Spatial periodicity in grid cell firing is explained by a neural sequence code of 2D trajectories

Abstract

Spatial periodicity in grid cell firing has been interpreted as a neural metric for space providing animals with a coordinate system in navigating physical and mental spaces. However, the specific computational problem being solved by grid cells has remained elusive. We here provide mathematical proof that spatial periodicity in grid cell firing is the only possible solution to a neural sequence code of 2D trajectories and that the hexagonal firing pattern of grid cells is the most parsimonious solution to such a sequence code. We thereby provide a teleological cause for the existence of grid cells and reveal the underlying nature of the global geometrical organization in grid maps as a direct consequence of a simple local sequence code using a minimal number of neurons. A sequence code by grid cells provides intuitive explanations for many previously puzzling experimental observations and may transform our thinking about grid cells.

INTRODUCTION

What is the nature of the problem being solved by grid cells?

Grid cells in the medial entorhinal cortex (MEC) (Fyhn et al., 2004; Hafting et al., 2005) and adjacent regions such as the pre- and parasubiculum (Boccara et al., 2010) are hypothesized to supply a “spatial metric” for cognitive map-based navigation and path integration (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Moser et al., 2017), episodic memory (Hasselmo, 2009; Eichenbaum and Cohen, 2014; Schiller et al., 2015), and navigating abstract feature spaces (Constantinescu et al., 2016; Hawkins et al., 2019; Rueckemann et al., 2021). Grid cells recorded in freely foraging animals fire at multiple locations in space so that the firing fields form a hexagonal lattice (Figure 1). Since their first discovery, the remarkable spatial periodicity in grid cell firing has been a topic of intense research (Moser et al., 2017). This research was fueled in part by awe of the beautiful symmetry and complexity displayed in the spatial firing pattern of a single cell. Moreover, research efforts were driven by the hope that understanding the underlying nature of grid cell firing would greatly advance our understanding of how the mammalian brain performs navigational computations and higher cognitive functions such as episodic memory.

Figure 1. The firing fields of a single grid cell in the medial entorhinal cortex form a hexagonal lattice in 2D space.

The typical grid cell data presented here were recorded using tetrodes from the medial entorhinal cortex of a freely foraging mouse (Dannenberg et al., 2019, 2020). A, Schematic drawing of a 1 m × 1m environment surrounded by walls in the presence of a single visual cue card. B, Trajectory plot visualizing grid cell spiking activity as a function of the animal’s location in space. The black line indicates the path taken by the animal during free exploration. Red dots indicate the locations on the animal’s path where action potentials (spikes) were generated by the recorded grid cell. C, Firing rate map of the spiking data shown in A. Data are visualized as 3 cm × 3 cm spatial bins, smoothed with a Gaussian kernel. Red color indicates a high firing rate; blue color indicates a low firing rate. Peak firing rate is 15 Hz; average firing rate is 1.9 Hz. D, Spatial autocorrelogram of the data shown in B. Red color indicates a high correlation value; blue color indicates a low correlation value. The geometric arrangement of firing fields can be described by falling on a hexagonal lattice that is rotated relative to the walls of the square environment.

However, currently existing mechanistic models of grid cell firing fall short of explaining the basic question of why grid cells exist in the first place. Most previous studies on grid cell function follow a traditional approach based on the well-founded assertion in biology that structure determines function. This approach has resulted in a vast literature describing properties of grid cells in multiple species and how these properties depend on internal neural circuit dynamics and external cues. However, this traditional approach has been proven notoriously difficult in identifying a teleological cause for the existence of grid cells in mammalian brains. Computational models of grid cells such as oscillatory interference models (O’Keefe and Burgess, 2005; Burgess et al., 2007; Giocomo et al., 2007; Hasselmo et al., 2007; Burgess, 2008) and continuous attractor models (Fuhs and Touretzky, 2006; Burak and Fiete, 2009; Shipston-Sharman et al., 2016) provide mechanistic explanations of how the spatial periodicity in firing can emerge from the structure of microcircuits within the superficial layers of the MEC (Zilli, 2012; Couey et al., 2013; Zutshi et al., 2018). However, these mechanistic models, too, leave a key question unanswered: What is the computational function, if any, of the spatial periodicity in grid cell firing? Consequently, functions of grid cells are often explained in generic terms and statements, such as that grid cells supply a path integration-based “metric for space” or provide a “coordinate system” for spatial mapping, memory-guided navigation (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Moser et al., 2017), and planning direct trajectories to goals (Erdem and Hasselmo, 2012; Bush et al., 2015).

The approach taken in this article to discover the computational goal of grid cells differs from those mechanistic modeling approaches and from traditional approaches in the grid cell literature that aim to assign functions to grid cells based on their properties. Instead, we turn the question on its head and ask the reverse question: What is an important function performed by the mammalian brain that could either not be performed at all or would be substantially more costly or inefficient to perform in the absence of grid cells? This approach follows the logic proposed by David Marr: “To phrase the matter in another way, an algorithm is likely to be understood more readily by understanding the nature of the problem being solved than by examining the mechanism (and hardware) in which it is embodied” (Marr, 2010, Chapter 1.2).

This article provides mathematical proof that, in Marr’s words, “the nature of the problem being solved” by grid cells is coding of trajectories in 2D space using cell sequences. By doing so, we offer a specific answer to the question of why grid cells have evolved in the mammalian brain. Thus, we provide a teleological cause for the existence of grid cells.

RESULTS

Does spatial periodicity in grid cell firing emerge from a cell sequence code of trajectories in 2D space?

To constrain our search for a function that requires grid cells or could not be performed efficiently without grid cells, we reasoned that this function shall rely on sequential activation of grid cells or grid cell assemblies, in short grid cell sequences. This reasoning rests on well-established experimental data on neural activity in the hippocampal formation showing that cell sequences can provide a fundamental neural syntax (Buzsáki, 2010) for cognitive operations. We further reasoned that, if a fundamental function of grid cells exists, such a function is very likely related to coding of trajectories. This reasoning rests on theoretical work demonstrating that theta sequences of grid cell populations can provide a movement-direction signal (Zutshi et al., 2017), and that temporal order of neural activity may be a necessary characteristic of representations generated by the hippocampal formation (Rueckemann et al., 2021). Moreover, data obtained from experiments using rodent animal models (Allen et al., 2014; Gil et al., 2018) and theoretical work (Sorscher et al., 2023) suggest that grid cells serve path integration and memory-guided navigation. A code for spatial trajectories by cell sequences that is usable across different environments would be very useful to keep track of changes in location relative to a starting point, i.e., path integration.

We therefore set out to provide mathematical proof (Box 1) that spatial periodicity in grid cell firing emerges from the assertion that cell sequences code for trajectories in 2D space under the constraint that the number of neurons in the brain is finite.

Box 1. Math notations.

A lemma is a mathematical statement that will be used to prove another result.

A proposition or theorem is a mathematical statement that can be proved using logical deduction from previously known results.

A proof is a logical argument using known results to generate new mathematical statements.

A plane is a flat surface extending infinitely far in two dimensions. Also referred to as ², since it can be assigned coordinates of the form (a, b) where a and b are real numbers.

A Euclidean metric is the usual notion of distance in the plane. Two points with coordinates, (x₁, y₁) and, (x₂, y₂) have distance $\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$.

Adding points means adding their coordinates, subtracting one point from another involves subtracting their coordinates.

A bijective map is a correspondence between two sets such that every point in one set is matched with exactly one point in the other set.

A geometric figure is a geometric object with a shape in the plane.

We work in ² (the plane), with the Euclidean metric.

Mathematical proof

Definition 1. Spatial firing field.

A spatial firing field of a neuron defines a specific region in space, where a neuron is active, i.e., the neuron responds to a specific spatial location of an animal with an increased rate of action potential firing.

Definition 2.1. Isometry.

An isometry is a bijective map f that preserves distance, that is for any two points x and y,

$$d\left(f\left(x\right),f\left(y\right)\right)=d\left(x,y\right).$$

We say that two geometric figures are geometrically congruent if there is an isometry between them. We will abbreviate this to congruent in what follows.

Remark 2.2.

The idea of isometry is that isometry preserves shape and size. In the plane, the only isometries are rotations, translations, reflections, the identity map, and compositions of these.

Definition 3.1. Kissing number.

Given a geometric figure, the kissing number is the largest number of non-overlapping figures congruent to the original geometric figure that can be arranged in the plane so that they all touch the original geometric figure.

Remark 3.2.

This usually refers to spheres embedded in various Euclidean spaces, but here we restrict to the plane and allow convex (see Definition 5) geometric figures other than circles.

Example 3.3.

The kissing number of a circle in the plane is 6, which is achieved using a hexagonal packing of circles ^31,32.

Definition 4.1. Lattice and lattice packing.

A lattice in the plane is an infinite set of points such that adding or subtracting any one point to/from another in the lattice returns another point in the lattice, any two points of the lattice are separated by a minimum distance, and any point in the plane is within a maximum distance of a lattice point.

A lattice packing is a packing of the plane by congruent geometric objects, such that the centers of the objects are located at the points of a lattice.

Example 4.2.

The points in the plane with integer coordinates form a lattice.

Example 4.3.

The tiling of the plane by equilateral triangles, squares, or hexagons is a lattice packing. So is the hexagonal circle packing, in which every circle is surrounded by six other circles touching it.

Lemma 4.4.

A lattice is invariant under isometries that take one point to another.

Lemma 4.5.

There are five types of a lattice in the plane (Kittel, 1966, Chapter 1) (Figures 2A–E).

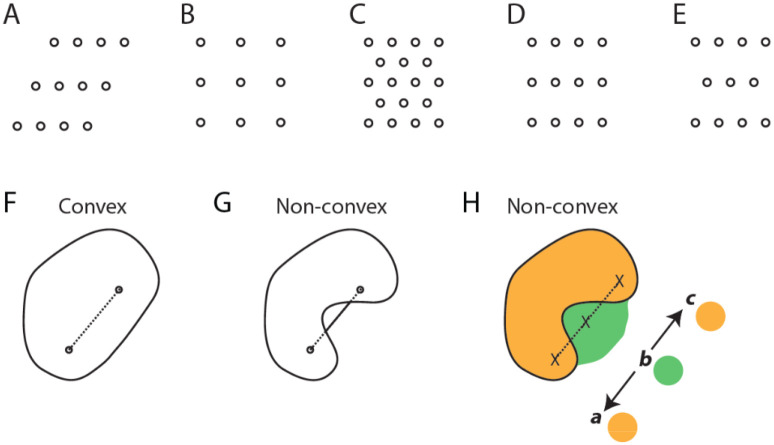
Figure 2. Trajectory coding by cell sequences requires a dense packing of convex firing fields.

A-E, Examples of the five types of lattices in the plane. A, Oblique. B, Square. C, Hexagonal. D, Rectangular. E, Centered rectangular. F,G, Examples of a convex and non-convex geometric object such as a possible spatial firing field of a neuron. H, A non-convex spatial firing field that results in an ambiguous cell sequence code for trajectories in space. In this example, two spatial firing fields of two cells are shown, indicated by green and orange colors. The three crosses mark three locations in space. The sequence green → orange can represent two opposite trajectories, namely b → a and b → c.

1. Oblique

2. Square

3. Hexagonal

4. Rectangular

5. Centered rectangular

Definition 5. Convexity.

A geometric object in the plane is convex if for any line segment whose endpoints lie on the object, the entirety of the line segment also lies on the object (Figures 2F–G).

Definition 6. Trajectory.

A trajectory is a path taken in space.

Definition 7.1. Cell sequence.

A cell sequence refers to continuous neural activity consisting of sequentially active cells or cell assemblies.

Remark 7.2.

In the context of a cell sequence, a “cell” within this sequence refers either to a single cell or a cell assembly. Cell assemblies can perform pattern completion and are thereby resistant to noise so that a cell assembly is activated robustly even if a single cell of this assembly fails to be activated at times.

Definition 8. Sequence coding of trajectories.

Sequence coding of trajectories is given if the identity of the next active cell in a cell sequence is uniquely determined by the current active cell and the velocity vector associated with the current trajectory (Figure 3).

Figure 3. Neural sequence code of trajectories in 2D space.

A, The animal’s current velocity vector determines the animal’s future trajectory. If the sequence code shall represent as many directions as possible with equal angular resolution from any given starting location, pairs of sequentially active cells need to represent six directions, e.g., North (N), Northeast (NE), Northwest (NW), West (W), Southwest (SW), and Southeast (SE). B, The current trajectory can be coded by pairs of sequentially active cells or cell assemblies. The next active cell in the sequence is uniquely determined by the current active cell and the velocity vector of the animal (Definition 8). C, All possible pairs of cells in the sequence code shown in B for the case that the current active cell is cell #1. The right panel shows how the sequence code displayed in B results in spatially periodic firing of all cells in the sequence. The example shown in C is marked with red and blue colors. D,E, Equal angular resolution of movement directions in trajectory coding by cell sequences requires an hexagonal lattice packing of firing fields. If a given firing field is surrounded by fewer or more than six firing fields that touch each other, opposite directions are represented with unequal resolution. D, In this example, moving from east → west can not be distinguished from the directions east → northwest and east → southwest because they are represented by the same cell sequence yellow → red. However, the opposite direction, west → east, is represented by three different cell sequences allowing for a finer angular resolution in the representation of movement direction. E, Congruent firing fields that surround each other symmetrically in a hexagonal lattice packing allow for equal angular resolution in the coding of trajectories by cell sequences.

Axioms (Table 1).

Table 1.

Axioms from which grid cell firing emerges as the most parsimonious solution to provide a code for trajectories in 2D space.

	Axiom	Remark/Example
Axiom 1	Cell sequences code for trajectories in 2D space.	This axiom states that the sequential activity of two cells, e.g., i → j, can unambiguously be interpreted by a downstream reader mechanism as a a code for one and only one trajectory, e.g., moving from place A to place B.
Axiom 2	The reverse cell sequence codes for the reverse trajectory.	If the cell sequence i → j codes for moving from place A to B, then the reverse cell sequence j → i codes for moving from place B to place A.
Axiom 3	Each cell’s firing field is surrounded symmetrically by a maximal number of other cell’s firing fields so that the angular resolution is constant and maximal across all directions.	This axiom means that a sequence code should represent each direction equally with no “gaps” in the representation (Figures 3D–E).
Axiom 4	The number of cells is finite.	Grid cells are densest in layer II of the medial entorhinal cortex (Sargolini et al., 2006), and this layer has been estimated to contain 24,000 and 58,000 neurons in mice and rats, respectively (Gatome et al., 2010).

Our goal is to provide a mathematical proof that spatial periodicity in grid cell firing emerges as a parsimonious solution to provide a code for trajectories in 2D space by cell sequences.

Proposition 9.1.

Assuming axioms 1 to 4, the firing fields of trajectory-coding cells must be congruent shapes in a hexagonal lattice packing.

Proof 9.2.

By Axiom 3, a particular firing field U is surrounded by the maximal number of other firing fields, each of which must be congruent to each other. This implies that every firing field around U is congruent. Since this holds for every firing field U, all firing fields must be congruent. To picture this, start with the firing fields around a single U, pick one of them V, and look at the firing fields around V. Continue in all directions to see that all firing fields must be congruent. Since each firing field U must be surrounded by the maximal number of firing fields, the kissing number of the arrangement must be maximal. Further, by the symmetry requirement, this must be achieved by a hexagonal lattice packing with a kissing number of 6 (Figures 3D–E). Any square lattice packing either has a kissing number of 4, or lacks symmetry between the “corner” firing fields and “side” firing fields. □

Lemma 10.1.

By axiom 1, the firing fields of trajectory-coding cells must be convex.

Proof 10.2.

If some cell has a non-convex firing field, a single cell sequence may code for more than one trajectory (Figure 2H). ^□

Theorem 11.1.

Assuming axioms 1 and 4, the firing fields of trajectory-coding cells must be spatially periodic, in the sense that starting at any point and continuing in a single direction, the initial sequence of locally active cells must eventually repeat with a repeat length of at least 3 (Figure 4).

Figure 4. Repeating sequences of cells coding for trajectories result in lattice packing of firing fields.

Left panels show firing fields of multiple cells in lattice packings that provide solutions to trajectory coding by cell sequences in 2D space. Mid panels show the cell sequences that code for the three major axes of direction in a dense packing of firing fields. Right panels highlight the firing fields of a single cell to visualize the lattice type formed by the firing fields. A, An example of seven cells and sequences with repeat length 7 along all three axes of direction. The resulting firing fields of single cells are arranged on a hexagonal lattice rotated by 10.9 degrees against one wall. This example only needs the minimum number of 7 cells to form unambiguous sequence codes of trajectories. B, An example of eight cells and sequences with repeat lengths 4 along one axis, and repeat length 8 along the two other axes of direction. The resulting firing fields are arranged on a centered rectangular lattice. C, An example of nine cells and sequences with repeat length 3 along all three axes of direction. The result is a symmetical grid (hexagonal lattice packing) of firing fields.

Proof.11.2.

Starting in a firing field of cell i and going along any set of firing fields, some cell must eventually become active again since the total number of cells is finite by axiom 4. Once there is a repeat of one cell’s firing field, the whole sequence of firing fields of all cells must repeat by axiom 1. This repeating sequence of locally active cells must at least have length 3 as if we had a repeat of length 2, we would have a sequence i, j, i. In this case i, j would represent two distinct trajectories, contradicting axiom 1. □

Remark.11.3.

This does not require symmetry in the sense that traveling in two different directions from cell i may give repeating sequences of two different lengths, as seen in Figure 4B, where the repeats have lengths 4 and 8, depending on the angle of travel from a given cell.

Lemma 12.1.

Every sequence of cells along one of the three major axes of the hexagonal lattice (from here on referred to as row or diagonal) must be either a translation of an existent sequence in a parallel axis or consist of a disjoint set of cells.

Proof 12.2.

Without loss of generality, if row A consists of cells 1, …, k repeating in this order, then any row that contains any cell from 1, …, k must contain the full repeat 1, …, k by axiom 1. So any row containing any cell from 1, …, k is a translation of row A, and any cell that does not contain them is disjoint from row A. □

Remark 12.3.

We will count the distance of a translation of a row A by starting at a cell a, passing to the cell diagonally down and to the right of cell a, and counting spaces moved right from here. Translations must be by 0,1,2,…, k − 1 spaces, where row A contains k cells.

Lemma 13.1.

If a row or diagonal of the hexagonal lattice is a translation of a neighboring row or diagonal, the translation must be by at least 2 and at most n − 3, where n is the repeat length.

Proof 13.2.

Translating by 0,1, n − 2, or n − 1 leads to a contradiction of axiom 1. □

Lemma 14.1.

Sequence repeats in parallel rows or diagonals must be of the same length.

Proof 14.2.

If two consecutive rows have sequence repeats of different lengths, say row A consists of 1, …, k and row B consists of k + 1, …, k + s, where k < s, then 1, k + 1 will appear in the 1 will appear in one repeat and 1, k + t will appear in the next, where t is not equal to 1. This contradicts axiom 1 (Figure 5A). □

Figure 5. The minimum number of distinct cells providing a sequence code of trajectories in 2D space is 7, and there are exactly 2 possible arrangements of the cells’ firing fields up to relabeling.

A, Repeat lengths that are smaller than 7 result in a violation of cell sequence coding of trajectories in that the resulting code is ambiguous and not unique. A red question mark indicates that no cell can be found for this position that would not violate the sequence code. Red numbers indicate that activity of this cell at the current position would violate sequence coding of trajectories due to ambiquity. Blue background color marks the sequential activity of 2 cells that violate cell sequence coding of trajectories (Definition 8) because the next active cell is not uniquely determined by the currently active cell in the sequence and the velocity vector associated with the current trajectory. B, If the repeat length is 7, there are three potential translations of the sequence in row 1 to fill up row 2 (Lemma 13.1). Only two of those three tranlsations result in an arrangement of cells (up to relabeling of cells) that creates a sequence code for trajectories in 2D space. These two arrangements are mirror images of each other (up to relabeling) and imply that the firing fields of each individual grid cell fall on the vertices of equilateral triangles, i.e., they form a hexagonal grid. C, Both possible arrangements of firing fields imply that grid patterns of other grid cells have the same spacing and rotation, and only differ in spatial phase (compare grid patterns of cell #1 and cell #6). The smallest angle between one grid axis and the boundary of a rectangular enclosure is 10.9 degrees if one sequence of cells is aligned with one of the borders of the enclosure.

Lemma 15.1.

The length of the sequence repeat in any row or diagonal must divide the number of cells. As a result, if the number n of cells is prime, the length of the sequence repeat in any row or diagonal must be of length n.

Proof 15.2.

Suppose the repeat length is less than n in some dimension. Without loss of generality, assume it is the horizontal direction, so that one row consists of 1,2,…, i repeating, for some i < n. Then every row must have repeat length i by Lemma 14.1. Since every row must consist of cells 1,2,…, i or be disjoint from the cells in other rows by Lemma 12.1, every cell will appear in exactly 1 of the distinct rows, so the length of the repeat in each row must divide n.

If n is prime, every row has repeat length dividing n. Since no row can have a repeat of length 1, every row has repeat length n.

Theorem 16.1.

The minimum number of distinct cells providing a sequence code of trajectories in 2D space is 7, and there are exactly 2 possible arrangements of the cells so that cell sequences code for trajectories in 2D space, up to relabeling of the cells.

Proof.16.2.

Given the requirement that each cell has 6 distinct cells around it, the minimum number of cells is 7.

By Lemma 15.1, the repeat length must be 7 in all directions. We may assume without loss of generality that row A consists of cells 1,2,… 7 (Figure 5B). Hence, every row is a translation of row A. By Lemma 13.1 and trial and error, there are two options (Figure 5B). □

DISCUSSION

A teleological cause for the existence of grid cells

We have provided mathematical proof that spatial periodicity in grid cell firing emerges as the only possible solution to provide a code for trajectories in 2D space by cell sequences. Within the space of all possible solutions, hexagonal symmetry in grid cell firing emerged as the most parsimonious solution. The hexagonal firing pattern of grid cells in 2D space is arguably their most intriguing property. Yet, despite decades of experimental and theoretical research, the fundamental nature of the computational problem solved by grid cells has remained largely elusive. Previous studies on grid cells have been fruitful in describing functional properties of grid cells and grid cell firing at the level of neuroanatomy, connectivity, neurophysiology, and circuit dynamics but have largely failed to provide an answer to why grid cells have evolved: what is the computational advantage of grid cells over other potential mechanisms or algorithmic implementations in the context of a computational goal? Previous investigations of grid cell function focused on mechanistic models that do not address the computational goal of or teleological cause for the existence of grid cells.

We therefore deviated from these traditional approaches of investigating grid cell properties and asked the reverse question: Is there a brain function that could either not be performed at all or would be substantially more costly or difficult to perform in the absence of grid cells? To constrain our search for such a function, we assumed that any coding mechanisms that operates on spatial firing requires cell sequences as a fundamental neural syntax in the brain (Buzsáki, 2010). Assuming that neural coding of trajectories in 2D space is important for animal navigation, we show that grid cells are the most effective solution. We demonstrate that just 7 neurons are sufficient to provide an unambiguous code for trajectories in 2D space and that the only two possible solutions with 7 neurons result in firing fields that fall on a hexagonal grid. Notably, these two solutions result in grid maps that are mirror images of each other up to relabeling the cells. Any other solutions to the problem would require at least 8 neurons, an increase in the number of neurons by more than 14%. Solutions with 8 or more neurons can result in other types of lattice packing (Figure 2), such as the oblique lattice or centered rectangular lattice that have also been observed in single unit recordings of freely behaving animals (Stensola et al., 2015). Code to compute and visualize “grid maps” of trajectory-coding cell sequence arrangements with up to 14 cells to help the community test some of our predictions against future datasets (Gleeson et al., 2017) has been made publicly available. Given the high energetic cost of neuronal activity, a solution with only 7 grid cells is evolutionarily advantageous and is thereofore expected to be the most frequently adopted neural code of spatial trajectories. We therefore provided a teleological cause for the existence of grid cells and an answer to the fundamental question of why grid cells have emerged in brains of navigating animals, namely that grid cells are the most parsimonious solution to sequence coding of trajectories in 2D space.

Sequence coding of trajectories by grid cells provides a mechanistic explanation for how grid cells serve path integration

If the step-by-step advancements from the currently active cell to the next cell in the grid cell sequence are caused by integrating velocity signals, grid cells perform path integration. The ensuing grid cell sequence is then the result of the path integration and can be interpreted as a sequence code by a downstream reader, potentially the hippocampus. Different grid cell modules integrate velocity signals at different (spatial) scales that are determined by the distance between the grid field centers of adjacent cells in the sequence. A sequence code of trajectories by grid cells therefore provides a mechanistic explanation for the functional role of grid cells in path integration. Notably, sequence coding of trajectories is not limited to physical space but could be useful for cognitive functions such as working memory or episodic memory that connects events into a cohesive story, consistent with experimental data demonstrating a grid-like code of conceptual knowledge space in humans (Constantinescu et al., 2016). A sequence code of trajectories by grid cells can thus explain data from human subjects that link reduced grid-like activity with path integration deficits observed in Alzheimer’s disease risk carriers (Kunz et al., 2015; Bierbrauer et al., 2020), and data from rodent experiments demonstrating that grid cell firing is reduced in a rodent animal model of Alzheimer’s disease (Ying et al., 2022, 2023).

Importantly, the grid pattern that we have found to emerge as the most parsimonious solution assuming axioms 1 to 4 (see Results), i.e., the solution to sequence coding of trajectories with a minimal number of neurons, mirrors experimental results on grid cells from animal experiments as we will discuss in the following paragraphs.

Sequence coding of trajectories predicts rotation of grid maps against a wall

On a single cell level, the solution to sequence coding is a symmetrical grid of firing fields, i.e., the distance between any two firing fields is constant, as observed in single unit recordings from freely behaving rodents (Hafting et al., 2005; Fyhn et al., 2008) and crawling Egyptian fruit bats (Yartsev et al., 2011). Moreover, if the trajectory-coding cell sequences are arranged parallel to a wall of a rectangular enclosure, the resulting grid is rotated so that the angle to the closest wall is 10.9 degrees (Table 2). This angle is close to an experimentally observed distribution of angles with a mean of 7.2 and a standard deviation of 3.5 degrees, and a reported median of 9.8 degrees in a highly familiar environment (Stensola et al., 2015; Dannenberg et al., 2020). Our sequence code model of grid cell firing thus provides a simple and intuitive answer to the otherwise puzzling observation that most grid field maps observed in freely behaving animals are rotated against the closest wall of a rectangular enclosure.

Table 2.

List of possible grid maps and properties of these grid maps given the total number of neurons participating in a trajectory-coding sequence in a rectangular environment. For each grid map that has a non-zero angle to a border, a reflection or 90°-rotation and reflection up to relabeling of the cells exist, and these additional possibilies are not included in this list.

# neurons	Repeat lengthsa	Lattice type	Smallest angle to a border of a rectangular environmentb
7	7, 7, 7	Hexagonal	10.9°
8	4, 8, 8	Centered rectangular	0°
	4, 8, 8	Oblique	10.9°
9	3, 3, 3	Hexagonal	0°
	3, 9, 9	Oblique	10.9°
	3, 9, 9	Oblique	13.9°
	3, 9, 9	Oblique	16.1°
10	5, 10, 10	Oblique	0°
	5, 10, 10	Oblique	10.9°
	5, 10, 10	Oblique	16.1°
11	11, 11, 11	Oblique	6.6°
	11, 11, 11	Oblique	10.9°
	11, 11, 11	Oblique	16.1°
12	6, 6, 6	Hexagonal	0°
	3, 12, 12	Rectangular	0°
	3, 12,12	Rectangular	10.9°
	3, 4, 12	Oblique	0°
	3, 4, 12	Oblique	13.9°
	4, 6, 12	Oblique	0°
	4, 6, 12	Oblique	6.6°
	4, 6, 12	Oblique	23.4°

^aRepeat lengths across the three major axes of the hexagonal lattice structure of densely packed firing fields.

^bThe smallest angle to a border of a rectangular environment assumes that one sequence of cells is arranged in parallel to one wall.

Sequence coding of trajectories predicts fragmentation of grid maps in 1D space

Another experimental observation related to the spatial geometry of grid fields that can be explained by a sequence code of trajectories is the fragmentation of grid cell maps in a multicompartment environment (Figure 6). As demonstrated by (Derdikman et al., 2009), the two-dimensional spatial periodicity in grid cell firing is replaced by one-dimensional (1D) spatial periodicity if movement through space is restricted to 1D trajectories along parallel alleys in a multi-compartment maze. Such a fragmentation of grid cell maps would be expected from a sequence code of trajectories since parallel trajectories would result in the same sequential activation of cells, and neural coding on a 1D tract is most efficient when sequences are aligned with the movement direction (Figure 6A). Likewise, grid cells have been shown to path integrate distances on a 1D circular track (Jacob et al., 2019), consistent with a cell sequence code of a trajectory along a 1D circular track (Figure 6B). Notably, (Jacob et al., 2019) report in their study that the field spacing of grid cells is increased in a 1D circular track compared to a 2D environment. The authors’ explanation is that field spacing is increased due to the lack of visual cues. However, an alternative explanation based on the sequence model of grid cell firing is that running through a cell sequence on a linear track would require to run through the complete sequence of cells until the sequence repeats (Figure 6C). Moreover, the cell sequence code of trajectories is consistent with an analysis of experimental data (Pröll et al., 2018) showing that firing fields of grid cells on a 1D linear track are compatible with a slice through a 2D hexagonal pattern. Specifically, a single hexagonal firing pattern explains lineartrack data if translational shifts of the pattern are allowed at turning points without a requirement of rotating or scaling the grid.

Figure 6. Transformation of a cell sequence code of trajectories from 2D space to 1D space.

A,B, A sequence of 7 different cells can code for a trajectory in a 1D compartmentalized “hairpin” maze (A) or a 1D circular track (B). Note that the distance between firing fields would increase in the 1D “hairpin” maze and 1D circular track compared to the distance between spatial firing fields in a 2D environment. Also note that cell sequences could undergo a phase reset at behaviorally relevant points, e.g., the turning points in the “hairpin” maze (A). C, The sequence of active cells in a 1D environment can be interpreted as a cross-section of the trajectory sequence code in a 2D space.

Furthermore, grid cells have been shown to code for traveled distance, elapsed time, or a combination of distance and time when animals run in place on a treadmill (Kraus et al., 2015). The firing pattern of grid cells as time or distance cells is remarkably similar to the firing pattern of grid cells that emerges when animals navigate 1D linear tracks after correcting for logarithmic expansion in grid field size over time. The fact that grid cells show repeating firing fields in other dimensions than physical space is consistent with a sequence code of trajectories in any type of dimension that has behavioral relevance for the animal. Experimental data (Kraus et al., 2015) demonstrate parallel coding of different dimensions by different grid cells, suggesting individual grid cell sequences can provide independent codes of trajectories through different dimensions, thereby enabling parallel processing of different cognitive functions.

Sequence coding of trajectories predicts rescaling and restructuring of grid maps in response to changes in a familiar environment

A cell sequence code of trajectories does not need to be rigid but instead can be malleable and rescaled in response to changes in the environment as long as the start and end points of the sequences are anchored to salient environmental landmarks. Thus, sequence coding of trajectories by grid cells provide an explanation of distortions of the grid pattern that are frequently observed in animal studies. Experiments in freely behaving rodents demonstrate that stretching or compression of enclosed environments result in stretching or compression of the grid map in the rescaled dimension. For instance, stretching or compressing the borders of a familiar open field recording arena resulted in an increase or decrease of the distance between firing fields in the rescaled dimension of the deformed enclosure (Barry et al., 2007; Stensola et al., 2015). Such distortions have been challenging to interpret under the assumption that grid cells provide a “spatial metric” or “coordinate system” for navigation. However, if we assume a cell sequence code of trajectories with start and end points of trajectories anchored to landmarks or environmental borders, distortions of the grid along the rescaled dimension would be expected. The sequence code of trajectories would remain the same if trajectories are defined relative to the borders of the environment (Figure 7A). Moreover, experimental data in rats show that grid maps that have been established in two adjacent compartments separated by a wall within the same larger environment merge once the wall is removed (Wernle et al., 2018). Merging of the two grid maps appeared to happen instantly resulting in local spatial periodicity and continuity between the two original maps (Wernle et al., 2018), as predicted by a sequence code of trajectories by grid cells.

Figure 7. Sequence coding of trajectories predicts rescaling and restructuring of grid maps in response to changes of a familiar environment.

A, Anchoring of cell sequences coding for trajectories to environmental borders predicts parametric rescaling of the grid pattern when an enclosure is deformed. Each color represents one grid cell, each circle represents one firing field. For clarity, the complete set of firing fields of a single cell is shown only for one grid cell shown in black. In addition, grid cell sequences are shown for all three major axes. Left panel, original maze configuration. Mid and right panel, the environment is compressed along the vertical or horizontal dimension resulting in a parametric deformation of firing fields and the grid pattern of firing fields along the vertical or horizontal dimension. B, Progressively faster advancement from the current active cell to the next active cell in the sequence code of trajectories results in progressive decrease in grid spacing and thereby a local distortion of the grid map. Open circles represent firing fields of grid cells along the three major axes. The red filled circle in the center represents a salient location such as a rewarded goal location toward which nearby grid fields gravitate.

Scaling of grids has also been observed in the form of an expansion, i.e., increased grid spacing between individual firing fields and increased field sizes, in response to novelty of the environment (Barry et al., 2012). Such scaling has also been reported in climbing rats foraging on a vertical wall (Casali et al., 2019). As the scaling of grids in response to scaling the borders of an environment is inconsistent with the hypothesis that grid cells provide a spatial metric for navigation or path integration, so is an expansion of grid fields in response to novelty. However, an increase in grid spacing in response to a novel environment can be explained easily by a cell sequence code of trajectories where firing fields are initially larger in novel environments and then become more refined once the space becomes familiar to the animal. Such changes in grid field size has been reported to co-occur, though to a lesser extent, with changes in the size of place cell firing fields in response to novel environments (Wilson and McNaughton, 1993; Karlsson and Frank, 2008; Barry et al., 2012). In summary, scaling of grids in response to deformations of the borders of the environment or in response to novelty can be explained by compression or expansion of firing fields combined with an increase or decrease in the grid spacing while maintaining the sequence code.

Furthermore, cell sequence coding of trajectories in 2D space provides an explanation of experimental data showing that grid fields move toward goal locations (Boccara et al., 2019) or restructure their spatial firing maps to incorporate the location of a learned reward (Butler et al., 2019). These data support the hypothesis that grid cells do not provide a simple metric of space. Instead, the spatial firing pattern of grid cells is malleable in response to relevant contextual features. Such local distortions of global grid patterns by salient locations have recently been compared to spacetime distortions by blackholes (Ginosar et al., 2023). We propose that such warping of grid maps is caused by an increased probability that the currently active grid cell activates the next grid cell in the sequence of trajectory-coding cells. This would result in a progressive decrease in grid spacing that could yield a gradual increase of overlap of grid fields or deformations of grid fields near a goal location, thereby causing local distortions in the grid map of a single grid cell. The result is that grid fields of a single grid cell appear to have moved closer to the goal location (Figure 7B). A cell sequence code of trajectories by grid cells is thus consistent with malleable grid maps because the spacing between adjacent firing fields can change gradually in response to local contextual features without compromising the sequence code. The same mechanism can explain shearing induced assymmetry and multiple alignment solutions that have been shown in experimental data (Stensola et al., 2015).

Sequence coding of trajectories predicts grid cell properties on the population level

In addition to properties of grid cell firing on the single cell level, the definition of sequence coding of trajectories implies an intriguing property of grid cells on the population level, namely that each grid cell’s collection of firing fields is geometrically congruent to any other grid cell’s collection of firing fields. This property mirrors experimental data from single unit recordings in rodents showing that adjacent firing field grid patterns of different anatomically close grid cells differ only in phase but have the same orientation and scale (Hafting et al., 2005). Moreover, experimental data have shown that grid cells cluster into autonomous modules with distinct scale, orientation, symmetry and theta frequency modulation (Stensola et al., 2012). If we assume that grid cells emerge from a cell sequence code of spatial trajectories, adjacent firing fields in that sequence would provide a discrete sequence of sampling points in the coding of trajectories, and the distance between the centers of two adjacent firing fields would determine the spatial resolution. Doubling the number of sampling points, i.e., doubling the number of firing fields per unit area for an individual grid cell, would double the spatial resolution (Williams, 1983). Conversely, dividing the number of firing fields per unit area in half would halve the spatial resolution. It would provide an advantage to animals if they could plan trajectories towards goals on different spatial scales to “zoom in” or “zoom out” on a cogntive map of their environment (Figure 8). This approach is analogous to mip mapping known from computer graphics (Box 2), where an image is sampled by a stack of images, each of which is represented with half the resolution of the previous to increase rendering performance. We propose that each grid module represents trajectories at progressively lower or higher resolution analagous to mipmaps in computer graphics to enable planning of trajectories across different spatial scales. To double or halve the spatial resolution in 2D space, the number of sampling points per area needs to double or be cut in half, respectively. Applied to grid cells, the number of firing fields per unit area would need to scale by a factor of 2 across grid modules. Because firing fields are densely packed, doubling the number of firing fields per unit area in 2D space would result in dividing the distance between two adjacent firing fields by a factor of √2 (Figure 8). This is exactly what has been observed experimentally (Stensola et al., 2015). Notably, in a 1D environment, doubling the number of firing fields per unit length would result in dividing the distance between two adjacent firing fields in half. It remains to be tested experimentally whether grid cell modules can adapt the scaling factor to optimize computational efficiency in multiscale representation of 1D environments.

Figure 8. Grid cell modules provide a pyramidal parametric sampling of 2D space enabling simultaneous multiscale representation of space.

The sampling of 2D space by grid fields is cut in half from module to module so that each grid cell module represents space at half of the resolution of the previous module. This resembles Gaussian pyramids or mip maps in computer vision (see Box 2). Representation of 2D space by different grid cell modules thereby allows the simultaneous representation of space at meaningful spatial resolutions in a computationally efficient way. The blue box represents a 1-m × 1-m square environment. Circles represent densely packed grid fields from multiple grid cells. Filled circles represent grid fields of a single grid cell. Grid fields are enlarged in space from module to module so that the total number of grid fields sampling the space approximately doubles from module to module. While the total number of grid fields doubles from module to module, the spacing between the grid fields of an individual grid cell increases by a factor of √2.

Box 2. Mip maps and scale-space theory.

In computer graphics, mip maps are stacks of images where each image is represented with half the number of pixels as the previous image in the sequence. The acronym “mip” is from the Latin phrase “multum in parvo,” meaning “many things in a small place.” Mip mapping was developed by (Williams, 1983) as a solution to map a 2D image onto a curved 3D surface. The problem that Williams addressed by mipmapping was twofold: As the projected scale of the surface increases, interpolation between the original samples of the source image becomes necessary, i.e. the resolution of the image needs to increase. Conversely, as the scale is reduced, approximation of multiple samples in the source is required, i.e., the resolution of the image needs to decrease. An analogy is to optimize the resolution of a picture when “zooming in” or “zooming out”. In order to reduce the computational effort, Williams proposed a pyramidal parametric sampling approach to create a stack of prefiltered source images. This approach is a solution to a special case of a more general problem, namely how to interpret images of real-world objects at a scale that enables the recognition of meaningful entities (Lindeberg, 2008). The theoretical framework for multi-scale representation of image data is scale-space theory (Lindeberg, 2008), a framework for multiscale image representation developed by the computer vision community. If we do not know a priori what scales of representation are relevant or if we quickly need to switch between relevant scales, a reasonable and computationally efficient approach is to consider representations at all scales simultaneously.

Sequence coding of trajectories in 3D space

There is no reason to assume that the sequence code of trajectories is restricted to 2D space. We have discussed in previous paragraphs how a sequence code of trajectories by grid cells can code for trajectories in 1D space. In principle, such a sequence code can be expanded to three-dimensional (3D) or higher dimensional spaces. However, there are multiple equally optimal possibilities to generate a close-packed arrangement of firing fields in 3D space (Stella and Treves, 2015; Weisstein, n.d.). A model based on a sequence code of trajectories by grid cells would therefore predict larger variability in spatial periodicity of grid cell firing in 3D space compared to 2D space. It remains to be determined whether specific solutions to cell sequence coding of trajectories in 3D space could result in local or global symmetries. (Grieves et al., 2021) demonstrated an irregular distribution of grid cell firing fields in rats exploring a 3D volumetric space. However, since sequences need to repeat, cell sequence coding of trajectories in 3D space predicts some degree of local order in the grid map of a single grid cell. Consistent with this prediction, experimental data show that grid cells recorded in flying bats exhibit fixed local distances between firing fields despite the lack of a global lattice arrangement of firing fields (Ginosar et al., 2021). Taken together, these experimental data are consistent with a sequence code of trajectories that expands to 3D space, even though this sequence coding may not need to result in a globally symmetric arrangement of the firing fields of a single cell.

The magical number 7

The most parsimonious solution to trajectory coding by cell sequences in 2D space is a sequence of 7 cells. Intriguingly, a sequence length of 7 matches the maximal number of items in a list that can be recalled easily by human subjects (Guilford and Dallenbach, 1925), and human subjects are often limited in terms of the amount of information they can receive, process, and remember (Miller, 1956). Theta-nested gamma cycles have been hypothesized to store short-term memories (Lisman and Idiart, 1995; Jensen and Lisman, 2005) so that each memory is stored in a different gamma subcycle nested within a single theta cycle. The existence of 7 cell sequences is consistent with the storage capacity of 7 chunks of information in working memory and with the occurrence of approximately 7 gamma cycles within a single cycle of hippocampal theta oscillations (Lisman and Buzsáki, 2008). In the hippocampus, these theta-nested gamma cycles mark the activity of distinct cell assemblies whose activities are correlated with a given spatial position (Bragin et al., 1995; Harris et al., 2003; Buzsáki and Tingley, 2018) along a spatial trajectory. Theta-nested gamma cycles have therefore been described as sub-units of neural circuit operations (Fernandez-Ruiz et al., 2023). The idea that sequential activation of cells can be used to code for trajectories has been previously employed in a simple connectionist model of the hippocampus that could successfully reconstruct an episodic memory trace by searching for a nearly shortest path in the space of remembered contexts (Samsonovich and Ascoli, 2005). This model used sequential activation of place cells in the hippocampus as a unifying neurophysiological mechanism underlying spatial navigation and episodic memory retrieval. We propose that a similar mechanism of cell sequences in the MEC can be employed to represent trajectories during spatial navigation and trajectories in mental space to enable abstract thinking and navigating memory space. Recruitment of grid modules with progressively larger grid spacing would then allow to code for arbitrarily long trajectories (at the cost of spatial precision) to serve spatial navigation or cogntive functions such as memory retrieval or goal directed planning.

Grid cell-like activity in artificial neural networks

Grid-like firing has recently been found to emerge in artificial neural networks that were trained to perform path integration under simple biologically plausible constraints, and such grid cells endowed agents with the ability to perform vector-based navigation (Banino et al., 2018; Sorscher et al., 2023). In contrast to the normative framework used by (Sorscher et al., 2023) that require specific hyperparameter choices to explain the emergence of grid-like units under anatomical constraints (see (Rylan Schaeffer et al., 2022) for a discussion), we have provided mathematical proof here that the emergence of lattice packings of firing fields is implied by a cell sequence code of trajectories in 2D space, and that the most parsimonious solution with only seven cells results in a hexagonal lattice packing of firing fields. Our proof does not require any assumptions about mechanistic implementations of the code of trajectories by cell sequences as defined by axioms 1 – 4. Any implementation that aims at providing a code for trajectories by cell sequences in a 2D space must result in a lattice packing of firing fields, and minimizing the required number of cells in that code must result in an hexagonal lattice of firing fields. We thereby have characterized coding of trajectories by cell sequences as a computational goal that requires grid cells to emerge under evolutionary pressure in living organisms navigating in 2D space. In artificial systems, other lattice configurations are possible, though significantly less computationally efficient. Therefore, we identified a teleological cause for the emergence of grid cells in the brain of navigating animals.

Code availability

Matlab code to plot “grid maps” that emerge as a result of sequence coding of trajectories is available on https://github.com/dannenberglab/grid-cell-sequences.