Abstract
We have compared distributions of sodium and potassium ions around double-stranded DNA simulated using fixed charge SPC/E, TIP3P, and OPC water models and Joung/Cheatham (J/C) ion parameter set, as well as Li/Merz HFE 6–12 (L/M HFE) ion parameters for OPC water. In all the simulations, the ion distributions are in qualitative agreement with Manning’s condensation theory and the Debye–Hückel theory, where expected. In agreement with experiment, binding affinity of monovalent ions to DNA does not depend on ion type in every solvent model. However, behavior of deeply bound ions, including ions bound to specific sites, depends strongly on the solvent model. In particular, the number of potassium ions in the minor groove of AT-tracts differs at least three-fold between the solvent models tested. The number of sodium ions associated with the DNA agrees quantitatively with experiment for OPC water model, followed closely by TIP3P+J/C; the largest deviation from experiment, ~ 10%, is seen for SPC/E+J/C. On the other hand, SPC/E+J/C model is most consistent (67%) with experimental potassium binding sites, followed by OPC+J/C (60%), TIP3P+J/C (53%) and OPC+L/M HFE (27%). The use of NBFIX correction with TIP3P+J/C improves its consistency with experiment. In summary, the choice of solvent model matters little for simulating the diffuse atmosphere of sodium and potassium ions around DNA, but ion distributions become increasingly sensitive to the solvent model near the helical axis. We offer an explanation for these trends. There is no single ”gold standard” solvent model, although OPC water with J/C ions or TIP3P with J/C + NBFIX may offer an imperfect compromise for practical simulations of ionic atmospheres around DNA.
Graphical Abstract
1. Introduction
Water, along with dissolved ions, is the primary solvent surrounding DNA, proteins, and other biomolecules in cells. Ions play multiple roles in determining the structure, dynamics and function of nucleic acids.1,2 In agreement with basic physical intuition, without the proper atmosphere of water and cations, DNA would not preserve its double-helical shape: strong repulsion between phosphate groups would rip the two strands apart.3 Under physiological conditions, counterions surround these negatively charged groups to screen the charge-charge repulsion. Counter-intuitively, multivalent ions can condense strongly repelling fragments of double-stranded DNA into globules.4–8 Under highly crowded conditions, monovalent counterions can also condense the DNA.9 Counterion-induced condensation of DNA or RNA facilitates the efficient packaging of nucleic acids inside cells and viruses.10–12 Counterion-induced condensation of nucleic acids is also important for delivering short interfering molecules of RNA for gene silencing13 and gene therapy for delivery of nucleic acids.14 In particular, some of the recently developed vaccines against SARS-CoV-2 consist of lipid nanoparticles with condensed mRNA inside.15–17 Mechanical properties of nucleic acids depend strongly, and sometimes unexpectedly, on the surrounding ionic atmosphere.18 For example, the persistence length of double-stranded DNA decreases with the concentration of trivalent ions in the ambient solution,19 but for double-stranded RNA the trend is just the opposite.18 Details of ionic atmosphere around DNA depend on its sequence.20 Monovalent ions are known to bind relatively strongly to specific sites on the DNA;21 guanine quadru-plexes are stabilized by specific binding of Na+ or K+ ions.22 Potassium ions were found to bind preferentially near previously identified magnesium binding sites in RNA.23 Specific sodium binding sites near the catalytic pocket of the hepatitis delta virus (HDV) ribozyme were identified.24,25
While some of the effects mentioned above can be readily accounted for within theories that describe diffuse distributions of ions around nucleic acids,26 other phenomena require knowledge of fine details of counterion distributions, including their specific binding modes.18,22,27,28 The nature of monovalent ions, e.g. Na+ vs. K+, appears unimportant in some cases,26 consistent with the experimental observation that different ions of the same charge generally form similar diffuse ionic atmospheres around DNA.29 At the same time, details of the ion distribution around DNA can be affected by the ionic radii;30 for example, different ions bind at the different depth in the minor groove.31 Monovalent ions are known to behave differently near GC-rich sequences and AT-tracts.21,32 Clear differences have been observed between the effect of monovalent ions such as K+ or Na+ on DNA condensation under crowded conditions,9 which may be caused by differences in distributions of K+ and Na+ around the DNA.33 Intriguingly, K+ ions, abundant in the cell nucleus, affect chromatin compaction differently from Na+, often used in in-vitro studies of chromatin components.34 An important motivation for this work is to lay the groundwork for future investigation of this phenomenon via atomistic simulations.
Atomistic Molecular Dynamics (MD) simulations are an indispensable tool for investigating ionic atmosphere around DNA,3,20,27,30,33,35–41 especially in view of the well known experimental difficulties in resolving biologically relevant monovalent ions around the DNA.21,42 The ability of these simulations to faithfully reproduce reality depends directly on the fidelity of the underlying DNA (gas-phase) force field, and, equally, of the solvent model.43 The latter is broken down further into specific representation of the liquid water itself (water model44–48) and of the dissolved ions.49–51 The influence of many existing force fields on structure and dynamics of nucleic acids has been explored extensively.43,52 The effect of monovalent ion types has also been explored, with the general conclusion being that simulated structure and dynamics of DNA is rather insensitive to the ion type41 over a relatively wide range of bulk salt concentrations.
At the same time, influence of water models themselves on outcomes of biomolecular simulations received less attention until recently, when it was discovered that the use of some of the ”third generation” general-purpose fixed-charge water models47,48 can lead to clear advances in resolving stubborn problems, such as achieving the right balance of RNA conformational populations53,54 or in reproducing structural ensembles of intrinsically disordered proteins.55 Given the importance of multiple aspects of ionic atmosphere around DNA for its function, the time is ripe to investigate in detail how simulated distributions of monovalent ions might depend on the water and ion models, including the third generation water models along with the matching ion models recently developed51,56 specifically for some of these newer water models.
Here we explore how the choice of non-polarizable water model and the corresponding ion parameters affects the computed distribution of two biologically important ions – K+ and Na+ – around double-stranded DNA. We look for similarities and differences between the ion distributions around the DNA, depending on the water and ion model. We also ask to what extend these solvent models can reproduce experimentally characterized nuances of ion distribution, and if some solvent models may be better than others in this respect.
To this end, we compare distributions of monovalent ions around DNA in systems with different 3-point water models TIP3P, SPC/E, OPC. For TIP3P and SPC/E water models, we use Joung/Cheatham ion parameter sets49 (referred to as J/C). These parameter sets were obtained by fitting solvation free energies, radial distribution functions, ion-water interaction energies and crystal lattice energies, and lattice constants for non-polarizable spherical ions.57 For OPC water model, we use two distinct ion parameter sets. One of them is the Joung/Cheatham ion parameter set developed for TIP4P-Ew water model,49 originally recommended for OPC in the absence of an OPC-specific ion set. The second ion set is a newer Li/Merz 6–12 HFE set51 (L/M HFE), which aims to reproduce experimental hydration free energies of the ions.
The Results section of this article is divided into two broad sections. First, we explore several aspects of ion distributions around DNA for which direct experimental reference for both Na+ and K+ is not yet available; the main goal of this part is to examine sensitivity of distributions to the choice of solvent model. Sensitivity to the DNA sequence is also looked into. Specifically, we analyze the diffuse distributions of counterions, their binding affinities to the DNA, as well as the degree of DNA neutralization by the bound counterions. In the second section, we compare aspects of simulated ion distributions directly against available experimental results, to rank the solvent models by their ability to reproduce experiment. We look at numbers of sodium ions associated with the DNA available from “ion counting” experiments.58 We check whether the calculated K+ affinity to the DNA is similar59 to that of Na+. We also examine, in detail, locations of potassium binding sites21 in the Drew-Dickerson dodecamer.
An explanation for the observed similarities and differences between ion distributions resulting from the different solvent models is provided, along with a relative ranking of the solvent models for each type of comparison with experiment.
2. Results and Discussion
In this work, we have examined various aspects of simulated Na+ and K+ distributions around double-stranded DNA in four different atomistic solvent models. To explore possible sequence effects, three different DNA fragments are considered: two different 25 b.p. B-form DNAs:27 poly(dA·dT) (referred to as ”polyA”) and (GCATCTGGGCTATAAAAGGGCGTCG) (referred to as ”mixed sequence”) and the Drew-Dickerson dodecamer (CGCGAATTGCGC). We simulated all three DNA duplexes in solution with Na+ and K+.
Since influence of water models and monovalent ions on the DNA structure was explored extensively in several previous works,41,52 here we have performed only a brief inspection of the simulated DNA structures to confirm that no gross distortions occur in any of the solvent models tested (results not shown).
2.1. Similarities and differences between ion distributions in different solvent models
Overall distributions of counterions around DNA
The simulated cation concentration as a function of the distance from the DNA helical axis for systems with 0.15 M bulk salt concentration is presented in Figure 1. The results for other systems are presented in Figure S1. Convergence of the ion distributions was verified (see Table S11 and Figures S5 and S6).
Figure 1:
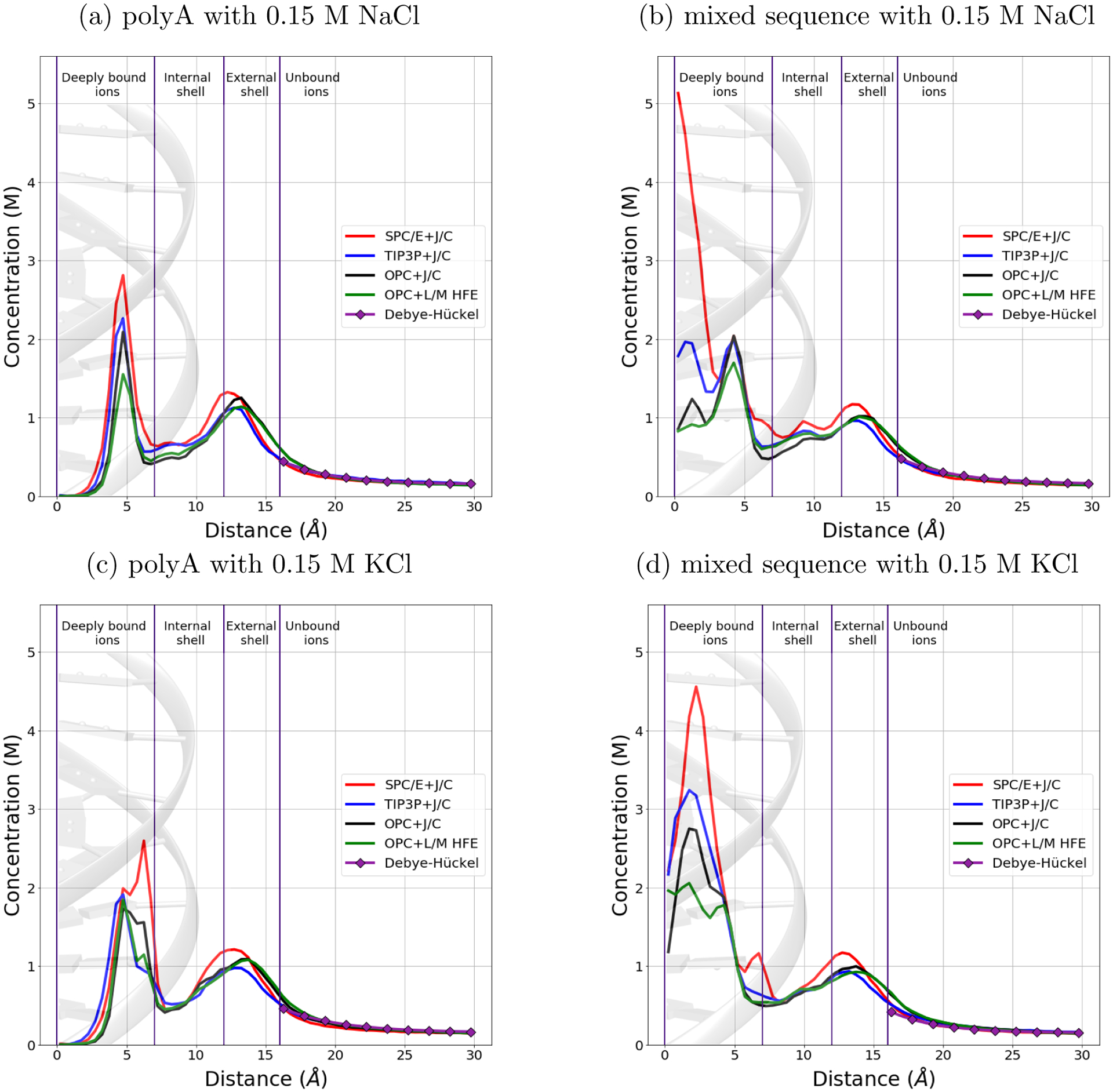
Dependence of sodium and potassium concentration on the distance from the DNA helical axis, from simulations in four different explicit solvent models – combinations of water models and sets of ion parameters. The bulk salt concentration is 0.15 M. All the distributions have almost the same shape beyond 7 Å from the DNA axis. In the order of solvent models SPC/E+J/C, TIP3P+J/C, OPC+J/C and OPC+L/M HFE, the concentration near the helical axis of the DNA drops down significantly regardless of the ion type and DNA sequence. The distribution corresponding to the Debye–Hückel theory is also shown for comparison. The names of the cylindrical shells around the DNA helical axis from Ref.27 are used here for notation convenience.
As we can see from the Figures 1 and S1, the distribution of ions in the internal (7–12 Å from the axis) and external (12–16 Å from the axis) shells is rather insensitive to the type of ion, DNA sequence or solvent model. Ions located near the negatively charged phosphate groups form the second peak of the distribution.20 Outside of the external shell, the ion distributions follow the Debye–Hückel theory, where the DNA with bound ions was treated as a spherical particle, see “Methods” for details.
The most significant differences between distributions of ions in different solvent models are observed near the axis of the DNA double helix. Following Ref.,27 we calculated the numbers of ”deeply bound” ions, located in the cylindrical shell within 7 Å of the helical axis, Figure 1. The results for the polyA sequence are shown in Table 1; see Table S1 for the mixed sequence. We have analyzed typical ion binding sites in the structures of mixed sequence and polyA DNA, Figure 2. The overall conclusion is that the set of ion-coordinating atoms does not depend on ion type, Na+ or K+, or on the solvent model, but the site occupancy does; the occupancy of Na+-binding sites is usually lower compared to that of the K+ sites.
Table 1:
Number of deeply bound ions in polyA DNA simulations. In the order SPC/E+J/C, TIP3P+J/C, OPC+J/C, OPC+L/M HFE, the number of deeply bound ions drops down significantly, regardless of the ion type. The error is the standard error of the mean (see Methods).
| Bulk salt concentration (M) | 0.15 | 0.5 | ||
|---|---|---|---|---|
| Ion type | Na+ | K+ | Na+ | K+ |
| SPC/E+J/C | 5.7 ± 0.2 | 7.1 ± 0.1 | 5.8 ± 0.1 | 6.8 ± 0.1 |
| TIP3P+J/C | 4.1 ± 0.1 | 4.7 ± 0.1 | 4.8 ± 0.1 | 4.9 ± 0.1 |
| OPC+J/C | 3.3 ± 0.1 | 4.7 ± 0.1 | 4.2 ± 0.2 | 4.3 ± 0.1 |
| OPC+L/M HFE | 3.0 ± 0.1 | 4.0 ± 0.1 | 3.9 ± 0.2 | 4.6 ± 0.1 |
Figure 2:
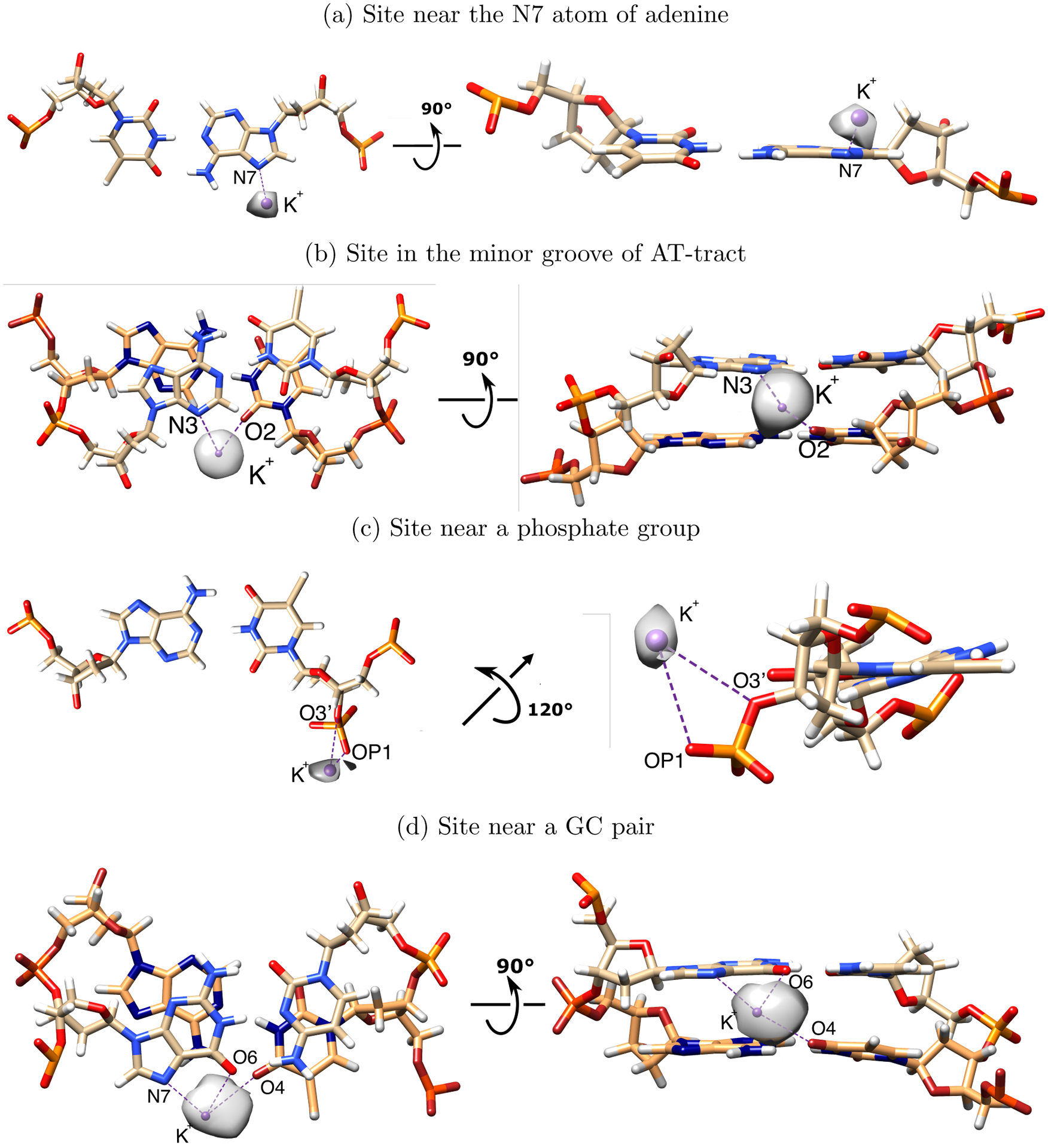
Typical K+ and Na+ binding sites in the dsDNA structure. Shown are the sites, for which the computed ion density is more than 5 electron charges per Å3. Sodium (not shown) is coordinated by the same sets of atoms, but the occupancy may differ significantly (generally lower). For visual clarity, the density maps of potassium near the binding sites are drawn at the different levels (a: 9 electron charges per Å3; b: 5 electron charges per Å3; c: 7.5 electron charges per Å3; d: 7 electron charges per Å3). Potassium location was fitted to the density map for the panel c; others were taken from the representative snapshots. The binding site near the GC-pair (d) corresponds to sites 1–3 and 10–12 in Figure 3. The binding site in the minor groove of the AT-tract (b) corresponds to site 7 in Figure 3
The number of deeply bound ions depends strongly on the solvent model. It decreases by 1.5–2 times from SPC/E+J/C to OPC+L/M HFE in the order of solvent models: SPC/E+J/C, TIP3P+J/C, OPC+J/C, OPC+L/M HFE. We also found noticeable dependence of the ion concentration near the helical axis on the nuances of DNA force field used, ff99bsc0 or ff99bsc1 (see Figure S3), although the strength of this dependence is weaker than the sensitivity to the solvent model. Ion distributions beyond 7 Å from DNA helical axis are nearly unaffected by the force-filed.
The DNA sequence also significantly affects the distribution of deeply bound ions, Figure 1. The first peak of the ion distribution is at 5 Å from the helical axis in the case of polyA DNA, and at 2–3 Å for the mixed sequence DNA. The difference in the first peak position can be explained as follows. The first peak of the ion distribution around the axis of polyA DNA is formed by the ions in the sites near N7 atom (see Figure 2). The mixed sequence DNA does not have as many AT-pairs with the specific structural motif as does the polyA sequence. At the same time, the mixed sequence DNA contains many GC-pairs, which form their own binding sites (see Figure 2). These sites are located very close to the DNA axis, and so even small differences in their occupancies significantly affect the ion concentration in the small volume near the axis, more so than do the occupancy differences of the binding sites further away from the axis. Thus, differences in binding site occupancies resulting from the use of different solvent models are amplified in the radial distribution near the helical axis; the amplification is stronger for the mixed sequence DNA compered to the polyA sequence. However, the average total numbers of deeply bound ions differ less between the two DNA sequences than between OPC+L/M HFE and SPC/E+J/C solvents for the same sequence.
Overall binding affinities of ions to DNA
We find that the computed ion-DNA binding affinity, see “Methods”, does not depend on the type of ion or the DNA sequence, Table 2 and Table S2. To within a fraction of kBT, there is no noticeable difference between the ion-DNA affinities for the four different solvent models, the maximum difference is about 0.2 kBT.
Table 2:
Calculated binding affinities of Na+ and K+ to polyA DNA. All values are in kBT units, and the standard error of the mean is 0.02 kBT. The binding affinity does not depend on the ion type, within the error, in all four solvents.
| ion type | Na+ | K+ | ||
|---|---|---|---|---|
| Bulk salt concentration (M) | 0.15 | 0.5 | 0.15 | 0.5 |
| SPC/E+J/C | −1.90 | −1.03 | −1.92 | −1.03 |
| TIP3P+J/C | −1.74 | −0.92 | −1.72 | −0.87 |
| OPC+J/C | −1.77 | −0.90 | −1.80 | −0.89 |
| OPC+L/M HFE | −1.75 | −0.90 | −1.74 | −0.86 |
The absolute value of the calculated binding affinity of Na+ and K+ to the DNA decreases with increasing bulk salt concentration, Table 2. A simple and intuitive, albeit glossing over details,58 explanation is that, as more counterions bind to the DNA, its net charge is reduced, thereby lowering the net attractive force acting on the remaining counterions in solution.
Degree of DNA charge neutralization by counterions
We have also calculated the degree of neutralization of the DNA charge by monovalent ions in our trajectories to compare these estimates with the prediction of Manning-Oosawa condensation theory.26 Dependence of the degree of neutralization of the DNA by counterions on the number of nucleotides excluded from the calculation can be found in Figure S9. In the theory the charged polymer is represented by a uniformly charged fiber of zero radius, and the bound ions are assumed to be in dynamic equilibrium with the ionic atmosphere around it. The degree of neutralization of the DNA charge does not depend noticeably on the sequence and type of ion, see Table S3. Table 3 contains the representative part of the results.
Table 3:
Calculated degree of polyA DNA charge neutralization by sodium ions. Units are %, statistical error is 4%. In SPC/E+J/C, the neutralization is noticeably higher than in the other solvents. All four solvent models are qualitatively consistent with Manning’s prediction,26 but neither model matches it quantitatively at 0.15 M bulk salt concentration.
| Solvent model | Bulk salt concentration (M) | |
|---|---|---|
| 0.5 | ||
| SPC/E+J/C | 86 | |
| TIP3P+J/C | 77 | |
| OPC+J/C | 79 | |
| OPC+L/M HFE | 75 | |
| Manning’s prediction | 76 | |
All four of the solvent models are in qualitative agreement with the the degree of DNA charge neutralization by monovalent ions predicted by Manning26 (76 %). At 0.15 M bulk salt concentration, none of the models agree with Manning’s prediction quantitatively, with SPC/E+J/C being closest. At 0.5 M salt, all of the solvent models except SPC/E+J/C are in good agreement with Manning’s prediction. The interpretation of the agreement is that all four of the solvent models provide a physically sound picture of counterion condensation onto the DNA; note that Manning’s theory itself is an insightful model based on clear and general physical principles, but still only an approximation to reality.60–63 At the same time, the variability of the predicted values by well established solvent models, near 15 % from Table 3, is not negligible, and should be reckoned with as one aims at a quantitative interpretation of atomistic explicit solvent simulations in this context. The above variability is smaller than that resulting from comparing a polarizable (Drude) and a non-polarizable (C36) force-fields.30
Dynamics of ions in different solvent models
To compare the dynamics of ions in our simulations, we have calculated the diffusion coefficients of Na+, K+ and Cl− in simulations with double-stranded DNA in different solvent models. The estimated diffusion coefficients of ions in trajectories with different DNA duplexes do not differ (Tables 4, S4 and S5.). Note that the calculation treats all of the ions on the same footing, regardless of their positions relative to the DNA, see “Methods”.
Table 4:
Diffusion coefficients (10−5 cm2/s) of monovalent ions in simulations with double-stranded mixed sequence DNA in different solvent models. The computed values are roughly two times larger in the simulations with TIP3P+J/C model compared to the other three solvents, where ion mobility is roughly the same.
| Bulk salt concentration (M) | 0.15 | 0.5 | 0.5 | ||
|---|---|---|---|---|---|
| Ion type | K+ | K+ | Cl− | ||
| SPC/E+J/C | 0.99 ± 0.01 | 1.14 ± 0.01 | 1.10 ± 0.01 | ||
| TIP3P+J/C | 1.76 ± 0.01 | 1.86 ± 0.01 | 1.96 ± 0.01 | ||
| OPC+J/C | 0.84 ± 0.01 | 0.94 ± 0.01 | 1.04 ± 0.01 | ||
| OPC+L/M HFE | 0.83 ± 0.01 | 0.88 ± 0.01 | 1.11 ± 0.01 | ||
Monovalent ions (Na+, K+ and Cl−) have almost the same diffusion coefficients in the trajectories obtained using all the solvent models except TIP3C+J/C. In simulations using the latter, the ions have diffusion coefficients that are roughly twice as large. This trend follows the dependence of self diffusion coefficient of water on the water model.47 Diffusion coefficients of ions were calculated earlier in trajectories obtained using TIP3P and SPC/E water;64 the ratios of the previously reported coefficients is essentially the same as the ones estimated from Table 4.
2.2. Comparison with available experiments
Number of sodium ions associated with dsDNA
Previously, the number of ions associated with a 24 b.p. mixed sequence double-stranded DNA was experimentally measured using buffer exchange method.58 We have counted DNA-associated sodium ions in every simulation with mixed sequence to compare their amount with experimental results (Table 5).
Table 5:
Number of DNA-associated sodium ions, in simulations of the mixed sequence DNA obtained using different solvent models. Standard errors of the mean are indicated. Agreement with experiment58 improves in the order: SPC/E+J/C, TIP3P+J/C, OPC+J/C, OPC+L/M HFE. Deviation from experiment is the largest for SPC/E+J/C. The experimental numbers were scaled to account for the 1 b.p. difference in length between the DNA fragment used in the experiment and that used in our simulation, see Methods.
| Bulk salt concentration (M) | 0.5 |
|---|---|
| SPC/E+J/C | 38.1 ± 0.5 |
| TIP3P+J/C | 32.6 ± 0.5 |
| OPC+J/C | 33.0 ± 0.5 |
| OPC+L/M HFE | 34.0 ± 0.5 |
| Experiment | 35 ± 3 |
Each of the solvent models correctly reproduces the counter-intuitive trend: the number of DNA-associated ions decreases as the bulk salt concentration increases; a detailed explanation of this trend can be found in the original experimental work.58 The number of ions associated with the DNA decreases from SPC/E+J/C to OPC+L/M HFE. Overall, OPC water model gives the best agreement with the experiment for both sets of ion parameters, Table 5.
The calculated ion-DNA binding affinities are consistent with the corresponding numbers of DNA-associated ions in the following sense: higher (by absolute value, beyond the error margin) binding affinity resulting from switching to a different solvent model, Table 2, leads to a greater number of DNA-associated ions, Table 5. For example, the noticeable relative decrease, 38.1/34.0 ≈ 1.12, of the number of DNA-associated Na+ ions at 0.5M salt in going from OPC to SPC/E, can be predicted, quantitatively, from the corresponding decrease in the computed binding affinity ΔΔG = −0.13kBT: e−ΔΔG/kBT ≈ 1.13.
Binding affinities of monovalent ions to DNA
In our simulations, ion binding affinity to the DNA, Table 2 and Table S2, does not depend on the type of ion or the DNA sequence. This independence of the DNA binding affinity of the ion type agrees with the experimental observation that diffusely bound counterions of the same valences produce very similar ionic atmosphere around DNA.29,65
Potassium-binding sites in DNA grooves
Experimental data on specific DNA sodium- and potassium-binding sites is limited. The most detailed information is usually obtained from X-ray crystallography experiments. Yet, the raw data are electron density maps, and their interpretation is sometimes ambiguous, especially if a certain putative binding site is not always fully occupied by the ion.66 Indeed, sodium is isoelectronic with water, while the distances to the surrounding atoms are smaller. On the other hand, potassium has more electrons, but typical distances to the surrounding atoms are similar to those of water. Because the assignment is complicated, heavier monovalent ions, such as Tl+, Rb+ or Cs+, which can be easily distinguished from water, are typically used in experiments. Tl+ is considered to be a good mimic for potassium (but not for sodium) due to similar ionic radii and biophysical properties.21
Crystallographic structure of the potassium form of the Drew-Dickerson dodecamer (CGC-GAATTCGCG) showed that there are potassium binding sites in the minor groove of the AT-tract both in ApT-site and ApA-sites.31 The Tl+-bound structure revealed a binding pocket in the ApT-site but not in the ApA-sites.21 Additional binding sites are observed in the major groove of GC-rich areas of DNA.21 Since available data for Tl+-bound sites is more reliable compared to Na+- or K+-bound sites due to more visible electron density of Tl+, we have compared our simulation results to Tl+ data. The experimentally observed binding sites are numbered for clarity, as shown in Figure 3. Note that the site numbers used in the original article21 are different, their correspondence to the site numbers in this work can be found in Table S7. While the dodecamer sequence is palyndromic, the experimentally observed ion binding sites are not arranged symmetrically.21 Presumably, this is the consequence of asymmetric packing in crystals. In the downstream analyses, binding sites symmetric to those observed in crystals are labeled ”sym”. They are expected to have the same ion binding properties as the experimentally observed ion binding sites.
Figure 3:
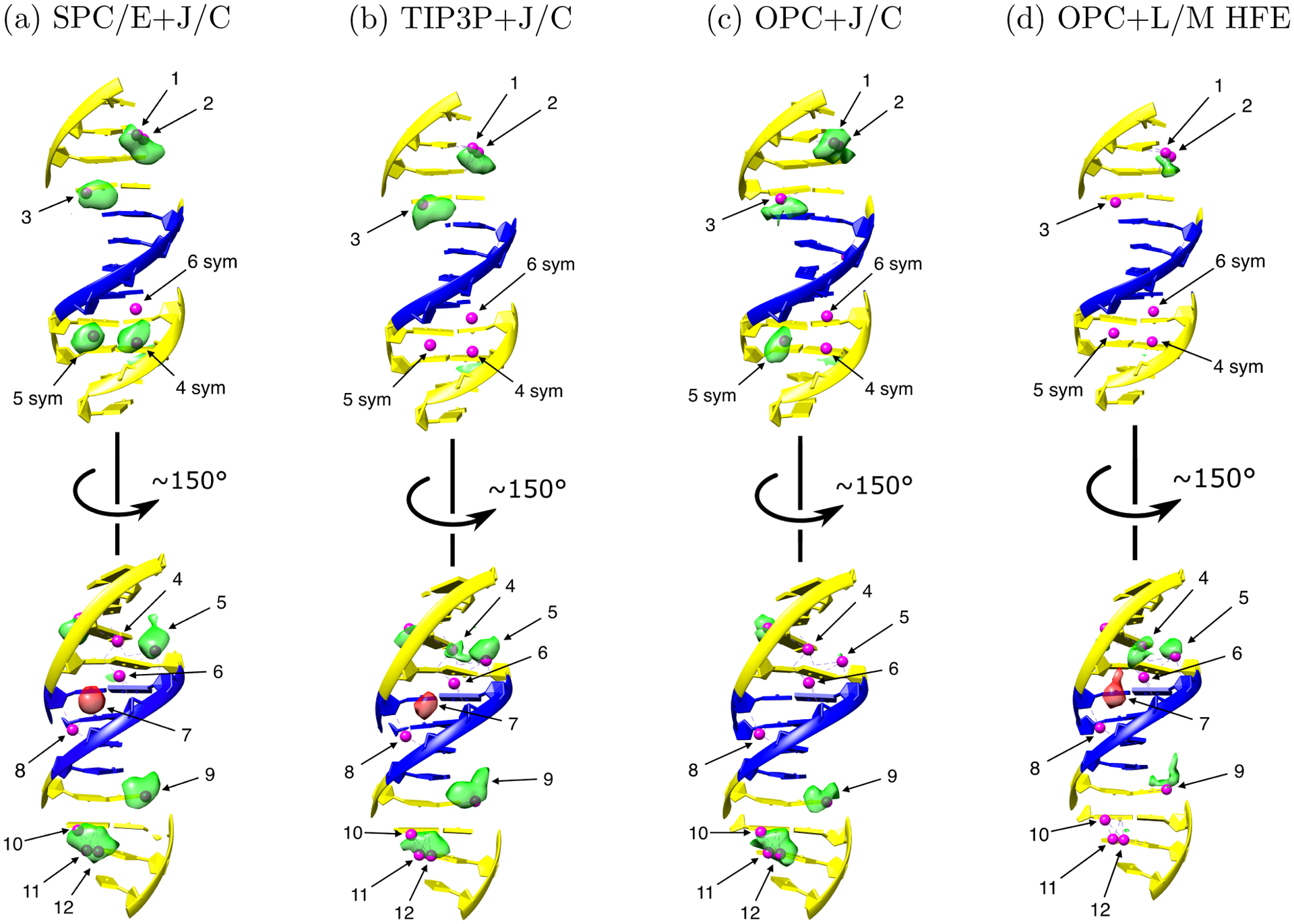
Probability electron density maps of potassium ions around the Drew-Dickerson dodecamer, estimated from the MD simulations in the four different solvent models. Green: density in simulated binding sites, which overlap with ones seen in experiment, red: density in the false positive site (# 7), which does not overlap with any experimental binding site in the reference structure. All the maps are drawn at the same level of 5 electron charges per Å3. Small magenta spheres are K+ binding sites suggested by experiment.21 Thymine and adenine are shown in blue. Guanine and cytosine are shown in yellow. In the order SPC/E+J/C, OPC+J/C, TIP3P+J/C, OPC+L/M HFE, the agreement of simulated K+ density with experiment decreases significantly: 67%, 60%, 53%, and 27%, respectively. Experimentally characterized sites were re-indexed for clarity as specified in Table S7. Here 4 sym, 5 sym and 6 sym are the binding sites located centrally symmetrically to the 4th, 5th and 6th sites near the symmetrically located nucleotides. The coordinating atoms for representative binding sites are shown in Figure 2.
In Figure 3 we compare, qualitatively, the density of potassium ions from our trajectories of the Drew-Dickerson dodecamer structure with the corresponding experimental ion binding sites. False positive sites are simulated binding sites with occupancy ≥ 0.1, which do not overlap with experimentally characterized sites. True positive sites have occupancy ≥ 0.1 and overlap with the corresponding binding sites seen in the experiment. Since the exact concentrations of buffer components in crystals, which affect the bound ion occupancies, are not known, and cannot be matched in simulations, and since, ultimately, Tl+ is not K+, we refrain from quantitative comparisons of our calculated and experimental site occupancies, summarized in Table S7. Instead, we only assert that in a faithful simulation the ions can be expected to be found near the experimentally characterized sites, Figure 3 and Table S6. This interpretation of simulation vs. experiment agreement leads to a semi-quantitative comparison presented here; more substantial claims would require additional experimental and modeling investigations.
As we can see from Figure 3, in the order of solvent models SPC/E+J/C, TIP3P+J/C, OPC+J/C, OPC+L/M HFE, the agreement with experiment decreases from 67% to 27% (see Table S6 for quantitative details). The most significant differences between the predictions of the solvent models are observed in the minor groove. Binding sites in this area contain almost no ions when OPC water model is used. In contrast, simulations in SPC/E water reveal a significant amount of potassium ions in the minor groove. Given the caveats outlined above, SPC/E water with J/C ions reproduces the experimental ion occupancies the most accurately of all four solvent models tested, at least qualitatively.
Generally, the reference structure21 shows that ions prefer to concentrate in the minor groove of AT-tract and in the major groove of GC-rich area. To compare our results with this general trend, we calculated the numbers of ions in minor grooves of AT-tracts of our DNAs and in major grooves of GC-rich areas of the mixed sequence (GCATCT(GGGC)GC−rich (TATAAAA)AT−tract(GGGCG)GC−richTCG), as well as in the minor groove of polyA sequence (see Tables S8 and S9).
The number of potassium ions in the major groove of the Drew-Dickerson dodecamer and 25 b.p. DNAs is largely independent of the solvent model, but the number of ions in the minor groove does depend on it, see Tables S7, S8 and S9. In OPC+L/M HFE solvent, the minor groove of the mixed sequence DNA contains almost no potassium ions, similarly to the minor groove of the dodecamer; this result does not agree with experimental findings.
While Na+ binding to B-DNA was explored experimentally,67 we are unaware of experimental binding data equivalent to the case of K+ discussed above; thus, we have not explored binding of Na+ to DNA to the same extent. Results of our limited simulations of Na+ binding to the Drew-Dickerson dodecamer are presented in the Figure S2.
2.3. The effects of NBFIX correction on the ion distributions
NBFIX corrections68–70 modify pair (cross-terms) parameters of the Lennard-Jones potential, which no longer follow the simple combination rules used in the models tested so far. These corrections were developed to best reproduce a set of experimental observables different from those used here for testing of the solvent models. The corrections were reported to result in improved accuracy of the simulations.70
To find out how the distribution of ions changes when using NBFIX (also called CUFIX) corrections to force fields, we applied the corrections to the TIP3P+J/C solvent model.68–70 This set of atomic parameters was developed using osmotic pressure of different solutions as a target value. Figure 4 shows the radial distributions of ions in TIP3P+J/C solvent model with and without the NBFIX corrections. We also counted the number of deeply bound ions in trajectories, Table 6.
Figure 4:
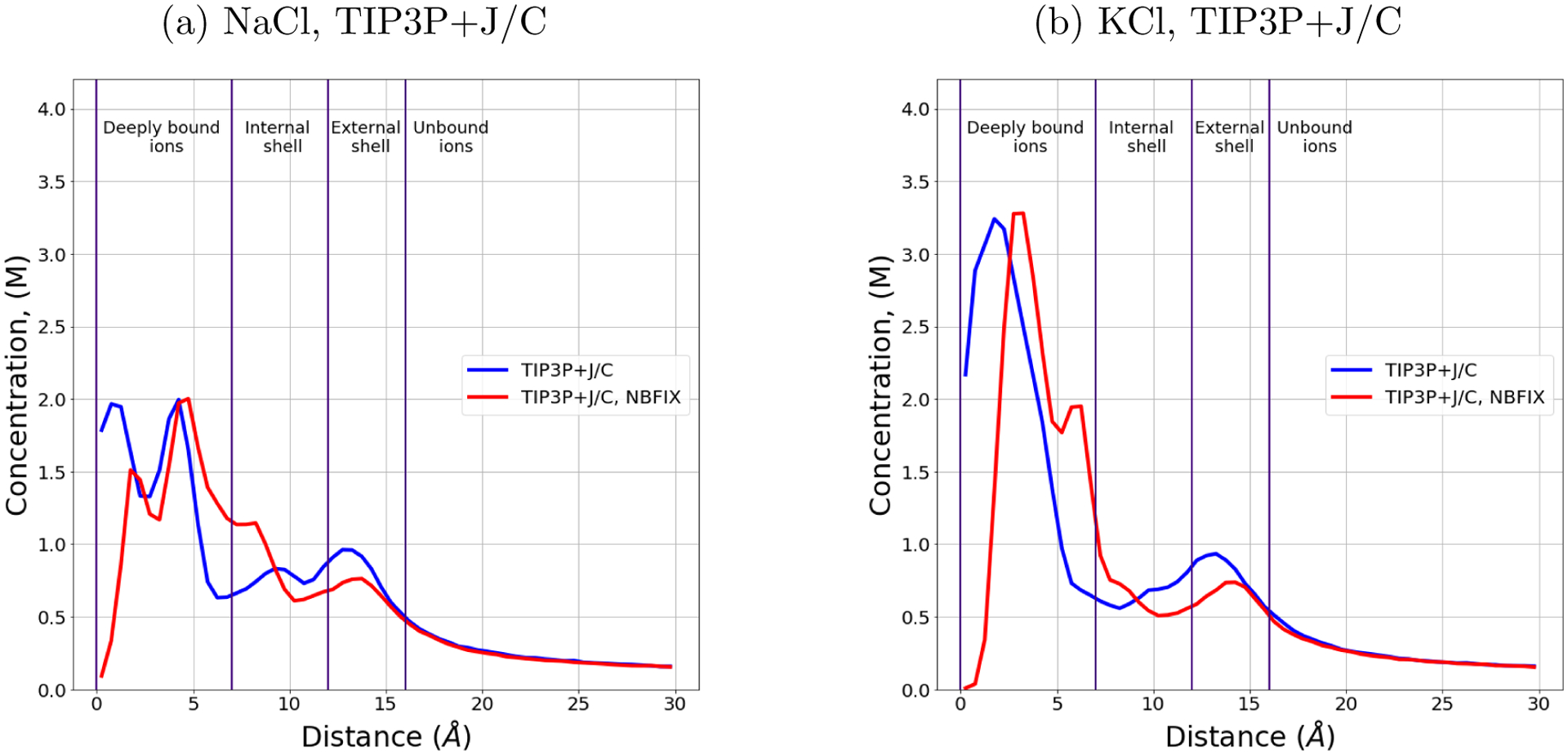
Dependence of sodium and potassium concentration on the distance from the DNA helical axis with and without the NBFIX corrections in TIP3P+J/C. The bulk salt concentration is 0.15 M. The distributions are identical beyond 15 Å from the DNA axis. The cylindrical shells around the DNA helical axis are named as in Figure 1.
Table 6:
Number of deeply bound ions in simulations of mixed DNA obtained using TIP3P+J/C solvent model with or without NBFIX corrections.
| Ion type | Na+ | K+ |
|---|---|---|
| TIP3P+J/C | 5.1±0.1 | 6.0±0.1 |
| TIP3P+J/C, NBFIX | 6.1±0.1 | 8.3±0.1 |
Deeply bound ions include ions in specific binding sites in the DNA structure. The use of NBFIX corrections for TIP3P+J/C solvent model led to an increase of the number of deeply bound ions observed in the simulations. To check if simulations carried out using TIP3P+J/C solvent with NBFIX corrections better reproduce experimentally characterized nuances of ion distributions, we generated a trajectory of Drew-Dickerson dodecamer in 0.5 M KCl using TIP3P+J/C solvent model with NBFIX corrections, just as we did for the other solvent models. Occupancies of binding sites in the DNA structure are presented in Tables S6 and S7. The correspondence between the binding sites in the trajectory obtained using TIP3P+J/C solvent with NBFIX corrections and the ones observed in experiment has improved to 60%.
We have also counted the number of ions associated with DNA in 0.15 M NaCl solution, which become 36.9 ± 0.5 (compared to 37 ± 2 in experiment) with the NBFIX correction turned on. Thus, NBFIX corrections for TIP3P+J/C solvent model makes distribution of ions more consistent with the available experimental results: the ”ion counting” experiment, mentioned before, and and crystallography experiment, see Tables S6 and S7. In summary, OPC+J/C model and TIP3P+J/C model with NBFIX corrections give the same agreement with X-ray experiment (60 %), and both models agree with the ”ion counting” experiment within the error margin.
Explanation for the general trends of sensitivity to the solvent model
The over-all numbers of monovalent counterions condensed onto the DNA, as well as their distributions beyond the distance to the DNA axis of ~ 10 Å ,are relatively insensitive to the solvent model. We argue that the insensitivity stems from the fact that this particular regime of ion-DNA interaction is controlled by counterion condensation, which, at its core, is agnostic to subtle details of the water or ion model used, as long as these are generally correct. Indeed, according to the simplest version of Manning’s condensation theory, the degree of DNA charge neutralization, Θ, by monovalent counterions is given by Θ = 1 − 1/ξ, where 72 Here, b is the average spacing between actual charged sites on the DNA, and the only parameter that characterizes the solvent (model) is its dielectric constant ϵ. For dsDNA in water at 300 K, the predicted degree of charge neutralization by monovalent counterions is about 0.76. At the next level of approximation,62 Θ shows some dependence on the bulk salt concentration and the over-all geometry of the DNA double-helix, but the latter is again insensitive to solvent models tested here, further supporting the relative insensitivity of Θ to the solvent model in our simulations. A relatively small, about 15 %, variability in the numbers of ions condensed onto the DNA, seen in our simulations, might be explained by the fact that model deviates from experiment for some of the water models tested.43 Once the requisite number of counterions condense onto the DNA, the remaining diffuse atmosphere of monovalent ions is well described by the linearized Poisson-Boltzmann model,71–74 which is also agnostic to the type of monovalent ion. Within the standard Poisson-Boltzmann approach the water model is specified by only two parameters: the dielectric constant and the water probe radius.
The logic becomes very different with respect to ions bound strongly to specific binding sites. This type of binding, often in the DNA grooves, implies at least partial dehydration of the ion; the associated free energy cost – the desolvation penalty – will factor into the local binding affinity. Thus, even a few % discrepancy between different ion models49,51 – out of nearly 150kBT experimental hydration energy for Na+ – can easily lead to several kBT of difference between the corresponding desolvation penalties and, hence, the corresponding sensitivity of the local binding affinities to the ion (and water) model. Even for two ion models that give exactly the same computed hydration free energy, the ion binding to the DNA may not be exactly the same. This is because these ion models may still differ in their LJ parameters, which, in turn, affects their interaction with DNA atoms, the effect being specific to the atom types found in the specific binding site.
Note that even though ion occupancies of some specific binding sites may differ noticeably between solvent models, the total number of counterions condensed onto the DNA can still be virtually the same. First, specific binding sites contribute relatively little to the total number of bound ions. Moreover, for the entire DNA fragment, differences between specific occupancies average out to some extent, reducing sensitivity to the solvent model for the aggregate characteristics of ion binding. Second, an increase in the deeply bound counterions contributes to the DNA neutralization, leading to fewer ions bound in the subsequent shells, to yield the same total according to counterion condensation theory.
3. Conclusions
In this work, we have compared distributions of sodium and potassium ions around double stranded DNA solvated in four different solvents – combinations of popular models of water and corresponding ion parameter sets. Our focus is specifically on ion distributions rather than on their effect on the DNA structure, which was explored in detail in several previous works.
We find that some features of simulated ion distributions are virtually independent of the solvent model, while others depend strongly on it. We have provided explanations for these trends.
In every solvent model tested, the DNA is found to have several electronegative competitive sites, around which the ions tend to form ”density clouds”, in agreement with experiment.75 The calculated binding affinity of ions to the DNA is virtually independent of the ion type in every solvent model tested; the similarity of K+ and Na+ binding affinities to double-stranded DNA is in agreement with experiment.59 The simulated binding affinity of ions to the DNA also does not depend significantly on the DNA sequence or the solvent model. Qualitatively, all four models are in agreement with Manning’s counterion condensation theory. At the same time, the variability of the predicted DNA charge neutralization by well established solvent models, ~ 15 % , is not completely negligible, and should be reckoned with as one aims at a quantitative interpretation of atomistic explicit solvent simulations in this context. Radial distributions of ions beyond 7 Å from the DNA helical axis do not depend significantly on the water model or ion parameters; for all four solvent models, the distribution of ions beyond 16 Å from the DNA helical axis is in near quantitative agreement with the Debye-Hückel theory. Typical functional groups that coordinate the ions are the same for different solvent models and do not depend on the ion type. Occupancies of the typical binding sites are affected by ion type and solvent model.
At the same time, ion distributions near the helical axis of DNA differ significantly between the solvent models, with the differences increasing for ions closer to the helical axis. In the following order of solvent models (water model + ion parameters) SPC/E+J/C, TIP3P+J/C, OPC+J/C, OPC+L/M HFE, the number of deeply bound ions decreases from 7–8 for SPC/E+J/C to 4–5 for OPC+L/M HFE. The number of ions in the minor groove of the AT-tract of the mixed sequence DNA reduces 3-fold in going from SPC/E+J/C to OPC+L/M HFE. In contrast to potassium, sodium does not appear to bind to distinct and specific binding sites in Drew-Dickerson dodecamer, at least in the one water model (SPC/E) where this effect was tested.
Distributions of deeply bound ions depend noticeably on the DNA sequence. Compared to the polyA DNA, in simulations of the mixed sequence DNA the first local maximum of the ion distribution is closer to the helical DNA axis by 2–3 Å for both ion types; the first maximum is also two times higher for ions in SPC/E+J/C solvent model in solutions with polyA than with the mixed sequence. However, the DNA sequence does not affect aggregate quantities, such as the total number of deeply bound ions and the degree of charge neutralization. The distribution of deeply bound ions also depends on the DNA force field noticeably, but this dependence is weaker than the dependence on the solvent model. At the same time, the average number of deeply bound ions is not affected significantly by switching the DNA force field from ff99bsc0 to ff99bsc1.
We also have compared the ability of the solvent models to reproduce several of experimentally characterized nuances of ion distributions around DNA. The number of simulated ions in the DNA minor grooves depends on the solvent models much more than does the number of ions in major grooves. Local distribution of ions depends on the type of ion significantly. The number of DNA-associated sodium ions in OPC water with L/M HFE ion parameter shows best quantitative agreement with the ”ion counting” experiment compared to the other three solvent models, while the deviation from experiment is the largest for SPC/E + J/C, with no quantitative agreement. The binding affinity of ions to DNA in the bulk salt concentration range between 0.15 M and 0.5 M and in all four tested solvent models does not depend on the ion type in agreement with experiment.59
We have identified potassium binding sites in the simulations, and compared them to what can be inferred from a specific experiment (X-ray).21 Qualitative agreement with the experiment decreases in the following order of the solvent models SPC/E+J/C, OPC+J/C, TIP3P+J/C, OPC+L/M HFE. Over-all, SPC/E water model with the J/C ion parameter set appears to reproduce the experimental specific K+ binding sites more clearly than the other solvent models tested. Difficulties in the interpretation of the available relevant experiments preclude us from making a stronger statement.
We have also examined the ability of NBFIX corrections to improve the agreement of the distribution of ions with the experimental references used here as the main accuracy metrics (generally distinct from those used in the parametrization of NBFIX). Correction for TIP3P+J/C solvent model has improved the agreement with both experimental references; the accuracy of the ion distribution obtained using TIP3P+J/C solvent with NBFIX corrections is the same as the one obtained using OPC+J/C solvent.
In summary, several features of ions distributions around double stranded DNA are virtually insensitive, or only weakly sensitive to the choice of water model and its ion parameters. Generally, the further is the ion from the DNA helical axis, the less influence the solvent model has; all four popular solvent models tested here are essentially interchangeable for simulating diffuse atmosphere of K+ and Na+ ions around the DNA. Several ”aggregate” characteristics of DNA-ion binding, including binding affinities, are weakly sensitive to the solvent model. The degree of DNA neutralization by counterions and the total number of ions associated with the DNA, do depend weakly on the solvent model; one can expect a 10 to 15 % sensitivity to the solvent model here. Solvent models can be rank ordered in their ability to reproduce experiment with respect to the total number of ions associated with the DNA.
At the same time, specific and relatively tight binding of monovalent ions to the DNA is highly sensitive to the solvent model. Even though direct comparison with relevant experiments is difficult for ions such as Na+ and K+, we have identified best and worst performing solvent models, at least qualitatively. While B-form DNA is a robust structure that may tolerate a degree of error in the specific ion binding, that may not be the case for other nucleic acid structures – their conformations and the associated transition can be sensitive to whether is give ion is in the right spot or not. Our findings should serve as a warning that popular solvent models may not be interchangeable in these situations.
Over-all, no single solvent model consistently outperforms the other three in their ability to reproduce the entire set of experimental characteristics of monovalent ion binding to double stranded DNA considered here.
We hope that this work will make it easier for practitioners to choose between available solvent models for atomistic simulations involving double-stranded DNA with K+ or Na+ counterions. As we have demonstrated, the choice depends on the scientific question the simulation is designed to address: for some questions, any of the four solvent models explored here may be equally appropriate, while for others choice of a specific solvent model can become critical. OPC+J/C solvent or TIP3P+J/C with NBFIX corrections might be suggested as an imperfect one-size-fits-all current compromise model in cases where several aspects of DNA-ion binding are relevant simultaneously. A more robust strategy may be to rely on consensus results obtained with two different solvent models.
Finally, in this work we have analyzed only a small, but arguably currently relevant, subset of possible combinations of popular DNA force fields, water and ion models. In particular, NBFIX correction was not explored as thoroughly as models based on “standard” combination rules. Also, the inclusion of electronic polarization effects, not considered here, may affect the ion distributions. In fact, beneficial effects of considering a fully polarizable DNA force-field were reported.30 We have also not examined the binding of monovalent ions to proteins or single stranded nucleic acids. Many of our specific conclusions, including the relative ability of the examined solvent models to reproduce relevant experiments, should be considered as strictly limited to double-stranded DNA. At the same time, some of the trends that rely on the basic physics of counterion condensation will likely hold beyond dsDNA, e.g. the predicted weak dependence of the ion distribution far from the solute on the choice of the solvent model. The testing protocols we have developed can be easily adopted to explore, on the same footing, new solvent models and their combinations.
Methods
3.1. All-atom MD simulations
MD simulations of two 25 b.p. long DNA duplexes, and of Drew-Dickerson dodecamer (DDD) were carried out using ff99bsc0 force field76 (unless otherwise specified). AMBER 1877 was used to generate most of the trajectories; versions 1677 and 1477 were used early in this work (with no discernible differences with respect to the outcomes relevant to this work). The 25 b.p. duplexes are constructed in canonical B-form using Nucleic Acid Builder (NAB).78 To analyze possible sequence dependence of the simulation outcomes, we used two different 25 b.p. long sequences: poly(dA·dT) (polyA in text) and (GCATCTGGGCTATAAAAGGGCGTCG) (mixed sequence in text). The PDB structure of the DDD was taken from X-ray structure 1JGR.21 Each DNA duplex was solvated with 22022 ± 40 water molecules. We used Joung/Cheatham ion parameter sets49 (J/C in text) (ion type, Rmin/2(Å), (kcal/mol)) for SPC/E (Na+, 1.212, 0.3526418; K+, 1.59, 0.4297054; Cl−,2.711, 0.0127850) and TIP3P (Na+, 1.369, 0.0874393; K+, 1.705, 0.1936829; Cl−, 2.513, 0.0355910) water models. For OPC water model two distinct ion parameter sets were used: J/C49 (Na+, 1.226, 0.1684375; K+, 1.590, 0.2794651; Cl−, 2.760, 0.0116615) and Li/Merz ion parameters (12–6 HFE set)51 (Na+, 1.432, 0.02154025; K+, 1.646, 0.10417397; Cl−, 2.298, 0.63661449) (L/M HFE in text). The LJ parameters of the last set were developed for OPC by Pengfei Li using the protocol in Ref.,51 and are slightly different from 12–6 HFE parameters for OPC reported recently in Ref.56 To calculate how many ions we should add to the system to reach the desired bulk salt concentration, we used SLTCAP79 method. For systems with 25 b.p. DNA that approach gave 221 Na+ or K+ and 173 Cl− to reach 0.5M, and 88 Na+ or K+ and 40 Cl− for 0.15M bulk salt concentration. For systems with the DDD and 0.5M bulk salt concentration, the numbers of added ions were 207 K+ or Na+ and 185 Cl−. A typical initial configuration without water is shown in Figure S4. After the initial minimization, each system was heated from 0 to 300 K in canonical ensemble (NVT) for 18 ps, and then equilibrated for 2 ps in the same ensemble. Then it was equilibrated for 40.06 ns in isothermal-isobaric ensemble (NPT) using Langevin dynamics with the collision frequency of 2−1 ps to reach 1 atm pressure. Periodic boundary conditions and the particle mesh Ewald method were used. After the equilibration, 100 ns (unless otherwise stated) long production trajectories were generated for each system using NPT ensemble. Convergence was checked on 1000 ns-long trajectories. The integration time-step was 2fs. During the heating, equilibration and production simulations, the 13th pair of nucleotides in 25 b.p. DNA, and the 7th pair in the dodecamer were restrained to their original positions with 1 kcal/mol/Å2 force constant to prevent drift of the duplex. Snapshots were saved every 10 ps along each trajectory.
3.2. Application of NBFIX corrections
We used the parameters for the TIP3P+J/C solvent model as distributed by the authors,70 following the recommended steps found at https://bionano.physics.illinois.edu/CUFIX .
Following the recommendations, we downloaded all the files and changed the paths in leaprc.DNA.bsc1.cufix to suitable for our case. We then added the command ”loadamber-params frcmod.ff99cufix” to the tleap script used to prepare the input coordinate and topology files. Details of the updated parameters are in Refs.68–70
3.3. Estimation of the ion diffusion coefficients
The diffusion coefficients were calculated using the diffusion utility in AMBER 16. The utility calculates the diffusion coefficient using the Einstein relation:
where n is the number of dimensions and MSD is the mean square displacement in time t. The diffusion coefficient represents the average over all the ions in simulation.
3.4. Trajectory analysis and calculation of ion distributions
For analysis of ion distribution around DNA we use Curves+ and Canion.80 Curves+ translates coordinates into a convenient curvilinear helicoidal system. Canion analyzes the curvilinear coordinates of ions and generates readable 1-dimensional and 2-dimensional graphs of the dependence of ion concentration on the coordinate along the axis of the DNA, angle, and distance from the helical axis of the DNA. It also produces density maps of ions around DNA. The output of Curves+ is also analyzed using package NumPy81 with Python 3. To compare numbers of deeply bound ions in the solutions with different solvent models we calculate the numbers of ions no further than 7 Å from DNA helical axis, see below how we obtain the mean and the error of the computed values. To calculate the ion distribution corresponding to the Debye–Hückel theory, we consider DNA as a spherical particle with a radius of 16 Å. The charge is located at the center of the sphere, and is equal to the sum of the charges of the DNA fragments and all of the bound ions in OPC + J/C solvent – ions inside a cylinder of 16 Angstroms in radius.
3.5. Analysis of the binding sites in the DDD
The 1JGR21 structure contains the Drew-Dickerson dodecamer (CGCGAATTGCGC) and Ti+ binding sites in the DNA. The dodecamer is palindromic, but not all the experimentally characterized sites have ”twin sites” near the same symmetry-related nucleotides. To determine where these additional sites should be, we took the 1JGR structure and its copy. Then we aligned one of the strands of original structure to complementary strand of the copy. The final structure included the 1JGR and its upside-down copy. Indexes of these additional symmetry-related sites contain the abbreviation ”sym”.
3.6. Ion binding affinities
To calculate the affinity, μ, of a given ion species to the DNA, we follow Ref.18
| (1) |
where C∞ is the bulk salt concentration, and Ccond is the concentration of the bound ions. The latter is estimated18 via
| (2) |
where Nion is the number of ions that are closer than 16 Å to the DNA helical axis, Vcyl is the volume of a cylinder of radius 16 Å and height 85 Å (corresponding to the dimensions of the 25 b.p. DNA fragment used), and VDNA is the volume of the DNA, calculated using ProteinVolume.82 The specific choice for the cutoff distance of 16 Å for monovalent ions that can be considered as bound to the DNA is consistent with the counterion condensation theory.60 While the absolute binding affinity computed via Eq. 1 is affected by the choice of the cutoff value, it does not affect our conclusions, which are based only on relative affinities – their changes with the solvent model and ion type.
3.7. Ion counting
Bai et al. experimentally measured the number of ions associated with a DNA using the buffer exchange method.58 Here, these numbers were multiplied by 24/23 – the ratio of the total charges of our DNA fragment (25 b.p. long) and one used in the actual experiment (24 b.p. long). For a direct comparison with the experiment, here we calculated the number of DNA-associated83 ions via:
| (3) |
where cNa+(∞) is the bulk salt concentration established using SLTCAP method,79 h is length of DNA (in our case it is 85 Å). The dependence of ion concentration, cNa+(r), on the distance to the DNA axis, was calculated by Curves+ and Canion programs.80
3.8. Estimation of computed values and their statistical errors
For each calculated value for which we seek estimate its statistical error, the error is estimated with the slicing method,84 from the MD trajectory of the mixed sequence DNA in OPC+L/M HFE ion set, at 0.15M KCl, see the SI for details. We assign the same statistical error to the corresponding average obtained in all other solvent models, for trajectories of the same length.
3.9. Occupancy of ion binding sites in simulations
Ion binding sites are defined as regions of space with the average charge density above the level of 5 electron charges per Å3. Charge density maps were generated using Canion.80 The densities were analyzed along the following coordinates: the distance along the DNA axis, the angle to the reference vector, which tracks the helical twist of the nucleic acid, and the distance from the DNA axis. Binding site boundaries were defined as the coordinates where the charge density drops to the half of its value at the maximum (see an example in Figure S8). We then counted the number of snapshots in the trajectory where the binding site was occupied by an ion. If the fraction of snapshots with bound ions was more than 0.1 of the total number of snapshots, the binding site was considered positive (occupied). If the binding pocket overlaps with the experimental binding site and it is positive, we call it ”true positive”. If a positive binding site does not overlap with any of the experimental sites, we call it ”false positive”.
3.10. Scoring the agreement with experimental K+ binding sites.
We count the number of true positive sites, and add 1 to it if the trajectory does not contain false positive sites. Then, we divide this score by 15 (the total number of experimental binding sites), and multiply by 100. The resulting score is percent agreement with the experimental data, see Table S6.
Supplementary Material
Acknowledgement
The authors thank Loren Dean Williams for an illuminating discussion on the limitations of experimental characterization of K+ binding sites in dsDNA. Funding from NIH R21GM134404 to A.V.O. is acknowledged. I.Yu.G. is supported by the Ministry of Science and Higher Education of the Russian Federation (agreement #075-00337-20-03, project FSMG-2020-0003). Authors also thank Khalid Mustafin for technical help.
Footnotes
Supporting Information Available
Supporting information contains Supporting Figures S1–S9 and Supporting Tables S1–S11 with detailed data on the ion distributions in simulations, as well as Supporting Text with a comparison of sodium and potassium behavior around the Drew-Dickerson dodecamer, and a comparison of the ion distributions around DNA obtained using different force fields. It also contains protocols of estimation of statistical errors and occupancies of potassium binding sites. This information is available free of charge via the Internet at http://pubs.acs.org
References
- (1).Sharp KA; Honig B Salt effects on nucleic acids. Current Opinion in Structural Biology 1995, 5, 323–328. [DOI] [PubMed] [Google Scholar]
- (2).Peters J; Maher J DNA curvature and flexibility in vitro and in vivo. Quarterly Reviews of Biophysics 2010, 43, 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Mocci F; Laaksonen A Insight into nucleic acid counterion interactions from inside molecular dynamics simulations is “worth its salt”. Soft Matter 2012, 8, 9268–9284. [Google Scholar]
- (4).Wilson RW; Bloomfield VA Counterion-induced condensation of deoxyribonucleic acid. A light-scattering study. Biochemistry 1979, 18, 2192–2196. [DOI] [PubMed] [Google Scholar]
- (5).Bloomfield VA Condensation of DNA by multivalent cations: Considerations on mechanism. Biopolymers 1991, 31, 1471–1481. [DOI] [PubMed] [Google Scholar]
- (6).Bloomfield VA DNA condensation by multivalent cations. Biopolymers 1997, 44, 269–282. [DOI] [PubMed] [Google Scholar]
- (7).Wong GCL; Pollack L Electrostatics of strongly charged biological polymers: ionmediated interactions and self-organization in nucleic acids and proteins. Annual review of physical chemistry 2010, 61, 171–189. [DOI] [PubMed] [Google Scholar]
- (8).Widom J; Baldwin RL Cation-induced toroidal condensation of DNA studies with Co3+(NH3)6. Journal of molecular biology 1980, 144, 431–453. [DOI] [PubMed] [Google Scholar]
- (9).Zinchenko AA; Yoshikawa K Na+ shows a markedly higher potential than K+ in DNA compaction in a crowded environment. Biophysical journal 2005, 88, 4118—4123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Luger K; Mäder AW; Richmond RK; Sargent DF; Richmond TJ Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature 1997, 389, 251–260. [DOI] [PubMed] [Google Scholar]
- (11).Borodavka A; Tuma R; Stockley PG Evidence that viral RNAs have evolved for efficient, two-stage packaging. Proceedings of the National Academy of Sciences 2012, 109, 15769–15774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Garmann RF; Comas-Garcia M; Gopal A; Knobler CM; Gelbart WM The Assembly Pathway of an Icosahedral Single-Stranded RNA Virus Depends on the Strength of Inter-Subunit Attractions. Journal of Molecular Biology 2014, 426, 1050–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Agrawal N; Dasaradhi PV; Mohmmed A; Malhotra P; Bhatnagar R; Mukherjee S RNA Interference: Biology, Mechanism, and Applications. Microbiology and Molecular Biology Reviews 2003, 67, 657–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Mansoori B; Sandoghchian S; Shotorbani B; Baradaran B RNA Interference and its Role in Cancer Therapy. advanced pharmaceutical bulletin 2014, 4, 313–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Hassett KJ; Benenato KE; Jacquinet E; Lee A; Woods A; Yuzhakov O; Hi-mansu S; Deterling J; Geilich BM; Ketova T; Mihai C; Lynn A; McFadyen I; Moore MJ; Senn JJ; Stanton MG; Almarsson Ö; Ciaramella G; Brito LA Optimization of Lipid Nanoparticles for Intramuscular Administration of mRNA Vaccines. Molecular Therapy - Nucleic Acids 2019, 15, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).McKay PF; Hu K; Blakney AK; Samnuan K; Brown JC; Penn R; Zhou J; Bouton CR; Rogers P; Polra K; Lin PJC; Barbosa C; Tam YK; Barclay WS; Shattock RJ Self-amplifying RNA SARS-CoV-2 lipid nanoparticle vaccine candidate induces high neutralizing antibody titers in mice. Nature Communications 2020, 11, 3523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Sahin U; Muik A; Derhovanessian E; Vogler I; Kranz LM; Vormehr M; Baum A; Pascal K; Quandt J; Maurus D; Brachtendorf S; Lörks V; Sikorski J; Hilker R; Becker D; Eller A-K; Grützner J; Boesler C; Rosenbaum C; Kühnle M-C; Luxemburger U; Kemmer-Brück A; Langer D; Bexon M; Bolte S; Karikó K; Palanche T; Fischer B; Schultz A; Shi P-Y; Fontes-Garfias C; Perez JL; Swanson KA; Loschko J; Scully IL; Cutler M; Kalina W; Kyrat-sous CA; Cooper D; Dormitzer PR; Jansen KU; Türeci Ö. COVID-19 vaccinë BNT162b1 elicits human antibody and TH1 T cell responses. Nature 2020, 586, 594–599. [DOI] [PubMed] [Google Scholar]
- (18).Drozdetski A; Tolokh I; Pollack L; Baker N; Onufriev A Opposing Effects of Multivalent Ions on the Flexibility of DNA and RNA. Physical Review Letters 2016, 117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Wenner JR; Williams MC; Rouzina I; Bloomfield VA Salt Dependence of the Elasticity and Overstretching Transition of Single DNA Molecules. Biophysical Journal 2002, 82, 3160–3169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Feig M; Pettitt BM Sodium and Chlorine Ions as Part of the DNA Solvation Shell. Biophysical Journal 1999, 77, 1769–1781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Howerton SB; Sines CC; VanDerveer D; Williams LD Locating Monovalent Cations in the Grooves of B-DNA,. Biochemistry 2001, 40, 10023–10031. [DOI] [PubMed] [Google Scholar]
- (22).Bhattacharyya D; Mirihana Arachchilage G; Basu S Metal Cations in G-Quadruplex Folding and Stability. Frontiers in Chemistry 2016, 4, 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Auffinger P; Bielecki L; Westhof E Symmetric K+ and Mg2+ Ion-binding Sites in the 5S rRNA Loop E Inferred from Molecular Dynamics Simulations. Journal of Molecular Biology 2004, 335, 555 – 571. [DOI] [PubMed] [Google Scholar]
- (24).Krasovska MV; Sefcikova J; Réblová K; Schneider B; Walter NG; Sponer J Cations and hydration in catalytic RNA: molecular dynamics of the hepatitis delta virus ribozyme. Biophysical journal 2006, 91, 626—638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Ke A; Ding F; Batchelor JD; Doudna JA Structural roles of monovalent cations in the HDV ribozyme. Structure 2007, 15, 281—287. [DOI] [PubMed] [Google Scholar]
- (26).Manning GS Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions II. Self-Diffusion of the Small Ions. The Journal of Chemical Physics 1969, 51, 934–938. [Google Scholar]
- (27).Tolokh I; Pabit S; Katz A; Chen A; Drozdetski A; Baker N; Pollack L; Onufriev A Why double-stranded RNA resists condensation. Nucleic acids research 2014, 42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Katz AM; Tolokh IS; Pabit SA; Baker N; Onufriev AV; Pollack L Spermine Condenses DNA, but Not RNA Duplexes. Biophysical Journal 2017, 112, 22–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Das R; Mills TT; Kwok LW; Maskel GS; Millett IS; Doniach S; Finkelstein KD; Herschlag D; Pollack L Counterion Distribution around DNA Probed by Solution X-Ray Scattering. Phys. Rev. Lett 2003, 90, 188103. [DOI] [PubMed] [Google Scholar]
- (30).Savelyev A; MacKerell AD Jr Differential Impact of the Monovalent Ions Li+, Na+, K+, and Rb+ on DNA Conformational Properties. The journal of physical chemistry letters 2015, 6, 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Shui X; Sines CC; McFail-Isom L; VanDerveer D; Williams LD Structure of the Potassium Form of CGCGAATTCGCG: DNA Deformation by Electrostatic Collapse around Inorganic Cations,. Biochemistry 1998, 37, 16877–16887. [DOI] [PubMed] [Google Scholar]
- (32).Hud NV; Sklenář V; Feigon J Localization of ammonium ions in the minor groove of DNA duplexes in solution and the origin of DNA A-tract bending. Journal of Molecular Biology 1999, 286, 651 – 660. [DOI] [PubMed] [Google Scholar]
- (33).Cheng Y; Korolev N; Nordenskiold L Similarities and differences in interaction of K+ and Na+ with condensed ordered DNA. A molecular dynamics computer simulation study. Nucleic Acids Res 2006, 34, 686–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Korolev N How potassium came to be the dominant biological cation: of metabolism, chemiosmosis, and cation selectivity since the beginnings of life. Bioessays 2021, 43, e2000108. [DOI] [PubMed] [Google Scholar]
- (35).Young MA; Jayaram B; Beveridge DL Intrusion of Counterions into the Spine of Hydration in the Minor Groove of B-DNA: Fractional Occupancy of Electronegative Pockets. Journal of the American Chemical Society 1997, 119, 59–69. [Google Scholar]
- (36).McConnell KJ; Beveridge DL DNA Structure: What’s in Charge? Journal of Molecular Biology 2000, 304, 803–820. [DOI] [PubMed] [Google Scholar]
- (37).Auffinger P; Westhof E Water and ion binding around RNA and DNA (C,G) oligomers. Journal of molecular biology 2000, 300, 1113–1131. [DOI] [PubMed] [Google Scholar]
- (38).Rueda M; Cubero E; Laughton CA; Orozco M Exploring the counterion atmosphere around DNA: what can be learned from molecular dynamics simulations? Biophysical journal 2004, 87, 800–811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Várnai P; Zakrzewska K DNA and its counterions: a molecular dynamics study. Nucleic acids research 2004, 32, 4269–4280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Dixit SB; Mezei M; Beveridge DL Studies of base pair sequence effects on DNA solvation based on all-atom molecular dynamics simulations. Journal of biosciences 2012, 37, 399–421. [DOI] [PubMed] [Google Scholar]
- (41).Galindo-Murillo R; Cheatham TE Lessons learned in atomistic simulation of double-stranded DNA: Solvation and salt concerns [Article v1.0]. Living journal of computational molecular science 2019, 1, 9974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).McFail-Isom L; Sines CC; Williams LD DNA structure: cations in charge? Current Opinion in Structural Biology 1999, 9, 298–304. [DOI] [PubMed] [Google Scholar]
- (43).Onufriev AV; Izadi S Water models for biomolecular simulations. WIREs Computational Molecular Science 2018, 8, e1347. [Google Scholar]
- (44).William LJ; Jayaraman C; Jeffry DM; Roger WI; Klein ML Comparison of simple potential functions for simulating liquid water. The Journal of Chemical Physics 1983, 79, 926–935. [Google Scholar]
- (45).Berendsen HJC; Grigera JR; Straatsma TP The missing term in effective pair potentials. The Journal of Physical Chemistry 1987, 91, 6269–6271. [Google Scholar]
- (46).Mahoney MW; Jorgensen WL A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. The Journal of Chemical Physics 2000, 112, 8910–8922. [Google Scholar]
- (47).Izadi S; Anandakrishnan R; Onufriev AV Building Water Models: A Different Approach. The Journal of Physical Chemistry Letters 2014, 5, 3863–3871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Wang LP; Martinez TJ; Pande VS Building Force Fields: An Automatic, Systematic, and Reproducible Approach. J Phys Chem Lett 2014, 5, 1885–1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Joung IS; Cheatham TE Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. The Journal of Physical Chemistry B 2008, 112, 9020–9041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Li P; Song LF; Merz KM Parameterization of Highly Charged Metal Ions Using the 12–6-4 LJ-Type Nonbonded Model in Explicit Water. The Journal of Physical Chemistry B 2015, 119, 883–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Li P; Song LF; Merz KM Systematic Parameterization of Monovalent Ions Employing the Nonbonded Model. Journal of Chemical Theory and Computation 2015, 11, 1645–1657. [DOI] [PubMed] [Google Scholar]
- (52).Galindo-Murillo R; Robertson JC; Zgarbová M; Šponer J; Otyepka M; Jurečka P; Cheatham TE 3rd Assessing the Current State of Amber Force Field Modifications for DNA. Journal of chemical theory and computation 2016, 12, 4114–4127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Bergonzo C; Cheatham TE Improved Force Field Parameters Lead to a Better Description of RNA Structure. Journal of Chemical Theory and Computation 2015, 11, 3969–3972. [DOI] [PubMed] [Google Scholar]
- (54).Yang C; Lim M; Kim E; Pak Y Predicting RNA Structures via a Simple van der Waals Correction to an All-Atom Force Field. Journal of Chemical Theory and Computation 2017, 13, 395–399. [DOI] [PubMed] [Google Scholar]
- (55).Shabane PS; Izadi S; Onufriev AV General Purpose Water Model Can Improve Atomistic Simulations of Intrinsically Disordered Proteins. Journal of Chemical Theory and Computation 2019, 15, 2620–2634. [DOI] [PubMed] [Google Scholar]
- (56).Sengupta A; Li Z; Song LF; Li P; Merz KM Parameterization of Monovalent Ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models. Journal of Chemical Information and Modeling 2021, 61, 869–880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Case D; Ben-Shalom I; Brozell S; Cerutti D; Cheatham T; V. C III; Darden T; Duke R; Ghoreishi D; Giambasu G; Giese T; Gilson M; Gohlke H; Goetz A; Greene D; Harris R; Homeyer N; Huang Y; Izadi S; Kovalenko A; Krasny R; Kurtzman T; Lee T; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Man V; Mermelstein D; Merz K; Miao Y; Monard G; Nguyen C; Nguyen H; Onufriev A; Pan F; Qi R; Roe D; Roitberg A; Sagui C; Schott-Verdugo S; Shen J; Simmerling C; Smith J; Swails J; Walker R; Wang J; Wei H; Wilson L; Wolf R; Wu X; Xiao L; Xiong Y; York D; Kollman P. AMBER 2019; 2019.
- (58).Bai Y; Greenfeld M; Travers KJ; Chu VB; Lipfert J; Doniach S; Herschlag D Quantitative and Comprehensive Decomposition of the Ion Atmosphere around Nucleic Acids. Journal of the American Chemical Society 2007, 129, 14981–14988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Korolev N; Lyubartsev AP; Rupprecht A; Nordenskïold L. Competitive Binding of Mg2+ , Ca2+, Na+, and K+ Ions to DNA in Oriented DNA Fibers: Experimental and Monte Carlo Simulation Results. Biophysical Journal 1999, 77, 2736–2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Anderson CF; Record MT Ion Distributions Around DNA and other Cylindrical Polyions: Theoretical Descriptions and Physical Implications. Annual Review of Biophysics and Biophysical Chemistry 1990, 19, 423–463. [DOI] [PubMed] [Google Scholar]
- (61).Hansen PL; Podgornik R; Parsegian VA Osmotic properties of DNA: Critical evaluation of counterion condensation theory. Physical Review E 2001, 64, 021907. [DOI] [PubMed] [Google Scholar]
- (62).Stigter D Evaluation of the counterion condensation theory of polyelectrolytes. Biophysical Journal 1995, 69, 380–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Sushko M; Thomas D; Pabit S; Pollack L; Onufriev A; Baker N The Role of Correlation and Solvation in Ion Interactions with B-DNA. Biophysical Journal 2016, 110, 315–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Joung IS; Cheatham TE 3rd Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. The journal of physical chemistry. B 2009, 113, 13279–13290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Korolev N; Lyubartsev AP; Rupprecht A; Nordenskïold, L. Competitive substitution of hexammine cobalt(III) for Na+ and K+ ions in oriented DNA fibers. Biopolymers 2001, 58, 268–278. [DOI] [PubMed] [Google Scholar]
- (66).Pascal A; D’Ascenzo L; Ennifar E Sodium and Potassium Interactions with Nucleic Acids; 2016; pp 167–201. [DOI] [PubMed] [Google Scholar]
- (67).Shui X; McFail-Isom L; Hu GG; Williams LD The B-DNA Dodecamer at High Resolution Reveals a Spine of Water on Sodium,. Biochemistry 1998, 37, 8341–8355. [DOI] [PubMed] [Google Scholar]
- (68).Yoo J; Aksimentiev A Improved Parameterization of Amine–Carboxylate and Amine–Phosphate Interactions for Molecular Dynamics Simulations Using the CHARMM and AMBER Force Fields. Journal of Chemical Theory and Computation 2016, 12, 430–443. [DOI] [PubMed] [Google Scholar]
- (69).Yoo J; Aksimentiev A Improved Parametrization of Li+, Na+, K+, and Mg2+ Ions for All-Atom Molecular Dynamics Simulations of Nucleic Acid Systems. The Journal of Physical Chemistry Letters 2012, 3, 45–50. [Google Scholar]
- (70).Yoo J; Aksimentiev A New tricks for old dogs: Improving the accuracy of biomolecular force fields by pair-specific corrections to non-bonded interactions. Physical Chemistry Chemical Physics 2018, 20, 8432–8449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Pack GR; Lamm G Counterion condensation theory revisited: Limits on its applicability. International Journal of Quantum Chemistry 1993, 48, 213–230. [Google Scholar]
- (72).Kirmizialtin S; Silalahi A; Elber R; Fenley M The Ionic Atmosphere around ARNA: Poisson-Boltzmann and Molecular Dynamics Simulations. Biophysical Journal 2012, 102, 829–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Deserno M; Holm C; May S Fraction of Condensed Counterions around a Charged Rod: Comparison of Poisson-Boltzmann Theory and Computer Simulations. Macromolecules 2000, 33, 199–206. [Google Scholar]
- (74).O’Shaughnessy B; Yang Q Manning-Oosawa Counterion Condensation. Phys. Rev. Lett 2005, 94, 48302. [DOI] [PubMed] [Google Scholar]
- (75).Maehigashi T; Hsiao C; Kruger Woods K; Moulaei T; Hud NV; Dean Williams L B-DNA structure is intrinsically polymorphic: even at the level of base pair positions. Nucleic Acids Research 2011, 40, 3714–3722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Pérez A; Marchán I; Svozil; Sponer J; Cheatham TE; Laughton CA; Orozco M Refinement of the AMBER Force Field for Nucleic Acids: Improving the Description of alpha/gamma Conformers. Biophysical Journal 2007, 92, 3817 – 3829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (77).Case DA; Cheatham TE 3rd; Darden T; Gohlke H; Luo R; Merz KM Jr; Onufriev A; Simmerling C; Wang B; Woods RJ The Amber biomolecular simulation programs. Journal of computational chemistry 2005, 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Macke TJ; Case DA Molecular Modeling of Nucleic Acids; ACS Symposium Series; American Chemical Society, 1997; Vol. 682; pp 24–379. [Google Scholar]
- (79).Schmit JD; Kariyawasam NL; Needham V; Smith PE SLTCAP: A Simple Method for Calculating the Number of Ions Needed for MD Simulation. Journal of Chemical Theory and Computation 2018, 14, 1823–1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Richard L; John HM; Marco P; Krystyna Z Analyzing ion distributions around DNA. Nucleic Acids Research 2015, 42, 8138–8149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).van der Walt S; Colbert SC; Varoquaux G The NumPy Array: A Structure for Efficient Numerical Computation. Computing in Science Engineering 2011, 13, 22–30. [Google Scholar]
- (82).Chen CR; Makhatadze GI ProteinVolume: calculating molecular van der Waals and void volumes in proteins. BMC Bioinformatics 2015, 16, 101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Yoo J; Aksimentiev A Competitive Binding of Cations to Duplex DNA Revealed through Molecular Dynamics Simulations. The Journal of Physical Chemistry B 2012, 116, 12946–12954. [DOI] [PubMed] [Google Scholar]
- (84).Straatsma T; Berendsen H; Stam A Estimation of statistical errors in molecular simulation calculations. Molecular Physics 1986, 57, 89–95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


