A COMPARISON OF PRINCIPAL COMPONENT METHODS BETWEEN MULTIPLE PHENOTYPE REGRESSION AND MULTIPLE SNP REGRESSION IN GENETIC ASSOCIATION STUDIES

Abstract

Principal component analysis (PCA) is a popular method for dimension reduction in unsupervised multivariate analysis. However, existing ad hoc uses of PCA in both multivariate regression (multiple outcomes) and multiple regression (multiple predictors) lack theoretical justification. The differences in the statistical properties of PCAs in these two regression settings are not well understood. In this paper we provide theoretical results on the power of PCA in genetic association testings in both multiple phenotype and SNP-set settings. The multiple phenotype setting refers to the case when one is interested in studying the association between a single SNP and multiple phenotypes as outcomes. The SNP-set setting refers to the case when one is interested in studying the association between multiple SNPs in a SNP set and a single phenotype as the outcome. We demonstrate analytically that the properties of the PC-based analysis in these two regression settings are substantially different. We show that the lower order PCs, that is, PCs with large eigenvalues, are generally preferred and lead to a higher power in the SNP-set setting, while the higher-order PCs, that is, PCs with small eigenvalues, are generally preferred in the multiple phenotype setting. We also investigate the power of three other popular statistical methods, the Wald test, the variance component test and the minimum $p$-value test, in both multiple phenotype and SNP-set settings. We use theoretical power, simulation studies, and two real data analyses to validate our findings.

1. Introduction.

In view of the rapid progression of massive data in genetic and genomic studies, developing statistical machinery to effectively leverage the correlation present in the data to boost analysis power becomes increasingly important. In this paper we focus on jointly testing multiple correlated quantities in two important settings which frequently arise in genetic association studies: the SNP-set setting, which tests for the association between a single phenotype and a set of single nucleotide polymorphisms (SNPs) in a genetic construct, for example, gene or network (Li and Leal (2008), Wu et al. (2011)), and the multiple phenotype setting, which tests for the association between a single SNP and multiple phenotypes, that is, pleiotropy (Aschard et al. (2014), Solovieff et al. (2013)). Despite having a similar set of statistical methods developed separately in each case, we explore the subtle but important differences in the methodology across the two cases. Specifically, principal component analysis (PCA) is a popular unsupervised dimension reduction method frequently used in both settings. However, little is known about how the performance of PCA differs in multiple phenotype regression as compared to multiple SNP regression, and when a PCA should be used in practice in each case as opposed to other methods, as well as which PC should be used. We investigate this problem in this paper.

There is an increasing interest to analyze multiple phenotypes jointly in genetic association studies to detect pleiotropic effects, as the power gain of joint analysis of multiple phenotypes has been demonstrated by several previous studies (Liu and Lin (2018, 2019), Schifano et al. (2013), Solovieff et al. (2013), Stephens (2013), Zhou and Stephens (2014), Zhu et al. (2015)). PCA has been used as a popular tool for dimension reduction in multiple phenotype analysis (Aschard et al. (2014), Karasik et al. (2012), Suo et al. (2013), Zhang et al. (2012), Liu and Lin (2019)). Aschard et al. (2014) found that combining multiple related phenotypes through their principal components identified significant top SNPs that were missed by individual phenotype association tests. Liu and Lin (2019) further proposed a series of PC based association tests for multiple phenotype studies using summary statistics from genome-wide association studies (GWASs).

In the case of a univariate phenotype outcome, SNPs in a genetic construct, such as gene or pathway, can be tested jointly which boosts analysis power by combining effects across multiple SNPs while also reducing the multiple testing burden. While true for GWASs, SNP-set testing is more important in sequencing studies where rare variant associations would be near impossible to detect without grouping signals within a SNP-set (Lee et al. (2014), Li and Leal (2008)). Due to linkage disequilibrium (LD), it is frequently the case that adjacent SNPs are in LD and correlated, complicating their joint analysis. There have been numerous statistical techniques developed for the purpose of properly accounting for LD/correlation when testing multiple SNPs simultaneously (Conneely and Boehnke (2007), Han, Kang and Eskin (2009), Moskvina and Schmidt (2008), Wu et al. (2011)). Dimension reduction can be a useful tool in these settings particularly for larger SNP-sets, and principal component regression is a commonly used dimension reduction approach for removing correlation among SNPs in a SNP-set, for example, a gene (Wang and Abbott (2008), Karacaören et al. (2011)). For example, in Karacaören et al. (2011), principal component regression was used in a QTL analysis to account for the LD between significant markers in a set of SNPs that was regressed on gene expression.

Despite its frequent usage throughout genetic association studies, there is little theoretical analysis on when using PCs is beneficial and when it is not in regression analysis, and how its performance differs in the multiple phenotype setting as compared to the multiple SNP setting. This renders PCA at the risk of potential power loss if used inappropriately. In this paper we investigate the circumstances under which PCA is effective in both the SNP-set and multiple phenotype settings. In addition, we address two other popular approaches in genetic epidemiology, variance component tests and min $p$-value tests. Upon first glance, all of these statistical methods have strong similarities across the two settings, but we will illuminate some crucial statistical differences.

In particular, we find that in the SNP-set setting, principal components with large eigenvalues tend to have increased power, whereas the opposite holds true in the multiple phenotype setting. The power of these methods are compared both theoretically and through simulation. In addition, we apply the concepts developed in this paper to both a lipids GWAS, which studies how a SNP affects multiple lipids, as well as a Breast Cancer GWAS by performing a gene-based analysis to study how the SNPs in a gene affect breast cancer risk. Henceforth, we refer to the SNP-set setting as “1:K” with reference its one outcome and $K$ predictors, and we similarly refer to the multiple phenotype setting as “K:1” for its $K$ outcomes and one predictor. In the 1:K setting, K usually represents the number of SNPs in a gene, while in the K:1 setting, K represents the number of phenotypes and is usually chosen based on the scientific question under study.

Section 2 compares the theoretical power of principal component tests in both the K:1 and 1:K settings. Section 3 discusses the crucial role of principal components in variance component tests, while again highlighting the stark differences between the K:1 and 1:K settings. Section 4 demonstrates these differences between the 1:K and K:1 settings through a series of power simulations. Finally, Section 5 shows these differences by comparing the analysis of two real data sets, one in the K:1 multiple phenotype setting (lipids GWAS) and one in the 1:K multiple SNP setting (breast cancer GWAS).

2. The power of PCA.

2.1. The K:1 multiple phenotype setting.

In the K:1 multiple phenotype setting, we consider testing the association between a particular SNP and a group of correlated phenotypes, that is, study pleiotropy. Suppose that we have measured $K$ continuous phenotypes on $n$ genotyped individuals. We first consider a model without covariates and then discuss the extension of the results to the covariate case. For the $i$th individual, we can use the following model to link a particular genotype to the $k$th phenotype:

$$Y_{ik}^{\left(P\right)}={\beta }_k^{\left(P\right)}{G}_i^{\left(P\right)}+{ϵ}_{ik}^{\left(P\right)},$$ (2.1)

where ${ϵ}_i^{\left(P\right)}={\left\{{ϵ}_{i1}^{\left(P\right)},\dots ,{ϵ}_{iK}^{\left(P\right)}\right\}}^T~N\left(0,{\Sigma }^{\left(P\right)}\right),Y_{ik}^{\left(P\right)}$ is the $k$th phenotype for the $i$th subject, $G_i^{\left(P\right)}$ is a scalar representing the genotype of a SNP of interest for the $i$th subject and ${\beta }_k^{\left(P\right)}$ is the regression coefficient for the genotype and the $k$th phenotype. We use the superscript $\left(P\right)$ to indicate this setting represents multiple phentoype regression and the K:1 setting. For notation simplicity, we assume that the $Y_{ik}^{\left(P\right)}$ have been standardized and the $G_i^{\left(P\right)}$ have been centered and scaled such that ${\sum }_{i=1}^n{\left\{G_i^{\left(P\right)}\right\}}^2=1$. Denote ${\beta }^{\left(P\right)}={\left\{{\beta }_1^{\left(P\right)},\dots ,{\beta }_K^{\left(P\right)}\right\}}^T$, $Y_k^{\left(P\right)}={\left\{Y_{1k}^{\left(P\right)},\dots ,Y_{nk}^{\left(P\right)}\right\}}^T$, and $G^{\left(P\right)}={\left\{G_1^{\left(P\right)},\dots ,G_n^{\left(P\right)}\right\}}^T$. To assess whether this particular SNP is associated with those $K$ phenotypes, we can formulate this problem as the following hypothesis testing:

$$H_0:{\beta }^{\left(P\right)}=0\text{ vs }{H}_1:{\beta }^{\left(P\right)}\ne 0.$$

Consider the following score statistics:

$$Z^{\left(P\right)}={\left\{Z_1^{\left(P\right)},Z_2^{\left(P\right)},\dots ,Z_K^{\left(P\right)}\right\}}^T,$$

where $Z_k^{\left(P\right)}={\left\{G^{\left(P\right)}\right\}}^T{Y}_k^{\left(P\right)}$ and its distribution is $Z_k^{\left(P\right)}~N\left\{{\mu }_k^{\left(P\right)},1\right\}$ where ${\mu }_k^{\left(P\right)}={\beta }_k^{\left(P\right)}$. For each fixed genetic variant, we have a random vector $Z^{\left(P\right)}={\left\{Z_1^{\left(P\right)},\dots ,Z_K^{\left(P\right)}\right\}}^T~N\left({\beta }^{\left(P\right)},{\Sigma }^{\left(P\right)}\right)$, where ${\mu }^{\left(P\right)}={\beta }^{\left(P\right)}$ is defined as the signal vector and does not depend on the correlation matrix. In what follows, we assume that the correlation matrix ${\Sigma }^{\left(P\right)}$ of $Z^{\left(P\right)}$ is known or can be consistently estimated. As sample sizes in GWAS are often large, the correlation matrix ${\Sigma }^{\left(P\right)}$ can be estimated very accurately using the GWAS phenotype-specific summary statistics and the bias and variance of the estimated ${\Sigma }^{\left(P\right)}$ have little effects on inference for ${\beta }^{\left(P\right)}$, and ${\Sigma }^{\left(P\right)}$ does not vary across SNPs (Liu and Lin (2018), Zhu et al. (2015)).

This correlation matrix ${\Sigma }^{\left(P\right)}$ can be decomposed as

$${\Sigma }^{\left(P\right)}=U^{\left(P\right)}{\Lambda }^{\left(P\right)}{\left\{U^{\left(P\right)}\right\}}^T=\sum _{k=1}^K{\lambda }_k^{\left(P\right)}{u}_k^{\left(P\right)}{\left\{u_k^{\left(P\right)}\right\}}^T,$$

where ${\Lambda }^{\left(P\right)}$ is a diagonal matrix $\text{diag}\left\{{\lambda }_1^{\left(P\right)},\dots ,{\lambda }_K^{\left(P\right)}\right\}$ whose elements represent the eigenvalues of ${\Sigma }^{\left(P\right)}$ and ${\lambda }_1^{\left(P\right)}\ge {\lambda }_2^{\left(P\right)}\ge \cdots \ge {\lambda }_K^{\left(P\right)}>0$, and $U^{\left(P\right)}$ is the normalized orthogonal matrix whose $k$th column $u_k^{\left(P\right)}$ represents the $k$th eigenvector associated with the $k$th largest eigenvalue. Then, the distribution of the portion of $Z^{\left(P\right)}$ along the $k$th principal component is given by

$$V_k^{\left(P\right)}={\left\{u_k^{\left(P\right)}\right\}}^T{Z}^{\left(P\right)}~N\left\{{\left(u_k^{\left(P\right)}\right)}^T{\beta }^{\left(P\right)},{\lambda }_k^{\left(P\right)}\right\},1\le k\le K.$$

There is a relationship between the principal components of the score test statistics $Z^{\left(P\right)}$ and the principal compoents of the $K$ phenotypes: Let $Y^{\left(P\right)}=\left(Y_1^{\left(P\right)},\dots ,Y_K^{\left(P\right)}\right)$ be the $n\times K$ phenotype matrix and note that $V_k^{\left(P\right)}={\left(Y^{\left(P\right)}{u}_k^{\left(P\right)}\right)}^T{G}^{\left(P\right)}={\left\{{\text{PC}}_k^{\left(P\right)}\right\}}^T{G}^{\left(P\right)}$, where ${\text{PC}}_k^{\left(P\right)}=Y^{\left(P\right)}{u}_k^{\left(P\right)}$ is the $k$th principal component of the $K$ phenotypes. This suggests that if one performs PCA analysis of the $K$ phenotypes and transforms the $K$ phenotypes $\left(Y_1^{\left(P\right)},\dots ,Y_K^{\left(P\right)}\right)$ to $K$ independent phenotype $\text{PCs}\left\{{\text{PC}}_1^{\left(P\right)},\dots ,{\text{PC}}_K^{\left(P\right)}\right\}$, then $V_k^{\left(P\right)}$ is equal to the score statistic obtained by regressing the $k$th phenotype ${\text{PC}}_k^{\left(P\right)}$ on the genotype $G^{\left(P\right)}$. This implies that whether a PC decomposition is done before or after testing, the resulting inference is the same.

Using the fact that ${\Vert u_k^{\left(P\right)}\Vert }^2=1$, the noncentrality parameter (ncp) of the $k$th phenotype $\text{PC}{V}_k^{\left(P\right)}$ under the alternative hypothesis is

$$\frac{{\left[{\left\{u_k^{\left(P\right)}\right\}}^T{\beta }^{\left(P\right)}\right]}^2}{{\lambda }_k^{\left(P\right)}}=\frac{{\Vert {\beta }^{\left(P\right)}\Vert }^2{\left\{\text{cos}\left({\theta }_k^{\left(P\right)}\right)\right\}}^2}{{\lambda }_k^{\left(P\right)}},$$

where ${\theta }_k^{\left(P\right)}$ is the $k$th principal angle defined as the angle between ${\beta }^{\left(P\right)}$ and the eigenvector $u_k^{\left(P\right)}$ first introduced by Liu and Lin (2019). Because the $k$th eigenvalue enters into the denominator of the $k$th ncp, excluding the effect of ${\theta }_k^{\left(P\right)}$, the first PC test statistic $V_1^{\left(P\right)}$ has the smallest ncp compared to the other PCs.

If we use $V_k^{\left(P\right)}$ as a testing statistic for the hypothesis $H_0:{\beta }^{\left(P\right)}=0$ vs. $H_a:{\beta }^{\left(P\right)}\ne 0$, then its theoretical power at significance level $\alpha$ is

$$\text{pr}\left(\left|V_k^{\left(P\right)}\right|>z_{1-\frac{\alpha }{2}}\mid H_a\right)=\Phi \left(z\frac{\alpha }{2}+\frac{\Vert {\beta }^{\left(P\right)}\Vert \cdot \left|\text{cos}\left({\theta }_k^{\left(P\right)}\right)\right|}{\sqrt{{\lambda }_k^{\left(P\right)}}}\right)+\Phi \left(z_{\frac{\alpha }{2}}-\frac{\Vert {\beta }^{\left(P\right)}\Vert \cdot \left|\text{cos}\left({\theta }_k^{\left(P\right)}\right)\right|}{\sqrt{{\lambda }_k^{\left(P\right)}}}\right),$$ (2.2)

where $\Phi (\cdot )$ is the cumulative distribution function of a standard normal random variable, and $z_{\alpha }$ is its $\alpha$ percentile. The power of this test depends on both the $k$th principal angle and the $k$th eigenvalue. Specifically, the test statistic $V_k^{\left(P\right)}$ is powerful if ${\theta }_k^{\left(P\right)}=0$ but is powerless if ${\theta }_k^{\left(P\right)}={90}^{\circ }$ (i.e., when $u_k^{\left(P\right)}$ is orthogonal to ${\beta }^{\left(P\right)}$), and the phenotype PCs with smaller eignvalues, that is, $V_k^{\left(P\right)}$ with larger $k$, are more likely to be powerful. This geometric perspective offered by equation (2.2) demonstrates why the test based on the first PC, without taking the true direction of $\beta$ into account, will have the least power of all the $K$ PCs in the K:1 setting due to it having the largest eigenvalue.

2.2. The 1:K SNP-set setting.

The difficulty of detecting single SNP effects in GWAS due to the tremendous multiple comparisons problem and weak SNP effects can be alleviated by changing the unit of analysis from a single SNP to meaningful groupings of SNPs. The most common choice of these groupings, or SNP-sets, is to combine the analysis of SNPs in the same gene. The number of SNPs in most GWAS is approximately 20 times larger than the number of genes, and therefore the multiple comparisons burden is greatly reduced by analyzing SNPs grouped by gene membership. Another benefit of analyzing SNP-set is the power gain by aggregating weak signal effects of multiple SNPs in a set, which is now becoming standard for rare variant association testings (Lee et al. (2014)).

A strong effort has been made to develop statistical methods for association testing in the SNP-set context. One primary difficulty is that often SNPs within the same gene are in LD. One popular approach uses a principal component decomposition in order to orthogonalize the genotype matrix. We outline and analyze this approach more closely here.

Consider the 1:K linear model, where a scalar phenotype $Y_i^{\left(S\right)}$ is regressed on $K$ SNPs in a SNP set $G_i^{\left(S\right)}={\left\{G_{i1}^{\left(S\right)},\dots ,G_{iK}^{\left(S\right)}\right\}}^T$ as

$$Y_i^{\left(S\right)}={\beta }_1^{\left(S\right)}{G}_{i1}^{\left(S\right)}+\cdots +{\beta }_K^{\left(S\right)}{G}_{iK}^{\left(S\right)}+{ϵ}_i^{\left(S\right)},$$ (2.3)

where ${ϵ}_i^{\left(S\right)}~N\left\{0,{\left({\sigma }^{\left(S\right)}\right)}^2\right\}$. We set $Y^{\left(S\right)}={\left\{Y_1^{\left(S\right)},\dots ,Y_n^{\left(S\right)}\right\}}^T$ to be the standardized phenotype vector and $G^{\left(S\right)}$ to be the $n$ by $K$ matrix of genotypes with columns centered and scaled such that ${\sum }_{i=1}^n{\left\{G_{ik}^{\left(S\right)}\right\}}^2=1$ for each $k$. We here use the superscript $\left(S\right)$ to indicate this setting represents 1:K SNP-set regression. Our goal is to test whether a group of SNPs $G_i^{\left(S\right)}$ is associated with the scalar phenotype $Y_i^{\left(S\right)}$, that is, to test the null hypothesis $H_0:{\beta }^{\left(S\right)}=0$ vs. $H_1:{\beta }^{\left(S\right)}\ne 0$, where ${\beta }^{\left(S\right)}={\left\{{\beta }_1^{\left(S\right)},\dots ,{\beta }_K^{\left(S\right)}\right\}}^T$.

Based on model (2.3), the score test statistic for ${\beta }^{\left(S\right)}$ is $Z^{\left(S\right)}={\left\{G^{\left(S\right)}\right\}}^T{Y}^{\left(S\right)}~N\left\{{\mu }^{\left(S\right)},{\Sigma }^{\left(S\right)}\right\}$, where ${\Sigma }^{\left(S\right)}={\left\{G^{\left(S\right)}\right\}}^T{G}^{\left(S\right)}$ is a $K\times K$ correlation matrix of the $K$ SNPs in a SNP set, and ${\mu }^{\left(S\right)}={\Sigma }^{\left(S\right)}{\beta }^{\left(S\right)}$. Note the covariance matrix ${\Sigma }^{\left(S\right)}$ appears in both the mean and the covariance of $Z^{\left(S\right)}$, while ${\Sigma }^{\left(P\right)}$ appears only in the covariance of $Z^{\left(P\right)}$.

Using spectral decomposition, we have

$${\Sigma }^{\left(S\right)}=U^{\left(S\right)}{\Lambda }^{\left(S\right)}{\left\{U^{\left(S\right)}\right\}}^T,$$

where $U^{\left(S\right)}$ is the eigenvector matrix whose $k$th column $u_k^{\left(S\right)}$ represents the $k$th eigenvector of ${\Sigma }^{\left(S\right)}$ and ${\Lambda }^{\left(S\right)}=\text{diag}\left\{{\lambda }_1^{\left(S\right)},\dots ,{\lambda }_K^{\left(S\right)}\right\}$ is a diagonal matrix whose diagonal elements are the ordered eigenvalues of ${\Sigma }^{\left(S\right)}$. Define $V_k^{\left(S\right)}$ as the portion of $Z^{\left(S\right)}$ along the $k$th principal component,

$$V_k^{\left(S\right)}={\left\{u_k^{\left(S\right)}\right\}}^T{Z}^{\left(S\right)}={\left\{G^{\left(S\right)}{u}_k^{\left(S\right)}\right\}}^T{Y}^{\left(S\right)}~N\left[{\lambda }_k^{\left(S\right)}{\left\{u_k^{\left(S\right)}\right\}}^T{\beta }^{\left(S\right)},{\lambda }_k^{\left(S\right)}\right].$$ (2.4)

In fact, suppose we first perform principal component analysis on the genotype matrix $G^{\left(S\right)}$ and obtain ${\text{PC}}_{ik}^{\left(S\right)}={\left\{G_i^{\left(S\right)}\right\}}^T{u}_k^{\left(S\right)}$, which is the $k$th principal component of the SNP-set of the $i$th subject. Then, regress $Y^{\left(S\right)}$ on these $K$ orthogonal genotype principal components as

$$Y_i^{\left(S\right)}={\gamma }_1^{\left(S\right)}{\text{PC}}_{i1}^{\left(S\right)}+\cdots +{\gamma }_K^{\left(S\right)}{\text{PC}}_{iK}^{\left(S\right)}+{ϵ}_i^{*},$$ (2.5)

where ${ϵ}_i^{*}~N\left(0,{\sigma }^{*2}\right)$. Then testing whether the set of SNPs $G_i^{\left(S\right)}$ is associated with the scalar phenotype $Y_i^{\left(S\right)}$, that is, testing the null hypothesis $H_0:{\beta }^{\left(S\right)}=0$ vs. $H_1:{\beta }^{\left(S\right)}\ne 0$ is equivalent to testing the null hypothesis $H_0:{\gamma }^{\left(S\right)}=0$ vs. $H_1:{\gamma }^{\left(S\right)}\ne 0$, where ${\gamma }^{\left(S\right)}={\left\{{\gamma }_1^{\left(S\right)},\dots ,{\gamma }_K^{\left(S\right)}\right\}}^T$. In other words, inference is the same for SNP-principal component regression as it is for the score tests on the original scale.

The power of using $V_k^{\left(S\right)}$ as a testing statistic is

$$\text{pr}\left\{\left|V_k^{\left(S\right)}\right|>z_{1-\frac{\alpha }{2}}\right\}=\Phi \left(z_{\frac{\alpha }{2}}+\sqrt{{\lambda }_k^{\left(S\right)}}{\left\{u_k^{\left(S\right)}\right\}}^T{\beta }^{\left(S\right)}\right)+\Phi \left(z_{\frac{\alpha }{2}}-\sqrt{{\lambda }_k^{\left(S\right)}}{\left\{u_k^{\left(S\right)}\right\}}^T{\beta }^{\left(S\right)}\right).$$ (2.6)

Analagous to the K:1 multiple phenotype regression setting, we have

$${\left\{u_k^{\left(S\right)}\right\}}^T{\beta }^{\left(S\right)}={\beta }^{\left(S\right)}\text{cos}\left({\theta }_k^{\left(S\right)}\right),$$

where ${\theta }_k^{\left(S\right)}$ is the principal angle between the $k$th eigenvector of ${\Sigma }^{\left(S\right)}$ and the effect vector ${\beta }^{\left(S\right)}$. If ${\theta }_k^{\left(S\right)}={90}^{\circ }$, then $V_k^{\left(S\right)}$ is powerless, and if ${\theta }_k^{\left(S\right)}=0$, then $V_k^{\left(S\right)}$ is powerful. This implies that a larger eigenvalue ${\lambda }_k^{\left(S\right)}$ leads to larger power, and the power is highest when ${\theta }_1^{\left(S\right)}=0$. This is the opposite of the conclusion found in the K:1 setting. This result shows that, for 1:K SNP-set regression, the PCs of SNPs with large eigenvalues have more power for detecting genetic association.

2.3. Differences and connections between 1:K and K:1 problems.

In both 1:K multiple SNP regression and K:1 multiple phenotype settings, we aim to test for the overall association between one variable and $K$ variables. In the 1:K SNP set setting, the PCA analysis is conducted on the genotype matrix to obtain orthogonal PC genotype scores, and then we can regress the scalar phenotype variable on those genotype PCs jointly. In the K:1 multiple phenotype setting, we first apply PCA on the multiple phenotypes and obtain orthogonal phenotype PCs and then regress each phenotype PC on the single SNP genotype variable.

There is an important difference when applying PCA in these two settings: correlation between explanatory variables has a different effect on inference than does correlation between outcome variables. In the K:1 setting, the $K$ variables are multiple phenotypes which are put on the left-hand side of the regression model as outcomes, and the one explanatory variable is the SNP genotype which is put on the right-hand side of the regression model. In contrast, in the 1:K setting there are $K$ explanatory variables, the multiple SNPs in the SNP-set, which are put on the right hand-side of the regression, while the one phenotype is still on the only outcome on the left-hand side of the regression model.

This difference leads to an asymmetry between the two settings. In the K:1 multiple phenotype regression setting, the correlation matrix among multiple phenotypes influences only the correlation matrix of the score testing statistics and has no influence on its mean vector, as the test statistic is $Z^{\left(P\right)}~N\left\{{\beta }^{\left(S\right)},{\Sigma }^{\left(P\right)}\right\}$. However, in the 1:K SNP-set regression setting the correlation matrix (LD) among the $K$ SNPs influences both the mean vector and correlation matrix of the score testing statistics, as the test statistic is $Z^{\left(S\right)}~N\left\{{\Sigma }^{\left(S\right)}{\beta }^{\left(S\right)},{\Sigma }^{\left(S\right)}\right\}$. This occurs because the Gaussian likelihood accounts for correlation between multivariate outcomes differently than it does for correlation between multiple explanatory variables, leading to the differences we see in the score equations and corresponding test statistics.

2.4. Extension to allow for covariate adjustment.

2.4.1. The K:1 setting.

In many cases covariates are included in the model to adjust for potential confounding factors. Suppose we denote the $q$-dimensional centered covariate row vector for individual $i$ as $X_i^{\left(P\right)}$, then we can model the relationship between genotype and phenotype adjusted for covariates as

$$Y_{ik}^{\left(P\right)}=X_i^{\left(P\right)}{\alpha }_k^{\left(P\right)}+G_i^{\left(P\right)}{\beta }_k^{\left(P\right)}+{ϵ}_{ik}^{\left(P\right)},$$ (2.7)

where ${\alpha }_k^{\left(P\right)}={\left\{{\alpha }_{k1},\dots ,{\alpha }_{kq}\right\}}^T$ are the covariate regression coefficients. Under $H_0:{\beta }^{\left(P\right)}=0$, the score test statistics are

$$Z_k^{\left(P\right)}={\left(G^{\left(P\right)}\right)}^T\left(Y_k^{\left(P\right)}-X^{\left(P\right)}{\widehat{\alpha }}_k^{\left(P\right)}\right),$$ (2.8)

where ${\widehat{\alpha }}_k^{\left(P\right)}$ is the maximum likelihood estimator under the null model $H_0$. Using matrix notation, we have

$$Z_k^{\left(P\right)}={\left(G^{\left(P\right)}\right)}^T\left[I-X^{\left(P\right)}{\left({\left(X^{\left(P\right)}\right)}^T{X}^{\left(P\right)}\right)}^{-1}{\left(X^{\left(P\right)}\right)}^T\right]Y_k^{\left(P\right)}.$$ (2.9)

Denote $a^{\left(P\right)}={\left(G^{\left(P\right)}\right)}^T\left[I-X^{\left(P\right)}{\left({\left(X^{\left(P\right)}\right)}^T{X}^{\left(P\right)}\right)}^{-1}{\left(X^{\left(P\right)}\right)}^T\right]$ to be the row vector of length $n$, then we can rewrite equation (2.9) as $Z_k^{\left(P\right)}=a^{\left(P\right)}{Y}_k^{\left(P\right)}$, which reduces to the setting in Section 2.1.

2.4.2. The 1:K setting.

To adjust for covariates in equation (2.3), we use ${\alpha }^{\left(S\right)}$ as a column vector of $q$ regression coefficients for the row vector $X_i^{\left(S\right)}$ of $q$ covariates

$$Y_i^{\left(S\right)}=X_i^{\left(S\right)}{\alpha }^{\left(S\right)}+G_i^{\left(S\right)}{\beta }^{\left(S\right)}+{ϵ}_i^{\left(S\right)}.$$ (2.10)

The score test statistics are

$$Z^{\left(S\right)}={\left(G^{\left(S\right)}\right)}^T\left(Y^{\left(S\right)}-X^{\left(S\right)}{\widehat{\alpha }}^{\left(S\right)}\right),$$ (2.11)

where ${\widehat{\alpha }}^{\left(S\right)}$ is the maximum likelihood estimator under the null model $H_0:{\beta }^{\left(S\right)}=0$. Similar to the K:1 setting, denote

$$a^{\left(S\right)}={\left(G^{\left(S\right)}\right)}^T\left[I-X^{\left(S\right)}{\left({\left(X^{\left(S\right)}\right)}^T{X}^{\left(S\right)}\right)}^{-1}{\left(X^{\left(S\right)}\right)}^T\right]$$

to be the row vector of length $n$, then we can rewrite equation (2.9) as $Z^{\left(S\right)}=a^{\left(S\right)}{Y}^{\left(S\right)}$, which can be treated in the same fashion of Section 2.2 and similar analysis can proceed.

3. The role of PCs in variance component tests.

Principal components play a similar role in variance component score tests in linear mixed models. In the K:1 setting, if ${\beta }^{\left(P\right)}$ from the multiple phenotype regression model (2.1) is such that each ${\beta }_j$ is assumed to follow an arbitrary distribution with mean 0 and variance ${\tau }^{\left(P\right)}$, where ${\tau }^{\left(P\right)}$ is the variance component, then testing for $H_0:{\beta }^{\left(P\right)}=0$ is equivalent testing for $H_0:{\tau }^{\left(P\right)}=0$ (Lin (1997)). Based on model (2.1), the variance component score test statistic for $H_0:{\tau }^{\left(P\right)}=0$ is (Huang and Lin (2013))

$$Q^{\left(P\right)}={\left\{Z^{\left(P\right)}\right\}}^T{\left\{{\Sigma }^{\left(P\right)}\right\}}^{-1}{\left\{{\Sigma }^{\left(P\right)}\right\}}^{-1}{Z}^{\left(P\right)}.$$

This can also be rewritten as

$$\begin{gathered} Q^{\left(P\right)}=\sum _{k=1}^K{\left[{\left\{Y^{\left(P\right)}{u}_k^{\left(P\right)}\right\}}^T{G}^{\left(P\right)}/{\lambda }_k^{\left(P\right)}\right]}^2 \\ =\sum _{k=1}^K{\left[G^T\left\{P{C}_k^{\left(P\right)}\right\}/{\lambda }_k^{\left(P\right)}\right]}^2 \\ =\sum _{k=1}^K{\left\{V_k^{\left(P\right)}/{\lambda }_k^{\left(P\right)}\right\}}^2, \end{gathered}$$

where $P{C}_k^{\left(P\right)},V_k^{\left(P\right)}$ and ${\lambda }_k^{\left(P\right)}$ are all defined in Section 2.1. This suggests that the variance component multiple phenotype test statistic $Q^{\left(P\right)}$ can be viewed as an inverse squared eigenvalue weighted quadratic combination of the $K$ phenotype PC score test statistics $V_k^{\left(P\right)}$.

The power of the multiple phenotype variance component test depends on both the $K$ principal angles ${\theta }_k^{\left(P\right)}$ as well as the phenotype eigenvalues ${\lambda }_k^{\left(P\right)}$. Its power is more robust with respect to the direction of the true unknown ${\beta }^{\left(P\right)}$ than the test based on a specific phenotype PC, in the sense that it can be powerful when the angle of the true ${\beta }^{\left(P\right)}$ lies in between phenotype PCs. Since the last phenotype PC has the largest weight in $Q^{\left(P\right)}$, the phenotype variance component test in the K:1 setting implicitly assumes that the phenotype PCs with smaller eigenvalues capture more association signals and, hence, weight them more. In fact, it weights the last phenotype ${\text{PC}}_K^{\left(P\right)}$ most. Similar assumptions are made by the multiple phenotype Wald test. If this underlying assumption is violated, like, for example, if the first PC actually has a small principal angle, then $Q^{\left(P\right)}$ will not be powerful.

The variance component test for a SNP set can be constructed similarly in the 1:K SNP set regression setting. Specifically, if ${\beta }^{\left(S\right)}$ from model (2.3) is such that each ${\beta }_j^{\left(S\right)}$ is assumed to follow an arbitrary distribution with mean 0 and variance ${\tau }^{\left(S\right)}$, where ${\tau }^{\left(S\right)}$ is the variance component, then testing for $H_0:{\beta }^{\left(S\right)}=0$ is equivalent to testing for $H_0:{\tau }^{\left(S\right)}=0$. Based on model (2.3), this SNP-set variance component test takes the form of the sequence kernel association test statistic (SKAT) (Wu et al. (2011))

$$Q^{\left(S\right)}={\left\{Y^{\left(S\right)}\right\}}^T{G}^{\left(S\right)}{\left\{G^{\left(S\right)}\right\}}^T{Y}^{\left(S\right)},$$ (3.2)

where a linear kernel is assumed and we have used the fact that $Y^{\left(S\right)}$ is scaled to have an unit variance. This leads to the simplified form of

$$Q^{\left(S\right)}={\left\{Z^{\left(S\right)}\right\}}^T{Z}^{\left(S\right)},$$

which can be rewritten as

$$\begin{gathered} Q^{\left(S\right)}=\sum _K^{k=1}{\lambda }_k^{\left(S\right)}{\left[{\left\{G^{\left(S\right)}{\mathit{u}}_k^{\left(S\right)}/\sqrt{{\lambda }_k^{\left(S\right)}}\right\}}^T{Y}^{\left(S\right)}\right]}^2 \\ =\sum _K^{k=1}{\left[{\left\{P{C}_k^{\left(S\right)}\right\}}^T{Y}^{\left(S\right)}\right]}^2 \\ =\sum _K^{k=1}{\left\{V_k^{\left(S\right)}\right\}}^2. \end{gathered}$$ (3.3)

Going from equation (3.2) to equation (3.3) can be realized by noting that $G^{\left(S\right)}{\left(G^{\left(S\right)}\right)}^T$ has the same eigenvalues as the component ${\left(G^{\left(S\right)}\right)}^T{G}^{\left(S\right)}$, except that the corresponding normalized eigenvectors are $G^{\left(S\right)}{u}_k^{\left(S\right)}/\sqrt{{\lambda }_k^{\left(S\right)}}$ instead of $u_k^{\left(S\right)}$. This can be seen by multiplying the left hand sides of the following equation by $G^{\left(S\right)}:{\left(G^{\left(S\right)}\right)}^T{G}^{\left(S\right)}{u}_k^{\left(S\right)}={\lambda }_k^{\left(S\right)}{u}_k^{\left(S\right)}$. Hence, equation (3.3) suggests that $Q^{\left(S\right)}$ can be viewed as a quadratic combination of the $K$ genotype PC score test statistics $V_k^{\left(S\right)}$ which have variance ${\lambda }_k^{\left(S\right)}$. This is in contrast to $Q^{\left(P\right)}$ of the K:1 multiple phenotype setting, where the inverse of the squared eigenvalues are used as weights in the sum.

To highlight the difference in the role of the eigenvalues in the two settings, it is interesting to note that, for multiple phenotypes, ${\lambda }_k$ is squared in the denominator of the K:1 variance component test while it is only implicitly present through the variance of $V_k^{\left(S\right)}$ in the 1:K case, that is,

$$Q^{\left(P\right)}=\sum _K^{k=1}{\left({\lambda }_k^{\left(P\right)}\right)}^{-2}{\left\{V_k^{\left(P\right)}\right\}}^2,$$

$$Q^{\left(S\right)}=\sum _K^{k=1}{\left\{V_k^{\left(S\right)}\right\}}^2.$$

The means are

$$\begin{gathered} E\left(Q^{\left(P\right)}\right)=\sum _K^{k=1}{\left({\lambda }_k^{\left(P\right)}\right)}^{-2}\left[{\lambda }_k^{\left(P\right)}+{\left\{{\left(u_k^{\left(P\right)}\right)}^T{\beta }^{\left(P\right)}\right\}}^2\right] \\ =\sum _K^{k=1}{\left({\lambda }_k^{\left(P\right)}\right)}^{-1}+\sum _K^{k=1}{\left({\lambda }_k^{\left(P\right)}\right)}^{-2}{\left\{{\left(u_k^{\left(P\right)}\right)}^T{\beta }^{\left(P\right)}\right\}}^2, \end{gathered}$$

$$E\left(Q^{\left(S\right)}\right)=\sum _K^{k=1}{\lambda }_k^{\left(S\right)}+\sum _K^{k=1}{\left({\lambda }_k^{\left(S\right)}\right)}^2{\left\{{\left(u_k^{\left(S\right)}\right)}^T{\beta }^{\left(S\right)}\right\}}^2.$$

In contrast, for the Wald test in the K:1 multiple phenotype setting

$${\text{Wald}}^{\left(P\right)}=\sum _{k=1}^K{\left({\lambda }_k^{\left(P\right)}\right)}^{-1}{\left\{V_k^{\left(P\right)}\right\}}^2,$$

and this is consistent with the Wald test in the 1:K SNP-set setting

$${\text{Wald}}^{\left(S\right)}=\sum _{k=1}^K{\left({\lambda }_k^{\left(S\right)}\right)}^{-1}{\left\{V_k^{\left(S\right)}\right\}}^2.$$

So, the Wald tests put more weight on the last PC in both settings. However, differences arise when examining the ncp for each test. The ncp of the Wald test of multiple phenotypes is influenced more by smaller eigenvalues, while the ncp of the Wald test of a SNP set is influenced more by larger eigenvalues:

$$E\left({\text{Wald}}^{\left(P\right)}\right)=K+\sum _K^{k=1}{\left({\lambda }_k^{\left(P\right)}\right)}^{-1}{\left\{{\left(u_k^{\left(P\right)}\right)}^T{\beta }^{\left(P\right)}\right\}}^2,$$

$$E\left({\text{Wald}}^{\left(S\right)}\right)=K+\sum _K^{k=1}{\lambda }_k^{\left(S\right)}{\left\{{\left(u_k^{\left(S\right)}\right)}^T{\beta }^{\left(S\right)}\right\}}^2.$$

Comparing the means of the test statistics, for K:1 multiple phenotype regression the power of the variance component test is influenced more by the last PC than the Wald test. On the other hand, for 1:K SNP-set regression the power of the variance component test is influenced more by the first PC than the corresponding Wald test.

The fundamental reason for the difference between the variance component test statistics of the two settings is best understood by looking at the variance component (VC) score test statistics directly. For the 1:K setting, the variance component score test statistic in equation (3.2) is based on the loglikelihood of $Y^{\left(S\right)}$, which is, apart from a constant

$$\ell \left({\beta }^{\left(S\right)}\mid Y^{\left(S\right)},G^{\left(S\right)}\right)=-\frac{1}{2}\sum _{i=1}^n{\left\{Y_i^{\left(S\right)}-G_i^{\left(S\right)}{\beta }^{\left(S\right)}\right\}}^2.$$

This likelihood does not contain ${\mathbf{\Sigma }}^{\left(S\right)}$, which appears only in the VC statistic (3.2) in its empirical form ${\left(G^{\left(S\right)}\right)}^T{G}^{\left(S\right)}$. On the other hand, the likelihood of $Y^{\left(P\right)}$ in the K:1 setting is, apart from a constant

$$\ell \left({\beta }^{\left(P\right)}\mid Y^{\left(P\right)},G^{\left(P\right)}\right)=-\frac{1}{2}\sum _n^{i=1}{\left(Y_i^{\left(P\right)}-G_i^{\left(P\right)}{\beta }^{\left(P\right)}\right)}^T{\left({\Sigma }^{\left(P\right)}\right)}^{-1}\left(Y_i^{\left(P\right)}-G_i^{\left(P\right)}{\beta }^{\left(P\right)}\right)-\frac{n}{2}\text{ln}\left\{{\Sigma }^{\left(P\right)}\right\}.$$

Here, ${\Sigma }^{\left(P\right)}$ enters directly into the likelihood itself. The stark difference in the two likelihood functions explains the differences in the variance component score tests as well as the PC and Wald tests.

4. Simulation studies.

In this section we first conduct simulation studies to assess the estimation accuracy of the eigenvalues and eigenvectors of the correlation matrix $\Sigma$ in the K:1 setting by using GWAS summary statistics. Second, we compare the finite sample performance of the PC-based tests in both the K:1 multiple phenotype setting and the 1:K multiple SNP setting. Specifically, we will show that the phenotype PCs with smaller eigenvalues are likely to play more important roles in the K:1 multiple phenotype association tests, while the genotype PCs with larger eigenvalues are likely to play more important roles in the 1:K SNP-set association tests.

First, the correlation matrix ${\Sigma }^{\left(P\right)}$ in Section 5.1 is set to be a true correlation matrix, and its eigenvalues and eigenvectors can be calculated, respectively. Our goal is to estimate the eigenvalues and eigenvectors using GWAS summary Z-scores. One million threedimensional multivariate normal Z-scores with mean zeros and correlation matrix equal to ${\Sigma }^{\left(P\right)}$ are generated mimicking GWAS Z-scores for one million SNPs. The correlation matrix can be estimated as ${\widehat{\Sigma }}^{\left(P\right)}$ using sample covariance matrix of those one million Z-score vectors (Liu and Lin (2018), Zhu et al. (2015)). The sample eigenvalues and eigenvectors can be computed as the eigenvalues and eigenvectors of the matrix ${\widehat{\Sigma }}^{\left(P\right)}$. To assess accuracy of estimation, we repeat this experiment for 1000 times. The bias of the three estimated eigenvalues is equal to the average of the difference between the true values and the estimated values over the 1000 experiments. The variability of the three estimated eigenvalues is calculated as the sample standard deviation of those estimated eigenvalues across the 1000 experiments.

For eigenvectors we use the normalized inner product (NIP) between two vectors to measure the accuracy of the estimation of the eigenvectors. For two vectors $u,v$, the normalized inner product is defined as $u\cdot v/\sqrt{u\cdot u}\sqrt{v\cdot v}$, where the ⋅ notation denotes inner product operation between two vectors of the same dimension. If two vectors are identical, then the NIP is equal to 1. The biases of the estimation of the three eigenvalues are: 3.61×10⁻⁵, −7.35×10⁻⁵,−5.14×10–5), and the standard errors are: 0.0021,0.0016,0.0005, respectively. The NIP for the three eigenvectors are: 0.9999910,0. 9999909,0. 9999995 and its standard errors are: 1.17×10⁻⁵, 1.17×10⁻⁵, 5.32×10⁻⁷. Simulation results show that the eigenvalues and eigenvectors can be accurately estimated.

In the K:1 multiple phenotype regression setting, we show numerically that the phenotype variance component (VC) test $Q^{\left(P\right)}$, which is designed to test for the association of a SNP and mulitple phenotypes without having a prior knowledge of the true direction of the effects ${\beta }^{\left(P\right)}$, gives more weights to the phenotype PCs with smaller eigenvalues. Hence, it favors the last phenotype PC-based test statistic $V_K^{\left(P\right)}$ more than the first phenotype PC-based test statistic $V_1^{\left(P\right)}$. Hence, the VC test in the K:1 setting will be most powerful if the last PC captures all the signals. Its performance is closer to the last phenotype PC-based test statistic $V_K^{\left(P\right)}$ than the first phenotype PC-based test statistic.

We considered an exchangeable correlation structure ${\Sigma }^{\left(S\right)}=\left(1-\rho \right)I+\rho 11^T$, where $\rho$ specifies the strength of the correlation. To demonstrate the theoretical results, we consider two extreme cases of ${\beta }^{\left(P\right)}:{\beta }^{\left(P\right)}=3\cdot u_1^{\left(P\right)}$ and ${\beta }^{\left(P\right)}=u_K^{\left(P\right)}$. In both cases we vary $\rho$ such that $\rho =0.1,0.2,\dots ,0.7,0.8$. The simulations are based on 10⁵ runs. We consider $K=10$ phenotypes. The results are summarized in Figure 1.

Fig. 1.

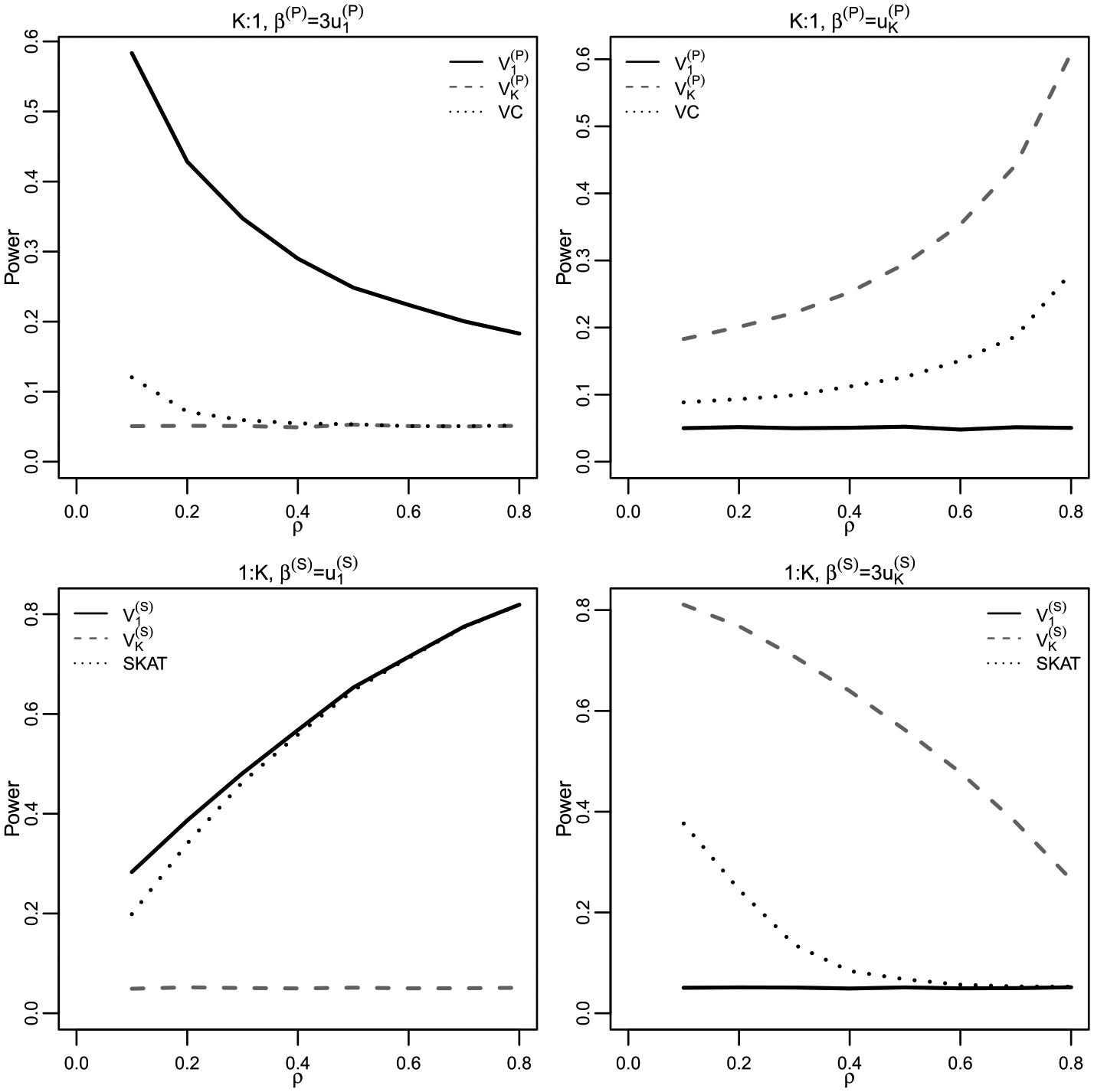
Power simulations demonstrating the relationship between PC tests and variance component tests. Set $K=10$, and consider the exchangeable correlation structure with a varying correlation coefficient $\rho$. For each ${\beta }^{\left(S\right)}$ (and ${\beta }^{\left(P\right)}$) and each $\rho$, 10⁵ simulations are used to estimate the power of each method empirically.

Next, we consider the 1:K SNP-set regression setting using the same exchangeable correlation structure. To demonstrate the theoretical results, we consider two extreme cases of ${\beta }^{\left(S\right)}:{\beta }^{\left(S\right)}=u_1^{\left(S\right)}$ and ${\beta }^{\left(S\right)}=3\cdot u_K^{\left(S\right)}$. With $K=10$ SNPs in a SNP set and simulations based on 10⁵ runs, the results are summarized in Figure 1.

As shown in Figure 1, in the K:1 multiple phenotype setting the last phenotype PC test statistic $V_K^{\left(P\right)}$ has a behavior closer to the phenotype VC test than the first phenotype PC test statistic $V_1^{\left(P\right)}$. When the last principal angle ${\theta }_K^{\left(P\right)}$ is zero, $V_K^{\left(P\right)}$ and the VC test are powerful while $V_1^{\left(P\right)}$ has little power. When the first principal angle ${\theta }_1^{\left(P\right)}$ is zero, $V_1^{\left(P\right)}$ is powerful while $V_K^{\left(P\right)}$ has little power. Also, note that when ${\beta }^{\left(P\right)}$ is in the direction of the first PC, signal strength needs to be three times larger in order to reach comparable power levels to when ${\beta }^{\left(P\right)}$ is in the direction of the last PC. This supports our theoretical findings in Section 2. The performance of the K:1 VC test is closer to that of $V_K^{\left(P\right)}$ but has more power when ${\beta }^{\left(P\right)}=3u_1^{\left(P\right)}$ due to the (albeit small) contribution from the first PC. In this case, when the between-phenotype correlation $\rho$ becomes larger, the phenotype VC test behaves more closely to $V_K^{\left(P\right)}$, reflecting the decrease in ${\lambda }_K^{\left(P\right)}$.

In the 1:K SNP-set regression setting, the first genotype PC-based test, $V_1^{\left(S\right)}$, has a behavior closer to the SNP-set variance component test, that is, the SKAT test, than does $V_K^{\left(S\right)}$. Specifically, when the first principal angle ${\theta }_1^{\left(S\right)}=0$, both $V_1^{\left(S\right)}$ and SKAT are more powerful than $V_K^{\left(S\right)}$, although SKAT is slightly less powerful than $V_1^{\left(S\right)}$. When ${\theta }_K^{\left(S\right)}=0,V_K^{\left(S\right)}$ is powerful while $V_1^{\left(S\right)}$ and SKAT have little power, although SKAT slightly outperforms $V_1^{\left(S\right)}$ here due to the small contribution from the last PC. Also, note that when ${\beta }^{\left(S\right)}$ is in the direction of the last PC, ${\beta }^{\left(S\right)}$ needs to be three times larger in order to reach comparable power levels to the case when ${\beta }^{\left(S\right)}=u_1^{\left(S\right)}$. As the between-SNP correlation (LD) $\rho$ increases, the behavior of SKAT becomes more closer to $V_1^{\left(S\right)}$ due to the increase of ${\lambda }_1^{\left(S\right)}$ which gives the first PC a higher weight in the SKAT test statistic $Q^{\left(S\right)}$. In all, SKAT can be viewed as very similar to $V_1^{\left(S\right)}$ while being a slightly more robust when the signal is orthogonal to the first PC.

It is also interesting to compare the variance component tests and the principal component tests with the minimum $p$-value test (MinP) in the 1:K and K:1 settings. The MinP test statistic is defined as the minimum $p$-value of the $K$ marginal test statistics $Z^{\left(S\right)}$ (or $Z^{\left(P\right)}$). One uses the distribution of the MinP test statistics to calculates the $p$-value of this test. The MinP test is conceived to perform better when the signals are sparse (Conneely and Boehnke (2007)). However, we will show that the accuracy of this notion is highly dependent on the correlation structure. In fact, the MinP test might be less powerful than the VC tests and the PC tests in the presence of sparse signals due to correlation. In the 1:K SNP-set regression setting, an additional reason for this result is that even if ${\beta }^{\left(S\right)}$ is sparse, ${\mu }^{\left(S\right)}={\Sigma }^{\left(S\right)}{\beta }^{\left(S\right)}$ may not be sparse. The opposite notion is also true: when ${\beta }^{\left(S\right)}$ (or ${\beta }^{\left(P\right)}$) is dense, it is not necessarily the case that VC and PC-based methods like $Q^{\left(S\right)}$ (or $Q^{\left(P\right)}$) outperform MinP.

We use the K:1 multiple phenotype regression setting to demonstrate these points for the dense case. Let $K=10$ and ${\mathbf{\Sigma }}^{\left(P\right)}$ be autocorrelated with $\rho =0.5$. First, consider the case where ${\beta }^{\left(P\right)}=1.9\cdot {[1,1,1,\dots ,1]}^T$ such that ${\theta }_K^{\left(P\right)}={90}^{\circ }$. In this case MinP has 76.1% power, while the phenotype VC test $Q^{\left(P\right)}$ has 14.9% power, the Wald test has 74.6% power and $V_K^{\left(P\right)}$ has 5.0% power (Figure 2). In this dense signal case MinP far outperforms both $Q^{\left(P\right)}$ and ${\text{PC}}_K^{\left(P\right)}$. At first glance this result appears counter to common perceptions of the MinP test being ideal in sparse signal settings. Second, consider a different dense signal case, where ${\beta }^{\left(P\right)}~{(1,-2,3,-4,5,-5,4,-3,2,-1)}^T$ such that ${\theta }_K^{\left(P\right)}={4.8}^{\circ }$. In this case MinP has 10.8% power, while $VC$ has 53.5% power, the Wald test has 36.6% power and $V_K^{\left(P\right)}$ has 82.5% power, which contradicts our first example and agrees with the prevailing intuition that MinP has lower power relative to $VC$ and PC-based methods when the signal is dense. As this intuition originally emerged from uncorrelated setting, it cannot be directly applied to correlated data.

Fig. 2.

The effect of ${\theta }_1^{\left(K\right)}$, the angle between ${\beta }^{\left(P\right)}$ and the last eigenvector $u_K^{\left(P\right)}$, on the power of association tests in the K:1 multiple phenotype regression setting. Both ${\beta }^{\left(P\right)}$ and $u_K^{\left(P\right)}$ are vectors in $R^{10}$, where there are $K=10$ phenotypes being tested. The correlation structure ${\Sigma }^{\left(P\right)}$ is autocorrelated with $\rho =0.5$. Power is calculated using 10⁵ simulations under the null distribution for each test at the significance level 0.05.

We use the 1:K SNP-set setting demonstrate the sparse case. We here set all SNPs to have pairwise correlation $\rho =0.8$ with one another, except for the first SNP which is independent of all others. We simulate power at the $\alpha =0.05$ level according to model (2.3) with ${\sigma }^2=8$, $K=10$ and $n=1000$. First, consider the ideal case for MinP where ${\beta }^{\left(S\right)}={[1,0,0,\dots ,0]}^T$ and, therefore, ${\mu }^{\left(S\right)}={[1,0,0,\dots ,0]}^T$. In this case MinP has 46.7% power, while the SKAT $Q^{\left(S\right)}$ has 8.2% power, the Wald test has 7.2% power and $V_1^{\left(S\right)}$ has 5.0% power. The poor performance of $Q^{\left(S\right)}$ and $V_1^{\left(S\right)}$ is due to the angle between the first eigenvector of ${\Sigma }^{\left(S\right)}$ and ${\beta }^{\left(S\right)}$ being orthogonal $\left({\theta }_1^{\left(S\right)}={90}^{\circ }\right)$ (Figure 3). If ${\beta }^{\left(S\right)}~{[0,31,32,\dots ,39]}^T$, then MinP has 59.2% power, while $Q^{\left(S\right)}$ has 61.2% power and $V_1^{\left(S\right)}$ has 61.8% power. The improvement of $Q^{\left(S\right)}$ and $V_1^{\left(S\right)}$ is due to a smaller angle between ${\beta }^{\left(S\right)}$ and the first eigenvector of ${\Sigma }^{\left(S\right)}\left({\theta }_1^{\left(S\right)}={4.2}^{\circ }\right)$. Based on these results it is clear that notions of signal sparsity/density and its effect on statistical power must always be conditional on the correlation and signal structure.

Fig. 3.

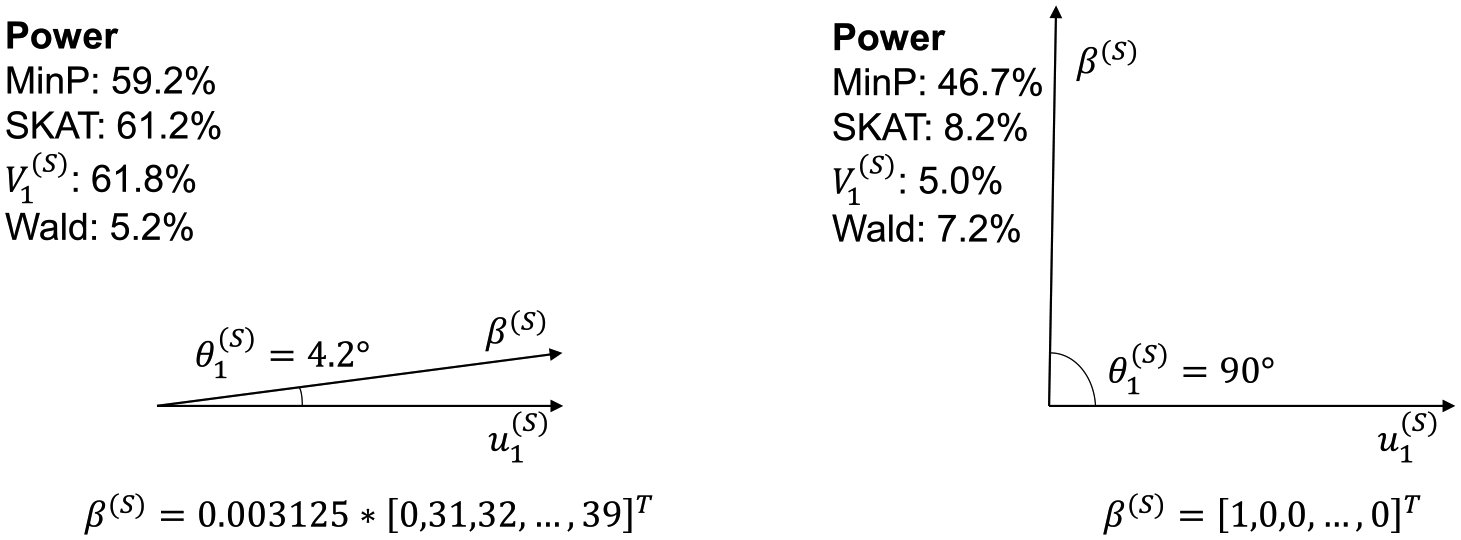
The effect of ${\theta }_1^{\left(S\right)}$, the angle between ${\beta }^{\left(S\right)}$ and the first eigenvector $u_1^{\left(S\right)}$, on the power of association tests in the 1:K SNP-set regression setting. Both ${\beta }^{\left(S\right)}$ and $u_1^{\left(S\right)}$ are vectors in $R^{10}$, where there are $K=10$ SNPs in a SNP-set. The correlation structure ${\Sigma }^{\left(S\right)}$ is exchangeable among nine SNPs with $\rho =0.8$, and they are independent of one SNP. Power is calculated using 10⁵ simulations under the null distribution for each test at the significance level 0.05.

Our simulation study results highlight the importance of using principal angles and eigenvalues to understand the power of $\text{PC}$-based tests in the K:1 and 1:K settings. We have demonstrated that the tests based on the first PC are more powerful in general in the 1:K setting while tests based on the the last PC are more powerful in general in the K:1 setting. We have also illustrated that although signal sparsity plays a role in determining the power of a test, using only signal sparsity to categorize the performance of PC-based tests and the MinP test without also considering the correlation structure is not appropriate.

5. Real data analysis.

In this section we compare the PC-based tests in K:1 and 1:K settings by analyzing two real data sets. The first data set is in the K:1 setting and contains GWAS summary statistics of three lipids traits where we are interested in studying individual SNP effects on multiple lipid phenotypes. The second data set is in the 1:K setting and is a breast cancer GWAS data set where we are interested in performing gene-level analysis of breast cancer risk across the genome.

5.1. The K:1 multiple phenotype setting.

Coronary artery disease is a leading cause of death in the U.S. and worldwide. Serum concentrations of high-density lipoprotein (HDL) cholesterol, low-density lipoprotein (LDL), total cholesterol (TC) and triglycerides (TG) are important risk factors for coronary artery disease and are therapeutic targets for drug development. Genetic analysis of those lipids levels can help identify genetic determinants of abnormal lipids levels. The publicly available global lipids GWAS data set contains the summary statistics ($Z$-scores) for these lipids traits calculated from more than 100,000 individuals of European ancestry (Teslovich et al. (2010)). Since LDL and TC are highly correlated with a correlation 0.88, we restrict the analysis to three phenotypes HDL, LDL and TG since LDL is of more clinical interest than TC.

The total number of genotyped or imputed SNPs is 269,1421, and for each SNP there are three phenotype-specific Z-scores corresponding to HDL, LDL and TG. The estimated correlation matrix between the three Z-scores using the sample correlation matrix over all the independent SNPs after LD pruning is as follows (Zhu et al. (2015)):

$${\Sigma }^{\left(P\right)}=\left(\begin{array}{ccc}1.00& -0.08& -0.42\\ -0.08& 1.00& 0.27\\ -0.42& 0.27& 1.00\end{array}\right)$$

The three eigenvalues of ${\Sigma }^{\left(P\right)}$ are ${\lambda }^{\left(P\right)}=\left(1.54,0.93,0.53\right)$, and the three corresponding eigenvectors are $u_1^{\left(P\right)}=\left(0.59,-0.43,-0.68\right),u_2^{\left(P\right)}=\left(-0.53,-0.84,0.07\right),u_1^{\left(P\right)}=$ $\left(0.60,-0.32,0.73\right)$. We apply several methods to analyze the data including the phenotype PC tests, the phenotype VC test $Q^{\left(P\right)}$ test and the MinP test to jointly analyze the three correlated Z-scores and to obtain corresponding overall $p$-values for testing the association between each SNP and the three lipids. The $p$-value of MinP cannot be more significant than the smallest individual $p$-value corresponding to each lipid which is one drawback of MinP in the sense that MinP cannot detect any additional SNPs. Due to linkage disequilibrium (LD), the SNPs identified might be in LD with each other. To obtain independent signals, we performed LD pruning using the LD threshold $r^2<0.01$ within 500kb region (Purcell et al. (2007)). Figure 4 presents the numbers of independent SNPs identified by each test. The first PC identified 38 SNPs, while 19 of them were also identified by the VC test; The third PC identified 46 SNPs, and all of them were also identified by the VC test.

Fig. 4.

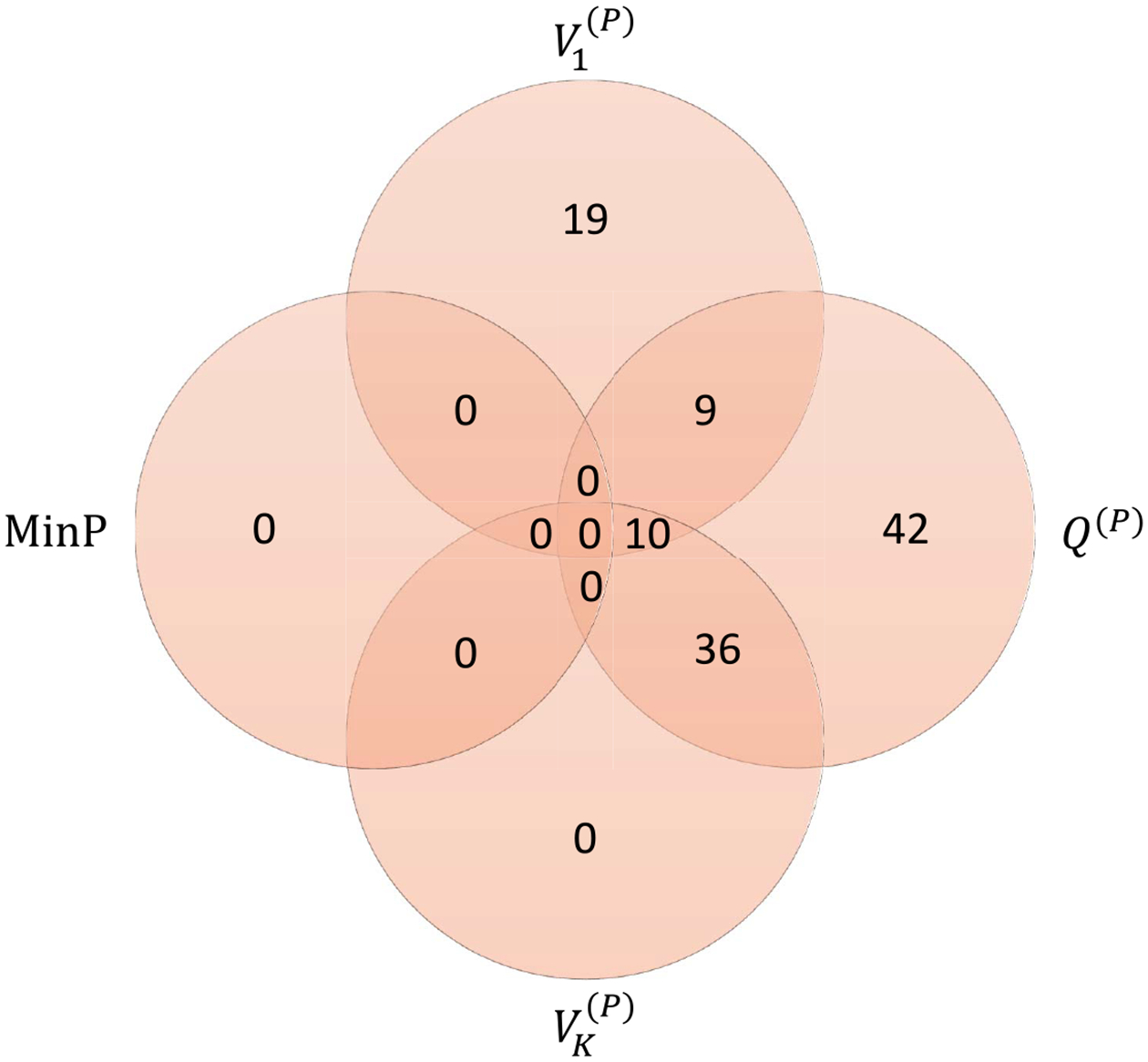
The number of novel independent SNPs detected by PC-based tests for the global lipids GWAS data in the K:1 setting. With $K=3$ different lipids, HDL, LDL and TG, multiple phenotype tests based on SNP-level association tests were performed: first and last PCs, VC and MinP.

To demonstrate the roles of principal angles on the power of the phenotype PC tests, we also compute the third empirical principal angle ${\hat{\theta }}_3^{\left(P\right)}$ which is estimated as the angle between $Z^{\left(P\right)}$ and the third eigenvector of the correlation matrix of $Z^{\left(P\right)}$. Table 1 summarizes the SNPs with the smallest principal angles ${\hat{\theta }}_3^{\left(P\right)}$ as well as the SNPs with top five largest principal angles ${\hat{\theta }}_3^{\left(P\right)}$. The first five SNPs, which have the smallest principal angles ${\hat{\theta }}_3^{\left(P\right)}$, can be detected by $V_3^{\left(P\right)}$ and $Q^{\left(P\right)}$ but not by MinP. They all have the third principal angles less than ${29}^{\circ }$. The $\text{VC}$ test $Q^{\left(P\right)}$ gives more weight to $V_3^{\left(P\right)}$ and also has very significant $p$-values. However, for the last five SNPs, which have the largest principal angles ${\hat{\theta }}_3^{\left(P\right)}$, their effects cannot be detected by $V_3^{\left(P\right)}$ or $Q^{\left(P\right)}$.

Table 1.

Joint Analysis of the GWAS summary statistics of three lipids levels in the K:1 multiple phenotype setting. The three lipids levels include HDL, LDL and TG. We use $Z^{\left(P\right)}$ as an estimate of the direction of $\beta$. The angle between $Z^{\left(P\right)}$ and $u_k^{\left(P\right)}$ is estimated as ${\hat{\theta }}_k^{\left(P\right)}$. SNPs with the smallest five principal angles ${\hat{\theta }}_3^{\left(P\right)}$ as well as the SNPs with the five largest principal angles ${\hat{\theta }}_3^{\left(P\right)}$ are displayed

SNP	CHR	MinP pval	$V_1^{\left(P\right)}\text{ pval}$	$V_3^{\left(P\right)}\text{ pval}$	$Q^{\left(P\right)}\text{ pval}$	${\hat{\theta }}_1^{\left(P\right)}$	${\hat{\theta }}_3^{\left(P\right)}$
rs7257916	19	2.19E-05	8.24E-01	2.90E-18	1.38E-19	87.52	6.21
rs13210634	6	5.58E-04	3.68E-01	9.61E-09	3.89E-09	75.51	20.56
rs804267	8	6.49E-05	1.72E-01	6.08E-09	2.90E-09	68.23	21.79
rs531117	11	1.51E-04	3.77E-01	1.25E-08	2.95E-09	76.25	25.92
rs1233489	6	7.83E-04	3.44E-01	2.07E-08	3.69E-09	75.44	28.98
rs6124245	20	1.42E-06	3.45E-03	9.04E-01	4.89E-04	48.84	89.10
rs2168711	18	1.14E-07	1.30E-06	8.28E-01	1.79E-04	29.86	88.69
rs12673863	7	1.11E-07	3.61E-03	8.28E-01	1.31E-04	51.95	88.45
rs7826687	8	8.08E-07	5.56E-09	7.32E-01	1.11E-03	4.35	88.03
rs17625826	2	1.22E-04	9.58E-08	5.49E-01	1.70E-03	11.64	86.29

This real data example well illustrates our theoretical finding that the variance component test favors the last PC in the K:1 setting and that the tests that favor the last PC generally are more powerful. It is clear that the principal angles provide a geometric perspective on the power of PC-based tests.

5.2. The 1:K SNP-set setting.

To illustrate the performance of genotype PC-based tests relative to principal angles for SNP-set analysis of a phenotype in the 1:K setting, we analyzed the 1145 postmenopausal women of European ancestry with breast cancer and 1142 controls from the Cancer Genetic Markers of Susceptibility (CGEM) GWAS (Hunter et al. (2007)). These women were genotyped at 528,173 loci using an Illumina HumanHap500 array. A logistic regression model is used for performing gene-level analysis by controlling for the covariates—age, postmenopausal hormone usage and the top three principal components to correct for population stratification (Price et al. (2006)). Let $X$ be the matrix of these covariates (with an additional column of 1s) and $W=\text{diag}\left\{{\hat{\pi }}_i\left(1-{\hat{\pi }}_1\right),\dots ,{\hat{\pi }}_n\left(1-{\hat{\pi }}_n\right)\right\}$ where ${\hat{\pi }}_i=E\left(Y_i^{\left(S\right)}\mid H_0,X^{\left(S\right)}\right)$ so that $P=W-W{X}^{\left(S\right)}{\left({\left(X^{\left(S\right)}\right)}^{T}W{X}^{\left(S\right)}\right)}^{-1}{\left(X^{\left(S\right)}\right)}^{T}W$. The marginal test statistics are

$$Z_j^{\left(S\right)}=\frac{{\left(G_j^{\left(S\right)}\right)}^T\left(Y^{\left(S\right)}-\hat{\pi }\right)}{\sqrt{{\left(G_j^{\left(S\right)}\right)}^{T}P{G}_j^{\left(S\right)}}},$$ (5.1)

where we estimate $\text{cov}\left(Z_j^{\left(S\right)},Z_k^{\left(S\right)}\right)={\sigma }_{jk}^{\left(S\right)}$, the $\left(j,k\right)$th component of ${\Sigma }^{\left(S\right)}$ by

$${\hat{\sigma }}_{jk}^{\left(S\right)}=\frac{{\left(G_j^{\left(S\right)}\right)}^{T}P{G}_k^{\left(S\right)}}{\sqrt{{\left(G_j^{\left(S\right)}\right)}^{T}P{G}_j^{\left(S\right)}}\sqrt{{\left(G_k^{\left(S\right)}\right)}^{T}P{G}_k^{\left(S\right)}}},$$

where $G_j^{\left(S\right)}$ and $G_k^{\left(S\right)}$ are the $j$th and $k$th column vectors of $G$, respectively.

We perform gene-level analysis across the genome, testing 15,890 genes with an average of 18 SNPs per gene, including the 20kb regions flanking each gene. We perform gene-level SNP set analysis using genotype PC tests $V_k^{\left(S\right)}$, $\text{SKAT}\left(Q^{\left(S\right)}\right)$ and MinP, and demonstrate the effect of the first principal angle ${\theta }_1^{\left(S\right)}$ on the performance of these tests.

We estimate ${\beta }^{\left(S\right)}$ by its MLE and estimate the first principal angle ${\theta }_1^{\left(S\right)}$ using the angle between ${\widehat{\beta }}^{\left(S\right)}$ and $u_1^{\left(S\right)}$. We compare in Table 2 the performance of $V_1^{\left(S\right)},V_K^{\left(S\right)},Q^{\left(S\right)}$ and MinP among the top gene hits. Despite lacking genome-wide significance, Figure 5 shows the similarity of performance between $V_1^{\left(S\right)}$ and SKAT while showing the differences when compared to both MinP and $V_K^{\left(S\right)}$. The performance of $V_K^{\left(S\right)}$ was strongest when ${\hat{\theta }}_K^{\left(S\right)}$ was further from 90°. When ${\hat{\theta }}_1^{\left(S\right)}$ is small $\left(<{20}^{\circ }\right)$, then ${\beta }^{\left(S\right)}$ is likely to share much of its direction with $u_1^{\left(S\right)}$. The $p$-values for both $Q^{\left(S\right)}$ and $V_1^{\left(S\right)}$ tend to be more significant than the $p$-value using MinP, although MinP still performs adequately. In contrast, when ${\hat{\theta }}_1^{\left(S\right)}$ is large (>70°), then ${\beta }^{\left(S\right)}$ is likely to be nearly orthogonal to $u_1^{\left(S\right)}$. This indicates that, even when the signal is strong, $V_1^{\left(S\right)}$ and $Q^{\left(S\right)}$ generally have almost no power while MinP has relatively small $p$-values. Overall, MinP appears to be robust to the value of ${\hat{\theta }}_1^{\left(S\right)}$, whereas $Q^{\left(S\right)}$ and $V_1^{\left(S\right)}$ are very sensitive and require the principal angle ${\theta }_1^{\left(S\right)}$ to be small. This sensitivity to ${\theta }_1^{\left(S\right)}$ reflects the important role of the principal angle in the theoretical power of equation (2.6). In addition, the smallest overall $p$-values occur for genes with small ${\theta }_1^{\left(S\right)}$ which supports the conclusion that tests based on the first PC or giving more weights to the first PC are more powerful in the 1:K setting.

Table 2.

Top breast cancer GWAS gene hits for competing methods compared to principal angles in the 1:K setting. Though ${\beta }^{\left(S\right)}$ is unknown, we use ${\hat{\beta }}^{\left(S\right)}$ as an estimate of ${\beta }^{\left(S\right)}$. The angle between ${\hat{\beta }}^{\left(S\right)}$ and $u_k^{\left(S\right)}$ is ${\hat{\theta }}_k^{\left(S\right)}$. The top 15 most significant genes, as determined by the smallest of the p-values of the four methods (first and last PCs, VC and MinP), are listed and sorted in increasing order by their ${\theta }_1^{\left(S\right)}$

Gene	K	MinP pval	$V_1^{\left(S\right)}\text{ pval}$	$V_K^{\left(S\right)}\text{ pval}$	$Q^{\left(S\right)}\text{ pval}$	${\hat{\theta }}_1^{\left(S\right)}$	${\hat{\theta }}_K^{\left(S\right)}$
STXBP1	9	4.00E-04	1.52E-04	9.25E-02	1.52E-03	6.3	88.9
PTCD3	12	2.66E-04	4.36E-05	8.45E-01	1.13E-04	7.7	89.9
POLR1A	16	4.00E-04	6.37E-05	1.54E-01	3.43E-04	9.0	90.0
TBK1	11	1.28E-03	3.59E-05	2.24E-01	5.44E-05	10.8	89.1
C11orf49	24	2.57E-03	3.11E-04	8.50E-01	3.84E-04	11.5	90.0
VAPB	25	7.53E-03	2.50E-04	1.34E-02	4.93E-04	15.7	89.8
XPOT	9	1.07E-03	2.04E-04	9.45E-02	1.59E-04	17.1	89.3
C1orf71	25	1.65E-02	1.19E-04	8.37E-01	6.40E-04	18.4	89.9
CNGA3	26	1.19E-03	1.33E-04	5.22E-01	1.36E-04	28.4	89.9
FGFR2	35	1.00E-04	8.15E-05	1.32E-01	3.88E-05	28.9	89.3
TMEM175	10	5.00E-04	5.05E-03	2.87E-04	2.96E-03	32.9	88.4
ZNF19	6	3.71E-02	4.55E-02	2.12E-04	3.54E-04	36.5	86.1
VWA3B	51	1.39E-03	1.23E-03	2.82E-01	2.10E-04	39.3	90.0
DACT1	9	1.26E-01	1.59E-01	1.55E-04	1.32E-01	44.9	75.6
DGKQ	9	3.31E-04	5.01E-01	1.22E-05	7.33E-03	80.1	87.0

Fig. 5.

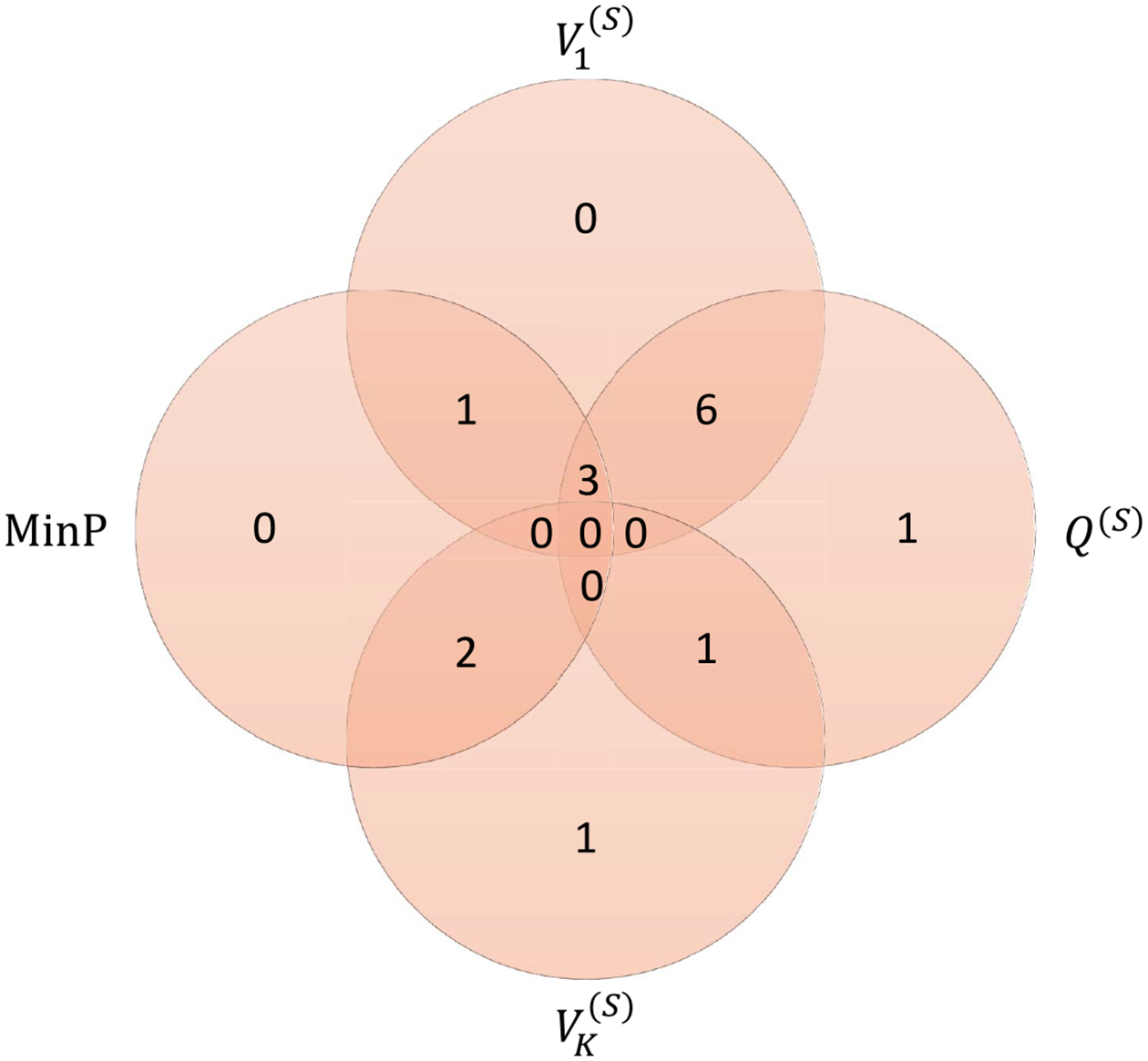
Venn Diagram for 1:K method similarity in the detection of the top genes in the breast cancer GWAS. The top 15 genes were determined by sorting the smallest p-values of all four methods: first and last PCs, SKAT and MinP. Among these genes, $p$-values less than 10⁻³ were counted for each method to produce the diagram.

6. Discussions.

In this paper we investigate the connections and differences between the association tests used in the analysis of multiple phenotypes in the K:1 setting and SNP-sets in the 1:K setting. In the multiple phenotype setting, we aim to assess the associations between a genetic variant and a group of correlated phenotypes; while in the SNP-set setting, we aim to assess the associations between a phenotype and a group of SNPs. At the first glance, these two problems seem to be the same statistically since they both aim at detecting an association between one variable and a group of variables. However, these two problems are very different in terms of the performances of various tests. Principal components based testing procedures have distinctive performance in the two settings. The higher order PC with small eigenvalues are generally preferred in multiple phenotype association studies, while the lower order PC with large eigenvalues are generally preferred in the SNP-set setting. A similar result holds for variance component tests in both settings. The variance component test $Q^{\left(P\right)}$ for multiple phenotypes gives the highest weight to the last PC and, therefore, implicitly assumes that the last PC is most informative, while $Q^{\left(S\right)}$ for SNP-set testing favors the first PC. The VC tests are more robust than single PC based tests, as they combine evidence across all the PCs and allow the unknown principal angles to be in between PCs. In practical data analysis settings, the relatively more robust variance component tests are recommended for use, such as the SKAT type test for SNP-set level association studies.

In both settings the correlation structures either among a group of SNPs or among multiple phenotypes play an important role in the performance of each test. Although the investigation of the statistical powers of a test in high dimensional settings is commonly categorized into dense and sparse regimes, this simple categorization can be misleading for correlated tests. A permutation of the signal vector, which would not alter sparsity, can drastically influence the power of many methods in the presence of correlation, such as for MinP and variance component tests. Indeed, correlation structure, signal strength and signal sparsity are all important factors in high-dimensional testing. Further research is required to investigate how they interplay in their effects on statistical powers of PC-based tests and other tests.

Jolliffe (1982) demonstrated using data examples that principal components with small variances can be as important as the ones with large variances in principal component regression; however, he did not provide any theoretical explanation for the observed empirical phenomenon. We have established the importance of principal angles, the angle between the principal components and the regression coefficient vector, in determining the power of many popular association tests.

It is worth noting that for the multiple phenotype problem (K : 1 setting), we regress multiple phenotypes on individual SNPs, following the traditional GWAS strategy. Our goal in this paper is not to identify which phenotypes that drive associations but to study whether and how to combine multiple phenotypes can boost power for detecting genetic association with a SNP. By modeling marginal SNP associations with multiple phenotypes, it is possible that the detected associations could be due to the correlation/linkage disequilibrium (LD) of a detected SNP with a different causal SNP nearby. This is an issue present with the entire traditional GWAS paradigm of analyzing one SNP at a time. Indeed, association does not necessarily mean causation. Fine mapping is an active area of research with the goal of identifying causal variants of genetic associations. The fine mapping effort becomes more feasible as the field moves into whole genome sequencing studies, such as the Genome Sequencing Program (GSP) of the National Human Genome Research Institute and the Trans-Omics Precision Medicine Program (TOPMed) of the National Heart, Lung and Blood Institute.

Though in this paper we considered only the 1:K and K:1 settings, of increasing interest is the K:J setting, where the association between K outcomes and J predictors is sought. This leads to a scenario where $Z$ is a K by J matrix as opposed to the K-dimensional vector like it is in the K:1 and 1:K settings. The models considered in this paper cannot be adequately adapted to this K:J setting, so future research is needed to allow for the analysis of both multiple phenotypes and SNP-sets simultaneously.