Abstract
The study of the brain's dynamical activity is opening a window to help the clinical assessment of patients with disorders of consciousness. For example, glucose uptake and the dysfunctional spread of naturalistic and synthetic stimuli has proven useful to characterize hampered consciousness. However, understanding of the mechanisms behind loss of consciousness following brain injury is still missing. Here, we study the propagation of endogenous and in‐silico exogenous perturbations in patients with disorders of consciousness, based upon directed and causal interactions estimated from resting‐state fMRI data, fitted to a linear model of activity propagation. We found that patients with disorders of consciousness suffer decreased capacity for neural propagation and responsiveness to events, and that this can be related to severe reduction of glucose metabolism as measured with [18F]FDG‐PET. In particular, we show that loss of consciousness is related to the malfunctioning of two neural circuits: the posterior cortical regions failing to convey information, in conjunction with reduced broadcasting of information from subcortical, temporal, parietal and frontal regions. These results shed light on the mechanisms behind disorders of consciousness, triangulating network function with basic measures of brain integrity and behavior.
Keywords: broadcasting of information, disorders of consciousness, in‐silico exogenous perturbations, integration of information
Propagation of neural events and network responses are disrupted in patients with disorders of consciousness. Loss of consciousness is related to the malfunctioning of two neural circuits: The posterior cortical regions fail to integrate information in altered consciousness and a breakdown of information broadcasting of subcortical cortical areas. Loss of network responses in these patients is related to glucose metabolism.
Abbreviations
- [18F]FDG‐PET
fluoro‐deoxyglucose positron emission tomography or glucose PET
- BOLD
BLOOD oxygenation level dependent
- CRS‐R
Coma recovery scale‐revised
- DoC
disorders of consciousness
- EC
effective connectivity
- fMRI
functional MRI
- HC
healthy control
- MCS
minimally conscious state
- MOU
multivariate Ornstein‐Uhlenbeck
- PCC
posterior cingulate cortex
- SC
structural connectivity
- UWS
unresponsive wakefulness syndrome
- τ
relaxation time constant
1. INTRODUCTION
Consciousness is a subjective experience. Internally perceived as the personal experience of “what is it like, to be you,” the definition of consciousness and its origin are still a matter of scientific and philosophical debates without consensus (Damasio & Meyer, 2009; Nagel, 1974; Tononi, 2004; Tononi et al., 2016). Within the clinical context, however, practitioners treating patients with severe brain injuries and disorders of consciousness (DoC) face the daily reality to help their patients in the best possible manner, regardless of the exact definition of consciousness. For that, it is important to better understand the mechanisms behind pathological loss of consciousness and its recovery, and to count with tangible correlates that accurately assess the state of the patients. The introduction of methods based on neuroimaging can help achieve these goals by providing complementary information to improve diagnosis and decision making (Owen & Coleman, 2008).
Behavioral assessment such as the response to sensory stimuli, pain or simple commands is the first line of action taken at bedside to evaluate patients. From this perspective, consciousness is often characterized based on two components: wakefulness (the level of arousal) and awareness (the content of one's conscious experience) (Demertzi et al., 2015; Laureys, 2005). Patients with severe brain injury can fall into a coma, which is characterized by the absence of both wakefulness and awareness. Patients surviving coma often recover signs of wakefulness, that is, eye‐opening, but without manifestation of awareness of the self nor of the environment. Such state is known as the unresponsive wakefulness syndrome (UWS) (Laureys, 2005). Some of these patients gradually regain awareness and progress into the so‐called minimally conscious state (MCS), showing a wider range of non‐reflexive behaviors such as visual pursuit, localization to pain or response to simple commands, although their ability to functionally communicate remains hampered (Laureys et al., 2004). While behavioral assessment is the standard approach for diagnosis of DoC patients, recently the use of glucose PET (i.e., [18F]FDG‐PET) has proven valuable to enhance the accuracy of the diagnosis (Thibaut et al., 2021). Along these lines, the value of auxiliary assessments such as neuroimaging methods are indicated to refine diagnosis (Giacino et al., 2018; Kondziella et al., 2020), and especially to gain understanding of the mechanisms behind the loss and the recovery of consciousness that might form the foundation for the development of new treatments.
In recent years, the study of the brain's dynamical activity is emerging as a promising approach to assess brain states. It is well‐known that neural activity is characterized by different frequency bands across sleep stages (Armitage, 1995) or cognitive processes, and that local field potentials display intercalated epochs of bursting activity followed by silent periods during anesthesia (Silva et al., 2010). Recent studies have shown that loss of consciousness leads to reduced spontaneous neural activity (Wenzel et al., 2019) and that functional connectivity between brain regions is also significantly reduced (Barttfeld et al., 2014; Bettinardi et al., 2015; Demertzi et al., 2015; Thibaut et al., 2021). Moreover, the patterns of fluctuating functional connectivity are altered during reduced consciousness, with functional patterns of shorter duration and more random transitions between them as compared to normal wakefulness (Barttfeld et al., 2014; Demertzi et al., 2019; López‐González et al., 2021; Luppi et al., 2019).
Observing how external perturbations propagate through the brain constitutes a window to probe brain dynamics and to evaluate their integrity in different states. For example, natural audio‐visual stimuli presented to subjects undergoing general anesthesia or within deep sleep are still processed in the sensory cortices but fail to integrate at the higher level cortical regions (Arena et al., 2021; Ishizawa et al., 2016; Krom et al., 2020; Pavone et al., 2017; Portas et al., 2000; Sela et al., 2016). Application of artificial perturbations such as transcranial magnetic stimulation triggers a response of the stimulated regions that is comparable across conditions, but a rapid decline in the propagation of the signals is found during deep sleep, anesthesia or in patients with DoC (Casali et al., 2013; Massimini et al., 2005). These observations have been successfully employed to classify the level of consciousness both in patients and during anesthesia (Casali et al., 2013). However, as the procedure focuses on the description of the whole‐brain responses by a single number—the perturbational complexity index—it misses the directionality of the evoked causal interactions. These causal interactions have been demonstrated to be sensitive to different states of consciousness and moreover to hold explanatory power with respect to their neural mechanisms (Seth et al., 2011; Signorelli et al., 2021).
In the present paper, we investigate the capacity of both endogenous and exogenous events to propagate throughout the brain in patients with DoC by use of model‐free and model‐based analyses of resting‐state activity, as measured via functional MRI. First, we studied how spontaneous endogenous events within the resting‐state blood oxygenation level dependent (BOLD) signals propagate and are subsequently integrated (Deco & Kringelbach, 2017). Also, we found that the intrinsic relaxation times of the BOLD signals exhibit a heterogeneous map of spatial distributions in the healthy brain that homogenises in patients, especially in the UWS group. Second, we employed a model‐based approach of linear propagation to estimate the pair‐wise effective connectivity between brain regions (Gilson et al., 2016; Gilson et al., 2019). Since effective connectivity captures the directional causal relations, we could simulate the asymmetrical propagation of exogenous perturbations in the brain in order to recognize changes in the ability of brain areas to ‘broadcast’ or to ‘receive’ converging information. In particular, we found two well‐differentiated subnetworks with altered propagation properties in the patients. The posterior regions of the cortex fail to convey information, while broadcasting of information is reduced in subcortical, temporal, parietal and frontal regions. We could confirm that these results correlate with the decrease in cerebral glucose metabolism as measured with [18F]FDG‐PET, reinforcing the evidence that the brain activity in patients with prolonged disorders of consciousness lack the sufficient capacity to propagate and subsequently integrate events, which are necessary conditions for conscious perception.
2. MATERIALS AND METHODS
2.1. Participants
We included subjects with a pathological reduction or loss of consciousness after severe brain injury, called disorders of consciousness (DoCs), as well as healthy control (HC) volunteers. Written informed consent was obtained from all HC participants and the legal representative of DoC patients for participation in the study. The local ethics committee from the University Hospital of Liège (Belgium) approved the study. This study includes 40 adult DoC patients, of which 26 were diagnosed as in minimally conscious state (MCS) (7 females, age range 23–73 years; mean age ± SD, 41 ± 13 years) and 14 were diagnosed with the unresponsive wakefulness syndrome (UWS) (7 females, age range 20–74 years; mean age ± SD, 49 ± 16 years). Besides, 33 age and gender‐matched healthy controls (HC) (13 females, age range 19–72 years; mean age ± SD, 40 ± 14 years) without premorbid neurological problems were included. The diagnosis of the DoC patients was confirmed through two standard approaches. The first is the repeated behavioral assessment using the Coma Recovery Scale‐Revised (CRS‐R) by trained clinicians and second, using Fluoro‐deoxyglucose Positron Emission Tomography (FDG‐PET) neuroimaging as an objective test to complement behavioral assessment according to the procedure described by Stender et al. (2014). Patients were behaviorally diagnosed through the best of at least five CRS‐R assessments evaluating auditory, visual, motor, oromotor function, communication and arousal (Giacino et al., 2004). Patients for whom these two diagnostic approaches disagreed were excluded from further analysis. Disorders of consciousness occur for a variety of reasons (etiology). Among the 40 patients 17 suffered from anoxia causing widespread neuronal death and 22 of traumatic brain injuries (TBI), that also were grouped with patients presenting with a DoC after a hemorrhagic stroke or cerebral vascular accident (CVA) leading to more focal lesions. Among the patients diagnosed with UWS, 11 suffered anoxia and 3 TBI whereas the MCS group consists of 6 patients with anoxia and 19 with TBI. Patient specific clinical information is presented in Table S1.
2.2. MRI data acquisition
Structural (T1 and diffusion weighted imaging, DWI) and functional MRI (fMRI) data was acquired on a Siemens 3T Trio scanner. The 3D T1‐weighted MP‐RAGE images (120 transversal slices, repetition time = 2300 ms, voxel size = 1.0 × 1.0 × 1.2 mm3, flip angle = 9°, field of view = 256 × 256 mm2) were acquired prior to the 10 min of BOLD fMRI resting state (i.e., task free) acquisition (EPI, gradient echo, volumes = 300, repetition time = 2000 ms, echo time = 30 ms, flip angle = 78°, voxel size = 3 × 3 × 3 mm3, field of view = 192 × 192 mm2, 32 transversal slices). Last, diffusion weighted MRI was acquired in 64 directions (b‐value =1000 s/mm2, voxel size = 1.8 × 1.8 × 3.3 mm3, field of view 230 × 230 mm2, repetition time 5700 ms, echo time 87 ms, 45 transverse slices, 128 × 128 matrix) preceded by a single unweighted image (b0).
2.3. MRI data analysis
2.3.1. MRI data preprocessing
Preprocessing was performed using MELODIC (Multivariate Exploratory Linear Optimized Decomposition into Independent Components) version 3.14, which is part of FMRIB's Software Library (FSL, http://fsl.fmrib.ox.ac.uk/fsl). The preprocessing consisted of the following steps: the first five functional images were discarded to reduce scanner inhomogeneity, motion correction was performed using MCFLIRT, non‐brain tissue was removed using BET, intensity was normalized, temporal band‐pass filtering with sigma 100 s was performed, spatial smoothing was applied using a 5 mm FWHM Gaussian kernel, rigid‐body registration and single‐session ICA with automatic dimensionality. Then noise components and lesion‐driven artifacts (e.g., head movement, metal, and physiological noise artifacts) were manually regressed out for each subject. Specifically, FSLeyes in Melodic mode was used to identify the single‐subject Independent Components (ICs) into “good” for cerebral signal, “bad” for noise or injury‐driven artifacts, and “unknown” for ambiguous components. Each component was evaluated based on the spatial map, the time series, and the temporal power spectrum (Griffanti et al., 2017). FIX was applied with default parameters to remove bad and lesion‐driven artifacts components (Griffanti et al., 2017). Then, the Shen et al. (2013) functional resting state atlas (without cerebellum) was used for parcellating the BOLD into n = 214 time series of cortical and subcortical brain areas in each individual's native EPI space (Finn et al., 2015). The cleaned functional data were co‐registered to the T1‐weighted structural image using FLIRT. Then, the T1‐weighted image was co‐registered to the standard MNI space by using FLIRT (12 DOF), and FNIRT. This transformation matrix was inverted and applied to warp the resting‐state atlas from MNI space to the single‐subject functional data. Finally, the time series for each of the 214 regions brain areas were extracted using custom‐made Matlab scripts using “fslmaths” and “fslmeants.”
2.3.2. Structural connectivity matrix
We computed an average whole‐brain structural connectivity matrix from all healthy participants as described in our previous study (López‐González et al., 2021). Briefly, the b0 image in native diffusion space was co‐registered to the T1 structural image using FLIRT. Next, the T1 structural image was co‐registered to the MNI space by using FLIRT and FNIRT. The resulting transformations were inverted and applied to warp the resting‐state atlas from MNI space to the native diffusion space using a nearest‐neighbor interpolation method. Then, analysis of diffusion images was performed using the FMRIB's Diffusion Toolbox (FDT) www.fmrib.ox.ac.uk/fsl. The structural connectivity matrices were then constructed for the same parcellation as employed to parcellate the BOLD signals, Shen et al. (2013) with n = 214 cortical and subcortical areas. The structural connectivity (SC) mask was obtained by averaging all HC subjects' SC matrix and applying a threshold of 80% to maintain the top 20% of strongest connections to binarize the SC. This SC mask was used to constrain the functional connectivity matrix for the whole brain EC computation.
2.3.3. Intrinsic ignition
Intrinsic ignition is a measure to quantify the level of integration elicited by spontaneously occurring local events in the brain's activity (Deco et al., 2017; Deco & Kringelbach, 2017). Given the BOLD signals measured during a resting‐state session, intrinsic ignition is calculated in three steps: (i) identification of intrinsic (endogenous) events occurring in the BOLD, (ii) calculation of the network integration elicited by each of the endogenous events and, (iii) intrinsic ignition is the average of integration evaluated over all events.
First, an intrinsic event is defined as a significant fluctuation spontaneously occurring in the resting‐state BOLD of a brain area. An event is said to occur in area i at time t’ whenever the signal surpasses a threshold of θ = 2 standard deviations. Second, the integration elicited by an event is obtained from the functional connectivity (FC) matrix (excluding region i) estimated in a short time window t′ → t′ + 4TR after the event occurrence. Specifically, the size of the largest connected component in the binarised FC matrix is calculated across all thresholds from one to zero. The integration elicited by the event is thus the area‐under‐the‐curve for the largest component sizes across thresholds. Here, FC is calculated as the phase‐locking value between two BOLD signals instead of employing Pearson's correlation. The phase‐locking approach allows to estimate an FC matrix at each time‐point and to avoid errors of computing correlation over short windows (Hindriks et al., 2016). Last, intrinsic ignition is the average of integration values obtained for all events identified.
For completeness, the analysis was repeated considering various thresholds from θ = 0.5 to θ = 2.5 standard deviations. When θ ≥ 2.5 no intrinsic events were observed in the BOLD of some subjects for each group (UWS = 8; MCS = 9 and HC = 7) and thus ignition could not be calculated.
2.3.4. Relaxation time constants (τ)
In order to obtain information about the operating regime of brain regions, we measured the relaxation time constant τ from the autocovariances of the BOLD signals. Specifically, τ represents the time a signal needs to decay towards its rest. The larger the τ the longer it takes for the activity of a region to decay and, the smaller it is the faster the activity decays. Given that and are the 0‐TR‐lag and the 1‐TR‐lag covariance matrices obtained from the empirical BOLD, the time constants are calculated as:
| (1) |
where corresponds to the slope of the linear regression of by .
2.3.5. Estimation of effective connectivity
The estimation of effective connectivity (EC) is a model‐based procedure that fits simulated data to empirical data by adjusting the pair‐wise connection strengths between the regions. Hence, EC represents the most likely set of connectivity strengths that—for the particular dynamical model employed—lead to simulation results closest to empirical data. In our case, we used the multivariate Ornsteing‐Uhlenbeck (MOU) process as the generative model of choice for the BOLD signals (Gilson et al., 2016). The MOU is a model of linear propagation in a network in which the activity is generated by injecting Gaussian noise at the regions. The MOU has been widely used to study the relation between the structural and functional connectivities (Barnett et al., 2009; Galán, 2008; Messé et al., 2014; Tononi & Sporns, 1994, 1996; Zamora‐López et al., 2010, 2016). Given a network of n regions and their connectivity matrix A (either binary or real weighted) the MOU is formally defined as:
| (2) |
where is the activity (BOLD signal) of a brain region i, is the time constant characterizing the rate of the exponential decay of the brain region and dB represents white noise given by covariance matrix B.
One of the main benefits of the MOU is that the 0‐lag and the 1‐lag covariance matrices of the system can be analytically calculated, thus avoiding the need to run time‐consuming numerical simulations to generate the signals from which the covariances are determined. Hence, MOU‐EC is a method that fits the model parameters (via a Lyapunov optimization procedure) in order to minimise the distance (L1‐norm) between the and empirically extracted from the BOLD, and the corresponding matrices estimated out of the MOU system (Adhikari et al., 2021; Gilson et al., 2016). In particular, the optimization procedure iteratively adjusts the pair‐wise connection strengths (weights of connectivity matrix A) and the levels of covariances of the Gaussian noise injected at each region (diagonal entries of matrix B). Thus, EC is the weighted connectivity matrix A' that results at the end of the iterative optimization process. Estimation of MOU‐EC was carried out using the pyMOU Python package, see the “Data availability statement.”
In this study, individual EC matrices were estimated for all HC participants, patients with UWS and partially recovered patients in MCS. A limitation of EC estimation for the whole‐brain is the large number of free parameters to be fitted, namely, the n 2 entries of the connectivity matrix A and the n 2 entries for the covariances of the Gaussian white noise inputs. Given the limited temporal resolution of the BOLD it becomes necessary to restrict the number of free parameters in order to avoid estimation “noise.” For that, the estimated EC (connectivity matrix A in Equation (2)) was constrained by the binarised average SC of the HC participants, tuning only the 20% strongest anatomical connections. Also, we restricted the optimization to the diagonal entries of the B matrix (i.e., input variances) assuming that each brain region receives an independent Gaussian white noise. As a consequence, the fitting involved 0.2n 2 + n free parameters, a 10% of the total.
2.3.6. In‐silico exogenous perturbational analysis
To investigate the propagation of perturbations throughout the brains of the HC participants and of the patients we employed a model‐based approach to study networks through the analysis of their responses to inputs (Gilson et al., 2019). The method considers the linear model of activity propagation in Equation (2). The second term of Equation (2), , represents the actual propagation of activity across the connectivity and how nodes influence each other. This mutual influence is exerted not only over direct connections or shortest paths as in the sense of graph distance, but it accounts for the activity propagated over all recurrent paths of different lengths. Indeed, as stated above, the matrix A can be either binary or weighted, thus comprising the general case of arbitrary connection strengths between regions. It shall be noted that when all values of A are positive this term diverges, leading to infinite network activity. On the contrary, the first term of Equation (2), is a leakage or dissipation term representing an exponential decay of the activity at each region, with the decay rate determined by . For small enough values of —say, fast enough leakage—the divergent behaviour of the second term is counterbalanced through this dissipation term. Thus, the goal is to study the transient response of a network to external perturbations as its activity raises in the short term and decays in the longer time.
For the analysis in this study, we consider the canonical case in which an external unit perturbation is applied to every brain region simultaneously and we studied the subsequent responses. Figure 1 summarises the conceptual rationale behind this perturbational approach using a small network as an example. At time every region receives a spike input of unit strength. In practice, this is achieved by setting the noise covariance matrix B to be the identity matrix, with all diagonal entries and otherwise. Taking advantage of the simplicity of the MOU process, as for the EC estimation, there is no need to run numerical simulations to obtain the network responses since they can be calculated analytically. The solution of the linear system in Equation (2) with initial conditions is given, in vector form, by where is the Jacobian matrix of the linear system and is the Dirac‐delta taking values when i = j, and otherwise. Assuming initial conditions we have that the matrix is the response function to a unit perturbation. Depending on the field of research, the unit response function is often named as the Green function (Selçuk Bayin, 2006) or the propagation kernel. Finally, since we are only interested in quantifying the part of the influence that nodes exert on each other through the connectivity, we regress out the trivial self‐responses of the regions to the external input, which is governed by the Jacobian of the first term, . Hence, we define the pair‐wise response function as
| (3) |
where is a normalization factor to compare across networks of different size. On the one hand, the pair‐wise elements represent the conditional, temporal response of area j to a unit perturbation applied on area i at time t = 0. This conditional pair‐wise response encompasses all network effects from i to j acting at different time scales along all recurrent paths of different lengths. On the other hand, at every time point t, is an matrix revealing how the spatio‐temporal interaction patterns that emerge from connectivity A evolve over time. See Figure 1a for illustration.
FIGURE 1.
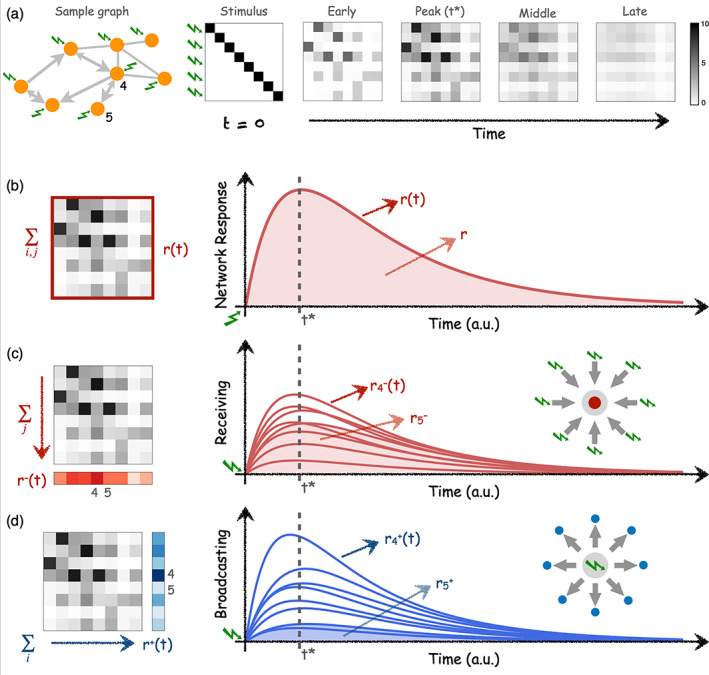
Network analysis via simulation of perturbation‐responses. (a) Temporal evolution of pair‐wise responses to an initial unit perturbations at time applied at every node of a sample network. The network is directed and weighted, thus pair‐wise responses are asymmetrical. The subsequent analysis of responses can be performed at different levels. (b) The global network response is computed as the sum of all pair‐wise responses at each time t. Global network response rapidly peaks at time t* and slowly decays as a consequence of the leakage term in Equation (2) resembling a dissipation of signal at the brain regions. is thus the total accumulated response in the network and is calculated as the integral (area‐under‐the‐curve) of . (c) The ‘Receiving’ capacity is the temporal response of one node to all the inputs applied at . It is thus a signature of how much of the network flows centralise at a given node, which is a (necessary but not sufficient) condition of a node to integrate information. is calculated as the column‐sum of the response matrices . (d) The ‘Broadcasting’ capacity the nodes represent the influence that node i exerts over the network by quantifying the amount of response elicited over all the nodes by an input applied at node i. Thus, is calculated as the row‐sum of the response matrices . For illustration, the behaviour of two nodes, and are highlighted. Node 4 is a central and node 5 is a ‘leaf’ only connected to node 4. As a consequence, node 4 has the largest receiving and broadcasting capacities in the network. A strong connection 4 → 5 implies that node 5 is very much influenced by the network (large receiving) but a weak connection 5 → 4 results in that node 5 can barely influence the other nodes (low broadcasting).
The response matrices contain much information about the architecture of the network and several measures can be extracted from them. Here, we focus on two simple metrics. First, the global network response representing the temporal evolution of the total amount of response propagated through the connectivity, Figure 1b. Thus, is computed as the sum of the pair‐wise responses of the matrix at every time point t:
| (4) |
Second, we characterise the temporal evolution of the response for every region. As this perturbational method accounts for arbitrary connectivity matrices A, either binary or weighted, it also naturally accounts for the case in which A represents a directed or an asymmetric connectivity. Therefore, for every region we can define both their input and output properties. We define the broadcasting and the receiving of a brain region as:
| (5) |
| (6) |
The receiving quantifies the temporal response of region i to all the inputs simultaneously applied at time , see Figure 1c. Hence, conceptually represents how sensitive is a region within the network. On the contrary, as illustrated in Figure 1d, the broadcasting quantifies the temporal response of the entire network due to the unit perturbation that was applied in region i at time . Thus, represents the influence that region i exerts over the whole network. While , and quantify the temporal evolution of the network and of the regional responses, the total responses , and are defined as the accumulated responses over time—say, the integral or area‐under‐the‐curve from to as illustrated by the shaded regions of Figure 1b–d.
In the present study, we applied the perturbational network analysis following the procedures in Gilson et al., 2019. The parameters of Equation (2) were constrained by information extracted from the empirical data. Namely, the connectivity matrices A were replaced by the EC matrices previously computed for each subject and the relaxation time constants were precomputed from the BOLD signals of the brain regions. The benefit of doing so is that the complete analysis and modeling pipeline is based on the same model, assumptions and limitations, thus allowing for a coherent interpretation of the results at every step (Gilson et al., 2020). All calculations were carried out using the NetDynFlow Python package, see the “Data availability statement.”
2.3.7. Metabolic index using [ 18F]FDG‐PET
Alongside the MRI analyses, we have estimated the cerebral glucose metabolism by means of the metabolic index for the best‐preserved hemisphere (MIBH) using [18F]FDG‐PET, that shows high accuracy to discriminate between UWS and MCS patients. To this end, data acquisition was performed with a Gemini PET‐CT (Philips Medical Systems) while receiving a bolus intravenous injection of FDG (185–370 MBq). The data was recorded in a single 12‐minute emission frame after a 30‐minute uptake phase and the images were corrected for attenuation (Annen et al., 2016; Stender et al., 2016). The following steps were followed to calculate MIBH (Stender et al., 2015, 2016). First, we created a population‐specific template for the patients (by taking all DoC patients) and control groups to overcome the problem of big deformations due to brain lesions and atrophy by following the approach of previous studies (Annen et al., 2016; Phillips et al., 2011, Stender et al., 2016; Thibaut et al., 2021). The population‐specific templates were built in three steps. First registering the [18F]FDG‐PET images of each subject to the 15O‐H2O‐PET‐template available in the SPM toolbox using an affine transformation individually for every subject. Then all the subject's coregistered images were averaged by group (i.e., HC, MCS, UWS) to create a study specific preliminary template. Secondly, an intermediate template was created by registering all individual [18F]FDG‐PET images to the aforementioned preliminary template using affine and non‐linear registration steps which was then averaged. Finally, the previous registration and averaging steps were iterated four times to create final population‐specific [18F]FDG‐PET templates (Phillips et al., 2011). After creating the template, individual images were registered to the appropriate template (for patients or healthy controls) with affine and non‐linear registration steps using Advanced Normalization Tools (ANTs version 2.0.3). Images were then segmented into the left and right cortical regions, extracerebral tissue and normalized based on the metabolism of the extracerebral tissue in reference to control as described by Stender and colleagues (Stender et al., 2016). Last, metabolic activity was scaled by setting the mean activity of extracerebral regions to an index value of 1 by transforming from 0 to 1. The MIBH was then computed as the highest mean metabolic activity out of the two hemispheres (Stender et al., 2015, 2016).
2.3.8. Statistical analyses
For the model‐free measures, the group differences were assessed using two‐sample t‐tests for the global intrinsic ignition and relaxation time constant τ at the whole brain level (Bonferroni correction for three groups). Specifically, we investigated local between group differences in regional relaxation time constant τ using two‐sample t‐tests with Bonferroni correction (p < 0.05) accounting for the number of regions (i.e., n = 214).
For the model‐based measures, we assessed between group differences for the EC links using two‐sample t‐tests with Bonferroni correction (p < 0.05) accounting for 20% of the number of the structural links between the brain regions (i.e., 9116 links). Then, we assessed between group differences in whole‐brain total (i.e., receiving and broadcasting) network response. The whole brain network response was calculated as the average network response across all the brain regions. An ANOVA with Tukey post hoc comparison, Bonferroni corrected for 200 time points of integration, was employed. Before assessing the local broadcasting and receiving differences, we first evaluated the effect of etiology (anoxia and TBI) versus diagnosis (UWS and MCS) for whole brain early peak responses (i.e., the maximum amplitude of the whole brain network response curve) and late whole brain network responses (i.e., from integration time 60–200 s [modeled time], based on the findings of the ANOVA described above) using a linear regression model as implemented in MATLAB (i.e., fitlm function). Both the mean effects for diagnosis and etiology were considered as well as their interaction. Regional modulation of the responses was evaluated only for factors with a significant main effect on global network response .
To investigate local broadcasting and receiving properties, we considered the area under the receiving and broadcasting curves (i.e., from integration time 60–200 s modeled time) separately for every brain region. We identified regions with relatively high difference in network responses within groups (i.e., HC, UWS and MCS separately) with a one‐sample t‐test (against the mean of all brain regions and subjects of the group) with Bonferroni correction (p < 0.05) accounting for the number of regions (i.e., n = 214). We identified the regional dominance for broadcasting and receiving by subtracting the areas (integral) between the regional receiving and the broadcasting curves, and performed a within‐group t‐test to identify regions with specific functional specialization (considered significant at p < 0.05 Bonferroni corrected for n = 214). Last, between group differences in regional receiving and broadcasting information were assessed with two‐sample t‐tests with Bonferroni correction (p < 0.05) accounting for the number of regions (i.e., n = 214).
We computed differences in the MIBH between UWS and MCS groups using a two‐sample t‐test. Finally, we correlate the MIBH and behavioral assessment (CRS‐R) values of DoC patients' with their network response (i.e., of regions with alterations as compared to healthy controls) using Pearson correlation (considered significant at p < 0.05) to explore if the brain network response measured using computational models is related to whole brain metabolism at rest and behavioral profile.
3. RESULTS
This study comprises resting‐state fMRI (eyes‐closed) of 33 healthy control (HC) subjects, 14 patients with unresponsive wakefulness syndrome (UWS) and 26 patients classified as in minimally conscious state (MCS). The diagnoses were made using repeated CRS‐R assessments and confirmed with FDG‐PET neuroimaging (Stender et al., 2014) to avoid including MCS* patients (i.e., patients who do not show behavioral signs of consciousness but with preserved brain metabolism suggesting that they might be conscious) (Thibaut et al., 2021).
3.1. Global integration of local endogenous events is hampered in lower conscious states
We started this study by investigating whether endogenous spontaneous events occurring locally propagate differently depending on the level of consciousness, across healthy controls, MCS or UWS patients. For that, we employed the intrinsic ignition measure which estimates the capacity for information integration elicited by spontaneously occurring local events in the brain's activity (Deco & Kringelbach, 2017). The level of global intrinsic ignition for one subject is calculated as the average integration triggered by all endogenous events identified during in a resting‐state session, Figure 2a. The whole brain intrinsic ignition is the average of all the brain region intrinsic ignition. The whole brain intrinsic ignition was lowest for patients with UWS, Figure 2b, implying that the endogenous BOLD events lead to a lower network response than in healthy controls and in MCS patients (HC = 0.82 ± 0.02, UWS = 0.78 ± 0.02, MCS = 0.79 ± 0.02, HC vs. UWS t(45) = 6.0, p < 0.0001, HC vs. MCS t(57) = 4.6, p < 0.0001, MCS vs. UWS t(38) = 2.0, p = 0.029). Also, it shall be noted that the number of observed intrinsic events was lowest in UWS, intermediate in MCS patients and highest in healthy controls (HC = 14.1 ± 3.6, UWS = 7.6 ± 2.9, MCS = 11.0 ± 3.6, HC vs. UWS t(45) = 5.9, p < 0.0001, HC vs. MCS t(57) = 3.3, p = 0.0017, MCS vs. UWS t(38) = 2.9, p = 0.0048). These results were obtained for events defined at BOLD signals overcoming a threshold θ = 2 standard deviations. Equivalent results were found considering other thresholds (θ = 0.5, 1.0 and 1.5), see Figure S1.
FIGURE 2.
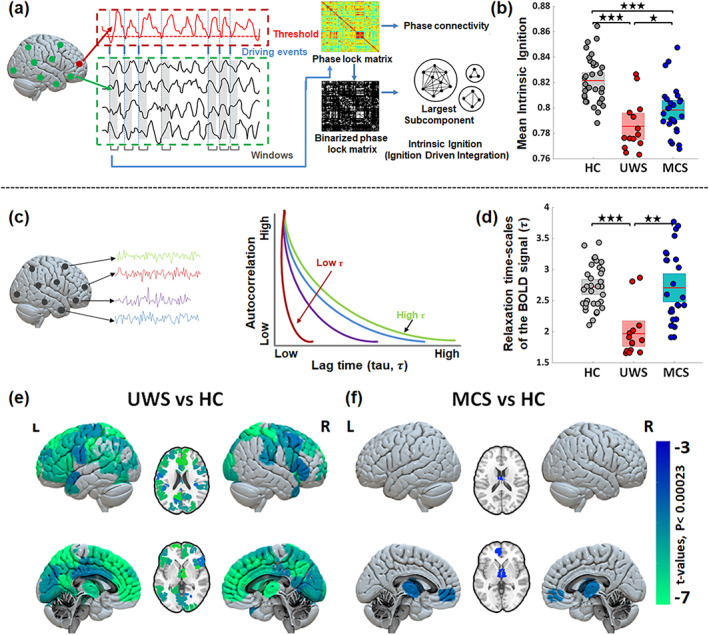
Changes in endogenous properties from resting‐state BOLD signals in healthy controls (HC), unresponsive wakefulness syndrome (UWS) and minimally conscious state (MCS). (a) Illustration of intrinsic ignition computation overview consisting of the identification of intrinsic (endogenous) events occurring in the BOLD and calculation of the network integration (using largest subcomponent of phase lag connectivity) elicited by each of the intrinsic events in a short time window. (b) Comparison of mean intrinsic ignition for the three groups, illustrating the reduced capacity to integrate endogenous spontaneous events in patients with DoC. (c) Representation of the relaxation (autocorrelation) time‐scales of the BOLD signals (τ). A shorter τ implies a faster decay of the signal and a lower memory depth. (d) At the whole‐brain level τ shows significant reductions in UWS and MCS patients compared to HC. Stars reflect the Bonferroni corrected (for three groups) significance levels (*p‐value < 0.05; **p‐value < 0.001; ***p‐value < 0.0001). (e, f) Maps of significant differences in regional distributions of τ between patients and controls. The color bar represents the t‐values of significant between‐group differences (Bonferroni corrected for 214 tests, p‐value = 0.05).
3.2. Shorter relaxation‐time of BOLD signals in low levels of consciousness
Alterations in the inherent time‐scales of signals can reveal changes in the underlying mechanisms controlling the local dynamics and determining their operating regime. Specifically, the autocovariance profile of the BOLD for one brain area estimates the duration for which the signal is altered before going back to pre‐event baseline activity (Murray et al., 2014), as illustrated in Figure 2c. Here, we measured the autocovariance time constant τ, also called the relaxation time or memory depth in the literature. Large τ implies a longer lingering effect of a signal after an event or perturbation before it decays, thus suggesting that the brain region might remain available for processing longer.
At a whole‐brain level, averaging over the for all regions in one subject, we found that τ was shorter in patients with UWS (1.96 ± 0.38) than in healthy controls (2.72 ± 0.35; t(45) = 6.5, p < 0.0001) and MCS patients (2.70 ± 0.58; t(38) = 4.2, p < 0.001), see Figure 2d. Looking at the spatial distributions, we found a heterogeneous gradient of in healthy controls with shorter time constants in subcortical areas ( ~ 1.5 s) and longer ( ~ 3.5 s) in the frontal and parietal areas, see Figure S2. Importantly, the diversity of relaxation times is lost in UWS with being homogeneously distributed and dominated by small values. Compared to healthy controls, the decrease of in patients with UWS was most predominant in the bilateral thalamus, right caudate, left hippocampus, parahippocampal gyrus, bilateral posterior, middle and anterior cingulate, insula, inferior, middle, superior and dorsolateral frontal areas, Figure 2e and Table S2. In the case of MCS patients shows a similar heterogeneous spatial distribution to that of HC, Figure S2. Compared to the healthy controls, in MCS patients was lower only in the bilateral thalamus and left medial prefrontal cortex, see Figure 2f and Table S2.
The results reported so far indicate a breakdown in the spatiotemporal structure of the BOLD signals that involves reduced propagation and integration capabilities of endogenous events in DoC patients, especially in the UWS group. For the remaining of the paper we shift to model‐based analyses.
3.3. Whole‐brain effective connectivity shows altered causal interactions in DoC patients
In order to identify alterations to the causal relations between the brain regions, we computed the whole‐brain effective connectivity (EC) from the resting‐state BOLD for each subject. In short, the estimation of EC consists of identifying the most likely connectivity that gives rise to the observed data, fitting a generative dynamical model. In our case, this implied to adjust the pair‐wise connection strengths between the brain regions through an optimization procedure such that the resulting covariances are closest to the empirical ones (Adhikari et al., 2021; Gilson et al., 2016), see Figure 3a. As the generative model of the signals we considered the multivariate Ornstein‐Uhlenbeck process in Equation (2). This is a model of noise diffusion on a network for which the covariance matrices can be analytically estimated, thus allowing for a fast optimization.
FIGURE 3.
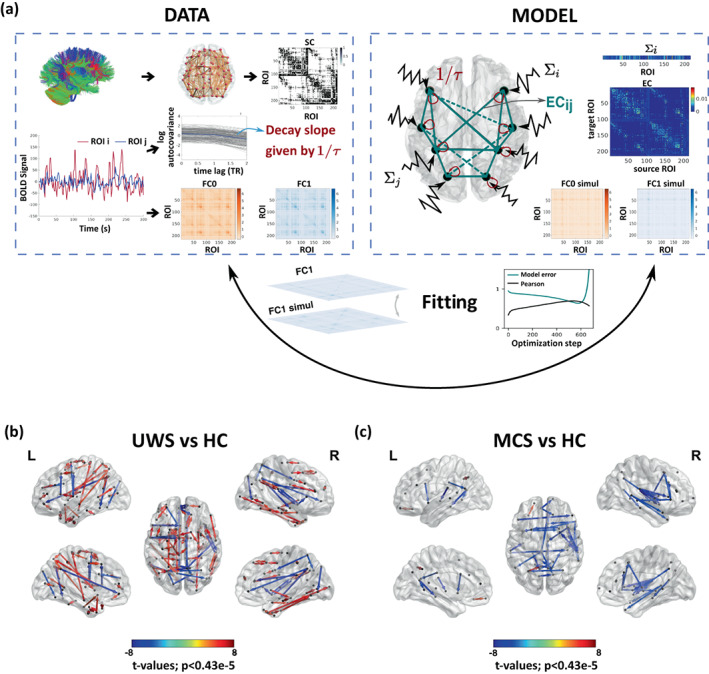
Comparison of effective connectivity (EC) between healthy controls and patients. (a) Schematic representation of the fitting procedure leading to estimation of EC. Considering a model of noise diffusion—the multivariate Ornstein‐Uhlenbeck process—the whole‐brain network model is constrained using structural connectivity obtained from diffusion imaging and then fitted to reproduce the empirical resting‐state data. In particular, to fit the zero‐lag and 1TR‐lag covariance matrices and , and the regional noise level ∑i. (b, c) Maps of significantly different EC connections between patients and controls. UWS patients show connections with both decreased and increased EC (decreased in fronto‐temporal, frontal–parietal and midline regions; increased in subcortical and wide cortical areas). Blue and red arrows indicate lower and higher EC, respectively, in patients as compared to HC subjects. MCS patients show decreased EC in fronto‐temporal and interhemispheric midline connections. The directional connections in the glass brain represents connections with significant between‐group differences (Bonferroni corrected for 11,395 tests, p‐value < 0.05) are represented.
At the whole‐brain level, averaging all the connections in a subject, we found that the EC of in patients with UWS was higher than for the healthy controls or than in MCS patients (HC = 0.015 ± 0.002, UWS = 0.019 ± 0.004, MCS = 0.014 ± 0.003; HC vs. UWS t(45) = −4.7, p < 0.0001, MCS vs. UWS t(38) = −4.0, p < 0.001). A closer inspection of the pair‐wise EC values revealed the presence of links that either increased or decreased in UWS with respect to the healthy controls, Figure 3b. The patients with UWS showed increased EC for connections in the subcortical (thalamus, caudate and putamen) and cortical regions, but also decreased EC in connections spanning posterior (i.e., parietal, occipital) to frontal (i.e., temporal and frontal) regions as well as between midline posterior regions (parietal, occipital) and middle frontal regions. The MCS patients showed especially lower EC in interactions from posterior to frontal and temporal regions and midline regions encompassing the middle prefrontal and posterior cortex and the thalamus, see Figure 3c, including regions important for long range connectivity and overlapping with key areas of the Default Mode Network (i.e., Posterior cortex, middle frontal, bilateral inferior parietal and temporal).
3.4. Altered spatiotemporal propagation of exogenous perturbations
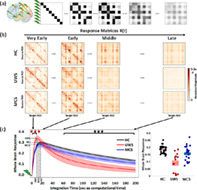
Having identified changes in specific pair‐wise EC connections for both UWS and MCS patients, the remaining question is how those alterations affect the propagation of information throughout the brain. To investigate this question, we performed an in‐silico perturbational study and evaluated how exogenous perturbations spread in the three conditions. For that, we considered again, as for the EC estimation, the multivariate Ornstein‐Uhlenbeck process to be the generative dynamical model of the brain activity. Applying a unit perturbation to every brain region at time , the pair‐wise responses are analytically estimated as in Equation (3). The resulting spatio‐temporal responses carry information of the spread of activity (Gilson et al., 2018, 2019), Figures 1a and 4a. Specifically, the pair‐wise elements represent the pair‐wise temporal response of area j to the unit perturbation applied on area i. This conditional response encompasses all network effects from i to j acting at different time scales over paths of different lengths. For the present study, the response analysis was performed on top of the EC matrices previously calculated for each participant—that is, the connectivity matrix A in Equation (2) is replaced by the corresponding EC matrix of the subject—over which the propagation takes place. Also, the regional time‐constants were constrained using the empirically calculated ones from the BOLD signals. First, we compared the global network response r(t) across the three conditions. The global response quantifies the sum of all pair‐wise responses over time, typically characterised by a rapid transient increase followed by a slow decay, Figure 1b. Second, since EC captures the weighted and asymmetric connection strengths between the brain regions, we also studied the temporal evolution of the input and output responses and of every region, Figure 1c,d, representing the receiving and the broadcasting capacities of the brain areas.
FIGURE 4.
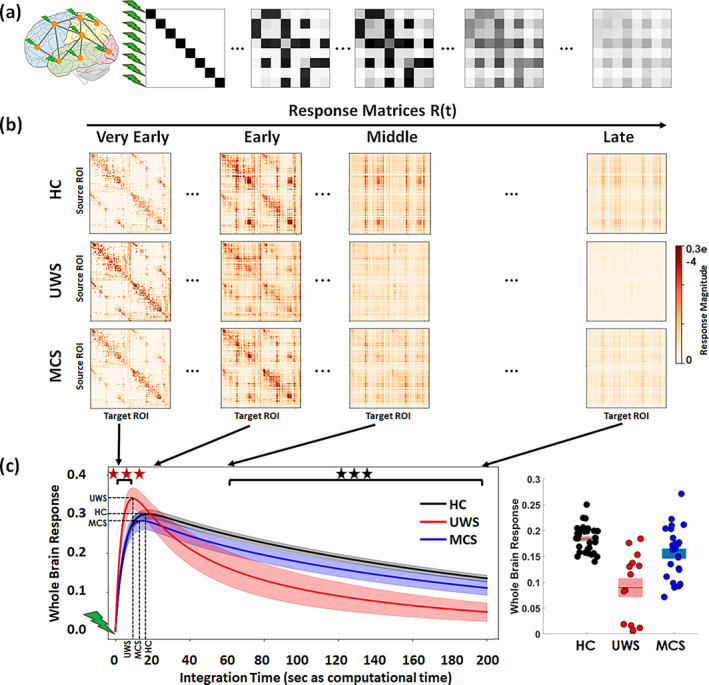
In‐silico propagation of exogenous perturbations. (a) Illustration of the propagation of simulated pair‐wise responses to initial unit perturbations at . Matrix elements represent the conditional response at region j due to the unit perturbation initially applied at region i. (b) Temporal evolution of the response matrices for healthy controls (HC) and patients (unresponsive wakefulness syndrome, UWS; minimally conscious state, MCS) at different times (early = 2 s, middle = 20 s, late 60 s and very late = 200 s). Note that here time corresponds to the arbitrary simulation time after the in‐silico perturbation is applied and thus it does not correspond to actual time, although the time‐constants governing the evolution were estimated from the BOLD signals. The colorbar represents the relative strength of the response between brain regions (unitless). (c) Whole brain response curves for the three study cases reflecting the sum of all pair‐wise responses at each time point post‐stimulus (left panel). Shaded areas represent the 95% confidence intervals across subjects. Black stars indicate a difference in global responses between all three groups (Bonferroni corrected for 100 tests/time points, p‐value = 0.05). Red stars indicate the early epoch during which UWS patients display a larger response than HC and MCS (Bonferroni corrected for 100 tests/time points, p‐value = 0.05). The bar graph represents area‐under‐the‐curve for the three global response curves in the time range t = 60–200 s, quantifying the differences across the three groups (right panel).
Sample response matrices for three participants are presented in Figure 4b. As seen, the patterns of responses are progressively reshaped over time for the three study groups—healthy controls, UWS patients and MCS patients. The group averaged global network responses are shown in Figure 4c. As expected, the global responses undergo a transient increase followed by a slower decay phase as the effects of the initial stimuli dissipate due to the leakage term of Equation (2). This relaxation is also observed in the homogenization of the response matrices at the longer latencies in Figure 4a. The global response curves for controls and MCS groups follow quite a similar behavior, both peaking at 18.2 ± 2.9 and 15.6 ± 3.7 s, respectively, and taking peak values 0.30 ± 0.03 and 0.28 ± 0.05. In the UWS group, the global response peaks sooner (10.6 ± 2.9 s) (HC vs. UWS t(45) = 8.2, p < 0.0001, HC vs. MCS t(57) = 3.0, p = 0.0036, MCS vs. UWS t(38) = 4.3, p < 0.001) and displays a higher peak (0.34 ± 0.05) (HC vs. UWS t(45) = −3.3, p = 0.0019, MCS vs. UWS t(38) = −3.1, p = 0.0031) than for the controls and MCS groups, but then it decays notably faster. Quantitatively, we found that the area‐under‐the‐curve in the time spanning 60–200 s (modeled time) significantly decreases for the UWS group (0.08 ± 0.06) and MCS patients (0.15 ± 0.04) compared to healthy controls (0.18 ± 0.02) (HC vs. UWS t(45) = 7.1, p < 0.0001, HC vs. MCS t(57) = 2.9, p = 0.005, MCS vs. UWS t(38) = 3.6, p < 0.001).
3.5. Broadcasting and integrative capabilities of brain regions across states of consciousness
Given that EC identifies the directed and weighted causal interactions, we could study the differentiated input and output responses— and —of each brain area in respect to the exogenous perturbations, see Figure 1c,d for illustration. First, in Figure 5a, the trajectories of the receiving and the broadcasting capacities for each brain region are compared plotting the two temporal trajectories against each other. Each panel shows the example for one participant. These results show that in the healthy participants some of the brain regions take a distinctive functional role, displaying either a dominant receiving or a broadcasting capacity. However, for the MCS and UWS patients such specialised regions are reduced or absent.
FIGURE 5.
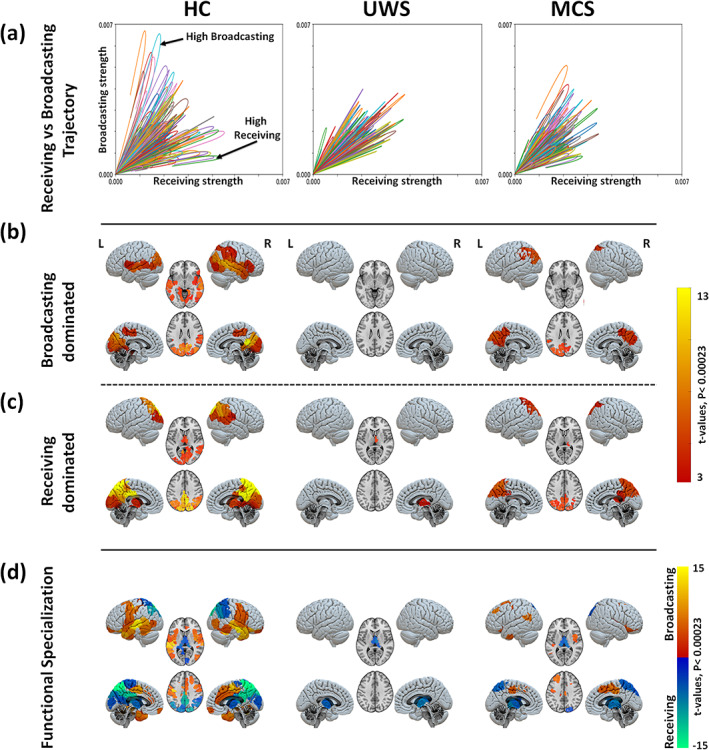
Region‐wise broadcasting and receiving capacities due to exogenous perturbations. (a) Comparison between the temporal trajectories of the receiving and the broadcasting for different brain regions. Results for one sample participant shown in each panel. In healthy controls, an asymmetry between the receiving and broadcasting of several areas is observed suggesting a specialised functional role of those areas. This functional differentiation is lost in patients with UWS. Note that the end of the network response curve is cut at the end of the simulation time (200 s). Maps of significantly large broadcasting (b) and receiving capacities (c) for the three study groups (healthy controls, HC; unresponsive wakefulness syndrome, UWS; and minimally conscious state, MCS). The color code represents the t‐values. Only regions with significantly high values are presented in each case (Bonferroni corrected p‐values < 0.05 for 214 tests (brain regions). (d) Maps of regional specialization estimated as the difference between the broadcasting and the receiving capacities of each brain region.
The group average receiving and broadcasting capacities for the three conditions are mapped in Figure 5b,c. In the healthy controls, we found a few brain regions with simultaneous large broadcasting and receiving capacities: the bilateral occipital, calcarine, lingual, cuneus, precuneus, superior and inferior parietal, right middle temporal. Only significant broadcasting capacity was found in the bilateral middle and superior temporal, right inferior temporal, left parahippocampal gyrus, bilateral insula, inferior parietal, right supramarginal and right inferior frontal areas. And, only significant receiving capacity was identified for the bilateral thalamus, posterior cingulate cortex (PCC), precuneus, middle cingulate and right supramarginal gyrus. In patients with UWS, however, we found that no brain region stands out either as a broadcaster or as a receiver; except for the thalamus which displays a relatively large receiving capacity. The group of MCS patients was characterized by a generalised reduction of both broadcasting and receiving capacities. A few areas displayed simultaneous significant receiving and broadcasting capacities: bilateral occipital, cuneus, bilateral superior and inferior parietal and precuneus. Preserved significant broadcasting was found in the left supramarginal area, Figure 5b, and significant receiving capacity was observed in the right thalamus, Figure 5c. See Table S3 for further details.
Figure 5d summarises the functional specialization of the brain regions, which was evaluated as the area between the broadcasting and receiving curves such that . The results suggest the presence of two distinct networks in healthy subjects: a receiving network prominently represented by the posterior cortex, the occipital cortex and the thalamus, and a broadcasting network encompassing parietal, temporal and frontal cortices. These two specialized functional networks show a strongly hampered flow in UWS patients with only preserved receiving capacity in the thalamus. In MCS patients, we observe that the two networks have been partially preserved, although flow in both receiving and broadcasting networks is diminished. The broadcasting network is smaller, yet the blueprint of the receiving network is largely preserved whereas these in MCS patients.
Having identified separate networks of brain areas specialised in either the integration or the broadcasting of activity, we finalise the model‐based perturbational analysis by directly comparing how these networks are altered in the patients, in respect to their configuration in the healthy controls, Figure 6. As compared to HC, broadcasting capacity was notably reduced in patients with UWS at the bilateral hippocampus, parahippocampal gyrus, thalamus, caudate, amygdala, putamen, insula, inferior/middle temporal, temporal pole, right superior temporal, fusiform, lingual, calcarine, occipital, anterior cingulate, right inferior and middle frontal cortices. The lack of broadcasting capacity of the subcortical regions evidences a reduced activity of the whole brain network. Regarding the receiving capacity was significantly reduced in patients with UWS at the bilateral precuneus, PCC, lingual, calcarine, fusiform, middle occipital, middle/anterior cingulum, inferior/superior parietal, supramarginal, middle temporal, inferior frontal cortices and the middle prefrontal cortex. These regions encompass primary visual and auditory areas, but also higher integration areas in the PCC that have an important hub function within the whole‐brain network, see Figure 6 and Table S4.
FIGURE 6.
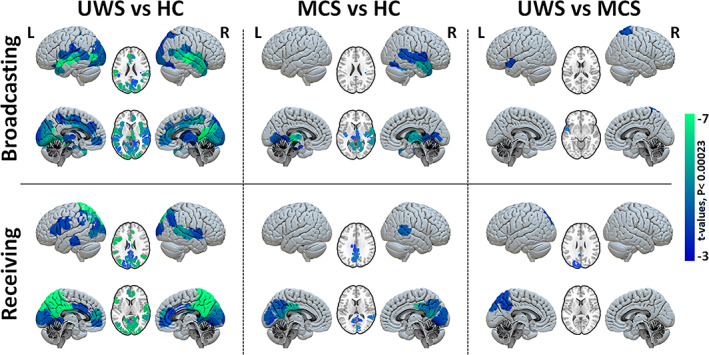
Group comparison of regional broadcasting and receiving capacities after exogenous perturbations. Maps of regional contrasts in broadcasting and receiving capacity between study groups. Color bar represents the t‐values for regions with significant between‐group differences (Bonferroni corrected p‐values < 0.05 for 214 tests (brain regions).
Compared to healthy controls the MCS patients showed a significant reduction for the broadcasting in the bilateral thalamus, parahippocampal gyrus, left hippocampus, bilateral insula, inferior/middle temporal, right superior temporal, bilateral fusiform and lingual cortices, Figure 6, middle column. We furthermore observed a reduced capacity to receive information in the bilateral precuneus, PCC, cuneus, right lingual, calcarine, bilateral middle cingulum and right middle temporal cortices. The comparison between MCS and UWS showed an additional significant reduction for patients with UWS in receiving and broadcasting of information at the left precuneus, occipital cortex, temporal and right superior parietal, Figure 6, right column; thus indicating that the information flow in these areas might be the most important contributors to conscious information processing.
3.6. Association of whole‐brain network responses to clinical measures
In order to better contextualise the data‐driven and the model‐based analyses reported in this study, we also searched for the relation to other aspects of clinical interest. We first evaluated if the whole brain responses (as in Figure 4c) are sensitive to etiology alongside the level of consciousness. Main and interaction effects of diagnosis and etiology on the peak value (i.e., early response) and late global brain responses (area‐under‐the‐curve in the 60–200 s of modeled time) were quantified using a linear regression model. We did not find significant differences for peak global responses for diagnosis (p = 0.405), etiology (p = 0.137), or the interaction between diagnosis and etiology (p = 0.258), the model r‐squared = 0.27 and model p‐value = 0.008. For the late global response, we noted significant differences in the case of diagnosis but neither in etiology nor in the interaction between diagnosis and etiology (p‐value for diagnosis = 0.0004, p‐value for etiology = 0.063, p‐value for interaction = 0.096; the model r‐squared = 0.32 and model p‐value = 0.0027). This confirms that the main differences in our analyses are due to diagnosis and ensured that the observed effects were mediated by the level of consciousness primarily, rather than by the effects of etiology. Indeed, looking at the global brain responses of individual subjects, we see that the anoxia and TBI subjects are diversely distributed in both UWS and MCS patient groups, Figure 7a. As etiology and the interaction between etiology and diagnosis were not significant, we did not explore their relationship with the regional responses further.
FIGURE 7.
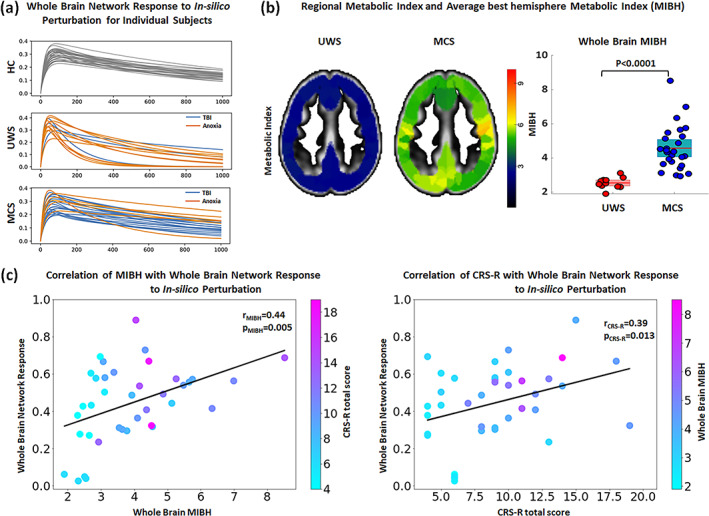
Association of the individual whole brain response curves of in‐silico perturbations and clinical variables. (a) Response curves for individual participants grouped by diagnostic including healthy controls (HC; top), unresponsive wakefulness syndrome (UWS; middle) and minimally conscious state (MCS; bottom) and colored by etiology in the case of DoC patients (Anoxia in orange and non‐Anoxia [e.g., TBI, hemorrhage] in blue). The whole‐brain responses of anoxia and TBI patients are heterogeneously distributed in both UWS and MCS groups. (b) Example for the MIBH images for a representative UWS and MCS patient. As also evident from the boxplot, glucose metabolism is minimal in UWS patients while partially preserved in MCS patients. (c) Correlation of whole brain response to simulated perturbation (y‐axis) with the metabolic index of the best hemisphere (MIBH; x‐axis) and individual data points are color coded according to the patient's CRS‐R total score (left panel). Similarly, correlation of whole brain response to In‐silico perturbation (y‐axis) with the CRS‐R total score (x‐axis) and individual data points are color coded according to the patient's MIBH index (right panel).
Since neural activity propagation requires the consumption of energy at the neural level, we quantified whole‐brain glucose metabolism (measured via glucose PET imaging) and assessed its relation to the integrative network response (measured as the whole‐brain computational response to perturbation). We first establish that the MIBH of UWS patients was significantly lower (2.53 ± 0.31) as compared to MCS patients (4.57 ± 1.32), (p < 0.0001), Figure 7b. Then, we compared the whole brain glucose PET MIBH values with the whole brain network response of the regions whose perturbation showed significantly altered flow in UWS patients. We noted positive correlations of whole brain network responses with the MIBH (r = 0.44, p = 0.005; Figure 7c, left column). To further explore the link of the network response with behavior observable at the bedside, we correlated the functional network response with CRS‐R scores obtained from behavioral evaluation. This also yielded a significant correlation (r = 0.39, p = 0.013 Figure 7c right column).
In summary, our model‐based analyses to estimate effective connectivity and to simulate in‐silico the response to exogenous perturbations can be related to basic biological measures and clinical observations, allowing us to identify specific directed pathways that are disrupted in patients with DoC.
4. DISCUSSION
In the present paper, we have studied the neural propagation of endogenous and exogenous perturbations in the brain using model‐free and model‐based analysis methods, applied to the problem of elucidating the mechanisms behind the loss of consciousness due to acquired brain injury and its partial recovery. The methods employed here add significant value to the dynamical approaches for two main reasons. First, they rely on simple observables—the resting‐state fMRI—thus bypassing the need to execute experimental exogenous stimulation protocols, for example, transcranial magnetic stimulation. Second, unlike previous approaches, they allowed us to investigate the directional causal interactions between brain regions, thus elucidating alterations in the broadcasting and the integrating capacities of individual areas or pathways, between normal awake and unconscious patients. Our main finding is that we could identify two distinct malfunctioning neural circuits in patients with DoC: the posterior cortical regions fail to convey information, in conjunction with reduced broadcasting of information from subcortical, temporal, parietal and frontal regions. These results show that patients with prolonged disorders of consciousness lack the capacity for the integration of events that would lead to conscious perception.
In healthy controls, we found that the relaxation time constants associated with the resting‐state BOLD signals display a graded spatial distribution with shorter relaxation times in subcortical areas and longer time constants in the frontal and in the parietal areas, Figure S2a. Accordingly, analysis of exogenous in‐silico perturbations revealed that the broadcasting of information flow is predominant in a broad range of cognitive modules, including the hippocampus, parahippocampal gyrus, temporal, posterior and inferior frontal regions. This subcortical–cortical loop has been proposed to mediate the sensory information to be globally ‘accessible’ to other cognitive functions through feedforward and feedback loops by the global neuronal workspace theory, and only when access to all cognitive modules occurs, sensory content is elevated to conscious perception (Dehaene et al., 2011; Dehaene & Changeux, 2011; Mashour et al., 2020). Although the activity in the posterior regions is highly influenced by perturbations, suggesting that they have a large cause‐effect capacity to receive and integrate the information flow, is one of the key principles of conscious perception in integration information theory (Oizumi et al., 2014; Tononi, 2004; Tononi et al., 2016).
Regarding the patients with unresponsive wakefulness syndrome (UWS), the results observed were very much altered. First, the propagation of endogenous events occurring in the resting‐state BOLD rapidly decays, avoiding their subsequent integration, Figure 2b. This is corroborated by the fact that the spatial distribution of relaxation times fades away in the UWS patients, with all areas taking short relaxation times (Figure 2d,e) and evidencing that local activity does not properly propagate along the network. Especially frontal, parietal and higher‐order cortices which ensure sensory information processing, need longer time to integrate diverse information (Hasson et al., 2008; Yeshurun et al., 2017). Second, effective connectivity is reduced overall but interestingly some effective subcortical–cortical connections were found to significantly increase, Figure 3b. The propagation of in‐silico exogenous perturbations showed a rapid and large initial response quickly followed by a fast decay, Figure 4c, since the activity fails to propagate throughout the network in a sustained manner. Such early hyper‐response has been previously seen in UWS patients (Di Perri et al., 2013) and in loss of consciousness due to generalized epilepsy possibly caused by excess electrical discharges in the brain (Moeller et al., 2008). The mechanism for this hyper‐response, Figure S3, is yet to be fully elucidated but it has been previously reported during loss of consciousness in different scenarios. For example, Kroeger and Amzica (2007) observed hypersensitivity to stimuli (sensory or mechanical) in cats during deep anesthesia. Their results suggested that during the periods of neural inactivity (the down states) both intra‐ and extra‐cellular (e.g., Ca2+) concentrations have the time to relax to basal levels allowing the neural tissue to respond the moment a stimulus is applied. Wollstadt et al., 2017 suggested that such hyper‐response could be due to lack of inhibition within and between subcortical–cortical areas in anesthetized ferrets (Wollstadt et al., 2017). The hyper‐response after stimulation is reminiscent of the empirical stimulation studies in DoC patients too. Activity after transcranial magnetic stimulation in unconsciousness states are characterized by a breakdown of cortical complexity (Casali et al., 2013; Massimini et al., 2005), hypothesized to be the result of low integration or lacking differentiation in neural activity. Such a network‐level interpretation might be relevant for the interpretation of our results as well, and after initial perturbation, a rapid decline in the brain's ability to process and broadcast stimuli is observed. Simply stated, even if the unconscious brain attempts to propagate activity throughout the network, it fails to integrate the input into conscious perception.
The patients in minimally conscious state (MCS) studied here went through a period of coma and UWS after brain injury, but later regained partial consciousness and cognitive functionalities. All the results found for the MCS patients show moderate alterations to those in the healthy participants, as expected from their partial functional recovery. The spatial gradient of relaxation time constants from the resting‐state BOLD is recovered, Figure S2, except shorter time constants were still found in the thalamus and the left medial prefrontal cortex. Effective connectivity was in general slightly below values observed in control subjects but a significant reduction was found remaining in frontoparietal connections and in between temporal regions, Figure 3c. Regional broadcasting and receiving capacities to in‐silico perturbations displayed a recovered scenario, see Figure 5 and Table S3. It is clinically relevant to understand why or how MCS patients could partially recover from the unresponsive wakefulness state. In the light of our results, it seems that a sufficient regain of the propagation of information leading to an increase in receiving and broadcasting of information at the left precuneus, occipital cortex, temporal and right superior parietal is instrumental for the recovery of conscious information processing, Figure 6.
In comparison with healthy controls, the patients with UWS showed a severe reduction of receiving information in posterior regions, which implies sensory information integration is already impaired at the level of sensory regions to the high‐level hub regions of the Default Mode Network (i.e., PCC and Precuneus). Indeed, the lack of receiving of information in the sensory areas hampers a stimulus or event to reach awareness, as integration of external inputs is a prerequisite for consciousness (Herbet et al., 2014). Our results provide a mechanistic explanation for how the ability to receive information in sensory and DMN hub regions alters cerebral information processing, which might be at the essence for the structural and functional anomalies in UWS. Although it is known that the PCC and the Precuneus have decreased structural, functional and metabolic integrity (Annen et al., 2016; Demertzi et al., 2015; López‐González et al., 2021; Luppi et al., 2019; Stender et al., 2014), our results show that the ability to receive information in sensory and DMN hub regions is reduced in UWS. On the other hand, broadcasting was reduced in the subcortical regions (i.e., thalamus, caudate, putamen) and regions involved in higher cognitive function (i.e., temporo‐parietal, anterior cingulate and frontal regions). This is aligned with the mesocircuit hypothesis (Schiff, 2010) which states that the feedforward connections between these regions play a key role in reaching levels of (cortical) activity that support the stimuli to access consciousness processing. This has been recently confirmed in macaques using intracraneal‐EEG, showing that integration at the thalamus, caudate, putamen and parietal cortex is a hallmark of conscious states (Afrasiabi et al., 2021). Our findings unravel that human consciousness also relies on the broadcasting capacities (i.e., from the thalamus, caudate and putamen) to support the transmission of activity, functional integration and recurrent activity between subcortical and cortical neurons, all of which is lost in UWS. Interestingly, we also noted a decrease in receiving and broadcasting capacities in the bilateral temporal areas for DoC patients. Recent studies also noted altered structural (Annen et al., 2018) and functional loss in the temporal area of DoC patients (Demertzi et al., 2015; Thibaut et al., 2021). To date, there is limited explanation for the involvement of the temporal cortex in consciousness. We speculate that a lesser involvement of the temporal areas in the information pathways could impede self‐awareness and memory.
From a clinical point of view, there is a variety of causes leading to disorders of consciousness. These are typically classified into two categories. On the one hand, anoxia is a generalized damage of brain tissue due to a temporary disruption of oxygen supply caused by, e.g., a heart attack or asphyxia. On the other hand, loss of consciousness can also occur as a result of focal brain lesions, e.g., traumatic brain injury, stroke or epilepsy. It is well‐known that the probability of (partial) recovery from UWS is larger for patients with focal lesions than for anoxic patients (Thibaut et al., 2021). This is reflected in the sample of patients here studied since 11 out of 14 patients with UWS are anoxic and 19 out of 26 patients in MCS suffered from focal brain injuries. However, the extent of damage is not a perfect predictor and the heterogeneity of lesions across patients calls for a better understanding of the mechanistic causes leading to the loss and the (partial) recovery of consciousness. We have explored the effects of etiology in our results and found that the diagnostic classification of the patients into UWS and MCS based on EC and on the propagation of perturbations significantly correlate, while this was not the case for etiology. Even though, at this point, we could not establish a link between etiology and network responses, perhaps due to a lack of data and heterogeneity within the data, hypothetically the evaluation of lesion‐specific alterations in network responses could help formulate more specific predictions about where propagation is significantly altered in reduced conscious states. Other samples including healthy volunteers under sedation could help narrowing down the location of possible consciousness mechanisms further as well.
Additionally, we have observed that activity propagation leading to consciousness is correlated to the presence of relatively widespread preserved glucose metabolism (Figure 7). This widespread preserved glucose metabolic rate is associated to the richness of signs of consciousness at the behavioral level, as commonly reported in the literature (Annen et al., 2016; Stender et al., 2016; Thibaut et al., 2021). The association of the complex model‐based assessment of network function to empirically measured brain metabolism and behavioral profiles in the first place suggests that the model is biologically relevant. Second, although a causal relation cannot be established to date, it is a first step towards the exploration of a potential mechanism behind the widespread altered glucose metabolism in DoC patients. However, the causal relationship between regional glucose metabolism and their broadcasting/receiving properties is still to be clarified. On the one hand, we could speculate that a significant disruption of the propagation of events along the neural network leads to a loss of metabolic demand, which is then observed via glucose PET. But, on the other hand, the opposite possibility also needs to be considered that the brain lesions could disrupt the metabolic supply chains, thus exhausting the capacity of the neural network to generate sufficient activity and responses. To be noted, both BOLD and FDG‐PET are related to metabolism and neural function, and a relationship between the two is to be expected. However, the latter is a more direct measure of metabolism. Another relevant difference is that the timescales of both the modalities are very different, which allows for a complementary interpretation of the findings. FDG‐PET presents the cumulative metabolism of gray matter at rest and is possibly related to the capacity for consciousness in an individual. We believe, the BOLD response after perturbation gives an indication of the state specific potential activity of specific brain areas (Bodart et al., 2017). Hence, the current assessment of activity propagation could be used to monitor patient's progress over time or in response to therapy.
Our in‐silico pertubational study revealed transient global changes to the propagation of activity, associated to glucose metabolism, that are similar to those we observed from the integration of endogenous events with the intrinsic ignition. In DoC patients, and especially for those with UWS, the brain's cause‐effect capacity to respond is significantly lower than during normal wakefulness in healthy subjects. It seems that the observed spatiotemporal alterations of local event processing also hamper global integration and whole brain neural responses; as observed both after in‐silico and endogenous perturbations. These results are in line with a number of empirical observations showing that during loss of consciousness due to sleep, anesthesia or brain damage, external natural (artificial perturbations) trigger normal neural responses in the area primary sensory cortices (in the area of application) but this initial activity fails to adequately propagate further impeding conscious integration and perception of the stimuli at higher cognitive levels (Arena et al., 2021; Casali et al., 2013; Ishizawa et al., 2016; Krom et al., 2020; Massimini et al., 2005; Pavone et al., 2017; Portas et al., 2000; Sela et al., 2016). In conclusion, the cerebral capacity of propagation and integration of local, naturally occurring events into the entire network is affected by reduced states of consciousness and shares similarities with both information integration theory (Tononi, 2004; Tononi et al., 2016) and global neuronal workspace theory (Dehaene et al., 2011; Mashour et al., 2020). Although these theories have distinct concepts of consciousness (Northoff et al., 2020; Northoff & Lamme, 2020; Winters, 2020), our results suggest that they might represent two sides of the same coin.
AUTHOR CONTRIBUTIONS
Rajanikant Panda, Ane López‐González, Jitka Annen, Gorka Zamora‐López, Matthieu Gilson, Gustavo Deco and Steven Laureys designed research. Jitka Annen, Steven Laureys and Gorka Zamora‐López supervised the research. Jitka Annen, Aurore Thibaut, Olivia Gosseries and the Coma Science Group Collaborators acquired the data. Rajanikant Panda, Ane López‐González and Anira Escrichs preprocessed the data. Rajanikant Panda, Ane López‐González, Jitka Annen, Gorka Zamora‐López and Gianluca Frasso analyzed the data. Matthieu Gilson and Gorka Zamora‐López designed the computational model and optimized the code as per this research study. Rajanikant Panda, Jitka Annen, Ane López‐González and Gorka Zamora‐López wrote the manuscript. All authors interpreted the results and contributed to the editing of the manuscript.
FUNDING INFORMATION
RP is a research fellow, OG and AT is research associate and SL is research director at F.R.S.‐FNRS. ALG and GD was supported by Swiss National Science Foundation Sinergia, grant no. 170873. SL and GD received funding from the European Union's Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 785907 (Human Brain Project SGA2) and No. 945539 (Human Brain Project SGA3). The study was further supported by the University and University Hospital of Liege, the Belgian National Funds for Scientific Research (FRS‐FNRS), Human Brain Project (HBP), the European Space Agency (ESA) and the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Programme, “Fondazione Europea di Ricerca Biomedica,” the Bial Foundation, the Mind Science Foundation and the European Commission, the Fund Generet, the King Baudouin Foundation, AstraZeneca foundation, Leon Fredericq foundation and the DOCMA project [EU‐H2020‐MSCA‐RISE‐778234]. GD acknowledges funding from the FLAG‐ERA JTC (PCI2018‐092891), the Spanish Ministry Project PSI2016‐75688‐P (AEI/FEDER), the Catalan Research Group Support 2017 SGR 1, and AWAKENING (PID2019‐105772GB‐I00, AEI FEDER EU) funded by the Spanish Ministry of Science, Innovation and Universities (MCIU), State Research Agency (AEI) and European Regional Development Funds (FEDER).
CONFLICT OF INTEREST STATEMENT
The authors report no conflict of interest.
Supporting information
Data S1. Supporting information.
ACKNOWLEDGMENTS
We would like to thank the healthy participants, the patients, their families, caregivers and treating clinicians for their participation in this study. The authors thank the whole staff from the ICU and Nuclear Medicine departments, University Hospital of Liège. We are highly grateful to the members of the Liège Coma Science Group for their assistance in clinical evaluations.
Coma Science Group Collaborators: Alice Barra, Charlotte Martial, Claire Bernard, Estelle Bonin, Emilie Szymkowicz, Jean‐Flory Luaba Tshibanda, Leandro Sanz, Marie Vitello, Roland Hustinx.
Panda, R. , López‐González, A. , Gilson, M. , Gosseries, O. , Thibaut, A. , Frasso, G. , Cecconi, B. , Escrichs, A. , Coma Science Group Collaborators , Deco, G. , Laureys, S. , Zamora‐López, G. , & Annen, J. (2023). Whole‐brain analyses indicate the impairment of posterior integration and thalamo‐frontotemporal broadcasting in disorders of consciousness. Human Brain Mapping, 44(11), 4352–4371. 10.1002/hbm.26386
Rajanikant Panda and Ane López‐González contributed equally.
Gorka Zamora‐López and Jitka Annen share supervision.
Coma Science Group Collaborators are listed in Acknowledgments section.
Contributor Information
Gorka Zamora‐López, Email: gorka@zamora-lopez.xyz.
Jitka Annen, Email: jitka.annen@uliege.be.
DATA AVAILABILITY STATEMENT
Data employed in this manuscript can be made available by the corresponding author on reasonable request. Regarding code, intrinsic ignition was calculated using MATLAB code available at https://github.com/RajanikantPanda/Ignition_and_Information_flow_for_DOC, estimation of effective connectivity was computed using the pyMOU Python package (https://github.com/mb-BCA/pyMOU) and the study of responses to exogenous perturbations was carried out using the NetDynFlow package in Python (https://github.com/mb-BCA/NetDynFlow). Both GitHub repositories for pyMOU and NetDynFlow contain usage tutorials in the form of Jupyter Notebooks. Usage of NetDynFlow and pyMOU functions in Python is available at https://github.com/RajanikantPanda/Ignition_and_Information_flow_for_DOC.
REFERENCES
- Adhikari, M. H. , Griffis, J. , Siegel, J. S. , Thiebaut de Schotten, M. , Deco, G. , Insabato, A. , Gilson, M. , & Corbetta, M. (2021). Effective connectivity extracts clinically relevant prognostic information from resting state activity in stroke. Brain Communications, 3, fcab233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afrasiabi, M. , Redinbaugh, M. J. , Phillips, J. M. , Kambi, N. A. , Mohanta, S. , Raz, A. , Haun, A. M. , & Saalmann, Y. B. (2021). Consciousness depends on integration between parietal cortex, striatum, and thalamus. Cell Systems, 12, 363–373.e11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Annen, J. , Frasso, G. , Crone, J. S. , Heine, L. , Di Perri, C. , Martial, C. , Cassol, H. , Demertzi, A. , Naccache, L. , & Laureys, S. (2018). Regional brain volumetry and brain function in severely brain‐injured patients. Annals of Neurology, 83, 842–853. [DOI] [PubMed] [Google Scholar]
- Annen, J. , Heine, L. , Ziegler, E. , Frasso, G. , Bahri, M. , Di Perri, C. , Stender, J. , Martial, C. , Wannez, S. , D'ostilio, K. , Amico, E. , Antonopoulos, G. , Bernard, C. , Tshibanda, F. , Hustinx, R. , & Laureys, S. (2016). Function–structure connectivity in patients with severe brain injury as measured by MRI‐DWI and FDG‐PET. Human Brain Mapping, 37, 3720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arena, A. , Comolatti, R. , Thon, S. , Casali, A. G. , & Storm, J. F. (2021). General anesthesia disrupts complex cortical dynamics in response to intracranial electrical stimulation in rats. eNeuro, 8. 10.1523/ENEURO.0343-20.2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armitage, R. (1995). The distribution of EEG frequencies in REM and NREM sleep stages in healthy young adults. Sleep, 18, 334–341. [DOI] [PubMed] [Google Scholar]
- Barnett, L. , Buckley, C. L. , & Bullock, S. (2009). Neural complexity and structural connectivity. Physical Review E, 79, 051914. [DOI] [PubMed] [Google Scholar]
- Barttfeld, P. , Uhrig, L. , Sitt, J. D. , Sigman, M. , Jarraya, B. , & Dehaene, S. (2014). Signature of consciousness in the dynamics of resting‐state brain activity. Proceedings of the National Academy of Sciences, 112, 201418031. http://www.pnas.org/content/early/2015/01/02/1418031112.short [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bettinardi, R. G. , Tort‐Colet, N. , Ruiz‐Mejias, M. , Sanchez‐Vives, M. V. , & Deco, G. (2015). Gradual emergence of spontaneous correlated brain activity during fading of general anesthesia in rats: Evidences from fMRI and local field potentials. NeuroImage, 114, 185–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodart, O. , Gosseries, O. , Wannez, S. , Thibaut, A. , Annen, J. , Boly, M. , Rosanova, M. , Casali, A. G. , Casarotto, S. , Tononi, G. , Massimini, M. , & Laureys, S. (2017). Measures of metabolism and complexity in the brain of patients with disorders of consciousness. NeuroImage: Clinical, 14, 354–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casali, A. G. , Gosseries, O. , Rosanova, M. , Boly, M. , Sarasso, S. , Casali, K. R. , Casarotto, S. , Bruno, M. A. , Laureys, S. , Tononi, G. , & Massimini, M. (2013). A theoretically based index of consciousness independent of sensory processing and behavior. Science Translational Medicine, 5, 198ra105. [DOI] [PubMed] [Google Scholar]
- Damasio, A. , & Meyer, K. (2009). Consciousness: An overview of the phenomenon and of its possible neural basis. The Neurology of Consciousness: Cognitive neuroscience and neuropathology, 3–14. [Google Scholar]
- Deco, G. , & Kringelbach, M. L. (2017). Hierarchy of information processing in the brain: A novel ‘intrinsic ignition’ framework. Neuron, 94, 961–968. [DOI] [PubMed] [Google Scholar]
- Deco, G. , Kringelbach, M. L. , Jirsa, V. K. , & Ritter, P. (2017). The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Scientific Reports, 7, 3095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene, S. , & Changeux, J. P. (2011). Experimental and theoretical approaches to conscious processing. Neuron, 70, 200–227. [DOI] [PubMed] [Google Scholar]
- Dehaene, S. , Changeux, J. P. , & Naccache, L. (2011). The global neuronal workspace model of conscious access: From neuronal architectures to clinical applications. Research and Perspectives in Neurosciences, 18, 55–84. [Google Scholar]
- Demertzi, A. , Antonopoulos, G. , Heine, L. , Voss, H. U. , Crone, J. S. , De Los, A. C. , Bahri, M. A. , Di Perri, C. , Vanhaudenhuyse, A. , Charland‐Verville, V. , Kronbichler, M. , Trinka, E. , Phillips, C. , Gomez, F. , Tshibanda, L. , Soddu, A. , Schiff, N. D. , Whitfield‐Gabrieli, S. , & Laureys, S. (2015). Intrinsic functional connectivity differentiates minimally conscious from unresponsive patients. Brain, 138, 2619–2631. [DOI] [PubMed] [Google Scholar]
- Demertzi, A. , Tagliazucchi, E. , Dehaene, S. , Deco, G. , Barttfeld, P. , Raimondo, F. , Martial, C. , Fernández‐Espejo, D. , Rohaut, B. , Voss, H. U. , Schiff, N. D. , Owen, A. M. , Laureys, S. , Naccache, L. , & Sitt, J. D. (2019). Human consciousness is supported by dynamic complex patterns of brain signal coordination. Science Advances, 5, eaat7603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Perri, C. , Bastianello, S. , Bartsch, A. J. , Pistarini, C. , Maggioni, G. , Magrassi, L. , Imberti, R. , Pichiecchio, A. , Vitali, P. , Laureys, S. , & Di Salle, F. (2013). Limbic hyperconnectivity in the vegetative state. Neurology, 81, 1417–1424. [DOI] [PubMed] [Google Scholar]
- Finn, E. S. , Shen, X. , Scheinost, D. , Rosenberg, M. D. , Huang, J. , Chun, M. M. , Papademetris, X. , Todd Constable, R. , & Author, N. N. (2015). Functional connectome fingerprinting: Identifying individuals based on patterns of brain connectivity HHS public access Author manuscript. Nature Neuroscience, 18, 1664–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galán, R. (2008). On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS One, 3, e2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giacino, J. T. , Kalmar, K. , & Whyte, J. (2004). The JFK coma recovery scale‐revised: Measurement characteristics and diagnostic utility. Archives of Physical Medicine and Rehabilitation, 85, 2020–2029. [DOI] [PubMed] [Google Scholar]
- Giacino, J. T. , Katz, D. I. , Schiff, N. D. , Whyte, J. , Ashman, E. J. , Ashwal, S. , Barbano, R. , Hammond, F. M. , Laureys, S. , Ling, G. S. F. , Nakase‐Richardson, R. , Seel, R. T. , Yablon, S. , Getchius, T. S. D. , Gronseth, G. S. , & Armstrong, M. J. (2018). Practice guideline update recommendations summary: Disorders of consciousness: Report of the guideline development, dissemination, and implementation Subcommittee of the American Academy of Neurology; the American Congress of Rehabilitation Medicine; and the National Institute on Disability, Independent Living, and Rehabilitation Research. Archives of Physical Medicine and Rehabilitation, 99, 1699–1709. [DOI] [PubMed] [Google Scholar]
- Gilson, M. , Kouvaris, N. E. , Deco, G. , Mangin, J. F. , Poupon, C. , Lefranc, S. , Rivière, D. , & Zamora‐López, G. (2019). Network analysis of whole‐brain fMRI dynamics: A new framework based on dynamic communicability. NeuroImage, 201, 116007. [DOI] [PubMed] [Google Scholar]
- Gilson, M. , Kouvaris, N. E. , Deco, G. , & Zamora‐López, G. (2018). Framework based on communicability and flow to analyze complex network dynamics. Physical Review E, 97. 10.1103/physreve.97.052301 [DOI] [PubMed] [Google Scholar]
- Gilson, M. , Moreno‐Bote, R. , Ponce‐Alvarez, A. , Ritter, P. , & Deco, G. (2016). Estimation of directed effective connectivity from fMRI functional connectivity hints at asymmetries of cortical connectome. PLoS Computational Biology, 12, e1004762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. , Zamora‐López, G. , Pallarés, V. , Adhikari, M. H. , Senden, M. , Tauste‐Campo, A. , Mantini, D. , Corbetta, M. , Deco, G. , & Insabato, A. (2020). Model‐based whole‐brain effective connectivity to study distributed cognition in health and disease. Network Neuroscience, 4(2), 338–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti, L. , Douaud, G. , Bijsterbosch, J. , Evangelisti, S. , Alfaro‐Almagro, F. , Glasser, M. F. , Duff, E. P. , Fitzgibbon, S. , Westphal, R. , Carone, D. , Beckmann, C. F. , & Smith, S. M. (2017). Hand classification of fMRI ICA noise components. NeuroImage, 154, 188–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson, U. , Yang, E. , Vallines, I. , Heeger, D. J. , & Rubin, N. (2008). A hierarchy of temporal receptive windows in human cortex. The Journal of Neuroscience, 28, 2539–2550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbet, G. , Lafargue, G. , de Champfleur, N. M. , Moritz‐Gasser, S. , le Bars, E. , Bonnetblanc, F. , & Duffau, H. (2014). Disrupting posterior cingulate connectivity disconnects consciousness from the external environment. Neuropsychologia, 56, 239–244. [DOI] [PubMed] [Google Scholar]
- Hindriks, R. , Adhikari, M. H. , Murayama, Y. , Ganzetti, M. , Mantini, D. , Logothetis, N. K. , & Deco, G. (2016). Can sliding‐window correlations reveal dynamic functional connectivity in resting‐state fMRI? NeuroImage, 127, 242–256. 10.1016/j.neuroimage.2015.11.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishizawa, Y. , Ahmed, O. J. , Patel, S. R. , Gale, J. T. , Sierra‐Mercado, D. , Brown, E. , & Eskandar, E. N. (2016). Dynamics of Propofol‐induced loss of consciousness across primate neocortex. The Journal of Neuroscience, 36, 7718–7726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondziella, D. , Bender, A. , Diserens, K. , van Erp, W. , Estraneo, A. , Formisano, R. , Laureys, S. , Naccache, L. , Ozturk, S. , Rohaut, B. , Sitt, J. D. , Stender, J. , Tiainen, M. , Rossetti, A. O. , Gosseries, O. , & Chatelle, C. (2020). European academy of neurology guideline on the diagnosis of coma and other disorders of consciousness. European Journal of Neurology, 27, 741–756. [DOI] [PubMed] [Google Scholar]
- Kroeger, D. , & Amzica, F. (2007). Hypersensitivity of the anesthesia‐induced comatose brain. The Journal of Neuroscience, 27, 10597–10607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krom, A. J. , Marmelshtein, A. , Gelbard‐Sagiv, H. , Tankus, A. , Hayat, H. , Hayat, D. , Matot, I. , Strauss, I. , Fahoum, F. , Soehle, M. , Bostrom, J. , Mormann, F. , Fried, I. , & Nir, Y. (2020). Anesthesia‐induced loss of consciousness disrupts auditory responses beyond primary cortex. Proceedings of the National Academy of Sciences of the United States of America, 117, 11780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laureys, S. (2005). The neural correlate of (un)awareness: Lessons from the vegetative state. Trends in Cognitive Sciences, 9, 556–559. [DOI] [PubMed] [Google Scholar]
- Laureys, S. , Owen, A. M. , & Schiff, N. D. (2004). Brain function in coma, vegetative state, and related disorders. Lancet Neurology, 3, 537–546. [DOI] [PubMed] [Google Scholar]
- López‐González, A. , Panda, R. , Ponce‐Alvarez, A. , Zamora‐López, G. , Escrichs, A. , Martial, C. , Thibaut, A. , Gosseries, O. , Kringelbach, M. L. , Annen, J. , Laureys, S. , & Deco, G. (2021). Loss of consciousness reduces the stability of brain hubs and the heterogeneity of brain dynamics. Communications Biology, 4, 2020.11.20.391482. 10.1101/2020.11.20.391482v1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luppi, A. I. , Craig, M. M. , Pappas, I. , Finoia, P. , Williams, G. B. , Allanson, J. , Pickard, J. D. , Owen, A. M. , Naci, L. , Menon, D. K. , & Stamatakis, E. A. (2019). Consciousness‐specific dynamic interactions of brain integration and functional diversity. Nature Communications, 10, 4616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mashour, G. A. , Roelfsema, P. , Changeux, J. P. , & Dehaene, S. (2020). Conscious processing and the global neuronal workspace hypothesis. Neuron, 105, 776–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massimini, M. , Ferrarelli, F. , Huber, R. , Esser, S. K. , Singh, H. , & Tononi, G. (2005). Breakdown of cortical effective connectivity during sleep. Science, 309, 2228–2232. [DOI] [PubMed] [Google Scholar]
- Messé, A. , Rudrauf, D. , Benali, H. , & Marrelec, G. (2014). Relating structure and function in the human brain: Relative contributions of anatomy, stationary dynamics, and non‐stationarities. PLoS Computational Biology, 10, e1003530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller, F. , Siebner, H. R. , Wolff, S. , Muhle, H. , Granert, O. , Jansen, O. , Stephani, U. , & Siniatchkin, M. (2008). Simultaneous EEG‐fMRI in drug‐naive children with newly diagnosed absence epilepsy. Epilepsia, 49, 1510–1519. [DOI] [PubMed] [Google Scholar]
- Murray, J. D. , Bernacchia, A. , Freedman, D. J. , Romo, R. , Wallis, J. D. , Cai, X. , Padoa‐Schioppa, C. , Pasternak, T. , Seo, H. , Lee, D. , & Wang, X. J. (2014). A hierarchy of intrinsic timescales across primate cortex. Nature Neuroscience, 17, 1661–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagel, T. (1974). What is it like to Be a bat? Philosophical Review, 83, 435. [Google Scholar]
- Northoff, G. , & Lamme, V. (2020). Neural signs and mechanisms of consciousness: Is there a potential convergence of theories of consciousness in sight? Neuroscience and Biobehavioral Reviews, 118, 568–587. [DOI] [PubMed] [Google Scholar]
- Northoff, G. , Wainio‐Theberge, S. , & Evers, K. (2020). Is temporo‐spatial dynamics the “common currency” of brain and mind? In quest of “spatiotemporal neuroscience”. Physics of Life Reviews, 33, 34–54. [DOI] [PubMed] [Google Scholar]
- Oizumi, M. , Albantakis, L. , & Tononi, G. (2014). From the phenomenology to the mechanisms of consciousness: Integrated information theory 3.0. PLoS Computational Biology, 10, e1003588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owen, A. M. , & Coleman, M. R. (2008). Functional neuroimaging of the vegetative state. Nature Reviews Neuroscience, 9, 235–243. [DOI] [PubMed] [Google Scholar]
- Pavone, K. J. , Su, L. , Gao, L. , Eromo, E. , Vazquez, R. , Rhee, J. , Hobbs, L. E. , Ibala, R. , Demircioglu, G. , Purdon, P. L. , Brown, E. N. , & Akeju, O. (2017). Lack of responsiveness during the onset and offset of Sevoflurane anesthesia is associated with decreased awake‐alpha oscillation power. Frontiers in Systems Neuroscience, 11, 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips, C. L. , Bruno, M. A. , Maquet, P. , Boly, M. , Noirhomme, Q. , Schnakers, C. , Vanhaudenhuyse, A. , Bonjean, M. , Hustinx, R. , Moonen, G. , Luxen, A. , & Laureys, S. (2011). “Relevance vector machine” consciousness classifier applied to cerebral metabolism of vegetative and locked‐in patients. NeuroImage, 56, 797–808. [DOI] [PubMed] [Google Scholar]
- Portas, C. M. , Krakow, K. , Allen, P. , Josephs, O. , Armony, J. L. , & Frith, C. D. (2000). Auditory processing across the sleep‐wake cycle: Simultaneous EEG and fMRI monitoring in humans. Neuron, 28, 991–999. [DOI] [PubMed] [Google Scholar]
- Schiff, N. D. (2010). Recovery of consciousness after brain injury: A mesocircuit hypothesis. Trends in Neurosciences, 33, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sela, Y. , Vyazovskiy, V. V. , Cirelli, C. , Tononi, G. , & Nir, Y. (2016). Responses in rat Core auditory cortex are preserved during sleep spindle oscillations. Sleep, 39, 1069–1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selçuk Bayin, S. (2006). Green's functions. In Mathematical methods in science and engineering. John Wiley & Sons, Inc. [Google Scholar]
- Seth, A. K. , Barrett, A. B. , & Barnett, L. (2011). Causal density and integrated information as measures of conscious level. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 369, 3748–3767. [DOI] [PubMed] [Google Scholar]
- Shen, X. , Tokoglu, F. , Papademetris, X. , & Constable, R. T. (2013). Groupwise whole‐brain parcellation from resting‐state fMRI data for network node identification. NeuroImage, 82, 403–415. 10.1016/j.neuroimage.2013.05.081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Signorelli, C. M. , Wang, Q. , & Khan, I. (2021). A compositional model of consciousness based on consciousness‐only. Entropy, 23, 308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva, A. , Cardoso‐Cruz, H. , Silva, F. , Galhardo, V. , & Antunes, L. (2010). Comparison of anesthetic depth indexes based on thalamocortical local field potentials in rats. Anesthesiology, 112, 355–363. [DOI] [PubMed] [Google Scholar]
- Stender, J. , Gosseries, O. , Bruno, M. A. , Charland‐Verville, V. , Vanhaudenhuyse, A. , Demertzi, A. , Chatelle, C. , Thonnard, M. , Thibaut, A. , Heine, L. , Soddu, A. , Boly, M. , Schnakers, C. , Gjedde, A. , & Laureys, S. (2014). Diagnostic precision of PET imaging and functional MRI in disorders of consciousness: A clinical validation study. Lancet, 384, 514–522. [DOI] [PubMed] [Google Scholar]
- Stender, J. , Kupers, R. , Rodell, A. , Thibaut, A. , Chatelle, C. , Bruno, M. A. , Gejl, M. , Bernard, C. , Hustinx, R. , Laureys, S. , & Gjedde, A. (2015). Quantitative rates of brain glucose metabolism distinguish minimally conscious from vegetative state patients. Journal of Cerebral Blood Flow and Metabolism, 35, 58–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stender, J. , Mortensen, K. N. N. , Thibaut, A. , Darkner, S. , Laureys, S. , Gjedde, A. , & Kupers, R. (2016). The minimal energetic requirement of sustained awareness after brain injury. Current Biology, 26, 1494–1499. [DOI] [PubMed] [Google Scholar]
- Thibaut, A. , Panda, R. , Annen, J. , Sanz, L. R. D. , Naccache, L. , Martial, C. , Chatelle, C. , Aubinet, C. , Bonin, E. A. C. , Barra, A. , Briand, M. M. , Cecconi, B. , Wannez, S. , Stender, J. , Laureys, S. , & Gosseries, O. (2021). Preservation of brain activity in unresponsive patients identifies MCS star. Annals of Neurology, 90, 89‐100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi, G. (2004). An information integration theory of consciousness. BMC Neuroscience, 5, 42. https://bmcneurosci.biomedcentral.com/articles/10.1186/1471-2202-5-42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi, G. , Boly, M. , Massimini, M. , & Koch, C. (2016). Integrated information theory: From consciousness to its physical substrate. Nature Reviews Neuroscience, 17, 450–461. [DOI] [PubMed] [Google Scholar]
- Tononi, G. , & Sporns, O. (1994). A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proceedings of the National Academy of Sciences of the United States of America, 91, 5033–5037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi, G. , Sporns, O. , & Edelman, G. M. (1996). A complexity measure for selective matching of signals by the brain. Proceedings of the National Academy of Sciences, 93, 3422–3427. 10.1073/pnas.93.8.3422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenzel, M. , Han, S. , Smith, E. H. , Hoel, E. , Greger, B. , House, P. A. , & Yuste, R. (2019). Reduced repertoire of cortical microstates and neuronal ensembles in medically induced loss of consciousness. Cell Systems, 8, 467–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winters, J. J. (2020). The temporally‐integrated causality landscape: A theoretical framework for consciousness and meaning. Consciousness and Cognition, 83, 102976. [DOI] [PubMed] [Google Scholar]
- Wollstadt, P. , Sellers, K. K. , Rudelt, L. , Priesemann, V. , Hutt, A. , Fröhlich, F. , & Wibral, M. (2017). Breakdown of local information processing may underlie isoflurane anesthesia effects. PLoS Computational Biology, 13, e1005511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeshurun, Y. , Nguyen, M. , & Hasson, U. (2017). Amplification of local changes along the timescale processing hierarchy. Proceedings of the National Academy of Sciences of the United States of America, 114, 9475–9480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamora‐López, G. , Chen, Y. , Deco, G. , Kringelbach, M. L. , & Zhou, C. S. (2016). Functional complexity emerging from anatomical constraints in the brain: The significance of network modularity and rich‐clubs. Scientific Reports, 6, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamora‐López, G. , Zhou, C. S. , & Kurths, J. (2010). Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Frontiers in Neuroinformatics, 4, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Supporting information.
Data Availability Statement
Data employed in this manuscript can be made available by the corresponding author on reasonable request. Regarding code, intrinsic ignition was calculated using MATLAB code available at https://github.com/RajanikantPanda/Ignition_and_Information_flow_for_DOC, estimation of effective connectivity was computed using the pyMOU Python package (https://github.com/mb-BCA/pyMOU) and the study of responses to exogenous perturbations was carried out using the NetDynFlow package in Python (https://github.com/mb-BCA/NetDynFlow). Both GitHub repositories for pyMOU and NetDynFlow contain usage tutorials in the form of Jupyter Notebooks. Usage of NetDynFlow and pyMOU functions in Python is available at https://github.com/RajanikantPanda/Ignition_and_Information_flow_for_DOC.


