A simplified log creep model for describing triaxial creep of mélange rocks

Abstract

This study aims to develop a simplified log creep model (LgCM) for predicting the triaxial three-stage creep behaviors of mélange rocks. The model was deduced from the creep deformation mechanism by considering the competition of strain rate hardening and damage during the steady and accelerating creep stages and was described by two simplified fractal functions. The model was then compared with the previous creep models on the uniaxial three-stage creep data of mortar, rock salt, and sandy shale, as well as the triaxial low-stress creep data of claystone. Afterward, the triaxial creep experimental results of the mélange rock samples were introduced to illustrate the process of calibrating the model in predicting the triaxial three-stage creep behaviors of mélange rocks. It was found the developed LgCM model showed good performance in predicting both the uniaxial and triaxial three-stage creep behaviors of rocks. The investigation reveals that the trend of the parameter $\beta$ can indicate three thresholds of the hardening and damaging effects, and provide the equation to reproduce the creep behavior of the mélange rock. The work contributes to understanding the time-dependent failure of underground rock mass in mélange rock formations.

1. Introduction

It is a significant issue to study the creep behavior of rocks. Most geoengineering structures need to keep long-term stability for their general operation. Some events of failure and instability of geoengineering constructs are caused by creep deformation [1,2]. Therefore, creep behavior is a great concern in researching the stability of geoengineering structures.

There are many articles that demonstrate the creep of soft rocks and hard rocks for decades in the current fields [3]. The creep behavior of the soft rocks reveals to include the decay, and steady and accelerated creep by many researchers [[4], [5], [6], [7], [8], [9]]. The creep test of the hard rock was conducted to demonstrate the mechanical behavior of the rocks subjected to the triaxial loading condition [[10], [11], [12], [13], [14], [15], [16]]. The previous articles reported the experimental results to illustrate the creep behaviors of rocks subjected to various environmental conditions. The various rock mechanics test methods were used to demonstrate the creep behavior of rocks under different axial stress and confined pressure [17,18]. Some articles contributed to understanding the influence of pore pressure on creep behaviors [19,20]. In recent years, many experts focused on the creep behavior of rock under the Thermal-Hydro-Mechanical coupled field [[21], [22], [23]]. These experimental studies were the basis of developing the model to represent the creep deformation process.

The creep behavior can be described by introducing an appropriate constitutive model. Many works contributed to the development of the corresponding constitutive creep models under certain geological environment conditions in the current field [[24], [25], [26]]. Up to now, two groups of creep models have been proposed, namely the component model the and empirical model [[27], [28], [29], [30]]. The basic part model can be categorized into four kinds: the Kelvin model, the Maxwell model, the Yield criteria model, and the Nonlinear model. With the combination of these basic models, complex creep behavior could be described [24,[31], [32], [33]]. The nonlinear creep model is a kind of special component creep model, which is composed of five components, including a hardening body and a damaging body. It could represent the hardening and damage effects during the creep process [34,35]. A nonlinear viscous-plastic body (NVPB) has been introduced to improve the nonlinear creep model for representing three-stage creep behaviors [[36], [37], [38]]. These models can contribute to obtaining an analytic solution for creep behaviors. However, the disadvantage of component mode is that the numerous parameters involved are difficult to determine.

Empirical models use different functions to define creep behaviors according to experiment results [[39], [40], [41], [42]]. Empirical models have fewer parameters, so it is easy to be applied to practical engineering [43,44]. However, the empirical models provided by the published articles could not represent the hardening effect and damage effect of the three-stage creep process. The failure time of creep is significant to understand the creep behavior [45,46]. Li and Yin proposed the time-to-failure creep model to emphasize the role of the creep lifetime [22]. Hashiba et al. established the equation of creep lifetime as a power function and illustrated the influence of water on the change of creep lifetime [47]. However, it might be required more deeply investigation to predict the creep lifetime of the mélange rock subjected to the different loading conditions.

In the present study, we established a simplified log creep model to represent the hardening effect and damage effect of the three-stage creep process under various loads. Its feasibility was verified by other empirical models. The result of validation showed to represent the creep behavior of the rocks including the decay, steady, and accelerated creep. This study carried out the triaxial compress creep test of the mélange rock for applying the model. By comparing the experiment result and the reproduction of the model, it illustrated the model to fully represent the creep behavior of the mélange rock, which is too small to discern the values of the steady-state creep and vague the accelerated creep until it occurs failure. Finally, this paper suggested that the trend of the parameters could indicate the criteria of the hardening and damage effect, and determined the long-term strength.

2. Model development considering strain hardening and damage

The previous studies showed that the typical creep behavior includes three stages: decelerated stage, steady-state stage, and accelerated stage [35,48]. The creep behavior depends on the loading condition. When the load is less than the threshold value, the accelerated stage can't occur. However, when the load approaches the instantaneous strength of the rock, the steady stage takes place as shown in Fig. 1.

Fig. 1.

The strain and strain rate during the creep of rock.

The total strain equals the sum of the elastic strain and the creep strain as follows.

$$\epsilon ={\epsilon }^e+{\epsilon }^{cr}$$ (1)

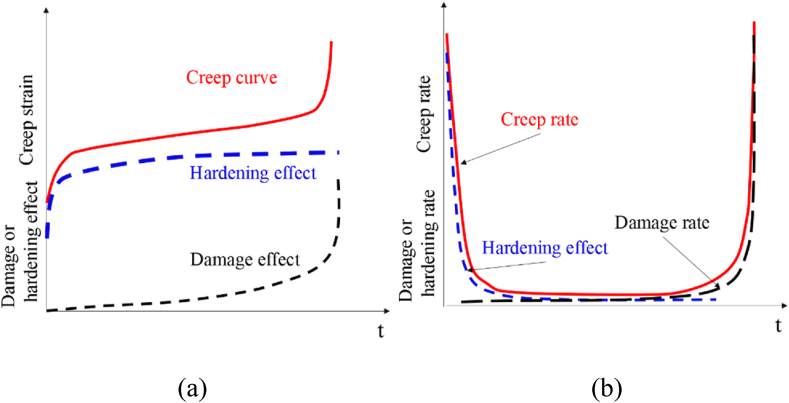
We assume that during the creep deformation of rocks, hardening and damage take place simultaneously [2,35,48,49]. On one hand of hardening, rock creep induces the compaction of the crack tip, which weakens the stress field at the crack gap while relaxing the crack initiation and propagation. The strain rate of the hardening effect decreases with time, which could be represented by a fractal function. The stress concentration induced by creep deformation at the crack promotes its initiation and propagation on the aspect of the damage. The strain rate of the damaging effect increases with time and could be represented by another fractal function. In this study, two fractal functions were adopted to describe the creep strain rate, which captures the hardening-damage coupled creep deformation, as shown in Fig. 2a and b.

Fig. 2.

Strain rate hardening and damage: (a)Creep strain during hardening-damage coupled creep process; (b) Strain rate during hardening-damage coupled creep process.

The LgCM model is derived as follows:

$${\epsilon }^{cr}={\epsilon }_d^{cr}+{\epsilon }_h^{cr}$$ (2)

$$\frac{\partial \epsilon }{\partial t}=\frac{\partial {\epsilon }_h^{cr}}{\partial t}+\frac{\partial {\epsilon }_d^{cr}}{\partial t}$$ (3)

In Eq (2), the ${\epsilon }^{cr}$, ${\epsilon }_d^{cr}$, ${\epsilon }_h^{cr}$ is total creep strain, the damage creep, and hardening creep, respectively. The strain rate, which decreases with time by the hardening effect, is described as a form of a fractal function.

$$\frac{\partial {\epsilon }_h^{cr}}{\partial t}=\frac{mn\beta }{1+\beta t}$$ (4)

The strain rate, which increases with time due to the damaging effect, is described as a form of another fractal function.

$$\frac{\partial {\epsilon }_d^{cr}}{\partial t}=\frac{m\alpha }{1-\alpha t}$$ (5)

where $\alpha$ and $\beta$ are parameters reflecting the rate of the damaging effect (unit;/h) and hardening effect (unit;/h), respectively. Moreover, these two parameters depend on loading conditions and material properties. $m$ and $n$ are fractal parameters, which are also related to loading conditions and material properties.

Substituting Eqs (4), (5) into Eq (3) yields:

$$\frac{\partial \epsilon }{\partial t}=\frac{m\alpha }{1-\alpha t}+\frac{mn\beta }{1+\beta t}$$ (6)

Integrating Eq (6) obtains Eq (7):

$$\underset{{\epsilon }_0}{\overset{\epsilon }{\int }}d\epsilon =\underset{0}{\overset{t}{\int }}\frac{m\alpha }{1-\alpha t}dt+\underset{0}{\overset{t}{\int }}\frac{mn\beta }{1+\beta t}dt$$ (7)

$$\epsilon \left(t\right)=\mathrm{m}\ln \frac{{\left(1+\beta t\right)}^n}{\left(1-\alpha t\right)}+C$$ (8)

The instantaneous elastic strain (${\epsilon }_0$) and the stress are related by Hooke's law.

$${\epsilon |}_{t=0}={\epsilon }^e=\frac{\sigma }{E}$$ (9)

The integration constant C in Eq (8) can be obtained as expressed in Eq (10) by introducing the initial condition Eq (9).

$$C={\epsilon }^e=\frac{\sigma }{E}$$ (10)

Therefore, the LgCM finally changes to

$$\epsilon \left(t\right)=\frac{\sigma }{E}+m\ln \frac{{\left(1+\beta t\right)}^n}{\left(1-\alpha t\right)}$$ (11)

In Eq (11), the parameters $\alpha$, $\beta$, $m$ and $n$ can be determined through the value of several onset points on creep curves in Fig. 1.

The first onset point indicates the creep behavior shifts from a hardening effect to a damaging effect and the strain rate keeps the continuity at the point. The strain rate decreases gradually with time before the shift point, and there is a strain rate (${\epsilon }_s^{\prime }$) at the onset point ($t_s$) and its value is a minimum in Fig. 1 as expressed in Eq (12). According to the characteristics of the local extreme value.

$${{\epsilon }_s^{\prime }|}_{t=t_s}={\frac{\partial \epsilon }{\partial t}|}_{t=t_s}$$ (12)

$${\frac{{\partial }^2\epsilon }{\partial t^2}|}_{t=t_s}=0$$ (13)

In Fig. 1, the second onset point indicates the instantaneous strain (${\epsilon }_0$) and the initial strain rate (${\epsilon }_0^{\prime }$) at the start point ($t=0$) as expressed in Eq (13).

$${\frac{\partial \epsilon }{\partial t}|}_{t=t_0}={\epsilon }_0^{\prime }$$ (14)

The third onset point corresponds to the creep failure in Fig. 1, where the strain rate quickly increases to infinity at the failure time ($t_f$)

$${\frac{\partial \epsilon }{\partial t}|}_{t=t_f}=\infty$$ (15)

Combining Eq. (5) and Eq. (16), the parameter $\alpha$ equals:

$$\alpha =\frac{1}{t_f}$$ (16)

Taking Eq. (14) ∼ (16) into account, other parameters are determined as follows.

To calculate the parameters, one needs to introduce Eq. (17). It is possible to calculate the parameters by using Eq. (18)∼(21).

$$n={\eta }^2$$ (17)

$${\eta }_{\mathrm{1,2}}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$ (18)

$$\{\begin{array}{l}a=\frac{{{\epsilon }_s}^{\prime }-{{\epsilon }_0}^{\prime }}{t_f-t_s}\\ b=\frac{t_s\left(\left({{\epsilon }_s}^{\prime }-{{\epsilon }_0}^{\prime }\right)+t_s{{\epsilon }_s}^{\prime }\right)}{t_f{\left(t_f-2t_s\right)}^2}\\ c=\frac{t_f\left(t_f-2t_s\right)\left({{\epsilon }_s}^{\prime }-{{\epsilon }_0}^{\prime }\right)-{t_s}^2{{\epsilon }_s}^{\prime }}{t_f{\left(t_f-2t_s\right)}^2}\end{array}$$ (19)

$$\beta =\frac{1}{\eta \left(t_f-2t_s\right)}$$ (20)

$$m=\frac{\left(t_f-t_s\right){\epsilon }_s^{\prime }}{\eta +1}$$ (21)

where, $\eta$, $a$, $b$, $c$, are the replacement variables.

As a result, the parameters are related to the specific value of creep deformation, such as the onset time ($t_s$), the strain rate at the onset point, (${\epsilon }_s^{\prime }$) and the creep lifetime ($t_f$) as shown in Fig. 1.

If stress is less than the threshold stress, creep failure may be impossible to occur, and creep behavior mainly includes the hardening effect. Thus, the creep lifetime has an infinite value and the equation of the creep strain can be rewritten as Eq (22), Eq (23).

$$\frac{\partial \epsilon }{\partial t}=\mathrm{m}\left(\frac{\beta n}{1+\beta t}\right)$$ (22)

$$\epsilon \left(t\right)=\frac{\sigma }{E}+m\ln {\left(1+\beta t\right)}^n$$ (23)

If the stress level is not high enough to trigger the tertiary creep in the creep experiment, Eq. (6), (11) turn into

$$\mathrm{m}\beta n={{\epsilon }_0}^{‘}$$ (24)

$${{\epsilon }_s}^{\prime }={\frac{\partial \epsilon }{\partial t}|}_{t=t_s}=\mathrm{m}\left(\frac{\beta n}{1+\beta t_s}\right)$$ (25)

$${\epsilon }_s={\epsilon \left(t\right)|}_{t=t_s}={\epsilon }_0+mn\ln \left(1+\beta t_s\right)$$ (26)

Rearranging Eqs. (24), (25), (26), the parameters under lower stress levels are written as Eq (27):

$$\{\begin{array}{l}\beta =\frac{{{\epsilon }_0}^{’}-{{\epsilon }_s}^{’}}{{{\epsilon }_s}^{’}{t}_s}\\ mn=\frac{{{\epsilon }_0}^{’}}{\beta }\end{array}$$ (27)

3. Model validation

In the previous section, we established the LgCM by taking the loading conditions into account. According to the loading conditions, it can account for the creep process for the two-stage creep under the low loading and the three-stage creep process under the high loading. Therefore, the validation of the LgCM is carried out on the aspect of the two-stage creep and three-stage creep.

3.1. Two-stage creep process

In this part, the data proposed in Ref. [11] is adopted to check the validity of the proposed model. When the load stress is smaller than a threshold, the creep model does not include the damage effect. The value $m\times n$ means the hardening effect. Therefore, the multiply of the parameters m and n is dealt a parameter.

3.2. Three-stage creep process

In this part, the utility of the Log Creep Model is further verified by using the data proposed by Ref. [48] The parameters of LgCM are determined by Eqs. (18), (19), (20), (21) and presented in Table 2.

Table 2.

Parameters of LgCM calculated from the curve of NDBM [47].

Model	Parameter	Cement-mortar	Rock salt-1 (Changshan)	Rock salt-2 (Changshan)	Sandy shale
Creep parameters in [47]	${\sigma }_0$ (MPa)	72	14.41	14.72	52.82
	${\epsilon }_0$ (10−3)	0.44	0.33	0.39	1.67
	$t_e$ (h)	182.77	342.84	149.34	5.453
	${\epsilon }_e$ (10−3)	2.43	0.47	0.55	2.19
	${{\epsilon }_e}^{\prime }$ (10−6/h)	3.41	0.14	0.39	16.4
	n	3.88	9.01	9.03	24.48
	m/10−2	0.5501	5.4052	5.4056	0.1667
	$t_f$ (/h)	705.5	1085.6	472.88	15.48
Parameters of Log Creep model	$\alpha$ (10−3/h)	1.487	0.927	2.105	64.75
	$\beta$ (/h)	471	12.16	32.8	2580
	n	0.1072	0.176	0.1662	0.5287
	m (/10−5)	128.3	7.481	9.0942	9.492
Calculated from reference [47] by the present study	${\epsilon }_s^{\prime }$ (10−3/h)	64.78	0.1601	0.4316	129.5

. Fig. 4a–d shows that LgCM can fully represent the three-stage creep deformation.

Fig. 4.

Strain curve of the NBDM (Cao et al., 2020) [47] and the log creep model. a) cement-motar, b) Changshan Rock salt-1, c) Changshan Rock salt-2, d) Sandy shale.

4. Model application

4.1. Experiment results of mélange rock

The previous sections demonstrated that the LgCM could describe the three-stage creep process and also reflect the characteristics of creep behavior under various loading conditions, such as low-stress, middle-stress, and high-stress levels. In this section, our work focuses on the utility of LgCM for reproducing the three-stage creep process of mélange rock.

Cylindrical mélange rock samples with 50 mm in height and 25 mm in diameter were tested in our work. The present work used two mélange rock samples (TM1-5-1, TM1-5-3), of which density, p-wave velocity, and porosity are respectively 2.7 g/cm³, 2.67 g/cm³, 6691.9 m/s, 6345.6 m/s, 13.11%, 9.25%, as Fig. 5b shows. The triaxial compressive tests were carried out in the soft rock-high/high-temperature rheology-seepage compressive triaxial system (Fig. 5a) designed at China Machinery Testing Equipment Co., Ltd.

Fig. 5.

Apparatus and samples; a) The soft rock-high/high-temperature rheology-seepage compressive triaxial system designed at China Machinery Testing Equipment Co., Ltd. b) Samples of mélange rock.

Triaxial compressive creep tests with two different confining pressures (5, 15 MPa) were performed. The deviatoric stresses are determined according to the mechanical strength of a series of mélange rocks. After increasing the deviatoric stress to the first-step axial stress at a constant stress rate of 10 MPa/min in the triaxial loading phase, it is maintained until the strain rate changes.

The results show that there is no tertiary creep in the creep behaviors under low deviatoric stresses (Axial stress 65.6 MPa, 74.2 MPa, 81.7 MPa in the test of TM1-5-3 sample). In the cases of a moderate load (with the deviatoric stress 90.1 MPa on TM1-5-3) and a high load (with the deviatoric stress as 107.8 MPa on TM1-5-1), tertiary creep occurs as shown in Fig. 6a and c.

Fig. 6.

Axial strain and strain rate evolution with time of single step creep of TM1-5-1 at Pc = 5 MPa, Axial stress 107.8 MPa and multistep creep of TM1-5-3 at Pc = 15 MPa with axial stress respectively of 65.6, 74.2, 81.7, 90.1 MPa.

The strain rate of the steady state creep increases with the increase of the axial stress. They are respectively 7.759 × 10⁻⁴/h and 1.0257 × 10⁻⁴/h under stress of 107.8 MPa and 90.1 MPa. The strain rate of the steady state creep also increases with the axial stress under low loading conditions (65.6, 74.2, 81.7 MPa) in the range of the order 10⁻⁶∼10⁻⁵/h as Fig. 6b and .d shows.

The experiment results show the creep failure behavior of the mélange rock. The creep lifetime depends on the loading level, they are 0.3186 h and 2.616 h under stress of 107.8 MPa and 90.1 MPa, respectively. The period of the accelerated stage is very short, which indicates the creep failure is brittle.

4.2. Parameters of LgCM

It needs to adjust the experiment data of the multi-step creep test for eliminating the influence of historical loads. In this paper, the data processing method used by Ref. [29] was adopted.

The sample subjected to the first-level constant load (${\sigma }^1$) alternates from the decaying creep stage to the stable creep stage after a duration, and the creep deformation generated during a period of first loading is ${\epsilon }^1$. The creep deformation of the specimen increases with time in the next-level load (${\sigma }^2={\sigma }^1+△\sigma$). If the load increases without increment of load ($△\sigma$) by the stress (${\sigma }^2$) in the first-level load, it probably equals to the sum of the creep strain (${\epsilon }^1$) and the increment creep strain ($△\epsilon$) with ${\epsilon }^1+△\epsilon$. Based on the above assumption, our work corrected the axial creep curves of all steps under different loading conditions, as shown in Fig. 7.

Fig. 7.

Comparison of axial strains of LgCM model and experimental data.

We obtained the parameters of LgCM from the corrected experiment data of TM1-5-1 and TM1-5-3 by applying Eqs. (16), (18) ∼ (21), (27). Table 4 shows the parameters determined by considering low-loading, middle-loading, and high-loading conditions. Fig. 7 shows the curve of creep deformation plotted under various loading conditions with the parameters listed in Table 3. It demonstrates that the LgCM has a utility to represent the creep behavior of the mélange rock under various loading conditions.

Table 4.

Characteristics of the multiple fractal parameters ($mn$).

Axial stress (MPa)	$mn$	$Y=mn\times {10}^4$	$X=\frac{\sigma -{\sigma }_h}{{\sigma }_c-\sigma }$
65.6	1.28E-05	0.128	0.16
74.2	3.52E-05	0.3516	0.4395
81.7	5.71E-05	0.5706	0.71325
90.1	1.45E-04	1.446	1.8075

Table 3.

Parameters of the LgCM model for samples of TM 1-5-1 and TM1-5-3.

Sample Number	Confining pressure (MPa)	Axial stress (MPa)	Onset points from tests				Parameters of LgCM
			${\epsilon }_0^{\prime }$ (/h)	${\epsilon }_s^{\prime }$ (/h)	$t_s$ (h)	$t_f$ (h)	$\beta$ (/h)	$n$	$m$	$\alpha$ (/h)
TM1-5-1	5	107.8	0.0043	7.759E-4	0.1542	0.3186	1266.3	0.889	6.566E-5	3.1387
TM1-5-3	15	65.6	1.03E-04	9.133E-7	13.22	–	8.48	1.28E-5		–
		74.2	0.0016	1.49E-5	4.86	–	45.64	3.516E-5		–
		81.7	0.0038	2.377E-5	4.78	–	67.13	5.706E-5		–
		90.1	0.0084	1.186E-4	1.827	2.58	61.78	5.463	2.647E-5	0.3876

4.3. Prediction of the damage strength and instantaneous strength

We focused on the relationship between the parameter $\beta$ of LgCM and the axial stress for estimating the characteristic in the change of the hardening effect. As a result, it reveals that the parameter increases with the increase of the axial stress before peak stress and decreases after that. For the quantitive analysis, this section introduced a power function as Eq. (28) and obtained the fitting curve as Fig. 8. Where, $u$ (unit, $h^{-1}{\left(N/m^2\right)}^{-2}$)is the coefficient for representing the trend of the parameter with the change of the stress loading.

$$\beta ={\beta }_{\max }-u{\left(\sigma -{\sigma }_d\right)}^2$$ (28)

From the results, we can obtain three values. When $\beta ={\beta }_{\max }$, the axial stress is 86.64 MPa; when $\beta =0$, the axial stresses are 64.26 MPa and 105.32 MPa, respectively in Fig. 8. The first value means that the creep behavior cannot include the damaging effect when the axial stress is lower than this value. Therefore, it might be the threshold of the damaging effect (${\sigma }_d$). The second value means that the creep behavior cannot include the hardening effect when the axial stress is less than this value. Thus, it might be the threshold of the hardening effect (${\sigma }_h$). The third value means that the creep behavior cannot include the hardening effect and the damaging effect when the axial stress is larger than it. Thus, it might be the instantaneous strength (${\sigma }_c$).

Fig. 8.

The fitting curve of the parameter $\beta$.

The previous articles show that the long-term strength is larger than 80% of the instantaneous strength. The threshold of damaging effect (${\sigma }_d$) is about 82.26% of the instantaneous strength (${\sigma }_c$). The result matches well with the previous article.

4.4. Prediction of creep lifetime

According to the above results, the creep lifetime increases with the decrease of the deviatoric stress, and it is very large when the deviatoric stress approach to threshold of the damaging effect. The creep lifetime decreases with the increase of the deviatoric stress and it approaches to zero at the instantaneous strength. We assume the relationship between the creep lifetime and the deviatoric stress as Eq (29);

$$t_f=q\frac{{\sigma }_c-\sigma }{\sigma -{\sigma }_d}$$ (29)

where $\sigma$ is the axial stress of the creep test, ${\sigma }_c$ is the threshold of instantaneous strength, ${\sigma }_d$ is the threshold of deviatoric stress to initiate the damaging effect, and k is the coefficient related to the properties of mélange rock. The coefficient $q$ (h) can be calculated with the threshold values mentioned above and $q=1.48$ (h).

4.5. Prediction of the fractal parameters

The fractal parameters ($mn$) increase with the increase of the axial stress. We used the variable X and Y (see Table 4) to illustrate the relationship between the fractal parameters ($mn$) and the axial stress. Fig. 9 shows that the correlation between the fractal parameters ($mn$) and the fractal variable of the axial stress is very high. The fractal parameters ($mn$) can be calculated as Eq (30):

$$mn=f\frac{\sigma -{\sigma }_h}{{\sigma }_c-\sigma }$$ (30)

Fig. 9.

Correlation between multiple parameters ($mn$) and the fractal variable of the axial stress.

According to Table 3 and Fig. 9, the fractal parameter $m$ only relates to the material properties because $m$ and $f$ are the values in the same order and $f$ is a constant. Therefore, the fractal parameters are determined as Eq (31).

$$\{\begin{array}{l}n=\frac{\sigma -{\sigma }_h}{{\sigma }_c-\sigma }\\ m=8\times {10}^{-5}\end{array}$$ (31)

5. Discussion

The result of the validation showed that the parameter $\beta$ decreased with the increase of the confined pressure as shown in Table 1, where it was 1311.9 (h⁻¹) with the deviatoric stress 21.2 MPa under the confined pressure 2 MPa, to 641.33 (h⁻¹) with the deviatoric stress 30.4 MPa under the confined pressure 6 MPa, and to 444.21 (h⁻¹) with the deviatoric stress 22.2 MPa under the confined pressure 12 MPa. But a trend of the parameter $\beta$ could not be understood from the creep strain curve by using the experiment data in Ref. [13] as Table 1 and Fig. 3 of section 3.1. In general, it might be understood that the hardening effect increase with the loading stress under confined pressure. However, the parameter of the hardening effect decreases with the increase of the deviatoric stress under the confined pressure 2 MPa and 6 MPa, and could not be shown a significant trend of it under 12 MPa. It might be because the creep strain curve includes the influence of history loading on the trend of parameters $\beta$ in the multi-step loading creep test.

Table 1.

Parameters of the fractal function ([11]) and LgCM.

Pc	q (MPa)	Fractal function (Liu et al., 2018) [11]				LgCM model			Absolute error of Δε1
		$a$ (E−08)	-$b$	Δε1(%)	creep time	mn (E−07)	$\beta$ (/h)	Δε1(%)
2 MPa (Fig. 3a)	21.2	4.0	1.269	0.052	143.16	3.726	1311.94	0.046	0.006
	26.7	8.0	1.243	0.099	143.34	7.64	1023.28	0.102	0.003
	31.6	10	1.166	0.162	163.95	10.58	500.77	0.175	0.007
	37.4	20	1.026	0.324	164.5	19.8	128.71	0.628	0.029
6 MPa (Fig. 3b)	30.4	10	1.203	0.089	143.16	10.05	641.33	0.12	0.031
	35.6	10	1.137	0.138	143.34	9.75	371.18	0.15	0.002
	41.3	10	1.101	0.166	163.95	9.73	267.03	0.18	0.014
	46.8	20	1.099	0.283	164.5	19.5	260.87	0.35	0.067
12 MPa (Fig. 3c)	22.2	10	1.168	0.197	71.57	8.566	444.21	0.18	0.017
	32.8	10	1.060	0.284	143.36	6.84	177.57	0.27	0.014
	43.2	20	1.162	0.382	144.83	25.8	472.12	0.358	0.024
	54.5	50	1.065	1.14	168.34	41.7	188.23	1.337	0.197

Fig. 3.

Strain rate curve of the creep test and the LgCM; The strain rate is described by a fractal function (${\epsilon }^{\prime }=a△T^b$) in Liu's work. For comparison, the parameters of LgCM are determined by using Eq. (28) as shown in Table 1. The ABS(Error) of the creep strain $△{\epsilon }_1$ between reference [13] and this work is calculated and presented in Table 1. The results show that the difference is negligible, which indicates the validity of the LgCM model under low-stress level.

The paper eliminated the creep strain of the mélange rock to the influence of the history loading on the trend of the parameter $\beta$ in the experiment creep test. As a result, the change of the parameter $\beta$ approached the parabolic curve as shown in Fig. 8. At last, it demonstrated the need to eliminate the influence of the loading history on the parameters of the model during determining the parameters of the LgCM.

The parabolic curve of the parameter $\beta$ trend could indicate three criteria values. These three criteria values are to apply an important role for represent the creep behavior of the mélange rock as Eq. (33). Especially when the loading deviatoric stress equals the damage criteria ${\sigma }_d$, the parameter $\alpha$ equals zeros, and the creep lifetime approach to infinity. So, the damage criteria mean the long-term strength at the confined pressure 15 MPa considering the definition of it.

$$\{\begin{array}{l}\epsilon \left(t\right)=\frac{\sigma }{E}+mn\ln \left(1+\beta t\right)\sigma <84.64\mathrm{M}\mathrm{P}\mathrm{a}\\ \epsilon \left(t\right)=\frac{\sigma }{E}+mn\ln \left(1+\beta t\right)-m\ln \left(1-\alpha t\right)\sigma \ge 84.64\mathrm{M}\mathrm{P}\mathrm{a}\end{array}$$ (32)

$$\{\begin{array}{l}\beta =66.45-0.1627\left(\sigma -84.64\right)\\ \mathrm{m}\mathrm{n}=8\times {10}^{-5}\times \frac{\sigma -64.26}{105.32-\sigma }\\ m=8\times {10}^{-5}\\ E=21.73\mathrm{G}\mathrm{P}\mathrm{a}\\ \alpha =0.676\times \frac{\sigma -84.64}{105.32-\sigma }\end{array}$$ (33)

This paper can calculate the parameters of the LgCM by using Eq (33) and submit into Eq (32) to reproduce the creep strain curve of the mélange rock under the confined pressure 15 MPa.

There is a lack of fully demonstrating the trend of parameters with the change of the confined pressure. In the future, it will need to conduct a series of creep tests of the mélange rocks under various confined pressure.

6. Conclusion

This article proposed a simplified LgCM to describe the creep behavior of mélange rocks under various loading conditions. The model was verified by comparing it with the existing models. The creep behavior was estimated by applying it to the analysis of the creep test of mélange rocks. The following conclusions were drawn.

• 1)The simplified LgCM proposed in the present study can describe the hardening-damaging effect during the multi-stage creep process. The model can represent three types of creep behavior under low, middle, and high loading conditions, including the decelerated, steady state, and accelerated creep stages.
• 2)It needs to adjust the experiment data of the multi-stage creep test for eliminating the influence of historical loads. The method adopted can help to accurately estimate the change of the parameters with the change of the axial stress.
• 3)It concludes that the trend of the parameters $\beta$ has a parabolic curve under a confined pressure and decreases the level with an increase of the confined pressure from validation and application work. And the trend of them indicates three thresholds of the hardening and damaging effect. The criteria of damaging effect might apply a role of long-term strength.

Nevertheless, this paper suggests the LgCM reproduces the creep behavior of the mélange rock, but there is a lack of experimental data for evaluating accurately the LgCM on quantity. In the future, many experiments need to determine the parameter of LgCM of the mélange rock subjected to the various loading condition.

Author contribution statement

Hyonsong OH: Conceived and designed the experiments; Performed the experiments; Wrote the paper.

Xin Wang: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Ming Wu; Fengjiao Liu: Performed the experiments; Analyzed and interpreted the data.

Jinhyok Jon; Tao Zeng: Analyzed and interpreted the data; Contributed reagents and materials.

Zaobao Liu: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.