The computational capabilities of many-to-many protein interaction networks

Summary

Many biological circuits comprise sets of protein variants that interact with one another in a many-to-many, or promiscuous, fashion. These architectures can provide powerful computational capabilities that are especially critical in multicellular organisms. Understanding the principles of biochemical computations in these circuits could allow more precise cellular control of cellular behaviors. However, these systems are inherently difficult to analyze, due to their large number of interacting molecular components, partial redundancies, and cell context dependence. Here, we discuss recent experimental and theoretical advances that are beginning to reveal how promiscuous circuits compute, what roles those computations play in natural biological contexts, and how promiscuous architectures can be applied for the design of synthetic multicellular behaviors.

TOC blurb:

Biological pathways comprise sets of protein variants that interact with one another in a many-to-many fashion to biochemically “compute” complex functions of protein inputs. Here, Klumpe et al. discuss recent experimental and theoretical advances that reveal how these circuit architectures compute, what roles those computations play in natural biological contexts, and how they can be applied to the design of synthetic multicellular behaviors.

Introduction

With the evolutionary transition from single cells to multicellular life, cells faced an expanded set of information-processing challenges. They had to support large numbers of distinct cell fates, decipher complex signals from other cells, and tailor their behavior depending on their own state, history, and local environment. Many of the protein circuits, or pathways, that evolved to address these challenges share a particular feature. They employ families of homologous, but subtly different, protein variants interacting in a many-to-many, or promiscuous, manner with one another, and with members of other protein families. These variants likely arose from duplications of simpler ancestral pathways^1-5 (Figure 1A). Typically, different cell types express different combinations of variants, generating a set of related, but distinct, versions of any given circuit⁶ (Figure 1B).While specific components and interactions within these circuits are often well-studied, it is still generally unknown how their components collectively respond to diverse combinations of inputs, and how those responses change depending on the specific components expressed in each cell context. Recent work is beginning to shed light on these issues, revealing how promiscuous circuits can support the complex information processing requirements of multicellular life.

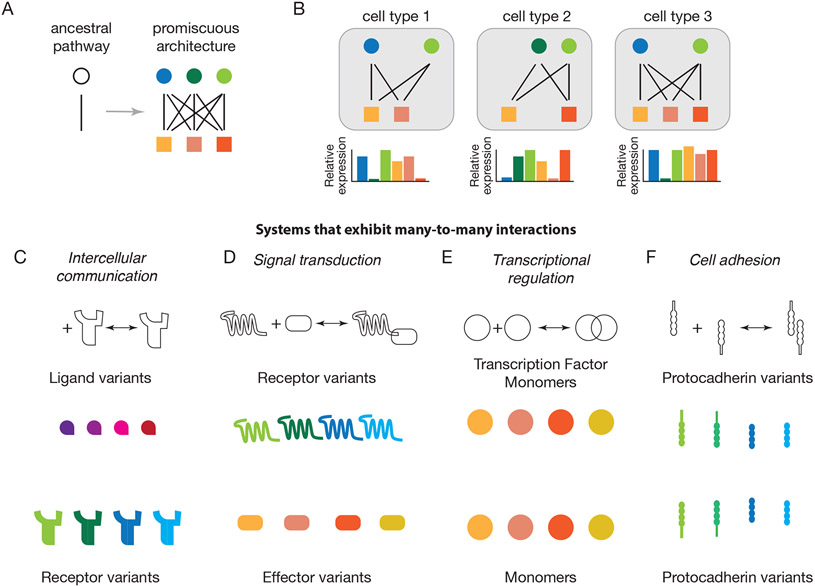
Figure 1: Diverse cellular pathways exhibit many-to-many interactions among protein families.

(A) Extant pathways, such as signaling from one component (circle) to another (square) can evolve from simpler ancestral pathways through gene duplications, resulting in many-to-many interaction networks (right).

(B) Different cell types (gray) typically express different protein variant profiles (schematic bar plots).

(C) Intercellular communication systems often comprise multiple ligand (upper) and receptor (lower) variants that interact in a many-to-many fashion, with each ligand binding to multiple receptors and each receptor binding to multiple ligand variants.

(D) In signal transduction systems, receptor variants (upper) interact with variant intracellular signal transducers, or effectors, in a many-to-many fashion.

(E) In cell adhesion processes, protocadherin variants interact with other protocadherins in adjacent cells, also in a many-to-many fashion.

(F) Eukaryotic transcription factor variants can often bind to one another to form a large repertoire of distinct dimers, each with distinct DNA binding specificities.

Promiscuous protein interaction circuits are prevalent throughout biology. Developmental cell-cell communication pathways such as Bone Morphogenetic Protein (BMP),⁷ Notch,⁸ JAK/STAT,^9,10 Wnt,^11,12 Fibroblast Growth Factor (FGF),¹³ and Epidermal Growth Factor (EGF),¹⁴ comprise sets of distinct ligands, each of which interacts promiscuously with multiple receptor variants (Figure 1C). Promiscuity is also conspicuous in the interactions of receptors with downstream effectors. For example, individual G-protein coupled receptors (GPCRs) interact with multiple effector G proteins in an overlapping, promiscuous manner¹⁵ (Figure 1D). Transcriptional regulation, too, is replete with promiscuity. Families of transcription factor variants, such as NF-κB, bHLH, bZIP, and POU/Sox, interact promiscuously to form diverse homo- and heterodimeric complexes (Figure 1E) that vary in their DNA binding specificity and activate or repress overlapping sets of target genes.^16-18 Transcription factors also interact promiscuously with co-factors, as has been analyzed extensively for the Mediator complex¹⁹ and the homeobox genes.²⁰ Extracellularly, families of Cadherin variants interact promiscuously with one another to control adhesion between adjacent cells^21-24 (Figure 1F). In many of these examples, proteins may form higher order, oligomeric complexes with more than two components, adding additional complexity to the system. These examples show that combinatorial protein networks occur at multiple levels with multiple protein families.

It can be tempting to regard protein interaction promiscuity more as a nuisance—perhaps an artifact of gene duplication in evolutionary history—than a feature. On the other hand, complexity science, neurobiology and artificial neural networks show that simple elements, connected together in a many-to-many fashion, can act as powerful computational systems.²⁵ By computation, we mean the ability to process input information encoded in multiple molecular signals in flexible and complex ways. Computations are usually understood to comprise three distinct levels: a function to be computed, an algorithm to implement that function, and the physical media that can execute that algorithm.²⁶ The first two are abstract descriptions of how inputs become outputs and are agnostic of physical implementation. By contrast, the properties of a particular physical medium may constrain the functions or algorithms it can implement. Here, we consider protein-protein dimerization networks as physical media for computation in cells, and discuss the algorithms and functions they can compute. We are interested in both what higher-level functions these networks support, as well as how this logic can be physically realized by a variety of protein families. In all these respects, we consider protein dimerization networks as a powerful architecture for computation in cells.

The interconnectedness of protein and metabolic networks within the cell has long been recognized as providing the potential for computations in cells.^27-29 Previous works have largely focused on how interacting biomolecules could implement aspects of digital computing, such as Boolean logic gates^27,30 or neural networks.^28,31 It has generally been more challenging to determine what computations are implemented natively by natural biomolecular circuits in living cells. Better understanding the range of native computations that arise in these settings could explain how cells, with many distinct properties from silicon chips, compute complex responses to their diverse input signals and, more specifically, how these computational capabilities address the unique challenges of multicellularity.

When many protein complexes can form through combinatorial dimerization of a smaller number of monomeric components, their distribution will in general depend on the abundances of each protein, their pairwise interaction strengths (e.g. affinities), as well as other inputs. These dependencies can be nonlinear and indirect, such that perturbing one protein level can affect the concentrations of complexes in which it does not appear. Further, distinct complexes can, in general, have distinct target specificities or activity levels. As a result, inputs that modulate one or more protein components can be processed by the combinatorial dimerization network in non-trivial ways to produce computations. These computations can support higher level functions in signaling, adhesion, and transcriptional regulation.^7,18,32,33

This type of computation occurs at two levels. First, within an individual cell or cell type, systems can compute a specific function of multi-protein inputs. Second, the function that is computed can vary between different cell states (i.e. be context-dependent). This is possible because cell states, in general, express different subsets of the circuit’s molecular components, as single-cell atlas data sets have revealed.⁶ Each configuration (and thus each cell state) may compute a distinct functional response to the same environmental inputs. A single combinatorial system then provides not just one cellular computation, but a whole repertoire of different computations in different cell states.

Here, we argue that combinatorial protein dimerization networks represent a general biological strategy to implement context-dependent computations in cells. We further show how this viewpoint provides a unifying framework to explain a diverse array of biological processes, including signaling, gene regulation, and cell-cell adhesion. More specifically, we first highlight recent work that reveals computations in promiscuous protein-protein interaction systems and how they arise. We then discuss possible biological functions of these computations. Finally, we explore experimental and computational approaches to understand and manipulate them.

Throughout, we focus on computations that emerge from networks of combinatorial protein-protein binding interactions within pathways. We omit additional complexity that can emerge through interactions between different pathways,³⁴ combinatorial allosteric control of individual protein activities,^35-37 as well as computations within enzymatic and metabolic networks. We also leave out important work in neural circuits such as olfaction, which depends on many-to-many interactions between odorants and receptors, as these systems rely on neural circuitry for most signal processing and receptor expression is limited to one per cell, precluding formation of diverse protein complexes. Lastly, because we primarily focus on protein-protein dimerization as a mechanism, we do not discuss the fascinating computational capabilities produced by other circuit features, such as the regulation of protein activity by co-factor binding, expression-mediated feedback, and post-translational modifications.

Promiscuous protein-protein interaction systems compute functions of multiple input proteins

Combinatorial protein networks are based on protein complex formation (Figure 1C-F, black and white illustrations). These systems consist of one or more sets of protein variants that can combinatorially assemble into a zoo of different protein complexes. In some cases, the complexes contain only one class of protein, of which there are many variants. For example, different bHLH transcription factors can promiscuously dimerize with one another to produce many distinct homo- and heterodimers (Figure 1E). In other cases, complexes contain two or more types of proteins, each of which may comprise many variants. For instance, a set of ligand variants can form many potential signaling complexes with a set of receptor variants (Figure 1C). In either case, each of the resulting complexes can exhibit a different level of activity or affect a different set of molecular targets. Further, when certain protein concentrations are limiting, competition to form complexes can lead to non-intuitive behaviors. Perturbing the abundance of one or more individual input protein components can directly affect the concentrations of complexes and indirectly affect the concentrations of other complexes. Considering certain proteins as “inputs” and the activity or effects of the complexes as “outputs,” the overall network can thereby perform a variety of input-output computations, depending on the concentrations of each component, and the binding energies or affinities for each possible interaction (Figure 2A).

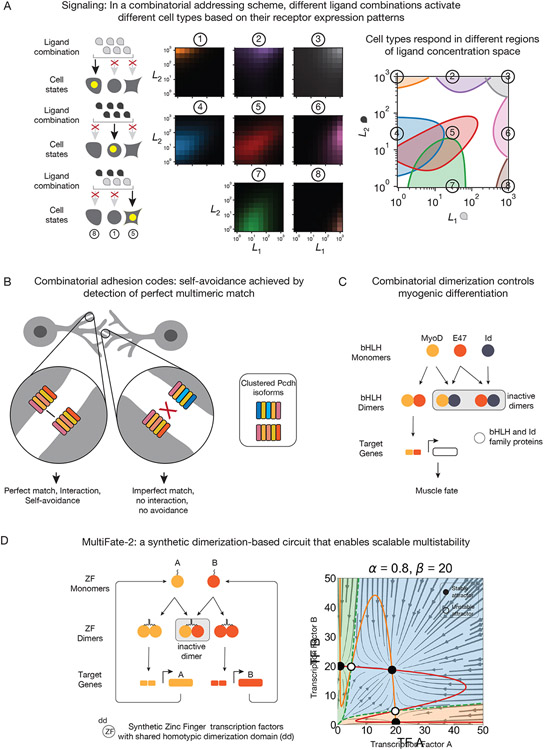
Figure 2: Many-to-many interaction systems can provide key functional capabilities.

(A) In cell-cell signaling, many-to-many interactions between ligands and receptors allow ligands mixtures to “address” messages to specific cell types, rather than broadcasting messages to any cell expressing receptors (left). This works by generating responses in specific regions of a multi-dimensional ligand concentration space. A model of BMP signaling showed that particular parameters for receptor-ligand interactions allow a single ligand pair to activate up to 8 distinct receptor configurations, depending on the ligand concentrations (middle, right). In each plot, the x- and y-axes show concentrations of two ligands, $L_1$ and $L_2$.

(B) In cell-cell adhesion, combinations of Pcdh isoforms (different colors) can encode cellular identity, allowing neurons to distinguish self from non-self.

(C) In gene regulation circuits, dimerization of bHLH transcription factors partitions the protein variants into active and inactive dimers. Perturbations of monomer expression can thus alter dimer abundance to produce nuanced effects on target gene expression.

(D) Naturally occurring protein-protein dimerization networks can guide the design of synthetic circuits for more complex computations. For example, the MultiFate-2 system includes a synthetic transcription mechanism that, like bHLH transcription factors, includes dimerization, DNA binding, and transcriptional activation domains. These programmed interactions (left) give rise to diverse stable cell states (right) defined by concentrations of active transcription factor dimers, analogous to differentiated cell states.

Mathematical models of competitive complex formation can capture many of the effects described above, allowing us to explore what kinds of computations are possible within different combinatorial protein network architectures. In addition, they reveal how those computations depend on the overall interaction architecture and biochemical parameters (Box 1). For example, models of receptor-ligand interactions have revealed how signaling pathways can compute Boolean and other types of combinatorial responses to multi-ligand inputs, two examples which we explore below. These examples show how diverse ligand-receptor affinities and signaling complex activities, defining features of combinatorial protein networks, can produce complex functions.

Box 1: Mathematical model of computation by promiscuous protein dimerization networks.

Promiscuous protein dimerization networks can implement diverse computations. To see how this works, consider a minimal system, inspired by signaling pathways, where one set of protein variants, $A_i$, analogous to ligands, acting as inputs, can bind to a second set of components, $B_j$, analogous to receptors, to form a combinatorial set of binary signaling complexes, $C_{ij}$. A similar formalism can represent other combinatorial dimerization and more complex multimerization networks. More specifically, we consider a system with two $A$ and two $B$ variants, generating four binding reactions (Box Figure 1A):

$$A_1+B_1\rightleftharpoons C_{11},A_1+B_2\rightleftharpoons C_{12},A_2+B_1\rightleftharpoons C_{21},A_2+B_2\rightleftharpoons C_{22}.$$

At equilibrium, these reactions lead to the equations $A_i{B}_j=k_{ij}{C}_{ij}$ where $k_{ij}$ denotes the affinity of binding of $A_i$ with $B_j$. We also assume that the total abundances of the components are at steady-state, i.e. that complex formation and dissociation are fast compared to the timescales of protein production and removal. Additionally, for analytical simplicity, we consider a regime in which the $A$ variants are supplied at a fixed concentration in a large extracellular volume, as could occur in the context of signaling, so that their concentrations are negligibly perturbed by binding to $B$ variants. However, similar functional behaviors can be obtained without this assumption. We then have the following conservation laws for the total $B$ abundances, $B_{1T}$ and $B_{2T}$:

$$B_1+C_{11}+C_{21}=B_{1T}{B}_2+C_{12}+C_{22}=B_{2T}.$$

From these equations, we obtain expressions for the concentrations of the free $B$ proteins as a function of the $A$ concentrations:

$$B_1=\frac{B_{1T}}{1+k_{11}{A}_1+k_{21}{A}_2},B_2=\frac{B_{2T}}{1+k_{12}{A}_1+k_{22}{A}_2}.$$ (1)

Assuming each complex, $C_{ij}$ signals with a specific activity, $e_{ij}$, the total output signal, $S$, is the sum of contributions from each complex,

$$S=e_{11}{C}_{11}+e_{12}{C}_{12}+e_{21}{C}_{21}+e_{22}{C}_{22}.$$

Finally, using the conservation laws (1), the expression for free receptors (2), and the equilibrium equations above, we can express the system output, $S$, in terms of the concentrations of the $A$ variants and the total abundances of $B_1$ and $B_2$.

$$S=\frac{e_{11}{B}_{1T}{k}_{11}{A}_1}{1+k_{11}{A}_1+k_{21}{A}_2}+\frac{e_{12}{B}_{2T}{k}_{12}{A}_1}{1+k_{12}{A}_1+k_{22}{A}_2}+\frac{e_{21}{B}_{1T}{k}_{21}{A}_2}{1+k_{11}{A}_1+k_{21}{A}_2}+\frac{e_{22}{B}_{2T}{k}_{22}{A}_2}{1+k_{12}{A}_1+k_{22}{A}_2}.$$ (2)

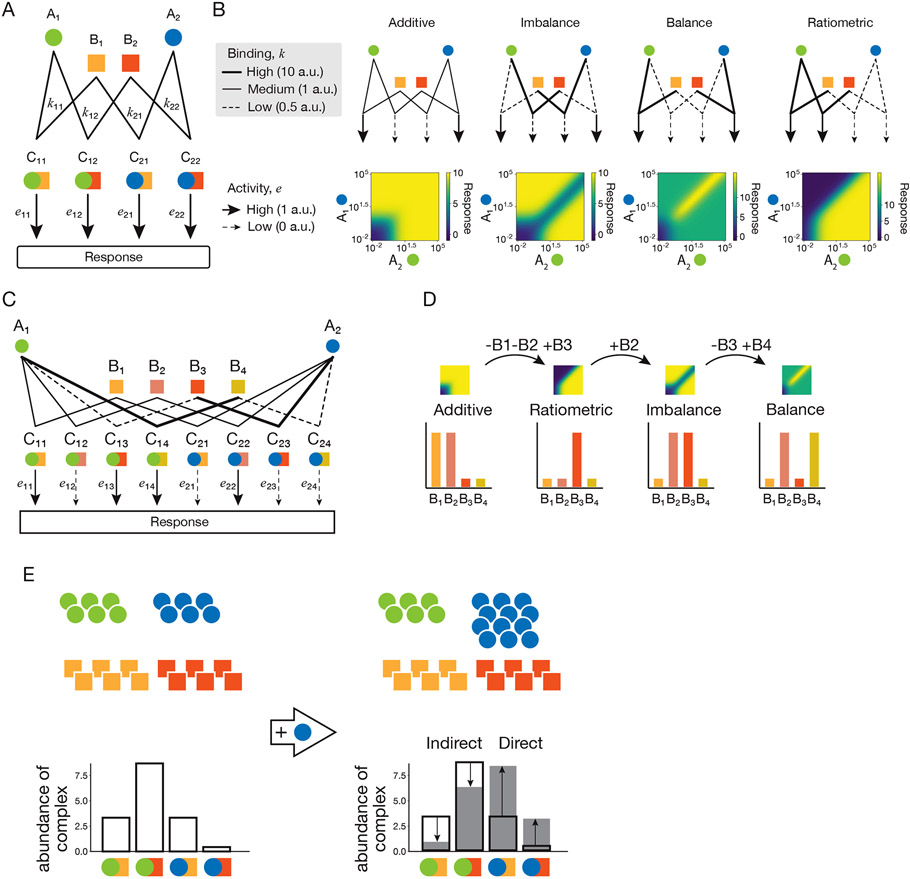
This simple model can represent at least four different classes of computation: additive, ratiometric, balance and imbalance responses (Box Figure 1B). For instance, when the activities of $C_{12}$ and $C_{21}$ are small compared to those of $C_{11}$ and $C_{22}$ (when each A component strongly activates a distinct B component), the system response can be approximated by the sum of two increasing functions, each hyperbolically increasing with one $A$ variant and cross-inhibited by the other:

$$S\approx \frac{e_{11}{B}_{1T}{k}_{11}{A}_1}{1+k_{11}{A}_1+k_{21}{A}_2}+\frac{e_{22}{B}_{2T}{k}_{22}{A}_2}{1+k_{12}{A}_1+k_{22}{A}_2}$$

In this limit, when the affinity coefficients have similar values, the system performs an additive computation (see Box Figure 1B, left). On the other hand, when the values of these coefficients differ from each other, and are chosen appropriately, the system can exhibit a balance or an imbalance response (Box Figure 1B, center). When $e_{21}$ and $e_{22}$ are small, the response of the circuit depends approximately on the ratio between $A_2$ and $A_1$:

$$S\approx \frac{e_{11}{B}_{1T}{k}_{11}{A}_1}{1+k_{11}{A}_1+k_{21}{A}_2}+\frac{e_{12}{B}_{2T}{k}_{12}{A}_1}{1+k_{12}{A}_1+k_{22}{A}_2}\approx \frac{e_{11}{B}_{1T}{k}_{11}+e_{12}{B}_{2T}{k}_{12}}{k_{11}+k_{21}(A_2∕A_1)}$$

where we have considered that $k_{11}=k_{12}$ and $k_{21}=k_{22}$, and have assumed $k_{ij}{A}_k\gg 1$. This behavior corresponds to a ratiometric computation (see Box Figure 1B, right).

In summary, this minimal model shows that specific sets of parameter values enable even simple promiscuous protein networks to operate in different computational modes. In particular, the four computational modes described above (additive, ratiometric, balance, and imbalanced) can be reached by selecting subsets of B components from a pool of only four variants, which interact with a single pair of A components (Box Figure 1C,D). This feature can be visualized by smoothly varying B levels and observing the resulting changes in computation (Supplementary Movie 1). In that way, computations in the A space depend on the context defined by the B levels. This model highlights the central importance of differences in parameters such as affinity, activity, and expression levels, which can be mediated by diverse mechanisms such as post-translational modification and expression-mediated feedbacks. Importantly, our model is not sensitive to the exact mechanism determining these parameters and can be expanded to explore more complicated protein binding architectures that lead to an even wider array of functions.

This simple model also reveals a feature of promiscuous protein networks that sets these computational systems apart from traditional neural networks. Specifically, because of the stoichiometric nature of the biochemical reactions, reflected in the conservation laws above, a change in the total abundance of one individual component can lead to a redistribution of other complexes (Box Figure 1E). This effect can be direct, affecting complexes containing the component whose abundance was perturbed, or indirect, impacting complexes in which the perturbed component does not appear. The resulting redistribution of components across complexes is absent in neural networks, whose components are not subject to conservation laws, but functions to strengthen the computational capabilities of promiscuous protein interaction networks.

Box figure: Mathematical model of computation by promiscuous protein dimerization networks.

(A) In a minimal promiscuous protein dimerization network, two A-type components (circles) interact with two B-type components (squares) to form complexes that induce a response. The binding affinities of the components $A_i$ and $B_j$ to form the complex $C_{ij}$ are denoted by $k_{ij}$, and their response activity levels are denoted by $e_{ij}$.

(B) Heatmaps representing the response of the minimal network as a function of the A concentrations. Parameter values are indicated by line weights, as indicated in the legend (a.u. = arbitrary units). All levels of B-type components are set at 10 a.u. The code to generate these plots can be found at https://github.com/dsb-lab/MinimalPromiscuousCircuit.

(C) All four distinct classes of computations shown in (B) can be generated by a single model with specific biochemical parameters using only four B-type components. Parameter values are indicated by line weights as in (B).

(D) By changing the expression levels of the B-type components the model can transition smoothly between the four computation classes. See also Movie S1.

(E) When the concentration of a ligand is increased (blue circles), the stoichiometric nature of the biochemical reaction results in a global redistribution of complexes. Outline bars and shaded bars show the amount of each complex before and after the increase in ligand, respectively. The increase results in direct effects on complexes containing the varying ligand (marked ‘Direct’). Additionally, the redistribution of complexes has indirect effects on complexes that do not contain the varying ligand (marked ‘Indirect’).

Computation of Boolean logic for two ligand inputs

An early theoretical study of combinatorial receptor-ligand interactions was performed by De Ronde et al.³⁸ The authors explored a set of ligand-receptor interaction architectures and compared their ability to produce different Boolean logic gates. To do this, they adapted the equilibrium statistical mechanics description of allostery, provided by the classical Monod-Wyman-Changeux model,³⁹ to describe how ligand binding alters the conformation of receptors to activate a pathway. In one scheme, they considered a dimer of two receptor subunits, in which one subunit could bind promiscuously to two ligand variants, while the other could bind only to one. By tuning the affinities of each ligand for each receptor, and the activities of the different possible complexes, the authors were able to generate all possible two-input Boolean logic functions. The most complex functional responses, such as XOR, required competition of two ligands to bind one of the receptor subunits. In this case, each ligand, presented individually, produced an activating receptor conformation. But when mixed together, one ligand outcompeted the other for its preferred subunit. The outcompeted ligand then bound its less preferred subunit and produced an inhibitory complex, leading to reduced activity when both ligands were present compared to the activity of each ligand alone. Simpler schemes, based on a single receptor or limited to homodimerization of receptors, exhibited more limited computational repertoires. These results demonstrated how ligands that promiscuously and competitively bind to heterodimeric receptors can perform a variety of multi-input computations.

Computation in the BMP signaling system

One example of computation in combinatorial protein networks occurs in the BMP pathway. This core cell-cell signaling pathway plays pivotal roles in a broad range of developmental, physiological, and disease processes. In mammals, BMP ligands are secreted by cells, diffuse through tissues to form morphogenetic gradients, and activate cognate receptors on signal-receiving cells. Critically, in most biological processes, cells are exposed to combinations of multiple BMP ligand variants, suggesting that the BMP signaling process could be inherently combinatorial.

To decipher these combinatorial input signals, cells express multiple variants of type I and type II receptor subunits, which assemble together with ligands to form signaling complexes, which activate downstream Smad transcription factors.⁴⁰ In humans, there are approximately 15 different ligand variants and 7 receptor variants (four type I and three type II), potentially generating thousands of distinct signaling complexes.^7,41-43 Moreover, these complexes likely vary quantitatively in their rates of Smad phosphorylation,⁷ as non-signaling (i.e. inactive) complexes have been shown to occur in the closely related TGFβ pathway.⁴⁴

This combinatorial complexity allows the BMP pathway to compute complex responses to multi-ligand combinations.⁴¹ For example, we found that in a mouse epithelial cell line, the ligand BMP4 strongly activates the BMP pathway, but its activity is blocked in a dose-dependent manner by another ligand, GDF5, such that pathway activity is approximately proportional to the ratio of BMP4 and GDF5 concentrations. This type of ratiometric response can occur when two ligands bind to the same receptor subunits with similar affinity, but one (in this case, BMP4) forms an active signaling complex while the other (GDF5) forms a non-activating partial complex, or a weakly-activating full complex. Similar types of antagonism have been reported for TGFβ ligands^45,46 and a related form of ratiometric sensing has been observed in yeast.⁴⁷

Experiments also revealed more complex computations. For example, BMP4 and BMP10 produce an “imbalance detector” response, in which either ligand can efficiently activate on its own, but the two ligands inhibit each other’s activity, neutralizing the response at a particular concentration ratio. (In this way the pathway is most active when the ligand’s concentrations are “imbalanced.”) Modeling showed that imbalance detection occurs in “incoherent” parameter regimes, where complexes that form with high affinity exhibit weak specific activity, while less preferred complexes are more active. In this regime, mixtures of the two ligands preferentially form their high affinity, but low activity complexes. By contrast, when either of the ligands is present alone, a mixture of strong and weak signaling complexes form, producing greater total activity. In the opposite “coherent” regime, where high affinity complexes also have high activity, the model predicts the opposite “balance detector” response, which was experimentally observed in a different cell line.⁴¹ Together, these results demonstrate that the promiscuous BMP pathway performs complex computations on multi-ligand inputs that can be explained in terms of an interplay between the affinity and activity of the various signaling complexes. These explanations for experimentally observed behaviors were consistent with a simplified model. Taken together, these modeling and experimental studies show how combinatorial ligand-receptor networks can compute responses to multiple ligands. However, further experimental validation will be necessary to definitively establish the underlying mechanisms that generate the observed responses.

Making computation contextual

Single-cell atlas projects have revealed the transcriptional expression profiles of diverse cell states.^48-52 Analysis of these profiles showed that the components of many combinatorial protein networks are expressed in distinct and often recurring configurations in different cell types.⁶ For example, in pathways such as BMP, Wnt, and Notch, multiple receptor variants are co-expressed in specific combinations. This observation provokes the question of whether cells that express distinct, but overlapping, sets of pathway components can perform different computations (Figure 2A).

Modeling of the BMP pathway showed that receptor expression levels could strongly impact the computation performed by the pathway (Box 1). Consistent with this prediction, perturbing the expression of individual receptors experimentally changed the computational response of the cell to different ligand combinations.^41,43 For example, knocking down the type II receptor BMPR2 changed an additive response to BMP4 and BMP9 into a ratiometric response. Similarly, ectopically expressing the type I receptor ACVRL1 converted an imbalance detector response function into an additive response. Analysis of cell lines also suggested that receptor expression profile dictates computation. Two otherwise unrelated cell lines with similar receptor profiles, one epithelial and one fibroblastic, exhibited similar multi-ligand integration responses. These differed qualitatively from responses of an embryonic stem cell line with a different receptor profile. Together, these results suggest that receptor expression profiles can (and likely do) control the type of computation that the BMP pathway performs on multiple ligand inputs.

This specific feature observed in signaling pathways suggests a more general feature of promiscuous protein-protein interaction networks. Indeed, earlier theoretical work on such networks showed that, in particular regimes, the steady-state concentrations of components depended more on protein abundance than the parameters of the protein-protein interactions themselves, suggesting that new network behaviors could be flexibly accessed by merely changing the concentration of different components.⁵³ Therefore, in addition to performing complex computations on multiple inputs, protein-protein dimerization networks also allow cells to reprogram those computations by varying the expression levels of pathway components. This ability to perform a range of computations on the same inputs allows different cell types to extract different types of information from the same environment, or a given cell type to change its behavior in different developmental or physiological contexts. Returning to the neural network analogy, this behavior roughly corresponds to different cell lines operating the same network topology with different weights to compute distinct functions.

Molecular promiscuity enables cell-cell specificity in communication pathways

One of the most basic capabilities of any communication system is the ability to address messages to particular recipients. For example, in the familiar case of email, we can send messages to individuals or groups. Cell-cell communication presents an analogous addressing challenge: how to use signals to selectively activate specific target cell types.

The simplest way to achieve such cell-specific “addressing” is a one-to-one ligand-receptor system in which each ligand variant activates a distinct receptor variant exclusively expressed by a single target cell type. This architecture reflects the strategy used in human engineered communication systems, where the goal is to avoid undesired crosstalk between communication channels.^54,55 It is also the basis for synthetic biological signaling systems such as synNotch, where each ‘ligand’ (cell surface protein) is recognized by a cognate antibody fused to its corresponding synNotch receptor.⁵⁶ By contrast, in many natural cell-cell communication pathways, each ligand variant activates multiple receptor variants, each cell type expresses multiple receptor variants, and each environment contains multiple ligand variants. Is such a system compatible with communication specificity in the presence of promiscuous interactions?

In a recent computational study, we sought to answer this question using a mathematical model of a BMP-inspired promiscuous signaling pathway.⁵⁷ This work revealed that molecular promiscuity counterintuitively generates a powerful, fundamentally combinatorial, addressing capability, in which ligand combinations activate cells expressing corresponding receptor combinations. In this system, just two ligand variants, present together at different concentrations, could orthogonally activate at least eight different cell types (Figure 2A). This occurs because cells with different receptor profiles can respond to different localized regions of ligand concentration space. These localized responses are in turn enabled by the computational capacity generated through promiscuous ligand-receptor interactions.

Increasing the number of receptor variants in the system allows more complex computational responses, and thereby increases the number of cell types that can be uniquely addressed by a given number of ligands. Key features that facilitate combinatorial addressing are (1) diverse activities for a given receptor, depending on the ligand that activates it, and (2) the existence of signaling complexes that form with high affinity but have low activity, and vice versa,⁵⁷ similar to the interplay observed in other models of BMP signaling described above.⁴¹

The addressing capabilities in the many-to-many architecture can far exceed what is possible in the seemingly simpler and more efficient one-to-one architecture, assuming the same number of ligand and receptor variants. This advantage becomes even stronger when one considers schemes in which a specific ligand combination activates multiple cell types (analogous to an email “mailing list”). For example, a particular combination of 2 ligands could selectively activate a subset of 3 cell types, showing that promiscuous interactions can produce versatile addressing schemes. Overall, these results suggest a picture in which different cell types “tune in” to specific combinations of ligands by expressing different receptor combinations. Different environments, with distinct combinations of ligands, can then preferentially activate one cell type, another, or both. Nonetheless, direct experimental tests will be necessary to confirm if evolved signaling capacities make use of this addressing capability.

Molecular promiscuity and cellular specificity in adhesion

Context-dependent computation also enables another important biological function: the ability of one cell to distinguish itself from other cells. For example, neural circuit assembly requires self-avoidance: individual neurons must physically contact other neurons but avoid contacting themselves.⁵⁸ To that end, neurons use unique sets of surface adhesion proteins to distinguish their own identity from that of other cells. In Drosophila, each neuron stochastically expresses a single isoform of the cell adhesion protein Dscam1 out of a large set (~19,000) of distinct isoforms. These isoforms interact homophilically (in a one-to-one manner), leading to contact-dependent repulsion for same-cell interactions. In this way, every isoform directly represents a single address.

By contrast, vertebrates use a combinatorial approach to generate a much larger set of addresses for unique neurons.⁵⁹ Each cell stochastically expresses ~15 different protocadherin variants from a much smaller set of 58 (in the case of the mouse) variants. Within the same cell (i.e. in cis), different variants interact promiscuously,⁶⁰ resulting in multimeric, heterogeneous protocadherin clusters. Each combination of expressed proteins represents a unique cellular identity. These protein variants interact in a many-to-many manner in cis, with each protein variant able to bind to all others. However, the multi-protein clusters exhibit a combinatorially homophilic interaction between juxtaposed cell membranes (in trans), such that a perfect match of all components is required for trans interactions, whether on the same or different cells (Figure 2B). By experimentally co-expressing sets of up to 5 different protocadherin variants, Thu et al. showed that only cells with identical expression patterns exhibit strong trans binding. Mismatch of a single isoform located on two juxtaposed membranes was sufficient to greatly diminish homophilic adhesion strength.^60,61 In this way, combinations of a few promiscuously interacting protocadherin isoforms in vertebrates provide neurons with a vast number of orthogonally interacting addresses and enable them to discriminate self from non-self. Recent work has shown that this mechanism might play more general roles in the mechanical organization of tissues during morphogenesis.⁶²

Transcription factor dimerization networks allow complex gene regulation

In a multicellular organism, combinatorial transcription factor dimerization networks could play a key role in enabling cell type specific gene regulatory responses to signals. For example, members of the bHLH transcription factor family share similar helix-loop-helix domains that allow the formation of many different dimers, as many as 30 in some systems.⁶³ These dimers can exhibit different transcriptional activities and DNA binding site preferences. Further, some bHLH factors lack DNA binding domains altogether, and therefore generate transcriptionally inactive dimers. Consistent with the mathematical models and other examples above, this combinatorial complex formation could allow cell context-dependent computational gene regulation responses. For example, key developmental pathways activate the expression of bHLH transcription factors, which can then form various homo- and heterodimers with themselves and one another. In this way, they provide a layer of combinatorial dimerization between signaling pathways and their genomic targets. For example, the Hes and Her genes are bHLH transcription factors that are activated by Notch, FGF, and other signaling pathways.⁶⁴ Once expressed, these transcription factors can then form dimers regulating the expression of downstream targets, as well as their own expression.

In many developmental processes, Hes and Her proteins negatively regulate their own expression, producing complex regulation of downstream gene targets. In somitogenesis, this autoregulation leads to synchronized oscillations in expression, which are necessary for the repetitive process of somitogenesis.⁶⁵ In neurogenesis, additional factors controlling the strength of this feedback can produce different outcomes in embryonic and adult stem cells.⁶⁶ However, though the negative feedback of Hes and Her genes plays a clear role in both somitogenesis and neurogenesis, it was insufficient to explain all the observed patterns of gene expression in these two processes.^33,67 This suggests that combinatorial interactions between bHLHs could play a key role in determining gene activation and dynamics. Below, we describe two examples where explicitly accounting for bHLH dimerization was necessary to explain the combinatorial and context-dependent effects of Hes and Her on their target genes.

In somitogenesis, knocking out Her1 or Her7 produces distinct effects, even though they promiscuously bind similar targets and have similar effects when overexpressed.³³ A careful study of Her1 and Her7 in zebrafish development revealed that they form many dimers, binding to themselves, each other, and a third binding partner, Hes6. This confirmed an earlier prediction of the existence of Her1-Her7 heterodimers to explain observed effects in zebrafish.⁶⁸ Most of the formed dimers are transcriptionally inactive. Only the Her7:Hes6 heterodimer and the Her1:Her1 homodimer have strong DNA binding activity and can regulate downstream expression of Her1 and Her7. Thus, while Her1 and Her7 bind similar DNA regions, their sequestration in a “dimer cloud” and competition for shared binding partners give them distinct roles in controlling gene expression, as Her7, but not Her1, is required for certain oscillations.

Dimerization of bHLHs can also be used to explain their context-dependent effects on their gene targets. Neural stem cells (NSCs) readily proliferate during embryonic development but are largely quiescent during adult neurogenesis. The Hes bHLH genes have two regulatory roles in this transition to quiescence: inhibiting their own expression and inhibiting the expression of proneural factors. Combinatorial bHLH dimerization is key to explaining how this circuit can produce different degrees of quiescence between the adult and embryonic states.⁶⁷ Specifically, Inhibitor of DNA-binding factors (IDs) have a helix-loop-helix domain that allows them to dimerize with bHLHs, but lack the basic domain that promotes DNA binding. Thus, IDs can dimerize with Hes proteins and alter their DNA binding properties. As a result, Hes-ID dimers can perform only one of Hes’s two regulatory roles, as they can inhibit expression of proneural factors but do not inhibit expression of Hes itself. This suggests that the expression of ID factors in adult NSCs stabilizes Hes expression, removing oscillations produced by its negative autoregulation, while more strongly repressing proneural factors, increasing the degree of quiescence.

Together, these examples highlight the complex gene regulation requirements for mammalian development and how bHLH dimerization supports those higher level functions. But key questions remain unclear: What computations are possible with bHLH and other combinatorial transcription factor dimerization architectures, and how do those computations enable developmental and physiological cell behaviors? What particular functions do these computations support, outside of achieving diverse patterns of gene expression? For example, dimerization networks can decouple the control of different aspects of circuit output, such as the period or amplitude of oscillations in somitogenesis^.33 Moreover, control of bHLH gene expression is also crucial to buffering these oscillations from the effects of bursty transcription^.69,70 How do these promiscuous dimerization networks integrate with other complex circuit features, such as autoregulation to produce oscillations of shared components? Experimental work is needed to systematically map bHLH dimerization networks, identify the functions they compute, and determine how those functions change depending on which factors are expressed in any given cell context. Moreover, the role of competitive dimerization in tuning DNA-binding and transcription factor activity can be applied to other transcription factor families, such as nuclear hormone receptors, which also exhibit complex dimerization patterns^.71,72 Such studies would allow us to understand transcription factor dimerization networks as predictable computational devices, and better control their behavior.

Synthetic combinatorial protein networks enable scalable multistability

Previously, most synthetic biological circuits have operated at the level of individual cells. However, recent advances have begun to enable the design of multicellular circuits that allow cells to operate in multiple states, communicate specifically with one another, and spatially organize into tissue-like structures. These multicellular behaviors will require increased computational capabilities, paralleling those that arose during the corresponding evolutionary transition to multicellularity. The same principles of computation by combinatorial protein networks could enable such synthetic circuits.

For example, we recently sought to create a synthetic cell fate control system that would generate multiple stable states^.73 To choose a design, we were inspired by two prevalent features of natural cell fate control systems: First, natural systems use promiscuous dimerization among transcription factors, such as bHLH factors, to generate a variety of dimers with different DNA binding specificities and activities, including inactive complexes^18,74,75 (Figure 2C). Second, they often include positive autoregulatory feedback loops in which dimers directly or indirectly activate expression of their own components. A minimal circuit design, termed MultiFate, embodies those two principles. It is based on a set of engineered zinc finger transcription factors that can promiscuously homo- and heterodimerize to form all possible dimers (Figure 2D, left panel). Homodimers positively regulate their own expression while heterodimers are inactive. Mathematical modeling showed that this circuit design could produce multiple stable attractors in the space of transcription factor concentrations (Figure 2D, right panel). Further, the number of states initially scales exponentially as 2^N-1, where N is the number of factors. This scaling is enabled in part by the use of dimerization for cross-inhibition among transcription factors. Eventually, this scaling becomes limited by the more rapid growth of inactive heterodimers compared to active homodimers. Consistent with the model, adding additional transcription factors to an existing experimental circuit expanded the number of states without re-engineering the existing system, with 2- and 3-factor circuits respectively generating 3 and 7 stable states. The synthetic system also recapitulated other aspects of natural cell fate control systems, such as progressive and irreversible differentiation. This work shows how combinatorial dimerization can play a key computational role in enabling multicellularity.

Studying promiscuous protein-protein interaction systems

Many biological systems possess the elements necessary for computation through combinatorial binding (Figure 3A, cf. Box 1). However, predicting and controlling the capabilities of these systems poses particular challenges and opportunities. First, these systems can contain many paralogs, whose subtle functional differences are not apparent in their highly similar structures and sequences. Second, the large number of combinatorial interactions, even for modest numbers of components, requires commensurately large datasets for qualitative mapping and quantitative measurement. Third, design of new modified protein variants could potentially expand network computations, but requires models that relate component sequences to their interaction parameters. Initial work has begun to address these three issues.

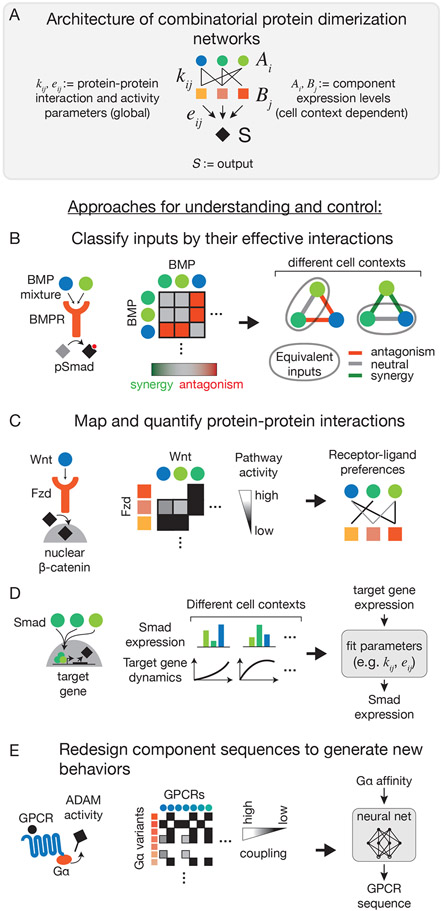
Figure 3: Strategies to understand and control combinatorial complexity of protein dimerization networks.

(A) In combinatorial protein dimerization networks, one set of protein variants ($A_i$) binds combinatorially to another set of protein variants ($B_j$); the resulting complexes produce a common output ($S$). Global parameters describe the protein-protein binding ($k_{ij}$) and complex activity ($e_{ij}$) parameters. The output of the network depends on the complex levels, and thus on the abundance of various components ($A_i,B_j$), which can vary between cell contexts.

(B) The functional differences between protein variants are often unclear because of the variants’ high sequence similarity. For example, the highly homologous BMP ligands activate a common output (pSmad), but can produce distinct effects in combinations. Mapping pairwise responses allows individual ligands to be classified by their effective interactions, highlighting functional differences between the ligands ⁴³. These differences are not global, but can vary between cell contexts.

(C) While all dimerizations are possible in principle, they do not necessarily produce output. For example, in the Wnt pathway, not all Wnt ligands bind and activate the associated receptors (Fzd). Exposing cell lines engineered to express only a single Fzd receptor to each Wnt ligand revealed patterns of receptor-ligand preferences that were not clear from protein sequence alone⁷⁹.

(D) Quantitatively predicting the output produced by protein-protein interactions requires careful parameterization of binding affinity and overall activity (i.e. kij, eij). Combining measurements of component abundance (Ai, Bj) with output dynamics (S) allows the inference of these parameters. For example, quantifying expression of Smad proteins and the expression of their downstream target genes fit a model that predicted target gene expression from Smad expression, and vice versa⁸⁰.

(E) Redesigning a given component’s sequence can alter its protein-protein interactions and, in some cases, produce entirely new responses and computations. The coupling interactions of 148 GPCRs with 11 Gα subunits were used to train a machine learning predictor of coupling strength. This model then guided the design of a less promiscuous GPCR, by generating GPCR sequences predicted to couple uniquely to a given Gα subunit¹⁵.

Classifying inputs by their effective interactions

The maintenance of multiple protein variants within networks suggests that they could perform unique functions, but differences between these components can be subtle and difficult to determine. Often, they have similar sequences and structures that do not provide obvious clues to the subtle differences in binding or activity that allow them to produce distinct effects. In other fields, comprehensive measurements of pairwise interactions have allowed functional systems-level classification of molecular components. For example, measuring the effects of a set of antibiotics, alone and in all pairwise combinations, on the growth of E. coli identified antagonistic and synergistic interactions.⁷⁶ These interactions were then used to classify antibiotics into equivalence groups, where drugs exhibiting the same pattern of interactions with other drugs are grouped together. Remarkably, this epistatic classification scheme—lacking any direct molecular information—matched that based on the drugs’ known biochemical mechanisms of action.

Inspired by such studies, we asked whether a similar functional classification of BMP ligands could be obtained by systematically and quantitatively analyzing BMP pathway responses in several cell lines to 10 BMP ligands, both individually and in all pairwise combinations.⁴³ In mouse embryonic stem cells (mESCs), many of the 10 ligands studied combined additively with one another, as if they were functionally interchangeable. However, even ligands that combined additively with one another sometimes interacted differently with other ligands. For example, BMP7 and BMP9 combined additively with each other, but either additively or synergistically, respectively, with BMP4, putting them into distinct equivalence groups. Altogether, this approach classified the full set of 10 ligands into 5 equivalence groups, with ligands within a group sharing both a similar individual potency and a similar pattern of effective interactions with other ligands (Figure 3B).

Are these equivalence groups intrinsic properties of the ligands, or are they contextual, depending on properties of the cell line and its receptor expression profile? In a second cell line, NMuMG, which exhibits a different BMP receptor expression profile, the ligands produced different pairwise responses. For example, BMP9 and BMP4 synergized in mESCs, but combined additively in NMuMG cells. More generally, NMuMG cells exhibited more antagonistic interactions between ligands. While the ligands could again be classified into five equivalence groups, these groups differed from those obtained in mES cells. More generally, expanding this analysis to a panel of five additional cell lines differing in their receptor expression profiles revealed the strong effect of receptor expression on ligand equivalence, with each of the 7 cell lines, some differing only in their receptor expression profiles, producing a distinct equivalence group classification. Evidently, cell context strongly impacts ligand equivalence.

This large dataset also provided insight into the effects of specific receptors on multi-ligand computation. For example, consistent with known ligand-receptor interactions, the BMPR1B receptor mediates signaling by the ligands GDF5, GDF6, and GDF7 by converting their antagonistic interactions to additive ones. Similarly, the ACVR1 and ACVRL1 receptors relieve non-additive interactions of BMP10 and BMP9, respectively. This phenotypic classification also proved useful in explaining previous results in the literature. For example, BMP9 was shown to functionally replace BMP10 during vasculature formation but not heart development^.77 This difference in the equivalence of BMP9 and BMP10 is consistent with observations that only when the receptor ACVRL1 is expressed, as it is in endothelial cells, do the two ligands fall into the same equivalence group. Taken together, these results underscore that BMP signaling is both combinatorial and contextual, as well as the power of effective interactions for revealing the spectrum of computational power in a given pathway and for individual ligands.

Mapping and quantifying protein-protein interactions

A key step in building a predictive model of combinatorial computations requires identifying which protein-protein complexes can form. However, even small changes in amino acid sequence can drastically affect protein binding affinity^.78 As a result, one cannot necessarily predict how strongly one pair of protein variants based on the binding strengths of their paralogs.

For example, Wnt signaling provides powerful instructive cues during development. The pathway includes 10 ligand variants, each of which could potentially bind and activate any of 9 Fzd receptor variants. In fact, however, the signaling activities of the ligands differ from one another and vary across different cell contexts^.11,12 To build a mechanistic understanding of the functional differences between Wnt ligands and Fzd receptors, Voloshanenko et al. engineered cells to express each Fzd receptor variant individually and then measured the activation of each receptor by each Wnt ligand.⁷⁹ This map showed that each ligand activated multiple receptors and that most receptors were activated by multiple ligands (Figure 3C). (Note that two receptors were not activated by any ligand and may provide other, possibly inhibitory, functions.) Moreover, many structurally homologous ligands, such as Wnt9a and Wnt9b, activated different sets of receptors. Thus, this approach revealed counter-intuitive interactions and revealed the diverse capabilities of these apparently similar ligand and receptor variants.

An accurate prediction of combinatorial computations requires knowing not only which complexes can form, but their relative affinities of formation and their output-producing activities ($k_{ij}$ and $e_{ij}$ in Box 1 and Figure 3A). Lucarelli et al. built such a model to predict the gene-specific dynamics of multiple targets of the TGFβ pathway. In TGFβ signaling, three variants of the Smad effector, Smad2/3/4, promiscuously assemble in different combinations to generate a family of 10 possible trimeric transcription factor complexes that differ in their genomic targets and activities. Predicting how the distribution of these trimers depends on the expression levels of the three components is essential for understanding computation within the pathway. Lucarelli et al. used mass spectrometry and co-immunoprecipitation to quantify the phosphorylation dynamics of Smad monomers.⁸⁰ The authors then used these data to fit a model in which monomers undergo pairwise association and dissociation (Figure 3D). Because each Smad2 and Smad3 monomer can be phosphorylated on two sites, many molecularly distinct complexes are possible. In fitting the model, they therefore used a standard regularization technique^81,82 to limit the number of nonzero parameters and focus on key Smad complexes. The resulting model predicted that three crucial Smad complexes, out of the possible 10, drove most target gene expression. Critically, the fit model could predict TGFβ activation of gene expression in other cell lines based solely on Smad expression levels. It could also make reverse predictions, correctly inferring that a tumor sample had elevated levels of Smad activation overall based on changes in its gene expression. These results provide hope that limited numbers of measurements can be sufficient to enable predictive, mechanistic modeling of combinatorial protein networks.

Redesigning component sequence to produce new behaviors

Machine learning methods show promise for identifying subtle patterns in the behavior of combinatorial protein networks and guiding the design of new signaling components. A clear example of this is recent work with GPCRs.¹⁵ These receptors promiscuously activate a variety of G-proteins, via interactions with the C-terminal tail of the Gα subunit. The authors quantified pathway activation by all possible pairs of 148 human GPCR and 11 Gα C-terminal domain variants, each fused to a common backbone. The sigmoidal signaling response to varying ligand concentrations allowed the authors to quantify the coupling between each receptor and each Gα variant. Training a machine learning model with these data identified sequence-specific coupling features, which the authors then used to forward design GPCR variants that coupled with a particular Gα variant of interest (Figure 3E). These results demonstrated how quantitative input-output measurements contain sufficient information to guide the design of new signaling components. Further, even though the underlying system is promiscuous, these results show that comprehensive analysis of promiscuous interactions, together with machine learning approaches, can enable the design of components with greater specificity.

Conclusions and future directions

In his 1995 review, “Protein molecules as computational elements in living cells,” Dennis Bray wrote, “Because proteins…integrate inputs and produce outputs it seems inescapable that the highly interconnected network of protein-based pathways in living cells will share some of the properties of neural nets.”²⁸ Here, we have seen how combinatorial protein networks can provide a versatile architecture for realizing neural-like computation at the protein level. Mounting experimental evidence shows that these systems can compute combinatorial functions of multiple input proteins. Furthermore, the computation can be reprogrammed by modulating the expression levels of circuit components. This ability allows cells to tailor computations to cell state and context, and support higher level functions such as addressing and self-avoidance. Critically, the elements necessary for combinatorial computation are present in a huge range of systems, the vast majority of which have not yet been systematically analyzed from this point of view.

In computer science, different neural network architectures have been developed to perform different kinds of computational tasks.⁸³ In a similar way, different combinatorial protein network architectures may be optimized to perform different classes of computation. For example, bHLH dimers often autoregulate their own expression, introducing direct feedback loops that allow the generation of stable attractors, while developmental signaling systems like BMP can use computation to selectively respond to different ligand combinations. Similarly, biological pathways may also operate over multiple timescales. For example, BMP can transmit signals on timescales of minutes to hours. Over the longer timescales of differentiation, cells can alter receptor expression, dynamically changing the ligand combinations they sense. Analysis of single-cell trajectories in developmental time courses could shed more light on such dynamic behaviors and on their potential to alter computational behavior.

Combinatorial protein networks differ in fundamental ways from their artificial neural network analogs. Because proteins have finite concentrations in cells, competition for binding can lead to indirect (or nonlocal) interactions across a set of promiscuously dimerizing proteins. That is, an increase in the level of one complex necessarily reduces the concentrations of alternative complexes. It would be interesting to understand how this architectural difference impacts the functional expressivity of the network, and whether the principles of combinatorial protein networks could be usefully imported into artificial neural networks for engineering applications.

Above, we focused on a single set, or “layer,” of promiscuously interacting proteins. Superficially, this contrasts with deep multi-layer neural network architectures. However, biological circuits can also contain multiple distinct layers of combinatorial dimerization, with one layer regulating the next. For example, the promiscuous ligand-receptor interactions in the BMP signaling system (layer 1) lead to promiscuous phosphorylation of a set of distinct Smad proteins by distinct signaling complexes (layer 2). These in turn promiscuously multimerize to form a variety of transcription factor complexes (layer 3). Finally, these complexes exhibit many-to-many binding relations with different target sites on the chromosome (layer 4). In this way, biological circuits achieve multiple layers of computation. It will be interesting to determine which aspects of the overall computation are performed at each level, and why. It may also be important to consider how computations are deployed across multicellular systems. Contextuality potentially allows each cell type to tailor the computation of a given pathway to its own needs. Experiments and models will both be central to exploring how computational modules within individual cells compose to generate more complex, and spatially extended, tissue level functions at a larger scale.⁸⁴

The paradigm of combinatorial protein networks can support at least two types of potential applications. First, the ability to develop predictive quantitative models of these systems could open up the ability to control cell behaviors with greater precision. Cell atlas projects have revealed the receptor expression profiles of most cell types. Promiscuous pathways are often involved in disease and targets for drug development. For example, mutations in the ACVR1 BMP receptor cause the disease fibrodysplasia ossificans progressiva (FOP). The discovery that these mutations cause disease by changing a non-signaling ligand-receptor complex into an signaling complex introduced important new approaches in the development of FOP therapeutics ^44,85. Understanding how potential perturbations of this and other pathways in each cell type and tissue environment change ligand perception could enable more rational design of therapeutic interventions. A second class of applications of this paradigm will undoubtedly unfold in synthetic biology, where systems of ever greater computational capacity are needed to enable more specific and controllable cell therapies.^86-91 The case of the MultiFate architecture discussed above shows a relatively simple example in which combinatorial protein networks can enable a complex dynamical behavior—multistability. But to program more complex multicellular systems, eventually rivaling those of the natural immune system, for instance, many more types of rapid protein-level computation will be needed.

The principal challenge in both analyzing and synthetically implementing combinatorial protein networks is the explosion of interactions and component expression contexts. Analytically, one approach is based on minimal, effective biophysical models that represent the essential components and interactions (Box 1), and are parameterized with empirical measurements. This approach requires systematic characterization of components, and relies on approximations or simplifications that may not be universally valid across all cell contexts. Alternatively, machine learning approaches based on high throughput measurements could potentially provide a mechanism-independent way to predict behaviors. These, too, suffer from the need for large data sets and may be limited in their predictive ability by the contents of the training data set. While such statistical models may not be immediately interpretable, they could nevertheless be valuable for design of experiments and therapeutics. For both modeling approaches, a key challenge is grappling with the strong contextuality of dimerization networks. Different cell types express different levels of circuit components, potentially generating a whole repertoire of different functional behaviors. It will therefore be critical to ensure that models can accurately predict circuit behavior across cell contexts.

Synthetically, designing combinatorial protein networks faces the challenges of imposing defined many-to-many interactions on a set of engineered protein components, and then regulating those components in different cell types. Engineering of combinatorial protein networks will benefit from growing libraries of well-characterized protein interaction domains,^92-94 and emerging methods to engineer complex protein-level circuits.^31,95-98 However, methods to assemble larger circuits in a more systematic way will be pivotal in expanding synthetic mammalian biology to multicellularity.

How “special” is the exact architecture and parameter values that characterize any given combinatorial protein network? At one extreme, it could be that in order to perform the required range of signal processing tasks within the organism, a combinatorial protein network needs to fine-tune its structure, affinities, activities, and other biochemical parameters. If one could replay the tape of evolution, in Stephen Jay Gould’s hypothetical metaphor, a closely equivalent network would have evolved with nearly identical parameters. On the other hand, it is possible that many different network topologies could provide the full diversity of computational functions for many or most possible parameter values. In this case, evolution might have stumbled upon a very different network design or parameter regime that nevertheless performs equivalent computations. In this case, the particular details of the pathways we observe would represent a contingent evolutionary artifact. Either way, it would be interesting to know whether the computational capacity of the system was more conserved or constrained than the molecular implementation.

Unlocking the full potential of promiscuous protein computation would provide a new lens to understand, predict, control, and ultimately program biological systems. Achieving this goal will require a combination of mathematical modeling, quantitative experimental analysis, and synthetic biology approaches. It will also require deeper analysis of the systems discussed above and extension of the paradigm to other systems that remain poorly characterized from this point of view. In the longer term, it will be interesting to see to what extent a unified paradigm can explain a broad diversity of promiscuous molecular circuits, built out of proteins and potentially other biological molecules as well.

Supplementary Material

1

Video S1. Receptor expression context controls computation in a many-to-many ligand-receptor network.