Abstract
Purpose
This study was conducted to evaluate the effect of alcohol consumption on breast cancer, adjusting for alcohol consumption misclassification bias and confounders.
Methods
This was a case-control study of 932 women with breast cancer and 1000 healthy control. Using probabilistic bias analysis method, the association between alcohol consumption and breast cancer was adjusted for the misclassification bias of alcohol consumption as well as a minimally sufficient set of adjustment of confounders derived from a causal directed acyclic graph. Population attributable fraction was estimated using the Miettinen’s Formula.
Results
Based on the conventional logistic regression model, the odds ratio estimate between alcohol consumption and breast cancer was 1.05 (95% CI: 0.57, 1.91). However, the adjusted estimates of odds ratio based on the probabilistic bias analysis ranged from 1.82 to 2.29 for non-differential and from 1.93 to 5.67 for differential misclassification. Population attributable fraction ranged from 1.51 to 2.57% using non-differential bias analysis and 1.54–3.56% based on differential bias analysis.
Conclusion
A marked measurement error was in self-reported alcohol consumption so after correcting misclassification bias, no evidence against independence between alcohol consumption and breast cancer changed to a substantial positive association.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12874-023-01978-6.
Keywords: Probabilistic bias analysis, Alcohol consumption, Breast cancer, Monte-Carlo sensitivity analysis, Population attributable fraction
Introduction
Breast cancer is the leading cause of death from cancer in women across the world accounting for 25% of the total new cancer cases and 15% of the total deaths from cancer [1]. The incidence of breast cancer varies up to five time in different parts of the world, being higher in developed countries; however, its incidence is on the rise in less developed countries, too [2]. Several studies investigated the risk factors of breast cancer and found that factors like childbearing, advanced age, high menopause age, low menarche age, low physical activity, high-fat diets, high BMI, positive family history, nulliparity, use of OCP, and smoking could play a role in its occurrence [2–6].
Alcohol consumption, as one of the risk factors of breast cancer, has drawn researchers’ attention in the past decade. However, there is still controversy about the association between alcohol consumption and breast cancer; some primary studies found a positive relationship [7–10] while others rejected any association [11–16]. Several researchers conducted different meta-analysis studies to address this controversy. Although most of these meta-analyses indicated a positive association [17–24], the majority were very weak [19, 20, 22–25]. This is while some other studies rejected any association between moderate alcohol consumption and breast cancer [25]. On the other hand, in addition to the fact that most of the studies failed to adjust for important confounders [24, 25], they also suffer from alcohol consumption misclassification due to self-reporting [17, 22, 23].
It is clear that the alcohol consumption may be underreported due to its social stigma. Several studies have found misclassification in alcohol consumption reporting [17, 22, 23], which may lead to biased effect estimates [26, 27] of alcohol consumption on breast cancer, explaining the contradictory results mentioned above. Therefore, statistical methods have been suggested to be used to correct misclassification bias secondary to self-reported alcohol consumption [28].
In general, two approaches have been developed to correct misclassification: Probabilistic Bias Analysis Method (PBAM) by Lash and Fox [29, 30], and Bayesian Method [31], by MacLehose [32] and Gustafson [11]. Both models can control the measurement bias but the PBAM, which is based on the Monte-Carlo simulation [12, 29, 30], is conceptually simpler and easier to perform. Studies have shown that in the case of selecting similar priors, the results of both models may be similar [33].
Simple bias analysis and multidimensional analysis [34] perform bias correction by using a set of few bias parameter (sensitivity and specificity) values, while PBAM creates simulation intervals that are adjusted for a probability distribution of bias parameters as well as random error and confounders through record-level correction of the misclassified exposure [30]. The general PBAM approach of Fox et al. [29] and Lash et al. [30] was developed for polytomous exposure variables.
Although several studies investigated the association between alcohol consumption and breast cancer [7–25], none of them have adjusted for the measurement bias secondary to the self-reported alcohol consumption. Therefore, this study was done to assess the effect of alcohol consumption on breast cancer after correcting alcohol consumption misclassification bias and adjusting for a set of confounders using PBAM.
Materials and methods
Design and sampling
This case-control study was performed in Tehran, Iran. The methodological details of the present study have already been published previously [35]. This study recruited 1000 patients with breast cancer as case, selected in an ongoing manner (incidence cases) from breast cancer detection clinics in Tehran, Iran, whose disease was diagnosed and confirmed by pathological study and/or a specialist and the same number of individuals without cancer as control, selected from the general population of all Tehran districts through proportional-to-size stratified random sampling. Cases included breast cancer patients aged 25–75 years old that expressed willingness to participate in the study and lived in Tehran. The exclusion criteria were pregnancy, other cancers in addition to breast cancer, and healthy women receiving preventive treatments for breast cancer. The study objectives were explained to the subjects and signed informed consent was obtained from all. The data collection tool was a researcher-made questionnaire with confirmed validity and reliability. However, we note that the misclassification problem in the question of alcohol consumption, which is closely related to the construct validity, exists as the question was subject to recall and under-reporting biases. A trained female research assistant made clinical measurements including weight and height. The questionnaire had seven sections, including (1) demographic and general data, (2) physical activity, (3) cigarettes and tobacco use as well as alcohol consumption, (4) diet, (5) pregnancy and past medical history data (history of breast diseases as well as the history of pregnancy along with the delivery date), (6) family history, and (7) clinical measurements including weight and height, weight at puberty (age 12), and weight at 20 and 30 years of age.
Statistical analysis
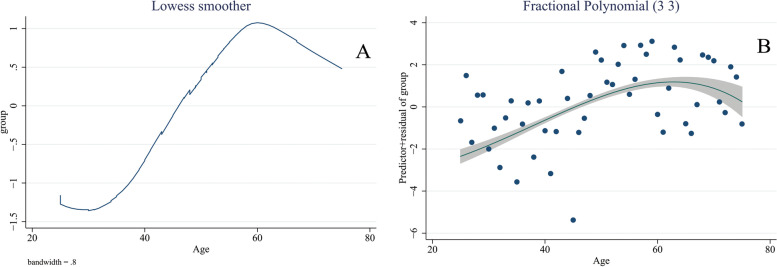
Some packages in the R software including foreign, doParallel, foreach, triangle, readstata13, MASS, Haven and SUMMER were used for statistical analysis. The relevant literature was searched to prepare a list of confounders. The DAGitty package was used to generate a casual directed acyclic graph (cDAG) [36–46]. The Pearl’s back-door criterion was applied to identify a minimally sufficient set for confounding adjustment [47]. Then, a conventional multivariable logistic regression model was fitted to assess the association of alcohol consumption and breast cancer, adjusted for the set of confounders and the result was reported as adjusted OR with 95% confidence interval [48, 49]. Locally weighted scatterplot smoother (LOWESS) and fractional polynomials were used to determine the appropriate scale for age [50]. Figure 1 presents the LOWESS and fractional polynomial plot for the association between age and breast cancer.
Fig. 1.
LOWESS (A) and fractional polynomial plot (B) for the association between age and breast cancer
Bias analysis using PBAM
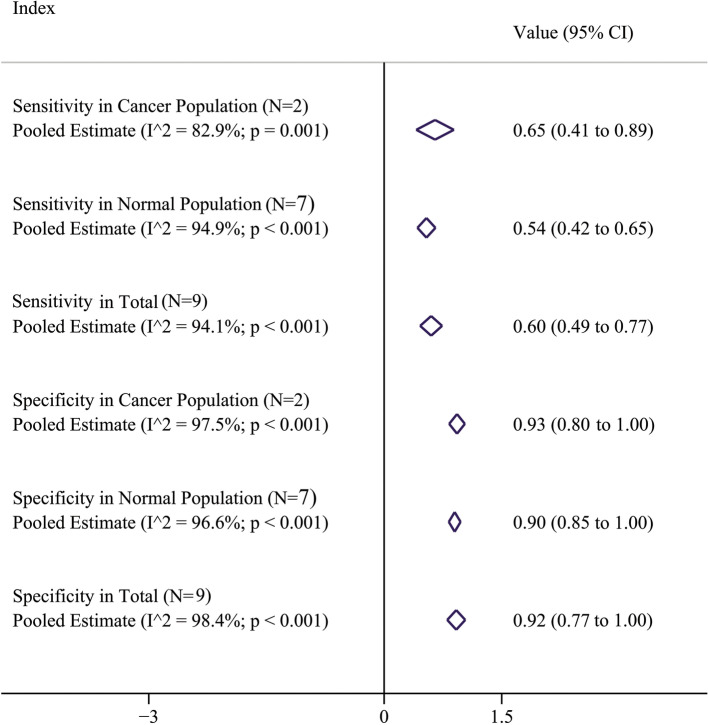
Step 1: A systematic literature review (without time and language restriction) was done in Scopus, PubMed, and Web of Science to determine the sensitivity and specificity of the question asking about self-reported alcohol consumption, using the following keywords: “sensitivity”, “specificity”, “self-reported alcohol consumption”, “validity”, “accuracy”, “measurement error” and “measurement bias”. The retrieved studies were screened in three stages, including titles, abstracts, and full texts. All the articles that reached the final stage were read carefully and the information such as sensitivity and specificity along with their confidence intervals, gold standard method, were collected. Then, an inverse-variance weighted random-effects model was applied to merge the results [51].
Step 2: According to the results of the systematic review, nine studies (Supplement 1) were included in the final analysis [52–60] two of which were done in cancer patients [52, 53] and seven were performed in the normal population [54–60]. The pooled estimate of specificity (95% CI) in cancer patients, normal population, and total were 93% (80, 100), 90% (85, 100), and 92% (77, 100), respectively. The estimates for sensitivity (95% CI) were 65% (41, 89), 54% (42, 65) and 60% (49, 77); respectively (Fig. 2).
Fig. 2.
Pooled estimates of specificity and sensitivity; pooled estimates in total was used for non-differential bias analysis and pooled estimates in cancer and normal subjects was used for differential bias analysis
Step 3: The probability distributions (including Triangular, Beta and Logit-logistic) were generated and their parameters were selected so that the median/mean of probability distribution was equal to the pooled estimate of specificity/sensitivity, and the dispersion becomes consistent with 95% confidence intervals. The pooled results obtained for cancer and normal populations were used to determine the distribution parameters in differential misclassification bias analysis and the results for the total population were used to determine the distribution parameters in non-differential misclassification bias analysis. Table 1 presents the probability distribution parameters for Triangular, Beta and Logit-logistic distributions. It should be noted that the correlation of sensitivity and specificity was set to be 0.8, 0.5 and 0.25 in both case and control groups in differential misclassification bias analysis.
Table 1.
The bias parameters for Triangular, Beta and Logit-logistic distributions in control and case groups
| Bias parameters (95% CI) | Group | Triangular distribution: min; max; mode | Beta distribution: alpha; beta | Logit-logistic distribution: location; scale | ||
|---|---|---|---|---|---|---|
| Type of misclassification | Differential |
Sensitivity 65% (41, 89) |
Case group | 0.41; 0.89; 0.65 | 9.21; 4.96 | 0.65; 0.0675 |
|
Specificity 93% (80, 100) |
0.80; 1; 0.93 | 46.74; 3.51 | 0.93; 0.0196 | |||
|
Sensitivity 54% (42, 65) |
Control group | 0.42; 0.65; 0.54 | 42.05; 35.82 | 0.54; 0.0309 | ||
|
Specificity 90% (85, 100) |
0.85; 1; 0.90 | 30.22; 3.36 | 0.90; 0.0281 | |||
| Non-differential |
Sensitivity 60% (49, 77) |
Both groups | 0.49; 0.77; 0.60 | 18.54; 12.36 | 0.60; 0.0478 | |
|
Specificity 92% (77, 100) |
0.77; 1; 0.92 | 39.87; 3.47 | 0.92; 0.0224 | |||
Step 4: A sensitivity/specificity matrix was generated to estimate the expected number of exposed and unexposed cases according to Formula 1.
| 1 |
where Sen and Spe refer to sensitivity and specificity, A is the expected number of exposed cases, B is the expected number of unexposed cases, A* is the observed number of exposed cases, and B* is the observed number of unexposed cases. Random values were selected for sensitivity and specificity from the probability distributions discussed in step 3 and plugged in Formula 1. Then, values A and B were obtained using Formula 1 based on Formulas 2 and 3: (see Supplement 2 for more explanations)
| 2 |
| 3 |
Step 5: Formulas 4 and 5 were used to calculate positive predictive value (PPV) and negative predictive value (NPV):
| 4 |
| 5 |
If there were out-of-range values for PPV and NPV (< 0 or > 1), the iteration process was discarded and steps 4 and 5 were repeated.
Step 6: The status of observed exposure in dataset and PPV/NPV were used to generate a new variable termed “expected exposure” in cases. The distribution of this variable was Bernoulli with the probability parameters equal to PPV for exposed and NPV for unexposed cases. Therefore, a uniform random variable Ui ranging from 0 to 1 was generated. For an exposed case, the value of expected exposure was considered 1 (exposed) if Ui<PPV and 0 (unexposed) otherwise. By contrast, for an unexposed case, the value of true exposure was considered 0 (unexposed) if Ui<NPV and 1 (exposed) otherwise. Steps 4–6 were repeated for estimation of true exposure in controls.
Step 7: The same conventional logistic regression model mentioned above was applied again using the expected exposure (alcohol consumption), generated through steps 1–6, instead of observed exposure, and adjusted OR with 95% confidence interval was reported.
Step 8: The adjusted OR obtained in Step 7 resulted from one round of analysis. The steps 4–7 were repeated applying probabilistic bias analysis and the Monte-Carlo technique to obtain a simulation interval. This procedure corrects the misclassification bias in self-reported alcohol consumption. Then, the 50th percentile of the OR distribution was used as the point estimate and the 2.5th and 97.5th percentiles as the Monte-Carlo sensitivity analysis (MCSA) interval [29].
This point estimate with MCSA interval was only adjusted for misclassification bias and confounders. To address random error, the bootstrap sampling was performed prior to step 4 so that confounding and misclassification adjustment in steps 4–8 were applied to each bootstrap samples. The 95% MCSA intervals incorporating bias and random error were calculated using the 2.5th and 97.5th percentiles over all bootstrap-Monte-Carlo samples. It should be mentioned that there were 500 bootstrap samples, and Monte-Carlo was repeated 1000 times in each bootstrap sample yielding 500,000 adjusted ORs.
Population Attributable Fraction (PAF)
The Miettinen Formula [61] was used for calculatiing PAF for alcohol consumption using Formula 6:
| 6 |
where is the prevalence of exposure in the case group and RR is the adjusted risk ratio. The proportion of alcohol consumers in the case group after misclassification bias correction in step 6 was used as estimate, and adjusted OR obtained in step 7 was considered as RR estimate based on the rarity assumption [62–64]. It is noteworthy that to calculate point estimate and MCSA interval for PAF, Monte-Carlo sampling and bootstrap technique were used.
Result
This study was conducted in 1000 healthy controls and 932 cases. The mean SD age of participants was 42.16 (9.49) years old in the control group and 50.40 (9.70) in the case group. The characteristics of the case and control groups have been presented in Table 2.
Table 2.
Characteristics of cases and controls
| Variables | No. (31) | |
|---|---|---|
| Control | Case | |
| Marital status | ||
| Married | 792 (79.2) | 744 (79.8) |
| Single | 133 (13.3) | 61 (6.5) |
| Divorced | 34 (3.4) | 47 (5.0) |
| Widow | 41 (4.1) | 80 (8.6) |
| Insurance | ||
| No | 107 (10.7) | 32 (3.4) |
| Yes | 893 (89.3) | 900 (96.6) |
| Education | ||
| Illiterate | 48 (4.8) | 55 (5.9) |
| Primary | 108 (10.8) | 163 (17.5) |
| Secondary | 158 (15.8) | 148 (15.9) |
| High school | 342 (34.2) | 316 (33.9) |
| Bachelor | 284 (28.4) | 200 (21.5) |
| More than bachelor | 60 (6.0) | 50 (5.4) |
| Job | ||
| Housekeeper | 723 (72.3) | 746 (80.0) |
| Government employed | 159 (15.9) | 96 (10.3) |
| Self employed | 108 (10.8) | 48 (5.2) |
| Retired | 10 (1.0) | 42 (4.5) |
| SES | ||
| Very low | 11 (1.1) | 25 (2.7) |
| Low | 68 (6.8) | 187 (20.1) |
| Middle | 273 (27.3) | 491 (52.7) |
| High | 638 (63.8) | 198 (21.2) |
| Very high | 10 (1.0) | 31 (3.3) |
| Alcohol | ||
| No | 971 (97.1) | 892 (95.7) |
| Yes | 29 (2.9) | 40 (4.3) |
| Physical activity | ||
| No | 891 (89.1) | 833 (89.4) |
| Yes | 109 (10.9) | 99 (10.6) |
| Smoking | ||
| No | 970 (97.0) | 890 (95.5) |
| Yes | 30 (3.0) | 42 (4.5) |
| Agea | 42.16 (9.49) | 50.40 (9.70) |
amean and SD
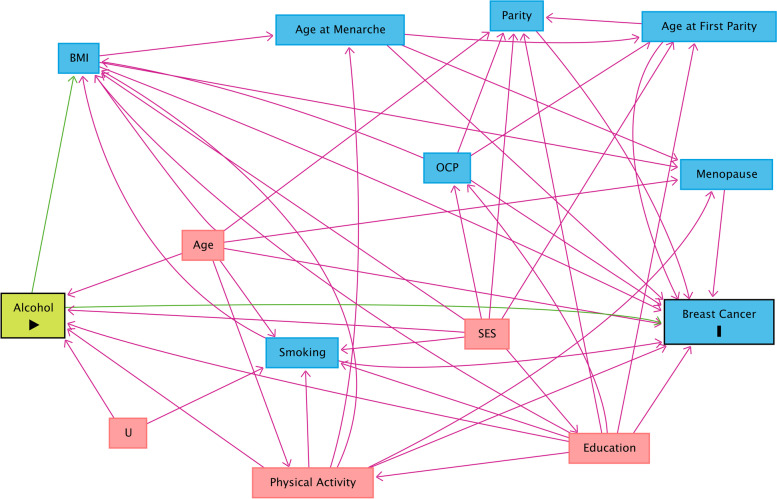
The causal diagram for the effect of alcohol consumption on breast cancer has been depicted in Fig. 3. According to this Figure, the minimally sufficient adjustment set included age, smoking, education level, physical activity, and socioeconomic status (SES).
Fig. 3.
Causal directed acyclic graph (cDAG) for the effect of alcohol consumption on breast cancer
Conventional and bias analyses
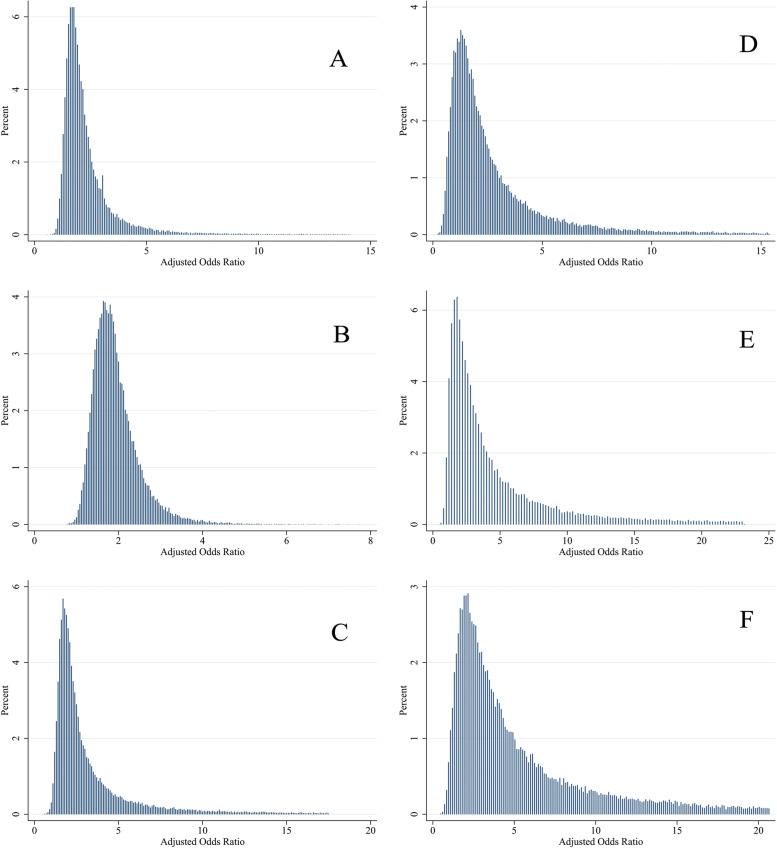
Table 3 presents the results of the conventional and bias analyses for the effect of alcohol consumption on breast cancer. Based on the conventional logistic regression analysis, the OR between alcohol consumption and breast cancer was 1.05 (95% CI: 0.57, 1.91) implying no evidence against the independence of breast cancer from alcohol consumption. According to the results of bias analysis, considering non-differential misclassification, the adjusted estimate of OR was 1.96 (MCSA interval: 1.20, 6.01) using Triangular distribution, 1.82 (MCSA interval: 1.20, 3.38) using Beta distribution, and 2.29 (MCSA interval: 1.23, 11.84) using Logit-logistic distribution for the bias parameter, indicating that alcohol consumption was a risk factor for breast cancer. On the contrary, considering differential misclassification with correlation 0.8, the adjusted OR estimates were 1.93 (MCSA interval: 0.67, 10.07), 2.99 (MCSA interval: 1.44, 17.74) and 3.65 (MCSA interval: 1.16, 17.42) using the Triangular, Beta and Logit-logistic distributions, respectively. The distribution of adjusted ORs using different bias parameters has been displayed in Fig. 4.
Table 3.
Adjusted odds ratio with 95% confidence interval or MCSA interval using conventional and probabilistic bias analyses. All estimates were obtained by adjusting for age, smoking, education level, physical activity and socioeconomic status
| Conventional analysis | Bias parameter distribution | Bias analysis (95% MCSA) | |||
|---|---|---|---|---|---|
| Non-differential | Differential (r = 0.8) | Differential (r = 0.5) | Differential (r = 0.25) | ||
| 1.05 (95% CI: 0.57, 1.91) | Triangular | 1.96 (1.20, 6.01) | 1.93 (0.67, 10.07) | 2.03 (0.97, 12.10) | 2.30 (1.28, 12.23) |
| Beta | 1.82 (1.20, 3.83) | 2.99 (1.11, 17.74) | 5.14 (3.53, 22.09) | 5.56 (3.88, 24.00) | |
| Logit-logistic | 2.29 (1.23, 11.84) | 3.65 (1.16, 17.42) | 5.20 (4.13, 18.00) | 5.67 (4.64, 18.30) | |
Fig. 4.
Distribution of ORs adjusted for measurement bias and confounding, assuming non-differential (A, B and C) and differential (D, E and F) misclassification errors. The distribution of bias parameter was assumed to be Triangular (A and D), Beta (B and E) and Logit-logistic (C and F)
Population attributable fraction
Table 4 shows PAF estimates with 95% confidence intervals using conventional and bias analyses. PAF estimate for alcohol consumption was 0.20% (95% CI: -3.24, 2.50) in conventional analysis. Considering Triangular, Beta and Logit-logistic distributions for the bias parameter in non-differential bias analysis, the PAF estimates for alcohol consumption were 1.76% (MCSA interval: 0.31, 5.27), 1.51% (MCSA interval: 0.27, 4.19) and 2.57% (MCSA interval: 0.37, 9.32), respectively; in differential bias analysis with correlation 0.8, they were 1.54% (MCSA interval: -0.91, 5.92), 2.85% (MCSA interval: 0.21, 6.81) and 3.32% (MCSA interval: 0.41, 6.85). Other values for differential scenario were shown in Table 4.
Table 4.
The estimates of population attributable fraction with 95% confidence intervals or MSCA intervals using conventional and bias analyses
| Conventional analysis | Bias parameter distribution | Bias analysis (95% MCSA) | |||
|---|---|---|---|---|---|
| Non-differential | Differential ( r = 0.8) | Differential ( r = 0.5) | Differential ( r = 0.25) | ||
| 0.20% (95% CI: -3.24, 2.50) | Triangular | 1.76% (0.31, 5.27) | 1.54% (-0.91, 5.92) | 1.53% (-0.03, 5.92) | 1.51% (0.23, 5.74) |
| Beta | 1.51% (0.27, 4.19) | 2.85% (0.21, 6.81) | 3.25% (0.20, 7.03) | 3.56% (1.09, 7.21) | |
| Logit-logistic | 2.57% (0.37, 9.32) | 3.32% (0.41, 6.85) | 2.57% (0.14, 6.34) | 2.58% (0.15, 6.35) | |
Discussion
In this study, we assess the effect of alcohol consumption on breast cancer after controlling three error sources including misclassification bias, confounders, and random error. The PBAM is a type of Monte-Carlo sensitivity analysis that is very similar to Bayesian methods [33, 65–67] and its results are affected by prior distributions [29, 33]. Therefore, the PBAM results depend on the distribution of sensitivity and specificity of the misclassified variable under question [68]. Using the same prior distributions for sensitivity and specificity parameters, the results of PBAM and Bayesian methods should be very similar [33]. Although different sources were used to determine the distribution of sensitivity and specificity, such as expert opinion and study validation, [26, 69] the medical literature seems to be one of the best sources [70]. The use of medical literature allows investigators to incorporate subjective data in their study while merging different sources can neutralize the effects of these judgments [29]. Different sources produce different results; therefore, in this study, to obtain more robust estimates of bias parameters, inverse variance weighting was used to merge these sources.
Based on the results of the conventional analysis in the present study, there was no evidence against independence of self-reported alcohol consumption and breast cancer. This finding was consistent with many previous reports [11–16]. However, it should be noted that case-control studies are prone to misclassification bias due to recall and underreporting [23, 71].
Cohort studies are much less prone to differential measurement error because exposure ascertainment occurs before the onset of the outcome (although differential measurement error can still occur due to dependence of exposure measurement on for some risk factors such as age) and prospective data collection should also reduce measurement error due to poor recall of past exposures [72]. However, similar to case–control studies of alcohol consumption and breast cancer, the results of cohort studies were inconsistent (the results have not been shown but available upon request).
Because of the inconsistent results and some limitations in primary studies, to evaluate the association between alcohol consumption and breast cancer, studies with higher levels of evidence, like meta-analyses, should be relied upon. Ziembicki et al. conducted a meta-analysis through merging 11 studies and found that alcohol consumption had a direct association with percent breast density. However, the effects of unmeasured confounders like smoking and measurement bias in alcohol consumption have not been controlled in the majority of meta-analyses [24]. Bagnardi et al. merged 49 studies and reported that alcohol consumption increased the risk of breast cancer; however, the authors discussed that they could not control the role of alcohol consumption underreporting and other confounders [17, 18]. Choi et al. merged 34 studies and found a positive association between alcohol consumption and breast cancer although this association was very weak (RR = 1.04; 95% CI: 1.01, 1.07), which was due to underreporting according to authors [25]. Another meta-analysis study found a positive association between alcohol consumption and breast cancer; nonetheless, they reported that misclassification and lack of adjustment for confounders were inevitable in primary studies [7].
The results of this study showed that alcohol consumption had a strong effect on breast cancer after adjusting misclassification bias and controlling confounders such as smoking. The range of adjusted OR estimates was 1.82 to 2.29 when controlling for non-differential misclassification and 1.93 to 5.67 when controlling for differential misclassification, suggesting that the effect the alcohol consumption was markedly underestimated if misclassification bias was not properly corrected.
Biologically, it seems that alcohol consumption increases epithelial cell proliferation resulting in dense tissue development in the breast through increased endogenous estrogen production [73], increased aromatase activity [74] and the components of the growth hormone-insulin-like growth factor [75] axis [76], resulting in increased risk of breast cancer [24].
A limited number of studies have used the PBAM for misclassification correction; hence, an extensive search failed to find similar results for comparison. However, this method has been applied in other studies with different context [4, 77–81]. De Silva et al. [79] reported a stronger association between maternal transfusion risk and inter-pregnancy interval after adjusting for severe maternal morbidity misclassification. One study [78] reported that the association between self-reported pre-pregnancy BMI and pregnancy outcomes was overestimated without considering misclassification. Pakzad et al. showed a strong association between smoking and breast cancer after smoking misclassification bias correction [4]. Nonetheless, Momoli et al. [80] and Bodnar et al. [77] found no marked change in the observed relationship after applying PBAM versus conventional methods.
This study estimated the PAF for alcohol consumption and breast cancer. It is clear that alcohol consumption is one of the most important risk factors of cancers. Daily consumption of up to 20 gr of alcohol (≤ 1.5 drinks) is responsible for 26–35% of alcohol-attributable cancer deaths [82]. Since PAF is a function of risk ratio (odds ratio for rare outcomes) and prevalence [83], its estimated prevalence may not show the actual prevalence because of alcohol consumption underreporting/recall bias. According to the recommendations of other studies [84], PAF calculation was done with misclassification correction. Based on the results, PAF ranged from 1.51 to 2.57% in non-differential bias analysis and from 1.54 to 3.56% in differential bias analysis. It means that if alcohol consumption had been eliminated, the risk of breast cancer would have been reduced by 1.5–3.6%. Van Gemert et al. found a PAF of 6.6% for alcohol consumption and breast cancer in the Netherlands [84]. Furthermore, Neutel et al. [85] conducted a study in Canadian women and estimated a PAF range of 2.7–2.6% for alcohol consumption and breast cancer during 1994–2006. PAF estimates for alcohol consumption were 2.8% and 6.4% in the Australian and UK woman in studies by Wilson et al. [86] and Parkin et al. [87], respectively. In a met-analysis by Key et al. [23], PAF estimates were 0.9–2.4% in the USA and 3.2–8.8% in the UK. There was a difference between the PAF estimates of the present study and the above studies, which could be secondary to differences in the prevalence of alcohol consumption in women.
The role of non-differential and differential misclassification was considered in this study. Differential exposure misclassification is more common in traditional case-control studies since the exposure data collection is done after disease diagnosis [26]. Considering a wide range of scenarios, in differential exposure misclassification, the correlation coefficient assumed to be 0.8, 0.5 and 0.25. The result showed that when correlation value increased, the result of differential misclassification will approach to that of non-differential misclassification.
Simple bias analysis can be performed by applying bias correction in each confounder stratum along with summarization. Nonetheless, this method takes a lot of time and does not consider the distribution of the bias parameters. Therefore, it may produce sparse data problems [69, 88, 89]. Other methods like empirical and Bayesian methods are more challenging in terms of calculations while bias correction can be done probabilistically in PBAM, considering distribution of bias parameters to impute the true exposure [29, 68]. This method is simpler and can be applied to estimate the association adjusted for multiple covariates using logistic regression, proportional hazards regression, and other popular modeling techniques [29]. In addition, Monte-Carlo simulations will make it possible to consider all misclassification sources resulting in more robust bias-adjusted estimates [68].
However, it should be noted that although Monte Carlo sensitivity analysis moved point estimates away from the null, the uncertainty interval were widened. In other words, taking into account the uncertainty due to measurement bias in the Monte Carlo approach led to a wider interval as expected.
A systematic search for the values of the bias parameter, using different distributions for the bias parameter, and assuming differential and non-differential misclassification error scenarios were some of the strong points of this study. In this study, a minimally sufficient adjustment set was detected using causal diagram [90] and their confounding bias was corrected using multiple logistic regression. To avoid over-adjustment bias, we did not adjust for the mediators on the pathway between alcohol consumption and breast cancer such as menopause or age at menopause. Finally, we carefully adjusted for the difference in age between cases and controls using LOWESS and fractional polynomials.
However, this study also suffered from some limitations. First there was some misclassification in using ever/never alcohol consumption instead of “number of drinks (bottle/can) of alcohol” which may reduce statistical power, induce a biased impression of dose-response, and change non-differential error to differential [91]. Also there was a considerable heterogeneity among included studies for the calculation of the bias parameters so the random-effects model was used. Moreover, the specificity in the case group was larger than in the control group, and only two studies for cancer patients were meta-analyzed to derive the bias parameters for the case group which is subject to small-sample bias. Also the studies in the meta-analysis were non-local and there is not a reliable study in Iran to determine how odds ratio will be changing by considering the local validations. In other words, it is difficult to perform a very meaningful adjustment for misclassification in the studied setting, and therefore validation studies specific to Iran seem warranted. Another limitation of the present study was inability to control for unmeasured confounding (e.g., diet) and misclassification in self-reporting confounders like smoking. We should note that presence of measurement error in a confounder like smoking will lead to residual confounding although our study objective was correcting alcohol consumption misclassification but not unmeasured confounding. We appreciate the misclassification error in smoking and alcohol is likely correlated which may increase the residual confounding [91]. However, the prevalence of smoking in women living in Tehran was 2.9% [92] and in Iranian woman was 3.6% [93] and so smoking probably cannot be a strong confounder (prevalence of smoking in our control group was 3%). We also calculated the E-value [94] i.e., the minimum strength of association, on the risk ratio (odds ratio for rare outcomes) scale, that an unmeasured confounder would need to have with both the exposure and outcome, conditional on the measured confounders, to fully explain away a specific exposure –outcome association. The results for different bias analysis scenarios have been presented in Table 5. The Table shows that smoking needs to have a large association (OR = 10.82 in one differential scenario) with both alcohol and breast cancer to fully explain the observed association between alcohol and breast cancer. It should be noted that the calculation of E-values assumes no adjustment was made for smoking although we did adjust for the self-reported smoking in the analysis.
Table 5.
E-Values for alcohol assuming no adjustment was made for this variable
| Bias parameter distribution | Bias analysis (95% MCSA ) | |||
|---|---|---|---|---|
| Non-differential | Differential (r = 0.8) | Differential (r = 0.5) | Differential (r = 0.25) | |
| Triangular | 3.30 (1.68, 11.49) | 3.27 (1.00, 19.62) | 3.48 (1.00, 23.69) | 4.03 (1.88, 23.95) |
| Beta | 3.04 (1.69, 7.12) | 5.43 (1.46, 34.93) | 9.75 (6.52, 43.67) | 10.61 (7.22, 47.49) |
| Logit-logistic | 4.01 (1.76, 23.16) | 6.76 (1.59, 34.33) | 9.87 (7.73, 35.49) | 10.82 (8.75, 36.09) |
Conclusion
Our conventional analysis showed no strong evidence of association between alcohol consumption and breast cancer although it is a well-known risk factor for several cancers. It seems that conventional analysis was unable to produce an unbiased estimate of association for sensitive exposures that are markedly prone to measurement error. According to PBAM, alcohol consumption was a strong risk factor for breast cancer with an OR of 1.82 to 5.67 in different scenarios. This study also found that 1.51–3.56% of breast cancers were attributed to alcohol consumption. Therefore, the breast cancer incidence can be reduced, although slightly in our population due to low prevalence of alcohol, through alcohol cessation programs. However, future confirmatory studies can provide more evidence for proper assessment of the effects of variables prone to misclassification bias and potentially encourage researchers to use PBAM methodology in the future.
Supplementary Information
Additional file 1: Supplement 1. Characteristics of included studies for calculating the bias parameters.
Additional file 2. Mathematical logic for obtaining the expected values from the sensitivity-specificity matrix.
Acknowledgements
This article was part of a PhD thesis entitled: “The effect of smoking on breast cancer by controlling smoking misclassification bias and adjusting for confounders using probabilistic bias analysis method” adopted by Tehran University of Medical Sciences by Registration number 240/1405.
Abbreviations
- BM
Bayesian Method
- PBAM
Probabilistic Bias Analysis Method
- cDAG
casual Directed Acyclic Graph
- LOWESS
LOcally WEighted Scatterplot Smoother
- CIs
Confidence Intervals
- PPV
Positive Predictive Value
- NPV
Negative Predictive Value
- MCSA
Monte-Carlo Sensitivity Analysis
- PAF
Population Attributable Fraction
- SES
Socio-Economic Status
Authors' contributions
RP and MAM designed the study. RP wrote the draft and SN, HS, NM, ME, MN, IP and MAM suggested revisions. All authors read and approved the final revision.
Funding
No.
Availability of data and materials
The all datasets and codes used during the current study are available from the corresponding author on reasonable request.
Declarations
Ethics approval and consent to participate
The study was approved by Ethics Committee of Tehran University of Medical Sciences (Ethics code: IR.TUMS.SPH.REC.1398.072). After explain of study objectives, Signed Informed consent was obtained from all study participants. Authors confirm that all procedures were carried out in accordance with relevant guidelines and regulations (Declaration of Helsinki).
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bray F, Ferlay J, Soerjomataram I, Siegel RL, Torre LA, Jemal A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J Clin. 2018;68(6):394–424. doi: 10.3322/caac.21492. [DOI] [PubMed] [Google Scholar]
- 2.Key TJ, Verkasalo PK, Banks E. Epidemiology of breast cancer. Lancet Oncol. 2001;2(3):133–40. doi: 10.1016/S1470-2045(00)00254-0. [DOI] [PubMed] [Google Scholar]
- 3.Nelson HD, Zakher B, Cantor A, Fu R, Griffin J, O’Meara ES, et al. Risk factors for breast cancer for women aged 40 to 49 years: a systematic review and meta-analysis. Ann Intern Med. 2012;156(9):635–48. doi: 10.7326/0003-4819-156-9-201205010-00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pakzad R, Nedjat S, Yaseri M, Salehiniya H, Mansournia N, Nazemipour M, et al. Effect of smoking on breast Cancer by adjusting for Smoking Misclassification Bias and Confounders using a probabilistic Bias Analysis Method. Clin Epidemiol. 2020;12:557–68. doi: 10.2147/CLEP.S252025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ahmadi Gharaei H, Dianatinasab M, Kouhestani SM, Fararouei M, Moameri H, Pakzad R, et al. Meta-analysis of the prevalence of depression among breast cancer survivors in Iran: an urgent need for community supportive care programs. Epidemiol Health. 2019;41:e2019030. doi: 10.4178/epih.e2019030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Almasi-Hashiani A, Nedjat S, Ghiasvand R, Safiri S, Nazemipour M, Mansournia N, Mansournia MA. The causal effect and impact of reproductive factors on breast cancer using super learner and targeted maximum likelihood estimation: a case-control study in Fars Province, Iran. BMC Public Health. 2021;21(1):1–8. [DOI] [PMC free article] [PubMed]
- 7.Allen NE, Beral V, Casabonne D, Kan SW, Reeves GK, Brown A, et al. Moderate alcohol intake and cancer incidence in women. J Natl Cancer Inst. 2009;101(5):296–305. doi: 10.1093/jnci/djn514. [DOI] [PubMed] [Google Scholar]
- 8.Chen WY, Rosner B, Hankinson SE, Colditz GA, Willett WC. Moderate alcohol consumption during adult life, drinking patterns, and breast cancer risk. JAMA. 2011;306(17):1884–90. doi: 10.1001/jama.2011.1590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Falk RT, Maas P, Schairer C, Chatterjee N, Mabie JE, Cunningham C, et al. Alcohol and risk of breast cancer in postmenopausal women: an analysis of etiological heterogeneity by multiple tumor characteristics. Am J Epidemiol. 2014;180(7):705–17. doi: 10.1093/aje/kwu189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hippisley-Cox J, Coupland C. Development and validation of risk prediction algorithms to estimate future risk of common cancers in men and women: prospective cohort study. BMJ open. 2015;5(3):e007825. doi: 10.1136/bmjopen-2015-007825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kawai M, Minami Y, Kakizaki M, Kakugawa Y, Nishino Y, Fukao A, et al. Alcohol consumption and breast cancer risk in japanese women: the Miyagi Cohort study. Breast Cancer Res Treat. 2011;128(3):817–25. doi: 10.1007/s10549-011-1381-x. [DOI] [PubMed] [Google Scholar]
- 12.Li CI, Chlebowski RT, Freiberg M, Johnson KC, Kuller L, Lane D, et al. Alcohol consumption and risk of postmenopausal breast cancer by subtype: the women’s health initiative observational study. J Natl Cancer Inst. 2010;102(18):1422–31. doi: 10.1093/jnci/djq316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu Y, Colditz GA, Rosner B, Berkey CS, Collins LC, Schnitt SJ, et al. Alcohol intake between menarche and first pregnancy: a prospective study of breast cancer risk. J Natl Cancer Inst. 2013;105(20):1571–8. doi: 10.1093/jnci/djt213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chhim A-S, Fassier P, Latino-Martel P, Druesne-Pecollo N, Zelek L, Duverger L, et al. Prospective association between alcohol intake and hormone-dependent cancer risk: modulation by dietary fiber intake. Am J Clin Nutr. 2015;102(1):182–9. doi: 10.3945/ajcn.114.098418. [DOI] [PubMed] [Google Scholar]
- 15.Nitta J, Nojima M, Ohnishi H, Mori M, Wakai K, Suzuki S, et al. Weight gain and alcohol drinking associations with breast cancer risk in japanese postmenopausal women-results from the Japan Collaborative Cohort (JACC) study. Asian Pac J Cancer Prev. 2016;17(3):1437–43. doi: 10.7314/APJCP.2016.17.3.1437. [DOI] [PubMed] [Google Scholar]
- 16.Shin A, Sandin S, Lof M, Margolis KL, Kim K, Couto E, et al. Alcohol consumption, body mass index and breast cancer risk by hormone receptor status: women’Lifestyle and Health Study. BMC Cancer. 2015;15(1):881. doi: 10.1186/s12885-015-1896-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bagnardi V, Blangiardo M, La Vecchia C, Corrao G. A meta-analysis of alcohol drinking and cancer risk. Br J Cancer. 2001;85(11):1700–5. doi: 10.1054/bjoc.2001.2140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bagnardi V, Blangiardo M, La Vecchia C, Corrao G. Alcohol consumption and the risk of cancer: a meta-analysis. Alcohol Res Health. 2001;25(4):263. [PMC free article] [PubMed] [Google Scholar]
- 19.Bagnardi V, Rota M, Botteri E, Tramacere I, Islami F, Fedirko V, et al. Light alcohol drinking and cancer: a meta-analysis. Ann Oncol. 2013;24(2):301–8. doi: 10.1093/annonc/mds337. [DOI] [PubMed] [Google Scholar]
- 20.Bagnardi V, Rota M, Botteri E, Tramacere I, Islami F, Fedirko V, et al. Alcohol consumption and site-specific cancer risk: a comprehensive dose–response meta-analysis. Br J Cancer. 2015;112(3):580–93. doi: 10.1038/bjc.2014.579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chu L, Ioannidis JP, Egilman AC, Vasiliou V, Ross JS, Wallach JD. Vibration of effects in epidemiologic studies of alcohol consumption and breast cancer risk. Int J Epidemiol. 2020;49(2):608–18. doi: 10.1093/ije/dyz271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Corrao G, Bagnardi V, Zambon A, La Vecchia C. A meta-analysis of alcohol consumption and the risk of 15 diseases. Prev Med. 2004;38(5):613–9. doi: 10.1016/j.ypmed.2003.11.027. [DOI] [PubMed] [Google Scholar]
- 23.Key J, Hodgson S, Omar RZ, Jensen TK, Thompson SG, Boobis AR, et al. Meta-analysis of studies of alcohol and breast cancer with consideration of the methodological issues. Cancer Causes Control. 2006;17(6):759–70. doi: 10.1007/s10552-006-0011-0. [DOI] [PubMed] [Google Scholar]
- 24.Ziembicki S, Zhu J, Tse E, Martin LJ, Minkin S, Boyd NF. The association between alcohol consumption and breast density: a systematic review and meta-analysis. Cancer Epidemiol Biomark Prev. 2017;26(2):170–8. doi: 10.1158/1055-9965.EPI-16-0522. [DOI] [PubMed] [Google Scholar]
- 25.Choi Y-J, Myung S-K, Lee J-H. Light alcohol drinking and risk of cancer: a meta-analysis of cohort studies. Breast Cancer Res Treat. 2018;50(2):474. doi: 10.4143/crt.2017.094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Blair A, Stewart P, Lubin JH, Forastiere F. Methodological issues regarding confounding and exposure misclassification in epidemiological studies of occupational exposures. Am J Ind Med. 2007;50(3):199–207. doi: 10.1002/ajim.20281. [DOI] [PubMed] [Google Scholar]
- 27.Jurek AM, Greenland S, Maldonado G. Brief report: how far from non-differential does exposure or disease misclassification have to be to bias measures of association away from the null? Int J Epidemiol. 2008;37(2):382–5. doi: 10.1093/ije/dym291. [DOI] [PubMed] [Google Scholar]
- 28.Luta G, Ford MB, Bondy M, Shields PG, Stamey JD. Bayesian sensitivity analysis methods to evaluate bias due to misclassification and missing data using informative priors and external validation data. Cancer Epidemiol. 2013;37(2):121–6. doi: 10.1016/j.canep.2012.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fox MP, Lash TL, Greenland S. A method to automate probabilistic sensitivity analyses of misclassified binary variables. Int J Epidemiol. 2005;34(6):1370–6. doi: 10.1093/ije/dyi184. [DOI] [PubMed] [Google Scholar]
- 30.Lash TL, Fox MP, Thwin SS, Geiger AM, Buist DS, Wei F, et al. Using probabilistic corrections to account for abstractor agreement in medical record reviews. Am J Epidemiol. 2007;165(12):1454–61. doi: 10.1093/aje/kwm034. [DOI] [PubMed] [Google Scholar]
- 31.Waern M, Rubenowitz E, Runeson B, Skoog I, Wilhelmson K, Allebeck P. Burden of illness and suicide in elderly people: case-control study. BMJ. 2002;324(7350):1355. doi: 10.1136/bmj.324.7350.1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MacLehose RF, Olshan AF, Herring AH, Honein MA, Shaw GM, Romitti PA. Bayesian methods for correcting misclassification an example from birth defects epidemiology. Epidemiology. 2009;20(1):27. doi: 10.1097/EDE.0b013e31818ab3b0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.MacLehose RF, Gustafson P. Is probabilistic bias analysis approximately bayesian? Epidemiology. 2012;23(1):151–8. doi: 10.1097/EDE.0b013e31823b539c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Greenland S. Basic methods for sensitivity analysis of biases. Int J Epidemiol. 1996;25(6):1107–16. doi: 10.1093/ije/25.6.1107. [DOI] [PubMed] [Google Scholar]
- 35.Salehiniya H, Haghighat S, Parsaeian M, Majdzadeh R, Mansournia M, Nedjat S. Iranian breast cancer risk assessment study (IRBCRAS): a case control study protocol. WCRJ. 2018;5:1–5. [Google Scholar]
- 36.Textor J, van der Zander B, Gilthorpe MS, Liśkiewicz M, Ellison GT. Robust causal inference using directed acyclic graphs: the R package ‘dagitty’. Int J Epidemiol. 2016;45(6):1887–94. doi: 10.1093/ije/dyw341. [DOI] [PubMed] [Google Scholar]
- 37.Etminan M, Collins GS, Mansournia MA. Using Causal Diagrams to improve the design and interpretation of Medical Research. Chest. 2020;158(1s):21–s8. doi: 10.1016/j.chest.2020.03.011. [DOI] [PubMed] [Google Scholar]
- 38.Mansournia MA, Hernán MA, Greenland S. Matched designs and causal diagrams. Int J Epidemiol. 2013;42(3):860–9. doi: 10.1093/ije/dyt083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mansournia MA, Higgins JP, Sterne JA, Hernán MA. Biases in randomized trials: a conversation between Trialists and Epidemiologists. Epidemiology. 2017;28(1):54–9. doi: 10.1097/EDE.0000000000000564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mansournia MA, Collins GS, Nielsen RO, Nazemipour M, Jewell NP, Altman DG, et al. CHecklist for statistical Assessment of Medical Papers: the CHAMP statement. Br J Sports Med. 2021;55(18):1002–3. doi: 10.1136/bjsports-2020-103651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Etminan M, Nazemipour M, Mansournia MA. Potential biases in studies of acid-suppressing drugs and COVID-19 infection. Gastroenterology. 2021;160(5):1443–6. doi: 10.1053/j.gastro.2020.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kyriacou DN, Greenland P, Mansournia MA. Using causal diagrams for biomedical research. Annals of Emergency Medicine. 2023;81(5):606–13. doi: 10.1016/j.annemergmed.2022.08.014. [DOI] [PubMed] [Google Scholar]
- 43.Etminan M, Brophy JM, Collins G, Nazemipour M, Mansournia MA. To adjust or not to adjust: the role of different Covariates in Cardiovascular Observational Studies. Am Heart J. 2021;237:62–7. doi: 10.1016/j.ahj.2021.03.008. [DOI] [PubMed] [Google Scholar]
- 44.Mansournia MA, Nazemipour M, Etminan M. Interaction contrasts and Collider Bias. Am J Epidemiol. 2022;191(10):1813–9. doi: 10.1093/aje/kwac103. [DOI] [PubMed] [Google Scholar]
- 45.Mansournia MA, Nazemipour M, Etminan M. Causal diagrams for immortal time bias. Int J Epidemiol. 2021;50(5):1405–9. doi: 10.1093/ije/dyab157. [DOI] [PubMed] [Google Scholar]
- 46.Mansournia MA, Nazemipour M, Etminan M. Time-fixed vs time-varying causal diagrams for immortal time bias. Int J Epidemiol. 2022;51(3):1030–1. doi: 10.1093/ije/dyac067. [DOI] [PubMed] [Google Scholar]
- 47.Pearl J. Causal inference in statistics: an overview. Stat Surv. 2009;3:96–146. doi: 10.1214/09-SS057. [DOI] [Google Scholar]
- 48.Greenland S, Mansournia MA, Joffe M. To curb research misreporting, replace significance and confidence by compatibility: a Preventive Medicine golden jubilee article. Prev Med. 2022;164:107127. doi: 10.1016/j.ypmed.2022.107127. [DOI] [PubMed] [Google Scholar]
- 49.Mansournia MA, Nazemipour M, Etminan M. P-value, compatibility, and S-value. Global Epidemiol. 2022;4:100085. doi: 10.1016/j.gloepi.2022.100085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mansournia MA, Collins GS, Nielsen RO, Nazemipour M, Jewell NP, Altman DG, et al. A CHecklist for statistical Assessment of Medical Papers (the CHAMP statement): explanation and elaboration. Br J Sports Med. 2021;55(18):1009–17. doi: 10.1136/bjsports-2020-103652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Harris RJ, Deeks JJ, Altman DG, Bradburn MJ, Harbord RM, Sterne JA. Metan: fixed-and random-effects meta-analysis. Stata J. 2008;8(1):3–28. doi: 10.1177/1536867X0800800102. [DOI] [Google Scholar]
- 52.Bonevski B, Campbell E, Sanson-Fisher R. The validity and reliability of an interactive computer tobacco and alcohol use survey in general practice. Addict Behav. 2010;35(5):492–8. doi: 10.1016/j.addbeh.2009.12.030. [DOI] [PubMed] [Google Scholar]
- 53.Osório FL, Lima MP, Chagas MHN. Screening tools for psychiatry disorders in cancer setting: caution when using. Psychiatry Res. 2015;229(3):739–42. doi: 10.1016/j.psychres.2015.08.009. [DOI] [PubMed] [Google Scholar]
- 54.Baggio S, Trächsel B, Rousson V, Rothen S, Studer J, Marmet S, et al. Identifying an accurate self-reported screening tool for alcohol use disorder: evidence from a swiss, male population‐based assessment. Addiction. 2020;115(3):426–36. doi: 10.1111/add.14864. [DOI] [PubMed] [Google Scholar]
- 55.Fleming MF, Barry KL. A three-sample test of a masked alcohol screening questionnaire. Alcohol Alcohol. 1991;26(1):81–91. [PubMed] [Google Scholar]
- 56.Karns-Wright TE, Dougherty DM, Hill-Kapturczak N, Mathias CW, Roache JD. The correspondence between transdermal alcohol monitoring and daily self-reported alcohol consumption. Addict Behav. 2018;85:147–52. doi: 10.1016/j.addbeh.2018.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.May PA, Hasken JM, De Vries MM, Marais AS, Stegall JM, Marsden D, et al. A utilitarian comparison of two alcohol use biomarkers with self-reported drinking history collected in antenatal clinics. Reproductive Toxicol (Elmsford NY) 2018;77:25–32. doi: 10.1016/j.reprotox.2018.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Oppolzer D, Santos C, Gallardo E, Passarinha L, Barroso M. Alcohol consumption assessment in a student population through combined hair analysis for ethyl glucuronide and fatty acid ethyl esters. Forensic Sci Int. 2019;294:39–47. doi: 10.1016/j.forsciint.2018.10.028. [DOI] [PubMed] [Google Scholar]
- 59.van de Luitgaarden IA, Beulens JW, Schrieks IC, Kieneker LM, Touw DJ, van Ballegooijen AJ, et al. Urinary ethyl glucuronide can be used as a biomarker of habitual alcohol consumption in the general population. J Nutr. 2019;149(12):2199–205. doi: 10.1093/jn/nxz146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Williams RJ, Nowatzki N. Validity of adolescent self-report of substance use. Subst Use Misuse. 2005;40(3):299–311. doi: 10.1081/JA-200049327. [DOI] [PubMed] [Google Scholar]
- 61.Miettinen OS. Proportion of disease caused or prevented by a given exposure, trait or intervention1. Am J Epidemiol. 1974;99(5):325–32. doi: 10.1093/oxfordjournals.aje.a121617. [DOI] [PubMed] [Google Scholar]
- 62.Mansournia MA, Altman DG. Population attributable fraction. BMJ (Clinical research ed) 2018;360:k757. doi: 10.1136/bmj.k757. [DOI] [PubMed] [Google Scholar]
- 63.Khosravi A, Nielsen RO, Mansournia MA. Methods matter: population attributable fraction (PAF) in sport and exercise medicine. Br J Sports Med. 2020:bjsports–2020. [DOI] [PubMed]
- 64.Khosravi A, Nazemipour M, Shinozaki T, Mansournia MA. Population attributable fraction in textbooks: time to revise. Global Epidemiol. 2021;3:100062. doi: 10.1016/j.gloepi.2021.100062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Navadeh S, Mirzazadeh A, McFarland W, Coffin P, Chehrazi M, Mohammad K, et al. Unsafe injection is Associated with higher HIV Testing after bayesian Adjustment for Unmeasured Confounding. Arch Iran Med. 2020;23(12):848–55. doi: 10.34172/aim.2020.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Moradzadeh R, Mansournia MA, Baghfalaki T, Nadrian H, Gustafson P, McCandless LC. The impact of maternal smoking during pregnancy on childhood asthma: adjusted for exposure misclassification; results from the National Health and Nutrition Examination Survey, 2011–2012. Ann Epidemiol. 2018;28(10):697–703. doi: 10.1016/j.annepidem.2018.07.011. [DOI] [PubMed] [Google Scholar]
- 67.Moradzadeh R, Mansournia MA, Baghfalaki T, Ghiasvand R, Noori-Daloii MR, Holakouie-Naieni K. Misclassification adjustment of family history of breast cancer in a case-control study: a Bayesian approach. Asian Pac J Cancer Prev. 2015;16(18):8221–6. doi: 10.7314/APJCP.2015.16.18.8221. [DOI] [PubMed] [Google Scholar]
- 68.Lash TL, Fink AK. Semi-automated sensitivity analysis to assess systematic errors in observational data. Epidemiology. 2003;14(4):451–8. doi: 10.1097/01.EDE.0000071419.41011.cf. [DOI] [PubMed] [Google Scholar]
- 69.Greenland S, Mansournia MA, Altman DG. Sparse data bias: a problem hiding in plain sight. BMJ (Clinical research ed) 2016;352:i1981. doi: 10.1136/bmj.i1981. [DOI] [PubMed] [Google Scholar]
- 70.Lash TL, Fox MP, MacLehose RF, Maldonado G, McCandless LC, Greenland S. Good practices for quantitative bias analysis. Int J Epidemiol. 2014;43(6):1969–85. doi: 10.1093/ije/dyu149. [DOI] [PubMed] [Google Scholar]
- 71.Chen C, Huang Y-B, Liu X-O, Gao Y, Dai H-J, Song F-J, et al. Active and passive smoking with breast cancer risk for chinese females: a systematic review and meta-analysis. Chin J Cancer. 2014;33(6):306–16. doi: 10.5732/cjc.013.10248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.White E, Hunt JR, Casso D. Exposure measurement in cohort studies: the challenges of prospective data collection. Epidemiol Rev. 1998;20(1):43–56. doi: 10.1093/oxfordjournals.epirev.a017971. [DOI] [PubMed] [Google Scholar]
- 73.Frydenberg H, Flote VG, Larsson IM, Barrett ES, Furberg A-S, Ursin G, et al. Alcohol consumption, endogenous estrogen and mammographic density among premenopausal women. Breast Cancer Res. 2015;17(1):103. doi: 10.1186/s13058-015-0620-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Qureshi SA, Couto E, Hofvind S, Wu AH, Ursin G. Alcohol intake and mammographic density in postmenopausal norwegian women. Breast Cancer Res Treat. 2012;131(3):993–1002. doi: 10.1007/s10549-011-1812-8. [DOI] [PubMed] [Google Scholar]
- 75.Kyu HH, Abate D, Abate KH, Abay SM, Abbafati C, Abbasi N, et al. Global, regional, and national disability-adjusted life-years (DALYs) for 359 diseases and injuries and healthy life expectancy (HALE) for 195 countries and territories, 1990–2017: a systematic analysis for the global burden of Disease Study 2017. The Lancet. 2018;392(10159):1859–922. doi: 10.1016/S0140-6736(18)32335-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Pollak M. Insulin-like growth factor physiology and cancer risk. Eur J Cancer. 2000;36(10):1224–8. doi: 10.1016/S0959-8049(00)00102-7. [DOI] [PubMed] [Google Scholar]
- 77.Bodnar LM, Himes KP, Abrams B, Lash TL, Parisi SM, Eckhardt CL, et al. Gestational weight gain and adverse birth outcomes in twin pregnancies. Obstet Gynecol. 2019;134(5):1075–86. doi: 10.1097/AOG.0000000000003504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Bodnar LM, Siega-Riz AM, Simhan HN, Diesel JC, Abrams B. The impact of exposure misclassification on Associations between Prepregnancy BMI and adverse pregnancy outcomes. Obesity. 2010;18(11):2184–90. doi: 10.1038/oby.2010.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.De Silva DA, Thoma ME. The association between interpregnancy interval and severe maternal morbidities using revised national birth certificate data: a probabilistic bias analysis. Paediat Perinat Epidemiol. 2020;34(4):469–80. doi: 10.1111/ppe.12560. [DOI] [PubMed] [Google Scholar]
- 80.Momoli F, Siemiatycki J, McBride ML, Parent M, Richardson L, Bedard D, et al. Probabilistic Multiple-Bias modeling Applied to the Canadian Data from the Interphone Study of Mobile phone Use and Risk of Glioma, Meningioma, Acoustic Neuroma, and parotid gland tumors. Am J Epidemiol. 2017;186(7):885–93. doi: 10.1093/aje/kwx157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Vlaar T, Elbaz A, Moisan F. Is the incidence of motor neuron disease higher in french military personnel? Amyotroph Lateral Scler Frontotemporal Degener. 2020;21(1–2):107–15. doi: 10.1080/21678421.2019.1675709. [DOI] [PubMed] [Google Scholar]
- 82.Nelson DE, Jarman DW, Rehm J, Greenfield TK, Rey G, Kerr WC, et al. Alcohol-attributable Cancer deaths and years of potential life lost in the United States. Am J Public Health. 2013;103(4):641–8. doi: 10.2105/AJPH.2012.301199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Northridge ME. Public health methods–attributable risk as a link between causality and public health action. Am J Public Health. 1995;85(9):1202–4. doi: 10.2105/AJPH.85.9.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.van Gemert WA, Lanting CI, Goldbohm RA, van den Brandt PA, Grooters HG, Kampman E, et al. The proportion of postmenopausal breast cancer cases in the Netherlands attributable to lifestyle-related risk factors. Breast Cancer Res Treat. 2015;152(1):155–62. doi: 10.1007/s10549-015-3447-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Neutel CI, Morrison H. Could recent decreases in breast Cancer incidence really be due to Lower HRT Use? Trends in attributable risk for modifiable breast Cancer risk factors in canadian women. Can J Public Health. 2010;101(5):405–9. doi: 10.1007/BF03404862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Wilson LF, Page AN, Dunn NAM, Pandeya N, Protani MM, Taylor RJ. Population attributable risk of modifiable risk factors associated with invasive breast cancer in women aged 45–69 years in Queensland, Australia. Maturitas. 2013;76(4):370–6. doi: 10.1016/j.maturitas.2013.09.002. [DOI] [PubMed] [Google Scholar]
- 87.Parkin DM. 1. The fraction of cancer attributable to lifestyle and environmental factors in the UK in 2010. Br J Cancer. 2011;105(2):S2–S5. doi: 10.1038/bjc.2011.474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Greenland S, Mansournia MA. Penalization, bias reduction, and default priors in logistic and related categorical and survival regressions. Stat Med. 2015;34(23):3133–43. doi: 10.1002/sim.6537. [DOI] [PubMed] [Google Scholar]
- 89.Mansournia MA, Geroldinger A, Greenland S, Heinze G. Separation in logistic regression: causes, Consequences, and control. Am J Epidemiol. 2018;187(4):864–70. doi: 10.1093/aje/kwx299. [DOI] [PubMed] [Google Scholar]
- 90.Bautista L, Bajwa P, Shafer M, Malecki K, McWilliams C, Palloni A. The relationship between chronic stress, hair cortisol and hypertension. Int J Cardiol. 2019;2:100012. doi: 10.1016/j.ijchy.2019.100012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Mansournia MA, Danaei G, Forouzanfar MH, Mahmoodi M, Jamali M, Mansournia N et al. Effect of physical activity on functional performance and knee pain in patients with osteoarthritis: analysis with marginal structural models. Epidemiology. 2012:631–40. [DOI] [PubMed]
- 92.Fotouhi A, Khabazkhoub M, Hashemi H, Mohammad K. The prevalence of cigarette smoking in residents of Tehran. Arch Iran Med. 2009;12(4):358–64. [PubMed] [Google Scholar]
- 93.Ahmadi J, Khalili H, Jooybar R, Namazi N, Mohammadagaei P. Prevalence of cigarette smoking in Iran. Psychol Rep. 2001;89(2):339–41. doi: 10.2466/PR0.89.6.339-341. [DOI] [PubMed] [Google Scholar]
- 94.VanderWeele TJ, Ding P. Sensitivity analysis in observational research: introducing the E-value. Ann Intern Med. 2017;167(4):268–74. doi: 10.7326/M16-2607. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1: Supplement 1. Characteristics of included studies for calculating the bias parameters.
Additional file 2. Mathematical logic for obtaining the expected values from the sensitivity-specificity matrix.
Data Availability Statement
The all datasets and codes used during the current study are available from the corresponding author on reasonable request.