Performance of different dental age estimation methods on Saudi children

Abstract

Aim

To evaluate and compare the performance of six dental age estimation methods (Moorrees, Fanning and Hunt, Demirjian, Gleiser and Hunt, Nolla, Chaillet et al., and Nicodemo et al.) on a sample of Saudi children.

Method

This cross-sectional study was based on the evaluation of a sample of 400 archived digital panoramic radiographs of healthy Saudi children (200 each from boys and girls) aged 6 to 15.99 years. Panoramic radiographs acquired during 2018–2021 were obtained from the information technology department of the dental clinics at King Saud University, Riyadh, Saudi Arabia. Dental age was evaluated using the six dental age estimation methods on the developing permanent dentition in both jaws of the left side. The accuracy of each method was assessed in relation to chronological age, and a comparison between these methods was made.

Result

For all the tested methods, significant differences were found between chronological and dental age (P<0.001). The mean difference between dental and chronological age was (-2.19 years) for Chaillet et al. method, (0.15 years) for the Demirjian method, (-1.01 years) for the Moorrees, Fanning and Hunt method, (-1.72 years) for Nicodemo et al. method, (-1.29 years) for Nolla method, and (-1.00 years) for Gleiser and Hunt method.

Conclusion

Among the tested methods, the accuracy in Saudi subjects was the highest for Demirjian’s method, followed by the Moorrees, Fanning and Hunt method. The methods proposed by Nicodemo et al., and Chaillet et al., were the least accurate.

INTRODUCTION

Age is determined by a person's date of birth and the amount of time or years elapsed from that date to any point in time and is termed chronological age (CA) (1). The CA can be estimated by determining the physiological age (1). Physiological age, also known as biological age, is based on the degree of maturation of different tissue systems. (2) Several biological ages have been developed, including skeletal, morphological, secondary sexual, and dental age (DA). (2)

DA is of particular interest to many scientific and clinical fields of application, including orthodontists and pediatric dentistry in choosing a timing and treatment plan, and in forensic dentistry, and pediatric endocrinology studies. (2) DA estimation is more reliable and genetically controlled than age estimation using skeletal indicators such as cervical vertebrae and hand-wrist bones. (3)

Additionally, DA can be determined by assessing tooth emergence or eruption in the oral cavity and observing the mineralization of developing teeth on radiographs. (4) Tooth mineralization is a more reliable indicator of dental maturity than emergence because it is not affected by factors such as ankylosis, early or delayed extraction of primary teeth, impaction, or crowding of permanent teeth. (2, 4)

Among all the methods used to estimate DA, such as visual, radiological, morphological, biochemical, and histological methods, the radiological method is a less invasive, simple, and reproducible and can be employed on both living and unknown dead. (5) Several radiological methods have been developed and studied to analyze dental mineralization as age indicator. The Demirjian method is the most widely used radiological method. Demirjian et al. (2) developed an eight-stage system in 1973 based on an analysis of French Canadian children. Chaillet et al. (6) obtained high accuracy in estimating DA in a Belgian population after adapting the Demirjian scores and using Belgian weighted scores. In 2005, Chaillet et al. (7) published international maturity curves for age estimation based on the evaluation of samples from eight different populations to overcome variations among different populations and use them when the ethnic origin of individuals is unknown. Nolla (8) created a DA system with 11 developmental stages, including tooth crypt staging, before the initial calcification.

Additionally, Gleiser and Hunt (9) devised a thirteen-stage system in 1955. Moorrees, Fanning, and Hunt (MFH) (4) evaluated dental development in 14 stages of mineralization, ranging from “cusp formation” to “root apex closure,” for the development of single and multirooted permanent teeth. In 1991, Smith (10) used MFH charts to develop tables showing the age at which each tooth reached each stage and a formula for age estimation, which made the MFH method easier to use. Nicodemo et al., in 1974 (11), provided a representative chart of the mineralization of all permanent teeth using eight developmental stages, with four stages each for the crown and the root.

Most DA estimation studies in the Saudi population have focused on the Demirjian method alone, and few studies have used and compared more than one method. Therefore, this study aimed to evaluate and compare the performance of six DA estimation methods that utilize the development of permanent teeth (MFH, Demirjian, Gleiser and Hunt, Nolla, Chaillet et al., and Nicodemo et al.) in a sample of Saudi children.

MATERIALS AND METHODS

Ethical Approval

The Institutional Review Board (E-21-6175) approved this study, followed by the approval of the College of Dentistry Research Center (PR 0124) at King Saud University.

Sample Selection And Size

This was a retrospective cross-sectional study involving children aged 6-15.99 years. Each chronological year was assigned to an individual group. A list of all Saudi patients aged (6–15.99 years) who had a panoramic radiograph acquired between 2018 and 2021 was obtained from the Information Technology department of the dental clinics at King Saud University. The inclusion and exclusion criteria were applied to the radiographs in reverse chronological order (from newest to oldest) until 400 cases were included. If a patient had multiple radiographs in the file, the oldest and most recent one that reflected the selection criteria were included.

The sample size was calculated for an effect size of 0.188 based on the Cohen equation and previous studies (12), at a level of significance of 0.05 and statistical power of 0.9. An analysis of variance (ANOVA) was performed for repeated measurements for ten age groups and the six methods, using GPower software. (13) The sample size in each age group was determined to be 40, which was subdivided into 20 boys and 20 girls; therefore, 400 digital panoramic radiographs (200 each from boys and girls) were used. The radiographs were initially assessed for the presence of radiographically visible exclusion criteria. The Salud file was then checked for other exclusion criteria in patients with acceptable radiographs. The radiographs were selected by ascending file number until each age group was completed.

Inclusion Criteria

The participants were selected following three main inclusion criteria: (1) Saudi patients, (2) children aged 6 to 15.99 years, and (3) presence of a panoramic radiograph in the Romexis server of the KSU College of Dentistry.

Exclusion Criteria

The exclusion criteria were as follows: (1) poor quality radiographs: the overlap of structures and presence of artifacts at the region of interest, (2) non-Saudi patients, (3) the presence of any systemic diseases or developmental conditions, (4) abnormal dental development including amelogenesis/dentinogenesis imperfecta, taurodontism, hypodontia, and hyperdontia, (5) presence of gross pathology related to the left side of the jaw or teeth, (6) presence of gross caries and periapical pathosis on the left side of the jaw, (7) presence of large restorations or crowns on the left side of the jaw, (8) early tooth extraction on the left side of the jaw, and (9) known previous orthodontic treatment.

Data Collection

Digital radiographs were analyzed with the naked eye for DA estimation. Planmeca Romexis 3.6.0.R software available at KSU was used. Each participant’s CA was calculated by subtracting the date of birth registered in the file from the date the radiograph was obtained and converted into a decimal system using the Eveleth and Tanner’s method. (14) The observer blinded the CA and entered them into a different spreadsheet until all 400 panoramic radiographs were assessed.

Each permanent tooth on the left side was evaluated to determine its developmental stage using the following methods: MFH (4), Nolla (8), Demirjian (2), Chaillet et al. (6), Gleiser and Hunt (15) and Nicodemo et al. (11)

Radiograph viewing conditions were standardized as follows:(1) if image adjustments had been made on the panoramic radiograph before data collection, all adjustments were undone; (2) viewing was done in a dimly-lit room; (3) the zoom level was standardized between methods; and (4) all age estimation methods were applied using the same contrast and density settings.

Statistical Analysis

All statistical analyses were performed using IBM SPSS Statistics for Windows version 28. The primary observer was trained and calibrated by a field expert. The main observer performed all measurements. To calculate the intra- and inter-examiner values, a 10% random sample of the digital radiographs was selected using random allocation software and re-evaluated after 2 weeks. Cohen’s kappa test was used to verify intra- and inter-observer agreements for all methods. (16)

The accuracy of each method was determined by the mean difference between DA and CA (bias). The DA was compared with the CA for each participant. The CA was subtracted from the DA, and a positive result indicated an overestimation, whereas a negative result indicated an underestimation. This difference and the absolute mean difference for each radiograph were tabulated. The absolute mean difference was used to assess the accuracy range by removing the canceling effect of equal, over, and underestimation. The standard deviation for each CA–year interval was also calculated. One-sample and paired t-tests were used to assess the accuracy of each method in each year interval for the entire sample.

An independent samples t-test was used to compare mean differences in CA and DA between the sexes. Repeated-measures ANOVA and post hoc analysis were used to compare DA and CA among five methods (excluding the Gleiser and Hunt method). The Bland–Altman plot was used to assess the agreement between each method and CA. Statistical significance was set at P<0.05.

RESULTS

Reliability Test

Intra-examiner Kappa values were 0.88 (MFH), 0.96 (Demirjian), 1.00 (Gleiser and Hunt), 0.97 (Nolla), 0.96 (Chaillet et al.), and 0.97 (Nicodemo et al.). For inter-examiner agreement, the Kappa values were 0.80 (MFH), 0.81 (Demirjian), 0.87 (Gleiser and Hunt), 0.78 (Nolla), 0.81 (Chaillet et al.), and 0.73 (Nicodemo et al.). These values are “substantial” or “almost perfect”. (16)

Description of Sample

A total of 400 digital radiographs were analyzed (200 each from boys and girls). All participants were divided into ten groups based on their CA and sex, with each group having an equal number of boys and girls (Table 1).

Table 1. Distribution of the study sample by chronological age (CA) and gender.

Group	Chronological Age (CA)/years	Males No.	Females No.	Total
1	6.00 – 6.99	20	20	40
2	7.00 – 7.99	20	20	40
3	8.00 – 8.99	20	20	40
4	9.00 – 9.99	20	20	40
5	10.00 – 10.99	20	20	40
6	11.00 – 11.99	20	20	40
7	12.00 – 12.99	20	20	40
8	13.00 – 13.99	20	20	40
9	14.00 – 14.99	20	20	40
10	15.00 – 15.99	20	20	40
Total		200	200	400

Accuracy of Each Method

The Chaillet et al. method underestimated CA by -2.03 years for boys and -2.35 years for girls (average, -2.19 years; P<0.001) (Tables 2 and 3) (Figs. 1, 2, and 3). The Chaillet et al. method underestimated the age of both sexes in all age groups (Table 4) (Fig. 4). A significant difference was found between boys and girls in the age groups of 12,13,14 and 15 years, where the mean difference was lower in boys than in girls (P=0.035, P=0.006, P<0.001, P<0.001, respectively) (Table 4).

Table 2. The accuracy of all methods for the entire sample expressed by Bias (the mean difference between dental age (DA) and chronological age (CA) in years) and the absolute mean difference between estimated and Real Age in years) using a one sample t-test.

Method	Measure of Accuracy	Mean	SD	p-value	95% C.I
					Lower	Upper
Chaillet et al	Bias	-2.19	0.98	<0.001	-2.28	-2.09
	Absolute difference	2.22	0.89	<0.001	2.14	2.31
Demirjian	Bias	0.15	0.63	<0.001	0.08	0.21
	Absolute difference	0.49	0.43	<0.001	0.44	0.53
Gleiser and Hunt	Bias	-1.00	1.20	<0.001	-1.15	-0.85
	Absolute difference	1.22	0.98	<0.001	1.20	1.34
MFH	Bias	-1.01	0.82	<0.001	-1.09	-0.93
	Absolute difference	1.06	0.75	<0.001	0.99	1.14
Nicodemo et al.	Bias	-1.72	1.86	<0.001	-1.91	-1.54
	Absolute difference	1.93	1.64	<0.001	1.76	2.09
Nolla	Bias	-1.29	0.83	<0.001	-1.37	-1.20
	Absolute difference	1.31	0.78	<0.001	1.24	1.39

Table 3. The Accuracy for Males and Females.

Method	Measure of Accuracy	Gender	Mean	SD	P-value
Chaillet et al.	Bias	Female	-2.35	1.16	0.002
		Male	-2.03	0.74
	Absolute difference	Female	2.42	0.98	<0.001
		Male	2.02	0.74
Demirjian	Bias	Female	0.11	0.65	0.219
		Male	0.18	0.61
	Absolute difference	Female	0.49	0.44	0.838
		Male	0.48	0.42
Gleiser and Hunt	Bias	Female	-1.16	1.19	0.042
		Male	-0.84	1.20
	Absolute difference	Female	1.31	0.02	0.162
		Male	1.13	0.93
MFH	Bias	Female	-1.14	0.85	0.001
		Male	-0.88	0.76
	Absolute difference	Female	1.18	0.79	0.001
		Male	0.94	0.68
Nicodemo et al.	Bias	Female	-1.65	1.87	0.401
		Male	-1.80	1.85
	Absolute difference	Female	1.88	1.63	0.579
		Male	1.97	1.66
Nolla	Bias	Female	-1.50	0.89	<0.001
		Male	-1.07	0.70
	Absolute difference	Female	1.53	0.84	<0.001
		Male	1.10	0.66

Figure 1.

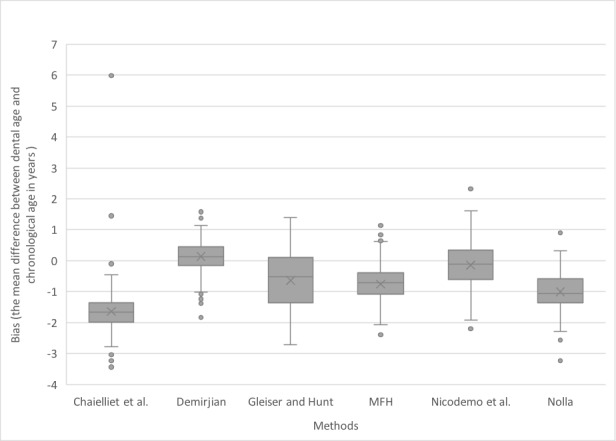
Box plot for the bias observed for each method

Figure 2.

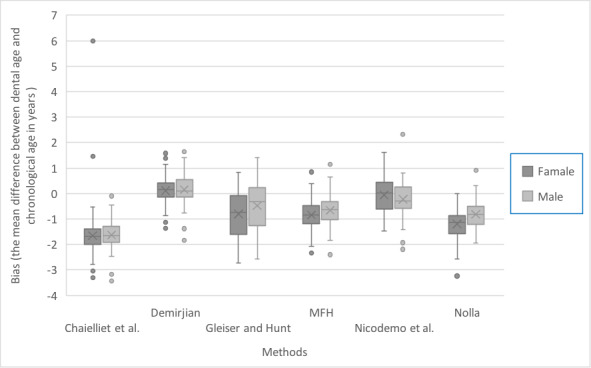
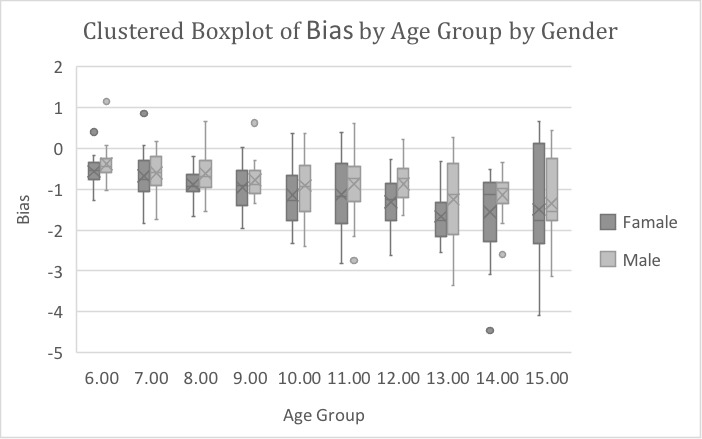
Box plot for the bias observed for each method stratified by sex

Figure 3.

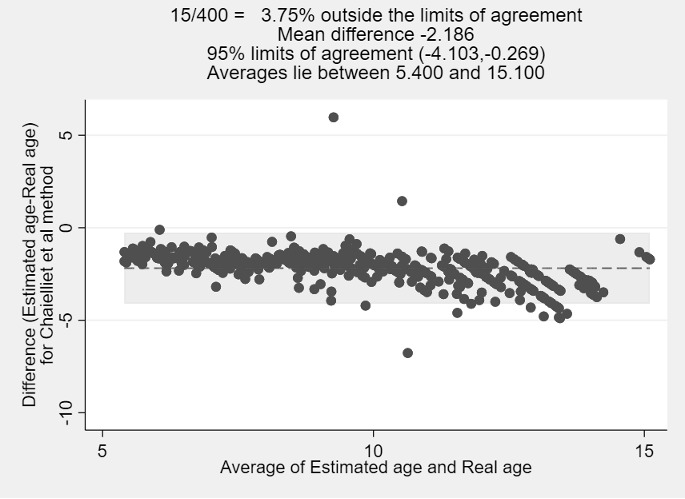
Bland-Altman plot the real age and estimated age for Chaillet et al. method

Table 4. The accuracy of Age Intervals of all methods for Males and females.

Categorical age midpoint	Method	Gender	N	Mean	SD	P-value	95% C.I
							Lower	Upper
6.5	Chaillet et al.	Female	20	-1.10	1.69	0.764	-0.66		0.90
		Male	20	-1.22	0.36
	Demirjian	Female	20	0.43	0.26	0.178	-0.33		0.06
		Male	20	0.56	0.35
	Gleiser and Hunt	Female	20	0.08	0.38	0.010	-0.69		-0.10
		Male	20	0.48	0.53
	MFH	Female	20	-0.57	0.36	0.165	-0.45		0.08
		Male	20	-0.38	0.46
	Nicodemo et al.	Female	20	0.55	0.40	0.672	-0.25		0.38
		Male	20	0.48	0.57
	Nolla	Female	20	-0.90	0.42	0.001	-0.76		-0.20
		Male	20	-0.42	0.45
7.5	Chaillet et al.	Female	20	-1.62	0.41	0.857	-0.28		0.23
		Male	20	-1.60	0.39
	Demirjian	Female	20	0.14	0.35	0.856	-0.20		0.24
		Male	20	0.12	0.32
	Gleiser and Hunt	Female	20	-0.02	0.64	0.311	-0.53		0.17
		Male	20	0.16	0.43
	MFH	Female	20	-0.68	0.58	0.687	-0.41		0.27
		Male	20	-0.61	0.49
	Nicodemo et al.	Female	20	0.39	0.43	0.048	0.00		0.55
		Male	20	0.11	0.43
	Nolla	Female	20	-1.08	0.47	0.071	-0.60		0.03
		Male	20	-0.80	0.50
8.5	Chaillet et al.	Female	20	-1.87	0.33	0.751	-0.34		0.25
		Male	20	-1.83	0.57
	Demirjian	Female	20	-0.19	0.41	0.290	-0.45		0.14
		Male	20	-0.03	0.50
	Gleiser and Hunt	Female	20	-0.65	0.32	<0.001	-0.72		-0.24
		Male	20	-0.16	0.43
	MFH	Female	20	-0.89	0.39	0.095	-0.58		0.05
		Male	20	-0.62	0.57
	Nicodemo et al.	Female	20	-0.01	0.42	0.311	-0.12		0.36
		Male	20	-0.13	0.33
	Nolla	Female	20	-1.44	0.40	<0.001	-0.84		-0.23
		Male	20	-0.90	0.53
9.5	Chaillet et al.	Female	20	-1.63	0.90	0.870	-0.48		0.41
		Male	20	-1.60	0.38
	Demirjian	Female	20	0.03	0.62	0.808	-0.40		0.32
		Male	20	0.08	0.49
	Gleiser and Hunt	Female	20	-1.36	0.55	0.016	-0.63		-0.07
		Male	20	-1.01	0.26
	MFH	Female	20	-0.96	0.52	0.239	-0.50		0.13
		Male	20	-0.78	0.46
	Nicodemo et al.	Female	20	-0.34	0.40	0.088	-0.03		0.41
		Male	20	-0.53	0.25
	Nolla	Female	20	-1.08	0.58	0.176	-0.57		0.08
		Male	20	-0.84	0.41
10.5	Chaillet et al.	Female	20	-2.03	0.63	0.477	-0.52		0.25
		Male	20	-1.90	0.56
	Demirjian	Female	20	0.15	0.83	0.634	-0.39		0.64
		Male	20	0.03	0.79
	Gleiser and Hunt	Female	20	-2.05	0.40	0.155	-0.43		0.07
		Male	20	-1.87	0.38
	MFH	Female	20	-1.14	0.73	0.321	-0.70		0.24
		Male	20	-0.91	0.73
	Nicodemo et al.	Female	20	-0.89	0.38	0.094	-0.04		0.48
		Male	20	-1.11	0.43
	Nolla	Female	20	-1.47	0.70	0.083	-0.74		0.05
		Male	20	-1.12	0.53
11.5	Chaillet et al.	Female	20	-2.27	0.57	0.469	-0.55		0.26
		Male	20	-2.12	0.68
	Demirjian	Female	20	0.36	0.96	0.422	-0.37		0.85
		Male	20	0.12	0.95
	Gleiser and Hunt	Female	20	-2.96	0.31	0.002	-0.50		-0.11
		Male	20	-2.66	0.30
	MFH	Female	20	-1.13	0.81	0.342	-0.77		0.27
		Male	20	-0.88	0.82
	Nicodemo et al.	Female	20	-1.62	0.29	0.151	-0.06		0.37
		Male	20	-1.77	0.37
	Nolla	Female	20	-2.02	0.88	0.012	-1.18		-0.16
		Male	20	-1.35	0.71
12.5	Chaillet et al.	Female	20	-2.47	0.51	0.035	-0.67		-0.03
		Male	20	-2.12	0.50
	Demirjian	Female	20	0.52	0.63	0.315	-0.19		0.57
		Male	20	0.33	0.54
	MFH	Female	20	-1.32	0.65	0.054	-0.90		0.01
		Male	20	-0.87	0.77
	Nicodemo et al.	Female	20	-2.37	0.34	0.113	-0.04		0.36
		Male	20	-2.53	0.29
	Nolla	Female	20	-1.90	0.96	0.079	-0.95		0.05
		Male	20	-1.45	0.57
13.5	Chaillet et al.	Female	20	-3.04	0.51	0.006	-0.93		-0.09
		Male	20	-2.48	0.77
	Demirjian	Female	20	0.09	0.39	0.772	-0.48		0.36
		Male	20	0.15	0.85
	MFH	Female	20	-1.67	0.61	0.121	-0.95		0.12
		Male	20	-1.26	0.99
	Nicodemo et al.	Female	20	-3.21	0.29	0.147	-0.05		0.34
		Male	20	-3.35	0.32
	Nolla	Female	20	-2.00	0.78	0.209	-0.96		0.22
		Male	20	-1.63	1.04
14.5	Chaillet et al.	Female	20	-3.48	0.84	<0.001	-1.38		-0.46
		Male	20	-2.56	0.58
	Demirjian	Female	20	0.04	0.47	0.080	-0.60		0.04
		Male	20	0.32	0.52
	MFH	Female	20	-1.57	1.00	0.115	-0.95		0.11
		Male	20	-1.14	0.60
	Nicodemo et al.	Female	20	-3.99	0.27	0.084	-0.02		0.34
		Male	20	-4.15	0.30
	Nolla	Female	20	-1.68	0.89	0.009	-1.07		-0.17
		Male	20	-1.06	0.46
15.5	Chaillet et al.	Female	20	-4.00	0.49	<0.001	-1.60		-0.76
		Male	20	-2.82	0.80
	Demirjian	Female	20	-0.50	0.67	<0.001	-1.02		-0.33
		Male	20	0.18	0.37
	MFH	Female	20	-1.50	1.52	0.719	-0.99		0.69
		Male	20	-1.35	1.04
	Nicodemo et al.	Female	20	-4.97	0.26	0.406	-0.09		0.22
		Male	20	-5.04	0.22
	Nolla	Female	20	-1.44	1.48	0.409	-1.09		0.46
		Male	20	-1.12	0.82

Figure 4.

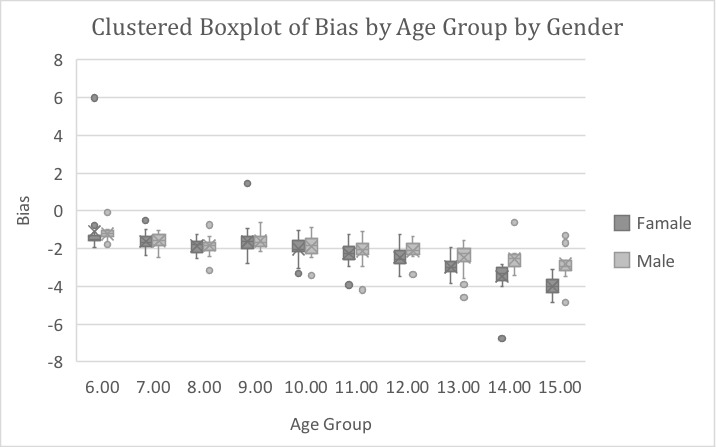
Box plot for the bias of Chaillet et al method stratified by sex and age

The Demirjian method overestimated CA by 0.18 years for boys and 0.11 years for girls (average, 0.15 years; P<0.001) (Tables 2 and 3) (Figs.1, 2 and 5). Overestimations were significant for the age groups of 6, 7, 12, and 14 years (P<0.001, P=0.034, P<0.001, and P=0.018, respectively). The Demirjian method overestimated CA for both sexes in all age groups, except for boys aged 8 years and girls aged 8 and 15 years, for whom an underestimation was observed (Table 4) (Fig.6). A significant difference was only found between boys and girls in the age group of 15 years, where the mean difference was lower in boys than in girls (P<0.001) (Table 4).

Figure 5.

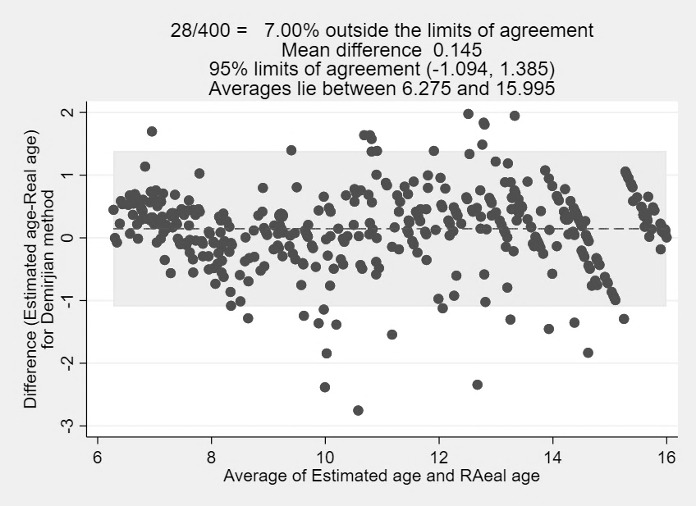
Bland-Altman plot the real age and estimated age for Demirjian method

Figure 6.

Box plot for the bias of Demirjian method stratified by sex and age

The MFH method also underestimated age by -0.88 years for boys and -1.14 years for girls (average, -1.01 years; P<0.001) (Tables 2 and 3) (Figs. 1,2 and 7). Underestimations were observed for both sexes in all age groups (Table 4) (Fig.8).

Figure 7.

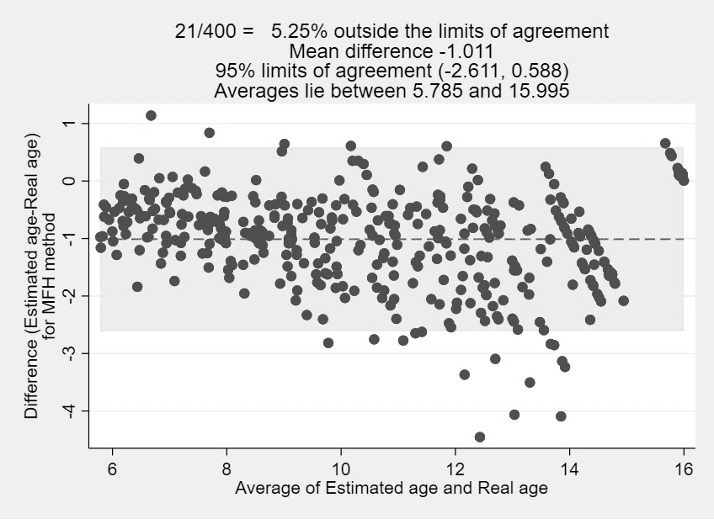
Bland-Altman plot the real age and estimated age for MFH method

Figure 8.

Box plot for the bias of MFH method stratified by sex and age

The Nicodemo et al. method underestimated CA by -1.80 years for boys and -1.65 years for girls (average, -1.72 years; P<0.001) (Tables 2 and 3) (Figs.1,2, and 9).

Figure 9.

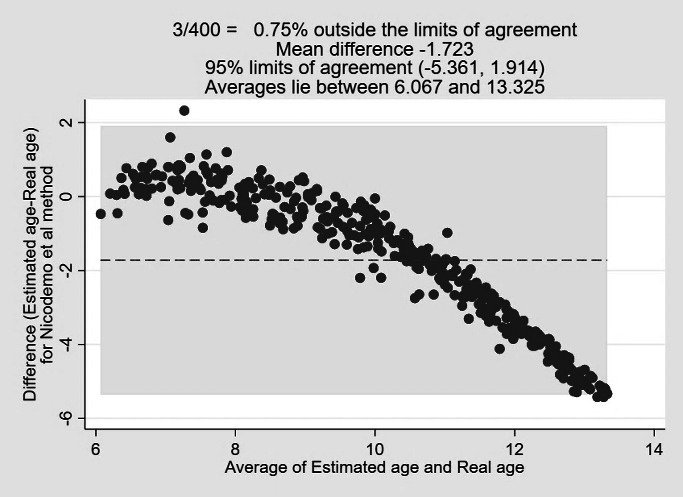
Bland-Altman plot the real age and estimated age for Nicodemo et al method

Underestimations were significant for the age groups of 9, 10, 11, 12, 13, 14, and 15 years (P<0.001). However, age was significantly overestimated in the age groups of 6 and 7 years (P≤0.001, P=0.001,respectively). A significant difference was found between boys and girls in the age group of 7 years, where the mean difference was lower in boys than in girls (P=0.048) (Table 4) (Fig.10).

Figure 10.

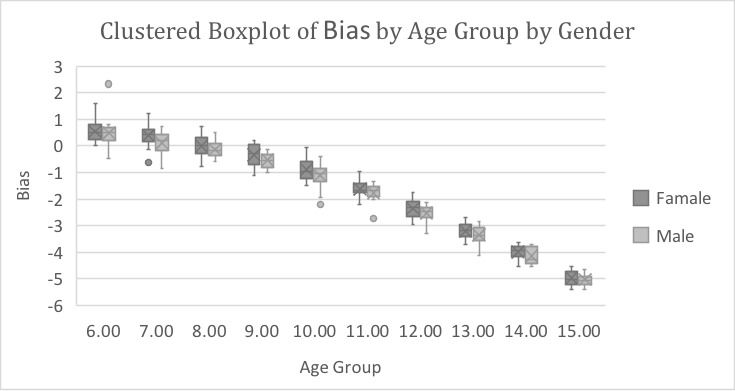
Box plot for the bias of Nicodemo et al. method stratified by sex and age

The Nolla method underestimated CA by -1.07 years for boys and -1.50 years for girls (average, -1.29 years; P<0.001) (Tables 2 and 3) (Figs. 1, 2 and 11). The Nolla method underestimated CA for both sexes in all age groups (Table 4) (Fig.12). A significant difference was found between boys and girls of age groups 6, 8, 11, and 14 years, where the mean difference was lower in boys than in girls (P=0.001, P<0.001, P=0.012, respectively). P=0.009, respectively) (Table 4).

Figure 11.

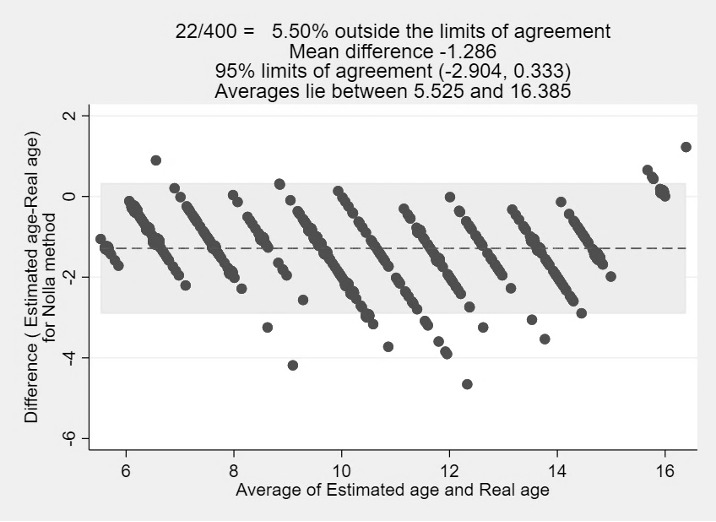
Bland-Altman plot the real age and estimated age for Nolla method

Figure 12.

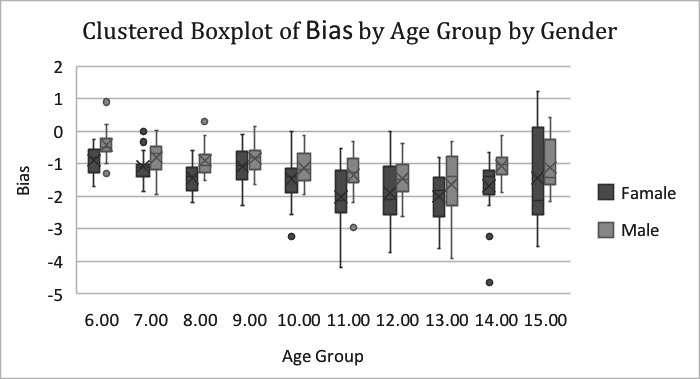
Box plot for the bias of Nolla method stratified by sex and age

The Gleiser and Hunt method underestimated CA by -0.84 years for boys and -1.16 years for girls (average, -1.00 years; P<0.001) (Tables 2 and 3) (Figs. 1, 2, and 13). The Gleiser and Hunt method underestimated CA for both sexes in all age groups, except for boys aged 6 and 7 years and girls aged 6 years, for whom an overestimation was found (Table 4) (Fig. 14). A significant difference was found between boys and girls of age groups 6, 8, and 9 years, where the mean difference was lower in girls aged 6 years and lower in boys aged 8 and 9 years (P=0.010, P<0.001, P=0.016, respectively) (Table 4).

Figure 13.

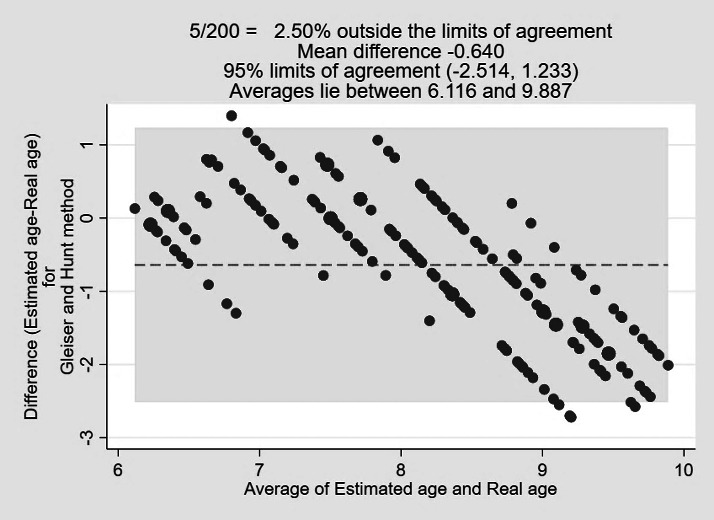
Bland-Altman plot the real age and estimated age for Gleiser and Hunt method

Figure 14.

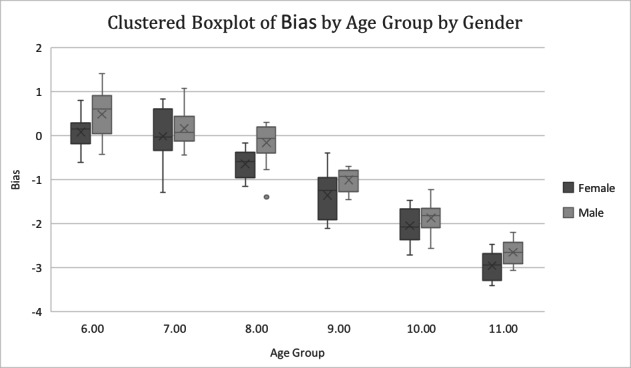
Box plot for the bias of Gleiser and Hunt stratified by sex and age

Comparison of Bias Between Different Methods

Significant differences in bias were found among the different methods. Post-hoc comparisons showed that there was a statistically significant difference in bias between all methods (P<0.001) (Table 5).

Table 5. Comparison of bias between different methods.

	Mean bias	SD	95% C.I		P-value
			Lower Bound	Upper Bound
Chaillet et al.	-2.19	0.98	-2.28	-2.09	<0.001
Demirjian	0.15	0.63	0.08	0.21
MFH	-1.01	0.82	-1.09	-0.93
Nicodemo et al.	-1.72	1.86	-1.91	-1.54
Nolla	-1.29	0.83	-1.37	-1.20

* The Gleiser and Hunt method was excluded from this comparison because all statistical analysis for this method was performed when the chronological age of subjects was ≤ 11.99, resulting in missing data above this age.

DISCUSSION

Age estimation is important in both forensic science and clinical practice. Knowing age could be helpful in several legal cases where it is necessary to differentiate a juvenile from an adult, cases of illegal immigration, and wrongly reported or manipulated ages in documents. According to the recommendations of the Study Group on Forensic Age Diagnostics, a forensic age estimate should consist of a physical examination, radiograph of the hand, and dental examination, including evaluation of a panoramic radiograph, if available. (17)

Dental maturation and emergence through the gingiva have long been recognized as the most useful criteria for estimating age. This approach is more favorable because teeth are less affected by environmental factors and hormonal disturbances than bones, and most techniques used are less invasive and simple to use (18). Many methods have been developed, providing results with various levels of accuracy and using different statistical procedures for age estimation based on tooth development in children and adolescents. (19)

Accuracy and precision are essential in DA assessment. Accuracy refers to the proximity of DA to CA. (20) We presented accuracy as the mean difference between DA and CA (bias) and the absolute mean difference between DA and CA. When assessing DA, it is essential to consider the precision of the age estimation method. Precision, also called reliability, is used in intra- and inter-observer reproducibility (21). The choice of tooth stage assessment is an important factor influencing reproducibility. Those described by Nicodemo et al. are the least detailed, thus showing lower precision in this study. The previous finding of lower precision for the Nolla’s method was not observed in this study (22, 23), probably because the addition of fractions to the Nolla score (0.2, 0.5, and 0.7) was not considered in the DA estimation. This was done because an increased number of stages in the Nolla method has been suggested to moderately decrease its precision while complicating the assessment and making it more subjective. (22) Moreover, in the present study, one examiner tested the performance of all the methods with almost perfect intra-examiner kappa values. One examiner controlled for errors attributable to inter-examiner differences.

The Demirjian Method:

The Demirjian method has been tested and applied to different populations for several years. It has been found to consistently overestimate age in various populations such as Croatia, Brazil, France, Italy, Kuwait, North Germany, Northern China, Portugal, Romania, South America, Spain, Sri Lanka and Turkey. (24–33) Liversidge et al. believed that the overestimation of DA in recent findings when Demirjian’s method was used in different populations may be partly explained by a positive secular trend in growth and development during the last 25 years. (36)

In contrast, in Eastern China, underestimation was generally demonstrated in boys and girls, except for the age group of 13–14.99 years in boys and 11–14.99 years in girls. (37) Additionally, Cruz-Landeira et al. reported an underestimation of age using this method in a Venezuelan Amerindian sample; however, they suggested that this finding may be due to the small sample size and ethnic origin of their sample. (38)

In Saudi Arabia, a study assessing DA in Riyadh in children between the ages of 8.5 to 17 years found an overestimation of 0.3 years for boys and 0.4 years for girls (39). Similar results were reported in Saudi children aged 4 to 14 years; however, the overestimation was 0.77 years for boys and 0.83 years for girls. (40) A study performed by Alshihri et al. in the Western Saudi Arabian population concluded that girls are 0.059 ± 1.26 years and boys are 0.66 ± 1.14 years ahead of the French‐Canadian children. (41) Alassiry et al. found that, in a sample of 298 Saudi children and adolescents between the ages of 3 and 15 years, the mean difference between DA and CA was 0.50 ± 1.57 years. The difference was 0.57 ± 1.48 years in boys and 0.44 ± 1.66 years in girls. (42)

In this study, Demirjian's method overestimated CA, consistent with the results of previous studies. The overestimation was more pronounced for the age groups of 6, 7, 12, and 14 years. The only underestimation was for the age groups of 8 and 15 years. The underestimation found in the age group of 15 years was similar to the results reported by Urzel and Bruzek. They explained that most children had reached a total maturity score of 100 and that no further scoring could be performed. (30)

The Nolla Method:

The Nolla method provided mixed results for various populations. When tested on Turkish children, Nolla’s method reported an underestimation of CA, with the mean age differences being -0.003 years for boys and -0.32 years for girls. (27) Maber et al. reported similar results of underestimation of CA by –0.87 years for boys and –1.18 years for girls in their study on 3–16.99 years old children of Bangladesh and British Caucasian ethnic origin (22). Hegde et al. reported a mean difference of -0.13 ± 0.80 years for boys and -0.30 ± 0.82 years for girls in Indian children aged 5 to 15 years. (23) Underestimations have also been found in South American, Portuguese, and Spanish populations. (31, 32)

However, overestimation of CA has also been reported in studies on Malaysian and south Indian populations. (43, 44) Moreover, in the Chinese population, overestimation and underestimation were observed in boys and girls, respectively. (26) In contrast to other studies, Nolla’s method was suitable for estimating CA of Brazilian children with due care, considering that the growth spurt commences at approximately 11 and 12 years. (33)

For the Saudi population, Yassin et al. reported that Nolla’s method underestimated CA in all age groups and both sexes, with an age difference of –2.68 months to –6 months in boys and –2.17 months to –4.24 months in girls. (45) This was similar to our study, where an underestimation was found in all age groups and sexes; however, the difference was more pronounced. The probable reason for these higher age differences in our results could be the different utilization of the method by not adding fractions to the staged scores of mineralization for each tooth.

The MFH method:

The MFH method underestimated CA in this study in all age groups and sexes, consistent with the results of several studies conducted in different populations. A study performed by Martínez GVM et al. in the Venezuela population found consistent age underestimation in all groups and sexes, with the variation ranging from 0.20 ± 1.14 to 7.61 ± 0.231 years. (32) Similar results were reported in three samples of South African children aged 3–16 years. (46)

Additionally, when tested on Mangalorean children, the MFH method significantly underestimated CA, with mean age differences of -3 years for boys and -2.9 years for girls. (47) Underestimation was also found in Kuwaiti children aged 5 to 15 years, with mean age differences of 1.01 years for girls and 0.89 years for boys (48). In a sample of American Caucasian children aged from 9 to 14 years, the MFH method underestimated CA by 2.3 years for girls and 1.9 years for boys. (49)

Contrary to other studies, Corral et al. concluded that the MFH method presented a high correlation coefficient between DA and CA, with a tendency to overestimate CA of Colombian children aged 5–16 years. (50) Although the MFH method has been tested in different populations, a literature search revealed that none of the studies had tested the accuracy of the MFH method for DA assessment in the Saudi population.

The Chaillet method:

In this study, Chaillet’s original standards for Belgian children were used; to obtain an increase in reliability, the 95th percentile of dental maturity was used to calculate DA.

Studies testing the Chaillet’s multi-ethnic international maturity standards method have reported overestimations of 0.28±0.90 and 0.37±1.04 years in boys and (0.09 ± 0.83) and (0.21± 1.07) years in girls of Bosnian-Herzegovinian and Spanish Caucasian populations, respectively. (38) However, underestimation has been reported in several populations, such as Venezuelan, Indians using Chaillet’s original standards for Belgian children and Kosovar populations. (30, 38, 51, 52)

In the present study, the underestimations were higher than those reported in previous studies that used Chaillet’s original standards for Belgian children. This difference between our results and those of the previous studies may be attributed to the 95% percentile being considered in this study. The higher the considered percentile level, the stronger the reliability, and the accuracy decreases as the reliability increases. (7)

The Gleiser and Hunt method:

In this method, age estimation uses the calcification of the permanent mandibular first molar only. In our study, all statistical analyses using the Gleiser and Hunt method were performed when the CA was ≤ 11.99 years. Because DA estimation is limited by tooth maturation, the mandibular first molar achieves its final maturation at 11 years. (53) Unlike the present study, previous studies tested the applicability of the Gleiser and Hunt dental staging system modified by Kohler on the second and third molars. (54, 55) Therefore, comparisons could not be made.

In this study, the Gleiser and Hunt method underestimated CA in both sexes, except for the age groups of 6 and 7 years, for which overestimations were obtained.

The Nicodemo et al. method:

The method proposed by Nicodemo et al. consistently underestimates age in various populations. When tested on Indian children, Nicodemo et al. reported an underestimation of CA for both sexes, and the differences were more pronounced in older groups (56). Kurita et al. and Silva et al. reported similar results of CA underestimation in their studies on the Brazilian population. (57, 58)

Our results are in accordance with previously published studies, where the Nicodemo et al. method underestimated CA for both sexes. Underestimations were also more pronounced in the older age groups. The only overestimation was for the age groups of 6 and 7 years.

Comparison between the methods:

Chaillet et al. considered a 1-year accuracy sufficient in forensic anthropology, whereas McKenna et al. commended ±0.5 years as more acceptable. (59, 60) An age estimation method is considered accurate if it predicts CA as closely as possible. In our study, the most accurate method was the Demirjian’s method, followed by the MFH method, whereas the Nicodemo et al. and Chaillet et al. methods were the least accurate. Moreover, repeated measures ANOVA verified the significant differences among the tested methods.

Most studies on DA estimation have compared only two different methods; few have studied the accuracy of six different methods simultaneously. Kelmendi et al. evaluated the accuracy of four Demirjian, Chaillet, and Willems methods for age estimation in Kosovo children. Their results indicated that the Demirjian method from 1973 was the least accurate among the six methods. (61) Kumaresan et al. tested the accuracy of five DA estimation methods (Demirjian, Willems, Nolla, Haavikko, and Cameriere) in 426 Malaysian children aged 5–15 years. The Demirjian method exhibited the lowest precision and accuracy among those tested. (44)

Several studies have compared the Demirjian and Nolla methods. Melo and Ata-Ali compared these two methods in a Spanish population and stated that both methods were accurate in estimating CA in a Spanish population, with an overestimation of age using the Demirjian method and an underestimation using the Nolla method. (62) Tomás et al. reported similar results for the Portuguese and Spanish samples. (31) Duruk et al. found that Nolla’s method was more accurate for CA estimation than Demirjian’s method in an Eastern Turkish population (27). Similar results were reported by Lopes et al. in Brazilian children aged 7–13 years. (33)

Additionally, Han et al. studied the accuracy of the Demirjian, Willems, and Nolla methods in a northern Chinese population. Among the three methods, the accuracy was the highest for the Nolla method. (26) However, Cortés et al. found that the Willems method was more appropriate when the three methods were tested in a Spanish ethnicity population. (63)

Additionally, Mohammed et al. concluded that Nolla’s method was more accurate in estimating DA in southern Indian children than Demirjian, Willems, and Haavikko’s methods. (43) Gutiérrez and Ortega-Pertuz studied the accuracy of three methods (Nolla, Moorrees et al. and Demirjian) in 512 Venezuelan children aged 6–18 years; their results indicated that the Demirjian method was the most accurate; whereas the Moorrees et al. method was the least accurate (32). In contrast, Tony et al. stated that neither the Demirjian nor the Moorrees et al. methods accurately estimated CA in their sample of contemporary American Caucasian children aged 9–14 years. (49)

Furthermore, Chaillet’s method was more appropriate for Spanish and Venezuelan children than the Demirjian method. (38) Nevertheless, Pinchi et al. found Willems and Demirjian methods as the most accurate, though they overestimated CA, compared to Cameriere and Haavikko's methods in the Italian population. (64)

The different results in various populations can be attributed to genetic variations, ethnicities, climate, and environmental factors, such as nutrition, dietary habits, and lifestyle, significantly influencing tooth development. Moreover, the uneven sample size of each age group may affect the accuracy of DA estimation. A previous finding that age can be more accurately predicted in younger children than in older children was observed in the present study for both sexes. This is mainly because more teeth continue to develop in this period, which can provide more information for DA estimation. For older age groups, most teeth had already completed their development; therefore, only a few teeth attributed to DA estimation, resulting in a large mean difference between DA and CA. Thus, DA estimation may be more accurate in studies with larger samples of younger patients.

Another possible reason could be age mimicry, a phenomenon in which the target population’s estimates tend to mimic the reference population’s age structure (the population upon which a method is based). (65) Liversidge et al. used this phenomenon to explain the poor performance of the MFH 1963 method in their study, which is one of the few radiographic studies from birth to the age of 25 years. (20)

Another explanation is the complexity of some of these methods. The methods of Demirjian, Chaillet, and Nolla involve a complex process of double numerical conversion. Additionally, not all maturity score values could be found in the conversion tables provided by Demirjian (1973), Chaillet (2004), and Nolla (1960); in these cases, we had to estimate the DA based on the closest smaller maturity score values, which might influence the accuracy of these methods. Moreover, the MFH method involves demanding steps for interpolating the attained values from the graphs, followed by calculating the predicted values from these interpolated values. The problem of inter-observer error in interpolation from graphs influences the accuracy of this method. However, the MFH method was more straightforward when the Smith tables were used.

One limitation of this study is that it was conducted in a geographically restricted sample. This study was conducted in Riyadh, Saudi Arabia and did not include other regions of Saudi Arabia. Hence, the results of this study cannot be generalized to the Saudi population. Further studies applying these methods to other Saudi Arabian regions would be beneficial. Additionally, computerized tools for calculating DA could be used instead of the classic method for a better workflow.