Abstract
为了解决目前肝脏肿瘤病理分级主要依靠穿刺活检、手术病理取材等侵入式方法的问题，提出了一种在非增强核磁共振图像（MRI）上进行肝脏肿瘤病理分级的定量分析方法。首先对采集到的 MRI 图像，由医生在专业软件中人工分割出病灶部位，对这些病灶部位提取高通量的 328 维图像特征，包括灰度、形状、纹理、小波等特征，利用最小绝对收缩和选择运算符（LASSO）和交叉验证方法从中挑选出对病理分级最有价值的特征，组成影像组学模型并融合临床信息实现对肿瘤高、低分化分类的定量分析。在 170 位肝脏肿瘤患者的 MRI 图像（T1 加权图像和 T2 加权图像）上进行实验，通过计算接收者操作特征（ROC）曲线下面积（AUC）来衡量模型的预测性能。结果表明，基于高通量图像特征的 LASSO 回归定量分析方法，在训练集上获得 AUC 为 0.909，在测试集上 AUC 为 0.800。挑选出来的图像特征组成的影像学标签可以对高、低分化进行自动分类，从而为医生提供了一种非侵入的辅助诊断方法，有助于预后判断和治疗方案的制定。
Keywords: 核磁共振图像, 病理分级, 肝脏肿瘤, LASSO回归, 影像组学
Abstract
In order to solve the pathological grading of hepatocellular carcinomas (HCC) which depends on biopsy or surgical pathology invasively, a quantitative analysis method based on radiomics signature was proposed for pathological grading of HCC in non-contrast magnetic resonance imaging (MRI) images. The MRI images were integrated to predict clinical outcomes using 328 radiomics features, quantifying tumour image intensity, shape and text, which are extracted from lesion by manual segmentation. Least absolute shrinkage and selection operator (LASSO) were used to select the most-predictive radiomics features for the pathological grading. A radiomics signature, a clinical model, and a combined model were built. The association between the radiomics signature and HCC grading was explored. This quantitative analysis method was validated in 170 consecutive patients (training dataset: n = 125; validation dataset, n = 45), and cross-validation with receiver operating characteristic (ROC) analysis was performed and the area under the ROC curve (AUC) was employed as the prediction metric. Through the proposed method, AUC was 0.909 in training dataset and 0.800 in validation dataset, respectively. Overall, the prediction performances by radiomics features showed statistically significant correlations with pathological grading. The results showed that radiomics signature was developed to be a significant predictor for HCC pathological grading, which may serve as a noninvasive complementary tool for clinical doctors in determining the prognosis and therapeutic strategy for HCC.
Keywords: magnetic resonance image, pathological grading, liver tumour, LASSO regression, radiomics
引言
肝脏肿瘤的早期诊断对制定治疗方案有着重要意义，对于已进展为中晚期的肿瘤，尽可能在治疗前明确肿瘤的分子生物学分型、分级等肿瘤异质性信息，可根据肿瘤的异质性选择合理的治疗方案，即精准治疗。临床实践表明肿瘤的病理分级信息与患者的疗效、预后密切相关，但依赖于穿刺活检、手术病理取材的病理分级方法并不适合于所有肿瘤人群的治疗前诊断。磁共振成像（magnetic resonance imaging，MRI）是一种常见的影像学诊断方法，但肉眼上对早期肝脏肿瘤的诊断仍存在局限性，对肿瘤异质性评估的价值并没有被完全挖掘出来。2012 年荷兰学者 Lambin 等[1]提出了放射组学的概念，同年 Kumar 等[2]将放射组学的定义扩展为影像组学。影像组学是以定量成像为基础的新兴技术，指的是高通量地从计算机断层扫描成像（computed tomography，CT）、MRI 等医学影像中提取影像特征，将传统的影像转换为可发掘的数据信息，通过定量分析来预测病理分级、分子生物学分型等。Doroshow 等[3]指出影像组学是转化医学未来发展方向之一。2014 年 Aerts 等[4]在《Nature》杂志上发布了一项根据定量的影像组学特征进行肿瘤分型的研究，结果显示大量的影像特征与患者预后有显著的联系，影像组学特征能够捕捉到肿瘤内部的异质性，并与基因表达的模式相关，并且某些特征在肺癌和头颈部肿瘤都存在。最近两三年基于影像组学的相关研究在对肿瘤的诊断、疗效评估、预后判断等方面已经显示出巨大的临床应用价值[5-7]。
影像组学的关键技术是提取高通量影像特征后的特征降维，可以利用各种机器学习算法来进行特征选择和分类模型构建。对于“高维”数据（特征变量数目远大于数据样本数量）而言，常见的方法比如支持向量机（support vector machine，SVM）、随机森林（random forest，RF）等，进行特征选择时无法同时满足模型的准确性、模型稳定性以及模型计算复杂度的要求[8]，岭回归虽然可以解决变量之间的多重共线性问题，但是它得到的解是非稀疏的，不能有效地降低特征变量的维度。Tibshirani[9-10]提出了一种称为最小绝对收缩和选择运算符（least absolute shrinkage and selection operator，LASSO）的变量选择方法，该方法在最小二乘估计的基础上加入 L1 正则化项，使用模型系数的绝对值函数作为惩罚策略来压缩模型系数，使一些与输出结果效应非常弱的回归系数变小，甚至变为零，因此 LASSO 可以提供一个稀疏解，很好地克服了传统方法的不足。王金甲等[11]提出采用 LASSO 模型用于肝病的分类，其分类正确率优于传统的模式识别方法；李静等[12]提出基于广义交互 LASSO 模型用于肝脏疾病分类；Liang 等[13]基于 LASSO 和影像组学对结直肠肿瘤的病理分级进行了预测；Guo 等[14]使用影像组学与基因组学联合基于 LASSO 模型预测浸润性乳腺癌的病理分级，取得了一些成果。
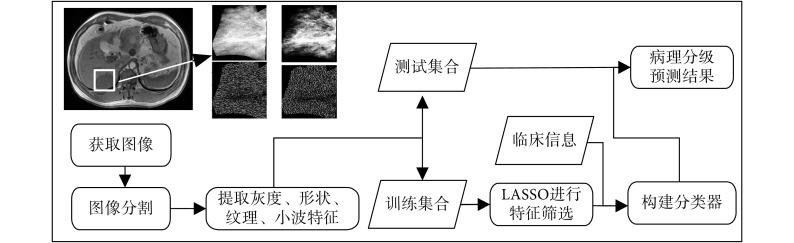
本文提出的肝脏肿瘤病理分级的定量分析方法主要是在非增强 T1 加权图像（T1 weighted MRI，T1WI）和 T2 加权图像（T2 weighted MRI，T2WI）上，采用手动方式将病灶部位分割出来，对分割出来的图像提取高通量的影像特征，通过 LASSO 算法，经过交叉验证从中筛选对病理分级最有关联的影像特征，并融合临床信息，构建分类器，对肝脏肿瘤的病理分级进行预测。图 1 给出了该方法的流程图。
图 1.
Flow chart of image processing for pathological grading
病理分级图像处理流程
1. 特征提取
对分割出来的病灶部位图像进行特征提取，特征主要分为四类：① 强度特征；② 形状和大小特征；③ 纹理特征；④ 小波特征。具体的特征描述见表 1 所示。
表 1. All features extracted from MRI images.
提取特征的具体描述
| 类型 | 特征具体描述 |
| 注：GLCM：灰度共生矩阵（gray level co-occurrence matrix）；GLRLM：灰度游程长度矩阵（gray level run-length matrix） | |
| 强度特征 | 能量、熵、峰度、最大值、均值、平均绝对偏差、中值、最小值、范围、均方根、偏度、标准差、一致性和方差 |
| 形状和大小特征 | 紧密度、球形的不均匀度、球形度、表面积和体积比值 |
| 纹理特征 | 基于 GLCM：主要有能量、熵、对比度、均匀度、自相关系数、相关系数、总平均值、方差、差异度；基于 GLRLM：主要有短游程强调、长游程强调、灰度不均匀度、游程长度不均匀性、游程百分比、低灰度级游程强度、高灰度级游程强度、短游程低灰度级强调、短游程高灰度级强调、长游程低灰度级强调、长游程高灰度级强调。 |
| 三维小波特征 | 图像经过三个方向上的小波分解后，计算强度和点奇异性特征 |
一阶统计特征用来描述肿瘤的强度特性，是描述 MRI 图像中肿瘤体素强度分布的通用和基础指标。形状和大小特征描述了病变区域的三维尺寸大小和形状，用于描述球形或者细长形状的肿瘤的特点。纹理特征主要基于 GLCM、GLRLM 进行计算和分析得到，由图像中体素强度值进行离散化得到相应的纹理统计矩阵，可以量化肿瘤内异质差异，由于在全部三维方向上计算这些特征，提供了图像中不同灰度级相对的位置信息，这个离散步骤不仅可以减少图像噪声，而且使所有肿瘤体素强度标准化，允许直接比较所计算的三维空间特征。三维小波特征是小波分解原图后计算每个分量的强度和点奇异性特征，关注图像内不同频域的特征。本文采用的是一种离散的、非抽取的三维小波变换，对于任何一幅 MRI 图像，原始图像 X 可以分解为 8 个分量，假设 L 表示低通滤波，H 表示高通滤波，8 个分量分别是 XLLL、XLLH、XLHL、XLHH、XHLL、XHLH、XHHL、XHHH。比如 XLLH 就是高通子带，它是沿 X 方向进行低通滤波、沿 Y 方向进行低通滤波、沿 Z 方向进行高通滤波得到的，可以表示如下：
 |
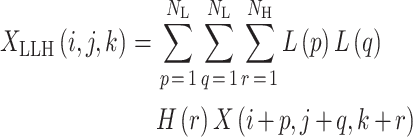1 |
其中 NL 表示低通滤波器的长度，NH 表示高通滤波器的长度。
上述提到的高通量特征是在 Matlab R2014b（Mathworks，Natick，美国）下编码完成的。
2. 模型与方法
经过对病灶部位图像进行特征提取，共提取了四大类共 328 维影像特征，但并非所有特征对于病理分级都是有用的，因此特征维度的降低十分必要。下面介绍特征选择的方法 LASSO 模型，LASSO 模型是在多元分析时，通过对变量系数的压缩，挑选出系数不为零的变量。
2.1. LASSO 的基本概念
假设已知数据
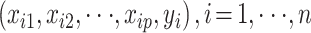，其中 xij 是预测变量，yi 是响应变量。同一般的回归方程一样，假设个体间是相互独立的，或者在给定预测变量 xij 的条件下，yi 是相互独立的。假设 xij 是标准化的，那么
 |
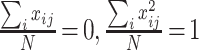2 |
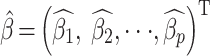，则LASSO估计
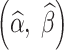可定义为：
 |
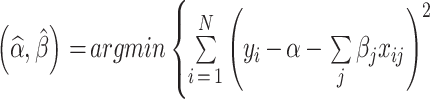3 |
同时满足
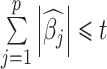的约束条件。其中 t ≥ 0 为惩罚参数，参数 t 在估计时用来控制收缩量，设
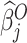为普通最小二乘估计值，记
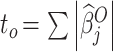，当 0 < t <
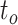，可以使一些回归系数收缩并趋向于 0，并且一些回归系数的估计值就等于 0，则 LASSO 估计就演变为下面的式子：
 |
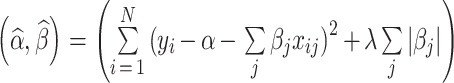4 |
其中
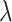> 0，参数
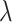和参数 t 是对应的，也即是参数
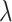对应的是模型的惩罚系数，当参数
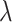越小时，模型的压缩程度越低，提取的特征越多，当参数
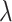越大时，对模型的压缩程度越大，提取的特征越少。例如当
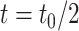时，效果会大致类似于寻找大小为
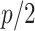的最优特征子集，也就是说变量集中一些变量的作用减小了，而且起作用的变量个数也仅大致为原来的二分之一。LASSO 模型的求解使用循环坐标下降法。
2.2. LASSO 参数 t 的估计
LASSO 估计中惩罚参数 t 的估计有两种方法：交叉验证法和广义交叉验证法。
假设
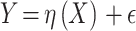，其中
，
。
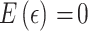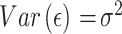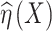估计的均方误差MSE定义如下：
 |
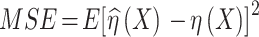5 |
MSE 的求解比较困难，预测误差 PSE 比较容易计算，并且和 MSE 是相关的。
 |
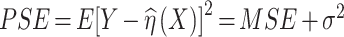6 |
最小化 PSE 相当于最小化 MSE。
惩罚参数 t 也叫做 LASSO 参数，它相当于是 LASSO 的收缩边界，
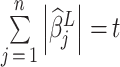，这里定义与参数 t 相关的另一个参数 s 作为归一化的 LASSO 参数，
 |
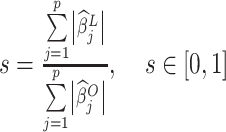7 |
2.2.1. 交叉验证
交叉验证的基本思想是把样本集分为两大类——训练集和验证集用来估计模型参数，其中训练集和验证集的角色不断地变换。
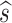表示最优的参数 s，比如一个 10 折交叉验证，样本集共分为 10 份，一份作为验证集，其余为训练集，然后不停地变换验证集，依次训练模型，在归一化参数 s 的条件下检索 LASSO，并且预测误差是由 s 从 0 到 1 不断变化估计出来的，选择产生最低预测误差估计值 PSE 所对应的
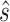作为最优解。
一个 N 折交叉验证的算法流程如下：
步骤 1：将全部数据样本 N 分为子样本集
；
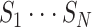步骤 2：
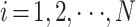，选择训练集
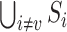训练模型，并用验证集 Sv 计算
；
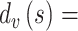
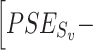
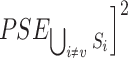步骤 3：在所有的
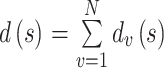中选择最小的 d（s）作为参数 s 的最优估计。
2.2.2. 广义交叉验证
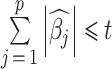的约束下，参数 s 的提出实际等价于在残差和或者残差平方上增加一个拉格朗日惩罚
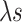，其中
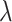取决于 t，因此在式（4）的基础上矩阵的表达形式为：
 |
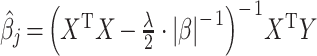8 |
在约束条件中适合
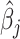的有效参数量 d（λ）可以用下面的式子进行近似：
 |
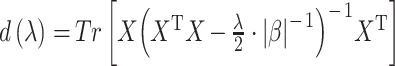9 |
可以构建广义交叉验证模型的统计方式：
 |
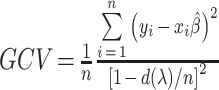10 |
LASSO 回归算法是由 R 语言编码完成，并在 R Version3.4.2（R Foundation for Statistical Computing）中实现的。
2.3. 病理分级分类模型构建
对手动分割出来的病灶部位图像进行高维特征提取，利用 LASSO 算法对肝脏肿瘤病理分级进行多元回归分析，挑选出对病理分级最有价值的影像特征。根据挑选出来的特征及其系数计算对病理分级进行预测的影像组学标签 Rad-score，根据影像组学标签进行分类测试。为了提高分类结果的准确率，将临床信息和影像组学标签进行融合，对病理分级进行分类预测。
临床模型指的是仅仅利用临床信息进行 Logistic 回归分析；影像组学模型是指提取高通量影像特征后，基于 LASSO 算法筛选特征后进行分类预测；融合模型指的是将影像组学模型得到的影像组学标签 Rad-score 和临床信息融合后进行 Logistic 回归分析。
2.4. 统计学方法介绍
患者样本数据在训练集和测试集上的分布对比情况，性别和高低分化情况对比使用卡方检验 Chi-squared test，年龄对比使用 Mann-Whitney U 检验。
通过三种模型得到的高分化和低分化患者的预测分数差异比较使用 Mann-Whitney U 检验，并且给出了四分位距（interquartile range，IQR）和中位值。
用接收者操作特征（receiver operating characteristic，ROC）曲线下面积（area under the curve，AUC）来衡量预测模型的性能，基于训练集设置最佳的分类阈值来计算 AUC，包括敏感性（sensitivity，SENS）、特异性（specificity，SPEC）、准确率（accuracy，ACC），然后将此阈值应用到测试集上，计算各个指标。AUC 大小的比较使用 Delong 测试，AUC 越大意味着分类的准确率越高，并给出了 AUC 的 95% 置信区间（confidence interval，CI）。
临床模型包含患者的年龄、性别、病灶大小、脉管癌栓、乙肝、血甲胎蛋白、假包膜、门脉癌栓、肝硬化、门脉高压等，利用 Logistic 回归进行多元因素分析，从中挑选与病理分级关联性最强的因素。临床模型加入影像组学标签 Rad-score 后，利用 Logistic 回归再一次进行多元因素分析，并给出了比值比 Odds Ratios。
统计分析使用 MedCalc16.2.0 软件完成（MedCalc software，http://www.medcalc.org），P < 0.05 表示差异有统计学意义。
3. 实验结果与分析
3.1. 实验数据
收集了 2012 年 1 月到 2016 年 12 月在河南省人民医院治疗过的肝脏肿瘤患者信息共 170 例，包含患者的 MRI 图像和临床信息，患者都已知晓本研究情况，合作医院也批准了本课题的研究，所有的数据都经过了数字化处理并对个人隐私进行了隐藏。患者样本入选实验的标准是：① 病理学诊断为肝细胞癌并具有明确的病理分级（Edmondson 分级）；② 在手术前一周行 MRI 检查，图像质量满足实验要求；③ 患者在手术之前没有经过治疗。高分化患者包括 Edmondson 等级为Ⅰ、Ⅰ-Ⅱ和Ⅱ的患者，低分化患者包括 Edmondson 等级为Ⅱ-Ⅲ、Ⅲ、Ⅲ-Ⅳ和Ⅳ的患者，进行高分化和低分化的二分类判别实验。采集图像使用的机器是通用医疗设备的 GE750 3.0T，原始图像格式为 DICOM 格式，图像分辨率为 512 * 512，扫描层厚为 7 mm，满足实验要求。由两位超过 10 年读片经验的放射科医师使用专业软件 ITK-SNAP3.0（http://www.itk-snap.org）对肿瘤病灶部位进行手动分割。患者临床信息主要包括患者的年龄、性别、病灶大小、脉管癌栓（有和无）、乙肝（有和无）、血甲胎蛋白（正常和升高）、假包膜（有、不完整、无）、门脉癌栓（有和无）、肝硬化（有、轻度、无）、门脉高压（有和无）等，临床信息取自于患者的病历管理系统。
通过程序将 170 例患者随机划分为训练集（125 例）和测试集（45 例），患者的情况描述如表 2 所示，训练集和测试集分布基本一致（P值均 > 0.05）。 图 2 显示了不同病理分级的肝脏肿瘤患者 T1WI 图像和 T2WI 图像，红色曲线标注区域为肿瘤区域。
表 2. Characteristics of patients in the training dataset and the validation dataset.
训练集和测试集患者情况对比
| 描述 | 训练集（n = 125） | 测试集（n = 45） | P 值 |
| 男性 | 104（83.20%） | 37（82.20%） | 0.881 |
| 女性 | 21（16.80%） | 8（17.78%） | |
| 年龄/岁 | 53（25～71） | 57（28～74） | 0.428 |
| 高分化患者 | 70（56.00%） | 25（55.56%） | 0.894 |
| 低分化患者 | 55（44.00%） | 20（44.44%） |
图 2.
MRI images of patients with hepatocellular carcinoma
肝脏肿瘤患者的 MRI 图像
3.2. 实验结果
LASSO 模型训练时采用 10 折交叉验证，选择 AUC 作为优化的目标，此时选出的模型作为病理分级的最优影像组学模型，利用模型筛选出来的特征及其系数计算基于影像组学的预测分数 Rad-score，进行肝脏肿瘤的病理分级。
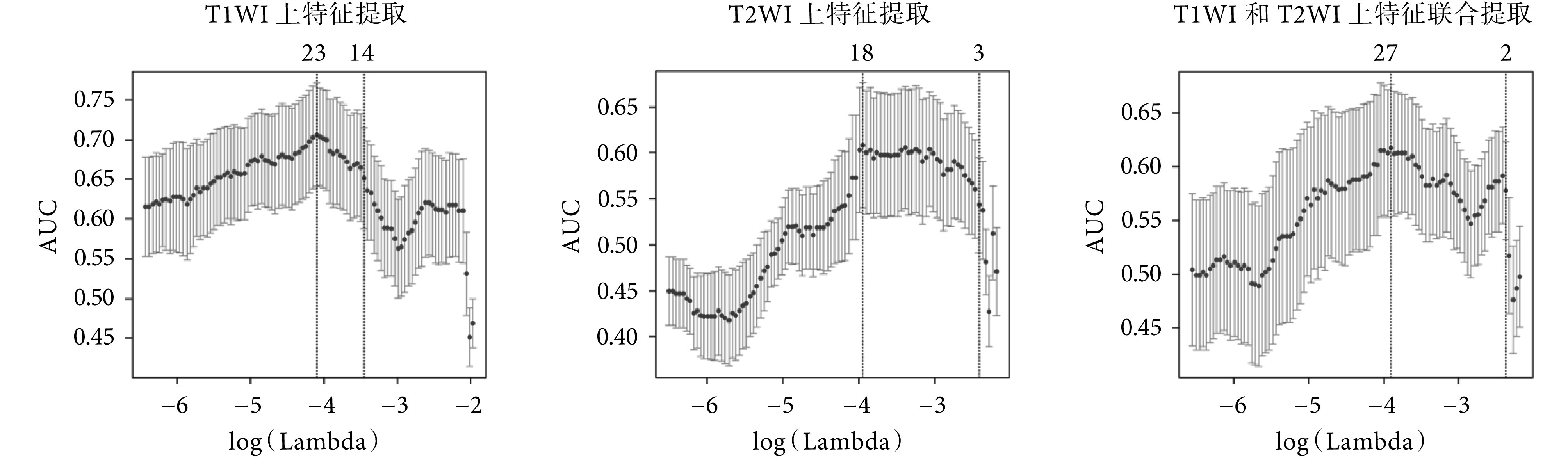
实验中使用了肝脏肿瘤患者的 T1WI 和 T2WI 图像，利用 LASSO 算法进行特征提取，构建分类模型，分别进行了 T1WI 特征筛选、T2WI 特征筛选以及 T1WI 和 T2WI 图像特征联合筛选三种实验，特征提取的结果如图 3 所示。横坐标表示参数 λ 的变化情况，纵坐标 AUC 表示模型的输出情况，曲线上方的数字表示模型提取特征的数量，从图中可看出，当参数 λ 逐渐变大时，模型的 AUC 在变化，特征数量在减少，即模型的压缩程度在增加。图中左侧虚线表示 AUC 最大时对应的取值和提取特征的数量，右侧虚线表示在 AUC 一倍标准误差时的特征提取情况，此时特征数量减少。选择左侧虚线对应的参数可以得到正确率最高的模型，选择右侧虚线对应的参数在保证一定准确率的同时可以精简模型，减少提取特征的数量，提高模型的计算效率。从图 3 可见，通过参数 λ，分别从 T1WI 的 328 维特征、T2WI 的 328 维特征以及 T1WI 和 T2WI 联合的 656 维特征中提取了 23、18、27 个特征。
图 3.
Feature selection using the LASSO logistic model
基于 LASSO 算法提取特征的结果
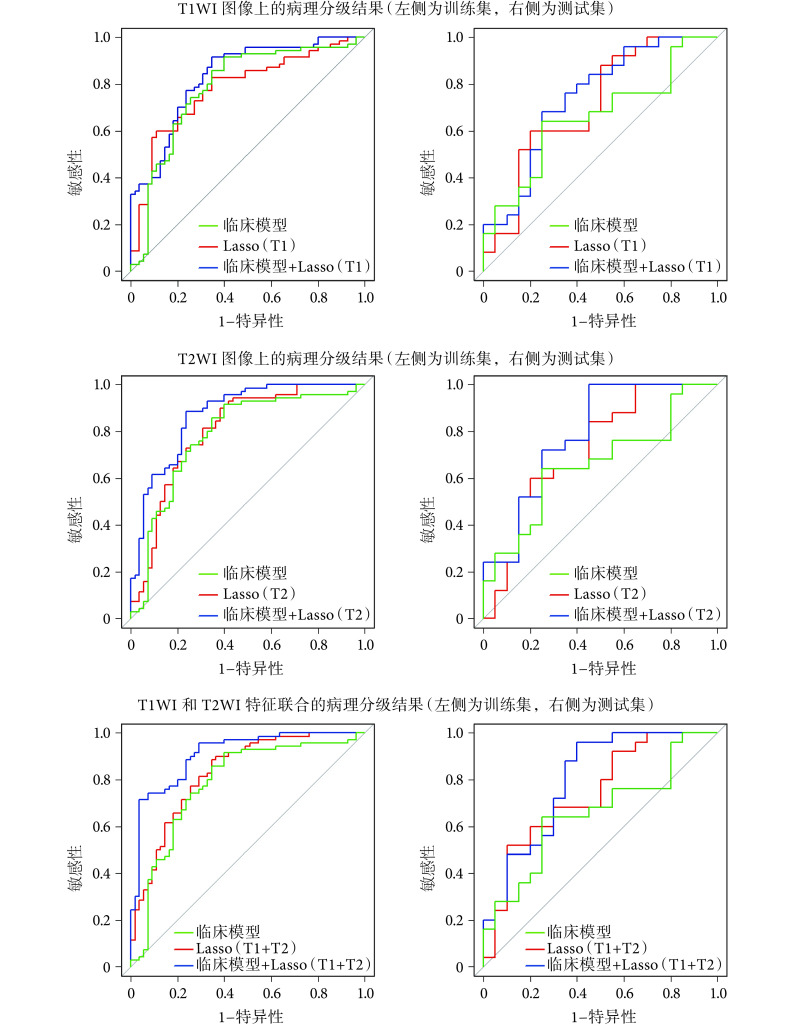
利用挑选出来的特征计算基于影像组学的预测标签 Rad-score，在临床模型、影像组学模型以及融合模型上进行了病理分级实验，结果如表 3 所示。在分类阈值为 − 0.868 8 时，融合模型取得了最高的分类结果，AUC 在训练集上为 0.909（敏感性 95.71%，特异性 70.91%，准确率 84.40%），在测试集上为 0.800（敏感性 85.00%，特异性 65.00%，准确率 76.11%）。 图 4 分别给出了在 T1WI 图像、T2WI 图像、T1WI 和 T2WI 图像特征联合上基于 LASSO 回归的影像组学模型病理分级结果以及融合临床信息的病理分级结果，可以看到，融合模型均比没有融合临床信息的影像组学模型准确率有一定的提升。
表 3. Pathological grading results.
病理分级结果
| 使用方法 | 分类阈值 | 训练集（n = 125） | 测试集（n = 45） | |||||||||
| 敏感性 | 特异性 | 准确率 | AUC（95%CI） | P 值 | 敏感性 | 特异性 | 准确率 | AUC（95%CI） | P 值 | |||
| 临床模型 | 0.507 9 | 80.00% | 65.45% | 72.20% | 0.784
（0.701，0.852） |
< 0.000 1 | 70.83% | 50.00% | 61.11% | 0.677
（0.519，0.810） |
0.032 0 | |
| 影像组学
模型（T1） |
0.638 9 | 57.14% | 85.45% | 69.60% | 0.812
（0.732，0.876） |
< 0.000 1 | 56.00% | 70.00% | 62.22% | 0.712
（0.558，0.837） |
0.009 1 | |
| 影像组学
模型（T2） |
0.108 6 | 81.43% | 63.64% | 73.60% | 0.804
（0.723，0.869） |
< 0.000 1 | 64.00% | 70.00% | 66.67% | 0.722
（0.568，0.845） |
0.005 9 | |
| 影像组学
模型（T1+T2） |
0.219 8 | 81.44% | 70.96% | 76.80% | 0.829
（0.752，0.891） |
< 0.000 1 | 60.00% | 80.00% | 68.89% | 0.742
（0.590，0.861） |
0.001 5 | |
| 融合模型（T1） | 0.219 2 | 78.57% | 72.37% | 75.36% | 0.831
（0.754，0.892） |
< 0.000 1 | 68.00% | 75.00% | 71.11% | 0.742
（0.590，0.861） |
0.001 6 | |
| 融合模型（T2） | 0.151 4 | 75.00% | 78.18% | 76.40% | 0.872
（0.801，0.925） |
< 0.000 1 | 70.00% | 75.00% | 72.22% | 0.786
（0.638，0.894） |
0.000 1 | |
| 融合模型
（T1+T2） |
– 0.868 8 | 95.71% | 70.91% | 84.40% | 0.909
（0.844，0.953） |
< 0.000 1 | 85.00% | 65.00% | 76.11% | 0.800
（0.654，0.904） |
< 0.000 1 | |
图 4.
The ROC curves of pathological grading results on the three experiments
三种实验的病理分级结果 ROC 曲线
表 4 给出了融合模型得出的预测分数在训练集和测试集上、不同年龄和性别的分布对比情况。表中给出了中位值和四分位距（P值均小于 0.05）。可以看到在训练集和测试集、男性和女性、年龄在 57 岁以上及 57 岁以下等范围内，低分化患者的预测分数高于高分化患者的预测分数，且高分化患者与低分化患者的分数差异较为明显，说明了本文提出的定量分析方法的有效性。
表 4. The Rad-score for the training dataset and validation dataset on combined model.
融合模型预测分数分布
| 描述 | 高分化患者 Median（IQR） | 低分化患者 Median（IQR） | P值 |
| 训练集 | – 1.863（– 3.447，0.002） | 1.926（0.697，3.246） | < 0.000 1 |
| 测试集 | – 2.702（– 5.128，0.439） | 1.684（– 0.655，2.890） | 0.000 5 |
| 男性 | – 1.835（– 3.581，– 0.251） | 1.808（0.267，3.246） | < 0.000 1 |
| 女性 | – 3.438（– 4.015，0.267） | 1.414（– 0.285，2.595） | < 0.000 1 |
| 年龄小于 57 岁 | – 1.490（– 3.447，– 0.497） | 1.536（0.154，2.737） | < 0.000 1 |
| 年龄大于 57 岁 | – 2.690（– 5.128，0.001） | 1.876（0.287，2.890） | < 0.000 1 |
表 5 给出了临床模型和融合模型进行病理分级时，多因素 Logistic 回归各个变量的系数、比值比 Odds Ratios 及 95% 置信区间，P 值小于 0.05 的变量被挑选出来组成回归方程。
表 5. Preoperative prediction models.
临床模型和融合模型的性能分析
| 变量名称 | 临床模型 | 融合模型（基于 T1WI 和 T2WI 特征联合） | |||||
| 系数 | Odds Ratios（95%CI） | P值 | 系数 | Odds Ratios（95%CI） | P值 | ||
| *表示P < 0.05 | |||||||
| 常数 | – 2.163 11 | 0.115（0.003，3.789） | 0.238 | – 0.450 67 | 0.637（0.005，61.424） | 0.848 | |
| 性别 | – 0.391 56 | 0.676（0.167，2.594） | 0.571 | 0.022 20 | 1.022（0.231，4.427） | 0.976 | |
| 年龄 | 0.005 70 | 1.006（0.963，1.050） | 0.794 | 0.008 44 | 1.008（0.953，1.067） | 0.766 | |
| 病灶大小 | 0.007 90 | 1.008（0.997，1.020） | 0.176 | – 0.004 95 | 0.995（0.981，1.008） | 0.477 | |
| 乙肝 | 1.184 82 | 3.270（0.700，17.553） | 0.144 | – 0.803 53 | 0.447（0.068，2.632） | 0.381 | |
| 甲胎蛋白 | 1.666 28 | 5.292（1.961，15.763） | 0.001* | 1.523 26 | 4.587（1.376，16.903） | 0.016* | |
| 包膜 | 0.025 34 | 1.026（0.374，2.835） | 0.961 | – 1.080 65 | 0.339（0.083，1.254） | 0.114 | |
| 包膜不完整 | 1.842 21 | 6.310（1.589，31.067） | 0.013* | – 0.112 53 | 0.893（0.186，4.322） | 0.886 | |
| 门脉癌栓 | 0.993 62 | 2.701（0.651，13.602） | 0.193 | 1.616 97 | 5.037（0.802，40.590） | 0.101 | |
| 轻度肝硬化 | – 0.492 00 | 0.611（0.055，6.779） | 0.683 | 1.480 47 | 4.395（0.147，184.825） | 0.411 | |
| 肝硬化 | – 1.325 42 | 0.265（0.037，1.739） | 0.169 | – 1.551 28 | 0.212（0.015，2.587） | 0.227 | |
| 门脉高压 | 0.920 06 | 2.509（0.972，6.761） | 0.061 | 1.177 46 | 3.246（1.083，10.328） | 0.038* | |
| 影像组学标签 | 3.630 04 | 37.715（10.243，195.415） | 0.000* | ||||
3.3. 实验分析与讨论
本研究提出了一种利用影像组学的肝脏肿瘤病理分级定量分析方法，在建立的模型中，设定定量的分类阈值后，通过肝脏肿瘤 MRI 图像可以预测病理分级情况。本文主要利用 LASSO 算法进行影像学特征的筛选，组成预测方程计算病理分级的影像学标签 Rad-score。实验结果证明这种方法可以很好地进行肝脏肿瘤的高、低分化二分类。
从表 3 可以看出，临床模型预测肝脏肿瘤病理分级的能力较差，说明临床信息对病理分级的贡献有限；表 5 中从临床模型的各个因素变量来看，挑选出了甲胎蛋白（P = 0.001）水平和不完整包膜情况（P = 0.013），前期也有相关文献[15]讨论了甲胎蛋白和肝脏肿瘤分期的关系。
在一些相关的研究中，使用图像纹理特征进行疾病预测的研究较多，如在结直肠癌 CT 图像上进行生存期预测[16]，以及在肺癌 CT 图像中进行分期预测[17]，都是单独使用纹理特征，并取得了不错的效果。本文提出的基于影像组学的病理分级方法，提取的特征不仅仅限于纹理特征，还有形状、灰度、小波等特征，特征的使用更全面更丰富，采用多种特征的联合分析，分类效果更好。从表 3 可以看出，基于影像组学的模型分类性能有了较大提升，说明影像组学对肝脏肿瘤病理分级的作用较为明显，MRI 图像内部蕴含的一些肉眼无法观察到的特征与肝脏肿瘤的病理分级有关联。Liang 等[13]提出基于影像组学模型的结直肠癌 CT 图像上的病理分级，在训练集上 AUC = 0.792，测试集上 AUC = 0.708，也说明了影像组学方法的有效性。陈舒婷[18]进行了基于影像组学模型的肝癌 CT 图像上 Edmondson 等级的预测，文章在进行高通量特征筛选时，只使用了简单的 U 检测方法，最终的分类结果 AUC 在训练集上为 0.765 6（n = 285），测试集上为 0.673 3（n = 127）。
传统的分析中临床信息和影像学特征是分开讨论的，将基于影像组学模型得到的影像学标签加入到临床信息中，进行病理分级的分析，可以形成很好的互补。从图 4 可以看出，在 T1WI、T2WI、T1WI 融合 T2WI 三组实验上，影像组学标签加入临床信息后，分类性能都有了提升。从表 3 可以看出，融合模型在 T1WI 融合 T2WI 实验上分类性能达到了最高。从表 5 可以看出，融合模型中挑选出来的因素是影像组学标签（P < 0.000 1）、AFP（ P = 0.016）和门脉高压（P = 0.038），说明将临床信息中甲胎蛋白等指标的检测与影像组学的结果融合在一起，可以提升基于影像组学的病理分级结果的准确性。
本文的研究方法是基于非增强 MRI 图像进行的，该方法也可以在其他模态的图像上进行分析，比如 CT 等。本文进行的是病理分级的研究，其他诸如病理分期、复发预测、生存期预测、疗效评估等都可以采用类似的方法。
4. 结束语
随着基因数据、图像数据等医疗大数据的出现，利用大数据进行肿瘤疾病诊断的价值还没有完全挖掘出来，影像组学为解决精准医学需求提供了新的思路。影像组学用到的关键技术是高通量特征提取后的降维方法，由于数据样本维度较高，当多个自变量有些相关时，模型计算可能出现多重共线性问题，当多重共线性严重时，模型的微小变化会造成系数估计的较大变化，使模型结果很不稳定，求解高度的多重共线性问题会造成计算困难，传统的回归无法正常地解决这类多重共线性问题，LASSO 回归算法则可以很好地解决这类问题，在尽量减少模型参数的同时还可以保持较高的识别准确率，很适合在影像组学中使用。本文采用 LASSO 回归算法，通过交叉验证可以很好地提取出对病理分级最有价值的特征，计算高、低分化二分类的影像组学标签，结合临床信息构造分类器，可实现对肝脏肿瘤病理分级的定量分析，结果表明影像组学特征可以很好地预测肝脏肿瘤患者的病理分级，该方法进一步挖掘了 MRI 图像中对诊断有意义的数据，提升了基于 MRI 图像的辅助诊断水平。
利益冲突声明：本文全体作者均声明不存在利益冲突。
Funding Statement
国家863计划项目（2012AA011603）；国家自然科学基金（61372172）
References
- 1.Lambin P, Rios-Velazquez E, Leijenaar R, et al Radiomics: extracting more information from medical images using advanced feature analysis. Eur J Cancer. 2012;48(4):441–446. doi: 10.1016/j.ejca.2011.11.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kumar V, Gu Yuhua, Basu S, et al Radiomics: the process and the challenges. Magn Reson Imaging. 2012;30(9):1234–1248. doi: 10.1016/j.mri.2012.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Doroshow J H, Kummar S Translational research in oncology-10 years of progress and future prospects. Nat Rev Clin Oncol. 2014;11(11):649–662. doi: 10.1038/nrclinonc.2014.158. [DOI] [PubMed] [Google Scholar]
- 4.Aerts H J, Velazquez E R, Leijenaar R T, et al Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat Commun. 2014;5:4006. doi: 10.1038/ncomms5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ganeshan B, Skogen K, Pressney I, et al Tumour heterogeneity in oesophageal cancer assessed by CT texture analysis: preliminary evidence of an association with tumour metabolism, stage, and survival. Clin Radiol. 2012;67(2):157–164. doi: 10.1016/j.crad.2011.08.012. [DOI] [PubMed] [Google Scholar]
- 6.Huang Y Q, Liang C H, He L, et al Development and validation of a radiomics nomogram for preoperative prediction of lymph node metastasis in colorectal cancer. J Clin Oncol. 2016;34(18):2157–2164. doi: 10.1200/JCO.2015.65.9128. [DOI] [PubMed] [Google Scholar]
- 7.Huang Yanqi, Liu Zaiyi, He Lan, et al Radiomics signature: a potential biomarker for the prediction of disease-free survival in early-stage (I or II) non-small cell lung cancer. Radiology. 2016;281(3):947–957. doi: 10.1148/radiol.2016152234. [DOI] [PubMed] [Google Scholar]
- 8.Fan Jianqing, Li Runze Variable selection via penalized likelihood. J Am Stat Assoc. 2001;96(4):1348–1360. [Google Scholar]
- 9.Tibshirani R Regression shrinkage and selection via the lasso. J R Statist Soc B. 1996;58(1):267–288. [Google Scholar]
- 10.Tibshirani R Regression shrinkage and selection via the lasso: a retrospective. J R Statist Soc B. 2011;73(3):273–282. doi: 10.1111/rssb.2011.73.issue-3. [DOI] [Google Scholar]
- 11.王金甲, 卢阳 特征交互lasso用于肝病分类. 生物医学工程学杂志. 2015;32(6):1227–1232. doi: 10.7507/1001-5515.20150218. [DOI] [PubMed] [Google Scholar]
- 12.李静, 仝晓云, 王金甲 基于交替方向乘子法的广义交互LASSO模型用于肝脏疾病分类. 生物医学工程学杂志. 2017;34(3):350–356. doi: 10.7507/1001-5515.201508026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liang Cuishan, Huang Yanqi, He Lan, et al The development and validation of a CT-based radiomics signature for the preoperative discrimination of stage I-II and stage III-IV colorectal cancer. Oncotarget. 2016;7(21):31401–31412. doi: 10.18632/oncotarget.8919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Guo Wentian, Li Hui, Zhu Yitan, et al Prediction of clinical phenotypes in invasive breast carcinomas from the integration of radiomics and genomics data. J Med Imaging. 2015;2(4):041007-1–041007-7. doi: 10.1117/1.JMI.2.4.041007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chang P E, Ong W C, Lui H F, et al Is the prognosis of young patients with hepatocellular carcinoma poorer than the prognosis of older patients? A comparative analysis of clinical characteristics, prognostic features, and survival outcome. J Gastroenterol. 2008;43(11):881–888. doi: 10.1007/s00535-008-2238-x. [DOI] [PubMed] [Google Scholar]
- 16.Ng F, Ganeshan B, Kozarski R, et al Assessment of primary colorectal cancer heterogeneity by using whole-tumor texture analysis: contrast-enhanced CT texture as a biomarker of 5-year survival. Radiology. 2013;266(1):177–184. doi: 10.1148/radiol.12120254. [DOI] [PubMed] [Google Scholar]
- 17.Dong Xinzhe, Xing Ligang, Wu Peipei, et al Three-dimensional positron emission tomography image texture analysis of esophageal squamous cell carcinoma: relationship between tumor 18F-fluorodeoxyglucose uptake heterogeneity, maximum standardized uptake value, and tumor stage. Nucl Med Commun. 2013;34(1):40–46. doi: 10.1097/MNM.0b013e32835ae50c. [DOI] [PubMed] [Google Scholar]
- 18.陈舒婷. 基于CT的影像组学在肝细胞癌病理分级及肝切除术预后预测的应用研究. 广州: 南方医科大学, 2017.