一种融合表面波变换与脉冲耦合神经网络的三维肺实质分割算法

Abstract

针对肺部病变及支气管干扰等因素导致的肺实质分割困难的问题，本文提出一种融合表面波（surfacelet）变换与脉冲耦合神经网络（PCNN）的肺实质分割算法。首先，通过 surfacelet 变换对三维肺部计算机断层扫描数据进行多尺度多方向分解，利用局部修正拉普拉斯算子选择处理后的子带系数增强图像的边缘特征；然后，经 surfacelet 逆变换得到增强后的图像作为 PCNN 的反馈输入；最后，通过循环迭代完成肺实质的分割。所提算法对公开数据集中的样本进行了测试。结果表明，本文算法的分割性能优于 surfacelet 变换边缘提取算法、三维区域生长算法和三维 U 形网络（U-NET）算法，能够有效抑制肺部病变及支气管的干扰，得到更完整的肺实质图像。

引言

从计算机断层扫描图像（computed tomography，CT）中准确地分割肺实质是计算机辅助诊断（computer aided diagnosis，CAD）技术的关键步骤，对于早期诊断肺癌等肺部疾病具有重要意义^[1-2]。另外，肺的边沿分割精度直接影响肺部体积测量的结果，而肺部体积的测量对研究气胸、肺气肿等疾病具有重要意义。肺实质分割方法主要分成三类：第一类是基于传统方法的肺实质分割，如阈值法^[3]、区域生长^[4]、边缘检测^[5]、活动轮廓^[6]等，各有一定缺陷。基于阈值的方法对噪声和成像伪影比较敏感^[7]，基于区域生长的方法易出现欠分割或过分割现象，基于边缘检测的方法易产生伪边界或边界丢失现象^[8]。第二类是不同方法相结合的肺实质分割。比如，Nizami 等^[9]提出使用小波框架与 K-均值（K-means）聚类相结合分割肺实质的算法；Birkbeck 等^[10]提出将统计学习与来自邻近解剖结构（心脏、肝脏、脾脏和肋骨）的解剖学约束相结合的算法；Zhou 等^[11]提出利用增强的阈值算法自动分割肺实质，然后通过纹理感知的活动轮廓模型平滑血管结构和肺部边界的算法。第三类是基于深度学习的方法。Kumar 等^[12]提出基于 U 形网络（U-NET）的深度卷积神经网络，可以实现对肺实质的自动分割，该模型采用数据增加（data augmentation）技术，使具有跳接结构的深度网络能够根据少量可用的医学图像进行像素分类。Kamal 等^[13]提出一种融合卷积和递归神经网络的三维混合 U-NET（three dimensional dense UNET，3D-denseUNET）框架，用于分割 CT 图像中的肺部肿瘤。Harrison 等^[14]引入一种基于全卷积神经网络（fully convolutional neural network，FCN）的渐进式整体嵌套网络（progressive holistically-nested networks，P-HNNs），用于分割肺组织病变。此外，近几年出现了将传统特征提取方法与深度学习方法融合的思路。比如，Ngo 等^[15]提出将深度置信网络与距离正则化水平集相结合，利用深度置信网络的学习结果驱动零水平集曲线演化进行肺实质的分割。但是，深度学习分割方法的性能依赖于可用的医学图像数量，对数据样本质量和计算能力的要求较高^[16]。

本文提出一种融合表面波（surfacelet）变换与脉冲耦合神经网络（pulse coupled neural network，PCNN）的三维肺实质分割方法，利用 surfacelet 变换和 PCNN 优势互补以提高肺实质分割的准确性。Surfacelet 变换是一种多分辨率变换，能够有效提取相邻帧间的多尺度多方向结构信息，可以通过对变换域各子带信息进行滤波以增强信号细节^[17]。脉冲耦合神经网络是一种特殊的神经网络，能够考虑像素之间灰度的几何分布选择合适的归类，有效分离对象和背景分布之间的重叠，准确提取感兴趣区域。所以，利用 surfacelet 变换增强 CT 图像的边缘与细节信息，可以弥补 PCNN 只考虑图像灰度信息的不足，从而能够减少 CT 图像中肺部病变及支气管的干扰，实现肺实质的精确分割。

1. 方法

1.1. 基于 surfacelet 变换的图像增强

Surfacelet 变换能够利用不同尺度、不同频率的方向子带准确地捕获 N 维信号中的面状奇异，具有平移不变性、完全重构、低冗余、多尺度多方向等性质^[18]。Surfacelet 变换的主要思想是将 N 维方向滤波器组（N-dimensional directional filter bank，NDFB）与多尺度金字塔结构结合，利用方向滤波器组实现金字塔形状的 N 维频域方向子带划分，利用多尺度金字塔结构实现多尺度分析与重构。本文主要考虑三维图像分割，所以下面介绍 surfacelet 变换的三维形式。

1.1.1. 三维方向滤波器组

三维方向滤波器组（three dimensional directional filter bank，3D-DFB）能够将三维信号的频谱分解为不同的方向子带。假设 n₁、n₂ 和 n₃ 分别表示三维空间域沿垂直方向、水平方向和深度方向相互正交的坐标轴，ω₁、ω₂ 和 ω₃ 是三维频域对应的坐标轴，则 3D-DFB 沿 ω₁ 轴的理想频率分解示意图如图 1 所示^[19]，分别表示沿（n₁，n₂）平面的二维理想楔形频率子带划分、沿（n₁，n₃）平面的二维理想楔形频率子带划分和金字塔形方向子带，将两个二维楔形频率子带划分进行重叠交叉，就会形成顶点对称的包含多个金字塔形方向子带（或通道）的沙漏滤波器（hourglass-shaped filter），深灰色部分表示其中的一个金字塔形子带（pyramid-shaped subband）。类似地，沿 ω₂ 轴和 ω₃ 轴的沙漏滤波器可以通过旋转沙漏滤波器得到。

图 1.

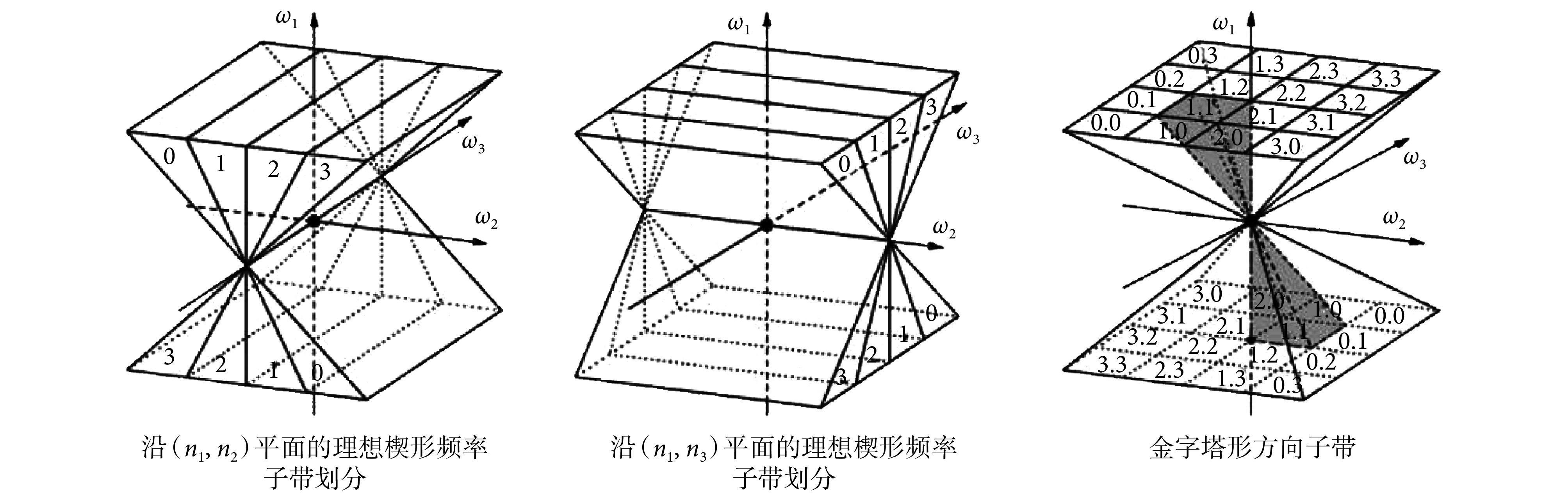
Schematic diagrams of pyramid-shaped frequency sub-band decomposition along ω₁ axis

沿 ω₁ 轴的金字塔形频率子带分解示意图

假设 a 表示如图 1 所示沿（n₁，n₂）平面的某一层二维滤波器的序号，l₂ 表示沿（n₁，n₂）方向的分解层数，b 表示如图 1 所示沿（n₁，n₃）平面的某一层二维滤波器的序号，l₃ 表示沿（n₁，n₃）方向的分解层数，则如图 1 所示沿（n₁，n₂）平面的楔形滤波器可以表示为 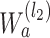（ω₁，ω₂），0 ≤ a< 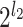，沿（n₁，n₃）平面的楔形滤波器可以表示为 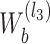（ω₁，ω₃），0 ≤ b< 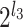。两个方向的分解层数决定沙漏滤波器包含的子带数（或通道数），沙漏滤波器可以根据分解层数和层序号表示为 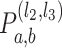。比如，l₂ = 2，l₃ = 2，则如图 1 所示的金字塔形方向子带共有 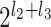=2⁴ = 16 个，其中用深灰色显示的子带下标号为 a = 1，b = 1，所以该子带可以用 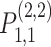表示。如图 1 所示的重叠交叉操作可以表示为两个楔形滤波器做乘积运算，如式（1）所示：

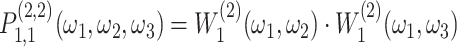1

在具体设计包含多个金字塔形状方向频域子带的沙漏滤波器时，需要两个步骤：

第一步，设计沙漏滤波器，首先采用平滑凯塞尔窗对二维辛格（sinc）函数进行截取，做二维傅里叶变换分别得到扇形结构的二维滤波器 E（ω₁，ω₂）和 E（ω₁，ω₃），然后将二者相乘得到沿 ω₁ 轴近似理想形状的沙漏滤波器 K（ω₁，ω₂，ω₃），如式（2）所示：

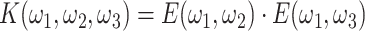2

另外，沿 ω₂ 轴和 ω₃ 轴的沙漏滤波器 K（ω₂，ω₃，ω₁）和 K（ω₃，ω₁，ω₂），可以由该滤波器旋转得到。将该沙漏滤波器代入如式（3）所示计算，对分解沙漏滤波器进行频率响应校正，如式（3）所示：

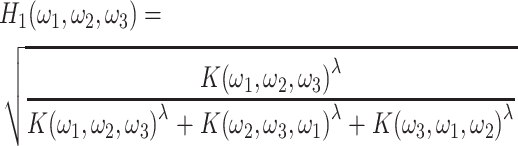3

用类似方法，可以获得沿 ω₂ 轴和 ω₃ 轴的沙漏分解滤波器 H₂（ω₁，ω₂，ω₃）和 H₃（ω₁，ω₂，ω₃）。以上三个滤波器可以彼此旋转得到，即 H₂（ω₁，ω₂，ω₃）=H₁（ω₂，ω₃，ω₁），H₃（ω₁，ω₂，ω₃）=H₁（ω₃，ω₁，ω₂）。如果要实现精确重建，约束条件如式（4）所示：

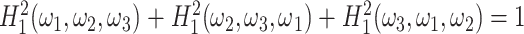4

重建（或合成）沙漏滤波器可以通过对分解滤波器进行坐标翻转获得。由于沙漏滤波器关于顶点对称，所以重建滤波器与分解滤波器相同，如式（5）所示：

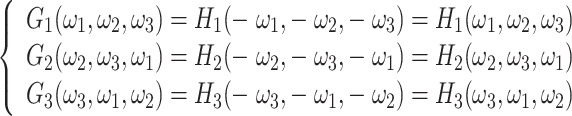5

第二步，利用二维迭代重采样棋盘格（iteratively resampled checkerboard，IRC）（符号记为：IRC）滤波器组对三维沙漏滤波器进行频带分解，获得一定数量的金字塔形子带通道。如果用 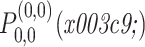表示待划分子带的三维沙漏滤波器，它可以表示为两个二维滤波器的乘积，如式（6）所示：

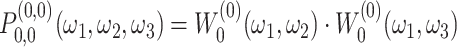6

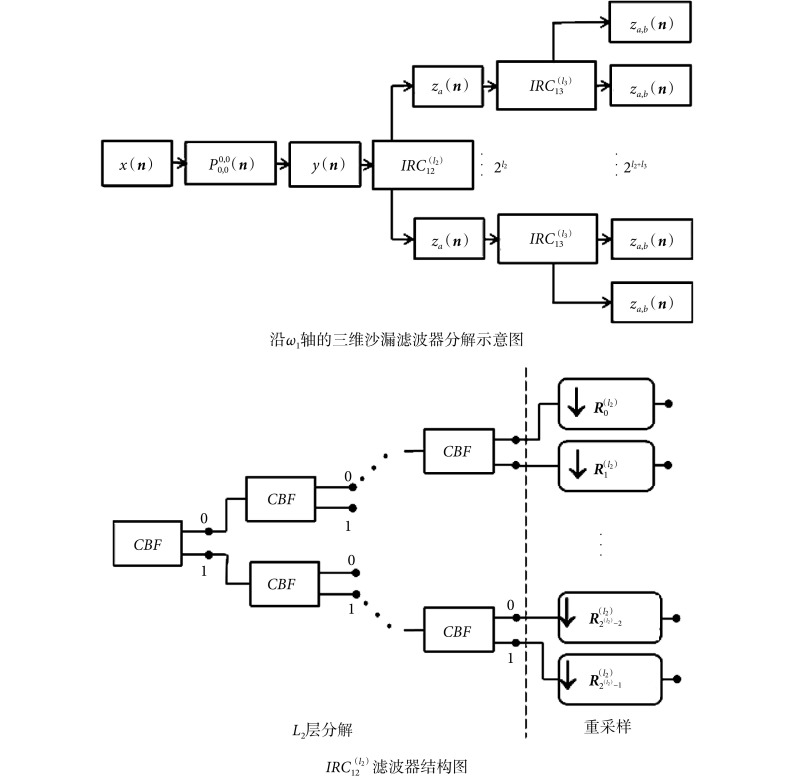
其通道数为 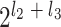=2⁰ = 1。该沙漏滤波器的子带分解过程如图 2 所示。如图 2 沿 ω₁ 轴三维沙漏滤波器分解示意图所示，输入信号 x（n）经三维沙漏滤波器 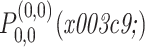做带通滤波，将输出信号 y（n）的频谱限制在沙漏形的带通范围内。然后，采用 IRC 滤波器以级联的方式进行子带切分。首先，利用 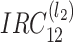沿（n₁，n₂）平面切分，子带通道数量为 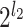个，每个通道对应的输出信号用z_a（n）表示（0≤a< 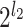）。然后，对这 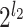个子带信号沿（n₁，n₃）平面切分。如果切分层数为 l₃，则输出的金字塔形子带通道数量为 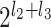个，每个通道对应的输出信号用 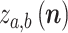表示（0≤b< 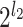）。IRC 由一定层数的二进制树级联组成，如图 2 中 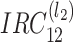滤波器结构图所示。沿（n₁，n₂）平面切分的 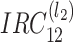采用 l₂ 层的二进制树级联分解，由双通道棋盘格滤波器组（checkerboard filter，CBF）（符号记为：CBF）实现分解，R 为重采样矩阵，负责在每个通道末尾对信号重采样。为得到如图 1 所示的理想金字塔形子带分解，IRC 滤波器需要满足以下两个条件：

图 2.

Schematic flow chart of decomposing the three-dimensional hourglass filter along ω₁ axis into multi-channel pyramid-shaped sub- bands

沿 ω₁ 轴三维沙漏滤波器金字塔形多通道子带分解过程示意图

（1）等价采样矩阵。 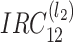第 k（0≤k< 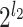）个通道的采样矩阵 M 需如式（7）所示：

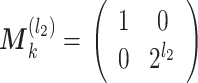7

其中，k 为通道数，l₂ 表示子带通道的数量为 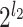个。

（2）楔形优化。设 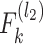为 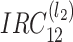第 k 个通道的等价滤波器，则如式（8）所示：

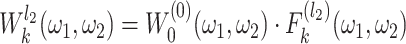8

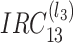的结构与 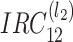一样，负责完成沿（n₁，n₃）平面的子带切分，切分层数为 l₃。以上的分解过程与重建过程是完全对称的。

1.1.2. Surfacelet 变换

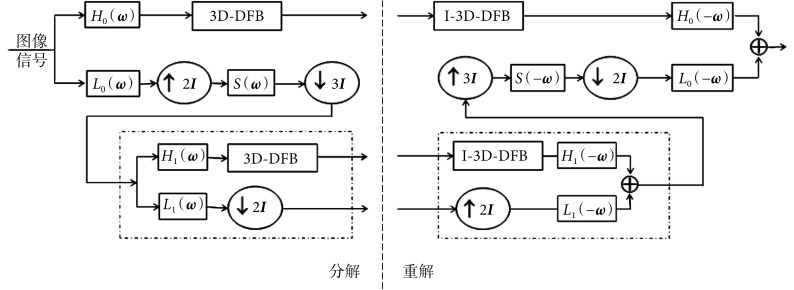
Lu 等^[19]将 NDFB 与多尺度分解相结合，提出了 surfacelet 变换。三维 surfacelet 变换及其逆变换如图 3 所示，其中L_i（ω）为低通滤波器，H_i（ω）为高通滤波器，分别用来实现多尺度分解得到对应信号的低频和高频部分。↑I 表示上采样，↓I 表示下采样。S（ω）为抗混叠滤波器，用来抑制上采样操作造成的混频干扰。信号在通过第一层的高通滤波器 H₀（ω）后经 3D-DFB 实现多方向分解，通过第一层的低通滤波器 L₀（ω）后，先进行 1.5 倍的下采样操作（即 2 倍上采样后进行 3 倍下采样操作，能够大幅减少频域混叠现象），后续分解采用 2 倍下采样，通过重复如图 3 所示虚线框中的分解过程，对信号实现更多级尺度的分解。此过程中，重建过程与分解过程是完全对称的。

图 3.

Schematic flow chart of the three-dimensional surfacelet transformation and its inverse transformation

三维 surfacelet 变换的分解与重建过程示意图

多维信号的采样操作通常定义为一个晶格，一个 N 维信号的晶格是一个大小为 N × N 的非奇异整数矩阵 I ［符号记为：LAT（I）］，如式（9）所示：

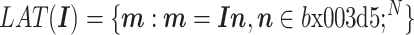9

其中，n =（n₁，n₂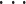， ，n_N）^T 为整数向量，输入信号 x ［n］经过 I 倍的下采样（或上采样）得到的下采样输出 y_d ［n］（或上采样输出 y_u ［n］）的表达式如式（10）所示：

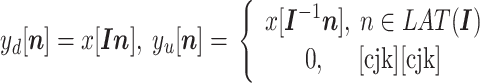10

低通滤波器 L_i（ω）的定义如式（11）所示：

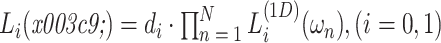11

其中，d₀ = 6^N/2，d₁ = 2^N/2，N 代表信号的维数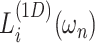， 是一个沿着 ω_n 轴的 1 维低通滤波器，如式（12）所示：

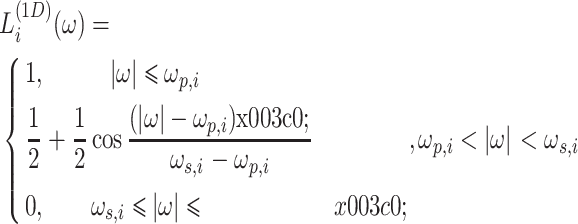12

其中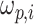， 为通带频率，当 i = 0，1 时，分别取值 π/3、π/4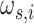； 为阻带频率，当 i = 0，1 时，分别取值 2π/3、π/2。同样，抗混叠滤波器 S（ω）的表达式为参数化形式与如式（13）所示相同的一维低通滤波器的可分离乘积，如式（14）所示：

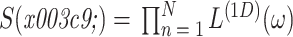13

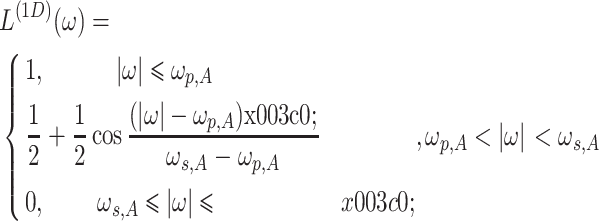14

其中，通带频率为 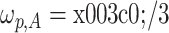，阻带频率为 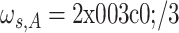。借助理想的多尺度重构条件，高通滤波器 H_i（ω）可以由低通滤波器 L_i（ω）获得^[19]，如式（15）所示：

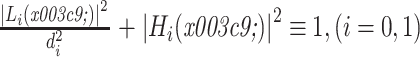15

Surfacelet 变换采用非整数的 1.5 倍下采样虽然能够减少频域混叠现象，但是冗余度较高，所以本文直接采用 2 倍下采样，两者冗余比约为 4.0∶3.4。本文使用像素为 512×512 的 CT 数据，假设其中一个数据有 64 帧，进行 2 层 surfacelet 分解，高低频子带大小分别为 256×256×32。高频子带在粗尺度得到 3 个主要方向子带，每个方向子带在细尺度内有 16 个不同的子带，这些子带分为 128×128×8、128×64×16、64×128×16 三种不同尺寸。

1.2. PCNN 模型

PCNN 模型是在哺乳动物视觉皮层模型的基础上修改得到的一种人工神经网络结构。与传统的神经元相比，PCNN 模型的每个神经元与图像的像素相对应，不需要任何训练。前馈神经网络采用一种单向多层结构，各神经元从输入层开始，接收前一级输入，并输出到下一级，直至输出层，整个网络中无反馈；反馈神经网络每个神经元同时将自身的输出信号作为输入反馈给其他神经元，需要工作一段时间才能达到稳定；相比于传统的前馈神经网络、反馈神经网络，PCNN 模型具有同步脉冲发放特性、线性相加和非线性相乘调制耦合等特性，对输入信息处理能力强，适合于图像处理^[20]。传统的 PCNN 模型结构比较复杂，控制参数多。本文采用一种基于最小交叉熵的简化 PCNN 模型，该模型的优点在于能够利用交叉熵原理自动计算模型的最佳迭代次数，提高了算法的自动化程度^[21]。该 PCNN 模型表达式如式（16）～（20）所示：

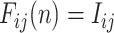16

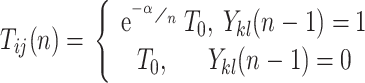17

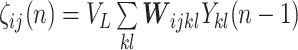18

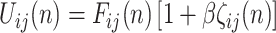19

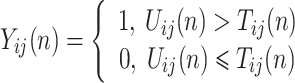20

其中，n 为迭代次数。ij 表示神经元在网络中位置的下标，kl 表示相邻神经元的下标。I_ij 为外部刺激，即与神经元相关联的像素的灰度值。ζ_ij（n）为神经元的连接输入，主要接收来自局部相邻神经元的输出信息 Y_kl （n − 1）。 V_L 表示连接输入的振幅，W 为 3×3 的内部连接矩阵，表示神经元之间的连接权值。U_ij 为内部活动项，β 是连接强度系数，需要手动设置参数。T_ij 为动态阈值，α = C/μ，C 为常数，μ 为图像平均灰度。α 在手动设置参数后，可以根据不同图像的平均灰度自适应调整。Y_ij 为神经元的脉冲输出。可以看出，PCNN 模型的点火像素控制主要由如式（20）所示的动态二值处理过程完成。与传统的根据图像灰度分布统计特性选择全局阈值或局部阈值进行二值化处理不同，PCNN 模型的二值化处理是迭代寻优过程中的一个步骤，阈值是自适应变化的，而且还充分考虑了邻域像素的灰度值。

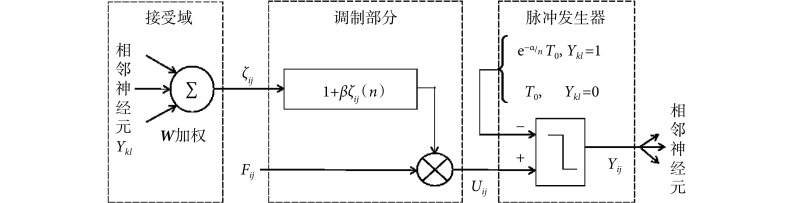
PCNN 模型中单个神经元的结构如图 4 所示。每个神经元均由接受域、调制部分与脉冲发生器组成。其中，接受域接收来自周围其他神经元的输入即连接输入 ζ_ij（n）的信息，调制部分对连接输入 ζ_ij（n）与馈送输入 F_ij（n）进行调制，得到神经元的内部活动项 U_ij，脉冲发生器用于判断该像素是否点火。从功能上看，PCNN 模型神经元的脉冲发生器与传统神经网络中的激励函数类似，区别在于传统神经网络的激励函数存在于每层结构和输出层，一般采用非线性函数来表示上层节点的输出与下层节点的输入之间的映射关系，而脉冲发生器是根据当前像素与相邻像素之间的灰度值相近程度判断该像素对应的神经元是否点火。

图 4.

A neuron model of the simplified PCNN

简化 PCNN 的神经元模型

当分割开始时，需要设置初始阈值（对于 CT 图像，该阈值一般设置为 255 的灰度值）和迭代次数 n。在第一次迭代过程中，每个神经元接收到与之对应像素灰度值的刺激，此时 ζ_ij 为 0，U_ij 不会大于 T₀，所以在第一次迭代中没有神经元脉冲。从第二次迭代开始，T_ij（n）以指数形式衰减，随着迭代次数的增加，使得 U_ij（n）大于 T_ij（n），因此会有神经元脉冲，脉冲的神经元会产生连接输入 ζ_ij（n）到相邻神经元，如果使得相邻神经元的内部活动项大于阈值，即说明它们具有相似的灰度值，从而产生同步脉冲，并且每个神经元在一个脉冲周期内只能点火一次。但是，在 PCNN 模型的迭代过程中，最优分割结果可能出现在预定迭代次数之前。所以，本文应用最小交叉熵准则来自动选择最优分割结果^[21-22]，在产生最优分割结果时自动停止迭代，可以节省计算时间，提高分割性能。最小交叉熵如式（21）所示：

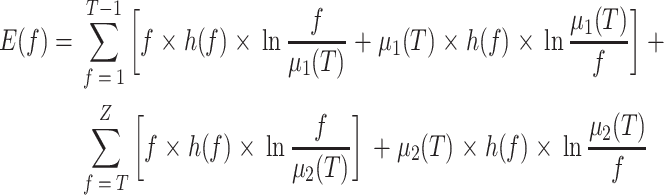21

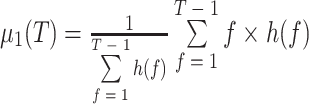22

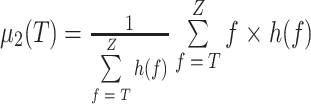23

其中，f 表示图像灰度值，h（f）表示灰度值为 f 的像素所占总像素的比值，Z 为灰度值上界（255），T = T_ij（n），μ₁（T）和 μ₂（T）为类内均值，分别代表分割结果中目标和背景的平均灰度，其计算公式如式（22）～（23）所示。当 E（f）为最小值时的迭代次数及阈值即为最佳迭代次数 n_best 及最佳阈值 T_best，而与其对应的输出 Y_ij（n_best）即为最佳结果。

1.3. 本文算法

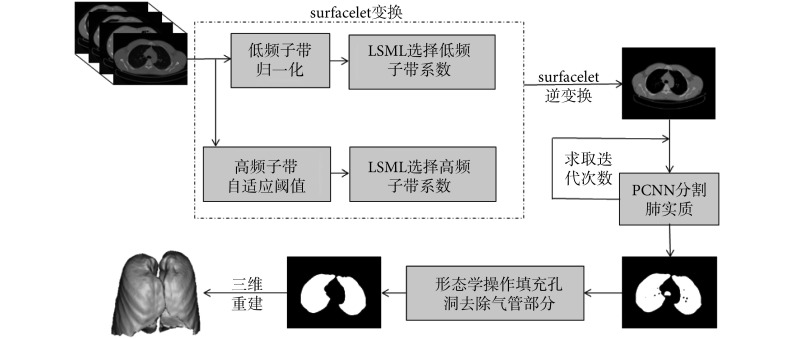
本文利用 surfacelet 变换的多尺度、多方向分解特性及局部修正拉普拉斯算子（local sum-modified-laplacian，LSML）增强三维 CT 图像中的边缘及细节信息，然后使用 PCNN 算法分割肺实质，算法流程如图 5 所示，具体步骤如下：

图 5.

Flow chart of the proposed algorithm

本文算法流程图

（1）使用 surfacelet 变换分解三维 CT 肺部数据，得到一系列高频与低频子带，分解的角度级别越高，产生的方向子带越多。实验表明，当 l = 2 即产生 3 × 2^2l = 48 个方向子带时，性能最优。

（2）对高频子带系数采取自适应阈值滤波处理，去除噪声干扰，设 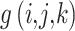为高频子带系数，自适应阈值 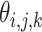的表达式如式（24）所示：

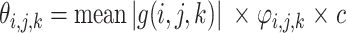24

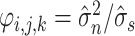25

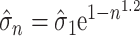26

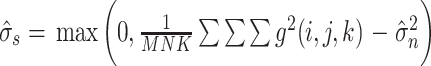27

其中，mean 为求平均值运算，c 为常数，经实验验证，c = 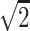时去噪效果最好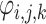， 为调整因子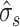， 是由极大似然估计得到的信号方差，M、N、K 分别为三维子带系数的长宽高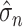， 为噪声方差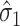， 为第一层分解系数的噪声方差，通过中值估计法得到，如式（28）所示：

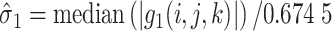28

为了降低稀疏系数幅值的波动，对低频子带系数 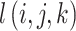做归一化处理，如式（29）所示：

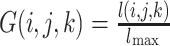29

其中，l_max 为低频子带系数中的最大值。

（3）LSML（以符号 LSML 表示）能够增强子带图像的边缘细节信息。利用 LSML 分别对得到的 surfacelet 变换域的低频和高频子带逐帧进行处理，在二维图像上处理的优点是能够在增强图像边缘特征的同时降低内存限制，LSML 的表达式如式（30）所示：

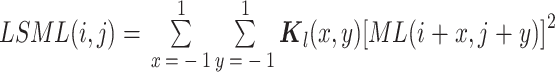30

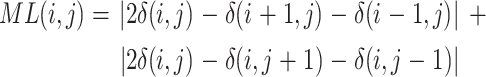31

32

其中，ML（.）为能量函数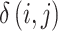， 是三维子带其中一帧在 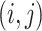处的分解系数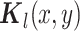， 是一个加权模板，用来突出中心像素， 。

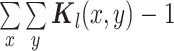（4）根据如式（15）所示的完全重构条件，经过 surfacelet 逆变换重建过程可以重建得到增强后的图像 P，并将其作为 PCNN 的输入。运行 PCNN 简化模型，计算每次迭代后的二值图像 Q 与图像 P 的交叉熵，将得到最小交叉熵时的迭代次数作为 PCNN 的最佳迭代次数，分割肺实质。

（5）基于形态学操作的方法填充肺实质孔洞，如式（33）所示：

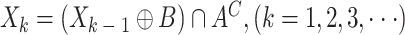33

其中，X₀ 是像素值全为 0 的图像，A 为待填充图像，A^C 为A 的补集，B 为四连通结构元。为了去除气管区域，对分割结果采用基于八邻域的区域统计方法，然后去除像素个数小于 1 500 的区域。

（6）基于体绘制方法实现三维重建。

2. 实验与结果分析

2.1. 实验数据

实验环境：笔记本电脑（Inspiron，Dell Inc.，美国）。

使用的软件系统：矩阵实验室软件 MATLAB R2017b（MathWorks Inc.，美国），微软 Visual Studio 2013（Microsoft Inc.，美国）。

实验数据：Kaggle 肺癌检测挑战赛上的公开数据集（网址：https://www.kaggle.com/c/data-science-bowl-2017/data）和肺部图像数据库联盟（lung image database consortium，LIDC）公开数据集（网址：https://wiki.cancerimagingarchive.net）。从每个数据集中随机选取各 10 组胸腔 CT 数据进行实验，图像大小为 512×512 像素。

2.2. 实验结果

为了有效评估本文所提算法性能，将其与三维 surfacelet 边缘提取算法（简称：文献[5]方法）、三维区域生长算法^[23]和三维 U-NET 算法进行比较^[24]。如图 6 所示，为 4 幅 CT 肺部切片（来自 Kaggle 数据集，图片尺寸为 512×512 像素）的分割结果。以手动分割结果为参照，当图像较为简单时，上述 4 种算法都能将完整肺实质分割出来，如图 6 切片 1 所示。当肺实质与气管存在粘连时，文献[5]方法与三维区域生长算法误将气管分割为肺实质，而三维 U-NET 算法与本文算法能较好地将肺实质分割出来，如图 6 切片 2 所示。当存在粘连且图像灰度不均匀，文献[5]方法误将气管分割为肺实质，而其他三种算法分割效果较好，如图 6 切片 3 所示。当存在肺实质粘连区域，且图像较模糊时，如图 6 切片 4 所示，文献[5]方法与三维区域生长算法在粘连区域分割失败，无法将左右肺区分开来，三维 U-NET 算法在切片 4 出现了欠分割现象，部分肺实质没有分割出来，而本文算法能够分割得到完整肺实质。

图 6.

Segmentation results comparison of four CT slices

四幅 CT 切片的分割结果比较

为了进行定量评估，本文从公开数据集 Kaggle 与 LIDC 中选取 20 组三维数据进行实验。从分割结果中随机选取 500 张二维 CT 肺部切片进行测试，并采用 3 个定量指标进行性能评估^[25]，即 Dice 相似度系数（dice similarity coefficient，DSC）（以符号 DSC 表示）、过分割率（over-segmentation，OS）（以符号 OS 表示）和欠分割率（under-segmentation，US）（以符号 US 表示）。这些指标的定义如式（34）～（36）所示：

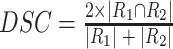34

其中，R₁ 表示算法分割结果，R₂ 表示手工分割结果。

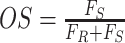35

其中，F_R 表示手工分割目标的面积或像素数，F_S 表示误分割为目标的面积或像素数。

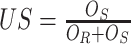36

其中，O_R 表示手工分割目标的面积或像素数，O_S 表示误分割为背景的面积或像素数。

4 种算法对 500 张测试图像的平均 DSC、平均 OS 和平均 US 如表 1 所示。可以看出，本文所提算法的 3 个定量指标均优于其他算法。与文献[5]方法、三维区域生长算法、三维 U-NET 算法相比，平均 DSC 分别提升 2.7%、1.5%、0.2%，平均 OS 分别减少 1.53%、0.51%、0.17%，平均 US 分别减少 1.1%、1.67%、0.79%。所以，本文所提算法的分割精确性有较明显的提升。由于三维 U-NET 分割算法需要大量带标签数据进行训练，且训练时间较长，所以本文所提算法在分割性能相近的情况下，具有计算成本小的优势。

表 1. Quantitative evaluation of four segmentation algorithms.

4 种分割算法的定量评估

算法	DSC	OS	US
文献[5]方法	0.952 0	0.018 4	0.029 7
三维区域生长算法	0.963 3	0.008 2	0.035 4
三维 U-NET 算法	0.976 9	0.004 8	0.026 6
本文算法	0.978 5	0.003 1	0.018 7

如图 7 所示，分别为 LIDC 公开数据集中三个肺部体数据（LIDC-IDEI-12，LIDC-IDEI-25，LIDC-IDEI-13）的三维重建结果，每个二维切片的尺寸为 512×512 像素，如图 7 所示。可以看到，文献[5]方法和三维区域生长算法受气管、支气管的影响，并受到图像中伪影的干扰，分割效果存在部分失真（三角箭头所指为误分割的气管部分）。三维 U-NET 算法可以较好地避免干扰，但是存在欠分割（圆点示意所指为缺失部分）。而通过与其他算法分割结果比较可以看出，本文算法能够解决上述问题，得到的分割效果更好。

图 7.

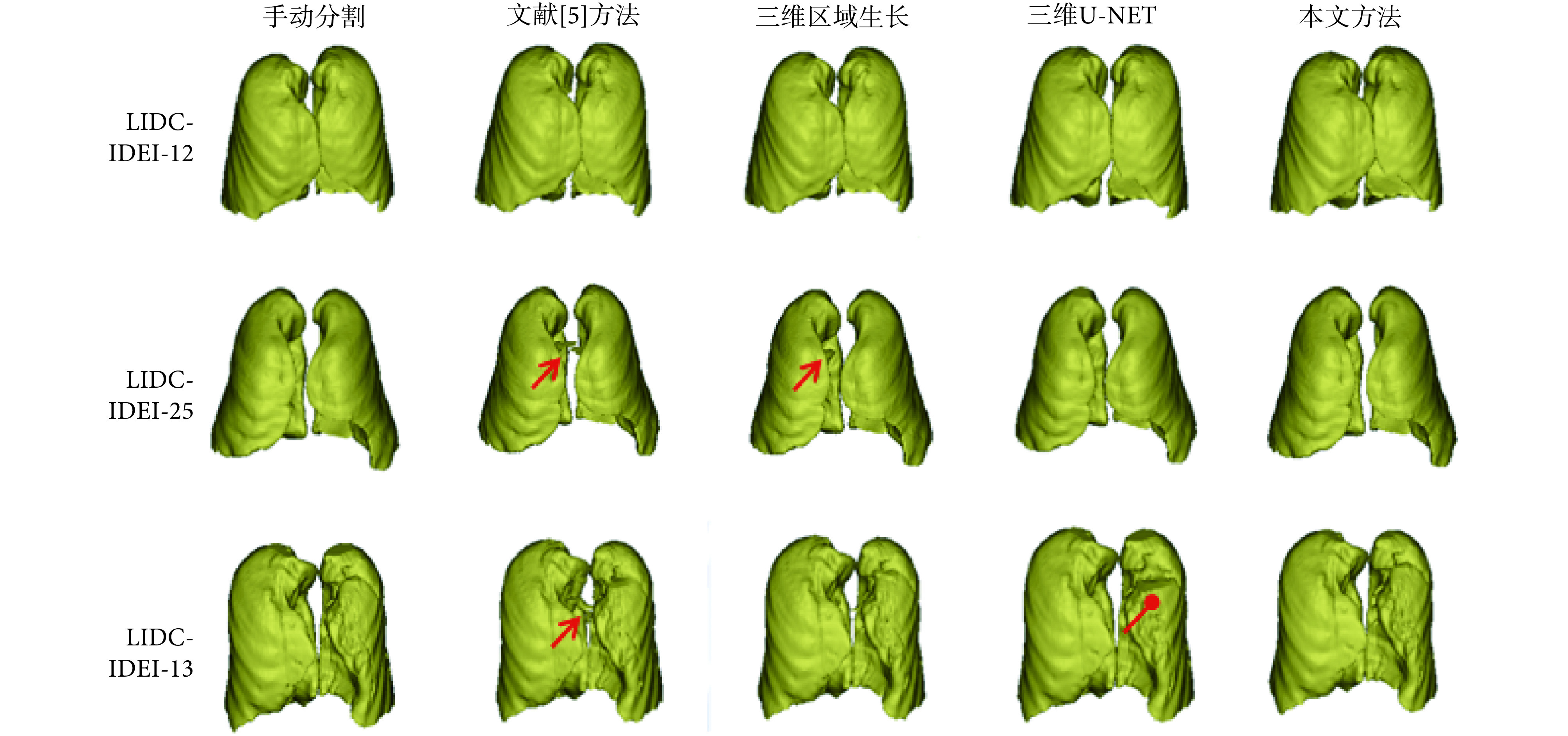
Three-dimensional segmentation and reconstruction results of three pulmonary volume data in LIDC

LIDC 公开数据集中三个肺部体数据的三维分割与重建结果

3. 讨论

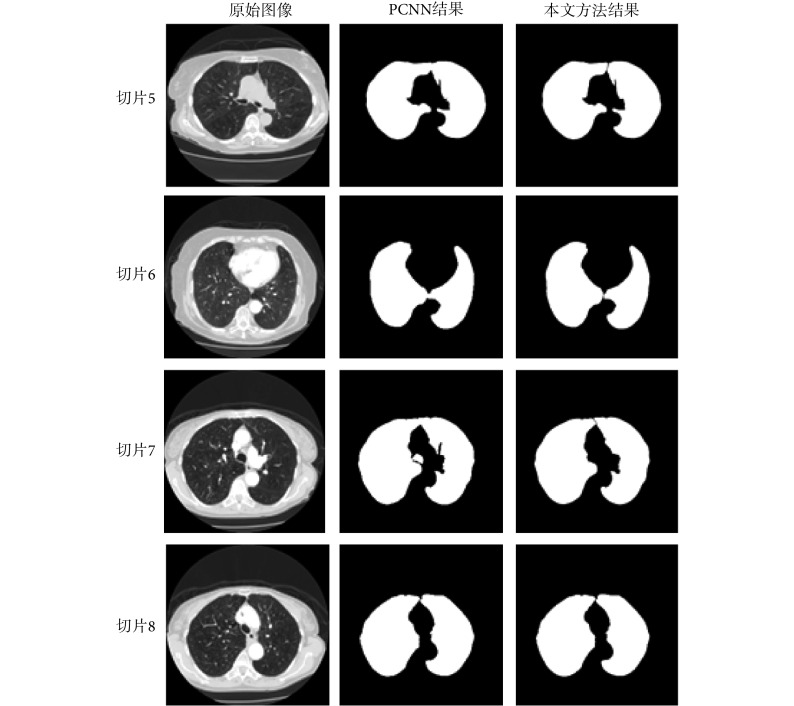
由于 PCNN 模型在循环迭代时以图像的灰度信息为依据，对灰度不均匀的图像难以区别模糊的目标边缘，分割质量较差。如图 8 第一列所示的双肺 CT 图像，灰度信息相近的左右肺在结构上非常靠近，二者之间的边缘比较模糊，如果单纯采用 PCNN 模型进行分割会出现大概率的分割失败。如图 8 第二列所示，4 幅切片图像中仅有第 4 行切片 8 的左右肺分割出来，其余三个切片图像均分割失败。本文利用改进的 surfacelet 变换算法可以增强图像的边缘与细节信息，将增强后的图像输入 PCNN 模型进行迭代，对模糊边缘的目标可以得到更为鲁棒有效的分割结果。此外，PCNN 模型分割不同的图像时都需要设置特定的参数，而一个三维医学影像数据包含几十甚至上百张二维图像，手工设置或调整参数耗时费力。本文所提算法可以根据图像特征自适应调整 PCNN 模型的动态阈值控制参数［如式（17）所示的 α 参数］，而且能够在迭代过程中根据最小交叉熵自动选择最佳分割结果，提高了 PCNN 模型处理三维数据的灵活性。

图 8.

Comparison of the proposed method with the PCNN

本文方法与 PCNN 方法的比较

如表 2 所示，为 4 种算法对 500 张切片的平均分割时间。这里，三维 U-NET 算法的计算时间指模型训练好之后的分割时间，没有包括数据标注和需要时间（约 51 h）。与文献[5]方法、三维区域生长算法、三维 U-NET 算法相比，本文算法的计算时间分别增加 1.17、7.45、7.93 s。这是由于 surfacelet 变换对三维数据分解与重建带来的计算成本增加，但是从分割算法的性能提升角度看，这种适量的计算成本增加是可以接受的。

表 2. Computational time of the four segmentation algorithms.

四种分割算法的分割时间

分割算法	计算时间/s
文献[5]方法	10.51
三维区域生长	4.23
三维 U-NET	3.75
本文算法	11.68

4. 结论

本文提出了一种融合 surfacelet 变换与 PCNN 模型的三维肺实质分割算法。该算法利用 surfacelet 变换的多尺度多方向分解特性增强 CT 图像的边缘与细节信息，有效地提升了 PCNN 模型分割肺实质的准确性。而且，PCNN 模型动态阈值控制参数的自动选择策略，以及利用最小交叉熵自动选择最佳分割结果可以有效减少人工干预，提高分割的鲁棒性和灵活性。通过与 surfacelet 变换边缘提取算法、三维区域生长分割算法和三维 U-NET 分割算法的实验比较，表明本文所提分割算法对三维 CT 肺实质分割具有更高的分割性能。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金资助项目（61471225）