用于日常体表监测的三维脊柱形态测量技术

Abstract

为了便于对人体的三维脊柱形态进行日常体表监测，本文提出一种利用“单相机，多视角”的方式构造立体视觉的脊柱形态测量方法。该方法通过移动单个相机使其从多个角度采集带有棘突标志点的人体后背图像，并基于“张正友标定法”和双目立体视觉的三角测距原理，求解出所有图像间两两对应的空间转换矩阵和标志点的三维坐标，由此推算出用于评估脊柱形态的脊柱评估角。试验结果表明，本文方法所得脊柱评估角误差在±3° 之内，结果与 X 线片测量法所得的柯布（Cobb）角相关性达 0.871。本文采用视觉检测算法，无放射性，且无需预先设定相机的拍摄位姿，操作简单。本文的研究成果可用于开发基于手机平台的智能监测系统，将适用于社区、学校、家庭等多种场合下的脊柱侧凸普查和患者的长期随访，为医生诊断病情、预测病情发展趋势、制定治疗方案提供参考。

引言

脊柱畸形是指脊柱在三个医学解剖面上偏离正常位置，其在青少年和儿童中发病率较高，会给少年儿童的脊柱健康带来损害，如果没有及时发现并进行干预治疗，病情将随着青少年生长期迅速发展，从而影响成年后的肢体外观甚至引起心肺疾病等多种并发症^[1-2]。目前，针对脊柱形态畸形的评估，在临床上主要由医生在患者的冠状面和矢状面 X 线片上绘制柯布（Cobb）角来实现^[3]。然而，X 线片测量法存在辐射暴露问题，已被证实会显著增加患者罹患恶性肿瘤的风险，不适用于长期随访检查^[4]。因此，国内外学者致力于研究非 X 线测量脊柱形态的方法，如表面形貌 (surface topography，ST) 测量法^[5]、核磁共振影像 (magnetic resonance imaging，MRI) 测量法^[6]、超声测量法^[7]等。虽然上述方法不具辐射性，但均需要较为庞大的专业设备，并需进行较为复杂的数据处理，而且同目前通用的临床方法一样，这些方法都要求患者到医院等指定地点进行脊柱形态测量，不便于家庭环境下的脊柱形态日常监测和学校大规模的普查，因此不利于对青少年脊柱畸形的早期发现以及治疗矫正过程中的随访观察。

视觉测量作为一种有效的测量手段已被广泛研究，将其应用于人体的脊柱形态测量，不仅能够避免人工测量误差、提高效率，还由于此类检测手段并无放射性从而不会增加受试者的辐射暴露风险^[8]。视觉测量系统按采用的相机数量可分为单目视觉系统和多目立体视觉系统^[9]。单目视觉系统测量时只需一个相机辅以适当的数据处理算法，具有结构简单、易于安装调试、计算量小等优点。Pan 等^[10]提出一种用于家庭环境下的基于单目视觉的脊柱评估方法，该方法使用相机采集一幅二维图像，利用该图像的边缘信息检测人体背部轮廓，将检测出的四条平滑非连续的轮廓曲线分成两组，其中一组代表腰部躯干的外轮廓曲线，另一组代表胸部和肩部躯干的外轮廓曲线，然后分别拟合出每组曲线的中心轴，用来表示脊柱形态。该方法无需人工标记，操作人员也无需具备专业的医学知识，但是由于人体背部外轮廓的中心轴和真实的脊柱形态之间存在明显差异，因此该方法的测量准确性较低。单一的二维图像因缺少深度信息，无法提供脊柱在矢状面中向前弯曲的情况，为了获得脊柱三维形态信息，Berryman 等^[11]开发了一种将结构光技术与单目视觉系统结合的新方法，所测得的临床参数精度可达 ± 1 mm，但此方法需要专用的结构光投影仪，不仅成本昂贵而且使得图像处理过程更为复杂。除了上述方法，多目立体视觉系统也可以很好地解决单目视觉系统缺少深度信息这一问题，其采用两部及以上的摄像机从不同的角度捕获空间目标，通过立体匹配算法计算出多幅图像中目标特征点对应的像素点之间的位置偏差，即可计算出空间目标的位置形状信息和深度信息。其中双目视觉系统由于存在匹配多义性问题，往往通过增加相机数目来减少错误匹配，提高测量的准确性。Zheng 等^[12]采用了三目立体视觉系统测量脊柱的三维畸形参数，利用运动平台在一系列预定义的角度下完成前屈试验，同时定义了椎间角分离（inter-vertebra angular separation，IVAS）并将其作为新的脊柱畸形评估指标，该指标与 Cobb 角之间呈强线性关系，因此具有一定的可行性和应用潜力。但是因为多目立体视觉系统拍摄目标的视场范围和测量精度受多部相机安装相对位置的制约，所以安装调试要求高，同时多相机的标定工作也极为复杂繁琐，导致多目立体视觉系统的环境适应性差，在三维脊柱形态测量领域中的应用受限^[13]。

为了简化多目立体视觉系统的结构并快速测量出脊柱的三维形态，本文基于多目立体视觉的几何原理，采用单个相机从不同角度进行拍摄的方法构建“单相机，多视角”的单目立体视觉系统。该方法首先通过移动单相机使其从多个角度采集多张图像，然后基于“张正友标定法”^[14]，以世界坐标系为基准通过处理棋盘格标定板上的角点数据实时求解相机外参数，获得每个拍摄位置的相机坐标系相对于世界坐标系之间的位姿关系，再基于双目立体视觉的三角测距原理，求解出多个拍摄位置间两两对应的空间转换矩阵，最终结合标志点的图像坐标计算出其在世界坐标系下的三维坐标值。与传统的多目立体视觉系统相比，本文所设计的测量系统只使用一台相机，且无需预先设定拍摄点，可选择任意视角进行拍摄，相机位姿在测量过程中进行动态标定，因此具有结构简单、便于移动、环境适应性好等优势，可用于社区、学校、家庭等多种场合下的脊柱侧凸普查和患者的长期随访，为医生诊断病情、预测病情发展趋势、制定治疗方案提供参考。

1. 基于视觉的脊柱形态测量

1.1. 脊柱形态测量方法的医学原理

在临床上，医生通常在 X 线片上绘制 Cobb 角来评估患者脊柱畸形的严重程度。Cobb 角测量方法如图1 左图所示，在 X 线片上找到脊柱的上、下端椎，即脊柱弯曲部分上部和下部倾斜角最大的椎体，然后在上端椎的上边缘和下端椎的下边缘各作一条延长线，这两条延长线的垂线所形成的夹角即为 Cobb 角，根据几何关系可知上述两条延长线形成的角度也是 Cobb 角。若将每个椎体用其轴线线段替代，依次连接相邻椎体轴线线段，可得到一条由多段折线近似表示的脊柱形态曲线，如图1 右图所示，找到多段折线上代表上、下端椎的轴线线段与竖直方向的夹角 和 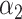，则 Cobb 角 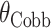可用公式 (1) 表示，具体如式（1）所示：

图 1.

Schematic of Cobb angle

Cobb 角示意图

1

由于椎体大致上左右对称，每个椎体中央位置均有棘突，两个相邻椎体的棘突间连线近似平行于椎体轴线，如图2 左图所示，因此本文用棘突间连线代替椎体的轴线，用棘突间连线构成的多段折线来表示脊柱形态。找到多段折线上代表上、下端椎的线段与竖直方向的夹角 和 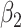，即可计算出近似 Cobb 角的脊柱评估角，如图2 右图所示，其计算公式如式 (2) 所示：

图 2.

Schematic of spine evaluation angle

脊柱评估角示意图

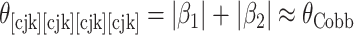2

若脊柱曲线上有多个弯曲，则选择计算出的最大脊柱评估角作为最终结果来评估脊柱形态，即只考虑主弯。

1.2. 基于“单相机，多视角”的脊柱形态测量算法原理

通过触摸人体后背皮肤可以确定棘突位置，然后在棘突处贴设标志点来标记棘突位置，最终利用相机标定技术获得标志点在世界坐标系中的坐标值。相机投影矩阵，表示的是一幅图像中标志点的像素坐标和其所对应的空间坐标之间的关系，如式 (3) 所示：

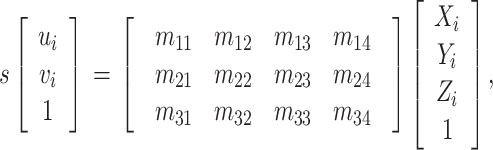3

式中，s是世界坐标系到图像坐标系的尺度因子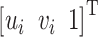； 是第i个标志的像素坐标的齐次矩阵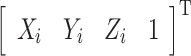； 是第i个标志的空间坐标的齐次矩阵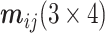； 是投影矩阵，利用“张正友标定法”确定相机的内、外参数进而可得出该投影矩阵，然后根据投影点的图像坐标即可计算出标志点的空间坐标。 的计算如式 (4) 所示：

4

式中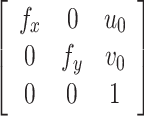， 是相机的内参数，在首次使用时通过标定获得； 为相机外参数，在每次拍摄后通过实时动态标定得到。求解公式 (3) 所得三元方程组如式 (5) 所示：

5

式中，u_i 和 v_i 分别代表第 i 个标志所处图像坐标的行数与列数，X_i、Y_i、Z_i 代表第 i 个标志所处的空间坐标值；m 代表相机参数矩阵中的元素。本文使用单相机从不同角度拍摄多幅图像，再由多幅图像求解公式 (5) 中的 ，用矩阵表示公式 (5) 的结果如式 (6) 所示：

6

式中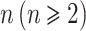， 是图像序号。其中，使用多幅图像进行计算的目的是减少由某幅具有较大误差的图像带来的影响。

1.3. 三维脊柱形态视觉测量系统的开发

为了实时获取相机外参数，参考“张正友标定法”，将世界坐标系建立在平面棋盘格上。世界坐标系如图3 所示，其原点为 O，X 轴和 Y 轴分别平行于棋盘格的两条垂直边，Z 轴垂直于棋盘平面，由于本文方法规定了棋盘格的大小和边长，所以棋盘格中角点的空间坐标也随之确定。在使用本文方法进行测量时首先需要将平面棋盘格固定在墙面上。在每次拍摄时，利用棋盘格上角点坐标信息实时求解相机拍摄时的外参数，进而利用公式 (6) 计算标志中心的空间坐标，获得标志空间坐标后即可根据公式 (2) 计算脊柱评估角。

图 3.

Schematic and flow chart of the measurement system

测量系统示意图与流程图

每次测量时，首先由脊柱科医生或经过医师培训的无临床经验的人员在受试者的棘突处贴设直径为 8 mm 的圆形标志，标记完成后让受试者面对墙面站立在棋盘格附近；然后操作人员使用单个相机从不同的角度对患者后背上的标志和墙上棋盘格进行拍摄，再将所采集图像导入程序进行处理得出测量结果。由于临床上通常利用正面 X 线片和侧面 X 线片测量 Cobb 角来评估患者冠状面和矢状面的脊柱畸形，因此为了便于后续对 X 线片测量法和本文所提方法进行比较，受试者站立时应尽量使人体冠状面与固定棋盘格的墙面保持平行，令世界坐标系的XOY平面平行于人体冠状面，YOZ平面平行于人体矢状面。

图像采集所需设备如下：① 一台相机：对相机类型没有要求，可以是家庭用数码相机或工业相机，也可以是智能手机的自带相机，相机的分辨率不低于 1280 × 720；② 6 × 8 的棋盘格一张，每个方格边长为 20 mm；③ 若干直径为 8 mm 圆形标记点。

本文测量方法有如下三个优点：① 通过简单培训即可使无临床经验的人员掌握贴设棘突标记的方法，贴设准确性可满足本试验要求；② 系统的所有设备成本低廉且容易获取，系统搭建简便快捷，大大提高了测量的便利性；③ 整个测量过程安全无辐射，不会增加受试者的辐射暴露风险，同一受试者可进行多次测量。综上所述，本方法的图像采集地点不局限于医院，测量可由经过培训的非专业人员进行，可用于日常生活中长期监测患者的脊柱形态变化。

1.4. 单相机立体视觉方法的有效性

为了验证本文所提方法的准确性和可重复性，分别进行了平面曲线测量实验和模拟人体背部测量试验。

1.4.1. 平面曲线装置实验

平面曲线实验装置如图4 所示，在平板 a 上首先贴一张坐标纸，再将一系列圆形标志贴在坐标纸上模拟表示一条脊柱曲线，由于棘突之间距离约 20～30 mm，所以将标志之间的距离也设置为 20～30 mm；然后在另一块平板 b 上粘贴棋盘格；最后将两块平板成一定倾角固定，并将平板 b 固定在墙面上。此时标志构成的离散曲线在XOY平面和YOZ平面上的投影均为一条曲线，测量出两块平板之间的角度后，即可用三角函数推导出标志点在如图4 所示的世界坐标系中的坐标，继而计算出冠状面和矢状面的实际脊柱评估角分别为 78.09° 和 14.62°。为了研究图幅数量对结果的影响，分别使用 2～8 幅图像进行七组实验，并分析比较七组实验的计算结果。每组实验中，从不同角度拍摄相应数量的图像进行 12 次重复实验来验证本文所提方法的可重复性。

图 4.

The device of plane curve

平面曲线装置

测量结果如表1 所示，误差是每个平面中实际脊柱评估角与测量值之间的差值，max(ε_xoy)和 max(ε_yoz) 代表了重复实验中XOY平面和YOZ平面计算的脊柱评估角误差的最大值，用于评价本文方法的准确性；均方差σ_xoy和σ_yoz描述了测量值的离散程度，用于衡量本文方法的可重复性。从表1 可以看出整体上ε_xoy比ε_yoz小，σ_xoy均在 1° 以内，表明XOY平面的测量数据更加准确、可重复性更好。当用于处理计算的图幅数量不少于五幅时，ε_xoy基本在 1° 之内，ε_yoz均在 2° 之内；此时σ_yoz也均在 1° 以内，表明同组实验中重复实验的重复误差结果波动较小。

表 1. Results obtained from different numbers of images.

不同数量图像计算结果

图像数量	max(εxoy)/(°)	max(εyoz)/(°)	σxoy/(°)	σyoz/(°)
2	−1.79	6.15	0.60	2.02
3	−1.83	3.13	0.67	1.31
4	−1.33	2.95	0.44	1.06
5	−0.78	1.77	0.27	0.64
6	−1.26	1.52	0.44	0.79
7	−0.94	0.95	0.31	0.59
8	−0.74	1.55	0.19	0.73

此外，为了保证每次拍摄的后背脊柱变形一致，在实际拍摄过程中需要受试者保持静止不动，然而随着拍摄图幅数量增多，其耗时也越长，受试者身体晃动的可能性越大，从而导致不同位置拍摄到的后背脊柱变形有差距，因此拍摄的图幅数量不宜过多。综合考虑，选择从五个角度拍摄图像来进行测量。

在临床上使用 X 线片测量法时，因操作者经验不同以及其对 X 线片图像解剖标志的判断差异，测量结果也会有较大差距，因此在临床诊断中 Cobb 角允许的测量误差范围为 ± 5° 以内。上述平面曲线装置实验结果表明，使用五幅图像进行图像处理与计算时，本文所用方法的测量误差不超过 ± 2°，因此本文采用的测量方法在原理上有效可行，可以为医生评估脊柱形态提供可信参考。

1.4.2. 人体模型装置实验

由于平面曲线装置与实际人体后背的复杂曲面有明显差异，因此为了更接近本文所提测量方法的实际应用场景，使用与真实人体颜色、形状和尺寸更为接近的人体模型进行皮肤表面标记实验。然而人体模型质地坚硬，无法发生变形来模拟脊柱畸形的背部形态，也无法通过触摸确定棘突位置，因此我们在人体模型后背处按照可能出现的脊柱畸形形态来贴标志，相邻标志之间的距离约 20～30 mm。将贴好标志的模型正面面对墙壁，并在墙上固定棋盘格，如图5 所示。根据 1.4.1 的实验结果，用相机从五个不同的角度拍摄同时包含模型后背和棋盘格的图片，然后将图像导入程序进行处理和计算，得到冠状面和矢状面的脊柱评估角。一共进行五组实验，每组实验中人体模型后背上由标志点构成的曲线形状各不相同，每组实验均进行 12 次，来验证本文方法的可重复性。

图 5.

Human body model experiment

人体模型实验

本文首先使用三坐标测量装置测得每组曲线中所有标志点的空间坐标，由此计算出该曲线的实际脊柱评估角度，测量三次求平均值作为最终结果，结果如表2 所示。

表 2. Actual angle of the marker curve.

标志曲线的实际角度

曲线序号	XOY平面实际角度/(°)	YOZ平面实际角度/(°)
1	31.59	40.58
2	29.91	46.15
3	39.52	37.92
4	30.15	42.70
5	31.64	43.09

使用本文方法的计算结果如表3 所示，从图中可知冠状面脊柱评估角的误差 ε_xoy 均在 ± 2° 以内，矢状面脊柱评估角的误差 ε_yoz 在 ± 2.8° 以内，综合误差不超过 ± 3°，说明本方法在近似实际情况的场景中具有较好的准确性。此外，冠状面均方差 σ_xoy 均在 0.6° 以内，矢状面均方差 σ_yoz 均在 1.4° 以内，说明本方法在近似实际情况的场景中具有较好的稳定性。

表 3. Results of the human back model experiment.

人体背部模型实验结果

曲线序号	max(εxoy)/(°)	max(εyoz)/(°)	σxoy/(°)	σyoz/(°)
1	−1.33	2.74	0.51	0.72
2	1.41	−2.32	0.49	0.94
3	−1.28	2.66	0.44	0.77
4	1.57	−2.04	0.46	1.06
5	1.60	−1.97	0.54	1.34

通过与 1.4.1 的模拟实验对比发现，人体模型实验结果稍大于平面曲线装置实验结果，这是由于人体模型实验中标志点位于复杂曲面而非光滑的平面，拍摄到的标志轮廓变得不规则，同时标志表面的阴影亮度也随之不同，因此在该环境下提取标志会产生误差，进而影响脊柱评估角的测量结果准确性。

综上所述，本文所提出的测量方法具有较好的准确性和可重复性，测量误差在允许范围内，可用于脊柱形态测量。

2. 医学试验验证

2.1. 试验方法

为了验证基于视觉的脊柱形态测量方法的可靠性，将本文方法应用于临床脊柱形态测量，对脊柱畸形患者进行试验并分析试验结果。本研究共招募了在上海长海医院脊柱外科就诊的 10 名脊柱侧凸患者（8 名女性，2 名男性）作为研究对象，所有受试者均知情并自愿参加试验。本次研究通过了第二军医大学生物医学研究伦理委员会的审查，并取得了医学伦理审查表。

对每位受试者在同一天内进行 9 次重复试验，试验的图像采集装置是 CCD 数字相机（MER-132-43U3M/C，北京大恒图像视觉有限公司，中国）。进行试验时，患者呈自然站立状态，医生首先在患者后背上通过触摸找到棘突位置并贴标志；然后让患者面对墙壁站立，提前在患者站立位置附近的墙面上固定平面棋盘格，使用相机对患者和棋盘格从不同的角度进行拍摄，拍摄图像如图6 所示。

图 6.

Scoliosis patient test

脊柱侧弯患者试验

2.2. 试验结果

2.2.1. 立体视觉法的可重复性

针对每位患者的 9 次重复试验的测量结果如表4 所示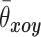， 和 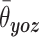分别代表每位患者在冠状面和矢状面 9 次测量脊柱评估角的平均值；σ_xoy 和σ_yoz分别代表每位患者 9 次测量脊柱评估角的冠状面均方差和矢状面均方差。其中冠状面和矢状面均方差最大值 max(σ_xoy) 和 max(σ_yoz) 分别为 2.01° 和 3.85°，证明本方法在实际应用中具有较好的稳定性，且冠状面稳定性比矢状面更好。

表 4. The mean and standard deviation of the spine evalua tion angle for all subjects.

所有受试者的脊柱评估角的平均值及均方差

患者序号	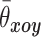/(°)	σxoy/(°)	/(°)	σyoz/(°)
1	52.38	0.46	51.67	3.85
2	41.75	2.01	57.04	2.82
3	42.75	1.57	45.59	3.45
4	23.76	0.72	24.66	2.27
5	56.82	0.90	40.84	2.84
6	38.42	0.58	37.86	1.49
7	27.15	0.45	54.63	1.62
8	29.43	1.49	32.79	0.90
9	29.91	0.32	32.22	0.69
10	34.45	0.36	44.89	0.95

2.2.2. 立体视觉法与 X 片法测量参数的比较

由于患者拍摄侧位 X 片时的身体姿态与本文试验所采用的站立姿态不同，且上海长海医院在进行矢状面测量时所采用的参数是胸椎后凸角 (thoracic kyphosis，TK)、胸腰后凸角 (thoracolumbar kyphosis，TLK) 和腰椎前凸角 (lumbar lodorsis，LL)，属于椎体前部畸形，与棘突所代表的椎体后部畸形在测量原理上差别较大，因此仅对每位患者用本文方法所测得的冠状面脊柱评估角的平均值 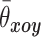和从患者正位 X 线片中测量所得的 Cobb 角进行比较，以此研究本文所提方法与 X 线片测量法之间的差异。两种方法测量的角度结果如表5 所示，数据呈现出一定的规律性，其中除了 2 号患者试验数据的差值为正值以外，其他试验的差值数据均为负，说明单目立体视觉方法测量的脊柱评估角一般比 X 线片测量法所得的 Cobb 角小，造成这一差异的主要原因可能是由于脊柱侧凸的同时会引起椎体的轴向旋转，且旋转方向一般偏向脊柱弯曲的凹侧。

表 5. Comparison of the angles obtained by two methods.

两种方法所得角度比较

患者序号	X 线片法/(°)	立体视觉法/(°)	差值/(°)
1	69.3	52.38	−16.92
2	26.6	41.75	15.15
3	44	42.75	−1.25
4	43	23.76	−19.24
5	53	48.09	−4.91
6	41.22	38.42	−2.8
7	33.17	27.15	−6.02
8	36.86	29.43	−7.43
9	42.24	29.91	−12.33
10	49.88	34.45	−15.43

脊柱侧弯按主弯所在位置可大致分为胸弯、胸腰弯、腰弯三种，根据 X 线片诊断结果所示，本试验中 8 位受试者的主弯为胸弯，4 号受试者与 7 号受试者的主弯为腰弯。所有试验中 4 号腰弯受试者的测量误差值最大，通过分析该患者的 X 片和相机拍摄的带有标志点的图像，本研究发现标志点所形成的曲线与 X 片中的脊柱中线有较大差异，由此分析针对腰弯的脊柱形态测量产生较大误差的原因可能是腰弯中脊柱弯曲处没有肋骨的支撑，更容易发生椎体轴向旋转，导致本文方法中用棘突连线表示的脊柱曲线与 X 线片测量法中用椎体所表示的脊柱曲线差异较大。

脊柱形态测量耗时也是影响日常监测便利性的一大因素，因此本研究也对比了本文试验方法与 X 线片测量法的耗时情况。本文患者试验耗时包括三个部分：① 标志点贴设耗时：标志均由脊柱科医生触诊贴设，耗时均不超过 5 min；② 图像采集耗时：单个患者图片每次采集 5 张图像，一共采集 9 组，进行 9 次重复实验，每组图像采集耗时均不超过 2 min；③ 图像处理及输出测量结果耗时：图像选择、相机外参数计算及脊柱形态角度由计算机程序依次计算输出，本文实验中 10 位受试者的程序运行时长均不超过 1 min。从布置试验场景到获得试验结果，每位患者 9 组实验的总时长均在 15～30 min 以内。上海长海医院采用临床影像分析软件 Surgimap 2.2.15.4（Nemaris Inc.，美国）测量 Cobb 角的平均时间为 (5.2 ± 0.7) min，使用传统测量方法的时间为 (8.8 ± 1.5) min^[15]，因此单就图像处理的耗时而言，本文所提出的方法耗时极少，图像采集后无需等待即可直接获得测量结果，便利性更高。

2.2.3. 立体视觉法与 X 线片测量法的相关性

在临床中胸弯是最常见的脊柱侧弯类型，为进一步评估本文方法，利用统计分析软件 IBM SPSS Statistics 25.0（IBM Inc.，美国）重点分析 7 位胸弯患者（患者序号：1、3、5、6、8、9、10）的测量结果。虽然 2 号患者的脊柱侧弯类型也为胸弯，但如 2.2.2 小节所述，由于该患者的脊柱评估角大于利用其 X 线片所测得的 Cobb 角，不符合大部分数据的变化特征，故作异常值处理，不列入此分析。本文采用配对样本t检验来分析本文方法测量的脊柱评估角和 X 线片测量法所得的 Cobb 角的相关性^[16]。由于样本数量较少，首先采用夏皮罗维尔克检验（Shapiro-Wilk test）进行正态性检验，如果实验数据服从正态分布，应有P ≥ 0.05；反之，P ≤ 0.05。7 位受试者用本文方法与 X 线片测量法所得角度的 Shapiro-Wilk 检验结果分别为 0.555 和 0.151，均大于 0.05，服从正态分布，因此两组样本均满足配对样本t检验的条件。将两种方法所得测量结果作为配对样本数据进行配对样本t检验，置信区间设置为 95%，结果如表6 所示，相关系数为 0.818 且相关系数检验的P < 0.05，可知两种方法所测得的角度之间强相关；配对样本 t检验结果的双尾概率P < 0.05，表明两种方法测得的角度平均值的差异具有统计学意义。

表 6. The results of paired sample correlation and t test .

配对样本相关性及 t 检验结果

配对样本	样本数	相关性	相关系数检验的概率P值	平均值差值	标准偏差差值	t	Sig.（双尾）
X 线片测量角度&视觉测量角度	7	0.818	0.025	8.724	6.223	3.709	0.010

3. 结论

由模拟实验和患者试验结果可以看出，本文所提方法具有较好的重复性和稳定性。模拟人体实验结果表明本文方法在原理上是可行的，且具有较好的测量精度，测量误差均在 ± 3° 以内；患者试验中得到的脊柱评估角与 X 线片测量所得的 Cobb 角的相关性达 0.818，表明本文所提出的单目立体视觉方法可用于脊柱形态测量，所测得的脊柱评估角能够用于衡量脊柱畸形的严重程度。由于此方法无放射性、不会增加受试者的辐射暴露风险，因此可以供脊柱侧凸患者长期使用来监测病情是否发展，同时为医生制定治疗方案提供一定参考。此外，由于本文的测量系统结构简单、设备成本低，而且非专业人员经由简单的培训即可完成棘突标记，无需医生指导也可以进行测量，因此本文方法可适用于家庭环境下的日常监测。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金资助项目（31870985）；上海市自然科学基金资助项目（16ZR1449100）