Abstract
Two fundamental difficulties when learning novel categories are deciding 1) what information is relevant, and 2) when to use that information. To overcome these difficulties, humans continuously make choices about which dimensions of information to selectively attend to, and monitor their relevance to the current goal. Although previous theories have specified how observers learn to attend to relevant dimensions over time, those theories have largely remained silent about how attention should be allocated on a within-trial basis, which dimensions of information should be sampled, and how the temporal ordering of information sampling influences learning. Here, we use the Adaptive Attention Representation Model (AARM) to demonstrate that a common set of mechanisms can be used to specify: 1) how the distribution of attention is updated between trials over the course of learning; and 2) how attention dynamically shifts among dimensions within-trial. We validate our proposed set of mechanisms by comparing AARM’s predictions to observed behavior across four case studies, which collectively encompass different theoretical aspects of selective attention. We use both eye-tracking and choice response data to provide a stringent test of how attention and decision processes dynamically interact during category learning. Specifically, how does attention to selected stimulus dimensions gives rise to decision dynamics, and in turn, how do decision dynamics influence our continuous choices about which dimensions to attend to via gaze fixations?
Keywords: categorization, learning, decision dynamics, eye tracking
Introduction
When asked to describe an object, we instinctively do so in terms of its components, or dimensions. To describe a jacket, we might note dimensions like its color or size, where its pockets are placed, or any insignia it has. When assigning objects to different categories, certain dimensions are often more relevant than others depending on the demands of the task. Distinguishing between spring and winter jackets, for example, might require us to specifically note dimensions like material, thickness, and types of closures, whereas distinguishing between formal and casual jackets might depend on dimensions like length and style.
How do we figure out which dimensions are relevant to a particular task, and how do we use that information to categorize new items? Theoretical accounts of category learning have suggested that over the course of experience with many items, humans gradually build up associations between features (i.e. “linen” and “wool” could be considered to be features of the “material” dimension) and the available category labels (i.e. spring and winter jackets). As more pairings between stimuli and category labels are presented, the observer learns that a subset of dimensions are particularly relevant for identifying category membership among all sources of information that are available.
Several models have described learning as a process of selectively attending to the most category-diagnostic dimensions to support an increase in accuracy across trials (e.g. Kruschke, 1992; Love, Medin, & Gureckis, 2004; R. Nosofsky, 1986). Although attention is often described as a latent mechanism, the general mode of learning via selective attention has garnered theoretical support from eye-tracking work. Results consistently show an increase in the proportions of fixations to task-relevant dimensions, which co-occur with increasing categorization accuracy (McColeman et al., 2014; Rehder & Hoffman, 2005a, 2005b). Despite these findings, the impact of learning on subsequent, generalized behaviors of information sampling and decision-making has remained under-explored. In other words, how does the knowledge we acquire through learning, such as memories of previous items and the task-relevance of individual dimensions, impact the manner in which we seek out information about new stimuli?
As suggested by Rehder and Hoffman (2005a, 2005b), one might reasonably assume that dimensions are fixated during each trial in proportion to their respective attention weights. Intriguing experimental work by Blair and colleagues (Blair, Watson, Walshe, & Maj, 2009; Chen, Meier, Blair, Watson, & Wood, 2013; McColeman et al., 2014; Meier & Blair, 2013), however, has indicated that there might be more to the story. In the paradigm illustrated in Figure 1A, stimuli were constructed using a hierarchical category structure where one superordinate dimension (i.e. rotation of the green square) indicated which of two subordinate dimensions was relevant to each trial (i.e. rotation of the orange triangle or the purple cross). While fixations were evenly distributed across dimensions early in the task, participants soon learned to consistently orient to the superordinate dimension as each new trial was presented (Figure 1B–C). Importantly, participants subsequently fixated to one subordinate dimension and ignored the other, depending on the feature identity of the superordinate dimension. In other words, participants tended to only fixate to the two dimensions that were relevant to each trial before making a response, despite all dimensions being equally predictive of category membership on average. These results indicate that humans not only prioritize the most relevant dimensions to make accurate categorization decisions, but also make ongoing decisions within-trial about which sources of information to sample next and when to terminate the sampling process with a response.
Figure 1. Within- and Between-trial Dynamics.
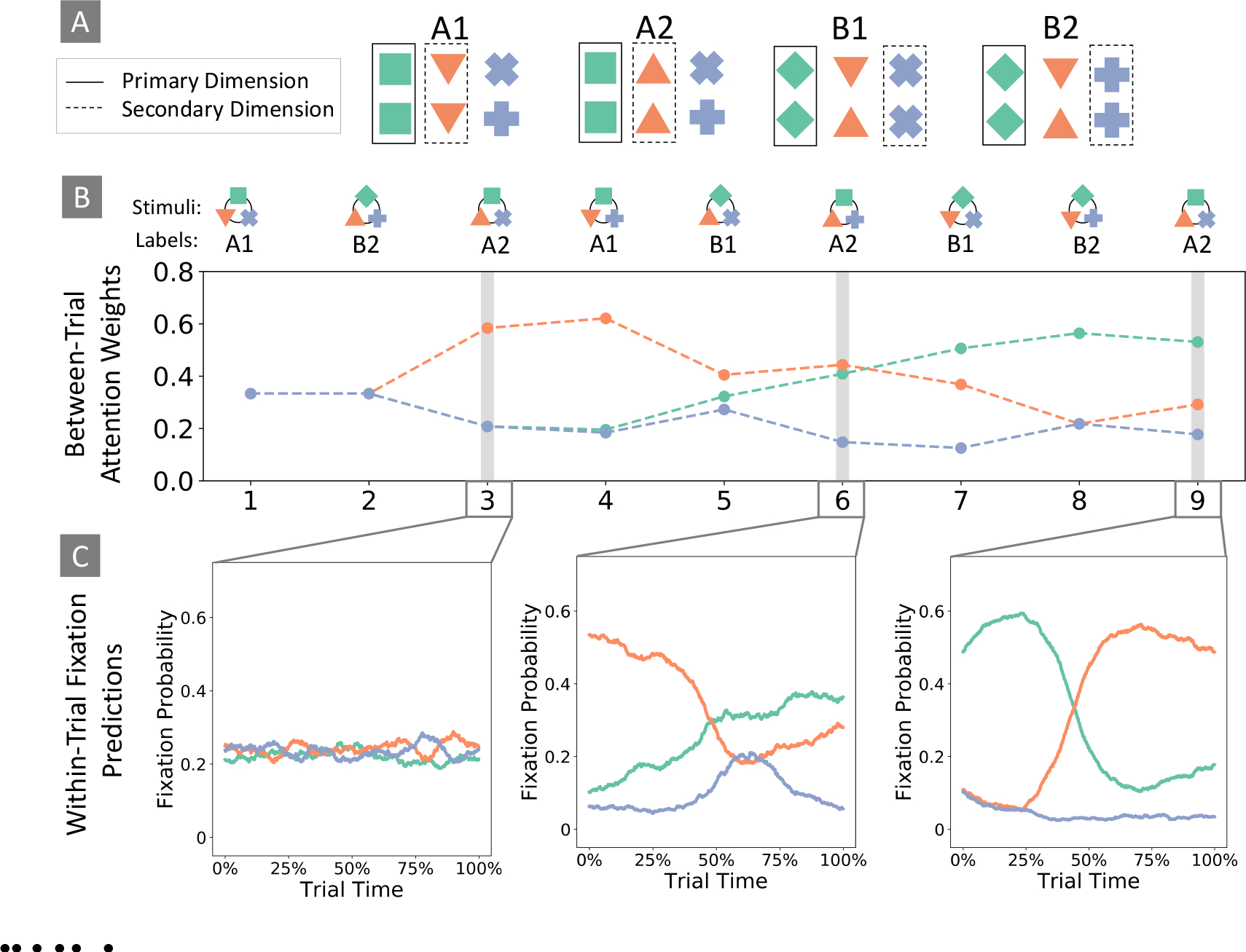
(A) Illustration of a hierarchical stimulus structure. Feature values (i.e. 0° or 45° rotation) in the superordinate dimension (green squares) indicated which of the two subordinate dimensions (orange triangles or purple crosses) were relevant for identifying category membership. (B) Attention weights generated by AARM’s between-trial module, given the sequence of stimuli shown in the top row. Weights were normalized for illustration. Line colors correspond to the colors of the stimulus dimensions. (C) 100 sequences of dimension fixations were generated using the within-trial module. Plots show mean fixation probabilities to each dimension as a function of the percentage of time within-trial, between stimulus onset and self-termination. Within-trial attention weights were initialized according to the outputs of the between-trial module for the relevant stimulus.
The goal of the current article is to establish a common set of mechanisms for allocating attention to relevant dimensions between-trials over the course of learning, and sampling sources of information within-trials over the course of individual decisions. We focus on the Adaptive Attention Representation Model (AARM), which was described and validated using data from five benchmark category learning paradigms in our previous work (Galdo, Weichart, Sloutsky, & Turner, 2021). AARM inherits its conceptual basis from context theory, which suggests that the feature and category information associated with previously-experienced items are stored in memory as discrete episodic traces (Medin & Schaffer, 1978). As a dynamic extension to the Generalized Context Model (GCM; R. Nosofsky, 1986), AARM describes how category representations are formed according to the similarity between new stimuli and stored exemplars, and are influenced by attention. The amount of attention allocated to each dimension is updated according to trial-level feedback, in a manner that is intended to optimize future responses with respect to the learner’s goals.
One major innovation of AARM is that it can be fit to both choice and eye-tracking data simultaneously, such that model-generated attention weights are informed by observed proportions of fixations to each dimension. With these constraints in place, Galdo et al. (2021) demonstrated that AARM could predict increasing proportions of fixations to task-relevant dimensions that co-occurred with increasing accuracy across paradigms of varying complexity (e.g. McColeman et al., 2014; Shepard, Hovland, & Jenkins, 1961). Like similar adaptive attention models of category learning (ALCOVE: Kruschke, 1992; SUSTAIN: Love et al., 2004), however, trial-level attention updates in AARM occur only after feedback has been observed. While attention weights on Trial may covary with proportions of fixations on Trial on average, the standard model lacks the specificity required to predict stimulus-dependent effects of information sampling like those observed by Blair et al. (2009). Here, we therefore extend the mechanisms of AARM that were presented by Galdo et al. (2021) to explain how humans use the knowledge acquired through experience to construct a representation of a new stimulus.
As illustrated in Figure 3, the current work presents the AARM framework as two interrelated modules: 1) a between-trial module to account for feedback-mediated changes in accuracy and attention; and 2) a within-trial module to account for information sampling and decision dynamics. Using insights from accumulation-to-bound decision models (e.g. Ratcliff, 1978) and theoretical notions of pattern completion (Estes, 1994), the within-trial module of AARM makes predictions about how participants use principles of attention to decide which dimensions of information to sample (i.e. via fixations), when to sample them, and when to make a response. Taking both modules of AARM together, the current article provides a comprehensive theoretical and computational framework for explaining how knowledge acquisition is fundamentally shaped by the experiences of the learner. Before introducing the mathematical details of AARM, we will first introduce four assumptions that are central to our approach.
Figure 3. Within- and Between-trial Modules of AARM.

(A) Between-trial updates to the category representation occur via influences of attention and decision components from the previous trial, in the context of feedback. (B) Within-trial updates require dynamic interactions among representation, attention, and decision components. First, the representation guides attention to a relevant dimension (1). Attention drives an encoding process for a fixated feature (2) to then update the amount of evidence (3) for each of a set of category responses. The representation is consulted (4) to guide subsequent attentional deployment.
Attention is the Mechanism of Learning
Categorization tasks provide a unique opportunity to study the relationship between learning and attention. From work with animals (Hall, 1991; Le Pelley, 2004) and humans (Bonardi, Graham, Hall, & Mitchell, 2005; Kruschke, 1996) demonstrating that learned dimension reliability influences how future stimuli are represented, we gain insight into how attention changes over the course of a task. In a standard type of categorization paradigm, stimuli are designed from a common set of dimensions, each of which can take on one of a unique set of possible feature values. In experiments conducted by Kruschke (1996), for example, stimuli were line drawings of box cars consisting of three dimensions, each of which could take on two possible features: height (tall or short), door position (left or right), and wheel color (black or white). Participants were asked to assign stimuli to arbitrary categories (e.g. categories ‘A’ and ‘B’) without receiving explicit instructions about how each category was defined. Instead, participants learned the experimentally-defined feature-to-category mapping through trial-and-error with corrective feedback, and learning was assessed through changes in accuracy over multiple trials.
For the sake of illustration, consider an example in which tall box cars belong to category A, and short box cars belong to category B. Assuming features are counterbalanced across dimensions, the only way a participant can achieve perfect accuracy is by categorizing stimuli according to the “height” dimension. Although a participant can categorize stimuli on the basis of another dimension like wheel color and be correct on a subset of trials by chance, humans do indeed achieve ceiling-level accuracy in these types of tasks when given sufficient training. In addition to simple “component” mappings (e.g. tall box cars belong to category A; short box cars belong to category B) humans can learn more complex “compound” mappings as well (XOR categories; e.g. short, black-wheeled and tall, white-wheeled box cars belong to category A; tall, black-wheeled and short, white-wheeled box cars belong to category B; Shepard et al., 1961). In general, findings across category learning studies have indicated that human learners 1) gradually acquire knowledge about which dimensions are relevant to the task; and 2) make categorization decisions according to which dimensions are perceived to be most relevant (see Ashby & Maddox, 2005; Markman & Ross, 2003, for review).
Category learning models often explain learning as a gradual shift in how stimuli are represented in psychological space. The influential GCM and its offspring have described successful categorization as a process of “stretching” multidimensional stimulus representations along relevant dimensions and “shrinking” them along irrelevant dimensions (Kruschke, 1992; Lamberts, 2000; R. Nosofsky, 1986; R. Nosofsky & Palmeri, 1997). As such, stimuli that differ along the relevant dimensions will be perceived as being more dissimilar to one another (i.e. belonging to different categories) than items that differ along the irrelevant dimensions. This manipulation of the psychological object representation comprises the definition of attention among many category learning models, such that allocating attention to a particular dimension distorts the representation across trials accordingly.
In GCM, categorization decisions are based on the perceived similarity between a stimulus probe and memory traces for exemplars with known category labels. The typical use of GCM in explaining attentional phenomena, however, has been to freely estimate attention weights independently across different blocks of an experiment. The model suggests that attention is distributed in a way that maximizes differences between categories and minimizes differences within categories, but does not specify a mechanism through which learning occurs. Instead, attention is allocated based on the properties of the category structure, and learning is retrospectively inferred. In the current article, we use intuitions from GCM to outline specific hypotheses about how learning and attention interact, suggesting that attention itself is the mechanism for learning.
The between-trial module of AARM uses gradient-based mechanisms to update attention upon observation of category feedback. Because the attention vector weights the influence of plausible feature-to-category mappings when the observer assigns an item to a category, gradient-based updating serves to reallocate attention on every trial in a manner that reduces the likelihood of future errors. As mentioned in the Introduction, our previous work demonstrated that AARM’s combination of iterative exemplar storage and attention updating were sufficient for predicting learning-related behaviors across paradigms of varying difficulty (Galdo et al., 2021; Shepard et al., 1961). Here, we additionally describe attention as the mechanism by which information is sampled from individual stimuli, such that fixations at each within-trial timestep are calculated directly from the model’s latent distribution of attention.
AARM’s specification of attention as the mechanism for learning departs conceptually from alternative rule-based classification and Bayesian updating accounts. Rule-based classification models seek to identify the boundary between categories, such that the category label can be determined through a conditional relation or weighted combination of feature values within the current stimulus (Goldberg & Jerrum, 1995; Vapnik, 1998). By contrast, the Bayesian approach is to construct an internal model of each category through iterative belief-updating, and assume that a latent category variable is responsible for generating a distribution of feature values (J. Anderson, 1991a; Oaksford & Chater, 1998; Tenenbaum & Griffiths, 2001). The Sampling Emergent Attention model (SEA; Braunlich & Love, 2021) combines intuitions from rule-based and Bayesian learning accounts to account for both information sampling and learning behaviors in the context of categorization problems. Like AARM, SEA consists of two interrelated parts: 1) a concept-learning component, which sorts stimuli into clusters (i.e. J. Anderson, 1991a) and determines the probability that a new item belongs to each one; and 2) a utility-sensitive sampling component, which performs preposterior analysis to balance the expected information gain of each dimension against a prespecified cost of additional sampling.
Because SEA provides a similarly comprehensive account of within-trial dynamics, we will refer to it throughout the introductory sections to provide theoretical contrast. In particular, we describe SEA as comprising a “rational” alternative to AARM’s “mechanistic” approach. As described by Sakamoto, Jones, and Love (2008), rational theories assume that humans learn to behave optimally within the constraints of the environment. Mechanistic theories, by contrast, aim to predict behavior by defining how information is processed and represented in the brain. For example, parameters representing costs in SEA are primarily used to instantiate different goals (e.g. responding accurately vs. responding quickly), but also comprise the time and effort involved in the perceptual encoding and processing of a stimulus feature. As such, if the observer elects to sample information from a dimension as a result of preposterior analysis, the relevant feature value is automatically used to update the observer’s state of belief about the identity of the stimulus. Feature encoding in SEA is therefore considered to be rational because it uses all known information about the task environment to select the action that will maximize gain and minimize loss: sample information, or make a choice. AARM’s within-trial module instead samples information from the dimension with the largest attention weight at each timestep. Attention weights are updated continuously throughout the trial, relative to an evolving working representation of the stimulus. Using familiar terms from the visual search literature (see Itti & Koch, 2001, for review), overt attention (i.e. describing the movement of the eyes) in AARM is explicitly linked to endogenous covert attention (i.e. reflecting latent, goal-directed processing). Encoding a feature value occurs as a function of the cumulative covert attention that is applied to an overtly attended spatial location. We consider feature encoding in AARM to be mechanistic by Sakamoto et al.’s definition because it occurs as a direct consequence of latent theoretical subprocesses. Whereas rational approaches are often considered to have an advantage of precision in terms of the predicted behavior and justification (J. Anderson, 1991b), mechanistic models are more appropriate for generating novel predictions and understanding nuanced behaviors (Sakamoto et al., 2008). Given the relative merits of each, we use this distinction to highlight how AARM’s mechanisms give rise to detailed predictions in various novel contexts.
Attention is Not a Zero-sum Game
Since seminal work by Sutherland and Mackintosh (1971), attention has often been understood as a fixed-quantity resource that observers use until its limit is reached. The authors presented the inverse hypothesis of animal learning, which described stimulus dimensions in terms of attention units that were modulated by reinforcement (e.g., food reward for correct category discrimination; Mackintosh & Little, 1969). Importantly, the theory imposed the constraint that attention activation across all dimensions must sum to a constant value, such that increasing the strength of one unit will decrease the strength of the others. Follow-up empirical and theoretical work by Mackintosh (1975), however, rejected the inverse hypothesis in light of evidence that attending to one dimension did not prevent learning of a second dimension in complex stimuli. Nevertheless, the convention of treating attention as a “zero-sum game” persists across many contemporary category learning models, such that attention weights across dimensions are constrained to sum to a constant of one (chosen arbitrarily by, for example, GCM). Similar intuitions about attention being represented as a constant sum have appeared in perceptual work as well; for example, the assumption that attending to a target stimulus in an array requires equivalent inhibition of distractors (White, Ratcliff, & Starns, 2011).
While we do not contest that attentional capacity limitations exist (i.e. as demonstrated in: Brydges et al., 2012; Janssens, De Loof, Boehler, Pourtois, & Verguts, 2018; Muller & von Muhlenen, 2000; Muller, von Muhlenen, & Geyer, 2007), there is little empirical evidence to suggest that the reserve of attention remains fixed across trials and tasks such that a sum-to-constant constraint is justified. Instead, an expansive literature has shown that task difficulty, perceptual load, and parallel processing affect the extent to which the capacity of the attention system becomes a limiting factor (see Chun, Golomb, & Turk-Browne, 2011, for review). For example, Lavie and colleagues (Lavie, 1995; Lavie & Cox, 1997; Lavie & Tsal, 1994) have shown that both relevant and irrelevant items are processed in visual search tasks when perceptual load is low, and inhibition of task-irrelevant items only occurs when perceptual load is sufficiently high. The sum-to-constant constraint, however, implies that the capacity limit is reached across tasks, regardless of difficulty.
Other studies have noted fluctuations in attention related to the stimuli themselves, including perceptual and emotional salience (Theeuwes, 1992, 2010), novelty (Johnston & Schwarting, 1997), and motion (B. Anderson, Laurent, & Yantis, 2011; Yantis & Egeth, 1999). For example, visual search work showed that the presence of high-salience, task-irrelevant cues significantly impaired subsequent overt attention to task-relevant targets relative to low-salience cues (Baker, Kim, & Hoffman, 2021; Most, Chun, Widders, & Zald, 2005). One interpretation of the results is that a greater quantity of covert attention continued to be allocated to the high-salience cues despite being removed from the screen before the target even appeared. Considering findings of flexible attention together, it is potentially overly constraining to assume that all attention is known and is entirely allocated to the stimuli intended by a given experimental manipulation, as would be required for inhibition to occur in the presence of a sum-to-constant constraint.
In line with connectionist models such as ALCOVE (Kruschke, 1992) and SUSTAIN (Love et al., 2004) which will be reviewed in detail below, AARM does not adhere to a sum-to-one constraint. Instead, attention to each dimension can fluctuate within- and between-trials depending on a learned history of predictive reliability, and the sum reserve of available attention is unconstrained. In previous work, Galdo et al. (2021) used model-fitting and comparison methods to evaluate various forms of attentional constraints during category learning. In addition to the standard sum-to-constant constraint, the authors implemented the following within AARM’s basic between-trial structure: 1) a norm-to-constant constraint, which allows for different forms of competition between dimensions in addition to the assumption of fixed-quantity attention (e.g. EXIT; Kruschke, 2001; Paskewitz & Jones, 2020); 2) LASSO regularization, which limits the number of dimensions that can be attended within a trial (Park & Casella, 2008); and 3) Ridge regularization, which imposes an upper bound on attention to individual dimensions (Busemeyer & Townsend, 1993). The results provided evidence against fixed-quantity attention constraints across five studies, with the model variant containing LASSO regularization and between-dimension competition performing the best overall. These results are considered to be consistent with findings from other empirical and modeling work, which similarly demonstrated that humans prefer to form representations based on a subset of the available dimensions (Lee, 2001; Shepard & Arabie, 1979; Sloutsky, 2003; Tversky, 1977; Ullman, Vidal-Naquet, & Sali, 2002). Galdo et al. (2021) therefore concluded that humans demonstrate a bias toward parsimonious solutions during learning, but nevertheless maintain some ability to flexibly allocate attention in order to improve performance.
We designed the within-trial module of AARM with these results in mind. While it is reasonable that capacity limitations or other factors could manifest in reduced sampling after training, the between-trial module is insufficient for explaining how humans decide when to terminate the information sampling process and commit to a choice during individual trials. The within-trial module predicts self-termination through a combination of stochastic feature imputation and thresholded evidence accumulation. In the decision-making literature, accumulation-to-bound models specify mechanisms through which an observer samples information from a stimulus through time, and a response is made when evidence in favor of a particular choice exceeds a prespecified threshold. Unlike standard implementations (Brown & Heathcote, 2008; Ratcliff, 1978; Usher & McClelland, 2001) or extensions to multi-attribute choice (Busemeyer & Townsend, 1993; Krajbich, Armel, & Rangel, 2010; Trueblood, Brown, & Heathcote, 2014), however, AARM makes no assumption that moment-to-moment samples of information are independent, but rather are integrated with information from other dimensions to activate memories of exemplars and contribute evidence toward a category response. To determine which sources of information to sample, AARM first forms expectations about which features might occur in each dimension (based on past exemplars), and randomly draws potential feature values into a working representation of the stimulus. The observer then orients to dimensions that provide additional evidence in favor of the leading category option at each timestep, and updates the working representation as features are encoded. This “confirmatory search” behavior naturally arises from the within-trial module’s gradient-based mechanisms for updating attention, as will be discussed in the Attention as an Optimization Problem section below. For now, it is sufficient to establish that AARM continuously reorients attention to encode stimulus features into its working representation, and self-terminates when it samples enough information to surpass a decision threshold.
Although SEA’s calculations are driven by predicted utility rather than a theoretical measure of attention, it is worth noting that SEA does not impose explicit constraints on its estimates of utility. The model instead implements parsimonious resource expenditure by 1) comparing the predicted utility of sampling a dimension to an expected cost; and 2) limiting the depth of forward search when predicting utility (i.e. what Braunlich and Love (2021) refer to as a “mypoic” rather than full preposterior analysis). Through ongoing utility calculations, SEA predicts self-termination when the potential gain of sampling any dimension no longer exceeds the potential cost of time and energy. Although this strategy is relatively efficient for low-dimensional stimuli, preposterior analysis requires the observer to determine the likelihood and category association of every possible combination of feature values across dimensions. This quickly incurs high computational cost as more dimensions are added, even when using the myopic strategy of only making predictions one step into the future. Although this forward computing is necessary to fulfill SEA’s intended purpose of identifying optimal sampling trajectories, AARM’s approach incorporates human-like biases in the interest of approximating observed behavior. Its approach is therefore readily extendable to tasks involving higher-dimensional stimuli, given that expected feature values are spontaneously retrieved from memory rather than being exhaustively considered.
In this way, AARM is similar to extensions to GCM that allow for sequential acquisition and retrieval of information. In the extended generalized context model (EGCM-RT Lamberts, 2000), stimulus dimensions are sampled sequentially to facilitate a gradual formation of a category representation through time. Similarly, the Exemplar-based Random Walk model (EBRW; R. Nosofsky & Palmeri, 1997) samples exemplars from memory and makes a decision when evidence surpasses a threshold. Unlike AARM, however, neither EGCM-RT nor EBRW have mechanisms for prioritizing dimensions according to task-relevance, strategically reorienting to additional dimensions within-trial, or self-terminating the sampling process. Instead, both models sample and encode all available stimulus information before making a choice. Relative to these examples, only AARM and SEA can account for these effects, all of which were observed in the studies of Blair et al. (2009).
Attention as an Optimization Problem
Alhough GCM made a major theoretical contribution by relating attention to learning, an open question remained as to how attention would change as learning occurred. After a few early attempts to solve this problem (Estes, 1986; Gluck & Bower, 1988), perhaps the most complete theoretical description was provided by ALCOVE (Kruschke, 1992). ALCOVE combines exemplar-like representations used by GCM with an adaptive reinforcement policy engineered by a connectionist architecture. The model consists of three layers, connected by intervening sets of weights: an input layer contains the stimulus features, a hidden layer contains a set of exemplars, and an output layer contains the model’s representation of a response probability. The set of weights that connect the latter two layers are referred to as “attention,” given that they fulfill a similar purpose to the attention weights in GCM. As in the typical connectionist approach, back propagation is used to alter both sets of weights after each new experience by minimizing a loss function that compares the response probability output from the model to a vector representing the true category label (e.g., provided by feedback). Over time, adjustments to the attention weights minimize the total number of categorization errors. This updating process can be thought of as a first-order optimization process, solved by gradient descent. The intuition of the problem solved by ALCOVE is that attention weights should move to a location in the abstract, multidimensional attention space that minimizes the squared loss function over time. Later, a similar procedure was assumed by SUSTAIN (Love et al., 2004).
Although ALCOVE has many similarities to GCM, a major departure is that it does not allow for explicit storage of new episodic events as they are experienced. Instead, ALCOVE presupposes that a set of basis exemplars are specified prior to learning, and the connection weights between experienced events and these basis exemplars are adjusted through time. As clarified by Turner (2019), most learning models take one of two forms: an “instance” representation, or a “strength” representation. The former consists of a class of models that assume that each new experience is captured in episodic memory, creating an “instance” of the event (Estes, 1994; Logan, 1988, 2002; Medin & Schaffer, 1978; R. Nosofsky, 1986). The latter consists of a class of models that simply adjusts a set of weights according to a rule, leaving no permanent storage of those events for future retrieval (D. Cohen, Dunbar, & McClelland, 1990; Rumelhart & McClelland, 1988). By this definition, ALCOVE is a strength-based model because it learns by modifying its weight structures over time.
When making efforts to distinguish between these two classes of theories, one pervasive problem is the confound between attention and representation. Specifically, encoded information affects the representation of the feature-to-category map, and this representation can subsequently drive the deployment of selective attention. In this way, an introspective learner may wonder during a task “Am I attending this dimension because I have learned that it is relevant, or is this dimension only relevant because I have attended to it before?” Assuming prototypical structure, strength-based models incur major theoretical limitations due to their lack of an explicit encoding structure for experienced events.
Recent research has begun to elucidate the interactions between the information that is stored, and the search for subsequent information. For example, Rich and Gureckis (2018) have shown that when only a subset of information is attended, subjects can fall into “learning traps” by inappropriately generalizing information to unattended dimensions. In other work, Turner et al. (2021) have shown that selective attention can cause subjects to falsely believe that one dimension is more relevant than it actually is, which can potentially eliminate a learner’s willingness to explore new dimensions of information. These results suggested that increasingly-selective deployment of attention across trials could be explained by the individual-specific history of encoded features and their learned relevance. The notion that attention orients based on an individual’s “selection history” has become a popular way of thinking about how selective attention should be deployed in response to one’s knowledge and one’s goals (Awh, Vogel, & Oh, 2006). If we apply such logic in the context of category learning, there clearly becomes a need to specify which experiences enter into an observer’s representation when determining how attention should orient.
To this end, AARM’s within-trial module enables confirmatory information search, which is well-documented in human learning (Lefebvre, Summerfield, & Bogacz, 2022; Nickerson, 1998; Talluri, Urai, Tsetsos, Usher, & Donner, 2018). Using similar mechanisms to ALCOVE, AARM’s between-trial module updates attention on each trial with respect to the correct category label, as provided by feedback. To extend the same mechanisms to account for sampling and decision dynamics, within-trial attention is first initialized with weights inherited from the previous trial. Attention is then updated at each timestep with respect to the category label that currently has the most evidence, given that the true category label is not known until after within-trial processes terminate in a response. As such, the observer reorients to dimensions that are expected to provide additional evidence for the category that is believed to be correct, given the current state of knowledge about the stimulus and previous exemplars.
By contrast, SEA specifies unbiased information search via preposterior analysis. The observer elects to sample dimensions that are expected to serve the overall goal (i.e. increase the probability of making a correct category response) in excess of the potential cost. Broader sampling beyond the relevant dimensions is made possible in the model by adjustment of an exploration parameter. The distinction between confirmatory and unbiased information search exemplifies the differences between AARM and SEA and their respective purposes. For example, developmental work has shown that while adults tend to categorize new items according to a perfectly-reliable dimension, children often make decisions in consideration of multiple dimensions with less regard for overall reliability (Blanco & Sloutsky, 2019; Deng & Sloutsky, 2015). While AARM can be used to identify which cognitive mechanisms potentially account for observed group-level differences in behavior, SEA can be used to assess the efficiency of the two strategies relative to rational predictions for behavior. Although confirmatory search in AARM provides a natural extension to between-trial mechanisms related error-minimization to account for the unsupervised aspects of within-trial dynamics, this notable departure from optimal sampling may have limitations beyond the context of category learning. These potential limitations and directions for future investigation on its relevance to human behavior are addressed in the General Discussion.
ALCOVE, SUSTAIN, AARM, and SEA all fundamentally specify learning as an optimization problem with respect to the observer’s goals, but use different mechanisms to solve it. Given that the models make very clear predictions for how dimensions of information are attended over time in order to predict learning (Braunlich & Love, 2021; Galdo et al., 2021; Kruschke, 1992; Love et al., 2004; Mack, Love, & Preston, 2016; Mack, Preston, & Love, 2013), constraining and adjucating between their respective theoretical assumptions potentially requires insights beyond what behavioral data alone can provide.
The Necessity of Eye-tracking Data
A central theme of this article is to use measures of gaze fixation as a guide for developing a model of category learning that considers both between- and within-trial dynamics. We are certainly not the first to use eye tracking data to shed light on theories of category learning (see Lai et al., 2013, for review). To investigate the connection between latent and observable correlates of attention, Rehder and Hoffman (2005a) collected eye tracking data while participants completed category learning tasks with different levels of complexity (Shepard et al., 1961). The authors demonstrated that eye tracking data can distinguish among alternative model-based assumptions about how attention is allocated at the beginning of the task as opposed to the end after learning has occurred. ALCOVE (Kruschke, 1992), for example, predicts that observers initially distribute attention evenly across all dimensions before identifying which dimensions are most relevant. An alternative theory outlined by the rule-plus-exception model (RULEX R. Nosofsky, Palmeri, & McKinley, 1994) assumes that observers implicitly form and test hypotheses during learning, and therefore predicts that observers would initially attend to a single dimension until its relevance could be sufficiently ascertained. It is important to note that these divergent assumptions could not have been examined with a measure as coarse as trial-level accuracy. One reason is that the distinction between pre- and post-learning was essential to the question of interest. Given that only the first trial contains information about attention in the absence of learning, using accuracy as the outcome measure would require conclusions to be heavily based on what is effectively a single data point. A second reason is that observers could use either an ALCOVE-like strategy of distributing attention evenly across dimensions, or a RULEX-like strategy of fixating on one dimension at random, and the predicted accuracy would be approximately equivalent on average. With eye-tracking data, however, Rehder and Hoffman identified fixation probabilities that were consistent with ALCOVE rather than RULEX: when considered in aggregate, participants fixated to all dimensions with approximately equal probability at the beginning of the task and attended only to the most relevant dimensions toward the end.
While the results of Rehder and Hoffman (2005a) relied on trial-level fixation probabilities, additional evidence suggests that gaze fixation data can be used as a continuous measure of within-trial attention as well (Blair et al., 2009; Chen et al., 2013; Krajbich et al., 2010; Krajbich & Rangel, 2011; Rehder & Hoffman, 2005a; S. Smith & Krajbich, 2019a, 2019b; Thomas, Molter, Krajbich, Heekeren, & Mohr, 2019). In work by Blair et al. (2009), gaze fixation data was recorded while participants completed a category learning task with hierarchically-organized stimulus dimensions (see Figure 1). As described in the Introduction of the current article, the feature value in one superordinate dimension indicated which of two subordinate dimensions would be relevant for determining the category label for each stimulus.
If one were to fit a model like ALCOVE, SUSTAIN, or AARM’s between-trial module to data from an experiment like this (see Palmeri, 1999, for an application of ALCOVE), we should expect the superordinate dimension to be preferentially weighted because it is relevant across all trials. The two subordinate dimensions would be weighted equally, but would receive lower weights than the superordinate dimension because they are each only relevant to 50% of trials (Figure 1B). If one were to predict proportions of gaze fixations directly from these attention weights, one might expect a high probability of fixating to the superordinate dimension, and lower, but equal, probabilities of fixating to the two subordinate dimensions. In reality, Blair et al. (2009) noted distinct stimulus effects on the trajectory of within-trial fixations, such that participants conditionally fixated to only one subordinate dimension per trial after observing the feature identity of the superordinate dimension (see Chen et al., 2013; McColeman et al., 2014; Meier & Blair, 2013, for replication). The results suggest that in addition to using learned information about dimension relevance to sample information, humans additionally prioritize dimensions dynamically within a trial in response to the stimulus itself. Although Braunlich and Love (2021) demonstrated that SEA could predict a reduction in the number of dimensions sampled within-trial across learning instances, the computationally-parsimonious “myopic” variant of SEA does not predict the ordering effects observed by Blair et al. (2009). Given that SEA considers all dimensions to have equal utility on average, it does not produce preferential orienting behaviors that are consistent with the hierarchical structure of the task. As we will show in Case Study 2, however, AARM’s within-trial module can produce stimulus-dependent information prioritization effects through its combination of attention-mediated orientation and confirmatory information search.
In light of empirical and theoretical work indicating that the hierarchical organization of information is ubiquitous in human learning (e.g. Barto & Mahadevan, 2003; Botvinick, 2012; Botvinick, Niv, & Barto, 2009), we suggest that the within-trial attention effects that emerge from hierarchical category structures can potentially make a more general statement about how humans sample information from naturalistic environments. For example, contextual features of the environment may serve as a set of superordinate dimensions for deciding which sources of information to attend when making judgements about new examples of recognizable objects that people encounter in everyday life. We therefore place particular emphasis on hierarchical category structures in the present article, given the distinct patterns of within-trial fixations observed by Blair et al. (2009) and theoretical generalizability to naturalistic attention and categorization principles.
As a final example to motivate the use of eye-tracking data in developing our theory of category learning, it is relevant to note that multiple modes of information sampling could yield inseparable patterns of behavior under certain conditions (Figure 2). Consider two hypothetical learners who are assigning four-dimensional stimuli to categories A and B. One dimension (D1) is perfectly reliable for determining category membership, such that an observer could achieve 100% accuracy by learning the appropriate D1 feature-to-category mapping (e.g., when , respond category “A”, and when , respond category “B”). The three other dimensions (D2, D3, and D4) are each 75% reliable for determining category membership. Learner 1 is very efficient; they identified the most reliable dimension, and exclusively sampled information from D1 after gaining experience with the task. In Figure 2A–B, we show an example in which a learner fixated to D1, and concurrently accumulated considerable evidence to support a Category “A” decision.
Figure 2. Information sampling and decision dynamics.

Hypothetical fixation paths were generated by AARM’s within-trial module, such that one of four spatially segregated dimensions was fixated at each timestep up to a response. Left panels show the probabilities of fixating to each dimension (y-axis), plotted as a function of percentage of time within-trial between stimulus onset and response (x-axis). Right panels show the decision evidence for each of two possible category choices as a result of the information sampling behavior (i.e. fixation paths) in corresponding left panels. Choice probability (y-axis) is plotted as a function of absolute time in milliseconds (x-axis). Dotted lines indicate when self-termination (i.e. a response) occurred. Each row shows the timecourses of fixations and decision evidence for: (A) a hypothetical subject who learned to attend to the deterministic (100% predictive of category; D1) dimension; (B) a hypothetical subject who received conflicting evidence across three probabilistic dimensions (D2, D3, and D4). Although each simulation reflects different information sampling behaviors, category A was selected in both examples.
By contrast to Learner 1, Learner 2 happened not to notice that D1 was the most reliable dimension. Instead, they found that by attending to some combination of D2, D3, and D4, they could achieve very high accuracy that in fact rivaled that of Learner 1. Figure 2C–D shows an example in which a learner prioritized D4, which provided some initial evidence for a “B” response. Sampling information from D2 subsequently contradicted the information in D4, and created uncertainty in the choice. To resolve this conflict, the learner sampled information from D3, which provided sufficient information for making an “A” response. Given that these two divergent learning profiles could yield identical accuracy, responses alone may say very little about whether or not a model is accurately capturing which dimensions are being attended. While different modes of information sampling could of course be dissociated by clever task design (e.g. Blanco & Sloutsky, 2019; Deng & Sloutsky, 2015), measures of attention such as those provided by eye tracking data provide strong constraints on how attention is deployed over time within a trial. In particular, a viable model of category learning that uses latent attention to predict behavioral changes should be able to account for multiple modes of observable attention allocation as well. We will further explore the impact of different sampling paths on response probability in Case Study 1.
The examples highlighted in this section seek to clarify that there are at least two problems in using behavioral data as the lone metric for validating the assumptions of attentional deployment. First, when stimuli are multidimensional, it is possible for many patterns of attention allocation to produce identical responses. Rehder and Hoffman (2005a) showed that eye tracking data could be used to support a broad distribution of attention early in the learning period, as opposed to a systematic testing of one dimension at a time. Relatedly, Figure 2 illustrated how different sequences of fixation patterns within a trial could ultimately produce the same category choice. Second, the determination of relevance may be highly contextualized within a trial, based on the properties of the stimulus itself rather than the feedback about the stimulus. A particularly striking example comes from hierarchical category learning experiments in which participants fixate to dimensions in a stimulus-dependent manner before feedback is even observed (Figure 1, Blair et al., 2009).
Despite overwhelming evidence that eye-tracking data provide a rich source of information about the timecourse of selective attention during individual decisions, few efforts have been made to extend the logic of categorization models to account for within-trial dynamics (but see Braunlich & Love, 2021). Taking these findings together, we assert that gaze fixations serve as a viable, necessary means for evaluating category learning models in terms of predicted attention allocation. By using eye-tracking data in the current work, we are equipped to examine the theoretical mechanisms put forth by AARM using a new standard of specificity, to which other models of category learning have been infrequently subjected.
Summary and Outline
We believe that no theory of human learning would be complete without a description about how selective attention should be deployed. The introductory sections have supported the notion that attention is a critical component for learning problems: it accelerates learning by identifying which dimensions are relevant, and thereby limits the time-consuming search for information when making decisions. Our conceptualization of how attention should be deployed follows those of Kruschke (1992), Love et al. (2004), and Galdo et al. (2021) by treating attention as an optimization problem. At face value, the problem of optimizing attention should be similar at the between- and within-trial level, but there are important differences in this optimization problem that make for an interesting challenge. Across trials, the learning problem is well defined: one needs only to specify how attention should be modified in response to feedback (i.e. supervised learning). However, within a trial, the problem is made more complex because the learner does not know the true category label until after they make a response, but must nevertheless decide which dimensions to sample (i.e. unsupervised learning).
The gold standard in solving these problems is some type of forward computing, where relevance is determined by considering all possible values of a dimension and then aggregating the results to form an expected utility of each (Nelson & Cottrell, 2007; Yang & Lengyel, 2016). SEA is perhaps the most striking display of this approach, wherein the utility of sampling is computed for all dimensions prior to making a decision to act (e.g., sample a dimension or make a response). Although this approach has considerable promise, one potential weakness is that it assumes an incredible amount of computation at each moment in time to assess the potential utility of every sampling outcome. It is possible that humans do indeed make these computations, but it certainly is not an economical approach if suitable heuristic alternatives were available, particularly in consideration of high-dimensional stimuli.
By contrast, AARM focuses on the representation of the current stimulus information rather than on the utility of would-be collected information. The rationale behind this strategy is that subjects maintain a sense of the distribution of features that occur within each dimension, and they use this distribution to form expectations about the current stimulus. By dynamically updating the expectations, a “working” representation can subserve attention and the search for subsequent information. To solve the unsupervised aspect of this problem, we critically assume that information is sought after in a confirmatory manner until category evidence surpasses a decision threshold. This assumption appears to be vital to our approach, as it naturally extends the between-trial module of AARM (Galdo et al., 2021) to account for within-trial dynamics.
To articulate our proposed framework, we consider how latent attention is updated between-trials to facilitate learning, and within-trials to facilitate individual categorization decisions. Although details and justification will be provided in the sections to follow, our theoretical framework can be summarized by the following core components:
Both within- and between-trial dynamics are described by a common set of mechanisms. Interactions among attention, representations, and decisions extend across timescales to account for how humans acquire information about individual stimuli, and learn the relevant information for distinguishing between categories.
Over the course of learning, humans form simplified stimulus representations composed of the dimensions that are most relevant to the current task. Within-trial dynamics of information sampling and decision making describe how these simplified representations are formed, such that only a subset of information needs to be attended before a categorization response is made.
Attention is optimized with respect to the current goal. Gradient-based mechanisms typically require the observation of feedback to update the attention weighting structure between-trials. If we extend the same logic to the within-trial level, we must define how the observer orients attention before the correct category label is known. We therefore describe how representations gradually evolve within-trial according to experience-based predictions and confirmatory information search.
Hierarchical category structures are ideal for studying within-trial dynamics, due to an implicit temporal ordering of relevant information. In addition to giving rise to gaze prioritization effects in an experimental setting, hierarchical structures are ubiquitous in nature. In particular, we suggest that in real-world scenarios, learners use environmental context as a superordinate cue for processing the dimensions of new stimuli.
To explicate these theoretical components, the remainder of this article is organized as follows. First, we discuss the mathematical details of AARM in terms of two separable but interacting modules. We begin with a description of how AARM is applied to between-trial learning, and then describe how expectations about features can be managed dynamically to create a working representation of the stimulus probe. We then describe how attention orients to confirm the existing beliefs about a stimulus to complete our description of within-trial dynamics. Second, we examine AARM’s ability to capture important empirical effects by simulating its behavior in four case studies. The case studies examine how attention is deployed in several unique situations: (1) when expectations are violated, (2) when relevance is contextualized within a stimulus (e.g., as in the hierarchical category learning task), (3) when multiple stimulus dimensions occupy the same location in space, and (4) when learning of stimulus dimensions occurs incidentally (e.g., dimensions are not relevant to the learning process but become relevant when tested). Third, we close with a discussion about future directions and alternative mechanisms.
Model Specification
We define the dynamics of category learning in terms of three components, as shown in Figure 3: 1) the representation describes how information is stored and maintained through a set of experiences; 2) attention describes what information contributes to the representation; and 3) the decision describes how information is used to generate an action (e.g. a response). To present the details of AARM, we separate our description into distinct between- and within-trial updating processes. First, as described by Galdo et al. (2021), the model updates its representation of stimuli in response to feedback on each successive trial (i.e., a between-trial update). This type of update entails (1) storing a new episodic trace containing the stimulus information on the current trial, (2) storing information about the category label (e.g., from feedback), and (3) updating the quantity of attention that is allocated to each dimension.
Second, the model maintains a representation of the current stimulus probe, which it updates through time as it encodes new information about each feature (i.e., a within-trial update). This type of update entails (1) an encoding process where attention is applied to a stimulus dimension in order to access the feature value contained therein, (2) an imputation process where the model uses the available information to form expectations about which feature values will occur in unattended dimensions, and (3) an attention rule that allows the model to reorient according to its updated knowledge and expectations about the current stimulus probe. We begin with a general overview of the between-trial module, and expand this model structure to accommodate within-trial dynamics. We then close this section by explaining how this expanded structure relates back to dynamics that occur across trials. For reference, a notation table and parameter definitions are provided in Appendix B.
Between-trial Updating Rule
The relevant mechanisms of AARM’s between-trial updating rule will be provided here, but we refer the reader to Galdo et al. (2021) for additional details. On each trial of a categorization task, the observer is asked to assign a -dimensional stimulus to one of categories. To do this, the observer is thought to retrieve memories of previously-experienced exemplars and their associated category labels (i.e. as supplied by corrective feedback).
As in GCM, AARM assumes that memories of stored exemplars are “activated” in proportion to their similarity to the current stimulus. Similarity is computed by way of a factorizable exponential kernel (R. Nosofsky, 1986; Shepard, 1987), such that activation of the nth exemplar in response to probe is
| (1) |
Here, is the specificity of the between-trial similarity kernel function, contains the memory strength associated with each exemplar, and quantifies the attention allocated to each of the stimulus dimensions. Although Galdo et al. (2021) assumed was determined by a weighting function that incorporates primacy and recency biases (Pooley, Lee, & Shankle, 2011), here we assumed all exemplars had equivalent memory strength to provide constraint in our simulation case studies.
The probability of choosing category is the summed similarity of the exemplars associated with that category, normalized by the total across all exemplars (i.e., a weighted average). Specifically, the choice probability associated with Category is
| (2) |
where is an indicator function returning a one if the statement is true and a zero otherwise.
After a response is made and feedback is observed, two actions occur. First, the features of stimulus are stored in exemplar matrix as a memory trace, and the true category label is stored in feedback matrix . Second, attention is updated in the direction of an error-gradient, similarly to the adaptive attention models described in the Attention as an optimization problem section (i.e. ALCOVE and SUSTAIN):
| (3) |
Here, is a positive constant describing a between-trial learning rate, and is a shorthand denoting a “gradient operator” for computing the set of partial derivatives of a loss function with respect to each element of the vector :
To define the loss function, ALCOVE and SUSTAIN use the so-called “humble teacher” rule, which allows for variability in category activation between exemplars. Specifically, more category-typical exemplars elicit greater activation than those that are more peripheral (Kruschke, 1992). For the purposes of our previous work on simplicity biases in human learning (Galdo et al., 2021), we instead selected a cross-entropy loss function because it allows for faster training and more reliable extension to multiclass problems than squared-loss alternatives (Demirkaya, Chen, & Symak, 2020). Given successful fits to behavioral and eye-tracking data with our previous specification for between-trial attention updating, we apply cross-entropy loss in the current work as well.
When using a soft-max rule (such as Luce-choice), the cross entropy loss function is simply the negative log likelihood of correct classification (Goodfellow, 2016):
where is the choice probability associated with the feedback given on the ith Trial (i.e., the correct response). Hence, to derive the gradient, we need only take the partial derivative of Equation 2 with respect to along each of the dimensions. We provide this derivation in Appendix A. Our update equation for the attention vector after observing feedback therefore becomes
| (4) |
We stress that this updating procedure departs from strength-based connectionist architectures in which back propagation solutions provide the rule to update the attention vector and hidden layer weights. As shown by Galdo et al. (2021), simply defining how attention should be updated across time within an instance representation is sufficient to capture categorization behavior.
Within-trial Updating Rule
Figure 3B illustrates the important components of the within-trial updating process, as well as its “default” temporal order (i.e., nodes with numbers). Upon stimulus presentation, a set of initial attention weights inherited from the previous trial of the between-trial module first dictates which information will be sampled, a process by which the eyes are oriented to the location of the prioritized dimension (Node 1 in Figure 3B). Once the eyes have fixated upon the intended dimension, an encoding process is initiated for the feature residing in that dimension. After a feature has been encoded, that information is passed to the representation (Node 2 in Figure 3B). Similarity-based activation of the stored exemplars is then used to calculate the total evidence for each category response (Node 3 in Figure 3B). The state of accumulated evidence at each moment in time is used to determine which dimension to orient to next. The model reorients attention in a confirmatory manner, according to which dimension is most likely to provide further evidence that would support whichever choice currently has the largest amount of supporting evidence. This dynamic process self-terminates and makes a response when a sufficient amount of evidence has accumulated for an option.
For ease of exposition, we organize this section into the following four stages of processing: Stimulus Encoding, Exemplar Activation, Evidence for Category Response, and Attention Orientation. Figure 4 provides an illustrative example of how each of these components contribute to within-trial dynamics, and we will use this figure as a working example to facilitate descriptions of each component.
Figure 4. Illustration of Within-trial Dynamics.

(A) An example stimulus is presented on the screen, and a stimulus dimension is sampled for processing (e.g. prioritized from the between-trial module). (B) The observer generates a working representation of the stimulus and predicts what features might occur in each dimension. As a feature is attended, predictions are replaced with true feature values. (C) Previously-stored exemplars are activated in proportion to their similarity to the probe. (F) The category labels associated with retrieved exemplars accrue noisy response evidence. (E) Attention updates to discriminate among the currently most active category options. (D) Gaze fixations are determined from the attention process, resulting in reorientation to new dimensions as needed to sample more category-relevant information.
Stimulus Encoding
Memory theories often describe the psychological representations of stored items or events as memory “traces,” which are organized into discrete features of perceptual, contextual, and conceptual information. While the contents of a memory trace cannot be directly observed, recall and recognition paradigms provide insight into which features are encoded under various conditions. For example, if a lure item is falsely recognized among previously-studied targets at test, it indicates overlap between the features of the lure and some subset of target memory traces (Deese, 1959; Roediger & McDermott, 1995). Additional work has shown that the distribution of features across stored traces and the extent to which they can be associated with one another influence which information will be encoded and subsequently retrieved (Dosher, 1984; Dosher & Rosedale, 1991; Greene & Tussing, 2001). With these insights in mind, a recent dynamic model of encoding and retrieval (Cox & Criss, 2020; Cox & Shiffrin, 2017) described trace formation as a time-varying process. Specifically, the iterative encoding of individual probe features selectively activates memory traces on the basis of similarity, and drives an evolving familiarity signal toward a recognition threshold. Similarly, AARM’s within-trial module was designed to build up an informative representation of the probe throughout the trial, using retrieval of previous exemplars to drive an evidence accumulation signal for making a category response.
Our specification of encoding in AARM’s within-trial module builds upon mechanisms of prediction and pattern completion observed in the hippocampus, in which previously-observed item representations are reinstated during encoding in order to fill-in missing information or properly orthogonalize overlapping cues (see Bowman & Zeithamova, 2020; Hunsaker & Kesner, 2013, for review). Prior to encoding any information about a new stimulus, we assume that a working representation is populated by experience-based expectations of feature values. Expectations are gradually replaced with the true features of the stimulus as they are attended and concurrently encoded over the course of the trial.
To incorporate the logic of pattern completion into AARM’s encoding mechanism, we follow a procedure outlined by Estes (1994). Borrowing his example, suppose an observer experiences the following three-dimensional stimuli: , , and . Suppose on Trial 4, the observer is presented with a partial stimulus and is asked to guess which feature value will occur in Dimension 3. We assume that an observer will predict the feature value based on memories of previous items and the current state of knowledge about the stimulus. To make and evaluate predictions, one can impute each feature value that was previously-observed in Dimension 3 (i.e. [1,2]) into the partial stimulus, and evaluate which feature value is more likely to represent the missing information.
Starting arbitrarily with a candidate feature value of 1 as shown in the table below, we compare the imputed stimulus (i.e. 111) to all stored exemplars and indicate whether the feature values match or mismatch in each dimension. In the Comparison column, “matches” and “mismatches” are indicated by values of 1 and respectively, where represents a baseline level of perceptual discriminability. We then compute the product across comparison values to determine the Similarity column below (Medin & Schaffer, 1978). Finally, we compute the sum similarity across all stored exemplars to determine the activation of imputed stimulus 111:
| Imputed Stimulus | Stored Exemplars | Comparison | Similarity |
|---|---|---|---|
|
| |||
| 111 | 111 | 1 | |
| 111 | 121 | ||
| 122 | |||
|
| |||
| Sum: | |||
Similarly, we can calculate the activation when “2” is the missing value using the same strategy:
| Imputed Stimulus | Stored Exemplars | Comparison | Similarity |
|---|---|---|---|
|
| |||
| 111 | |||
| 112 | 121 | ||
| 122 | |||
|
| |||
| Sum: | |||
The probability of selecting a value is simply the activation of its respective imputed stimulus, normalized by the total activation across all candidates. In our example, the probability that the stimulus has a feature value of 1 in Dimension 3 (i.e., ) is
As long as is small enough to indicate sufficient perceptual discriminability among candidate feature values, will approach 1 in the current example. In other words, when asked to complete the partial stimulus , the observer is most likely to respond “1”.
In extending the intuition of Estes’s example for the purposes of dynamic encoding, it is necessary to distinguish between the “true” identity of the stimulus and a “working” representation that changes through time. As in our description of the between-trial module, we use the notation to denote the true identity of the probe on the ith trial. We denote the working representation of the stimulus probe at Timestep of Trial as , and omit the “” trial notation for convenience. We next require a general expression for the probability that a candidate feature value will occur in a particular dimension. We define the set of unique feature values that were previously observed in Dimension as . We then use the equation
| (5) |
to calculate activation of stored feature value in response to an imputed feature value , drawn from . This equation is a more general form of the exemplar activation calculation provided in Equation 1. Here, however, is the within-trial specificity of the similarity kernel function, indicates the encoding status of exemplar features, and indicates the attention weight at moment . We will describe how attention changes through time in the Attention Orientation section, but for now it is sufficient to acknowledge that attention is updated throughout the trial and will affect how stimuli are encoded.
Using the relation , the probability that the “true” feature value is equal to is
| (6) |
Note that Equation 6 takes the same form as the feature probability calculation from Estes’s example. Here, the numerator is simply the activation associated with an imputed feature value , and the denominator is the total activation associated with all values in . To specify a feature value in the working representation at moment , we randomly draw a value from the distribution defined by the probability mass function in Equation 6. Importantly, a new value of is re-drawn at each timestep within the trial, such that the working representation is non-stationary. This imputation process continues until sufficient attention has been applied to Dimension for a true feature value to be encoded, at which point is predominantly represented in (see Attention Orientation section). Although Equation 6 expresses the pattern matching probabilities for discrete feature values, it can easily be extended to continuous values by replacing the summation over the set to be an integration over the space , in the same way that the similarity kernel (e.g., Equation 5) was generalized from Medin and Schaffer’s 1978 context model to Nosofsky’s 1986 GCM. We demonstrate an extension to a paradigm with continuously-valued dimensions in Case Study 3.
Our specification of a prediction-based working representation is somewhat related to utility predictions in SEA. Both models assume the observer maintains an ongoing sense of what features might occur in each dimension, with an associated likelihood of occurrence that depends on the state of knowledge about the current stimulus. One critical distinction is how each model uses these insights to decide which sources of information to sample. While SEA requires a pairwise assessment of every possible combination of features in order to determine a single utility prediction for each dimension, AARM’s working representation is more reflective of spontaneous, noisy retrieval of features that are unbounded by specific exemplar representations. As such, our approach has a similar intuition to Monte Carlo algorithms in which probability distributions are approximated through repeated sampling, some specifications of which can be recursively updated as more information is obtained (Doucet, de Freitas, & Gordon, 2001; Gilks, Richardson, & Spiegelhalter, 1996). Random sampling approaches have been suggested to provide an advantage of cognitive plausibility over rational models on the grounds of computational parsimony (Sanborn, Griffiths, & Navarro, 2010). Relative to SEA, the feature imputation strategy in AARM is arguably more consistent with the capabilities of resource-limited humans because there is no requirement that every possible feature combination is assessed within the working representation. Expected or observed feature values are instead drawn from a distribution, and attention and decision components update accordingly.
Our specification is also similar to other extensions to GCM that were designed to characterize the timecourse of stimulus encoding during category learning tasks (Brockdorff & Lamberts, 2000; A. Cohen & Nosofsky, 2003; Lamberts, 2000). As mentioned previously, the EGCM-RT (Lamberts, 2000) incorporated a stochastic stimulus representation mechanism into GCM, which results in a similarity output that changes throughout the trial as probe dimensions are encoded. Unlike AARM, however, EGCM-RT does not specify a precise order in which dimensions should be encoded, only that encoding is sequential and that all feature values of the stimulus need to be encoded before a response is made. A variant of EBRW (R. Nosofsky & Palmeri, 1997) for perceptual encoding (EBRW-PE A. Cohen & Nosofsky, 2003) contains similar stochastic dimension-sampling mechanisms, such that exemplars race toward a threshold at rates that are proportional to their total similarity to the probe. At each timestep within a trial, there is an increasing probability that a feature will be encoded and thus included in the continuous similarity calculation. As such, encoding a feature value within the stimulus representation is strictly probabilistic, whereas AARM offers a mechanism for encoding individual feature values that is driven by attention and is gated by gaze fixations.
Instead of populating the working representation with random draws from an expected distribution of feature values, an alternative approach would have been to define the working representation as an empty vector prior to encoding. The retrieving effectively from memory model (REM; Shiffrin & Steyvers, 1997), for example, assumes that observers begin with an empty trace consisting of a vector with all zeros. Over time, the zero elements of the trace are replaced with samples from a pre-specified distribution (e.g., a Geometric distribution) with properties intended to reflect the details of the stimulus set. In the context of a model designed to capture within-trial dynamics, however, we found that the expectation-formation component of the working representation was essential for the model to reorient to additional dimensions after processing the first. In hierarchical paradigms like the one illustrated in Figure 1 (Blair et al., 2009), various iterations of the model in which the stimulus representation was initialized with an uninformed (e.g. zero or average) basis vector provided no impetus for the model to reorient to one dimension over the other. As we will show in Case Study 2, our implementation achieves human-like reorientation to the stimulus-relevant subordinate dimension by updating its feature predictions after initial encoding, and fixating to a second dimension through confirmatory search.
Figure 4B illustrates how the encoding dynamics occur in AARM’s within-trial module after initial orientation to a dimension (e.g. food source; Figure 4A) when an observer is categorizing images of animals. Before a new image is even presented, the observer has some expectation about what feature values each dimension could possibly take on, given their experience with previous stimuli. After the food source dimension is sufficiently attended and the observer encodes the “true” feature value (e.g. acorn), the working representation of the stimulus is updated to accommodate this information. As shown in Figure 4C and discussed below, this shift in the probe representation directly affects which stored exemplars are subsequently activated to facilitate the reorientation of attention.
Exemplar Activation
We assume that encoding (and by extension, attention) is the primary mechanism driving memory activation of previously-stored exemplars. This is in contrast to EBRW (R. Nosofsky & Palmeri, 1997) which assumes that the similarity of previously stored exemplars to the stimulus probe is what dictates how frequently each exemplar is retrieved. In AARM, attention is what guides the similarity computation itself, causing potentially rapid nonlinear activation in both the activation of past exemplars and the evidence for a category response.
Exemplars are activated in a nearly identical way as described in the between-trial case (see Equation 1), with the one exception that activation is based on the working representation of the stimulus probe, , and not the true contents of the stimulus probe itself. In addition, activation is expressed as a function of time, given by
| (7) |
where we denote the attentional state at Time as .
As discussed in the previous section, the working stimulus representation in AARM’s within-trial module is non-stationary and gradually comes to resemble the stimulus’s true identity as features are encoded. As a consequence, the distribution of expected feature values in Equation 6 will change dynamically through time and affect which dimensions are prioritized, given the information available at Time . Pertaining to the hierarchical paradigm shown in Figure 1 (Blair et al., 2009), Figure 5 shows how attention and exemplar activation mutually impact one another. At the beginning of the trial, memories for all exemplars are equally active (left panel, ). Attention initially orients to the D1 dimension (right panel; x-axis) per weights inherited form the between-trial module. As the working representation is updated with D1 feature information, there is a concurrent retrieval bias for exemplars belonging to “A” categories (left panel, and ). When attention then updates again, the observer will reorient to D2 in an effort to distinguish between the categories associated with the most active exemplars (right panel; y-axis). When sufficient attention is applied to encode the feature value of D2, exemplars with similar features in both D1 and D2 are selectively activated (left panel, and ).
Figure 5. Illustration of Attention Gradient.

(A) Heatmaps show the activation of each unique exemplar in the task paradigm shown in Figure 1. Y-axis labels show trial numbers and the feedback associated with each exemplar. Activation at 4 different time points within an individual trial are shown, given a probe with a true category label of A2. (B) The plot shows the progression of within-trial attention weights assigned to dimensions D1 and D2, which are the relevant dimensions for determining the category membership of the given stimulus. As time progresses (as indicated by black arrows), the attention weights (x- and y-axis values) move in a direction to support a category response (contour values).
To account for potentially imprecise mappings between the visual properties of matching probe and exemplar features, we incorporated the notion of perceptual variability into the calculation for exemplar activation (Equation 7). As it stands, the distance calculation within Equation 7 assumes the observer will perceive all matching feature values in a precisely identical way. This is unlikely to be the case for human subjects, whose visual perception depends on noisy neuronal firing and elements of bottom-up salience. For example, stimuli like Gabor patches (see Case Study 3) that allow for continuous dimensions of frequency and tilt angle are unlikely to be mapped to their true feature values such that all stimuli are precisely distinguishable. When attempting to generate human-like behavior in our case studies, we therefore added random noise drawn from a normal distribution with standard deviation to the distance calculation at each Time . SEA provides an alternative method for accounting for imprecise feature perception and storage, in that memories are stored as clusters (J. Anderson, 1991a) and the likelihood of a stimulus belonging to each cluster is represented as a continuously-updated distribution of belief. The probability that a given stimulus belongs to a particular category is determined by a weighted combination of cluster probabilities. Uncertainty is therefore inherent to the Bayesian belief-updating process in SEA, whereas AARM assumes precise mappings between stimulus and exemplar features unless otherwise specified (e.g. with noise).
In summary, exemplars that are more similar to the working representation of the probe will be more strongly activated in AARM, and will have more relevance to the response choice. As a simplification of Figure 5, Figure 4C provides an illustration of how exemplar activation occurs. After the “acorn” feature is encoded as the food source of the probe stimulus, memories for animals that eat acorns are selectively activated, (e.g. chipmunks and squirrels) whereas memory traces for animals that eat cheese are deactivated (e.g. rats). In the next section, we will discuss how exemplar retrieval manifests in the accumulation of evidence in favor of an available category label.
Evidence for Category Response
We assume within-trial choice probability is calculated in a way that mirrors the between-trial case (see Equation 2). Here, however, we reconceptualize “choice probability” as “decision evidence”, and specify evidence at each time point using the following equation:
| (8) |
where is defined in Equation 7. The numerator represents the activation of the subset of exemplars associated with feedback , and the denominator represents the total activation across all stored exemplars.
EGCM-RT (Lamberts, 2000) uses a similar calculation to Equation 8 to approximate within-trial dynamics, and the output is interpreted as a probability of making each possible response, given an RT. In order to implement self-termination behavior into AARM’s within-trial module, we instead assume that for each Category represents category evidence that accumulates up to a threshold. Alternative specifications would have been to use a race-like structure and calculate decision evidence as the sum of category-relevant exemplar activation without normalization (Brown & Heathcote, 2008; Usher & McClelland, 2001), or apply a log ratio calculation similar to the sequential probability ratio test (SPRT; Wald & Wolfowitz, 1948). For our purposes of extending mechanisms for between-trial learning to account for within-trial sampling dynamics, however, it was important to use the same specification of the choice rule in order to ensure predictable behavior of the gradient-based attention update that will be discussed in the next section.
In specifying a decision rule, several options were available for consideration. We adopted a simple relative decision rule, such that the difference between the response with the largest evidence minus the response with the second largest evidence must be greater than some value, called . This specification is similar to extensions of the Drift Diffusion Model (DDM Ratcliff, 1978) and the SPRT for modeling multialternative choice, in which the decision terminates according to a thresholded distance between the two leading outcomes (McMillen & Holmes, 2006). Other approaches would have been to apply an absolute decision rule in which the threshold were applied to evidence for the leading option, or to apply a threshold to the distance between evidence for the leading option and the average evidence across alternatives (Niwa & Ditterich, 2008). Through testing, we found that our chosen specification provided the most stringent requirement for category-disambiguating evidence, such that multiple sources of task-relevant information were consistently sampled before decisions were made in a manner that was reflective of observed behavior.
Returning to Figure 4, panel C shows the activation of memories for exemplars that match the features of the current stimulus. Panel F shows how exemplar activation dynamically affects category evidence. Here, the observer maps the most active exemplars to the “squirrel” and “chipmunk” categories, respectively, thus increasing the probability of making a “squirrel” or “chipmunk” response. The probability of responding “rat” concurrently decreases, given that the corresponding exemplars do not match the current stimulus with respect to the encoded food source: acorn. As we will describe in the next section, category evidence at each timestep is used to continuously update attention and concurrent information sampling behaviors.
Attention Orientation
On a between-trial basis, the attention vector reflects the quantity of attention deployed to each stimulus dimension on the ith trial. We assume that attention in the within-trial module initially orients according to learned experiences, which are synthesized by these between-trial attention weights. For example, if a subject learns that the most relevant stimulus dimension is likely to occur in a particular spatial location across trials, the subject could begin orienting attention to this location in an anticipatory fashion before a stimulus is even revealed on trial . 1 To keep the notation for between- and within-trial dynamics separate, we use to denote the within-trial attention vector at the tth moment in time, and we have dropped the superscript designating trial number for convenience. To initialize on Trial , we set , such that the within-trial module is initialized with normalized between-trial weights from the most recent update. We made this choice in order to inform orientation in the within-trial module using between-trial weights, but in a way that does not make strong assumptions about scale equivalence between feedback-based and search-related updates to attention.
Because it is central to our theory that between-trial learning and within-trial information sampling involve a common set of mechanisms, we needed a way to modify the feedback-based attention update mechanism in Equation 3 to account for the unsupervised aspect of within-trial dynamics. The between-trial module reduces the probability of future errors by redistributing the attention weights in a gradient-based manner, given the model’s predicted response probabilities for each available option as well as the true category label. Because the true category label is not known by the observer until after the within-trial process terminates, however, we made the choice to calculate the within-trial attention update in reference to the model’s current best guess about the true category label.
Using Equation 8 as the definition of momentary evidence, we define a dynamic loss function as
| (9) |
where is the gradient-based update vector, and denotes maximum evidence across response options at moment . Mirroring Equation 4, attention is updated at each timestep using the equation
| (10) |
where is the within-trial learning rate. Because fixations are calculated directly from the attention update described by Equation 9, this specification supports confirmatory search behavior, such that attention will orient toward the dimensions that supports further gains in evidence for the leading accumulator. We acknowledge that other, more balanced approaches could have been taken instead. For example, we could have calculated a separate vector that maximizes evidence for each of the candidate category labels. In this case, the update to attention in Equation 10 could have been the sum or a weighted combination of all vectors, or we could have applied a maximum gain selection criterion similar to SEA. While alternative approaches merit additional investigation in future work, the selected implementation is consistent with observed confirmatory biases in human learning (Lefebvre et al., 2022; Nickerson, 1998; Talluri et al., 2018), has an advantage of computational parsimony over some unbiased alternatives, and was demonstrably sufficient for predicting human-like attention dynamics across the four simulation case studies that will be presented in sections to follow.
An important contribution of our work is to put forth a generative framework that makes explicit predictions for what dimensions will be fixated at each moment in time. To achieve this, we must consider two cases of dimension spatial arrangements. In the first case, stimulus dimensions are separated into different spatial locations (i.e. segregated dimensions). Here, eye tracking measures provide direct measures of attention for specific dimensions, assuming only one spatial location can realistically be fixated at a time. In the second case, stimulus dimensions overlap in space (i.e. integrated dimensions). Here, fixation information cannot distinguish between dimensions that are selectively attended (i.e. via covert attention), and dimensions that are ignored.
In the segregated case, we can identify the fixated dimension directly from the most recent update to the attention vector. Letting denote the fixation index for each Dimension at Time , we can define
In other words, we assume that a fixation will be directed toward the dimension that provides the largest absolute amount of information, according to one’s current representation.
In the integrated case, the specification is similar but additionally accounts for the fact that at least one subset of dimensions spatially overlap. Letting denote the set of dimensions that have a spatial location that is identical to that of the most informative dimension, we can specify
Hence, if one dimension is deemed to be the most informative at a given moment in time, then any dimensions that occupy the same location in space (i.e. shape and color dimensions of a particular item) will also be fixated within same moment.
The distinction between the segregated and integrated cases exemplifies the fact that fixation data provide only minimal constraints on encoding. Although fixating to a dimension is a necessary condition for encoding a feature value, it is not guaranteed to be sufficient. In the case of selective attention, an observer could be overtly fixating on a particular spatial location, but only attending covertly to a subset of information contained there (e.g. selectively attending to the “face” or “scene” components of overlapping face-scene stimuli, Rutman, Clapp, Chadick, & Gazzaley, 2010). In these cases, it would be problematic to assume that fixation data alone gives us complete and direct information about how time spent looking at a dimension relates to the probability of encoding. Given these considerations, we assume that encoding is based on a thresholded, cumulative sum of attention over the course of dwell time, such that
Hence, when the cumulative attention applied to a fixated dimension exceeds the threshold , a feature is considered to be “encoded”. After a trial terminates , the information in is stored in so that only encoded feature values can be imputed on subsequent trials (Equation 7). As discussed in the Attention is the mechanism of learning section, this specification is considerate of findings of improved memory for items that are covertly attended through endogenous means (Addleman, Tao, Remington, & Jiang, 2018; Botta, Martin-Arevalo, Lupianez, & Bartolomeo, 2019; Foster, Bsales, & Awh, 2020). Recent neuroimaging work has suggested, however, that both endogenous and exogenous (i.e. related to salience) modes of covert attention facilitate perceptual encoding, but endogenous attention uniquely facilitates subsequent readout of visual information, such as what would be required for a category judgement (Dugue, Merriam, Heeger, & Carrasco, 2020). While we do not account for the potential impact of exogenous covert attention on encoding probability here, this is a topic of future work that will be considered in the General Discussion.
Relating encoding dynamics back to the working representation of the stimulus probe as described in Stimulus Encoding, we again note that encoding a feature alters the distribution of values that are imputed into the working probe representation . At the beginning of a trial when the feature value that occupies dimension has not been encoded yet, will be equal to zero, and feature values will be imputed into with probability (Equation 6). After the cumulative attention applied to the spatial location of dimension exceeds is set to 1 to indicate that a feature was encoded. From that point on, the value will be imputed into the working representation with probability , where represents encoding fidelity. With the remaining probability , we assume that feature values will continue to be drawn from the distribution of previously-observed values.
Mathematically, we can write this process as a mixture of two probability mass functions, one containing a distribution over all expected feature values in , and one defining a Dirac delta distribution
where all probability mass is centered at the true representation . Hence, we can write the mixture of these two distributions as
With this specification, the working representation of a probe dimension continues to be stochastic after the encoding threshold has been surpassed, but is biased in the direction of the true stimulus feature value with magnitude . This allows the observer to continue to represent feature values that have occurred within the broader task context with some probability, even after the true feature value of the stimulus is known. This appears to be important in situations where novel features or combinations of features are introduced (e.g. Case Studies 1 and 4), such that the observer is able to reorient if the fixated dimension provides information with unknown or contrary category information. For these types of situations, SEA contains a mechanism for a “sampling bonus,” which can be artificially imposed to induce continued sampling. AARM’s proposed way of balancing encoded stimulus information with available task feature information, however, naturally produces reorientation behavior in the presence of novel stimuli without modification.
A brief example of how attention reorients within a trial is shown in Figure 4E. Essentially, attention orients to the dimensions that have the best chance of resolving the conflict among the active choice options. In this case, the first encoded dimension (i.e., the food source) activated the chipmunk and squirrel categories, and so the deliberation now turns toward dimensions that accentuate differences between them. In this example, the next most important dimension is the tail. Attention therefore reorients to the tail dimension so that it will be subsequently fixated in Figure 4D. Additional elaboration of the attention updating process is provided in Figure 5 using the stimulus structure from Figure 1, as described in the Exemplar Activation section. In summary, the gradient update is initially maximized in Dimension D1, given that D1 is relevant to categorization across all exemplars . After a D1 feature value is encoded for the current stimulus, exemplars from categories “A1” and “A2” are selectively activated on the basis of similarity to the encoded information ( and ). Attention then reorients to D2 in order to distinguish between the two most active categories, and encoding a D2 feature value facilitates retrieval of exemplars from category “A2” ( and ).
Summary
In this section, we provided the technical details of AARM as they relate to between- and within-trial dynamics. Although the notation can become complex when dealing with dynamics at two different time scales, the intuition of the model is far simpler. When provided with a stimulus (Figure 4A), observers sample information selectively in order to make an accurate and time-effective choice. With experience, observers learn to prioritize dimensions that help them separate stimuli into categories.
When faced with a choice, observers deploy selective attention in a manner that is consistent with a learned prioritization map, and begin encoding relevant stimulus features. As shown in Figure 4B, the encoding process constructs a psychological representation of the stimulus probe, which in turn activates memory traces of similar exemplars (Figure 4C). The retrieved exemplars are typically associated with a category label, such that the observer can accumulate evidence for a response (Figure 4F). For complex stimuli, these response options compete for selection, and necessitate the recruitment of additional stimulus dimensions. Consequently, attention reorients to the dimensions that would facilitate a comparison among the most competitive options (Figure 4E) and can produce a shift in the fixated location (Figure 4D). This process continues until a decision threshold is reached, based on the relative difference between the evidence among the response options.
In the next part of the article, we describe the results of four theoretical case studies that demonstrate how the between- and within-trial modules of AARM contribute to human-like predictions of choice and eye-tracking behavior across a comprehensive set of challenging scenarios. Case studies are divided into two sections to explicate the theoretical tenets of AARM: 1) humans seek out information about new stimuli in a manner that is influenced by their individual learning experiences; and 2) attention is sensitive to hierarchically-organized information, such that the current state of knowledge guides future information sampling.
This study was not preregistered. Model code will be made available upon publication at https://github.com/MbCN-lab. The data used in Case Study 1 will be available upon reasonable request. The data used in Case Study 2 were made freely available online by Meier and Blair (2013) at https://doi.org/10.1016/j.cognition.2012.09.014.
Experience-based Representations
Empirical and modeling work has demonstrated that humans tend to form representations based on a subset of the available dimensions (Lee, 2001; Shepard & Arabie, 1979; Sloutsky, 2003; Tversky, 1977; Ullman et al., 2002). In support of this idea, eye-tracking work has shown that after sufficient training with the structure of a task, humans tend to fixate to only a few informative dimensions before making a response (Blair et al., 2009; Rehder & Hoffman, 2005a, 2005b). Even without consideration of the relationship between endogenous covert attention and encoding fidelity, it stands to reason that features that are overtly fixated are more likely to be stored in memory for later use (Irwin, 1996; Loftus, 1985). In cases where multiple sources of information might be equally sufficient for correctly identifying the category label across trials (see Figure 2 for a hypothetical example), the extent to which features are encoded from each dimension across training instances potentially impact how the observer elects to sample information from stimuli encountered at test.
The relationship between the storage of individual memories and generalized representations has garnered great interest, particularly in regards to the role of the hippocampus in both episodic inference and concept formation (Bowman & Zeithamova, 2018; Mack et al., 2016; Mack, Love, & Preston, 2018; Schapiro, Turk-Browne, Botvinick, & Norman, 2017). Several theoretical accounts have suggested that generalization decisions do not require the formation of integrated concept representations, but rather can be achieved by the encoding and strategic retrieval of discrete memory traces for past exemplars (Hintzman, n.d.; Kruschke, 1992; Kumaran & McClelland, 2012; R. Nosofsky, 1988). While some fMRI work has supported exemplar-based accounts by identifying similar hippocampal activation for both recognition and categorization judgements (Mack et al., 2013; N. Nosofsky, Little, & James, 2012), other work has provided evidence of associative inference functions of the hippocampus that arguably extend beyond item-specific memory storage. For example, repetition effects in the hippocampus have provided evidence that overlap between the current stimulus and existing memories impact how new items are encoded (Richter, Chanales, & Kuhl, n.d.; Zeithamova, Dominick, & Preston, 2012; Zeithamova, Manthuruthil, & Preston, 2016; Zeithamova & Preston, 2017). In addition to encoding new information in reference to recent experiences, other work has provided evidence that humans make predictions about future events that are shaped by memories of the past (De Brigard et al., 2016; Van Hoeck et al., 2013), often recruiting the same networks that are involved in encoding and retrieval (De Brigard, Addis, Ford, Schacter, & Giovanello, 2013; De Brigard, Spreng, Mitchell, & Schacter, 2015).
Given these insights on the impact of memory on category representations, Case Study 1 investigates memory-dependent sampling and decision dynamics in a category learning paradigm with multiple informative dimensions (Blanco & Sloutsky, 2019). In its original presentation by Galdo et al. (2021), the between-trial module of AARM is not equipped to account for variability in feature encoding over the course of learning. With the within-trial module, however, we can gain insight into how feature encoding variability related to selective attention during training might give rise to different patterns of information sampling behaviors in the presence of novel stimuli.
Case Study 1: Dimension Biases
To investigate the impact of attention-mediated encoding variability on subsequent information sampling and retrieval, we used a paradigm that was developed by Blanco and Sloutsky (2019) to investigate developmental changes in learning strategies. Here, we discuss behavioral and eye-tracking data that were collected from a cohort of 38 adults while they completed the same paradigm (Blanco, Turner, & Sloutsky, under review). The task paradigm will be summarized here, but the reader is directed to Blanco and Sloutsky (2019) for additional details.
As illustrated in Figure 6, categories were defined with a rule-plus-similarity structure, such that one “Deterministic” dimension was perfectly predictive of category membership, and five “Probabilistic” dimensions provided good but imperfect category information across trials (80% cue validity). An additional “Irrelevant” dimension contained the same feature value across stimuli, and therefore contained no category-diagnostic information. Stimuli were images of alien-like characters that were composed of seven dimensions: antenna, head, body, button, hands, feet, and tail. Each dimension could take on one of a discrete set of features that varied on the basis of color and shape (i.e. the terminal ends of antennae could be either beige rectangles or gray triangles; hands could be either blue crosses or red half-moons, etc.). During the instructions, participants were informed that they would be seeing different creatures called Flurps and Jalets, and that their task was to figure out which species each creature belonged to. Participants also received instructions about the category structure. The features of each dimension were shown to participants in isolation, along with the message that “most” (for Probabilistic dimensions) or “all” (for the Deterministic dimension) creatures belonging to a particular category shared that feature. No information about the Irrelevant dimension was provided during the instructions.
Figure 6. Paradigm and Stimuli used in Case Study 1.

(A) Illustration of stimuli, which participants were asked to sort into fictional “Flurp” and “Jalet” species types. Each stimulus contained seven dimensions (antennae, head, button, body, hands, feet, and tail). In Phase 1, one dimension (e.g. feet; outlined by solid box) was deterministic, one was irrelevant (e.g. button; outlined by dashed box), and five were probabilistic (all un-outlined features) in their mappings to category labels. After an undisclosed “switch,” the deterministic dimension from Phase 1 became irrelevant in Phase 2 and the irrelevant dimension became deterministic. (B) Characteristics of stimuli presented at test. Match items were drawn directly from the training set, such that deterministic and probabilistic dimensions carried the same feature-to-category mappings. Conflict items contained novel configurations of features, such that the deterministic and probabilistic dimensions were associated with opposite category mappings. In the table, unique feature values within each dimension are indicated by 0s, 1s and 2s.
The task was divided into two phases with complementary sets of stimuli. Each stimulus in Phase 1 had a Phase 2 counterpart that contained the identical configuration of Probabilistic features, and was mapped to the same category label. The Deterministic and Irrelevant dimensions, however, switched roles between Phases 1 and 2. As shown in Figure 6A, for example, “feet” features that were Deterministic in Phase 1 were replaced with a novel Irrelevant feature in Phase 2, and the Irrelevant “button” feature that occurred in all Phase 1 stimuli was replaced with one of two novel Deterministic features in Phase 2. Participants were not informed that the switch would occur, and did not receive any explicit instructions about the post-switch feature mappings.
Each phase consisted of a training stage (with feedback), followed by a testing stage (without feedback). In the training stages, each of 10 unique items (5 from each category) from the relevant stimulus set were presented 3 times in random order (30 trials total). All stimuli were presented in the center of the screen, and each dimension occupied the same spatial location across trials. Participants made category responses by pressing buttons on a controller. After a response was made, participants were given corrective feedback. During Phase 1 training, feedback was very descriptive in an effort to encourage both attention to the overall appearance of the stimulus as well as the Deterministic dimension. For correct responses, feedback took the form of: “Correct this is a Flurp. It looks like a Flurp and has the Flurp feet.” Feedback following incorrect response took the form: “Oops this is actually a Jalet. It looks like a Jalet and has the Jalet feet.” Feedback during Phase 2 training was simplified so that participants were free to learn the post-switch feature-to-category mappings on their own. As such, feedback for a correct response was: “Correct this is a Flurp,” and feedback for an incorrect response was: “Oops this is actually a Jalet.”
Testing stages consisted of 10 trials from each of 2 conditions that were presented in random order (20 trials total). Participants responded to each item by selecting a category label, but no feedback was provided. Items in the “Match” condition were identical to the stimuli presented during training. Items in the “Conflict” condition contained novel configurations of previously-encountered features. As shown in Figure 6B, each Conflict item contained a feature in the Deterministic dimension that predicted one category label, and features in the Probabilistic dimensions that predicted the opposite category label.
Continuous eye-tracking data was collected while participants completed the task using an EyeLink 1000 eye tracker, with a sampling rate of 250 Hz. To preprocess the data, 8 non-overlapping rectangular areas of interest were defined to comprise the spatial locations of features in each dimension. 6 out of 7 dimensions occupied only one AOI, and the “hands” dimension occupied two. Fixation points were mapped to a particular dimension if they fell within the bounds of the relevant AOI, and were otherwise excluded from analysis.
In the sections to follow, we consider the data from Blanco et al. (under review) in two parts. Case Study 1A uses data from the training and testing stages of Phase 1 to observe how information sampling during training relates to response probabilities in the presence of previously-seen items (Match) and novel configurations of features (Conflict). Case Study 1B uses data from the transition between the testing stage of Phase 1 to the training stage of Phase 2 to observe how participants redistribute attention after the most reliable source of information suddenly becomes irrelevant for identifying category membership. In both sections, we provide simulation results from AARM alongside the observed data in order to demonstrate the model’s ability to predict human-like information sampling and decision behaviors. Throughout, we will refer to Deterministic, Probabilistic, and Irrelevant dimensions as “D,” “P,” and “I,” respectively.
Case Study 1A: Conflicting Information
The within-trial module of AARM makes specific predictions about how feature encoding over the course of learning impacts information sampling behaviors and decision processes in the presence of new stimuli. The paradigm developed by Blanco and Sloutsky (2019) provides a unique opportunity to test these predictions, given that multiple dimensions provide information that is independently relevant to the task. Like the example provided in Figure 2, participants may achieve similarly high accuracy during training whether they selectively attend to the D dimension, a subset of P dimensions, or a combination of the two. In addition to the emergence of fixation preferences for particular dimensions, responses to test items in the current paradigm provide insight into how attention was distributed. Specifically, test items drawn from the Conflict condition contain a combination of features that are associated with opposite category labels. Responses consistent with information in the D dimension (i.e. rule-based responses) could therefore be interpreted as evidence that the participant learned to selectively attend to that dimension during training. Similar logic holds for the P dimension as well, such that selective attention to any combination of P dimensions could manifest in P-consistent responses.
For our purposes, we performed analyses and simulations that were considerate of individual differences in fixation preferences at test. Because feedback was only provided during training, we considered fixations at test to be a stable indicator of post-learning dimension-level attention. A histogram of fixation preferences across subjects is shown in Figure 7A. Considering only the first 10 test trials of Phase 1, we observed a relatively balanced distribution of fixation preferences for the D dimension as determined by normalized dwell times in the form (mean=0.541, min=0.00, max=1.00). We organized subjects into 3 groups on the basis of these fixation preferences: Group 1) Looking preference for P dimensions (; 12 subjects); Group 2) Mixed looking preference (, 12 subjects); and Group 3) Looking preference for P dimensions (, 14 subjects). Panels B-D of Figure 7 show mean trajectories of fixations within Phase 1 test trials (line plots) and subsequent response proportions to Match and Conflict stimuli (bar plots) for Groups 1, 2, and 3, respectively. Within-trial fixations to each of the 7 stimulus dimensions were calculated as percentages of the RT, binned by steps of 0.1%, averaged across trials, and smoothed using a moving window of size 1%. P dimensions were rank-ordered within-subject according to mean fixation probability across trials prior to aggregation in an effort to account for spurious differences among P dimension preferences when interpreting the results.
Figure 7. Case Study 1A: Conflicting information.

(A) Subject-level mean proportions of fixations to the deterministic dimension. (B-D) Left panels show mean proportions of fixations (y-axis) to each of the seven dimensions through time. Right panels show observed means and 95% CIs of proportions of rule-based (i.e. responses consistent with the deterministic feature) responses across match and conflict trials. (E-F) Fixation and response data were generated using AARM’s within-trial module. (H-J) Mean proportions of fixations to the deterministic, probabilistic, and irrelevant dimensions across observed (filled bars) and model-generated (unfilled bars) trials, collapsing across groups. (H) Fixation proportions across match trials. (I) Fixation proportions across conflict trials on which responses were consistent with the deterministic dimension. (J) Fixation proportions across conflict trials on which responses were consistent with the majority of probabilistic dimensions.
To simulate fixations and responses with AARM, we used a single set of parameters across subjects for the between-trial module (Table B2, Appendix B). Though other approaches could have been taken, we made this choice in an effort to isolate individual differences in sampling trajectories to feature-level encoding fidelity, as used by the within-trial module to make predictions about what features might occur in currently-unseen dimensions. For each subject, we interpolated the number of encoded D features across unique training stimuli based on each subject’s observed mean proportion of fixations to D at test (Figure 7A). Subject-level proportions of D fixations were split into quantiles and mapped to a discrete value between 5 and 9 (inclusive) to represent the number of unique training trials out of a possible 10 on which the D feature was perfectly encoded (i.e. fewer fixations to D at test implied fewer D features were encoded during training). The matrix , which contains the encoding status for the features of the stored exemplars (Equation 5), was then modified for each subject accordingly. A random selection of elements in the column of corresponding to the D dimension were set to 1 (meaning “encoded”), and were otherwise set to 0 (meaning “unencoded”). All elements in that corresponded to P and I dimensions were set to 1. We then simulated 1000 Match and Conflict trials for each subject. The parameter values and initialized attention weights used for our simulations were otherwise fixed across subjects and task conditions, and were optimized with respect to the observed patterns of data in aggregate. Because no feedback was given at test, trials were simulated in isolation without subsequent updating of the stored exemplars in matrix . Parameter values used for our simulations are provided in Table B2, Appendix B.
As shown in Figure 7E–G, AARM’s predictions reflect several important elements of the observed data. By simply accounting for encoding variability for feature values observed in the D dimension, AARM was able to predict the observed effect of increasing proportions of fixations to D from Group 1 to Group 3. Considering response probabilities, AARM further predicted the observed effect of increasing proportions of rule-based responses to conflict trials from Group 1 to Group 3. Although there are discrepancies between the observed data and the simulations in terms of, for example, the probabilities of initial fixations and mean response probabilities within each group, we consider these results to be promising overall. While we intentionally relegated individual differences in test behavior to encoding efficiency and held all other mechanisms constant, future work will more thoroughly investigate how partial encoding of individual items impacts the trajectory of between-trial learning in addition to within-trial sampling.
For our current purposes of qualitatively assessing AARM’s theoretical assumptions about within-trial dynamics, Figure 7H–J provide a proof-of-concept. Proportions of observed and simulated (same simulations shown in Panels E-G) fixations to D, P, and I dimensions were averaged across subjects within each test condition of Phase 1. Panel H shows that correct responses to Match stimuli (D and P features have matching category mappings) were preceded by a slight fixation preference for D compared to P when the data are considered in aggregate. Because D and P dimensions carried opposite category mappings on Conflict trials, we back-sorted the data by response in order to observe potential differences in fixation probabilities. Panel I shows that responses consistent with the D feature-to-category mapping were preceded by a fixation preference for D over P dimensions. Panel J shows the opposite fixation bias, such that responses consistent with the P feature-to-category mapping were preceded by a fixation preference for the P dimensions over D. As shown by the unfilled bars in Panels H-J, AARM predicts patterns of response-dependent fixations that closely match what we see in the data.
Here, we demonstrated AARM’s predictions about attention allocation and decision making as a result of successful learning and encoding efficacy. In the decision making literature, the widely-supported integrate-to-bound perspective suggests that information is sampled from multiple sources of information within a trial, and choices are made when the cumulative evidence in favor of one option exceeds a predetermined threshold (e.g. Ratcliff, 1978). Other work used eye-tracking methods to show that proportions of fixations to two competing options in value- and preference-based decision tasks are directly related to choice probability (Krajbich et al., 2010; Krajbich & Rangel, 2011; S. Smith & Krajbich, 2019a, 2019b; Thomas et al., 2019). Extending this logic to categorization decisions, the intuition is simple: if an observer doesn’t look at a particular dimension during a trial, the unseen feature will not contribute to the choice. While models that conceptualize attention as trial-level weights can adequately predict average proportions of responses in a variety of cases, the relationship between attention weights and information sampling behaviors has remained under-explored. AARM, however, makes specific predictions about which stimulus dimensions will be prioritized, attended, and sampled within a trial, and how sampling affects subsequent responses in the presence of new stimuli. Our simulations show that AARM not only predicts the same contingency between fixations and responses that are observed across experimental conditions of information consistency (Figure 7H–J), but can also predict individual differences in dimension prioritization as a result of encoding individual features (Figure 7E–G).
Case Study 1B: Shifting Information Relevance
We next explored how within- and between-trial attention dynamics interact over the course of learning. Previous work has demonstrated that adult learners use selective attention to prioritize the most relevant information (e.g. Desimone & Duncan, 1995) and can adapt to changing categorization rules via set-shifting (e.g. Chiu & Yantis, 2009). Although engaging selective attention can lead to faster, more efficient categorization, it can also result in learned inattention (A. Hoffman & Rehder, 2010). When an observer ignores a dimension after learning that it is uninformative for the task, it is often difficult for the observer to identify if and when the ignored feature becomes relevant at some point in the future.
The Blanco and Sloutsky (2019) paradigm provides an opportunity to observe how learners adapt to abrupt changes in information relevance when the the D and I dimensions from Phase 1 switch roles during the transition to Phase 2. With the addition of eye-tracking data (Blanco et al., under review), we gain additional insight into how selective attention and feature encoding modulate the impact of the switch on information sampling. Here, we discuss the observed effects of the switch on information sampling behaviors, and how these effects are explained by AARM. For clarity, we refer to the dimension that was Deterministic in Phase 1 and Irrelevant in Phase 2 as “D/I,” and we refer to its counterpart as “I/D.” The observed and model-predicted fixation results that are relevant to the current discussion are shown in Figure 8. Note that all panels in Figure 8 show data from the final trial in Phase 1 (Trial 20 of the Phase 1 test stage) and the first three trials in Phase 2, separated by a vertical black line.
Figure 8. Case Study 1B: Shifting Information Relevance.

The final trial of Phase 1 and the first three trials of Phase 2 are of primary interest. In all panels, the vertical black bar represents the “switch” from Phase 1 (left) to Phase 2 (right). (A) Between-trial module-generated attention weights (points) for unique stimulus configurations. (B) 100 sequences of within-trial fixation and decision behaviors were generated by the within-trial module, using the specific sequence of stimulus configurations that each participant experienced. (C) Within-trial probabilities of fixating to each dimension were aggregated across subjects, and plotted as a function of percentage of observed response time. (D-H) Data and simulations for two groups, specified according to the proportion of fixations to D dimensions during the latter 10 trials of Phase 1 test. Group 1 showed a looking preference for D, whereas Group 2 showed a looking preference for P. Probabilities of fixating to the deterministic (D and G), or any of the five probabilistic (E and H) dimensions were averaged across observed (filled bars) and model-generated (unfilled bars) sequences.
We first discuss the observed results, as shown in Figure 8 C and D–H. Although participants were not informed of the switch, the aggregate data shown in Figure 8C indicate that participants quickly realized that the dimension that was most reliable for identifying category membership in Phase 1 (left-most panel; green line) was no longer reliable in Phase 2 (remaining panels; purple line). Across the four trials of interest, we observe a steady decrease in the proportion of fixations to the D/I dimension. This awareness, however, did not extend to the change in relevance for the formerly Irrelevant dimension: participants continued to ignore I/D in Phase 2, presumably as a result of learned-inattention incurred during Phase 1 (A. Hoffman & Rehder, 2010). Instead, participants reoriented attention to a P dimension after the switch. Prioritization of P and inattention to I/D persisted across the entirety of Phase 2, beyond the initial three training trials shown in Figure 8 (mean proportion of fixations across Phase 2: I/D=0.168, P=0.629, D/I=0.203).
In Case Study 1A, we observed how dimension-level fixation preferences related to choice behavior during Conflict trials. We expected to observe related effects in the current case study, such that participants who tended to fixate to D during Phase 1 would demonstrate larger effects of attention reorientation after the switch to Phase 2. We specified two groups on the basis of proportions of D/I fixations across the last ten test trials of Phase 1. This differs from the group delineations in Case Study 1A (proportions of D fixations across the first ten test trials of Phase 1) in order to be considerate of potential effects of the Conflict trials on information sampling. Here, we specify Group 1) Looking preference for , and Group 2) Looking preference for P . As shown in Figure 8D–E, Group 1 showed rapid deprioritization of D/I across the trials of interest, such that the mean proportion of fixations to D/I dropped from 0.72 to 0.14. This was accompanied by increased prioritization of P, such that the mean proportion of fixations across P dimensions rose from 0.26 to 0.78. Switch effects were substantially less severe in Group 2, as shown in the left panels of Figure 8G–H. The mean proportion of fixations to D/I dropped from 0.26 to to 0.12 over the relevant trials, and the mean proportion of fixations to the P dimensions increased slightly from 0.72 to 0.81 over the same period.
To simulate data in AARM, we first used the between-trial module to determine a set of initialization weights for the 4 trials of interest. As in Case Study 1A, we made the decision to relegate differences in sampling behavior to mechanisms for feature prediction in the within-trial module. As such, the set of weights from the between-trial module were generated with a single set of parameters, and were therefore constant across all subject-level simulations. Figure 8A shows the progression of attention weights generated by the between-trial updating mechanism in AARM, given the 10 unique training stimuli in Phase 1 and three training trials in Phase 2. Over the course of Phase 1, the model learns to increase attention to D/I and decrease attention to I/D. Following the switch, attention to D/I decreases and is redistributed among the P dimensions, while attention to the I/D dimension remains consistently low.
For within-trial simulations, each subject’s proportion of D/I fixations during the last 10 test trials of Phase 1 was mapped to a discrete value between 6 and 9 (inclusive) to represent the number of training trials out of a possible 10 on which the D/I feature was encoded (i.e. fewer fixations to D at test implied fewer D features were encoded during Phase 1). The feature encoding matrix, , was then modified as described in Case Study 1A. We probed the within-trial module with the exact sequence of stimuli that each participant actually observed; specifically, the last test trial of Phase 1 and the first three training trials of Phase 2. For each simulated trial, the model outputs were: 1) a category response; 2) a response time equal to the number of iterations between initialization and self-termination; 3) a vector of predicted fixations with length equal to the RT, in which each element corresponded to a discrete dimension; and 4) a binary vector , which indicated whether each dimension was encoded or not by the end of the trial. After each trial in a sequence, the feature-identity of the probe was appended to the matrix of stored exemplars along with the corrective category feedback received by the participant. Similarly, was appended to the exemplar encoding matrix, . Elements that were set to 0 in functioned as a mask over the corresponding feature values in , such that feature information about a stimulus in a sequence was only accessible to the model on subsequent trials if it was encoded. We simulated 1000 sequences of the four relevant trials for each subject. All simulations used the same set of parameters, which were optimized with respect to the observed data in aggregate (Table B2, Appendix B).
Figure 8B shows the model-predicted time course of fixation probabilities within each trial, averaged across subjects. At the end of Phase 1, the model predicts initial orientation to D/I on the basis of learned relevance (green line), but gradually reorients to a P dimension upon observing that the novel feature value in D/I is no longer relevant in Phase 2 (purple line). In Figure 8D–H, we observe that the model additionally predicts stronger effects of D/I-deprioritization and corresponding prioritization of P in Group 1 compared to Group 2. Despite minor qualitative discrepancies considering the precise timecourse of fixation probabilities, we consider these effects to be consistent with the observed data. With AARM’s specification, the necessity of redistributing attention after the switch is contingent upon the extent to which the observer encoded features in the D/I dimension to begin with.
Hierarchical Category Structures
For decades, it has been known that hierarchical structures play an important role in guiding goal-directed behaviors, such that humans instinctively use superordinate sources of information to determine appropriate actions (e.g. Estes, 1972; Lashley, 1951; Miller, Galanter, & Pribram, 1960). In task-cueing and task-switching paradigms, for example, humans are able to engage in different sets of rule-based behaviors in response to a stimulus-independent indicator (see Monsell, 2003, for review). In work by Meiran (1996), participants learned to classify digit stimuli as either odd/even or high/low depending on the shape or color of a background cue. While the authors observed notable switch costs, such that participants were slower to respond on the first trial after a rule-switch, participants were indeed able to learn the mapping between background cues and the current rule in both predictable and unpredictable conditions of subtask sequences (see Allport, Styles, & Hsieh, 1994; Rogers & Monsell, 1995, for similar results). Given that digit stimuli were drawn from a common distribution across odd/even and high/low subtasks, one interpretation of Meiran’s (1996) results is that the feature value of the background cue served as a hierarchically-superordinate indicator of whether participants should attend to the digit’s parity or magnitude on each trial.
Other work has suggested that humans use sources of contextual information to determine how to selectively allocate attention as well (e.g. Chun & Jiang, 1998; Chun & Turk-Browne, 2007; Crump, Milliken, Leboe-McGowan, Lebowe-McGowan, & Gao, 2018; Egner, 2008; Vecera, Cosman, Vatterott, & Roper, 2014). In a contextual-cueing task conducted by Chun and Jiang (1998), for example, participants were able to use the global arrangement of stimuli as a cue for identifying the spatial location of a visual search target. These results are in line with seminal theories of memory and attention, in which contextual cues are bound to stimuli during encoding, and influence automatic attentional processing at test (Norman, 1968; Norman & Shallice, 1986; Shiffrin & Schneider, 1977).
In the three case studies to follow, we will use AARM to explore how hierarchical category structures give rise to distinct patterns of information sampling behaviors and within-trial changes in selective attention. We will first discuss results originally reported by Blair et al. (2009), which showed that humans prioritize information in a manner that is consistent with hierarchically-organized stimulus dimensions. We will then expand the concept of hierarchical structures to environmental context as a superordinate dimension for determining how to appropriately distribute attention across the dimensions of the stimulus itself.
Case Study 2: Dimension Prioritization
In Case Studies 1A and 1B, we discussed how learning and memory impact the way humans decide which dimensions to sample when provided with a new stimulus. Case Study 2 further considers how the feature information contained within the current stimulus can impact the path and timecourse of attention allocation. As shown in Figure 1C, for example, hierarchically-organized category structures contain jointly-deterministic dimensions, such that the feature value contained in the superordinate (green squares) dimension indicates which of the available subordinate dimensions (orange triangles or purple crosses) is relevant to category membership. Such structures are ideal for studying within-trial dynamics, as they give rise to distinct temporal ordering effects of dimension sampling behaviors between stimuli.
First, we present eye-tracking data from 41 subjects that were provided freely online by Meier and Blair (2013). The “1:1 condition” (equal frequency across category exemplars during training; Experiment 2) used the same stimuli and study design that were originally developed by Blair and colleagues (2009). Stimuli were fictional microorganisms, each containing a triad of equally-spaced dimensions (organelles). Each dimension could take on one of two possible features, resulting in 8 unique stimulus configurations. Stimuli were assigned to 4 categories (A1, A2, B1, and B2) based on a hierarchical category structure, such that one dimension (D1) indicated membership in an A or a B category, the second dimension (D2) differentiated between A1 and A2, and the third dimension (D3) differentiated between B1 and B2 (i.e. Figure 1). Participants completed 480 trials with feedback, and were excluded from further analyses if they failed to exceed an accuracy criterion of 80% within the latter 120 trials (10 subjects; Meier and Blair (2013)). Following the analyses presented by the original Blair et al. (2009) study, we aggregated fixations to each dimension separately across category A and B items in the final 72 trials of the experiment. Mean fixation probabilities shown in Figure 9A, reflect striking differences in dimension prioritization between trial types. Replicating the findings from Blair et al. (2009), the results from Meier and Blair (2013) show that participants tended to fixate to the superordinate dimension first, then shift their gaze to the subordinate dimension that was relevant to the current trial while ignoring the alternative.
Figure 9. Case Study 2: Hierarchical Category Structures.

(A) Observed fixation data from Experiment 2 (1:1 condition) from Meier and Blair (2013) while participants categorized stimuli that belonged to categorized A (left panel) and B (right panel). (B) Within-trial fixation predictions generated by AARM, aggregated across 1000 probes from categories A (left panel) and B (right panel). (C) Means and 95%CIs of dwell times to each stimulus dimension in milliseconds, calculated across category A (left set of bars) and B (right set of bars) trials. Filled bars show observed data and unfilled bars show model predictions.
For our simulations with AARM’s within-trial module, we first used the between-trial module to generate post-learning initialization weights after a single exposure to all 8 unique stimulus configurations. After normalization (see Attention Orientation section) D1 received the highest weight (0.505) and D2 and D3 each received lower but equivalent weights (0.248). We then used the within-trial module to simulate 1000 isolated trials without feedback using A- and B-labeled probes as inputs. Outputs of each simulated trial were: 1) a category response; 2) an RT equal to the number of iterations between initialization and self-termination; and 3) a vector of predicted fixations with length equal to the RT, in which each element corresponded to a discrete dimension (i.e. D1, D2, or D3). For generating dwell times, iteration units were converted to milliseconds by simple scalar multiplication.
The simulated paths of fixations generated by AARM shown in Figure 9B closely resemble the observed behavior shown in Figure 9A. Across A and B probes, the model predicts a fixation bias toward the superordinate D1 dimension for the first 30–40% of the trial’s full duration before reorienting to the relevant D2 or D3 dimension. As a reconfiguration of the results shown in Figure 9A–B, Figure 9C shows total dwell times to each dimension, averaged across trials. Both observed (filled bars) and model-predicted (unfilled bars) results show approximately equal dwell times (600–650ms) for the two dimensions that were relevant to each trial (D1 and D2 for category A stimuli; D1 and D3 for category B stimuli) and substantially shorter dwell times for the irrelevant dimension (D3 for category A stimuli; D2 for category B stimuli).
Blair et al.’s (2009) original study provided compelling evidence that humans allocate attention in way that 1) favors features that are relevant within the current trial; and 2) is observable via within-trial gaze fixation paths. Until recently (see Braunlich & Love, 2021), however, category learning models have not been subjected to constraints related to temporal ordering of prioritized dimensions. By explicitly defining how mechanisms for between-trial attention weights manifest in distinct paths of information sampling, AARM demonstrates the unique ability to relate latent theoretical constructs of attention to observable time courses of within-trial behavior.
Case Study 3: Task Cueing
Here, we extend the concept of hierarchical structures to contextual cues as a superordinate dimension. Specifically, we used AARM to simulate response data across a set of rule-based (RB) and information-integration (II) subtasks in which a context dimension (i.e. background color) indicated which stimulus information was relevant for categorizing a common set of stimuli. While 2-dimensional RB tasks require observers to categorize stimuli on the basis of a single dimension only, II tasks require integration of feature information across multiple dimensions (Ashby, Alfonso-Reese, & Waldron, 1998; Maddox & Ashby, 2004; D. Smith et al., 2012). Humans and nonhuman primates have demonstrated an ability to learn both RB and II tasks, but are notably faster and more accurate at learning in the former case (Maddox & Ashby, 2004; D. Smith et al., 2012). Even when stimulus dimensions co-occur in space, behavioral evidence suggests that humans can selectively attend to task-relevant dimensions while ignoring the others (Ashby & Maddox, 2005).
We designed a simulation paradigm after O’Donoghue, Broschard, and Wasserman (2020) to provide what we consider to be a clear demonstration of context-dependent learning and selective attention with AARM. However, we do not draw comparisons to observed data in the current case study. Given that data from O’Donoghue et al. (2020) were collected from pigeons rather than humans in an effort to study behavior in the absence of an analytic category learning system, we do not expect a model of human category learning like AARM to produce analogous behavioral results. Instead, the goal of Case Study 3 is to demonstrate AARM’s ability to extend to categorization problems with 1) continuously-valued dimensions; 2) spatially co-occurring dimensions; and 3) multiple levels of trial complexity (where II trials are assumed to be more complex than RB).
Figure 10A illustrates the hypothetical paradigm used here. Each point represents a combination of frequency (x-axis) and tilt angle (y-axis) feature values for a single Gabor patch that was created from a common, normally-distributed stimulus space across trials. Contexts 1 and 2 denote RB subtasks, such that category membership was determined by high vs. low frequency or large vs. small tilt angle, respectively. Contexts 3 and 4 denote II subtasks, such that category membership was determined by the integration of both frequency and tilt angle information.
Figure 10. Case Study 3: Task Cueing.

(A) Illustration of stimuli and category delineations from four sub-tasks of a hypothetical experiment. Points represent Gabor patch stimuli that each take on a frequency value (x-axis) and a rotation angle value (y-axis). Background colors served as an indicator of the categorization rule for each sub-task: frequency distinguished between categories A and B in Context 1 (rule-based), angle distinguished between categories C and D in Context 2 (rule-based), and both frequency and angle were necessary for distinguishing between categories E and F in Context 3, and categories G and H in Context 4 (information integration). (B) Mean encoding probabilities of each dimension (y-axis) plotted as a function of the percentage of time in between stimulus onset and response (x-axis). Solid, dotted, and dashed lines represent context, frequency, and angle dimensions, respectively. (C) Probabilities of making an A-H response (y-axis) plotted as a function of the percentage of time within-trial between stimulus onset and response (x-axis). Each color represents an available category label, as shown in panel A.
To represent Gabor patches that varied continuously on frequency and tilt angle dimensions, we randomly drew 400 points () from a bivariate normal distribution with means of 0 and standard deviations of 1. One hundred points were randomly allocated to each of the 4 contexts, and category labels were assigned according to the relevant rule as follows:
| Context | Rule | Category |
|---|---|---|
|
| ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
Training stimuli with category labels were stored as rows of exemplar matrix , with the first two elements taking on continuous values, and the third element taking on a discrete value between 1 and 4 (inclusive) to represent context. All 400 training stimuli were iteratively introduced to AARM’s between-trial module, and the post-training weights for each dimension were: 0.195 (X; frequency), 0.194 (Y; tilt angle), and 0.611 (context). As in the previous case studies, attention weights in the within-trial module were initialized to the post-training values determined by the between-trial module. Four probes were each introduced to the within-trial module 1000 times without feedback. Feature values corresponding to the and dimensions were set to 1 across probes (shown as crosses in Figure 10A), and context feature values corresponded to each of the 4 unique contexts in the task. By contrast to the previous case studies in which dimensions were spatially-segregated, encoding probability was not gated by the output of the error gradient (i.e. gaze fixations). Instead, both attention weights and encoding probability were continuously updated throughout the trial for all dimensions simultaneously, given that context, tilt, and angle dimensions co-occurred in space. Outputs of each simulation were: 1) a category choice (A-H); 2) a matrix of choice probabilities across categories at each timestep prior to self-termination; 3) an RT (number of iterations); and 4) a binary matrix indicating whether each dimension was encoded.
Within-trial averages of dimension encoding and choice probability across simulated trials are shown in Figure 10. As a reflection of the inherently hierarchical structure of the paradigm, we observe that context is prioritized across both RB (Contexts 1 and 2) and II (Contexts 3 and 4) subtasks, as illustrated by consistently early encoding of the context dimension (approximately 25% of the response time; Panel B). Analogues of selective attention emerge, however, when we observe which stimulus dimensions were encoded in each context. In accordance with the RB category structure learned in Context 1, the model tended to encode the frequency (X) dimension but not the tilt angle (Y) dimension across probes. By contrast, the model encoded tilt angle but not frequency when presented with a probe in Context 2. Humans are known to engage similar selective attention processes in the presence of integrated dimensions (see van Moorselaar & Slagter, 2020, for recent review), and these effects are accompanied by reduced subsequent memory for task-irrelevant stimulus features (e.g. Olivers, Peters, Houtkamp, & Roelfsema, 2011; van Moorselaar, Theeuwes, & Olivers, 2014).
While context and only one stimulus dimension were encoded in RB Contexts 1 and 2, both frequency and tilt angle dimensions were encoded when probes were presented in II Contexts 3 and 4. This behavior is appropriate given the demands of the two II subtasks, in which integration of both stimulus dimensions is required to correctly identify category membership. Given probes with identical frequency and tilt angle feature values, AARM predicts maximum probabilities of correctly responding “B”, “C”, and “F” when presented in Contexts 1, 2, and 3, respectively. Because the stimulus probe is located on the category boundary in Context 4, AARM predicted an equal probability of selecting categories G or H at the time of the response. Overall, the timecourses of choice probability predicted by AARM indicate both successful mapping of context to relevant candidate responses, as well as successful adoption of learned RB and II categorization rules.
The current case study is similar in scope to Case Study 2 in that context serves as a superordinate hierarchical indicator of the rule. Case Study 3 was meant to build upon the results of Case Study 2 in two important ways: 1) the RB vs. II distinction demonstrates that AARM encodes spatially co-occurring dimensions independently or simultaneously, depending on the demands of the task; and 2) the use of continuous dimensions demonstrates that AARM can generalize learned information to categorization decisions about novel stimuli. Although the exact combination of probe feature values introduced at test were never observed during training, AARM was still able to use information about context to engage selective attention (Figure 10B) and predict responses consistent with learned RB and II subtasks (Figure 10C). Building upon the simulation results presented here, Case Study 4 will investigate how the nature of the learning environment can potentially modulate attention to context during training, and subsequent context-dependent behavior at test.
Case Study 4: Incidental Context
By design, context in Case Study 3 indicated the rule that was relevant to each stimulus, and was therefore relevant to category membership itself. Empirical evidence has further suggested that environmental context plays a role in memory encoding and retrieval even when context is not directly relevant to the goals of the task (i.e. Godden & Baddeley, 1975; S. Smith, Glenberg, & Bjork, 1978). These effects extend from complex-place to simple computerized manipulations of context as well (i.e. background color: Dulsky, 1935; Murnane, Phelps, and Malmberg, 1999; Isarida and Isarida, 2007; screen location: Dix and Aggleton, 1999; font size: Perfect, 1996). In the memory literature, these two types of context have been characterized as “local” and “global” context, respectively (Baddeley, 1982; Eich, 1985; Murnane et al., 1999). Whereas local context is associated with a subset of items and influences the representation of stimuli during encoding, global context refers to aspects of the learning environment that are independent of the to-be-remembered information (Hockley, 2008). Building from our examination of local context in Case Study 3, Case Study 4 tests the extent to which AARM can predict context-related differences in behavior, even if context is not identified as an independently-relevant dimension during learning.
Case Study 4A: Context Integration
In the current case study, we focus on a paradigm that was developed by Sloutsky and Fisher (2008) to examine context-dependent generalization of learned concepts in 4- to 5-year-old children. Global contextual features (i.e. the color of a background rectangle and the stimulus’s location on the computer screen; Figure 11A) co-occurred with categorization rules during training but were not independently relevant to the task. In the presence of novel test items with conflicting stimulus features, however, observed response biases indicated that participants had indeed learned the contingencies between contexts and categorization rules. Simulations with AARM provide an explanation for how the observed pattern of results might occur.
Figure 11. Case Study 4: Incidental Context.
Figure adapted with permission from Child Development. (A) Illustration of contexts. (B) Training stimuli. Stimuli were triads of items, and the task was to select one of the two choice options (top two items) that matched the target (bottom item) according to a rule. Yellow arrows indicate a path from the target to the correct choice option. (C) Test stimuli. Note that identical stimulus configurations were shown in Contexts 1 and 2, but yellow arrows indicate that different responses are appropriate according to the context. (D) Hypothetical training stimuli for simulation purposes. (E) Attention weights generated by the between-trial module of AARM before (left bar) and after exposure to each set of training stimuli and their category labels. Each color represents a stimulus dimension, and larger segment heights correspond to larger attention weights. (F) Observed proportions of shape-based responses in each context. (G-H) Model-generated proportions of shape-based responses in each context at test, following Training A and B. The context dimension in our simulations was either considered to be integrated (perceptually overlapping) with the dimensions of the stimulus triad (G) or segregated (separate in space and requiring independent perceptual processing) from the dimensions of the stimulus triad (H).
Stimuli were triads of items, with each item varying on the basis of shape (circle or triangle) and color (red or blue). Triads consisted of a target and two choice options, and the task on each trial was to select the choice option that matched the target on either the shape or the color dimension. Forty-two participants underwent training in which they responded to two types of trials with feedback: 1) in Context 1, all items in a triad had the same color, and participants had to respond on the basis of shape (Figure 11B, top: yellow arrows show paths from target to correct response); 2) in Context 2, items had the same shape, and participants had to respond on the basis of color (Figure 11B, bottom). After 48 training trials, participants completed 16 test trials without feedback. By contrast to the training phase in which triad items only varied on a single dimension per trial, test triads were ambiguous. As shown in Figure 11C, one choice option matched the target on the basis of shape (and mismatched on color) while the other matched the target according to a rule. Half of the participants completed the test phase in Context 1, and the other half in Context 2. As a baseline, a separate group of 32 participants completed the test phase in both contexts after receiving no training at all. The behavioral results of the test phase are shown in Figure 11F. When tested in Context 1, participants who underwent training were more likely to respond on the basis of shape than the untrained participants. When tested in Context 2, trained participants were more likely to respond on the basis of color than the untrained participants.
We ran simulations with AARM using two sets of training stimuli. Here, we discuss simulation results from Training Set A, which had the same characteristics as the training stimuli described above. Results from simulations that used the hypothetical Training Set B will be discussed in Case Study 4B. We first introduced each unique training stimulus to the between-trial module to generate initialized weights for the within-trial module. Because context co-occurred with the relevant target dimension and therefore did not contain independently relevant information, AARM allocated minimal attention to context. As shown in Figure 11E (Training A), the shape and color of the target received the highest attention weights (0.312), and context received the lowest weight (0.040), with shape and color of the choice options falling in between (0.084). After initializing the within-trial model’s attention weights, probe stimuli containing each of the two possible context feature values were introduced to the model separately. Within each of the two probes, one choice option matched an arbitrarily-chosen target according to shape, and the other choice option matched the target according to color as follows:
| Item | Dimension | Probe 1 Features | Probe 2 Features |
|---|---|---|---|
|
| |||
| context | 0 | 1 | |
| Target | shape | 0 | 0 |
| color | 0 | 0 | |
| Option 1 | shape | 0 | 0 |
| color | 1 | 1 | |
| Option 2 | shape | 1 | 1 |
| color | 0 | 0 | |
Using each probe, we ran 1000 independent within-trial simulations without feedback. Each simulated trial yielded a binary response corresponding to either the left or the right choice option in the stimulus triad.
We assumed that shape and color of a given triad item could be encoded simultaneously, given that they occupied the same location in space. Mechanisms for contextual encoding, however, were much less straightforward. We therefore performed two sets of simulations using Training Set A, each representing a different hypothesis for how context is processed and encoded. In one set, contextual information was considered to be integrated with the item-level information at each respective spatial location, such that the probability of encoding context was updated continuously within-trial. In the other set, context was considered to be a segregated dimension, such that the observer had to fixate to context independently from the items in the triad in order to encode its information. As shown in Panel G, AARM predicts behavioral results that are consistent with the observed data when contextual information is integrated with stimulus information. Specifically, AARM predicts a higher proportion of shape-based responses to test items presented in Context 1 compared to Context 2. When context is considered to be a segregated dimension, however, Figure 11H shows that AARM does not predict the observed response bias on ambiguous test items following Training A. Instead, the model predicts an approximately equal probability of making a shape-based response in both Contexts 1 and 2. Because context is not independently relevant to the task during training and the observer has therefore not learned to explicitly attend to it, context will only be used during the decision process if it is encoded by other, passive means. Our results suggest that attention in AARM is a possible mechanism for the effects of global context on behavior, such that contextual information can be passively encoded along with the features of a stimulus despite a lack of known predictive utility at the time of learning.
Case Study 4B: Context Relevance
We ran an additional set of simulations using a hypothetical Training Set B, in which context was a hierarchically-superordinate indicator of whether shape or color was relevant on each trial. Training B stimuli were configured identically to the test set in Sloutsky and Fisher (2008), such that one choice option matched the target according to shape, and the other choice option matched the target according to color (Figure 11D). Although observed responses using the alternative Training B were not published, we performed these additional simulations to provide direct contrast between the influences of global and local context in AARM’s specification. We first used the between-trial module to calculate a set of attention weights after observing all 16 unique stimuli in Training B. As shown in Figure 11E, the context dimension was assigned the highest weight (0.471) followed by target shape and color (0.168) and shape and color of the two choice options (0.048). The post-training weights from the between-trial module were used to initialize the within-trial model on 1000 simulations. We used the same two probes that were used to examine the learning effects of Training A.
As previously described, context was implemented as an integrated- (passively encoded along with fixated stimulus information) or segregated (encoding requires independent fixation) dimension in two separate sets of simulations. AARM predicts the same pattern of responses at test as a result of Training B, regardless of whether context is considered to be an integrated (Figure 11G) or a segregated (Figure 11H) dimension: in both cases, AARM predicts a higher proportion of shape-based responses when triads are presented in Context 1 compared to Context 2. Because the model is able to learn the hierarchical structure of the Training B stimulus set in which context is the superordinate dimension, it responds to test stimuli by orienting to and encoding context independently from the items in the triad. Therefore, Training B does not require AARM to overcome reduced attention to context via passive encoding related to feature integration.
As part of a study that investigated context-mediated transfer of learning in categorization tasks, George and Kruschke (2012) used model simulations to demonstrate that the results from Sloutsky and Fisher (2008) could be explained by associative learning alone, without the involvement of additional selective attention mechanisms. More specifically, the authors used two associative learning models (Pearce, 1994; Rescorla & Wagner, 1972) to show that context-consistent responses at test could arise on the basis of asymmetrical feature-level similarity between the given test stimulus and a subset of training items. As shown by our AARM simulations in which context is instantiated as an independent dimension relative to the elements of the stimulus triad, however, the influence of context on behavior is not guaranteed from the experimental design of Sloutsky and Fisher (2008) (Figure 11H). If we can, for the purposes of argument, assume that the role of attention is ubiquitous in category learning, AARM’s within-trial mechanisms offer an alternative to the purely association-based explanation provided by George and Kruschke (2012) that overcomes reduced attention to context incurred as a result of training. By incorporating global context as an integrated dimension that is peripherally attended during item-level processing at test, AARM predicts context-mediated patterns of behavior consistent with the results of Sloutsky and Fisher (2008) (Figure 11G). Although several studies have found evidence that global context during learning influences future decision-making behavior (Geiselman & Glenny, 1977; George & Kruschke, 2012; Murnane & Phelps, 1993, 1994; S. Smith, 1986; S. Smith & Vela, 1992), other studies observed the opposite pattern of results (Griffiths & Le Pelley, 2009; S. Smith & Vela, 2001). Given that AARM makes dissociable predictions about the influence of global context depending on the extent of feature integration, AARM can potentially be used in future work to identify which elements of context are bound to stimuli during encoding, and which are not.
General Discussion
The between-trial module of AARM comprises a theoretical framework for how attention allocation, decision making, and item representations interact to facilitate learning. Here, we extended AARM to account for within-trial dynamics as well: specifically, the mutually-influential timecourses of dimension-level information sampling and response evidence. Like AARM’s between-trial module, several models predict learning as a consequence of the strategic manipulation of attentional resources over the course of a task. Most, however, do not make explicit assumptions about how the latent distribution of attention might affect how dimensions are prioritized within a trial. AARM therefore stands apart from other accounts of category learning because it seeks to close the loop between updating latent attention according to trial-level feedback, and subsequently deploying attentional resources to acquire relevant information when the next stimulus appears.
As discussed in the introductory sections, there were four overarching theoretical components to the current work. First, both within- and between-trial dynamics are described by a common set of mechanisms. For AARM to be viable, it was important that the within-trial module be constructed from the same cognitive machinery and operations that were purported by our previous work to be engaged in service of the broader learning problem (Galdo et al., 2021). As such, the Model Specification section provides a core set of mechanisms that operates at multiple timescales to explain how humans both learn about new categories, and acquire information about new stimuli.
Second, humans form simplified representations of stimuli from the features that are perceived to be relevant to the task. Given our previous findings that dimensions compete for attention and that only the attended subset appears to contribute to categorization decisions, the within-trial module was necessary to explain how strategic reorientation and self-termination behaviors might emerge. We therefore specified dynamic processes through which attention, decision evidence, and an evolving stimulus representation inform one another, but only until the observer has acquired enough information about the stimulus to map it to a particular category.
Third, attention allocation is optimized with respect to a goal. The learning problem in the between-trial case is well defined, such that the observer can conceivably redistribute attention upon observation of feedback in an effort to reduce the probability of future errors. Indeed, rational theories of psychological processes predict behaviors via optimization of a cost function given some set of environmental constraints (Sakamoto et al., 2008; Sanborn et al., 2010). The costs of sampling information from a feature that provides support for an incorrect category label cannot be ascertained and avoided, however, before the correct label has been provided by feedback. The within-trial module therefore assumes observers seek additional support for the category label that they believe to be correct at each moment in time. The result is a parsimonious extension to attention optimization that is consistent with observable human biases of confirmatory search.
Fourth, attention processes are sensitive to hierarchical structures. Given eye-tracking results showing distinct temporal ordering effects that are consistent with hierarchical structures (Blair et al., 2009), it was important that the within-trial module be able to produce similar trajectories of orienting. In several of our case studies (i.e. 2, 3, and 4), hierarchical organization of information via selective attention was essential for producing the expected patterns of information sampling behaviors and responses. We argue that hierarchical structures are not a special case of experimental manipulations, but are rather ubiquitous in nature given observable impacts of environmental context on information processing and behavior.
Across four case studies, we used model simulations to demonstrate AARM’s capacity for predicting plausible patterns of behavioral responses (Case Studies 3 and 4), eye-tracking data (Case Study 1B), or both simultaneously (Case Studies 1A and 2). Our preliminary results provide qualitative support for the within-trial mechanisms proposed by AARM. In Case Study 1, we demonstrated how individual differences in information sampling and response probabilities could emerge due to selective attention and encoding variability, despite all participants experiencing the same stimuli during training. In Case Study 2, we showed that distinct temporal ordering effects of information sampling emerge in the presence of hierarchical stimuli through a combination of experience-biased orienting and mechanisms for ongoing feature predictions. Case Study 3 used hypothetical stimuli to present the possibility that even when dimensions co-occur in space, selective attention could be a mechanism through which only the information that is relevant to individual trials will be encoded and concurrently contribute to the choice. Case Study 4 explored how contextual features could bias decisions at test even if they were not explicitly attended during training. If contextual features are considered to be integrated with the stimuli of interest, they could be passively encoded and subsequently accessed to provide orienting cues if an ambiguous stimulus should occur in the future. In the sections to follow, we will discuss the implications of our results and suggest future extensions that pertain to AARM’s component mechanisms.
Self-Termination
Most models of category learning assume that observers access all feature information across stimulus dimensions when making category judgements. While this may be plausible in laboratory tasks that include stimuli with only a few dimensions, it is potentially unreasonable to assume that humans encode all available perceptual information from the complex stimuli that they encounter in the real world. To make efficient decisions, humans therefore need to identify the dimensions of information that are relevant to their current goals. Using variants of AARM that instantiated different modes of simplicity bias, Galdo et al. (2021) provided evidence that humans tend toward low-dimensional representations as they learn. One interpretation of these findings is that while humans strive to achieve high accuracy in a task setting, they concurrently seek to reduce time and resource expenditure on individual trials (Boureau, Sokol-Hessner, & Daw, 2015; Cisek, Puskas, & El-Lurr, 2009; Thura, Beauregard-Racine, Fradet, & Cisek, 2012; Yau et al., 2021).
Given evidence that memories for past events influence how we make predictions about the environment (S. Smith & Vela, 1992) and encode new information (Bowman & Zeithamova, 2020), it stands to reason that the construction and storage of low-dimensional representations might bear a meaningful impact on how the observer interfaces with new stimuli. In Case Study 1, we used the within-trial module of AARM to investigate the potential impact of feature-level encoding variability on subsequent information sampling behaviors in a paradigm with multiple independently-relevant sources of information (Blanco & Sloutsky, 2019). In particular, we manipulated the extent to which previously-presented features of the deterministic dimension were successfully encoded in memory, such that they were accessible when the observer forms expectations about what features a new stimulus might take on. If humans form simplified representations based on only a few dimensions, our hypothesis was that selective attention to a subset of probabilistic dimensions would yield reduced encoding of deterministic features across trials, whereas selective attention to the deterministic dimension would yield a high probability of encoding its features. Although attention was initialized with the same values across simulations, we found that manipulating feature expectations via the encoding structure of the model was sufficient for predicting notable differences in fixation paths when new stimuli were presented. Importantly, this manipulation also produced differences in proportions of responses in the presence of novel stimuli with conflicting feature-to-category mappings (Case Study 1A), and the extent of reorientation after a categorization rule-change (Case Study 1B) that were consistent with observed effects.
Two contributions of the within-trial module, then, are that it 1) provides an explanation for how low-dimensional representations are formed through self-terminating attention and decision processes; and 2) allows us to investigate potential impacts of low-dimensional representations on how observers seek out information and respond when presented with new stimuli. While our interest in the current paper was to articulate a theory for how learned information (i.e. memories and goal-directed attention) fundamentally shapes how future knowledge is sought after and acquired, the effects of partial or variable encoding of individual stimuli during learning requires further investigation. The between-trial module of AARM and other iterations of GCM allow for variable memory strength at the level of the global stimulus, such that traces of exemplars are subject to decay as they recede into the past. It is generally assumed, however, that all features are encoded and are available for similarity comparisons as new stimuli are presented. As a future direction, we will therefore use insights provided by the current work to extend the between-trial module of AARM to problems of partial encoding. In high-dimensional environments in particular, the sources of information that are fixated and encoded early in learning may have profound impacts on how attention is selectively distributed in the future. As such, accounting for partial encoding during the learning process would be essential for assessing the relative contributions of initialized attention weights and feature-level memory in generating patterns of behavior like those observed in Case Study 1.
Confirmatory Search
We have made efforts to contrast AARM with SEA, an alternative theory of learning and information sampling (Braunlich & Love, 2021). As a rational account, SEA’s purpose is to identify the most cost-effective action within a set of environmental constraints (Sakamoto et al., 2008). While the two models often make similar predictions, AARM fulfills a different purpose of characterizing plausible mechanisms that manifest in human-like behaviors. Its base implementation was therefore designed to be amenable to influences from observable biases in human learning, whereas SEA was developed to generate optimal sampling paths under various environmental conditions. One major way that AARM departs from SEA is the specification of confirmatory information search. Although unbiased approaches could have been taken, behavioral effects of confirmatory search have been widely observed in causal judgement tasks (Rabin & Schrag, 1999; Schustack & Sternberg, 1981; Shaklee & Fischhoff, 1982; Wason & Johnson-Laird, 1972), and more recently in visual search as well (Rajsic, Taylor, & Pratt, 2017; Rajsic, Wilson, & Pratt, 2015).
Although the two models have not been directly compared, both AARM and SEA have been shown to produce human-like behaviors of reorientation and self-termination in the presence of hierarchical stimuli from Blair et al. (2009). The manner in which the models perform the task after training, however, differ in interesting ways. As discussed in Case Study 2 and the examples provided in the Within-trial Updating Rule section, AARM’s between-trial module upweights attention to the superordinate dimension over the course of training upon observing its relevance to the categorization response on every trial. The within-trial module therefore orients to the superordinate dimension on the basis of post-training attention weight. When sufficient cumulative attention is applied for a feature value to be encoded, active retrieval of similar exemplars coupled with ongoing updates to attention causes the observer to reorient to a subordinate dimension, depending on the feature identity that was encoded from the superordinate dimension. After accumulating sufficient evidence for a single category label, the model self-terminates with a response.
Braunlich and Love (2021) performed two sets of simulations of the paradigm from Blair et al. (2009): one using the standard model with full preposterior search, and the other using the myopic version of the model. The standard model forecasts all possible sequences of feature values across dimensions at trial onset, calculates the probability of observing each response via cluster activation, and condenses that information into an expected utility of sampling each dimension. The observer then samples information from the dimension with the maximum utility, or terminates the search process in a response if no available dimensions are expected to provide gain beyond a prespecified cost of sampling. The myopic version of the model works similarly to the standard version of SEA, except that feature predictions are made only one step into the future instead of the full projected dimension sequences. Given the massive computational load of full preposterior search, the myopic variant of the model was presented in an effort to account for human-like limitations on memory and attention resources.
As shown in Figure 9, AARM predicted trajectories of fixations and dwell times that were consistent with the hierarchical structure of the task, varied appropriately between trial types, and consistently self-terminated after the two trial-relevant features were encoded. We consider the level of detail at which AARM is able to predict behavior to be an advantage of its mechanistic approach; as shown in Figure 9, its predictions closely match the observed timecourse of sampling behavior across participants. The timecourse of orientation is, in fact, central to AARM’s specification as feature encoding is calculated as a function of cumulative attention. SEA, by contrast, only makes predictions about the order in which features are sampled before a response is made. This level of specificity is of course sufficient for a rational account, as the model was designed to determine the probability of discrete actions (e.g. sample a dimension; make a response) given a particular goal and task environment. As such, the standard version of SEA was reported to make predictions that were consistent with observed post-learning behavior insofar as it sampled the superordinate dimension first, self-terminated after sampling the two relevant dimensions on each trial, and correctly categorized items on 93.3% of trials (Braunlich & Love, 2021).
The more parsimonious myopic variant, however, was less successful. Because a one-step forecast produces equal utility predictions across dimensions, the myopic model only oriented to the superordinate dimension on one third of the trials. Across a majority of trials, however, the myopic model generated fixation trajectories that were not consistent with the observed effects shown in Figure 9. This discrepancy potentially highlights an important instance in which human behavior departs from the optimal action sequence, even when capacity limitations are considered. The myopic model does not predict effects of initial orientation that are consistent with the hierarchical design of the task because its balanced, single-step prediction determines that all dimensions are equally likely to support a correct response. While this explanatory issue can be overcome by exhaustive preposterior search, AARM produces the target pattern of behavior by incorporating human-like biases and a non-stationary working representation of the stimulus.
Confirmatory search mechanisms in AARM supported behaviors in Blair et al.’s paradigm that were consistent with rational predictions provided by full preposterior search in SEA, but this approach has potential limitations. For instance, it is often the case that false negatives incur a greater cost than false positives, such that disconfirmatory search would be advantageous. Real-world medical diagnosis is an extreme example, but this balance of costs is relevant to various recognition-primed decision-making tasks as well (Fadde, 2009). Additionally, work investigating search strategies has shown that while people tend to maximize probability gain (that is, sample dimensions that yield the highest probability of a correct response), strategies that maximize information gain or impact are used in some cases as well (Nelson, McKenzie, Cottrell, & Sejnowski, 2010). Although confirmatory search was an effective way of extending the error-minimization updating rule from the between-trial module of AARM to account for the unsupervised aspect of within-trial dynamics, it may not be a viable solution in all contexts.
Given the diverging theoretical bases of AARM and SEA, a direction of future work will be to conduct quantified comparisons between their predictions. Because SEA determines optimal behaviors with respect to the environment while AARM is more flexible with regards to the influences of individual biases, comparing the predictions of these two models may provide important insight into when and why humans deviate from optimal modes of behavior. One potential avenue is to compare AARM and SEA’s predictions in a task like the one designed by Blanco and Sloutsky (2019) and discussed in Case Study 1. Both models can purportedly produce learning traps such that an initially-irrelevant dimension continues to be ignored even if it becomes relevant at some point in the future. Nevertheless, the switch from Phase 1 to Phase 2 in the Blanco and Sloutsky (2019) paradigm might provide interesting contrast between AARM and SEA because the optimal behavior is not well defined. When the deterministic dimension is no longer relevant, is it more advantageous to exploit a probabilistic dimension and at least be correct on a subset of trials, or re-explore in order to find the new deterministic dimension?
Endogenous Covert Attention
The proposed AARM framework specifies how latent attention dynamics might give rise to patterns of gaze fixations. It is therefore relevant to highlight the theoretical distinction between overt and covert attention, as it exists in the visual search literature. Whereas covert attention is a latent psychological construct that may be distributed according to feature salience (exogenous) or in a goal-directed (endogenous) manner, overt attention refers specifically to the movements of the eyes (see Itti & Koch, 2001, for review). Previous work has indicated that overt shifts of attention, or saccades, are preceded by covert shifts in attention resulting from anticipation of a visual target’s spatial location (Deubel & Schneider, 1996; J. Hoffman & Subramaniam, 1995). To explain these results, the influential premotor theory suggests that overt and covert attention are tightly coupled, such that they involve a common set of processing and planning streams and the only difference is the motor processes that are specific to overt attention (Rizzolatti, Riggio, Dascola, & Umilta, 1987; Rizzolatti, Riggio, & Sheliga, 1994). With these insights in mind, we assumed that latent attention in the within-trial module was continuously updated for all dimensions simultaneously, but fixations were directed to the spatial location corresponding to the most informative dimension. Synchronous updates to latent attention across dimensions, therefore, could result in changes to the fixated location. In light of work demonstrating more successful encoding of task-relevant features that incur selective attention over the course of learning (Deng & Sloutsky, 2015), we additionally specified that feature encoding occurs as a function of cumulative latent attention. With this specification, it is possible to overtly attend to a feature, but to fail to encode it if endogenous covert attention is low.
The decoupling of overt and endogenous covert attention is exemplified by Case Study 3, in which multiple stimulus dimensions could occupy the same location in space, but differed in terms of their relevance to the current trial. In the example, angle, frequency, and context dimensions all overlapped in space and thus could be fixated simultaneously. Nevertheless, as shown in Figure 10B, the angle and frequency dimensions were only encoded when they were necessary for identifying the appropriate category label within the relevant task context. Behavioral and neuroimaging work has supported the idea that humans can selectively attend to a subset of dimensions occupying a common spatial location as well. For example, Rutman et al. (2010) collected EEG data while participants viewed overlapping face and scene stimuli. The authors identified ERP differences depending on whether participants were cued to focus on the face or the scene, and these differences correlated with subsequent memory for cued and uncued stimulus components (see Gazzaley & Nobre, 2012, for additional review).
Although the current specification of AARM’s within-trial module assumed feature encoding was determined from endogenous covert attention alone, influences of feature-level salience are likely to play a role as well. Dugue et al. (2020), for example, recently found that both endogenous and exogenous covert attention facilitate encoding, but endogenous attention uniquely facilitates the read-out of feature information. Future work will therefore investigate the extent to which overt attention and feature encoding in AARM should be determined from covert attention in general (i.e. both endogenous and exogenous), or endogenous covert attention specifically. One potential avenue is to contrast fixations to salient features early and late in learning. Studies have shown that overt attention initially orients to salient features, but that these effects can be overcome by increasing endogenous covert attention to task-relevant dimensions (Theeuwes, 2010; Vanunu, Hotaling, Le Pelley, & Newell, 2021). With AARM’s specification for unconstrained total attention (see Attention is not a zero-sum game), it would be possible to specify a different baseline attention value for each dimension. This would bias information sampling to salient dimensions early in the task, and overcoming this bias would depend on the observer’s ability to explore the other dimensions rather than exploiting information from the salient dimensions alone.
Conclusions
With the specification of the between- and within-trial modules of AARM that were outlined here, we have provided a comprehensive theory for how learning fundamentally affects how humans interact with their environment, both in terms of the dimensions they attend to and the decisions that they make.
AARM stands apart from previous models of category learning in that it presents a common set of mechanisms that operates at both between- and within-trial timescales of attention allocation and decision making. Our theory broadly suggests that as humans learn, they make decisions on the basis of simplified representations of the stimuli they encounter. These simplified representations gradually emerge through a combination of selective attention to relevant dimensions, and early-termination of information search when an evidence threshold is reached. Accumulation of category evidence occurs concurrently with confirmatory information search, such that humans intuitively direct their attention toward dimensions that are expected to support their current beliefs. When testing AARM’s theoretical predictions, we focused on hierarchical category structures in particular, due to the natural emergence of temporal ordering effects alongside attention updating. Beyond the results presented here, we believe that AARM comprises a broader theoretical statement about how humans learn in naturalistic environments as well, with contextual dimensions serving as superordinate cues to guide information sampling. This work serves to highlight aspects of category learning that are frequently overlooked, but are crucial for gaining a complete understanding of how humans acquire knowledge about the world, and how that knowledge guides their behaviors.
Author Note
This work was supported by a CAREER Award from the National Science Foundation (BMT). Preliminary results were first presented at the Annual Meeting of the Mathematical Psychological Society on July 1, 2021 (ERW). An early version of the manuscript was posted on PsyArXiv on June 29, 2021 and is accessible at http://doi.org/10.31234/osf.io/94csh. This study was not preregistered. Model code will be made available upon publication at https://github.com/MbCN-lab. The data used in Case Study 1 will be available upon reasonable request. The data used in Case Study 2 were made freely available online by Meier and Blair (2013) at https://doi.org/10.1016/j.cognition.2012.09.014.
Appendix A
Starting with Equation 2 where evidence for Category on Trial is a weighted sum of exemplar activations and their associated category labels, we need to compute the partial derivative of this ratio to specify how the attention vector should change so as to minimize the cross entropy loss. Although we used vector representation in the main text, our derivation here will show the partial derivative on a dimension-wise basis. Letting again denote the feedback provided on the ith trial, the partial derivative of the cross entropy loss is
Here, the partial derivative operator can be applied linearly to each individual element within the summations, and so we need only compute the derivative of the activation expression in Equation 1 for a single exemplar:
The partial derivative in Equation 9 can be calculated in a similar manner, where here the feedback associated with Trial would be replaced with the index corresponding to the leading accumulator at Time .
Appendix B
Table B1. Nomenclature.
Reference table for the notation used in the technical specifications.
| Indices | |
| trial | |
| dimension | |
| feature | |
| exemplar | |
| within-trial timestep | |
| category label | |
|
| |
| Task Environment | |
| number of dimensions per stimulus | |
| number of possible category labels | |
| set of dimensions at spatial location | |
|
| |
| Common Elements | |
| true stimulus representation | |
| episodic memory trace | |
| feedback | |
| exemplar memory strength | |
| between-trial attention weight | |
| exemplar activation | |
| category evidence | |
| number of exemplars stored | |
| number of observed features | |
|
| |
| Additional Within-Trial Elements | |
| working stimulus representation | |
| within-trial attention weight | |
| exemplar dimension encoding | |
| imputed feature value | |
| imputed feature activation | |
| within-trial gradient update value | |
| dimension fixation prediction (True/False) | |
| feature encoding status (True/False) | |
Table B2. Parameter Values.
Table of parameter values that were used to simulate behavioral and eye-tracking data in each case study.
| Case Study |
|||||||
|---|---|---|---|---|---|---|---|
| Parameter | Description | 1A | 1B | 2 | 3 | 4A | 4B |
| kernel specificity (between-trial) | 0.05 | 0.02 | 1.50 | 0.01 | 1.50 | 1.50 | |
| learning rate (between-trial) | 2.50 | 2.00 | 1.50 | 0.001 | 0.20 | 0.20 | |
| kernel specificity (within-trial) | 0.20 | 0.20 | 0.35 | 0.25 | 0.24 | 0.24 | |
| learning rate (within-trial) | 0.20 | 0.20 | 0.08 | 0.20 | 0.17 | 0.17 | |
| encoding threshold | 62 | 62 | 28 | 202 | 74 | 74 | |
| feature sampling bias | 0.70 | 0.70 | 0.80 | 0.95 | 0.70 | 0.70 | |
| evidence threshold | 0.90 | 0.90 | 0.99 | 0.99 | 0.90 | 0.90 | |
| perceptual variability | 0.10 | 0.10 | 0.15 | 0.10 | 0.10 | 0.10 | |
Footnotes
It would be possible to define attention as a global optimization process for each individual trial; however, the presence of anticipatory attention orientation suggests to us that attention can be roughly approximated as a combination of single updates across trials, along with attention on each trial that is inherited from the between-trial dynamics. In other contexts, global definitions of the relevance of dimensions may prove more effective.
References
- Addleman D, Tao J, Remington R, & Jiang Y (2018). Explicit goal-driven attention, unlike implicitly learned attention, spreads to secondary tasks. Journal of Experimental Psychology: Human Perception and Performance, 44(3), 356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allport A, Styles E, & Hsieh S (1994). Shifting intentional set: Exploring the dynamic control of tasks. In Umilta C & Moscovitch M (Eds.), Attention and performance xv: Conscious and nonconscious information processing (p. 421–452). Cambridge, MA: MIT Press. [Google Scholar]
- Anderson B, Laurent P, & Yantis S (2011). Value-driven attentional capture. Proceedings of the National Academy of Sciences, 108(25), 10367–10371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson J (1991a). The adaptive nature of human categorization. Psychological Review, 98, 409–429. [Google Scholar]
- Anderson J (1991b). Is human cognition adaptive? Behavioral & Brain Sciences, 14, 471–484. [Google Scholar]
- Ashby G, Alfonso-Reese L, & Waldron E (1998). A neuropsychological theory of multiple systems in category learning. Psychological Review, 105(3), 442–481. [DOI] [PubMed] [Google Scholar]
- Ashby G, & Maddox T (2005). Human category learning. Annual Review of Psychology, 56, 149–178. [DOI] [PubMed] [Google Scholar]
- Awh E, Vogel E, & Oh S-H (2006). Interactions between attention and working memory. Neuroscience, 139(1), 201–208. [DOI] [PubMed] [Google Scholar]
- Baddeley A (1982). Domains of recollection. Psychological Review, 89(6), 708–729. [Google Scholar]
- Baker A, Kim M, & Hoffman J (2021). Searching for emotional salience. Cognition, 214, 104730. [DOI] [PubMed] [Google Scholar]
- Barto A, & Mahadevan S (2003). Recent advances in hierarchical reinforcement learning. Discrete Event Dynamic Systems, 13(1), 41–77. [Google Scholar]
- Blair M, Watson M, Walshe R, & Maj F (2009). Extremely selective attention: Eye-tracking studies of the dynamic allocation of attention to stimulus features in categorization. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35(5), 1196–1206. [DOI] [PubMed] [Google Scholar]
- Blanco N, & Sloutsky V (2019). Adaptive flexibility in category learning? Young children exhibit smaller costs of selective attention than adults. Developmental Psychology, 55(10), 2060–2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanco N, Turner B, & Sloutsky V (under review). The benefits of immature cognitive control: How distrubuted attention guards against learning traps. [DOI] [PMC free article] [PubMed]
- Bonardi C, Graham S, Hall G, & Mitchell C (2005). Acquired distinctiveness and equivalence in human discrimination learning: Evidence for an attentional process. Psychonomic Bulletin & Review, 12, 88–92. [DOI] [PubMed] [Google Scholar]
- Botta F, Martin-Arevalo E, Lupianez J, & Bartolomeo P (2019). Does spatial attention modulate sensory memory? PLoS One, 14(7), e0219504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick M (2012). Hierarchical reinforcement learning and decision making. Current Opinion in Neurobiology, 22(6), 956–962. [DOI] [PubMed] [Google Scholar]
- Botvinick M, Niv Y, & Barto A (2009). Hierarchically organized behavior and its neural foundations: A reinforcement learning perspective. Cognition, 113(3), 262–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boureau Y, Sokol-Hessner P, & Daw N (2015). Deciding how to decide: Self-conrol and meta-decision making. Trends in Cognitive Sciences, 19(11), 700–710. [DOI] [PubMed] [Google Scholar]
- Bowman C, & Zeithamova D (2018). Abstract memory representations in the ventromedial prefrontal cortex and hippocampus support concept generalization. Journal of Neuroscience, 38(10), 2605–2614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman C, & Zeithamova D (2020). Training set coherence and set size effects on concept generalization and recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46, 1442–1464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braunlich K, & Love B (2021). Bidirectional influences of information-sampling and concept learning. Psychological Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockdorff N, & Lamberts K (2000). A feature-sampling account of the time course of old-new recognition judgments. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26(1), 77–102. [DOI] [PubMed] [Google Scholar]
- Brown S, & Heathcote A (2008). The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178. [DOI] [PubMed] [Google Scholar]
- Brydges C, Clunies-Ross K, Clohessy M, Lo Z, Nguyen A, Rousset C, . . . Fox A (2012). Dissociable components of cognitive control: An event-related potential (erp) study of response inhibition and interference suppression. PLOS ONE, 7(3), e34428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busemeyer J, & Townsend J (1993). Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review, 100, 492. [DOI] [PubMed] [Google Scholar]
- Chen L, Meier K, Blair M, Watson M, & Wood M (2013). Temporal characteristics of overt attentional behavior during category learning. Attention, Perception, & Psychophysics, 75(2), 244–256. [DOI] [PubMed] [Google Scholar]
- Chiu Y-C, & Yantis S (2009). A domain-independent source of cognitive control for task sets: Shifting spatial attention and switching categorization rules. Journal of Neuroscience, 29(12), 3930–3938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun M, Golomb J, & Turk-Browne N (2011). A taxonomy of external and internal attention. Annual Review of Psychology, 62, 73–101. [DOI] [PubMed] [Google Scholar]
- Chun M, & Jiang Y (1998). Contextual cueing: Implicit learning and memory of visual context guides spatial attention. Cognitive Psychology, 36(1), 28–71. [DOI] [PubMed] [Google Scholar]
- Chun M, & Turk-Browne N (2007). Interactions between attention and memory. Current Opinion in Neurobiology, 17(2), 177–184. [DOI] [PubMed] [Google Scholar]
- Cisek P, Puskas G, & El-Lurr S (2009). Decisions in changing conditions: The urgency-gating model. Journal of Neuroscience, 29(37), 11560–11571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen A, & Nosofsky R (2003). An extension of the exemplar-based random-walk model to separable-dimension stimuli. Journal of Mathematical Psychology, 47(2), 150–165. [Google Scholar]
- Cohen D, Dunbar K, & McClelland J (1990). On the control of automatic processes: A parallel distributed processing account of the stroop effect. Psychological Review, 97(3), 332. [DOI] [PubMed] [Google Scholar]
- Cox G, & Criss A (2020). Similarity leads to correlated processing: A dynamic model of encoding and recognition of episodic associations. Psychological Review, 127(5), 792–828. [DOI] [PubMed] [Google Scholar]
- Cox G, & Shiffrin R (2017). A dynamic approach to recognition memory. Psychological Review, 124(6), 795. [DOI] [PubMed] [Google Scholar]
- Crump M, Milliken B, Leboe-McGowan J, Lebowe-McGowan L, & Gao X (2018). Context-dependent control of attention capture: Evidence from proportion congruent effects. Canadian Journal of Experimental Psychology, 72(2), 91–104. [DOI] [PubMed] [Google Scholar]
- De Brigard F, Addis D, Ford J, Schacter D, & Giovanello K (2013). Remembering what could have happened: Neural correlates of episodic counterfactual thinking. Neuropsychologia, 51(12), 2401–2414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Brigard F, Giovanello K, Stewart G, Lockrow A, O’Brien M, & Spreng R (2016). Characterizing the subjective experience of episodic past, future, and counterfactual thinking in healthy younger and older adults. Quarterly Journal of Experimental Psychology, 69(12), 2358–2375. [DOI] [PubMed] [Google Scholar]
- De Brigard F, Spreng R, Mitchell J, & Schacter D (2015). Neural activity associated with self, other, and object-based counterfactual thinking. NeuroImage, 109, 12–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deese J (1959). On the prediction of occurrence of particular verbal intrusions in immediate recall. Journal of Experimental Psychology, 58(1), 17–22. [DOI] [PubMed] [Google Scholar]
- Demirkaya A, Chen J, & Symak S (2020, March). Exploring the role of loss functions in multiclass classification. In 2020 54th annual conference on information sciences and systems (ciss) (p. 1–5). IEEE. [Google Scholar]
- Deng W, & Sloutsky V (2015). The development of categorization: Effects of classification and inference training on category representation. Developmental Psychology, 51(3), 392–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desimone R, & Duncan J (1995). Neural mechanisms of selective visual attention. Annual Review of Neuroscience, 18(1), 193–222. [DOI] [PubMed] [Google Scholar]
- Deubel H, & Schneider W (1996). Saccade target selection and object recognition: Evidence for a common attentional mechanism. Vision Research, 36, 1827–1837. [DOI] [PubMed] [Google Scholar]
- Dix S, & Aggleton J (1999). Extending the spontaneous preference test of recognition: Evidence of object-location and object-context recognition. Behavioral Brain Research, 99(2), 191–200. [DOI] [PubMed] [Google Scholar]
- Dosher B (1984). Discriminating preexperimental (semantic) from learned (episodic) associations: A speed-accuracy study. Cognitive Psychology, 16(4), 519–555. [Google Scholar]
- Dosher B, & Rosedale G (1991). Judgments of semantic and episodic relatedness: Common time-course and failure of segregation. Journal of Memory and Language, 30(2), 125–160. [Google Scholar]
- Doucet A, de Freitas N, & Gordon N (2001). Sequental monte carlo methods in practice. Springer. [Google Scholar]
- Dugue L, Merriam E, Heeger D, & Carrasco M (2020). Differential impact of endogenous and exogenous attention on activity in human visual cortex. Scientific Reports, 10(21274). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dulsky S (1935). The effect of a change of background on recall and relearning. Journal of Experimental Psychology, 18(6), 725–740. [Google Scholar]
- Egner T (2008). Multiple conflict-driven control mechanisms in the human brain. Trends in Cognitive Sciences, 12(10), 374–380. [DOI] [PubMed] [Google Scholar]
- Eich E (1985). Context, memory, and integrated item/context imagery. Journal of Experimental Psychology: Learning, Memory, and Cognition, 11(4), 764–770. [Google Scholar]
- Estes W (1972). An associative basis for coding and organization in memory. In Melton A & Martin E (Eds.), Coding processes in human memory (p. 161–190). Washington DC: Winston & Sons. [Google Scholar]
- Estes W (1986). Array models for category learning. Cognitive Psychology, 18(4), 500–549. [DOI] [PubMed] [Google Scholar]
- Estes W (1994). Classification and cognition. Oxford University Press. [Google Scholar]
- Fadde P (2009). Instructional design for advanced learners: Training recognition skills to hasten expertise. Educational Technology Research and Development, 57(3), 359–376. [Google Scholar]
- Foster J, Bsales E, & Awh E (2020). Covert spatial attention speeds target individuation. Journal of Neuroscience, 40(13), 2717–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galdo M, Weichart E, Sloutsky V, & Turner B (2021). The quest for simplicity in human learning: Identifying the constraints on attention. (DOI: 10.31234/osf.io/xgfmb) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazzaley A, & Nobre A (2012). Top-down modulation: Bridging selective attention and working memory. Trends in Cognitive Sciences, 16(2), 129–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiselman R, & Glenny J (1977). Effects of imagining speakers’ voices on the retention of words presented visually. Memory & Cognition, 5(5), 499–504. [DOI] [PubMed] [Google Scholar]
- George D, & Kruschke J (2012). Contextual modulation of attention in human category learning. Learning & Behavior, 40(4), 530–541. [DOI] [PubMed] [Google Scholar]
- Gilks W, Richardson S, & Spiegelhalter J (1996). Markov chain monte carlo in practice. Chapman and Hall. [Google Scholar]
- Gluck M, & Bower G (1988). From conditioning to category learning: An adaptive network model. Journal of Experimental Psychology: General, 117(3), 227. [DOI] [PubMed] [Google Scholar]
- Godden D, & Baddeley A (1975). Context-dependent memory in two natural enviornments: On land and underwater. British Journal of Psychology, 66(3), 325–331. [Google Scholar]
- Goldberg P, & Jerrum M (1995). Bounding the vc dimension of concept classes parameterized by real numbers. Machine Learning, 18, 131–148. [Google Scholar]
- Goodfellow I (2016). Deep learning (Vol. 1) (No. 2). Cambridge, MA: MIT Press. [Google Scholar]
- Greene R, & Tussing A (2001). Similarity and associative recognition. Journal of Memory and Language, 45(4), 573–584. [Google Scholar]
- Griffiths O, & Le Pelley M (2009). Attentional changes in blocking are not a consequence of lateral inhibition. Learning & Behavior, 37(1), 27–41. [DOI] [PubMed] [Google Scholar]
- Hall G (1991). Perceptual and associative learning. Oxford University Press. [Google Scholar]
- Hintzman D (n.d.). Minerva 2: A simulation model of human memory. Behavior Research Methods, Instruments, & Computers, 16(2), 96–101. [Google Scholar]
- Hockley W (2008). The effects of environmental context on recognition memory and claims of remembering. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34(6), 1412–1429. [DOI] [PubMed] [Google Scholar]
- Hoffman A, & Rehder B (2010). The costs of supervised classification: The effect of learning task on concaptual flexibility. Journal of Experimental Psychology: General, 139(2), 319–340. [DOI] [PubMed] [Google Scholar]
- Hoffman J, & Subramaniam B (1995). The role of visual attention in saccadic eye movements. Perception & Psychophysics, 57, 787–795. [DOI] [PubMed] [Google Scholar]
- Hunsaker M, & Kesner R (2013). The operation of pattern separation and pattern completion processes associated with different attributes or domains of memory. Neuroscience & Biobehavioral Reviews, 37(1), 36–58. [DOI] [PubMed] [Google Scholar]
- Irwin D (1996). Integrating information across saccadic eye movements. Current Directions in Psychological Science, 5(3), 94–100. [Google Scholar]
- Isarida T, & Isarida T (2007). Environmental context effects of background color in free recall. Memory & Cognition, 35(7), 1620–1629. [DOI] [PubMed] [Google Scholar]
- Itti L, & Koch C (2001). Computational modelling of visual attention. Nature Reviews Neuroscience, 2, 194–203. [DOI] [PubMed] [Google Scholar]
- Janssens C, De Loof E, Boehler N, Pourtois G, & Verguts T (2018). Occipital alpha power reveals fast attentional inhibition of incongruent distractors. Psychophysiology, 55(3), e13011. [DOI] [PubMed] [Google Scholar]
- Johnston W, & Schwarting I (1997). Novel popout: An enigma for conventional theories of attention. Journal of Experimental Psychology: Human Perception and Performance, 23(3), 622. [Google Scholar]
- Krajbich I, Armel C, & Rangel A (2010). Visual fixations and the computation and comparison of value in simple choice. Nature Neuroscience, 13, 1292–1298. [DOI] [PubMed] [Google Scholar]
- Krajbich I, & Rangel A (2011). Multiatternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based choice. Proceedings of the National Academy of Sciences of the United States of America, 108, 13852–13857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruschke J (1992). Alcove: An exemplar-based connectionist model of category learning. Psychological Review, 99(1), 22–44. [DOI] [PubMed] [Google Scholar]
- Kruschke J (1996). Dimensional relevance shifts in category learning. Connection Science, 201–223. [Google Scholar]
- Kruschke J (2001). Toward a unified model of attention in associative learning. Journal of Mathematical Psychology, 45, 812–863. [Google Scholar]
- Kumaran D, & McClelland J (2012). Generalization through the recurrent interaction of episodic memories: A model of the hippocampal system. Psychological Review, 119(3), 573–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai M-L, Tsai M-J, Yang F-Y, Hsu C-Y, Liu T-C, Lee S, . . . Tsai C-C (2013). A review of using eye-tracking technology in exploring learning from 2000 to 2012. Educational Research Review, 10, 90–115. [Google Scholar]
- Lamberts K (2000). Information-accumulation theory of speeded categorization. Psychological Review, 107(2), 227–260. [DOI] [PubMed] [Google Scholar]
- Lashley K (1951). The problem of serial order in behavior. In Jeffress L (Ed.), Cerebral mechanisms in behavior: The hixon symposium (p. 112–136). New York, NY: Wiley. [Google Scholar]
- Lavie N (1995). Perceptual load as a necessary condition for selective attention. Journal of Experimental Psychology: Human Perception and Performance, 21(4), 451. [DOI] [PubMed] [Google Scholar]
- Lavie N, & Cox S (1997). On the efficiency of visual selective attention: Efficient visual search leads to inefficient distractor rejection. Psychological Science, 8(5), 395–396. [Google Scholar]
- Lavie N, & Tsal Y (1994). Perceptual load as a major determinant of the locus of selection in visual space. Perception & Psychophysics, 56(2), 183–197. [DOI] [PubMed] [Google Scholar]
- Lee M (2001). On the complexity of additive clustering models. Journal of Mathematical Psychology, 45, 131–148. [DOI] [PubMed] [Google Scholar]
- Lefebvre G, Summerfield C, & Bogacz R (2022). A normative account of computation bias during reinforcement learning. Neural Computation, 34(2), 307–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Pelley M (2004). The role of associative history in models of associative learning: A selective review and hybrid model. Quarterly Journal of Experimental Psychology, 57B, 193–243. [DOI] [PubMed] [Google Scholar]
- Loftus G (1985). Picture perception: Effects of luminance on available information and information-extraction rate. Journal of Experimental Psychology: General, 114(3), 342. [DOI] [PubMed] [Google Scholar]
- Logan G (1988). Toward an instance theory of automatization. Psychological Review, 95(4), 492. [Google Scholar]
- Logan G (2002). An instance theory of attention and memory. Psychological Review, 109(2), 376. [DOI] [PubMed] [Google Scholar]
- Love B, Medin D, & Gureckis T (2004). Sustain: A network model of category learning. Psychological Review, 111(2), 309. [DOI] [PubMed] [Google Scholar]
- Mack M, Love B, & Preston A (2016). Dynamic updating of hippocampal object representations relfects new conceptual knowledge. Proceedings of the National Academy of Sciences, 113(46), 13203–13208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mack M, Love B, & Preston A (2018). Building concepts one episode at a time: The hippocampus and concept formation. Neuroscience Letters, 260, 31–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mack M, Preston A, & Love B (2013). Decoding the brain’s algorithm for categorization from its neural implementation. Current Biology, 23(20), 2023–2027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackintosh N (1975). A theory of attention: Variations in the associability of stimuli with reinforcement. Psychological Review, 82(4), 276. [Google Scholar]
- Mackintosh N, & Little L (1969). Intradimensional and extradimensional shift learning by pigeons. Psychonomic Science, 14(1), 5–6. [Google Scholar]
- Maddox T, & Ashby G (2004). Dissociating explicit and procedural-learning based systems of perceptual category learning. Behavioral Processes, 66(3), 309–3332. [DOI] [PubMed] [Google Scholar]
- Markman A, & Ross B (2003). Category use and category learning. Psychological Bulletin, 129(4), 592–613. [DOI] [PubMed] [Google Scholar]
- McColeman C, Barnes J, Chen L, Meier K, Walshe R, & Blair M (2014). Learning-induced changes in attentional allocation during categorization: A sizable catalog of attention change as measured by eye movements. PloS one, 9(1), e83302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillen T, & Holmes P (2006). The dynamics of choice among multiple alternatives. Journal of Mathematical Psychology, 50, 30–57. [Google Scholar]
- Medin D, & Schaffer M (1978). Context theory of classification learning. Psychological Review, 85(3), 207. [Google Scholar]
- Meier K, & Blair M (2013). Waiting and weighting: Information sampling is a balance between efficiency and error-reduction. Cognition, 126(2), 219–325. [DOI] [PubMed] [Google Scholar]
- Meiran N (1996). Reconfiguration of processing mode prior to task performance. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22(6), 1423–1442. [Google Scholar]
- Miller G, Galanter E, & Pribram K (1960). Plans and the structure of behavior. New York, NY: Holt, Rinehart, & Winston. [Google Scholar]
- Monsell S (2003). Task switching. Trends in Cognitive Sciences, 7(3), 134–140. [DOI] [PubMed] [Google Scholar]
- Most S, Chun M, Widders D, & Zald D (2005). Attentional rubbernecking: Cognitive control and personality in emotion-induced blindness. Psychonomic Bulletin & Review, 12(4), 654–661. [DOI] [PubMed] [Google Scholar]
- Muller H, & von Muhlenen A (2000). Probing distractor inhibition in visual search: Inhibition of return. Journal of Experimental Psychology: Human Perception and Performance, 26(5), 1591–1605. [DOI] [PubMed] [Google Scholar]
- Muller H, von Muhlenen A, & Geyer T (2007). Top-down inhibition of search distractors in parallel visual search. Perception & Psychophysics, 69(8), 1373–1388. [DOI] [PubMed] [Google Scholar]
- Murnane K, & Phelps M (1993). A global activation approach to the effect of changes in environmental context on recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 19(4), 882–894. [Google Scholar]
- Murnane K, & Phelps M (1994). When does a different environmental context make a difference in recognition? a global activation model. Memory & Cognition, 22(5), 584–590. [DOI] [PubMed] [Google Scholar]
- Murnane K, Phelps M, & Malmberg K (1999). Context-dependent recognition memory: The ice theory. Journal of Experimental Psychology: General, 128(4), 403–415. [DOI] [PubMed] [Google Scholar]
- Nelson J, & Cottrell G (2007). A probabilistic model of eye movements in concept formation. Neurocomputing, 70, 2256–2272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson J, McKenzie C, Cottrell G, & Sejnowski T (2010). Experience matters: Information acquisition optimizes probability gain. Psychological Science, 21(7), 960–969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickerson R (1998). Confirmation bias: A ubiquitous phenomenon in many guises. Review of General Psychology, 2, 175–220. [Google Scholar]
- Niwa M, & Ditterich J (2008). Perceptual decisions between multiple directions of visual motion. Journal of Neuroscience, 28, 4435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman D (1968). Toward a theory of memory and attention. Psychological Review, 75(6), 522–536. [Google Scholar]
- Norman D, & Shallice T (1986). Attention to action. In Consciousness and self-regulation (p. 1–18). Boston, MA: Springer. [Google Scholar]
- Nosofsky N, Little D, & James T (2012). Activation in the neural network responsible for categorization and recognition reflects parameter changes. Proceedings of the National Academy of Sciences, 109(1), 333–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nosofsky R (1986). Attention, similarity, and the identification-categorization relationship. Journal of Experimental Psychology: General, 115(1), 39–57. [DOI] [PubMed] [Google Scholar]
- Nosofsky R (1988). Exemplar-based accounts of relations between classification, recognition, and typicality. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14(4), 700–708. [Google Scholar]
- Nosofsky R, & Palmeri T (1997). An exemplar-based random walk model of speeded classification. Psychological Review, 104(2), 266–300. [DOI] [PubMed] [Google Scholar]
- Nosofsky R, Palmeri T, & McKinley S (1994). Rule-plus-exception model of classification learning. Psychological Review, 101, 53–79. [DOI] [PubMed] [Google Scholar]
- Oaksford M, & Chater N (Eds.). (1998). Rational models of cognition. Oxford University Press. [Google Scholar]
- O’Donoghue E, Broschard M, & Wasserman E (2020). Pigeons exhibit flexibility but not rule formation in dimensional learning, stimulus generalization, and task switching. Journal of Experimental Psychology: Animal Learning and Cognition, 46(2), 107–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivers C, Peters J, Houtkamp R, & Roelfsema P (2011). Different states in visual working memory: When it guides attention and when it does not. Trends in Cognitive Sciences, 15(7), 327–334. [DOI] [PubMed] [Google Scholar]
- Palmeri T (1999). Learning categories at different hierarchical levels: A comparison of category learning models. Psychonomic Bulletin & Review, 6(3), 495–503. [DOI] [PubMed] [Google Scholar]
- Park T, & Casella G (2008). The bayesian lasso. Journal of the American Statistical Association, 103, 681–686. [Google Scholar]
- Paskewitz S, & Jones M (2020). Dissecting EXIT. Journal of Mathematical Psychology, 97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce J (1994). Similarity and discrimination: A selective review and a connectionist model. Psychological Review, 101(4), 587–607. [DOI] [PubMed] [Google Scholar]
- Perfect T (1996). Does context discriminate recollection from familiarity in recognition memory. The Quarterly Journal of Experimental Psychology: Section A, 49(3), 797–813. [DOI] [PubMed] [Google Scholar]
- Pooley J, Lee M, & Shankle W (2011). Understanding memory impairment with memory models and hierarchical bayesian analysis. Journal of Mathematical Psychology, 55, 47–56. [Google Scholar]
- Rabin M, & Schrag J (1999). First impressions matter: A model of confirmatory bias. The Quarterly Journal of Economics, 114(1), 37–82. [Google Scholar]
- Rajsic J, Taylor E, & Pratt J (2017). Out of sight, out of mind: Matching bias underlies confirmatory visual search. Attention, Perception, & Psychophysics, 79(2), 498–507. [DOI] [PubMed] [Google Scholar]
- Rajsic J, Wilson D, & Pratt J (2015). Confirmation bias in visual search. Journal of Experimental Psychology: Human Perception and Performance, 41(5), 1353–1364. [DOI] [PubMed] [Google Scholar]
- Ratcliff R (1978). A theory of memory retrieval. Psychological Review, 85(2), 59–108. [Google Scholar]
- Rehder B, & Hoffman A (2005a). Eyetracking and selective attention in category learning. Cognitive Psychology, 51(1), 1–41. [DOI] [PubMed] [Google Scholar]
- Rehder B, & Hoffman A (2005b). Thirty-something categorization results explained: Attention, eyetracking, and models of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 811–829. [DOI] [PubMed] [Google Scholar]
- Rescorla R, & Wagner A (1972). A theory of pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In Black A & Prokasy W (Eds.), Classical conditioning ii: Current research and theory (p. 64–99). New York, NY: Appleton-Century-Crofts. [Google Scholar]
- Rich A, & Gureckis T (2018). The limits of learning: Exploration, generalization, and the development of learning traps. Journal of Experimental Psychology: General, 147, 1553. [DOI] [PubMed] [Google Scholar]
- Richter F, Chanales A, & Kuhl B (n.d.). Predicting the integration of overlapping memories by decoding mnemonic processing states during learning. NeuroImage, 124, 323–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzolatti G, Riggio L, Dascola I, & Umilta C (1987). Reorienting attention across the horizontal and vertical meridians: Evidence in favor of a premotor theory of attention. Neuropsychologia, 25(1), 31–40. [DOI] [PubMed] [Google Scholar]
- Rizzolatti G, Riggio L, & Sheliga B (1994). Space and selective attention. In Umilta C & Moscovitch M (Eds.), Attention and performance xv: Conscious and nonconscious information processing (p. 231–264). MIT Press. [Google Scholar]
- Roediger H, & McDermott K (1995). Creating false memories: Remembering words not presented in lists. Journal of Experimental Psychology: Learning, Memory and Cognition, 21(4), 803. [Google Scholar]
- Rogers R, & Monsell S (1995). Costs of a predictable switch between simple cognitive tasks. Journal of Experimental Psychology: General, 124(2), 207–231. [Google Scholar]
- Rumelhart D, & McClelland J (1988). Parallel distributed processing. IEEE. [Google Scholar]
- Rutman A, Clapp W, Chadick J, & Gazzaley A (2010). Early top-down control of visual processing predicts working memory performance. Journal of Cognitive Neuroscience, 22(6), 1224–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakamoto Y, Jones M, & Love B (2008). Putting the psychology back into psychological models: Mechanistic versus rational approaches. Memory & Cognition, 36(6), 1057–1065. [DOI] [PubMed] [Google Scholar]
- Sanborn A, Griffiths T, & Navarro D (2010). Rational approximations to rational models: Alternative algorithms for category learning. Psychological Review, 117(4), 1144. [DOI] [PubMed] [Google Scholar]
- Schapiro A, Turk-Browne N, Botvinick M, & Norman K (2017). Complementary learning systems within the hippocampus: A neural network modelling approach to reconciling episodic memory with statistical learning. Philosophical Transactions of the Royal Society B: Biological Sciences, 372(1711), 20160049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schustack M, & Sternberg R (1981). Evaluation of evidence in causal inference. Journal of Experimental Psychology: General, 110(1), 101–120. [Google Scholar]
- Shaklee H, & Fischhoff B (1982). Strategies of information search in causal analysis. Memory & Cognition, 10(6), 520–530. [Google Scholar]
- Shepard R (1987). Toward a universal law of generalization for psychological science. Science, 237, 1317–1323. [DOI] [PubMed] [Google Scholar]
- Shepard R, & Arabie P (1979). Additive clustering: Representation of similarities as a combination of discrete overlapping properties. Psychological Review, 86(2), 87–123. [Google Scholar]
- Shepard R, Hovland C, & Jenkins H (1961). Learning and memorization of classifications. Psychological Mongraphs: General and Applied, 75(13). [Google Scholar]
- Shiffrin R, & Schneider W (1977). Controlled and automatic human information processing: Ii. perceptual learning, automatic attending and a general theory. Psychological Review, 84(2), 127–190. [Google Scholar]
- Shiffrin R, & Steyvers M (1997). A model for recognition memory: Rem–retrieving effectively from memory. Psychonomic Bulletin & Review, 4(2), 145–166. [DOI] [PubMed] [Google Scholar]
- Sloutsky V (2003). The role of similarity in the development of categorization. Trends in Cognitive Science, 7, 246–558. [DOI] [PubMed] [Google Scholar]
- Sloutsky V, & Fisher A (2008). Attentional learning and flexible induction: How mundane mechanisms give rise to smart behaviors. Child Development, 79(3), 639–651. [DOI] [PubMed] [Google Scholar]
- Smith D, Berg M, Cook R, Murphy M, Crossley M, Boomer J, & Spiering B (2012). Implicit and explicit categorization: A tale of four species. Neuroscience & Biobehavioral Reviews, 36(10), 2355–2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith S (1986). Environmental context-dependent recognition memory using a short-term memory task for input. Memory & Cognition, 14(4), 347–354. [DOI] [PubMed] [Google Scholar]
- Smith S, Glenberg A, & Bjork R (1978). Environmental context and human memory. Memory & Cognition, 6(4), 342–353. [Google Scholar]
- Smith S, & Krajbich I (2019a). Gaze amplifies value in decision making. Psychological Science, 30, 116–128. [DOI] [PubMed] [Google Scholar]
- Smith S, & Krajbich I (2019b). Gaze-informed modeling of preference learning and prediction. Journal of Neuroscience, Psychology, and Economics, 12, 143–158. [Google Scholar]
- Smith S, & Vela E (1992). Environmental context-dependent eyewitness recognition. Applied Cognitive Psychology, 6(2), 125–139. [Google Scholar]
- Smith S, & Vela E (2001). Environmental and context-dependent memory: A review and meta-analysis. Psychonomic Bulletin & Review, 8(2), 203–220. [DOI] [PubMed] [Google Scholar]
- Sutherland N, & Mackintosh N (1971). Mechanisms of animal discrimination learning. Academic Press. [Google Scholar]
- Talluri B, Urai A, Tsetsos K, Usher M, & Donner T (2018). Confirmation bias through selective overweighting of choice-consistent evidence. Current Biology, 28(19), 3128–3135. [DOI] [PubMed] [Google Scholar]
- Tenenbaum J, & Griffiths T (2001). Generalization, similarity, and bayesian inference. The Behavioral and Brain Sciences, 24(4), 629–640. [DOI] [PubMed] [Google Scholar]
- Theeuwes J (1992). Perceptual selectivity for color and form. Perception & Psychophysics, 51(6), 599–606. [DOI] [PubMed] [Google Scholar]
- Theeuwes J (2010). Top-down and bottom-up control of visual selection. Acta Psychologica, 135(2), 77–99. [DOI] [PubMed] [Google Scholar]
- Thomas A, Molter F, Krajbich I, Heekeren H, & Mohr P (2019). Gaze bias differences capture individual choice behavior. Nature Human Behavior, 3, 625–635. [DOI] [PubMed] [Google Scholar]
- Thura D, Beauregard-Racine J, Fradet C-W, & Cisek P (2012). Decision making by urgency gating: Theory and experimental support. Journal of Neurophysiology, 108(11), 2912–2930. [DOI] [PubMed] [Google Scholar]
- Trueblood J, Brown S, & Heathcote A (2014). Multiattribute linear ballistic accumulator model of context effects in multialternative choice. Psychological Review, 121(2), 179–205. [DOI] [PubMed] [Google Scholar]
- Turner B (2019). Toward a common representational framework for adaptation. Psychological Review, 126(5), 660. [DOI] [PubMed] [Google Scholar]
- Turner B, Kvam P, Unger L, Sloutsky V, Ralston R, & Blanco N (2021). Cognitive inertia: How loops among attention, representation, and decision making distort reality. (DOI: 10.31234/osf.io/8zvey) [DOI] [Google Scholar]
- Tversky A (1977). Features of similarity. Psychological Review, 84, 327–352. [Google Scholar]
- Ullman S, Vidal-Naquet M, & Sali E (2002). Visual features of intermediate complexity and their use in classification. Nature Neuroscience, 5(7), 682–687. [DOI] [PubMed] [Google Scholar]
- Usher M, & McClelland J (2001). The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review, 108(3), 550. [DOI] [PubMed] [Google Scholar]
- Van Hoeck N, Ma N, Ampe L, Baetens K, Vandekerckhove M, & Van Overwalle F (2013). Counterfactual thinking: An fmri study on changing the past for a better future. Social Cognitive and Affective Neuroscience, 8(5), 556–564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Moorselaar D, & Slagter H (2020). Inhibition in selective attention. Annals of the New York Academy of Sciences, 1464(1), 204–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Moorselaar D, Theeuwes J, & Olivers C (2014). In competition for the attentional template: Can multiple items within visual working memory guide attention? Journal of Experimental Psychology: Human Perception and Performance, 40(4), 1450–1464. [DOI] [PubMed] [Google Scholar]
- Vanunu Y, Hotaling J, Le Pelley M, & Newell B (2021). How top-down and bottom-up attention modulate risky choice. Proceedings of the National Academy of Sciences, 118(39). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik V (1998). Statistical learning theory. John Wiley & Sons. [Google Scholar]
- Vecera S, Cosman J, Vatterott D, & Roper Z (2014). The control of visual attention: Toward a unified account. Psychology of learning and motivation, 60, 303–347. [Google Scholar]
- Wald A, & Wolfowitz J (1948). Optimal character of the sequential probability ratio test. Annals of Mathematical Statistics, 19, 326–339. [Google Scholar]
- Wason P, & Johnson-Laird P (1972). Psychology of reasoning: Structure and content (Vol. 86). Cambridge, MA: Harvard University Press. [Google Scholar]
- White C, Ratcliff R, & Starns J (2011). Diffusion models of the flanker task: Discrete versus gradual attention selection. Cognitive Psychology, 63(4), 210–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang S, & Lengyel M (2016). Active sensing in the categorization of visual patterns. eLife, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yantis S, & Egeth H (1999). On the distinction between visual salience and stimulus-driven attentional capture. Journal of Experimental Psychology: Human Perception and Performance, 25(3), 661. [DOI] [PubMed] [Google Scholar]
- Yau Y, Hinault T, Madeline T, Cisek P, Fellows L, & Dagher A (2021). Evidence and urgency related eeg signals during dynamic decision-making in humans. Journal of Neuroscience, 41(26), 5711–5722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeithamova D, Dominick A, & Preston A (2012). Hippocampal and ventral medial preforntal activation during retrieval-mediated learning supports novel inference. Neuron, 75(1), 168–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeithamova D, Manthuruthil C, & Preston A (2016). Repetition suppression in the medial temporal lobe and midbrain is altered by event overlap. Hippocampus, 26(11), 1464–1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeithamova D, & Preston A (2017). Temporal proximity promotes integration of overlapping events. Journal of Cognitive Neuroscience, 29(8), 1311–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]


