Cyclic voltammetry, square wave voltammetry or electrochemical impedance spectroscopy? Interrogating electrochemical approaches for the determination of electron transfer rates of immobilized redox proteins

Abstract

In this article, we cross-examine three well-established electrochemical approaches, namely cyclic voltammetry (CV), cyclic square-wave voltammetry (SWV) and electrochemical impedance spectroscopy (EIS) to dissect the electron transfer (ET) rate of electrostatically immobilized cytochrome c on Ag electrodes. A detailed analysis supported by simulations of redox transition provided three distinct values for the heterogeneous electron transfer (HET) rate constant of cyt c interfaced on COOH-terminated C₁₀-long alkanethiol, i.e., k_HET= 47.8 (±2,91) s⁻¹ in CV, k_HET= 64.8 (±1,27) s⁻¹ in SWV, and k_HET= 26.5 s⁻¹ in EIS. We discuss the obtained discrepancies obtained from electrochemical methods and compare them with the data from spectro-electrochemical experiments. A comprehensive selection list is created from which the most applicable approach can be chosen for studying proteins of interest. CV is most applicable to study the interfaced proteins exhibiting k_HET of ca. 0.5 - 70 s⁻¹, SWV is suitable for a broader range of k_HET of 5 – 120 s⁻¹ and EIS for k_HET of 0.5 to 5 s⁻¹ if alkanethiols are used as immobilization strategy.

1. Introduction

Interfacing redox proteins and microorganisms on electrodes revolutionized the field of bioelectrochemistry and its application in biotechnological industry. The powerful concept of transforming chemical energy from molecules via immobilized enzymes/microbes to electrical energy has been implemented in the electrochemical biosensor [1] and biofuel cell [2], [3], [4], [5], [6], [7], [8], [9] technologies. In parallel, it enriched the research with a tool of a direct measure of the electrocatalytic performance of metalloproteins [10], [11], [12], [13], [14] or electro-active microbes [10,15], often providing their mechanistic details [16] as well. One of the most critical aspects governing the performance of such systems is the efficient electronic communication between the electrode and the redox-active site in the biomolecule. Electronic communication or, in other words, the possibility of transferring an electron from a donor to acceptor (i.e., in this case, electrode and redox-active center) is primarily governed by the heterogeneous electron transfer (HET) rate. The closer the distance between donor and acceptor, the faster is HET and the bioelectrochemical system is better performing [3,[17], [18], [19], [20]] Since HET is intrinsically not a native process, there is no unified strategy for interfacing proteins on electrodes. A custom-made solution must be tailored for each protein of interest in a way to enable efficient HET. Equally crucial is the choice of the method to precisely assess the HET rates of interfaced biomolecules to ensure the advancement of the field.

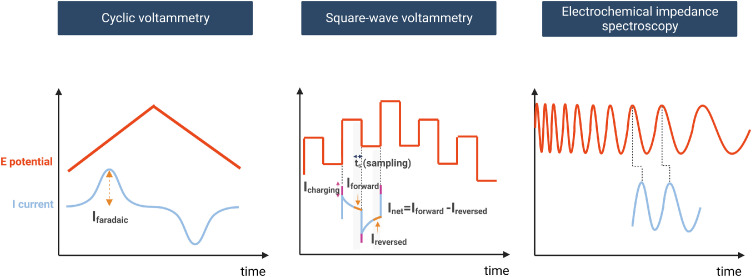
Electrochemical methods are the most direct and information-rich experimental approaches to studying redox transformations and their kinetics in (bio)chemistry. Over the last decades, the popularity of electrochemistry significantly increased as it provides means to inject or remove an electron from a molecule of interest in a thermodynamically controlled way by precisely regulating the magnitude of the applied electromotive force to drive a redox reaction, being particularly attractive in the field of green (bio)chemistry (check ref. [21] for a historical perspective on voltammetry). Moreover, the potential perturbation can be achieved in numerous ways (Fig. 1). In its simplest and most often employed form, cyclic voltammetry (CV), the potential magnitude is changed linearly in time and the current response has a bell-shape distribution. However, the detected current encompasses information on the charge flow due to not only faradaic, i.e. ET, but also all non-faradaic processes, which might influence the determination of the HET rate constants. Other, more advanced approaches make use of the periodic perturbation of the potential. In cyclic square wave voltammetry (SWV) (Fig. 1, middle), the potential is applied as a waveform composed of large amplitude differential pulses coordinated in a staircase fashion. This enables dissecting the current response into non-faradaic (Fig. 1, middle, I_charging) and faradaic responses occurring earlier and later in probed time, respectively. In turn, in electrochemical impedance spectroscopy (EIS) (Fig. 1, right), the potential is applied as a sinusoidal perturbation of a certain frequency range, and a current response (shifted in phase) is expressed in terms of impedance, from which the resistance and capacitance of charge transfer transition can be directly derived and with that the kinetics of HET.

Fig. 1.

Potential (E) perturbation and a current (I) response as a function of time in electrochemical methods: Cyclic voltammetry (left), cyclic square wave voltammetry (SWV) (middle), and electrochemical impedance spectroscopy (EIS) (right). In CV, the orange arrow marks an amplitude of faradaic current. In cyclic SWV, the detailed current components are marked: charging (non-faradaic) current in pink, the current sampled at the end of a forward pulse (I_forward) and at the end of a reversed pulse (I_reversed) in orange.

In this article, we cross-examine these three electrochemical approaches (CV, SWV and EIS) to determine the kinetic rate constant of the HET of interfaced redox proteins on electrodes. We offer a new simulation-based approach to analyzing data from CV and cyclic SWV and further compare such an approach to standard, well-established experimental data analysis methods. We further discuss their advantages and disadvantages regarding experimental detection, simplicity, and reliability of deriving values of kinetic rates and compare such approaches to other methods combining electrochemistry with spectroscopy. As a model protein, we chose cytochrome c (cyt c), which has been well and extensively studied to date, and it was immobilized on electrodes via various immobilization procedures. [22], [23], [24], [25], [26] We aim to present the reader with the pros and cons of each method and their data analysis such that the most appropriate approach can be applied to the system of their choice.

2. Materials and methods

2.1. Reagents and chemicals

11-mercaptoundecanoic acid (11-MUA), 6-mercaptohexanoic acid (6-MHA), 6-mercaptohexanol (6-MCH), and cytochrome c (cyt c) from the bovine heart were purchased from Sigma-Aldrich. EtOH of the highest purity (99.8%) purchased from Fisher Scientific was used for the preparation of ethanolic solutions for the construction of self-assembled monolayers (SAMs). The following buffers were used for protein incubation and measurements: 12.5 mM potassium phosphate buffer (pH 8.0) and 50 mM potassium phosphate buffer (pH 8.0).

2.2. Immobilization of cytochrome c on electrodes

Ag disc electrodes of geometrical active area of ca. 0.25 cm² (purchased from PINE research) were prepared by mechanical polishing of the surface and subsequent electrochemical roughening via consecutive reductive (at applied −320 mV vs. Ag|AgCl) and oxidative (at applied +320 mV) steps as described previously [27] and tested on many further examples [28], [29], [30], [31], [32]. First, the electrodes were sonicated for 10 mins in EtOH to remove impurities adsorbed to the electrode surface. Electrodes were then incubated in the SAM solution composed of either a) 11-mercaptoundecanoic acid and 6-mercaptohexanol (3:7, M/M) or b) 6-mercaptohexanoic acid and 6-mercaptohexanol (3:7, M/M) for 16 h on ice under stirring. Oxygen was removed from the SAM-EtOH solution by purging it with Ar for 5 mins prior to incubation. After removing the electrode from the SAM solution, it was rinsed with EtOH and MilliQ H₂O. Electrodes were then incubated in a protein solution composed of ca. 40–50 µM of cyt c in pH 8.0 12.5 mM potassium phosphate buffer for 2 h while gently stirring at room temperature.

2.3. Electrochemical measurements

All electrochemical measurements were performed using a PINE Research WaveDriver 200 potentiostat. The three-electrode cell was composed of a working Ag disc electrode as described above, a Pt counter electrode and a Ag|AgCl (3 M KCl) electrode as a reference electrode. The total volume of the electrochemical cell was ca. 150 ml. The buffer used for measurements was 50 mM potassium phosphate at pH 8.0. CV, SWV, and EIS were performed at least 2 or 3 times. Obtained kinetic rates are averaged. CV experiments were performed sweeping the potential between −150 mV to 150 mV and backwards with a scan rate of 10 mV/s to 3.5 V/s. SWV parameters of frequency-sweep experiment: E_amplitude=20 mV, E_step=2 mV, fr.=5.7–250 Hz, sampling time t_s=0.5 ms. EIS spectra were collected in a frequency range between 0.1 Hz to 1 MHz with potential amplitude of E_AC=10 mV (RMS). E_DC is as stated in the results section.

2.4. Simulations

Simulations were performed using DigiElch 8FD Software. CV and SWV simulations were based on the Butler-Volmer equation for adsorbed redox species. Parameters: E⁰=0.18 V, α=0.5 (if not stated otherwise), electrode surface area=2.5 cm², C_DL=19µF, R=4.5 Ω, k_ET= 1–80 s⁻¹, Г=3E-7 M/cm².

3. Model system and theoretical background

3.1. Model system – cytochrome c and its immobilization on the ag electrode

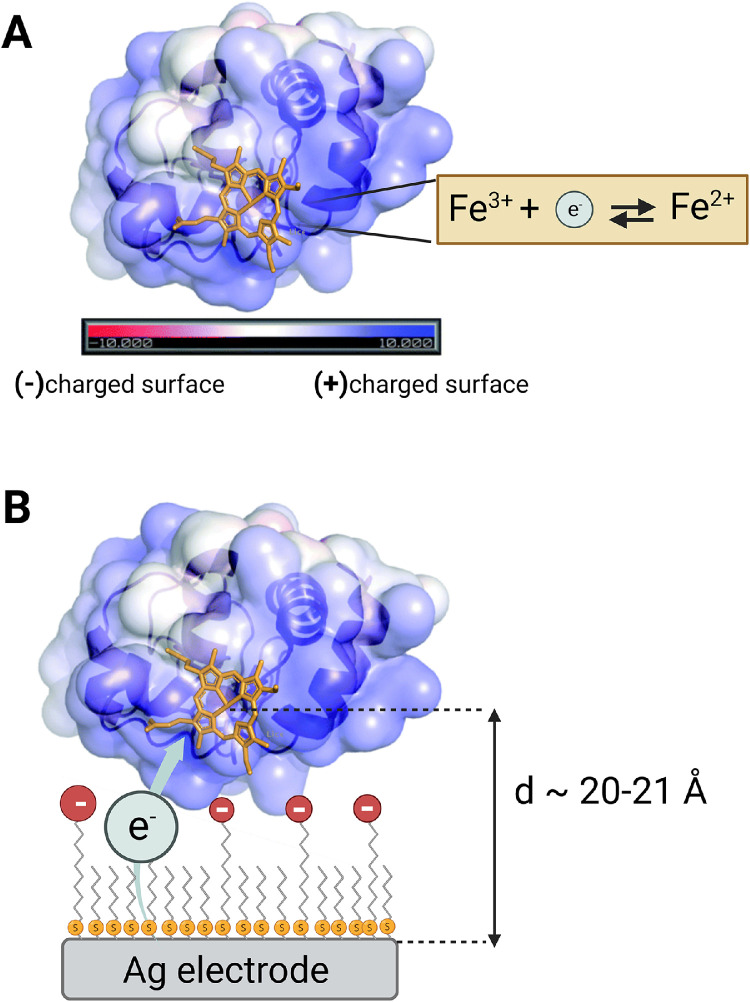
Cytochrome c (cyt c) is a well-characterized redox protein by electrochemical methods. It is a small, soluble protein (ca. 12 kDa) serving as an electron carrier in the mitochondrial respiratory chain. As such, it is ubiquitous in plants, fungi, and higher organisms. Under physiological conditions, an electron is transferred between cyt c and its natural electron acceptor (cytochrome c oxidase (CcO)) with the rate constant of ca. k_ET = 7000–50,000 s⁻¹. [33,34] The redox-active cofactor of cyt c is a heme type c, in which a Fe-heme site experiences a change of the oxidation state (Fig. 2) that can be controlled by applying an electromotive force during the electrochemical experiment.

Fig. 2.

(A) Structure of cyt c with positively-charged surface marked in blue and negatively-charged surface in red. Heme is presented in orange (pdb id: 1hrc; prepared in Pymol). (B) Schematic representation of electrostatically immobilized cytochrome c on the Ag electrode coated with 11-mercaptoundecanoic acid/6-mercaptohexanol. Heterogenous electron transfer (HET) step between the electrode and the heme active site is represented by the gray arrow. The approximate distance (d) between the Fe and the Ag surface is calculated to equal ca. 21 Å.

To accomplish direct HET and thus efficient ET rates, various immobilization strategies have been employed including electrostatic [22], [23], [24] or covalent [25] attachment of cyt c to the Ag or Au electrode surface and exhibited satisfactory current density in voltammetry of interfaced cyt c with various HET rates. In this work, we employed electrostatic attachment of protein to a Ag electrode. Although, Au is more commonly used as a working electrode in the bioelectrochemical field, we have chosen Ag to be able to directly compare our results to reported data from surface-enhanced resonance Raman (SERR) measurements of interfaced cyt c on nanostructured Ag. We have immobilized cyt c on longer and shorter alkanethiol with a negatively charged groups: 1) 11-MUA (HS-(CH₂)_10—COOH) mixed with 6-MCH (HS-(CH₂)_6—OH), and 2) 6-MHA (HS-(CH₂)_10—COOH) mixed with 6-MCH (HS-(CH₂)_6—OH) to electrostatically attach the positively charged surface of the cyt c; a strategy that mimics the natural interaction of docking of cyt c to CcO in the respiratory chain (Fig. 2). Such an immobilization ensures i) preserved thermodynamic properties of Fe-heme [25], and ii) favorable orientation of cyt c to achieve rapid HET rates [17,35]. The dilution of the anionic charge of SAM with shorter chains with hydrophobic or hydrophilic head groups has been shown computationally to enhance the surface coverage and quality of SAM distribution on the metal surface [36]. Moreover, it has been experimentally confirmed that diluting the -COOH terminated longer thiols, but not shorter ones (i.e.(CH₂)₅COOH) with shorter hydrophilic head groups increases the HET rate in electrostatically interfaced cyt c. [18]

3.2. Theory of electron transfer in bioelectrochemical systems

A large number of studies by Bowden [22], Armstrong [12] and others have shown that the HET rate constant k_ET in bioelectrochemical experiments can be well approximated by Marcus theory in biological frame [37] extended for bioelectrochemical systems [38]:

$$k_{ET}\propto \frac{1}{\left(\exp \left[\frac{\left(E-E_i\right)F}{RT}\right]+1\right)}*\text{exp}\left[-\beta d\right]*\text{exp}\left[-\frac{\Delta G^{‡}}{RT}\right]$$ (1)

where: E- applied potential, E_i- energy of a specific Fermi level of the metal electrode, β - tunneling decay parameter, d – separation distance of the reactants, $\Delta {\mathrm{G}}^{‡}$- activation energy, F, R and T have their usual meaning). The expression is composed of three main terms: the first exponential term describes the probability of occupancy of Fermi levels in the electrode, the second exponential function describes the dependence of the electron transfer rate on the electron tunneling barrier, and the third exponential function is dependent on the activation energy related to the driving force (ΔG⁰) and reorganization energy (λ) parameters. Many bioelectrochemical studies focus on optimizing the distance of the active site to the electrode surface as it can directly influence the possibility of yielding direct ET [3,19]. In this work, we have also used two lengths ((CH₂)_nCOOH, n=5 and n = 10) of SAM to test the faster and slower HET rates resulting from different distances between the Fe-heme and the electrode surface in electrochemical experiments. The distances can be estimated to equal ca. 16.4 Å of n = 10 SAM chain length [39], ca. 8.2 Å of n=5 SAM chain length and ca. 5 Å distance from the SAM head group to the heme center. As expected, previously, slower HET rates were detected for n=10 SAM (k_HET = 43 s⁻¹ on Ag) and faster HET rates for n=5 SAM (k_HET = 270 s⁻¹ on Ag). [40]

According to Marcus theory, the activation energy-dependent term is related to the driving force (ΔG⁰) and reorganization energy (λ) parameters according to

$$\Delta G^{‡}=\frac{\lambda }{4}{\left[1+\frac{\Delta G^0}{\lambda }\right]}^2$$ (2)

In electrochemical systems, the driving force can be expressed as

$$\Delta G^0=nF\left(E-E_0^{{}^{\prime }}\right)$$ (3)

where n is the number of electrons transferred between redox site and the electrode, E is the applied potential and E₀^’ stands for the standard midpoint potential of a redox couple. Invoking Butler-Volmer expression of current-potential (I-E) characteristics in the electrochemical experiment, it becomes evident how this term can be evaluated. The current density ($j=\frac{I}{A}\left[\frac{A}{c{m}^2}\right],$where A – electrode surface area) is related to the kinetics of cathodic and anodic process according to [41]:

$$j=k_0[C_o\exp \left(-\alpha f\left(E-E_0^{\prime }\right)\right)-C_R\exp \left(1-\alpha f\left(E-E_0^{\prime }\right)\right)$$ (4)

where f = F/RT, C_O and C_R is the surface concentration of oxidized and reduced species respectively and $\alpha$ represents a symmetry coefficient independent of the applied potential.

4. Results and discussion

In the following sections, the data from experiments of cyt c immobilized on (CH₂)₁₀-long SAMs are graphically shown, and data from experiments on shorter (CH₂)₅-long SAMs can be found in SI.

4.1. Cyclic voltammetry (CV)

CV represents the simplest version of voltammetry in which current (I) is recorded as a response of sweeping the potential (E) with a defined scan rate ($v=\frac{\Delta E}{\Delta t}$, ΔE- potential step, Δt – time unit). It has been routinely employed to characterize the redox proteins adsorbed on biocompatibly coated electrodes, often referred to as protein film voltammetry [12,42]. From a series of voltammograms recorded at various scan rates, the themodynamics and kinetics of electron transfer can be obtained. The middle of peak-to-peak separation informs about the midpoint potential of a redox transition, which on the example of a monolayer of cyt c adsorbed on Ag electrode equals E_1/2° ∼ 17–18 mV (vs. Ag|AgCl) for (CH₂)₁₀-long SAMs (Fig. 3A) and E_1/2° ∼ 20 mV for (CH₂)₅-long SAMs. These results are comparable to the literature [22,26]. The voltammograms of cyt c immobilized on longer SAMs represent almost ideal quasi-reversible behavior based on the full width at half maximum (FWHM) equal to ca. 84 mV. For the ideal Nernstian behavior, this value equals 90.6 mV/n [41]. As such, derived from our data n=1.07 reflects on close to uniform orientation of the adsorbed electroactive protein. If protein orientation on the electrode would be heterogenous, we would expect multiple redox transitions, which would result in broadened redox peaks in voltammograms [43]. FWHM of voltammograms of cyt c adsorbed on shorter chains equal to ca. 50 mV, which is far from ideal Nernstian behavior for 1 e⁻ redox transition. Such discrepancies in the shape of voltammograms might originate from more complex scenario of cyt c electrostatically attached on shorter (n<10) chains, which are: (1) an increased population of the non-native state of cyt c, denoted as B2, in which the Met-axial ligand is lost [44,45] and 2) presence of an additional step involving a conformational change of cyt c preceding the ET step which becomes rate-limiting step [46].

Fig. 3.

Cyclic voltammetry of cyt c interfaced on 11-MUA/6-MCH-coated Ag electrode. A) Experimental voltammograms recorded at series of scan rates from 150 mV/s to 3 V/S. B) Laviron analysis in which the anodic and cathodic peak potential is plotted vs. log(scan rate). The red dots represent the experimental data and gray dots are derived from simulated voltammograms at various scan rates (0.01–4 V/s). The green dashed line marks peak-to-peak separation ΔE_p at 1.5 V/s.

The kinetics of HET can be derived from the detected current which is governed by the Butler-Volmer equation (Eq. (4)). However, the measured current is a sum of faradaic (ET) processes in the system and all non-faradaic processes including charging of the electrical double layer or other effects related to the mass transport if a redox couple is not directly adsorbed on the electrode surface. As such, the analysis of the voltammogram might prove a complex task. A popular [6,46,47] approach of deriving k_HET, offered by Laviron [48,49], entails the detection of a series of voltammograms at varying scan rates (Fig. 3A). At slower scan rates, the voltammogram exhibits totally symmetric peaks in respect to the x-axis for reversible redox couple confined at the electrode surface, and the current's amplitude of both faradaic and charging (capacitive; non-faradaic) components are small. As the current response increase with the scan rate, the current of redox peaks become more distinct at higher scan rates, but the capacitive current also increases (Fig. 3A). In terms of the peak postion, at higher scan rates at which the sweep rate surpasses the HET rate, peak separation begins to occur. As such, from the plot of peak-to-peak potential separation vs log(scan rate) the k_HET can be calculated. On the example of interfaced cyt c, we present this approach (Fig. 3B, red dots and Fig. S3A). Fitting a linear function to the slope of E at peak max vs log (scan rate) at sufficiently high scan rates, the α coefficient can be determined (Fig. S1). Knowing α, which equals 0.5 for a totally symmetric cathodic and anodic process, the k_HET can be calculated according to

$$k_{HET}=\frac{\alpha nF{\nu }_C}{RT}=\frac{\left(1-\alpha \right)nF{\nu }_A,}{RT}$$ (5)

where ν_A and ν_C stand for the value of scan rate where the fitted linear function crosses the x-axis. Applying such analysis, we obtained a value of α =0.51–0.52 (Fig. S1) and ca. k = 10 (±3,30) s⁻¹ for longer chains, and α =0.64 and k = 20 s⁻¹ (Fig. S3A) for shorter chains. It is worth noting, that Laviron [48] stated that determination of α coefficient and k_HET is only valid for ∆E_p > 200 mV, which is rarely achieved experimentally. To further test this approach and estimation of α coefficient, we simulated voltammograms (DigiElch software; BV equation for adsorbed species) of adsorbed redox couple with defined k but varying α (0.2< α <0.8, Fig. S2) and analyzed the data using Laviron approach. Unfortunately, the analysis did not yield the original α value which resulted in the faulty estimation of k_HET using Eq. (5). Fig. S2 presents how the large deviation from ideal α, i.e. α=0.8 or α=0.2, results in not very pronounced difference in slopes of E at peak max vs. log(scan rate) in comparison to plots for α=0.5 for ∆E_p below 200 mV. Such discrepancy indicates how the determination of α and thus derived HET rate constants for fast kinetic processes might appear inaccurate.

As an alternative approach of deriving k_HET from our experiments, we simulated a series of voltammograms varying k_HET (8–80 s⁻¹) at various scan rates and plotted the derived peak-to-peak (ΔE_p) separation vs log(scan rate) (Fig. 3B, gray dots). Plotting the ΔE_p vs corresponding kinetic rate constants yields a trend (Fig. 4), which only slightly differs for processes with α other than 0.5 and it can be modeled using an exponential function. At slower scan rates (0.15 V/s or 0.25 V/s) the changes in the ΔE_p are distinct for the k from 0.5 s⁻¹ to up to 15 s⁻¹(Fig. 4D and Fig. 4E). At a faster scan rate of 1.5 V/s (Fig. 4B), the ΔE_p differs at faster kinetic rate constants of up to 70 s⁻¹. Using this derived function and the ΔE_p of 33.61 mV at a scan rate of 1.5 V/s (Fig. 3B), the kinetic rate from our experimental data yields the rate constant of k_HET = 47.80 (±2,91) s⁻¹ for longer SAM chains(Fig. 4, blue dot) and ΔE_p of 38 mV and k_HET of ca. 62 s⁻¹ for shorter SAM chains.

Fig. 4.

Peak-to-peak separation ΔE_p derived from simulated voltammograms with various scan rates (orange: 2.5 V/s, green: 1.5 V/s, red 0.5 V/s, blue: 0.25 V/s, purple: 0.15 V/s) plotted vs. heterogeneous ET rate (k_HET). Colored dots represent simulated data with α=0.5, gray dots stand for α=0.2 (or α=0.8). Fitted exponential function is used to estimate k_HET rate from experimental data.

We postulate that such simple analysis provides an alternative approach of determination of the HET rate of immobilized redox proteins in which there is no need of calculating α coefficient. Nevertheless, it is worth noting the general disadvantage of using CV for kinetics analysis; scan rates of up to 0.25 V/s are applicable to derive small k values of 0.5 – 10 s⁻¹, whereas a fast sweeping rate (up to 3 V/s) needs to be applied to derive the k values larger than 30 s⁻¹ to up to 100 s⁻¹ (Fig. 4A, 4B).

4.2. Square wave voltammetry (SWV)

Square wave voltammetry (SWV) offers an attractive alternative to CV through which the contribution of nonfaradaic current in voltammogram can be minimized. Instead of linearly sweeping the potential with a defined scan rate, the potential is applied as a waveform of certain pulse amplitude (E_amp) and width (t_p) in a staircase fashion: in a first cycle a positive E_amp pulse is followed by an oppositely directed negative E_amp pulse of equal magnitude, followed by a next cycle starting at an increased potential according to a E_step value (Fig. S4, check reviews of Mirceski et al. [50,51] or Gulaboski [52] for more details). In cyclic SWV, the potential waveform is scanned in the positive direction, and in addtion, followed by a scan in negative direction (Fig. S5). The current is measured at the end of each jump (t_s), so that for one cycle, the current is probed two times: at the end of the positive potential jump (I_forward) and at the end of the negative potential jump (I_reversed). In the SWV voltammogram, the net current (I_net=I_forward-I_reversed) is plotted vs. potential (Fig. 5A); thus, the contribution from the non-faradaic process is absent, if the frequency is small enough. The obtained voltammogram can be analyzed in terms of the peak current and the peak potential. However, both values do not carry the same information as in the ‘usual’ CV voltammogram. Apart from subtracting the charging current, and enhancing the faradaic current in I_net, each potential value refers to the middle potential of positive and negative potential jumps. As a result, the presented normalized current response is more sensitive to the faradaic process, the shape of the cathodic and anodic wave is more symmetrical in respect to x-axis (up to certain potential amplitude, see below) and thus information about the redox transition can be more easily obtained (Fig. 5A). SWV is also an elegant electrochemical method to evaluate the mechanism of surface electrode mechanisms coupled to chemical reactions, as reviewed in detail by Gulaboski et al. [53,54] but not applicable in this work. In SWV, the scan rate is modulated by a change of pulse width t_p, and it is defined as potential step divided by t_p ($v=\frac{E_{step}}{t_p}$).

Fig. 5.

Square wave voltammetry of cyt c interfaced on 11-MUA/6-MCH-coated Ag electrode. A) Experimental voltammograms recorded at a series of frequencies from 5.7 to 40 Hz. B) Normalized peak current (I_p/f) vs. log(f) from experimental voltammograms (blue). Gray dashed lines represent the fr. at I_{p max} of simulated SWVs at various k_HET rates which are marked in green. C) Function of frequency at max I_p/f vs. the corresponding k_HET derived from simulated SWV voltammograms. Blue dot represents experimental data.

There are two strategies of performing a SWV experiment, either by varying the frequency (f = 1/t_p) or the potential amplitude E_amp.. Kinetic rate constants can be derived from both approaches. [51,55] We first present the frequency-sweep approach on the example of adsorbed cyt c. SWV voltammograms were recorded at a series of frequencies in the range of f = 5.7 – 250 Hz (corresponding to scan rate v = 11–500 mV/s) from which the net current I_net and the peak current (I_p) were analyzed as a function of frequency (Fig. S6 and Fig. S7). It has been shown that the electrode kinetic parameter (w_ET, do not confuse with angular frequency w) of adsorbed electroactive species is a function of frequency (w_ET=k_ET/f). Plotting the peak current divided by frequency vs log(fr.) generates a bell-shaped curve from which the maximum of the current can be estimated (Fig. 5B and Fig. S8 for cyt c interfaced on longer SAM and Fig. S9 for cyt c interfaced on shorter SAM). Note that in such analysis faradaic and non-faradaic currents become independently plotted, as faradaic current occurs at lower frequencies (0-ca. 150 Hz) and non-faradaic current dominates the voltammogram at higher frequencies than 150 Hz (Fig. S7). The frequency at the maximum is a linear function of HET rate constant as shown here for the data from simulated voltammograms (Fig. 5C and Fig. S10). The frequency at max I_p/f is independent of the potential amplitude (Fig. S11) and α coefficient (Fig. S12) [56]. Such analysis yielded the kinetic rate constant of k_HET = 64.86 (±1,27) s⁻¹ (Fig. 5C, blue dot) in all three repetitions of the experiment for longer SAM chains and k_HET = 86.22 s⁻¹ for shorter SAM chains. In principle, the total net current can be also analyzed in the similar fashion, however at high frequencies the contribution of charging current cannot be easily separated from the net current (Fig. S7).

Mirceski et al. proposed a second strategy for evaluating the kinetics of electrode-confined redox species, an amplitude-based approach, in which the potential amplitude is modulated and the scan rate remains constant [56,57]. He has shown, that the net peak current (I_net) increases nonlinearly with the increasing amplitude (E_amp). Normalizing the values of I_p and ΔE_p over applied potential amplitude generates a curve with a maximum from which electrode kinetic parameter ω_ET can be calculated. However, analysis of our data did not yield a satisfactory curve from which k_HET could be estimated (not shown).

There are numerous benefits of employing SWV to study the redox properties of redox couple. A higher amplitude of current response can be modulated by increasing the potential amplitude E_amp (Fig. S11). There is no need to determine α coefficient for estimating k_HET. Using the frequency-sweep approach, the use of slower scan rates (up to 20 mV/s in comparison to ca. 1.5 V/s in CV experiment of adsorbed cyt c) is sufficient to determine kinetics of HET.

4.3. Electrochemical impedance spectroscopy (EIS)

The most information-rich technique that can be used to characterize the electrochemical system is electrochemical impedance spectroscopy (EIS). Similar to SWV, the potential is applied as a waveform, but it has a sinusoidal shape. This sinusoidal perturbation is defined by its frequency f and the amplitude dE around a specified DC potential E_DC (E = E_DC + dE*sin(2*pi*f)). The information about current response to the applied E sinusoid is expressed in terms of electrical impedance Z, i.e. the ratio between voltage perturbation and current response, or in other words, the frequency-dependent resistance. As such, in EIS the impedance Z is recorded as a function of the frequency, typically in a range from 0.1 to 10⁶ Hz (at constant Edc and dE), resulting in an impedance spectrum. The results can be represented as an electric circuit of resistive and capacitive components in the system. As such, analysis of the EIS data entails fitting different electrical circuit models that provide the best description of the measured impedance to extract parameters that control the charge-transfer reaction. In certain cases, impedance data can be evaluated in a model-independent fashion, by extracting results directly from an appropriate representation (see below).

To interpret EIS spectra of interfaced cyt c on the electrodes, we first fitted our data with the simplified Randles circuit (Fig. 6A, inset) composed of solution resistance (R_sol), the capacitance of the double-layer (C_dl) representing the non-faradaic current, and resistance of the charge-transfer R_ct (Fig. 6A). The last parameter is minimal at the midpoint potential of redox transition, which here is 20 mV for cyt c interfaced on both SAMs. In the next step, we represented the measured impedance spectra at the E_DC of 20 mV in the form of the frequency-normalized Cole-Cole plot (Fig. 6B and Fig. S13B; dark purple) which is a plot of the real part of admittance (Y-admittance, Y = 1/Z) vs. the imaginary part of admittance, each divided by the angular frequency (w=2pf). The ideal Cole-Cole plot should be composed of two semi-circles. At high frequencies (low imaginary admittances) the semicircle corresponds to the response of the solution and at low frequencies (high imaginary admittances) the semicircle reports on the charge-transfer process. To extract the R_ct with minimal data manipulation and in a model-independent fashion, one can remove the contribution from the solution resistance. [58] To achieve this, we subtracted the resistance of the solution from the real impedance of the original data, since it contributes in an additive fashion. We derived the value of R_sol from the Nyquist plot, but it is also possible to use the result from the fit of the Randles circuit above. This correction generated a new curve (Fig. 6B and Fig. S13B, light purple). From the frequency at the maximum of so-derived semi-circle, the HET rate constant can be estimated [58] according to k_HET= πf. As such, we obtained the value of ca. k_HET = 26 s⁻¹ for cyt c interfaced on 11-MUA coated electrodes and ca. k_HET = 497.6 s ^− 1 for cyt c interfaced on 6-MCH electrodes (Fig. S13B).

Fig. 6.

Electrochemical impedance spectroscopy of cyt c interfaced on 11-MUA/6-MCH-coated Ag electrode. A) Resistance of charge-transfer element as a function of applied potential obtained from the fit of simplified Randles circuit presented in the inset picture. B) Frequency-normalized Cole-Cole plot at applied 20 mV. The dark purple circle represents the raw data. The light purple circle represents the solution resistance corrected data. Dashed line labeled fr_HET marks the frequency of the middle of the circle from which the k_HET can be estimated. C) HET rate constants as a function of applied potential, which has been estimated from fitting the complete Randles circuit (inset) to EIS data.

As an alternative approach, we fitted the complete Randles circuit to impedance spectra collected at the E_DC of 20±15 mV (Fig. 6C), keeping the value of solution resistance constant (R_sol=108 Ω for cyt c immobilized on 11-MUA-coated electrodes) allowing only the values of R_ct, C_DL and C_ct to change. Describing the charge-transfer as resistive and capacitive elements allows estimation of the HET rate constant according to $k_{HET}=\frac{1}{2R_{CT}{C}_{CT}}$. [58,59] For cyt c adsorbed on the electrode, the maximum value of k_HET=27 s⁻¹ (for cyt c interfaced on 11-MUA-coated electrode) and k_HET=0.39 s⁻ (for cyt c interfaced on 6-MHA-coated electrodes) was obtained at applied 20 mV (Fig. 6C).

Both approaches of i) analyzing the solution-corrected Cole-Cole plot and ii) fitting the Randles Circuit to impedance spectra, yielded almost the same kinetic rate constants for the cyt c interfaced on longer SAM, which are however different from CV and SWV experiments. It is worth noting, that in contrast to CV and SWV, in which to various extent a contribution of charging current in detected current is present, in EIS the charging current of double-layer formation is reflected in the capacitive element of SAM coating. As such, the value can significantly differ depending on the packing and quality of alkanethiol attached to a metal surface, the length of its chain and ion permeability. [60] In certain cases, when the contribution of the capacitive element of coating in EIS spectra is large enough [58], i.e. larger than the capacitive element C_ct of electron transfer process, both values cannot be easily distinguished and as such the k_HET rate cannot be precisely determined.

Although EIS offers the most precise description of the electrochemical system, the accuracy of the approach is highly dependent on the correct description of all the elements in the circuit.

4.4. Critical assessment of obtained kinetic rates using electrochemistry and comparison to spectro-electrochemical approaches

Employing three different electrochemical approaches to determine HET rate constant of interfaced cyt c either on 11-MUA/6-MCH or 6-MHA/6-MHA-coated electrodes resulted in a diverse results of k_HET ∼ 10 – 65 s⁻¹ for longer SAM (Table 1) and k_HET ∼ 19 – 497 s⁻¹ for shorter SAM (Table S1). In general, the frequency-based SWV approach yielded kinetic rate constant more than 4–6 times larger than Laviron analysis of CV. Such large discrepancies could originate from the model system, i.e. conformational or rotational changes of the protein matrix prior to the electron transfer, which has been shown to occur for shorter SAM like 6-MHA [40], or heterogeneity of the results reflects the technical capabilities of the used method. The first scenario is likely the case for cyt c on shorter SAMs (n=5) as electron tunneling through such a short distance between the heme moiety and the electrode surface becomes faster than other processes, i.e. structural changes preceding ET step, known as conformational gating. Such a scenario, however, does not occur for cyt c interfaced on a longer alkanethiol chain (number of C atoms ≥11) as electric field-dependent reorientation does not occur at longer distances and adsorption of only one electroactive state of cyt c is preserved (out of two possibilities) [17]. In other words, under conditions of cyt c adsorbed on longer SAM, the applied potential in electrochemical experiments induces primarily HET reaction and the observed differences must reflect some other effects not related to the protein itself which we discuss below.

Table 1.

HET rate constant of cyt c immobilized on 11-MUA-coated electrodes obtained using electrochemical and spectro-electrochemical approaches.

Method	kHET / s−1	Source
CV: Laviron Simulations	10 (±3,30) 47.8 (±2,91) – 1.5 V/s 58	This study
SWV	64.86 (±1,27)	This study
EIS: Cole-Cole plot Randles Circuit	26 27	This study
CV	40a	[40]
SERR	42a 43a	[26,40]

^acyt c immobilized on pure 11-mercaptoundecanoic acid.

The results from CV yielded two very different values of k_HET (ca. 10 s⁻¹ and ca. 47.80 s⁻¹ for cyt c on 11-MUA, and ca. 19 s⁻¹ and 62 s⁻¹ for cyt c on 6-MHA) obtained from Laviron analysis and simulation-based approach, respectively. In the seminal publication of Laviron [49], it is stated, that determination of α coefficient and k_HET is only valid for ∆E_p > 200 mV which is difficult to obtain experimentally. In this work, the high scan rates had to be employ to observe significant ∆E_p with the value of 33.61 mV at a scan rate of 1.5 V/s for 11-MUA. As such, a reliable Laviron analysis, in particular determination of α coefficient could not be performed. The simulation-based approach, presented here, overcame such limitations, and a more reasonable value of k_HET = 47.80 s⁻¹ has been obtained. Such an approach is also applicable to systems exhibiting low HET rates, as for such low scan rate as 0.15 V/s, ∆E_p of 0.02 - 0.14 V corresponds to k_HET of 0.5 to ca. 10 s⁻¹ (Fig. 4E), and as fast HET rates as ca. 60–70 s⁻¹ that could be detected by scan rates of 2.5 V/s (Fig. 4A). However, under such a high scan rates conditions, there is a large contribution of solution resistance due to complexity of iR drop compensation. [61] Thus, the result could be overestimated. The rate reported in literature k_HET=40 s⁻¹ [26] lies very close to obtained results. However, the published rate refers to cyt c interfaced on pure 11-MUA coated electrodes. In this regard, it has been postulated that dilution of longer -COOH terminated SAM monolayer, as in the case of this work, helps to obtain faster HET rates of interfaced cyt c due to higher concentration of available -COO⁻ groups. [18] This explains why the k_het for cyt on mixed 11-MUA/6-MCH monolayer (this study) is slightly higher (by 8 s⁻¹) than for cyt c on pure 11-MUA.

The frequency-based approach SWV allowed to determine the k_HET of ca. 65 s⁻¹ for cyt c interfaced on 11-MUA-coated electrodes. SWV proved to be very useful as it is a method which intrinsically allows for deconvolution of current into faradaic and nonfaradaic process. Furthermore, the HET estimation is straightforward as the frequency at the highest faradaic current response directly informs about the kinetic rate, as shown in this work for simulations-derived linear fit function (Fig. 5C). Moreover, the analysis is independent of a coefficient and applied potential amplitude. Another advantage is negligible contribution from the solution resistance, due to application of much lower scan rates (up to 20 mV/s) than in CV experiment. In this regard, it is evident from Fig S6 and Fig. S7 how the faradaic response can be separated from other contributions occurring at high frequencies of potential perturbation. In sum, SWV is an appropriate method to determine HET rates in the range of 5–120 s⁻¹ (Fig. 7) in which the lower limit reflects the technical limitations and the upper limit reflects the frequencies at which capacitive current becomes dominant in voltammograms.

Fig. 7.

The applicability of electrochemical methods to study interfaced redox proteins exhibiting k_HET ∼ 0 – 120 s⁻¹ when immobilized on alkanethiols.

The HET rate constant derived from EIS is more than 2x smaller than from SWV. The method of data analysis (model-independent Cole-Cole plot or fitting Randles circuit) has no effect on estimated HET rate as both values are almost identical. It is, thus, very unlikely that in this work the accuracy of EIS is compromised through the fitting of equivalent electrical circuit. However, in EIS the detected current is sensitive to all capacitors in the system. As such if there is significant overlap between the capacitive contributions of current response, their deconvolution becomes difficult which affects the accuracy of HET estimation. Unfortunately, the charging current of cyt c interfaced on C₁₁-long SAM monolayer has relatively high capacitance (ca. 25 µF) in comparison to capacitance of charge transfer (ca. 12 µF). This is visualized in original Cole-Cole plot (Fig. 6B) in which two semi-circles partly overlay each other. As a consequence, Cole-Cole plot represents convoluted processes from which the precise estimation of the charge transfer process is hindered. For cyt c interfaced on shorter SAM chains, the effect is even more pronounced and it leads to even higher overestimation of k_HET rate constant (Fig. S13B). As a comparison, the capacitance of double-layer is smaller for longer chains [24] from which estimated HET rate resembles the HET rate from CV experiment. As such EIS is an appropriate method to estimate relatively low HET rates (Fig. 7) in which the capacitance of SAM monolayer and capacitance of charge-transfer process can be well separated.

Combining electrochemistry with spectroscopy often allows to overcome the limitations of application of solely electrochemical methods. Directly probing the structural changes of redox protein underdoing redox transition in a time-dependent fashion upon potential jump allows the precise estimation of HET rate constant. [29,62] As such, only the faradaic response is detected, and there is no need of subtracting non-faradaic processes. Surface-enhanced methods allow detection of monolayer of sample interfaced on noble-metal support. Most common approaches are surface-enhanced resonance Raman spectroscopy (SERR) or surface-enhanced infrared absorption spectroscopy (SEIRA). [63] In such spectro-electrochemical methods, the intensity of spectral peaks informs about the concentration of oxidized or reduced species However, this is also a disadvantage of these methods, since the change of the concentration of redox species might be a reflection of another process like reorientation or complete desorption of the enzymes from the electrode surface.

5. Conclusions

The HET rate constant can be estimated using all electrochemical methods, however not every method is the most suited to the redox protein of interest. In this work, we examined most-known approaches for detection of HET rate constant of cyt c electrostatically interfaced on electrodes: CV, SWV, and EIS.

Electrochemical CV is an appropriate technique to determine slower k_HET using Laviron analysis in which a coefficient can be confidently estimated. i.e. for ∆E_p > 200 mV. As is it experimentally dificult to obtain such values, we have introduced simulation-based approach of estimating HET rates, in which ∆E_p detected at 5 various scan rates (0.15 V/s, 0.25 V/s, 0.5 V/s, 1.5 V/s and 2.5 V/s) directly informs about k_HET rate constant. As such, slow rates of ca. 0.5 – 10 s⁻¹ can be probed at slower scan rates and the rates as fast as ca. 70–80 s⁻¹ can be probed at fast dcan rates (2.5 V/s).

Freuquency-based cyclic SWV has been found to be a more reliable electrochemical technique for the estimation of k_het within the range of 0–120 s⁻¹ or higher due to straight-forward subtraction of non-faradaic current. For the EIS to offer a reliable estimation, the charging capacitance must be significantly smaller than the capacitance of the charge transfer.

Data availability

Data will be made available on request.

Supporting Information

Supplementary information is attached

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.