Epigenetic switching with asymmetric bridging interactions

Abstract

Gene expression states are often stably sustained in cis despite massively disruptive events like DNA replication. This is achieved by on-going enzymatic activity that maintains parts of the DNA in either heterochromatic (packed) or euchromatic (free) states, each of which is stabilized by both positive feedback and bridging interactions between individual nucleosomes. In contrast to condensed matter, however, the dynamics is not only governed by equilibrium binding interactions but is also mediated by enzymes that recognize and act on specific amino acid tails of the nucleosomes. The mechanical result is that some nucleosomes can bind to one another and form tightly packed polymer configurations, whereas others remain unbound and form free, noncompact polymer configurations. Here, we study the consequences of such an asymmetric interaction pattern on the dynamics of epigenetic switching. We develop a 3D polymer model and show that traits associated with epigenetic switching, such as bistability and epigenetic memory, are permitted by such a model. We find, however, that the experimentally observed burst-like nature of some epigenetic switches is difficult to reproduce by this biologically motivated interaction. Instead, the behavior seen in experiments can be explained by introducing partial confinement, which particularly affects the euchromatic regions of the chromosome.

Significance

Parts of the DNA chain can be maintained in a free (euchromatic) or packed (heterochromatic) state. In the free state, the gene can easily be read and expressed, whereas in the packed state, the gene is inaccessible and effectively silenced. The stable maintenance of these states is achieved by positive feedback and bridging interactions between the nucleosomes of the DNA. This paper studies the dynamics of switching from the free state to the packed state, and it shows that asymmetric interactions between active and silenced nucleosomes lead to a linearly spreading dynamics, which contrasts with experimentally known behavior. In contrast, if the effects of confinement of DNA are included, the observed burst-like dynamics appear.

Introduction

Epigenetics is the study of mitotically heritable gene expression states that are not a result of underlying changes in the DNA sequence (1,2,3). In particular, nucleosome-mediated epigenetics focuses on the genetic regulation of a local region of the genome, i.e., in cis. It primarily deals with histone modifications and small chemical groups or polypeptides that are attached to histone tails by chromatin-modifying enzymes. Many chromatin modifiers can both catalyze the addition of modifications (write) and bind to (read) nucleosomes that carry the same modification that they write. This read-write property enables positive feedback, allowing modifications to spread from nucleation sites over large chromosomal distances (4, 5).

A modification of particular importance is the methylation of histone H3K9 (H3K9me), since it maintains large chromosomal regions in a heterochromatic state. This modification noticeably competes with an alternative acetylated modification, H3K9ac, and together, these modifications play a central role in our understanding of epigenetics and heterochromatin formation (5,6,7,8,9).

In particular, the generation of quantitative spatiotemporal data has led to the development of a stochastic model that has been adapted to address the mating-type model system in mutants of S. pombe (5, 10,11,12)). This model framework has also been applied to other organisms and read-write systems, including vernalization in Arbidopsis (13,14,15), Polycomb and Trithorax systems in animals (16), and olfactory neurons in mice (17).

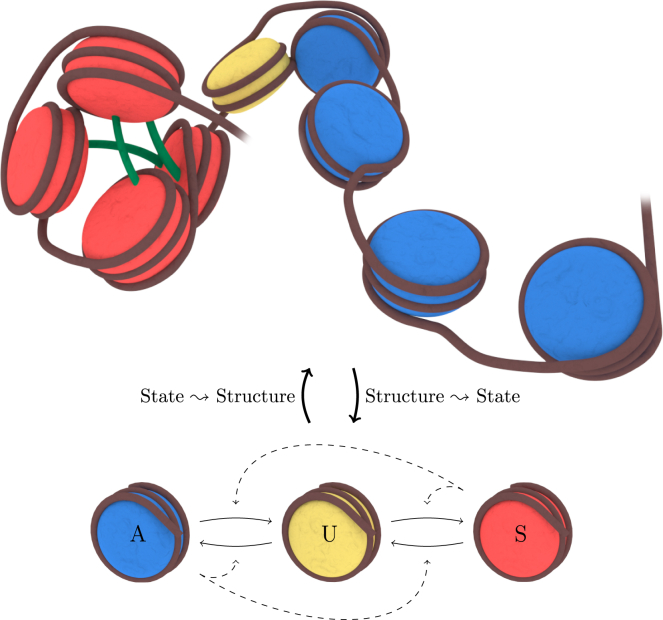
In addition to the positive feedback provided by the read-write enzymes, modeling has uncovered cooperativity and nonlocal nucleosome interactions to be required for bistable, mitotically heritable chromosomal regions. Cooperativity is a result of the three-state structure of the model, where each nucleosome can be in either the A (active/acetylated), U (unmodified), or S (silent/methylated) state, so that each A(S)-nucleosome needs to be converted twice to become an S(A)-nucleosome, as illustrated schematically in Fig. 1. Here, A-state monomers (blue) are representative of nucleosomes that have been acetylated, U-state monomers (yellow) represent unmodified nucleosomes, and S-state monomers (red) represent nucleosomes carrying an H3K9me mark. Lastly, interactions between nucleosomes (dashed arrows in Fig. 1) constitute the ability for nucleosomes to recruit enzymes and attempt to modify the states of other nucleosomes, which is possible not only between adjacent nucleosomes on the DNA, but also over long distances, as permitted by the 3D structure of the DNA polymer, as illustrated in the top of Fig. 1.

Figure 1.

A section of DNA (brown) with its associated nucleosomes. A-state (blue) and U-state (yellow) nucleosomes form polymers that exhibit an open structure, whereas the S-state (red) nucleosomes form polymers that exhibit a closely packed structure. The packing emerges from enzymatic bridging interactions (green), for instance mediated by Swi6^HP1 in S. pombe, Sir2 in S. cerevisiae, and HP1 in mammalian cells. Note that S-state nucleosomes can bind to up to two other S-state nucleosomes. To see this figure in color, go online.

A theoretical description of the stochastic recruitment rules between A-U-S nucleosomes was introduced by Dodd et al. (5) in a model that simplified the DNA polymer into a 0D structure, distinguishing only between local (nearest-neighbor) and global (long-range) interactions. Nonlocal interactions are believed to be a consequence of the folding of the chromatin fiber, thus bringing linearly distant nucleosomes in close spatial proximity to each other (18). The frequency of self-interactions, in turn, depends on the chromatin state in that the more densely packed heterochromatic state increases the probability of distant nucleosomes coming close to each other compared with the more open euchromatic state. This codependence of nucleosome state and structure is especially important during heterochromatin formation, where density and nonlocal nucleosomal interactions coevolve into a condensed globule that is later maintained.

To understand the effects of this complex feedback between spatial dynamics and nucleosome state, the 3D polymer structure must be explicitly modeled. Starting with (19, 20), there are now several models that couple polymer dynamics, state-specific bindings, and the active modifications of these interactions performed by read-write enzymes (21,22,23,24,25). These models couple the model of Ref. (5) with actual dynamics of chromosome rearrangement and spatial interactions in three dimensions. The models also assume symmetric interaction patterns in which silent nucleosomes attract silent nucleosomes, and active nucleosomes attract active nucleosomes.

The overall features of the aforementioned models are a reinforced bistability of each of the two possible polymer states of an isolated region of the chromosome, as well as the prediction of a condensed polymer configuration dominated by either the transcriptionally active euchromatin or the transcriptionally silent heterochromatin. However, although heterochromatin is indeed a condensed form of chromatin, euchromatin is much more loosely packed, enabling transcription factors and the transcriptional machinery to bind and express the residing genes. The packed heterochromatic structure arises from the evolutionarily conserved H3K9me reader Swi6^HP1, which binds to two spatially proximal nucleosomes, whereas there is no equivalent bridging for the active euchromatic state. Motivated by this underlying asymmetry where only methylated nucleosomes are subject to bridging-induced condensation, we here explore a slightly modified scenario of the polymer dynamics, where we respect that an active region of the chromosome is in a euchromatic and thus more flexible state, whereas a silent region is in a more tightly bound heterochromatic state (26, 27).

The asymmetry between the two states has been observed experimentally, e.g., using chromatin conformation capture analysis (27), by studying the diffusion constant in the two environments (28), and by studying the segregation fidelities of active and silent marks during cell division (29). Likewise, theoretical studies of chromatin structure have examined this asymmetry in systems with static methylation profiles (30,31,32). In our dynamic system, we will see that these systematic differences in chromatin structure challenge the nature and stability of the transitions between the euchromatic and heterochromatic states.

Materials and methods

Model

Polymer dynamics

We represent the genetic region as a 3D polymer of length N = 40, where each monomer represents one (or possibly more) nucleosome(s). The monomers can be in one of three states: A, U, or S, with polymers consisting mainly of A-state monomers being active and mainly of S-state monomers being silent. All monomers interact repulsively with one another, and additionally, S-state monomers can form attractive interaction pairs with a maximum of two other S-state monomers, which corresponds to bridging interactions between nucleosomes. The maximum value of two bridging interactions is motivated by the assumption that the interactions are mediated by the two tails of the nucleosomes that can carry H3K9me marks. The interaction “bonds” are only formed within a threshold distance and are assigned dynamically during simulation in such a way that the total distance between all bonded pairs is minimized.

The distance ${\ell }_0$ between neighboring monomers sets the scale of the system, and (without loss of generality) we take this to be unity. We work in the inelastic limit and thus only allow monomers to rotate perpendicularly to the distance vector between their two neighboring monomers (end-point monomers are allowed free movement with the constraint that the distance to the only neighbor be equal to ${\ell }_0$).

The dynamics of the polymer is described by an over-damped Langevin equation of the form

$$\mathrm{d}{\mathit{X}}_i\left(t\right)=-{\nabla }_{{\mathit{X}}_i}U\left(\mathit{X}\left(t\right)\right)\mathrm{d}t+\mathrm{d}{\mathit{W}}_i\left(t\right)\text{,}$$ (1)

where ${\mathit{X}}_i$ is the position of the i’th monomer, U is the aggregate potential function, and $\mathit{W}$ is a Wiener process satisfying $⟨{\mathit{W}}_i\left(t\right)⟩=0$ and $⟨{\mathit{W}}_i\left(t\right)·{\mathit{W}}_i\left(t^{\prime }\right)⟩=3{\sigma }^2\delta \left(t-t^{\prime }\right)$, with σ setting the diffusive noise scale. Equation (1) is then solved using the Euler-Maruyama method. We note that this procedure contrasts with those of previous studies, which tend to employ lattice polymer models (23, 24).

The potential U depends on the positions and states of all other monomers:

$$U\propto \left[\sum _{ij}{e}^{\frac{-4r_{ij}}{{\ell }_0}}-\sum _{ij\in \text{bonds}}{e}^{\frac{-4b{r}_{ij}}{{\ell }_0}}\right]\text{.}$$ (2)

Here, the terms in the first summation account for repulsion between all monomers, and the terms in the second summation account for attraction for the S-state monomers that form bonds. For bonded monomers, the two exponential terms create a potential well with an equilibrium distance equal to ${\ell }_0/2$, ensured by setting $b=-\text{LambertW}\left(-2e^{-2}\right))/2$. We note that U, as specified here, does not constitute the total potential, as, again, adjacent monomers in the polymer are constrained to be distance ${\ell }_0$ from one another.

Nucleosome dynamics

The monomer states evolve dynamically due to both recruited conversation steps, the rate of which depends on the states of spatially close monomers, and noisy conversion steps, which happen independently of the current polymer state configuration. The possible states, A-U-S, are ordered, and conversions between A and S have to go through U, as illustrated in Fig. 1. The state dynamics closely follows the rules laid out in Ref. (5), which can be summarized as follows.

Recruited conversion — with rate $r_{\mathrm{R}}$, a randomly selected (recruiting) monomer attempts the conversion of a randomly selected (recruited) monomer within the recruitment distance of $2{\ell }_0$. If the recruiting monomer state is S, the state of the recruited monomer is changed one step (in the possible reactions) toward S with probability p. Likewise, if the recruiting monomer state is A, the state of the recruited monomer is changed one step (in the possible reactions) toward A with probability $1-p$. If the recruiting monomer state is U, no conversion is performed.

Noisy conversion — with rate $r_{\mathrm{N}}$, a random monomer undergoes noisy conversion. A- and U-state monomers are converted one step toward S with probability p, and likewise, S- and U-state monomers are converted one step toward A with probability $1-p$.

The requirement that monomers participating in a recruited conversion must be within the recruitment distance $2{\ell }_0$ of each other results in a naturally emergent distance dependence for nucleosome conversions. In contrast to the model of Ref. (5), our conversion rates are not equal. The extra parameter is introduced to balance the effects of the asymmetric spatial structure of active and silent polymers, the latter of which exhibit closer packing and thus an inherent higher probability of successful recruited conversions. In other words, setting $p=\frac{1}{2}$ would not create symmetric behavior for the two competing states. We further note that the same probability p is used for both recruited and noisy conversions. This simplifies the model and further reflects the assumption that both types of conversions are mediated by the same enzymatic reactions and that their rates are similarly affected by the local enzyme concentrations.

Results

Asymmetric state behavior

First, we consider the asymmetry in the behavior of the monomers of different states. Fig. 2 illustrates the monomer state dynamics of recruited conversions for polymers with all monomers initialized in state A [Fig. 2 a] and S [Fig. 2 b]. Defining a polymer to be active if $\ge 90\%$ of the monomers are in the A state and silent if $\ge 90\%$ of the monomers are in the S state, we observe that the polymers maintain their initial state during the simulations: the system is bistable in the sense that both active and silent polymers remain active and silent, respectively.

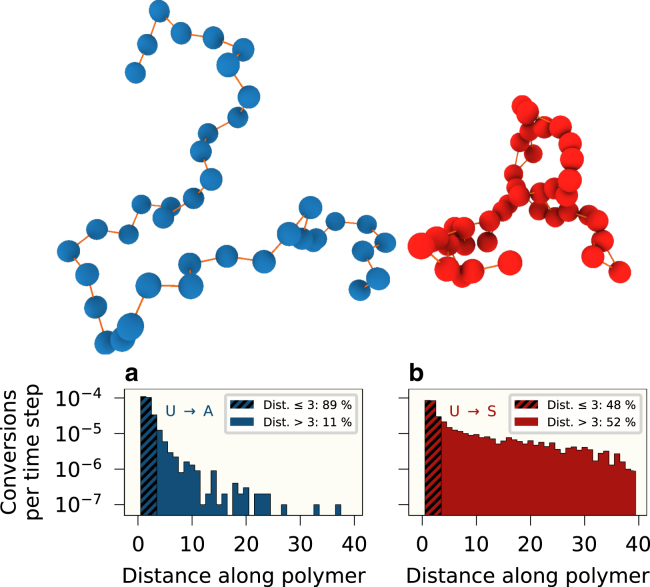
Figure 2.

Number of successful recruited conversions per time step as a function of the distance along the DNA polymer for (a) the U to A reaction, with all monomers initially in the A state, and (b) the U to S reaction, with all monomers initially in the S state. On top are shown representative 3D polymer structures for (a) all monomers in the A state and (b) all monomers in the S state. Parameters: $R_{\mathrm{R}}=8.50$, $p=0.41$, RMS $\approx$ 4.0. To see this figure in color, go online.

Tracking the number of successful recruited conversions for a given reaction as a function of distance along the polymers, we observe that the probability for a recruited conversion to occur decreases with the distance along the polymer, albeit very differently for either type of polymer. For the silent polymer (Fig. 2 b), we find that the number of conversions decays much more slowly. The number of conversions for local interactions (here defined as distance $\le 3$) make up $\sim 89$ % of the total conversions for the active polymer, but only $\sim 48$ % for the silent polymer. At a distance of 10, the number of conversions is different by an order of magnitude, and at distances $>30$, conversions are still stably occurring only for the silent polymer ($\sim {10}^{-6}$ per time step). This behavior is expected, since the monomers in the silent polymer form many bonds, which in turn forces the monomers closer together on average than what is the case for the active polymer.

Here our model differs markedly from previous models: for models that do not implement spatial dynamics directly (5, 11), special parameters are needed to separately model local and global reactions. Likewise, for models that explicitly employ 3D polymer structures (19−21,23−25)), we believe that ours is the first model to combine dynamic nucleosome states with the biologically relevant fact that silent and active polymers exhibit different local spatial behavior due to bridging, which in turn results in different global polymer structures.

The cenH region

To put our model in the context of experiments, we consider data on the mating-type region in S. pombe, which relies on a special nucleation region known as cenH. With the activation of cenH, the mating-type region becomes stably heterochromatic, and the re-establishment of the heterochromatic state from an artificially created euchromatic state has been studied experimentally (10, 11). Without the cenH region in the $K\Delta$ mutant (6, 33, 34), the mating-type region is bistable, and it can thus exist either in the euchromatic or the heterochromatic state at a given time. The timescale of the switching between the two states is of order once per 2000 generations of the yeast cell cycle (6, 34). The cenH region occupies about 20% of the $\sim {10}^2$ nucleosomes in the wild-type mating-type region, which in our system of 40 monomers corresponds to a cenH region of 6–8 S-state monomers. We will further simplify the dynamics by never allowing the monomers in the cenH region to change to a different state, thus approximating the relatively high rate of heterochromatic nucleation of this region in real systems (10).

As mentioned, the active and the silent states of the polymer are each extremely stable. However, with the activation of the cenH region, this stability changes fundamentally, as the overall polymer state becomes biased toward the silent state. The simulations now show the spreading of the S state to the rest of the polymer when initializing in the active state. This recapitulates the experimental observation of (10). Polymers with activated cenH regions are thus monostable in the silent state. Fig. 3 a shows a representative time-space plot of the process. The switch from active to silent happens gradually with the S-states spreading linearly with time from the central cenH region to the rest of the polymer. This behavior, however, contrasts with what is seen in experiments on S. pombe, where instead a stochastic and sudden, burst-like, switch is observed (11).

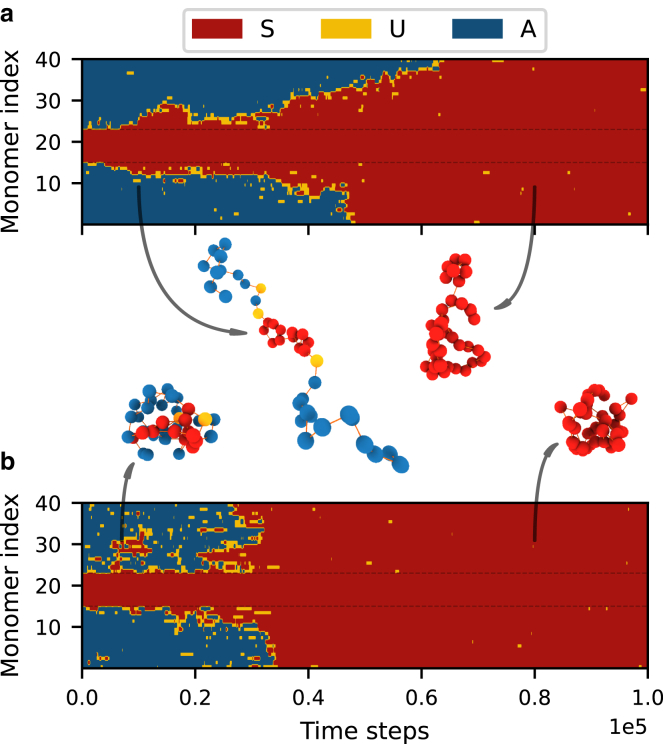
Figure 3.

Time-space plots showing the development of polymers with a cenH region of size 8 (dotted lines). (a) No external pressure leads to few interactions between monomers and the gradual spreading of the S state. (b) With the external pressure, we see many interactions between monomers and a sudden, stochastic switch of the entire polymer from active to silent. 3D polymer structures representing the different regimes are shown in the middle. Parameters: as in Fig. 2, except: RMS $\approx$ 4.0 (a) and $\approx$ 2.0 (b). To see this figure in color, go online.

External pressure

Burst-like switching has previously been observed in models where active and silent polymers behave symmetrically (11), and we therefore expect this behavior to be mediated by global interactions also within the active polymers. In the present model, however, global interactions for A-state monomers occur very infrequently, due to the absence of bridging interactions.

Instead we look for alternative explanations. One possibility could be the tight packing of DNA in the nucleus, which indicates that external forces are at play, compressing the polymer. To investigate this, we introduce an effective external pressure that accounts for environmental (steric) forces acting on the DNA chain, modeled by a potential term,

$$U_{\text{pressure}}\propto \sum _i\parallel {\mathit{X}}_i{\parallel }^2\text{.}$$ (3)

With the inclusion of this term, the silencing behavior is qualitatively altered, as shown in Fig. 3 b. We observe the same permanent switch from the active to the silent state but now also see burst-like behavior, with the switch occurring over a much smaller time interval. We furthermore observe significantly more noise in the state-conversion interactions (seen as “patches” of U- and S-state monomers). The increased number of patches indicates a higher number of global interactions. We quantify pressure by the effect it has on the radius of gyration, i.e., the root mean-square (RMS) of the monomer distances to the center of mass. The highest pressure we consider reduces the average RMS of the polymer from $\approx 4.0$ to $\approx 2.0$.

Switching statistics

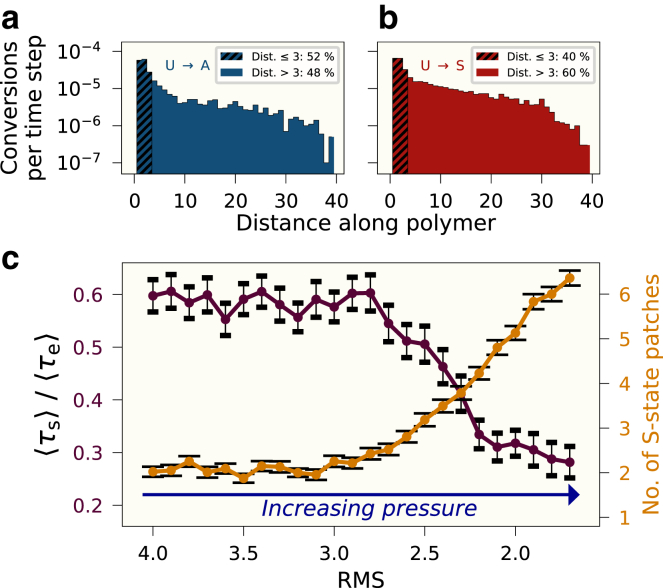
We now move on to study the effects of pressure quantitatively. In Fig. 4 a and b, we compare the number of successful recruited conversions for polymers with the cenH region inactive, using a pressure term such that RMS $\approx 2.0$, for the U to A reaction, with initially active polymers [Fig. 4 a], and the U to S reaction, with initially silent polymers [Fig. 4 b]. As in Fig. 2, we observe that the probability for a recruited conversion to occur generally decreases by the distance along the polymer, as a result of the 3D dynamics. However, we now also observe that with significant pressure present, the number of conversions decays much more slowly than for polymers with no external pressure, in both cases (compare with Fig. 2). The number of global conversions where the external pressure is present is significantly higher than when it is not present; for the initially active polymer in Fig. 4 a, the number of conversions for interactions of distance $\le 3$ ($\approx$ 52%) is now comparable to the number of conversions for distances of $>3$ ($\approx$ 48%), where previously (Fig. 2), where the conversions were dominated by small-distance interactions, the corresponding values were $\approx$ 89% and $\approx$ 11%, respectively. A change from Fig. 2 can also be observed in the number of conversions for the silent polymer in Fig. 4 b, where the number of conversions of distance $>3$ has increased from $\approx$ 52% to $\approx$ 60%, indicating a distinct pressure effect in addition to the compaction resulting from bridging interactions. Lastly it is worth noting that the behavior of the active polymer in Fig. 4 a is similar to the behavior of the silent polymer in Fig. 2 b, which indicates that pressurized active polymers can achieve similar “globalness” as silent polymers.

Figure 4.

Number of successful recruited conversions per time step as a function of the distance along the DNA polymer with external pressure for the (a) U to A and (b) U to S reactions. (c) Ratio of the average switching time to average establishment time, as well as the average number of S state patches (at switching initialization) as a function of RMS. The averages are taken over 100 simulations. Error bars indicate uncertainty of the mean values. Parameters: as in Fig. 2, except: RMS $\approx$ 2.0 (a) and (b). To see this figure in color, go online.

To quantify the effects of pressure on the switching behavior, we define ${\tau }_x$ as the first time at which x % of the monomers were in the S state. With this, we define the “establishment time,” ${\tau }_{\mathrm{e}}={\tau }_{90}$, and the “switching time,” ${\tau }_{\mathrm{s}}={\tau }_{90}-{\tau }_{50}$, since we assume that when at least 50% of the monomers are in the S state, a switch is overwhelmingly likely to occur. Burst-like switching is characterized by short switching times compared with establishment times.

In Fig. 4 c, we quantify the time spent during the switch in comparison to the total time of heterochromatin establishment by considering $⟨{\tau }_s⟩/⟨{\tau }_e⟩$. As mentioned, the overall state switching of the DNA chain during heterochromatin establishment occurs stochastically and in a burst-like manner, and this ratio reflects the degree to which this occurs for the polymers. Here we observe that for RMS $\ge 3.0$, the ratio stays relatively constant at approximately 0.6 and then falls to approximately 0.3 for RMS $\le 2.2$, marking a more distinct switching event. This recapitulates the behavior seen in Fig. 3. Next, we investigate the number of isolated, contiguous S-state patches (or regions) of any size in the polymer at ${\tau }_{50}\text{.}$ At high pressure, the higher levels of global interactions lead to a more patched landscape (Fig. 3 b). Fig. 4 c shows this effect as a function of external pressure. We observe that the number of S-state patches is markedly higher for lower RMS values, averaging more than six patches, whereas the number falls as the RMS grows; when the RMS is above 3, the average number of patches falls to about two. Taking into account that any random state conversion to an S state results in a patch of size 1, the average value of about two patches indicates that the S state spreads almost entirely between nearest neighbors. There are very few, if any, recruited conversions that occur over longer distances. This corroborates the results from Fig. 4 a and b.

In summary, the results seen here constitute further evidence that pressure and its consequences in the shape of polymer compression are a viable explanation for burst-like state switching.

Establishment time statistics

In Fig. 5 a, we quantify the results from simulations of 5000 polymers initialized in the active state, with cenH regions of size 6–8. Here the fraction of nonswitched (active) polymers, which we compare for pressures corresponding to RMS $\approx 2.0$ and RMS $\approx 4.0$, is tracked as a function of time. First we observe that the 3D polymer model presented in this paper reproduces the exponentially decaying behavior of the establishment time seen in (11), for all systems. In addition, we find that the smaller the fraction of cenH to system size is, the larger is the mean establishment time for the given system. This qualitatively matches the behavior seen in experimental data, as shown in the inset of Fig. 5 a.

Figure 5.

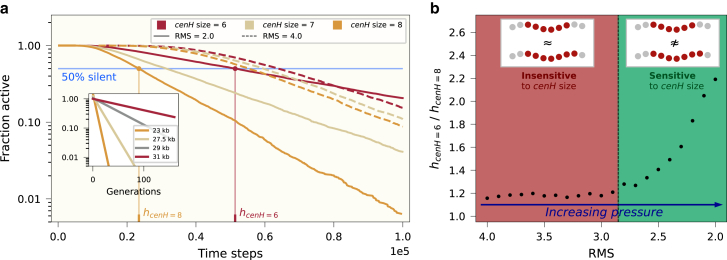
The influence of cenH size and pressure on establishment times. (a) The fraction of active polymers as a function of time steps for different cenH sizes, as well as different RMS values. Values are computed from 5000 simulations. (a, inset) Experimental data from (11). (For the 29-kb system, data from the SH4 strain is used.) Corresponding system sizes are indicated by matching colors. (b) Fractions of times where polymers are 50% silent for cenH values 8 and 6. Parameters: $R_{\mathrm{R}}=8.50$, $p=0.41$, number of simulations = 5000. To see this figure in color, go online.

Furthermore, there is a clear difference in the observed behavior for different values of RMS. For RMS $\approx$ 2.0, the slopes for the different cenH sizes are markedly different, whereas for RMS $\approx$ 4.0, the slopes are almost identical. This can again be attributed to the fact that without compression, the spreading of the S state in active polymers can almost exclusively happen from neighbor to neighbor. The effect on the establishment times when increasing the cenH size is thus a time reduction, since, trivially, fewer nucleosomes need to be converted. With pressure effects, and thus a smaller RMS, there are more global interactions and recruitment conversions, and we find that this leads to a nontrivial dependency for the establishment time on the cenH length, which indeed is what is correspondingly seen in experimental data.

Finally, we quantify the effect of pressure on the behavior of the slopes of the establishment times. We here define the “half-silent time,” h, as the first time at which half of the polymers in the ensemble become silent. Note that steeper slopes follow from lower establishment times, and thus also from lower half-silent times. In Fig. 5 b, we evaluate the ratio of the half-silent times of systems with cenH size = 6 and cenH size = 8, as a function of RMS. For RMS $\approx$ 4.0–2.8, the ratio is close to 1, which matches the similar slopes seen in Fig. 5 a. However, above RMS $\approx$ 2.8, the values rise abruptly, indicating a fundamental change in the behavior of the system, akin to a phase transition. This indicates that conversion interactions become sufficiently long-range to facilitate the burst-like switching behavior for the polymers, corresponding to an effective onset of substantial nonlocal read-write activity along the DNA. Thus we find two regimes of polymer confinement: at low pressures nearest-neighbor conversion interactions dominate and the switching dynamics is insensitive to the cenH size. In contrast, above a critical pressure, the temporal dynamics of switching becomes sensitive to the cenH nucleation region size.

Discussion

In this paper we have introduced a model framework that allows us to discuss the asymmetry of the dynamics of euchromatic and heterochromatic polymer states in an isolated region of the chromosome. Our model predicts a systematic difference in recruitment dynamics for the condensed silent polymer compared with open active polymer, when confinement of the polymer is not taken into consideration. Recruitment between nucleosomes in active polymers is effectively driven by interactions between close neighbors, whereas recruitment in silent polymers typically occurs over longer distances.

For bistable epigenetic behavior to emerge, the relatively high rate of conversion interactions for nucleosomes in a heterochromatic region of the chromosome needs to be balanced by a higher enzymatic conversion rate for the nucleosomes in a euchromatic region. Furthermore, long-range conversion interactions are necessary to observe the stochastic burst-like behavior seen in real epigenetic switches (5). Our study shows that such long-range interactions are very unlikely to occur in open polymers, irrespective of the state of the recruiting nucleosome. Thus a few S nucleosomes cannot induce a sudden change in the whole system, and the resulting euchromatic-heterochromatic switches therefore become gradual rather than burst-like. To explain the discrepancy between our model and experiments (11), we considered an externally induced compaction mechanism. In a real eukaryotic nucleus, this may be provided by the overall confinement of the genome reflected in high volume fractions (35) compared with the one predicted by free random polymers with its associated Flory scaling (36). Our model further predicts that the heterogeneously varying density of chromatin between different regions of the nucleus (35) could have the implication that burst-like silencing (11) is more likely in dense regions, whereas linearly spreading silencing dynamics (37) is more likely in sparser regions.

As a further demonstration of the consequence of confinement, we link our model directly to the experiments of Ref. (11) and include a cenH region. Our model highlights that the rate of silencing in the unconfined regime with linear spreading would be nearly independent of the size of the cenH region relative to the size of the total system. However, with confinement, we obtain a strong dependency, thereby reproducing the experimentally observed effect.

When simulating a system that encompasses both the timescales of polymer dynamics and enzymatic read-write activity, the model dynamics should in principle accommodate timescales from the milliseconds of nucleosome movements to minutes, which characterize the typical rate of collapse of euchromatin to heterochromatin (22, 38). The separation of timescales between polymer dynamics and nucleosome dynamics is thus on the order of $\sim {10}^5$. For computational feasibility, however, we choose parameters that correspond to a separation on the order of $\sim {10}^3$. Concretely, in our system, the characteristic timescale to move a monomer a distance ${\ell }_0$ is $\sim {10}^1$ time steps, whereas the timescale of nucleosome state conversions is $\sim {10}^4$. Due to this reduction in the difference in timescales, our model is not quantitatively true to biology, in that the kinetic constants used correspond to undersampling the large space of possible polymer configurations.

Our 3D polymer model differs from previous models (19, 23−25)) in that we try to explicitly account for the following observations: 1) in systems such as S. pombe and Polycomb, there is no evidence that nucleosomes corresponding to A-state monomers form bridging interactions with other nucleosomes, and 2) the bridging interactions rely on modifications on the histone tails, which we believe can happen at maximally two locations per nucleosome. The resulting structures thus have an inherent asymmetry between active and silent polymers, and the silent, condensed polymers are more open than they would have been if many-body (more than two) interactions were permitted.

The widest perspective of our model is the predicted feature of confinement-dependent epigenetic switching dynamics. H3K9me ChIP-seq profiles often show two qualitatively distinct shapes in the same organism. For example, in S. pombe, block-like, uniformly distributed enrichment of H3K9me at centromeres and the mating-type region coexists with smaller, bell-shaped H3K9me enrichment profiles of heterochromatic islands (39). Moreover, both types of ChIP-seq profiles show enrichment with the same enzymes like Clr4 or Swi6. However, the more bell-shaped enrichment pattern is thought to emerge from linear, nearest-neighbor only spreading from a nucleation site (37), whereas the uniform enrichment patterns emerge from burst-like establishment of heterochromatin (5, 11), requiring nonlocal interactions of nucleosomes. How to reconcile these two suggested modes of heterochromatin establishment is a challenge. Based on our findings, we speculate that switching between the two modes is possible within the same system, e.g., mediated by changing the allowed conformations of the polymer in the micro-environment of a given Swi6/Clr4 target region. One may even speculate that these changes might be mediated by a liquid-liquid phase separation, which has been recently suggested to play a role in heterochromatin formation and maintenance (40,41,42).

Editor: Helmut Schiessel.