Multitask Deep Ensemble Prediction of Molecular Energetics in Solution: From Quantum Mechanics to Experimental Properties

Abstract

The last few years have witnessed significant advances in developing machine learning methods for molecular energetics predictions, including calculated electronic energies with high-level quantum mechanical methods and experimental properties, such as solvation free energy and logP. Typically, task-specific machine learning models are developed for distinct prediction tasks. In this work, we present a multi-task deep ensemble model sPhysNet-MT-ens5, which can simultaneously and accurately predict electronic energies of molecules in the gas, water, and octanol phases, as well as transfer free energies at both calculated and experimental levels. On the calculated dataset Frag20-solv-678k, which is developed in this work and contains 678,916 molecular conformations up to 20 heavy atoms and their properties calculated at B3LYP/6–31G* level of theory with continuum solvent models, sPhysNet-MT-ens5 predicts density functional theory (DFT)-level electronic energies directly from force field optimized geometry within chemical accuracy. On the experimental datasets, sPhysNet-MT-ens5 achieves state-of-the-art performances, which predicts both experimental hydration free energy with RMSE of 0.620 kcal/mol on the FreeSolv dataset and experimental logP with RMSE of 0.393 on the PHYSPROP dataset. Furthermore, sPhysNet-MT-ens5 also provides a reasonable estimation of model uncertainty which shows correlations with prediction error. Finally, by analyzing the atomic contributions of its predictions, we find that the developed deep learning model is aware of the chemical environment of each atom by assigning reasonable atomic contributions consistent with our chemical knowledge.

Graphical Abstract

Introduction

To accurately and rapidly predict molecular energetics has been of great interest in computational chemistry. Theoretically, molecular energetics can be calculated by solving the Schrödinger equation $\mathscr{H}\left(\left\{Z_I,{\mathit{R}}_{\mathit{I}}\right\}\right)\mathrm{\Psi }=E\mathrm{\Psi }$ of the system, where $\left\{Z_I\right\}$ is the set of nuclear charges and $\left\{{\mathit{R}}_{\mathit{I}}\right\}$ is the set of atomic positions. Unfortunately, the exact solution of this equation is intractable for most chemical systems and numerical approximations require the tradeoff between accuracy and computational efficiency.^1–4 In recent years, researchers have shown great interest in developing machine learning (ML) approaches for energetics prediction.^5–10 Instead of explicitly solving the Schrödinger equation for energetics calculation $\mathscr{H}\left(\left\{Z_I,{\mathit{R}}_{\mathit{I}}\right\}\right)\stackrel{\mathrm{\Psi }}{\to }E$, machine learning methods^11–22 can learn the mapping from the geometry to the energetics of the system directly $\left\{Z_I,{\mathit{R}}_{\mathit{I}}\right\}\stackrel{ML}{\to }E$. Recently, deep learning (DL) methods, which directly utilize the atomic coordinates $\left\{{\mathit{R}}_{\mathit{I}}\right\}$ and type $\left\{Z_{\text{I}}\right\}$ and predict molecular energetics in an end-to-end fashion, are gaining increasing popularity. In 2017, deep tensor neural network (DTNN)²³ achieved Mean-Absolute-Error (MAE) of less than 1 kcal/mol (chemical accuracy) on the QM9 benchmark dataset,^24–26 which contains minimized structures and molecular properties in the gas phase calculated using the DFT method at the B3LYP/6–31G(2df, p) level of theory for 133,885 molecules composed of H, C, N, O, and F with no larger than nine heavy atoms. Subsequently, many DL models such as MPNN,²⁷ SchNet,²⁸ HIP-NN,²⁹ MGCN,³⁰ DTNN_7ib,³¹ PhysNet,³² DimeNet,³³ and DimeNet++³⁴ have been developed for the end-to-end prediction of molecular energetics, with DimeNet++ achieving as low as 0.15 kcal/mol MAE on the QM9 benchmark dataset. However, these highly accurate deep learning models developed based on the QM9 dataset require the input of the DFT optimized geometries for their accurate energetics prediction, and thus the original motivation for developing ML and DL models is not fully achieved: reducing the computational cost of high-level Quantum Mechanical (QM) calculations. To address this problem, we previously demonstrated³¹ that it was possible to predict DFT-level electronic energy directly from Merck Molecular Force Field³ (MMFF) optimized geometry. We then further pushed the limit of molecular energetics prediction by developing the Frag20 dataset,³⁵ which contains over half a million molecules composed of elements H, B, C, N, O, F, P, S, Cl, and Br with up to 20 heavy atoms. Eventually, we obtained a DL model named sPhysNet which can predict DFT-level energies directly from the MMFF-optimized geometry of molecules. The model achieved close to chemical accuracy performance on real-world datasets, turning out to be a promising tool to explore the chemical space with 3D molecular geometries for calculated energetics. On the other hand, experimental transfer free energies, such as hydration free energy and logP, are typically treated as separate tasks by ML models with completely different architectures.^36–43

In this work, motivated by traditional molecular modeling methods which utilize the direct relationship between absolute energies and transfer energies,^44–47 we present sPhysNet-MT, a multitask DL model which predicts molecular electronic energies in gas, water, and octanol phases directly and corresponding transfer free energies indirectly, from MMFF-optimized molecule geometries. Unlike some previous multitask models for less correlated tasks that usually perform worse than their single-task variants,^{32, 33} well-correlated tasks facilitate the model for simultaneous predictions,^{48, 49} and the tasks in sPhysNet-MT benefit from mutual learning which help the model to achieve better performance. After training on our prepared Frag20–678k-solv dataset containing over 678,000 molecular conformations labeled with calculated DFT-level energetics in gas, water, and octanol phases, sPhysNet-MT achieves a MAE of less than 0.6 kcal/mol on molecular electronic energy predictions and MAE of less than 0.2 kcal/mol on the transfer free energies between phases. For the experimental energetics, we develop a multitask training set combining experimental hydration free energy from FreeSolv⁵⁰ dataset and experimental logP from PHYSPROP^{51, 52} to fully utilize the limited amount of experimental data. After fine-tuning⁵³ on the experimental dataset, the model can simultaneously predict hydration free energy with $\mathit{0.359}\pm \mathit{0.063}$ kcal/mol MAE and $\mathit{0.620}\pm \mathit{0.140}$ kcal/mol RMSE (Root-Mean-Squared-Error), as well as logP with $\mathit{0.242}\pm \mathit{0.004}$ MAE and $\mathit{0.393}\pm \mathit{0.012}$ RMSE from MMFF-optimized molecular geometries, achieving state-of-the-art performance for both tasks. Further analysis shows that the model is aware of the chemical environment of atoms in the molecule by assigning atomic contributions consistent with our chemical knowledge. Corresponding source code and datasets are freely available at https://www.nyu.edu/projects/yzhang/IMA.

Dataset

Multitask training set for calculated energetics: Frag20-solv-678k.

In order to simultaneously predict both molecular electronic energies and transfer free energies, we develop Frag20-solv-678k, a multi-task training set that contains 678,916 conformations and their calculated energetics in gas, water, and octanol phase (Table 1, Supplementary Figure 1). The conformations come from the following three sources: 565,896 conformations are generated from the 565,438 unique molecules in the Frag20 dataset³⁵ which contains molecules up to 20 heavy atoms carefully selected from ZINC,^54–56 and PubChem^{57, 58} based on the number of heavy atoms, extended-functional groups, and fragment frequency;³⁵ 39,816 conformations are generated from 33,572 unique molecules in CSD20 dataset which contains molecules up to 20 heavy atoms selected from the Cambridge Structure Database;⁵⁹ the rest 73,204 conformations are generated in this work from 11,939 unique molecules selected from CSD20 dataset. The distributions of the number of heavy atoms and elements in the training datasets are shown in Supplementary Figure 1. More Frag20-solv-678K dataset construction details are described in Supplementary Information.

Table 1. Datasets that are used for model training and evaluation.

$E_{gas}$: gas phase electronic energy;$E_{water}$: water phase electronic energy;$E_{oct}$: octanol phase electronic energy. The $\mathrm{\Delta }E$ terms are defined in Equation 1. DFT: the property is calculated by DFT method; EXP: the property is measured by experiments; CAL: the property is calculated indirectly from Equation 1 or Equation 3.

		Frag20-solv-678k				FreeSolv-PHYSPROP-14k
		Frag20	CSD20	Conf20	Together	FreeSolv	PHYSPROP	Together
Source		35	35,59	This work	This work	50	60	This work
#Mols		565,438	33,572	11,939	599,010	640	14,500	14,339
#Confs		565,896	39,816	73,204	678,916	640	14,500	14,339
Geometries	MMFF	Y	Y	Y	Y	Y	Y	Y
	DFT	Y	Y	Y	Y	Y	N	N
Properties	$E_{gas}$	DFT	DFT	DFT	DFT	DFT	DFT	DFT
	$E_{water}$	DFT	DFT	DFT	DFT	---	---	CAL
	$E_{oct}$	DFT	DFT	DFT	DFT	---	---	CAL
	$\mathrm{\Delta }{E}_{gas\to water}$	CAL	CAL	CAL	CAL	EXP	---	EXP
	$\mathrm{\Delta }{E}_{gas\to oct}$	CAL	CAL	CAL	CAL	---	---	CAL
	$\mathrm{\Delta }{E}_{oct\to water}$	CAL	CAL	CAL	CAL	---	EXP	EXP

The label generation protocol is shown in Figure 1. We perform single-point energy calculations at B3LYP/6–31G* level with Gaussian16⁶¹ in gas ($E_{gas}$), water ($E_{water}$), and 1-octanol ($E_{oct}$) phase. The solvents are modeled with Universal Solvation Model (SMD)⁶². The calculated single-point electronic energies are then used to calculate the transfer free energies between phases, resulting in six labels for each of the 678,916 conformations. The transfer free energies are defined as:

$$\mathrm{\Delta }{E}_{solv1\to solv2}=E_{solv2}-E_{solv1}, solv1,solv2\in \left\{gas, water, oct\right\}$$ Equation 1

Figure 1.

Frag20-solv-678k dataset generation protocol. A. 3D Geometry generation protocol. B. Single-point energy calculation in three phases. C. The post calculation to generate the transfer free energy terms.

$E_{gas}$: gas phase electronic energy;$E_{water}$: water phase electronic energy;$E_{oct}$: octanol phase electronic energy. The $\mathrm{\Delta }E$ terms are defined in Equation 1.

Multitask training set for experimental energetics: FreeSolv-PHYSPROP-14k.

To fully utilize the limited amount of existing chemical knowledge at the experimental level for multitask training, we combine the compounds in FreeSolv⁵⁰ and PHYSPROP^{51, 52} datasets to develop a multi-tasking data set for experimental transfer free energies (Table 1). FreeSolv⁵⁰ dataset contains experimental hydration free energies ($\mathrm{\Delta }{E}_{gas\to water}$) for around 640 fragment-like neutral molecules. The molecules are selected from prior literature and curated to correct a number of errors and redundancies. The PHYSPROP^{51, 52} dataset contains around 14,500 molecules and their experimental logP which is further curated following an established protocol^{60, 63} including removal of inorganics and mixtures, structural conversion and cleaning, normalization of specific chemotypes, removal of duplicates and manual inspection. The experimental octanol to water transfer free energy is calculated from experimental logP by the following thermodynamic equation.⁴⁷

$$\text{Δ}{E}_{oct\to water}=RTln\left(10\right)*logP$$ Equation 2

Where R is the ideal gas constant and T is the temperature assumed to be 298.15K in this work.

As shown in Figure 2 A and B, for each compound in the combined dataset, the MMFF conformations are generated with ETKDG and optimized with MMFF. Unlike Frag20 where only one conformation is generated for each molecule, here up to 300 geometries are generated for each molecule and the one with the lowest MMFF-level energy is selected.

Figure 2.

Experimental dataset generation protocol. A. Up to 300 conformations are generated with ETKDG⁶⁴ in RDKit⁶⁵ and optimized with MMFF94. B. The one conformation with the lowest MMFF level energy is selected for each compound. C. Label calculation if the molecule is presented in both datasets.

As shown in Figure 2 C, if the molecules are presented in both datasets, both $\mathrm{\Delta }{E}_{gas\to water}$ and $\mathrm{\Delta }{E}_{oct\to water}$ are available, so all six labels can be calculated as long as we can obtain the gas-phase electronic energies. For those molecules, the gas-phase single-point DFT calculation is performed to calculate the gas phase electronic energies $E_{gas}$ and the electronic energies in other phases are calculated following these equations derived from Equation 1.

$$\begin{gathered} E_{water}=E_{gas}+\mathrm{\Delta }{E}_{gas\to water} \\ {E}_{oct}=E_{water}-\mathrm{\Delta }{E}_{oct\to water} \end{gathered}$$ Equation 3

For those molecules presented in only one dataset, we do not perform further calculation and all labels other than the corresponding experimental transfer free energies are marked unavailable. The combined FreeSolv-PHYSPROP dataset contains 14,339 molecules with 13,700 molecules exclusively in PHYSPROP dataset, 165 molecules only in FreeSolv dataset, and 474 molecules in both datasets.

Model and Training

sPhysNet-MT model.

Inspired by the thermodynamic relationships between the properties as described in Equation 1 and Equation 2, we develop sPhysNet-MT, a multitasking DL model which predicts electronic energies directly and transfer free energies indirectly.

Architecture.

Figure 3 shows an overview of sPhysNet-MT. Initially, the N atoms in a molecule go through an embedding matrix and are embedded into vectors ${\mathit{h}}_{\mathit{1}}^{\mathit{0}}, \dots , {\mathit{h}}_{\mathit{N}}^{\mathit{0}}$ (node embedding). The distances between each atom pair are expanded with radial basis functions (RBFs) into vectors $\{\mathit{g}\left(r_{ij}\right)|i, j\in \left\{1, 2,\dots ,N\right\}, r_{ij}<10\text{Å}\}$ (edge embedding). The node embeddings are then updated by three interaction modules with message passing, residual layers, and gate layers. The node embeddings of the final layer go through the output layer to predict targeted properties. For each input conformation, sPhysNet-MT directly predicts three values: gas phase electronic energy ${\widehat{E}}_{gas}$, water phase electronic energy ${\widehat{E}}_{water}$ and octanol phase electronic energy ${\widehat{E}}_{oct}$ and calculates the transfer free energies based on Equation 1.

Figure 3.

Overview of sPhysNet-MT model architecture and training procedure. A. The architecture of sPhysNet-MT. The model takes the 3D coordinate and the atomic number of each atom and predicts the three electronic energies in three phases. B. The loss function for multitask training (Equation 4). C and D. The single-task scenarios when the energetics are partially available on the experimental dataset.

Figure 4 shows the detailed architecture of each layer in sPhysNet-MT. The embedding layer contains an embedding matrix $\mathit{e}\in {\mathit{R}}^{94\times F}$, where 94 is the maximum supported atomic number and $F=160$ is the feature dimension. Each atom with atomic number $Z_i$ will be encoded into a vector ${\mathit{h}}_{\mathit{i}}^{\mathit{0}}\in {\mathit{R}}^F$, where $i\in N$ is the atom index of the molecule of N atoms. The Euclidean distances between each atom pair within a cutoff of $r_{cut}=10\text{Å}$ are expanded into vectors using RBFs (Figure 4 A) of the form:

$$g_k\left(r_{ij}\right)=\varphi \left(r_{ij}\right)\cdot \text{exp}\left(-{\beta }_k{\left(\exp \left(-r_{ij}\right)-{\mu }_k\right)}^2\right)$$

Figure 4.

The detailed architecture of the layers in sPhysNet-MT. A. RBF expansion layer. Distances between atom pairs are expanded into vectors. B. Embedding layer. The atoms are embedded into vectors based on their atomic number. C. Interaction layer. sPhysNet-MT contains three interaction layers with message passing, residual layers, and gate layers. D. Output layer. The updated node embeddings go through the output layer to predict target properties. E. Residual layer architecture used in A and B.

Where $k\in \left\{1, 2, \dots ,K\right\}$ , and $K=64$ is the total number of RBFs to map each distance pair $r_{ij}$ to a vector $\mathit{g}\left(r_{ij}\right)\in {\mathit{R}}^K$. ${\mu }_k$ and ${\beta }_k$ are learnable parameters that specify the center and width of $g_k\left(r_{ij}\right)$. The centers ${\mu }_k$ are initialized to K equally spaced values between $\text{exp}\left(-r_{cut}\right)$ and 1, and all widths ${\beta }_k$ are initialized to ${\left(2K^{-1}\left(1-\exp \left(-r_{cut}\right)\right)\right)}^{-2}$. $\varphi \left(r_{ij}\right)$ is a smooth cutoff function defined as:

$$\varphi \left(r_{ij}\right)=\left\{\begin{array}{c}1-6{\left(\frac{r_{ij}}{r_{cut}}\right)}^5+15{\left(\frac{r_{ij}}{r_{cut}}\right)}^4-10{\left(\frac{r_{ij}}{r_{cut}}\right)}^3 r_{ij}<r_{cut}\\ 0 r_{ij}>r_{cut}\end{array}\right.$$

The encoded atom embeddings ${\mathit{h}}_{\mathit{i}}^{\text{0}}$ and edge embeddings $\mathit{g}\left(r_{ij}\right)$ then go through 3 interaction layers as shown in Figure 4 C. The node embedding of each atom is first updated through message passing based on the node embeddings of its neighbors as well as the expanded distances:

$${\tilde{\mathit{h}}}_{\mathit{i}}^{\mathit{m}}=\mathit{\sigma }\left({\mathit{W}}_{\mathit{I}}\mathit{\sigma }\left({\mathit{h}}_{\mathit{i}}^{\mathit{m}}\right)+{\mathit{b}}_{\mathit{I}}\right)+\sum _{j\ne i}\mathit{G}\mathit{g}\left({\mathit{r}}_{\mathit{i}\mathit{j}}\right)\circ \mathit{\sigma }\left({\mathit{W}}_{\mathit{J}}\mathit{\sigma }\left({\mathit{h}}_{\mathit{j}}^{\mathit{m}}\right)+{\mathit{b}}_{\mathit{J}}\right)$$

Where ${\mathit{W}}_{\mathit{I}},{\mathit{W}}_{\mathit{J}}\in {\mathit{R}}^{F\times F}$, ${\mathit{b}}_{\mathit{I}}, {\mathit{b}}_{\mathit{J}}\in {\mathit{R}}^F$, and $\mathit{G}\in {\mathit{R}}^{F\times K}$ are all trainable parameters. $\circ$ denotes the Hadamard product. $\sigma \left(■\right)$ is the shifted softplus activation function which operates on every element of the tensor:

$$\sigma \left(x\right)=\log \left(e^x+1\right)-\log 2$$

The updated atom embeddings ${\tilde{\mathit{h}}}_{\mathit{i}}^{\mathit{m}}$ go through a residual layer (Figure 4 E), an activation operation, a linear layer, a gating layer controlled by a learnable gating vector u, and another residual layer. The output of the interaction layer ${\tilde{\mathit{h}}}_{\mathit{i}}^{\mathit{m}\text{+1}}$ will be used as the input of next interaction layer or the output layer.

After three interaction layers, an output layer is used to predict the properties from the atom embeddings. The final linear transformation in the output layer uses a matrix $W_{final}\in R^{3\times F}$ for the atom-level raw prediction of electronic energies in gas, water, and octanol phases ${\mathit{y}}_{\mathit{i}}\in {\mathit{R}}^3$. The raw predictions are then scaled and shifted before summed up to the final molecule properties:

$$\begin{array}{c}{\widehat{E}}_{gas}\\ {\widehat{E}}_{water}\\ {\widehat{E}}_{oct}\end{array}=\sum _{i=1}^N\left(s_{Z_i}\circ {\mathit{y}}_{\mathit{i}}+c_{Zi}\right)$$

Where $s_{Z_i}$ and $c_{Zi}$ are learnable element-specific scale and shift parameters, and N is the total number atoms in the molecule.

Training on calculated data.

Since all three electronic energies and three transfer free energies are available in the calculated dataset, the objective of the training is to optimize the loss function:

$$L=L_1+\lambda \cdot L_2$$ Equation 4

$$L_1=\left|{\widehat{E}}_{gas}-E_{gas}^{ref}\right|+\left|{\widehat{E}}_{water}-E_{water}^{ref}\right|+\left|{\widehat{E}}_{oct}-E_{oct}^{ref}\right|$$ Equation 5

$$L_2=\left|\text{Δ}{\widehat{E}}_{gas\to water}-\text{Δ}{E}_{gas\to water}^{ref}\right|+\left|\text{Δ}{\widehat{E}}_{gas\to oct}-\text{Δ}{E}_{gas\to oct}^{ref}\right|+\left|\text{Δ}{\widehat{E}}_{oct\to water}-\text{Δ}{E}_{oct\to water}^{ref}\right|$$ Equation 6

Here $L_1$ is the Mean Absolute Error (MAE) of three direct prediction terms and $L_2$ is the MAE of three transfer free energy terms. $\lambda =23.061$ is a hyperparameter that makes the model focus more on the energy difference terms than the direct terms. We have tried other $\lambda$ values including 10, 50, and 100, and very similar results were observed. All E and $\text{Δ}E$ terms are in the unit of electron volt (eV) during training. The detailed optimization hyperparameters are included in Supplementary Table 1.

Frag20-solv-678k provides both MMFF and DFT-optimized geometries as input, as mentioned above, a model trained with DFT-optimized geometry would be impractical to use. Therefore, we chose MMFF-optimized geometry as the input for training.

We randomly split Frag20-solv-678k into a training/validation/testing set of 658,916/10,000/10,000. In each epoch, the model is trained on the training split and evaluated on the validation set, and the model with the lowest validation loss is saved as the best model for testing. No early stopping is implemented so the model is trained until reaching the time limit (36 hours on a Tesla V100-SXM2–16GB) or 1000 epochs, whichever comes first.

Training on experimental data.

The model is initialized with the weights of the trained model on Frag20-solv-678k, and is trained with the same loss function as Equation 4. However, as shown in Figure 2C, only 474 molecules have all six labels available. For the remaining 165 molecules in FreeSolv and 13,700 molecules in PHYSPROP, only the corresponding transfer free energy is available, therefore, we mask out the unavailable terms in calculating the loss.

Due to the imbalance between the number of hydration free energy data and the logP data, we apply the random oversampling⁶⁶ strategy to make sure the molecules in the two datasets have a closer chance of being sampled during training. Aside from the oversampling, the model is optimized with slightly different hyperparameters included in Supplementary Table 1.

Deep Ensemble.

Deep ensemble⁶⁷ is used to further improve the model performance and also provide calibration of model uncertainty. Five independent models are randomly initialized and trained with identical hyperparameters and training data. During prediction, the average of all five models is used as the ensemble prediction and the standard deviation is used as the ensemble model uncertainty.

In this paper, sPhysNet-MT-ens5 stands for a deep ensemble of five independent models and sPhysNet-MT stands for a single model.

Results and Discussion

Calculated Energetics Prediction.

After training sPhysNet-MT and sPhysNet-MT-ens5 as described above, we test the model on the reserved test set composed of 10,000 molecules of Frag20-solv-678k. As shown in Table 2, sPhysNet-MT predicts electronic energies with MAE of 0.7 kcal/mol and transfer free energies with MAE of 0.2 kcal/mol. Deep ensemble further improves the model performance on all tasks: sPhysNet-MT-ens5 predicts electronic energies with MAE of less than 0.6 kcal/mol and three transfer electronic energy terms with MAE of 0.187 kcal/mol, 0.145 kcal/mol, and 0.079 kcal/mol, respectively.

Table 2.

The test performance on the Frag20-solv-678k dataset. sPhysNet-MT-ens5 is a deep ensemble of five sPhysNet-MT models. The errors are reported in kcal/mol.

Model	Metric	Target
		$E_{gas}$	$E_{water}$	$E_{oct}$	$\mathrm{\Delta }{E}_{gas\to water}$	$\mathrm{\Delta }{E}_{gas\to oct}$	$\mathrm{\Delta }{E}_{oct\to water}$
On the test set of Frag20-solv-678k
sPhysNet-MT	MAE	0.719	0.691	0.695	0.205	0.161	0.086
	RMSE	1.143	1.074	1.087	0.377	0.300	0.139
sPhysNet-MT-ens5	MAE	0.599	0.571	0.573	0.187	0.145	0.079
	RMSE	0.993	0.932	0.943	0.357	0.283	0.131

Experimental Energetics Prediction.

Following the multi-task training strategy described above, we further fine-tuned the model for the multitask prediction of experimental properties. To be consistent with previous publications, we perform 50 independent runs with random splits and then report both mean and standard deviation performance on the testing splits. As shown in Table 3, our sPhysNet-MT-ens5 model predicts experimental hydration free energy with RMSE of 0.620±0.140 kcal/mol and logP with RMSE of 0.393±0.012, achieving state-of-the-art performance on both tasks.

Table 3.

The test performance on the FreeSolv-PHYSPROP dataset. Each model is trained on 50 random splits and the mean and standard deviation are reported. sPhysNet-MT-ens5 is a deep ensemble of five sPhysNet-MT models. The errors in hydration free energies are reported in kcal/mol and the errors in logP are reported in log unit.

Ref.	Model	Target
		Hydration (FreeSolv)		logP (PHYSPROP)
		MAE	RMSE	MAE	RMSE
	sPhysNet-MT	0.392±0.064	0.663±0.135	0.262±0.006	0.421±0.017
	sPhysNet-MT-ens5	0.359±0.063	0.620±0.140	0.242±0.004	0.393±0.012
Previous hydration free energy prediction models
36	SVM	---	0.852±0.171	---	---
	XGBoost	---	1.025±0.185	---	---
	RF	---	1.143±0.230	---	---
	DNN	---	1.013±0.197	---	---
	GCN	---	1.149±0.262	---	---
	GAT	---	1.304±0.272	---	---
	MPNN	---	1.327±0.279	---	---
	Attentive FP	---	1.091±0.191	---	---
40	3DGCN	0.575±0.053	0.824±0.140	---	---
42	AGBT	0.594±0.090	0.994±0.217	---	---
39	D-MPNN	---	0.998±0.207	---	---
37, 68	weave	---	1.220±0.280	---	---
43	A3D-PNAConv	0.417±0.066	0.719±0.168	---	---
69	FML	0.570	---	---	---
Previous logP prediction models
70	QSPR	---	---	---	0.78
60	GraphCNN	---	---	---	0.56
71	$DN{N}_{taut}$	---	---	---	0.47±0.02
	$DN{N}_{mono}$	---	---	---	0.50±0.02
72	OPERA	---	---	---	0.78

Atom contribution analysis for model prediction explanation.

One of the disadvantages of DL models is the difficulty of model explanation because of the complex architecture and the huge number of parameters. Fortunately, sPhysNet-MT-ens5 directly predicts atom-level energetics and sums them over for the molecular energetics, which allows us to break out the model prediction back into atom-level contributions for further explanation. As shown in Figure 5, we select 3 examples and visualize the predicted atomic contributions for both tasks. For aspirin (row 1), most of the hydration free energy is contributed by the four oxygen atoms, while the oxygen atom in the hydroxyl group has the highest contribution, which is reasonable because it can dissociate or form hydrogen bonds. The two oxygen atoms in the carbonyl group also show strong contributions, which is consistent with the fact that they are hydrogen bond acceptors. For hexose (row 2), all the hydroxyl group oxygens are assigned strong contributions to the hydration free energy, and the single ether oxygen is also assigned relatively weaker (lighter in color) contributions. Conversely, as an extremely non-polar compound, all atoms in carbon tetrafluoride show positive contributions to the solvation energy. The logP contributions show very similar trends to the hydration free energy prediction. In summary, from the atomic contribution analysis, the model is aware of different atomic types and chemical environments, showing predictions consistent with our chemical knowledge. It should be noted that atomic contribution analysis is solely used for model prediction explanation and is different from Energy Decomposition Analysis.^{73, 74}

Figure 5.

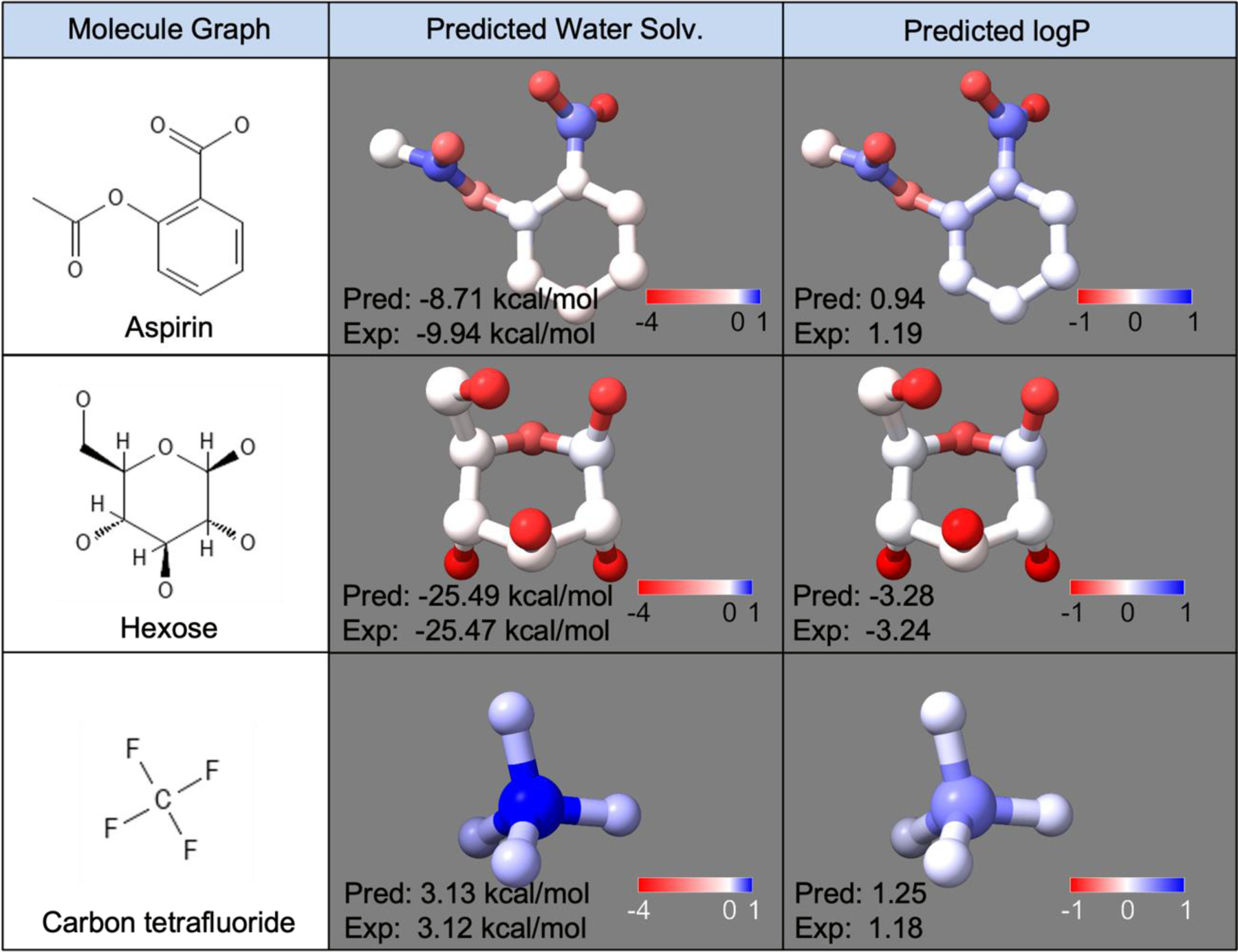
The atomic contributions assigned by sPhysNet-MT-ens5 on both hydration free energy prediction and logP prediction for aspirin, hexose, and carbon tetrafluoride.

Uncertainty analysis.

Uncertainty prediction is a popular topic in DL models.^{29, 34, 75–85} As a deep ensemble model,⁶⁷ sPhysNet-MT-ens5 provides a measure of model uncertainty. Supplementary Figure 2 and Supplementary Figure 3 show the relationship between prediction errors and uncertainties on the calculated dataset and the experimental dataset respectively. Statistically, when the model uncertainty increases, both cumulative and interval error increase, which means those molecules with higher uncertainties have higher expected errors than those molecules with lower uncertainties.

Conclusion

In this work, we present sPhysNet-MT-ens5, a deep ensemble model which can simultaneously predict electronic energies and transfer free energies. The model unifies these tasks which are typically treated separately by other ML and DL models. On the calculated dataset, the model benefits from mutual learning and achieves chemical accuracy on predictions of both electronic energies and transfer free energies with MMFF-optimized geometries as input. On the experimental dataset, the model fully utilizes the limited amount of experimental data through multitasking and outperforms existing models on both experimental hydration free energies and logP predictions. Further decomposition of atomic contribution also reveals that the model learns reasonable chemical knowledge by assigning meaningful values for different atoms based on the atom properties and their chemical environment. Our work not only produces a useful computational model for electronic energies and transfer free energies prediction directly from MMFF-optimized geometry, but also provides a multitasking protocol for ML and DL model design to learn a more robust molecular representation.

Several limitations of our method are also worth future research. As discussed by Ulrich et al,⁷¹ if a compound is ionizable, the octanol-water partition coefficient (logD) would be dependent on the pH of the solvent and the pKa of the compound, and a more complex model would be needed for logD prediction. Stemming from this problem, sPhysNet-MT does not explicitly use the total charge of the system as input, as a result, it would be challenging for the model to predict the properties of ionizable compounds which tend to be charged in water solution. Therefore, the model should be upgraded to sense charged molecules to further deal with the system where compounds are ionizable.