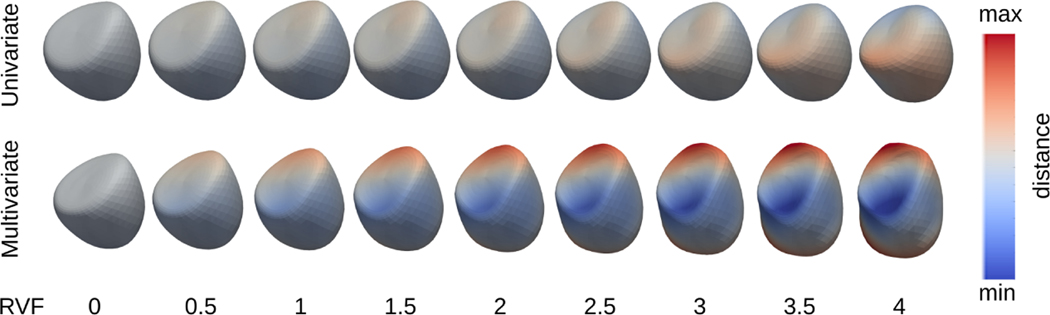Hierarchical Geodesic Polynomial Model for Multilevel Analysis of Longitudinal Shape

Abstract

Longitudinal analysis is a core aspect of many medical applications for understanding the relationship between an anatomical subject’s function and its trajectory of shape change over time. Whereas mixed-effects (or hierarchical) modeling is the statistical method of choice for analysis of longitudinal data, we here propose its extension as hierarchical geodesic polynomial model (HGPM) for multilevel analyses of longitudinal shape data. 3D shapes are transformed to a non-Euclidean shape space for regression analysis using geodesics on a high dimensional Riemannian manifold. At the subject-wise level, each individual trajectory of shape change is represented by a univariate geodesic polynomial model on timestamps. At the population level, multivariate polynomial expansion is applied to uni/multivariate geodesic polynomial models for both anchor points and tangent vectors. As such, the trajectory of an individual subject’s shape changes over time can be modeled accurately with a reduced number of parameters, and population-level effects from multiple covariates on trajectories can be well captured. The implemented HGPM is validated on synthetic examples of points on a unit 3D sphere. Further tests on clinical 4D right ventricular data show that HGPM is capable of capturing observable effects on shapes attributed to changes in covariates, which are consistent with qualitative clinical evaluations. HGPM demonstrates its effectiveness in modeling shape changes at both subject-wise and population levels, which is promising for future studies of the relationship between shape changes over time and the level of dysfunction severity on anatomical objects associated with disease.

1. Introduction

Studying change over time is a core aspect of many medical applications. Trajectories of change are followed in studies of childhood development, aging, and disease development. This can involve sampling a cross-sectional population to estimate a possible time course. However, such cross-sectional studies may show large variability across the population and may not properly reflect the nature of longitudinal changes of individuals. On the other hand, longitudinal studies involve following subjects over time, allowing to capture subject-wise trajectories as well as at the population level. Longitudinal study design comes with data challenges such as staggered time points, missing time points, and subjects with different number of observations. Dedicated modeling schemes are needed to correctly account for the correlated measurement within subjects. These models are known as mixed-effects or hierarchical models and have shown great promise for modeling derived measure in medical imaging studies [1,17].

Several models have been explored for longitudinal analysis of higher dimension data [3,4,11,13,16,18]. Two main directions have been followed. First, dedicated methods with a specific data representation in mind such as diffeomorphisms on images or shapes. Image or shape change is represented as continuous diffeomorphic deformations at the subject and population level. The second methodological direction are intrinsic Riemannian models which may be adapted to new data representations from a variety of manifold representations. These models require the definition of a few key manifold specific operations, to be discussed in Section 2, in order to be applied to new data types. In this work, we favor this second approach due to the potential for extension to new data representations and thus a variety of clinical problems.

In this paper we propose to extend the hierarchical multi-geodesic model in [11] by applying polynomial expansion at both subject-wise and population levels, with the aim of modeling shape trajectories associated to changes in related covariates, such as sex, cognitive scores, or disease severity. Our development of polynomial regression allows for more flexibility in data-matching than the traditional geodesic model, while still enabling the choice of geodesic as a polynomial of degree 1. The polynomial expansions at different model levels are inherently compatible with the hierarchical modeling framework where subjects may have a different number of observations. Due to the non-Euclidean nature of the shape space, a fast and efficient model estimation algorithm similar to the computation of the Fréchet mean is implemented. We validate our method on synthetic data as well as clinical data right ventricle shape change over the cardiac cycle as it relates to covariates such as dysfunction severity. This promises to meet a currently unmet need of clinical researchers to correlate geometry with function.

2. Methods

2.1. Shape Space and Geodesics

We define shape space as the pre-shape space of Kendall space [12] with rotations removed. As such, the final shapes are obtained by removing their translation, rotation, and similarity components through partial procrustes alignment. The shape space is formed as a hyper-sphere and can be treated as a high dimensional Riemannian manifold $M$. Performing geodesic regressions in the shape space allows for efficient computation with proven Kendall-space equivalence as indicated in [8,15]. A geodesic on $M$ is a zero-acceleration curve with the minimizing property that there is no curve shorter than a geodesic between any two points within a small neighborhood. Three geodesic-related operations are extensively used in this work: exponential map, log map, and parallel transport. An exponential map $Exp(p,v)=q$ maps a shape $p\in M$ to another shape $q\in M$ in the direction and magnitude of a tangent vector $v$. A log map $Log(p,q)=v$ is the inverse of the exponential map in which two shapes $p$ and $q$ are given and the unique tangent vector that maps $p$ to $q$ is obtained. The Riemannian distance between the two shapes is then defined as the L2-norm of their log map $d(p,q)=\parallel Log(p,q)\parallel$. The parallel transport operation ${\psi }_{p\to q}(u)$ transports a tangent vector $u\in T_{p}M$ from $p$ to $q$ while maintaining angle and scale preservation properties. For rigorous and complete definitions, please see [2].

2.2. Hierarchical Geodesic Model for Manifold-valued Data

Geodesic regression is very similar to linear regression in Euclidean space, with analogies of the anchor point to the intercept and tangent vector to the slope. In a similar way, multilevel models could be constructed in a “geodesic” way by following the framework of hierarchical linear models [19]. In this study, we further extend geodesic regressions in [11] to higher order polynomial versions at both the subject-specific trajectory level and the population level for better adaptability in the modeling of longitudinal data with covariate induced variability. Unlike the Riemannian polynomial described in [9,10] where the polynomial is defined in a differential manner with covariant derivatives, our polynomial expansions are applied to the tangent vectors under the geodesic regression model in an algebraic form, making them straightforward and consistent to fit into different levels of the hierarchical model. Thus, geodesic polynomial regression in this study refers to expanding the composition of tangent vectors in their hyper-tangent space with polynomials of different orders.

Subject-wise Level Model

We first perform geodesic polynomial regression at the subject-wise level (level 1). The nth order polynomial model on subject-specific trajectory $Y_k$ is formulated as

$$Y_k=Exp\left(\widehat{a_k},\sum _{p=1}^n\widehat{b_{kp}}{t}^p\right)$$ (1)

where ${\widehat{a}}_k$ is the anchor point of subject-specific trajectory $k$, ${\widehat{b}}_{kp}$ is the tangent vector of the $p\text{th}$ polynomial term and $t$ is the independent time variable. Given the input observations ${\mathit{y}}_{\mathit{k}}$, ${\widehat{a}}_k$ and ${\widehat{b}}_{kp}$’s are estimated by least squares geodesic regression

$$\left({\widehat{a}}_k,{\widehat{\mathit{b}}}_{\mathit{k}}\right)=\underset{a_k,{\mathit{b}}_{\mathit{k}}}{\text{argmin}}\sum _{i=1}^{N_{obs}}{d}^2\left(y_{ki},Exp\left(a_k,\sum _{p=1}^n{b}_{kp}{t}_{ki}^p\right)\right)$$ (2)

where ${\widehat{\mathit{b}}}_{\mathit{k}}\left({\mathit{b}}_{\mathit{k}}\right)$ is the combined representation of all ${\widehat{b}}_{kp}\left(b_{kp}\right)$, $y_{ki}$ and $t_{ki}$ are the $i\text{th}$ observation and corresponding time variable in ${\mathit{y}}_{\mathit{k}}$. Note that due to the number of free parameters in the regressing polynomial, $N_{obs}\ge n+1$ is required to avoid singularity in the solution.

Population Level Model

At population level (level 2), let the subject trajectories be associated with a set of $m$ covariates $\mathit{\eta }=\left\{{\eta }_1,{\eta }_2,\dots ,{\eta }_m\right\}$, the final form of the hierarchical geodesic polynomial model can be written as

$$Y=Exp\left(Exp\left(f(\mathit{\eta }),\sum _{p=1}^n{g}_p(\mathit{\eta })t^p\right),ϵ\right)$$ (3)

where $f(\mathit{\eta })$ and $g_p(\mathit{\eta })$ are the models for the anchor point and the basis tangent vector of polynomial order $p$ respectively. Technically speaking, the two models do not necessarily share the same set of covariates to allow for more flexible regression. However, in most cases, the same set of covariates would be used for both models if there is no compelling indication that a specific covariate is solely associated with one of the models. We promote both the anchor point model and the tangent vector model with quadratic expansion on the covariates. The aim is to associate each model with higher order terms of the covariates as well as cross terms to accurately model their combined effects on subject trajectories.

Anchor Point Model

The anchor point model with quadratic expansion on $m$ covariates is written as

$$f(\mathit{\eta })=Exp\left({\widehat{\beta }}_0,\sum _{i=1}^m\left({\widehat{\beta }}_i{\eta }_i+{\widehat{\beta }}_{ii}{\eta }_i^2\right)+\sum _{i=1}^{m-1}\sum _{j=i+1}^m{\widehat{\beta }}_{ij}{\eta }_i{\eta }_j\right)$$ (4)

where ${\widehat{\beta }}_0\in M$ is a base anchor point and ${\widehat{\beta }}_i$, ${\widehat{\beta }}_{ii}$, ${\widehat{\beta }}_{ij}\in T_{{\widehat{\beta }}_0}M$ are basis vectors of the anchor point polynomial. These coefficients can be estimated from the results of subject-specific trajectory regression as

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}\sum _{k=1}^{N_s}{d}^2\left(f\left({\mathit{\eta }}_{\mathit{k}}\right),{\widehat{a}}_k\right)$$ (5)

where ${\mathit{\eta }}_{\mathit{k}}$ and ${\widehat{a}}_k$ are the covariates and regressed anchor point of subject $k$, $N_s$ is the total number of input subject trajectories and $\widehat{\mathit{\beta }}$ is the combined representation of ${\widehat{\beta }}_0$, ${\widehat{\beta }}_i$, ${\widehat{\beta }}_{ii}$, ${\widehat{\beta }}_{ij}$ in the anchor point model.

Tangent Vector Model

Recall that the $\widehat{{\mathit{b}}_{\mathit{k}}}$ is the combined representation of the $n$ tangent vector bases of different orders from the level 1 regression. Thus, there are $n$ corresponding tangent vector models at the population level $G(\mathit{\eta })=\left\{g_1(\mathit{\eta }),g_2(\mathit{\eta }),\dots ,g_n(\mathit{\eta })\right\}$. Each tangent vector model with quadratic expansion on $m$ associated covariates can be formulated as

$$g_{\left(\mathit{\eta }\right)}={\psi }_{{\widehat{\beta }}_0\to f(\mathit{\eta })}\left(g_{{\widehat{\beta }}_0}(\mathit{\eta })\right)$$ (6)

$$g_{{\widehat{\beta }}_0}(\mathit{\eta })={\widehat{\gamma }}_0+\sum _{i=1}^m\left({\widehat{\gamma }}_i{\eta }_i+{\widehat{\gamma }}_{ii}{\eta }_i^2\right)+\sum _{i=1}^{m-1}\sum _{j=i+1}^m{\widehat{\gamma }}_{ij}{\eta }_i{\eta }_j$$ (7)

where $g\in T_{f(\mathit{\eta })}M$ and $g_{{\widehat{\beta }}_0}\in T_{{\widehat{\beta }}_0}M$ are the tangent vectors at $f(\mathit{\eta })$ and ${\widehat{\beta }}_0$ respectively, ${\widehat{\gamma }}_0$, ${\widehat{\gamma }}_i$, ${\widehat{\gamma }}_{ii}$, ${\widehat{\gamma }}_{ij}\in T_{{\widehat{\beta }}_0}M$ are bases of the tangent vector polynomial at ${\widehat{\beta }}_0$. Note that the subscript referring to the order of the polynomial model $p$ is omitted here for readability purposes. From the above formulation, the final tangent vector basis is obtained by calculating a tangent vector at ${\widehat{\beta }}_0$ from the polynomial model and then transporting it to the corresponding anchor point $f(\mathit{\eta })$ by a parallel transport function ${\psi }_{{\widehat{\beta }}_0\to f(\mathit{\eta })}$ defined on $M$. This is due to the consideration that subject-specific tangent vectors must be comparable with each other to perform regression in a consistent manner. Therefore, we need to transport all of them to the same tangent vector space $T_{{\widehat{\beta }}_0}M$ for the regression calculation, as well as to transport them to their corresponding anchor point $f(\mathit{\eta })$ in the forward calculation. Due to the existence of the parallel transport functions and the fact that regressed subject-specific anchor points ${\widehat{a}}_k$ do not necessarily lie on $f(\mathit{\eta })$, the actual tangent vector ${\tilde{b}}_k$ being used for regression calculation is obtained as

$${\tilde{b}}_k={\psi }_{f\left({\mathit{\eta }}_k\right)\to {\widehat{\beta }}_0}\left({\psi }_{{\widehat{a}}_k\to f\left({\mathit{\eta }}_k\right)}\left({\widehat{b}}_k\right)\right)$$ (8)

so that all ${\tilde{b}}_k\in T_{{\widehat{\beta }}_0}M$. Stop-over transport avoids arbitrary rotation from direct transport ${\psi }_{{\widehat{a}}_k\to {\widehat{\beta }}_0}$, explained in [11]. Regression on the basis tangent vector of a specific polynomial order is then formulated as

$$\widehat{\mathit{\gamma }}=\underset{\mathit{\gamma }}{\text{argmin}}\sum _{k=1}^{N_s}{\Vert g_{{\widehat{\beta }}_0}\left({\mathit{\eta }}_{\mathit{k}}\right)-\widetilde{b_k}\Vert }^2$$ (9)

where $\widehat{\mathit{\gamma }}$ is the combined representation of ${\widehat{\gamma }}_0$, ${\widehat{\gamma }}_i$, ${\widehat{\gamma }}_{ii}$, and ${\widehat{\gamma }}_{ij}$.

Iterative Optimization Scheme

Since our shape space is constructed as a Riemannian manifold and thus not Euclidean, there exists no closed-form solution for such geodesic polynomial regressions on subject-wise trajectory and anchor point model. Similar to the calculation of Fréchet mean, we employ an iterative solution scheme for obtaining the optimal parameters in Eq. (2) and Eq. (5). The algorithm 1 illustrates how the parameters are updated over iterations. Note that the function Least Squares Polynomial Fitting depends on ${\omega }_0$, which means that all points in $\mathit{y}$ are transformed to the hyper-tangent space at ${\omega }_0$ using a log map for calculating new parameters ${\mathit{\omega }}_{\mathit{\text{new}}}$.

$R^2$ and Hypothesis Testing

At subject-wise level, the $R^2$ is calculated using the Fréchet variance[14], intrinsically defined by

$$var\left(y_i\right)=\underset{y\in M}{\min }\frac{1}{N}\sum _{i=1}^{N}d{\left(\overline{y},y_i\right)}^2$$ (10)

Algorithm 1:

Iterative solution scheme

$$var\left({ϵ}_i\right)=\underset{y\in M}{\min }\frac{1}{N}\sum _{i=1}^{N}d{\left({\widehat{y}}_i,y_i\right)}^2$$ (11)

$$R^2=1-\frac{var\left({ϵ}_i\right)}{var\left(y_i\right)}$$ (12)

where $\overline{y}$ is the Fréchet mean, ${\widehat{y}}_i$ is the regressed point $i$, and ${ϵ}_i$ is the error between ${\widehat{y}}_i$ and observation point $y_i$. To test statistical significance of fitting a geodesic polynomial model with respect to time, hypothesis test is conducted against the null hypothesis $H_0$: $t$ is irrelevant to change in shape using the permutation approach described in [6,7].

3. Results and Discussion

3.1. Test on Low Dimensional Synthetic Data

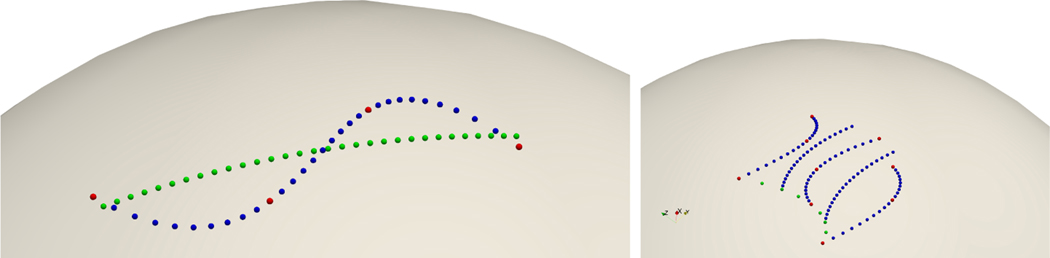
In order to validate as well as to visualize our hierarchical geodesic polynomial model, we first test our implementation on points on the unit sphere. Points on the sphere represent shapes with only one 3D point and the sphere is the corresponding shape space. On the left of Fig. 1 shows the result from fitting four input points (red) with geodesic model (green) and 3rd order geodesic polynomial model (blue) respectively. The four input points have integer times steps ranging from 0 to 3. The 3rd order geodesic polynomial is able to fit the input points almost perfectly, whereas as the linear geodesic model can only fit the inputs in a least square sense, which is similar to the case in Euclidean space.

Fig. 1:

Left) Results from fitting input points (red) with geodesic model (green) and 3rd order polynomial model (blue). Right) Fitting three input trajectories (red) with hierarchical geodesic polynomial model. Green points represent changes in anchor point location with respect to the covariate values ranging from 0 to 2, and the blue points show changes in regressed subject-specific trajectory with respect to the covariate values.

The right of Fig. 1 shows regression results from fitting three input trajectories with a hierarchical geodesic polynomial model. Each input trajectory contains three points with integer timestamps ranging from 0 to 2. The three input trajectories represent trajectories with integer covariate values ranging from 0 to 2 respectively. A quadratic model is used at both the subject-specific and the population level. The green points on the left of Fig. 1 also show the changes in anchor points from fitting a quadratic model, with covariate values ranging from 0 to 2 with an interval of 0.25. The blue points demonstrate the changes in regressed trajectories for covariates ranging from 0 to 2 with an interval of 0.5. Given the three input trajectories, our hierarchical geodesic polynomial model is capable of fitting the inputs perfectly with a quadratic model at both subject-wise level and population level.

3.2. Analysis of 4D Pediatric Right Ventricular Data

The shape of the right ventricle (RV) is known to influence the function of the tricuspid valve, but precise shape-based characterization of the RV in Hypoplastic left heart syndrome (HLHS) has not been described. The 4D trajectories of 94 pediatric RVs are acquired from 3D echocardiogram-based speckle tracking, and then transfered into the TOMTEC imaging system for the computation of the 3D models of the RV chamber. Each acquisition contains approximately one cardiac cycle, with 10 to 30 captured frames. Due to some incomplete cardiac cycle acquisitions as well as the fact that some obtained cardiac cycles do not perfectly repeat themselves from the end to the start point, the data is divided into two subsets, the systolic and diastolic phases. Since lengths of individual cardiac cycles can be different, we standardize trajectories for each systolic and diastolic phase with equally-spaced 50 frames in each trajectory [5]. As such, we finally obtain 58 systolic and 36 diastolic trajectories for hierarchical geodesic regression analysis. To evaluate the impact our polynomial model, we compare to the geodesic model [11], as to our knowledge it is the only longitudinal shape model that incorporates multiple covariates.

Subject-wise Model

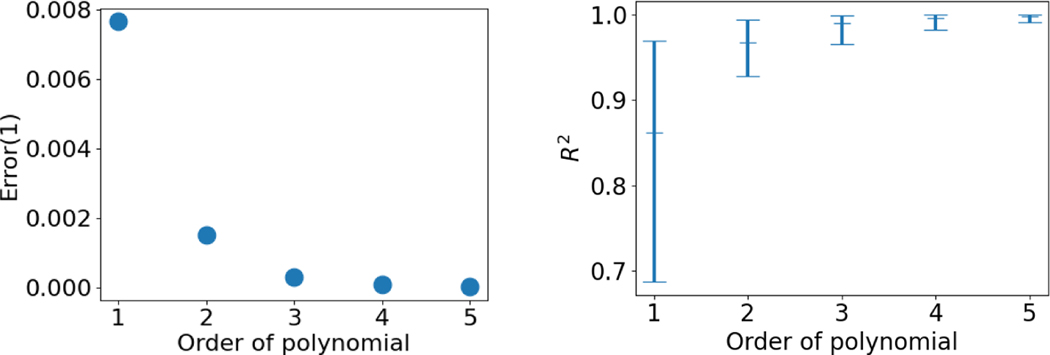
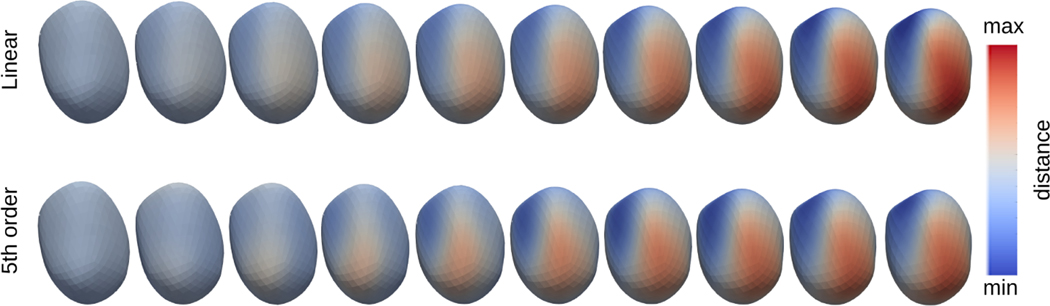
We first fit a polynomial model to subject-specific trajectories with the left of Fig. 2 showing the resulting error from fitting models to a representative single subject trajectory. As the order of polynomial model increases, the regression error decreases significantly from 7.65 × 10⁻³ (1st order) to 3.82×10⁻⁵ (5th order) with a 99.5% reduction (unitless because shapes are normalized to unit size). Fig. 3 shows that the trajectory from a higher order polynomial regression exhibits more nonlinearity than the geodesic model, as expected. Though not obvious, it is observed that the maximum distance point shifts from the left to the right side of the shape in the polynomial model, whereas the most distant point remains the same point in the geodesic model throughout time. The right of Fig. 2 shows the ranges and the mean values of the R² across the systole population, which indicates that trajectories of shape change over time better matches observed data with models of higher order.

Fig. 2:

Left) Error in fitting a single subject trajectory with respect to the order of the polynomial model. Right) Means and ranges of $R^2$ from fitting systole population with models of different orders.

Fig. 3:

A geodesic and a 5th order polynomial model on the systolic trajectory of a representative subject. Color indicates distance to the initial shape.

Anchor Point Model

As more samples are desirable for regression analysis, we first test our anchor point model on all end systolic and end diastolic shapes in both systolic and diastolic trajectories. Two covariates from the demographics are chosen for level 2 models: tricuspid regurgitation severity (TRS) and right ventricle function (RVF) take on values shown in Table 1.

Table 1:

Relationship between qualitative clinical assessments in the demographics to numerical values used in polynomial model fitting.

Covariate Value	TRS	RVF
0	Trivial	Normal
1	Mild	Low normal
1.5	Mild to moderate	Low normal to mildly diminished
2	Moderate	Mildly diminished
2.5	Moderate to severe	Mildly to moderately diminished
3	Severe	Moderately diminished
3.5		Moderately to severely diminished
4		Severely diminished

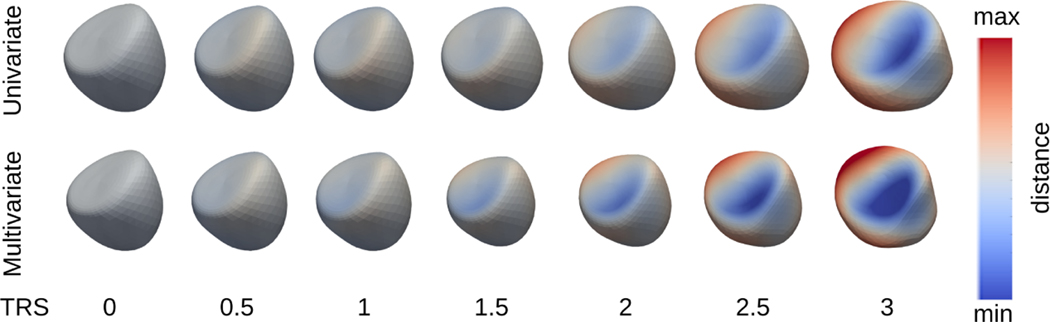
We fit both geodesic linear models and quadratic polynomial models to the end systolic and end diastolic shapes, with the RVF and/or TRS as covariates. Table 2 shows regression errors. It can be seen that (i) quadratic models lead to smaller errors than geodesic models, and (ii) model fitting with respect to TRS leads to smaller errors than the ones with respect to RVF, which indicates the shape changes are better aligned with changes in TRS, and (iii) regressions using both covariates outperform those using single covariate, in terms of model fitting, which is expected as more independent covariates are taken into account. From visual observations of the shape changes, similar to the results from fitting polynomial model to subject specific trajectories, the higher order polynomial model fitting including covariates yield more nonlinear changes in the end systolic and end diastolic shapes. While RV shape changes with respect to RVF is smoother, shape changes associated with TRS shows more local variability over time, leading to an obvious compressed edge between the RV top region and the septal wall at the most severe level of tricuspid regurgitation.

Table 2:

Error from fitting multivariate polynomial model to anchor points.

Phase	Covariates	Linear model errors(1)	Quadratic model errors(1)
End diastole	RVF	5.521	5.487
	TRS	5.515	5.442
	RVF & TRS	5.454	5.208
End systole	RVF	5.178	5.138
	TRS	5.147	5.062
	RVF & TRS	5.102	4.840

It is also observed that changes in shape with respect to the same covariates from multivariate regression are more prominent. Fig. 4 and 5 show that the multivariate regressions yield more observable changes in shapes as the covariate-specific changes of the shape are co-captured by different covariates separately.

Fig. 4:

Univariate and multivariate geodesic polynomial regression results for end diastolic shapes at different RVF severities.

Fig. 5:

Univariate and multivariate geodesic polynomial regression results for end diastolic shapes at different levels of TRS.

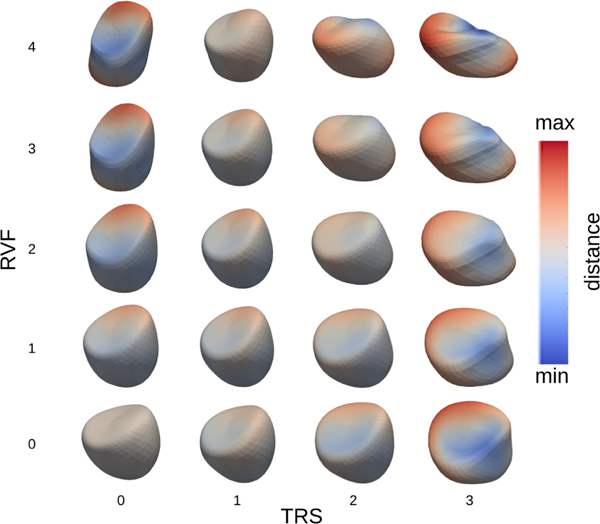
Fig. 6 shows the full spectrum of how the shape of the RV changes with respect to different values of the covariates at end diastole. Due to the sparsity and large variability in the input data set, extrapolating RV shape to extreme values of both covariates leads to a non-feasible real world shape as no such combination appeared in the input data set.

Fig. 6:

Full spectrum of end diastolic shapes at various levels of RVF and TRS.

3.3. Future Work

There are a few aspects that can be further extended to our current work. First, the current parallel transport of tangent vectors is computed along the geodesic between the start and end points. Meanwhile at the population level, it is also possible that the directions of the tangent vectors are dependent on the anchor points’ trajectories, in which parallel transport should be computed along a certain path on the Riemannian manifold (e.g. the regressed anchor point’s trajectory in the single covariate case). In the case with multiple covariates, the choice of the path requires further study. Second, if scale is a key factor to consider in the shape model, it is also feasible to append a scale factor to the existing model, which is regarded as an additional entry in shape space, and the solution process would be almost identical to the other entries in the anchor point or tangent vector. As we collect more data, we will also investigate modeling growth or pathology models of HLHS over a larger time period (i.e. years) instead of the cardiac cycle.

4. Conclusions

In comparison with previous geodesic models, polynomial regression leads to more accurate and flexible data-matching results at both subject-wise and population levels. Population-level regression with respect to multiple covariates leads to clearer separation between covariate effects on the shapes as indicated from validation on 4D right ventricular data. The regressed model is able to yield results that are consistent with qualitative clinical evaluations.

Given the sparsity and large variability in the input right ventricular data set, extrapolating shapes outside of the input covariate combination range may lead to irregular reconstructed shapes, which is understandable. The proposed HPGM model can be further extended with higher order polynomial expansion on covariates as well as using other basis functions (eg. kernel functions) for better fitting on the input. Overall, the proposed HGPM can be used for multilevel analysis of longitudinal shape data, leading to interpretable results relating functions (covariates) with shape trajectories, thus being promising for a variety of relevant clinical research in the future.