Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2023 Jun 16;8(26):23925–23935. doi: 10.1021/acsomega.3c02411

AQDnet: Deep Neural Network for Protein–Ligand Docking Simulation

Koji Shiota †, Akira Suma †, Hiroyuki Ogawa †, Takuya Yamaguchi †, Akio Iida †, Takahiro Hata †, Mutsuyoshi Matsushita †, Tatsuya Akutsu ‡, Masaru Tateno †,*
PMCID: PMC10324054  PMID: 37426216

Abstract

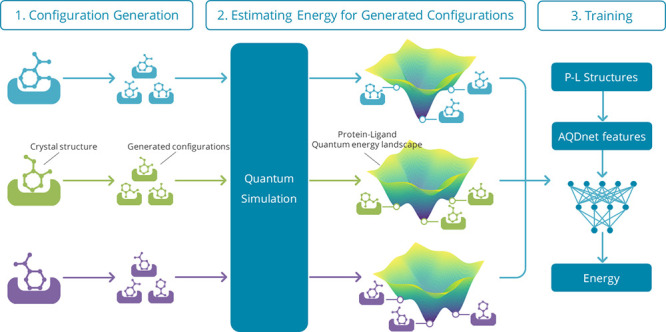
graphic file with name ao3c02411_0006.jpg

We have developed an innovative system, AI QM Docking Net (AQDnet), which utilizes the three-dimensional structure of protein–ligand complexes to predict binding affinity. This system is novel in two respects: first, it significantly expands the training dataset by generating thousands of diverse ligand configurations for each protein–ligand complex and subsequently determining the binding energy of each configuration through quantum computation. Second, we have devised a method that incorporates the atom-centered symmetry function (ACSF), highly effective in describing molecular energies, for the prediction of protein–ligand interactions. These advancements have enabled us to effectively train a neural network to learn the protein–ligand quantum energy landscape (P–L QEL). Consequently, we have achieved a 92.6% top 1 success rate in the CASF-2016 docking power, placing first among all models assessed in the CASF-2016, thus demonstrating the exceptional docking performance of our model.

Introduction

Virtual screening (VS) is a computational approach that facilitates the identification of bioactive compounds that bind to a specific target protein from an extensive library of compounds. This method can significantly expedite the drug discovery process and reduce the expenses, the time, and effort required to evaluate compounds in assays.1 Recently, various attempts have been made to leverage the achievements of computer vision and natural language processing technologies, such as convolutional neural networks2 and transformers,3 for VS. One of the key objectives of VS is to predict the binding affinity of protein–ligand (P–L) interactions. Several VS techniques have been proposed, based on physicochemical calculations and machine learning.4−8 Recently, methods based on deep learning have shown remarkable success in this field. Nonetheless, the accuracy of binding affinity prediction by deep learning models remains inadequate and demands significant improvement. The cause of this inadequacy lies in the absence of an established learning methodology and an insufficient number of training samples.

Behler discussed the three essential requirements for artificial intelligence (AI) to predict the potential energy, including invariant predictions for system rotation and translation, invariant predictions regardless of the atom processing order, and a unique representation of the three-dimensional molecular structure.9 Various approaches have been developed to represent the molecular structure as graphs,8,10 but they may not effectively use the exact relative positions of numerous atoms. Another approach is to use 3D convolutional neural networks (3DCNNs) to process molecular structures as three-dimensional images to predict binding affinity.5,7 However, 3DCNNs are not invariant to molecule rotation and translation and may neglect energy changes due to slight differences in interatomic distances. Various attempts have been made to predict binding affinity by processing the ligand and protein separately.6 However, these approaches fail to consider the intricate three-dimensional structure of the ligand–protein complex. OnionNet11,12 is an invariant method to system rotation and translation and the order of atoms processed, which predicts binding affinity by counting the number of the elements’ contacts that exists at a particular distance as a feature. However, this method uses shells in 0.5 Å increments to determine distances and cannot recognize differences in atomic coordinates smaller than 0.5 Å.

The atom-centered symmetry function (ACSF)13 satisfies all three of the above requirements and has proven effective in predicting molecular energies. However, while ACSF has been successfully applied to single-molecule systems, it cannot be directly employed for predicting P–L binding affinity. Furthermore, some of the reported methods for the application of ACSF to predict P–L bond affinity do not fully utilize the information on protein-side atoms. Nonetheless, ACSF possesses two desirable features that are useful in predicting P–L bond affinity: accounting for three-body interactions and generating high-resolution features that can even detect small differences in atomic coordinates.

The majority of current methodologies for predicting the activity of ligand–protein complexes rely solely on information regarding two-body interactions.11,12 However, P–L intermolecular interactions are essentially many-body interactions. Although many-body interactions are known to play a significant role in predicting the physical properties of chemical compounds, they have rarely been taken into account when predicting binding affinity. Therefore, it is necessary to establish a method to utilize the information of not only two-body interactions but also three- or more-body interactions for the prediction of binding affinity. ACSF extracts features by utilizing information pertaining to the distances between three atoms and the angles they form. This enables the model to account for the interactions between the three bodies, making it highly advantageous in predicting P–L bond affinity.

Binding affinity predictions are applied in tight collaboration with molecular docking programs. However, many of these prediction systems rely on other docking programs to predict the most stable conformation, and only a few are capable of evaluating protein–ligand docking. Those systems only predict the binding affinity using the most stable conformation predicted by other docking programs. It is thus imperative to develop a method that can predict both the most stable conformation and the binding affinity of P–L complexes, as few machine learning systems currently exist that can accomplish this task.

One of the reasons why evaluating the stability of P–L complexes is challenging is because differences in binding stability must be predicted from small differences in atomic coordinates. Previously reported machine-learning methods for predicting binding affinity are based on grids of 1 Å increments14 or shells of 0.5 Å increments,11,12 and are unable to recognize small differences in atomic coordinates. As a result, these methods are unable to evaluate protein–ligand docking. In this respect, ACSFs can generate high-resolution features that take into account the slightest difference in atomic coordinates because the distance between two atoms is represented by the outputs of the multiple Gaussian functions. Thus, the use of ACSF in predicting P–L binding affinity allows us to evaluate the stability of the P–L complex and even predict the most stable conformation.

In databases such as PDBbind,15 which are commonly employed as training datasets, approximately 20,000 combinations of ligand–protein complex structures and binding affinities are archived. In contrast, while more than 1.5 million training samples are commonly used for image recognition,16 a meager number of samples are available for training in the domain of binding affinity prediction. Thus, there is an urgent need to increase the number of training samples and develop methods for data augmentation.

Previous methods for predicting the binding affinity of P–L complexes using machine learning have basically used only crystal structures registered in databases as training data.7,11,12 However, as mentioned before, the number of complexes registered in the database is limited. This makes it difficult to prepare a sufficient amount of training data by using crystal structures alone. In addition, the VS needs to evaluate not only the crystal structure but also the configurations of the transition process before reaching the most stable configuration. For this reason, it is not appropriate to train the model for VS only on the most stable configurations. In this paper, we propose a new data augmentation method that generates a large number of configurations based on a single crystal structure registered in a database. The challenge here is how to label the generated configurations. To address this challenge, we have devised a method of estimating the change of stability of each generated configuration compared to that of the most stable pose using quantum chemical calculation. By using this method, we were able to generate more than 1000 configurations for a single crystal structure and successfully expand the training dataset by labeling each of them.

In labeling the configurations generated by the above method, we used semiempirical quantum mechanics (SQM)/COSMO to estimate the change of stability from the most stable pose. This method is a scoring function that combines a quantitative SQM description of various noncovalent interactions with an implicit COSMO solvation approach.17 This is an extremely accurate method of predicting the most stable conformation in P–L docking. In the P–L docking task, where a root-mean-square deviations (RMSD) of 2 Å or greater from the native binding pose is the criterion for false positives, SQM/COSMO showed a substantially lower number of false positives than classical SFs such as AutoDock Vina and Glide. These outcomes suggest that SQM/COSMO is adept at correctly identifying the native binding pose among decoys for each protein–ligand system.

The energy difference between the generated configurations and the most stable poses estimated by SQM/COSMO was used for labeling. This approach not only serves as a data augmentation method but also as a novel approach to train the model using the protein–ligand quantum energy landscape (P–L QEL) dataset calculated by SQM/COSMO.

This study is novel in two ways. The first is the development of a method that applies ACSF to the prediction of P–L binding affinity prediction. Second, quantum mechanics (QM) simulations were used to extend the data and overcome the lack of training data. These two points have enabled us to successfully learn the P–L QEL. As a result, our model was superior to all others evaluated on the CASF-2016 docking power benchmark.18

Results and Discussion

We trained two different AQDnet models, depending on the task being evaluated. The docking AQDnet, which is a model specialized for the evaluation of docking power, was used for the evaluation of docking power and screening power. Similarly, the scoring AQDnet was used to evaluate scoring power. The only difference between the docking AQDnet and the scoring AQDnet is the training data. Details are described in the data filtering section of method.

Docking Power

During training the docking AQDnet, the Pearson correlation coefficient (PCC), root mean square error (RMSE), and the loss function (PCC_RMSE) described below were monitored. Finally, the loss function of validation dataset was minimized at epoch 27 (Table S1); hence, we adopted the model of this epoch.

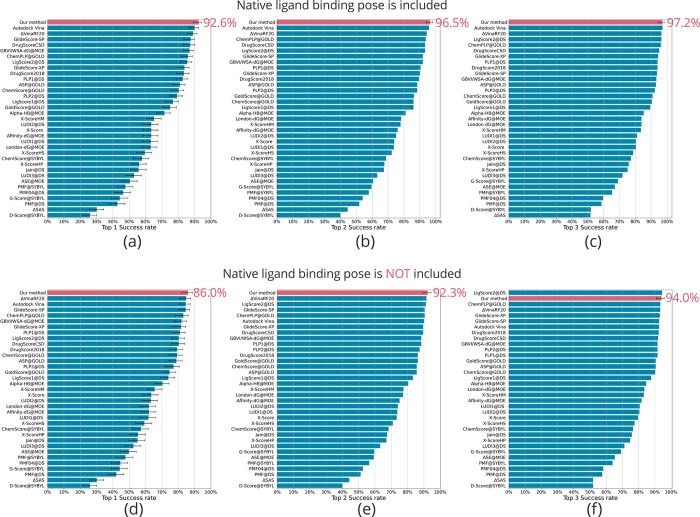
For the evaluation of our model, we used the CASF-2016 benchmark dataset.18 Notably, our model achieved a top 1 success rate of 92.6% in the docking power test, surpassing all other evaluated symmetry functions (SFs) in the CASF-2016 (Figure 1a). Additionally, our model demonstrated top 2 and top 3 success rates of 96.5 and 97.2%, respectively, ranking first in both categories (Figure 1b,c). These outstanding results are attributed to the successful learning of the P–L QEL by the model, facilitated by our data augmentation method.

Figure 1.

Figure 1

Open in a new tab

CASF-2016 docking power of AQDnet model. CASF-2016 docking power test performance (top 1/2/3 success rates) of the AQDnet model (colored pink) and other scoring functions. (a–c) Top 1/2/3 success rates when the native ligand binding pose is included. (d–f) Top 1/2/3 success rates when the native ligand binding pose is not included. Error bars indicate 90% confidence intervals obtained from 10,000 replicated bootstrapping samples. The 90% confidence intervals are derived from the CASF-201618 results. However, error bars are not shown for those that do not provide 90% confidence intervals in CASF2016 (e.g., Top2 success rate). Adapted with permission from Ref (18).

The attempt to expand the data by generating numerous configurations from crystal structure appears clearly beneficial in overcoming the insufficient number of training samples. However, this has not been achieved so far due to the difficulty of labeling. In this study, we developed a method of labeling the generated configurations by calculating the energy difference from the most stable pose using SQM/COSMO and correcting it using the experimental pKa. This labeling strategy can be employed in various existing machine-learning methods for predicting pKa from crystal structures. It is of great significance as it has the potential to substantially enhance the performance of docking tasks, which pose difficulties for many of the current machine-learning approaches. Although the proposed data expansion technique has the drawback of necessitating a substantial amount of time for calculation, it is expected to be incorporated into diverse machine learning methods in the future.

DeepBSP19 uses a simple data augmentation method using configuration generation. This method utilizes the RMSDs from crystal structures as labels. While this method is very easy to prepare data for, it is not trained to predict binding affinity and therefore cannot compare binding affinity between ligands. Therefore, it is not possible to evaluate the scoring power and screening power of CASF-2016. In contrast, our method can compare binding affinities among complexes. In fact, we achieved the 4th place in the screening power test of the top 1% enrichment factor, indicating that our method can be used to compare binding affinities between complexes.

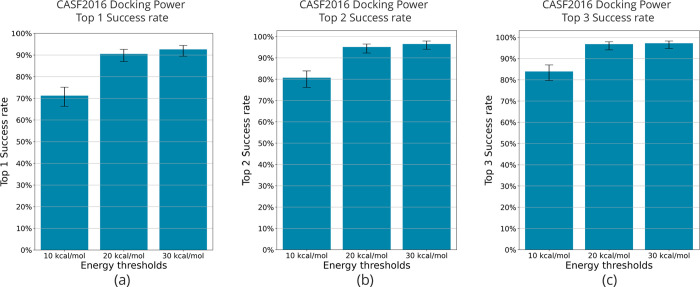
In learning the energy landscapes, the amount of high-energy unstable conformation to be included in the training data is very important. To determine the optimal value of this energy threshold, we conducted filtration under three different conditions. As outlined in the methods, we designated ΔE as the variation between the lowest energy conformation for each complex and the corresponding conformation’s energy. Filtering of the training data was performed under the following three conditions: ΔE < 10 kcal/mol, ΔE < 20 kcal/mol, and ΔE <30 kcal/mol. For the RMSDs, all the data were filtered under the consistent condition (<2.5 Å). The model was then trained on each of the training datasets. In this case, the number of training data differed across the three conditions. Although the quantity of training data increases as the ΔE threshold elevates, this tendency is also apparent in actual VS, making it valuable to explore the optimal values, including the effect of the increase in the number of training data points.

The results of the docking power evaluation under three different energy thresholds are shown in Figure 2. The model trained on filtered training data with ΔE < 30 kcal/mol had a docking power top 1 success rate of 92.6%, the highest success rate among the three conditions. The model trained with training data filtered by ΔE < 10 kcal/mol had the lowest docking power top 1 success rate of 71.2%. A success rate of 90.5% was obtained for ΔE < 20 kcal/mol, which is not as good as that for ΔE < 30 kcal/mol, but still good. From these results, it was observed that docking performance tended to increase as the ΔE filtering threshold was increased.

Figure 2.

Figure 2

Open in a new tab

Comparison of CASF-2016 docking power by energy threshold. The threshold for energy filtering was varied and used to compare CASF-2016 docking power in terms of (a) top 1 success rate, (b) top 2 success rate, and (c) top 3 success rate. Error bars indicate 90% confidence intervals obtained from 10,000 replicated bootstrapping samples.

Scoring Power

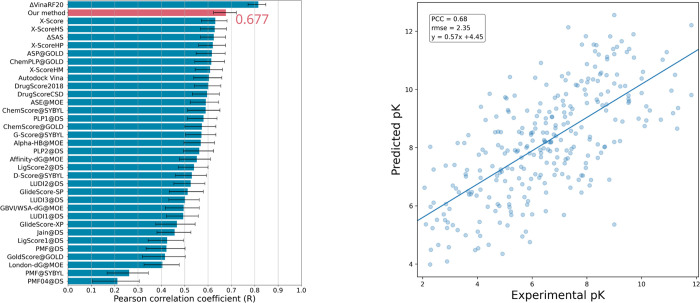
During training, the scoring AQDnet, PCC, RMSE and the loss function described below were monitored. Finally, the loss function (PCC_RMSE) of the validation dataset was minimized at epoch 33 (Table S2); hence, we adopted the model of this epoch. In the scoring power test, our scoring AQDnet achieved 0.677. This is the 2nd best result among the SFs evaluated in the CASF-2016 (Figure 3). Note that the best scoring power of the docking AQDnet was about 0.63, while that of the scoring AQDnet was 0.047 higher.

Figure 3.

Figure 3

Open in a new tab

CASF-2016 scoring power of AQDnet model. Comparison of AQDnet with the scoring functions listed in CASF-2016 (left panel). Error bars indicate 90% confidence intervals obtained from 10,000 replicated bootstrapping samples. Scatter plot of CASF-2016 “coreset” experimental values (horizontal axis) and predicted values by AQDnet (vertical axis) (right panel). Error bars indicate 90% confidence interval obtained from 10,000 replicated bootstrapping samples. The 90% confidence intervals are derived from the CASF-201618 results. Adapted with permission from Ref (18).

The scoring AQDnet was trained using only the conformations that were very close to the crystal structure data (ΔE < 2 kcal/mol, RMSD < 2.5 Å). To improve scoring performance, it is necessary to learn as many different protein–ligand systems as possible, rather than learning many different conformations of the same protein–ligand combination, as in the training data for the docking AQDnet. Comparing the scoring power of the docking AQDnet with that of the scoring AQDnet, which was trained by adding samples with relatively high energy, the scoring power of the scoring AQDnet is higher. A tendency toward better scoring power emerged when filtering with very low ΔE values, in contrast to the docking power, which improved when filtering with higher ΔE values. These results suggest that it is challenging to improve both the docking power results and the scoring power results with a single model at this time. Our future objective is to enhance the scoring power of the docking AQDnet by augmenting the training dataset, enabling a single model to perform superiorly in both docking and scoring evaluations.

In this case, AQDnet’s CASF-2016 scoring power was 0.68. After CASF-2016 was published, many machine-learning methods have been evaluated using CASF-2016. For example, Pufnucy,14 which learns the 3D structure of the protein–ligand complex using a 3DCNN, achieves a scoring power PCC of 0.780, and InteractionGraphNet (IGN),20 which learns the structure of the P–L complex as a graph, achieved a scoring power PCC of 0.837. The current best is extended connectivity interaction features (ECIF),21 which learns the count values of contacts between atoms represented in detail as features in gradient boosting decision tree (GBDT), achieving a PCC of 0.866.

Our method is apparently not competitive in terms of the scoring power compared to the current state-of-the-art methods. However, it is important to emphasize that before utilizing such methods, it is necessary to provide the most stable, or near-stable, structures of the protein–ligand complex, like its crystal structure, for accurately evaluating protein–ligand affinity. In fact, current state-of-the-art methods do not exhibit exceptional docking performance, unlike AQDnet, requiring the “true” structure of the protein–ligand complex for accurately determining protein–ligand affinity with these approaches. In contrast, the AQDnet system exhibits the significant performance in the identification of the most stable pose as shown in the docking power result. This was established in the AQDnet system by combining the quantum docking techniques. This is an exclusive feature of our AQDnet system, compared with the other state-of-the-art methods, and also critical for the actual use in the practical VS workflow.

Screening Power

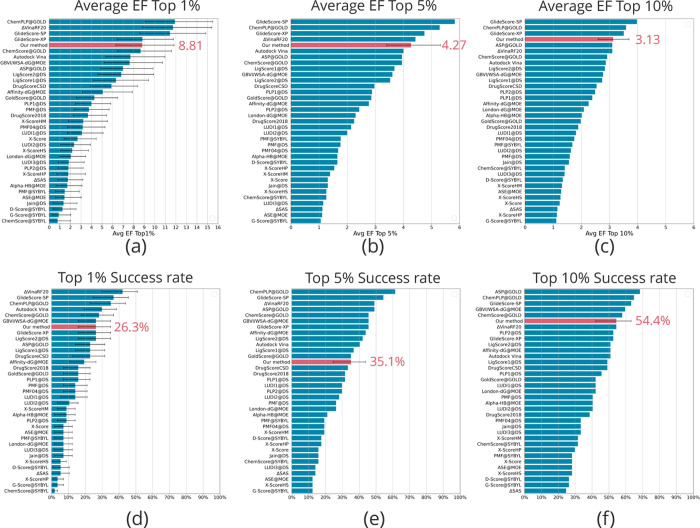
Screening power was evaluated using the docking AQDnet. In the forward screening power test, our model’s screening power average enrichment factor top 1% was 8.81, placing it in the 4th position among the SFs evaluated by the updated CASF-2016 (Figure 4a).

Figure 4.

Figure 4

Open in a new tab

CASF-2016 screening power of the AQDnet model. Average enrichment factor (EF) top 1/5/10% performance (a–c) and top 1/5/10% success rate performance (d–f) of the AQDnet model (colored pink) and other scoring functions on the CASF-2016 screening power test. Error bars indicate 90% confidence intervals obtained from 10,000 replicated bootstrapping samples. Error bars indicate 90% confidence intervals obtained from 10,000 replicated bootstrapping samples. The 90% confidence intervals are derived from the CASF-201618 results. However, error bars are not shown for those that do not provide 90% confidence intervals in CASF2016 (e.g., Average EF Top 5%). Adapted with permission from Ref (18).

The CASF2016 screening power test sample was generated by cross-docking 285 ligands against 95 proteins, and it has not been experimentally shown whether the decoys are truly inactive. It is also reported that there are serious biases in the dataset using a decoy, but it is unclear how CASF-2016 addresses this issue. Therefore, as another reliable indicator, we conducted a validation with the LIT-PCBA22 dataset. In order to compare our method with the current state-of-the-art machine-learning-based method in screening power, we compared the results of the five scoring functions (Surflex-Dock,23 Pafnucy,24 Deltavina,25 IFP,26 and GRIM27) evaluated in Bret and co-workers28 Details of the method are described in the method section. AQDnet predictions were made for all 15 targets included in the LIT-PCBA and compared using an enrichment factor (EF) of 1% as metric. The results are shown in Figure S1. Although it fell short of Pafnucy and Deltavina for 11 of the 15 targets, it outperformed the other 5 SFs for ESR1-antagonist, MTORC1 and TP53. Thus, evaluation results of CASF-2016 and LIT-PCBA show a reasonable screening performance of our method (also see the last part in the Scoring Power section).

We discuss below how the methodology can be improved from a developmental standpoint and its prospective applications. There are three ways to improve this methodology.

First, a small number of complexes was currently used to generate the training data. Most of the existing methods that use PDBbind as the source of training data use about 12,000 complexes. In contrast, we used only 1123 complexes herein as training data due to computational reasons. By creating a training dataset based on a larger number of complexes, we expect to achieve improved results in scoring power and screening power.

Second, our method presently neglects the energy difference between the free and bound states of the ligand. To accurately compare ligand binding affinities, it is crucial to consider the energy differences, specifically requiring an understanding of the ligand’s topology to ascertain its distortion. However, the presented algorithm in AQDnet solely considers the distance between the protein atoms and the ligand atoms, without accounting for the covalent bonding of the ligand atoms. This limitation could potentially hinder the scoring power and screening power of the model, highlighting the need for a feature extraction approach that incorporates the topology of ligands to further enhance the methodology. This work is actually ongoing in our lab.

Third, our method does not recognize the exposed moiety of the ligand molecule from the protein pocket. Feature extraction is performed for protein atoms within 12 Å of each atom of the ligand and regions lacking protein atoms within 12 Å of ligand atoms are disregarded. This is a major challenge in predicting the binding affinity of relatively large molecules such as peptides. For example, even if two ligands are in the same conformation in a protein pocket, the stability of one that fits completely in the protein pocket and another with a large hydrophobic segment exposed outside the pocket may differ significantly. However, AQDnet predicts that the two would have the same binding affinity. Therefore, implementing measures such as increasing the cutoff distance is necessary when dealing with large ligand molecules.

Conclusions

In this study, we devised a novel approach for predicting the P–L binding affinity by applying ACSF, which is suitable for describing the energy of a single molecule. This method takes into account not only two-body interactions but also three-body interactions and generates high-resolution features that clearly represent changes in atomic coordinates of 0.1 Å or smaller. In these two respects, this method proves valuable for VS applications. Additionally, we have devised a data augmentation technique that leverages configuration generation and QM calculations, thereby overcoming the shortage of training data for P–L binding affinity prediction. We believe that this method has great value in that it can be easily integrated into existing machine-learning methods and enhance their performance.

Our method was evaluated by the CASF-2016 dataset and ranked first in the docking power test of the top 1 success rate and fourth in the screening power test of the top 1% EF. Note here that our method achieves the above results by creating training data based on the crystal structures of only 1123 complexes. Actually, this is the smallest number of training data used by any machine learning method, which suggests that our method can learn features originated from the QM-based first principles (i.e., the quantum field) found in P–L interactions. Accordingly, further increase in the number of training data will enable us to effectively obtain higher performance.

Moreover, the presented method does not take ligand characteristics into account and predicts affinities only with information on P–L interactions, which is unfavorable for scoring and screening performance. Nevertheless, the obtained achievements were within an acceptable level even for the actual use of the presented system. Thus, our method is also promising in terms of improvements in the scoring and screening performance by incorporating a ligand energy feature, which leads to the involvement of how much the docked ligand is destabilized from the most stable conformation of the free ligand.

Note herein that prior to performing most of current machine-learning-based P–L docking methods including state-of-the-art ones, one needs to provide the most stable structures (or structure that is close to being native) of the P–L complexes, such as the crystal structures of the complexes, for the appropriate evaluation of the P–L affinity. In fact, present state-of-the-art methods for the P–L docking task do not exhibit excellent docking performance (whereas the AQDnet system does, as described in this report), and thus do require the “true” (native) structures of the P–L complexes for obtaining the appropriate P–L affinity. In contrast, the AQDnet system discriminates the most appropriate pose among other many poses, as shown in the presented docking score data. This is an exclusive feature of our AQDnet system in the actual VS workflow, compared with those of the other state-of-the-art methods.

Method

Feature Extraction of Protein-Ligand Complexes

Feature extraction was conducted on the three-dimensional structure of the ligand–protein complex. MDTraj29 was used to read the PDB files and calculate the interatomic distances. The Gaussian function calculation and other processes were implemented using NumPy. The three-dimensional structures were prepared using PDB files that contain both ligand and protein information. The feature extraction method used in this study consisted of two main parts: the radial part, which contains information on the distance between two atoms, and the angular part, which contains information on the distance and angle between three atoms. These two parts are explained below. Figure S2 shows a graphical representation of the features.

Radial Part

The radial part uses the interatomic distance between one atom on the ligand side and one atom on the protein side as the input of the multiple Gaussian functions, with the output vector being the feature value of the radial part. The feature extraction process is as follows. First, the distance between all ligand atoms and protein atoms is calculated. Next, all pairs with distances below a specified threshold (Rc) are obtained. For each pair, the elements of the ligand atom and the protein atom are retrieved, and the radial symmetry function is calculated using the interatomic distance of the two atoms (Rij) as input.

graphic file with name ao3c02411_m001.jpg
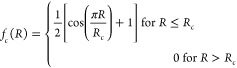graphic file with name ao3c02411_m002.jpg 1

The cutoff function, fc includes Rc as the cutoff radius—a hyperparameter that determines which atoms are considered based on their distance. Rs is a hyperparameter that adjusts the peak of the Gaussian functions. In this process, multiple Rs are used to output multidimensional features for each pair. Finally, features with the same combinations of ligand-side element, protein element, and Rs are summed to produce the final feature as shown below.

graphic file with name ao3c02411_m003.jpg 2

where El is the element type of the ligand-side atom, Ep is the element type of the protein-side atom, LEl is the set of all the El atoms on the ligand side, PEp is the set of all the Ep atoms on the protein side, and Rs(k) is the kth Rs. The name of the feature with El for the ligand-side atom, Ep for the protein-side atom, and Rs for Rs is defined as El_Ep_k. For example, the feature N_C_3 is characterized by a combination of a ligand-side nitrogen atom, a protein-side carbon atom, and R_s as Rs(3). As a result, a feature vector with (Nelement × NRs) dimensions is obtained, where Nelement is the number of elemental species considered, and NRs is the number of Rs values.

Angular Part

The feature value of the angular part is generated using the interatomic distance between a ligand-side atom and two protein-side atoms, as well as the angle between the three atoms. The feature extraction procedure is as follows. First, the distance between all ligand atoms and protein atoms is calculated. Next, all combinations of two protein-side atoms with distances less than a certain threshold (Rc) from any ligand-side atom are obtained. For the resulting triplet of one ligand-side atom and two protein-side atoms, the interatomic distances Rij and Rik, the angle between the three atoms θjik, and the element type of each atom are obtained. For each triplet, the following angular symmetry function with Rij, Rik, and θjik as inputs is calculated.

graphic file with name ao3c02411_m004.jpg 3

where fc is the same cutoff function as that of the radial part. R_s is a hyperparameter that adjusts the peak of the Gaussian function, and θs is a hyperparameter that modifies the phase of the Cosine function. In this process, multiple Rs and θs are used to output multidimensional features for each triplet. Finally, the features with the same combination of ligand side element, protein elements, Rs, and θs are summed up to get the final feature value as shown below.

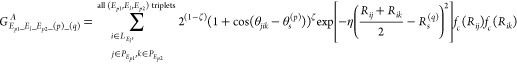graphic file with name ao3c02411_m005.jpg 4

where El represents the element type of the ligand-side atom, Ep1 and Ep2 are the element types of the protein-side atoms. LEl is the set of all the El atoms on the ligand side, PEp1 and PEp2 are the sets of all the Ep1 atoms on the protein side and all the Ep2 atoms on the protein side, respectively. θs(p) is the pth θs value and Rs is the qth Rs value. The feature comprising El for the ligand-side atom, Ep1 and Ep2 for the protein-side atoms, θs(p) for θs and Rs for Rs is named as Ep1_El_Ep2_p_q. For example, the feature where the ligand-side atom is carbon, the protein-side atoms are hydrogen and nitrogen, θs is θs(1), and Rs is Rs is defined as H_C_N_1_2. As a result, we get a feature vector with 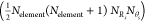Inline graphic dimensions, where Nelement is the number of elemental species considered, NRs is the number of Rs values, and Nθs is the number of θs values.

Exporting Features to Files

For memory efficiency reasons, the features are exported as TFRecords files.

Parameters

For feature extraction, we targeted seven elements for feature extraction, H, C, N, O, P, S, Cl, and Zn, while the remaining elements were collectively represented as Dummy (Du). Consequently, eight-element types, H, C, N, O, P, S, Cl, Zn, and Du, were used for El and Ep above. The Rc parameters were set to 12 Å for radial part and 6 Å for angular parts. The R_s parameters for the radial part are [0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5, 10.0, 10.5, 11.0, 11.5]. Regarding the angular part, the Rs parameters are [0.5, 2.5, 4.5] and the θs parameters are a sequence of numbers from 0 to 2π divided into 8 equal segments [0.0, 0.785, 1. 570, 2.356, 3.142, 3.927, 4.7124, 5.4978].

Dataset Preparation

Quantum Docking Simulation

P–L complex structures were obtained from the PDBbind database.15,30 For each complex, hydrogen atoms were added using the Protonate 3D module in the Molecular Operating Environment (MOE) suite, and the structural data of the complex were intensively augmented by performing the docking simulations as follows. The partial charges of each atom were assigned by mmff94x force field. Over 1000 configurations were generated from each complex by Smina,31 which is a fork of AutoDock Vina.32 The configurations were energy-minimized using Amber 18 (http://ambermd.org/) with ff99SBildn force field33 for proteins, the second generation of the general AMBER force field (GAFF2)34 for ligands. With protein coordinates fixed, the energy of the ligand was minimized. The energy of each configuration was calculated with PM6-D3H4X/COSMO in MOPAC (http://openmopac.net/). In order to improve the calculation accuracy, solvation energy was compensated by the effective surface tension coefficient ξ = 0.046,35 which was also coupled with our correction scheme depending on the P–L QEL (more detailed descriptions are provided elsewhere).

Labeling of the Generated Configurations

In this paper, experimentally obtained values are represented as variables without dashes (e.g., pKa), while values corrected by ΔE are represented as variables with dashes (e.g., pKa′). From the experimentally measured binding affinity (Kd), ΔG is calculated using eq 5, where R is the gas constant and T is the temperature.

graphic file with name ao3c02411_m007.jpg 5

The lowest energy conformation generated from a single ligand is defined as the reference configuration for that ligand. For other configurations, the difference in energy (ΔE) between each configuration and the reference configuration was calculated. The corrected energy label of each configuration, ΔG′, is then calculated using eq 6.

graphic file with name ao3c02411_m008.jpg 6

The configurations except for the reference configuration were labeled with ΔG′, while the reference configuration was labeled with ΔG. If necessary, pseudo-Kd (Kd′) and pseudo-pKa (pKa′) corrected by ΔE are obtained using the following equations.

graphic file with name ao3c02411_m009.jpg 7
graphic file with name ao3c02411_m010.jpg 8

PDB Preparation of CASF-2016 Dataset

Ligand Mol2 files were converted to PDB files by Open Babel. Subsequently, protein PDB files and ligand PDB file were merged to generate complex PDB files. The −log Kd/Ki registered in PDBbind was converted to ΔG using eq 5 and used as the correct label. In both docking decoy and screening decoy, one ligand Mol2 file contains multiple ligand structures. Therefore, we parsed each structure and created PDB files containing one ligand structure per file. These parsed ligand PDB files were merged with the corresponding protein PDB file to establish the complex PDB file.

PDB Preparation of LIT-PCBA Dataset

The smi file of ligand was loaded using RDkit (https://www.rdkit.org) to generate 3Dconformation and add hydrogens. The files were then saved as sdf files. All template PDB files were protonated by MOE. Then, docking of ligand to protein was performed using gnina.36 If multiple templates were given in the target, docking was performed on all templates. The docked ligands were then saved as sdf files. Ligand Mol2 files were converted to PDB files by Open Babel. Subsequently, protein PDB files and ligand PDB file were merged to generate complex PDB files.

Evaluation Method

Evaluation by CASF-2016

We evaluated scoring power, docking power and screening power of CASF-2016 in order to facilitate comparison with existing methods. Features were extracted from PDB files generated by the method described in PDB preparation of CASF-2016 dataset. The predicted values were formed using the method described in the CASF-2016 update study,18 and the docking power, screening power, and scoring power were evaluated. The docking AQDnet, which is a model specialized for the evaluation of docking power, was used for the evaluation of docking power and screening power. Similarly, the scoring AQDnet was used to evaluate scoring power. The only difference between the docking AQDnet and the scoring AQDnet is the training data. The structure and hyperparameter of these two models remain the same. The differences between the two models are discussed in the data splitting and data filtering sections.

Data Splitting

The data were divided into test sets, valid set, and train set with reference to OnionNet and Pufnucy’s method.

We carried out data augmentation on 1223 complexes, excluding those in the CASF-2016 and CASF-2013 core sets. During the data expansion process, each complex generated approximately 5000 conformations. We divided the complexes into trainset, validation set, and test set in the following manner.

The trainset for the docking AQDnet consisted of 1123 complexes from the augmented data. For the scoring AQDnet, we included 16,306 crystal structures that were not present in the validation set, CASF-2016 core set, or CASF-2013 core set. However, we did not add any crystal structures to the docking AQDnet’s trainset.

The validation set for the docking AQDnet was composed of 100 randomly-selected complexes from the initial 1223 complexes. Additionally, the scoring AQDnet’s valid set contained crystal structures of these 100 complexes and 900 other randomly chosen complexes, totaling 1000 complexes.

Lastly, the test set included the CASF-2016 core set and the CASF-2013 core set. The summary of the aforementioned divisions is presented in Table 1. The PDBIDs of the complexes used for the test set, validation set and training set for both the docking-specific and scoring AQDnet are listed in Tables S3–S7.

Table 1. Differences between the Training Data of the Docking AQDnet and that of the Scoring AQDnet.

  docking AQDnet scoring AQDnet
number of expanded complexes (PDBIDs) in validation set 100 100
number of expanded complexes (PDBIDs) in training set 1123 1123
crystal structures added no yes
number of crystal structures in validation set 0 1000
number of crystal structures in training set 0 16,306
energy filtering <30 kcal/mol <2 kcal/mol
RMSD filtering <2.5 Å <2.0 Å
number of configurations in validation set 89,740 20,995
number of configurations in training set 940,038 247,393
Open in a new tab

Data Filtering

We defined ΔE for each configuration as the difference between the minimum energy among the configurations generated for each complex and the energy of the corresponding configuration. For example, if configurations A, B, and C have energies of −7, −5, and −4, respectively, the ΔE values for configurations A, B, and C would be 0, 2, and 3, as configuration A possesses the minimum energy among the three. Given the impracticality of utilizing all generated configurations for training from a computational standpoint, RMSD from each crystal structure and ΔE were used to filter the data. Different filtering criteria were used for the training data of the docking-specific and scoring AQDnet. For the training and validation sets of the docking AQDnet, we used conformations with ΔE less than 30 kcal/mol and RMSD less than 2.5 Å. For the docking AQDnet’s training and validation sets, conformations with ΔE values below 30 kcal/mol and RMSD values under 2.5 Å were utilized.

For the scoring AQDnet’s training and validation sets, conformations with ΔE values below 2 kcal/mol and RMSD values under 2.0 Å were employed. The validation set for the docking AQDnet contains 100 PDBIDs and a total of 89,740 configurations. The training set for the docking AQDnet comprises 1123 PDBIDs and a total of 940,038 configurations. The validation set for the scoring AQDnet consists of 1000 PDBIDs and 20,995 total configurations. The training set for the scoring AQDnet includes 16,306 PDBIDs and 247,393 total configurations.

Neural Network Model

All of the following models were built and trained in TensorFlow 2.3.2. The architecture of the deep neural network (DNN) is presented in Figure S3. The DNN model employed in this project consists of 18 sub-DNNs, which process the radial or angular features of each corresponding element, and one output DNN that summarizes the outputs of the 18 sub-DNNs. Specifically, 9 of the sub-DNNs process radial features and correspond to different elements (H, C, N, O, P, S, Cl, Zn, and Dummy), responsible for processing the features when the atom on the ligand side is the target element. The remaining 9 sub-DNNs process angular features and are responsible for processing features when the atom on the ligand side is the target element, in a similar manner to the sub-DNNs that process radial features above. All 18 sub-DNNs share the same structure, and their details are described below.

Sub-DNN Structure

A dropout layer is used after the input layer with a dropout rate of 0.05. Each DNN consists of 6 blocks featuring the residual learning mechanism. As illustrated in Figure S4, a block comprises one dense layer with 500 nodes, a batch normalization layer, and a dropout layer with a dropout rate of 0.15. A sub-DNN is a stack of 6 of these blocks, and outputs a 10-dimensional tensor. The output DNN consists of three dense layers with 256 nodes, taking the above-mentioned 18 sub-DNN’s outputs as input and produces a one-dimensional output. In order to prevent the over fit problem, spectral normalization and L2 regularization are implemented in all the above dense layers with the λ parameter of L2 regularization set at 0.1.

Preprocessing

Feature preprocessing procedure are depicted in Figure S3. The features are separated into 18 subsets based on radial or angular features and ligand side element types, which are then input into the corresponding DNN. Radial features are segregated into nine groups using El of the feature name El_Ep_k, while angular features are divided into nine groups based on El of the feature name Ep1_El_Ep2_p_q. Each segregated feature group is subsequently input into the DNN responsible for processing El features.

Loss Function (PCC_RMSE)

A loss function combining correlation coefficient R and RMSE, as utilized in OnionNet,11 was adopted. We call this loss function PCC_RMSE. The equation is as follows:

graphic file with name ao3c02411_m011.jpg 9

where R represents the correlation coefficient, RMSE denotes the root mean square error, and α is the coefficient determining the R and RMSE ratio, with values ranging between 0 and 1. All models in this study were trained with α = 0.7.

Model Training

Each model underwent 200 epochs of training with early stopping set at 20 epochs. The initial learning rate value was set at 1e–3, and the learning rate was multiplied by 0.2 if the validation loss failed to improve for five epochs.

Acknowledgments

K.S. thanks Dr. Shohei Oie for the fruitful discussion.

Data Availability Statement

The code for AQDnet feature extraction, model training, and inference with trained models can be accessed on GitHub (https://github.com/koji11235/AQDnet). Due to the data size constraints, only a subset of the PDB files and features used for training have been uploaded.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c02411.

  • Table S1: Transition of loss function during training of docking AQDnet. Table S2: Transition of loss function during training of scoring AQDnet. Table S3: PDB IDs used for test set. Table S4: PDB IDs used for validation set of docking AQDnet. Table S5: PDB IDs used for train set of docking AQDnet. Table S6: PDB IDs used for validation set of scoring AQDnet (data augmented). Table S7: PDB IDs used for validation set of scoring AQDnet (crystal structure). Table S8: PDB IDs used for train set of scoring AQDnet (data augmented). Table S9: PDB IDs used for train set of scoring AQDnet (crystal structure) Figure S1: Comparison of AQDnet performance on the LIT-PCBA data set. Figure S2: A graphical representation of the AQDnet features. Figure S3: A simplified schematic of the structure of the deep neural network of AQDnet. Figure S4: A schematic of residual dense block (PDF)

The authors declare no competing financial interest.

This paper was originally published ASAP on June 16, 2023. Additional minor corrections were received, and the corrected version reposted on June 20, 2023.

Supplementary Material

ao3c02411_si_001.pdf (763.5KB, pdf)

References

  1. Gimeno A.; Ojeda-Montes M. J.; Tomas-Hernandez S.; Cereto-Massague A.; Beltran-Debon R.; Mulero M.; Pujadas G.; Garcia-Vallve S. The Light and Dark Sides of Virtual Screening: What Is There to Know?. Int. J. Mol. Sci. 2019, 20, 1375. 10.3390/ijms20061375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Krizhevsky A.; Sutskever I.; Hinton G. E.. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, 2012; Vol. 1.
  3. Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser L. U.; Polosukhin I.. Attention is All you Need, 2017.
  4. a Jones D.; Kim H.; Zhang X.; Zemla A.; Stevenson G.; Bennett W. F. D.; Kirshner D.; Wong S. E.; Lightstone F. C.; Allen J. E. Improved Protein-Ligand Binding Affinity Prediction with Structure-Based Deep Fusion Inference. J. Chem. Inf. Model. 2021, 61, 1583–1592. 10.1021/acs.jcim.0c01306. [DOI] [PubMed] [Google Scholar]; b Feinberg E. N.; Sur D.; Wu Z.; Husic B. E.; Mai H.; Li Y.; Sun S.; Yang J.; Ramsundar B.; Pande V. S. PotentialNet for Molecular Property Prediction. ACS Cent. Sci. 2018, 4, 1520–1530. 10.1021/acscentsci.8b00507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ragoza M.; Hochuli J.; Idrobo E.; Sunseri J.; Koes D. R. Protein-Ligand Scoring with Convolutional Neural Networks. J. Chem. Inf. Model. 2017, 57, 942–957. 10.1021/acs.jcim.6b00740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. a Lee I.; Keum J.; Nam H. DeepConv-DTI: Prediction of drug-target interactions via deep learning with convolution on protein sequences. PLoS Comput. Biol. 2019, 15, e1007129 10.1371/journal.pcbi.1007129. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Ozturk H.; Ozgur A.; Ozkirimli E. DeepDTA: deep drug-target binding affinity prediction. Bioinformatics 2018, 34, i821–i829. 10.1093/bioinformatics/bty59. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jimenez J.; Skalic M.; Martinez-Rosell G.; De Fabritiis G. K(DEEP): Protein-Ligand Absolute Binding Affinity Prediction via 3D-Convolutional Neural Networks. J. Chem. Inf. Model. 2018, 58, 287–296. 10.1021/acs.jcim.7b00650. [DOI] [PubMed] [Google Scholar]
  8. Torng W.; Altman R. B. Graph Convolutional Neural Networks for Predicting Drug-Target Interactions. J. Chem. Inf. Model. 2019, 59, 4131–4149. 10.1021/acs.jcim.9b00628. [DOI] [PubMed] [Google Scholar]
  9. Behler J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. 10.1002/qua.24890. [DOI] [Google Scholar]
  10. Jiang D.; Hsieh C. Y.; Wu Z.; Kang Y.; Wang J.; Wang E.; Liao B.; Shen C.; Xu L.; Wu J.; et al. InteractionGraphNet: A Novel and Efficient Deep Graph Representation Learning Framework for Accurate Protein-Ligand Interaction Predictions. J. Med. Chem. 2021, 64, 18209–18232. 10.1021/acs.jmedchem.1c01830. [DOI] [PubMed] [Google Scholar]
  11. Zheng L.; Fan J.; Mu Y. OnionNet: a Multiple-Layer Intermolecular-Contact-Based Convolutional Neural Network for Protein-Ligand Binding Affinity Prediction. ACS Omega 2019, 4, 15956–15965. 10.1021/acsomega.9b01997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Wang Z.; Zheng L.; Liu Y.; Qu Y.; Li Y. Q.; Zhao M.; Mu Y.; Li W. OnionNet-2: A Convolutional Neural Network Model for Predicting Protein-Ligand Binding Affinity Based on Residue-Atom Contacting Shells. Front. Chem. 2021, 9, 753002 10.3389/fchem.2021.753002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. a Behler J.; Parrinello M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]; b Smith J. S.; Isayev O.; Roitberg A. E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 2017, 8, 3192–3203. 10.1039/C6SC05720A. [DOI] [PMC free article] [PubMed] [Google Scholar]; c Gao X.; Ramezanghorbani F.; Isayev O.; Smith J. S.; Roitberg A. E. TorchANI: A Free and Open Source PyTorch-Based Deep Learning Implementation of the ANI Neural Network Potentials. J. Chem. Inf. Model. 2020, 60, 3408–3415. 10.1021/acs.jcim.0c00451. [DOI] [PubMed] [Google Scholar]
  14. Stepniewska-Dziubinska M. M.; Zielenkiewicz P.; Siedlecki P. Development and evaluation of a deep learning model for protein–ligand binding affinity prediction. Bioinformatics 2018, 34, 3666–3674. 10.1093/bioinformatics/bty374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wang R.; Fang X.; Lu Y.; Wang S. The PDBbind database: Collection of binding affinities for protein-ligand complexes with known three-dimensional structures. J. Med. Chem. 2004, 47, 2977–2980. 10.1021/jm030580l. [DOI] [PubMed] [Google Scholar]; 15163179
  16. a Russakovsky O.; Deng J.; Su H.; Krause J.; Satheesh S.; Ma S.; Huang Z.; Karpathy A.; Khosla A.; Bernstein M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vision 2015, 115, 211–252. 10.1007/s11263-015-0816-y. [DOI] [Google Scholar]; b Kuznetsova A.; Rom H.; Alldrin N.; Uijlings J.; Krasin I.; Pont-Tuset J.; Kamali S.; Popov S.; Malloci M.; Kolesnikov A.; et al. The Open Images Dataset V4: Unified Image Classification, Object Detection, and Visual Relationship Detection at Scale. Int. J. Comput. Vision 2020, 128, 1956–1981. 10.1007/s11263-020-01316-z. [DOI] [Google Scholar]
  17. a Pecina A.; Meier R.; Fanfrlik J.; Lepsik M.; Rezac J.; Hobza P.; Baldauf C. The SQM/COSMO filter: reliable native pose identification based on the quantum-mechanical description of protein-ligand interactions and implicit COSMO solvation. Chem. Commun. 2016, 52, 3312–3315. 10.1039/c5cc09499b. [DOI] [PubMed] [Google Scholar]; b Pecina A.; Haldar S.; Fanfrlik J.; Meier R.; Rezac J.; Lepsik M.; Hobza P. SQM/COSMO Scoring Function at the DFTB3-D3H4 Level: Unique Identification of Native Protein-Ligand Poses. J. Chem. Inf. Model. 2017, 57, 127–132. 10.1021/acs.jcim.6b00513. [DOI] [PubMed] [Google Scholar]; c Ajani H.; Pecina A.; Eyrilmez S. M.; Fanfrlik J.; Haldar S.; Rezac J.; Hobza P.; Lepsik M. Superior Performance of the SQM/COSMO Scoring Functions in Native Pose Recognition of Diverse Protein-Ligand Complexes in Cognate Docking. ACS Omega 2017, 2, 4022–4029. 10.1021/acsomega.7b00503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Su M.; Yang Q.; Du Y.; Feng G.; Liu Z.; Li Y.; Wang R. Comparative Assessment of Scoring Functions: The CASF-2016 Update. J. Chem. Inf. Model. 2019, 59, 895–913. 10.1021/acs.jcim.8b00545. [DOI] [PubMed] [Google Scholar]
  19. Bao J.; He X.; Zhang J. Z. H. DeepBSP-a Machine Learning Method for Accurate Prediction of Protein-Ligand Docking Structures. J. Chem. Inf. Model. 2021, 61, 2231–2240. 10.1021/acs.jcim.1c00334. [DOI] [PubMed] [Google Scholar]
  20. Jiang D.; Hsieh C. Y.; Wu Z.; Kang Y.; Wang J.; Wang E.; Liao B.; Shen C.; Xu L.; Wu J.; et al. InteractionGraphNet: A Novel and Efficient Deep Graph Representation Learning Framework for Accurate Protein-Ligand Interaction Predictions. J. Med. Chem. 2021, 64, 18209–18232. 10.1021/acs.jmedchem.1c01830. [DOI] [PubMed] [Google Scholar]
  21. Sanchez-Cruz N.; Medina-Franco J. L.; Mestres J.; Barril X. Extended connectivity interaction features: improving binding affinity prediction through chemical description. Bioinformatics 2021, 37, 1376–1382. 10.1093/bioinformatics/btaa982. [DOI] [PubMed] [Google Scholar]
  22. Tran-Nguyen V. K.; Jacquemard C.; Rognan D. LIT-PCBA: An Unbiased Data Set for Machine Learning and Virtual Screening. J. Chem. Inf. Model. 2020, 60, 4263–4273. 10.1021/acs.jcim.0c00155. [DOI] [PubMed] [Google Scholar]
  23. Jain A. N. Surflex-Dock 2.1: robust performance from ligand energetic modeling, ring flexibility, and knowledge-based search. J. Comput.-Aided Mol. Des. 2007, 21, 281–306. 10.1007/s10822-007-9114-2. [DOI] [PubMed] [Google Scholar]
  24. Stepniewska-Dziubinska M. M.; Zielenkiewicz P.; Siedlecki P. Development and evaluation of a deep learning model for protein-ligand binding affinity prediction. Bioinformatics 2018, 34, 3666–3674. 10.1093/bioinformatics/bty374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wang C.; Zhang Y. Improving scoring-docking-screening powers of protein-ligand scoring functions using random forest. J. Comput. Chem. 2017, 38, 169–177. 10.1002/jcc.24667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Marcou G.; Rognan D. Optimizing fragment and scaffold docking by use of molecular interaction fingerprints. J. Chem. Inf. Model. 2007, 47, 195–207. 10.1021/ci600342e. [DOI] [PubMed] [Google Scholar]
  27. Desaphy J.; Raimbaud E.; Ducrot P.; Rognan D. Encoding protein-ligand interaction patterns in fingerprints and graphs. J. Chem. Inf. Model. 2013, 53, 623–637. 10.1021/ci300566n. [DOI] [PubMed] [Google Scholar]
  28. Tran-Nguyen V. K.; Bret G.; Rognan D. True Accuracy of Fast Scoring Functions to Predict High-Throughput Screening Data from Docking Poses: The Simpler the Better. J. Chem. Inf. Model. 2021, 61, 2788–2797. 10.1021/acs.jcim.1c00292. [DOI] [PubMed] [Google Scholar]
  29. Robert T. M.; Kyle A. B.; Matthew P. H.; Christoph K.; Jason M. S.; Carlos X. H.; Christian R. S.; Lee-Ping W.; Thomas J. L.; Vijay S. P. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Liu Z.; Li Y.; Han L.; Li J.; Liu J.; Zhao Z.; Nie W.; Liu Y.; Wang R. PDB-wide collection of binding data: current status of the PDBbind database. Bioinformatics 2015, 31, 405–412. 10.1093/bioinformatics/btu626. [DOI] [PubMed] [Google Scholar]
  31. Koes D. R.; Baumgartner M. P.; Camacho C. J. Lessons Learned in Empirical Scoring with smina from the CSAR 2011 Benchmarking Exercise. J. Chem. Inf. Model. 2013, 53, 1893–1904. 10.1021/ci300604z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Trott O.; Olson A. J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2009, 31, 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins: Struct., Funct., Bioinf. 2010, 78, 1950–1958. 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. He X.; Man V. H.; Yang W.; Lee T.-S.; Wang J. A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys. 2020, 153, 114502. 10.1063/5.0019056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kříž K.; Řezáč J. Reparametrization of the COSMO Solvent Model for Semiempirical Methods PM6 and PM7. J. Chem. Inf. Model. 2019, 59, 229–235. 10.1021/acs.jcim.8b00681. [DOI] [PubMed] [Google Scholar]
  36. McNutt A. T.; Francoeur P.; Aggarwal R.; Masuda T.; Meli R.; Ragoza M.; Sunseri J.; Koes D. R. GNINA 1.0: molecular docking with deep learning. Aust. J. Chem. 2021, 13, 43. 10.1186/s13321-021-00522-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao3c02411_si_001.pdf (763.5KB, pdf)

Data Availability Statement

The code for AQDnet feature extraction, model training, and inference with trained models can be accessed on GitHub (https://github.com/koji11235/AQDnet). Due to the data size constraints, only a subset of the PDB files and features used for training have been uploaded.

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES