Abstract

Therapeutic peptides and proteins derived from either endogenous hormones, such as insulin, or de novo design via display technologies occupy a distinct pharmaceutical space in between small molecules and large proteins such as antibodies. Optimizing the pharmacokinetic (PK) profile of drug candidates is of high importance when it comes to prioritizing lead candidates, and machine-learning models can provide a relevant tool to accelerate the drug design process. Predicting PK parameters of proteins remains difficult due to the complex factors that influence PK properties; furthermore, the data sets are small compared to the variety of compounds in the protein space. This study describes a novel combination of molecular descriptors for proteins such as insulin analogs, where many contained chemical modifications, e.g., attached small molecules for protraction of the half-life. The underlying data set consisted of 640 structural diverse insulin analogs, of which around half had attached small molecules. Other analogs were conjugated to peptides, amino acid extensions, or fragment crystallizable regions. The PK parameters clearance (CL), half-life (T1/2), and mean residence time (MRT) could be predicted by using classical machine-learning models such as Random Forest (RF) and Artificial Neural Networks (ANN) with root-mean-square errors of CL of 0.60 and 0.68 (log units) and average fold errors of 2.5 and 2.9 for RF and ANN, respectively. Both random and temporal data splittings were employed to evaluate ideal and prospective model performance with the best models, regardless of data splitting, achieving a minimum of 70% of predictions within a twofold error. The tested molecular representations include (1) global physiochemical descriptors combined with descriptors encoding the amino acid composition of the insulin analogs, (2) physiochemical descriptors of the attached small molecule, (3) protein language model (evolutionary scale modeling) embedding of the amino acid sequence of the molecules, and (4) a natural language processing inspired embedding (mol2vec) of the attached small molecule. Encoding the attached small molecule via (2) or (4) significantly improved the predictions, while the benefit of using the protein language model-based encoding (3) depended on the used machine-learning model. The most important molecular descriptors were identified as descriptors related to the molecular size of both the protein and protraction part using Shapley additive explanations values. Overall, the results show that combining representations of proteins and small molecules was key for PK predictions of insulin analogs.
1. Introduction
Optimizing pharmacokinetic (PK) properties of lead candidates is an important aspect of the multiobjective drug design challenge.1,2 Prediction models of PK parameters can accelerate the drug development process and potentially reduce the number of labor-intensive and costly in vivo experiments.3 While several published studies describe the PK prediction of small molecules,4−6 less is published for proteins or peptides.7 Strategies to protract the PK properties of protein therapeutics include conjugation to larger proteins, e.g., fragment crystallizable (Fc) region or lipidation, by attaching small molecules such as fatty acid side chains.8,9 Examples for the latter include long-acting insulin analogs such as degludec (Figure 1) or GLP-1 analogs such as semaglutide.10 The presence of conjugated proteins or added fatty acid side chains creates a practical challenge for machine-learning models as commonly used encoding mechanisms for biologics series are not applicable. For instance, sequence-based descriptors that encode the physical–chemical properties of amino acids on the residue level do not capture chemical modifications such as fatty acid acylations. In turn, global physical–chemical properties such as molecular weight and charge might not capture underlying sequential information from the amino acid residues.
Figure 1.
Examples of insulin analogs. Insulin Aspart (a) has a single substitution compared to human insulin in which proline is replaced with aspartate at position B28. Insulin Degludec (b) in which threonine is deleted at position B30 and 16-carbon fatty diacid is added via a glutamic acid linker. Insulin-0327 (c) has an arginine substitution at B29, removed threonine at B30, added lysine at A22, and a 20-carbon fatty acid added via a glutamic acid linker. Color red indicates amino acid residues which have been removed compared to human insulin (gray). Green refers to items added compared to human insulin. Solid lines represent disulfide bonds. See the Supporting Information (Tables S1 and S2) for descriptors and PK parameters for the analog-dosed iv in rat.
In the field of small molecules, machine learning provides a cardinal tool for various molecular property predictions,11 and several studies describe the prediction of PK parameters, using different encodings.4,5,12−14 Ye et al.5 used extended connectivity fingerprints (ECFPs) along with eight mainly physiochemical descriptors, while Wang et al.12 employed the Molecular Operating Environment (MOE) software15 for calculation of molecular representation. Wang et al.13 in turn used Morgan and Molecular ACCess System (MACCS)16 fingerprints, an embedding of Simplified Molecular-Input Line-Entry System (SMILES) as well as a molecular graph representation to predict PK-related properties such as aqueous solubility, lipophilicity, and membrane permeability.17
For biologics, such as proteins, encoding of the amino acid sequence,18 graph representation,19 and representation using protein-embeddings have been used to predict biological properties.20 Examples of PK-related end points include a deep-learning approach by Khurana et al.21 for sequence-based solubility classification of proteins using Convolutional Neural Networks (CNN). Additionally, fully connected layers were used to incorporate physiochemical and structural information from numeric molecular descriptors. A recent approach utilizes Graph Convolutional Networks to perform slightly better than other sequence-based models when classifying solubility of a protein.19 A large comparison between machine-learning and deep-learning models on experimentally observed properties of proteins, carried out by Xu et al.,22 suggested that sequence-based amino acid property-related descriptors modeled with a 1D-CNN is a suitable setup for protein design tasks. The effects of using different representations of molecules along with different machine-learning models have thus been widely investigated for both small-molecule drugs and proteins. However, to our knowledge, representing molecules as a combination of proteins and small molecules for downstream machine-learning modeling tasks is not described in the literature. In this work, molecular representations were investigated for proteins using a comprehensive PK data set from Novo Nordisk of a diverse set of insulin analogs. We combined knowledge from small-molecule literature and recent developments on protein–drug design and property prediction using machine learning to investigate the best representation methods for PK parameter prediction of therapeutic proteins.
2. Materials and Methods
2.1. Data
The PK data set in this analysis consists of 640 unique insulin analogs tested in rats by intravenous (iv) injection and the following PK parameters: Cl (clearance), T1/2 (elimination half-life), and MRT (mean residence time). The historical data originate from 16 different discovery projects at Novo Nordisk from 2008 to 2021 and consist of mutation variants in the insulin backbone and attached extensions via either fatty acid side chains (∼50%), peptides (∼25%), or fragment crystallizable (Fc) region attachment (∼10%) (Table 1).
Table 1. Insulin Analogs in Groups According to Protraction Modificationsa.
| backbone
mutationsb |
CL (min/mL/kg) | T1/2 (h) | MRT (h) | |||||
|---|---|---|---|---|---|---|---|---|
| group name | n | 0–1 | 2–3 | 4–5 | ≥6 | mean [SDc] | mean [SDc] | mean [SDc] |
| no attachments | 9 | 1 | 5 | 3 | 0 | 23.5 [6.51] | 0.41 [0.19] | 0.34 [0.14] |
| acylation | 338 | 20 | 182 | 107 | 29 | 0.43 [0.17] | 7.53 [0.89] | 9.10 [0.99] |
| peptide attachment | 154 | 9 | 29 | 62 | 54 | 0.26 [0.054] | 6.08 [0.63] | 7.37 [0.78] |
| amino acid extension | 35 | 30 | 1 | 0 | 4 | 2.7 [0.43] | 2.14 [0.35] | 1.04 [0.38] |
| Fc region attachments | 60 | 5 | 7 | 8 | 40 | 0.06 [0.011] | 47.7 [6.51] | 50.2 [6.26] |
| others | 44 | 23 | 9 | 8 | 4 | 7.8 [2.09] | 2.55 [0.61] | 2.12 [0.46] |
Mean and standard deviation (SD) of all three PK parameters, clearance (CL), half-life (T1/2), and mean residence time (MRT) are calculated for each of the insulin groups along with the number of backbone mutations.
Number of backbone mutations compared to human insulin.
Estimated standard deviations (SD) by the square-root of mean of variances.
Generally, insulin analogs with no attachments have a fast PK with short half-life (mean = 0.41 h), short MRT (mean = 0.34 h), and high Cl (23.5 min/mL/kg). All other groups provided modifications to the analog that protracted the PK resulting in longer half-life and MRT and lower Cl. This is especially pronounced for analogs with Fc region attachments to the insulin. The modifications to insulin provide a highly diverse data set in terms of molecular sequences as well as kinetics.
Figure 1 shows the structure of three insulin analogs that have different kinetics. Figure 1a illustrates insulin Aspart23 which belongs to the group of insulin analogs without any attachments (Table 1). This analog has a single amino acid substitution compared to human insulin. Two examples of analogs with a small-molecule protractor (acylation) are given in Figure 1b and Figure 1c with insulin Degludec24 and insulin-0327,25 respectively. These three insulin analogs, together with human insulin, have publicly available iv PK data in rat which is provided in the Supporting Information (Table S1) along with the molecular descriptors used in this analysis (Tables S1 and S2).
2.2. PK Parameters
The following three PK parameters were selected for investigation: clearance (CL) (mL/min/kg), elimination half-time (T1/2) (h), and mean residence time (MRT) (h) from iv studies in rat. All three PK parameters were (natural) log transformed and provided as mean estimates based on noncompartmental analysis (NCA) of individual animal concentration–time profiles applying WinNonlin (Certara, CA, U.S.). The calculation of the area under the plasma concentration–time curve extrapolated to infinity (AUC) was based on the “linear-up log-down”26 method, and uniform weighting was used for estimation of the terminal rate constant. MRT extrapolated to infinity was calculated as the area under the first moment curve (AUMC) extrapolated to infinity divided by the AUC. The PK parameters are highly correlated as in agreement with the general understanding of the three PK parameters and their relations.27 The observed correlations were 0.95 between MRT and T1/2, −0.93 between CL and MRT, and a correlation of −0.89 between CL and T1/2.
2.3. Molecular Representations and Encoding
The descriptors were divided into four descriptor space categories DS1–DS4, each describing either the amino acid backbone (DS1 and DS3) or attached fatty acid side chain (DS2 and DS4) components of the insulin analog (Table 2). DS1 and DS2 are molecular descriptors, encoding the physical–chemical properties of the backbone and fatty acid side chain, respectively, whereas DS3 and DS4 are learned embeddings based on the amino acid backbone or chemical nature of the respective molecule. DS1 contains 15 mainly physicochemical descriptors calculated on the molecule, including molecular descriptors such as size, charge, and hydrophobicity. DS2 consists of seven physicochemical descriptors calculated solely on the fatty acid side chain using the RDkit28 package in Python. An exhaustive list of all descriptors from DS1 and DS2 is provided in the Supporting Information (Tables S3 and S4). The extended-connectivity fingerprint with bond diameter 4 (EFCP4)29 was considered an alternative to descriptors in DS2 but with comparable performance (Figure S1); DS2 was favored due to more straightforward interpretation of physiochemical descriptors.
Table 2. Different Descriptor Spaces (DS) Used to Represent the 2D Structure of Insulin Analogsa,b.
| name | type of descriptors | examples | descriptor space dimension |
|---|---|---|---|
| DS1 | overall numeric molecular descriptors calculated from the entire sequence of the insulin analogs | size, charge, hydrophobicity | 15 |
| DS2 | physiochemical molecular descriptors of the fatty acid side chain (acylation group) | surface area, LogP, molecular weight | 7 |
| DS3 | NLP embedding approach ESM-1b,30 encoding the entire backbone sequence (insulin and attached amino acids/sequences) | GIVEQCCTSICSL | 1280 |
| DS4 | SMILES representation of the fatty acid side chain Mol2Vec31 used for embedding of SMILES | NC(C)C(=O)O | 100 |
Abbrevations: NLP, Natural Language Processing; ESM, Evolutionary Scale Modeling; SMILES, Simplified Molecular-Input Line-Entry System.
For more details on descriptors, see Supporting Information Table S3, Table S4, and Figure S3.
DS3 utilizes the ESM-1b30 to encode from the sequence backbone, using an embedding length of 1280. For this, the sequence part of the insulin analog and attachments such as peptide and antibody moieties are concatenated to one sequence. Residue-based encoding such as one-hot and z-scales was also considered but did not provide better performance (Figure S2). DS4 encoded the fatty side chain utilizing a natural language processing approach called mol2vec,31 originally developed for small molecules. Here, the SMILES representation of the fatty acid side chain is encoded using mol2vec and an embedding length of 100. For examples of DS3 and DS4 encodings, see the Supporting Information (Figure S3).
All possible combinations of the molecular representations DS1–DS4 (15 in total) were investigated. Below, e.g., DS1234 is used as a notation for the ML model utilizing representations from all sources, i.e., DS1, DS2, DS3, and DS4.
2.4. Models
Two different machine-learning models were explored to predict PK parameters: Random Forest (RF)32 and Artificial Neural Network (ANN).33
2.4.1. Random Forest (RF)
RF is an ensemble of decision trees using a selected number of randomly sampled variables in each decision split. A total of 200 decision trees were trained on subsamples of data using bootstrapping, and the outputs were averaged to fit into a regression task. The number of features (maxf) in each split and the minimum number of observations in a leaf node (minleaf) were considered hyperparameters and tuned by evaluating all combinations of a prespecified search space provided in the Supporting Information (Table S5). To include information from amino acid sequences (DS3) and SMILES representations (DS4) in RF, a principal component analysis (PCA) was performed on the embedding space, and the top 20 principal components for each type of descriptor were included as features. The effects of using PCA on the embeddings are considered in the Supporting Information (Figure S4), indicating that the RF model performance benefited from the PCA reduction.
2.4.2. Artificial Neural Network (ANN)
Fully connected layers were used for the numerical descriptors DS1 and DS2, while one-dimensional convolutional neural networks (1D-CNN) were used for the sequential amino acid and SMILES representations with two CNN layers (DS3 and DS4). The number of fully connected layers (Fc) to model the numerical molecular descriptors was determined in the hyperparameter search allowing for one or two fully connected layers. The models were trained using the Adam optimizer with L2 regularization on the loss function. All ANN models were trained with a max epoch of 200 with early stopping. Batch-normalization, dropout, and ReLU activation34 were used between all layers excluding the final output layer. The output layer size was set to three, one for each of the PK parameters. The information from the CNN filters was converted to numeric format using a fully connected layer before being parsed to the output layer. Dropout, L2 regularization, batch size, learning rate, and the sizes of the fully connected hidden layers were considered hyperparameters and tuned using the optuna implementation of the Tree-Structured Parzen Estimator (TPE)35 for 30 iterations. Due to the large embedding size of ESM-1b, max-pooling was applied between CNN layers of DS3 with a kernel size equal to the kernel filter size. When molecular descriptors contained both a numeric and a sequential representation, e.g., DS13, the fully connected layers from the different representations were concatenated before the output layer. A table of the optimal hyperparameters and the search space can be found in Table S5 (Supporting Information).
2.5. Model Evaluation
Model evaluation and selection were performed in a nested cross-validation (CV) setup with five folds with random splits. Thus, the five test sets contain 128 analogs each, and the remaining 512 analogs are used for training/validation in each fold. The data splits were identical for RF and ANN to ensure model evaluation on the exact same data. Once the optimal hyperparameter setting for each fold was found, the model was retrained on the entire training/validation data set and evaluated on the test set for that fold. The root-mean-square error (RMSE) was used to evaluate the model performance on the five test sets as well as model selection during the hyperparameter search and is defined as
| 1 |
where N is the number of
insulin analogs,  is the ith (log) prediction,
and yi is the ith (log) measured PK value.
is the ith (log) prediction,
and yi is the ith (log) measured PK value.
Fold error (FE) and average fold error (AFE) are calculated with
where 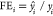 if
if 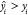 and
and 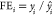 if
if 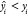 .
.
Additionally, the modeling was carried out with temporal data splits to evaluate the prospective modeling performance.36 In this way, the model was trained on data acquired before a specific date and tested solely on data after that date. The temporal data splits can be seen in the Supporting Information (Figure S5). An overview of the full process from molecular representation to modeling and evaluation can be seen in Figure 2.
Figure 2.

Overview of the modeling flow for PK parameter prediction. The insulin analogs were represented using four different descriptor spaces, scaled and fed to the machine-learning models Random Forest (RF) and Artificial Neural Network (ANN). Evaluation was done using fivefold nested cross-validation.
2.5.1. Extraction of Feature Importance via Shapley Additive Explanations
SHapley Additive exPlanations (SHAP) values were used to identify the most important features for the PK parameter predictions.37 The method provides explanations for contributions of the descriptors as well as the contribution of each observation on all three PK parameters. For ANN, the DeepExplainer37 was used to approximate the conditional expectations of SHAP whereas the Tree Shap implementation38 was used for Random Forest. SHAP values were calculated by retraining the model on the full data set and evaluating SHAP values for all data. The hyperparameters for this model were set to the median of the best hyperparameters learned from the nested cross-validation procedure; see Table S5 (Supporting Information) for exact hyperparameters. Because we combined many molecular descriptors from different sources, correlation between some of the descriptors was inevitable. Evaluation of SHAP values for correlated features is an active research field39,40 with no ”golden standard” framework. In this work, we grouped highly correlated descriptors and summed up the SHAP values within those groups as suggested by the main author of SHAP.41 Correlation structures for the numeric descriptors DS12 as well as the full descriptor space DS1234 can be seen in the Supporting Information (Figures S6 and S7).
2.5.2. Evaluation Using Paired t Test
For comparison of model performance, we employ a paired t test on RMSE values of the outer test sets from the nested CV procedure. This approach assumes independent test scores, which is well-known not to be completely true when using cross-validation.42 The effects of different evaluation methods are investigated in Dietterich et al. (1998),43 and it is found that paired t tests on the same data folds are feasible but slightly optimistic in finding a difference between models. The p-values were subject to Benjamini–Hochberg (BH) correction for multiple testing44 with a false discovery rate of 5%.
2.5.3. Mean Predictor Model and Experimental Error
The model RMSE values were compared to experimental error (highest achievable model performance) and a simple mean predictor model using the mean of training data as predictions on the test set (lowest model performance). Each PK observation is a mean value of repeated experiments of the same analog in different rats. Using the standard deviations associated with each PK observation, we can calculate the variance in log space.45
where f is the natural logarithm function, y is the PK observation, and σy is the standard deviation of each PK observation. Taking the mean of the variances and subsequent square root yields the mean standard deviation in log space which we denote “experimental error”. A 95% confidence interval is also provided assuming normality of the standard deviations around the mean estimate.
3. Results
PK parameters (Cl, T1/2, and MRT) measured in rats could be predicted by machine-learning models based on molecular representations of insulin analogs all with RMSE in the 0.5–1 range with both random and temporal data splits (Figure 3). The two data-splitting strategies overall gave comparable results with a slight increase in median and variance of the test set RMSE values for temporal data splits. The lowest median RMSE for the five test folds is found using DS124 (RF) and DS1234 (ANN) for both random and temporal splits. Due to highly correlated PK parameters, the following results highlight only clearance (CL) while results for T1/2 and MRT can be seen in the Supporting Information.
Figure 3.
Model performance on clearance (CL) measured as root-mean-square error (RMSE) on test sets on all combinations of descriptors using both Random Forest (RF) and Artificial Neural Network (ANN). Random data splits are seen in (a) and temporal splits in (b). Standard deviation of CL observations was used to define a region of experimental error while a mean predictor model defines the lowest model performance threshold. Zoomed in areas (black box) of the best performing models can be seen as the bottom two figures. For descriptor space categories, see Table 2.
Predicting PK using only molecular descriptors from DS1 gave a solid baseline performance that outperformed all other combinations of representations that did not include DS1. Figure 3 shows a boxplot of the outer test scores from the cross-validation procedure for CL for all combinations of molecular representations for both RF and ANN models. See the Supporting Information (Figures S8 and S9) for T1/2 and MRT, respectively. The region of experimental error, measured in log RMSE, was between 0 and 0.29 for CL, between 0 and 0.38 for T1/2, and between 0 and 0.24 for MRT. The mean predictor model gave a median log RMSE of 1.38 for CL, 1.44 for T1/2, and 1.42 for MRT using random data splits. The equivalent mean predictor model performances for temporal splits were 1.44 for CL, 1.48 for T1/2, and 1.45 for MRT. Clearly, using representations exclusively from the backbone amino acid sequence (DS3) or protractor (DS2 or DS4) exhibited inferior performance for both the RF and ANN. For this reason, Figure 3 also shows a zoomed in area of the selected groups of descriptor sets that provided the lowest test errors (all including DS1).
Prediction accuracy measured in fold-error is provided in Table 3 for the best performing descriptor sets DS124 and DS1234 for RF and ANN, respectively. The percentage distribution of fold errors between RF and ANN is similar across although the average fold error for RF, ranging from 1.9 to 3.3 depending on PK parameter and splitting strategy, is lower compared to the 2.2–3.5 for ANN. Model performance was seen to drop for temporal data splits compared to random splits but still has a minimum 70% of data points predicted within twofold error.
Table 3. Prediction Accuracy for Random Forest (DS124) and ANN (DS1234) Models for Both Random and Temporal Data Splits for All Three PK Parameters.
| model | parameter | average fold error | within twofold error (%) | within threefold error (%) | within fivefold error (%) |
|---|---|---|---|---|---|
| random splits | |||||
| RF(DS124) | CL | 2.5 | 84 | 91 | 95 |
| T1/2 | 1.9 | 90 | 95 | 97 | |
| MRT | 1.9 | 90 | 95 | 97 | |
| ANN(DS1234) | CL | 2.9 | 83 | 90 | 93 |
| T1/2 | 2.2 | 86 | 92 | 95 | |
| MRT | 2.2 | 86 | 92 | 95 | |
| temporal splits | |||||
| RF(DS124) | CL | 3.3 | 70 | 84 | 92 |
| T1/2 | 2.5 | 79 | 90 | 96 | |
| MRT | 2.5 | 82 | 89 | 95 | |
| ANN(DS1234) | CL | 3.5 | 70 | 80 | 88 |
| T1/2 | 2.6 | 73 | 84 | 90 | |
| MRT | 2.6 | 74 | 84 | 91 |
The model performances between descriptor sets for random and temporal splitting are similar, Therefore, the following results focus only on random splitting.
3.1. Comparison between Models
We compared the performance of the two different models for each descriptor set. In the following, we only consider the seven descriptor sets which include DS1 as these are clearly seen to be the most interesting molecular representation combinations (Figure 3a). Generally, RF and ANN performed on par with only DS13 being significantly different (p-value = 0.03). The other descriptor sets had no significant difference in performance between RF and ANN, all with p-values above 0.07. The lowest median test RMSE score was found for DS124 for RF and DS1234 for ANN.
3.2. Comparison of Descriptor Sets
The performance difference was pronounced depending on the choice of molecular representation. Figure 4 shows all p-values from paired t test for both RF (upper triangle) and ANN (lower triangle) where black boxes highlight the significant p-values after Benjamini–Hochberg correction.
Figure 4.

P-values from paired t test between descriptor sets. Results from Random Forest (RF) models in the upper triangle (blue color scale) and results from Artificial Neural Network (ANN) models in the lower triangle (red color scale). Black boxes indicate a significant p-value after Benjamini–Hochberg (BH) correction.
For ANN, Figure 4 shows that DS124 and DS1234 both performed significantly better than DS1 and DS12 only (p-value = 0.018 and 0.0098, respectively). This indicates that the model benefited from encodings of both DS3 and DS4 compared to purely numeric descriptors in DS12. However, no significant difference between DS1234 and the other well performing descriptor sets was observed after BH correction for multiple testing: DS124 (p-value = 0.12) and DS14 (p-value = 0.05). For RF models, only DS124 with the lowest median test score was significantly better than baseline DS1 (p-value = 0.011). However, no significant difference between DS124 and models with similar median test scores was observed: DS1234 (p-value = 0.11), DS12 (p-value = 0.12), DS134 (p-value = 0.23), and DS14 (p-value = 0.21). The hyperparameters for ANN using DS1234 and RF using DS124 can be seen in Table S5 (Supporting Information). The gain in performance on test sets for these two models compared to DS1 is visualized as observed/predicted scatter plot on PK parameter clearance in Figure 5. Here, it is seen how the mean RMSE of the five test sets drops substantially from 0.9 to 0.68 for ANN and from 0.74 to 0.60 for RF. The four insulin analogs with publicly available rat iv data are highlighted in Figure 5 and show better prediction error for all compounds except insulin-0327 for RF and insulin Degludec for ANN when compared to baseline DS1. Figures for PK parameters T1/2 and MRT can be seen in Figures S10 and S11 (Supporting Information).
Figure 5.
Observed against predicted data from all test sets during nested cross-validation for the PK parameter clearance. Red dashed line for twofold error in log space. Comparison of baseline descriptor set (left) versus optimal descriptor set (right) for both RF (top row) and ANN (bottom row). The four insulin analogs with publicly available rat iv PK data are highlighted by color/symbol (see Supporting Information Tables S1 and S2 for descriptors and rat PK data). Figures for half-life and mean resident time can be seen in the Supporting Information (Figures S9 and S10).
3.3. Model Performance on Individual Insulin Groups
Random Forest models on descriptor DS124 were also trained on the individual groups from Table 1 and compared to the RF models trained on all data. The models were evaluated on data from the individual groups, and the results can be seen in Table 4.
Table 4. Mean of the Five Test RMSE from Nested Cross-Validation Procedure for RF-DS124 on Each PK Parameter, Clearance (CL), Half-life (T1/2), and Mean Residence Time (MRT)a.
| CL |
T1/2 |
MRT |
|||||
|---|---|---|---|---|---|---|---|
| group | n | all data | only group | all data | only group | all data | only group |
| acylation | 338 | 0.48 | 0.50 | 0.45 | 0.45 | 0.46 | 0.47 |
| peptide attachments | 154 | 0.57 | 0.52 | 0.34 | 0.32 | 0.42 | 0.34 |
| amino acid extensions | 35 | 0.55 | 0.51 | 0.69 | 0.65 | 0.56 | 0.52 |
| Fc region attachments | 60 | 0.53 | 0.50 | 0.41 | 0.36 | 0.50 | 0.50 |
| other | 44 | 1.09 | 1.38 | 0.70 | 0.90 | 0.71 | 0.88 |
| all groups | 640 | 0.59 | 0.48 | 0.49 | |||
The model was trained on all data (all data) as well as purely on the individual group (only group) and evaluated on data from the individual groups in both cases. For fair comparison, the test sets in the “only group” evaluation were a subset of the test sets in the ”all data” evaluation. Group ”no attachments” was not included due to the very low number of observations (n = 9). For results on ANN-DS1234, see the Supporting Information (Table S6).
Acylation, amino acid extension, and Fc region attachment groups all showed similar performance for training on all data versus training only on the specific group whereas a small decrease was seen the peptide attachment group when trained on this group only. Group “other” clearly benefited from training on all data compared to training on this group only with an improvement of RMSE of 0.29, 0.20, and 0.17 for the PK parameters CL, T1/2, and MRT, respectively. Similar results were observed for the ANN model on DS1234 (Supporting Information Table S6).
3.4. Molecular Features for PK Predictions
Having established RF with DS124 and ANN with DS1234 as the two best performing models, we proceed to investigate the individual molecular descriptor contributions to the PK parameter predictions by calculating SHAP values.
With highly correlated PK parameters, it was expected that many of the important molecular descriptors were the same across the PK parameters. Therefore, the SHAP values for clearance (CL) are shown in Figure 6, and those for T1/2 and MRT are shown in the Supporting Information (Figures S12 and S13). Generally, for both models, descriptors related to the molecular size of both the backbone as well as the attached fatty acid are among the top SHAP features. It was seen that large insulin analogs, with large fatty acids attached, provided a lower clearance. The average molecular weight for insulin with fatty acid attachments was 6329 g/mol and 16 315 g/mol for peptide attachment analogs, and Fc-attached analogs had an average weight of 59 473 g/mol. Thus, the data set clearly reflected a wide range of conjugations that sought to minimize clearance with the increased size of both the backbone and the small-molecule attachments being the most influential descriptors. SHAP dependence plots in Figure 6c, 6d, and 6e shows SHAP values for selected descriptors against the descriptor values for the RF model on descriptor set DS124. Results for human insulin and insulin Aspart are left out of Figure 6e, DS2_mollogp, as these analogs do not have protractors. It is seen from Figure 6d, DS2_num, that analogs without attachments generally have higher clearance, while it is evident from Figure 6c and 6e that low negative charge of backbone amino acids and high lipophilicity of the protractor result in lower clearance.
Figure 6.
Top 10 SHAP values for clearance (CL) on the best performing model for both Random Forest using DS124 (a) and Neural Network using DS1234 (b). Each point is an observation placed on the x-axis according to SHAP value. Colors indicate magnitude of the original feature value with dark colors for low feature values and light colors for high feature values. Correlated features are grouped together, and the SHAP values are summed. Further details on the descriptors can be found in the Supporting Information (Tables S3 and S4). Parts (c), (d), and (e) present SHAP dependence plots to interpret selected important descriptors for CL prediction using RF on DS124. Four insulin analogs with publicly available rat iv PK data are given in color and symbol.
4. Discussion
4.1. Model Extrapolation
Given the standard random-splitting strategy described in the Materials and Methods section, the developed models were not supposed to make predictions for very different types of proteins but rather to predict on new variants within the explored chemical space. Temporal data splits are known to better reflect true prospective model performance.36 Therefore, temporal data splits were calculated to create a more challenging modeling setup and to ensure the proposed models and descriptors to be practically applicable in drug discovery. From Figure 3 it is seen that the RMSE remained between 0.5 and 1 log units for temporal splits, and DS124 and DS1234 still had the lowest median RMSE test score for RF and ANN, respectively. As expected, a small decrease in performance for all combinations of molecular descriptors was observed for the temporal data split compared to random. This indicates that predicting outside of a known chemical space is a difficult problem, and it is likely that larger data sets as well as methods that handle distribution shifts better are required to achieve models that, ideally, extrapolate to new compounds. Although numerous such high-quality public PK data sets exist for small molecules,3 only a few exists for protein/peptides,46,47 while no public data sets incorporate in vivo PK parameters for proteins with chemical modifications as presented in this analysis.
For the best RF model, an average fold error of 2.5 for CL predictions is comparable to Physiologically Based Pharmacokinetic (PBPK) modeling and allometric scaling on small molecules along with 84% of predictions within twofold, which is also considered reasonable performance in PBPK literature.48,49Figure 5 shows good performance (R2 = 0.82) of clearance predictions although the models underpredict high-clearance analogs. Such analogs are underrepresented in the data set, as seen from Table 1, and a part of these belong to the “other group” which is the most diverse of the insulin analog groups. Furthermore, high-clearance analogs, with half-life values of a few minutes, are generally more difficult to measure accurately. From small-molecule clearance predictions, better RMSE values on test sets have been obtained12 (with bias on low CL observations), and Figure 3a suggests that further improvements could be expected given the margin from the best models (RMSE around 0.5–0.6) to the experimental error range. However, with reasonable model performance even on a diverse data set of insulin analogs, we are confident that the presented model and descriptors carry practical value for the drug design processes.
Additional experiments were carried out by training the models on individual groups from Table 1 rather than the entire data set as seen throughout this analysis (Table 4). Training on all groups provided on par performance compared to training on the insulin groups “acylation”, “amino acid extensions”, and ”Fc-region attachments”. The ”other” group represented a diverse set of insulin analogs conjugated to, e.g., poly(ethylene glycol) (PEG) or complex carbohydrates or small-molecule albumin binders. RMSE for this group was lower when training on all data compared to the individual group, thus indicating that prediction on such a diverse group of insulin analogs benefited from information in the full data set. In order to reassure that the proposed machine-learning models learned from the sequential information, we compared RF and ANN with a K-Nearest-Neighbor (KNN) model only on the backbone embedding space (DS3). This resulted in inferior performance compared to ANN and RF on DS3 (Figure S14) as well as on the best performing descriptor sets (Figure S15), thereby indicating that the proposed methods learned information beyond sequence similarity.
4.2. Best Molecular Representations for Each Machine-Learning Model
In our study, the best Random Forest and the best ANN model did not show significantly different model performance, which is in agreement with previous PK studies for small-molecules drugs.4Figure 3a shows that PK parameter prediction on highly diverse protein data sets requires comprehensive combinations of information from different sources. Combining information from all four sources (DS1234) produced the lowest test RMSE error using the neural network approach. On the other hand, Random Forest performed the best when excluding information from the backbone amino acid embedding (DS124). We hypothesize that this could be due to the large embedding space produced by ESM-1b not being able to remain meaningful in a much smaller, PCA reduced, space. For ANN, the sequential nature of 1D-CNN was able to utilize the information from the backbone amino acid embedding and left DS1234 as the representation with the lowest median RMSE test score. Thus, regardless of modeling choice, a good generalization to unseen insulin analogs was best achieved with a comprehensive set of molecular descriptors combining both protein and small-molecule descriptors. Modeling performance using a baseline descriptor set, DS1, was compared to EFCP4 descriptors from the domain of small molecules. Results are summarized in Figure S16 where modeling performance using DS1 is shown to perform on par with ECFP4 descriptors. This reassures DS1 as a valid baseline descriptor set while being more interpretable for proteins compared to atomic-based descriptors such as ECFP4.
4.3. Practical Implications of Feature Importance
The feature importance analyses based on SHAP values revealed that molecular size related features like molecular weight of both the protein part and the small-molecule/protractor part together with lipophobicity features such as polar surface area (tPSA) and (mollogp) for the fatty acid were important for clearance predictions in both the Random Forest and Artificial Neural Network models. Larger protein part and longer fatty acid result in lower clearance and longer T1/2 and MRT. The results go well with the general understanding of insulin receptor affinity and PK for insulin analogs.50,51 For design directions, feature importance, such as, e.g., SHAP analysis, can be applied to identify which feature(s) are important for the predictions. The model trained on all data can be used to investigate feature importance as a general guidance; e.g., less negative charge for the amino acids in the insulin backbone or more lipophobicity in the protractor leads to lower CL, as presented in Figure 6. Thus, knowledge on feature importance can be used to design mutations and protractors for new analogs. The partial dependence plots in Figure 6c, d, and e are examples of the dependence between clearance response and a set of input features of interest, marginalizing over the values of all other input features (the “complement” features). Intuitively, we can interpret the partial dependence as the expected clearance response as a function of the input features of interest, and such plots can be used for design guidance for chemists. For example, for a new insulin analog where we use the presented model, we can see what features that are main contributors for changing of clearance (e.g., the lipophilicity and number of protractors), and then we can focus on those features and design the next molecules accordingly to further improve their PK properties.
4.4. Protraction Mechanisms for Insulin Analogs
Three main protraction mechanisms have been applied for the insulin analogs in the present data set: acylation or lipidation,8,52 covalent conjugation of proteins, peptides, or repeats of selected polar amino acids,53,54 and conjugation/fusion to long-lived macromolecules like fragment crystallizable (Fc) regions.55,56 Especially the insulin analogs with Fc attachments had high molecular weight (mean 60 000 g/mol; almost 10 times higher than for the acylated insulin analogs), and the increased size leads to reduced renal clearance and increased half-life by cellular recycling via the Fc receptor; this group had the lowest mean clearance (Table 1). More than half of the analogs in the data set had fatty acid protractors, and fatty acids are widely used to prolong the half-life for therapeutic peptides and protein;8 e.g., the acylated insulin analog for once weekly dosing, Icodec, has a C20 diacyl acid protractor together with three backbone mutations, and for this analog a half-life of 196 h is observed in humans.51 Important features from the fatty acid side chain were in addition to size, lipophobicity and confirming the general understanding that longer fatty acid protractor results in lower clearance and longer half-life. For example, changing from a C16 to C20 fatty acid on the same insulin backbone results in decreased receptor affinity and increased iv half-life in rat from 1.3 to 12 h50 compared to ca. 15 min iv half-life for human insulin in rat57 (Supporting Information, Table S1). Insulin is known to have receptor-mediated clearance,58 and for most analogs there will therefore be high correlation between in vitro insulin receptor affinity and in vivo clearance. For receptor affinity, solvent-exposed residues, B12, B13, and B16, of the insulin B-chain alfa helix were the positions most affected by substitutions.59 Applying the ESM-1b embedding does not allow an exact mapping between position in embedding space and amino acid residues in the insulin backbone.30 ESM-1b embedding was employed due to the alignment-free nature60 and because the approach showed no significant difference in performance compared to One-Hot-Encoding (OHE) and Z-scale encoding (Supporting Information, Figure S2). However, for a better understanding of the effects of mutations in exact locations such as before-mentioned B-chain residues, one would have to use other embeddings, e.g., sequence alignment followed by OHE.
4.5. Future Work
Receptor-mediated clearance for insulin analogs61 makes it natural to describe the clearance and related PK parameters through the molecular structure as shown in this analysis. It would therefore be interesting to explore the ability of the molecular descriptors from this study to generalize to other therapeutic proteins which have a different clearance mechanism. Furthermore, generalization to proteins attached with small molecules other than fatty acid side chains would be of great interest. Insulin receptor affinity in vitro data is expected to be of key importance for in vivo PK prediction of the receptor-mediated clearance for insulin analogs. To investigate a combination of in silico features and in vitro receptor affinity data for improvement of the here-presented PK prediction models is therefore an obvious next step.
5. Conclusion
Molecular representations of insulin analogs with small-molecule attachments have been investigated for the purpose of predicting iv PK parameters in rats. Descriptors contained classical physiochemical molecular descriptors as well as embeddings of amino acid and SMILES sequences. This resulted in four different data sources for each insulin analog that together provided a comprehensive molecular representation for therapeutic proteins with different protraction schemes. In order to evaluate the importance of each descriptor component, all combinations of descriptor sets were compared using both Random Forest and neural networks on PK parameter predictions. This study shows that, by including information from multiple sources of the molecule, we were able to obtain significantly better performance compared to standard physiochemical molecular descriptors. Fold errors highlighted that the best models achieved 83–90% and 70–82% of predictions within twofold error for random and temporal data splits, respectively. We found that including a mol2vec embedding of the SMILES representation of the fatty acid side chain enhanced model prediction performance of the Random Forest model. For neural networks, a 1D-CNN on both an ESM-1b embedding of amino acid sequence as well as the mol2vec embedding of SMILES representation of the attached small molecules provided significantly better prediction performances compared to the standard numeric protein descriptors. From a drug design perspective, the longest half-life protraction and lowest clearance of the mechanisms in the present data set are achieved by attaching the large fragment crystallization (Fc) region. For the acylation protraction group, large and multiple fatty acid attachments with high lipophobicity provide the longest half-life. Overall, we highlight the importance of the representation of therapeutic proteins when employing machine-learning-based PK parameter prediction.
Acknowledgments
This work was supported by Innovation Fund Denmark grant 0153-00027B. O.W.’s work was funded in part by the Novo Nordisk Foundation through the Center for Basic Machine Learning Research in Life Science (NNF20OC0062606). We are thankful for the skilled performance of rat iv studies and bioanalysis from Novo Nordisk colleagues in pharmacology and research bioanalysis departments.
Data Availability Statement
2D structure and PK data on the four insulin analogs with publicly available iv data in rat are available on Github along with the code.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c01218.
Details of molecular descriptors for DS1 and DS2; hyperparameters for the best models; correlation structure for the full data set; feature importance analysis for the best models using SHAP; and table of publicly available insulin analogs with iv rat PK data (PDF)
The authors declare the following competing financial interest(s): KAE, KMB, KI, MT, NRK, SF & HHFR are all employees and minor stockholders at Novo Nordisk A/S. Only a very small number of therapeutic proteins with small-molecule attachments has publicly available in vivo PK data. The manuscript is therefore based on Novo Nordisk A/S proprietary data.
Supplementary Material
References
- Chen H.; Engkvist O.; Wang Y.; Olivecrona M.; Blaschke T. The rise of deep learning in drug discovery. Drug Discovery Today 2018, 23, 1241–1250. 10.1016/j.drudis.2018.01.039. [DOI] [PubMed] [Google Scholar]
- Lipinski C. F.; Maltarollo V. G.; Oliveira P. R.; da Silva A. B. F.; Honorio K. M. Advances and Perspectives in Applying Deep Learning for Drug Design and Discovery. Front. Robot. AI 2019, 6, 00108. 10.3389/frobt.2019.00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danishuddin; Kumar V.; Faheem M.; Woo Lee K. A decade of machine learning-based predictive models for human pharmacokinetics: Advances and challenges. Drug Discovery Today 2022, 27, 529–537. 10.1016/j.drudis.2021.09.013. [DOI] [PubMed] [Google Scholar]
- Schneckener S.; Grimbs S.; Hey J.; Menz S.; Osmers M.; Schaper S.; Hillisch A.; Göller A. H. Prediction of Oral Bioavailability in Rats: Transferring Insights from in Vitro Correlations to (Deep) Machine Learning Models Using in Silico Model Outputs and Chemical Structure Parameters. Journal of Chemical Information and Modeling 2019, 59, 4893–4905. 10.1021/acs.jcim.9b00460. [DOI] [PubMed] [Google Scholar]
- Ye Z.; Yang Y.; Li X.; Cao D.; Ouyang D. An Integrated Transfer Learning and Multitask Learning Approach for Pharmacokinetic Parameter Prediction. Mol. Pharmaceutics 2019, 16, 533–541. 10.1021/acs.molpharmaceut.8b00816. [DOI] [PubMed] [Google Scholar]
- Kosugi Y.; Hosea N. Prediction of oral pharmacokinetics using a combination of in silico descriptors and in vitro ADME properties. Molecular Pharmaceutics 2021, 18, 1071–1079. 10.1021/acs.molpharmaceut.0c01009. [DOI] [PubMed] [Google Scholar]
- Grinshpun B.; Thorsteinson N.; Pereira J. N.; Rippmann F.; Nannemann D.; Sood V. D.; Fomekong Nanfack Y. Identifying biophysical assays and in silico properties that enrich for slow clearance in clinical-stage therapeutic antibodies. MAbs 2021, 13, 1932230. 10.1080/19420862.2021.1932230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtzhals P.; Østergaard S.; Nishimura E.; Kjeldsen T. Derivatization with fatty acids in peptide and protein drug discovery. Nat. Rev. Drug Discov. 2023, 22, 59. 10.1038/s41573-022-00529-w. [DOI] [PubMed] [Google Scholar]
- Muttenthaler M.; King G. F.; Adams D. J.; Alewood P. F. Trends in peptide drug discovery. Nature reviews Drug discovery 2021, 20, 309–325. 10.1038/s41573-020-00135-8. [DOI] [PubMed] [Google Scholar]
- Lau J.; Bloch P.; Schaffer L.; Pettersson I.; Spetzler J.; Kofoed J.; Madsen K.; Knudsen L. B.; McGuire J.; Steensgaard D. B.; et al. Discovery of the once-weekly glucagon-like peptide-1 (GLP-1) analogue semaglutide. Journal of medicinal chemistry 2015, 58, 7370–7380. 10.1021/acs.jmedchem.5b00726. [DOI] [PubMed] [Google Scholar]
- Brown N.; Ertl P.; Lewis R.; Luksch T.; Reker D.; Schneider N. Artificial intelligence in chemistry and drug design. Journal of Computer-aided Molecular Design 2020, 34, 709–715. 10.1007/s10822-020-00317-x. [DOI] [PubMed] [Google Scholar]
- Wang Y.; Liu H.; Fan Y.; Chen X.; Yang Y.; Zhu L.; Zhao J.; Chen Y.; Zhang Y. Silico Prediction of Human Intravenous Pharmacokinetic Parameters with Improved Accuracy. Journal of Chemical Information and Modeling 2019, 59, 3968–3980. 10.1021/acs.jcim.9b00300. [DOI] [PubMed] [Google Scholar]
- Wang X.; Liu M.; Zhang L.; Wang Y.; Li Y.; Lu T. Optimizing Pharmacokinetic Property Prediction Based on Integrated Datasets and a Deep Learning Approach. Journal of Chemical Information and Modeling 2020, 60, 4603–4613. 10.1021/acs.jcim.0c00568. [DOI] [PubMed] [Google Scholar]
- Miljković F.; Martinsson A.; Obrezanova O.; Williamson B.; Johnson M.; Sykes A.; Bender A.; Greene N. Machine Learning Models for Human in Vivo Pharmacokinetic Parameters with In-House Validation. Molecular Pharmaceutics 2021, 18, 4520–4530. 10.1021/acs.molpharmaceut.1c00718. [DOI] [PubMed] [Google Scholar]
- Vilar S.; Cozza G.; Moro S. Medicinal chemistry and the molecular operating environment (MOE): application of QSAR and molecular docking to drug discovery. Current topics in medicinal chemistry 2008, 8, 1555–1572. 10.2174/156802608786786624. [DOI] [PubMed] [Google Scholar]
- Durant J. L.; Leland B. A.; Henry D. R.; Nourse J. G. Reoptimization of MDL keys for use in drug discovery. Journal of chemical information and computer sciences 2002, 42, 1273–1280. 10.1021/ci010132r. [DOI] [PubMed] [Google Scholar]
- Kearnes S.; McCloskey K.; Berndl M.; Pande V.; Riley P. Molecular graph convolutions: moving beyond fingerprints. Journal of computer-aided molecular design 2016, 30, 595–608. 10.1007/s10822-016-9938-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elabd H.; Bromberg Y.; Hoarfrost A.; Lenz T.; Franke A.; Wendorff M. Amino acid encoding for deep learning applications. Bmc Bioinformatics 2020, 21, 235. 10.1186/s12859-020-03546-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.; Zheng S.; Zhao H.; Yang Y. Structure-aware protein solubility prediction from sequence through graph convolutional network and predicted contact map. J. Cheminform. 2021, 13, 7. 10.1186/s13321-021-00488-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang K. K.; Wu Z.; Bedbrook C. N.; Arnold F. H. Learned protein embeddings for machine learning. Bioinformatics 2018, 34, 2642–2648. 10.1093/bioinformatics/bty178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khurana S.; Rawi R.; Kunji K.; Chuang G.-Y.; Bensmail H.; Mall R. DeepSol: a deep learning framework for sequence-based protein solubility prediction. Bioinformatics 2018, 34, 2605–2613. 10.1093/bioinformatics/bty166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y.; Verma D.; Sheridan R. P.; Liaw A.; Ma J.; Marshall N. M.; McIntosh J.; Sherer E. C.; Svetnik V.; Johnston J. M. Deep Dive into Machine Learning Models for Protein Engineering. Journal of Chemical Information and Modeling 2020, 60, 2773–2790. 10.1021/acs.jcim.0c00073. [DOI] [PubMed] [Google Scholar]
- Mudaliar S. R.; Lindberg F. A.; Joyce M.; Beerdsen P.; Strange P.; Lin A.; Henry R. R. Insulin aspart (B28 asp-insulin): a fast-acting analog of human insulin: absorption kinetics and action profile compared with regular human insulin in healthy nondiabetic subjects. Diabetes care 1999, 22, 1501–1506. 10.2337/diacare.22.9.1501. [DOI] [PubMed] [Google Scholar]
- Tambascia M. A.; Eliaschewitz F. G. Degludec: The new ultra-long insulin analogue. Diabetol. Metab Syndr. 2015, 7, 57. 10.1186/s13098-015-0037-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgerton D. S.; Scott M.; Farmer B.; Williams P. E.; Madsen P.; Kjeldsen T.; Brand C. L.; Fledelius C.; Nishimura E.; Cherrington A. D. Targeting insulin to the liver corrects defects in glucose metabolism caused by peripheral insulin delivery. JCI insight 2019, 4, e126974. 10.1172/jci.insight.126974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowland M.; Tozer T. N.. Clinical pharmacokinetics/pharmacodynamics; Lippincott Williams and Wilkins: Philadelphia, PA, 2005. [Google Scholar]
- Reisfeld B.; Mayeno A. N. In Computational Toxicology; Reisfeld B., Mayeno A. N., Eds.; Humana Press: Totowa, NJ, 2012; Vol. I, pp 377–391. [Google Scholar]
- Landrum G.; et al. Rdkit: Open-source cheminformatics software; 2016.
- Rogers D.; Hahn M. Extended-connectivity fingerprints. Journal of chemical information and modeling 2010, 50, 742–754. 10.1021/ci100050t. [DOI] [PubMed] [Google Scholar]
- Rives A.; Meier J.; Sercu T.; Goyal S.; Lin Z.; Liu J.; Guo D.; Ott M.; Zitnick C. L.; Ma J.; et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. U.S.A. 2021, 118, 118. 10.1073/pnas.2016239118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeger S.; Fulle S.; Turk S. Mol2vec: Unsupervised Machine Learning Approach with Chemical Intuition. Journal of Chemical Information and Modeling 2018, 58, 27–35. 10.1021/acs.jcim.7b00616. [DOI] [PubMed] [Google Scholar]
- Breiman L. Random forests. Machine learning 2001, 45, 5–32. 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Alom M. Z.; Taha T. M.; Yakopcic C.; Westberg S.; Sidike P.; Nasrin M. S.; Hasan M.; Van Essen B. C.; Awwal A. A. S.; Asari V. K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. 10.3390/electronics8030292. [DOI] [Google Scholar]
- Nair V.; Hinton G. E.. Rectified linear units improve restricted boltzmann machines. Proceedings of the 27th international conference on machine learning (ICML-10); 2010; pp 807–814.
- Akiba T.; Sano S.; Yanase T.; Ohta T.; Koyama M.. Optuna: A next-generation hyperparameter optimization framework. Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining; 2019; pp 2623–2631.
- Sheridan R. P. Time-Split Cross-Validation as a Method for Estimating the Goodness of Prospective Prediction. Journal of Chemical Information and Modeling 2013, 53, 783–790. 10.1021/ci400084k. [DOI] [PubMed] [Google Scholar]
- Lundberg S. M.; Lee S.-I. In Advances in Neural Information Processing Systems 30; Guyon I., Luxburg U. V., Bengio S., Wallach H., Fergus R., Vishwanathan S., Garnett R., Eds.; Curran Associates, Inc.: Red Hook, NY, 2017; pp 4765–4774. [Google Scholar]
- Lundberg S. M.; Erion G.; Chen H.; DeGrave A.; Prutkin J. M.; Nair B.; Katz R.; Himmelfarb J.; Bansal N.; Lee S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56. 10.1038/s42256-019-0138-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aas K.; Jullum M.; Løland A. Explaining individual predictions when features are dependent: More accurate approximations to Shapley values. Artificial Intelligence 2021, 298, 103502. 10.1016/j.artint.2021.103502. [DOI] [Google Scholar]
- Giudici P.; Raffinetti E. Shapley-Lorenz eXplainable artificial intelligence. Expert Systems with Applications 2021, 167, 114104. 10.1016/j.eswa.2020.114104. [DOI] [Google Scholar]
- Lundberg S.Comment on Interpretable Machine Learning with XGBoost. 2018; https://medium.com/@scottmlundberg/good-question-6229a343819f.
- Bengio Y.; Grandvalet Y.. No unbiased estimator of the variance of k-fold cross-validation. Adv. Neural Inf. Process. Syst. 2003, 16. [Google Scholar]
- Dietterich T. G. Approximate statistical tests for comparing supervised classification learning algorithms. Neural computation 1998, 10, 1895–1923. 10.1162/089976698300017197. [DOI] [PubMed] [Google Scholar]
- Benjamini Y.; Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995, 57, 289–300. 10.1111/j.2517-6161.1995.tb02031.x. [DOI] [Google Scholar]
- Harris D. C.Quantitative chemical analysis; Macmillan: New York, 2003. [Google Scholar]
- Usmani S. S.; Bedi G.; Samuel J. S.; Singh S.; Kalra S.; Kumar P.; Ahuja A. A.; Sharma M.; Gautam A.; Raghava G. P. THPdb: Database of FDA-approved peptide and protein therapeutics. Plos One 2017, 12, e0181748 10.1371/journal.pone.0181748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathur D.; Singh S.; Mehta A.; Agrawal P.; Raghava G. P. In silico approaches for predicting the half-life of natural and modified peptides in blood. PloS one 2018, 13, e0196829 10.1371/journal.pone.0196829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones H. M.; Parrott N.; Jorga K.; Lavé T. A novel strategy for physiologically based predictions of human pharmacokinetics. Clinical pharmacokinetics 2006, 45, 511–542. 10.2165/00003088-200645050-00006. [DOI] [PubMed] [Google Scholar]
- Jones H. M.; Gardner I. B.; Collard W. T.; Stanley P.; Oxley P.; Hosea N. A.; Plowchalk D.; Gernhardt S.; Lin J.; Dickins M.; et al. Simulation of human intravenous and oral pharmacokinetics of 21 diverse compounds using physiologically based pharmacokinetic modelling. Clinical pharmacokinetics 2011, 50, 331–347. 10.2165/11539680-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Kjeldsen T. B.; et al. Engineering of Orally Available, Ultralong-Acting Insulin Analogues: Discovery of OI338 and OI320. J. Med. Chem. 2021, 64, 616–628. 10.1021/acs.jmedchem.0c01576. [DOI] [PubMed] [Google Scholar]
- Kjeldsen T. B.; Hubalek F.; Hjørringgaard C. U.; Tagmose T. M.; Nishimura E.; Stidsen C. E.; Porsgaard T.; Fledelius C.; Refsgaard H. H.; Gram-Nielsen S.; et al. Molecular engineering of insulin icodec, the first acylated insulin analog for once-weekly administration in humans. J. Med. Chem. 2021, 64, 8942–8950. 10.1021/acs.jmedchem.1c00257. [DOI] [PubMed] [Google Scholar]
- Bech E. M.; Pedersen S. L.; Jensen K. J. Chemical Strategies for Half-Life Extension of Biopharmaceuticals: Lipidation and Its Alternatives. ACS Medicinal Chemistry Letters 2018, 9, 577–580. 10.1021/acsmedchemlett.8b00226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binder U.; Skerra A. PASylation®: A versatile technology to extend drug delivery. Curr. Opin. Colloid Interface Sci. 2017, 31, 10–17. 10.1016/j.cocis.2017.06.004. [DOI] [Google Scholar]
- Kjeldsen T. B.; Hoeg-Jensen T.; Vinther T. N.; Hubalek F.; Pettersson I.. Insulins with polar recombinant extensions. US Patent 11,208,452, 2021.
- Kontermann R. E. Half-life extended biotherapeutics. Expert opinion on biological therapy 2016, 16, 903–915. 10.1517/14712598.2016.1165661. [DOI] [PubMed] [Google Scholar]
- Levin D.; Golding B.; Strome S. E.; Sauna Z. E. Fc fusion as a platform technology: potential for modulating immunogenicity. Trends in biotechnology 2015, 33, 27–34. 10.1016/j.tibtech.2014.11.001. [DOI] [PubMed] [Google Scholar]
- Novo Nordisk A/S.Compund sharing. https://www.novonordisk.com/partnering-and-open-innovation/compound-sharing/compound-details.31607368417373.html, accessed: 2022–08–11.
- Menting J. G.; Whittaker J.; Margetts M. B.; Whittaker L. J.; Kong G. K.-W.; Smith B. J.; Watson C. J.; Žáková L.; Kletvíková E.; Jiráček J.; et al. How insulin engages its primary binding site on the insulin receptor. Nature 2013, 493, 241–245. 10.1038/nature11781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glendorf T.; Sørensen A. R.; Nishimura E.; Pettersson I.; Kjeldsen T. Importance of the Solvent-Exposed Residues of the Insulin B Chain -Helix for Receptor Binding. Biochemistry 2008, 47, 4743–4751. 10.1021/bi800054z. [DOI] [PubMed] [Google Scholar]
- Høie M. H.; Kiehl E. N.; Petersen B.; Nielsen M.; Winther O.; Nielsen H.; Hallgren J.; Marcatili P. NetSurfP-3.0: accurate and fast prediction of protein structural features by protein language models and deep learning. Nucleic Acids Res. 2022, 50, W510–W515. 10.1093/nar/gkac439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meijer R. I.; Barrett E. J. The insulin receptor mediates insulin’s early plasma clearance by liver, muscle, and kidney. Biomedicines 2021, 9, 37. 10.3390/biomedicines9010037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
2D structure and PK data on the four insulin analogs with publicly available iv data in rat are available on Github along with the code.






