Recent Advances in 2D Material Theory, Synthesis, Properties, and Applications

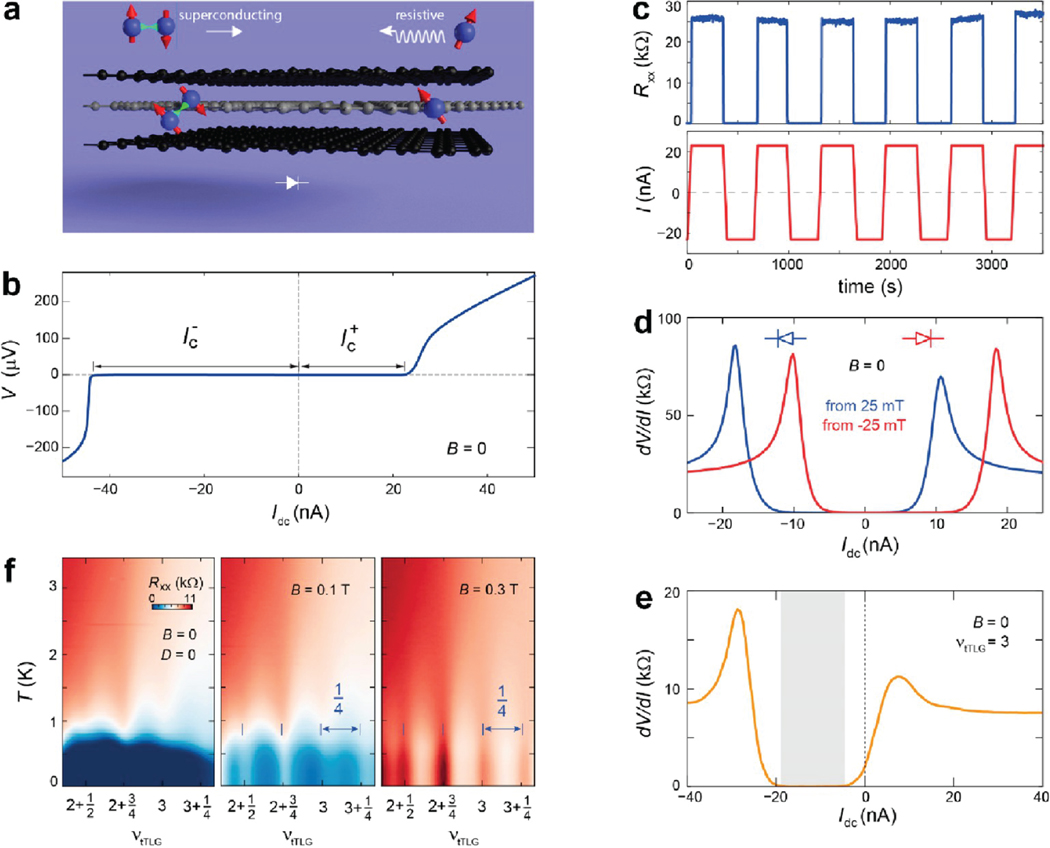
Abstract

Two-dimensional (2D) material research is rapidly evolving to broaden the spectrum of emergent 2D systems. Here, we review recent advances in the theory, synthesis, characterization, device, and quantum physics of 2D materials and their heterostructures. First, we shed insight into modeling of defects and intercalants, focusing on their formation pathways and strategic functionalities. We also review machine learning for synthesis and sensing applications of 2D materials. In addition, we highlight important development in the synthesis, processing, and characterization of various 2D materials (e.g., MXnenes, magnetic compounds, epitaxial layers, low-symmetry crystals, etc.) and discuss oxidation and strain gradient engineering in 2D materials. Next, we discuss the optical and phonon properties of 2D materials controlled by material inhomogeneity and give examples of multidimensional imaging and biosensing equipped with machine learning analysis based on 2D platforms. We then provide updates on mix-dimensional heterostructures using 2D building blocks for next-generation logic/memory devices and the quantum anomalous Hall devices of high-quality magnetic topological insulators, followed by advances in small twist-angle homojunctions and their exciting quantum transport. Finally, we provide the perspectives and future work on several topics mentioned in this review.

Graphical Abstract

INTRODUCTION

Two-dimensional materials (2D materials) are thermodynamically stable as atomically or molecularly thin layered structures and exhibit properties different from their bulk counterparts. From the seminal papers^1,2 to current 2D materials research, it is evident that graphene, hexagonal boron nitride (hBN), 2D transition metal dichalcogenides (TMDs),³ and metal carbides and nitrides (MXenes) are currently the most common building blocks in this field. In the past decade, magnetic 2D materials,⁵ 2D metals,⁶ layered topological insulators (TIs),⁷ and 2D moiré van der Waals (vdW) heterostructures⁸ are at the front lines of research in this material family. Additionally, more have been theoretically predicted to exist and await exploration.⁹ 2D materials and their heterostructures cover an extensive range of properties from metals to semimetals, semiconductors, insulators, and TIs that can be tailored through layer number, surface morphology, strain engineering, heterostructures, and emerging material processing. Besides their pristine form, heterogeneities such as impurities, dopants, structural defects, disorders, and interfaces may be controlled through substitutional doping and defect engineering to engineer electronic structures, induce magnetization, and trigger quantum phenomena in host materials.¹⁰ As a result, 2D materials are a rich platform for a broad spectrum of research from theory to next-generation (opto)electronics, fundamental physics, sensors, energy, and artificial intelligence and machine learning. The substantial interest in this field is reflected in the publication record: The number of publications relevant to 2D materials has increased from merely ≈1900 in 2004, to ≈9000 in 2013, and over 49,000 in 2021.^11,12 As 2D materials science and technology expands with this spectacular pace, it is necessary to connect experts with different disciplines in conferences or workshops frequently to enhance synergy and work together toward a promising future in this field. This review reflects the views of a group of theoretical and experimental experts on advanced 2D materials interdisciplinary efforts as summarized in Figure 1.

Figure 1.

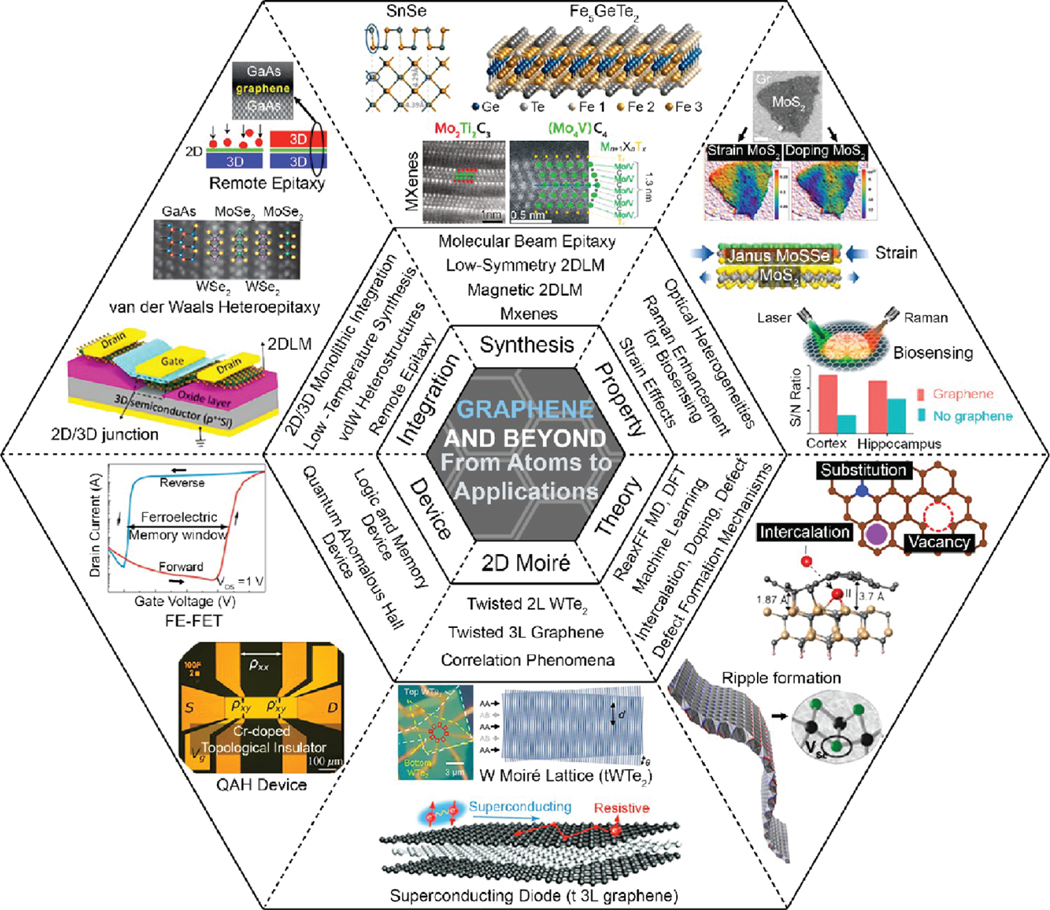
Overview of the scope of this review. We focus on the recent advancements in the field of two-dimensional layered materials (2DLM) learned from the Graphene and Beyond workshop at the Pennsylvania State University in 2022. The topics relevant to 2DLM in this review cover the fields of theory, synthesis and processing, material properties, material Integration, device study, and twisted 2D heterostructures.

Initially, we will discuss the theoretical aspect of 2D materials, including predicting properties introduced by defects and impurities in 2D materials, large-scale computations with reactive force field potentials to understand growth and intercalation mechanisms, and artificial intelligence (AI) and machine learning (ML) in 2D material research. Calculations and theoretical modeling are more important than ever to guide the search for 2D materials useful for energy applications and future devices and to deconvolute complicated growth and processing steps. In subsequent sections focused on material synthesis, we discuss some 2D materials that can be synthesized in large area or quantity, including MXenes prepared by chemical exfoliation of MAX-phase crystals and synthesis and doping of TIs and TMDs using molecular beam epitaxy (MBE) and metalorganic chemical vapor deposition (MOCVD). Additionally, low-symmetry SnS crystals, magnetic ${\text{Fe}}_n{\text{GeTe}}_3$ ($n=3–5$) layered materials, magnetically doped TMDs, and utilization of intermediate 2D layers for remote epitaxy are discussed.

Further, we examine 2D material characterization and applications, including optical properties of asymmetric 2D materials, 2D surfaces for biosensing, and strain engineering for tuning their band structures. Thanks to Se-S ion exchange¹³ and confinement heteroepitaxy¹⁴ techniques, structurally asymmetric 2D materials, such as Janus monolayers (e.g., SeMoS and SMoSe) and 2D metals (e.g., Ga and In) confined in graphene/SiC interface, can be realized and studied optically by Raman spectroscopy, optical measurements, second harmonic generation, etc. Because of their atomic thickness and high surface-to-volume nature, both their phonon and band structure are very sensitive to slight changes in electron doping and strain when they interface with other materials, which serve as the foundation for scalable sensing.

Finally, we summarize efforts on the physics and devices of relevant quantum materials grown via MBE and bulk crystal growth. First, we show some of recent progress in mixed-dimensional heterostructures, including 2D materials combined with single metal atoms or quantum dots (so-called zero-dimensional materials, 0D) into 0D/2D platforms for sensing and electronic doping and hybrid 2D/3D electronic material integration for logic and memory devices. Second, we highlight ${\text{Mn}}_2{\text{Bi}}_2{\text{Te}}_4$—an emerging intrinsic magnetic TI—and its ferro- and antiferromagnetic properties. Third, we provide an overview on the quantum anomalous Hall effect in magnetically doped TIs and its metrological applicability without an external magnetic field. Then, we review two emerging 2D homojunctions made of and their unique moiré physics: graphene trilayer with each layer twisted by ≈1–2° and $T_{\text{d}}-{\text{WTe}}_2$ bilayer with each layer twisted by ≈5°. Due to the rapid advancement of this field, this review only summarizes the most recent breakthroughs in 2D materials discussed at the 2022 Penn State Graphene and Beyond Workshop. At the end of the review, we provide perspectives and future works. While discussions on earlier works are not provided, they can be found in our prior reviews. ^11,12,15,16

DISCUSSION

1. Theory and Computation.

1.1. Modeling Intercalation, Defects, and Doping in 2D Materials.

Theoretical calculations are not only tools for designing future materials but also for modifying their properties. In layered compounds, some of the most powerful engineering techniques to tailor material properties—which we will emphasize in this section— are intercalation, doping, and defects (Figure 2). In this subsection, we will give an overview on computational predictions of intercalation and defect engineering in 2D materials, highlighting their potential impact on next-generation technologies by tailoring structural, electronic, optoelectronic, magnetic, and catalytic properties.

Figure 2.

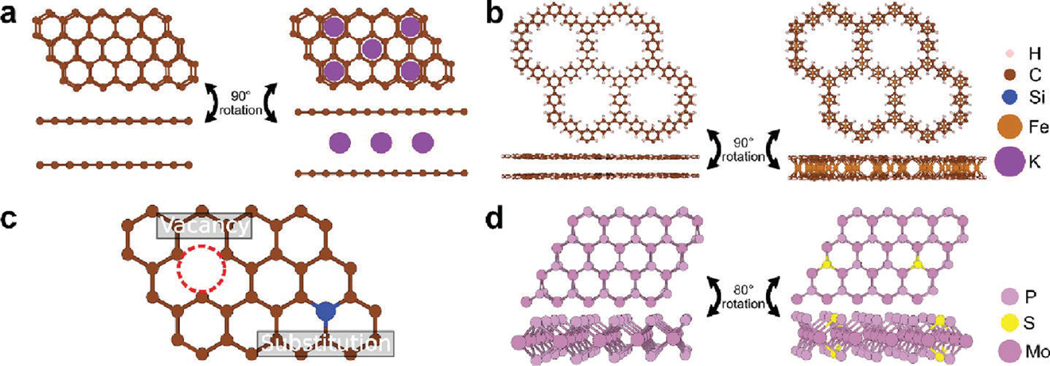
Modeling intercalation, defects, and doping in 2D materials. (a) Bilayer graphene before (left) and after (right) intercalation. The figure includes a top view (top) and a side view (bottom). (b) “All-benzene” 2D-COF before (left) and after (right) intercalation. Intercalated atoms are placed at the centroid of each benzene ring. The figure includes a top view (top) and a side view (bottom). (c) Defective graphene layer showing a vacancy and a silicon substitution. (d) Pristine (left) and S-doped (right) MoP. The figure includes a top view (top) and a triclinic view (bottom).

1.1.1. Intercalation.

Monolayer graphene (MLG) possesses several attractive material features; however, the lack of property tunability and limited chemical space limits its progress. By contrast, bilayer graphene (BLG), constructed by stacking two MLGs, is an effortless form to drastically expand the electronic flexibility of 2D carbon-based systems. Moreover, BLG allows for intercalation as a viable technique to perform material modification (Figure 2a). Unlike doping and adsorption, intercalation is the attempt to control material properties via taking advantage of the vdW-regulated space between BLG layers. What is more open-ended, few-layer graphene (FLG) can provide scenarios for investigating staging and cointercalation, especially in the realm of electrodes for energy storage.^17,18

Regarding electronic properties, graphene-based materials decorated with intercalants were found to present a controllable position of Dirac point from the Fermi level.¹⁹ This provided a way to discover candidates for various semiconductor applications, especially for interconnect technologies such as integrated circuits. Pakhira et al.²⁰ systematically simulated 2D slab and bulk BLG systems intercalated with a series of transition metal (TM) via density functional theory (DFT) calculations. Their calculations predict high thermodynamic stability and Dirac cone tunability in the intercalated systems, as shown in Figure 3a. Since the electrons distributed near the Fermi energy can drastically affect the position of the Dirac point, distinguishing the electron density around the Fermi level becomes significant. Their results also indicate that the main electron density contributions around the Fermi level derive from the $p_z$ subshell of carbon and 3d subshells of intercalated TMs. Controlling the type and concentration of TMs within BLG indeed offers an interesting approach to modulating electric properties.

Figure 3.

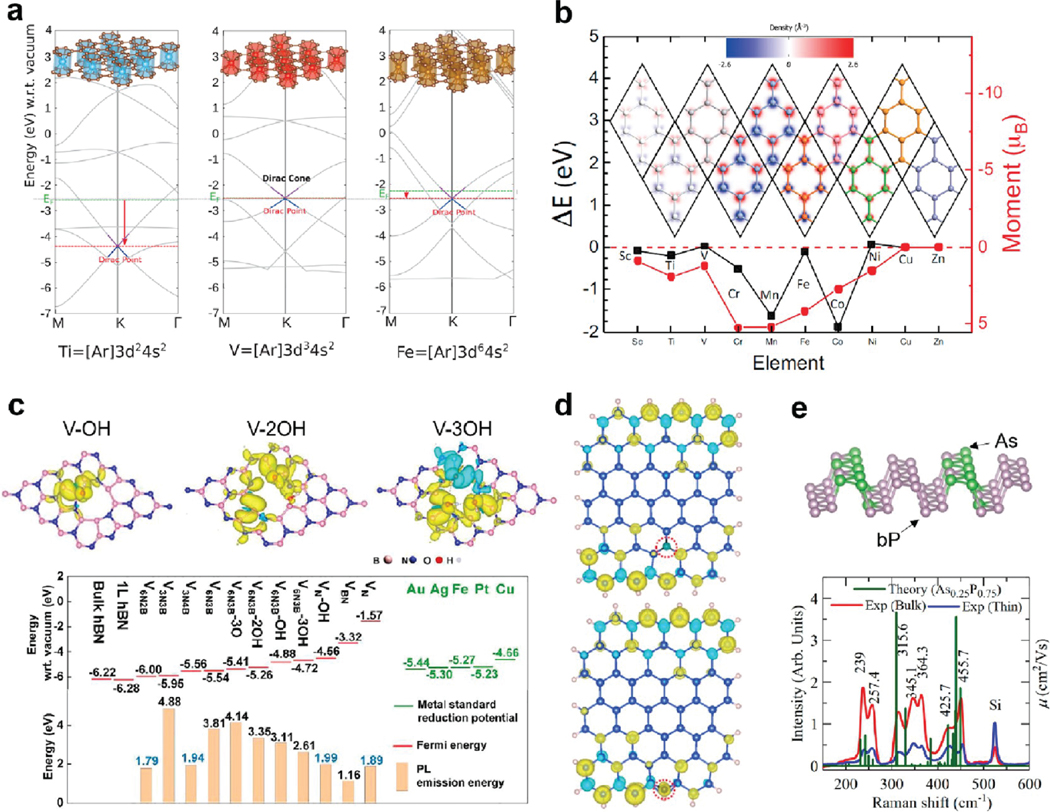
Theory-predicted properties of functionalized 2D materials. (a) The shifted Dirac points of BLG with Ti/V/Fe intercalants relative to pristine BLG with inserted structures. Reproduced with permission from ref 20. Copyright 2018 American Chemical Society. (b) The magnetic moment and energetic ground states of various TM-intercalated BLG. Reproduced with permission under a nonexclusive license to distribute from ref 22. Copyright 2019 arXiv. (c) The spin density of BN with functionalized vacancies, and the shifting Fermi energy of d-BNs with distinct type, size, and functional groups of the vacancies. Reproduced with permission under a Creative Commons CC-BY 4.0 License from ref 34. Copyright 2021 Elsevier. (d) The spin density relies on the position of carbon dopant(s) within MLS. Reproduced with permission from ref 39. Copyright 2020 American Chemical Society. (e) The distribution of As dopants within b-P and its theoretical Raman spectra relative to experimental counterpart. Reproduced with permission from ref 40. Copyright 2019 Royal Society of Chemistry.

Furthermore, the shift in the chemical potential of graphene caused by atomic intercalants was considered for inducing superconductivity.²¹ The intercalation of alkali and alkaline metals within few-layer graphene (FLG), whose $p$ band crossings at the Fermi energy contribute to superconducting behavior, was well-studied. Inspired by this, Lucht et al.²² implied that the hybridization of $d$ bands deriving from TMs could have a similar mechanism to construct superconductive systems. By comparing established superconducting systems with their theoretical results of first-row TM-intercalated BLG in the aspects of lattice constant and interlayer band energy, they found that Sc, Ti, and V are promising intercalants to promote superconductivity. The $d$ orbital electrons of these intercalants were believed to constrain the interlayer band energies below the Fermi level via the interaction with $p$ orbitals of graphene, inducing superconductive behavior. On the other hand, other TMs with more $d$ orbital electrons did not present superconductivity, as they alleviated such hybridization by having more paired electrons, enlarging the interlayer distance to an inappropriate level for superconductivity. Other parameters, such as number of layers, concentration of TMs, or even cointercalation, could be starting points for sharpening the mechanism and precise property modulation in graphene and other 2D materials.

Moreover, structures that interacted with TMs were proven to display noticeable magnetic properties due to the coupling of their $d$ orbital electrons with graphene.²³ The study by Lucht et al.²² also simulated how the magnetic features of BLG were influenced by several TM-intercalants, further defining their corresponding magnetic ground states. Briefly, in Figure 3b, $\text{Cr}$, $\text{Mn}$, and $\text{Co}$ were found to have larger magnetic moments while $\text{Cu}$ and $\text{Zn}$ have moments approaching zero. These differences in their magnetic moments stem from the number of unpaired electrons. For instance, $\text{Zn}$ has fully occupied orbitals, resulting in a lack of $d-s{p}^2$ hybridization when interacting with graphene. In addition, among first-row TMs, $\text{V}$ and $\text{Ni}$ are the only two having ferromagnetic configurations and the remaining first-row TMs are antiferromagnetic. BLG with TM intercalants is, after all, a pioneer in magnetic alteration.

Another family of materials where TM-intercalation was predicted to yield promising electronic properties is 2D covalent organic frameworks (2D-COFs), which are porous crystalline materials comprised of organic bridging linkers. The structural features of 2D-COFs are shown in Figure 2b. These compounds have become increasingly popular in the past two decades due to their porous architecture, high surface area, and unique tunability.²⁴ These properties have led to various use-cases, including catalysis,²⁵ energy storage,²⁶ molecular sensors,²⁷ and biomedical applications.²⁸ What makes 2D-COFs stand out is that their monomers are covalently bonded in a 2D sheet, with almost perfect “eclipsed” stacking due to $\pi -\pi$ out-of-plane interactions, generating 1D columns that are ideal for charge and exciton transport.

The electronic properties of 2D-COFs are traditionally modified by changing the organic linkers that make up the layers²⁹ or modifying the length of their chains.³⁰ However, this generally does not solve the main issue for their application as porous electronic materials: e.g., intrinsically low conductivity and charge-carrier mobility. Nevertheless, there is potential to bypass these problems by intercalating the 2D-COF layers with transition metals (see Figure 2b), which yields electronic properties that range from insulating to conducting.^31,32 Pakhira et al.³¹ showed that the systematic addition of $\text{Fe}$ in the centroid of the COF rings produced a drastic change to the Fermi level and band morphology of these structures. For example, they found that a pure triazine-benzene-boroxine COF’s insulating behavior (2.6 eV indirect band gap) is modified to a semiconductor (1.18 eV direct band gap) with the addition of $\text{Fe}$ atoms at the centroid of all rings in the unit cell. Furthermore, the band structures show a reversal in the conduction band curvature and a change in the relative position of the Fermi level. Intercalated 2D-COF architectures presented band gaps as small as ≈0.3 eV and as large as ≈2.6 eV, with several intermediate values. In addition, through vibrational analysis, these materials were also predicted to be thermodynamically stable. Their excellent electronic tunability and dynamic stability present an interesting opportunity to use layered COFs as nanoporous electronics and optoelectronics.

Intercalation can also be used to achieve higher reactivity during catalysis. One reaction of great interest is “water splitting” (also known as oxygen evolution reaction). Carrying out this reaction efficiently could decrease the current cost of hydrogen for fuel cells, attacking one of society’s current issues: clean-energy production. A promising 2D material that stands out for this application is birnessite: a layered, ion-intercalated manganese oxide. Birnessite acts by mimicking plant’s photosystem II. This natural system captures solar energy to oxidize water, a reaction that occurs in the Oxygen Evolution Center: a cubane-like structure comprised of ${\text{Mn}}_4{\text{O}}_8\text{Ca}$. Birnessite has a similar structure, composed of ion-intercalated ${\text{MnO}}_2$ tetrahedra. Birnessite intercalated with different cations was theoretically studied by Lucht et al.³³ who discovered that Sr, Ca, B and Al-intercalated birnessites have valence bands with a band alignment suitable for water splitting. In addition to its water-splitting capabilities, bulk birnessite intercalated with boron has a direct band gap of about 2 eV, which has suitable properties for light-capture. An analysis of monolayer birnessite further revealed that Mg and Sr-intercalations present an indirect-to-direct band gap transition when reducing the bulk to a slab, with direct band gap energies of 2.19 and 2.69 eV, respectively, which are also suitable for light capture. The theoretically predicted band alignments and band gaps for birnessite predict its ability to perform both oxygen evolution and light capture simultaneously, which could lead to materials that can carry out photocatalytically activated oxygen evolution, comprising a step toward achieving artificial photosynthesis.

1..1.2. Defects.

Defects are generally seen as undesired, as it is usually difficult to control and predict their effect on materials’ properties. However, for 2D materials, defects such as vacancies, dopants, and substitutions are effective methods to alter and fine-tune materials’ properties. Vacancies, in particular, can induce an electric potential that reshapes the electron distribution, and further changes the materials’ electric and chemical properties (Figure 2c). For example, Lei et al.³⁴ activated chemically inert BN via the decoration of vacancies, which could be applied to the reduction of metal cations for the hydrogen evolution reaction (HER). Based on their DFT calculation, a high spin density, which can represent unpaired electrons or free radicals, was surrounding the vacancies; this indicates vacancy-induced reactivity. Most interestingly, the Fermi energy level of defective-BN (d-BN) could be finely shifted from −6.28 to −1.57 eV by controlling the type, size, and functional groups (functionalization) of the vacancies as shown in Figure 3c. Overall, localized free radicals and a tunable band alignment could aim to achieve several metal reductions ($\text{Fe}$, $\text{Cu}$, $\text{Au}$, $\text{Ag}$, and $\text{Pt}$) with different redox potentials. Aside from d-BN, other defective 2D materials that have been predicted as excellent electrocatalysts for hydrogen evolution include ${\text{MoS}}_2$ with S vacancies,³⁵ ${\text{PtSe}}_2$ with Pd/Pt substitutions,³⁶ and ${\text{MoSi}}_2{\text{N}}_4$ with nitrogen vacancies.³⁷ All these examples require defects to boost their electrochemical activity for hydrogen evolution, making defects essential to engineer properties of 2D materials.

On the other hand, doping is the introduction of a small amount of impurities into a material. Doping is well-known for aiding in the design of field-effect transistors (FETs), as it can help calibrate 2D materials’ electric features, such as electronic transport, with dilute concentrations of dopants.³⁸ Recent studies showed that 2D materials’ properties affected by the introduction of dopants were not only dependent upon the concentration of dopants (which had been widely studied in the past), but also on the atomic position of impurities in the structure. A first-principle study³⁹ in 2020 defined how the structures and properties including band gap, formation energy, and magnetism were influenced by the position of carbon dopant(s) within monolayer Si (MLS), as shown in Figure 3d. Silicon-carbon substitution at the edge sites was found to be more energetically preferable, interestingly, these substitutions generated high neighboring spin density around the doping site. Also, the authors found that reducing the distance between two dopants leads to a more distorted and unstable geometry of carbon-doped MLS. More significantly, they concluded that if a doping site breaks the symmetry of the whole structure more, more band degeneracies can be broken, inducing a larger band gap. Apart from the substitution site of a dopant, its distribution can determine advanced features for electronics as well. For instance, Pradhan et al.⁴⁰ unveiled a certain distribution of As dopants within black phosphorus (b-P) that could contribute to not only an appropriate band gap for FETs, but also an anisotropic fast carrier mobility, which can range from 300 to 600 cm² V⁻¹ s⁻¹. In order to define such As dopant arrangements, they took advantage of theoretical techniques to compute the Raman spectra of designed models, and find the structure that agreed with their experimental Raman results, as shown in Figure 3e. To some degree, the clustering of As atoms is more stable and presents an anisotropic transport property that is gate-voltage dependent for 25% arsenic doped b-P. Finally, another doped 2D material that has shown promising properties is S-doped MoP (Figure 2d). Through theoretical and experimental results, it was found that the addition of S atoms in MoP leads to a smaller band gap (0.67 eV in S-doped MoP compared to 2.18 and 2.07 eV for pure ${\text{MoS}}_2$ and MoP, respectively), and high electron mobility near the Fermi level due to rectification of electron accumulation at the conduction and valence bands.⁴¹ These properties are highly favorable for hydrogen evolution catalysis. Cluster model computations also elucidate the amount of dopant with the best catalytic activity. In particular, the authors found that a small percentage of S dopant (5% S) in MoP leads to a more favorable HER rate-limiting (Volmer) step during the reaction, compared to 10% S-doped MoP, pure ${\text{MoS}}_2$, and pure MoP.

1.2. High-Speed and Large-Scale Modeling for 2D Materials Based on ReaxFF.

Understanding the effect of operating conditions such as temperature, pressure, flow rate, and gas-composition on 2D material growth kinetics is challenging. Modeling and simulation can improve the atomic-level understanding of the morphology and characteristics of a resultant structure and thus enhance the ability for better control of the complex growth process of 2D materials. The ReaxFF reactive force field, originally developed by van Duin et al.,⁴² is a computationally efficient means that captures the covalent bond breaking and reforming by updating the bond order at each molecular dynamic iteration, in contrast to nonreactive potentials. Therefore, ReaxFF molecular dynamics (MD) simulations are highly effective in capturing detailed chemical events, reaction pathways, and product formation during gas-phase and gas/condensed phase simulations, for systems up to ≈10⁶ atoms and for time scales not accessible to first-principles based techniques. This ReaxFF potential can simulate the nucleation and growth and intercalation of 2D materials, which involves both gas-phase and surface interactions, as a function of local chemical environment, helping in predicting effective growth protocol.^43–46 It features vdW interactions which particularly enables the simulation of multilayer vdW hetero- and homostructures.^44,46 Additionally, ReaxFF provides thermodynamic and kinetic insight into fundamental solid-phase phenomena observed in 2D materials such as atomic intercalation, grain boundary (GB), defect formation and diffusion, stress induced lattice distortions, morphological evolution of 2D domains as a function of local chemical environment during the growth. Also, ReaxFF differs from the so-called “first generation” reactive force fields such as Tersoff^47,48 and Brenner⁴⁹ by applying a significantly longer-ranged bond-order relationship, which makes it possible to achieve accurate reaction kinetics. The ReaxFF framework has been successfully applied to a wide range of 2D systems^50–52 and their defect formation, growth mechanisms and characterization, as shown in the following examples.

1.2.1. Kinetics of Ga Intercalation through Graphene.

Nayir et al.^46,52 used a combination of ReaxFF- and DFT-based simulations to study defects in graphene, which can act as pathways for Ga intercalation into the interface between graphene and SiC. The results show that the sizes of vacancy defects ranging from single carbon vacancy (SV) to multiple carbon vacancy (3 and 4 V) can affect the thermodynamic and kinetic preference of intercalant between the adsorption on graphene surface or the intercalation at the interface. For example, the diffusion of a relatively large Ga atom through small sized defects (<3 V) is kinetically hindered, where Ga encounters a kinetic barrier. However, the potential energy of the system monotonically decreases as Ga approaches to graphene with larger sized defects (>double vacancy, DV) and the diffusion through graphene layer is nearly barrierless (Figure 4a). This suggests that defect engineering provides an effective way to lower the temperature required for intercalation, by consequence, energy savings and cost reduction during 2D material intercalation.

Figure 4.

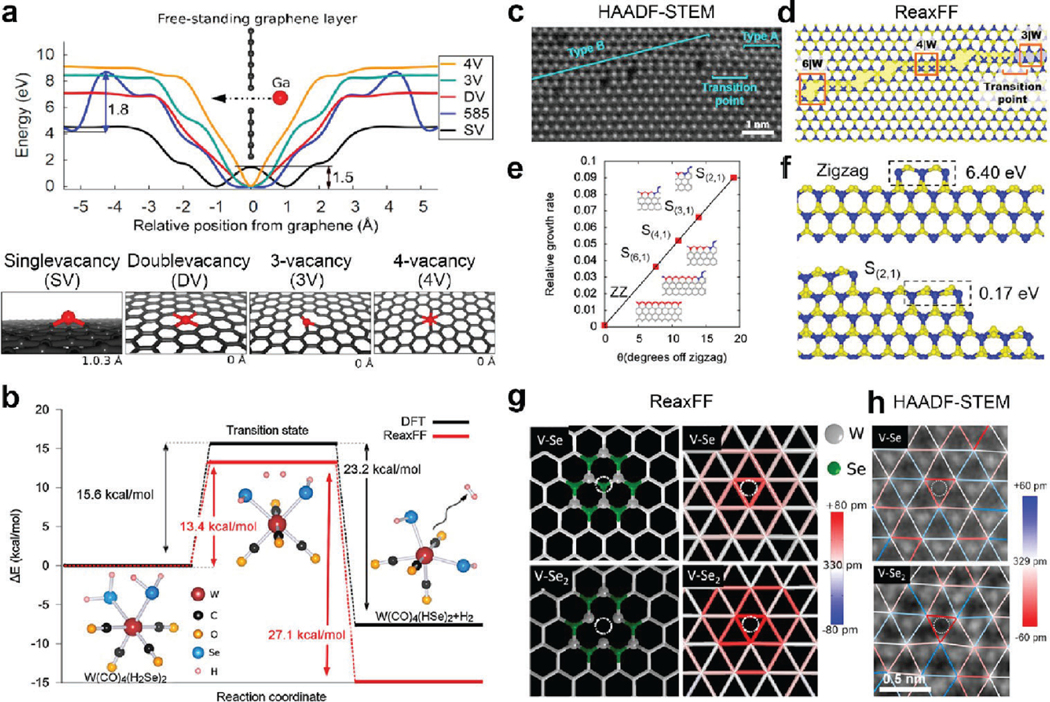
Examples of ReaxFF applications to 2D materials. (a) Ga diffusion through a free-standing defective graphene. The graph shows a potential energy barrier for Ga diffusion into defective graphene sites: SV, DV, 5-8-5, 3 and 4 V at 0 Å. Ga diffusion realizes from right to left in the graph The images at the bottoms show the most stable Ga adsorption on SV at 1.03 Å, DV at 0 Å, 3 V at 0 Å, and 4 V model at 0 Å, respectively. Adapted with permission from ref 46. Copyright 2022 Elsevier. (b) ReaxFF and DFT predicted reaction pathway for hydrogen release from the $\text{W}{(\text{CO})}_4{\left({\text{H}}_2\text{Se}\right)}_2$ molecule. Adapted with permission from ref 43. Copyright 2019 Elsevier. (c) ADF-STEM image showing type A and B GBs, as well as the transition point between them. (d) ReaxFF MD simulation equilibrated at 300 K of the structure shown in (c). (e) Computed relative growth rate of the slanted edge structures with respect to the sulfur-terminated zigzag (ZZ) edge as a function of slanted angle, $\theta$. S(2,1), S(3,1), S(4,1), and S(6,1) are the slanted edges characterized by the translational vector (n, 1) of the 2H-${\text{WS}}_2$ lattice, where n is the number of the zigzag units along the a1 direction, and a 2-component vector contains only one zigzag unit in the GB of interest (f) Illustrations of the formation energy for adding atoms (enclosed in the dashed rectangular boxes) onto the reference sulfur terminated ZZ and S(2,1) slanted edges, respectively. Adapted with permission from ref 51. Copyright 2021 American Chemical Society. (g) Ball-stick representations and W—W bond displacement maps of V-Se and $\text{V}-{\text{Se}}_2$ point defects based on ReaxFF methods. (h) HAADF-STEM images with overlaid maps of the distances between neighboring W atoms of V-Se and $\text{V}-{\text{Se}}_2$. In (g,h) The vacancies are marked by dotted white circles. Adapted with permission from ref 44. Copyright 2020 American Chemical Society.

1.2.2. MOCVD Growth of ${\text{WSe}}_2$.

A combination of ReaxFF- and DFT-based chemical kinetic models developed by Xuan et al.⁴³ provides a fundamental insight into kinetic properties of elementary reaction pathways leading to the ${\text{WSe}}_2$ formation from $\text{W}{(\text{CO})}_6$ and ${\text{H}}_2\text{Se}$ precursors. During MOCVD at elevated temperatures, CO ligands will dissociate from $\text{W}{(\text{CO})}_6$ and ${\text{H}}_2\text{Se}$ will rapidly fill in the ensuing vacancies in W-carbonyl, resulting in intermediate $\text{W}{(\text{CO})}_x{\left({\text{H}}_2\text{Se}\right)}_y$, molecules. Continuous ${\text{H}}_2$ release from the $\text{W}{(\text{CO})}_x{\left({\text{H}}_2\text{Se}\right)}_y$ is a key event that could determine the growth rate of 2D ${\text{WSe}}_2$. The model in Figure 4b shows that ${\text{H}}_2$ release from $\text{W}{(\text{CO})}_4{\left({\text{H}}_2\text{Se}\right)}_2$ with a kinetic energy barrier of 13.4 kcal/mol at the ReaxFF results in a more stable product, $\text{W}{(\text{CO})}_4{(\text{HSe})}_2$. The reverse reaction may also occur, as pure ${\text{H}}_2$ environment is used in the process. However, for $\text{W}{(\text{CO})}_4{(\text{HSe})}_2+{\text{H}}_2\to \text{W}{(\text{CO})}_4{\left({\text{H}}_2\text{Se}\right)}_2$, the barrier for the reverse reaction is higher, 27.1 kcal/mol in ReaxFF. Based on simulations, these reactions are generally exothermic with a lower activation energy than their reverse reactions, indicating that ${\text{H}}_2$ release is thermodynamically favorable. After all ${\text{H}}_2$ and CO ligands are released from the intermediate molecules, stable 2D ${\text{WSe}}_2$ films can grow on substrates.

1.2.3. Grain Boundary and Defects in 2D TMDs.

Hickey et al.⁵¹ uncovered invisible translational defect arrays in nearly single-orientation, coalesced monolayer ${\text{WS}}_2$ films with high-angle annular dark field (HAADF) scanning transmission electron microscopy (STEM) imaging and used ReaxFF MD simulations at 300 K to create the same irregular translational GB (Figure 4c,d). There are two types of GBs: one has vacancy line defects, and the other adopts a rectangular arrangement of W atoms, 4IW, at the boundary and is stabilized by 6IW rings that cause steps in the GB. The latter is comprised of the slanted edges with angles within the range of 0 to 30°, deviated from the zigzag edge. The ReaxFF MD calculations show that the kink concentration significantly affects the stability of slanted edges as shown in Figure 4e,f where the growth rate is linearly correlated to the kink concentration. In a Sulfur-rich environment, given the high-cost energy required for the first nucleus formation, the most stable ZZ structure, whose edge atoms are passivated by Sulfur atoms, is the slowest to grow while the slanted edge with a highest kink concentration is expected to grow fastest. The analysis in the aforementioned work indicates that growth of the S-ZZ edge requires a long time to complete its linear formation. Therefore, even though the slanted edges are less stable edge structures and should disappear quickly during the growth process according to the growth conditions, shorter growth time or slower flow rate of the gas-phase precursors, most likely, may not allow flakes to complete their zigzag linear formation, thus, grains with the slanted edges may survive during the growth to meet at the GB.

The ReaxFF reactive potential was used to simulate point defects in a 2D ${\text{WSe}}_2$ to study their influence on local strain. Figure 4g presents the atomic configurations and the ReaxFF-based bond displacement maps of single Se vacancy (${\text{V}}_{\text{Se}}$) and double Se vacancy (${\text{V}}_{\text{Se}2}$) in ${\text{WSe}}_2$. The loss of Se of two defect types drives bond contraction between adjacent W atoms and reduces W—W distances by about 15 and 24%, respectively, as the unsaturated W atoms marked by red triangles radially contract toward the chalcogen vacancies in the maps. These strain effects are consistent with STEM imaging, which shows that the distances between three W atoms adjacent to the ${\text{V}}_{\text{Se}}$ and ${\text{V}}_{\text{Se}2}$ are contracted by approximately 10 and 18%, respectively, in good agreement with the ReaxFF results.

1.3. Artificial Intelligence and Machine Learning in 2D Materials Research.

In recent years, exploiting artificial intelligence (AI), machine learning (ML), data mining, and other data-driven approaches has steadily grown its presence in various aspects of 2D materials research. With traditional materials development commonly taking 1—2 decades to develop from conception to completion,⁵³ a different approach for the creation of 2D materials research needed to be considered to reduce research time. On the one hand, the Materials Genome Initiative has provided a strong impetus for creating databases and screening methods for materials with specific functionalities. On the other hand, rapid progresses in Industry 4.0 provides matured methods for instruments and data-science to meld seamlessly to streamline manufacturing and other complex industrial processes. Given the advent of easy-to-use ML tools,⁵⁴ these emerging statistical approaches have been utilized to speed up material development processes—even reducing some experimental optimizations down to just 8 h.⁵⁵ We next describe recent developments in various aspects of 2D materials research where applications of ML can accelerate and/or enable scientific and technological advances.

1.3.1. Machine Learning in 2D Material Theory.

With the availability of high-performance computing, data mining, pattern recognition, and other search algorithms are being used frequently to computationally “discover” materials, including 2D materials. These theoretical works in 2D materials have led to collaborative efforts to provide shareable DFT information using databases.⁵⁶ More importantly, such shareable resources have led to a standardization of processes for the community—effectively establishing generally accepted structures of data. These standardized data structures allow for the sharing of data across many different platforms in DFT, which is conducive to the integration of ML algorithms. Applying the data from these databases, many groups have effectively utilized ML to predict physical properties of a lattice structure,⁵⁷ replicated electron scattering in a DFT+U model,⁵⁸ and even exploited crystal graph convolutional neural networks to study nearly 45,000 2D structures to discover compositions suitable for photovoltaics.⁵⁹ Advancing this field forward, Suzuki et al.⁶⁰ have developed methods for achieving machine-learned exchange correlation (XC) functionals for time-dependent DFT (TD-DFT) calculations using neural networks. Given that XC inaccuracies have been a consistent issue in DFT, XC functionals derived from experimental data and fit through ML algorithms stand to serve the long-standing issue of understanding unknown systems, potentially without the need for energy convergence, drastically reducing computational time while increasing accuracy of simulations. In keeping with the recent progress with magic-angle moiré superlattice engineering, ML approaches are being blended with theory and computational approaches to achieve high-throughput searches of multiply stacked, multiangle 2D materials with specific, desired properties.⁶¹ With increasing computing powers, more difficult and also more accurate calculations of functionalities will become achievable, thanks to the growing collaboration between computational physicists and data scientists.

1.3.2. Machine Learning in 2D Material Synthesis.

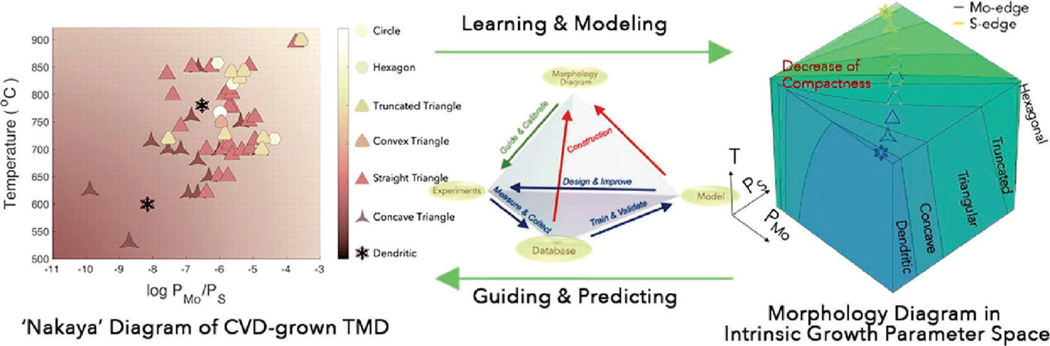
Utilizing ML in the synthesis of 2D materials may not only be considered useful but also a requirement for future discoveries. Predictable synthesis of 2D materials depends on precise control over a combination of experimental parameters. In micromechanical exfoliation techniques, 2D flakes (e.g., graphene) are usually transferred onto a flat substrate from a bulk crystal (like graphite). In this case, the shape and size of both the bulk source and the transferred 2D layer are random. This randomness makes developing/training machine-learning algorithms that could assist fabrication of identical 2D layers a considerable challenge. In this case, ML approaches are more useful for automated searching specific candidates in from a dense ensemble of mixed-thickness flakes. For example, masked convolutional neural networks techniques applied to optical microscopy images can provide high-probability identification of various monolayer flakes (e.g., graphene, hBN, ${\text{MoS}}_2$, and ${\text{WTe}}_2$) from a collection of flakes of various thicknesses exfoliated onto a flat ${\text{SiO}}_2/\text{Si}$ substrate.⁶² In contrast, chemical vapor deposition (CVD), MOCVD, plasma-enhanced CVD, MBE, sputtering or other reactor-based synthesis of 2D materials can have a larger range of controllable parameters in their 2D crystal growth recipes (e.g., temperature, pressure, flow rate of carrier and reactant gases, ramp-rates, and several other design of experimental or DoE parameters). Here, trial-and-error approaches to optimize the DoE parameters for a specific type of outcome (i.e., crystal quality, yield, reproducibility, or large-area coverage, etc.) for each type of reactor can be daunting. Traditional DoE methods,^63–65 even with Latin-hypercube sampling (LHS),⁶⁶ require a large input of samples to be useful. Because of this, Bayesian Optimization (BO)^67–71 with Gaussian Processes (GP) tends to be the preferred method of experimental optimization of materials due to its ability to work with smaller sample sizes. While this technique has yielded promising results from previous research,^72–77 a shortfall of this approach is the computational requirements associated with it. A computational training cost of $O\left(N^3\right)$ with BO of GP⁷⁸ is not technically very challenging but it would be preferable to have a training cost of $O(N)$ for lower budget research groups, which will require a creative shift from BO to simpler feedforward Neural Networks (NN).⁷⁹ Since NNs typically require large data sets for training, one approach could be to simplify the problem into smaller subsets of problems. For example, the objective of one subset could be to find correlations between the ratio of precursor material ${\text{P}}_x/{\text{P}}_y$ to the resulting shape of the flakes, i.e., triangular, polygonal, or dendritic, as was suggested in a recent perspective on 2D materials,⁸⁰ with the idea articulated in Figure 5. A second subset of machine-learning guided experiments could then aim to find correlations between the DoE parameters (precursor quantity, temperature, flow rate, ramp-rate, growth duration, etc.), and the resulting in situ conditions of ${\text{P}}_x/{\text{P}}_y$ at the growth surface. Finally, a third set of ML-guided experiments will then need to find correlations between shapes of seed crystals versus their propensity for eventually growing into large-area, uniform, and/or high-quality 2D layers on a given substrate, depending on the required target outcome. A combination of these three kinds of ML-guided experiments is likely going to help provide the best correlation between DoE parameters and final 2D material outcomes.

Figure 5.

Proposed ML framework for understanding the correlation between the ratio of precursors in this case partial pressure of Mo versus S sources in a CVD reactor, and the resulting shape of the grown crystal. Reproduced with permission from ref 80. Copyright 2020 Elsevier.

1.3.3. Machine Learning Used with 2D Materials.

In contrast to utilizing ML to discover 2D materials, 2D materials have recently been used in conjunction with, and even as, ML algorithms. It has been shown recently that the optical transmittance of TMDs can be exploited to allow for accurate light source color identification by training an ML model to identify wavelengths based off measurements from the single-cell silicon photodetector with an accuracy of 99%—effectively drastically reducing the cost of accurate color identification systems⁸¹ (Figure 6). Given that most modern cameras utilize Bayer filters over complementary metal-oxide-semiconductor (CMOS) sensors, it takes four Si photodiodes to measure the color of a single pixel in a modern camera. It is then feasible to presume that using this ML technique with TMDs filters could possibly reduce camera sensor surface area by one-quarter, while retaining similar light intensity response and color accuracy. In recent years, many researchers have also shown the viability of using 2D materials themselves to develop hardware-based neuromorphic systems.⁸² Mennel et al.⁸³ even developed an Artificial Neural Network (ANN) for identifying images—allowing for low-power training cost and ultrafast analysis—boasting some computations as fast as 50 ns. According to Mennel, this time is only limited due to the onboard clock. Given these emerging technologies, the future of ML for 2D material development may, intriguingly, be done so by 2D materials.

Figure 6.

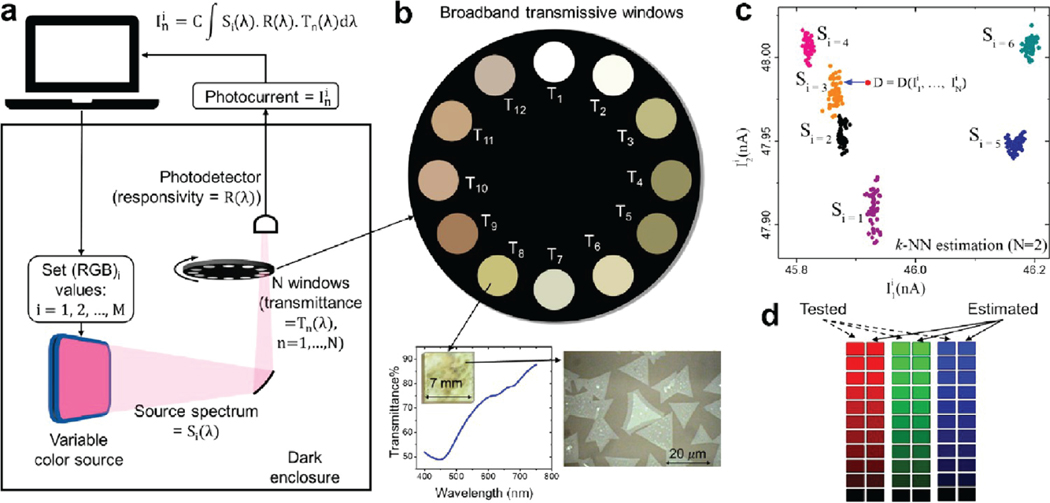
Artificial eye (or, A-Eye), an instrument that uses a nondispersive method for achieving accurate classification, reproduction, and spectral estimation of color by exploiting engineered variations in optical transmittances of 2D materials. (a) Schematics of data collection system in dark enclosure. The RGB colors are generated via a python code on a screen, the generated lights are allowed to pass through a set of transmissive windows, one at a time; then the transmitted lights are collected by the single photodetector. The signals are collected with the same computer. The measured photocurrent is related to the generated incident spectrum, the transmittance of the window, and the responsivity of the photodetector, via the given formulas. (b) Transmissive windows mounted on a disk (top). Transmittance curve and real-size optical image of one of a typical transmissive window made of CVD-grown TMDs, as well as microscopic image from a segment of this transmissive window (bottom). (c) Application of k-nearest neighbor ($k$-NN) method with $k=1$, where only two transmissive windows ($n=1,2$ out of N) and five groups of data $\left(S_{i=1-5}\right)$ are shown. For each i, an N-dimensional data point $S_i=S_i\left(I_1^i,I_2^i,\dots ,I_N^i\right)$ for ${\text{RGB}}_{\text{i}}$ is generated and stored. The data points with similar colors group together in the training set. Here, $S_i=3$ is the nearest neighbor class for the test sample $\text{D}=\text{D}(I_1^i,I_2^i,\dots I_N^i)$. (d) A small set of tested single colors, red, green, and blue (left columns in each column pair), with their corresponding estimated colors (right columns in each column pair), using the methods outlined in panels (a)-(c). Adapted and modified with permission from ref 81. Copyright 2022 Elsevier.

2. Synthesis and Processing.

2.1. MXenes with Multiple M-Elements: Composition—Structure—Property Relationships.

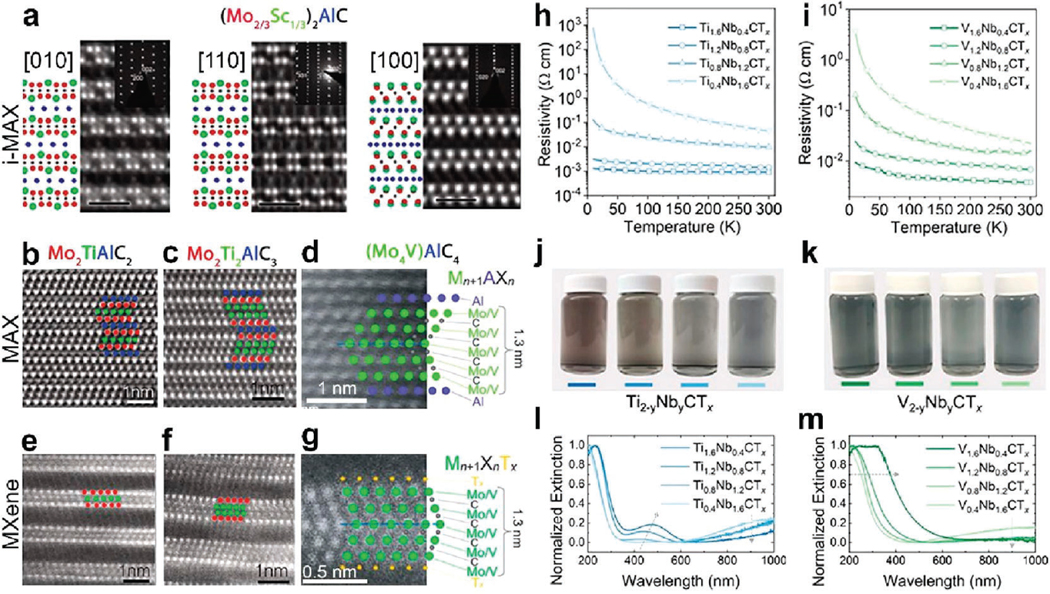
MXenes are an emergent, and potentially the largest, class of 2D materials discovered to date.⁸⁴ This class of transition metal carbides, nitrides, and carbonitrides has the general formula ${\text{M}}_{n+1}{\text{X}}_n{\text{T}}_x$ where $\text{M}$ is an early transition metal ($\text{Ti}$, $\text{V}$, $\text{Nb}$, $\text{Ta}$, etc.), $\text{X}$ is $\text{C}$ and/or $\text{N}$, ${\text{T}}_x$ represents the surface functional groups (typically $\text{O}$, $\text{OH}$, $\text{F}$, and $\text{Cl}$), and $n=1-4$.⁸⁵ MXenes are produced by a top-down synthesis approach where ${\text{M}}_{n+1}{\text{AX}}_n$ (MAX;⁸⁶ A is typically Al, but can be Si or Ga) phase precursors are selectively etched via wet HF-containing mixtures,⁸⁷ molten salt,⁸⁸ halogenation,⁸⁹ and others.⁹⁰ MXenes have been widely studied due to their desirable properties, such as hydrophilicity (soluble in water with no additives or surfactants),⁹¹ ease of processing (able to be used in any conventional water-based route, e.g., spray coating, dip coating, vacuum filtration),⁹¹ scalability (no change in properties as batch size is increased),^92,93 and desirable optical (tunable plasmon resonance, optical response in visible region, electro-chromic nature),^94–96 electrical (>20,000 S/cm conductivity, metallic-like response to cryogenic temperatures, magnetic transitions), ^94,96,97 and mechanical properties (around 0.4 TPa Young’s modulus from solution processed materials).^97,98 Due to these properties, MXenes have found widespread use in a variety of fields, including electrochemical energy storage,⁹⁹ electromagnetic interference shielding,¹⁰⁰ medicine,^101,102 environmental remediation,^103,104 additives to composites, etc.^105,106 To date, more than 30 stoichiometric MXenes have been discovered, in addition to a theoretical infinite number of solid-solution MXenes. In addition to single-M MXenes, there are broadly three classes of multi-M MXenes: i-MXenes (in-plane ordered divacancy MXenes; Figure 7a), ordered double transition metal MXenes (out-of-plane ordered MXenes; Figure 7b,c,e,f), and solid-solution MXenes (Figure 7d,g).

Figure 7.

Structures and properties of MXenes. (a) High-resolution scanning transmission electron microscopy (HRSTEM) and corresponding selected area electron diffraction (SAED) patterns of ${\left({\text{Mo}}_{2/3}{\text{Sc}}_{1/3}\right)}_2\text{AlC}$ i-MAX phase along the [010], [110], and [100] crystal orientation, together with schematics based on a monoclinic $\text{C}2/c$ symmetry. The red, green, blue, and black spheres in the schematics are Mo, Sc, Al, and C, respectively. (b) HRSTEM of ${\text{Mo}}_2{\text{TiAlC}}_2$ (c) ${\text{Mo}}_2{\text{Ti}}_2{\text{AlC}}_3$, and (d) ${\text{Mo}}_4{\text{VAlC}}_4\text{MAX}$ phases. STEM images of (e) ${\text{Mo}}_2{\text{TiC}}_2{\text{T}}_x$, (f) ${\text{Mo}}_2{\text{Ti}}_2{\text{C}}_3{\text{T}}_x$, and (g) ${\text{Mo}}_4{\text{VC}}_4{\text{T}}_x$ MXenes. For the panels (b, c, e, f), the blue, red, and green spheres represent Al, Mo, and Ti, respectively. For the panels (d, g), the green, blue and orange spheres represent Mo/V, Al and surface terminations ${\text{T}}_x$. Images in (d) and (g) demonstrate a herringbone-type structure with an atomic schematic and mirror plane shown by solid circles on the right and a dashed line, respectively. Reproduced (adapted) with permission from ref 97. Copyright 2021 Elsevier. (h, i) The temperature dependent electrical properties of (h) ${\text{Ti}}_{2-\text{y}}{\text{Nb}}_y{\text{CT}}_x$ and (i) ${\text{V}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$. (j, k) The optical properties of solid-solution (j) ${\text{Ti}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ and (k) ${\text{V}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ colloidal solutions in deionized water. In all three systems, the gradual change in color resulting from the different stoichiometries can be observed. (l, m) The quantitative UV-vis spectra normalized to a maximum extinction of 1 of the (l) ${\text{Ti}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ and (m) ${\text{V}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ systems. For all systems, multiple features are visible with a nonlinear shift in the absorbance with changes in the composition. Reproduced (adapted) with permission from ref 96. Copyright 2020 American Chemical Society.

2.1.1. In-Plane Ordered MXenes (I-MXenes).

I-MXenes are synthesized from ${\left({\text{M}}_{2/3}^{\prime }{\text{M}}_{1/3}^{\prime \prime }\right)}_2\text{AlC}$ I-MAX phases, where ${\text{M}}^{\prime }$ is $\text{Mo}$, $\text{W}$, $\text{V}$, $\text{Cr}$, and ${\text{M}}^{″}$ is $\text{Sc}$, $\text{Zr}$ or $\text{Y}$, or some lanthanides. These structures occur due to the difference in atomic size between ${\text{M}}^{\prime }$ and ${\text{M}}^{″}$. The most common i-MAX phases are ${\left({\text{Mo}}_{2/3}{\text{Sc}}_{1/3}\right)}_2\text{AlC}$ (Figure 4a)¹⁰⁷ or ${\left({\text{Mo}}_{2/3}{\text{Y}}_{1/3}\right)}_2\text{AlC}$,¹⁰⁸ but there a number of others have also been produced.^109,110 These materials, when etched, can lead to two different structures, either ${\left({\text{Mo}}_{2/3}{\text{Sc}}_{1/3}\right)}_2{\text{CT}}_x$ or ${\text{Mo}}_{4/3}{\text{CT}}_x$, depending on the etchant time and concentration.¹¹¹ This leads to a benefit, where the effect of controlled defects in MXenes can be studied. The i-MXenes have positive and negative properties—due to the highly defective nature, these MXenes tend to be more chemically active, especially for catalysis.¹¹⁰ However, due to their defective nature, they also tend to be less stable.¹¹² For example, ${\text{Mo}}_{4/3}{\text{CT}}_x$ has a volumetric (gravimetric) capacitance of 1153 F cm⁻³ (339 F g⁻¹),¹⁰⁷ which is ≈65% higher than ${\text{Mo}}_2{\text{CT}}_x$. Further studies have shown that the enhanced capacitance and energy density of ${\text{Mo}}_{4/3}{\text{CT}}_x$ comes at the expense of lower stability and a faster discharge rate.¹¹³

2.1.2. Out-of-Plane Ordered MXenes.

Out-of-plane ordered MXenes have two elements that do not intermix in the M layers (Figure 7b,c,e,f), such as ${\text{Mo}}_2{\text{Ti}}_2{\text{C}}_3{\text{T}}_x$, ${\text{Mo}}_2{\text{TiC}}_2{\text{T}}_x$, ${\text{Mo}}_2{\text{ScC}}_2{\text{T}}_x$,¹¹⁴ or ${\text{Cr}}_2{\text{TiC}}_2{\text{T}}_x$. For these, the $\text{Cr}$ (or $\text{Mo}$) is on the outer layer with $\text{Ti}$ (or $\text{Sc}$) on the inner layer. These MXenes are beneficial because they offer unique chemistries that cannot be easily attained in single-M MXenes.^115,116 Moreover, it was shown that the inner layer affects the electronic properties of the outer layer transition metal.¹¹⁷ This class of MXenes also has different properties than single-M MXenes, such as modified plasmon resonance.⁹⁵ ${\text{Mo}}_2{\text{TiC}}_2{\text{T}}_x$ has a transverse surface plasmon resonance at 476 nm, whereas ${\text{Ti}}_3{\text{C}}_2{\text{T}}_x$ is at 780 nm. Based on this, ${\text{Mo}}_2{\text{TiC}}_2{\text{T}}_x$ should have a higher free electron density, but experimentally this has not been confirmed, electrical conductivity points to the opposite (≈1500 S/cm for ${\text{Mo}}_2{\text{TiC}}_2{\text{T}}_x$ against >20,000 S/cm for ${\text{Ti}}_3{\text{C}}_2{\text{T}}_x$),¹¹⁸ ${\text{Cr}}_2{\text{TiC}}_2{\text{T}}_x$ was also shown to be unique among MXenes; it is the only MXene that was experimentally shown to have a magnetic transition resulting from the MXene itself.¹¹⁶

2.1.3. Solid-Solution MXenes.

Solid-solution MXenes have uniform, random mixing of the two M elements within their entire structure (Figure 7d,g). There have been a number of solid-solution MXenes synthesized already, including ${\text{Ti}}_{2-y}{\text{Nb}}_y{\text{T}}_x$,⁹⁶ ${\text{Nb}}_{2-y}{\text{V}}_y{\text{T}}_x$,⁹⁶ ${\text{Ti}}_{2-y}{\text{V}}_y{\text{T}}_x$,⁹⁶ ${\text{Ti}}_{3-y}{\text{Ta}}_y{\text{T}}_x$,¹¹⁹ ${\text{Mo}}_{4-y}{\text{V}}_y{\text{T}}_x$,¹²⁰ ${\text{Nb}}_{4-y}{\text{Zr}}_y{\text{T}}_x$,¹²¹ ${\text{Nb}}_{4-y}{\text{Ti}}_y{\text{T}}_x$,¹²¹ and ${\text{Mo}}_4{\text{VC}}_4{\text{T}}_x$,⁸⁵ it is noteworthy that this class of MXenes is the only one that spans $n=1-4$ to date. This is noteworthy: for MXenes, the only case where $n=4$ observed to date was a solid-solution MXene, ${\text{Mo}}_4{\text{VC}}_4{\text{T}}_x$.⁸⁵ This MXene is stable only at a narrow compositional range, a variance of 5% in either direction of the M element causes impurity MAX phases to form. It also has a structure unlike other MAX/MXene—it is twinned at the middle M-site, a structural motif that has never been observed before. Moreover, in terms of properties it is also exceptional, it has a higher thermal stability than any other MXene, is resistant to the electron-withdrawing effect of organic intercalants, and has low optical absorbance over the entire studied range (out to near-infrared).⁸⁵

In solid-solution MXenes, some properties appear to be linearly related to the chemistry, while others are nonlinear. The conductivity is one property that monotonically varies with the chemistry. Typically, ${\text{Nb}}_2{\text{CT}}_x$ has a low conductivity (≈ 25 S/cm), while ${\text{V}}_2{\text{CT}}_x$ and ${\text{Ti}}_2{\text{CT}}_x$ are substantially higher (>1000 S/cm).^95,122,123 As the Nb content in ${\text{Ti}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ and ${\text{V}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ increases, the conductivity correspondingly decreases (Figure 7h,i).^96,123 This trend continues over the entire compositional range, and all films show similar temperature response. But, interestingly there are a variety of properties that are not linearly related to the composition. For single-M MXenes, there is a single plasmon resonance peak that is related to the free electron density of the MXene, and is affected by the etching/delamination approach.⁹⁶ While, for solid-solution MXenes (Figure 7j,k), there are instead two plasmon resonance peaks (Figure 7l,m). Using ${\text{Ti}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ as an example, there is one peak around 550 nm (similar to ${\text{Ti}}_2{\text{CT}}_x$) and a second in the near IRregion (similar to ${\text{Nb}}_2{\text{CT}}_x$), but both are slightly shifted, due to the interactions of the metals with each other.⁹⁷ This is due to the modification of the electronic states of the metals due to the other metal, as was recently shown with electron energy loss spectroscopy (EELS)¹²⁴ in addition to computational predictions.⁹⁷ Interestingly, the same trend with EELS does not occur with ${\text{Nb}}_{2-y}{\text{V}}_y{\text{CT}}_x$, meaning that the interactions depend on the specific metals themselves. Thus, to fully understand and predict the specific properties that solid-solution MXenes will have, it is imperative to continue fundamental studies.

The electrochemical performance of solid-solution MXenes also benefits from the multiple chemistries.^120,125 For certain MXenes, such as ${\text{Ti}}_2{\text{CT}}_x$ and ${\text{V}}_2{\text{CT}}_x$, they have high capacitance, but are unstable. ${\text{Nb}}_2{\text{CT}}_x$ is highly stable but has lower capacitance. Thus, combining the two can alleviate the negatives of both chemistries. For ${\text{Ti}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$ and ${\text{V}}_{2-y}{\text{Nb}}_y{\text{CT}}_x$, the cyclic voltammograms (CVs) are directly related to the MXene chemistry. Depending on the specific chemistry, the volumetric (gravimetric) capacitance ranged from 680 to 1070 F cm⁻³ (245–490 F g⁻¹) in $3{\text{M H}}_2{\text{SO}}_4$.¹²⁵ Interestingly, in some cases, middle compositions outperformed both extremes in capacitance: ${\text{V}}_{1.2}{\text{Nb}}_{0.8}{\text{CTT}}_x$ and ${\text{Ti}}_{1.6}{\text{Nb}}_{0.4}{\text{CT}}_x$ outperformed ${\text{Ti}}_2{\text{CT}}_x$, ${\text{V}}_2{\text{CT}}_x$, or ${\text{Nb}}_2{\text{CT}}_x$ in these studies. This implies that some synergistic effect is occurring within solid-solution MXenes, giving them enhanced performance. A similar case where a middle composition outperforms other extremes was also observed in ${\text{Mo}}_{4-y}{\text{V}}_y{\text{C}}_3{\text{T}}_x$.¹²⁰

2.2. Controlling the Structure and Phase of Low-Symmetry 2D Materials.

Low-symmetry 2D materials with in-plane anisotropic crystal structures possess a distinct functionality because of their in-plane direction-dependent properties. Low-symmetry 2D materials include black phosphorus, certain TMDs including rhenium disulfide (${\text{ReS}}_2$) and diselenide (${\text{ReSe}}_2$), and monochalcogenides of the group IV elements Ge and Sn.^126,127 Here, we focus on the Sn monochalcogenide semiconductors SnSe and SnS. Their crystal structure resembles a perturbed rock-salt, with ferroelectric and ferroelastic distortions and substantial phonon anharmonicity, which make these materials interesting for ferroelectrics, thermoelectrics, and photonics.^128–130 The orthorhombic, ground state crystal structure is thermodynamically adjacent to different phases with higher symmetry and distinct properties, suggesting the possibility of facile phase control and phase-change functionality.¹³¹

We visualize the crystal structure in Figure 8a-d. The top view (Figure 8a) illustrates the shape and symmetry of the in-plane unit cell. The in-plane unit cell is a rectangle with dissimilar lattice constants ranging from 3.9 to 4.5 Å, depending on the chalcogen and crystal thickness. Each 2D sheet in the crystal structure contains two layers of atoms (Figure 8j,k), and the out-of-plane lattice constant is perpendicular to the layers, forming the overall orthorhombic crystal structure. The arrangement of Sn-Se bonds, distorted from the high-symmetry rock-salt structure (Figure 8j), results in net polarization along the longer in-plane armchair direction.¹³² The unit cell contains two sheets with opposing polarity (called AB stacking), so that the crystal is antiferroelectric and centrosymmetric (i.e., nonpolar). In Figure 8d we visualize the ${\text{SnSe}}_7$ coordination polyhedron, with both short-bonds and long-bonds within each 2D sheet, and longer bonds linking the sheets.¹³³

Figure 8.

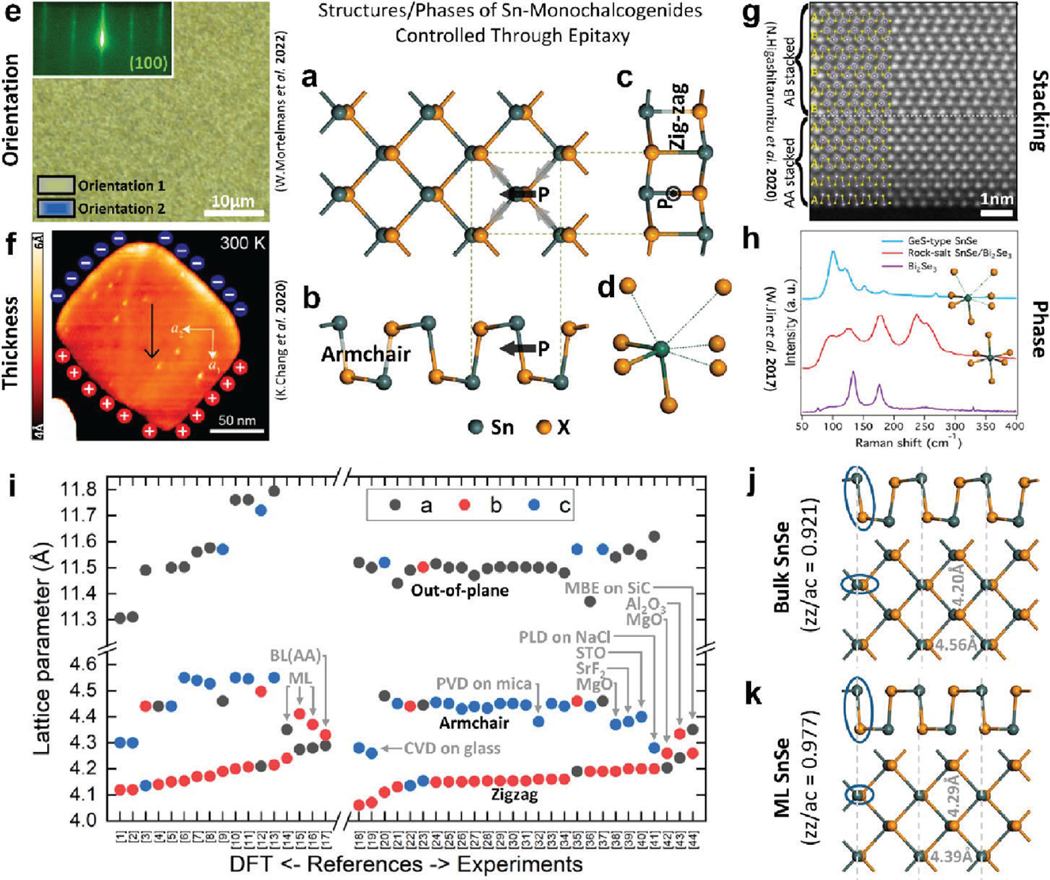
Controlling the structure and phase of Sn monochalcogenides through epitaxy. (a) Top view showing the in-plane unit cell in dashed lines, orientation of the polar bonds, and the net in-plane polarization within a single sheet. (b, c) Visualizing the in-plane armchair and zigzag directions. (d) The ${\text{SnSe}}_7$ coordination polyhedron. Reproduced with permission from ref 134. Copyright 2022 American Chemical Society. (e-h) Demonstrations of structure and phase control through epitaxy: (e) eliminating twin domains. Reproduced with permission from ref 134. Copyright 2022 American Chemical Society. (f) realizing ferroelectricity in monolayers. Reproduced with permission from ref 135. Copyright 2020 American Chemical Society. (g) making a multilayer, polar crystal with metastable layer stacking. Reproduced with permission under a Creative Commons CC-BY 4.0 License from ref 136. Copyright 2020 Springer Nature. (h) Making a topological crystalline insulator by stabilizing the rock-salt phase. Reproduced with permission under a Creative Commons Attribution 4.0 International license from ref 137. Copyright 2017 American Physical Society. (i) Reported lattice constants ordered from smallest to largest along the armchair direction and separated into results reported by theory (left) and experiments (right). Gray arrows give more information on the simulated/measured samples. (j, k) Cross-section and plan-view images of SnSe simulated by DFT for the case of (j) bulk and (k) monolayer. The armchair lattice constants are visualized using gray dashed lines, and the reduced in-plane anisotropy in the monolayer case is highlighted using blue ovals. Note that there is no consensus in the literature on crystal indexing.

The properties and functionality exclusive to these low-symmetry 2D materials can be accessed by controlling the structure and phase through epitaxial growth (Figure 8e-h). The ferroelastic distortion that creates the distinction between armchair and zigzag directions leads to a system of 90° twin boundaries, across which these directions (and their associated anisotropic properties) exchange. Mortelmans et al.¹³⁴ showed that these 90° twins in SnSe can be eliminated by epitaxial growth on a substrate with a rectangular and lattice-matched in-plane unit cell (Figure 8e), making possible large-area thin films with uniform in-plane anisotropy. Chang et al.¹³⁵ demonstrated through epitaxial growth on 6H-SiC(0001) that monolayers of SnSe are indeed polar (Figure 8f), and exhibit in-plane ferroelectricity at room temperature. The antiferroelectric, AB-stacked crystal structure implies that polar crystals can only be achieved in the monolayer limit. However, Higashitarumizu et al.¹³⁶ observed AA stacking in multilayer SnS crystals grown on mica, thereby realizing polar and ferroelectric SnS beyond the monolayer limit, with intriguing possibilities for the optical and optoelectronic properties (Figure 8g). Jin et al.¹³⁷ demonstrated that this nonequilibrium rock-salt phase can be stabilized through epitaxial film growth (Figure 8h). These results highlight that a multitude of structures and phases can be accessed through epitaxy, creating possibilities for fundamental study and device technology.

Within the orthorhombic ground state structure, the in-plane lattice constants and the measure of in-plane anisotropy are remarkably sensitive to crystal thickness and likely also growth conditions. Areview of SnSe lattice constants reported by theory (left) and experiments (right) is provided in Figure 8i. The data are ordered from smallest (4.12 Å for theory, 4.06 Å for experiment) to largest (4.29 Å for theory, 4.26 Å for experiment) lattice constant along the zigzag direction. From the presented theoretical work, we see that the lattice constants in the zigzag and armchair directions approach closer to each other in monolayer and bilayer SnSe, compared to the bulk.^138,139 In other words, on decreasing the crystal thickness, the in-pane symmetry approaches square, bringing the crystal closer to the rock-salt structure. This trend is confirmed by experimental observations on thin films grown using CVD and physical vapor deposition (PVD), compared to measurements on thicker films and bulk crystals.^140,141 The out-of-plane lattice constant generally increases along with increasing in-plane lattice constants.

In Figure 8j,kwe present DFT simulations that illustrate and quantify the tendency of SnSe to have reduced in-plane anisotropy for thinner crystals. Bulk SnSe has in-plane lattice constants of 4.20 and 4.56 Å, in a ratio of 0.921; results for 2D SnSe are 4.29 and 4.39 Å, in a ratio of 0.977. This approach toward square symmetry manifests as a reduced staggering, and Sn—Se out-of-plane bonds that approach perpendicular relative to the layers (highlighted by blue ovals), which reduces the in-plane polarization (Figure 8a) control of SnX structure and phase through epitaxy may enable a range of useful applications. The in-plane ferroelastic distortion of single-crystal thin films can be used for “domain change” applications, whereby the armchair and zigzag directions are switched (exchange of short- and long-bonds within the plane) on a picosecond time scale by pulsed light, leveraging the dielectric anisotropy to realize a diffusionless, martensitic, nonthermal, nonresonant switching process.¹⁴² Such “domain change” functionality could be useful for low-injection-loss optical phase control in photonic integrated circuits.¹⁴³ Ferroelectric monolayer and AA-stacked multilayer crystals could be used for electro-optic phase modulation, nonlinear optics, and concepts in ferroelectric nonvolatile memory.¹⁴⁴ The topological crystalline insulator phases could enable high-responsivity infrared optical detectors.¹⁴⁵ Control of crystal anisotropy could also enable fundamental understanding and applications of thermoelectricity in SnX materials, for waste heat energy harvesting.¹⁴⁶

2.3. Epitaxial Growth of Wafer-Scale TMD Monolayers by MOCVD.

Epitaxial TMD monolayers (${\text{MoS}}_2$, ${\text{WS}}_2$, ${\text{WSe}}_2$) at the wafer scale is of significant interest for device applications. MOCVD is a promising approach for TMD growth as it enables the use of high substrate temperatures (700—1000 °C) and chalcogen/metal ratios (10³—10⁵)^147,148 that are beneficial for epitaxy. In addition, the flow rate of precursors can be modulated during growth to enhance the surface diffusion of metal-containing species and control the lateral growth rate of TMD domains.¹⁴⁷ C-plane sapphire has emerged as a promising substrate for TMD epitaxy due to its crystallographic compatibility and good chemical stability in the CVD environment. In addition, steps on the sapphire surface can be used to induce a preferred alignment of TMD domains resulting in a significant reduction in inversion domains in the films.^149,150

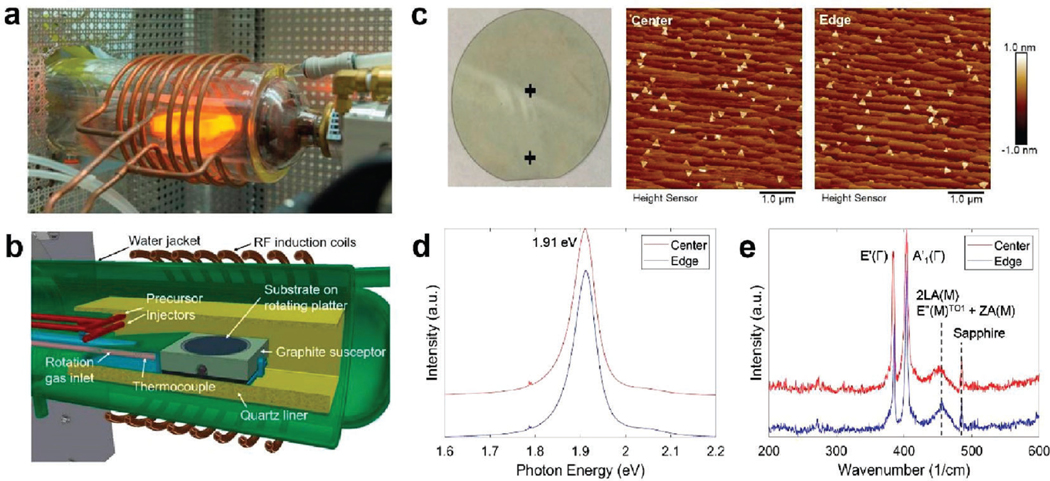
MOCVD growth of wafer-scale TMDs has been carried out using a cold-wall horizontal quartz tube reactor that includes an induction-heated rotating SiC-coated graphite susceptor as shown in Figure 9a,b, which is available in the Penn State 2D Crystal Consortium facility.¹⁵¹ The precursors used include metal hexacarbonyls ($\text{Mo}{(\text{CO})}_6$ and $\text{W}{(\text{CO})}_6$) and hydrides (${\text{H}}_2\text{Se}$ and ${\text{H}}_2\text{S}$) with ${\text{H}}_2$ as the carrier gas. The cold wall geometry, reduced reactor pressure (50—200Torr) and separate gas injectors are beneficial to reduce the extent of gas phase prereactions that occur between the carbonyls and hydrides.⁴³ Epitaxial growth of monolayer ${\text{MoS}}_2$,¹⁵² ${\text{WS}}_2$,¹⁵³ and ${\text{WSe}}_2$¹⁵⁴ on 2” c-plane sapphire miscut ±0.2° toward the m-axis has been demonstrated at growth temperatures in the range of 800—1000 °C. For example, epitaxial ${\text{MoS}}_2$ films grown under these conditions consist of a uniform monolayer across the entire 2” diameter wafer with small triangular bilayers at a surface coverage of <15% (Figure 9c). Undulations in the surface morphology of the monolayer arise from the steps on the sapphire surface. Room temperature photoluminescence (PL) spectra (Figure 9d) obtained at the center and the edge of the 2” sapphire contain an emission peak at 1.91 eV associated with the Aexciton of 1L ${\text{MoS}}_2$.¹⁵⁵ Raman spectra (Figure 9e) obtained at the center and edge of the wafer show the characteristic modes for 1L ${\text{MoS}}_2$. All of these results indicate the quality and monolayer thickness can be uniform across the entire wafer.

Figure 9.

MOCVD for epitaxial 2D TMD semiconductors. (a) photo and (b) schematic of horizontal cold wall MOCVD reactor used for TMD growth. (c) Surface morphology of ${\text{MoS}}_2$ monolayer grown on 2” c-plane sapphire at center and edge of the wafer (locations indicated by + in photo). Room temperature (d) PL and (e) Raman spectra obtained at the center and edge of the wafer show spatially uniform monolayer thickness across the wafer.

The availability of wafer-scale MOCVD-grown epitaxial TMD monolayers films has enabled a variety of studies that benefit from high quality large area films that can be readily transferred off the growth substrates for device fabrication and testing. This includes benchmarking studies of FET performance,¹⁵⁶ 2D memtransistors for Baynesian networks,^157,158 large area vdW superlattices,¹⁵⁹ localized quantum emitters,¹⁵⁹ and 2D photodetectors for biomimetic sensing platforms.¹⁶⁰

2.4. Substitutional Doping and Alloying 2D Materials for Device Applications.

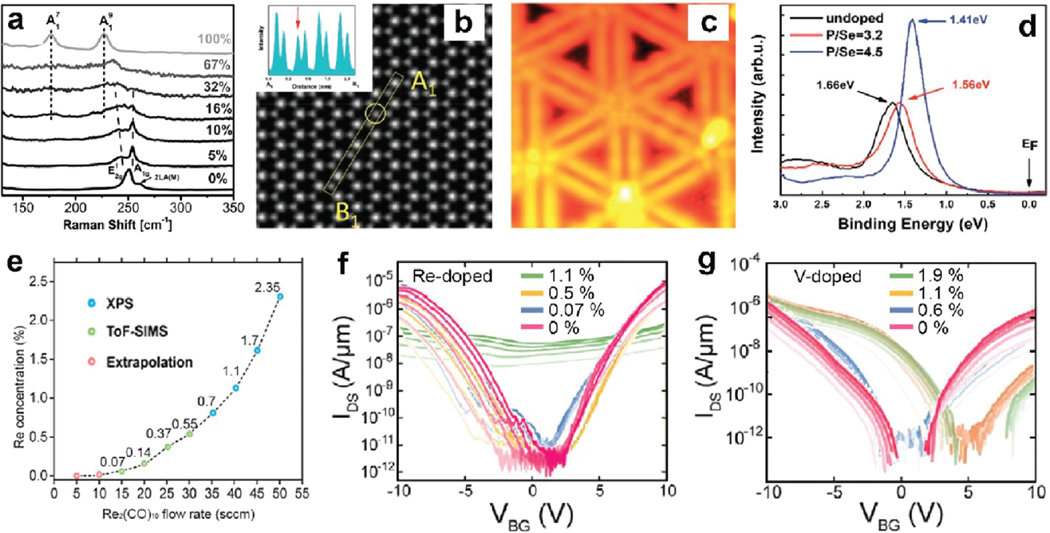
Ion implantation is a standard semiconducting technique to achieve small-depth channel postgrowth electronic doping on Si using energetic ion beams. However, the high energy beams in traditional ion implantation techniques will lead to significant damage for 2D materials and would require postimplantation thermal annealing to recover crystallinity. Bottom-up doping or alloying of 2D materials can be achieved through MBE and MOCVD in a homogeneous and repeatable fashion by codelivery and control of multiple source materials and their flux ratios. First, in an attempt to demonstrate the potential of MBE to grow TMD alloys at back-end-of-line (BEOL) temperatures (<550 °C) and highlight relevant challenges, Barton et al.¹⁶¹ reported ${\text{WSe}}_{(2-x)}{\text{Te}}_x$ alloys grown at $T=250°\text{C}$. For $\text{Te}<14\%$, a stable alloy in the semiconducting 2H phase was achieved while for $\text{Te}>79\%$ a semimetallic 1T′ phase was found to be stable. Interestingly, for Te in the range of 14 to 79% a miscibility gap was observed which resulted in a phase separation between two different alloys having different crystal structures and composition, as shown by Raman data in Figure 10a. The metallic alloys can be very useful to make low resistance contacts by increasing the film conductivity significantly.

Figure 10.

Doping and alloying 2D materials for electrical applications. (a) Raman spectra of ${\text{WSe}}_{(2-\text{x})}{\text{Te}}_x$ alloys showing a transition from the semiconducting 2H phase to the semimetallic 1T' phase as a function of increasing Te concentration. Adapted from ref 161. Copyright 2019 IOP Publishing Ltd. (b) ADF-STEM image and corresponding intensity profiles along the boxed region showing a P atom sitting at a Se site. (c) STM image of P-doped ${\text{MoSe}}_2$ (sample bias: —1.0 V, size: 10 X 10 nm²). The hexagonal structure of ${\text{MoSe}}_2$ remained intact after doping. (d) UPS of the undoped, lightly doped (P/Se flux ratio ≈3.2), and heavily doped (P/Se ≈4.5)-doped ${\text{MoSe}}_2$, showing a p-type behavior. Panels (b)—(d) were adapted with permission from ref 162. Copyright 2020 John Wiley & Sons, Inc. (e) The doping concentration of Re in ${\text{WSe}}_2$ from X-ray photoemission spectroscopy (XPS), secondary ion mass spectrometry (SIMS), and extrapolated points are plotted as a function of ${\mathrm{Re}}_2{(\text{CO})}_{10}$ flow rate during ${\text{WSe}}_2$ growth. (f) Transfer characteristics of pristine and Redoped ${\text{WSe}}_2$ field-effect transistors. While ambipolar conduction in the pristine and lightly Redoped ${\text{WSe}}_2$ films is demonstrated, at higher Re concentrations device performance is degraded due to the increasing impurity scattering. Panels (e) and (f) were adapted and modified with permission from ref 164. Copyright 2020, Wiley-VCH. (g) Transfer characteristics of the pristine ${\text{WSe}}_2$ film at different drain voltages (1—5 V) display ambipolar conduction. However, the n-branch degrades as V concentration increases and transistors gradually become p-type. All transistors were on 50 nm ALD ${\text{Al}}_2{\text{O}}_3$. Reproduced with permission from ref 165. Copyright 2021, Wiley-VCH.

Recently, substitutional doping of TMDs has been gaining popularity for a variety of applications. Xia et al.¹⁶² demonstrated phosphorus (P) doping in a monolayer of ${\text{MoSe}}_2$ by codepositing P, Mo, and Se on a variety of substrates to tune the electrical conductivity. As shown in Figure 10b, P substitution at the Se sites was confirmed through annual dark field scanning transmission electron microscopy (ADF-STEM).¹⁶² The cluster setup of the MBE system, combining scanning tunneling microscopy (STM) and ultraviolet photo-electron spectroscopy (UPS), allowed them to perform in-depth characterization without exposing the samples to air. As confirmed by STM (Figure 10c), P doping did not affect the hexagonal structure or inversion domain boundaries of the ${\text{MoSe}}_2$, nor generated any apparent P clusters within or on the surface of the ${\text{MoSe}}_2$. In contrast to other reports where dopants prefer to segregate at domain boundaries,¹⁶³ very uniform doping was achieved. UPS measurements showed a clear p-type behavior where the valence band maxima gradually moved closer to the Fermi level ($E_{\text{F}}$) as a function of P doping (Figure 10d).¹⁶² To have such fine control over tuning the electrical conductivity and $E_{\text{F}}$ through doping is highly desirable to control the threshold voltages and ON-current density in TMD-based transistors.

Recently, controllable substitutional doping of TMDs with transition metal elements during MOCVD for modulating TMDs-based transistors has been demonstrated. Kozhakhmetov et al.^164,165 introduced ${\mathrm{Re}}_2{(\text{CO})}_{10}$ and ${\text{V}}_2{\left({\text{C}}_5{\text{H}}_5\right)}_2$ during ${\text{WSe}}_2$ growth to substitute W with Re and V for n- and p-type doping, respectively. Furthermore, by controlling carrier gas flow going through the bubblers of precursors that provide dopants, dopant concentrations can be tuned the parts per million to the percentage level in ${\text{WSe}}_2$ (Figure 10e). Furthermore, to understand the impact of dopant types and concentrations on the transport of 2D ${\text{WSe}}_2$, Kozhakhmetov et al.^164,165 established the relationship between dopant concentration and transfer characteristics for both Re- and V-doped ${\text{WSe}}_2$ using back-gate-FET (BGFET). The pristine ${\text{WSe}}_2$ BGFETs exhibit ambipolar transfer characteristics and remain the same until both Re and V concentrations exceed 1%. While standard semiconductor doping level for Si is at the ppm level (<0.1%), the doping for 2D semiconductors is relatively ineffective due to the quantum confinement effect and reduced dielectric screening.¹⁶⁶ This could be alleviated by encapsulation with high-$\kappa$ dielectric materials,¹⁶⁶ alloying TMDs with high dopant concentrations,¹⁶⁷ or few-layer thick TMDs. Nevertheless, contrary to high energy ions or high temperature diffusion processes normally used in the CMOS-compatible processes, in situ substitutional doping during MBE and MOCVD can maintain the highest crystallinity of TMDs and control dopant concentration well.

2.5. Native Oxide Formation of Semiconducting TMDs.

Like most metals in the galvanic series, and nearly all well-developed semiconductors, the surfaces of TMDs are prone to oxidation. Oxidation of TMDs is a long-appreciated and still outstanding challenge in present-day applications of TMDs for solid-state lubrication and desulfurization catalysis. In general, the TMD surface is more easily oxidized as the chalcogen decreases in electronegativity (descending in the periodic table) from S, to Se, to Te. Group VI compounds containing Mo and W have a larger formation energy of sulfur vacancies and are more stable compared to nongroup IV compounds containing Hf, Zr, Ti, and Nb.¹⁶⁸ The oxidation of synthetic thin films is more pronounced than that of bulk single crystals, due to accelerated oxidation at random GBs, twin boundaries, and other crystallographic defects.¹⁶⁹ Control over oxidation is therefore a further reason to address the challenges of nucleation and growth in TMD thin film crystal growth, for future applications in microelectronics, optoelectronics, and photonics. ¹⁷⁰

In particular, for microelectronics, the sustained academic research activity and the increasing attention from industry increase the urgency of understanding and controlling the processing and properties of TMD native oxides. In some situations, such as applications of monolayer crystals of highly oxygen-sensitive compounds (e.g., ${\text{MoTe}}_2$, ${\text{TiS}}_2$), oxidation must be avoided entirely, and therefore oxidation rates even in nominally oxygen-free environments should be quantified.^171,172 In other situations, such as applications of multilayer crystals of less-oxygen-sensitive compounds (e.g., ${\text{WS}}_2$ field effect transistors), controlled oxidation could be beneficial, and research is ongoing into oxidation methods including thermal, UV/ozone, and plasma-assisted.^173–176 The processes of TMD native oxidation are quite different, on the atomic scale, from the long-studied native oxidation processes in legacy semiconductors, Si chief among them. Some of the oxides in question are volatile, such as ${\text{MoO}}_3$ that evaporates more readily than either Mo or ${\text{MoS}}_2$. The oxides of Mo and W can form with wide variations in oxygen content, leading to wide variations in electronic conductivity, which is detrimental for dielectric functionality but may be useful for resistive switching. Further, TMD oxidation is accompanied by chalcogen loss. The expelled chalcogen may leave the system as a volatile gas (e.g., ${\text{SO}}_2$), or segregate as an additional (and likely unwanted) solid phase.

A lesson learned from Si microelectronics is that, if at all possible, we should make use of semiconductor native oxides. Particularly for semiconducting TMDs for which the native oxides maybe useful dielectrics (or even ferroelectrics), there is opportunity in better understanding the processing—property relationships that control dielectric response, leakage, and interface quality. For TMDs for which the native oxides have easily varied conductivity, there is opportunity in developing resistive switching functionality for memory and neuromorphic computing, or in developing native oxide electrodes. It took decades to develop ${\text{SiO}}_2$ as a reliable dielectric for Si CMOS technology. With the much wider processing and property space for TMD native oxides than for traditional semiconductors, we look forward to many years of productive research and development.

2.6. Remote Epitaxy Using 2D Materials as an Intermediate Layer.

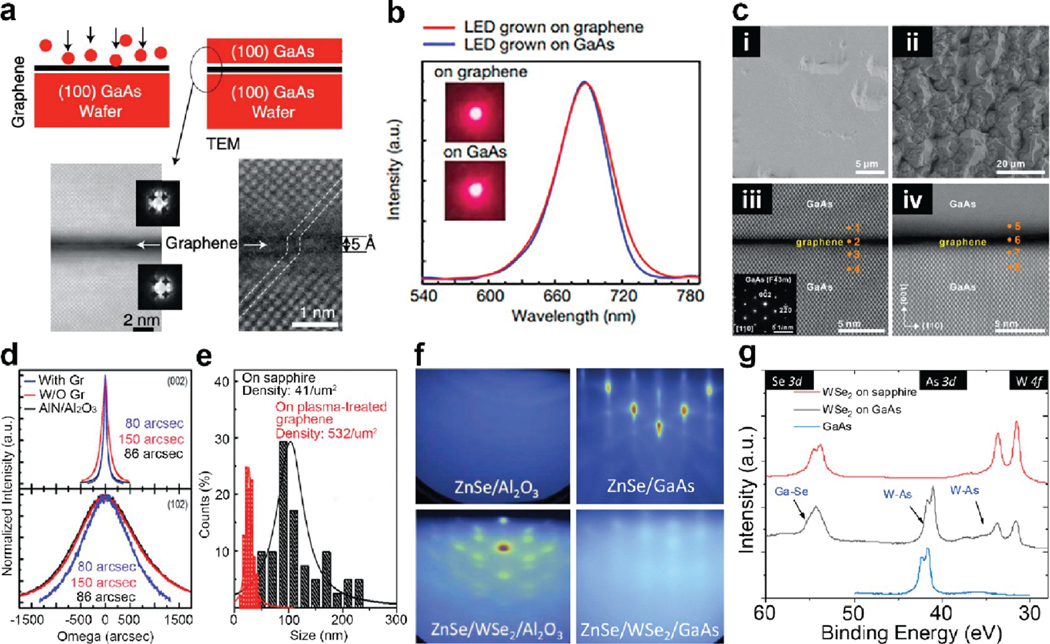
Remote epitaxy, utilizing a 2D/3D heterostructure, is an emerging technology that uses 2D materials as an intermediate layer to grow and later isolate single-crystal, freestanding 3D thin films in a nondestructive manner. In 2017, Kim et al.¹⁷⁷ revealed that thin films of different properties/functionalities can be grown, exfoliated, and heterogeneously stacked as required.¹⁷⁸ As shown in Figure 11a, a thin layer of graphene was used to partially screen the electrostatic potential fluctuations from the GaAs (100) substrate for homoepitaxial growth of GaAs (100).¹⁷⁷ Since the surface fluctuations of the substrate were not fully suppressed, adatoms on graphene were still able to interact with the substrate lattice to grow in an epitaxial manner with the same crystal orientation as the substrate. Additionally, unlike traditional epitaxy in which a strong bond exists between the epilayer and the substrate, the dangling bond free inert surface of graphene facilitated an easy detachment of the epilayer. An advantage of remote epitaxy is that adding a graphene intermediate layer between a grown film and its host wafer does not degrade the device performance of grown films (Figure 11b).¹⁷⁹ This area that had originally started from homoepitaxy of GaAs with graphene as an intermediate layer has now expanded to a variety of epitaxial materials (e.g., GaAs,¹⁸⁰ III-N,¹⁸¹ and oxide ultrathin films¹⁸²) and intermediate 2D layers (e.g., hBN¹⁸³ and TMDs¹⁸⁴).

Figure 11.

2D materials as the intermediate layer of remote epitaxy. (a) Illustration of remote epitaxy of GaAs and cross-sectional TEM at GaAs/graphene/GaAs interface. Adapted with permission from ref 178. Copyright 2019 Springer Nature. (b) Electroluminescence spectra of GaAs LEDs prepared directly on GaAs (red curve) and graphene through remote epitaxy on GaAs (blue curve). Inset shows pictures of working LEDs grown on both substrates. Adapted and modified with permission from ref 179. Copyright 2022 AIP Publishing LLC. (c) Scanning electron microscopy (SEM) (i, ii) and STEM (iii, iv) comparison of GaAs epitaxy using dry (i, iii) and wet (ii, iv) transferred graphene as an intermediate layer. The quality is significantly better on dry transferred graphene. Adapted and modified with permission from ref 180. Copyright 2021 AIP Publishing LLC. (d) X-ray diffraction rocking curves of the (002) and (102) planes for the aluminum nitride (AlN) growth on different templates. Quality is improved on the graphene template. (e) AlN nucleation and grain size comparison for direct growth on sapphire and remote epitaxy using plasma-treated graphene. Larger grain sizes on graphene enabled higher quality growth of the AlN film. (d, e) Adapted with permission from ref 181. Copyright 2020 AIP Publishing LLC. (f) Improvement in growth quality of MBE grown ZnSe by using an MBE grown 2D ${\text{WSe}}_2$ as a template. The reflection high-energy electron diffraction pattern transitions from Debye rings to streaky dots confirming better quality of the film when grown on ${\text{WSe}}_2$. (g) A comparison of ZnSe grown directly on GaAs with one grown using ${\text{WSe}}_2$ as an intermediate layer. (h) XPS comparison of ZnSe shown in panel (g). A reaction between the ${\text{WSe}}_2$ and the GaAs substrate can be clearly observed in the form of W-As and Ga-Se chemical states in the XPS. (f-h) Adapted with permission from ref 187. Copyright 2021 IEEE.

Since remote epitaxy is facilitated by the intermediate 2D film, the quality of this layer is one of the most important variables dictating the crystallinity of the grown epilayer. As shown in Figure 11c for remote epitaxy of GaAs, oxide formation at the substrate and interface of wet transferred graphene altered the effective distance between GaAs and the substrate to compromise the growth quality. In contrast, when GaAs was grown on dry-transferred graphene, which is less susceptible to oxidation, better quality was achieved. In a different report on remote epitaxy of GaN microcrystals, Jeong et al.¹⁸⁵ reported that when the 2D film is defective or has pinholes in it, a fraction of the grown structures could not be exfoliated and remained stuck on the substrate because of a direct covalent epitaxy through the defective region which made it difficult to reuse the substrate as well. Moreover, when there is an irregularity in the thickness of the 2D layer, such that there are regions where the thickness is greater than the critical thickness for remote interaction, epitaxy in those areas will not take place.¹⁸⁶ All these reports, consistently stress the elimination of transferred vdW layers and highlight the importance of contamination-free, uniformly grown 2D layers as the ideal pathway for reliable remote epitaxy.¹⁸⁷

Though remote epitaxy is still in its early stage of development, it is already showing potential for a variety of applications such as the growth of free-standing devices, flexible electronics, and light-emitting diodes (LEDs).¹⁷⁸ In addition to this, remote epitaxy can help improve the overall growth quality of a material as well. An increase in the crystallinity and grain size of the epi-film have been observed when an intermediate 2D layer is used (Figure 11d,e).¹⁸¹ Zhou et al.^184,187 used a MBE grown intermediate ${\text{WSe}}_2$ layer to improve the growth quality of zinc selenide (ZnSe) on sapphire at BEOL compatible temperatures (Figure 11f). ZnSe is a promising p-type semiconductor and is sought after as a channel material for BEOL transistors. The atomically thin, inert surface of ${\text{WSe}}_2$ enabled the long-range diffusion of adatoms at relatively lower temperatures to improve the crystallinity of the film. It is important to mention here that not only the quality of the intermediate layer, but the inertness of the substrate is also a critical factor to grow high quality epilayers. In contrast with the relatively chemically inert substrate sapphire, ZnSe growth on GaAs with a ${\text{WSe}}_2$ intermediate layer resulted in a degraded quality of the epilayer. Although GaAs and ZnSe are lattice matched (Figure 11g), the ${\text{WSe}}_2$ growth process reacted with the GaAs substrate, formed unwanted Ge-Se (Figure 11h), and failed to provide a pristine, dandling bond-free template for the epilayer to grow with high quality.

2.7. Challenges for Growing High-Quality 2D Materials on 3D Substrates by Thin-Film Deposition.

Among the bottom-up approaches of fabricating 2D materials and structures, CVD and PVD are commonly used, as they generally produce high quality thin films with relatively simple equipment and low maintenance costs. However, for some layered materials such as TIs, MBE is preferred for its extremely high purity,¹⁸⁸ precise control on doping,¹⁸⁹ and capability of creating atomically sharp interfaces¹⁹⁰ in heterostructures. Chalcogenide-based TIs like ${\text{Bi}}_2{\text{Se}}_3$ have hexagonal in-plane crystal structure with vdW bonds between each layer. They are of interest because their band structure comprises a bulkband gap andlinear-dispersed surface states crossed within.¹⁹¹ To exploit these surface states, we need wafer-scale thin films that are atomically smooth with few defects, similar to the needs for other layered materials. Unlike a conventional 3D semiconductor system, synthesis of these layered materials proceeds by vdW epitaxy in which a vdW gap exists between the material and the substrate, relaxing the lattice-matching constraint. However, the substrate still must be properly treated and growth conditions (substrate temperature, flux ratios, etc.) must be carefully chosen such that the material grows in the expected orientation.¹⁹²

Here, we will take the growth of ${\text{Bi}}_2{\text{Se}}_3$ by MBE as an example; however, many of the problems and solutions we discuss are applicable to other layered materials. ${\text{Bi}}_2{\text{Se}}_3$ has a crystal structure comprising sequentially covalently bonded quintuple layers (QL) of Se(1)-Bi-Se(2)-Bi-Se(1); the QLs are connected to each other by vdW bonds. ${\text{Bi}}_2{\text{Se}}_3$ has been successfully grown on sapphire,¹⁹³ GaAs,¹⁹⁴ Si,¹⁹⁵ and other substrates,^196,197 even with considerable lattice mismatch. However, these films tend to suffer from three major types of structural defects, all of which increase electron scattering and reduce TI device quality. The first step is the formation of twin defects. Because ${\text{Bi}}_2{\text{Se}}_3$ has a hexagonal in-plan crystal structure, it can nucleate in two different orientations rotated by 60 degrees with respect to each other with equal probability. When these domains coalesce, dislocations arise which can lead to electron scattering. Twin defects can be mitigated by selecting more lattice-matched substrates with pregrowth treatment to align substrate step edges,^198,199 or by using vicinal substrates with regular step edges to promote step-flow growth mode.²⁰⁰ However, vicinal substrates lead to additional difficulties as described below.

The second structural defect is terraced growth, in which a second or third layer begins to grow before the first layer has finished leading to a “wedding cake” morphology. This arises due to the presence of Ehrlich-Schwoebel (ES) barriers.^201,202 The ES barrier is the energy barrier for an adatom to cross an atomic step to a lower terrace.²⁰³ If the ES barrier is large compared to the in-plane diffusion barrier, adatoms are more likely to form a “daughter” island on incomplete “parent” island rather than move downward to fill the gap and smooth the film.²⁰⁴ The typical way to reduce the ES barrier is by using a surfactant such as Bi, In, or Sb.²⁰⁵ However, all three of these metals will incorporate into chalcogenide-based materials rather than acting as a surfactant. We instead take an alternative approach to reducing the root-mean square roughness of the film: reducing in-plane adatom diffusion. Nucleating the film at a low temperature, then growing the rest of the film at a higher temperature and/or by increasing growth rates both reduce in-plane diffusion and thereby reduce the film roughness. It is possible that other materials could be used as surfactants to further improve film morphology.

Another unwelcome morphology often witnessed in TI films is the spiral growth. In conventional materials, spiral growth almost always originates from screw dislocations.²⁰⁶ For vdW materials, these types of dislocations should be mitigated by the vdW gaps. However, when the growth front of a TI domain encounters the step edge of the substrate, it can “pin” the domain. The six sides of the hexagonal in-plane ${\text{Bi}}_2{\text{Se}}_3$ crystal structure are not equivalent. One set of three sides grows faster than the other set due to a higher density of dangling bonds. If the domain encounters a step at the wrong angle, this difference in edge growth rate will result in spiral growth.²⁰⁷ It is possible that substrates with step heights equal to the thickness of a QL would reduce the spiral formation. These defects can also be mitigated by pretreating the substrate such that all the atomic steps are aligned, though challenges will still arise when domains coalesce if the substrate step height does not equal the c-axis lattice constant of the film.

In addition to these structural defects, ${\text{Bi}}_2{\text{Se}}_3$ films are often n-type doped due to selenium vacancies, surface oxidation, and/or band bending at the top and bottom interfaces. These unwanted carriers can pin the Fermi level above the Dirac point into the bulk conduction band, obscuring the signal from the surface states. There are several ways to mitigate the doping. A cracker source can be deployed to promote incorporation of the selenium atoms.²⁰⁸ A capping layer such as elemental selenium²⁰⁹ or other materials including oxides and polymers can be deposited on the ${\text{Bi}}_2{\text{Se}}_3$ surface to suppress oxygen exchange or contaminant adsorption. In addition, one can also introduce a lattice-matched trivially insulating buffer layer (e.g., ${\left({\text{Bi}}_{1-x}{\text{In}}_x\right)}_2{\text{Se}}_3$) between the substrate and the ${\text{Bi}}_2{\text{Se}}_3$ film to reduce defects and band bending at the interface.²¹⁰ Through a combination of these efforts, background doping in ${\text{Bi}}_2{\text{Se}}_3$ films has steadily decreased such that the Fermi energy is often found in the bulk band gap. As noted above, vdW epitaxy has been widely adopted for other 2D material synthesis such as elemental 2D materials like silicene,²¹¹ stanene,²¹² antimonene,²¹³ and TMDs.^214,215 With the extremely accurate control over material flux, MBE is also capable of creating functional heterostructures and superlattices based on 2D materials for optic and electronic applications, especially when the interface plays a critical role as in the 2D system.^216,217 Overall, MBE growth of layered materials has progressed significantly over the past decade. Using a detailed understanding of the unique challenges and opportunities presented by vdW epitaxy, the future for MBE growth of functional vdW devices is bright.

2.8. Ternary Magnetic Layered Compounds Grown by MBE.

The quest for layered ferromagnets, one of the functionalities more recently pursued within the class of 2D materials, is to demonstrate a robust ferromagnetic order at room temperature. The initial question was if indeed ferromagnetism can be stabilized in the single atomic layer limit at finite temperatures. This presence of magnetic order would represent a violation of the Mermin-Wagner theorem,²¹⁸ i.e. the inability to establish any long-range magnetic order if an isotropic and finite-range Heisenberg exchange interaction is present. An alternative interpretation would be that 2D materials are simply not well captured by this theorem, and rather the highly anisotropic bond geometry inherent to 2D materials along with a finite thickness even in the single 2D layer limit would be enough to stabilize magnetic order, rendering a rigorous application of the theorem as not suitable. In any case, it is to be expected that magnetic order in 2D materials will not be very robust and potentially limited to a regime significantly lower than room temperature.

The experimental confirmation of ferromagnetism in atomically thin layers of the layered magnetic materials ${\text{CrI}}_3$²¹⁹ and ${\text{Cr}}_2{\text{Ge}}_2{\text{Te}}_6$²²⁰ in 2017 were widely considered fundamental breakthroughs, which led to an intensification of activities aimed at the further exploration of the field of 2D magnetism. Pioneering research activities have identified several vdW ferromagnets exhibiting insulating, semiconducting, and metallic ground states, both in the form of bulk single crystals as well as atomically thin flakes and films.²²¹ This is particularly exciting because vdW materials are considered an ideal playground for fundamental exploration of magnetic spin-on-lattice phenomena in the 2D limit, including the study of exotic magnetic ground states and magnetic phase transitions,²²² and they are also host of topologically nontrivial spin configurations (skyrmions).²²³ Aside from the exciting possibilities to explore fundamental physics questions, therefore pushing the horizon of our understanding of magnetism in 2D systems, research on these materials is also anticipated to stir up perspectives and avenues toward realization of ultracompact magnetic devices with relevance in spintronics and emerging quantum technologies. Here, one fascinating aspect is the fabrication of multifunctional vdW heterostructures by combining them and other 2D crystals like graphene and TMDs into vdW stacks, in which proximity-induced coupling effects across atomically smooth interfaces of layered materials can tailor magnetism by heterostructure design.²²⁴

Most 2D ferromagnets experimentally realized and investigated so far have Curie temperatures ($T_{\text{C}}$) well below 300 K even in the bulk regime,²²⁵ a constraint that hinders their practical applications. Hence, there is an urgency in finding materials that can furnish long-range ferromagnetic order in a robust fashion above room temperature and within a thickness range from a few nanometers down to the single layer limit. Additionally, the 2D material of choice should allow for a straightforward, easy to control, and high-quality wafer-scale synthesis that should be stable in ambient conditions. Hence, beyond the growth of bulk single crystals and subsequent exfoliation, the utilization of thin film synthesis methods, such as MBE and CVD, is highly desirable.

The development of a precise deposition route with atomic level control is also key for assessing fundamental phenomena in these materials. This thickness range of interest, namely from few layers down to the single layer limit, seems to be difficult to access via standard exfoliation schemes in various 2D crystals including some vdW magnets. The structural and chemical stability is an additional, important aspect to advance the field toward technological realization. For example, the fast degradation commonly observed in chromium halides upon air exposure²²⁶ presents a great challenge for the development of reliable device fabrication routes. To be compatible with the envisioned device application, it is necessary to find magnetic 2D materials with superior chemical stability and robust magnetic order well above room temperature that will facilitate their realistic exploration for future technologies.

TMDs with sizable free carrier concentrations, such as $1\text{T}-{\text{VSe}}_2$,²²⁷ $1\text{T}-{\text{CrTe}}_2$,²²⁸ and ${\text{Fe}}_n{\text{GeTe}}_2$ ($3\ge n\ge 5$),²²⁹ show excellent prospect for the envisioned applications as they can exhibit ferromagnetic order around or even above 300 K. Recently, unique insights have been reported on the origin of magnetism in $1\text{T}-{\text{VSe}}_2$.²³⁰ It has been shown for $2\text{D}{\text{VSe}}_2$ synthesized via MBE on ${\text{MoS}}_2$ that postgrowth anneals promoted Se desorption, which induced the formation of a reconstructed surface. Since the magnetic signal was absent in pristine, i.e. unreconstructed, layers, the formation of 1D line defects were assumed to originate a ferromagnetic response at 300 K. This suggests that alternative methods offering local control, such as focused ion beam,²³¹ could be utilized to introduce magnetic defects in a controlled fashion and with high spatial precision in the 2D lattice of $1\text{T}-{\text{VSe}}_2$. These recent reports indicate that the development of reproducible protocols for scalable synthesis and defect creation are indeed challenging. On the one hand it represents a critical roadblock that needs to be overcome for the future exploration of vdW magnets, while at the same time this research area offers fertile grounds to make further ground-breaking discoveries in magnetic 2D materials.

Capping layers were required to prevent unintentional oxidation and to avoid inactivation of magnetic defects.²³² Interestingly, degradation of magnetic properties upon air exposure was found less critical for $1\text{T}-{\text{CrTe}}_2$,²³³ although for long-term operation the use of capping layers seems inevitable as well. Like ${\text{VSe}}_2$, ${\text{CrTe}}_2$ assumes the conventional configuration of TMDs, schematically depicted in Figure 12a. Importantly, $1\text{T}-{\text{CrTe}}_2$ crystals were reported to exhibit Curie temperatures around 300 K in the bulk form, which remained close to room temperature for exfoliated flakes as thin as 8 nm.²²⁸ Interestingly, Zhang et al.²³⁴ observed room-temperature ferromagnetism of few-layer-thick ${\text{CrTe}}_2$ films grown by MBE on bilayer epitaxial graphene on SiC, while $T_{\text{C}}$ decreases to about 200 K when the thickness is reduced to a single layer, shown in Figure 12b,c. An intriguing aspect in the available reports is that a robust out-of-plane anisotropy was usually observed for epitaxially grown material. This is in marked difference from bulk crystals and corresponding ultrathin flakes, which always displayed an in-plane magnetic anisotropy. Specifically, Meng et al.²³⁵ reported a transition from an in-plane to an out-of-plane magnetocrystal-line easy axis in CVD-grown $1\text{T}-{\text{CrTe}}_2$ islands for thicknesses ≤10 nm. The origin of an out-of-plane anisotropy, which has not been observed in exfoliated flakes, has been associated with an enhanced magnetic anisotropic energy in the 2D limit, which can better resist thermal fluctuations and therefore help mediating a long-range ferromagnetic order. Further investigations are required to understand these peculiar observations and existing discrepancies. Considering the rich phase diagram of the Cr-Te system, which also includes the existence of stable phases with Cr atoms intercalated between chromium telluride layers,²³⁶ the existence of intermixed phases and/or thickness-dependent phase transitions occurring during epitaxial growth could possibly explain the differences in the magnetic properties observed so far.

Figure 12.

Properties of layered magnetic compounds. (a) Schematic depiction of a single layer of $1\text{T}-{\text{CrTe}}_2$. (b) Temperature-dependent magnetization curves of ${\text{CrTe}}_2$ films with different thicknesses in a magnetic field of 1 kOe oriented along the out-of-plane direction. A high $T_{\text{C}}$ close to room temperature was found for a trilayer. (c) Temperature-dependent magnetic hysteresis loops for a 7-layer-thick film with a magnetic field applied along the film normal. Panels (b) and (c) were reproduced with permission under a Creative Commons CC-BY 4.0 License from ref 234. Copyright 2021 Springer Nature. (d) Schematic depiction of a single layer of ${\text{Fe}}_5{\text{GeTe}}_2$. Temperature-dependent (e) remanent magnetization and (f) magnetic hysteresis loops of bilayer ${\text{Fe}}_5{\text{GeTe}}_2$ grown on c-plane sapphire by MBE. Panels (e) and (f) were reproduced with permission under a Creative Commons CC-BY 4.0 License from ref 229. Copyright 2022 Springer Nature. (g) The anomalous Hall effect (AHE) measured for ${\text{Fe}}_3{\text{GeTe}}_2/\text{Gr}$ at different temperatures. For clarity, the resistance curves are successively shifted up by 2.5Ω for temperatures ≥5 K. The square hysteresis loop of the AHE contribution in the Hall resistance $R_{\text{XY}}$ is due to a strong out-of-plane magnetic anisotropy and superimposed onto the negative linear slope arising from the ordinary Hall response of the free carriers in ${\text{Fe}}_3{\text{GeTe}}_2/\text{Gr}$. (h) Coercive field ${\mu }_0\cdot H_{\text{C}}$ and saturation resistance $\text{Δ}{R}_{\text{AHE}}$ from the AHE contribution as a function of temperature for ${\text{Fe}}_3{\text{GeTe}}_2/\text{Gr}$. (i) Hall resistance $R_{\text{XY}}$ in the high field limit of the ${\text{Fe}}_3{\text{GeTe}}_2/\text{Gr}$ heterostructure showing Quantum Hall effect plateaus, indicating a high carrier mobility in Gr and thus the ability to preserve the functionality of the vdW templates after the growth of ${\text{Fe}}_3{\text{GeTe}}_2$ by MBE.²³⁸ The Landau level index is assigned to every plateau. Reproduced with permission under a Creative Commons Attribution 4.0 license from ref 238. Copyright 2021 IOP Publishing.

The ferromagnetic metal ${\text{Fe}}_n{\text{GeTe}}_2$ is yet another very relevant contender as a 2D material with an above room temperature ferromagnetic order. This is not only because of the high transition temperatures it can exhibit, but also due to the flexibility it offers to tailor magnetic properties via structural and chemical design within the individual vdW layers. As proposed by Seo et al.,²³⁷ a single layer of ${\text{Fe}}_n{\text{GeTe}}_2$ can be considered as a specific material representation of a more general layered structure, in which a mechanical backbone is formed from a nonmagnetic and a chalcogen element—here Ge and Te with the chemical composition of a dichalcogen crystal—that is “filled” with magnetic elements—here Fe—that mediate the exchange interaction and ultimately originate the long-range magnet order. A schematic of the atomic arrangement is shown in Figure 12d. A 3D-like network of magnetic elements confined within a 2D layer is formed in such a way that only vdW interaction are present for the interlayer interaction. Tuning the $\text{Fe}$ content within the layers has been experimentally realized, and until now, ${\text{Fe}}_n{\text{GeTe}}_2$ with $n$ values ranging from 3 to 5 was experimentally demonstrated.^229,237,238

Recently, changes in the magnetic properties as a function of thickness have been assessed. The general trend confirmed by several studies is a decrease in $T_{\text{C}}$ when the 2D limit is reached.^239,240 For monolayer-thick ${\text{Fe}}_3{\text{GeTe}}_2$, $T_{\text{C}}$ values ranging from 20 to 126 K have been reported, depending on the measurement technique and method utilized for synthesis (either MBE growth on Ge(111)²³⁹ or mechanical exfoliation²⁴⁰). A bilayer of ${\text{Fe}}_5{\text{GeTe}}_2$ grown epitaxially on c-plane sapphire exhibited a record-high $T_{\text{C}}$ of around 230 K (Figure 12e,f).²²⁹ Systematic studies are needed to unambiguously identify the critical thickness for $T_{\text{C}}$ reduction for the different ${\text{Fe}}_n{\text{GeTe}}_2$ structures, as well as other contributing factors such as substrate type and capping layers. Such insights into ${\text{Fe}}_n{\text{GeTe}}_2$ become even more desirable, since it exhibits good stability in air. Furthermore, electrostatic gating of ${\text{Fe}}_n{\text{GeTe}}_2$ using ionic liquids has demonstrated that Curie temperatures can be further increased up to room temperature.²⁴⁰ One promising path to engineer the intrinsic magnetic properties of ${\text{Fe}}_n{\text{GeTe}}_2$ is by substituting $\text{Fe}$ with transition metal elements possessing a strong magnetic moment as well. Co- and Ni-doping in ${\text{Fe}}_{5-x}{\text{GeTe}}_2$ bulk crystals²⁴¹ allowed for a rich variety of modifications in magnetism depending on the dopant content and type, from ferromagnetic-antiferromagnetic exchange to $T_{\text{C}}$ boosting well above room temperature (Chen et al.²⁴¹ recently reported a $T_{\text{C}}$ around 476 K for Ni-doped ${\text{Fe}}_5{\text{GeTe}}_2$ crystals). Further efforts should now be put on the realization atomically thin layers of doped ${\text{Fe}}_n{\text{GeTe}}_2$ with uniform intra- and interlayer dopant distribution.

Progress has also been made in large-scale bottom-up growth of ${\text{Fe}}_n{\text{GeTe}}_2$. MBE has so far been the method of choice for the epitaxial growth of continuous, large-area films utilizing the “3D” substrates. ^{229,238,239,242} For example, c-plane sapphire has been used for the growth of ${\text{Fe}}_5{\text{GeTe}}_2$ epitaxial films.²²⁹ A Curie temperature of 300 K was reported, in good agreement with values obtained for bulk crystals.²⁴³ ${\text{Fe}}_n{\text{GeTe}}_2$ synthesized directly on a 2D material surface has also been realized.²³⁸ A robust out-of-plane magnetic anisotropy and $T_{\text{C}}$ around 220 K were measured for ${\text{Fe}}_3{\text{GeTe}}_2$ films grown on epitaxial graphene on SiC at relatively low growth temperatures around 300 °C. The high structural and electronic quality of the heterostructures was also confirmed by the observation of the quantum Hall effect in graphene, see Figure 12g—i. This is a key step toward the realization of epitaxial vdW heterostructures with pure and sharp interfaces, where proximity-induced phenomena can be used as a tool for tailoring magnetism. In this regard it remains of particular interest to develop synthesis of atomically thin, all-epitaxial heterostructures combining ${\text{Fe}}_n{\text{GeTe}}_2$ not only with graphene but also with wafer-scale 2D crystals such as TMDs and hBN to realize the vision of highly functional vdW heterostructures, in which proximity-induced coupling across atomically smooth interfaces of layered materials with different properties enable unique functionalities²²⁴ that can be further tuned by external applied fields.

2.9. 2D Magnets and Controversies.

Magnetism in the 2D limit is a desired property to build an all 2D-integarated chip capable of performing logic operations as well as storing the information.²⁴⁴ Although, a variety of 2D materials have been predicted and experimentally realized as room temperature magnets, the origin of this magnetism is under intense debate in the community. ^245,246 The case of ${\text{VSe}}_2$ is one such example. Bonilla²⁴⁷ and Duvjir²⁴⁸ independently report magnetism in MBE grown ${\text{VSe}}_2$ monolayers on a variety of substrates, where magnetometry characterization using vibrating sample magnetometer (VSM) and superconducting quantum interference device (SQUID) showed magnetic hysteresis at room temperature suggesting ferromagnetic order. However, later investigations by Batzill’s group reported that pristine ${\text{VSe}}_2$ did not show magnetism. Instead, the magnetism arose following postgrowth annealing and Se vacancy formation in the film.^245,249 This was confirmed in studies on pristine ${\text{VSe}}_2$ using a different characterization technique of X-ray magnetic circular dichroism (XMCD), which indicate the absence of any magnetic moments on the V atoms in pristine 2D ${\text{VSe}}_2$.^250,251 Further evidence comes from angle-resolved photoemission spectroscopy (ARPES) measurements where no spin-polarized bands are found in 2D ${\text{VSe}}_2$.^251,252 Lastly, the reported observation of a charge density wave (CDW) in monolayer ${\text{VSe}}_2$, which competes with the ferromagnetic ground state of the system to suppress it, supports the claim of the nonmagnetic nature of pristine ${\text{VSe}}_2$.^252,253 Thus, many reports demonstrate that the pristine ${\text{VSe}}_2$ is nonmagnetic. It is important to mention here that such a lack of intrinsic ferromagnetism is reported for other systems as well, where different artifacts such as edge states, surface adsorbates, and point defects were responsible for the magnetic effects.^254,255

Magnetic impurity-doped semiconductors, commonly known as dilute magnetic semiconductors (DMS), have also been suggested as another platform to search for RT 2D magnetism. Once again, the literature on 2D DMS is similarly filled with controversies and inconsistencies, in both theory and experiments. For example, Tiwari et al.²⁵⁷ used first-principles calculations to predict that >18% atomic substitution of vanadium for W in a monolayer of ${\text{WSe}}_2$ should give an out-of-plane RT ferromagnet. However, MBE grown 2D ${\text{WSe}}_2$ with about 30 atomic % V substitution does not show any magnetism for temperatures as low as 100 K (Figure 13a). In contrast, several other groups have observed RT ferromagnetism for V doping levels in the range of 0.1–1% that are far below what DFT predicts for RT Curie temperatures.^258,259 On the other hand, recently, point defects in the form of Se vacancies in CVD grown V-doped ${\text{WSe}}_2$ created by thermal annealing were found to be responsible for magnetism in this system (Figure 13b,c).²⁵⁶ As the MBE growth is usually performed in a high chalcogen flux environment, Se vacancy concentrations are likely too low to show any vacancy induced magnetism and may explain why MBE V-doped ${\text{WSe}}_2$ films do not exhibit ferromagnetism. In short, while RT 2D magnets are coveted elements for memory and spintronic devices, the literature is rife with inconsistent and sometimes contradicting observations.

Figure 13.

Quality versus magnetism in 2D TMDs. (a) Temperature dependent M versus H loops for a MBE grown, 30% V-doped 2D ${\text{WSe}}_2$ on sapphire showing the absence of any ferromagnetism at 100 K. (b) As-grown V-doped 2D ${\text{WSe}}_2$ sample grown on ${\text{SiO}}_2/\text{Si}$ was intentionally annealed to create Se vacancies. (c) Magnetic force microscopy (MFM) phase images measured at 120 K for as-grown and 500 °C annealed 0.5% V-doped ${\text{WSe}}_2$ are compared: The as-grown ${\text{WSe}}_2$ exhibits a negligible MFM phase contrast with respect to the ${\text{SiO}}_2/\text{Si}$. In contrast, the annealed ${\text{WSe}}_2$ exhibits a distinct magnetic domain contrast, confirming ferromagnetism in the annealed sample. Panels (b) and (c) were adapted and modified with permission from ref 256. Copyright 2022 John Wiley & Sons, Inc.

3. Strain Engineering, Symmetry Breaking, and Biosensing.

3.1. Strain and Strain Gradient Engineering in 2D Materials.

Strain engineering has been shown as a neat and effective approach in tuning or engineering the physical properties of 2D materials. The ability to reach large elastic strain in 2D materials has led to various scientific progresses in materials science, which include the editing of Berry connection/curvature and topological Dirac states, tuning of metal—insulator and magnetic phase transition, direct—indirect electronic band structure evolution, and the realization of the flexo-photovoltaic effect, with details discussed in the paragraphs below.

3.1.1. Colossal Strains and Strain Gradients in 2D Materials.

In bulk materials, an elastic strain $\ll 1\%$ can be sustained due to a large number of intrinsic defects (e.g, cracks and dislocations) either on the surface or inside the material.²⁶⁰ These defects multiplicate rapidly once deformation occurs (e.g., dislocation multiplicated by Frank-Read source). However, in low dimensional nanoscale materials, thermodynamic equilibrium shape can be easily reached and less defects are expected to be formed during the crystal growth. When deformed, for example, defect creation is largely dominated by surface dislocation nucleation, not by growth and propagation as the case of bulk crystals, making them much stronger than their bulk counterparts. Large elastic strains of above 1% have been widely demonstrated in low dimensional ceramic materials.

Figure 14a shows the experimental measured elastic strains in representative 2D materials such as graphene, transition metal dichalcogenides, and other layered materials. Lee et al.²⁶¹ and Perez Garza et al.²⁶² reported elastic strains of above 10% in graphene or few-layer graphene by nanoindentation and a tensile microelectromechanical system, respectively. Similarly, Bertolazzi et al.²⁶³ reported that elastic strains in ${\text{MoS}}_2$ monolayer reaches above 10% by nanoindentation using an atomic force microscope (AFM) tip. Researchers have reported many other methods, such as bending,²⁶⁴ bulking,²⁶⁵ and using substrates with grating²⁶⁶ and nanocones,²⁶⁷ to generate elastic strains in graphene and ${\text{MoS}}_2$. Large elastic strains have been reported in other TMDs (${\text{MoSe}}_2$,^268,269 ${\text{MoTe}}_2$,^270–272 ${\text{WS}}_2$, ^273,274 ${\text{WSe}}_2$, ^268,275,276 ${\text{WTe}}_2$, ²⁷⁷ ${\text{ReSe}}_2$, ²⁷⁸ and ${\text{Bi}}_2{\text{Se}}_3$²⁷⁹), black phosphorus (BP),^280,281 layered magnets ($\text{CrSBr}$,²⁸² ${\text{Fe}}_3{\text{GeTe}}_2$²⁸³), and layered halide (${\text{PbI}}_2$²⁸⁴), as plotted in Figure 14a as a function of thickness. In general, the measured elastic strain limits increase with decreasing thicknesses of samples.

Figure 14.

Large elastic strains and strain gradients in 2D materials. (a) Experimental measured elastic strains in representative 2D materials as a function of thickness. Here 2D materials include graphene,^261,262,266 ${\text{MoS}}_2$,^{263,265,267,289} ${\text{MoSe}}_2$,^268,269 ${\text{MoTe}}_2$,^270–272 ${\text{WS}}_2$,^273,274 ${\text{WSe}}_2$,^268,275,276 ${\text{WTe}}_2$,²⁷⁷ ${\text{ReSe}}_2$,²⁷⁸ ${\text{Bi}}_2{\text{Se}}_3$,²⁷⁹ $\text{BP}$,^280,281 $\text{CrSBr}$,²⁸² ${\text{Fe}}_3{\text{GeTe}}_2$,²⁸³ and ${\text{PbI}}_2$.²⁹⁵ Strain and strain gradient engineering in 2D materials. (a) Schematics of band structures ($\text{K}$ for crystal momentum) before (left) and after (right) applying a strain (band gap engineering). Blue dashed curves represent the original bands. (b) Schematics of band structures ($x$ for distance) before (left) and after (right) applying a local strain (a funneling effect). (c) Schematics of symmetries before (left) and after (right) applying a strain gradient. The strain gradient induces a spontaneous electrical polarization (P) (flexoelectric effect). (d) Atomic structures of transition metal dichalcogenides before (2H semiconducting phase, left) and after (1T′ metallic phase, right) applying a strain (semiconductor-metal transition). (e) Schematics of magnetic phases before (FM, left) and after (AFM, right) applying a strain (FM-AFM transition). (f) Schematics of band diagrams before (left) after (right) applying a strain. (g) Schottky barrier heights formed at contacts are tuned by strain due to strain-induced polarization in piezoelectric materials.

Although elastic strain has been studied widely in most 2D materials, the strain gradient has received much less attention. In bulk crystals, the strain gradient can normally only reach below 0.1 m⁻¹, which is often induced by mechanical bending.²⁶⁴ However, with reducing the sample thickness, a large elastic strain gradient can be created. Incredibly, large strain gradients of up to ≈10⁶ m⁻¹ and ≈10⁵ m⁻¹ are possible in ${\text{MoS}}_2$²⁸⁵ and freestanding film of ${\text{BiFeO}}_3$,²⁸⁶ respectively, whereas a bulk crystal such as ${\text{MAPbBr}}_3$²⁶⁴ can only manage strain gradients of <0.1 m⁻¹ Normally, when strains are generated in local regions in 2D materials (such as nanoindentation and buckling), strain gradients are formed simultaneously. These strain gradients should not be ignored and may play an important role on some physical properties. For example, strain gradient can break the inversion symmetry of a material and induce a spontaneous electrical polarization (flexoelectric effect), leading to intriguing phenomena such as flexo-photovoltaic effect (bulk photovoltaic effect coupled with flexoelectric effect).^285–287 Therefore, relevant studies on strain gradient-property relations on 2D materials are highly desired.

By introducing strain in a material, one can modify the lattice constant, atom position, symmetry, and space group. All these parameters determine the Hamiltonian of the system and thus can be used to design or tune its electronic structure. For example, by introducing compressive strain, a smaller lattice constant could increase orbital overlapping, thus leading to a larger band gap. The tensor form of strain can be used to design or lower the symmetry of the system while symmetry breaking is sometimes accompanied by the emergence of interesting physical properties. Strain gradient naturally breaks the inversion symmetry of materials and could be used to design polarization or Berry connection.²⁸⁸ When spin—orbit coupling is considered, by tuning the symmetry of the crystal, strain or strain engineering could be used to design the topological properties of material. In 2D materials, strain and strain gradient have been demonstrated to be able to tune the electron—lattice interactions, band structure, phonon behaviors, magnetic ordering, spin-momentum coupling, and topological parameters.

The strain—band gap relation is one of the most widely investigated topics in 2D materials.^{265,274,280,289} By applying a uniaxial tensile mechanical strain $\epsilon$ in a monolayer ${\text{MoS}}_2$ (Figure 14b), Conley et al.²⁸⁹ reported a nearly linear decrease of around 45 meV/% in the optical band gap of the monolayer. A pronounced decrease in the PL intensity with increasing tensile strain suggests a possible direct-to-indirect transition in this material. If strain is applied at a local region, e.g., by nanoindentation using an AFM tip, a funneling effect can be induced (Figure 14c), ²⁹⁰ where photoexcited electron and holes can migrate to the center and then they may recombine or they can be collected by electrodes. Based on this funneling effect, Li et al.²⁶⁷ designed and fabricated a 2D ${\text{MoS}}_2$ strained crystal by transferring ${\text{MoS}}_2$ monolayer onto a ${\text{SiO}}_2$ nanocone array. The authors demonstrated broadband light absorption and efficient funneling effect at maximum strain points in this strained crystal.²⁶⁷ Finally, this effect can lead to efficient funneling of excitons to generate single photon emission in nonuniformly strained monolayer ${\text{WSe}}_2$,^291,292 and trions in nonuniformly strained monolayer ${\text{WS}}_2$.²⁷³ Strain gradients can also tune the point group of a material (flexoelectric effect, Figure 14d). By using this method, Jiang et al.²⁸⁵ reported a large strain gradient of up to 10⁻⁶ m⁻¹ in a strain gradient-engineered ${\text{MoS}}_2$ sheet, leading to a flexo-photovoltaic effect. The 2D materials with nonuniform strains induced by nanoindentation, buckling and substrate with nanocones reported previously, also have strain gradients. The flexoelectric effect in these 2D materials may play in important role on some intriguing phenomena. By modifying the thermodynamic energy landscape, strain can tune phase transition temperature in 2D materials, such as a structural $2\text{H}-1{\text{T}}^{\prime }$ phase transition (Figure 14e) with a proper strain in TMDs. It is suggested that the activation energy for $2\text{H}-1{\text{T}}^{\prime }$ phase transition can be modulated by strain: tensile strain lowers the energy barrier height.²⁹³ The structural phase transition is often accompanied by electronic phase transition-metal—semiconductor transition, important for the development of fast-switching transistors.²⁹³ By using strain-tuned phase transition in ${\text{MoTe}}_2$, Hou et al.²⁷¹ fabricated ${\text{MoTe}}_2$ phase change transistor and achieved nonvolatile conductivity change $G_{\text{on}}/G_{\text{off}}$ of near 10⁷. Through tuning the interlayer or intralayer magnetic exchange interaction, strain can control magnetic phases in 2D materials, including a ferromagnetic (FM) to antiferromagnetic (AFM) phase transition (Figure 14f).²⁸² As a final example of how strain impacts electronic properties, strain in piezoelectric 2D materials can also be used to tune the Schottky barrier heights when Schottky contacts are formed (Figure 14g). Wu et al.²⁹⁴ reported the piezoelectricity in 2D ${\text{MoS}}_2$ and demonstrated an asymmetric carrier transport under strains in this device indicating a piezotronic effect in 2D ${\text{MoS}}_2$. Besides, strain can tune Dirac surface states and control exciton—phonon coupling in ${\text{Bi}}_2{\text{Se}}_3$ films, as reported by Flototto et al. ²⁷⁹ Strain can control exciton-phonon coupling in monolayer transition metal dichalcogenides, as reported by Niehues et al.²⁶⁸

3.2. Second Harmonic Generation in 2D Materials.

Here, we discuss recent research progress and challenges in the second harmonic generation (SHG) of 2D materials. For a more comprehensive review of nonlinear properties, the readers are referred to several excellent previous reviews on 3D bulk²⁹⁶ and 2D materials.²⁹⁷ SHG describes a coherent frequency-doubling process when intense light passes through a material. As a higher-order process compared with linear optical response, SHG involves more complexities in interpreting experimental measurements and theoretical calculations. However, the initial appeal of studying SHG in 2D materials was simple: SHG relies on inversion asymmetry, commonly found in monolayers and not their bulk layered parents.²⁹⁸ Within a monolayer with inversion asymmetry, any local disruptions to the lattice will also modulate ${\chi }^{(2)}$,^299–301 promoting SHG to be a defect characterization method that is more efficient and less destructive than transmission electron microscopy methods.³⁰⁰ One experimental difficulty is that there is no direct readout of ${\chi }^{(2)}$ from experiments: the extraction of ${\chi }^{(2)}$ from experimental measurements of SHG requires a model of the second harmonic radiation field driven by the polarization of the material. One common “bulk” model originating from Boyd’s classic text is to treat a monolayer as a bulk material with a thickness (e.g., 0.65 nm per layer for ${\text{MoS}}_2$), as has been done for ${\text{MoS}}_2$,³⁰² GaSe,³⁰³ and InSe.³⁰⁴ This bulk model has been shown to severely over-estimate ${\chi }^{(2)}$ compared with a more careful treatment using a “sheet” model.³⁰⁵ For example, ${\chi }^{(2)}$ for ${\text{MoS}}_2$ was over-estimated to be 10⁵ pm/V using the bulk model, while the sheet model yields 6 pm/V (static³⁰⁶) or 40–100 pm/V (on resonance).³⁰⁶ Fortunately, Clark et al.³⁰⁶ also prescribes how to convert the bulk-model-derived ${\chi }^{(2)}$ to sheet-model-derived ones. Applying this conversion to GaSe, and InSe has achieved better agreement with theory results.³⁰⁷ Other methods were reported too: a model based on the Green’s function of a sheet source has estimated ${\chi }^{(2)}$ to be around 10⁴ pm/V for 2D TMDs³⁰⁸ at 800 nm excitation,³⁰⁹ 2 orders of magnitude larger than the on-resonance ${\chi }^{(2)}$ for TMDs extracted from the sheet model. At present it is not clear why these models yield ${\chi }^{(2)}$ values that appear inconsistent with both the bulk and sheet models.

The initial successful characterizations of SHG in 2D materials also brought focus to maximizing ${\chi }^{(2)}$ for potential applications in frequency doubling. Typically, measured ${\chi }^{(2)}$ were compared with that of industry-standard nonlinear crystals like barium borate (BBO) or potassium dihydrogen phosphate (KDP). However, ${\chi }^{(2)}$ is not the only metric of an ideal nonlinear crystal. A sufficiently large bandgap is required to ensure transparency and withstand laser-induced damage; adequate birefringence is necessary for phase matching; a crystal growth protocol that minimizes defect population is needed to reduce defect absorption. Even if one only considers two metrics—${\chi }^{(2)}$ and bandgap—the known trade-off relationship³¹⁰ between them means that large ${\chi }^{(2)}$ values reported in the literature are frequently obtained at the implicit cost of a smaller bandgap.

A fairer metric should therefore be how far ${\chi }^{(2)}$ exceeds the ${\chi }^{(2)}$-bandgap trade-off. One way to quantify this is to report ${\chi }^{(2)}$ normalized by the bandgap, as is done in Taghizadeh et al.³¹¹ Overall, we recommend that future research compare ${\chi }^{(2)}$ in the context of the material’s bandgap. For example, in the case of 2D metals, in-plane ${\chi }^{(2)}$ components of 4.8 and 3.8 nm²/V were measured for 2D Ga and In intercalated between a SiC substrate and a graphene cap.³¹² These values, in a fair comparison with other zero-gap materials systems, are larger than the in-plane ${\chi }^{(2)}$ of metal surfaces such as Al(111), estimated to be 0.2 nm²/V. For the case of metal thiophosphates, He et al.³¹³ demonstrated that the bulk layered compound ${\text{SnP}}_{\text{2}}{\text{S}}_6$ achieves a large ${\chi }^{(2)}$ for its bandgap (2.3 eV). Its ${\chi }^{(2)}$ is on the order of 53 pm/V, larger than other common infrared nonlinear crystals with similar bandgaps, such as ${\text{AgGaS}}_2$ and ${\text{AgGaSe}}_2$. ${\text{SnP}}_2{\text{S}}_6$ also has a high laser-induced damage threshold, three times greater than that in ${\text{ZnGeP}}_2$, a commercially available nonlinear optical crystal.³¹³ Along with a large bandgap and laser damage threshold, the synthetic method is also important when considering 2D crystals for frequency doubling and other nonlinear optical applications. For example, it has recently been shown that few-layer ${\text{MoS}}_2$ exfoliated through a solution-phase redox process can exhibit saturable SHG and multiphoton absorption up to 10th order.³¹⁴ Polyoxometalate clusters which are formed during the redox exfoliation process and adsorb onto the 2D material flakes were implicated in the unusual nonlinear optical properties. Saturable SHG and multiphoton absorption were not observed in ${\text{MoS}}_2$ prepared by CVD, demonstrating that the choice of synthesis method can not only enhance or suppress the magnitude of existing nonlinear optical properties in 2D materials but also enable interesting phenomena.

3.3. Symmetry Breaking in 2D Materials.

Symmetry reduction can introduce exotic physical and chemical properties. For instance, the breaking of inversion symmetry in twisted BLG led to strongly correlated states due to moiré superlattice formation.³¹⁵ While low-symmetry 2D materials exist (e.g., SnS, ${\text{PdSe}}_2$, and ${\text{WTe}}_2$), there was a lack of 2D materials with mirror symmetry breaking because they were metastable. Thanks to recent advancement in synthesis methods for 2D materials, researchers can break the mirror symmetry of monolayers and unleash functionalities that cannot be achieved by traditional thin film techniques. This section covers two examples of 2D materials with structural symmetry breaking and their properties. First, Janus TMDs (e.g., SWSe, SeMoS) are one example of structural asymmetry enabled by surface treatments such as annealing with sulfur vapor³¹⁶ or low-energy selenium implantation¹³ performed on ${\text{WSe}}_2$ or ${\text{MoS}}_2$. The mirror symmetry breaking in Janus TMDs leads to an intrinsic vertical dipole moment that induces a wealth of unique properties that are not normally accessible and enhance the vdW coupling in heterostructures.³¹⁶ Second, air-stable 2D polar metals (e.g., Ga, In) in between epitaxial graphene and SiC with one side covalently binding to SiC and the other side that interacts with graphene by vdW forces are made possible by confined heteroepitaxy (CHet).⁵⁰ Due to different bond environments on both surfaces of half-vdW 2D metals, the out-of-plane metal— metal bond changes by near 10%,³¹² resulting in symmetry breaking and a large nonlinear optical response. Both cases demonstrate the optical and photonic properties can be controlled precisely at the submonolayer level.

3.3.1. Janus TMD Heterostructures.

Janus TMDs is an example of broken mirror symmetry enabled by surface modification. It is a type of TMD material in which the transition metal is sandwiched between two different species of chalcogen. When Janus TMDs are assembled with other 2D materials into heterobilayers, different interfaces can be formed because of the structural asymmetry (Figure 15a). Zhang et al.³¹⁶ demonstrated that the dipole moment of Janus SeMoS enhanced the vdW coupling in a $\text{SeMoS}/{\text{MoS}}_2$ heterostructure synthesized by thermal selenization of bilayer ${\text{MoS}}_2$. The interlayer force constant of $\text{SeMoS}/{\text{MoS}}_2$ related to the interlayer shear and breathing modes was larger by 13.2% than that of as-grown bilayer ${\text{MoS}}_2$ due to the intrinsic dipole moment.³¹⁶ As the intrinsic dipole is perpendicular to the basal plane, the same group showed that this vdW coupling is dependent on which side of Janus TMDs was interacting with their pristine counterparts as well as their twisted angles (Figure 15b).³¹⁷ For a Janus TMD transferred onto a pristine TMD, the ${\text{MoS}}_2$ exhibited a better vdW interaction with the sulfur side of SeMoS, as shown by the higher interlayer phonon frequencies in Figure 15c, due to a shorter interlayer spacing. DFT calculations also revealed that the intrinsic dipole led to an interfacial electric field (Figure 15d), promoting charge transfer between layers when ${\text{MoS}}_2$ was in contact with the sulfur side of MoSSe.³¹⁷ The modulated vdW coupling and charge transfer of Janus TMDs showcase the great potential for manipulation of electron dynamics in a variety of optoelectronic devices. Besides the experimentally probed optical properties, the intrinsic dipole moment was predicted to contribute to robust Rashba spin splitting independent of the applied electric field and strain,³¹⁸ which is important for spintronic devices, such as spin filters, spin FETs, and spin-resolved photodetectors. Theoretical predictions also suggested that Janus TMDs displayed great potential for applications including photocatalytic water-splitting, hydrogen evolution reaction, and gas sensing.

Figure 15.

Emerging optical phenomena of asymmetric 2D materials. (a) Illustration of $\text{SeMoS}/{\text{MoS}}_2$ (SS) and $\text{SMoSe}/{\text{MoS}}_2$ (Se/S) heterobilayers. (b) The shear and breathing mode frequencies of interlayer shear and breathing modes of S/S heterobilayer at two twisted angles $(\theta )$, which is defined as the angle between the zigzag directions of SeMoS and ${\text{MoS}}_2$. (c) The breathing mode frequencies of S/S and Se/S heterobilayers fabricated by transfer stacking. (d) The charge density difference of the above Janus heterostructures with S/S and Se/S interfaces predicted by DFT calculations shows the direction of the interfacial electric field. Panels (a)-(d) were reproduced with permission from ref 317. Copyright 2021 American Chemical Society. (e) STEM image depicting the structure of 2D Ga PMet, consisting of three atomic layers of gallium on a SiC substrate capped with bilayer graphene, along with calculated charge density and schematic of bonding character. Reproduced with permission from ref 312. Copyright 2020 American Chemical Society.

3.3.2. 2D Polar Metal Heterostructures.

While nano-structured metals are ubiquitous in technologies for sensing, catalysis, and nonlinear optics, 2D elemental metals are understudied compared to other 2D materials. The reduced dimensionality of 2D metals may offer advantages for highly tunable plasmonics,³¹⁹ photocatalysis,⁶ enhanced magnetism,⁵ and superconductivity.³²⁰ However, unlike other materials which are well-known in both 2D and 3D forms, traditional metals do not have an intrinsically layered bulk structure. Therefore, 2D metals are difficult to synthesize and often unstable, which has limited them to small lateral dimensions and high vacuum environments, hindering their applicability.³²¹ Epitaxial graphene grown on SiC can be physically decoupled from the SiC by intercalating atoms, such as F, O, and H,³²² to the graphene/SiC interface. Although this interface can improve the stability of intercalated ultrathin metals,¹⁴ metal intercalation has not been studied actively.

Recently, atomically thin, air-stable metals have been realized through CHet.⁵⁰ These 2D polar metal heterostructures (2D-PMets) consist of a few atomic layers of metal that are epitaxial to a SiC substrate and capped with bilayer graphene (Figure 15e). The components of the heterostructure are crucial to the properties of the 2D metals: registry to the SiC substrate results in the metal layers adopting a strained hexagonal lattice, while the graphene protects the metal from oxidation. As a result, 2D-PMets offer opportunities for both fundamental studies of the properties of crystalline metals in lattice configurations not achievable in bulk and expanded studies of 2D metals beyond gold under ambient conditions. Since the introduction of 2D-PMets, their properties including superconductivity,⁵⁰ nonlinear optical phenomena,³¹² potential epsilon-near-zero modes,³²³ and tunable optical resonances and energy dissipation have been reported.³²⁴ 2D-PMets, such as Ga and In, exhibit extremely efficient nonlinear optical transduction, with ${\chi }^{(2)}$ of 3 to 5 nm/V.³¹² 2D-Ga and -In also outperform other metal SHG sources like gold nanorods and graphene-coated gold films (1000 and 100X higher ${\chi }^{(2)}$, respectively) and industry standards like ${\text{LiNbO}}_3$ (100X higher ${\chi }^{(2)}$).³²⁵ Nonlinear optical microscopy has revealed in-plane and out-of-plane symmetry breaking in 2D-PMets which allows the large second-order response and determines the polarization plane of the emission.³¹²

As the family of 2D-PMets grows to include more elements, nonlinear optical microscopy will continue to enable fast, noninvasive characterization of the quality and crystal structure of intercalated metals. The structural information obtained through polarization-resolved SHG microscopy may be complemented by wide-field hyperspectral nonlinear imaging, which can be performed with diffraction-limited and subdiffraction spatial resolution through Fourier transform nonlinear optical microscopy.^326,327 These combined modalities may address further remaining questions about 2D-PMets, such as the influence of metal thickness on the properties of the 2D metal heterostructures and the possibility of enhancing the intrinsically strong light—matter interactions of 2D-PMets through the formation of hybrid resonances.

3.4. Biosensing Applications.

2D materials’ surfaces have low roughness and are dangling bond-free, which are more desirable than 3D substrates to host small molecules and biological materials to avoid unnecessary material binding and improve surface adsorption. Additionally, 2D materials exhibit characteristic Raman peaks (e.g., G band and 2D band of graphene and ${\text{E}}_{2\text{g}}$ band and ${\text{A}}_{1\text{g}}$ band of 2D ${\text{MoS}}_2$) whose position and width are very sensitive to changes in doping, strain, environment effects, and materials heterogeneity (e.g., substitutional doping, alloying, and vdW heterostructure formation). Therefore, Raman peaks of 2D materials and in some cases PL of 2D semiconductors are used as indicators in nondestructive sensing including photodetectors, strain sensors, and biosensing. In the following, we discuss biosensing of small molecules and biomolecules on 2D surfaces using Raman characterization³²⁸ and learn from Ignatova et al.³²⁹ about using multi-imaging techniques to understand the nonuniformities in ${\text{MoS}}_2$/graphene bilayers. Since 2D materials are scalable, transferrable, and air-stable thanks to the continuous improvement of their manufacturing, it is possible to realize them as large-area biosensors in the near future.

3.4.1. Raman Enhancement through 2D Surfaces.

2D materials have attracted substantial interest in the field of biological sensing because of their large surface-to-volume ratio, superior electrical transport, strong surface adsorption, and biocompatibility.³³⁰ These excellent attributes meet the demands of rapid and accurate biomolecular sensing, which requires high multiplexity and specificity. For the detection of infectious diseases, the challenge is to detect rapidly and remotely to minimize unnecessary contacts and reduce the transmission rate.³³¹ While for other diseases with unknown origin, Alzheimer’s disease, for instance, it is challenging to provide additional information that pinpoints reliable disease biomarkers for early detection.³³² However, realizing such sensing functionality needs a reliable technique tool to obtain fingerprinting signals of biological samples and efficient interaction between the sensing media and biomolecules. Facing these challenges, Raman enhancement through 2D materials offers an effective approach for chemical sensing of biomolecules with high multiplexity, specificity, and signal-to-noise ratios.³²⁸ An example of Raman enhancement through 2D materials is the surface-enhanced Raman scattering (SERS),³³³ in which the Raman signals of analyte molecules can be significantly enhanced by contacting graphene and other 2D crystals (Figure 16a). This sensing mechanism relies on the dipole—dipole interaction and charge transfer between 2D materials and molecules.³³⁴ Since the discovery of graphene-enhanced Raman scattering (GERS), a plethora of 2D materials including graphene and TMDs (${\text{WSe}}_2$, ${\text{SnS}}_2$, ${\text{WTe}}_2$) have exhibited the capability to strengthen the Raman signals of a wide range of small molecules (Figure 16b).^{330,328,335,336}

Figure 16.

Biosensing based on Raman enhancement through 2D materials. (a) GERS of Phthalocyanine. Adapted and modified with permission from ref 333. Copyright 2015 American Chemical Society. (b) Raman enhancement of CuPc using different 2D materials. Adapted and modified with permission from ref 335. Copyright 2019 American Chemical Society. (c) The Raman signals obtained from different brain regions showed a better signal-to-noise ratio when graphene was in contact with the brain slice. Different ML classifiers showed higher accuracy in distinguishing mice with and without Alzheimer's disease. Adapted and modified with permission from ref 338. Copyright 2022 American Chemical Society.

The application of Raman enhancement through 2D materials is not limited to small molecules. It can be widely applied to a range of biological samples, such as macromolecules,³³⁷ tissues,³³⁸ and cerebrospinal fluid.³³⁹ Huang et al. demonstrated the enhancement of blood constituent proteins, including hemoglobin and albumin based on their unique structures and oxidation states.³⁴⁰ Wang et al.³³⁸ showed that 2D materials can also be used to enhance the signal-to-noise ratio of Raman signals in mouse brains with Alzheimer’s disease (Figure 16c). The accuracy of machine learning (ML) classification for brain tissues with and without Alzheimer’s disease was also increased from 77 to 98% by applying graphene.³³⁸ Moreover, this work identified biomarkers specific to Alzheimer’s disease, including Amyloid-$\beta$ and Tau, and other potential biomarkers that have been confirmed by other biochemical studies. Equipped with ML analysis,³³⁸ enhanced Raman response can accelerate the understanding of disease pathology, the control of viral transmission, and the development of therapeutics. Aside from being applied to biochemical sensing, 2D materials have been extensively explored in the landscape of other biomedical applications, such as bioimaging,³⁴¹ tissue engineering,³⁴² and drug delivery,³⁴³ continuing to attract interdisciplinary research interest.

3.4.1. The Role of Optical Nonuniformities in vdW Heterostructures for Multidimensional Imaging.

2D heterostructures were shown to operate in a multimodal regime—producing several signals in response to a single analyte, allowing for reporting the analyte in a complex media.¹⁰ Multiplexed sensing of doxorubicin, a common cancer drug, was demonstrated by Ignatova et al.³²⁹ using a 2D material vertical heterostructure. A biosensor composed of monolayer ${\text{MoS}}_2$ coated with graphene utilized GERS, ${\text{MoS}}_2$ photoluminescence (PL), and graphene Raman shift signals to report drug molecules with a 60 nM threshold. A multiplexing approach has enabled reporting the drug in the mixed solution with a “contaminant” organic molecule.³⁴⁴ However, this method could suffer from the above-mentioned local fluctuations of material properties at the nanoscale. The nonuniformities that influence device performance can be divided in two groups: inherited during synthesis (intrinsic) and acquired during device fabrication process. Intrinsic nonuniformities include atomic impurities, lattice defects,^46,52,345 GBs, wrinkles and ruptures that result in strain, doping and/or charge transfer, often possessing variation at the nanometer scale. Acquired nonuniformities that come from the transfer process and nanofabrication can be partially eliminated by post-transfer cleaning procedures (annealing) or by using Soxhlet extractor³⁴⁶ for improving quality of transfer. Despite efforts to remove contaminants, typical resultant materials are not perfect, leading to variability in optical signaling and high noise in biosensors.

Ignatova et al.³²⁹ applied multidimensional imaging analysis to unveil mechanisms of the local fluctuations of optical response (PL, Raman) of a biosensor. Typical Raman spectra of graphene-${\text{MoS}}_2$ heterostructure are shown in Figure 17a,b (insets show maps of a ${\text{MoS}}_2$ island and locations of single-point spectra of the main plot). Advanced fitting procedure described previously^347,348 was used to determine the local values of strain and doping for graphene and ${\text{MoS}}_2$ materials across the whole heterostructure. Furthermore, the splitting of the G- and 2D-Raman bands of graphene yields the shear (nonisotropic) component of the strain (Figure 17b). Generated maps in Figure 17d—h show correlation between the sources of local optical fluctuation and morphology of the sample, as determined by high resolution infrared scattering scanning near-field optical microscopy (sSNOM) image (Figure 17c). Charge doping and components of graphene strain clearly vary across the ${\text{MoS}}_2$ island, consistent with the Kelvin probe force microscopy (KPFM) results (Figure 17i) and sSNOM (not shown). The cross-correlation of KPFM and sSNOM data allows quantification of the variation of in Fermi level of graphene above the ${\text{MoS}}_2$ island at nanoscale resolution impossible for KPFM or Raman microscopy along. The presented study suggests that to improve the performance of devices and sensors based on 2D heterostructures, nonuniformity of doping and strain—two major mechanisms for optical signal variation—must be addressed. Strain-free and doping-free transfer methods are also needed.

Figure 17.

Multidimensional imaging on ${\text{MoS}}_2$/graphene. (a) ${\text{MoS}}_2$ Raman spectrum, fitted with E1 and A-bands, (inset) A-band intensity map; (b) Raman spectra for graphene off/on ${\text{MoS}}_2$ island, fitted by G (orange), ${\text{D}}^{\prime }$ (pink) and 2D (green) bands, (inset) Raman map of 2D-amplitude showing the island location; (c) KPFM (a) KPFM image; (d—f) calculated graphene doping, hydrostatic and shear strain maps, overlaid with scanning electron microscopy image; (g, h) doping and strain for ${\text{MoS}}_2$ layer overlaid with SEM image; (i) sSNOM phase image of the same area. All scale bars are 1 μm. Reproduced with permission from ref 329. Copyright 2022 American Chemical Society.

4. Multidimensional Heterostructures.

4.1. 0D/2D Heterostructures.

Mixed-dimensional 0D/2D heterostructures formed by the stacking of 2D materials with 0D nanoparticles constitute a class of nanomaterials that offers multifunctionality that goes beyond those of 2D heterostructure systems.³⁴⁹ The class of 0D materials that can be stacked on 2D materials primarily consist of fullerenes, organic molecules, quantum dots (QD), atomic clusters, and atoms.³⁵⁰ In principle, due to the lack of lattice matching and processing compatibility limitations, a large panel of radically different materials can be stacked to form mixed-dimensional 0D/2D heterostructures with diverse properties.³⁴⁹ Mixed-dimensional 0D/2D heterostructures have attracted attention in the fields of catalysis, molecular sensing, quantum information, optoelectronics, and energy conversion and storage due to their unique properties.^351,352

The recent work by Kolli et al.³⁵³ is a typical example representing a mixed-dimensional 0D/2D heterostructure between ${\text{SnS}}_2$ QDs and 2D ${\text{MoS}}_2$. The ${\text{SnS}}_2$-QDs prepared using solution-processing method were spin coated on ${\text{MoS}}_2$ monolayers grown on ${\text{SiO}}_2/\text{Si}$ by the CVD technique, to form the mixed-dimensional 0D/2D ${\text{SnS}}_2$-QDs/${\text{MoS}}_2$ heterostructure. The 0D/2D heterostructure of ${\text{SnS}}_2$-QDs/monolayer ${\text{MoS}}_2$ was fabricated for high-performance and broadband (UV—visible—near-infrared (NIR)) photodetector, with photo-responsivity for UV, visible, and NIR regions of ~278, ~435, and ~189 A/W, respectively. Monolayer ${\text{MoS}}_2$ is visible- and NIR-light-sensitive, and discretely distributed ${\text{SnS}}_2$-QDs extends the photodetection range to the UV region, thus broadening the photodetection range of ${\text{SnS}}_2\text{-QDs}/{\text{MoS}}_2$ from UV to NIR. The excellent performance of the fabricated ${\text{SnS}}_2$-QDs/monolayer ${\text{MoS}}_2$ hybrid photodetector is attributed to the band bending and built-in potential created at the junction of ${\text{SnS}}_2$-QDs and ${\text{MoS}}_2$ (Figure 18a), which enhances the injection and separation efficiency of the photoexcited charge carriers.

Figure 18.

Mixed-dimensional 0D/2D heterostructures. (a) Schematic illustration of ${\text{SnS}}_2$-QDs and monolayer ${\text{MoS}}_2$ band structure after the formation of heterojunction with proposed e—h pair separation. Reproduced with permission from ref 353. Copyright 2022 American Chemical Society. (b) Representative high magnifications STEM-ADF images of hBN-AgPt where the atomically dispersed Pt atoms in the Ag-Pt cluster are highlighted with red dashed circles. Reproduced with permission under a Creative Commons Attribution 4.0 International license (CC BY 4.0) from ref 34. Copyright 2021 Elsevier. (c) An annular dark-field TEM image of a ~0.6 at. % Au-doped ${\text{MoS}}_2$ monolayer. Au adatom (indicated by arrows) were found to be located on top of the Mo (i), S (ii), and hollow-center site (iii), respectively. (d) LDOS of the Au dopant atoms at their considered atomic structures. The blue and red plots are for the spin up and spin down components, respectively. The filled curves indicate occupied states. Panels (c) and (d) were adapted and modified with permission from ref 356. Copyright 2014 John Wiley & Sons, Inc.

Metallic nanoclusters and/or atomically dispersed metal atoms confined on 2D materials is also a promising avenue for mixed dimensional heterostructures for catalysis, molecular sensing, and energy storage due to their highly efficient metal utilization.³⁵⁴ Reducing the metallic particle size to metallic nanoclusters and single metal atoms increases the exposed surface atoms, modifies the surface electronic and atomic structure, and creates defects.,³⁵⁵ The strong metal—2D material support interaction and quantum size effects can lead to exceptionally distinct chemical, physical and electronic properties relative to nanoparticles and bulk metals. Lei et al.³⁴ showed a typical example of a mixed-dimensional 0D/2D heterostructure based on metallic nanoclusters and atomically dispersed metal atoms confined on 2D materials between hexagonal boron nitride (hBN) and various metals including, $\text{Fe}$, $\text{Cu}$, $\text{Au}$, $\text{Ag}$, and $\text{Pt}$. In this report, the hBN/AgPt nanoclusters (Figure 18b) demonstrated excellent hydrogen evolution reaction (HER) activity, with an onset potential better than all other heterostructures (87 mV) due to the robust anchoring of atomically dispersed Pt atoms, improved electrical conductivity from the $\text{Ag}$, and the synergetic effects between hBN and AgPt.

Single metal atom sites attached on a 2D material matrix in a mixed-dimensional 0D/2D heterostructure can also be used to tune the electronic structure of the 2D material host matrix. A typical example representing a 0D/2D heterostructure in which attaching single metal atoms are attached onto a 2D matrix to tune the electronic structure of the host matrix is an Au single atom/monolayer ${\text{MoS}}_2$ hybrid.^356,357 For example, Lin et al. prepared Au dopants on the surface of a ${\text{MoS}}_2$ monolayer and confirmed the position of Au adatoms can be on top of the $\text{Mo}$, $\text{S}$, and hollow-centers (HC) of ${\text{MoS}}_2$ in the TEM image (Figure 18c). To investigate the impact of Au adatoms on the electronic structure of 2D ${\text{MoS}}_2$, the authors simulated local density of states (LDOS) around Au adatoms on ${\text{MoS}}_2$ (Figure 18d). The LDOS around Au adatoms at the Mo, S, and HC sites exhibit the gap states inside the bandgap of ${\text{MoS}}_2$, which can act as p-type doping sources to compensate the n-type nature of ${\text{MoS}}_2$. Recently, Liu et al.³⁵⁷ reported a spontaneous defect-free functionalization method consisting of attaching Au single atoms to monolayers of semiconducting ${\text{MoS}}_2$ by using S-Au-Cl coordination complexes and confirmed the doping effect of Au single atoms with ${\text{MoS}}_2$ FETs. The output characteristics of the Au-${\text{MoS}}_2$ BGFETs showed that the Au single atoms led to the transfer of electrons from ${\text{MoS}}_2$ to $\text{Au}$, as the threshold voltage was shifted toward negative voltages with Au dopants, which introduced p-type doping to the functionalized ${\text{MoS}}_2$ monolayers.³⁵⁷ Moreover, the degree of n- and p-type doping in the ${\text{MoS}}_2$ matrix can be finetuned by choosing the transition metal single atom attached and by varying their concentrations, thus controlling the electronic band structure of ${\text{MoS}}_2$.³⁵⁸

4.2. 2D/3D Heterojunction Devices.

The advent of 2D materials has attracted considerable attention in design exploration for highly scaled FETs, thanks to the enhanced electrostatic control over bulk 3D semiconductors due to their atomically thin bodies and self-passivated surfaces.^359,360 However, introduction of 2D materials is quite challenging since high material quality, stable, complementary doping are not readily available for them, while Si and III-V technology is very much established in terms of doping type and doping density control.^361,362 Hence, it is natural to explore 2D semiconductors and 3D bulk semiconductors as complementary counterparts in next-generation logic device architectures. In this regard there have been considerable efforts by the community for the exploration of 2D/3D heterojunctions for next-generation logic and memory devices.

4.2.1. Logic Devices.

A fundamental thermionic limit defined by the so-called Boltzmann tyranny of the subthreshold slope (SS) at 60 mV dec⁻¹ in single band transport devices such as metal-oxide-semiconductor FET (MOSFETs) not only precludes further scaling down the supply voltage but also increases overall power density and consumption in MOSFET-based circuits.³⁶³ Tunneling field-effect transistors (TFETs) is the primary approach to overcome the fundamental thermionic limits, in which the current conducts through band-to-band tunneling (BTBT) rather than the thermionic emission in single band transport devices.³⁶⁴ To allow strong direct BTBT transport, TFET devices are normally made of p-i-n homo or heterojunctions in which the intrinsic layer should have superior tunability subject to electrostatic modulation and ease of miniaturization in lateral dimensions.³⁶⁵ 2D semiconductors have great electrostatic control due to their ultrathin body and low static dielectric constants, which makes them ideal candidates for the intrinsic region of the TFET devices. However, unlike 3D semiconductors, the lack of stable and complementary doping in 2D materials makes the “all-2D” vdW heterojunction not compelling for the TFET device configuration. Hence, it is natural to combine 2D semiconductors with 3D bulk semiconductors for exploring next-generation TFET architectures, in which 2D semiconductors work as the intrinsic region and the heavily doped regions are made of 3D bulk semiconductors. Miao et al.³⁶⁶ recently reported a 2D/3D heterojunction TFET as shown in Figure 19a, in which the heterojunction was made of unintentionally n-doped 2D-InSe and heavily doped (p++) Si. As shown in Figure 19b, the 2D/3D heterojunction TFET was observed to have as an average SS of 34 mV/decade over four decades of drain current with a minimum SS of as low as 6.4 mV/decade, which are both below the fundamental thermionic limit at 60 mV/decade. Further, the devices showed a high current on/off ratio of 10⁵ for sub-60 mV/decade and a high on-state current density of 0.3 μA/μm, while most other TFETs including ones made using 2D/3D junctions have long been limited by low on/off ratios for sub-60 mV/decade operation and low on-current density.^367,368 The extracted SS slope in Miao et al. is nearly independent of temperature (Figure 19c),³⁶⁶ which unambiguously confirmed that the observed transport in the InSe/Si heterojunction TFETs was dominated by BTBT.

Figure 19.

2D/3D heterojunctions for logic devices. (a) 3D schematic of a 2D/3D TFET based on 2D n-type InSe and 3D p++ Si. (b) the 2D/3D heterojunction TFET was observed to have as an average SS of 34 mV/decade over four decades of drain current with a minimum SS of as low as 6.4mV/decade. (c) Extracted SS versus temperature in InSe/Si 2D/3D heterojunction TFET. Panels (a)-(c) were reproduced with permission from ref 366. Copyright 2022 Springer Nature. (d) Schematic view of $\text{HZO}/{\text{MoS}}_2$ NCFET. (e) Transfer characteristics of the $\text{HZO}/{\text{MoS}}_2$ NCFET measured at room temperature and at drain voltage of 0.1 V at different gate voltage sweep speeds. (f) Extracted SS versus drain current in the $\text{HZO}/{\text{MoS}}_2$ NCFET. Panels (d)-(f) were reproduced with permission from ref 369. Copyright 2018 Springer Nature.

Another mechanism for inducing steep SS (<60 mV/dec) switching is by adding a ferroelectric thin layer to the gate stack of a MOSFET, which is so-called negative-capacitance FET (NCFET).³⁷⁰ In a NCFET, the semiconductor channel surface potential can be amplified more than the gate voltage as the ferroelectric thin layer contributes a negative capacitance, which leads to a SS < 60 mV dec⁻¹ at room temperature in the device.^369,370 However, it remains challenging to design a stable NCFET by proper design of capacitance matching to simultaneously achieve the steep SS and the nonhysteretic 1-V characteristics. 2D semiconductors may offer a promising solution to those challenges, thanks to their low static dielectric constants, flatness of the body capacitance, and compatibility to the junction-less transistor architecture. Recently, Si et al.³⁶⁹ reported a 2D steep-slope transistor by using ${\text{MoS}}_2$ as a semiconductor channel and a 2D ferroelectric hafnium zirconium oxide layer (HZO) in the gate dielectric stack (Figure 19d). As shown in Figure 19e, the demonstrated ${\text{MoS}}_2$ NCFET showed a steep-slope in both forward sweep and reverse sweep and it was also observed to exhibit near hysteresis-free transfer characteristics, which indicates a good capacitance matching by using an atomic thin channel in a NCFET. The SS was extracted for both forward sweep (average SS ≈ 52.3 mV dec⁻¹) and reverse sweep (average SS ≈ 57.6 mV dec⁻¹) and those two values <60 mV dec⁻¹ indicated subthermionic subthreshold slope has been overcome and provided strong evidence that the observed steep SS is the result of a NC effect (Figure 19f).

4.2.2. Memory Devices.

The discussed advantages of 2D semiconductors not only manifest themselves in highly scaled and energy efficient logic devices and circuits but also make them appealing for transistor-backboned emerging memory technologies such as Static Random-Access Memory (SRAM), Dynamic RAM (DRAM), and Floating-Gate FET (FGFET).^371–373 Marega et al.³⁷⁴ reported a floating-gate memory device based on a junction-less transistor architecture with wafer-scale 2D ${\text{MoS}}_2$ as the channel and an additional metal gate as the floating gate in the gate stack, as shown in Figure 20a. The gate stack (from the bottom to the top) was comprising of a bottom control gate, a 30 nm-thick 3D ${\text{HfO}}_2$ blocking oxide layer, the floating gate, a 7 nm-thick ${\text{HfO}}_2$ tunnel oxide layer, and the ${\text{MoS}}_2$ channel. The distinguishable memory states in FGFET memory are achieved by the programmable transistor threshold voltage controlled by the amount of charge stored in the 3D charge trap layer. The total shift of the memory threshold voltage was estimated to be a memory window of 10.6 V, when observed at 1 nA (Figure 20b). Further, the authors also demonstrated that various logic operations can be directly performed using the reconfigurable memory elements. Programming of the FGFETs (positive shift in the threshold voltage) is achieved by injecting electrons into the floating gate with the application of a positive voltage pulse on the gate; erase of the FGFETs (negative shift in the threshold voltage) is achieved by extracting electrons from the floating gate with the application of a negative voltage pulse on the gate (Figure 20c).

Figure 20.

2D/3D heterojunctions for memory devices. (a) 3D schematic of a FGFETs device based on MOCVD-grown monolayer ${\text{MoS}}_2$. (b) Transfer characteristic of the FGFET acquired for two different gate voltage sweep directions, showing a memory window of 10.6 V when observing at 1 nA constant current. (c) Simplified band diagrams of ${\text{MoS}}_2$ FGFETs for both programming (left panel) and erasing (right panel). Reproduced with permission from ref 374. Copyright 2020 Springer Nature. (d) Schematic view of a $\text{AlScN}/{\text{MoS}}_2$ FE-FET. (e) Transfer characteristic of the $\text{AlScN}/{\text{MoS}}_2$ FE-FET acquired for two different gate voltage sweep directions, showing a memory window more than 4 MV/cm. (f) Retention measurement on $\text{AlScN}/{\text{MoS}}_2$ FE-FET by monitoring the drain current for varying time intervals up to 10⁵ s. (g) Calculated ratio of depolarization field over coercive field in three different ${\text{MoS}}_2$ FE-FET cases: (1) $\text{AlScN}/{\text{MoS}}_2$; (2) ${\text{HfO}}_2/{\text{MoS}}_2$; (3) $\text{PZT}/{\text{MoS}}_2$. Reproduced with permission from ref 375. Copyright 2020 American Chemical Society. (h) Polarization charges distribution (left) and band diagram (right) in a FeS-FET in polarization down and polarization up states. (i) The demonstrated FeS-FETs showed a high on/off ratio of over 10⁸ and a large memory window of over 1 MV/cm. Reproduced with permission from ref 376. Copyright 2019 Springer Nature. (j) Illustration of an atomristor consisting of a mono or few layer TMD or h-BN sandwiched between conducting electrodes. The structure can produce nonvolatile memory effect. Reproduced with permission from ref 377. Copyright 2019 Springer Nature.

The ferroelectric FET (FE-FET) is another emerging memory technology that could take advantage of the 2D semiconductor-based junction-less transistor architecture when integrated with 3D crystalline ferroelectric dielectrics. In FE-FETs, the information is stored by the amount of remnant polarization in a ferroelectric layer, which controls the transistor threshold voltage in the device.³⁷⁸ Despite their emergence in 1963, subsequent efforts to produce a practical, compact FE-FET have been plagued by poor retention due to large depolarization fields and incompatibility with CMOS process integration.³⁷⁹ By implementing 2D semiconductors as the channel to the FE-FETs, the depolarization fields can be minimized because of their low dielectric constants, fully depleted ultrathin bodies, and the flatness of the body capacitance. In addition, due to the absence of the surface dangling bonds, vdW 2D semiconductors such as ${\text{MoS}}_2$ can be transferred via wet- or dry-transfer schemes onto arbitrary substrates at room temperature, which makes them a great candidate for transistor channel in CMOS front end of line (FEOL) and BEOL process compatible technology. Among 2D/3D FE-FETs, Liu et al.³⁷⁵ has recently reported high-performance devices that integrates an atomically thin ${\text{MoS}}_2$ channel on top of a 3D wurtzite structure AlScN ferroelectric (Figure 20d). The devices showed a normalized memory window of 3 MV/cm and concurrently a current on/off ratio of near 10⁶, stable memory states up to 10⁴ cycles and state retention up to 10⁵ s as shown in Figure 20e,f. 2D semiconductor channel combined with large coercive field 3D ferroelectrics^380,381 can present as an ideal scenario for long retention in FE-FETs, as shown by the calculated ratio of depolarization field over coercive field in three different FE-FET cases in Figure 20g. By theoretical simulations, Liu et al.³⁷⁵ also show that the ratio of the depolarization field over the coercive field can be less than 1, while keeping a wide and stable memory window, even the AlScN ferroelectric layer is scaled down to 10 nm, which makes them ideal also for high voltage scaled devices.

As discussed above, the depolarization field combined with cycling endurance are two of the main issues slowing down the commercialization of FE-FETs in nonvolatile memory applications. Another option to potentially minimize the effects of the depolarization field is by using ultrathin ferroelectric semiconductors as the channel material in the ferroelectric transistor rather than using ferroelectric dielectric as gate material. Si et al.³⁷⁶ reported a ferroelectric semiconductor FET (FeS-FET), in which the polarization that stores the information in the FeS-FETs exists in the $\alpha -{\text{In}}_2{\text{Se}}_3$ ferroelectric semiconductor. Although FE-FET and FeS-FET have similar counter-clock hysteresis loops in their transfer curve, the operation mechanism of a FeS-FET (Figure 20h) fundamentally differs from a FE-FET: in a FeS-FET, the polarization charges accumulate at both the bottom- and top-surface of the 2D ferroelectric semiconductor, and they simultaneously determine the drain current due to the ultrathin body of the 2D ferroelectrics semiconductor, while only the polarization charges at the ferroelectric/semiconductor interface play a role in the electrostatics. The demonstrated FeS-FETs showed a high on/off ratio of over 10⁸ and a large memory window of over 1 MV/cm with a low operation voltage as shown in Figure 20i.

In addition, 2D materials such as TMDs and h-BN are suitable to realize vertical memristors consisting of one or more layers sandwiched between 3D conductive electrodes.^382–384 These memristors are sometimes referred to as atomristors (Figure 20j), a colloquial term to describe resistance switching effect in an atomically thin material, with monolayer h-BN representing the thinnest memristor active layer. ³⁸⁵ Since the initial atomristor report in 2017,³⁸² there have been much progress in advancing the understanding, performance, and applications of these memory devices. Atomic-resolution studies reveal that metal ion adsorption into native vacancy defects in 2D monolayers are responsible for nonvolatile resistance switching effect, arising from a phenomenon termed virtual conductive point effect,³⁸⁶ an atomic scale version of conductive bridge effect in conductive bridging random access memory (CBRAM) devices. Hence, the atomristor effect can be considered an application of defect, otherwise known as defectronics, where defect engineering can be utilized to optimize device performance.³⁸⁷ It is likely alternative mechanisms could also result in a memristor effect including conductive-bridge formation from metal diffusion along GBs in few-layer 2D materials to more exotic atomic distortions that can trigger resistance switching ^388–391

The performance of 2D memristors has similarly progressed over the past years with demonstrations of low switching energies, low switching voltages, and low switching currents suitable for diverse applications.^{384,392–394} In terms of reliability, a months-long retention has been demonstrated with the potential for indefinite retention with engineered devices and interfaces.³⁹⁵ The endurance of 2D memristors is still at a nascent stage with current cyclability in the 100 to 1000 s of switching cycles for mono or few layers.³⁹² Thicker films of TMDs with partial oxidation have afforded more than a million cycles.³⁹⁶ For applications, wafer-scale demonstration of cross-bar arrays for artificial neural networks for neuromorphic computing have been reported with character recognition approaching the accuracy limit.³⁹² Likewise, nonvolatile switches for high-frequency applications in the 5G and 6G communication spectrum with a bandwidth up to around 500 GHz and data transmission of 100 Gb/s has been reported. ^395,397

5. Magnetic Topological Insulators and Twisted vdW Heterostructures.

5.1. ${\text{MnBi}}_2{\text{Te}}_4$: An Intrinsic Magnetic Topological Insulator.

Research on quantum materials has been at the frontiers of materials science and condensed matter physics since exotic functional properties of quantum materials are not only fundamentally important but also have wide prospects for applications in information and energy technologies. Magnetic topological insulators are a type of recently discovered quantum materials in which a combination of magnetism and nontrivial band topology can create a variety of topological quantum states, such as a quantum anomalous Hall insulator (QAHI) and an axion insulator.³⁹⁸ Since QAHI can support dissipationless charge transport without an external magnetic field, it carries great promise for applications in energy-saving electronic and spintronic devices. Although magnetic doping into topological insulators (TIs) and the interface magnetic proximity effect in heterostructures have been employed to demonstrate the QAHI, the chemical inhomogeneity of magnetic doping leads to small exchange gaps,^399,400 thus limiting the working temperature of the quantum anomalous Hall state. This disadvantage has inspired the search for topological materials with intrinsic magnetism.

${\text{MnBi}}_2{\text{Te}}_4$ has recently been investigated as an emerging intrinsic magnetic TI.^401–403 It is a layered ternary tetradymite compound, crystallizing in a rhombohedral structure with the space group R3m, and its structure is built of the stacking of Te-Bi-Te-Mn-Te-Bi-Te septuple layers (SLs) along the $c$-axis (Figure 21a,b). Given that the SLs are coupled through the vdW force, ${\text{MnBi}}_2{\text{Te}}_4$ can be easily exfoliated into thin flakes. This material exhibits an antiferromagnetic (AFM) order below $T_{\text{N}}=25\text{K}$ (Figure 21e), with in-plane ferromagnetic (FM) coupling and out-of-plane AFM coupling.⁴⁰⁴ Such a magnetic order is intimately coupled with band topology, which was predicted to yield a large exchange gap (Figure 21c) and various topological quantum states, as discussed below. Since ${\text{MnBi}}_2{\text{Te}}_4$ is a metastable phase, its crystal can be obtained only by quenching the crystals grown in the slowly cooling down process of the melt with a stoichiometric composition.^401,404 However, single crystals grown using this method are small and thin. The other problem with this method is the presence of intergrowth between ${\text{MnBi}}_2{\text{Te}}_4$ and ${\text{Bi}}_2{\text{Te}}_3$. Soon after, Yan et al.⁴⁰⁵ developed an effective growth protocol for growing large ${\text{MnBi}}_2{\text{Te}}_4$ crystals. They used ${\text{Bi}}_2{\text{Te}}_3$ as a flux to grow ${\text{MnBi}}_2{\text{Te}}_4$ crystals. Crystals grown using this flux method have significantly larger lateral dimensions (up to a few millimeters) and can be easily exfoliated, which is critical to nanodevice fabrications and exploration of emerging topological quantum states in its 2D limit. The availability of such high-quality crystals has enabled observation of various topological quantum states in ${\text{MnBi}}_2{\text{Te}}_4$, including the QAHI, the axion insulator, the high number of Chern insulators ($C=2$), as well as the layer Hall effect.^406–409

Figure 21.

Crystal and magnetic properties of magnetic TIs. (a) Crystal and magnetic structure of ${\text{MnBi}}_2{\text{Te}}_4$. (b) HAADF-STEM image taken from the [100] zone axis of ${\text{MnBi}}_2{\text{Te}}_4$. Reproduced with permission under a Creative Commons Attribution 4.0 International license from ref 404. Copyright 2019 American Physical Society. (c) Spin-resolved electronic structure of the ${\text{MnBi}}_2{\text{Te}}_4$ (0001) surface. Reproduced with permission from ref 401. Copyright 2019 Springer Nature. (d) Composition dependence of carrier density $n$ and transport mobility ${\mu }_{\text{H}}$ of $\text{Mn}{\left({\text{Bi}}_{1-x}{\text{Sb}}_x\right)}_2{\text{Te}}_4$. Inset: Flux-grown crystals’ image. Reproduced with permission under a Creative Commons Attribution 4.0 International license from ref 410. Copyright 2021 American Physical Society (e, f) Field-cooled (FC) and zero-field-cooled (ZFC) temperature dependences of magnetic susceptibility $\chi$ with magnetic field aligned parallel to the $c$-axis ($H//c$) for (e) ${\text{MnBi}}_2{\text{Te}}_4$⁴⁰⁴ and (f) $\text{Mn}{\left({\text{Bi}}_{0.1}{\text{Sb}}_{0.9}\right)}_2{\text{Te}}_4$, respectively. Panel (f) was reproduced with permission from ref 411. Copyright 2020 American Physical Society.

In addition to the 2D topological states noted above, ${\text{MnBi}}_2{\text{Te}}_4$ is also predicted to host a long-sought, ideal time-reversal symmetry breaking Weyl semimetal (WSM) with one pair of Weyl nodes in bulk when its AFM order is coerced into FM order by a magnetic field parallel to the c-axis.^402,403 Zhang et al.⁴⁰² suggest that this FM WSM can be either type-I or type-II, depending on the lattice parameters. Recent theoretical studies further predict that such a Weyl state can be tuned by the field orientation but disappears as the field is rotated to the in-plane direction.⁴¹² However, there has been no experimental evidence that supports the presence of the Weyl state in the FM phase driven by the c-axis magnetic field in ${\text{MnBi}}_2{\text{Te}}_4$. This is because the Weyl nodes are far from the Fermi surface due to self-doping effects in pristine ${\text{MnBi}}_2{\text{Te}}_4$.^404,405

Several groups have shown that it is possible to tune the chemical potential of ${\text{MnBi}}_2{\text{Te}}_4$ by doping Sb to the Bi site, similar to the ${(\text{Bi},\text{Sb})}_2{\text{Te}}_3$ system.^410,413,414 Lee et al.⁴¹⁰ have shown that single crystals of $\text{Mn}{\left({\text{Bi}}_{1-x}{\text{Sb}}_x\right)}_2{\text{Te}}_4$ (MBST, $0\le x\le 1$) with controlled chemical potentials can be grown using ${\text{Sb}}_2{\text{Te}}_3-{\text{Bi}}_2{\text{Te}}_3$ as a flux, similar to the growth protocol reported by Yan et al.⁴¹⁴ To achieve a desired chemical potential, the $\text{Sb}$ concentration and the temperature for centrifuging need to be tuned to appropriate values. Empirically, large MBST single crystals with lateral dimensions being up to 10 mm can be grown using the molar ratio of $\text{Mn:Sb:Bi:Te}$ in 1:5x:5(1-x):16.^410,413 Carefully tuning of the centrifugation temperatures for each $x$ is critically important since the melting points of both fluxes and $Mn{\left({\text{Bi}}_{1-x}{\text{Sb}}_x\right)}_2{\text{Te}}_4$ are very close. Given that the melting points of ${\text{Bi}}_2{\text{Te}}_3$ and ${\text{Sb}}_2{\text{Te}}_3$ are 585 and 620 °C, respectively, the excessive flux is separated by centrifuging in the range of 590 to 620 °C, depending on x. Higher centrifugation temperatures are used for the samples with higher Sb content. It is worth noting that ramping down quickly below the solidification temperatures and then ramping up to the desired centrifugation temperature in higher Sb-content alloy can lead to high density of Mn occupation at the Sb sites (e.g., antisite defects), which favors a ferromagnetic exchange between Mn layers.^{411,415–417}

While ${\text{MnBi}}_2{\text{Te}}_4$ is electron-doped, as the Sb concentration increases, the chemical potential of $\text{Mn}{\left({\text{Bi}}_{1-x}{\text{Sb}}_x\right)}_2{\text{Te}}_4$ is tuned from the bulk conduction band to the bulk valence band passing through the charge neutral point near $x$ equal to 0.3. Through fine-tuning of chemical potential by Sb substitution for Bi, Lee et al.⁴¹⁰ observed transport hallmarks of the predicted ideal Weyl state in the lightly hole-doped samples with $x=0.26$ (Figure 21d), including a large intrinsic anomalous Hall effect and chiral anomaly. The Weyl state in $\text{Mn}{\left({\text{Bi}}_{1-x}{\text{Sb}}_x\right)}_2{\text{Te}}_4$ is of particular interest because it is the least complicated possible manifestation of a Weyl phase, hosting only one pair of Weyl nodes at the Fermi level and having no interference from other trivial bands near the Fermi level. Therefore, it is an ideal model system for further study of Weyl Fermion physics. The magnetic phase of $\text{Mn}{\left({\text{Bi}}_{1-x}{\text{Sb}}_x\right)}_2{\text{Te}}_4$ is also dependent on Sb concentration. For $x<0.9$ the systems exhibit an A-type AFM order similar to that seen in the pristine compound ${\text{MnBi}}_2{\text{Te}}_4$. However, for $0.9\le x\le 1.0$, an FM phase with $T_{\text{c}}=26-46\text{K}$ (Figure 21f) is accessible due to the Mn-Sb antisite defect-mediated layered FM coupling, as noted above.^415–417 The realization of the FM phase in MBST is an important step toward understanding intrinsic ferromagnetic topological insulators, which opens up opportunities for engineering topological states in this vdW ferromagnet and related family members ${\text{MnBi}}_{2n}{\text{Te}}_{3n+1}$.

5.2. Quantum Anomalous Hall Effect in Magnetically Doped Topological Insulators.

The quantum Hall effect has been in the eye of the scientific community for nearly half a century, and materials hosting a 2D electron system could exhibit it. Graphene and gallium arsenide heterostructures were among the more popular material systems for performing quantum Hall research. Many applications of the quantum Hall effect, notably electrical metrology, have required strong magnetic fields for the quantized plateaus to be exhibited in a robust way.⁴¹⁸ This requirement has limited the extent to which an experimental apparatus may be simplified, namely in the necessity of an electromagnet. Emerging thin materials, like magnetically doped topological insulators (MTIs), are known to exhibit the quantum Hall effect at zero magnetic field. This phenomenon, known as the quantum anomalous Hall effect (QAHE), is linked to the breaking of time-reversal symmetry and the opening of an energy gap that can accommodate the existence of topological surface states.^419–421

Under typical circumstances, the formed energy gap closes in physical locations where the component of the magnetization normal to the surface changes direction. This implies that for material systems nearing the 2D limit, assuming they have relatively uniform out-of-plane magnetization, this transition occurs at the edges of the material system. Therefore, the edges of a suitable material system would then enable the QAHE to be exhibited and observed. Electrically, its longitudinal transport would be ideally dissipationless given that its corresponding quantization conditions are ${\sigma }_{xy}=e^2/h$ and ${\sigma }_{xx}=0$. Thus, in the context of metrology, the QAHE could become the basis for a future resistance standard, at most needing only a small permanent magnet to activate a quantized resistance value.^422–424 Ultimately, such metrologically suitable devices could operate at zero-field for measurements, making the dissemination of the ohm more economical and portable.

The details of how the QAHE arises are obviously more nuanced when compared with the conventional integer quantum Hall effect. As summarized by Kou et al.,⁴²⁵ there are two main approaches for introducing magnetic exchange that allows one to break surface states’ time-reversal symmetry. The first approach is by means of magnetic proximity, typically achieved by adding in a topologically trivial magnetic material, which locally aligns the relevant electrons’ spin moments out of plane. The second approach involves the incorporation of magnetic ions into the host material system.⁴¹⁹ Currently, MTIs that are used in electrical metrology have been grown by MBE,⁴²⁶ presumably due to the method’s advantages vis-à-vis its nonequilibrium physical deposition, accurate layer thickness and doping control, and wafer-scale growth capability.

As mentioned earlier, most quantum Hall applications based on graphene devices will generally need a sufficiently strong magnetic field to observe any robust quantum behavior. This limitation is inherently tied to the band structure of graphene. However, with the QAHE, one may observe a physical manifestation of a material’s topologically nontrivial electronic structure without needing an electromagnet to break time-reversal symmetry. There are several types of materials that exhibit the QAHE, with some being classified among the following categories: doped MTIs, intrinsic MTIs, and twisted vdW layered systems. Some key recent results involve materials that display a quantized resistance plateau at zero-field suitable for metrology measurements, with some recent work already mentioned. ^422,424

Recent work by Fox et al.⁴²⁴ explored the metrological applicability of the QAHE in a MTI-based thin film. Using a cryogenic current comparator, or an apparatus that allows for the precise comparison of two electrical currents (and thus, two resistances), the group measured the quantization of the Hall resistance to within one part per million and, at smaller electrical currents, measured the longitudinal resistivity to be under 10 mΩ at zero magnetic field. Some of these acquired data are shown in Figure 22a.b. A breakdown of the quantized state was induced by gradually increasing the current density past a critical value. It was thought that this effect was due to electron heating in parallel bulk current flow. This work furthered the understanding of MTIs by gaining comprehension for the physical mechanisms that ultimately contribute to these devices’ limitations, including thermal activation, bulk dissipation, and variable-range hopping. Gotz et al.⁴²² also sought to present a metrologically comprehensive measurement at zero-field of a MTI (in this case, it was V-doped ${(\text{Bi},\text{Sb})}_2{\text{Te}}_3$). When the difference of the QAHE resistance was measured as compared to the von Klitzing constant $\left(R_{\text{K}}\right)$, a value of $0.176\mu \text{Ω}/\text{Ω}\pm 0.25\mu \text{Ω}/\text{Ω}$ was obtained. Some of these data are shown in Figure 22c.

Figure 22.

Summary of QAHE measurements of MTI-based films. (a) Cryogenic current comparator data are shown for Hall measurements in an example device using a 100 nA current at 21 mK. The plateau in the upper panel shows the deviation from $R_{\text{K}}$. The inset shows a magnified view of the Hall resistance deviations in the center of the plateau $(\nu =1)$. The bottom panel shows the logarithmic behavior of the deviations as one departs from the optimal gate voltage. (b) The longitudinal resistivity for the same device. Data are displayed on a linear and log scale in the top and bottom panels, respectively. All error bars show the standard uncertainty and are omitted when they are smaller than the data point. Reproduced with permission from ref 424. Copyright 2018 by the American Physical Society. (c) Topological insulator at the $\nu =1$ plateau data. Currents of 5 and 10 nA were used in both orthogonal and diagonal configurations. The colored rectangles represent the weighted average and standard deviation of the data from those configurations. Reproduced from ref 422 with the permission of AIP Publishing. (d—h) Quantization accuracy of the QAHE-based resistance standard. (d) The normalized deviation $\text{Δ}R/R_{\text{K}}$ are shown (top panel shows conventional quantum Hall effect). The error bars correspond to the combined standard uncertainty and $N$ denotes the number of data points used for averaging. (e) The dependence of $\text{Δ}R/R_{\text{K}}$ on the source-drain current (I) is shown, with the error bars corresponding to the standard deviation of $N=200$ measurements. (f) The current dependence of the longitudinal resistance $\left({\rho }_{xx}\right)$ is shown at a temperature of 20 mK. The longitudinal resistivity was measured by using the upper (U1—U5) and lower (L1—L5) pairs of voltage contacts. The error bars are the standard deviation of $N=20$ measurements. (g) The relationship between $\text{Δ}R$ and ${\rho }_{xx}$ shown with a red line as the linear fitting result. (h) Temperature dependence of ${\rho }_{xx}$ measured at $0.5\mu \text{A}$ using the upper pair of voltage contacts (U1—U5). The error bars are the standard deviation of $N=20$ measurements. Reproduced with permission from ref 423. Copyright 2022 Springer Nature.

Two other recent works surrounding MTIs and the quality of their exhibited QAHE plateaus come from Okazaki et al. and Rodenbach et al.^423,427 In the former, the group demonstrates a precision of $10\text{nΩ}/\text{Ω}$ for the $\nu =1$ plateau of the QAHE. Furthermore, they directly compared both the QAHE and QHE from a conventional device to confirm their observations. These results are shown in Figure 22d-h. In Rodenbach et al.,⁴²⁷ extensive analyses on the surrounding elements of metrological measurements, namely noise measurements, are summarized and shown in Figure 23. These works are crucial to understand for eventually realizing a zero-field quantum resistance standard. One of the last remaining limitations to be lifted are the stringent temperature requirements, which are currently in the 10 to 100 mK range. Fijalkowski et al.⁴²⁸ show that the chiral edge channels associated with the QAHE continue to exist without applied magnetic field up to the Curie temperature (about 20 K) of bulk ferromagnetism in their TI system. This conclusion was reached through a careful analysis of nonlocal voltages in Corbino-type devices. It was also found that thermally activated bulk conductance was mostly responsible for quantization breakdown. These results show promise on the availability of topological protection from MTI edge channels for developing a resistance standard.

Figure 23.

Summary of the precision measurements of (a) ${\rho }_{xx}$ and (b) the QAHE over the previous few years. Applied currents vary, and the following MTI measurements are represented: 2018 NIST/Stanford (purple),⁴²⁴ PTB/UW (black),⁴²² 2022 NIST/Stanford (red and blue),⁴²⁷ and 2022 NMIJ and partners (olive).⁴²³ The light green region in panel (b) marks the boundary for data points going beneath one part in 10⁷. All error bars represent $k=1$ type A and B combined uncertainties. Adapted with permission under Creative Commons Attribution 4.0 International license from ref 427. Copyright 2022 American Physical Society.

5.3. Superconducting Diode Effect in Twisted Trilayer-Graphene Homojunctions.

Within BCS theory and for most known superconductors, time-reversal symmetry is a key ingredient to the formation of Cooper pairs.^429,430 Nonetheless, superconductivity can survive moderate time-reversal symmetry breaking perturbations, e.g., resulting from the proximity to a ferromagnet or from an applied external magnetic field. The microscopic coexistence between superconductivity and ferromagnetism in a single electron liquid, however, is very rare in nature.^431–433 Time-reversal symmetry also implies that the critical current for forward, $I_c^{+}$, and backward direct current (DC) bias, $I_c^{-}$, are identical. If, however, it is broken in the superconductor along with inversion symmetry, $I_c^{+}\ne I_c^{-}$ becomes possible. In that case, applying a DC current $I_{DC}$ with $\left|I_{DC}\right|$ between $I_c^{+},$ and $I_c^{+},$, will lead to dissipationless superconducting transport for one sign of $I_{DC}$ and resistive behavior for the other. Such “superconducting diode” behavior has been reported in previous works where time-reversal symmetry is explicitly broken by applying an external magnetic field or proximitizing with a magnetic material.^434–436 Alternatively, diode effect has been demonstrated in Josephson junctions.^437–439 Notably, the superconducting diode effect at zero-field in a uniform, junction-free sample would be a strong indication of the microscopic coexistence between superconductivity and spontaneous time-reversal symmetry breaking. Such a zero-field superconducting diode effect was recently observed in small twisted angle trilayer graphene,⁴⁴⁰ where the authors demonstrated a prominent diode effect that was intrinsic to the superconducting phase and could reach reasonably large current asymmetries, with $\left|I_c^{+}-I_c^{-}\right|/\left(I_c^{+}+I_c^{-}\right)$ approaching 1.

In the mirror-symmetric twisted trilayer graphene (tTLG) sample (Figure 24a), the middle graphene layer is rotationally misaligned with the outer layers by an angle of $\theta ={1.25}^{\circ }$, which is detuned from the magic angle of 1.55°.⁴⁴⁰ The zero-field superconducting diode is evidenced by the nonreciprocal current—voltage characteristic, as shown in Figure 24b. At $B=0$, the superconducting critical current, defined as the peak position in the differential resistance $\text{d}V/\text{d}I$, is around 10 nA with forward biased current flow but increases dramatically to around 90 nA when the current flow is reversed. Such nonreciprocity enables a diode-like switching between dissipationless and resistive transport behaviors, when a DC current of 22 nA alternates between forward and reverse bias directions, as shown in Figure 24c. Notably, the alternating behavior remains robust for more than an hour, indicating that the zero-field superconducting diode effect is nonvolatile.

Figure 24.

Nonreciprocity and superconducting diode effect. (a) Schematic diagram showing the superconducting diode effect. Cooper pairing is only stable when current flows from left to right. As a result, the transport response across the sample is dissipationless when current flows from left to right, whereas a resistive behavior is observed when current direction is reversed. (b) Differential resistance as a function of DC current bias of the superconducting phase at $B=0.I_c^{+}$ and $I_c^{-}$ are the critical current with positive and negative DC current bias, respectively. The asymmetry in $I_c^{+}$ and $I_c^{-}$ shows the nonreciprocity. (c) Demonstration of robust zero-field superconducting diode effect. (d, e) Field-training of the superconducting diode: (d) After a positive (negative) field training, the superconducting diode remains as a reverse (forward) diode as shown in the blue (red) curve. (e) Extremely high diode efficiency at large doping, as the zero-resistance regime (shaded part) has shifted totally to the negative current side. (f) Interplay between superconductivity and density-wave state. Longitudinal resistance as a function of temperature and doping, at different magnetic fields. As the magnetic field increases, superconductivity is suppressed and density-wave state (resistance oscillations with 1/4 periodicity) takes over at the low temperature range. Adapted with permission from ref 440. Copyright 2022 Springer Nature.

As shown in Figure 24d, the sign of nonreciprocity at zero-field can be reversed by training with an external magnetic field. After training with a negative magnetic field of −25 mT, which is then set to zero, the superconducting phase behaves like a forward diode, with the critical current being larger with a positive DC current bias. Conversely, a reverse diode behavior is observed after training with a positive magnetic field of 25 mT. The dependence on the magnetic field history offers unambiguous evidence for an underlying spontaneous time-reversal symmetry breaking. Moreover, a prominent diode effect is observed throughout the density regime of the superconducting phase, indicating an origin that is intrinsic to the moiré system.⁴⁴⁰ An extreme nonreciprocal behavior can be achieved by tuning the carrier concentration of the system by electrostatic doping. As shown in Figure 24e, the sample is resistive at zero current bias but becomes superconducting in the presence of a negative DC current bias.

Since the presence of either time-reversal or 2-fold rotation/inversion symmetry guarantees reciprocal superconducting transport, the zero-field superconducting diode effect implies that both time-reversal and 2-fold rotation symmetry are broken in the superconducting state of the tTLG sample. The mechanism underlying the superconducting diode effect is therefore constrained by these broken symmetries, which can be understood by considering the possible symmetry-breaking instabilities of moiré electrons.⁴⁴⁰ The simplest possible scenario is that the system spontaneously develops an imbalance of its two valleys, which breaks both of the aforementioned symmetries. Then, a superconducting phase emerging from a valley-imbalanced Fermi surface will exhibit a zero-field superconducting diode effect. Due to the multitude of internal “flavor” degrees of freedom—resulting from the spin, valley, and conduction-valence-band quantum numbers of the band structure—there is a whole plethora of such possible candidate instabilities in tTLG.^440,441 A careful consideration of the trainability of the observed diode effect⁴⁴⁰ leaves only a single candidate phase that is symmetry-equivalent to the valley-imbalance case discussed above.

The zero-field superconducting diode effect is observed in the so-called small twisted angle regime. In stark contrast with the magic-angle regime, the phenomenon of Dirac revival is mostly absent in the small twist angle regime. Instead of correlated insulators appearing at every integer moiré filling, the moiré band is populated with density wave states that exhibit a density modulation of 1/2 and 1/4 moiré fillings. This gives rise to an interesting coexistence between the superconducting and density wave states. As superconductivity is suppressed by the application of an external magnetic field, a series of density wave states are evidenced by the observation of resistance peaks appearing at integer multiple of 1/4 moiré filling,⁴⁴⁰ as shown in Figure 24f. The onset temperature of these resistance peaks, which defines the melting transition of the underlying density wave order, coincides with the transition temperature of the superconducting phase. It is argued that these density-wave states likely compete against the superconducting state, since the critical temperature of the superconducting phase do not show the same density modulation as the density wave order. Nevertheless, the simultaneous presence of the density wave order and the superconducting phase in the phase space of the small-angle tTLG provides more constraints for theoretical models aiming to understand the origin of superconductivity in a graphene moiré band.

In summary, the intrinsic zero-field superconducting diode effect in small-angle tTLG demonstrates the microscopic coexistence of superconductivity and spontaneous time-reversal symmetry breaking. This discovery not only provides a platform with superconducting diode effect for potential applications but also draws our attention to the unique behavior of the superconductivity in this system and hopefully brings us closer to deciphering the nature of strongly correlated moiré physics.

5.4. Moiré Luttinger Liquids in Twisted ${\text{WTe}}_2$ Bilayers.

The Luttinger liquid (LL) model^442,443 offers a powerful tool to study interacting electrons in 1D metals, which are distinct from 2D or 3D metals that are typically captured by the Fermi liquid theory. An interesting question is whether the LL physics could be stabilized down to the lowest temperature in some strongly correlated 2D or 3D systems, as investigated by Philip W. Anderson.⁴⁴⁴ Approaches based on coupled-wire models,⁴⁴⁵ which consist of a 2D array of 1D LLs, have been developed to investigate this fundamental question theoretically.^445–449 The experimental realization of high-quality arrays of 1D wires necessary for investigating various coupled wire models remains challenging as they require many identical wires to be strictly arranged with crystalline quality at both nano and microscopic scales. Experimental tests of many interesting ideas^450–452 along this direction remain uncharted.

Significant experimental progress has been made recently based on 2D moiré quantum engineering. The study utilizes a unique moiré material consisting of twisted bilayer ${\text{WTe}}_2$ (${\text{tWTe}}_2$).⁴⁵³ With an elongated rectangular unit cell, monolayer ${\text{WTe}}_2$ is known to exhibit rich physics including topology,^454–456 superconductivity,^457,458 and strong correlations.^459,460 As shown in Figure 25a, 2D ${\text{WTe}}_2$ has a sandwiched structure, in which the middle layer hosts the W atoms that form 1D zigzag chains. Figure 25b illustrates the moiré superlattice of the ${\text{tWTe}}_2$ twisted at a small angle of near 5° (for simplicity, only the two layers of W atoms of ${\text{tWTe}}_2$ are shown). Clearly, the moiré supercell is an enlarged rectangle, with a size tunable by twist angles. Figure 25c confirms the formation of such an anisotropic moiré pattern via a conductive atomic force microscopy image. Transport studies indeed revealed a highly anisotropic phase and LL behaviors in the hole-rich state of ${\text{tWTe}}_2$ devices near this twist angle.⁴⁵³ With carefully designed and fabricated devices (Figure 25d,e), Wang et al.⁴⁵³ showed that an exceptionally large transport anisotropy with a four-probe resistance ratio of close to 10³ along the two orthogonal directions (Figure 25f) was observed in the hole-doped regime (Figure 25g,h) but not in the electron-doped regime. Moreover, the across-wire conductance obeys power-law dependence on temperature down to 1.8 K, and the differential conductance under varying applied d.c. bias and temperature shows the universal power-law scaling behavior (Figure 25i,j) expected for LL physics.⁴⁴² Both the anisotropy and the interaction strength are highly tunable in the ${\text{tWTe}}_2$ moiré structure, by knobs, e.g., doping density and twisted angle.⁴⁵³ The ${\text{tWTe}}_2$ system offers a high-quality, high-controllable platform for studying the intriguing physics related to various coupled-LL models.

Figure 25.

Luttinger liquid behavior in ${\text{tWTe}}_2$ moiré system. (a) The crystal structure for monolayer ${\text{WTe}}_2$. The W atoms are sandwiched by two Te atom layers. From the top view, the W atoms (blue) form zigzag chains. The dashed square denotes the unit cell. (b) Moiré superlattice of ${\text{tWTe}}_2$, where only the W atoms are shown. The alternating AA and AB 1D stripes are illustrated. (c) conductive AFM image of a ${\text{tWTe}}_2$ sample. (d) Optical image of a typical device, with the contact regions marked with red solid lines and the two layers of ${\text{WTe}}_2$ with yellow and white dashed lines, respectively. (e) Cartoon illustration of the device structure. From bottom to top: bottom graphite, bottom hBN, electrodes, thin hBN, ${\text{tWTe}}_2$, top hBN, and top graphite. (f) Measurement configuration for the hard and easy directions. The squares denote the contacts, and the gray lines indicate the moiré stripes. s, source; d, drain. (g) Four-probe resistance of the hard and easy direction shown in panel (f), measured at 1.8 K, as a function of the gate-induced doping density $n_{\text{g}}$ of the device. (h) The anisotropy ratio, $R_{\text{hard}}/R_{\text{easy}}$ with $R_{\text{hard}}$ and $R_{\text{easy}}$ in g, versus $n_{\text{g}}$. (i) The across-wire differential conductance $\text{d}I/\text{d}V$ measured under different d.c. bias and temperature, with the doping fixed on the hole side. (j) Scaled differential conductance $(\text{d}I/\text{d}V)/T^{\text{a}}$, plot against $\text{eV}/k_{\text{B}}T$ (same data in panel (i)), showing that all the data collapse into one curve. Adapted with permission from ref 453. Copyright 2022 Springer Nature.

An immediate question from the moiré LLs in the ${\text{tWTe}}_2$ is whether such a 2D anisotropic LL behavior could be stabilized down to millikelvin temperature, one crucial question in the study of non-Fermi liquid physics.^446–448 An exciting future direction is to search for unconventional quantum oscillations and quantum Hall states in such a non-Fermi liquid system.^449–451 The physics of spin-charge separation^442,443 is another interesting direction to pursue here in such a 2D setting. Other predictions in coupled wire models, including topological phases⁴⁶¹ and quantum spin liquids,⁴⁶² are also of potential future interest. On the material side, ventures in other rectangular moiré lattices, such as twisted GeSe,⁴⁶³ twisted $T_{\text{d}}-{\text{MoTe}}_2$, twisted phosphorene, $T_{\text{d}}-{\text{MoTe}}_2/T_{\text{d}}-{\text{WTe}}_2$ heterostructure, also deserve careful studies as they may develop imilar phenomena.

PERSPECTIVES AND FUTURE WORK

This review provides the recent progress of theory, synthesis, heterostructures, characterization, sensing, devices, and physical properties of 2D materials. There continue to be many interesting breakthroughs in recent months and years, including MD simulations and machine learning for 2D materials synthesis and applications. Theory is becoming inseparable from experimental studies and is now key to design materials, predict device performances, and optimize processing. Additionally, remote epitaxy using 2D materials as the intermediate layer and wafer-scale synthesis of 2D TMDs by MOCVD also established their own fields and continue to emerge. However, as we are moving forward in 2D materials’ science and technology, many challenges still require interdisciplinary efforts and collaborations to be addressed. For examples, some challenges regarding synthesis of high-quality 2D films and introduction of magnetic properties into TMDs have been mentioned in sections 2.7 and 2.9, respectively. Here, we provide perspectives on the future research directions that we may pursue.

Material Theory.

Computationally we find that intercalation, doping, and defects provide an efficient platform for tailoring 2D materials’ properties. However, for intercalation, there are still open questions about staging and cointercalation in common materials such as multilayer graphene, which could potentially provide further property control. Defects, on the other hand, can be difficult to simulate at the atomic level, especially when working with charged point defects, where long-range artificial interactions occur. There are several schemes that have been proposed to correct for this; however, it is still an unanswered question and requires continuous investigation.

Artificial Intelligence and Machine Learning for 2D Materials.

While many solutions have been devised in the 2D material world with the utilization of ML, the field of condensed matter still has a lot of room to grow with these mathematical tools. As demonstrated in recent publications,⁵⁸ it becomes apparent that ML algorithms could conceivably be trained to refine potential energies in DFT calculations, suggesting a feasibility to derive a generalized exchange correlations through ML—arguably the holy grail of DFT work—thus reducing computational load and greatly increasing accuracy. In synthesis, Bayesian optimization (BO) seems to be the prevailing technique. Though, it could be noted that—with a high computational cost—it would be beneficial to migrate away from BO and toward neural networks. Unfortunately, without any training data or a large quantity of pre-existing samples, this is not possible. Therefore, a proposed solution could be to mimic the theoretical community in devising an open, centralized, and normalized database structure. In case of applications, availability of diverse ML tools on 2D materials and devices provides the exciting possibility that not only will be we able to improve traditional applications but also explore autonomous material synthesis and processing.

Optimizing ReaxFF Parameters with Guidance from Machine Learning.

Developing the ReaxFF force field, like other empirical potentials, has been challenging due to the many-body character of the potential energy function and the high dimensionality of the force field parametrization. Obtaining an accurate, transferable, and efficient ReaxFF is therefore critical to atomic scale simulations. Molecular dynamics simulations are an effective method to test the performance of a force field at hand. In the future, a data-driven approach that combines ML, DFT, ab initio, and classic MD simulations needs to be developed for active learning of force field. Besides the ML algorithm, inclusion of ab initio MD simulations to this framework will significantly accelerate the force field development process, particularly for gas-phase reactions. ML will automate the force field training workflow which consists of the evaluation of models taken from MD simulations in comparison with DFT and the identification of the non-DFT matched data, followed by the generation of DFT data and their addition to training set in order to reoptimize force field parameters. Thus, it is necessary to enhance the accuracy and quality of force field parameters by active learning.

Automatic Analysis of ReaxFF Simulations with Machine Learning.

Studies using MD simulations usually require large-size and long-time runs that generate large amounts of data. Their postprocessing, especially when the investigation is coupled with rare events of interest like chemical reactions, costs significant efforts. Machine learning methods can automate analysis of ReaxFF simulations, helping with extracting and classifying outliers and unique features in simulations of materials. Our future work will focus on ML automated postprocessing of ReaxFF simulations to better manage and interpret our data, then connecting them to experimental efforts.

Continuous Exploration of MXenes Properties.

In section 2.1, we learn that the family of MXenes is enormously large. There is still significant work to be done to understand the relationship between their chemistry and properties. While more than 30 stoichiometric MXenes have been discovered, in addition to a variety of solid-solution MXenes, there is still ample room for exploring MXenes. Computationally it is expected that there will be more ordered and solid-solution MXenes discovered for each structure: ${\text{M}}_2{\text{XT}}_x$, ${\text{M}}_3{\text{X}}_2{\text{T}}_x$, ${\text{M}}_4{\text{X}}_3{\text{T}}_x$, and ${\text{M}}_5{\text{X}}_4{\text{T}}_x$.^464,465 For some specific chemistries, there are predictions of ferromagnetism, topological semiconductors, and others, depending on the specific chemistry and surface chemistry.^466,467 Additional effort must be placed on the synthesis and discovery of these materials. Generally, multipleM chemistry represents the future of MXenes with desired properties. Thus, additional systematic studies are needed to determine the specific relationships and effects different chemistries have on MXene properties and need incorporated into computational models to further guide experimental studies.

Making Magnetic Layered Compounds with High Curie Temperatures.

Adding more $\text{Fe}$ into ${\text{Fe}}_n{\text{GeTe}}_2$ is expected to enhance the strength of the exchange interaction present and consequently allows one to push toward higher Curie temperatures ($T_{\text{C}}$). Indeed, from ${\text{Fe}}_3{\text{GeTe}}_2$ to ${\text{Fe}}_5{\text{GeTe}}_2$ with thicknesses around 10 nm or thicker, $T_{\text{C}}$ was found to generally increase from about 220 K to about 300 K. These promising $T_{\text{C}}$ values are expected to further increase with increasing $\text{Fe}$ content to values up to and even beyond 500 K.⁴⁶⁸ Recent theoretical studies also predicted that ${\text{Fe}}_6{\text{GeTe}}_2$ and ${\text{Fe}}_7{\text{GeTe}}_2$ are stable 2D phases.⁴⁶⁸ However, experimental validation is lacking. In-depth studies that correlate structure, specifically the precise atomic arrangement of nearest neighbor $\text{Fe}$ facilitating the magnetic coupling, and the resulting magnetic properties at the mesoscopic scale, in particular $T_{\text{C}}$, magneto-crystalline anisotropy, coercive fields, remanence and magnetic domain structure, will establish the structure—property relationship in these material systems and help form a comprehensive understanding of magnetic phenomena in these material systems.

Strain Engineering for 2D Materials.

To tune the structural or electronic phases of materials, strain is as important as temperature. The six independent strain components and 18 independent strain gradients provide a vast design space to explore or engineer the thermodynamic landscape of materials and their properties. So far, most strain engineering or strain gradient engineering studies have been focused on utilizing one or two independent components. There are a plenty of uncharted spaces yet to be explored. Experimental challenges exist in realizing a multistrain or multistrain gradient tuned system. While both mechanical bending/stretching and epitaxial growth can lead to the design of one or two independent strain or strain gradient components, there is no reliable experimental approach to realize a complex designed strain or strain gradient pattern. Further, the vdW or quasi vdW bonding nature of these 2D materials makes it difficult to introduce long-lasting strain without delamination subject to thermal or mechanical cycling.

To reproduce the technical successes of strain engineering in Si transistors or III-V quantum well layers, one also must be able to produce the strain and strain gradients at the large or wafer scale. For this, mechanical stretching or similar local approaches involving the use of a sharp mechanical tip or structure may be replaced by large scale strain engineering approaches such as epitaxy using lattice mismatched substrates that are widely used in commercial III-V quantum well systems. Most works on the epilayer—substrate interaction in 2D materials have been focused on graphene or ${\text{MoS}}_2$. When the interlayer interactions in 2D materials become strong, it has been found that some epitaxial 2D layers may take epitaxial strains as high as a few percent.^469,470 However, it is unclear how and why such large strain even exists. Further efforts are needed to understand the materials chemistry and epitaxy science of 2D materials for strain engineering. Though strain, in theory, can be produced at a large scale for 2D systems, the strain gradient, by its nature, prevents its development beyond the nanometer scale. Due to this reason, works on strain gradient engineering of 2D materials have been focused on the small scale. A potential strategy in the mass production of the strain gradient is to separate a large piece of 2D materials into many nanoscale pieces with each serving as an active component carrying a large enough strain gradient. This approach, though, may bring complexity in devices fabrication, especially if the out-of-plane dimension is needed in designing the strain gradient.

SHG in 2D Materials.

One future challenge is seeking a rational design principle for materials with large ${\chi }^{(2)}$ that could exceed the current apparent upper boundaries of the ${\chi }^{(2)}$-bandgap trade-off, with initial efforts focusing on cataloging materials data for ${\chi }^{(2)}$ and bandgap through high-throughput computation, as has been carried out for 3D bulk materials in Naccarato et al.⁴⁷¹ One empirical observation related to dimensionality is that, among materials with similar bandgaps, ${\chi }^{(2)}$ tend to be larger for lower-dimensional materials since they host more pronounced singularities in their low-energy excitation spectra that contribute to a nonresonant nonlinear response.⁴⁷² It is unclear to what degree this strategy would apply since, by extrapolation, one may expect molecular systems to achieve the largest ${\chi }^{(2)}$, yet there have been no reports demonstrating this.

2D/3D Electronic Devices.

The marriage of 2D semiconductors with crystalline 3D materials is a rich area of exploration not just from the perspective of basic interface physics but also in terms of high-performance device applications. In terms of logic devices, the appeal of TFETs with a steep SS concurrently with a high on/off current ratio and a high on-current density is a worthy and impactful goal. Further studies and investigations are warranted to scale the devices and optimize contact, junction, and dielectric—semiconductor interfaces in addition to pursuing high quality, near-intrinsic, phase pure and scalable growth of 2D semiconductors. From the perspective of memory devices, the appeal of low-depolarization fields in atomically thin bodies combined with transferrable, high quality layered semiconductors makes it worthwhile to pursue interfaces between 2D semiconductors and 3D ferro-electrics. Additionally, 3D ferroelectrics that have low-static dielectric constants and high remnant polarizations that can be integrated with the 2D semiconductors are equally important to attain long retention. The grand challenges in this area, pertain once again to scaling the 2D materials to wafer scales as well as retaining device performance for highly voltage and area-scaled devices. Finally, 2D ferroelectric semiconductors are another very promising class of materials, and their junctions with 3D semiconductors and 3D ferroelectric dielectrics will be beneficial to device design and applications.

MTI Devices.

In the ideal case, MTI-based devices will make disseminating the ohm more economical and portable and will, more importantly, serve as a basis for a compact quantum ampere, an electrical standard that has been even more limited in its versatility than resistance or voltage standards, primarily because they are based on single electron transistors. For instance, at present, the global accessibility of the quantum ampere is constrained to mostly National Metrology Institutes.⁴⁷³ Other limitations that may possibly be overcome by using MTIs include the sub-nA currents typically associated from the aforementioned single electron transistors and the Josephson voltage standard’s aversion to magnetism, which would complicate its integration with a graphene-based resistance standard in a single cryostat. The work that comes from MTIs and any other 2D material system that exhibits the QAHE will help to move forward the realization of the quantum SI in terms of electrical standards. The realization of a compact quantum ampere through integration of devices operable in a zero-field environment will impact how calibration services are provided for industry.

Going forward, three research directions can emerge from among following efforts: (1) Identification of the physical limitations of the many promising materials, both through experimental and theoretical means. For instance, computing the defect behavior and the impact of disorder on Hall quantization would provide invaluable knowledge to materials growers. (2) Optimization of the best QAHE materials for device applications. In theory, knowledge from the first listed research direction (1) would provide a feedback loop with which one could narrow down the list of systems with immediate promise, allowing researchers the ability to determine dominant sources of nonideal behavior (e.g., point defects, magnetic order inhomogeneity such as domain walls, etc.). (3) Testing of applied QAHE technologies. Although the QAHE has been understood much more in recent times, there are still vast amounts of interdisciplinary work required to harness the effect in a way that enables the adoption of relevant 2D material systems for future technological advances.