Structured cerebellar connectivity supports resilient pattern separation

Summary

The cerebellum is thought to detect and correct errors between intended and executed commands^1,2 and is critical for social behaviors, cognition and emotion^3–6. Computations for motor control must be performed quickly to correct errors in real time and should be sensitive to small differences between patterns for fine error correction while being resilient to noise⁷. Influential theories of cerebellar information processing have largely assumed random network connectivity, which increases the encoding capacity of the network’s first layer^8–13. However, maximizing encoding capacity reduces resiliency to noise⁷. To understand how neuronal circuits address this fundamental tradeoff, we mapped the feedforward connectivity in the mouse cerebellar cortex using automated large-scale transmission electron microscopy (EM) and convolutional neural network-based image segmentation. We found that both the input and output layers of the circuit exhibit redundant and selective connectivity motifs, which contrast with prevailing models. Numerical simulations suggest these redundant, non-random connectivity motifs increase resilience to noise at a negligible cost to overall encoding capacity. This work reveals how neuronal network structure can support a trade-off between encoding capacity and redundancy, unveiling principles of biological network architecture with implications for artificial neural network design.

Seminal work in the 1960s and 70s^14,15 provided the basis for influential theories of cerebellar information processing^8,9. At the input layer, a relatively small number of mossy fibers (MFs, input neurons) are hypothesized to be randomly sampled by a massive numbers of granule cells (GrCs, parallel fibers) resulting in expansion recoding (Fig. 1a,b). Through non-linear activation of the GrCs, expansion recoding projects MF sensory and motor information into a high dimensional representation facilitating pattern separation^10–13,16 (Fig. 1c). At the output layer, each Purkinje cell (PC, readout neuron) integrates tens of thousands of GrC inputs to form appropriate associations^8,9,17 and are the sole output of the cerebellar cortex (Fig. 1a,b). Association learning is hypothesized to occur through linear decoding¹⁷ and reinforcement learning rules^6,18,19 and may help generate subnetworks of PCs suitable for ensemble learning^20,21. This network architecture of expansion and re-convergence is also seen in the mushroom body of fly and the electrosensory lobe of electric fish^13,22–24, suggesting that cerebellar architecture exemplifies a general principle of neuronal circuit organization critical for separating neuronal activity patterns before associative learning. Indeed, these input and output layers are similar to convolutional and linear output layers in artificial deep neural network architectures²⁵ (Extended Data Fig. 1).

Figure 1. Reconstruction of feedforward circuitry in the cerebellar cortex using large-scale electron microscopy.

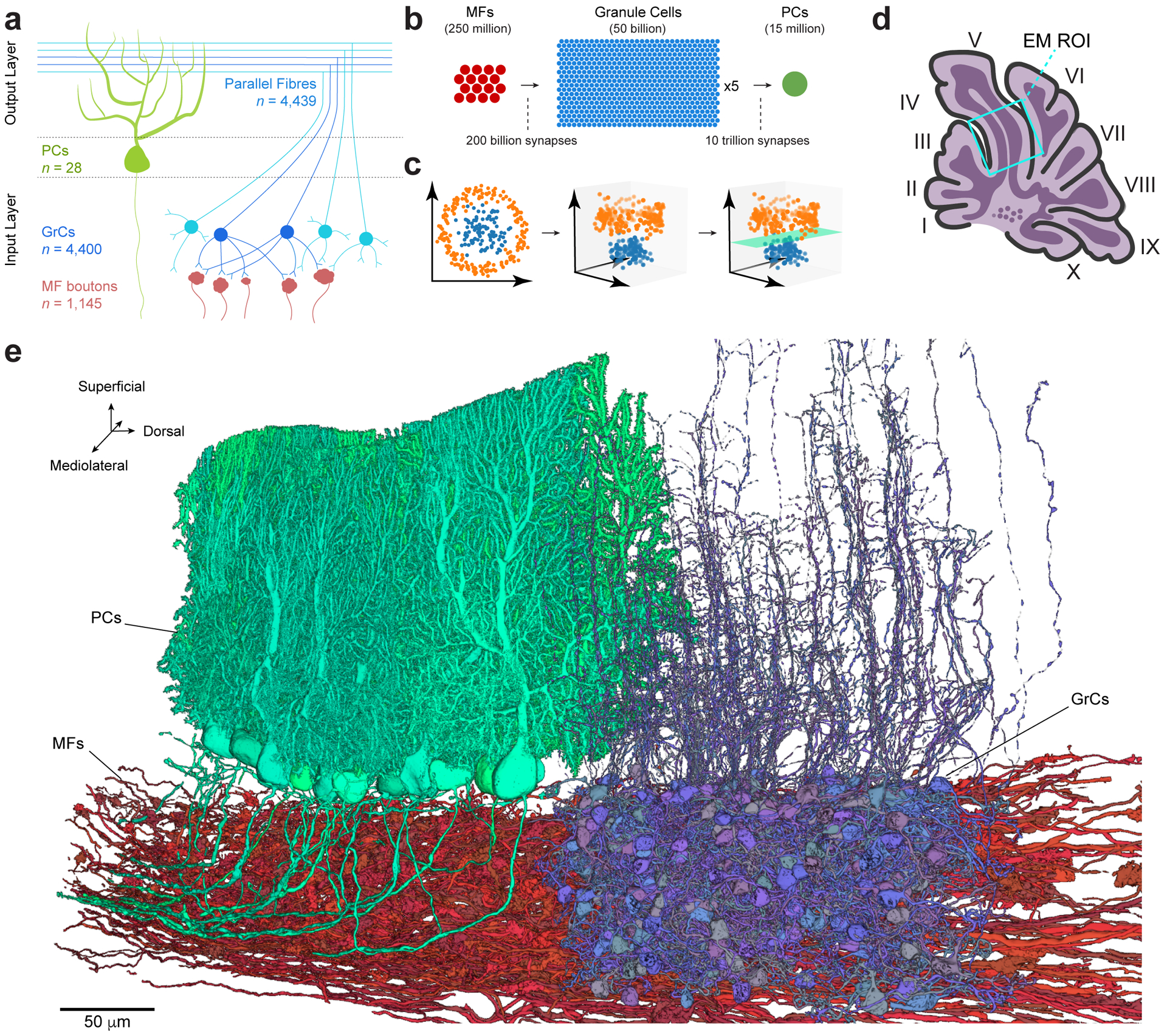
a, Schematic depicting wiring of feedforward neurons in the cerebellar cortex. Granule cells (GrCs, blue circles) sample mossy fiber (MF) boutons (red) and project their axons into the molecular layer where they bifurcate to form parallel fibers. GrC axons make synaptic contacts onto Purkinje cells (PCs, green), which are the sole output of the cerebellar cortex. The number (n) of reconstructed objects (MF boutons and parallel fibers) or cells with cell bodies (GrCs and PCs) in our dataset is shown. b, Expansion and convergence of the cerebellar cortex feedforward network. The number of circles is proportional to the number of neurons in the estimated global population²⁰. At the local circuit scale, however, divergence of single MF boutons to GrCs is less (ratio ~1:3), and convergence of GrCs to PCs is higher (ratio 50,000–200,000:1). c, Illustrative data showing how two input representations in 2D (left) once projected into 3D (middle) can be linearly separated (right, green plane). Marr & Albus^8,9 hypothesize that the MF→GrC dimensionality expansion supports pattern separation and the GrC→PC convergence performs pattern association. d, Schematic of a parasagittal section through the vermis of mouse cerebellum with the location of the EM dataset (Extended Data Fig. 2a) outlined (cyan box). e, 3D rendering of representative EM reconstructions of PCs (green), GrCs (blue) and MFs (red). Non-overlapping GrCs and PCs were rendered for clarity.

Information theoretical models usually assume that MF→GrC connectivity is random in order to maximize the encoding capacity of the input layer of the network^8–11,13. However, maximizing encoding capacity makes networks less resilient to noise⁷. To understand how the cerebellar cortex balances the tradeoff between encoding capacity and resilience, we mapped the precise synaptic connectivity across both input (MF→GrC) and output (GrC→PC) layers of the feedforward circuit in the cerebellar cortex.

3D EM reconstruction

We generated a synapse-resolution EM dataset that contains a proximal portion of lobule V from the adult mouse vermis (Fig. 1d, Extended Data Fig. 2a). The sample was cut into 1176 serial parasagittal sections, each ~45 nm thick and imaged at a resolution of 4 × 4 nm² per pixel. The dataset was aligned into a 37.2 trillion voxel volume spanning ~28 million μm³ (Supplementary Video 1). To facilitate analysis, we densely segmented neurons using artificial neural networks (Fig. 1e, Extended Data Fig. 2). To process a large EM dataset efficiently, we developed a scalable framework to process the dataset in parallel (Extended Data Fig. 2c) and a proofreading platform (Extended Data Fig. 2d) for targeted neuron reconstruction (Extended Data Fig. 2e). We predicted synapse locations and their weights using a separate artificial neural network trained to identify synapses based on their ultrastructural features (Extended Data Fig. 2f and 4a,b) with high accuracy (precision: 95.4%, recall: 92.2%, f-score: 93.8%). In total, we reconstructed >5,500 neurons (Fig. 1a,e) and analyzed >150,000 synapses (116,571 MF bouton→GrC and 34,932 GrC→PC) constituting >36,000 unitary connections (13,385 MF bouton→GrC and 23,365 GrC→PC).

Structured MF→GrC connectivity

We first tested the hypothesis that feedforward connectivity in the input layer (MFs→GrCs) was random. To do so, we densely reconstructed neurons in the GrC layer and identified MFs and GrCs based on morphology¹⁵ (Fig. 2a,b, Extended Data Fig. 3a,b, Supplementary Data 1-2, Video 2). The basic properties of GrCs and MFs were consistent with prior findings^11,26. GrCs had 4.38 ± 1.00 (mean ± SD) dendrites (Extended Data Fig. 3c), each of which ended in a “claw” that wrapped around and received 10.4 ± 5.6 (mean ± SD) synapses from a single MF bouton (Extended Data Fig. 4). GrC dendrites measured 21.7 ± 8.5 μm (mean ± SD) from the cell body center to the center of the presynaptic MF bouton (Extended Data Fig. 3d,e). Individual MF boutons were sampled by 14.8 ± 8.4 (mean ± SD) GrCs. Though MF collaterals give rise to multiple boutons in the GrC layer, MF boutons are typically spaced such that the likelihood of individual GrCs innervated by multiple boutons from the same MF is low^11,15,27. While a subset of MF boutons in the dataset belonged to the same MF axons (n = 182 out of 784 boutons), we found that GrCs rarely received inputs from different boutons of the same MF axon (n = 20 out of 4400) in the dataset. Notably, our subsequent analyses did not significantly change when we considered MF boutons independently or combined MF boutons arising from the same reconstructed axons (data not shown), so for the remainder of our analysis we focus on MF boutons. Additionally, we found a small fraction (8.8%) of MF boutons have axon collaterals that each make one or two synapses onto dendrites and claws of GrCs; however, the vast majority of synapses were from the main MF boutons (Extended Data Fig. 5).

Figure 2. EM reconstructions reveal GrCs redundantly sample MF boutons.

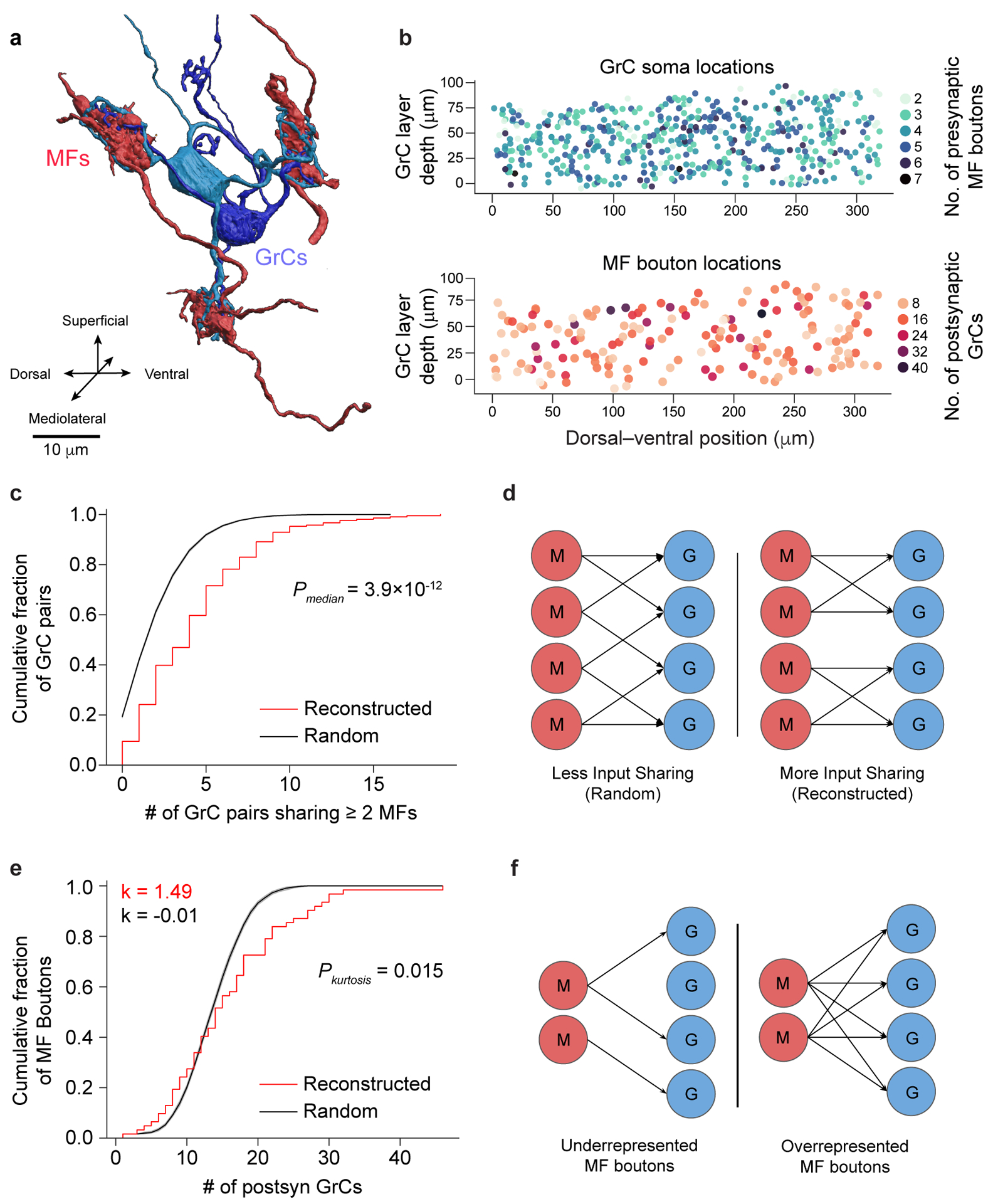
a, 3D rendering of two GrCs (blue) sharing three common MF bouton inputs (red). b, Locations of GrCs (top, n = 4,400, color coded to show the number of dendrites) and MF boutons (bottom, n = 1,145, color coded to show the number of postsynaptic GrCs per bouton). Only neurons in the center 10 μm in the mediolateral axis are plotted for clarity. Within a 320 × 80 × 50 μm subvolume, there are 2,397 GrCs and 784 MF boutons, giving a density of 1,870,000 GrCs and 612,000 MF boutons per mm³ and a ratio of 3.06 GrCs per MF bouton. c, Cumulative distribution of MF bouton input redundancy, counting the number of GrC pairs sharing at least 2 MF boutons for each GrC. To minimize edge-effects, only the centermost GrCs (n = 211, Methods) are included in this analysis. GrCs in the reconstructed network (red line) share significantly more MF boutons than connectomically-constrained random models (Radius model Extended Data Figure 3, black line; p = 3.94 × 10⁻¹², two-sided Wilcoxon rank-sum test, Methods). Here, and throughout the figures shaded regions represent the bootstrapped 95% confidence interval around data mean unless otherwise stated. d, Illustration of redundant sampling in c showing pairs of GrCs sharing 2 common MF inputs (right) vs sharing 1 common MF input (left). e, Cumulative distribution of postsynaptic GrCs per MF bouton. The reconstructed distribution (red line) is compared with a random model (black line, as in c). To minimize edge effects, only connections from the centermost MF boutons are counted (n = 62). Kurtosis (k), a unitless measure of amount of distribution in the tails, is significantly higher in the reconstructed network than the random model suggesting over- and under-sampling of MF boutons by GrCs (p = 0.0146, n = 62, two-sided Permutation test, Methods). f, Selective subsampling of MF boutons by the GrCs in e creates underrepresented and overrepresented subpopulations.

Recent theoretical work has assumed unstructured MF→GrC connectivity, which implies low levels of shared MF bouton inputs between GrCs^12,13,28 even when considering the limited reach of their dendrites^11,26. We found GrC pairs shared 2 or more MF bouton inputs more often than predicted by anatomically-constrained random connectivity¹¹ (reconstructed: 4.43 ± 3.63, shuffled: 2.34 ± 2.08, mean ± SD; p = 3.9 × 10⁻¹², n = 211, two-sided Wilcoxon rank-sum test, Fig. 2c,d, Extended Data Fig. 3f–h). The distribution of sharing is consistently higher across different numbers of shared inputs and synapse prediction accuracies (Extended Data Fig. 3i–m, Extended Data Fig. 6a, Extended Data Fig. 7a). Oversharing of inputs among GrCs implies an overconvergence of MF boutons (Extended Data Fig. 6b), and suggests that GrC activity is more correlated than expected, in opposition to the prediction that MF→GrC encoding minimizes population correlations to maximize encoding capacity^7–9,12,13.

Furthermore, we found that MF boutons were not sampled uniformly: the most connected third of MF boutons had 4 times as many postsynaptic GrCs as the least connected third of MF boutons (Extended Data Fig. 3n). To rule out the possibility that MF boutons simply had high variability in the number of postsynaptic partners (σ²: 0.522 vs. 0.297 (reconstructed vs. random), p = 0.001, permutation test, n = 62), we quantified the overrepresentation of MF boutons by GrCs with their kurtosis and skew measuring prevalence of outliers and asymmetry of the distributions respectively and found each to be significantly greater than those of random connectivity models (kurtosis: 1.49 vs. −0.01 (reconstructed vs. random), p = 0.0146; skew: 0.963 vs 0.233 (reconstructed vs. random), p = 0.0178; permutation tests, Fig. 2e, Extended Data Fig. 3f,o, Extended Data Fig. 7b). By overrepresenting inputs from select MF boutons, these inputs are redundantly encoded by more GrCs, influencing more of the GrC coding space (Fig. 2f). Select MF boutons may be more informative or reliable, potentially enhancing noise resiliency of specific inputs. In summary, we found oversharing and overrepresentation to be two redundant wiring motifs that permit expansion coding in the input layer to be more robust to noise and may partially explain low dimensional GrC activity recently reported in vivo^29–31.

Selective GrC→PC connectivity

In the output layer, given that adjacent PC dendrites share many potential GrC axon inputs (Fig. 1e, Fig. 3a), we hypothesized that there are redundant and non-random motifs within the GrC→PC connectivity that could contribute to PC synchrony^32–34. Given the convergence of PCs to downstream deep cerebellar nuclei (DCN), we propose that structured GrC→PC connectivity can give rise to groups of partially redundant PCs to produce more accurate pattern associations. To test these hypotheses, we densely reconstructed the connectivity between GrC axons and PCs (Supplementary Data 2-3 and Videos 2-3). Reconstructed GrC axons were categorized as either “local” or “non-local”. Local GrC axons (n = 541) had cell bodies within the EM volume, while non-local GrC axons (n = 4,439) were parallel fibers without a cell body identified within the dataset. Dendrites of reconstructed PCs (n = 153 total, n = 28 with somas) ramified across an area of 208 ± 5.2 μm by 158 ± 19.5 μm (mean ± SD) in height and width (Supplementary Data 3), consistent with light microscopy¹⁵. A common assumption used in computational models is that all GrC-PC pairs that contact each other make synapses^13,17. However, we found the connectivity rate was 49 ± 4.4% (mean ± SD) (Fig. 3a,c, Extended Data Fig. 8a), with each GrC→PC connection typically comprising one or two synapses (Extended Data Fig. 4c), consistent with prior work^35–37. The lack of all-to-all GrC→PC connectivity raised the question of how selective these unitary connections are and how this selectivity constrains information processing and plasticity mechanisms in the circuit.

Figure 3. GrC input selectivity predicts PC subnetworks.

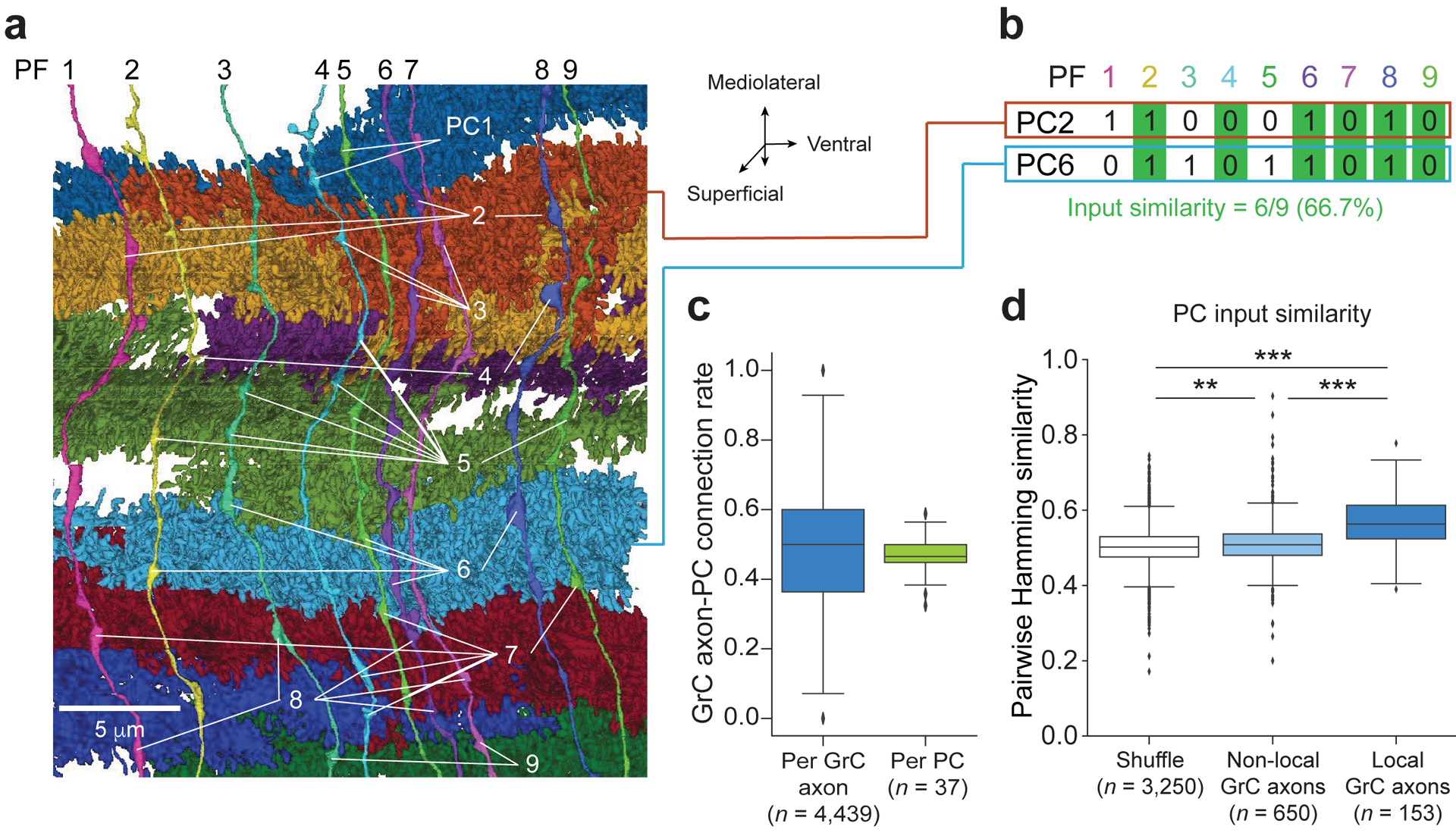
a, 3D rendering of nine GrC axons, nine PCs, and the locations of synapses (white lines) connecting them. Note, unlabeled axonal varicosities are presynaptic to non-PC neurons (e.g., molecular layer interneurons). b, Calculation of Hamming similarity as a pairwise metric to compare the similarity of two binary patterns. The example compares the postsynaptic connectivity pattern between two PCs from different parallel fibers (PFs) where a “1” denotes a connection and a “0” denotes the lack of connection. c, Box plot (25th, 50th and 75th percentiles with whiskers extended to points within 1.5 IQRs) of the ratio of GrC→PC synapses to the total number of times a GrC axon and PC pair contact (touch) one another (Methods). Left: synapse ratio per GrC. Right: synapse ratio per PC. d, Similarity of GrC inputs between pairs of PCs with at least 30 common GrC axon contacts comparing shuffled input connectivity, non-local GrC axons, and local GrC axons. All three populations are significantly different (p = 1.25 × 10⁻⁵⁶, Kruskal-Wallis test; p = 0.00433, shuffle vs. non-local GrC axons; p = 9.16 × 10⁻³², non-local GrC axons vs. local GrC axons; p = 4.91 × 10⁻⁶¹, shuffle vs. non-local GrC axons; Dunn’s post hoc tests, Bonferroni corrected for multiple comparisons).

To examine selectivity in GrC→PC connectivity, we compared pairs of PCs by using Hamming similarity as a metric to quantify the similarity in their GrC input populations, which accounts for both connected and non-connected GrC-PC pairs (Fig. 3b). PC input patterns from local and non-local GrC axons were significantly more similar than shuffled controls, and local GrCs have significantly more similar connection patterns onto PCs than non-local GrC axons (Fig. 3d; local: 0.567 ± 0.071, non-local: 0.513 ± 0.065, shuffled: 0.503 ± 0.056 (mean ± SD); local GrC axons vs. shuffle, p = 4.9 × 10⁻⁶¹; non-local GrC axons vs. shuffle, p = 0.0043; non-local GrC axons vs. local GrC axons; p = 9.1 × 10⁻³²; Kruskal-Wallis and Dunn’s post hoc tests, Bonferroni corrected for multiple comparisons), suggesting that PCs exhibit input selectivity. Then, when comparing pairs of GrCs based on the PCs to which they provide input, we detected a small yet significant trend suggesting that sharing MF inputs influences GrC→PC connectivity (Extended Data Fig. 8b, p = 1.1 × 10⁻⁴, Kruskal-Wallis test). The difference between local and non-local inputs may be related to the differences in dimensionality recorded from localized GrC cell bodies^30,31 versus GrC axons in the molecular layer³⁸.

Modeling network capacity & resilience

To explore the functional implications of the observed connectivity, we modeled pattern separation, a hypothesized function of the expanded representation from MFs to GrCs^8–13 (Fig. 1c). We used dimensionality^12,13 to quantify network encoding capacity, and signal-to-noise ratio (SNR) to quantify pattern separation performance and robustness to noise (Fig. 4a). We computed the dimensionality of the GrC population for input patterns with different levels of variability to better understand how the system separates similar versus different input patterns. It has been suggested that random connectivity maximizes dimensionality^7,13, which predicts the observed redundant and selective connectivity motifs would decrease dimensionality. Although the reconstructed network showed lower dimensionality than random connectivity when the variability between input patterns was large, overall the reconstructed network preserved high dimensionality, particularly for less variable input patterns (Fig. 4b, Extended Data Fig. 9a). We next investigated amplification of selected inputs and noise resiliency as two possible benefits of redundant and selective connectivity. Examining over- and under-represented MF inputs separately, we found that dimensionality for overrepresented MF inputs increased, allowing them to utilize more of the encoding space (Fig. 4c), and increasing their pattern separability performance (Extended Data Fig. 9b). This may help with discriminating similar input patterns and possibly increase resilience to noise⁷. Furthermore, we found redundant oversharing of inputs increased noise robustness for a subset of the GrCs (Extended Data Fig. 9c,d), which may help increase reliability. Finally, we explored how the observed selective GrC-PC subsampling (Fig. 3c,d) could influence decoding from the perspective of PCs. Selective GrC-PC subsampling (Extended Data Fig. 9e) substantially increases pattern separability compared to random-subsampling or all-to-all connectivity (Fig. 4d, Extended Data Fig. 9f). Interestingly, the observed absence of roughly half of potential GrC axon inputs only slightly decreased dimensionality (Extended Data Fig. 9g,h). This suggests a preservation of information across layers by the network that may be supported by the redundant and selective connectivity motifs of the input layer.

Figure 4. Structured redundancy increases SNR of specific and small input differences.

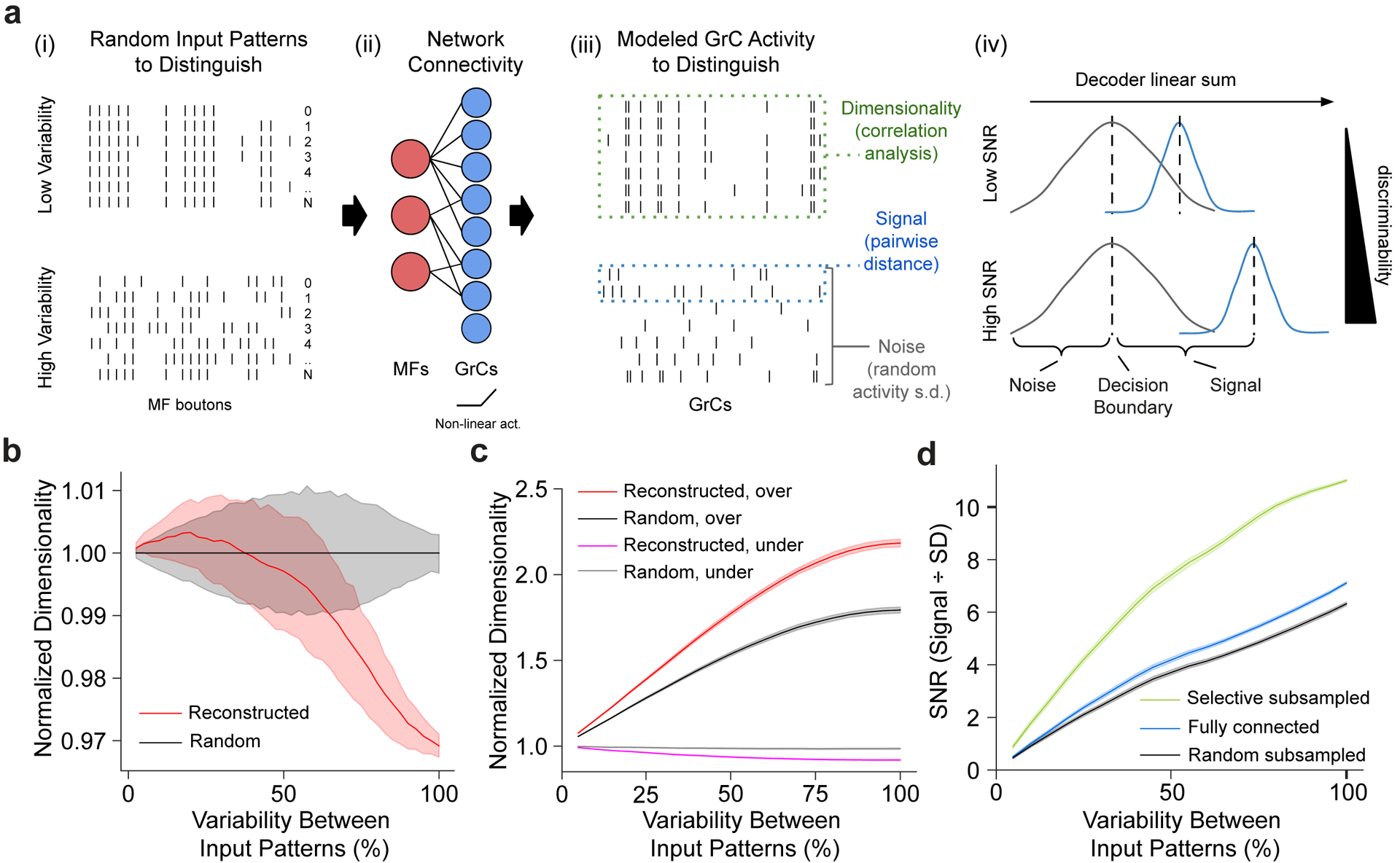
a, Dimensionality and signal-to-noise (SNR) analysis. (i) Binary input patterns, modeled with different levels of variability. (ii) Input patterns are non-linearly transformed by the MF-GrC network to produce modeled GrC activity^7,13. (iii) Output activity is analyzed for dimensionality¹³ (how correlated the activity matrix is), signal (how different each output pattern is from each other), and noise (SD of the linear sum of each pattern). (iv) Illustrative histogram of the linear sum of postsynaptic GrC-PC activity. Higher signal relative to noise implies better discriminability. b, Relative dimensionality of the GrC population as a function of variability between modeled MF input activity patterns (0% denotes no difference and 100% denotes uncorrelated randomized patterns) comparing the reconstructed (red) to connectomically-constrained randomly connected models (black) normalized to the random model. c, Relative dimensionality of the GrC population as a function of variability between MF input patterns, comparing overrepresented (top-third, red and black) vs underrepresented (bottom-third, magenta and gray) most connected MF boutons in the reconstructed (red and magenta) vs random (black and gray) connectivity models. Dimensionality is normalized by the underrepresented population in the random connectivity model. d, Modeled SNR (Methods) as a function of variability between input patterns, measuring separability of GrC activity between models with selective (green), no (blue), and random (black) subsampling (Extended Data Figure 9e).

Discussion

In summary, we found two connectivity motifs in the input layer: redundant oversharing of inputs among GrCs (Fig. 2c), and selective overrepresentation of specific MF boutons (Fig. 2e). Computational analyses suggest these features support a trade-off between network capacity and robustness, possibly to combat input variability and synaptic noise^37,39. These findings run counter to prevailing models of random connectivity where dimensionality is solely maximized^8–13 and may partially explain recent findings of lower-than-expected dimensionality of in vivo GrC activity^29–31. Selective overrepresentation of MF boutons, in addition to increasing redundancy of signals from more informative inputs, could also be a mechanism for differential integration of multimodal MFs^40,41. Our findings are also compatible with the hypothesis of activity-dependent synaptic plasticity underlying learned representational changes in MF-GrC connectivity^6,42. Future studies incorporating long-range connectivity^40,41,43 and functional characterization^30,31 may reveal why some MF boutons are oversampled relative to others.

At the output layer, we found the connectivity rate of GrC to PCs to be ~50% (Fig. 3c) and observed some input similarity between adjacent PCs, consistent with learning occurring in the output layer^8,9 (Fig. 3d). For neighboring PCs, a balance of similar, but non-identical inputs may serve to ensure variability and non-convergent learning, enabling a trade-off between specificity and generality. This may allow downstream cells in the DCN to more effectively implement ensemble learning, a machine learning approach where many weak and redundant learners (i.e. PCs) are pooled to make a more accurate prediction^20,21.

In conclusion, we examined the feedforward connectivity of the cerebellum at synapse resolution, unveiling the role of non-random redundancy within a circuit that was hypothesized to rely on randomness for optimal performance. This is consistent with non-random biases detected in the parallel fiber system of the fruit fly^44,45, suggesting a conserved principle of circuit architecture across species. Beyond the feedforward network, we expect continued analysis of the dataset will enable the comprehensive examination of cell types making up the cerebellar network^{14–16,46–49}. Considering its similarities to modern deep learning architectures (Extended Data Fig. 1), our findings of structured connectivity may help to improve artificial intelligence algorithms, build and constrain more complete circuit models, and further our understanding of learning rules^6,18,19 underlying cerebellar motor control and cognitive function^3,6,42,50.

Methods

Experimental animals.

Experimental procedures were approved by the Harvard Medical School Institutional Animal Care and Use Committee and performed in accordance with the Guide for Animal Care and Use of Laboratory Animals and the animal welfare guidelines of the National Institutes of Health. The mouse (Mus musculus) used in this study was a P40 male C57BL/6J (Jackson Laboratory) housed on a normal light–dark cycle with an ambient temperature of 18–23°C with 40–60% humidity.

Sample preparation.

The specimen was prepared for EM as described previously^51,52. We used an enhanced rOTO protocol for heavy metal staining^51,53 followed by dehydration in a graded ethanol series and embedding in LX112 resin (Ladd Research Industries). The sample was polymerized at 60°C for 3 days.

Sectioning and imaging.

The EM dataset of the cerebellum (Fig. 1d,e, Extended Data Fig. 2a) was collected and imaged using the GridTape pipeline for automated serial-section TEM⁵². In brief, embedded samples were trimmed (Trim 90, Diatome). Serial ~45 nm-thick sections were cut using a 35° diamond knife (Diatome) and collected onto LUXFilm-coated GridTape (Luxel Corporation). A total of 1176 sections were cut for a total of ~49.5 μm total sample thickness. There were 91 single-section losses, 20 instances of adjacent two-section losses, 5 instances of adjacent three-section losses, 2 instances of adjacent four-section losses, and 1 instance of an adjacent five-section loss. Folds, staining artifacts, and cracks occasionally occurred during section processing, but were typically isolated to section edges and therefore not problematic.

Sections were imaged on a JEOL 1200EX transmission electron microscope at 120 kV accelerating potential at 2,500× magnification using a reel-to-reel GridTape stage and a 2 × 2 array of sCMOS cameras (Zyla 4.2, Andor) at 4.3 nm/pixel⁵². Imaging required 521 hours of acquisition on a single tape-based transmission electron microscope with a camera array. The EM images were then stitched together and aligned into a continuous volume using the software AlignTK (https://mmbios.pitt.edu/software#aligntk).

The aligned EM sections were then first imported into CATMAID⁵⁴, then to Zarr (github.com/zarr-developers/zarr-python) and N5 containers (github.com/saalfeldlab/n5) for visualization and segmentation.

Automated segmentation.

We adapted an automated segmentation workflow based on a segmentation pipeline for TEM data^55,56. In brief, the pipeline consists of three steps: (1) affinity prediction, fragment extraction (over-segmentation), and agglomeration. The affinity prediction uses a 3D U-net convolutional neural network (CNN)⁵⁷ to predict a “connected-ness” probability of each voxel to adjacent voxels. An over-segmentation graph is then produced through a watershed algorithm (2D per-section), and agglomeration is performed iteratively using the “mean affinity” metric⁵⁸ set at 0.5 threshold (segments are only joined when their immediate boundary has affinity greater than 0.5). We modified the original code⁵⁶ (without local shape descriptors) to optimize for runtime performance and to adapt to our supercomputing cluster environment (Harvard Medical School Research Computing). The input to the network is a two-fold downsampled in XY images (effective resolution 8 × 8 × 40 nm); we found the decrease in size and performance to outweigh a minor reduction in accuracy.

Affinity CNN training.

We trained the CNN using a two-step process: bootstrapped ground truth (GT), and subsequent refinement based on skeleton GT. A set of bootstrapped GT was first created by applying a trained CREMI network (https://cremi.org/) directly on several subvolumes of the dataset, then applying manual corrections using Armitage/BrainMaps (Google internal tool). Training on these bootstrapped GT volumes generated an over-segmenting network.

To further improve the accuracy of the network, we scaled up the GT coverage to include 2 regions in the GrC layer, 3 regions in the molecular layer, and 1 region in the Purkinje cell layer – each 6 × 6 × 6 μm (1536 × 1536 × 150 voxels) in size. To accurately and efficiently proofread these volumes, we developed a skeleton-based GT method where we used the connectivity of the manually annotated point-wise skeletons of neurons to correct for errors of the bootstrapped network output. First, human tracers produced dense skeletons of the GT volumes using CATMAID⁵⁴. To correct for split errors, the bootstrapped outputs were agglomerated at very high thresholds (0.7–0.9) to produce an under-segmented graph. Then the GT skeletons are used to correct merge errors, producing an output that can be reviewed and used for improved network training. We iteratively performed the annotation-train-review loop several times per volume as needed (sometimes without further annotation) to converge on a set of high-quality GT volumes.

Using the above GT volumes and supplementary volumes (to be described later), we trained the network using gunpowder (https://github.com/funkey/gunpowder). We used the CREMI network architecture for TEM images⁵⁵. In brief, the U-net had four levels of resolution with downsampling factors in xyz of (3,3,1), (3,3,1), and (3,3,3). The topmost level had 12 feature maps, with the subsequent levels increasing the number of feature maps by 5 fold. Each layer was composed of two convolution passes with kernel sizes of (3,3,3) followed by a rectified linear unit (ReLU) activation function. A final convolution of kernel size (1,1,1) with 3 feature maps and a sigmoid function produced the affinity probability map. The mini batch input size was 268 × 268 × 84 pixels, and the output size was 56 × 56 × 48 pixels. An Adam optimizer was used with learning rate = 0.5 × 10⁻⁴, beta1 = 0.95, beta2 = 0.999, epsilon = 10⁻⁸. Gunpowder’s built-in augmentations were used to enable more varied training samples – these include elastic deformation, rotation in the z-axis, artificial slip/shift misalignment, mirroring, transpose, and intensity scale and shift, and missing sections. We also wrote and added duplicated augmentation that randomly selects a section and duplicates it up to 5 times. This is to simulate missing sections where, during deployment, missing sections are replaced with adjacent non-missing data sections. We trained the network to 350,000 iterations.

To evaluate performance of the neural network on unseen data, we further densely traced GT skeletons in another 9 cutouts in various regions of the GrC layer - each spanning 6 × 6 × 6 μm (1536 × 1536 × 150 voxels) in size - and used custom code to evaluate split and merge errors. Compared with other metrics like VOI or RAND index, comparing the number of topological errors is a more direct assessment of the amount of time that proofreaders will take to correct split and merge errors. Plus, producing skeleton GT cutouts is faster, allowing us to make more GT in less time. Evaluating across different artificial neural network parameters, we found that our best segmentation network, at an agglomeration threshold of 0.5, produces an average of 2.33 false merges and 27 false splits per cutout (Extended Data Fig. 2e). Analyzing the results in depth, we found that most false splits belong to small axons at locations with poorly aligned or missing sections.

Supplementary ground truth sub-volumes.

Beyond the targeted performance evaluation with the nine GT cutouts as described above and before deploying the network across the entire dataset, we had to address problems with segmenting (1) myelin that spans across large regions of the dataset often resulting in merge errors, (2) broken blood vessels that resulted in merge errors with surrounding neurons, (3) darkly stained mitochondria that can make adjacent neuron membranes ambiguous, and (4) GrC axons that are sometimes darkly stained.

To address myelin, we produced 3 additional volumes of regions with dense myelin labeled and trained the network to predict low (i.e., zero) affinity for myelin-containing voxels; the fragment extraction step was then modified to remove fragments that have averaged affinity (average of x, y, z affinity values) less than 0.3. The removal of these fragments reduced myelin-related merge errors.

Blood vessels are relatively large structures in EM that are typically easy to segment. Broken capillaries (during serial sectioning), however, can produce artifacts with misalignments, blending with surrounding neurites and producing merge errors. To address this problem, we used Ilastik⁵⁹ to train a machine learning model (random forest) on 32-fold XY downsampled EM images (effective resolution 128 × 128 × 40 nm) to detect blood vessel voxels and mask them out from the affinity prediction prior to the fragment extraction step.

Mitochondria are often darkly stained in the EM dataset. Because the network is trained to predict high affinities for electron-dense membranous structures including mitochondria, the network can under-predict neuron boundaries when mitochondria are right next to the boundaries creating conditions that can be ambiguous even to human experts. We sparsely annotated an additional GT cutout (3 × 6 × 3 μm in size) with dense mitochondria for training the segmentation network. To our surprise, this worked well without further masking agglomeration or other post processing steps.

Last, there were an infrequent number of GrC axons that were partially darkly stained. These would often be normally stained proximal to the soma but became more darkly stained distally before becoming normally stained again along the ascending portion of the axon. Human annotators can often trace these axons reliably, but they generated errors by the initially trained segmentation network. To mitigate this problem, we made a skeleton GT cutout specifically targeting a region dense with dark GrC axons and added it to the training procedure. Except for regions where multiple darkened axons come together to form a tight bundle of axons, this was effective for segmenting isolated dark axons, speeding up the bulk of the GrC axon reconstruction process.

Large-scale parallel processing deployment.

To efficiently run the trained CNN and other steps in the automated segmentation pipeline across a large dataset, we developed Daisy⁶⁰, an open-source work scheduler that can divide the input dataset into spatial chunks and operate on them in parallel (Extended Data Fig. 2c). We developed Daisy with the following design requirements: (1) be scalable and efficient across thousands of workers, (2) be able to tolerate worker and scheduler failures and resumable across reboots, (3) be extensible to non-segmentation tasks, (4) be Python-native for ease of integration with the existing pipelines, and (5) be able to provide on-the-fly dependency calculation between computational stages. At the time of development, no existing tools met such requirements.

Targeted neuron reconstruction and proofreading.

Although split and merge errors exist in the automated segmentation, such errors are usually easy for humans to recognize in 3D visualizations of reconstructed neurons. Thus, proofreading automated segmentation results is typically faster than manual tracing. That said, merge errors – especially between big neurons and in regions not well-represented by the GT – are endemic for large EM volumes, requiring a low merge-threshold (which creates more split errors), sophisticated un-merge algorithms, and/or exorbitant person-hours to proofread and diagnose where the merge errors happen. These obstacles make using automated large-scale segmentation inaccessible to labs with less resources.

To combat the merge error problem, we developed merge-deferred segmentation (MD-Seg) proofreading method, a novel workflow that pre-agglomerates fragments only in local blocks (4 × 8 × 8 μm in this work) and defers inter-block merge decisions to proofreaders. In this manner, if there is a merge error, it is limited to the local block and not automatically propagated to hundreds of other blocks which may contain even more merge errors. While deferred, inter-block merge decisions of each neuron are still computed and on-line accessible to proofreaders through a hot key in the user interface, which is based on Neuroglancer (https://github.com/google/neuroglancer) (Extended Data Fig. 2d).

By deferring merge decisions across the dataset, MD-Seg allowed us to focus proofreading, targeting regions and cells of interest. Although conventional proofreading can also target specific neurons, because agglomeration is performed globally, a generally high-quality assurance (QA) is needed to be performed for all neurons prior to proofreading to minimize excessive errors among these neurons to the neurons of interest. This pre-proofreading QA burden can be excessive for projects with fewer GT and resources, preventing the start of proofreading. In contrast, in MD-Seg, errors between non-targeted neurons do not affect segmentation quality of targeted neurons in most cases. Furthermore, because local blocks are agglomerated separately, it is easier to run segmentation for parts of the dataset, or re-run and update segmentations for specific regions without affecting on-going proofreading progress.

To reconstruct neurons in MD-Seg, MFs, GrCs, and PCs were first identified manually based on their stereotypical morphological characteristics¹⁵ (Fig. 1f, Supplementary Data 1-3 and Videos 2-3). Proofreaders typically started by selecting a neuron fragment (contained within a single block), and sequentially ‘grew’ the neuron by adding computed merge decisions of fragments in adjacent blocks through a hot-key. During each growth step, the 3D morphology of the neuron was visualized and checked for errors. When merge errors occur, the blocks containing the merge are ‘frozen’ to prevent growth from the merged segment. When a neuron branch stops growing (has no continuations), the proofreader inspects the end of the branch to check for missed continuations (split errors). In this way, both split and merge errors can be corrected.

At any time during growth steps, the proofreader can associate annotations like “uncertain continuations” (potential split errors) as well as periodically save the partial progress of the reconstructed neurons into an on-line database. Upon saving, MD-Seg automatically checks if the neuron overlaps with any existing saved neurons, and reports a failure back to the proofreader, enforcing an invariance that any single fragments can only belong to one neuron object. For neurons with higher complexity and overlapping branches (such as a Purkinje cell), to decrease cognitive load, proofreaders saved the neuron as simpler sub-objects (e.g., purkinje_0.axon, purkinje_0.dendrite_0, …). Once a neuron is marked as completed, a reviewer then loads the neuron to check for possible split or merge errors in a second independent review. Gallery of example reconstructions of MFs, GrCs, and PCs are provided (Supplementary Data 1-3 and Videos 2-3).

Using this pipeline, we reconstructed 153 PCs (total; 28 with somas), 784 MF boutons and 2,397 GrCs based on morphology. 550 of the 784 MF boutons are from unique MFs, with rare instances of GrCs receiving input from different boutons belonging to the same MF (n = 20). 541 of the 2,397 GrCs had axons extending into the molecular layer. We also reconstructed 4,439 axons from GrCs whose cell bodies were not present in our volume.

Automated synapse prediction.

We adapted an artificial neural network for synapse prediction on mammalian brain datasets using synful⁶¹. We modified the algorithm to predict synaptic clefts from pointwise ground truth annotations and identified pre- and post-synaptic partners by applying the synapse directionality prediction on the cerebellum dataset. We used webKnossos⁶² to make rough synaptic cleft masks and trained the network to predict these cleft masks. We found that training the network to identify the synaptic clefts produced more generalizable results than either pre- or post-synaptic point predictions and removed ambiguity of one-to-many or many-to-one synapses if only the pre- or post-synaptic partners are predicted. For the network architecture, we used the “small” network size and the cross-entropy loss. We downsampled the GT cutouts by a factor of four in the x- and y-dimension for an effective resolution of 16 × 16 × 40 nm prior to training. Consequently, we reduced the downsampling factors of the U-Net to (2,2,1), (2,2,1), and (2,2,3).

To train and evaluate the synapse prediction network, we annotated nine GT cutouts of the GrC layer (GCL; previously used for evaluating the automated segmentation network, see above), two more of the molecular layer (ML), and one more of the PC layer (PCL) – all of which are 6 × 6 × 6 μm. Five of the GCL cutouts and one of the ML cutouts were used for training – the rest were used for evaluation. Because of the efficiency of pointwise GT generation, we were able to produce a large amount of GT for both training and evaluation. The synapse predictions exhibited excellent accuracy (precision: 95.4%, recall: 92.2%, F-score: 0.938; Extended Data Fig. 2f), exceeding that of other TEM datasets^52,61 (F-score: ~0.60–0.75) and FIB-SEM datasets⁶³ (precision/recall: ~60–93%). It must be noted, however, that other datasets are of Drosophila, which have smaller and more numerous synapses that lead to disagreements even among expert annotators^61,63. Inspecting the synapse predictions, we found that prediction “errors” are typically ambiguous GCL synapses consistent with errors found evaluating synapse predictions elsewhere⁶³. In contrast, there were no mispredictions in the ML evaluation dataset where synapses are both larger and clearer in EM (Extended Data Fig. 4).

To conduct a sensitivity analysis of the automated synapse prediction, we evaluated the robustness of our results with different prediction thresholds to artificially add false positive (FP) and false negative (FN) synapses to the predicted network connectivity graph (Extended Data Fig. 7). In our prediction framework, each synapse is scored by how confident the detected synapse is and how big it is (i.e., score is the sum of the confidence value of the connected components); synapses with scores above this threshold are recognized while those below this threshold are ignored. We can combine predictions from multiple thresholds together to simulate a model with specific accuracy values. For example, if threshold_a produced a graph with a 20% FP rate and threshold_b produced one with a 20% FN rate, to get an 80% accurate model that has 20% FP and 20% FN rates, we take the default model and subtract synapses that were not detected with threshold_a and add synapses that were falsely detected with threshold_b. We then tested models with FP/FN rates at 10%, 20%, …, 90% to represent models with 90%, 80%, …, 10% accuracy. Note, however, that since the lowest threshold possible can only produce 30% FP rate, models with less than 70% accuracy only had 30% FP rate.

Quantifying MF→GrC connectivity.

We used the reconstructed neurons and the automated synapse predictions to map the connectivity between MF boutons and GrCs. The center of mass of GrCs cell bodies were manually annotated. To accurately get the center of mass of MF boutons, we first collected all MF→GrC synapses (i.e., synapses onto non-GrC neurons were filtered out) associated with a single MF, clustered them into individual boutons through DBSCAN⁶⁴ with parameters eps = 8 μm and min samples = 2, then averaged the synapse locations of each bouton to get the bouton’s center of mass.

MF bouton - GrC connectivity proofreading.

Beyond optimizing the neural network to minimize false positive (FP) and false negative (FN) rates, we also performed synapse count thresholding and targeted proofreading to more accurately determine binary connectivity between MF boutons and GrCs. Considering that each MF bouton to GrC connection has multiple synapses (Extended Data Fig. 4c) and that FPs often would only result in connections with single synapses, simple thresholding would make binary connectivity identification robust even with some FNs. However, we considered two additional factors. First, when MF boutons are at the edge of the volume, only a partial number of synapses are visible, increasing the need for a lower threshold. Second, MF boutons can make axon collaterals that make 1 to 2 synapses onto GrC dendrites either without “claws”; with claws connecting to different MF boutons than the collateral; or with claws connecting to the same MF (Extended Data Fig. 5). Considering these factors, we set the minimum automatic synapse threshold of MF bouton→GrC connections to 3, and then manually validated 2-synapse connections.

Spatial distribution of connectivity.

To get the spatial distribution of GrC dendrites in Extended Data Fig. 3e, for each GrC, we quantified the spatial displacement (Euclidean distance) of each MF bouton connected to it. To avoid edge effects, we defined margins where we removed from our analysis GrCs within 200 μm of the reconstruction boundaries in the X-axis. We further only counted the GrCs that are either at the top (or bottom) 10 μm of the dataset in Z, removed connections to MFs that are above (or below) the GrC centers of mass in Z, then combined the two distributions together. The Y margins do not need to be accounted for since they are natural boundaries. Since the dataset has a Z thickness of 49.5 μm, this method allows unbiased measurement of dendrite distribution of up to 200 μm in X and 39.5 μm in Z. Taken together, we found that GrCs preferentially connect with MF boutons spread in the dorsal-ventral axis rather than in the medial-lateral or the anterior-posterior axis, consistent with previous reports²⁶.

Counting presynaptic and postsynaptic partners.

In Fig. 2e, we counted the number of postsynaptic GrCs connected to each MF bouton. To avoid edge effects, we defined margins to not include in the analysis MF boutons within 60 μm and 20 μm to the reconstruction boundaries in X- and Z-axis respectively (Y margins do not need to be accounted for since they are natural boundaries). As shown in Extended Data Fig. 3e, these margins capture the extent of the dendritic reach of GrC dendrites. For Fig. 2e, only connections from the centermost MF boutons are counted (n = 62, though we used all surrounding GrCs n = 4,400). Similarly, for Extended Data Fig. 3c,d and Fig. 2, we removed analysis GrCs that are within 60 μm and 20 μm of the reconstruction boundaries in X- and Z-axis respectively. Note that the reconstructed distribution is plotted as an empirical CDF with discrete numbers of connected neuron pairs, while the random distribution is plotted as CDFs with error shaded across randomly generated networks.

Counting input redundancy between GrCs.

In Fig. 2c, we analyzed the MF bouton input redundancy to each GrC by counting the number of other GrCs sharing 2 or more MF inputs. To avoid the edge effects, even though we computed input redundancy using the entire GrC (n = 4,400) and MF (n = 1,145) population, we only counted the sharings of the centermost n = 211 GrCs.

MF→GrC random connectivity models.

To compare with the observed connectivity in Fig. 2, we developed random connectivity models (Extended Data Fig. 3f). The “Radius” models are based on random spherical sampling connecting GrCs to MF boutons closest to a single given dendrite length^11–13,26. “Radius-Average” uses the average dendrite length from our EM reconstructions. The “Radius-Distribution” model is similar, but it uses dendrite lengths drawn from the reconstructed distribution. In the “Vector-Shuffle” model, the dendrite targets of each GrC are drawn (with replacement) from the observed distribution of the spatial displacements between connected GrCs and MF boutons (Extended Data Fig. 3e). In all models, the locations of GrCs/MF boutons and the number of dendrites per GrC are maintained to be the same as the reconstructed graph, the margin of searching for MF boutons is set to 10 μm, and there are no double connections between any MF bouton→GrC pair.

MF axon collaterals → GrC proofreading.

To obtain the distributions in Extended Data Fig. 5c–e,h, we densely proofread 68 MF boutons within a 12,000 μm³ subvolume and determined whether a bouton made axon collaterals of at least 10 μm in length, how many boutons there are within a collateral axon, and whether they made synapses onto GrCs. We then quantified whether the synapses are located at the GrC dendrite claws or trunks, and whether the dendrite made a claw or not.

Quantification of GrC→PC connectivity.

Similar to MF→GrC connectivity analysis, we used automated segmentation and synapse detection to map GrC→PC connectivity.

GrC→PC connectivity proofreading.

Since the majority of GrC→PC connections consist of single synapses (Extended Data Fig. 4c), it was necessary to proofread GrC→PC synapses to minimize false negative errors. Virtually all false negatives consist of synapses from a GrC axon onto “orphaned” PC spines that are not connected to their PC dendrite. To correct these errors, we found all synapse locations between the reconstructed GrC axons to orphaned segments, and manually proofread them.

GrC axon to PC touches.

To find locations where GrC axons touch PCs and have the potential, but do not make synapses, we computed and utilized mesh representations of neuron segmentations, where neuron meshes consist of a reduced set of vertices that describe their boundaries. Touches between two neuron meshes were then determined through thresholding the shortest distance between the two sets of vertices; this threshold was set to 10 pixels (at 16 nm mesh resolution) to account for the mesh coordinate approximations. To reduce the number of all-to-all comparisons and improve performance, we simplified vertex locations through downsampling to make rough predictions of distances and prune vertices prior to calculating the exact distances.

GrC→PC random connectivity models.

To make the “Shuffle” model (i.e., the configuration model) in Fig. 3d, for each PC, we shuffled the “connected” status among all connected and touching GrCs preserving the total number of connected GrCs per PC. We shuffled only connected and touching neurons to preserve the spatial constraints on connectivity (i.e., PCs have limited dendrite spans and do not touch all GrC axons in the dataset).

Computing Hamming similarity.

To measure similarity between pairs of PCs in terms of their GrC input populations (Fig. 3), and pairs of GrCs in terms of the PCs to which they provide input (Extended Data Fig. 8b), we used Hamming similarity. We used this metric to give connections and the absence of connections equal influence in assessing the similarity of connectivity patterns. Hamming similarity is defined as the inverse of Hamming distance⁶⁵ normalized to the length of the vectors:

$$\text{Hamming similarity = 1 - }\left(\text{Hamming distance/vector length}\right)$$

For example, to compare the input similarity of two PCs which might have different sets of potential presynaptic GrC axons due to differences in the location of their dendrites, we first filtered out all axons that are not either connected to or touching both PCs, prior to computing the Hamming similarity score. Similarly for the comparing GrC pairs, we computed the Hamming similarity between the output vectors of two GrCs after filtering out all PCs that were neither connected to nor touched by both GrCs (Extended Data Fig. 8b). For Fig. 3d, we further filtered out PC pairs that had less than 30 common connected or touching GrC axons to minimize Poisson noise in the analyzed distributions.

Numerical analyses.

We developed a simulation framework to generate modeled input and output activity patterns of the MF→GrC layer given the reconstructed (and randomized) MF bouton→GrC connectivity. In all analyses in Fig. 4 and Extended Data Fig. 9 (with the exception of Extended Data Fig. 9c–d), to decrease edge effects where GrCs near the edge of the reconstruction boundaries showed fewer inputs (e.g., GrCs that had four dendrites, but only one is observable) and MFs near edges showed fewer outputs (e.g., boutons with only a portion contained in the EM volume), we used a subset of the reconstructed MFs and GrCs for our simulations. We used only the GrCs within the center 200 μm in the X dimension and 34 μm in the Z dimension, which totaled 1459 neurons, and MF boutons within the center 240 μm in the X dimension and 44 μm in the Z dimension totalling 630 boutons. While this graph is most representative of the EM sample, the overall MF input sharing among GrCs was not as high as observed in Fig. 2a and Extended Data Fig. 3g–m because of GrCs near the edges. To better test the high MF input sharing principle in Extended Data Fig. 9c–d we constructed a 120 × 80 × 120 μm MF-GrC graph by taking the GrCs and MF boutons in the center 120 × 80 × 40 um and replicate these node positions 3 fold along the Z (mediolateral) axis for a graph with 2541 GrCs and 771 MF boutons. With this graph we tested two models, one with high MF input sharing and one with normal (as expected from random wiring) MF input sharing. To achieve high input sharing while preserving the observed distributions of GrC dendrites (Extended Data Fig. 3c), GrC dendrite lengths (Extended Data Fig. 3d), and MF bouton sizes (Fig. 2e), we randomly added extra dendrite (26% more for this graph) to achieve the observed level of sharing (Fig. 2c and Extended Data Fig. 3l,m) then pruned away⁶⁶ those that least contributed to MF sharing. On each iteration, we randomized the graph by shuffling the dendrite and bouton size distributions and randomly connecting GrCs to MF boutons with a distance sampled from the observed dendrite length distribution.

We assumed the MF input pattern to be binary with a mean activity level of 50%, consistent with prior work^12,13. Each GrC integrates its inputs with equal weights based on the reconstructed (or randomized) connectivity graph. We assumed a binary output GrC activation function^12,13 but with an activity level of 30% instead of 10% to be more consistent with recent in vivo recordings^30,31. To maintain a steady-state activity level in a GrC population with a varying number of dendrites per neuron (as observed in Extended Data Fig. 3c), we tuned the activation threshold of each GrC by simulating 512 random input patterns and getting the average number of spiking inputs that would produce a 30% activity level for this neuron. Because the MF inputs are binary, however, a single threshold will not produce the precise 30% activity level. As an example, in our configuration, for GrCs with 5 dendrites, an activation threshold of 3 produces a 54% activation rate while a threshold of 4 would produce a 21% activation rate. It is then necessary to further divide the GrC population into an x% population of “low” and a 1-x% population of “high” activation level. In the above example, we solved for x% where .21 * x% + .54 * (1 - x%) = .30, then randomly choose x% of GrCs to have an activation threshold of 3 and 1 - x% to have 4. Such random assignment of “low” and “high” activation levels allowed us to overcome limitations in previous work^12,13.

Computing dimensionality.

Dimensionality is a measure of the number of independent variables embedded in a population’s activity which we used to quantify network encoding capacity. To compute the dimensionality of the population activity matrix x = (x₀, x₁, …) describing activity of the MF or GrC population across trials, we used a previously defined equation¹³.

$$\text{dim}\left(x\right)\text{=}{\text{(Σ}{\lambda }_{\text{i}}\text{)}}^{\text{2}}\text{÷}\text{Σ}{{\lambda }_i}^2$$

where 𝜆_i are the eigenvalues of the covariance matrix of x. We also computed population correlation¹² as:

$$\text{popcorr}\left(x\right)\text{=}\raisebox{1ex}{$\text{N}$}\!\left/ \!\raisebox{-1ex}{$\text{N-1}$}\right.\times \text{((max(}\surd {\lambda }_{\text{i}}\text{)}\text{÷}\text{Σ}\surd {\lambda }_{\text{i}}\text{)}-{\text{1/}}_{\text{N}}\text{)}$$

where N is the number of neurons in the population.

For Fig. 4b,c and Extended Data Fig. 9g, we sought to quantify the dimensionality of the GrC population when given a set of MF input vectors that are different by a specific f_variability factor, where low f_variability means highly similar input vectors and high f_variability means highly different input vectors. To achieve this, we constructed the input MF population activity matrix m as follows. For each simulation trial, a base vector m₀ was randomly generated: each element in m₀ was drawn independently as a binary number from a Bernoulli distribution with probability p = 0.5. Derived vectors m_i (n = 512 vectors) were then generated from m₀ by randomly selecting f_variability * len(m₀) elements and randomly rerolling their binary values. In this manner, vectors created with f_variability = 1.0 would be entirely uncorrelated to the base input pattern. Each data point (e.g., for each input pattern difference) consisted of the average of 100 such simulation trials and the resulting 95% confidence interval.

For Fig. 4c and Extended Data 6b, variability was restricted and normalized to the 33% MF subpopulation being tested (random, over-, and under-sampled). Within a trial, the variation of MF activity vectors m_i was sampled from said fixed MF bouton subpopulations. This was slightly different for Fig. 4b where the variation of MF activity vectors m_i was sampled across the entire MF population, even if the effective f_variability was the same. For Extended Data Fig. 9g, to measure dimensionality of a varying GrC population size with a parameter y%, we ran MF→GrC simulation as above, but only performed dimensionality analysis on a random y% subset of the GrCs. The subset is re-randomized for each trial and MF input variability is 100%.

For Extended Data Fig. 9a, we modeled MF inputs as continuous variables representing input spiking frequencies¹³. Like the binary input model, we also performed GrC activation threshold tuning to produce a precise coding level for the GrC population (i.e., 30%), though we did not need “low” and “high” assignments since inputs are continuous. In this experiment, we sought to quantify the GrC population correlation/stability when given a set of inputs that were the same, but corrupted by an f_noise factor (a higher population correlation value could denote higher noise resilience and learning generalization⁴⁴). Compared to Fig. 4b, besides using continuous input variables versus discrete variables, the other primary difference is that in this study all inputs were changed (% magnitude based on f_noise), while in the binary study a subset of the input was flipped (% based on f_variability). Specifically, for each simulation trial, we generated a random input vector m₀ with a uniform distribution from 0 to 1. Derived input vectors m_i were then generated by adding m₀ to a random noise vector n_i (also using a uniform distribution) multiplied by the noise factor f_noise:

$$m_i=(\text{1}-f\_noise)\times m_0+\left(f\_noise\times n_i\right)$$

The noise factor f_noise effectively controls the degree of difference between input vectors within the MF activity matrix m. At low f_noise, m is more static, while at high f_noise, m is composed of more independently drawn random input vectors.

Computing learned signal size.

We computed SNR with the signal size defined as the maximum linear distance of GrC representations between two input patterns and noise defined as the variation of the modeled binary activity^12,13 of the GrC population. It is thought that the GrC population activity is normalized through inhibition from the Golgi cells^8,9, and thus we tuned the GrC population to have the same mean activity across input MF patterns. Assuming equal weights, the presynaptic sum of GrC activations is expected to be the same across patterns. To differentiate patterns, it is theorized that PCs can manipulate their synaptic weights to affect (increase or decrease) the postsynaptic linear sum of specific GrC activation^{7–9,13,17,20,67}. For simplicity, these analyses assumed that GrC inputs were equal in strength. However, we note that some GrC inputs may be more influential than others⁶⁸ (cf.^69,70) and that >25% of unitary connections have multiple synapses (Extended Data Fig. 4c) which would further improve SNR of these inputs.

For Fig. 4d and Extended Data Fig. 9c–d, we modeled the PCs linear/logistic regression models with multiple variables (input GrCs) and binary outputs (PC firing low/high). The models assumed a linear relationship between the input patterns and the outputs, hence the “linear sum.” The model’s predictive power is maximized when the weights/parameters of the model maximize the difference between the input patterns, and so we defined and measured “learned signal size” as the maximum difference of the linear sums.

In Fig. 4d, the objective is to measure SNR of the difference or discriminatory power of the GrC population when encoding MF vectors which can be similar or different based on a variability factor f_variability. Given two GrC activation vectors g_j and g_k, and a set of weights w, the linear sum difference is:

$${\text{LearnedDiff}}_{\text{j}\to \text{k}}={\text{Σ}}_{\text{i}}\left(g_{ji}-g_{ki}\right)\times w_i$$

Given the constraints that weights are positive (GrC→PC synapses are excitatory) and that weights range from 0.0 to 1.0, the max learned difference from g_j to g_k would be:

$${\text{MaxLearnedDiff}}_{\text{j}\to \text{k}}\text{=}{\text{Σ}}_{\text{i}}\left(g_{ji}-g_{ki}\right)\text{ if}{g}_{ji}>g_{ki}$$

Alternatively, the max learned difference from g_k to g_j is:

MaxLearnedDiff_k→j = Σ_i (g_ki - g_ji) if g_ki > g_ji

For simplicity and without loss of generality we simply calculated a combined metric, which equates to the Hamming distance between two GrC activation vectors when GrC activation vectors are binary and weights are between 0.0 and 1.0:

$$\text{MaxLearnedDiff}\text{=}\text{HammingDistance}\left({\text{g}}_{\text{j}}\text{,}{\text{g}}_{\text{k}}\right)$$

For each simulation trial, we generated a base input MF vector m₀ and a set of derived vectors m_{1, .., n} (n = 512) as described previously. We then computed the pairwise Hamming distance of the resulting GrC activation vector g₀ against g_{1, 2, .., n} to measure the average and variance of responses. Each data point (e.g., for each input pattern difference) consists of 40 such simulation trials and the resulting 95% confidence interval. For the “selective subsampled” model in Fig. 4d, we chose the 50% subset of GrCs that would produce the greatest Hamming distance across the derived activation vectors m_{1, .., n} to m₀.

In Extended Data Fig. 9c–d, the objective was to measure the robustness of the GrCs encoding a number of input patterns when they are corrupted by noise (f_variability). We then scored and ranked the GrCs with a robustness_score to show that SNR is higher and more concentrated in a smaller subpopulation of GrCs in the high MF input sharing models than in the low input sharing model. Given m_1..n (n = 8 in this study) random input patterns, we computed the noisy patterns as described for Fig. 4b,c twenty times each, ten used for ranking GrCs (ranking patterns) and then for computing SNR (testing patterns). These input patterns are then used to compute the resulting GrC activation vectors. To estimate the most robust GrC subpopulation, we compute robustness_score by ranking each GrC by its probability to be activated across all ranking patterns - GrCs that are most consistently activated here should also be robust across testing patterns, and PCs that made synapses to these GrCs will also more reliably have a high SNR linear sum with respect to MF input patterns. After ranking, for each subpopulation_threshold, we computed SNR on the subpopulation_threshold of GrCs with the highest robustness_score: signal is the difference between the linear sum of activations across testing patterns and background patterns, and noise is the standard deviation of the activations across background patterns (see “Computing noise” below). Note, we included a pattern_size parameter that controls whether a randomly selected pattern_size subset of inputs is relevant (and kept constant during noise additions) and the rest of the input is irrelevant (and replaced with random inputs during noise additions). Extended Data Fig. 9c–d used an example pattern_size of 0.3 but the general trend was seen in all pattern_size that we tested (data not shown).

Computing noise.

For Fig. 4d and Extended Data Fig. 9c–d, we computed noise as the magnitude of variation of the modeled GrC activity across random background MF input patterns. To calculate the standard deviation of background activity noise, we ran simulations of 512 random MF input patterns and calculated the standard deviation of the sums of GrC outputs.

Prediction accuracy.

To evaluate prediction accuracy in Extended Data Fig. 9f,h, we used gunpowder (https://github.com/funkey/gunpowder), JAX⁷¹, Haiku⁷², Optax⁷³, and Chex⁷³. As above, we trained the output decoder as a linear layer with stochastic gradient descent using the output of the MF-GrC model as the input. The task was a standard binary classification where the network discriminates two classes of MF input patterns, where MF patterns were randomly varied, with different levels of variability, starting from a randomly chosen input vector. A standard sigmoid activation function was used. For comparison, we picked the number of test patterns that resulted in ~90% accuracy performance at 100% variability, which was 800 patterns. Each model was trained for 300 epochs with 5% MF noise augmentation on each batch, with a learning rate of 1 × 10⁻². The models are evaluated with different noise than in training. Since accuracy varied from run to run, we ran each model 20 times to produce averages and bootstrapped 95% confidence intervals. To better approximate the performance of a Purkinje cell decoder, we further modified the weight update mechanism to restrict the input weights to be positive with a logistic/sigmoid activation function that centers on a positive value sigmoid_center instead of on zero because GrC->PC synapses are excitatory and the activation of many GrCs are needed to influence the firing rate of PCs. We then defined max_weight, the maximum value of any individual synapse weight to be:

$$max\_weight=1/num\_grcs\times 1/activation\_rate\times sigmoid\_center\times weight\_scale$$

The first and second term normalize max_weight to the total number of GrCs and activation_rate respectively. The third term scales this by the sigmoid_center value, essentially controlling the steepness of the sigmoid function. Lastly, the fourth term controls synapse strength. In these simulations, we set weight_scale to be 4, which means that at activation_rate = 30%, 7.5% (30% ÷ 4) of the inputs would need to be activated at max weight to reach the center of the sigmoid function.

Statistics and reproducibility.

We did not use statistical methods to pre-determine sample sizes. Technical limitations made it only feasible to analyze one mouse in this study. However, connectivity trends were observed for many different neurons, and significance was tested with statistical tests (Wilcoxon rank-sum, Kruskal-Wallis, and permutation tests). Our study did not contain experimental groups, so randomization and blinding do not apply.

Extended Data

Extended Data Figure 1. Similarity between a convolutional neural network and the cerebellar feedforward network.

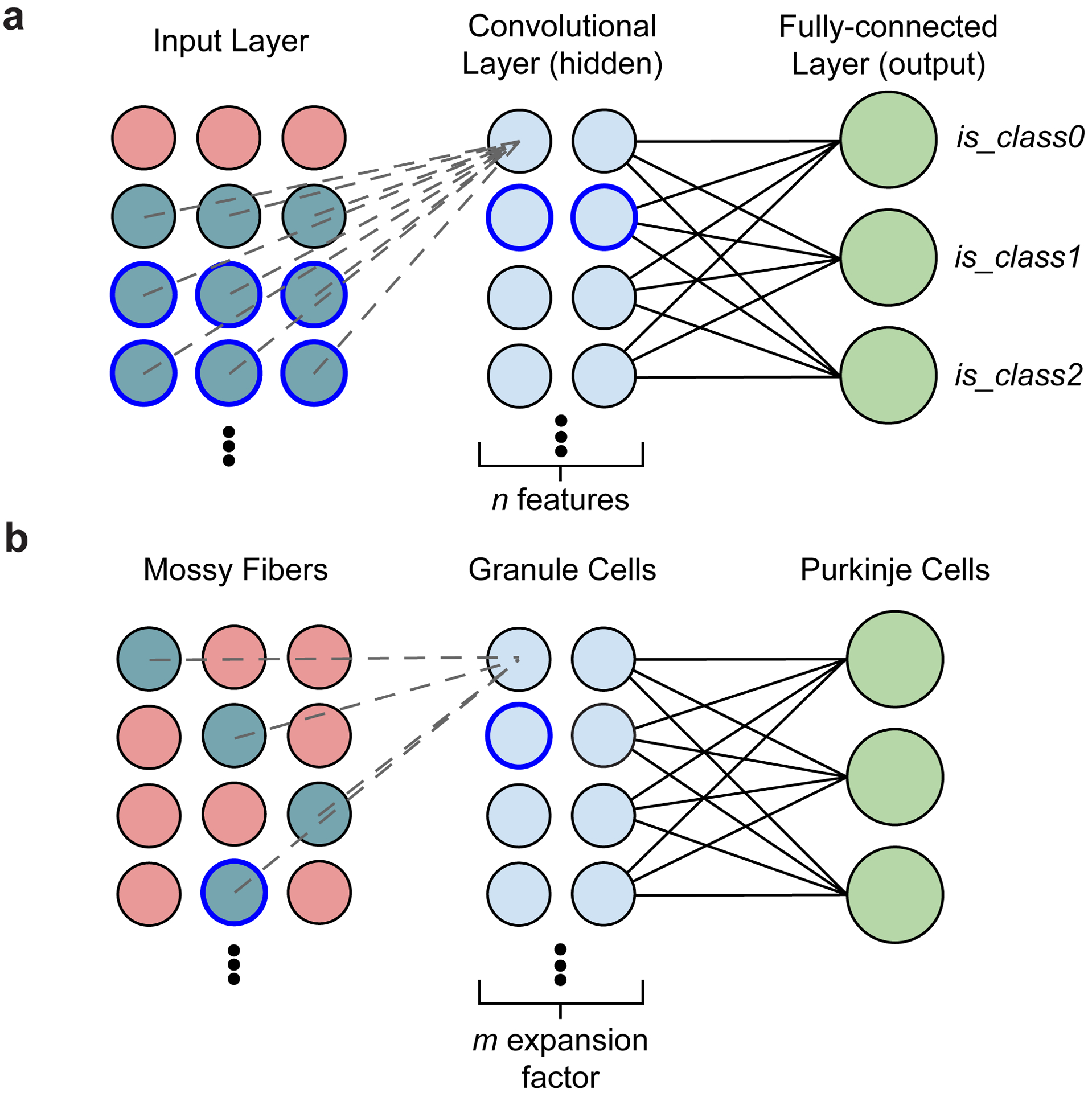
a, Diagram of a simple convolutional neural network with one convolutional layer (input→hidden) and one fully connected layer (hidden→output). The input (left) is made up of a single-channel 2D grid of neurons. The convolutional layer (middle) is made up of neurons each sampling a small local grid of the input (e.g., nine inputs when a 3×3 filter is used, cyan colored circles). This is notably different from a multi-layer perceptron network where the input and the hidden layer are fully connected - the convolution allows an increase in features while decreasing computational cost. Due to the small field of view of each convolutional layer neuron, adjacent neurons share a significant amount of inputs with each other. To increase capacity of the hidden layer, the convolutional neurons can be replicated by n times (typically parameterized as n features). Finally, the output neurons (right) are fully connected with neurons in the preceding convolutional layer. For a classification network, each label (class) is associated with a single binary output neuron for both training and inference. b, Diagram of the cerebellar feedforward network. Mossy fibers (MFs; left) can be considered a 2D grid of sensory and afferent command inputs typically of mixed modalities^40,41. Granule cells (GrCs; middle) sample only ~4 MF inputs each. The total number of GrCs is estimated to be hundreds of times more than the number of MFs (Fig. 1b), represented by an expansion factor m. Finally, Purkinje cells (PCs; right) - output neurons of the cerebellar cortex - receive input from tens to hundreds of thousands of GrC axons that pass by PC dendrites.

Extended Data Figure 2. Automated segmentation and synapse prediction.

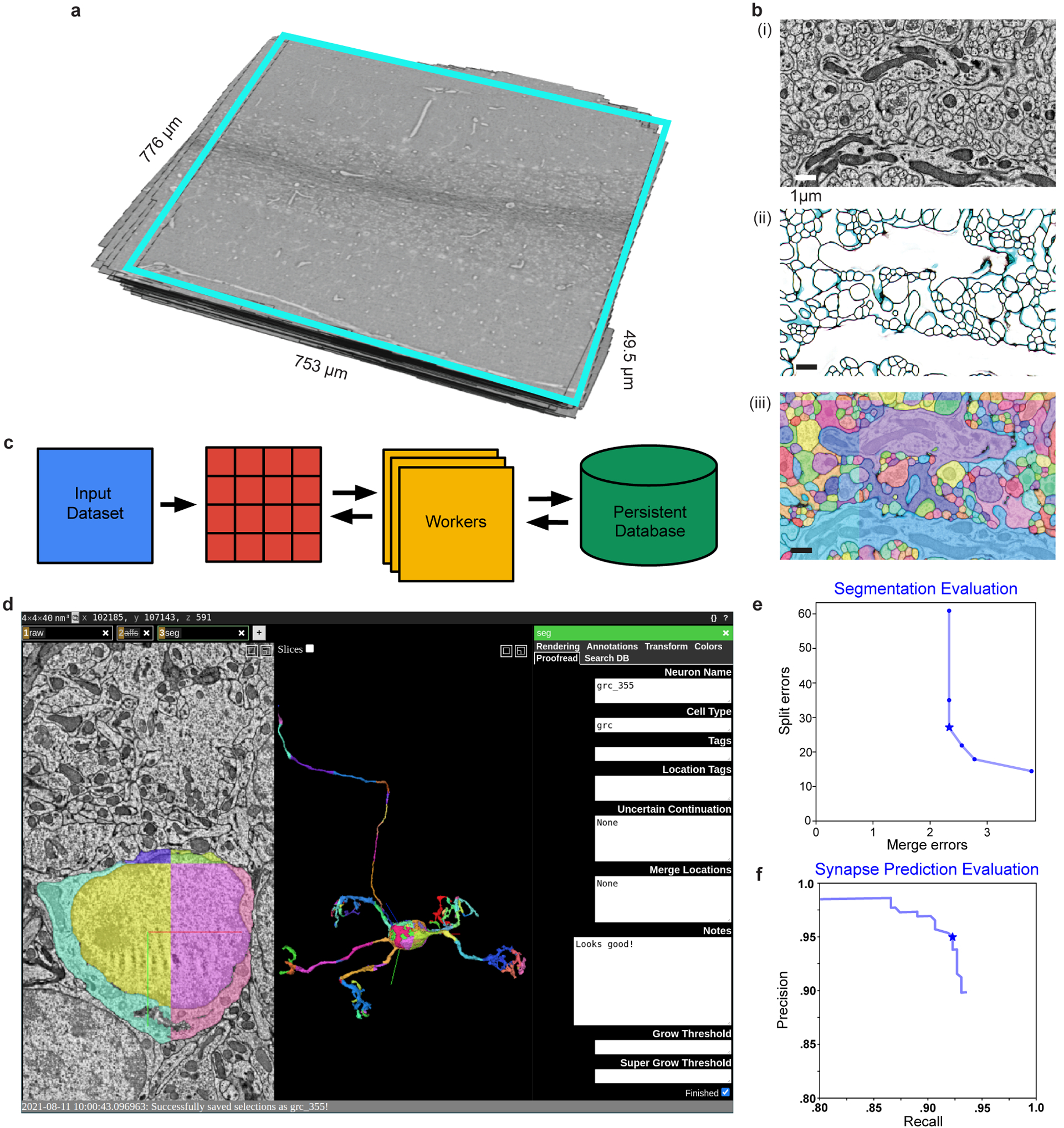
a, Serial-section electron microscopy (EM) dataset from lobule V from the cyan boxed region in Fig. 1d. b, The 3D reconstruction segmentation pipeline. (i) EM image data, (ii) boundary affinities, and (iii) automated segmentation output. c, Parallelized volume processing using Daisy. The input dataset is divided into small blocks, on which multiple workers can dynamically query and work. Block completion status and output data are efficiently stored into a persistent database or on disk directly from the workers without going through the centralized scheduler process. d, Example view of targeted neuron reconstruction using merge-deferred segmentation (MD-Seg). Neurons are first segmented as small blocks, and inter-block merge decisions are deferred to proofreaders. This is illustrated by the different colored segments of the displayed neuron. The user interface is based on Neuroglancer, modified to provide the segment “grow” functionality, and to integrate an interface to the database keeping track of neuron name, cell type, completion status, notes, and which agglomeration threshold to use for “growing”, as well as searching for neurons based on different criteria and recoloring segments of a single neuron to a single color (“Search DB” and “Color” tabs, not shown). e, Automated segmentation evaluation; plot points denote agglomeration thresholds. Average number of merge and split errors of (n = 9) 6 μm³ test volumes. We used a threshold (star) with 2.33 merges and 27 splits per 6 μm³ for proofreading. f, Automated synapse prediction evaluation; plot points denote connected component thresholds. Precision and recall curve for the synapse inference network. We achieved high synapse prediction accuracy with precision: 95.4% and recall: 92.2%, and an f-score: 93.8% (star)..

Extended Data Figure 3. MF→GrC wiring, convergence, and null models.

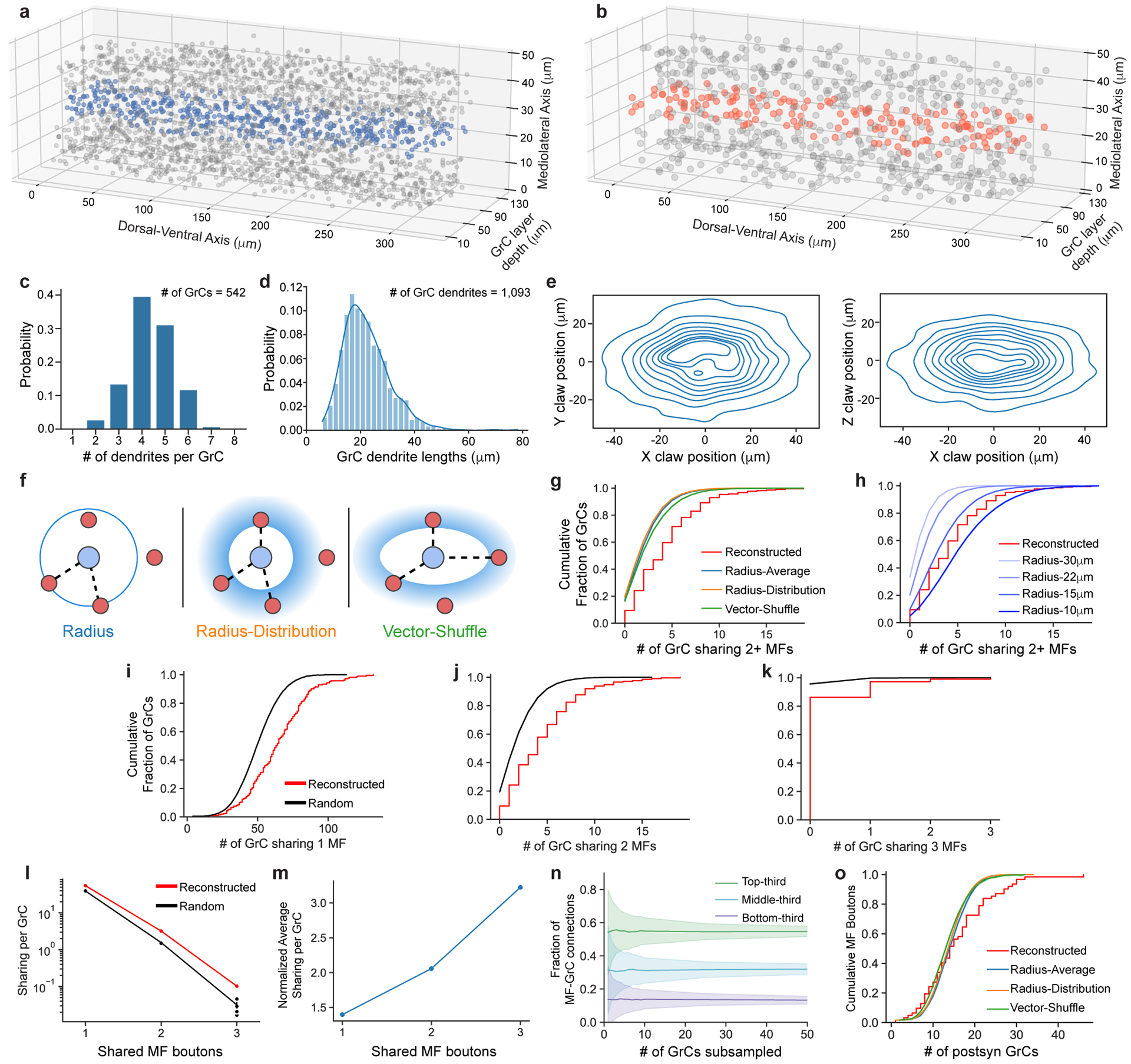
a,b, 3D plot of the locations of GrC somas and centers of MF boutons reconstructed in the 320 × 80 × 50 μm subvolume. Blue and orange dots indicate the GrCs and MF boutons respectively in the center 10 μm in the mediolateral axis, as plotted in Fig. 2b. c, Distribution of the number of dendrites per GrC (n = 542). d, Distribution of GrC dendrite lengths (n = 1093). e, Anisotropic positioning of MF bouton→GrC inputs (claws), showing elongated distribution in the dorsal-ventral axis (X) relative to both anterior-posterior (Y) and medio-lateral (Z) axes. Contour lines represent 10% intervals in the distribution. f, MF→GrC random models used for comparison with the reconstructed connectivity. (Methods). g, Similar to Fig. 2c, but with random models from f added. h, Similar to g, but with Radius models of different dendrite lengths. i, Cumulative distribution of MF bouton input redundancy counting the number of GrC pairs sharing 1 MF bouton (similar to Fig. 2c). j, Similar to i, but for 2 MF boutons. k, Similar to i, but for 3 MF boutons. l, Average number of GrC pairs sharing 1, 2, or 3 common MF bouton inputs, comparing reconstructed against the Radius random connectivity model described in d. m, Average sharing of GrCs in the reconstructed network as in l, but normalized to random networks. n, Average fractional distribution of inputs to GrCs from different MF bouton types (categorized as the top-third, middle-third, and bottom third most connected boutons) as a function of GrC sampling size. GrCs were randomly subsampled to produce input composition distributions, with error shadings representing SD. o, Same as Fig. 2e, but with random models from f added.

Extended Data Figure 4. MF→GrC and GrC→PC synaptic connectivity.

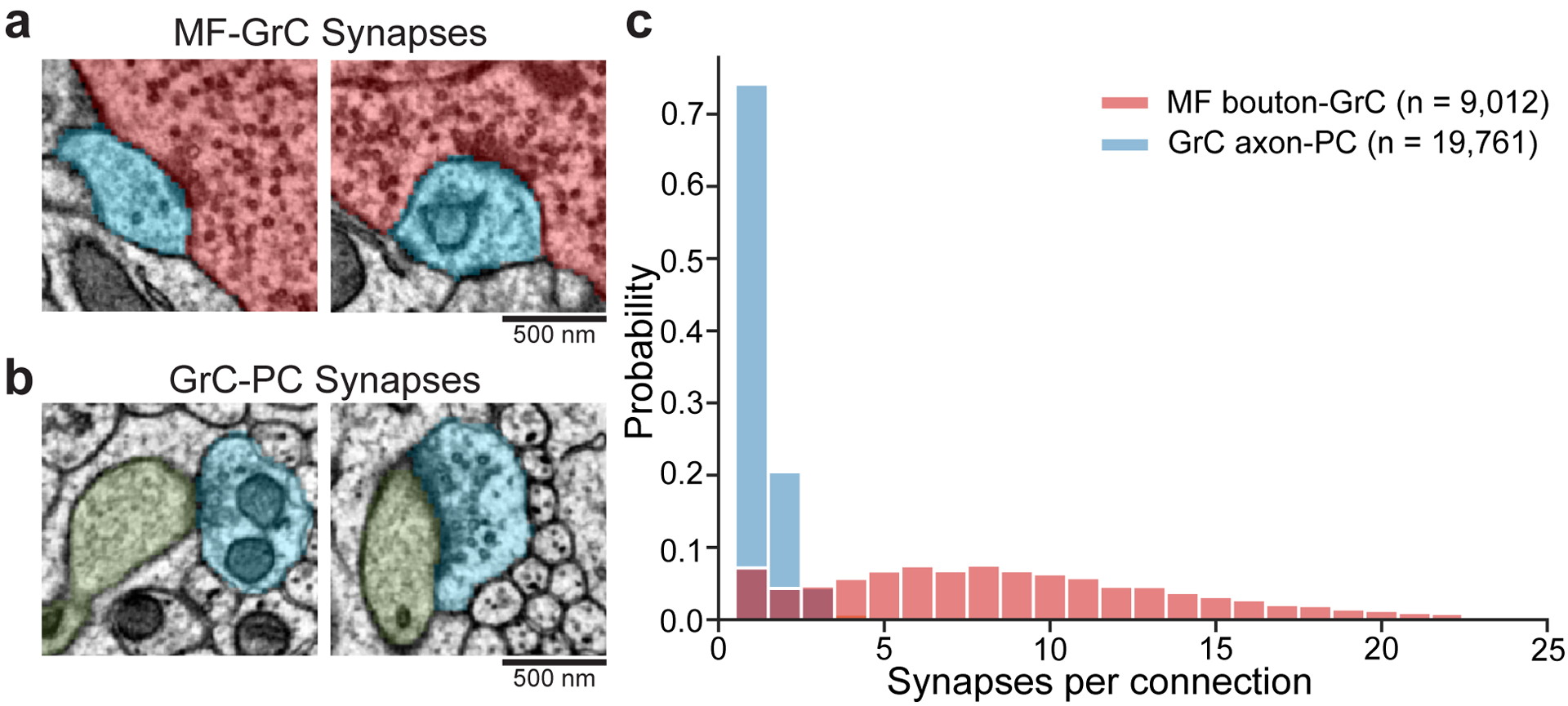
a, Example EM micrographs of MF (red) to GrC (blue) synapses. b, Example EM micrographs of GrC (blue) to PC (green) synapses. c, Distributions of the number of synapses per connection of the two synapse types. We analyzed (n = 9012) MF→GrC and (n = 19761) GrC→PC synapses in one volumetric EM dataset from one animal. The median of MF→GrC is nine synapses, while GrC→PC is one. Over 97% of GrC→PC unitary connections have 1 to 2 synapses, though instances of 3 to 6 synapses per connection, while rare, do occur.

Extended Data Figure 5. MF collateral axons connectivity to GrCs.

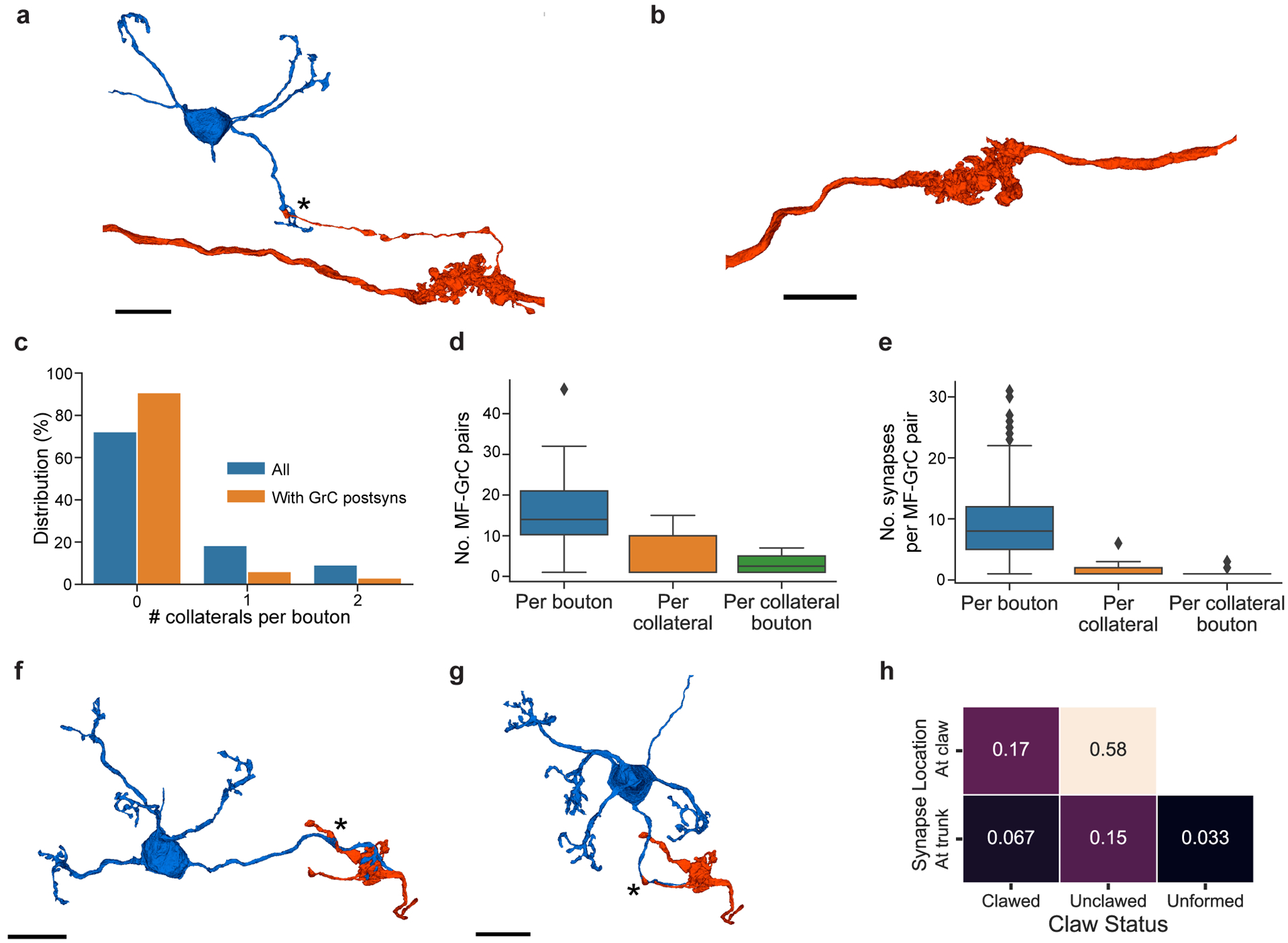
a, 3D rendering of a MF (red) bouton, with an axon collateral making synapses onto a GrC (blue) dendrite near a claw. Asterisks denote the location of synapses. b, Rendering of a MF bouton with no axon collaterals. c, Distribution of number of collaterals per MF bouton (n = 63); a MF bouton can have multiple axon collaterals, and each collateral may or may not make synapses onto GrCs. d, Box plot (25th, 50th and 75th percentiles with whiskers extended to points within 1.5 IQRs) of the number of MF-GrC connections: per MF bouton (n = 63), per axon collateral (n = 8), and per each bouton in a collateral (n = 16). e, Box plot of the number of synapses in each MF-GrC connection: per MF bouton (n = 978), per collateral (n = 28), and per bouton in collateral axons (n = 51). Due to the low frequency of axon collaterals, GrC targets, and the number of synapses per GrC target, it is unlikely that MF axon collaterals to GrCs represent a major route of signal propagation. f, Example of an axon collateral making synapses to a GrC on the trunk, and with more synapses formed on the claw. g, Example of a connection on the trunk of the dendrite, with no claw. h, Joint probability distribution of the synapse location of MF axon collaterals onto GrCs (on claw vs. trunk) and whether or not the dendrite made a claw onto the same MF bouton, or did not have claws (unformed claws). These examples of MF axon collateral connections to GrCs could represent different states of MF→GrC rewiring, supporting the hypothesis that MF→GrC wiring adapts to changing MF input representation^6,42. Scale bars are 10 μm.

Extended Data Figure 6. MF→GrC oversharing and convergence vs null models.

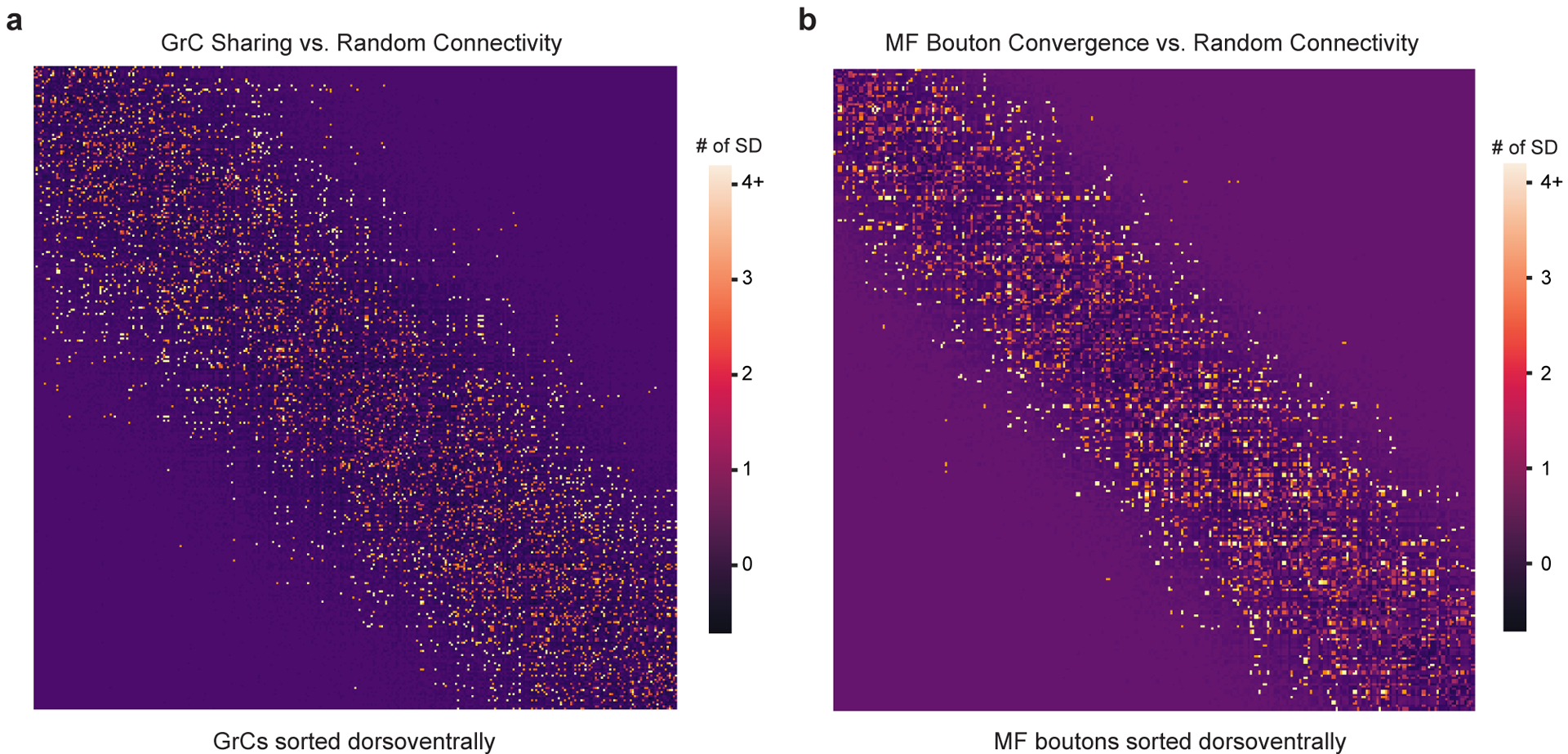
a, GrC input sharing relative to random connectivity. The matrix shows the degree of input sharing between GrCs (centermost n = 550, sorted by soma position dorsoventrally). The color scale for each cell in the matrix uses the z-score (reconstructed # of sharing minus random mean divided by the SD). b, MF bouton output convergence relative to random connectivity. The matrix shows the degree of output convergence between MF boutons (centermost n = 234, sorted by soma position dorsoventrally). The color scale uses the z-score as in a.

Extended Data Figure 7. Synapse prediction sensitivity analysis.

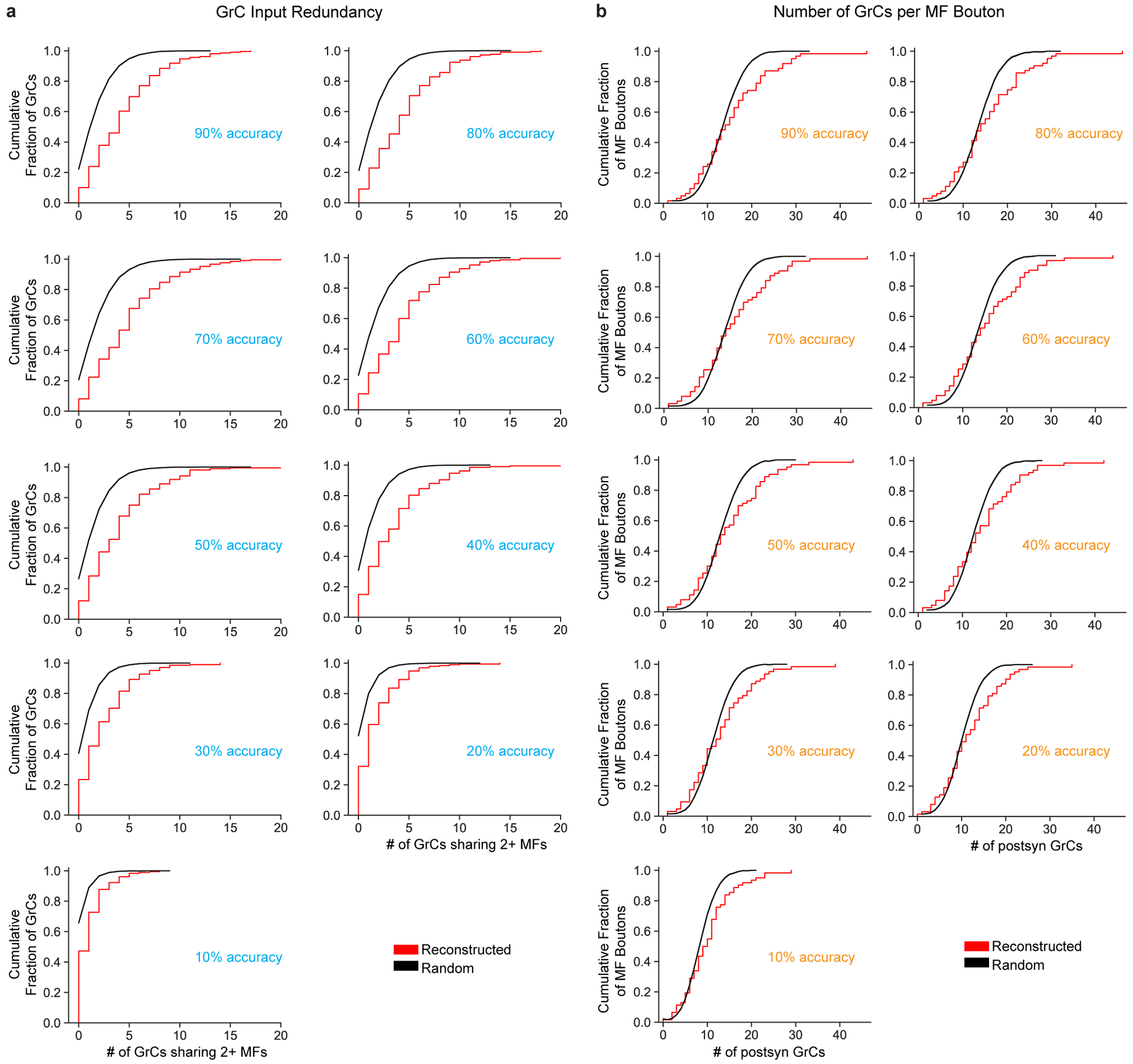
a, Cumulative distributions of MF bouton input redundancy as in Fig. 2c but across synapse prediction accuracies ranging from 90% to 10%. We artificially added false positives (FPs) and false negatives (FNs) to the network (Extended Data Fig. 2f) to achieve different accuracies (Methods). b, Cumulative distribution of postsynaptic GrCs per MF bouton as in Fig. 2e but across synapse prediction accuracies. As shown in a and b, we found that the results were consistent across models and only changed substantially when the FP/FN rates increased past 60%. We propose two reasons our results are robust across model prediction accuracies. First, MF-GrC connections are typically composed of multiple synapses (10 on average, Extended Data Fig. 4c). Since we used at least 3 synapses as a threshold for determining connectivity, even with significant missing, undetected synapses (eg. 50%), the remaining synapses are still reliable to reflect binary connectivity. Second, random and spurious false positive predictions are unlikely to coincide to cross the 3-synapse threshold. One interesting implication is that strongly selective features do not require perfect synapse prediction. This is consistent with connectomes in Drosophila where synapse prediction accuracy is ~60% and that connections are typically consist of multiple synapses which means that even with significant missing, undetected synapses (eg. 50%), the remaining synapses are sufficiently reliable to indicate connectivity.

Extended Data Figure 8. GrC→PC wiring and similarity of inputs to PCs.

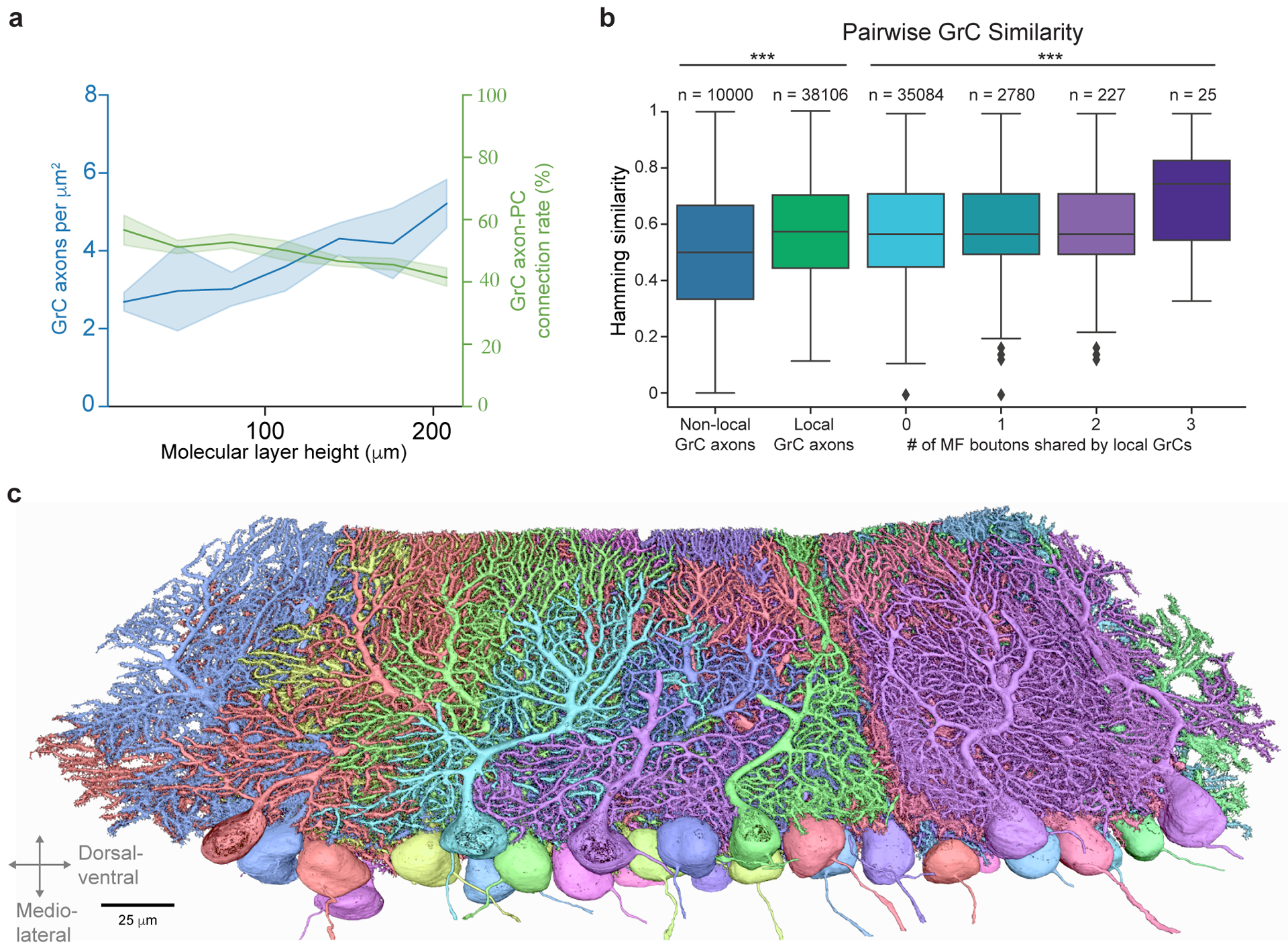
a, Plot of density GrC axons and GrC→PC connectivity rate as a function of height in the molecular layer between the pial surface and PC layer. Across molecular heights, the average axon density is 3.73 ± 1.23 per μm² (mean ± SD), and the average connection rate is 49.12 ± 4.39% (mean ± SD). Using these numbers and the average area of PC dendrites, we calculated ~125,000 GrC axons pass through the dendritic arbor of each reconstructed PC. At an average connectivity rate of 49%, only about 60,000 GrC axons were connected to each PC, 3–5× less than typically assumed in models of the cerebellar cortex^17,67,74. b, Box plot (25th, 50th and 75th percentiles with whiskers extended to points within 1.5 IQRs) of pairwise Hamming similarity between PC postsynaptic targets of non-local GrC axons, and local GrC axons with different numbers of shared MF bouton inputs. Across local GrCs sharing 0, 1, 2, and 3 MF boutons, Hamming similarity means = p = 0.0001137, Kruskal-Wallis H-test. 0-shared vs 1-shared p = 0.0132, 0-shared vs 3-shared p = 0.00797, 1-shared vs 3-shared p = 0.0186, 2-shared vs 3-shared p = 0.0309, other pairings p > 0.05, Dunn’s post hoc tests, Bonferroni corrected for multiple comparisons. c, 3D rendering of EM reconstructed PCs arbitrarily colored.

Extended Data Figure 9. MF-GrC-PC simulations.

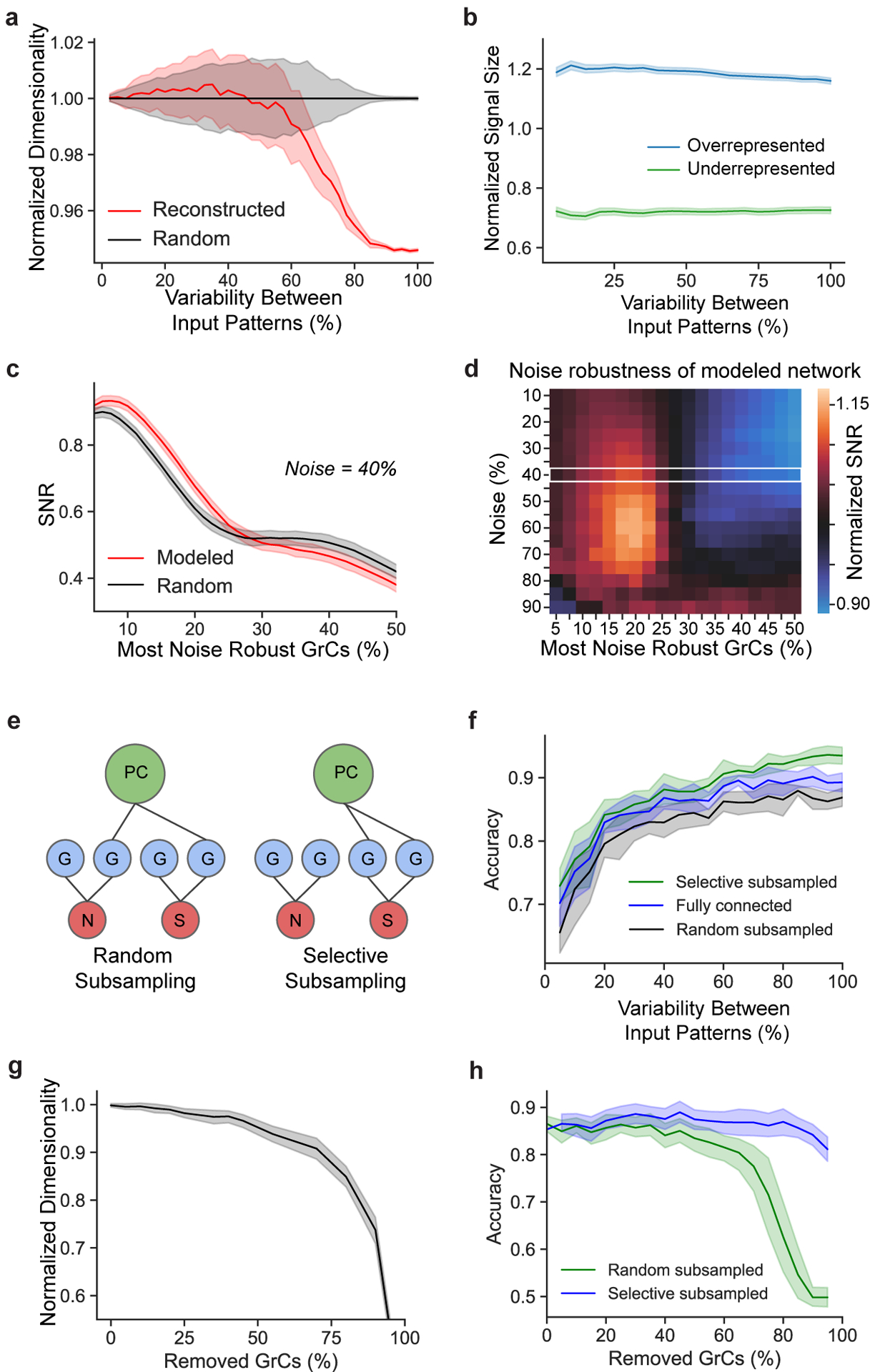
a, Normalized dimensionality of GrCs as a function of input variability using a continuous model of spike frequency¹³. Noise was modeled as the degree of variation of spiking frequency across all MF inputs (Methods). b, Modeled learned signal size (Methods) as a function of variability between MF input patterns, comparing pattern separation performance between overrepresented (top-third most connected) and underrepresented (bottom-third) MF boutons. Signal size from the reconstructed network is normalized by the random connectivity model for each population separately. c-d, SNR analyses of modeled MF-GrC networks, measuring noise robustness with (Modeled) or without (Random) redundant oversharing of MF inputs (Fig. 2c,d). SNR was computed across GrC subpopulations ranked by robustness (Methods) at a 40% noise level in c, and across GrC subpopulations and noise levels in d (normalized to SNRs of the “random” model at each noise level and subpopulation). The white box in d denotes the noise level shown in c. Redundant oversharing helps PCs learn more reliably by encoding the most robust signals in a subset of more correlated GrCs. e, Binary GrC→PC selective subsampling increases SNR. Left: PCs (green) randomly subsample GrCs (blue) with MF (red) inputs containing signal (S) or noise (N). Right: PCs connect to GrCs encoding signal-relevant MFs, leading to a higher SNR (Fig. 4d). f, Prediction accuracy of a linear neural network trained on output patterns of the GrCs as a function of MF input variability, comparing performance of MF-GrC networks between models that were fully connected, randomly subsampled with 50% connectivity, and selective subsampled with 50% connectivity, all as a function of MF input variability. g, Dimensionality of the GrC population as a function of the percentage of GrCs randomly removed, normalized to the dimensionality with 100% of the population. h, Prediction accuracy as in f comparing performance of MF-GrC networks between randomly and selectively subsampled models as a function of a percentage of randomly removed GrCs.

Data Availability

The EM dataset is publicly available at the BossDB (https://bossdb.org/) repository: https://bossdb.org/project/nguyen_thomas2022. Source data for Figs. 2c,e, 3c,d, and 4b,c,d are provided with the paper. Further directions for accessing neuron 3D renderings and derived neuron connectivity graphs are available at https://github.com/htem/cb2_project_analysis.