Convergence in determining enzyme functional descriptors across Kemp eliminase variants

Abstract

Molecular simulations have been extensively employed to accelerate biocatalytic discoveries. Enzyme functional descriptors derived from molecular simulations have been leveraged to guide the search for beneficial enzyme mutants. However, the ideal active-site region size for computing the descriptors over multiple enzyme variants remains untested. Here, we conducted convergence tests for dynamics-derived and electrostatic descriptors on 18 Kemp eliminase variants across six active-site regions with various boundary distances to the substrate. The tested descriptors include the root-mean-square deviation of the active-site region, the solvent accessible surface area ratio between the substrate and active site, and the projection of the electric field (EF) on the breaking C–H bond. All descriptors were evaluated using molecular mechanics methods. To understand the effects of electronic structure, the EF was also evaluated using quantum mechanics/molecular mechanics methods. The descriptor values were computed for 18 Kemp eliminase variants. Spearman correlation matrices were used to determine the region size condition under which further expansion of the region boundary does not substantially change the ranking of descriptor values. We observed that protein dynamics-derived descriptors, including RMSD_{active_site} and SASA_ratio, converge at a distance cutoff of 5 Å from the substrate. The electrostatic descriptor, EF_C–H, converges at 6 Å using molecular mechanics methods with truncated enzyme models and 4 Å using quantum mechanics/molecular mechanics methods with whole enzyme model. This study serves as a future reference to determine descriptors for predictive modeling of enzyme engineering.

1. Introduction

Enzymes have been widely used as biocatalysts for chemical synthesis [1–3], biomass conversion [4–7], polymer upcycling [8–11], drug functionalization [12–15], and food allergy treatment [16–18]. Wild-type enzymes usually exhibit low specificity for converting non-native substrate and feeble activity for catalyzing new-to-nature reactions. Experimental strategies of enzyme engineering, such as random mutagenesis [19–21], gene shuffling/recombination [22, 23], CASTing [24, 25], and directed evolution [26–29], have been leveraged to optimize enzymes’ capability for accommodating non-native substrates or catalyzing new-to-nature reactions. These strategies require extensive efforts for screening and selecting mutants to achieve desired functions. To accelerate biocatalytic discovery, molecular simulations [30–34] have been augmented with the campaign of biocatalytic discovery. The catalytic actions of enzyme catalysis can be elucidated and quantified using descriptors, including folding stability [35], binding affinity [36–38], activation barriers [39, 40], protein dynamics and correlated motions [41–49], electric field (EF) [50–55], charge transfer [54, 56], and more. These descriptors, derived from quantum mechanical (QM) or molecular mechanical (MM) simulations, have guided the search for beneficial mutants [57, 58]. They also serve as critical features for data-driven enzyme engineering.

For example, protein dynamics-derived descriptors and EFs have been extensively studied, because they were found to correlate with enzyme catalytic efficiency [50, 58–60]. Additionally, their computation is more efficient than that of activation barriers, whose convergence requires intensive conformational sampling and electronic structure calculations. A common descriptor for protein dynamics is the root-mean-square deviation of the active-site region (RMSD_{active_site}). RMSD_{active_site} quantifies the structural fluctuation of protein backbones or sidechains relative to a reference structure. The fluctuation is associated with the B-factor of protein structure determined from crystallography. In an analysis of catalytic residues in 178 enzyme active sites [59], Bartlett et al showed that the active-site residues of efficient enzymes generally have a lower B-factor. As such, a lower RMSD_{active_site} should be expected for efficient mutant enzymes and designer enzymes in catalysis, albeit the catalytic efficiency may drop under very low RMSD_{active_site}range [61]. Besides RMSD_{active_site}, our group identified a new descriptor to evaluate the overall impact of protein dynamics on substrate positioning [58]. The descriptor, defined as solvent accessible surface area ratio of substrate to active-site residues (SASA_ratio), can be obtained from molecular dynamics (MD) simulations. Using lactonase as a model system, our previous work shows that SASA_ratio can guide the search of optimal enzyme mutants with enhanced specificity for non-native substrates. Besides protein dynamics, the role of electrostatic environments was reported as a critical factor in mediating enzyme catalysis [62]. Linear correlation was observed between the magnitude of EF in the reaction center and the free energy barrier in ketosteroid isomerase and serine protease [50].

Despite the broad applications of simulation-derived descriptors in guiding enzyme engineering, converging the computation of descriptors in QM and MM simulations is a non-trivial task. Failure of achieving convergence hampers reproducibility of computational outcomes and may misguide experimental designs. This issue is particularly significant for QM-based calculations due to their high computational cost. Benchmarks have been performed to investigate the selection of QM regions that converge the computation of electronic structure descriptors (e.g. partial charge [63–67], charge transfer [67], charge density [66], bond valence [67], and electrostatic potential), energetic properties (e.g. energy barrier, reaction energy, and free energy) [64, 65, 67–75], geometries [64, 73, 74], and nuclear magnetic resonance (NMR) shielding [76, 77] in various model enzymes (peroxidase, methyltransferases, cytochrome P450, and deacetylase) [67]. Rational QM region selection approaches have also been developed, including charge shift analysis [78], Fukui shift analysis [78], and point charge variation analysis [79].

The benchmark studies on descriptors have been mostly performed on wild-type enzymes [72]. However, to understand or predict mutation effects, it is essential to perform convergence tests over multiple enzyme variants. Ideally, the selected active-site region for computing QM or MM properties should be large enough so that further expanding the region size does not substantially change the order of descriptor values across different enzyme variants. In this work, using 18 variants of Kemp eliminase [80], we investigated whether the ranking of descriptor values across enzyme variants approaches convergence as the increase of active-site region sizes used in descriptor computation. We first sampled conformational ensembles for 18 variants using classical molecular dynamics. Based on the sampled conformers, protein dynamics-derived descriptors (i.e. RMSD_{active_site} and SASA_ratio) and electronic structure-derived descriptors (i.e. EF along the breaking C–H bond) were evaluated using different sizes of active-site region based on MM or QM methods. For each descriptor, the Spearman correlation matrix was computed to examine the trend of convergence. The study informs the conditions under which different descriptors can be calculated with high fidelity for predicting the impact of mutations on catalytic functions. In addition, as the interplay between protein dynamics and electronic structures emerges as a new direction of study [81, 82], the convergence trend investigated in the current study might inspire the development of new strategies to predict computationally demanding QM properties using MM-derived properties.

2. Computational methods

Protein Structure and Preparation

The crystal structure of KE07-R7-2 was obtained from the Protein Data Bank (PDB ID: 5D38) [56]. All the crystallizing water molecules were removed. To make the amino acid sequence consistent with the original KE07 design [30], the N-terminal alanine was changed to methionine and the residues following Leu253 on the C-terminal were removed. The crystal structure [30] of KE07 in complex with the substrate 5-nitrobenzisoxazole was aligned relative to the KE07-R7-2 crystal structure using PyMol [83]. The coordinates of the substrate were used to construct the KE07-R7-2-substrate complex. The complex was then prepared with the AMBER 18 tleap [84] utility for MD simulations. AMBER ff14SB force field was used for the protein [85]. Parameters for the substrate were obtained using the generalized AMBER force field [86, 87]. The substrate structure was downloaded from PDB under the H5J entry (5-nitro-1,2-benzoxazole). The atomic charges were determined by the AM1-BCC model [88]. The missing atoms were also complemented with tleap.

Molecular Dynamics Simulations

MD simulations for each of the 18 variant-substrate complexes were conducted with a high throughput enzyme modeling platform, EnzyHTP [89]. The 18 variants include one KE07-R7-2 as the ‘wild-type’ and 17 of its mutants, including S48N, H201A, H201K, K222A, R16Q, N25S, I52A, M62A, H84Y, K132N, I199S, I199F, I199A, K132M, K162A, L170A, E185A (supporting information, table S1 and .zip file). Specifically, EnzyHTP automatically generates the structures of enzyme mutants based on the original structure and performs MD simulations using AMBER 18 [84]. The SHAKE algorithm was applied to constrain all the hydrogen-containing bonds [90]. To sample the near transition state conformations throughout the simulations, geometric restraints between the substrate and key amino acid residues were applied from minimization to production runs (supporting information, figure S1). The enzyme complexes were then solvated in a periodic octahedron box with a 10 Å buffer of TIP3P water and were neutralized with Na⁺ counterions. For each variant complex, the whole solvent box was first relaxed using steepest descent method for 10 000 steps followed by conjugate gradient method for another 10 000 steps. After minimization, each box was heated from 0 to 293.15 K within 36 ps with constant volume, equilibrated for 4 ps under constant volume at 293.15 K, and further equilibrated at 293.15 K and 1 atm for 1 ns. In addition to the geometric restraints mentioned above, the backbone C_α, C and N of the amide group were also restrained with a 2 kcal mol⁻¹ Å⁻² weight from the minimization to equilibration. After equilibration, we carried out production runs for 110 ns and output the trajectories every 100 ps. The snapshots derived from the last 100 ns of the production run were used for analyses. This yields a total of 1000 snapshots for each production run. All simulations were performed with a time step of 2 fs. The Langevin thermostat [91] and Berendsen barostat [92] were used throughout the simulations. For each of the 18 variant-substrate complexes, five parallel MD runs were conducted with different random seeds, yielding a total sampling time of 500 ns and 5000 snapshots.

QM/MM Calculations

We conducted QM/MM single-point electronic structure calculations for 500 snapshots sampled from MD production runs with a 1 ns interval. Each snapshot resulted from MD sampling was converted to an image in which the enzyme-substrate complex occupies the center of the box using autoimage function of AMBER cpptraj utility [93]. QM/MM single-point energies were calculated using TeraChem [94, 95]. The electrostatic interactions between the QM and MM region were treated with the electrostatic embedding method [62]. The QM/MM boundaries cut the backbone C–N bond of the amide group. To cap the unbonded atoms in the QM region, explicit H atoms were placed along the bond vector connecting the QM and MM atoms, and the resulting N–H and C–H bond lengths were set to be 1.09 Å. At the same time, the point charges originally belonging to the QM-region-bonded amide C and N atoms in the MM region were removed, and their charges were redistributed evenly on the remaining MM atoms except for those covalently bonded to the deleted MM amide C and N atoms. The electronic structures were described using the range-separated exchange-correlation functional ωPBEh [96] (ω = 0.2 bohr⁻¹) with 6–31 G(d) [97]. This combination of method and basis set has been validated in the study of large-scale electronic structure effects in catechol O-methyltransferase, cytochrome P450cam, lysozyme, and DNA methyltransferase [65, 67]. The restrained electrostatic potential (RESP) point charges [98] of each snapshot were calculated for QM residue EF analyses.

Descriptor Calculations and Analyses

We selected six active-site regions whose boundary’s distance to the substrate surface ranges from 3 to 8 Å with a 1 Å interval. For all 18 variants, the active-site regions were classified based on the averaged MD structure of KE07-R7-2. A residue is selected in the region if any one of its heavy atoms is within the distance cutoff from its nearest substrate heavy atom. Based on each of the active-site region, we calculated the enzyme functional descriptors, including mass weighted root-mean-square deviation of an active-site region (RMSD_{active_site}, in Å), solvent accessible surface area ratio between substrate and active-site residues (SASA_ratio, in Ų), and EF along the breaking C–H bond (EF_C–H, in MV cm⁻¹). The values of each descriptor were first evaluated on individual conformational snapshots, and then averaged over sampled classical MD or QM/MM snapshots (supporting information, tables S2–S5).

For RMSD_{active_site}, we included all the heavy atoms of the amino acid residues. The reference structure was averaged from sampled MD snapshots. The SASA_ratio was calculated based on the ratio of SASA_sub (substrate’s SASA) to SASA_protein (protein residues’ SASA). SASA was quantified using the Shrake and Rupley algorithm [99] embedded in the python library MDTraj [100]. The probe radius was 1.4 Å and the surface of each atom was represented by 5000 grid points. EF_C–H was calculated to be the projected EF strength at the middle point of the breaking C–H bond of the substrate 5-nitrobenzisoxazole. The bond vector direction points from C to H. We separately computed EF_C–H based on RESP charges either derived from molecular mechanics force field or single-point electronic structure calculation. For MM-derived EF_C–H, the EF_C–H was summed over from all atoms in the selected active-site region based on the RESP charges used in the classical force field. For QM/MM-derived EF_C–H, the EF_C–H was summed over from all atoms in the QM and MM region. The EF contributions from the capping H atoms were not included.

For each active-site region, the averaged descriptor values were computed and then ranked across 18 enzyme variants from 1 to 18. The Spearman correlation coefficient ρ was calculated as $1-\frac{6\sum d_i^2}{n\left(n^2-1\right)}$ where d_i is the rank difference for the ith enzyme variant and n = 18 is the total number of enzyme variants. Spearman correlation matrix for each descriptor was computed that contains the correlation coefficients for each pair of the active-site regions.

3. Results and discussion

3.1. Kemp eliminase variants as the model system

As the first known de novo-designed enzyme, Kemp eliminase catalyzes the conversion of benzisoxazole to cyanophenol via C–H deprotonation followed by ring opening (figure 1 top right) [30]. Multiple generations of Kemp eliminase have been reported [30, 42, 51, 52, 56, 80, 101–103]. Some well-known examples include the KE family designed using the ‘inside-out’ protocol by Baker, Houk, Tawfik, and co-workers [30], the HG family using iterative protocol by Hilvert, Houk, Mayo and co-workers [31], and the AlleyCat family using the minimalist approach by Korendovych, Degrado, and coworkers [32, 103]. From their initial reports, the most efficient enzyme variants were identified to be KE07-R7-2 (k_cat/K_M 2590 M⁻¹ s⁻¹), HG-3 (k_cat/K_M 430 M⁻¹ s⁻¹), and AlleyCat (i.e. k_cat/K_M = 128.4 M⁻¹ s⁻¹). All three families of Kemp eliminase involve a general acid-base mechanism, in which the substrate 5-nitrobenzisoxazole is deprotonated by a nearby carboxylate (side chain of Glu or Asp) to form 2-hydroxy-5-nitrobenzonitrile via one single transition state (figure 1, top-right). Nonetheless, they involve a different set of active site residues for substrate deprotonation and binding.

Figure 1.

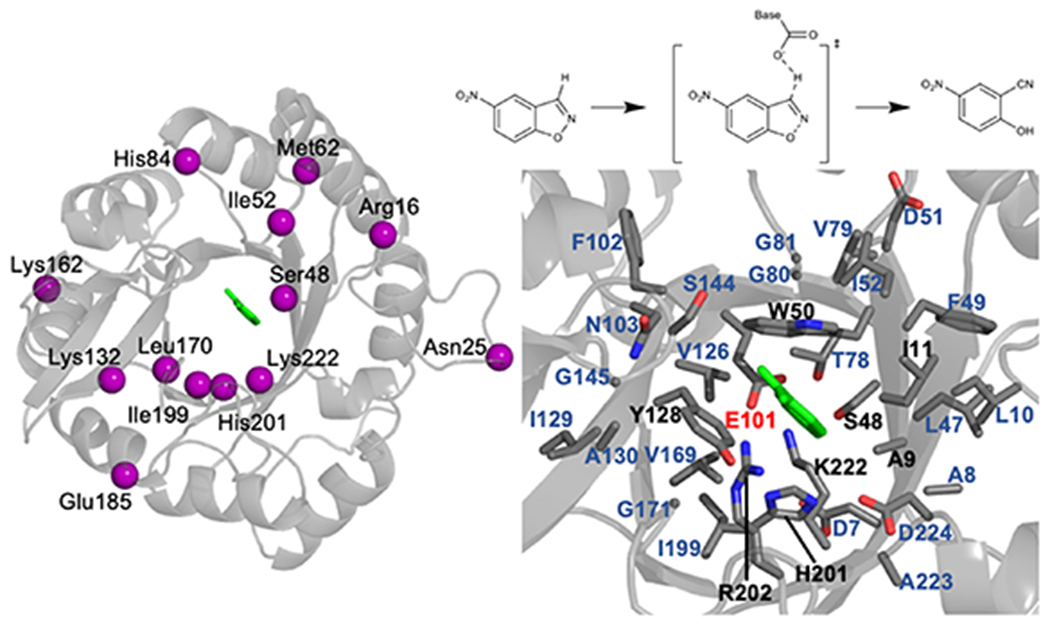
Mutation spots, catalyzed reaction, and active site residues of Kemp eliminase KE07-R7-2. (Left) Spatial distribution of mutation spots. The C_α atom of each site is shown in purple sphere, and the substrate is shown in green sticks. (Top-right) Catalyzed Kemp elimination reaction. The single transition state involves the deprotonation of a carbon atom. The transition state is stabilized by a general base from an amino acid side chain. The partial negative charge on the oxygen atom is stabilized by a hydrogen bond donor, which can be an amino acid side chain or a solvent water molecule. (Bottom-right) Active site residues are shown in stick. The substrate is shown in green, and the rest of the residues are shown in gray. The catalytic base is labeled in red. The residues that are within 5 Å from the substrate are labeled in black. The residues that are between 6 and 8 Å from the substrate are labeled in darker blue.

We chose the model system to be a member of the KE family, KE07-R7-2 [30, 56], and 17 of its variants with single amino acid substitution reported by Head-Gordon and coworkers [80]. KE07-R7-2 was derived from seven rounds of directed evolution based on a computationally designed enzyme scaffold KE07. In KE07-R7-2 and its variants, the carboxylic sidechain of Glu101 serves as the catalytic base (figure 1, bottom-right). These variants were selected in the benchmark for three reasons. First, the mutational spots of the variants span over a wide range of spatial proximity to the substrate (i.e. 3–23 Å, figure 1, left and supporting information, table S1). Both close and distal mutations are thus considered in the study. Second, although modeling has been performed for KE07-R7-2 to infer mutational hotspots based on correlated residue motion [80], protein dynamics and electronic structures for the 17 variants of KE07-R7-2 have not been investigated. Third, the kinetic parameters (i.e. k_cat or K_M) for these variants are known experimentally [80]. This implies that the mutation does not abolish the structural and catalytic integrity of Kemp eliminase. The crystal structure for KE07-R7-2 can be used as a scaffold for mimicking the mutant structures. Notably, although Kemp eliminase is the only model enzyme used in the current study, the general acid-base mechanism of Kemp eliminase represents a general mechanistic scheme shared by hydrolases, isomerases, and many other types of enzymes. As such, the convergence trend identified here can be potentially applied to other cases.

For KE07-R7-2 and its variants, the greater enzyme active site region entails 32 residues, including 6 polar, 20 non-polar, and 6 charged residues (figure 1, bottom-right and supporting information, table S6). By design, Glu101, Lys222 and Trp50 directly participate in the reaction or stabilize the transition state [30]. Glu101 is the general base that deprotonates the substrate. Lys222 is the H-bond donor to stabilize the phenoxide intermediate. Trp50 is the π-stacking residue to stabilize the substrate binding and charge-separated transition state. Four polar residues are observed within 5 Å of the substrate, including Tyr128, Ser48, His201, and Arg202. They likely stabilize the substrate binding or transition state with electrostatic or polar interactions. In addition, a total of eight polar (i.e. Glu101, Lys222, Tyr128, Ser48, His201, Arg202, Asp224, Asn103) and four charged (i.e. Glu101, Lys222, Arg202, Asp224) residues are found within 5.5 Å from the substrate. These residues mediate the EF environment exerted on the breaking CℓH bond. Besides dispersion interactions, the nonpolar residues likely contribute to the active site dynamics as described by RMSD_{active_site} and SASA_ratio.

3.2. Region selection for descriptor calculation

To calculate simulation-derived descriptors, an active-site region should be defined first. In this study, the calculations of RMSD_{active_site}, SASA_ratio, and MM-derived EF_C–H involve only the residues classified within a defined active-site region. The calculation of QM/MM-derived EF_C–H involves treatment of the active-site region residues using quantum mechanics and the rest of the enzyme residues using molecular mechanics.

To benchmark the region size effect, the active-site regions were defined based on the residues’ spatial proximity to the substrate (see section 2, Descriptor Calculations and Analyses). We selected six active-site regions whose boundaries to the substrate range from 3 to 8 Å (with 1 Å interval)—they are named C3–C8, respectively (figure 2). The residues were consistently selected by referencing KE07-R7-2. For C3, only Glu101 is included. Glu101 serves as the catalytic base to deprotonate the residue. Notably, throughout the MD simulations, a distance constraint was applied between Glu101 and the substrate to maintain their favorable catalytic pose. Compared to C3, C4 involves an expansion of seven additional residues. Among these residues, Lys222 and Trp50 appear in the original design of theozyme [30]. These two residues, cooperating with His201, Tyr128, and Ser48, likely facilitate proton transfer needed for the general acid-base mechanism. Unlike C3 which bears a −1 charge, C4 is charge neutral due to the addition of Lys222. In C5, only one additional residue Arg202 is included. This indicates that the catalytic core of KE involves a relatively compact inner cluster of residues surrounding the substrate. The positive charge introduced by Arg202 in C5 is neutralized by Asp224 in the C6 region. Notably, among the newly added residues in C6, three (i.e. Leu10, Phe49, and Val169) out of five are non-polar. This trend is also observed in C7 and C8. For the new additions, only two residues (i.e. Ser144 and Thr78) out of eight are polar in C7; two (i.e. Asp7 and Asp51) out of ten are polar in C8. The excessive number of non-polar residues in the greater active-site region contribute to the stability of Kemp eliminase.

Figure 2.

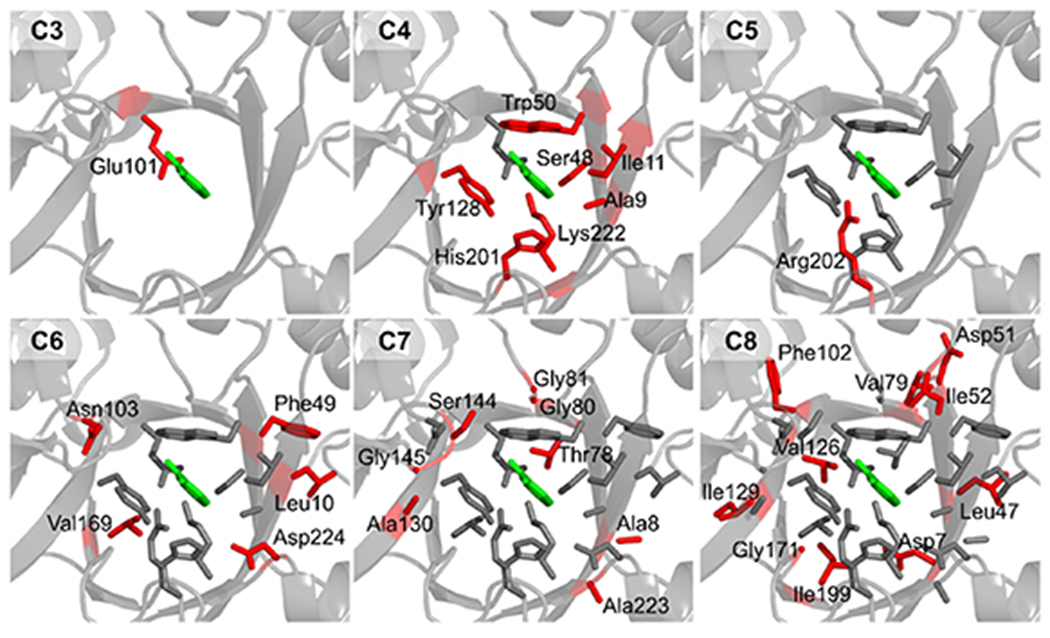
Six active-site regions with various boundary distances to the substrate. The distances used here range from 3 to 8 Å; the regions are named C3–C8, respectively. For each region, the selected residues are shown in stick. Compared to an adjacent region with a smaller size, the newly-added residues shown in red stick and labeled with a residue name; the existing residues are shown in gray stick.

The total number of atoms ranges from 31 in C3 to 495 in C8 (table 1). The region size tested here is comparable to or greater than the optimal region sizes determined from previous benchmark studies, including DNA methyltransferase by Solt et al [68]. (300 atoms), histone deacetylase by Morgenstern et al [66]. (200 atoms), and catechol O-methyltransferase by Kulik et al [64]. (500–600 atoms) and Jindal and Warshel [72]. (60 atoms). Notably, the size effect mentioned above was determined to be optimal for QM-derived quantities, including charge transfer, electron density, reaction enthalpy, and so on. In contrast, the size effects investigated in this study emphasize both MM-derived and QM/MM-derived features.

Table 1.

Number of residues, number of atoms, and net charge for the six active-site regions of KE07-R7-2 with different region sizes. Substrate atoms are counted in the number of atoms.

Cutoff (Å)	Number of residues	Number of atoms	Net Charge
3	1	31	−1
4	8	155	0
5	9	179	1
6	14	260	0
7	22	336	0
8	32	495	−2

For each of the six active-site regions, we computed the average descriptor values for the 18 KE07-R7-2 variants based on their conformational ensembles (supporting information, tables S3–S6). We investigated how the ranking of descriptor values across the 18 variants varies with the increase of region size. Instead of benchmarking a certain molecular property against its reference value, this study intends to identify a condition of region size under which further expanding the region boundary minimally changes the ranking of descriptor values across enzyme variants. Notably, the region size condition for a converged trend does not guarantee the convergence of individual property values. Nonetheless, the mutation effect can be reasonably inferred under this condition to guide enzyme engineering.

3.3. Descriptor of protein dynamics: RMSD_{active_site} and SASA_ratio

We first investigated the dynamics-derived descriptors, RMSD_{active_site} and SASA_ratio. They represent different aspects of protein dynamics. RMSD_{active_site} informs the conformational fluctuation of active site residues, while SASA_ratio informs the dynamic positioning and fitness of substrate in the active site.

Figure 3 shows the Spearman correlation matrix for RMSD_{active_site} (left) and SASA_ratio (right). Each element of the matrix represents a Spearman correlation coefficient (i.e. ρ) between descriptor values derived from two regions with a distinct size. For RMSD_{active_site}, a high ρ value (i.e. ⩾0.70) is observed for almost all pairs of regions except those that involve C3. The moderate ρ values between C3 and C5–C8 (i.e. 0.4–0.6) are caused by the small size of C3 that involves only one residue in the region (i.e. Glu101). The correlation coefficients tend to be higher for regions that are close in size (e.g. ρ > 0.9 for C5–C6, C6–C7, and C7–C8) and lower for regions with a larger size gap (e.g. ρ = 0.40 for C3–C8 and 0.73 for C4–C8). Notably, it is unexpected that the correlation coefficient is still as high as 0.40 between C3 and C8 because their numbers of residues differ by 31 and of atoms by 464. This indicates that the RMSD_{active_site} ranking calculated from C3 can still partially inform the ranking of dynamic fluctuation exhibited by larger-sized regions. This is likely caused by the collective motions of residues in the enzyme active site, where all residues are somewhat interconnected in a complex, dynamic network.

Figure 3.

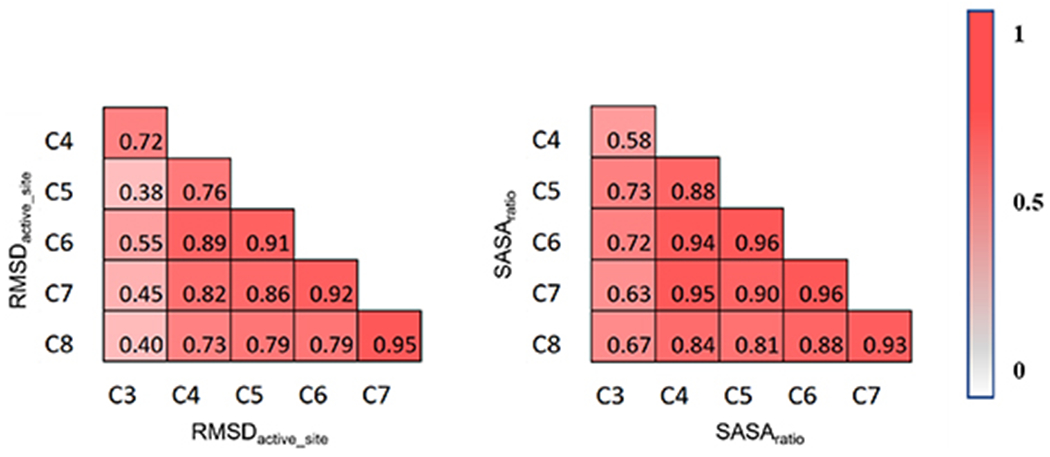
Spearman correlation matrices for protein dynamics-derived descriptors, RMSD_{active_site} (left) and SASA_ratio (right). Each matrix element represents a Spearman correlation coefficient for a pair of active-site regions with a distinct size. The magnitude of the correlation is coded by a gradient color bar that ranges from 0 (white) to 1 (red).

Unlike RMSD_{active_site}, which emphasizes protein dynamics, SASA_ratio represents the interplay of dynamic motion between substrate and its surrounding active-site residues. The Spearman correlation matrix of SASA_ratio shows a similar trend to that of RMSD_{active_site} (figure 3, right). For each pair of regions, the Spearman correlation coefficient of SASA_ratio is generally greater than that of RMSD_{active_site}. The ρ values are greater for correlations between larger regions that are closer in size (e.g. ρ = 0.96, 0.96, and 0.93 for C5–C6, C6–C7, and C7–C8, respectively). Notably, the SASA_ratio is computed by the SASA ratio of substrate to active-site residues. For different active-site regions, the SASA value of the substrate always remains constant. This helps dampen the perturbation of expanding region size on the ranking of descriptor values across variants.

To determine a convergence cutoff for computing dynamics-derived descriptors, we investigated the change of Spearman correlation coefficients between adjacent active-site regions versus the increase of region size (figure 4). For both RMSD_{active_site} and SASA_ratio, the correlation coefficient appears greater than 0.90 after C5 (i.e. 5.0 Å from the substrate). With a Spearman ρ value greater than 0.90, the ranking of descriptor values computed from one active-site region is largely preserved in another. As such, the convergence cutoff for dynamics-derived descriptors is determined to be 5.0 Å. Notably, from C5 to C8, the atomic charge varies from 1 (C5), to 0 (C6 and C7), then to −2 (i.e. C8). The correlation coefficients remain high even between regions of different charges. This observation confirms that the dynamics-derived descriptors used here are approximately independent from electrostatic effects—they are insensitive to electrostatic perturbation in the protein environment.

Figure 4.

Spearman correlation coefficients for the dynamics-derived descriptors, RMSD_{active_site} (left) and SASA_ratio (right) between regions that are close in size. The red dashed line indicates the convergence cutoff of 0.90.

3.4. Descriptor of electrostatic environment: EF along breaking C–H bond

Next, we investigated the descriptor for enzyme electrostatics, EF_C–H, the EF along the breaking C–H bond. The interior EF in Kemp eliminase has been proposed as a factor to stabilize the developing dipole moment along the C–H bond [52]. Optimizing the EF through mutagenesis has also been demonstrated as an effective strategy to improve enzyme catalytic efficiency [52, 104].

Figure 5 shows the Spearman correlation matrix for EF_C–H that were separately computed using MM (left) and QM/MM (right) method. MM-derived EF_C–H involves only the local residues that are classified in the active-site region. This approach is similar to the distance cutoff method used in Rosetta score functions for computing electrostatic interactions [105]. QM/MM-derived EF_C–H employs QM to treat residues in the active-site region and MM for residues in the rest of the enzyme. This approach incorporates the effects of long-range electrostatics. Notably, to ensure a consistent comparison, the same set of MD-derived snapshots was used in the calculations for both MM- and QM/MM-derived EF_C–H values. In our test cases, the QM/MM optimization consistently increases the resulting EF_C–H values by a few tens of MV cm⁻¹ (supporting information, table S7).

Figure 5.

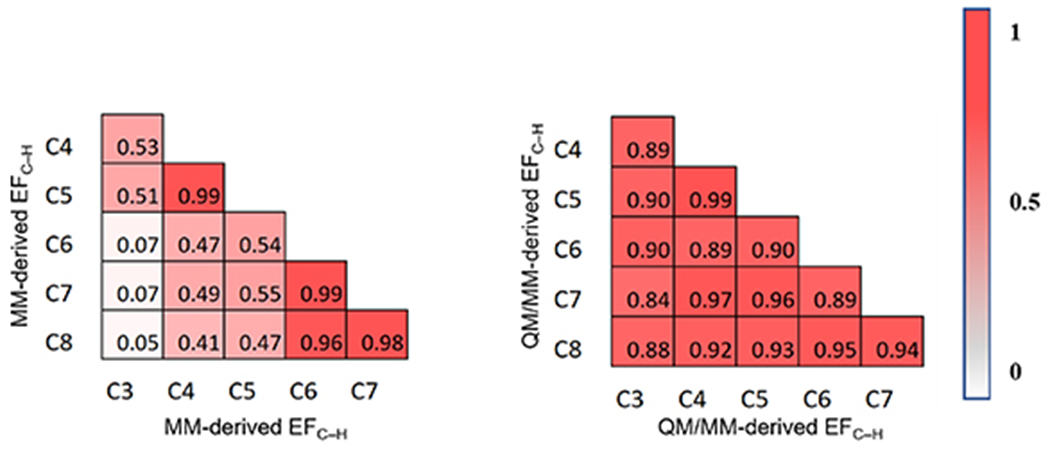
Spearman correlation matrix for MM-derived EF_C–H (left) and QM/MM-derived EF_C–H (right). Each matrix element represents a Spearman correlation coefficient for a pair of active-site regions with different region sizes. The magnitude of the correlation is coded by a gradient color bar that ranges from 0 (white) to 1 (red).

Unlike dynamics-derived descriptors, low correlation coefficients are more frequently observed between active-site regions of different sizes, especially between regions with a larger size gap. For example, the Spearman ρ values for C3–C6 (i.e. differ by 13 residues), C3–C7 (i.e. differ by 21 residues), and C3–C8 (i.e. differ by 31 residues) are 0.07, 0.07, and 0.05, respectively, for MM-derived EF_C–H (figure 5, left). The low correlation strength indicates that the ranking of EF_C–H values derived from a smaller active-site region cannot be used to infer the ranking from a larger active-site region. Different from dynamics-derived descriptors, the EF depends more sensitively on the active-site regions used in the calculation. From C3 to larger active-site regions, individual residues added to the active site region, especially polar and charged residues, can significantly affect the representation of mutation effects on interior enzyme electrostatics.

Similar to dynamics-derived descriptors, the Spearman ρ values are greater for correlations of EF_C–H rankings between larger regions that are closer in size. The ρ values for C4–C5, C6–C7, and C7–C8 are 0.99, 0.99, and 0.98, respectively, for MM-derived EF_C–H (figure 5, left); and are 0.99, 0.89, and 0.94, respectively, for QM/MM-derived EF_C–H (figure 5, right). Interestingly, the rankings derived from C4 to C5 are highly consistent, albeit their difference in the total charge of active-site residues by −1. The charge difference is caused by the addition of Arg202 in C5. Despite having a +1 charge, Arg202 has a trivial influence on EF_C–H due to it being perpendicular to the breaking C–H bond vector. For C6–C7 and C7–C8, the newly added residues are mostly nonpolar and are distant from the breaking C–H bond in the substrate (i.e. >6.3 Å). As EF strength is inversely proportional to the square of the distance, the impact of remote residues dies off quickly. As such, a consistent ranking of EF_C–H values is observed between regions beyond C6. For MM-derived EF_C–H, the Spearman ρ value for C5–C6 (i.e. 0.54) is significantly lower than that for C4–C5 or C6–C7 (figure 5, left). This is because the newly added charged residue in C6, Asp224, is positioned along the direction of the breaking C–H bond vector. As such, the impact of Asp224 on the ranking of EF_C–H values is substantial. Notably, the drop of Spearman ρ value for C5–C6 was also observed for Mulliken charge-based QM/MM-derived EF_C–H values (supporting information, table S8 and figure S2), albeit the correlation coefficients remain consistently high (i.e. >0.90) for larger QM regions.

By comparing the Spearman ρ values for C4–C5, C5–C6, and C7–C8, the results show that for both MM-and QM/MM-derived EF_C–H values, the ranking is dependent more on the spatial distribution of charged residues relative to the breaking C–H bond than on the total atomic charge in the active-site regions. This finding can potentially help rational identification of residues for tuning interior enzyme EFs for selective bond activation. To determine a convergence cutoff for computing electrostatic descriptors (i.e. for MM- and QM/MM-derived EF_C–H), we investigated the change of Spearman correlation coefficients between adjacent active-site regions versus the increase of region size (figure 6). Consistent with the dynamics-derived descriptors, we adopted a Spearman ρ value of 0.90 as the criterion for determining the convergence cutoff. For MM-derived EF_C–H with truncated enzyme models, the convergence occurs at 6 Å. For QM/MM-derived EF_C–H with whole enzyme models, the correlation coefficients are consistently high even at minimal QM region C3/C4 (figure 6, right). This indicates that MM charges are sufficiently accurate and can even replace QM-derived RESP charges in describing the ranking of EF values across different mutants (supporting information, figure S3). The results are likely caused by the fact that the reactant state of Kemp eliminase does not involve longer-range charge transfer with residues in the greater protein environment. The trend of correlation likely changes when the deprotonation transition state is bound to the active site.

Figure 6.

Spearman correlation coefficients for the dynamics-derived descriptors, MM-derived EF_C–H (left) and QM/MM-derived EF_C–H (right) between regions that are close in size. The red dashed line indicates the convergence cutoff of 0.90.

However, we should note that the computed EF values are still dependent on the QM region selection. As such, we investigated the trend of convergence for absolute QM/MM-derived EF_C–H values under different QM region sizes (supporting information, figure S4). The distribution of EF values systematically drops as the QM region enlarges from C3 to C4 and becomes steady until the QM region size hits C7 where the distribution bumps up due to reorganization of active site residues (i.e. Ala9, Thr78, Gly80, and Asp224). Combining the region size benchmark of correlation matrix and absolute EF values, we determine C4 as the convergence cutoff. To examine the influence of MM region, we calculated the C4-based QM/MM-derived EF_C–H values under different MM region sizes (supporting information, table S9 and figure S5). The ρ values for C4–C5, C6–C7, C7–C8, and C8-whole enzyme are 0.93, 0.98, 0.99, and 0.95, respectively. This result shows that the ranking of EF values across mutants is not sensitive to MM region sizes.

To pinpoint the origin of the difference between MM- and QM/MM-derived EF_C–H values at the QM region of C4, we calculated the atomic RESP charges derived from both MM and QM methods based on the KE07-R7-2 wild-type. The atoms with the top ten largest deviations are backbone atoms residing on the QM/MM boundary (supporting information, table S10). Although the QM/MM boundary effects do not appear to influence the ranking of EF values across mutants, larger QM region should be used when the actual values of physical properties are of interest to the research.

Considering the low computational cost of MM-derived EF_C–H values, we would recommend a hybrid approach for future practice of computational enzyme engineering. This hybrid approach involves using MM-derived EF_C–H values (of the whole enzyme) for pre-screening of a large number of mutants, followed by assessment of QM/MM-derived EF_C–H values to identify mutants for experimental tests. For reactions with stronger polarization and charge transfer, a larger QM region may be used, but the region size could potentially be reduced by using rational QM determination approaches such as charge shift analysis [78], Fukui shift analysis [78], and point charge variation analysis [79].

4. Conclusions

In this work, we investigated how large an active-site region should be to converge the description of mutation effects on enzyme dynamics and electrostatics. For 18 KE07-R7-2 variants, dynamics-derived descriptors (RMSD_{active_site} and SASA_ratio, both derived from classical MD) and electrostatic descriptors (MM- and QM/MM-derived EF_C–H were computed across six active-site regions with various boundary distances (i.e. 3–8 Å) to the substrate. For each descriptor, we employed the Spearman correlation matrix to determine the region size condition under which further expansion of the region boundary does not substantially change the ranking of descriptor values.

Using a Spearman ρ value of 0.9 as a criterion for convergence, we observed that the ranking for RMSD_{active_site} and SASA_ratio converges at 5 Å; MM- and QM/MM-derived EF_C–H converge at 6.0 and 4.0 Å, respectively. The ranking of EF_C–H values derived from MM charges (i.e. including all atoms in the enzyme) is predictive to that from QM/MM charges, albeit the absolute EF values still exhibit dependence on the QM region sizes. As such, we recommend a hybrid approach for future practice of computational enzyme engineering, which involves a pre-screening of a large number of mutants based on MM-derived EF_C–H values, followed by an assessment of QM/MM-derived EF_C–H values on a smaller number of pre-screened mutants. Notably, the convergence of rankings does not ensure the convergence of measured descriptor values. Nonetheless, the ranking is most useful to guide experimental selection of function-enhancing enzyme mutants. Additionally, the current study emphasizes a designer enzyme, Kemp eliminase. Future studies should entail more types of enzymes with various catalytic actions.

Data availability statement

The data that support the findings of this study are openly available at the following URL/DOI: 10.5281/zenodo.7140835.