A modular strategy for distributed, embodied control of electronics-free soft robots

Abstract

Robots typically interact with their environments via feedback loops consisting of electronic sensors, microcontrollers, and actuators, which can be bulky and complex. Researchers have sought new strategies for achieving autonomous sensing and control in next-generation soft robots. We describe here an electronics-free approach for autonomous control of soft robots, whose compositional and structural features embody the sensing, control, and actuation feedback loop of their soft bodies. Specifically, we design multiple modular control units that are regulated by responsive materials such as liquid crystal elastomers. These modules enable the robot to sense and respond to different external stimuli (light, heat, and solvents), causing autonomous changes to the robot’s trajectory. By combining multiple types of control modules, complex responses can be achieved, such as logical evaluations that require multiple events to occur in the environment before an action is performed. This framework for embodied control offers a new strategy toward autonomous soft robots that operate in uncertain or dynamic environments.

An approach for designing electronics-free soft robots that autonomously choose their trajectories is described.

INTRODUCTION

Soft robotics has become a notable area of research in recent years, with the potential to enable robots with a number of promising characteristics (1, 2), such as resilience to large deformation (3, 4), safe human-machine interaction (5, 6), environmental adaptability (7, 8), novel and adaptable locomotion strategies (9, 10), and resistance to impact (11, 12). Versatile deformable structures and actuating materials have been adopted in the design and fabrication of soft robots, including pneumatic and hydraulic actuators (13–15), dielectric elastomer actuators (16, 17), liquid crystal elastomers (LCEs) (18–20), magnetic actuators (21, 22), and hydrogels (23, 24). Numerous useful functionalities have been demonstrated in soft robots, including gripping (25, 26), crawling (27, 28), jumping (29, 30), and shape adaptability (31, 32).

However, to sense and respond to the environment, most soft robotic systems rely heavily on traditional mechatronics (fig. S1): Solid-state sensors capture inputs from the environment; these signals are routed to an electronic processor; the processor then uses the inputs to make decisions and issue commands to actuators. These sensing, control, and actuation feedback loops require complex integrated systems that may limit the function and form factor of the robot (16, 27, 33, 34). Typically, these mechatronic devices consist of rigid electronic components and peripheral circuits that can be bulky, expensive, and mechanically incompatible with soft materials (35). In addition, these electronics may be undesirable for work in certain harsh environments, e.g., due to the potential for spark ignition (mines and nuclear reactors) or in environments in which metal may be incompatible or limiting (magnetic resonance imaging machines, water, and other solvents) (36). Moreover, for applications in which the robot is intended to directly change shape or function in response to its environment, an electronic sensing, control, and actuation strategy can be extremely complex and requires a large number of transduction steps. The same problems arise for microrobots or other robots with unique form factors that might be incompatible with conventional electronics (37).

Nature provides inspiration for the design of autonomous capabilities based on embodiment rather than traditional electronics. Instead of using electronic components, biological systems interact with the environment via physical intelligence, directly embodying many of the sensing, processing, and actuating functions in spatially distributed features of the physical body (37, 38). Embodying physical intelligence provides unique advantages, including simplicity and scalability (38, 39). This strategy has been recently applied to soft robotic systems (40, 41). For instance, Drotman et al. (42) developed untethered soft-legged quadruped robots that reverse their direction of motion when a wall is contacted. Rothemund et al. (43) designed and fabricated a mechanical bistable valve that enables simple logic circuits and demonstrated how these can be applied in soft grippers and crawlers. In parallel, nascent ideas in mechanical metamaterials have been developed that blur the distinction between robotics and materials (44, 45). These mechanical metamaterials embody transduction and control functions in their engineered architecture, allowing the materials to use environmental inputs for mechanical computation and autonomous adaptation (46–50). For example, recent work has demonstrated environmentally responsive mechanical logic (48, 51, 52), including an artificial “flytrap” that can autonomously actuate when it senses specified environmental stimuli.

In this work, we build on the above advances in intelligent mechanical metamaterials and embodied logic to create an electronics-free soft autonomous robot (Fig. 1).

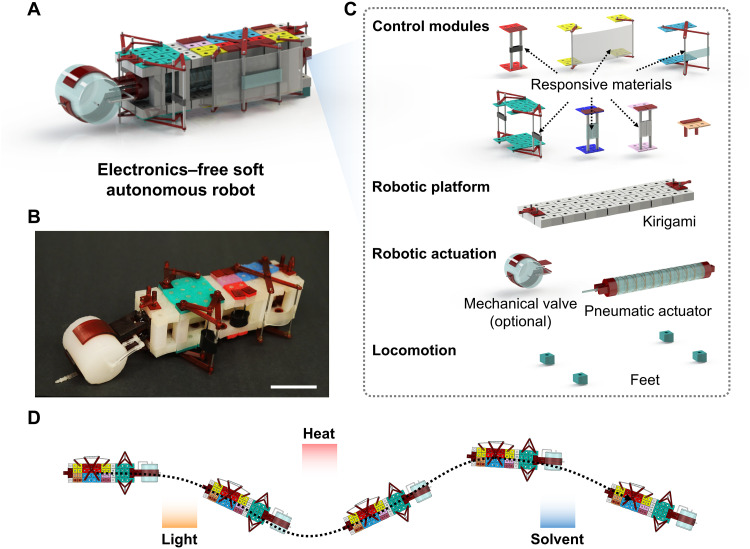
Fig. 1. Design of an electronics-free soft autonomous robot.

(A and B) A schematic and image, respectively, of the soft robot. (C) The soft robot comprises multiple types of control modules (with responsive materials), a kirigami-inspired body, a pneumatic actuator (mechanical valve is optional), and feet (to enable locomotion). (D) Autonomous motion of the soft robot in response to various external stimuli (light, heat and solvent). Scale bar (B), 5 cm.

We accomplish this by designing modular control units that incorporate soft responsive materials, such as LCEs that respond to heat or light (via the photothermal effect), hydrogels, and silicones [polydimethylsiloxane (PDMS)], and distributing these units throughout the soft body of the robot (Fig. 1).

The robot body itself consists of a kirigami-inspired architecture based on the rotating squares mechanism (53–55), which serves as a flexible and convenient platform for the reconfigurable, modular control units (Fig. 1). The control modules constrain the local rotation of the kirigami when activated by stimuli-responsive materials.

The behavior of the robot in response to environmental inputs is a function of the spatial distribution (and interactions) of the control modules. The trajectory of the robot is thereby governed by a distributed computational event, comprising a logical combination of distinct environmental inputs. This framework provides a new strategy for achieving autonomous, electronics-free soft robots that can operate in dynamic or uncertain environments following a variety of control objectives.

RESULTS

Design and operational principle

The design of the electronics-free autonomous robot is shown in Fig. 1. This robot comprises four components: a kirigami-inspired body, a pneumatic actuator (equipped with a bistable mechanical valve), multiple types of control modules (with integrated responsive materials), and feet to enable locomotion. The pneumatic actuator is sandwiched between two layers of the kirigami. It can generate periodic extension and contraction when pressurized air is applied, which in turn expands or contracts the kirigami body. The kirigami body accommodates the changing dimensions of the actuator via the internal rotation of the squares. The bistable valve (Fig. 1) is optional (see discussion later), but it can translate a constant pressure source into a periodic inflation/deflation of the pneumatic actuator (43); hence, an electronic pressure controller is not required. The feet underneath the body of the robot enable it to move forward due to anisotropic friction between the robot and ground (fig. S2) (43). Control modules can be added, moved, or removed from the kirigami body, imparting different functionality to the robot. Each of these modules integrates stimuli-responsive materials, which act as sensors for stimuli such as light, heat, and solvents (Fig. 2). These materials can activate or deactivate mechanical constraints, which in turn induce bending in the kirigami during pneumatic actuation. The placement of these control modules in the kirigami thereby enables the robot to sense and respond to these stimuli, and, based on the location and type of control modules, to autonomously change its trajectory of locomotion (Fig. 2). In this work, we mainly focus on the use of LCEs to sense and respond to heat or light. However, the design principle can be applied to a broad range of external stimuli using multiple responsive materials (see the Supplementary Materials for examples).

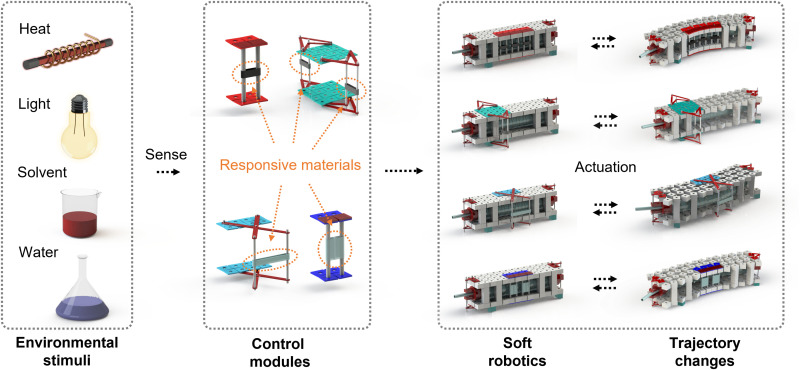
Fig. 2. Operating principle of electronics-free soft autonomous robots.

Multiple control modules (with responsive materials) allow the soft robots to respond to their surrounding environments (heat, light, and solvents). Control modules activate in response to local stimuli, which mechanically constrain the actuating kirigami, causing changes to the curvature of the robot, and, as a result, to its trajectory.

Several important parameters affect the behavior of the kirigami robot and the efficacy of the control modules, including the hinge thickness of the kirigami, the constraints applied to the square units, and the size of the kirigami. Before deciding on a final set of parameters for the robot, we experimentally and numerically characterized the effect of these parameters, with details provided in the Supplementary Materials. In brief, we built a discrete model that treats the kirigami squares as rigid bodies and the thin hinges as elastic springs (fig. S3). The discrete model is then nondimensionalized to identify the fundamental parameters that intrinsically dictate the mechanical behavior of the kirigami platform, thus providing useful guidelines for the design of the kirigami body (figs. S4 and S5). We also performed finite element analysis (FEA), which has the advantage of validating the experimental data more precisely, but which is computationally expensive, and therefore less efficient than the discrete model for parametric studies (figs. S6 to S8). Results from these methods are discussed where appropriate below and described in more detail in the Supplementary Materials.

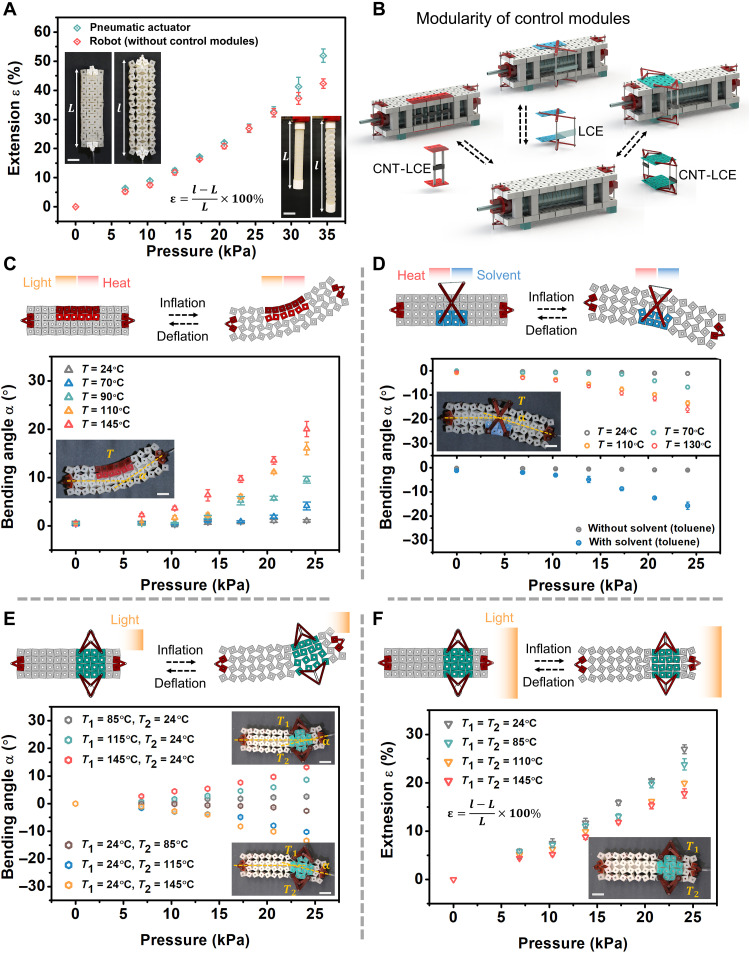
The inflation/deflation cycle of the pneumatic actuator powers the locomotion of the robot. When no relevant stimuli are present, inflation of the pneumatic actuator causes rotation of the kirigami squares and associated lengthening of the robot body. The extension of the platform is dependent on the pressure in the pneumatic actuator. We define the extension ratio (ε) as ε ≡ (l − L)/L × 100%, where L is the length of the initial state and l is the length of the pressurized state. We measure the extension ratio (ε) as a function of the applied pressure, both for the pneumatic actuator and for the assembled robot (without any control modules, Fig. 3A). To accurately quantify this relationship, the pressure in the pneumatic actuator for these tests is precisely controlled using a custom fluid control system (fig. S9). The ability of the kirigami to extend with the actuator is a function of hinge thickness. We characterized this effect experimentally and numerically (using both our discrete model and FEA). The experimental results show that smaller hinge thicknesses (1 mm) can generate a large extension ratio (27%) without causing buckling of the pneumatic actuator (fig. S10). Both the discrete model and FEA agree with experiments, i.e., that the hinge thickness should be as thin as possible to allow efficient extension (e.g., fig. S10) (56). As shown in Fig. 3A, when the pressure is below 25 kPa, the extension ratio of the pneumatic actuator is comparable to the robot. Further increasing the pressure may lead to buckling of the actuator, resulting in bending of the robot body. This can cause the robot to turn. The maximum operational pressure of the pneumatic actuator is therefore set to 25 kPa.

Fig. 3. Physical shape changes of soft autonomous robots in response to environmental inputs.

(A) The extension ratio ε of the pneumatic actuator and the robot (without any control modules) as a function of applied pressure. (B) Multiple types of modular control units are developed. They can be easily attached to or removed from the body of the robot. (C) As one example, a control module can sense and respond to heat or light. (D) In this example, a different control module design causes the robot to bend away from heat or solvents. (E and F) In another example, a control module is designed to bend the robot so that its end will align toward a light. Scale bars (A), (C), (D), (E) and (F), 2 cm.

The autonomous robot is designed to achieve sensing and control solely from the action of the control modules. The behavior of the robot in response to a particular stimulus depends both on the types of control modules present in the robot and on their location. Multiple types of control modules are developed to provide different moving strategies. They can be easily attached to or removed from the body of a given robot (Fig. 3B and movie S1), showing the simplicity of the entire robotic system. It is worth noting that the modularity of the control units enables a robot to achieve different moving strategies in response to a given set of environmental stimuli, without the need of fabricating a new robot. Furthermore, new control modules could be designed, beyond those that we have introduced in this work, which could enable new types of responses or enable responsiveness to additional stimuli. The responsive materials in the control modules sense and actuate when they encounter relevant environmental stimuli. In this way, the control modules that are distributed throughout the robot influence its shape, thereby enabling it to autonomously change its trajectory.

We experimentally and numerically characterized how different mechanical constraints on the rotation of the kirigami squares affect the bending angle (figs. S11 to S13). The first example of a control module, shown in Fig. 3C, locally prevents the kirigami from opening if light or heat is applied. This is enabled by a strip of carbon nanotube doped liquid crystal elastomer (CNT-LCE) in the control module, which contracts if heat or light is present above a given threshold (see figs. S14 to S20 for detailed characterizations). As shown in Fig. 3C, if the light and heat in the environment are minimal, the CNT-LCE does not contract (the control module is not active), allowing the kirigami squares to rotate freely everywhere. This leads to uniform extension of the robot body as the pneumatic actuator inflates (no bending). If the temperature is elevated, the CNT-LCE strip contracts, causing the control module to locally inhibit the motion of the squares, producing bending when the robot is actuated. To quantify this effect, we measured the bending angle α as a function of temperature (Fig. 3C). At a given pressure, the bending angle of the robot is larger when the temperature is higher, because the LCE actuates to a larger strain (fig. S15). The length of the CNT-LCE strip is a critical design parameter (fig. S21). In addition, the bending angle of the robot was measured during repeated inflation/deflation cycles (fig. S22), showing no obvious degradation of the control module.

By simply changing the type of control module, the robot can behave entirely differently in response to the same environmental stimulus. For example, Fig. 3D and fig. S23 show a control module that causes the robot to bend in the opposite direction than the previous example.

The relationship between the bending angle α and pressure is plotted in Fig. 3D. In addition to heat, the LCE can contract when exposed to other stimuli, such as the toluene, due to a nematic-isotropic phase transition (57–59), resulting in bending of the robot when pneumatically actuated (Fig. 3D).

A third type of control module is shown in Fig. 3 (E and F). Here, two CNT-LCE strips are used in the module and distributed to each side. If the control module is illuminated more on one side than the other, the CNT-LCE strip on that side contracts more than the strip on the other side. As a result, the robot bends toward the light source (Fig. 3E). Note that as with all responsive materials, there is an operational range for the relevant stimuli (e.g., temperature) outside of which the materials will not behave as designed (e.g., the robot will not bend when the temperature of the LCEs is so high that both have fully contracted). If the light is directly in front of the robot (Fig. 3F), then the two CNT-LCE strips contract equally, so the robot does not bend. The extension ratio (ε) of the robot is measured and shown in Fig. 3F.

Autonomous changes to trajectory in response to environmental inputs

Feet are added to the bottom of the robot to translate the cyclic inflation and deflation of the pneumatic actuator into locomotion. As shown in movie S2, the robot walks straight if no control modules are present.

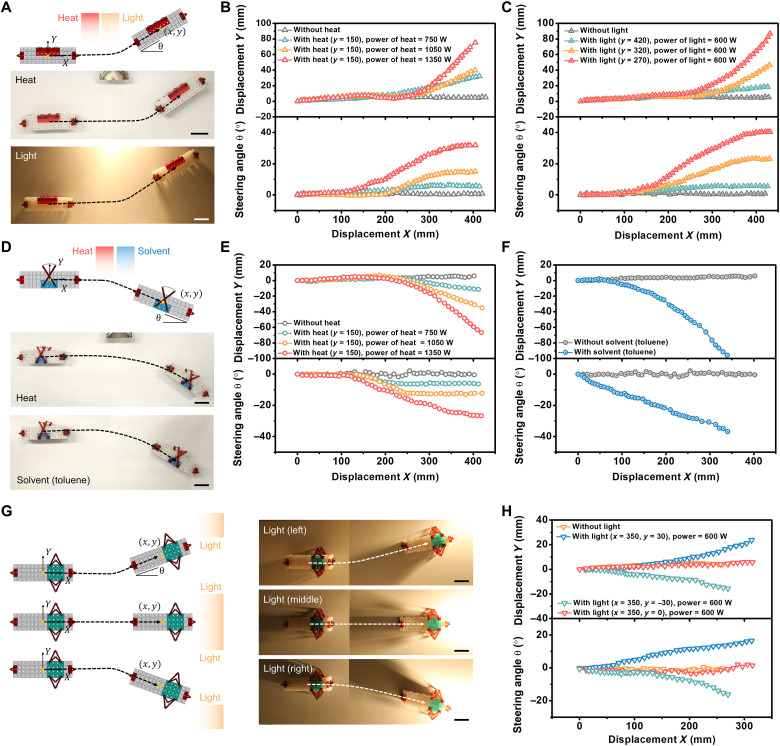
In Fig. 4, we show the effect of the control modules of Fig. 3 on the trajectory of the robot. First, we demonstrate how the robot can autonomously steer its trajectory closer to light or heat (Fig. 4A and movie S3) using the control module of Fig. 3C. When no appreciable heat or light is present in the local environment, the robot walks forward. However, if the control module receives a large flux of heat or light, then the CNT-LCE strip contracts, inhibiting the squares in contact with the module from opening when the pneumatic actuator inflates. The rest of the robot body can still expand, however, inducing bending. The trajectory of the robot therefore bends toward the stimulus (Fig. 4A). The trajectory of the robot is shown in Fig. 4 (B and C) as a function of the power of the heat source (Fig. 4B) and as a function of the distance between the robot and the light source (Fig. 4C). Since the CNT-LCE contracts more at higher temperatures, the bending angle of the robot is larger when the power is higher or the distance is smaller. To confirm the repeatability of the trajectories for a given set of conditions, we tested some trajectories up to 20 times with the same light conditions, finding minimal trajectory variations. The standard deviation of the trajectories in these trials was less than 5% of the body length of the robot (fig. S24).

Fig. 4. Autonomous changes to trajectory in response to environmental inputs.

(A) The schematic and experimental images show that the robot can autonomously steer its trajectory closer to light or heat. (B) The trajectories (displacement and steering angle) of the robot as a function of the power of the heat source. (C) The trajectories (displacement and steering angle) of the robot as a function of the distance y (in millimeter scale) between the light source and the initial trajectory of the robot. (D) The second type of control module causes the robot to autonomously steer away from a heat source or the solvent toluene. (E and F) The trajectories (displacement and steering angle) of the robot under different stimuli (heat or toluene). (G) The third type of control module causes the robot to autonomously steer directly toward a light source. (H) The trajectories (displacement and steering angle) of the robot in environments with different locations of the light source. Scale bars (A), (D), and (G), 5 cm.

As in Fig. 3, simply by changing the type of control module, we can cause the trajectory to bend away from the stimulus. Figure 4 (D to F) shows trajectories of the robot that occur when the control module of Fig. 3D is used instead of the module of Fig. 3C. This module inhibits the rotation of the squares on the side of the robot that is opposite to the stimuli. This causes the robot to autonomously steer its path away from stimuli (Fig. 4D and movie S4). These trajectory changes are quantified in Fig. 4 (E and F).

The third type of control module, introduced in Fig. 3 (E and F), allows the robot to steer itself directly toward a stimulus, as demonstrated in Fig. 4 (G and H) and movie S5.

Note that this same module also enables steering in dynamic environments, e.g., in which the intensity or location of the light sources is changing (fig. S25).

Last, we note that all of the control modules above have made use of LCEs. However, in principle, the LCEs in the control modules can be replaced with other responsive materials, such as hydrogels and PDMS, enabling analogous robot responses in the presence of water or other solvents, respectively (figs. S26 to S28). In this work, as a simple proof of concept, we made control modules with hydrogels and silicones instead of LCEs. These control modules were submerged in water (hydrogels) or nonpolar solvents (silicones) for 2 hours and 15 min, respectively, and then reattached to the robot body. As shown in fig. S26, the flexible strip generates tension due to the swelling of the materials, which prevents the opening of the kirigami. As a result, the kirigami bends when the actuator is inflated (figs. S27 and S28). We demonstrate this behavior in figs. S29 and S30. Given the large number of stimuli-responsive materials that have been developed, the control modules could respond to a large variety of other stimuli, including magnetic fields (22) and pH (60).

It is worth noting that the robot exhibits relatively slow locomotion speed (1 mm/s). This rate was chosen to accommodate the slow response time of the actuating materials that regulate the control modules. For example, at the millimeter to centimeter length scales of this design, the CNT-LCE composites actuate in response to light on the order of 100 s. Hence, at these length scales, the robot should move at a rate such that its immediate environment changes at comparable time scales. Whether or not this time scale is “fast enough” or “slow enough” depends on the application and the intrinsic time scale of the environment. The response time can be changed by patterning the responsive materials, or changing their length scale, potentially down to millisecond time scales (51). However, the response time is also coupled with the mechanical properties of the responsive materials. Reducing the length scale of the responsive materials may reduce the force that they can exert on the kirigami. This may, in turn, require that the compliance of the kirigami be structurally increased (e.g., via thinning of the hinges or of the kirigami itself) to maintain mechanical compatibility.

Embodying multistimuli-responsive logic via control modules

As shown above, the control modules are designed to produce mechanical constraints within the robot body, altering how it deforms and thereby its trajectory. The mutual interactions produced by multiple control modules throughout the body can be very complex. However, these interactions also offer a strategy for implementing more nuanced control objectives, despite the lack of electronics in these robots. The competing actions of multiple control units can be viewed as a computational event that is distributed throughout the robot body.

To demonstrate this behavior more concretely, we consider a simplified example in which control modules are only placed along the robot’s right or left side (near the center) and only heat or light are used as inputs. Since heat or light can be applied to either side, there are four total environmental inputs: heat applied to the left side (“input A”), light applied to the left side (“input B”), heat applied to the right side (“input C”), and light applied to the right side (“input D”). Boolean values of “1” or “0” for a given input indicate that the input is, or is not, present, respectively. We also define an “output” value, for which “0” indicates that the robot is moving forward along a straight trajectory, while output values of “1” and “−1” indicate that the robot is steering left or right, respectively.

With four boolean inputs, there are a total of 16 possible combinations of input values. The output associated with each combination of inputs is determined by the choice of control modules placed at the input sites. The aggregate effect of all control modules determines the map from the inputs to the outputs. These relationships can be summarized in “truth tables,” as shown, for example, in fig. S31.

As a first simple example, we configure the robot using only one control module (the module of Fig. 3C), placed on the left side of the robot. The complete truth table for this configuration (for all 16 combinations of inputs) is shown in fig. S31A. Heat and/or light can be sensed on the left side of the robot (e.g., inputs A and B are allowed to be either 0 or 1). However, since there is no control module on the right side of the robot, changing the values for inputs C and D has no effect on the robot. Hence, we can use an abbreviated truth table to fully define the response of the robot (see fig. S32). This configuration behaves as an “OR” operation. When the robot is exposed to heat or light from the left side (i.e., input A and/or input B are nonzero), the robot bends due to the contraction of the CNT-LCEs, causing it to steer left (fig. S33).

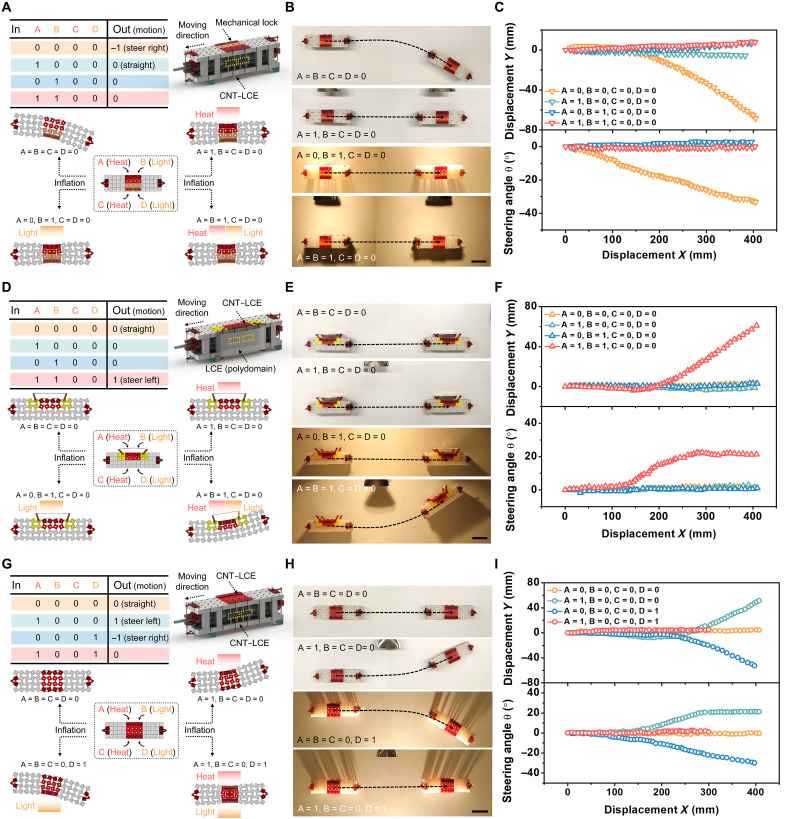
Next, we add a second control module to the robot, as shown in Fig. 5A. The new module is a passive control module that acts like a mechanical lock on the right side of the robot. It does not sense or respond to stimuli, but instead causes the robot to bend right by default when the pneumatic actuator inflates, even without environmental stimuli (i.e., the output is −1 even when the inputs A = B = C = D = 0). Consequently, the robot steers right when heat or light are below the threshold. The complete truth table for all possible inputs is shown in fig. S31B. However, as in the previous example, since the inputs on the right side are not sensed, the values of inputs C and D have no effect. The abbreviated truth table is shown in Fig. 5A and fig. S34. If the control module on the left side is exposed to heat and/or light (i.e., input A and/or input B are nonzero) the squares across from the lock are also inhibited from opening when the pneumatic actuator inflates. In this case, the mechanical constraints on the two sides cancel one another, causing the robot to remain straight when the pneumatic actuator is pressurized, giving a straight trajectory (Fig. 5, B and C, and movie S6). This configuration behaves as a “NOR” operation.

Fig. 5. Embodying distributed, multistimuli-responsive logic via interaction of multiple control modules.

Interactions of multiple control modules can be complex (see complete truth tables in fig. S31). Here are a few simplified examples: (A) The combination of a “mechanical lock” control module and the CNT-LCE module of Fig. 3C causes the robot’s steering to obey a NOR response. (B and C) Experimental images and trajectories, respectively, of the robot with different heat/light inputs. (D) In another example, a “mask” control module is used in conjunction with the CNT-LCE module of Fig. 3C to steer in accordance with an AND strategy [for the environment shown in (E)]. (E and F) Experimental images and trajectories, respectively, of the robot with different heat/light inputs. (G) In another example, two identical control modules (actuated by heat or light) are distributed symmetrically along the two sides of the robot body, which enable the robot to realize XOR response. (H and I) Experimental images and trajectories, respectively, of the robot with different heat/light inputs. Scale bars (B), (E), and (H), 5 cm.

More complex examples of mechanical logic can be achieved with other combinations of control modules. For example, the decision for the robot to turn can obey AND logic by adding a mask module (an opaque polydomain LCE) exterior to the CNT-LCE control module used in the previous examples, as shown in Fig. 5D and figs. S31C and S35. When the temperature is greater than 150°C, the mask layer (opaque polydomain LCE) becomes transparent (fig. S36), as demonstrated previously (61). If only heat is applied to the left side of the robot (i.e., inputs A = 1 and B = 0), the mask layer becomes transparent, but also blocks enough of the heat that the CNT-LCE module inside does not activate. Consequently, the robot walks forward along a straight trajectory (Fig. 5, E and F). The same thing occurs if only light is applied (A = 0 and B = 1), since the mask layer remains opaque. Only when heat and light are both present on the left side (A = B = 1) will the robot steer left (see Fig. 5, D to F, and movie S7), since the heat causes the mask module to become transparent, allowing the light to reach and activate the inner control module. As with all active materials, there is a particular time scale and intensity range that defines their operational relevance. In this case, we have to tune the distance between the robot and light source to prevent overheating from occurring too rapidly. Note, in this example, inputs C and D have no effect, since no control modules are present on the right side of the robot. However, if the two control units on the left were duplicated on the right side, the same AND logic with respect to inputs C and D would govern whether the robot steers right (and in the case in which all inputs A = B = C = D = 1, the two sides would cancel, allowing the robot to proceed straight ahead). Moreover, the AND response of Fig. 5 (D to F) can be made into a NAND response by adding a mechanical lock to the right side (as demonstrated in figs. S31D, S37, and S38). In this case, the robot will only move straight ahead if both heat and light are present on the left side, otherwise it will turn right.

As a final example, we consider using two of the CNT-LCE control modules of Fig. 3C, one on each side of the robot (Fig. 5G and fig. S39). The robot bends only when exactly one side of the robot is subjected to light or heat (for example, A = 1 and B = C = D = 0 or A = B = C = 0 and D = 1), causing the robot to steer left or right (Fig. 5, H and I). If the control modules on both sides are actuated (e.g., A = 1, B = C = 0, and D = 1), the two effects cancel, and the robot continues to move straight forward. The complete truth table for this system is shown in fig. S31E. See also movie S8.

We again note that all of the different behaviors described above were obtained using the same robot. Only the type and locations of the modular control units were varied.

Examples of autonomous trajectory changes in robots integrated with multiple control modules

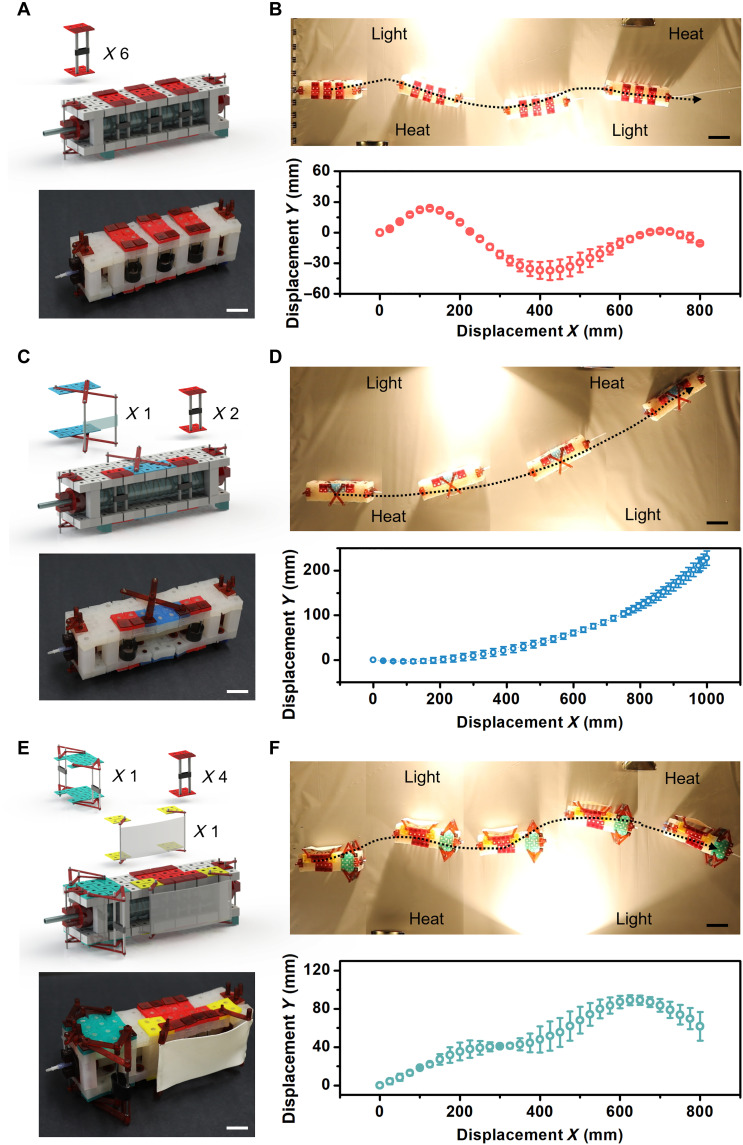
Last, we demonstrate autonomous trajectory changes of the electronics-free robot as it passes through a more complex environment. Light and heat sources are placed along both sides of the robot’s path. In the first example, we evenly distribute control modules (with CNT-LCE strips) throughout the soft body of the robot, as shown in Fig. 6A. This specific design causes the robot to be “attracted” by the heat and light sources. This results in a “zigzag” trajectory, as shown in Fig. 6B and movie S9. A different moving strategy can be achieved by rearranging the control modules, as shown in Fig. 6C. In this case, the control modules are only placed along one side of the robot, including modules that bend the trajectory toward stimuli (i.e., Fig. 3C) and a module that bends the trajectory away from stimuli (i.e., Fig. 3D). This design causes the robot to steer left whenever heat or light are encountered (Fig. 6D and movie S9). Next, we use three different modules to give the robot an AND response, as shown in Fig. 6E. These include control modules that bend the trajectory toward stimuli (i.e., Fig. 3C), a mask module (i.e., the polydomain LCE of Fig. 5D), and the module that causes the robot to steer directly toward stimuli (i.e., Fig. 3, E and F). When this configuration is used, the robot first moves toward the light, causing the body to steer left. Then, the robot moves straight forward, due to the effects of the mask module. As the robot begins to sense the light source to the right, the trajectory begins to turn right (see Fig. 6F and movie S9). The autonomous motion of the robot can be reprogrammed simply by changing the distribution and types of control modules in the kirigami robot body. The error bars in the trajectories of Fig. 6, (B, D, and F) are the standard deviations of the positions upon performing the experiments three times.

Fig. 6. Demonstration of repeatable autonomous trajectory changes for the robot configured with different control modules moving through environments with multiple stimuli.

(A, C, and E) show the robot configured with different modular control units. (B, D, and F) show experimental images and trajectories that result from these designs. Scale bars (A), (C), and (E) 2 cm. Scale bars (B), (D), and (F), 5 cm.

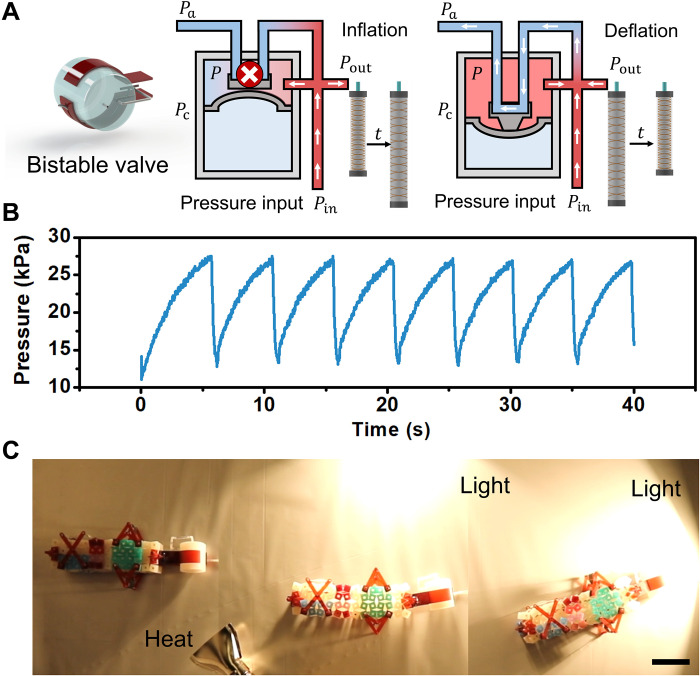
Last, we note that while the robot itself does not have onboard electronics, it is tethered to a pneumatic device that is electronically controlled. However, as has been previously demonstrated by others (42), the pneumatic controller can be eliminated by integrating a bistable valve with the robot (Fig. 7). When the membrane of the valve bends upward, it blocks the pneumatic tube inside the top chamber. As a result, the pressurized air flows into the actuator, inflating the pneumatic actuator. Once the pressure of the top chamber reaches a critical pressure P_c, the membrane snaps, the air tube in the top chamber is no longer blocked, and the pressurized air can flow out to the atmosphere, deflating the pneumatic actuator (Fig. 7A). This bistable valve thereby converts a constant pressure input to a periodically varying pressure output, providing the necessary sequential inflation-deflation of the pneumatic actuator (Fig. 7B). With the bistable valve and the control modules, this robot can autonomously change its trajectory in a complex manner without any electronics (Fig. 7C, figs. S40 and S41, and movie S10).

Fig. 7. The integration of a bistable valve with the autonomous robot.

(A) The working mechanism of the mechanical bistable valve. When the membrane bends upward, it blocks the pneumatic tube inside the top chamber. As a result, the pressurized air flows into the actuator, inflating the pneumatic actuator. Once the pressure of the top chamber reaches a critical pressure P_c, the membrane snaps, the air tube in the top chamber is no longer blocked, and the pressurized air can flow out to the atmosphere, deflating the pneumatic actuator. (B) The bistable valve translates a constant pressure input to a periodically varying pressure output (supplied to the pneumatic actuator). (C) Demonstration of autonomous motion in response to various light and heat sources. Scale bar (C), 5 cm.

DISCUSSION

In this work, we have shown how a kirigami-based soft robot can autonomously navigate through an environment using modular control units distributed throughout its body. These control modules can make use of different types of responsive materials, enabling the robot to sense and respond to stimuli such as light, heat, water, and solvents. Different control responses can be imparted to the robot simply by changing the positions and types of control modules. We also showed that simple computational capabilities (e.g., “turn toward heat, but only if light is also present”) can be embodied in the robot via the interactions of multiple control units. Last, by also incorporating a mechanical bistable valve, the robot can autonomously navigate without any electronic components. Previous work has demonstrated the use of a similar bistable valve to autonomously reverse the moving direction of a robot when it walks into a wall (42), a clear example of an autonomous interaction of a robot with its environment. In our work, we develop a collection of modular control units that enable the robot to sense and respond to multiple environmental stimuli (light, heat, water, and solvent). These control modules are interchangeable, providing a wide variety of robot-environment interaction inputs and programmable moving strategies. Our framework opens up a new strategy for working toward full autonomy in soft robotic systems.

The current version of the soft robot is tethered to an external pneumatic source. We note, however, that the robot could be made untethered, following strategies already outlined in the literature, especially since the robot only requires a constant pressure source thanks to the bistable valve. The robot could provide its own pneumatic source via a chemical reaction, such as hydrogen peroxide (39) or by carrying a small compressed gas source (42). Another current limitation of this robot is its large physical size (the squares in the kirigami are centimeter scale), which is the practical result of our current manufacturing technique. We note, however, that the mechanical response of the kirigami body and the basic control strategy (i.e., using variable mechanical constraints to manipulate that mechanical response) are scale independent. Hence, similar robots could, in principle, be scaled to smaller length scales using advanced manufacturing methods such as photolithography, two-photon polymerization, etc., which may broaden the application of the proposed control strategy to biomedical engineering and other areas making novel use of small soft robots. Future work can also investigate the use of the proposed control strategy under a broader range of environmental stimuli. In addition, we note that most of the analysis, modeling, and experimentation assumed that the robot exists in a two-dimensional (2D) world (i.e., stimuli are in the same plane as the robot body). However, in principle, there is no such restriction, and 3D effects could certainly be included in the future. For example, fig. S42 illustrates one mechanism that could translate out-of-plane phenomena into trajectory changes of the robot. Last, although we only demonstrate control of trajectory in this work, such electronics-free sense-control-act response loops could be readily adopted to change the function, morphology, or other behaviors of robots.

MATERIALS AND METHODS

Fabrication of the pneumatic actuator

The fabrication process of the pneumatic actuator is based on (62) (see fig. S43). Briefly, we design a mold using SolidWorks and print it using a MakerGear M3 3D printer. The uncured silicone precursor (Ecoflex 30, Smooth-On Inc.) is poured into the mold and cured for 24 hours. This results in a silicone elastomer tube with a helix concave fiber groove. Then, we wrap a kevlar fiber following the predesigned helix trace on the tube to constrain the radial expansion of the actuator resulting in axial extension. The two ends of the kevlar fiber are fixed to the silicone using Sil-poxy (Smooth-On Inc.). Using this approach, the fiber angle can be precisely controlled. The total height of the helix is 120 mm, the pitch is 8 mm, and the diameter is 19 mm. This corresponds to a total length of 1806 mm for the kevlar fiber. After that, the silicone tube (wound with fiber) is reinserted into the mold. Additional uncured precursor is injected into the mold to seal the kevlar fiber. After 24 hours, the silicone tube is taken out and sealed with two caps using Sil-poxy. Last, a fitting is inserted into the cap, which is connected to the external pneumatic source.

Fabrication of kirigami platform

As shown in fig. S44, the uncured silicone precursor (Dragonskin 10, Smooth-On, Inc.) is poured into the 3D-printed mold. Then, we ensure all excess silicone is removed. After 24 hours, the cured specimens are taken out and prepared for further use.

Assembly of the electronics-free soft autonomous robot

The entire structure of the soft robot is shown in fig. S45. The pneumatic actuator is sandwiched between two layers of kirigami. The vertical columns (made from silicone) are placed at both sides of the pneumatic actuator to constrain the actuator during extension. For the connection between the kirigami and the pneumatic actuator, 3D printed parts (R11, EnvisionTec) are designed and fabricated (fig. S45). All the squares can freely rotate and open when pressurized air is applied to the pneumatic actuator.

Fabrication of the control modules

The control modules include silicones, responsive materials (LCEs, hydrogels, and/or PDMS), rigid rods, and 3D-printed parts. The silicone layer of the kirigami is fabricated by pouring the mixture of silicone precursor and dye (Ecoflex 30, Smooth-On Inc.) into the mold. The silicone is peeled off from the mold after 24 hours. For the 3D-printed part, we use a digital light processing printer (EnvisionTec) to fabricate the rigid parts. The detailed fabrication and assembly of each control module can be found in figs. S46 to S51. The control modules can be repeatedly switched on and off by suitable inputs in the environment, with no discernible change in performance (figs. S22 and S24). The practical maximum operational temperature of the control module is set to 150°C. Further increasing the temperature will cause softening of the 3D-printed parts. Other materials could be substituted to increase this operational temperature, if that were necessary for a particular application.

Mechanical integration of the control modules with the soft autonomous robot

Integration of the control modules with the soft robot is shown in fig. S52 and movie S1. The top and bottom layers of the control module (blue color in fig. S52) are attached to the kirigami body of the robot. Eight cylindrical pins (diameter, 4 mm) are used to connect the control module and kirigami robot. The process can be easily performed in reverse to remove a module.

Fabrication of the mechanical bistable valve

The mechanical bistable valve receives a constant pressure as input and outputs a periodic pressure variation due to an internal instability, as reported previously (43). We fabricate the bistable valve based on (42). We pour the silicone precursor (Dragonskin 10, Smooth-On Inc.) into a 3D-printed mold and cure. Air tubes are glued to the membrane in the middle of the valve using Sil-poxy (Smooth-On Inc.). The cap of the valve is subsequently glued to the main body of the bistable valve. Last, we connect the air pathway.

The measurement of the elongation, bending angle, and trajectory of the soft robot

The pneumatic actuator of the robot is pressurized using a custom fluid control system to precisely control the pressure (fig. S9). To measure the elongation ε and bending angle α of the robot, we use a digital camera (Canon 80D) to capture images of the robot during its inflation. We characterized the bending angle of the robot at each pressure by analyzing the images, using ImageJ. The results are shown in Fig. 3.

To measure the trajectory of the soft robot, we use a digital camera to record the video. We extract the video frames images from the video after one cycle. We track the center point of the robot to keep track of its location (using ImageJ). The results are shown in Figs. 4 to 6.

Synthesis of LCEs

1,4-Bis-[4-(3-acryloyloxypropyloxy)benzoyloxy]-2-methylbenzene (RM257) (Wilshire company, 95%), (2-hydroxyethoxy)-2-methylpropiophenone (HHMP; Sigma-Aldrich, 98%), 2,2′-(ethylenedioxy) diethanethiol (EDDET; Sigma-Aldrich, 95%), pentaerythritol tetrakis (3-mercaptopropionate) (PETMP; Sigma-Aldrich, 95%), dipropylamine (DPA; Sigma-Aldrich, 98%), and multiwalled CNTs (MWCNT, Sigma-Aldrich, >98%) are used as received without purification. We use a glass mold and VHB (3M, 4905 and 4910) as spacer for controlling the thickness of the LCE sample.

We prepare the LCE film following (63) with a few modifications. Ten grams of liquid crystal mesogen RM257 and 0.078-g of photoinitiator HHMP are added to toluene. The mixture is dissolved in an oven at 85°C. A 0.03-g MWCNTs can also be added into the mixture to make the LCEs light-responsive. A 1.9017-g chain extender EDDET, 1.52-g cross-linker PETMP, and 0.0324-g catalyst DPA are added to the mixture. The mixture is stirred and degassed and poured into a glass mold (1 mm thickness). After 24 hours of curing, the solvent (toluene) is evaporated from the LCE in an oven set to 85°C for 12 hours. This results in a loosely cross-linked, polydomain LCE thin film. To align and fix the alignment of the liquid crystal mesogen, the loosely cross-linked LCE is stretched to λ = 2 and exposed to ultraviolet (UV) irradiation for 1 hour. This results in a monodomain LCE. LCE strips can be made by cutting the monodomain LCE sheet. The actuation performance of the LCE is shown in fig. S15. If a polydomain LCE is desired (e.g., as in the mask control module), then it is placed under the UV light for 1 hour without stretching, finishing the second cross-linking step.

Synthesis of hydrogels

Acrylamide (>99%; Arcos, USA), alginate (FMC Biopolymer, LF 10/60, USA), N,N′ -methylenebis (acrylamide) (MBAA) (Sigma-Aldrich, USA), ammonium persulfate (>98%; Sigma-Aldrich, USA), N,N,N′,N′-tetramethylethylenediamine (TEMED) (>99%; Sigma-Aldrich, USA), and calcium sulfate dihydrate (98%; Sigma Aldrich, USA) are used without further purification.

The double network hydrogel is synthesized following (64) with some modification (65). An 8-g acrylamide, 1-g alginate, 0.0048-g cross-linker MBAA, and 0.02-g thermal initiator are dissolved into 51 g of deionized water. The mixture is stirred for 2 hours until all the components are fully dissolved. The mixture is marked as solution 1. Then, 0.02-g initiator accelerator TEMED and 0.1328-g ionic cross-linker calcium sulfate dihydrate are dissolved into 5 g of deionized water. The mixture is sonicated for 2 min and marked as solution 2. After that, solution 1 and solution 2 are mixed and poured into a 3D-printed polylactic acid (PLA) mold with dimensions 5 mm by 4 mm by 10 mm. The specimen is left at room temperature (24°C) for 24 hours, covered by a glass slide, to polymerize the gel.

The measurement of the actuation strain of the CNT-LCE and LCE film

A hot plate is used to measure the actuation strain of the CNT-LCE and LCE film at different temperatures. At each temperature, we wait 3 min to ensure the length of the LCEs has reached an equilibrium. The length is measured by taking an optical image (Canon 80D) then using ImageJ. The results of the actuation strain are shown in fig. S15.

The response speed of the CNT-LCE film

The actuation strain of the CNT-LCE film versus time is shown in fig. S18A for different light intensities. In the experiment, we change the distance between the light source and the CNT-LCE film. When the light is switched on, the actuation strain of the CNT-LCE gradually increases, eventually reaching a steady-state plateau value after 100 s. After the light is switched off, the actuation strain drops to 0 within 160 s. During these tests, we also measure the maximum surface temperature of the CNT-LCE film using an infrared (IR) camera (FLIR E54), as shown in fig. S18B. When the light is turned on, the surface temperature increases, and reaches steady state within 100 s. After the light is switched off, the temperature gradually decreases to room temperature (24°C) within 160 s.

The mechanical properties of the CNT-LCE and LCE film at different temperatures

The force-displacement relationship of the CNT-LCE and LCE films are measured using an Instron Model 5564. At room temperature (24°C), the sample size of the films is 45 mm by 15 mm by 1 mm. In the experiment, we use light and heat to increase the temperature of the films. The IR camera (FLIR E54) is used to capture the surface temperature. Stretching is begun once the temperature reaches the intended steady-state target temperature.

The force-displacement relationship of the CNT-LCE film is shown in fig. S19A. After the temperature is sufficiently increased, the material undergoes a nematic-isotropic phase transition. At this point, the CNT-LCE become softer, causing the maximum force to decrease from 50 to 10 N. Figure S19B shows the stress-strain relationship of the CNT-LCE film at different temperatures. Both the mechanical strength and the stretchability of the CNT-LCE decreases as a function of temperature. The mechanical strength decreases from 3 to 0.4 MPa when the temperature is increased from 24° to 145°C, while the stretchability decreases from 62 to 28% when the temperature is increased from 24° to 145°C. Similarly, the force-displacement and stress-strain relationship of the LCE film is shown in fig. S20.

Characterization of the force-strain relationship of the kirigami

The force-strain relationship of the kirigami is measured using an Instron Model 5564. The loading speed is set to 1 mm/s. The force-strain relationships are shown for different hinge thicknesses in fig. S10. The initial length of one set of squares is 20 mm.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S52

Legends for movies S1 to S10

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S10