Abstract
Polygenic scores (PGSs) are individual-level measures that aggregate the genome-wide genetic predisposition to a given trait. As PGS have predominantly been developed using European-ancestry samples, trait prediction using such European ancestry-derived PGS is less accurate in non-European ancestry individuals. Although there has been recent progress in combining multiple PGS trained on distinct populations, the problem of how to maximize performance given a multiple-ancestry cohort is largely unexplored. Here, we investigate the effect of sample size and ancestry composition on PGS performance for fifteen traits in UK Biobank. For some traits, PGS estimated using a relatively small African-ancestry training set outperformed, on an African-ancestry test set, PGS estimated using a much larger European-ancestry only training set. We observe similar, but not identical, results when considering other minority-ancestry groups within UK Biobank. Our results emphasise the importance of targeted data collection from underrepresented groups in order to address existing disparities in PGS performance.
Subject terms: Genomics, Predictive markers, Genetic variation
There are challenges with transferring genetic risk scores from ancestry in which they were generated to another. Here, the authors investigate the use of multi-ancestry versus single-ancestry training sets to construct polygenic scores and find that the optimal strategy varies across traits.
Introduction
Polygenic scores (PGS) are composite, quantitative measures that aim to predict complex traits from genetic data. As well as providing insights into the genetic architecture of complex traits, PGS have considerable clinical potential for screening and prevention strategies1,2. Largely driven by significant increases in sample sizes, the predictive utility of PGS has improved substantially in recent years for a variety of traits3, including cardiovascular disease4, breast cancer5, and type I diabetes6.
These improvements, however, have largely been limited to populations of European ancestry7–9, reflecting the lack of diversity in genomic samples collected to date9. Moreover, predictive performance decreases with genetic distance from the training population10–12. The lack of transferability of PGS across ancestries may be due to a number of factors, including population differences in allele frequencies and linkage disequilibrium (LD)9,11. While there is some evidence that common causal variants have similar effects across ancestries9,13, other studies have suggested that the underlying variant effects may in fact differ across ancestries14–16, which may be due to gene-by-gene or gene-by-environment (GxE) interactions17,18. In addition, GxE interactions for people of African ancestry may be different between those living in the UK and those living in South Africa, say. This lack of transferability raises one of the most important technical and ethical challenges in the clinical utility and applications of PGS due to their potential to exacerbate health inequalities9.
There are major, ongoing initiatives to collect genomic data from traditionally under-represented groups, such H3Africa19, that aim to address the lack of global genetic diversity in research data. However, it may take many years to collect sufficient data to reduce the disparities in PGS performance. Statistical methods may provide an alternative, short-term, cost-effective and complementary potential solution to mitigate against the negative effects of the lack of diversity in genomic datasets, by using modelling techniques to make use of all the existing data available, while allowing for some differences between groups.
There has been a growing interest in statistical methods to improve the transferability of PGS, which have thus far focused on GWAS-derived PGS, i.e. PGS based on summary statistics from a genome-wide association study (GWAS). These integrate results from GWAS trained on distinct populations at different stages of the PGS estimation. For example, Grinde et al. use European GWAS results to select variants, and then estimate the variant weights using the non-European GWAS results20. Márquez-Luna et al. propose a ‘multi-ethnic’ PGS by combining scores trained separately on different populations21. Weissbrod et al. expand on this approach by further leveraging functionally informed fine-mapping to estimate the PGS weights22. In a related approach, Ruan et al. incorporate LD information to directly estimate effect sizes using GWAS results from two or more populations23. To account for admixture, Cavazos & Witte propose local ancestry weighting to construct individualised PGS24. These efforts have yielded promising improvements in PGS performance, though there remains a significant gap in predictive accuracy between European and non European target populations.
Here, we investigate the use of multiple-ancestry datasets, such as UK Biobank25, to estimate PGS for a range of anthropometric, blood-sample, and disease traits, with the explicit objective of improving predictive accuracy for under-represented ancestries. Specifically, we ask whether there are consistent optimal strategies for borrowing information across ancestry groups to maximize prediction accuracy in groups that have small sample sizes in available resources. For each trait, we construct training sets with varying numbers of individuals from each ancestry to assess the effect of sample size and composition on PGS accuracy, using both simulated data and data from UK Biobank25. Moreover, and to counteract the imbalance of ancestries in a multiple-ancestry training set, we investigate the use of an importance reweighting approach that places more weight on underrepresented ancestries during training. Importance reweighting is a standard statistical technique used in survey sampling that aims to account for differences between the sampling population and the population of interest26. Given the availability of individual-level information in biobanks, we estimate PGS using regularised regression applied to full genotype and covariate data (as opposed to genome-wide association summary statistics) to avoid introducing additional artefacts into our analysis via the reliance on assumptions about genotype and covariate correlation structure (including LD) and GWAS methodology.
Our results show that the impact of sample size and composition on predictive performance is highly variable across traits. For some traits, polygenic scores estimated using a relatively small number of minority-ancestry individuals outperformed on a minority-ancestry test set scores estimated using a much larger number of European-ancestry individuals. Moreover, adding European-ancestry individuals to the training set did not always improve performance and in some cases even led to poorer performance. Although importance weighting yields moderate improvement in performance for some traits, we find that sample size is a much more prominent factor, highlighting the limitations of statistical corrections and the importance of collecting more data from a more diverse range of participants.
Results
Overview of methods
To investigate the effect of sample size and ancestry composition on polygenic score performance, we used both simulated data and real data from UK Biobank25. We initially focus on PGS strategy for African-ancestry groups, given that predictive accuracy using European-ancestry PGS is consistently worst out of all the major ancestry groups9,12. Simulated data was generated using the simulation engine msprime27 in the standard library of population genetic simulation models stdpopsim v0.1.228 to generate African-ancestry and European-ancestry genotypes. We also considered a range of quantitative and binary traits from UK Biobank, using imputed genotypes along with inferred genetic ancestry labels made available by the Pan-UKBB initiative29.
For both the simulated and real data, we constructed a range of training sets controlling the number of European-ancestry and minority-ancestry individuals. We considered three types of training sets: a single-ancestry set consisting only of European-ancestry individuals, a single-ancestry set consisting of minority-ancestry individuals, and a dual-ancestry set consisting of both European-ancestry and minority-ancestry individuals. We denote a PGS trained on a XYZ-ancestry training set as PGSXYZ—for example PGSEUR. Similarly, we refer to a PGS trained on a dual-ancestry (respectively minority-ancestry) training set as PGSdual (respectively PGSmin).
For each training set, we estimated PGS using L1-regularised regression, also known as the LASSO30, which has previously been used in the context of genetic risk prediction (see for example31–34). To account for the imbalance in sample size numbers in the dual-ancestry training sets, we also estimated PGS using an importance reweighted LASSO, upweighting the non-European-ancestry individuals. Following Martin et al.9, we assessed the predictive performance of a PGS using partial r2 relative to a covariate-only model. See Fig. 1 for a schematic diagram of the methods used and “Methods” for full details.
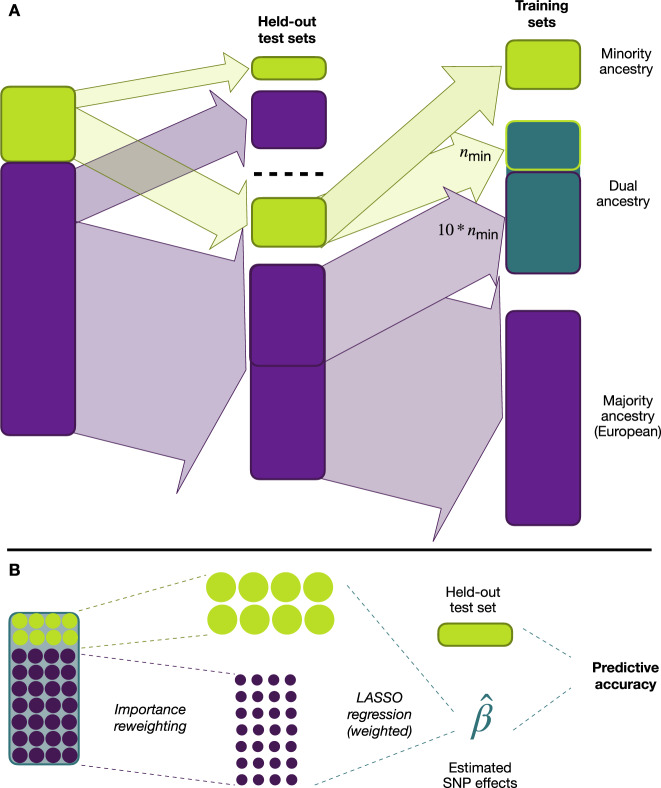
Fig. 1. Overview of methods.
A To evaluate the different PGSs, we performed various splits of the available data. Firstly, we held out test sets of 20% of individuals in each ancestry group. From the remaining 80%, we constructed three types of training sets: a single-ancestry set consisting only of European-ancestry individuals (purple block), a single-ancestry set consisting of non-European-ancestry individuals (yellow block), and a dual-ancestry set consisting of both European-ancestry and non-European-ancestry individuals (blue block). For each training set, we used another 20% of the data to select the regularisation parameter in the LASSO. B For the dual-ancestry training set, we used an importance weighted LASSO, assigning higher weights to individuals in the minority-ancestry group. See Methods for full details.
Single-ancestry PGS can outperform dual-ancestry PGS despite being trained on fewer individuals
We first set out to evaluate the relative performance of single-ancestry PGS versus dual-ancestry PGS through simulation. An important factor in the lack of transferability of PGS across ancestries is the difference in causal effect sizes11, with the correlation of causal effect sizes between ancestry groups, ρ, has been estimated to be significantly less than one across a range of common traits15,16. We simulated traits by randomly selecting p0 = 100 SNPs to be causal and then generating effect sizes for these SNPs such that that overall heritability across the entire population was h2 = 0.3. To assess the impact of differences in causal effect sizes on the relative predictive performance of PGS strategies, we varied the trans-ancestry causal effect correlation, ρ = 0.5, 0.6, …, 1.0, generating 10 quantitative traits for each value. We assume that all causal variants are genotyped, thus avoiding any differences in PGS accuracy that may arise from imperfect tagging11. We note that in practice imputation does not fully address the issue of imperfect tagging, due to differences in imputation quality across ancestry groups7,9.
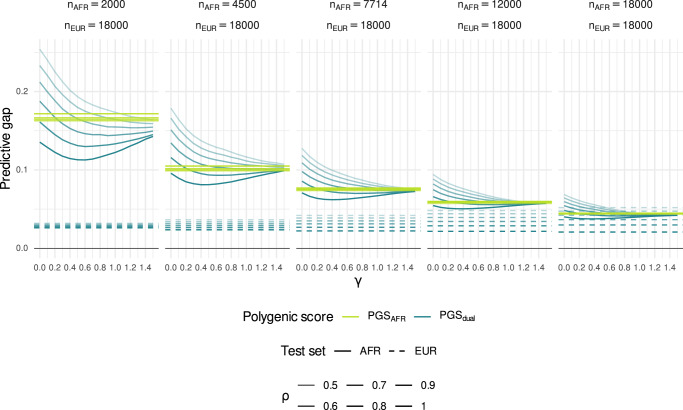
For each trait we created five African-ancestry training sets with nAFR = 2000, 4500, 7714, 12,000, 18,000 African-ancestry individuals. We also created five dual-ancestry training sets made up of the corresponding African-ancestry training set supplemented with nEUR = 18,000 European-ancestry individuals. To obtain PGS from the African-ancestry training sets, we used unweighted LASSO regression, while for the dual-ancestry training sets, we used the importance reweighted LASSO with γ = 0, 0.1, …, 1.5. The case γ = 0 corresponds to no reweighting, that is, the standard LASSO. The case γ = 1 corresponds to inverse proportion reweighting, so that in total, African-ancestry individuals and European-ancestry individuals have equal weight. Note that the African-ancestry training set is equivalent to the limiting case γ → ∞ whereby zero weight is placed on European-ancestry individuals. We quantified predictive performance of a PGS for a given ancestry group in terms of the predictive gap: the difference between variance explained by the PGS, r2, and SNP heritability h2 (the maximal variance explained by any PGS). See “Simulation study” for full details.
For both PGSAFR and PGSdual, the predictive gap for African-ancestry individuals decreased substantially as the number of African-ancestry individuals in the training sets increased (Fig. 2). For example, when nAFR = 2000 and the correlation between genetic effects ρ was 0.7, the mean predictive gap of the unweighted PGSdual (γ = 0) was just over 0.21 for the African-ancestry test sets, compared to 0.03 for the European-ancestry test sets. While the performance on Europeans did not change markedly as the number of African-ancestry training set individuals increased, the African-ancestry predictive gap fell to ~0.11 and 0.06 when nAFR = 7 714 and nAFR = 18,000 respectively. As expected, the discrepancy between the two ancestry groups decreased as the correlation ρ between the ancestry-specific genetic effects increased.
Fig. 2. Simulation study: predictive gap against number of African-ancestry individuals in training set.
Each panel corresponds to a different number of African-ancestry training set individuals from nAFR = 2000 to nAFR = 18,000. The training sets for PGSdual (blue lines) consisted of the corresponding African-ancestry training set for PGSAFR (yellow lines), along with nEUR = 18,000 European-ancestry individuals. Each line represents the mean predictive gap across 50 repetitions. The horizontal dashed lines correspond to the predictive gap for European-ancestry (EUR) test sets based on an unweighted LASSO, while the solid lines correspond to the predictive gap for African-ancestry (AFR) test sets. The parameter γ corresponds to the degree of reweighting used in the reweighted LASSO for PGSdual. The correlation of genetic effects between ancestries ρ was varied from 0.5 (lighter lines) to 1 (darker lines).
In the absence of reweighting (γ = 0), PGSAFR generally outperformed PGSdual, despite the latter being trained on more individuals—the dual-ancestry training sets consist of the African-ancestry training sets along with 18,000 European-ancestry individuals. This was particularly evident when the correlation between ancestry-specific genetic effects was lower (ρ = 0.5).
Importance reweighting generally had a positive impact on predictive performance, reducing the difference between PGSAFR and PGSdual. When the number of African-ancestry training individuals was low (nAFR = 2000), the importance-reweighted PGSdual outperformed PGSAFR when the correlation between ancestry-specific genetic effects was relatively high (ρ ≥ 0.7). When ρ = 0.7, the relative amount of improvement with reweighting was stable as nAFR increased: for nAFR = 2000, the predictive gap was reduced by 27% (from 0.21 at γ = 0, to 0.15 at γ = 1.4), while for nAFR = 18,000, the predictive gap was reduced by 29% (from 0.060 at γ = 0, to 0.042 at γ = 1.4). In contrast, when ρ = 1, the relative amount of improvement with reweighting was decreased as nAFR increased: for nAFR = 2000, the predictive gap was reduced by 16% (from 0.14 at γ = 0, to 0.11 at γ = 0.5), while for nAFR = 18,000, the predictive gap was only reduced by 7% (from 0.040 at γ = 0, to 0.038 at γ = 0.4). We highlight that importance reweighting reduced the predictive gap even when the effect sizes were the same across ancestries (ρ = 1), indicating that the procedure can partially correct for ancestry-specific differences in allele frequencies and LD structure.
The effect on predictive performance depended on the degree of reweighting, quantified by γ. As γ increased from 0 to 1.5, the predictive gap typically decreased. When the correlation between ancestry-specific genetic effects was high (ρ ≥ 0.9) and the number of African-ancestry samples low (nAFR = 2000), the predictive gap increased again for larger values of γ. This reflects a crucial trade-off of importance reweighting in this context: while the bias of African-ancestry genetic effect estimates may be lower with more reweighting, the increased variance of the weights results in a lower effective sample size. The effect of reweighting was relatively small compared to the effect of increased sample size. For nAFR = 2000 and ρ = 0.7, reweighting reduced the predictive gap from 0.21 to 0.15. The same improvement for the unweighted PGSdual was seen when increasing the number of African-ancestry individuals to nAFR = 4500, though we note that the PGSAFR with nAFR = 4500 had an even lower predictive gap of 0.10.
To investigate the impact of different genetic architectures on these results, we performed supplementary studies varying the heritability h2 = 0.1, 0.3, 0.5, and the polygenicity (i.e. number of causal SNPs) p0 = 10, 100, 1000 (Supplementary Figs. 1 and 2 respectively). We observed a similar pattern of results, with importance reweighting having a positive impact on predictive performance when the number of African-ancestry training individuals was low. For a fixed genetic correlation ρ = 0.8, the impact of reweighting was generally larger when heritability was high, and when the number of causal SNPs was lower. In particular, we note that the impact of reweighting was minimal when h2 = 0.1. This is likely a reflection of the LASSO’s reduced ability to estimate small effect sizes as opposed to large effect sizes.
This simulation study illustrates the relative performance of PGSAFR and PGSdual as a function of (i) the number of minority-ancestry individuals in the respective training sets and (ii) the correlation of genetic effects between ancestries. For both PGSAFR and PGSdual, the between-ancestry disparity in predictive performance decreased as the number of minority-ancestry individuals in the training set increased. Despite being trained on fewer individuals, the PGSAFR tended to outperform PGSdual, particularly when the correlation between ancestry-specific genetic effects was low. Importance reweighting generally reduced the predictive gap of PGSdual, especially when the sample size imbalance between ancestries was high. As this imbalance decreased, however, the reweighted PGSdual did not outperform PGSAFR.
Adding individuals from one ancestry does not always improve PGS performance for a different ancestry
Next, we sought to examine whether, even without reweighting, prediction performance in an underrepresented ancestry group can be boosted by including individuals from a different ancestry among the training samples. To do so, we used data from UK Biobank, estimating a range of PGS based on varying numbers of training individuals for a variety of traits (Table 1; see Methods for a description of how the traits were selected). In this analysis we focused on African-ancestry and European-ancestry individuals, where genetic ancestry labels were taken from Pan-UKBB. Note that the number of individuals from each ancestry with non-missing trait values varied across traits (see Table 1). For example, there are 6178 African-ancestry individuals and 361,699 European-ancestry individuals with non-missing data for height, compared to 5748 African-ancestry individuals and 345,862 European-ancestry individuals with non-missing data for high light scatter reticulocyte count.
Table 1.
Number of individuals with non-missing trait value in UK Biobank by genetic ancestry group
| Ancestry | Trait | Total | Cases | h2 |
|---|---|---|---|---|
| AFR | Height | 6178 | 0.4603 | |
| AMR | Height | 981 | ||
| CSA | Height | 8082 | 0.5709 | |
| EAS | Height | 2689 | 0.4415 | |
| EUR | Height | 361699 | ||
| MID | Height | 1543 | ||
| AFR | Mean corpuscular volume (MCV) | 5912 | 0.4465 | |
| AMR | Mean corpuscular volume (MCV) | 958 | 0.8142 | |
| CSA | Mean corpuscular volume (MCV) | 7956 | 0.3716 | |
| EAS | Mean corpuscular volume (MCV) | 2622 | 0.2414 | |
| EUR | Mean corpuscular volume (MCV) | 351672 | 0.1215 | |
| MID | Mean corpuscular volume (MCV) | 1513 | 0.7393 | |
| AFR | Asthma | 6257 | 741 | 0.0255 |
| AMR | Asthma | 989 | 106 | 0.0610 |
| CSA | Asthma | 8285 | 1017 | 0.0340 |
| EAS | Asthma | 2700 | 236 | 0.0170 |
| EUR | Asthma | 362511 | 42248 | 0.0748 |
| MID | Asthma | 1567 | 174 | 0.0301 |
| AFR | Female genital prolapse (FGP) | 3665 | 93 | 0.1222 |
| AMR | Female genital prolapse (FGP) | 641 | 27 | |
| CSA | Female genital prolapse (FGP) | 3793 | 170 | |
| EAS | Female genital prolapse (FGP) | 1786 | 31 | |
| EUR | Female genital prolapse (FGP) | 194734 | 11043 | 0.0675 |
| MID | Female genital prolapse (FGP) | 662 | 33 | |
| AFR | Body mass index (BMI) | 6168 | 0.3838 | |
| EUR | Body mass index (BMI) | 361306 | 0.1090 | |
| AFR | Eosinophill percentage | 5893 | 0.0739 | |
| EUR | Eosinophill percentage | 351038 | 0.0958 | |
| AFR | Erythrocyte distribution width | 5912 | 0.1331 | |
| EUR | Erythrocyte distribution width | 351672 | 0.0936 | |
| AFR | Lymphocyte count | 5893 | 0.1896 | |
| EUR | Lymphocyte count | 351033 | 0.0962 | |
| AFR | Monocyte count | 5893 | 0.2451 | |
| EUR | Monocyte count | 351033 | 0.1105 | |
| AFR | Mean platelet volume (MPV) | 5912 | 0.3315 | |
| EUR | Mean platelet volume (MPV) | 351669 | 0.2062 | |
| AFR | Platelet crit | 5912 | 0.2090 | |
| EUR | Platelet crit | 351670 | 0.1298 | |
| AFR | High light scatter reticulocyte count | 5748 | 0.3758 | |
| EUR | High light scatter reticulocyte count | 345862 | 0.0967 | |
| AFR | Atrial fibrillation (AFib) | 6257 | 125 | 0.0797 |
| EUR | Atrial fibrillation (AFib) | 362511 | 16476 | 0.0880 |
| AFR | Diverticular disease of the intestine (DDI) | 6257 | 285 | 0.0247 |
| EUR | Diverticular disease of the intestine (DDI) | 362511 | 30413 | 0.0615 |
| AFR | Hypothyroidism | 6257 | 124 | 0.0308 |
| EUR | Hypothyroidism | 362511 | 17496 | 0.1243 |
First, we held the number of European-ancestry individuals fixed, and constructed six training sets by varying the number of African-ancestry individuals from 0% to 80% of the total number of African-ancestry individuals with non-missing data for the trait in question. The number of European-ancestry individuals was chosen such that the largest training set had a 90-10 split between European- and African-ancestry individuals. Considering height again as an example, this corresponded to keeping the number of European-ancestry individuals fixed at 44,487 and varying the number of African-ancestry individuals from 0 to 4 942. For each training set, we used the unweighted LASSO to generate PGSs, and evaluated predictive performance in terms of variance explained on held-out test sets for each ancestry.
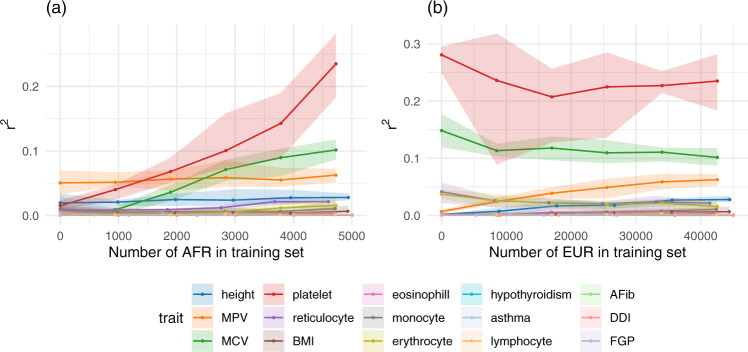
The predictive performance on African-ancestry individuals increased for five traits: height, mean corpuscular volume (MCV), female genital prolapse (FGP), high light scatter reticulocyte count (reticulocyte), and platelet crit (platelet) (Fig. 3a). For the remainder of the traits, predictive performance stayed largely stable.
Fig. 3. Predictive performance for African-ancestry individuals against sample size for 15 traits in UK Biobank.
a We fixed the number of European-ancestry (EUR) individuals in the training set at ~50,000 (26,388 for female genital prolapse (FGP)) and varied the number of African-ancestry (AFR) individuals from 0 to ~4700 (2900). The predictive performance, evaluated in terms of partial r2, on African-ancestry individuals increased markedly for mean corpuscular volume (MCV) and platelet crit; and stayed largely stable (or increased slightly) for the remainder. b Here, we instead fixed the number of African-ancestry individuals in the training set at ~4700 (2900 for FGP) for each trait and varied the number of European-ancestry individuals so that the proportion of European-ancestry individuals in the training set ranged from 0% to 90%. The effect on performance on African-ancestry individuals again varied by trait, showing a clear improvement for MPV and height, and a moderate decrease for MCV. Error bars correspond to the range across five cross-validation rounds of training set construction and PGS estimation. Phenotype acronyms: mean platelet volume (MPV), mean corpuscular volume (MCV), body mass index (BMI), atrial fibrillation (AFib), diverticular disease of the intestine (DDI), female genital prolapse (FGP).
Next, we performed complementary analyses in which we held the number of African-ancestry individuals fixed at 80% of the total number of African-ancestry individuals with non-missing data for the trait in question. We again constructed six training sets, now varying the number of European-ancestry individuals so that the proportion of European-ancestry individuals in the training set ranged from 0% to 90%.
Predictive performance on African-ancestry individuals only increased markedly for height and mean platelet volume (MPV), with the improvement for MPV appearing to tail off between the two largest training sets. For three traits (mean corpuscular volume, reticulocyte count, erythrocyte distribution width), predictive performance worsened as European-ancestry individuals were added to the training set. For the remainder of the traits, predictive performance stayed mostly constant.
These results demonstrate that, for some traits, the potential for increasing prediction performance by including samples from a different population can be limited. They also highlight substantial between-trait heterogeneity in response, suggestive of major differences in genetic architecture.
Optimal ancestry composition of training sets varies among traits in UK Biobank
Next, we set out to assess the relative performance of single- versus dual-ancestry PGS in empirical data by considering the UK Biobank traits analysed in the previous section. We first considered three training sets: (i) a European-ancestry training set of ~300,000 European-ancestry individuals, (ii) a African-ancestry training set of ~5000 African-ancestry individuals, and (iii) a dual-ancestry training set made up of the African-ancestry training set combined with European-ancestry individuals so that the proportion of African-ancestry individuals was 10%. For the latter, we opted for this 90-10 split—thus not using all the available European-ancestry individuals—following the previous analysis that indicated the limited benefit to African-ancestry predictive performance of adding European-ancestry individuals to the training set. A secondary motivation was to limit the imbalance between the two ancestries in order to evaluate the effect of importance weighting. We used the importance weighted LASSO with γ = 0, 0.2, …, 1 to construct PGSdual, while for the single-ancestry training sets we just considered the standard, unweighted LASSO. In a supplementary analysis on a subset of the traits, we also estimated dual-ancestry PGS trained on the combination of the European-ancestry training set and the African-ancestry training set, using both the unweighted and reweighted LASSO (Supplementary Fig. 3). We found that for this subset there was limited benefit over either the European-ancestry only training set, or the smaller dual-ancestry training set with only 50k European-ancestry individuals. Moreover, although the LASSO is a relatively efficient algorithm for constructing PGS using individual-level data, it nevertheless took over 210 CPU hours to fit the PGS for height on the full dual-ancestry training set, compared to 40 CPU hours on the smaller dual-ancestry training set.
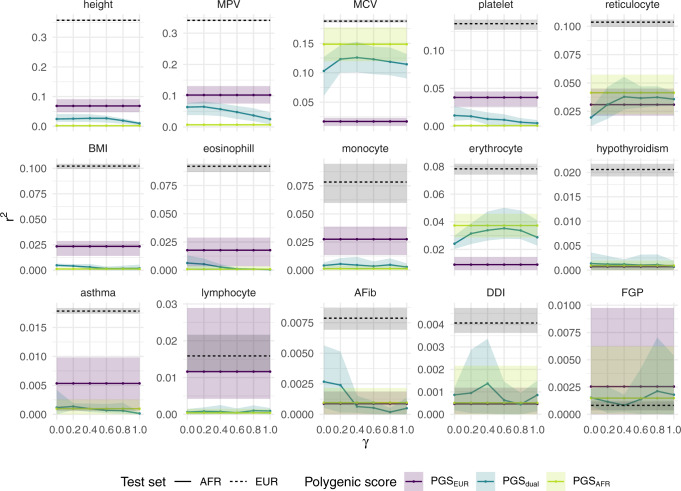
Figure 4 illustrates the predictive performance of the three above PGS for the 15 UK Biobank traits. In terms of African-ancestry predictive utility, PGSAFR outperformed PGSEUR on two traits—MCV, and erythrocyte distribution width (erythrocyte)—despite the former sample size being orders of magnitude smaller (n ≈ 5000 versus n ≈ 300,000). For both of these traits, the unweighted PGSdual performed the same as or slightly worse than PGSAFR. While importance reweighting yielded a moderate improvement, the reweighted PGSdual did not outperform PGSAFR.
Fig. 4. Partial r2 for PGSEUR, PGSdual, and PGSAFR on 15 traits in UK Biobank.
Predictive performance on an African-ancestry (AFR) test set is shown by the solid lines. The dashed lines correspond to predictive performance on a European-ancestry (EUR) test set using PGSEUR. The single-ancestry scores were estimated using a standard, unweighted LASSO. The dual-ancestry scores were constructed using an importance weighted LASSO with various degrees of reweighting γ. Traits are ordered according to partial r2 of PGSEUR on the European-ancestry test set (note the varying y-axes). Error bars correspond to the range across five cross-validation rounds of training set construction and PGS estimation. Phenotype acronyms: mean platelet volume (MPV), mean corpuscular volume (MCV), body mass index (BMI), atrial fibrillation (AFib), diverticular disease of the intestine (DDI), female genital prolapse (FGP).
For four other traits—high light scatter reticulocyte count (reticulocyte), hypothyroidism, atrial fibrillation (AFib), and and diverticular disease of intestine (DDI)—the predictive performance of all three PGS was largely similar. For the remaining traits—height, MPV, body mass index (BMI), eosinophill percentage, monocyte count, asthma and lymphocyte count—PGSEUR performed best. We note that predictive accuracy of PGSEUR for European-ancestry individuals was the same or higher than any of the PGS for African-ancestry individuals, consistent with previous investigations into the between-ancestry disparities of polygenic scores7,9.
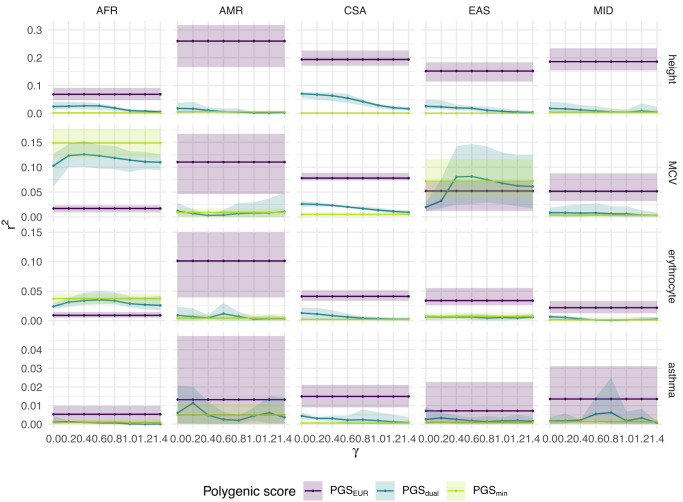
To explore whether the variability in optimal PGS strategy extended to other subpopulations, we focused in on four of the above traits (height, MPV, asthma, and erythrocyte distribution width) and ran the above analyses using different minority-ancestry groups: Admixed American ancestry (AMR), Central/South Asian ancestry (CSA), East Asian ancestry (EAS), and Middle Eastern ancestry (MID).
Figure 5 shows the predictive performance on the four traits across the five minority ancestry groups. For both height and asthma, PGSEUR had the best predictive performance for each of ancestry groups, with partial r2 for height varying from r2 = 0.08 for the African-ancestry group to r2 = 0.25 for the Admixed American ancestry group. For both erythrocyte distribution width and mean corpuscular volume in African-ancestry individuals, the PGSmin and the reweighted PGSdual outperformed PGSEUR, which offered almost no predictive utility. With the exception of mean corpuscular volume in East Asian ancestry individuals, where performance was similar between the different PGS, PGSEUR was consistently the best strategy for the remaining minority-ancestry groups. Results were qualitatively identical when using only genotyped SNPs instead of the full imputed sequence (Supplementary Fig. 4).
Fig. 5. Partial r2 for PGSEUR, PGSdual, and PGSmin on four traits in UK Biobank for five minority-ancestry groups.
The single-ancestry scores were estimated using a standard, unweighted LASSO. The dual-ancestry scores were constructed using an importance weighted LASSO with various degrees of reweighting γ. Error bars correspond to the range across five cross-validation rounds of training set construction and PGS estimation. The four traits considered are height, MCV, asthma, and erythrocyte distribution width. We used inferred genetic ancestry labels from Pan-UKBB, with participants divided into six groups: European ancestry (EUR), African ancestry (AFR), Admixed American ancestry (AMR), Central/South Asian ancestry (CSA), East Asian ancestry (EAS), and Middle Eastern ancestry (MID).
Differences in trait architecture explain variable performance by ancestry
Finally, to investigate the reasons why optimal training approaches vary across traits, we investigated the contribution of variants at different allele frequencies to variance explained. Specifically, we measured the partial r2 for different subsets of variants grouped by minor allele frequency (MAF) in a given ancestry group. For each ancestry group, we grouped variants into four sets: ‘rare’ (MAF ≤ 1%), ‘uncommon’ (1% < MAF ≤ 5%), ‘intermediate’ (5% < MAF ≤ 20%), and ‘common’ (MAF > 20%). Given a set of variants and the genotype matrix of the test set X, let denote the submatrix given by the columns of X that are in . For a set of variants , we define to be the score associated with the variant set , where is the vector of variant effects obtained from the LASSO. We then defined the partial r2 attributable to variant set to be the difference in r2 between models
| 1 |
| 2 |
where y is the vector of trait values, and M is the matrix of covariates (age, sex, the first ten genetic principal components (PCs), and interactions between sex and the ten genetic PCs) for the test set. We note that because we are considering the same set of variants for each trait, observed differences among traits in composition likely reflect differences in trait architecture, rather than differences in how the studies were performed.
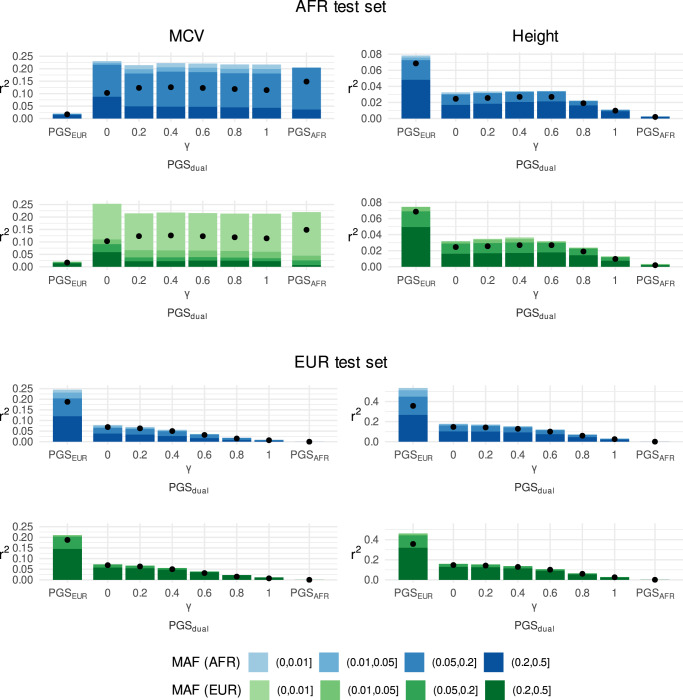
Figure 6 illustrates the contribution to variance explained by different segments of the ancestry-specific allele frequency spectra for the PGS for mean corpuscular volume and height. We observe striking differences between these traits in the contribution of different allele frequency segments. For MCV in African-ancestry individuals, the majority of the variance explained in each of the polygenic scores was due to variants that were intermediate or common in African-ancestry individuals (see top row, left). Notably, over half the contribution to variance explained of the African-ancestry and PGSdual could be attributed to variants that have MAF < 5% in the European-ancestry subgroup (second row, left). Conversely, variance explained in the European-ancestry subgroup was driven by variants that are intermediate or common in European-ancestry individuals (fourth row, left). And approximately one quarter of the variance explained could be attributed to variants with MAF < 5% in African-ancestry individuals.
Fig. 6. Allele frequency composition of variance explained by single- and dual-ancestry PGS.
Results shown for mean corpuscular volume (left) and height (right) in a African-ancestry test set (AFR; top) and a European-ancestry test set (EUR; bottom). The black dots represent partial r2 for all the variants, i.e. the entire polygenic score. Variants were grouped according to their minor allele frequency (MAF) in African-ancestry individuals (blue palette) or in European-ancestry individuals (green palette). Each bar represents the sum of the partial r2 values for each subset of variants in a given polygenic score. Note that the bars are stacked, and the height of the bar is generally higher than corresponding dot due to LD between variants. The parameter γ corresponds to the degree of reweighting used in the reweighted LASSO for PGSdual.
In contrast, for height we find that variance explained in European-ancestry individuals has an allele frequency decomposition with a slightly greater contribution of variants that are common in European-ancestry individuals (bottom row, right). But, variance explained in African-ancestry individuals is dominated by variants that are common (MAF > 5%) in both populations (top two rows, right). The effect of reweighting follows a similar pattern; for MCV shifting variance explained towards variants that are higher-frequency in the African-ancestry individuals (and considerably rarer in European-ancestry individuals) and, for height, tending to favour variants that are common in both groups.
These results suggest differences in genetic architecture between the two traits. For mean corpuscular volume, the variance explained by PGSdual and PGSAFR could largely be attributed to variants that were relatively common in African-ancestry individuals but rare in European-ancestry individuals. Since the number of African-ancestry individuals in these training sets was relatively small, this suggests that the corresponding effect sizes are comparatively large. On the other hand, the variance explained by each of the height PGS could be attributed to variants that were common in both European-ancestry and African-ancestry individuals. We found similar patterns for the other minority ancestries (Supplementary Figs. 5–8). Specifically, for traits and ancestries where PGSmin outperformed the PGSEUR, more variance could be attributed to variants that are more common in the minority ancestry group. We also found substantial differences across traits in the implied liability variance between PGSEUR and PGSmin (Supplementary Table 1). Such differences in trait architecture are indicative of variation in the evolutionary and selective forces that have shaped trait variation35–37.
Discussion
The lack of diversity in human genetic studies has been brought into focus by a number of articles (e.g.9,38–40), revealing that around 86% of all GWAS participants are of European descent. In the context of polygenic scores, this bias has been reflected in the lack of transferability of scores across ancestries: PGS developed using European-ancestry samples tend to perform poorly in non-European ancestry test sets7–9. Correspondingly, our results found that, for a range of traits, PGS estimated using European-ancestry individuals performed relatively poorly on other non-European ancestry groups. Although recent improvements in predictive performance across a number of traits indicate the potential clinical utility of PGS2,3,5,6, the disparity in PGS accuracy across ancestry groups, raises serious technical, clinical and ethical issues, with likely substantial impacts on health inequalities if left unaddressed9.
Recent investigations into statistical methods have sought to construct improved PGS using the available data with the aim of reducing this disparity in predictive accuracy. Previous studies on the lack of transferability of PGS have generally estimated scores using summary statistics from genome-wide association studies of single-ancestry populations7–9. These summary statistic approaches are often highly efficient computationally and typically achieve highly competitive predictive performance relative to full genotype approaches34,41–43. A number of methods to construct PGS by combining GWAS results from distinct ancestry groups have recently been developed, demonstrating improved prediction accuracy on the minority-ancestry group22–24.
However, the question of how to optimally construct PGS directly from multiple-ancestry training data has largely been unexplored. That is, to maximise predictive accuracy for a minority-ancestry group, is it better to employ a PGS trained on just the minority-ancestry individuals or a combination of the minority-ancestry individuals and the majority-ancestry individuals? To investigate this, we compared the prediction accuracy of PGS trained on different subsets of the available data. This was possible due to the availability of individual-level genetic data in UK Biobank, accompanied by a wide range of phenotypic measurements. This in turn allowed us to vary the number of individuals of each ancestry in each training set and thus to assess the effect of sample size and composition on PGS predictive performance for a range of quantitative and binary traits. Moreover, the use of individual-level data to estimate PGS, as opposed to the more standard approach of using external GWAS summary statistics, avoids making any assumptions such as common LD structure or phenotype definition from the GWAS population and target population (though see ref. 44 for a method that combines both approaches to improve polygenic prediction). A potential drawback of using an individual-level approach was the considerable computational cost associated with constructing the PGS, which may be impractical in the context of large-scale biobanks of increasing diversity.
It is worth noting that UK Biobank consists of an older subset of the UK population recruited on a voluntary basis in response to postal invitations. As a result, UK Biobank is not a representative sample of the wider UK population, displaying a bias towards individuals who are healthier, wealthier, and who self-report their ethnicity as white45. We further note that the absolute number of non-European-ancestry individuals in UK Biobank is considerably smaller than those of European-ancestry. Our findings are thus limited by the ancestral diversity of UK Biobank and more work is required to investigate optimal PGS strategies in more balanced multi-ancestry genomic datasets.
Our primary finding is that, in terms of minority-ancestry prediction performance, traits vary substantially in their optimal strategy for combining data across ancestries. Through simulation, we have shown that a PGS trained on a small minority-ancestry training set may outperform a much larger European-ancestry training set. Moreover, there are plausible regions of parameter space, notably where effect sizes are correlated across ancestry groups but not identical, where reweighting strategies can boost prediction performance using a multiple-ancestry training set. However, when applied to empirical data from the UK Biobank, relatively weak benefit from reweighting was observed. Rather, traits fell into two broad categories for which the minority-ancestry PGS outperformed the majority-ancestry PGS, or vice versa. For those in the first category, the most valuable training data was the small dataset from the minority group alone (and where performance decreases by the inclusion of any individuals of the majority—here European-ancestry). For those in the second category (such as height), the best performance in the underrepresented group was achieved by training in the much larger majority group, though note this still represented a substantial decrease in absolute performance relative to the majority European-ancestry group. When the minority group was African-ancestry individuals, the first category, though smaller, included important biomarkers such as MCV. Moreover, for a given trait, the optimal strategy varied by ancestry. For MCV for example, PGSEUR outperformed the PGSmin for Admixed American-, Central/South Asian- and Middle Eastern-ancestry groups, while the reverse was true for the African-ancestry group. For the East Asian-ancestry group, the PGS displayed similar performance.
These findings raise the question of why the optimal strategy varies across traits and ancestry groups. Recent studies have ascribed the overall lack of PGS transferability to a number of factors, including population-level differences in allele frequencies, LD patterns, location of causal variants, and effect sizes9–12,14,15. We found that the variability across traits could be at least partially explained by differences in the allele frequency pattern of causal variants or, more precisely, variants in LD with a causal variant. Specifically, we found that for some traits, such as height, most predictive utility could be attributed to variants that were relatively common (MAF > 5%) in both European- and African-ancestry individuals. For other traits, such as MCV, the predictive utility could be attributed to variants that were common in African-ancestry individuals but rare in European-ancestry individuals. This points to why PGSEUR for MCV performed much worse than the corresponding PGSAFR, despite being trained on a much larger number of individuals. We also note that the minority-ancestry PGS and reweighted dual-ancestry PGS performed particularly well for blood cell traits. This may be due to the influence of relatively few loci that have large phenotypic effects and strong differences in allele frequency between populations indicative of strong evolutionary selective pressure (such as has been shown for the DARC (Duffy) locus46). For such traits, a strategy that emphasises the minority-ancestry data may be favoured. Further work is needed, however, to determine the precise nature of differences in optimal strategy and the relation with trans-ancestry differences in genetic architecture.
Our findings highlight the limitations of statistical corrections alone in reducing the disparities of PGS performance between ancestries. There are numerous sources of potential bias that adversely affect the application of an analytical pipeline to individuals of minority and/or underrepresented groups, including problem selection, data collection, outcome definition, model development and lack of real-world impact assessments and considerations47. Therefore, statistical solutions must be considered in combination with efforts to address the global health research funding gap48, diversity of the bioinformatics workforce49 and assessing the impact and translation of analyses to real-world data50 in addition to efforts to increase the number of non-European-ancestry participants in genetic research. Each of these partial solutions, in combination, provide essential contributions to reduce and remove opportunities for negative effects on health inequalities, particular amongst those from different ancestry groups51.
It is becoming increasingly clear that the vast disparities in PGS performance can only be bridged by improving the diversity of human genetic datasets9. An important consideration surrounds future sampling strategy: whose genomes should we aim to sequence to reduce existing disparities in polygenic prediction accuracy? Our findings indicate that increasing the number of samples from minority-ancestry groups can lead to significant improvements in prediction performance. Moreover, even within the same ancestry group, PGSs do not always generalise across other characteristics such as age, sex and socio-economic status52, pointing to the need of more diversity across multiple axes both alongside and within genetic ancestry.
Perhaps counter-intuitively, with more diverse data, statistical tools such as importance reweighting may eventually play a more important role as we seek to boost predictive utility by using all the available data. Reweighting strategies have the benefit of overcoming the lack of universal definitions of race, ethnicity and ancestry, which causes considerable confusion and imprecision53,54. The categorisation of individuals into discrete ancestry groups to explain differences between behaviours and exposures may be unhelpful55, whereas continuous representations of genetic ancestry56,57 enable identification of areas of genetic ancestry where performance is stronger or weaker as well as how the trait itself varies across ancestry. Ultimately, approaches to genetic prediction must acknowledge both the many similarities of human biology, but also the differences in history, cultural heritage, exposure, and behaviour that can lead to certain factors being of greater relevance for particular groups of individuals.
Methods
PGS Estimation using the LASSO
To construct PGSs from full genotype data, we use L1-penalised regression, also known as the LASSO30. The LASSO has previously been used in the context of genetic prediction (see for example refs. 12,31–34 and references therein) and is suitable for high-dimensional problems where one expects the number of non-zero predictors to be small relative to the number of total predictors. Although there exist other full genotype PGS methods such as linear mixed models (see e.g. ref. 58), we focus on the LASSO largely for its computational efficiency. We provide an analysis of predictive performance versus sample size, focusing on differences in predictive performance between European-ancestry individuals and non-European-ancestry individuals.
We first briefly recap the LASSO algorithm for constructing polygenic scores. Let n be the number of individuals in the training set. Denote to be the matrix of q covariates, X to be the n × p genotype matrix, and y to be the n-vector of observed phenotype values. We assume a linear relationship between the phenotype and predictors,
| 3 |
where θ is a q-vector of covariate effects, β is a p-vector of variant effects, and ϵ is an environmental noise term with mean 0.
The LASSO aims to minimise the objective function,
| 4 |
with respect to (θ, β), where λ is a regularisation parameter. The purpose of the ∣∣β∣∣1 term is to penalise large values of ∣β∣ and thus encourage sparse solutions, that is, solutions with a relatively low number of non-zero coefficients. Note that the parameters θ are not penalised. The choice of λ controls the degree of penalisation with higher values of λ encouraging smaller values of β. To select λ, we applied an 80-20 training-validation split to the training set, generating a path of solutions for a range of values of λ using the training split, and then selecting the value of λ that maximises r2 (for quantitative traits) or the Area Under the Curve (AUC; for binary traits) on the validation split.
We optimise (4) using the R packages glmnet59 and snpnet34 on simulated and real data respectively. The snpnet package is an extension of glmnet designed to interface directly with the PLINK software60,61 to handle large-scale single nucleotide polymorphism datasets such as the genotype data in UK Biobank. Using the default package settings and following the guidance in34, we did not standardise the genotypes before fitting.
Multiple-ancestry datasets
The above description assumes that the genetic effects β are the same for all individuals. While this assumption may be reasonable within a single ancestry group, it is unlikely to hold more generally. We consider a hypothetical model that allows genetic effects to vary among individuals. To this end, we introduce a low-dimensional latent variable z representing the ancestry of a given individual. For an individual i,
| 5 |
where (θ( ⋅ ), β( ⋅ )) are now vector-valued functions parameterised by z. The only assumption we make about these functions is one of continuity, so that individuals with similar ancestry have similar covariate and genetic effects. Otherwise, we do not make any explicit statements regarding the form of the functions.
In this paper, we consider the special case with J = 2 ancestry groups, such that . We denote (θ(zi), β(zi)) = (θ(j), β(j)) for an individual i in ancestry group j. Using superscripts to denote the ancestry group (for example, y(j) is the vector of observed phenotypes for group j),
| 6 |
Denoting nj to be the number of individuals of ancestry j in the training set, we assume n1 > n2 to reflect a European-ancestry dominated training set. Applying the standard LASSO to such a training set, we would expect the estimate to be closer to (θ(1), β(1)) than to (θ(2), β(2)). All else being equal, this would result in better predictive performance for test individuals in group 1.
Importance reweighting
We return for a moment to the more general model in Equation (5). Suppose we wish to construct a polygenic score for a test set with ancestry distribution πTE(z) given a training set of observations from individuals with ancestry z1, …, zn, how should one obtain a single estimate for (θ, β)? Our proposed approach is to use importance reweighting, a statistical technique commonly used in survey sampling26. Importance reweighting aims to account for distributional differences between the sampling population and the population of interest by assigning weights to each of the samples in the training data. Here, we assign each of the training individuals a weight wi that quantifies the similarity of the ancestry variable zi to the test set ancestries, with individuals who have a similar ancestry to the test set assigned a higher weight. More concretely, assuming an ancestry distribution πTR( ⋅ ) on the training set, we set
| 7 |
Note that we do not have access to the distributions πTR, πTE so in practice we must approximate (7). Given weights wi, to estimate (θ, β), we minimise the following weighted LASSO objective function:
| 8 |
In this work, we consider only the special case with two ancestry groups (Eqn. (6)), specifying importance weights w1, w2 such that w2 ≥ w1 with the aim of improving estimates for group 2, i.e. the underrepresented group. Specifically, we use weights of the form:
| 9 |
where γ is a hyperparameter that controls the degree of reweighting. We normalised the weights so that n1w1 + n2w2 = n1 + n2. With these weights, we thus minimise the objective function,
| 10 |
with respect to (θ, β).
Simulation study
To evaluate the effect of importance reweighting on PGS performance under various settings, we undertook a simulation study. We used the simulation engine msprime27 in the standard library of population genetic simulation models stdpopsim v0.1.228 to generate African-ancestry and European-ancestry genotypes, following a similar simulation framework to that used by Martin et al.7. For each ancestry group, we generated a total of 200,000 genotypes for chromosome 20, based on a three-population ‘out-of-Africa’ demographic model62, using a mean mutation rate of 1.29 × 10−8 and a recombination map of GRCh37. This recombination map is from the Phase II Hapmap project and is based on 3.1 million genotyped SNPs from 270 individuals across four populations (Nigeria, Beijing, Japan, northern and western Europe)63. Note that this particular simulation model also generates genotypes for East Asian individuals but we do not use these in our analysis. To reduce the computational burden, we used only the first 10% of the chromosome, applying a minor allele frequency (MAF) threshold to filter out any SNPs that had a MAF of <1% in each ancestry group, resulting in a total of 189, 765 variants.
We simulated phenotypes from these genotypes assuming a normal linear model,
| 11 |
where . The noise variance parameter σ2 controls the SNP heritability for each ancestry group and was chosen to yield an average SNP heritability of 0.3 across the groups. To reflect the sparsity of genetic effects, we randomly selected p0 = 100 of the p = 189, 765 variants to be causal. Motivated by Trochet et al.64, we drew the causal effect sizes from a bivariate normal distribution to model the similarity of genetic effects between ancestries. Denoting to be the indices of the causal SNPs, and we have the equation
| 12 |
where ρ is the correlation between the ancestry-specific genetic effects. We set for i ∉ C. For each value of ρ = 0.5, 0.6, …, 1.0, we repeated the above procedure 5 times to generate 5 quantitative traits.
To investigate the effect of sample size, for each trait we created five training sets with nEUR = 18,000 randomly selected individuals of European ancestry and nAFR = 2000, 4500, 7714, 12,000, 18,000 randomly selected individuals of African ancestry. For each of these training sets, we computed weights , and where γ is a hyperparameter controlling the degree of reweighting. To investigate the impact of reweighting, we varied γ = 0, 0.1, …, 1.5. Note that γ = 1 corresponds to inverse proportion reweighting when nAFR = 2000 and nEUR = 18,000. We normalised the weights to ensure that their sum equalled n, in line with the unweighted case.
To assess predictive performance for each ancestry, we constructed an African-ancestry test set and a European-ancestry test set by randomly selecting 2000 individuals from each ancestry out of those not included in the training set. We used the proportion of variance explained, denoted r2, as the measure of predictive performance,
| 13 |
where denotes the sample variance. Note that this is equivalent to the partial r2 relative to an intercept-only covariate model. For ρ = 0.5, 0.6, …, 1.0, we repeated the above process 5 times with different randomly selected individuals in the training and test sets to calculate a mean r2 for each trait.
In supplementary studies to investigate the role of heritability and polygenicity, i.e. the number of causal SNPs, we repeated the above analyses with the correlation between the ancestry-specific genetic effects fixed at ρ = 0.8, and varying the overall heritability h2 = 0.1, 0.3, 0.5 and the number of causal SNPs p0 = 10, 100, 1000 respectively.
UK Biobank
The UK Biobank is a large-scale cohort study with genomic and phenotypic data collected on ~500,000 individuals aged 40-69 at the time of recruitment25. We used inferred genetic ancestry labels made available by the Pan-UKBB initiative29. These labels were derived based on reference data from the 1000 Genomes Project65 and the Human Genome Diversity Project (HGDP)66. Briefly, principal component analysis (PCA) was performed on unrelated individuals in the combined reference dataset, and a random forest classifier was trained on the first 6 principal components (PCs) using continental ancestry metadata. UK Biobank individuals were then projected onto this reference PC space and given initial ancestry assignments based on the random forest classifier. These assignments were then adjusted by removing outliers. Full details can be found on the Pan-UKBB website29.
Phenotypes
We investigated a range of quantitative and binary traits available in our UK Biobank project (UKB Application Number 12788). To select these, we applied the following procedure. We first filtered out traits with estimated SNP heritability of <5% or a ‘low’ confidence rating for the SNP heritability estimate, as reported on the Neale Lab UKB SNP-Heritability Browser67,68. To ensure that the traits under investigation were not highly correlated with each other, we used genetic correlation estimates available on the Neale Lab UKBB Genetic Correlation Browser69,70. Specifically, working from the most heritable traits to the least heritable, we iteratively removed a trait if it had an estimated genetic correlation of >0.5 with any remaining trait of higher heritability. Of the remaining traits, we selected the top 10 most heritable quantitative traits: height, mean corpuscular volume (MCV), body mass index (BMI), eosinophill percentage, erythrocyte distribution width (erythrocyte), lymphocyte count, monocyte count, mean platelet volume (MPV), platelet crit, and high light scatter reticulocyte count (reticulocyte). We also selected the top 5 most heritable binary traits: asthma, female genital prolapse (FGP), atrial fibrillation (AFib), diverticular disease of the intestine (DDI), and hypothyroidism. For our African-ancestry analyses, we investigated all 15 of these traits, while for the other minority-ancestry analyses, we focused in on 4 traits: height, mean corpuscular volume, erythrocyte distribution width, and asthma.
Genotypes and covariates
We used imputed genotypes from UK Biobank, filtering out individuals and variants according to quality-control metrics used by the Pan-UKBB initiative29. Firstly, we removed individuals who were identified as displaying sex chromosome aneuploidy. We also removed individuals who were flagged as related by Pan-UKBB. Within each ancestry group, related individuals were identified using PC-Relate71 with k = 10 and a minimum individual MAF of 5%. We filtered out variants that were not deemed to be of ‘high quality’ according to Pan-UKBB, retaining those with an INFO score of at least 0.8 and with an allele count of at least 20 per population. We also removed variants that had a MAF of <1% in both the European-ancestry group and the minority-ancestry group under analysis. To control for population structure, we included the following covariates in our model: age, sex, the first ten genetic principal components (PCs), and interactions between sex and the ten genetic PCs.
Construction of training sets
To assess the effect of sample size and composition on PGS performance, we used subsets of the above data as training sets, controlling the number of European-ancestry and minority-ancestry individuals. The remaining individuals were then used as a held-out test set. For each trait, we constructed three types of training sets using individuals with non-missing data for that particular trait. The first two types of training sets were single-ancestry datasets, one consisting solely of European-ancestry individuals and the other consisting solely of minority-ancestry individuals.
European-ancestry A random sample comprising 80% of the quality-controlled European-ancestry individuals.
Minority-ancestry A random sample comprising 80% of the respective quality-controlled minority-ancestry individuals.
Dual-ancestry This set consisted of both minority-ancestry individuals and European-ancestry individuals. The basic form of this training set was made up of the minority-ancestry training set described above, combined with European-ancestry individuals so that the proportion of minority-ancestry individuals was 10%. The European-ancestry individuals were matched to the minority-ancestry individuals on age and sex. We also considered variations of this training set by removing a proportion of either the European-ancestry individuals or the minority-ancestry individuals (see Results for more details).
For each dataset, we further removed variants with a MAF of <0.1% or a missing genotype call rate of <5%. Note that, as a result, the sets of variants generally differed by training set. For the single-ancestry datasets, we used the standard, unweighted LASSO to construct the PGS. For the dual-ancestry datasets, we used the weighted LASSO with γ = 0, 0.2, 0.4, 0.6, 0.8, 1. Note that γ = 0 corresponds to the unweighted LASSO.
Predictive accuracy
We evaluated predictive accuracy of each PGS by ancestry group using individuals that were not included in the corresponding training sets. To assess the genetic predictive accuracy of a PGS, we calculated the partial r2 attributable to the PGS, relative to a covariate-only model, following Martin et al.9. Specifically, we fit the following nested linear models (or the equivalent logistic models for binary traits),
| 14 |
| 15 |
where M is the covariate matrix and is the vector consisting of polygenic scores for each individual in the test set. We took the partial r2 (or the Cox and Snell pseudo-r2 for binary traits) between models (14) and (15) as our measure of predictive accuracy. To obtain more reliable estimates, we performed 5-fold cross-validation. That is, we repeated five times the process of training set construction and PGS estimation to obtain five estimates of partial r2, and report the mean and the range of these estimates.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Acknowledgements
This research was funded in whole, or in part, by the UKRI [EP/R018561/1; UK Engineering and Physical Sciences Research Council (EPSRC) Bayes4Health programme] (B.L., C.H., G.M.) and the Wellcome Trust [100956/Z/13/Z] (G.M.). The computational aspects of this research were supported by the Wellcome Trust Core Award Grant Number 203141/Z/16/Z and the NIHR Oxford BRC. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. B.L. also gratefully acknowledges funding from Jesus College, Oxford. C.H. was also supported by The Alan Turing Institute, Health Data Research UK, the Medical Research Council UK, and AI for Science and Government UK Research and Innovation (UKRI). G.M. was also supported by the Li Ka Shing Foundation. For the purpose of Open Access, the author has applied a CC BY public copyright license to any Author Accepted Manuscript version arising from this submission.
Author contributions
B.L., G.M., and C.H. designed the study. B.L. carried out the analyses. M.M., G.M., and C.H. provided critical feedback and framing. All authors contributed to writing and editing of the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Data availability
This research has been conducted using data from UK Biobank, a major biomedical database, under application 1278825. The UK Biobank data are available under restricted access; access can be obtained by researchers upon application—see https://www.ukbiobank.ac.uk/enable-your-research. The genetic correlation estimates from the Neale Lab UKBB Genetic Correlation Browser69,70 are available at https://ukbb-rg.hail.is/. The heritability estimates from the Neale Lab UKB SNP-Heritability Browser67,68 are available at https://nealelab.github.io/UKBB_ldsc/downloads.html. The ancestry-specific heritability estimates and inferred genetic ancestry labels for UK Biobank individuals from the Pan-UKBB initiative29 are available at are available at https://pan.ukbb.broadinstitute.org/downloads. The recombination map of GRCh37 is available as part of the stdpopsim python library—see https://popsim-consortium.github.io/stdpopsim-docs.
Code availability
The code used to generate these results is available at https://github.com/brieuclehmann/pgs_transferability/releases/tag/v0.1. To construct the PGS, we used the glmnet R package v4.1 (for simulated data), and a slight adaptation of the snpnet R package34 v0.3.0 available at https://github.com/brieuclehmann/snpnet (for UK Biobank data). To generate simulated data, we used the msprime simulation engine via the stdpopsim v0.1.2 python library—see https://popsim-consortium.github.io/stdpopsim-docs/. To preprocess the UK Biobank genetic data, we made use of both PLINK v1.9 and PLINK v2.0, available at https://www.cog-genomics.org/plink/.
Competing interests
G.M. is a director of and shareholder in Genomics PLC, and is a partner in Peptide Groove LLP. M.M. is a Programme Lead for the Diverse Data initiative at Genomics England Ltd. B.L. and C.H. declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Gil McVean, Chris Holmes.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-023-38930-7.
References
- 1.Chatterjee N, Shi J, García-Closas M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 2016;17:392–406. doi: 10.1038/nrg.2016.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Torkamani Ali, Wineinger NE, Topol EJ. The personal and clinical utility of polygenic risk scores. Nat. Rev. Genet. 2018;19:581–590. doi: 10.1038/s41576-018-0018-x. [DOI] [PubMed] [Google Scholar]
- 3.Khera AV, et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018;50:1219–1224. doi: 10.1038/s41588-018-0183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Knowles JW, Ashley EA. Cardiovascular disease: The rise of the genetic risk score. PLoS Med. 2018;15:1–7. doi: 10.1371/journal.pmed.1002546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Maas P, et al. Breast cancer risk from modifiable and nonmodifiable risk factors among white women in the United States. JAMA Oncol. 2016;2:1295–1302. doi: 10.1001/jamaoncol.2016.1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sharp SA, et al. Development and standardization of an improved Type 1 diabetes genetic risk score for use in newborn screening and incident diagnosis. Diabetes Care. 2019;42:200–207. doi: 10.2337/dc18-1785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Martin AR, et al. Human demographic history impacts genetic risk prediction across diverse populations. Am. J. Hum. Genet. 2017;100:635–649. doi: 10.1016/j.ajhg.2017.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Duncan L, et al. Analysis of polygenic risk score usage and performance in diverse human populations. Nat. Commun. 2019;10:3328. doi: 10.1038/s41467-019-11112-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Martin AR, et al. Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet. 2019;51:584–591. doi: 10.1038/s41588-019-0379-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Scutari M, Mackay Ian, Balding D. Using genetic distance to infer the accuracy of genomic prediction. PLoS Genet. 2016;12:1–19. doi: 10.1371/journal.pgen.1006288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang Y, et al. Theoretical and empirical quantification of the accuracy of polygenic scores in ancestry divergent populations. Nat. Commun. 2020;11:3865. doi: 10.1038/s41467-020-17719-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Privé F, et al. Portability of 245 polygenic scores when derived from the UK Biobank and applied to 9 ancestry groups from the same cohort. Am. J. Hum. Genet. 2022;109:12–23. doi: 10.1016/j.ajhg.2021.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shi H, et al. Localizing components of shared transethnic genetic architecture of complex traits from GWAS summary data. Am. J. Hum. Genet. 2020;106:805–817. doi: 10.1016/j.ajhg.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Carlson CS, et al. Generalization and dilution of association results from European GWAS in populations of non-European ancestry: The PAGE Study. PLoS Biol. 2013;11:1–11. doi: 10.1371/journal.pbio.1001661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brown BC, Ye C, Price AL, Zaitlen N. Transethnic genetic-correlation estimates from summary statistics. Am. J. Hum. Genet. 2016;99:76–88. doi: 10.1016/j.ajhg.2016.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Galinsky KJ, et al. Estimating cross-population genetic correlations of causal effect sizes. Genet. Epidemiol. 2019;43:180–188. doi: 10.1002/gepi.22173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Franks PW, Pearson E, Florez JC. Gene-environment and gene-treatment interactions in type 2 diabetes: progress, pitfalls, and prospects. Diabetes Care. 2013;36:1413–1421. doi: 10.2337/dc12-2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bentley AR, et al. Multi-ancestry genome-wide gene-smoking interaction study of 387,272 individuals identifies new loci associated with serum lipids. Nat. Genet. 2019;51:636–648. doi: 10.1038/s41588-019-0378-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.H3 Africa Consortium. Enabling the genomic revolution in Africa. Science. 2014;344:1346–1348. doi: 10.1126/science.1251546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Grinde KE, et al. Generalizing polygenic risk scores from Europeans to Hispanics/Latinos. Genet. Epidemiol. 2019;43:50–62. doi: 10.1002/gepi.22166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Márquez-Luna C, Loh Po-Ru. Multiethnic polygenic risk scores improve risk prediction in diverse populations. Genet. Epidemiol. 2017;41:811–823. doi: 10.1002/gepi.22083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Weissbrod O, et al. Leveraging fine-mapping and multipopulation training data to improve cross-population polygenic risk scores. Nat. Genet. 2022;54:450–458. doi: 10.1038/s41588-022-01036-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ruan Y, et al. Improving polygenic prediction in ancestrally diverse populations. Nat. Genet. 2022;54:573–580. doi: 10.1038/s41588-022-01054-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cavazos TB, Witte JS. Inclusion of variants discovered from diverse populations improves polygenic risk score transferability. Hum. Genet. Genomics Adv. 2021;2:100017. doi: 10.1016/j.xhgg.2020.100017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bycroft C, et al. The UK Biobank resource with deep phenotyping and genomic data. Nature. 2018;562:203–209. doi: 10.1038/s41586-018-0579-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Scheaffer, Richard L., Mendenhall III, William, Ott, R Lyman. and Gerow, Kenneth G. Elementary survey sampling. Cengage Learning, (2011).
- 27.Kelleher J, Etheridge AM, McVean G. Efficient coalescent simulation and genealogical analysis for large sample sizes. PLoS Comput Biol. 2016;12:1–22. doi: 10.1371/journal.pcbi.1004842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Adrion JR, et al. A community-maintained standard library of population genetic models. eLife. 2020;9:e54967. doi: 10.7554/eLife.54967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.The Pan-UKBB team. Pan UKBB. https://pan.ukbb.broadinstitute.org (2020).
- 30.Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc.: Ser. B (Methodol.) 1996;58:267–288. [Google Scholar]
- 31.Waldmann P, et al. AUTALASSO: an automatic adaptive LASSO for genome-wide prediction. BMC Bioinforma. 2019;20:167. doi: 10.1186/s12859-019-2743-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Okser S, et al. Regularized machine learning in the genetic prediction of complex traits. PLOS Genet. 2014;10:1–9. doi: 10.1371/journal.pgen.1004754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Privé F, Aschard H, Blum MGB. Efficient implementation of penalized regression for genetic risk prediction. Genetics. 2019;212:65–74. doi: 10.1534/genetics.119.302019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Qian J, et al. A fast and scalable framework for large-scale and ultrahigh-dimensional sparse regression with application to the UK Biobank. PLoS Genet. 2020;16:1–31. doi: 10.1371/journal.pgen.1009141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Simons YB, Bullaughey K, Hudson RR, Sella G. A population genetic interpretation of GWAS findings for human quantitative traits. PLoS Biol. 2018;16:1–20. doi: 10.1371/journal.pbio.2002985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zeng Jian, et al. Signatures of negative selection in the genetic architecture of human complex traits. Nat. Genet. 2018;50:746–753. doi: 10.1038/s41588-018-0101-4. [DOI] [PubMed] [Google Scholar]
- 37.Schoech AP, et al. Quantification of frequency-dependent genetic architectures in 25 UK Biobank traits reveals action of negative selection. Nat. Commun. 2019;10:790. doi: 10.1038/s41467-019-08424-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Need AC, Goldstein DB. Next generation disparities in human genomics: concerns and remedies. Trends Genet. 2009;25:489–494. doi: 10.1016/j.tig.2009.09.012. [DOI] [PubMed] [Google Scholar]
- 39.Popejoy AB, Fullerton SM. Genomics is failing on diversity. Nature. 2016;538:161–164. doi: 10.1038/538161a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fatumo S, et al. A roadmap to increase diversity in genomic studies. Nat. Med. 2022;28:243–250. doi: 10.1038/s41591-021-01672-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lloyd-Jones LR, et al. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun. 2019;10:5086. doi: 10.1038/s41467-019-12653-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mak T, Porsch R, Choi S, Zhou X, Sham P. Polygenic scores via penalized regression on summary statistics. Genet. Epidemiol. 2017;41:469–480. doi: 10.1002/gepi.22050. [DOI] [PubMed] [Google Scholar]
- 43.Vilhjálmsson BJ, et al. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am. J. Hum. Genet. 2015;97:576–592. doi: 10.1016/j.ajhg.2015.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Albi nana C, et al. Leveraging both individual-level genetic data and GWAS summary statistics increases polygenic prediction. Am. J. Hum. Genet. 2021;108:1001–1011. doi: 10.1016/j.ajhg.2021.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fry A, et al. Comparison of sociodemographic and health-related characteristics of UK biobank participants with those of the general population. Am. J. Epidemiol. 2017;186:1026–1034. doi: 10.1093/aje/kwx246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.McManus KF, et al. Population genetic analysis of the darc locus (duffy) reveals adaptation from standing variation associated with malaria resistance in humans. PLoS Genet. 2017;13:1–27. doi: 10.1371/journal.pgen.1006560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen IY, et al. Ethical machine learning in healthcare. Annu. Rev. Biomed. Data Sci. 2021;4:123–144. doi: 10.1146/annurev-biodatasci-092820-114757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vidyasagar D. Global notes: the 10/90 gap disparities in global health research. J. Perinatol. 2006;26:55–56. doi: 10.1038/sj.jp.7211402. [DOI] [PubMed] [Google Scholar]
- 49.Hofstra Bas, et al. The diversity–innovation paradox in science. Proc. Natl Acad. Sci. 2020;117:9284–9291. doi: 10.1073/pnas.1915378117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Obermeyer Z, Powers B, Vogeli C, Mullainathan S. Dissecting racial bias in an algorithm used to manage the health of populations. Science. 2019;366:447–453. doi: 10.1126/science.aax2342. [DOI] [PubMed] [Google Scholar]
- 51.Peterson RE, et al. Genome-wide association studies in ancestrally diverse populations: opportunities, methods, pitfalls, and recommendations. Cell. 2019;179:589–603. doi: 10.1016/j.cell.2019.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mostafavi H, et al. Variable prediction accuracy of polygenic scores within an ancestry group. eLife. 2020;9(Jan.):48376. doi: 10.7554/eLife.48376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mathieson I, Scally A. What is ancestry? PLoS Genet. 2020;16:1–6. doi: 10.1371/journal.pgen.1008624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mersha TB, Abebe T. Self-reported race/ethnicity in the age of genomic research: its potential impact on understanding health disparities. Hum. Genomics. 2015;9:1. doi: 10.1186/s40246-014-0023-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Foster MW, Sharp RR. Race, ethnicity, and genomics: Social classifications as proxies of biological heterogeneity. Genome Res. 2002;12:844–850. doi: 10.1101/gr.99202. [DOI] [PubMed] [Google Scholar]
- 56.Belbin GM, et al. Toward a fine-scale population health monitoring system. Cell. 2021;184:2068–2083.e11. doi: 10.1016/j.cell.2021.03.034. [DOI] [PubMed] [Google Scholar]
- 57.Lewis AnnaCF, et al. Getting genetic ancestry right for science and society. Science. 2022;376:250–252. doi: 10.1126/science.abm7530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhou X, Carbonetto P, Stephens M. Polygenic modeling with Bayesian sparse linear mixed models. PLOS Genet. 2013;9:1–14. doi: 10.1371/journal.pgen.1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Friedman JH, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010;33:1–22. doi: 10.18637/jss.v033.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Chang CC, et al. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience. 2015;4:7. doi: 10.1186/s13742-015-0047-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chang, C & Shaun P. PLINK 1.90 betawww.cog-genomics.org/plink/1.9/ (2023).
- 62.Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 2009;5:1–11. doi: 10.1371/journal.pgen.1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.The International HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Trochet Holly, et al. Bayesian meta-analysis across genome-wide association studies of diverse phenotypes. Genet. Epidemiol. 2019;43:532–547. doi: 10.1002/gepi.22202. [DOI] [PubMed] [Google Scholar]
- 65.Auton Adam, et al. A global reference for human genetic variation. Nature. 2015;526:68–74. doi: 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Cann HM, et al. A human genome diversity cell line panel. Science. 2002;296:261–262. doi: 10.1126/science.296.5566.261b. [DOI] [PubMed] [Google Scholar]
- 67.Bulik-Sullivan BK, et al. LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 2015;47:291–295. doi: 10.1038/ng.3211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.The Neale Lab. UK Biobank Heritability Browser. https://nealelab.github.io/UKBB_ldsc/ (2019).
- 69.Bulik-Sullivan B, et al. An atlas of genetic correlations across human diseases and traits. Nat. Genet. 2015;47:1236–1241. doi: 10.1038/ng.3406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.The Neale Lab. UK Biobank Genetic Correlation Browser. https://ukbb-rg.hail.is/ (2019).
- 71.Conomos MP, Reiner AP, Weir BS, Thornton TA. Model-free estimation of recent genetic relatedness. Am. J. Hum. Genet. 2016;98:127–148. doi: 10.1016/j.ajhg.2015.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zhou Wei, et al. Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic association studies. Nat. Genet. 2018;50:1335–1341. doi: 10.1038/s41588-018-0184-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This research has been conducted using data from UK Biobank, a major biomedical database, under application 1278825. The UK Biobank data are available under restricted access; access can be obtained by researchers upon application—see https://www.ukbiobank.ac.uk/enable-your-research. The genetic correlation estimates from the Neale Lab UKBB Genetic Correlation Browser69,70 are available at https://ukbb-rg.hail.is/. The heritability estimates from the Neale Lab UKB SNP-Heritability Browser67,68 are available at https://nealelab.github.io/UKBB_ldsc/downloads.html. The ancestry-specific heritability estimates and inferred genetic ancestry labels for UK Biobank individuals from the Pan-UKBB initiative29 are available at are available at https://pan.ukbb.broadinstitute.org/downloads. The recombination map of GRCh37 is available as part of the stdpopsim python library—see https://popsim-consortium.github.io/stdpopsim-docs.
The code used to generate these results is available at https://github.com/brieuclehmann/pgs_transferability/releases/tag/v0.1. To construct the PGS, we used the glmnet R package v4.1 (for simulated data), and a slight adaptation of the snpnet R package34 v0.3.0 available at https://github.com/brieuclehmann/snpnet (for UK Biobank data). To generate simulated data, we used the msprime simulation engine via the stdpopsim v0.1.2 python library—see https://popsim-consortium.github.io/stdpopsim-docs/. To preprocess the UK Biobank genetic data, we made use of both PLINK v1.9 and PLINK v2.0, available at https://www.cog-genomics.org/plink/.