Abstract
Micromixers play an imperative role in chemical and biomedical systems. Designing compact micromixers for laminar flows owning a low Reynolds number is more challenging than flows with higher turbulence. Machine learning models can enable the optimization of the designs and capabilities of microfluidic systems by receiving input from a training library and producing algorithms that can predict the outcomes prior to the fabrication process to minimize development cost and time. Here, an educational interactive microfluidic module is developed to enable the design of compact and efficient micromixers at low Reynolds regimes for Newtonian and non-Newtonian fluids. The optimization of Newtonian fluids designs was based on a machine learning model, which was trained by simulating and calculating the mixing index of 1890 different micromixer designs. This approach utilized a combination of six design parameters and the results as an input data set to a two-layer deep neural network with 100 nodes in each hidden layer. A trained model was achieved with R2 = 0.9543 that can be used to predict the mixing index and find the optimal parameters needed to design micromixers. Non-Newtonian fluid cases were also optimized using 56700 simulated designs with eight varying input parameters, reduced to 1890 designs, and then trained using the same deep neural network used for Newtonian fluids to obtain R2 = 0.9063. The framework was subsequently used as an interactive educational module, demonstrating a well-structured integration of technology-based modules such as using artificial intelligence in the engineering curriculum, which can highly contribute to engineering education.
I. INTRODUCTION
Micromixers are miniaturized microfluidic components that enable rapid and enhanced mixing of fluids in micro-scale flows for chemical, biological, and medical applications.1–3 While turbulence occurring within flows with high Reynolds number (Re) allows for enhanced mixing, low Re regimes mostly depend on diffusion, which results in slow mixing within lengthy microchannels.4 Therefore, developing compact micromixers that enable efficient mixing of liquids and gases in low Re regimes is an arduous task. Active micromixers use external stimuli such as acoustic,5–7 magnetic,8–10 thermal,11–13 and electric14–16 fields to effectively and rapidly mix fluids. On the other hand, passive micromixers utilize the innate properties of fluids, including inertial, viscous, and diffusive forces.17,18 These types of micromixers exploit the energy of driving pressure, which is already available in the microfluidic system that contains the micromixer.19 This approach eliminates the need for complicated and costly manufacturing processes associated with active micromixers. Additionally, passive micromixers enable the fabrication of tinier and compact micro-total analysis systems (μTAS) and lab on chip (LoC) setups since they do not require any external equipment to create force fields.20,21 The fluidic forces that control the micromixing process can be achieved by employing complex geometries such as helices, curves, and corners along the microchannels.22 3D shapes such as serpentines,23 tesla structures,24 crossing manifolds,25 and cascaded structures26 can also be implemented in passive micromixer designs. Alternatively, 2D passive micromixers are amenable to facile manufacturing schemes without compromising the mixing efficiency by implementing repeating curves and obstacles or widening and narrowing cross sections.
Machine learning (ML) is a subdivision of artificial intelligence (AI), where algorithms are trained to autonomously improve by learning from previous trials to optimize or predict an outcome that results from multiple input parameters. ML has been actively utilized in medical and biomedical fields,27–29 such as the prediction of diseases based on big data,30 delegating the computational tasks in tough conditions for providing faster analysis and forecasting the data,31 cancer diagnosis.32,33 In combination with image processing, ML can be used for the prediction of microneedle features for drug delivery34 and medical imaging applications.35 ML techniques are usually divided into two main categories: (i) regression, in which the outcome to be predicted is a continuous variable, or (ii) classification, where the aim is to predict whether the outcome belongs to one of two or more classes.36 Additionally, ML can be categorized based on the aim and training approach into supervised, semi-supervised, unsupervised, and reinforced learning.37 ML has been used to optimize designs and understand the impact of design and manufacturing parameters on products.38,39 For instance, 3D-printed structures were analyzed using ML to detect and prevent design errors.40 Furthermore, ML was used to fine-tune the design of microstructures to optimize their mechanical properties.41 The other applications of ML include the design 3D-printed surrogates42 and the optimization 3D-printed biomimetic microfibrillar adhesives.43 Similarly, ML can augment the analyses of the effect of different geometrical parameters on the mixing capabilities of passive micromixers to optimize their designs.
AI has the potential to enhance the learning outcomes of engineering students.44,45 For example, AI-powered simulations can provide a more realistic and immersive learning experience than traditional methods.46 AI can also help personalize the learning experience to individual students' needs, allowing them to progress at their own pace and receive targeted feedback.47 This study presents a well-structured integration of technology-based modules such as using artificial intelligence in the engineering curriculum, which can highly contribute to engineering education. In addition, AI has the potential to revolutionize engineering research and development. In this regard, we used the ML-based optimization of the mixing performance of micromixers at low Re regimes for Newtonian and non-Newtonian fluids to develop an interactive educational module for students (Fig. 1). Micromixers with 58590 combinations of five geometrical parameters and three fluidic parameters were simulated. The mixing efficiency and compactness of each design were calculated and utilized to create a training data library for ML. After being trained, the ML algorithm evaluated the optimum geometrical parameters for improved mixing of preferred fluids (Newtonian or non-Newtonian) in low Re regimes with a miniaturized design. Finally, this ML-based optimization algorithm was developed into an educational user interface. We demonstrated that this new method of AI-based education can enhance students' learning outcomes and improve their problem-solving skills.
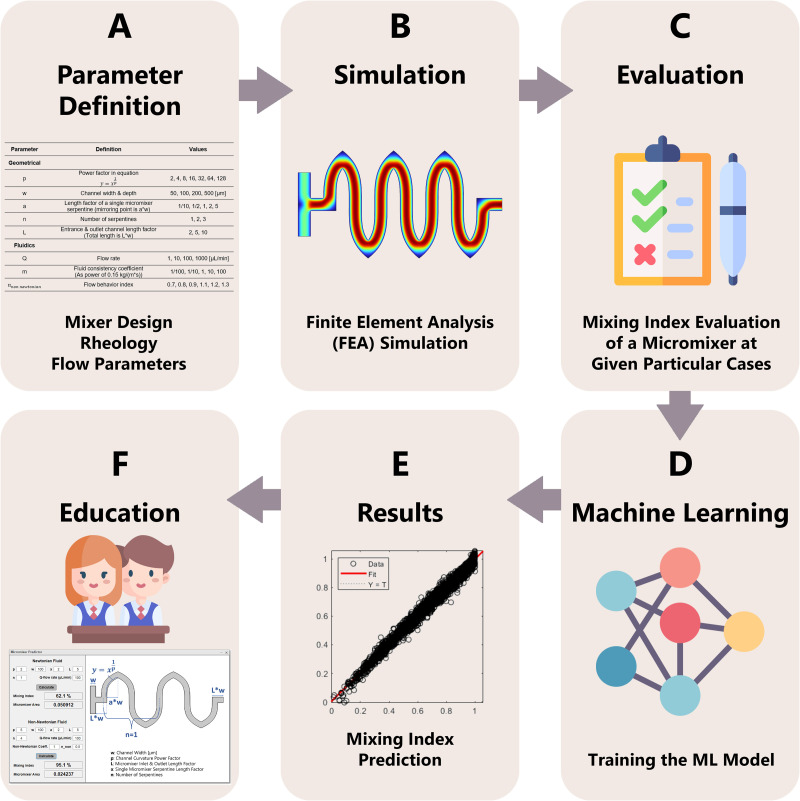
FIG. 1.
Workflow of the educational module. (a) First parameters affecting the micromixer study were defined and organized. (b) Finite element analysis (FEA) was used for simulating the micromixer setups. (c) For given particular cases of the micromixer, the mixing index was evaluated. (d) The data were used for training a machine learning (ML) model. (e) Results of the ML model were used to create (f) a novel interactive educational module for students.
II. METHODS
A. Geometric design
A parametrically changeable microchannel geometry was rendered in the 2D module of COMSOL Multiphysics. The design was composed of two inlets—a T-junction that merges flow from two inlets into the micromixer entrance channel and the micromixer—and an outlet channel [Fig. 2(a)]. The dimensions of the channels were determined by multipliers of the channel width (w). The lengths of the vertical inlet channels were equal to 5*w, while the lengths of the micromixer entrance channel and outlet channel was determined by the factor of L (length = L*w). The curvature of the micromixers was based on Eq. (1), and it was drawn with the parametric curve function [Fig. 2(b)],
| (1) |
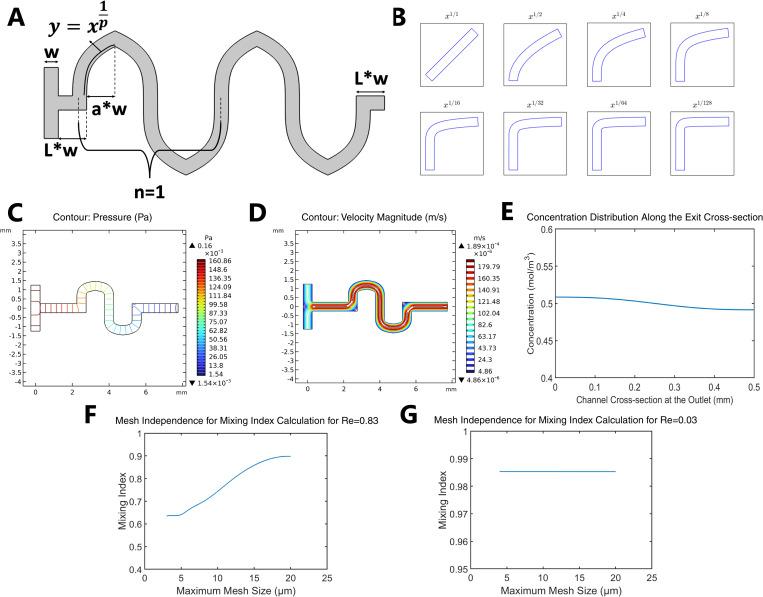
FIG. 2.
Simulation procedure. (a) Demonstration of the microchannel geometry with changeable parameters. (b) Depiction of the micromixer profiles. (c) Pressure contour plot. (d) Velocity streamline plot. (e) Concentration distribution along the vertical cross section for the case of p = 16, a = 1, L = 5, n = 1, Q = 1 μL min−1, and w = 500 μm. 0–1 on the x axis corresponds to the top-bottom line at the outlet cross section. (f) Mesh independence study for Re = 0.83, p = 16, a = 5, L = 5, n = 3, w = 200 μm, and Q = 10 μL min−1 case. (g) Mesh independence study for Re = 0.033, p = 16, a = 5, L = 5, n = 1, w = 500 μm, and Q = 1 μL min−1 case.
Since a parallel curve to the existing curve with a distance equal to w in between is needed to create a closed area, the parametric representation of a parallel curve with a distance of w was formulated by implementing and into Eq. (2), which yields Eq. (3),
| (2) |
| (3) |
The length of a micromixer curve was limited to factor a, which determined the maximum x-coordinate of the curve . The number of the serpentines of the microchannels was determined with factor n.
B. Flow simulations
Creeping Flow and Transport of Diluted Species modules of COMSOL Multiphysics were implemented to evaluate the passive mixing ability of micromixers. These modules were chosen since they enabled researchers to successfully generate the simulation results that match experimental findings for a wide range of Re numbers and micromixer designs.48–53 The parametrically changeable microchannel geometry was created as a 2D area, and the domain was assigned as the fluid that would be simulated. As boundary conditions, flows that contain concentrations of 0 and 1 mol m−3 were assigned to the bottom and top inlets, respectively, with the flow rate of Q. The exit of the microchannel was assigned as a single outlet with zero pressure as the boundary condition, while all the remaining boundaries were assigned as channel walls based on the properties of polydimethylsiloxane (PDMS). Equation (4) was used to compute a fully developed flow profile, where the inertial terms were neglected to reproduce a small Re (Stokes) flow, while the second term on the right-hand side of the equation was added to approximate the shallowness of microfluidic channels ( is equal to w, yielding a microchannel with a square cross section). P, μ, and U represent the pressure, the dynamic viscosity, and the velocity, respectively [Figs. 2(c) and 2(d)],
| (4) |
The diffusion equation with convection mechanism [Eq. (5)] was used to compute the transport of diluted species, where D is the diffusion coefficient, U is the velocity, and c is the concentration. The accuracy and efficiency of numerical solutions are influenced by the properties of the mesh utilized for discretizing the governing equations and boundary conditions. Although the accuracy of solutions tends to improve as the mesh size approaches zero, this leads to a significant increase in computational requirements such as time and memory, which are closely tied to the number of nodes in the model. To address this, the optimal mesh was determined by performing a mesh independence study that examined the balance between the accuracy of the solution and the computational demands [Figs. 2(f) and 2(g)]. Since the geometry of the micromixer is altered in this study in order to examine the impact of the microchannel design on the output mixing index, the mesh independency analysis has been carried out using the model's maximum element size ( ). The mesh analysis was conducted on two models with parameters that yield the highest and lowest Re cases, which are Re = 0.83, W = 200 μm, a = 5, L = 5, n = 3, p = 16, and Q = 10 μl min−1 and Re = 0.03, W = 500 μm, a = 5, L = 5, n = 3, p = 16, and Q = 1 μl min−1, respectively. Using free quadratic mesh elements, the analysis showed that the calculated mixing index becomes stable with and does not change significantly with further mesh refinement; hence, was enough to carry out the simulations,
| (5) |
Simulations for Newtonian fluids were conducted with the fluidic properties of the water where the density was 1000 kg m−3, the dynamic viscosity was , and the diffusion coefficient was set to 10−9 m2 s−1. The Newtonian simulations were ran by sweeping over the geometrical parameters of p from 1st to 7th powers of 2; w for values of ; L for values of ; n for values of ; and a for values of values of , with the flow rate (Q) values of 1 and 10 μl min−1. Within these 2520 combinations, models that contain w of 50 and 100 μm and Q of 10 μl min−1 were excluded due to the uncertainty of the used module for Re > 1, yielding 1890 different simulations. On the other hand, the power-law viscosity model [Eq. (6)] was used to simulate non-Newtonian fluids, where m is the fluid consistency coefficient, n is the flow behavior index, and γ is the shear rate. In addition to all geometrical values that are used in Newtonian models, m values of 0.01, 0.1, 1, 10, and 100th powers of 0.15 kg m−1 s−1 were added to parametric sweep in non-Newtonian models. Furthermore, n values of 0.7, 0.8, and 0.9 were added to mimic shear thickening fluids, while values of 1.1, 1.2, and 1.3 were used for replicating shear thinning fluids (Table I). Eventually, 56 700 non-Newtonian simulations were performed to train the ML algorithm,
| (6) |
TABLE I.
Nomenclature of parametrically sweep values.
| Parameter | Definition | Values |
|---|---|---|
| Geometrical factor | ||
| P | Power factor in equation | 2, 4, 8, 16, 32, 64, 128 |
| W | Channel width and depth | 50, 100, 200, 500 μma |
| A | Length factor of a single micromixer serpentine (mirroring point is a*w) | 1/10, 1/2, 1, 2, 5 |
| N | Number of serpentines | 1, 2, 3 |
| L | Entrance and outlet channel length factor (total length is L*w) | 2, 5, 10 |
| Fluidics | ||
| Q | Flow rate | 1, 10 (μL min−1)a |
| M | Fluid consistency coefficient [as a power of 0.15 kg/(m*s)] | 1/100, 1/10, 1, 10, 100 |
| n non-Newtonian | Flow behavior index | 0.7, 0.8, 0.9, 1.1, 1.2, 1.3 |
Combinations with w values of 50 and 100 μm were excluded for Q = 10 μL min−1 due to computational limitations.
The mixing index (M) was calculated with the variation in the concentration over the vertical crossline at the outlet of the microchannel with Eqs. (7) and (8)18 [Fig. 2(e)]. N represents the number of data points, while c represents the concentrations at respected data points. The value of was calculated with the concentration data at the vertical crossline of the T-junction, where the variation was maximum. The calculated M value varied between 0 and 1 where 1 represents perfect mixing. In addition to M, the total area ( ) spanned by each micromixer design was calculated using Eq. (9),
| (7) |
| (8) |
| (9) |
C. ML-Based parameter optimization
The data used to train the ML model were extracted from the simulation results. For Newtonian fluids, a combination of six input parameters was used to calculate the mixing index of 1890 different micromixer designs. To train the ML model, the Regression Learner toolbox (MATLAB) was initially used to find the most suitable model. After training all the available models in the toolbox, including linear regression, neural networks, regression trees, support vector machines, and Gaussian process regression, the best performing models were found to be neural networks and regression trees. A neural network model was adopted as the ML model. For a more customized model, a MATLAB's Neural Network Fitter toolbox was then used to train a neural network by setting the hyperparameters manually, which were the number of hidden layers, neurons, and optimization mathematical process. In particular, two hidden layers were used with 100 hidden neurons in each of them, while Bayesian regularization was used for optimization since it has high generalization capabilities. The data were split into 70% for training and 30% for validation, and the neural network was trained accordingly. The non-Newtonian fluids data included 56 700 different designs, which had the same six input parameters used for Newtonian fluids with the addition of two extra parameters related to non-Newtonian fluids, resulting in a total of eight input parameters. The data were then reduced to 1890 designs to be comparable with the results of the Newtonian fluids data, and a deep neural network with the same hyperparameters of the neural networks used for Newtonian fluids was also used for training an ML model.
D. GUI design
To enable the trained ML model to be effectively used for mixing index prediction, a graphical user interface (GUI) was developed using the App Designer tool (MATLAB). The GUI enables the employment of the ML model by non-programmers, where a diagram of an example micromixer is shown to illustrate the meaning of each of the six input parameters. The user can choose between using a Newtonian and non-Newtonian fluid, which has six or eight input parameters, respectively. For each parameter, a text box with the name of the corresponding parameter is included, allowing the user to enter the desired value, taking into consideration the upper and lower limits of the parameters and whether they can be integers or real numbers, where the GUI rejects any incompatible values. The trained ML model was integrated with the GUI in such a way that after entering all the six or eight parameters, when the user clicks the “Calculate” button, the developed function is called to input the entered parameters into the trained ML model, calculate the predicted mixing index, and show the result to the user. An additional text box was added to show the area spanned by the micromixer for both Newtonian and non-Newtonian by implementing a function within the GUI that calculates that area based on Eq. (9).
E. Educational module
Through the developed GUI, an educational module was designed for micromixer optimization. By the employment of this module, a group of students were trained. Prior to the study, consent was taken from all the students to process their information for educational and research purposes. The participants consisted of 18 undergraduates and graduates enrolled in the course “Fundamentals of Microfluidics” at Koç University. The students were asked to find the optimum mixing index by changing the parameters and running the code to obtain the results using a set of instructive problems (Table II). Students were asked to evaluate their experience in the module,54 using the five-point Likert scale questionnaire survey (Table III) by indicating their degree of accordance ranging from strongly agree to strongly disagree.
TABLE II.
Questions offered to students as an instruction to interact with the educational module.
| # | Please consider Newtonian fluids for questions 1, 2, 3. |
| 1 | Please set the Q = 10 μL min−1, w = 100 μm, a = 2, L = 5, n = 1 and observe the effect of p (in other words, the effect of the curvature profile on micromixing performance). What is the effect of increasing p on mixing performance? |
| 2 | Please set p = 2 and Q = 10 μL min−1 and play with w, a, L, and n values. Please state the most and the least effective geometrical parameters on mixing performance. |
| 3 | Please try to find a set of parameters that gives the mixing performance for flow rates of 1000, 100, 10, and 1 μL min−1. The mixing index can go up to %99. Please try to spend at most 60 s for each flow rate value. |
| 4 | Please apply the parameters that you found in question 3 for Q = 1 μL min−1 to the non-Newtonian fluid case. Keep the non-Newtonian coefficient 1 and evaluate mixing performance for various values of the flow behavior index between nindex = 0.7 (shear thickening fluid) and nindex = 1.3 (shear thinning fluid). Try to observe whether the mixing index is different for shear thinning and shear thickening fluids. |
| 5 | Repeat question 4 for Q = 1 μL min−1. Please compare the effect of the non-Newtonian fluid characteristic for different flow rates. What might be the reason if you observe any difference? |
| 6 | For Q = 1 μL min−1 and nindex = 0.7, please vary the fluid consistency coefficient as powers of 10 (e.g., 10−2, 10−1, and 103). Does the fluid consistency coefficient affect the mixing performance of the micromixer? |
| 7 | Please repeat question 6 for Q = 1 μL min−1 and nindex = 1.3. Is the effect of fluid consistency coefficient the same for shear thickening and shear thinning fluids? |
| 8 | Do you think micromixers that were designed for Newtonian fluids should be re-designed when used with a non-Newtonian fluid based on your understanding from the app? |
| 9 | Did you have previous background about micromixers (their design and application)? |
TABLE III.
Survey questionnaire used for assessing the introduced education module. Legend: 1 = strongly disagree; 2 = disagree; 3 = neither agree nor disagree; 4 = agree; and 5 = strongly agree.
| # | Statement | How much do you agree with the statement? | ||||
|---|---|---|---|---|---|---|
| 1 | The module helped me to understand mixing optimization idea. | 1 | 2 | 3 | 4 | 5 |
| 2 | The legend figure given in the software was informative. | 1 | 2 | 3 | 4 | 5 |
| 3 | The problems given to me were clear. | 1 | 2 | 3 | 4 | 5 |
| 4 | The education module was interesting and involving. | 1 | 2 | 3 | 4 | 5 |
| 5 | The software graphical user interface is easy to use. | 1 | 2 | 3 | 4 | 5 |
| 6 | I could understand the different parameters that are used for optimization of mixers. | 1 | 2 | 3 | 4 | 5 |
| 7 | I was able to run the software by myself. | 1 | 2 | 3 | 4 | 5 |
| 8 | I could figure out how to work with the software easily. | 1 | 2 | 3 | 4 | 5 |
| 9 | I could understand how the entered parameters affect mixing. | 1 | 2 | 3 | 4 | 5 |
| 10 | I was able to optimize the mixer design independently. | 1 | 2 | 3 | 4 | 5 |
III. RESULTS
A combination of parameters in Table I enabled the simulation of micromixer structures with Re numbers ranging from 0.033 to 0.83. The mesh independence study showed that the mesh setting did not have a significant effect on simulating low Re flows [Figs. 3(f) and 3(g)]. However, for Re > 1 flows, the reduced mesh quality has shown a detrimental effect on the simulation results. By utilizing the meshing setting described in Sec. II B, we were able to achieve comparable results to the best quality meshing setup, while also managing to maintain a reasonable computational load for the vast number of simulations. Velocity and pressure profiles were generated using Eq. (4). [Figs. 2(c) and 2(d)]. The area covered by the micromixer structure was 4 mm2 in the largest structure while the smallest design merely crossed 0.0046 mm2. For the Newtonian simulations, the lowest M was determined as 0.13 in the case of , and ( ), while M of ∼1 was reached for multiple cases. On the other hand, the smallest M in non-Newtonian simulations was calculated as 0.17 in the case of , , , and ( ). As expected, the most effective geometrical parameter on M was the number of serpentines (n). Nevertheless, increasing n also expanded the total area covered by the six micromixers, which is not desired for applications that possess spatial limitations. Therefore, minor effects of other geometrical and fluidic parameters on M were investigated with ML. The output of 1890 Newtonian and 56 700 non-Newtonian simulations (later reduced to 1890) was documented as a library, which was used to train the ML model.
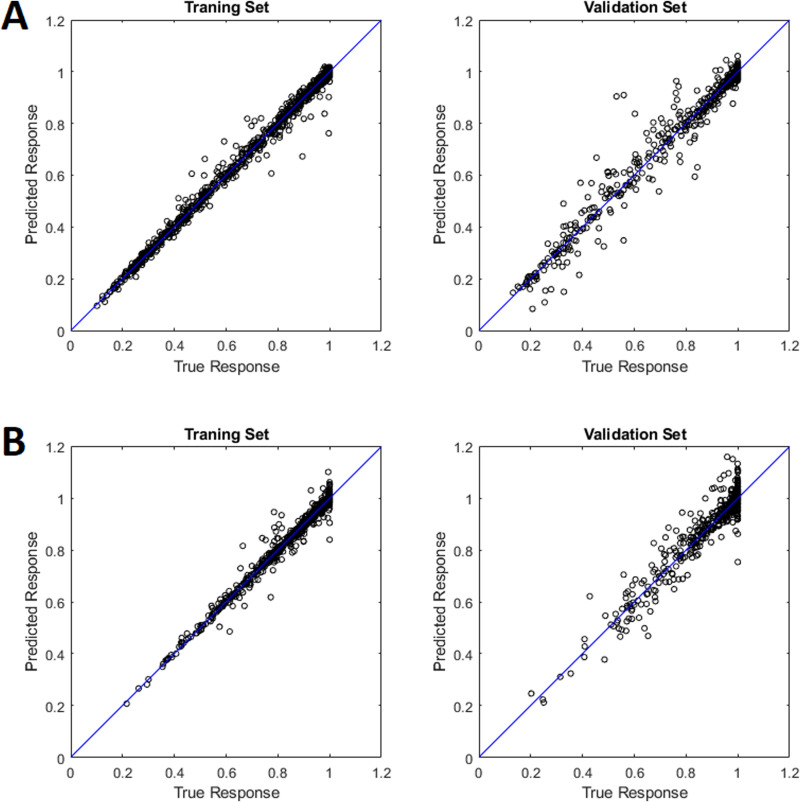
FIG. 3.
True vs predicted responses of the training (left) and validation (right) subsets after training the neural network models for (a) Newtonian fluids data and (b) non-Newtonian fluids data.
After training all the models available in the Regression Learner toolbox of MATLAB, the R2 values were checked as an indicator for the prediction power of the ML models: R2 = 1 means perfect prediction and R2 = 0 means completely wrong prediction. As a result, the models that yielded the highest R2 values were neural network and regression trees, with R2 values of 0.94 and 0.93, respectively. In some cases, neural networks predicted the mixing index to be slightly higher than the maximum possible mixing index, which was 1, but not more than 1.07. On the other hand, although regression tree prediction did not exceed 1, its predicted values were always restricted by the mixing indexes provided by the training data set. The over-prediction of the neural network was not significant, while its R2 value was higher than that of the regression tree. The customized neural network yielded a higher R2 value than when it was trained with the regression toolbox, indicating R2 = 0.9543 [Fig. 3(a)]. On the other hand, training the data from non-Newtonian simulations with different models in the regression toolbox showed a lower R2 of 0.9063 [Fig. 3(b)]. In addition to R2, mean absolute error, mean absolute percentage error, and root mean square error metrics were also calculated and reported in Table IV.
TABLE IV.
Neural networks training metrics for Newtonian and non-Newtonian fluids.
| R2 | Mean absolute error (MAE) | Mean absolute percentage error (MAPE) | Root mean square error (RMSE) | ||
|---|---|---|---|---|---|
| Newtonian data | Training set (70%) | 0.9939 | 0.0111 | 1.7901 | 0.0204 |
| Validation set (30%) | 0.9543 | 0.0282 | 5.0187 | 0.0552 | |
| Non-Newtonian data | Training set (70%) | 0.9789 | 0.0089 | 1.0520 | 0.0199 |
| Validation set (30%) | 0.9063 | 0.0282 | 3.4744 | 0.0442 |
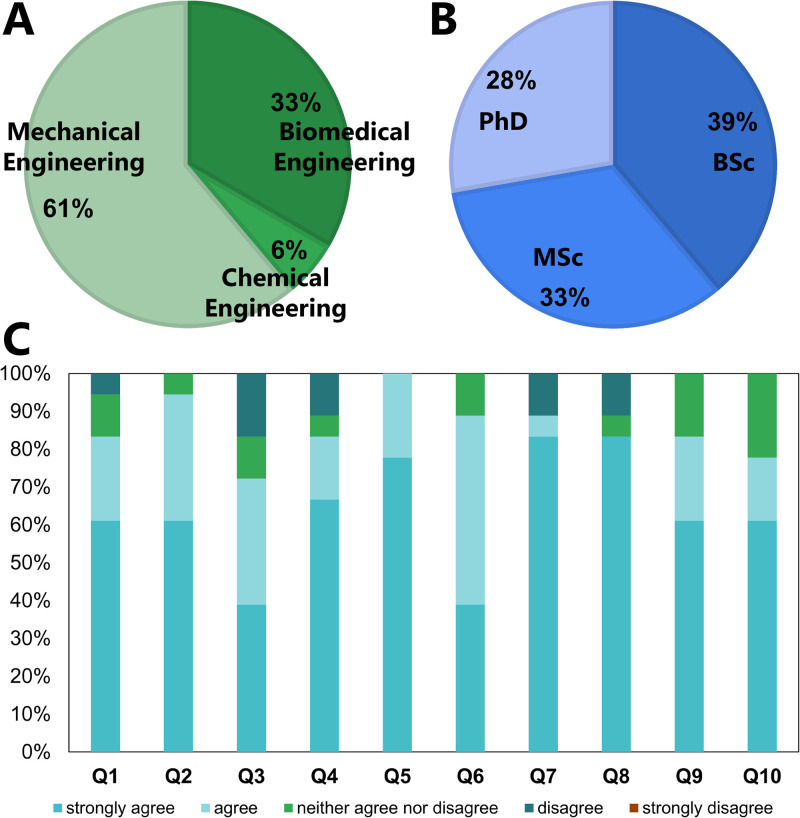
Using the five parameters affecting geometrical properties and one characteristic of the fluid flow, a graphical user interface (GUI) was developed based on the ML model for the prediction of new results when these parameters were altered (Fig. 4). The developed GUI included two sections for Newtonian fluids and non-Newtonian fluids. The user without any programming background could enter the desired parameters. Upon pressing the “Calculate” button, two results would be updated: the predicted mixing index as percentage and the area spanned by the micromixer in mm2. The developed GUI was used as an interactive educational module for micromixers. The subject major and degree of students attending the class are illustrated in Figs. 5(a) and 5(b). The analysis of feedback using the survey (Table III) indicated overall satisfaction with the presented educational module [Fig. 5(c)]. For example, ∼80% of students expressed that they strongly agreed or agreed that the educational module helped them to acquire key concepts to understand mixing optimization. Furthermore, more than 85% of the students indicated that they could figure out how to work with the software independently without any assistance.
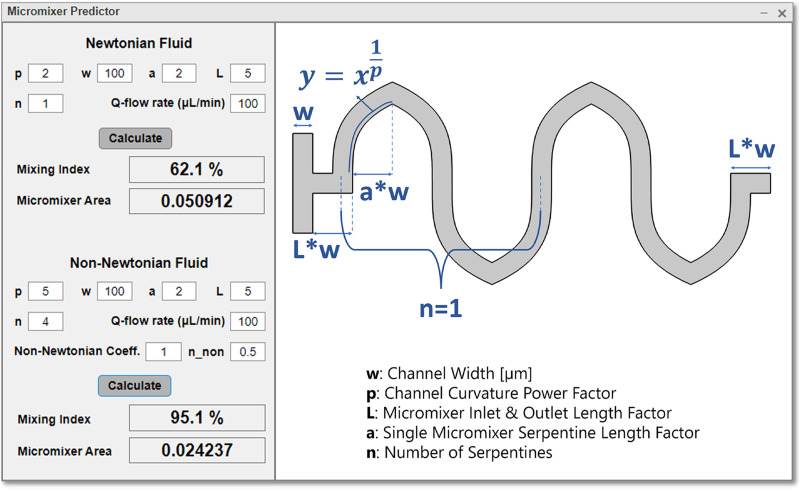
FIG. 4.
The graphical user interface (GUI) that was developed as the educational tool. The parameters affecting the effectiveness of mixing, including five geometrical parameters and the flow rate, are chosen from the left tab. The ML model predicts new results when these parameters are altered. The GUI includes two separate sections for Newtonian fluids and non-Newtonian fluids. Users enter their desired parameters in the appropriate sections and upon pressing the “Calculate” button, the predicted mixing index result based on the ML model appears as percentage next to this button.
FIG. 5.
The developed ML-enabled interactive educational module was presented to a class in a course open to (a) engineering students with various backgrounds and (b) including both undergraduate and graduate students. (c) After interacting with the module, the students' responses to the survey were analyzed to validate the feedback from the module and evaluate the satisfaction of the students.
IV. CONCLUSIONS
ML-based optimization of mixing performance of micromixers at low Re regimes for Newtonian and non-Newtonian fluids was demonstrated to develop an interactive educational module. This simulation module was used for training undergraduate and graduate students in microfluidic concepts and geometries. The obtained results from the survey demonstrated a higher level of understanding of key concepts in microfluidics. The developed module enabled the students to enhance their understanding of microfluidic chips and the optimization of micromixer designs. Students' feedback on the educational module was highly positive. The application of AI techniques in education can be a supplementary approach in addition to conventional content-heavy teaching methods.
ACKNOWLEDGMENTS
S. T. acknowledges Tubitak 2232 International Fellowship for Outstanding Researchers Award (No. 118C391), Alexander von Humboldt Research Fellowship for Experienced Researchers, Marie Skłodowska-Curie Individual Fellowship (No. 101003361), and Royal Academy Newton-Katip Çelebi Transforming Systems Through Partnership Award (No. 120N019) for the financial support of this research. Opinions, interpretations, conclusions, and recommendations are those of the author and are not necessarily endorsed by the TÜBİTAK. This work was partially supported by Science Academy's Young Scientist Awards Program (BAGEP), Outstanding Young Scientists Awards (GEBİP), and Bilim Kahramanlari Dernegi the Young Scientist Award. This study was conducted using the service and infrastructure of Koç University Translational Medicine Research Center (KUTTAM). The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript apart from those disclosed. Some elements in Fig. 1 have been designed using free resources from flaticon.com.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Mehmet Tugrul Birtek and M. Munzer Alseed have contributed equally to this work.
Mehmet Tugrul Birtek: Data curation (equal); Software (equal); Writing – original draft (equal). M. Munzer Alseed: Data curation (equal); Software (equal); Writing – original draft (equal). Misagh Rezapour Sarabi: Visualization (equal); Writing – original draft (equal). Abdollah Ahmadpour: Software (equal); Writing – review & editing (equal). Ali K. Yetisen: Conceptualization (equal); Funding acquisition (equal); Project administration (equal); Supervision (equal); Writing – review & editing (equal). Savas Tasoglu: Conceptualization (equal); Funding acquisition (equal); Project administration (equal); Software (equal); Supervision (equal); Writing – review & editing (equal).
Author Contributions
Mehmet Tugrul Birtek: Data curation (equal); Software (equal); Writing – original draft (equal). M. Munzer Alseed: Data curation (equal); Software (equal); Writing – original draft (equal). Misagh Rezapour Sarabi: Visualization (equal); Writing – original draft (equal). Abdollah Ahmadpour: Software (equal); Writing – review & editing (equal). Ali K. Yetisen: Conceptualization (equal); Funding acquisition (equal); Project administration (equal); Supervision (equal); Writing – review & editing (equal). Savas Tasoglu: Conceptualization (equal); Funding acquisition (equal); Project administration (equal); Software (equal); Supervision (equal); Writing – review & editing (equal).
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Cai G. et al. , “A review on micromixers,” Micromachines 8(9), 274 (2017). 10.3390/mi8090274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee C. Y. and Fu L. M., “Recent advances and applications of micromixers,” Sens. Actuators B 259, 677–702 (2018). 10.1016/j.snb.2017.12.034 [DOI] [Google Scholar]
- 3.Sokullu E. et al. , “Microfluidic invasion chemotaxis platform for 3D neurovascular co-culture,” Fluids 7(7), 238 (2022). 10.3390/fluids7070238 [DOI] [Google Scholar]
- 4.Chen X. Y. and Zhang L., “A review on micromixers actuated with magnetic nanomaterials,” Microchim. Acta 184(10), 3639–3649 (2017). 10.1007/s00604-017-2462-2 [DOI] [Google Scholar]
- 5.Yaralioglu G. G. et al. , “Ultrasonic mixing in microfluidic channels using integrated transducers,” Anal. Chem. 76(13), 3694–3698 (2004). 10.1021/ac035220k [DOI] [PubMed] [Google Scholar]
- 6.Ahmed D. et al. , “A millisecond micromixer via single-bubble-based acoustic streaming,” Lab Chip 9(18), 2738–2741 (2009). 10.1039/b903687c [DOI] [PubMed] [Google Scholar]
- 7.Ang K. M. et al. , “Amplitude modulation schemes for enhancing acoustically-driven microcentrifugation and micromixing,” Biomicrofluidics 10(5), 054106 (2016). 10.1063/1.4963103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boroun S. and Larachi F., “Enhancing liquid micromixing using low-frequency rotating nanoparticles,” AIChE J. 63(1), 337–346 (2017). 10.1002/aic.15456 [DOI] [Google Scholar]
- 9.Hejazian M. and Nguyen N. T., “A rapid magnetofluidic micromixer using diluted ferrofluid,” Micromachines 8(2), 37 (2017). 10.3390/mi8020037 [DOI] [Google Scholar]
- 10.Jeon H., Massoudi M., and Kim J., “Magneto-hydrodynamics-driven mixing of a reagent and a phosphate-buffered solution: A computational study,” Appl. Math. Comput. 298, 261–271 (2017). 10.1016/j.amc.2016.11.026 [DOI] [Google Scholar]
- 11.Huang C. H. and Tsou C., “The implementation of a thermal bubble actuated microfluidic chip with microvalve, micropump and micromixer,” Sens. Actuators A 210, 147–156 (2014). 10.1016/j.sna.2014.02.015 [DOI] [Google Scholar]
- 12.Meng J. Y. et al. , “AC electrothermal mixing for high conductive biofluids by arc-electrodes,” J. Micromech. Microeng. 28(6), 065004 (2018). 10.1088/1361-6439/aab39b [DOI] [Google Scholar]
- 13.Kunti G., Bhattacharya A., and Chakraborty S., “Electrothermally actuated moving contact line dynamics over chemically patterned surfaces with resistive heaters,” Phys. Fluids 30(6), 062004 (2018). 10.1063/1.5028172 [DOI] [Google Scholar]
- 14.Matsubara K. and Narumi T., “Microfluidic mixing using unsteady electroosmotic vortices produced by a staggered array of electrodes,” Chem. Eng. J. 288, 638–647 (2016). 10.1016/j.cej.2015.12.013 [DOI] [Google Scholar]
- 15.Zhao W. et al. , “Rapid mixing by turbulent-like electrokinetic microflow,” Chem. Eng. Sci. 165, 113–121 (2017). 10.1016/j.ces.2017.02.027 [DOI] [Google Scholar]
- 16.Same S. et al. , “Halloysite clay nanotube in regenerative medicine for tissue and wound healing,” Ceram. Int. 48(21), 31065–31079 (2022). 10.1016/j.ceramint.2022.05.037 [DOI] [Google Scholar]
- 17.Bazaz S. R. et al. , “A hybrid micromixer with planar mixing units,” RSC Adv. 8(58), 33103–33120 (2018). 10.1039/C8RA05763J [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Raza W., Hossain S., and Kim K. Y., “A review of passive micromixers with a comparative analysis,” Micromachines 11(5), 455 (2020). 10.3390/mi11050455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lee C. Y. et al. , “Passive mixers in microfluidic systems: A review,” Chem. Eng. J. 288, 146–160 (2016). 10.1016/j.cej.2015.10.122 [DOI] [Google Scholar]
- 20.Chen X. Y. and Li T. C., “A novel passive micromixer designed by applying an optimization algorithm to the zigzag microchannel,” Chem. Eng. J. 313, 1406–1414 (2017). 10.1016/j.cej.2016.11.052 [DOI] [Google Scholar]
- 21.Sarabi M. R. et al. , “Disposable paper-based microfluidics for fertility testing,” iScience 25(9), 104986 (2022). 10.1016/j.isci.2022.104986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sokullu E. et al. , “3D engineered neural co-culture model and neurovascular effects of marine fungi-derived citreohybridonol,” AIP Adv. 12(9), 095102 (2022). 10.1063/5.0100452 [DOI] [Google Scholar]
- 23.Liu R. H. et al. , “Passive mixing in a three-dimensional serpentine microchannel,” J. Microelectromech. Syst. 9(2), 190–197 (2000). 10.1109/84.846699 [DOI] [Google Scholar]
- 24.Yang A. S. et al. , “A high-performance micromixer using three-dimensional tesla structures for bio-applications,” Chem. Eng. J. 263, 444–451 (2015). 10.1016/j.cej.2014.11.034 [DOI] [Google Scholar]
- 25.Lim T. W. et al. , “Three-dimensionally crossing manifold micro-mixer for fast mixing in a short channel length,” Lab Chip 11(1), 100–103 (2011). 10.1039/C005325M [DOI] [PubMed] [Google Scholar]
- 26.Sadabadi H., Packirisamy M., and Wüthrich R., “High performance cascaded PDMS micromixer based on split-and-recombination flows for lab-on-a-chip applications,” RSC Adv. 3(20), 7296 (2013). 10.1039/c3ra40910d [DOI] [Google Scholar]
- 27.Yu K. H., Beam A. L., and Kohane I. S., “Artificial intelligence in healthcare,” Nat. Biomed. Eng. 2(10), 719–731 (2018). 10.1038/s41551-018-0305-z [DOI] [PubMed] [Google Scholar]
- 28.Rezapour Sarabi M., Nakhjavani S. A., and Tasoglu S., “3D-printed microneedles for point-of-care biosensing applications,” Micromachines 13(7), 1099 (2022). 10.3390/mi13071099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Esteva A. et al. , “A guide to deep learning in healthcare,” Nat. Med. 25(1), 24–29 (2019). 10.1038/s41591-018-0316-z [DOI] [PubMed] [Google Scholar]
- 30.Chen M. et al. , “Disease prediction by machine learning over big data from healthcare communities,” IEEE Access 5, 8869–8879 (2017). 10.1109/ACCESS.2017.2694446 [DOI] [Google Scholar]
- 31.Sarabi M. R., Yetisen A. K., and Tasoglu S., “Magnetic levitation for space exploration,” Trends Biotechnol. 40(8), 915–917 (2022). 10.1016/j.tibtech.2022.03.010 [DOI] [PubMed] [Google Scholar]
- 32.Liao Z. J. et al. , “Cancer diagnosis through IsomiR expression with machine learning method,” Curr. Bioinf. 13(1), 57–63 (2018). 10.2174/1574893611666160609081155 [DOI] [Google Scholar]
- 33.Osareh A. and Shadgar B., “Machine learning techniques to diagnose breast cancer,” in 2010 5th International Symposium on Health Informatics and Bioinformatics (IEEE, Piscataway, NJ, 2010). 10.1109/HIBIT.2010.5478895 [DOI] [Google Scholar]
- 34.Sarabi R. et al. , “Machine learning-enabled prediction of 3D-printed microneedle features,” Biosensors 12(7), 491 (2022). 10.3390/bios12070491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ranschaert E. R., Morozov S., and Algra P. R., Artificial Intelligence in Medical Imaging: Opportunities, Applications and Risks (Springer, 2019). [Google Scholar]
- 36.Mohri M., Rostamizadeh A., and Talwalkar A., Foundations of Machine Learning (MIT press, 2018). [Google Scholar]
- 37.Bonaccorso G., Machine Learning Algorithms (Packt Publishing Ltd, 2017). [Google Scholar]
- 38.Goh G. D., Sing S. L., and Yeong W. Y., “A review on machine learning in 3D printing: Applications, potential, and challenges,” Artif. Intell. Rev. 54(1), 63–94 (2020). 10.1007/s10462-020-09876-9 [DOI] [Google Scholar]
- 39.Yigci D. et al. , “3D bioprinted glioma models,” Prog. Biomed. Eng. 4(4), 042001 (2022). 10.1088/2516-1091/ac7833 [DOI] [Google Scholar]
- 40.Shi Y. et al. , “Manufacturability analysis for additive manufacturing using a novel feature recognition technique,” Comput. Aided Des. Appl. 15(6), 941–952 (2018). 10.1080/16864360.2018.1462574 [DOI] [Google Scholar]
- 41.Gan Z. T. et al. , “Data-driven microstructure and microhardness design in additive manufacturing using a self-organizing map,” Engineering 5(4), 730–735 (2019). 10.1016/j.eng.2019.03.014 [DOI] [Google Scholar]
- 42.Sarlo R. and Tarazaga P. A., “A neural network approach to 3D printed surrogate systems,” in Topics in Modal Analysis & Testing (Springer, 2016), Vol. 10, pp. 215–222. [Google Scholar]
- 43.Son D., Liimatainen V., and Sitti M., “Machine learning-based and experimentally validated optimal adhesive fibril designs,” Small 17(39), 2102867 (2021). 10.1002/smll.202102867 [DOI] [PubMed] [Google Scholar]
- 44.Chen X., “Two decades of artificial intelligence in education,” Educ. Technol. Soc. 25, 28–47 (2022; available at https://www.jstor.org/stable/48647028. [Google Scholar]
- 45.Roll I. and Wylie R., “Evolution and revolution in artificial intelligence in education,” Int. J. Artif. Intell. Educ. 26, 582–599 (2016). 10.1007/s40593-016-0110-3 [DOI] [Google Scholar]
- 46.Chen L., Chen P., and Lin Z., “Artificial intelligence in education: A review,” IEEE Access 8, 75264–75278 (2020). 10.1109/ACCESS.2020.2988510 [DOI] [Google Scholar]
- 47.Owoc M. L., Sawicka A., and Weichbroth P., “Artificial intelligence technologies in education: Benefits, challenges and strategies of implementation,” in Artificial Intelligence for Knowledge Management: 7th IFIP WG 12.6 International Workshop, AI4KM 2019, Held at IJCAI 2019, Macao, China, 11 August 2019 (Springer, 2021), Revised Selected Papers. [Google Scholar]
- 48.Xie H., Zhao X., and Yang H., “Experimental and numerical study on a planar passive micromixer with semicircle mixing elements,” in 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (IEEE, Piscataway, NJ, 2010). 10.1109/AIM.2010.5695817 [DOI] [Google Scholar]
- 49.Chen J. et al. , “Crosswise ridge micromixers with split and recombination helical flows,” Chem. Eng. Sci. 66(10), 2164–2176 (2011). 10.1016/j.ces.2011.02.022 [DOI] [Google Scholar]
- 50.Tran-Minh N., Dong T., and Karlsen F., “An efficient passive planar micromixer with ellipse-like micropillars for continuous mixing of human blood,” Comput. Methods Programs Biomed. 117(1), 20–29 (2014). 10.1016/j.cmpb.2014.05.007 [DOI] [PubMed] [Google Scholar]
- 51.Le The H. et al. , “An effective passive micromixer with shifted trapezoidal blades using wide Reynolds number range,” Chem. Eng. Res. Des. 93, 1–11 (2015). 10.1016/j.cherd.2014.12.003 [DOI] [Google Scholar]
- 52.The H. L. et al. , “Geometric effects on mixing performance in a novel passive micromixer with trapezoidal-zigzag channels,” J. Micromech. Microeng. 25(9), 094004 (2015). 10.1088/0960-1317/25/9/094004 [DOI] [Google Scholar]
- 53.Liao Y., Mechulam Y., and Lassalle-Kaiser B., “A millisecond passive micromixer with low flow rate, low sample consumption and easy fabrication,” Sci. Rep. 11(1), 20119 (2021). 10.1038/s41598-021-99471-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Golman B. and Yermukhambetova A., “An excel VBA-based educational module for simulation and energy optimization of spray drying process,” Comput. Appl. Eng. Educ. 27(5), 1103–1112 (2019). 10.1002/cae.22139 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.