Abstract
We develop a framework for the design of optimized alchemical transformation pathways in free energy simulations using non-linear mixing and a new functional form for so-called “softcore” potentials. We describe the implementation and testing of this framework in the GPU-accelerated AMBER software suite. The new optimized alchemical transformation pathways integrate a number of important features, including: 1) the use of smoothstep functions to stabilize behavior near the transformation end points, 2) consistent power scaling of Coulomb and Lennard-Jones (LJ) interactions with unitless control parameters to maintain balance of electrostatic attractions and exchange repulsions, 3) pairwise form based on the LJ contact radius for the effective interaction distance with separation-shifted scaling, and 4) rigorous smoothing of the potential at the non-bonded cut-off boundary. The new softcore potential form is combined with smoothly transforming non-linear λ weights for mixing specific potential energy terms, along with flexible λ-scheduling features, to enable robust and stable alchemical transformation pathways. The resulting pathways are demonstrated and tested, and shown to be superior to the traditional methods in terms of numerical stability and minimal variance of the free energy estimates for all cases considered. The framework presented here can be used to design new alchemical enhanced sampling methods, and leveraged in robust free energy workflows for large ligand datasets.
Graphical Abstract
1. Introduction
Alchemical free energy simulations are an integral part of computer aided drug design, particularly at the stage of lead refinement where they are used to rank the binding affinity of compounds to their targets, and in some cases make predictions about selectivity and off-target effects.1-8 As a result, there is great activity in the field to develop a wide range of methods for which to improve the accuracy, robustness and throughput of these simulations.2,9-13 Alchemical free energy methods leverage the property that the free energy is a state function to enable non-physical thermodynamic pathways to be constructed that are amenable to computation. So while, in principle, the free energy is independent of transformation pathway, in practice the choice of pathway is crucial. For example, whereas the direct calculation of the binding free energy of a ligand along a physical pathway can be considerably challenging and computationally intensive to achieve with high precision (although there has been much progress in this area14-16), it is often easier to compute the “alchemical” transformation between two similar ligands, both in the bound and unbound states, to arrive at the desired free energy difference (Fig. 1). In this way, the relative binding free energy17 (RBFE) can be computed with sampling requirements that are often less intensive and more precise than the calculation of an absolute binding free energy (ABFE) whether along a physical pathway that would provide additional information about binding kinetics, or alchemical pathway where the ligand is “annihilated” in the bound state and in solution. Analogously, the relative and absolute solvation free energy (RSFE and ASFE, respectively) can be computed considering transformations in the gas phase and in solution. These cycles are illustrated in Figure 1.
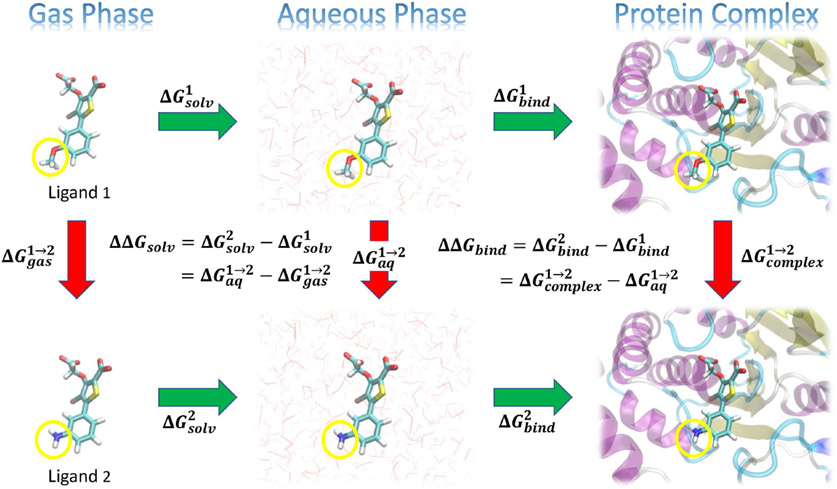
Figure 1:
Illustration of a thermodynamic cycle for a relative solvation free energy, RSFE (ΔΔGsolv) and relative binding free energy, RBFE (ΔΔGbind) for two ligands (“Ligand 1” and “Ligand 2”). The green arrows represent the absolute solvation free energy, ASFE (ΔGsolv) and absolute binding free energy, ABFE (ΔGbind) of each ligand (indicated by superscripts) that involve changing their environment from gas to aqueous phase, or from unbound in the aqueous phase to bound in a complex with the protein target, respectively. These quantities are experimentally measurable, but are challenging to directly compute as the change in the environment can be considerably complicated. The red arrows represent alchemical transformations where Ligand 1 is mutated into a similar Ligand 2 in a fixed environment. These transformations are frequently more amenable to practical computations. The yellow circles in the figures indicate the region of each ligand that undergoes the most significant changes in the alchemical transformation, and would likely be modeled using a so-called “softcore potential” during the transformation.
Alchemical free energy simulations typically require atoms to be created and/or annihilated during the transformation process - or more precisely, transformed into a so-called “dummy atoms”.18 Dummy atoms are placeholders that are designed to interact with the real atoms of the physical system only through select bonded interactions such that they do not alter the relative free energy (i.e., they do not introduce a net potential of mean force on any of the real atoms). Transformations of real atoms into dummy atoms can be especially challenging if there is poor phase space overlap of neighboring states along the transformation coordinate.18-22 This issue is not restricted to only transformations of real atoms into dummy atoms (which is an extreme case), it can also occur in transformations between two real atoms that have significantly different force field parameters.
A number of strategies have been explored to develop robust, stable transformation pathways in alchemical free energy simulations, including use of so-called “softcore potentials” with separation-shifted scaling,23-25 parameter interpolation,26 short-range switching,27 or capping the short-range interactions,28,29 and non-linear mixing of the endpoint potentials. 30-34 Recent studies have shown that adverse effects of these problematic transitions can lead to large variance and in some cases order/disorder transitions along the alchemical path that can hinder sampling and convergence of free energy estimates.29 Very recently, a λ-enveloping distribution sampling method,35-37 which is related to approaches to optimize minimum variance pathways in alchemical transformations,38-40 has been explored as an alternative coupling scheme to more conventional λ-intermediate states.
There are many strategies for performing free energy simulations,2,4 and in turn choosing appropriate alchemical transformation pathways. In the present work we will develop robust alchemical pathways (including new softcore potentials) that are particularly useful for “concerted” alchemical transformations (sometimes referred to as “one-step” or “unified” procedures) where all non-bonded terms (e.g., electrostatic and Lennard-Jones) terms occur synchronously. This differs from “stepwise” transformations (sometimes referred to as “multistep” or “split” procedures) where transformation of electrostatic and Lennard-Jones terms occur asynchronously; for example, in a 3-step “decharge/LJ/recharge” transformation. Concerted transformations are particularly useful in relative binding free energy calculations as they avoid weakly bound states that may require additional restraints. Nonetheless, the methods presented here are not restricted to purely concerted transformations, and as will be shown below, have been integrated into a powerful λ-scheduling framework in AMBER that enables the design of customized alchemical transformations for different energy terms that are seamlessly integrated with existing enhanced sampling tools such as replica exchange.
In the present work, we develop new highly robust alchemical transformation pathways that are designed to overcome commonly encountered classes of problems23,27,30,31,33 designated here as endpoint catastrophes, particle collapses, and large gradient-jumps. This work builds on our previously developed smoothstep softcore potentials,41 but introduces a number of important improvements, including: 1) consistent power scaling of Coulomb (Coul) and Lennard-Jones (LJ) interactions with unitless control parameters to maintain balance of electrostatic attractions and exchange repulsions, 2) introduction of a pairwise form based on the LJ contact radius for the effective interaction distance with separation-shifted scaling, and 3) rigorous smoothing of the softcore potential at the non-bonded cut-off boundary. We test the new alchemical transformation pathway on a number of systems in both the context of thermodynamic integration (TI) and free energy perturbation (FEP), and compare results to other commonly used pathways and softcore potentials.
The remainder of the manuscript is organized as follows. Section 2 outlines the key theoretical background. Section 3 provides details of the computational methods. Section 4 presents results and discussion for a series of test cases and comparison with other methods. Section 5 concludes with a summary of main points and direction for next developments. The methods presented here are available for beta testing in the Drug Discovery Boost upgrade to the AMBER software suite, and will be integrated into the next official AMBER release.
2. Theory
This section summarizes the theoretical background for the alchemical transformation pathway framework and provides implementation-level details. In particular, we develop alchemical transformation pathways that combine non-linear mixing of different potential energy terms and a new smoothstep softcore potential to enable robust, stable free energies to be computed. Section 2.1 summarizes the necessary theoretical background and establishes a notational convention that enables precise definition of specific energy terms, transforming regions and interacting sets of atoms that form the λ-dependent potential energy and transformation pathway. Section 2.2 describes flexible, stable forms and λ-scheduling of the weight functions used to mix different potential energy terms. Section 2.3 describes the new functional form for the softcore potentials. Together, the weights along with the softcore potentials form the foundation of the new alchemical transformation pathways that are developed and tested in the Results and Discussion.
2.1. Background and notation
This section presents the necessary theoretical background as well as develops a notation that enables precise identification of the energy terms and interacting sets of atoms that form the basis of different alchemical transformation pathways. The discussion of the alchemical transformation pathway here will be in the context of thermodynamic integration (TI)42,43 using a hybrid single-dual-topology34 implementation in AMBER22. Nonetheless, the improvement in phase space overlap between states along the pathway are transferable to other FEP methods with traditional BAR,44,45 MBAR46,47 and formally equivalent unbinned weighted histogram analysis methods (UWHAM),48 as well as their recent extensions that enable large-scale network-wide analysis using a constrained variational approach (BARnet and MBARnet).49
In practice, TI and FEP methods generally require taking incremental steps along a alchemical transformation pathway parameterized by a coordinate λ that varies between 0 and 1. The end states at λ values of 0 and 1 are generally physical “real states”, i.e., chemically distinct molecules with distinct compositions. Alternatively, the continuum of states for 0 < λ < 1 are non-physical “alchemical states”. The free energy change, ΔA0→1, between states “0” and “1” can be achieved through integration of the thermodynamic derivative as:
| (1) |
where rN = r1, r2 … rN represent the Cartesian positions of each particle, the second integral involves the derivative of the potential energy U with respect to the parameter λ that smoothly connects the end states λ = 0 and λ = 1, and the sum indicates numerical integration over M quadrature points (λk, for k = 1, … M) with associated weights wk. While the free energy is a state function, and formally is invariant to the pathway connecting states, in practical simulations the thermodynamic averages in eq 1 are extremely sensitive to the pathway, and similar issues arise for FEP methods. The λ-dependent total potential energy U (rN; λ) can be written as
| (2) |
where the individual state energies, U0(rN; λ) and U1(rN; λ) are given in terms of their energy term components (indexed by t) as
| (3) |
and similarly for U1(rN; λ). In eq 3, the subscript t sums over different potential energy terms summarized in Table 1. These individual state energy terms in general can have an explicit non-linear λ-dependence that arises from the form of the softcore potential that is used, as will be described in section 2.3. In addition, in the expression for the λ-dependent total potential energy U(rN; λ), each of the energy terms U0/1,t(rN; λ) has a λ-dependent weight (“mixing term”) associated with it, W0/1,t(λ), the form of which will be described in more detail in section 2.2 below.
Table 1:
Definition of potential energy terms and their abbreviations used as subscripts.a
| Energy Term | Index | Description | Collective Term |
|---|---|---|---|
| Ubond | 7 | Bond stretch | Bonded (b) Ub = Ubond + Uang + Utor |
| Uang | 6 | Angle bend | |
| Utor | 5 | Torsion rotate (proper/improper) | |
| ULJ | 4 | Lennard-Jones | Non-bonded (nb) Unb = Udir + U1−4Ele + ULJ + U1−4LJ |
| U 1−4LJ | 3 | 1-4 Lennard-Jones | |
| Udir | 2 | PME direct/real space | |
| U 1−4Ele | 1 | 1-4 Electrostatic | |
| Urec | 0 | PME reciprocal space |
Absence of an energy term subscript indicates all energy terms (i.e., summation over all energy terms, index t = 0, … 7). The bonded and non-bonded terms are “short” and “inter-mediate” ranged, respectively, and kept track of with array lists, the latter for which is set by a distance cut-off and updated dynamically when needed. Note under these definitions, the 1-4 Ele and 1-4 LJ terms are considered part of the non-bonded terms, and the total electrostatic energy (UEle) is not purely a “non-bonded” term as it contains also the non-local reciprocal space term. i.e., UEle = Udir + U1−4Ele + Urec.
Each of the energy terms in Table 1, with the exception of Urec, involves a straight-forward summation over the relevant sets of atoms to compute 2-body, 3-body or 4-body interactions. In the case of free energy simulations, we need to further distinguish between contributions to the energy that are made from different non-overlapping sets of atoms. Specifically, we need to subdivide the system into two main subdivisions: one region is alchemically transforming, whereas the remainder of the system is immutable (I), i.e., not transforming. Within the hybrid single-dual-topology, the immutable region is represented by a single “topology” and set of coordinates. The transforming region of the system is represented by a formal dual topology and separate sets of coordinates for each state, and is further subdivided into constrained coordinate/common core (CC) and the separable-coordinate/softcore (SC) regions (in previous work13 we used the the abbreviations TC and TS, but feel that SC and CC are more straight forward). The SC, CC and I regions are illustrated in Fig. 2. The CC region has corresponding atoms in each topology constrained to have the same positions in order to facilitate phase space overlap between states during the alchemical transformation. The SC region, on the other hand, has separable independent coordinates for each topology that can adopt different conformations and do not directly interact with one another.
Figure 2:
Illustration of a transformation between two ligands (L66 and L67) bound to a protein target (PTP1B) showing the softcore (SC, blue and red), common core (CC, green) and immutable (I, gray) regions. There are two SC regions (red for L67 on the left, and blue for L66 on the right) that represent functional groups that are annihilated/created during the transformation and involve separate topologies and coordinates. In the end states where the atoms of the SC region are transformed into non-interacting “dummy” atoms, their colors are grayed out. The middle panel depicts an intermediate λ value for which the SC regions of L66 and L67 are partially transformed, as depicted by their partial translucency. The CC region is transforming as well (as the force field parameters are changing from those of L67 to L66), but the atoms share a common set of coordinates within a single topology in order to reduce the amount of phase space sampling. The immutable region is the protein and surrounding solvent that are not transforming. The coordinates of the SC, CC and I regions are all treated dynamically at every stage of the alchemical transformation which is conducted in a series of simulations (“ λ windows”) each at different values of the alchemical transformation coordinate λ that varies from 0 to 1 and controls the potential energy.
For example, if two drug molecules involved in an alchemical transformation (e.g., as shown in Fig. 2) share a common chemical core of atoms such as an aromatic ring and differ only by certain attached substituents for which atoms between the topologies cannot easily be mapped, then the CC region would contain the atoms of the common aromatic ring and the SC region would contain the atoms of the different substituents. In the alchemical transformation of λ : 0 → 1, the SC atoms of state “0” are “turned off” by mutating the real atoms of state “0” into so-called “dummy atoms”,18 while at the same time the SC atoms of state “1” are being “turned on” in a synchronous counter-transformation. The dummy atoms do not interact with their environment, with the exception of certain bonded interactions that must obey the constraint conditions that they introduce no net potential of mean force onto any non-dummy atom. Often this separable dual-coordinate approach requires the introduction of “softcore potentials”,24,41 i.e., explicit non-linear λ-dependent terms to “soften” the interaction of these atoms with their surroundings. These are most often employed for non-bonded interactions such as LJ and Ele (or in the case of PME electrostatics, often just the Udir term), but other forms have also been developed for bonds and other energy terms.23,24,33
Thus the system can be divided into non-overlapping regions described in Table 2: I (immutable), CC (transforming constrained/common core) and SC (transforming separable/softcore). The I region has the same atomic coordinates, parameters and internal potential energy for both states 0 and 1. The CC region can have different parameters between states 0 and 1, but the coordinates of mapped atoms are constrained to be the same. The SC region also can have different parameters between states 0 and 1, but unlike the CC region each state has its own separable set of atomic coordinates.
Table 2:
Energy decomposition terms based on non-overlapping sets of atoms comprising the separable-coordinate/softcore (SC), constrained coordinate/common core (CC) and immutable (I) regions.a
| Energy | Region/Interactions | Description |
|---|---|---|
| USC | Internal energy of the SC region | Each of the contributing bonded or non-bonded internal energy terms arises from a set of atoms that are contained within indicated region; i.e., all atoms of the term belong to the indicated region. |
| UCC | Internal energy of the CC region | |
| UI | Internal energy of the I region | |
| U(CC+I) | Internal energy of the CC+I region | |
| USC/(CC+1) | Interaction energy between SC and (CC+I) regions: USC/(CC+I) = USC/CC + USC/I |
Each of the contributing bonded or non-bonded interaction energy terms arises from a set of atoms that span the SC and combined (CC+I) regions; i.e., some belong to the SC region, while others in the same term belong to the (CC+I) region. |
The three regions are as follows: 1) (SC) Separable coordinate/softcore region that is transforming with λ and is treated with separable coordinates within the dual topology framework; 2) (CC) Constrained coordinate/common core region that is transforming with λ but that shares the same coordinates within the dual topology framework (making it effectively a single topology); and 3) (I) Immutable (not transforming with λ). Regions can be combined as a union of atom sets with the “+” operator; e.g., (SC+CC) combines the SC and CC regions, and (SC+CC+I) would imply all regions (and hence atoms) of the system. The energy decomposition involves using the superscripts UX to indicate either an internal energy within the region “X”, or an interaction energy UX/Y between regions “X” and “Y”. Thus in its most expanded form, the total potential energy can be written as U = USC + UCC + UI + USC/CC + USC/I + UCC/I. Note the absence of subscripts indicates a summation over all energy terms in Table 1; however, the superscript notation can also be applied to energy terms individually. It is assumed, for the convenience and simplification of our notation, that the SC, Cc and I regions are defined in such a way that no individual 3-body or 4-body term spans all three regions (e.g., there is no angle bending term that has one atom in each of the SC, CC and I regions).
To facilitate development of the framework for enabling improved alchemical transformation pathways, we now introduce a system whereby we use subscripts to indicate the state (“0” or “1”) and (optionally) the specific term in the potential energy as described in Table 1, and superscripts to indicate the specific atoms involved in the energy term interaction. The state of the system and specific energy terms follow the general form or where the state is indicated as either 0 or 1, the energy term is designated an appropriate abbreviation index (t) as indicated in Table 1, and the superscript “X” indicates an internal potential energy for region “X” and “X/Y” indicates the interaction energy between regions “X” and “Y” as indicated in Table 2.
Using this notation, the individual state “0” energy, U0 (rN; λ) can be expanded as
| (4) |
and similarly for U1(rN; λ). Note that U0(rN; λ) is the potential energy of the state “0” topology written as (possibly) having an explicit λ dependence (e.g., through a softcore potential or parameter interpolation26 form). The general expanded form of the λ-dependent total potential energy U(rN; λ) can be written as
| (5) |
The above equation is general in the sense that it assumes a possible explicit non-linear λ-dependence for any of the energy terms. In the framework presented here that has been implemented into the AMBER Drug Discovery Boost package to AMBER22 (and will be officially available in the a future AMBER release), only the terms that involve non-bonded interaction involving the SC region will potentially use softcore potentials, and hence have an explicit non-linear λ dependence. Further, as mentioned previously, in the current presentation, the PME reciprocal space term is not decomposed into regional contributions. With these conditions, the specific λ-dependent total potential energy U(rN; λ) can be written as
| (6) |
2.2. λ-dependent weight functions for scaling potential energy components
This section describes the λ-dependent weight functions and the control flags that allow their manipulation in free energy simulations in AMBER. The next subsection 2.2.1 introduces the family of smoothstep functions and describe their most relevant properties that will be exploited to develop the λ-dependent weight functions in the following subsection 2.2.2. In subsection 2.2.3, these weight functions are then generalized to operate on specific sub-ranges of λ between 0 and 1 to form a flexible λ-scheduling framework.
2.2.1. Smoothstep functions
Consider the family of smoothstep functions of orders P (P = 0, 1, 2, …) defined as the polynomial functions (up to P = 4 shown):
| (7) |
The smoothstep functions are monotonically increasing functions that have desirable 0 and 1 endpoint values and vanishing endpoint derivative properties:
| (8) |
In addition, the smoothstep functions obey the symmetry condition
| (9) |
A smoothstep function with a higher order will have a smoother function curve and smaller derivatives near 0 and 1 but a larger derivative in between. The zero-order (P = 0) smooth-step function is in fact simply linear with constant slope, including at the endpoints, which can lead to endpoint catastrophe problems. As illustrated in previous work,41 the second order smoothstep function (P = 2) overall offers a good balance between smooth vanishing derivatives at the endpoints, and modest derivatives for intermediate values of λ. AMBER22 offers the flexibility to choose different smoothstep functions through the λ-scheduling mechanism described below.
2.2.2. Form of the λ-dependent weight functions
We now describe a general form for the weight functions W(λ), where we only retain the 0 and 1 subscript to indicate the state. The weight functions are defined in term of the smoothstep functions as
| (10) |
| (11) |
In the above equation, we drop the explicit superscripts and subscripts in eq 6 that can be controlled by different flags available to the user in AMBER22. Previous work has illustrated that use of smoothstep functions of order greater than 0 (i.e., a weight function that goes beyond the simple linear λ-dependence and has vanishing derivatives at the endpoints), affords improvement of the the transformation pathway, particularly at the endpoints where large variation in < ∂U/∂λ >λ can occur.41 These weight functions both operate within the range 0 ≤ λ ≤ 1 (they have constant endpoint values outside of this range), and satisfy the normalization condition:
| (12) |
and the symmetry condition:
| (13) |
2.2.3. λ-scheduling of weight functions
In some cases, it is desirable to have the flexibility to apply more complicated λ schedules that operate over a subinterval of λ values between 0 and 1. The generalized λ scheduling weight for W0 can be defined so that it is changing only within the interval λmin ≤ λ ≤ λmax as
| (14) |
where 0 ≤ λmin ≤ λmax ≤ 1. In the current framework, the complementary weight function W1(λ) can be selected to either satisfy the normalization condition (eq 12), or the symmetry condition (eq 13) above. Only if the interval z(λ) is centered at λ = 0.5 are both the normalization and symmetry conditions simultaneously satisfied. The Drug Discovery Boost package in AMBER22 allows flexible λ scheduling of this form for different energy components. The detailed usage can be found in the updated AMBER22 manual.50
2.3. New softcore potential form
With a flexible form of the weight functions in eq 6 described, we now turn to a presentation of a new functional form for the softcore potentials that provide the explicit λ-dependence in the potential energy terms in eq 4. In the current framework, softcore potentials are developed for both the LJ and non-bonded electrostatic interactions (i.e., the direct/real space component of the PME method). Hence, the main terms that are affected by the softcore potentials are those contained in the non-bonded interactions between the SC and (CC+I) regions, i.e., those terms present in . Formally, these terms can also be present in the internal energy of the SC region, if these terms are being “turned off” to form the “dummy state”. In principle, the internal potential energy interactions in the dummy state are arbitrary so long as they are treated consistently in different legs of the thermodynamic cycle that are subtracted. However, in practice, choice of the interactions in the dummy state are important, and should be selected to minimize the volume of phase space needed to sample the dummy state while at the same time avoiding sampling traps (multiple distinct free energy basins separated by high barriers) that could lead to inconsistent results. In fact, with the proper choice of potential energy interactions in the dummy state, together with well-established generalized ensemble methods such as Hamiltonian replica exchange51-53 can lead to powerful new alchemical enhanced sampling methods. These issues will be explored in next paper in this series.54 For the present paper, the dummy state was created by scaling (i.e., “turning off”) electrostatic interactions, and in some cases also torsion angle and 1-4 LJ terms, but keeping other bonded and normal LJ terms in place. Hence, the new form of the softcore potential will affect mainly the term, which, as results presented later in the paper will show, has a profound affect on the free energy estimates.
The LJ, Coulomb and PME direct-space interactions for a set of interacting point particles i and j separated by a distance rij are given by
| (15) |
| (16) |
and
| (17) |
where σij and ϵij are the pairwise LJ contact distance and well depth, respectively, and qi and qj are the partial charges of particles i and j, respectively, er f c() is the complementary error function and κ is the Ewald coefficient.
To soften these pairwise particle-particle interactions, a parametric form for the separation-shifted scaling is used to modify the effective interaction distance. A commonly used form23,24 is given by
| (18) |
and
| (19) |
where n and m are positive integers and α and β are adjustable positive semi-definite parameters (note that α is unitless whereas β has units of distance raised to the power of m). The value of n = 6 and m = 2 are often used, and have been the default values in AMBER until the present work. We will demonstrate later in the manuscript how this softcore potential can lead to numerical instabilities, and discuss ongoing efforts and progress to improve the methods.
We introduce the following modified form of the separation-shifted scaling that leads to considerable improvement:
| (20) |
and
| (21) |
where αLJ and αCoul are the corresponding unitless parameters, S2 is the 2nd-order smooth-step function in eq 7, and fSW(rij) is a switching function designed to smoothly return to the normal rij, and thus long-ranged behavior, by the end of the cutoff
| (22) |
where Rcut,i is the distance that the switching function begins switching and Rcut,f is the final distance where the switching ends (returning the effective interaction distance to be rij). Henceforth, we will set Rcut,f = Rcut, and Rcut,i = Rcut − 2 Å, respectively.
The form of the new softcore potential is thus
| (23) |
| (24) |
and
| (25) |
Most free energy simulations in the condensed phase are performed under periodic boundary conditions and use the PME method55,56 to treat long-ranged electrostatic interactions, in which case the electrostatic softcore potentials described here apply to the Udir term (eq 25). If, on the other hand, PME electrostatics is not used, then the electrostatic softcore potential apply to the UCoul term (eq 24).
3. Methods
Throughout the manuscript, we will explore alchemical free energy calculations using concerted transformation pathways. The new alchemical transformation pathway and softcore potential developed here will be compared to several previously developed methods, including the softcore potential method of Steinbrecher, Joung and Case24 with default parameters used in AMBER18, as well as modified parameters developed by Ebert and Labute,57 and a modified smoothstep softcore potential41 used in AMBER20. The present method builds on the latter, but deviates in functional form to include a universal pairwise interaction with consistent power scaling of Coulomb and Lennard-Jones interactions with unitless control parameters and rigorous smoothing of the potential at the non-bonded cut-off boundary. All simulations in the present work were performed with the pmemd.cuda module of AMBER Drug Discovery Boost package (AMBER DD Boost)13 as a modified software patch to AMBER20 that now has been fully implemented and is available in AMBER22.50
3.1. Three example molecular systems
We examine transformations involving three small molecules as test systems. The first test case (denoted “DPT/0”) involves the vanishing transformation of 3,4-diphenyltoluene, a bulky hydrophobic molecule, into a dummy state. The second test case (denoted “Na+/0”) involves the vanishing transformation of Na+, a small ion strongly interacting with its environment, into a dummy state. The third test case (denoted “L51c/h”) involves the alchemical transformation between two factor Xa ligands, L51c → L51h in solution, which involves the migration of charged functional groups from one region of the ligand to another.58 The hydration free energy simulations for DPT/0, Na+/0 and L51c/h were modeled using the GAFF force field11,59 with the AM1-BCC charges60,61 and solvated with TIP3P62 waters (DPT/0, Na+/0 and L51c/h systems contained 2114, 6101 and 1511 water molecules, respectively). All the initial structures for gaseous simulations were prepared by stripping water from those equilibrated structures in the aqueous phase with a periodic box. Alchemical free energy calculations were performed for different softcore potential methods using single-step concerted transformations in a series of 21 alchemical states equally spaced along the λ dimension ranging from 0 to 1 (Δλ = 0.05). The system in each transformation was first energy minimized with 1000 steps which the steepest descent method was used, then the initial conformations for each λ window (total 21 windows) were sequentially generated with 5 ps pre-equilibration with NVT ensemble. Each window was run in the NVT ensemble at 298 K through Langevin thermostat with a friction constant of 5.0 ps−1 for 5.2 ns with the first 200 ps discarded prior to analysis, in order to get 5 ns of production sampling. The long-range electrostatics were evaluated with the particle mesh Ewald (PME) method.55,56 A cutoff of 10 Å was used for non-bonded interactions, including the direct space PME terms and particles interacting through softcore potentials. All simulations were performed using a 1 fs integration time step, and only the bonds and angle involving hydrogens of water molecules were constrained with the SHAKE algorithm.63,64
3.2. Relative hydration and binding free energy simulations
We examine six possible transformations between four ligands (L66, L67, L74 and L75) that target binding to protein tyrosine phosphatase 1B (PTP1B)65,66 with softcore regions for each transformation selected using a variant of the maximum common substructure search algorithm67 as implemented in the Cheminformatics software RDKit.68 Specifically, an “extended” MCS atom-mapping algorithm we developed is used that builds on the original MCS algorithm and excludes from the “maximum overlap” region atoms that differ either in chemical identity or hybridization, and further enforces the condition that for each ligand, the same softcore and common core regions are used consistently for every transformation in the network involving that ligand. We refer to this atom-mapping procedures as MCS-Enw. Initial structures were taken from the published data66 and simulations were prepared using the AMBER ff14SB,69 GAFF270 force fields. Ligands and ligand-protein complexes were solvated using TIP4P-Ew71 water and an initial buffer size of 20 and 16 Å, respectively. Any remaining net charge of the system was first neutralized and then solvated as 0.15 M ion concentration by addition of Na+ or Cl− as appropriate. A minimization with Cartesian restraints relative to the starting structure were applied to all ligand and protein heavy atoms with force constant of 5 kcal/mol/Å2, and followed by another minimization without any restraint at λ=0. After two steps of minimization (5000 steps of steepest descent for each minimization), two short 5 ps equilibration were performed and followed by 500 ps equilibration with NPT ensemble. The system then was heated at a fixed volume with 300 k. After the heating stage, a 500 ps equilibration with NPT ensemble was performed and followed by 2 ns annealing. The annealing was heated to 600 K in the first 50 ps, then stayed with 600 K for another 100 ps, and eventually cooled down to 300 K in the last 50 ps. After the annealing stage, the restraint on the ligand and protein heavy atoms was reduced to zero in five steps over 1 ns. After the above procedure was performed at λ=0, the sequentially minimization, equilibration and heating were performed, which mean the initial structure for each λ window was taken from the equilibrated structure of the last λ window. For each λ window, the minimized with 5000 steps which the steepest descent method was used, then two short 5 ps equilibration were performed and followed by 500 ps equilibration with NPT ensemble and heated to 300 K. Alchemical free energy calculations were performed for different softcore potential methods using single-step concerted transformations in a series of 21 alchemical states equally spaced along the λ dimension ranging from 0 to 1 (Δλ =0.05). Each window was run independently (with different initial velocities) 4 times in the NPT ensemble at 300 K through Langevin thermostat with a friction constant of 2.0 ps−1 for 5 ns with the first half of data discarded prior to analysis. The long-range electrostatics were evaluated with the particle mesh Ewald (PME) method.55,56 A cutoff of 10 Å was used for non-bonded interactions, including the direct space PME terms and particles interacting through softcore potentials. Only the bonds involving hydrogen were constrained with the SHAKE algorithm63,64 except the atoms of ligands, and all simulations were performed using a 1 fs integration time step.
3.3. Absolute hydration free energy simulations
We examine absolute hydration free energy calculations for four molecules taken or modified from FreeSolv database.72 Initial structures were taken from FreeSolv72 and simulations were prepared using the AMBER ff14SB,69 GAFF force field11,59 with the AM1-BCC charges.60,61 The systems were solvated with TIP3P62 water and an initial buffer size of 20 Å. The equilibration procedure was in the same way as for relative binding free energy simulations. Alchemical free energy calculations were performed for different softcore potential methods using concerted scheme in a series of 21 alchemical states equally spaced along the λ dimension ranging from 0 to 1 (Δλ =0.05). Each window was run independently (with different initial velocities) 4 times in the NPT ensemble at 300 K through Langevin theromostat with a friction constant of 2.0 ps−1 for 2.7 ns with the first 0.2 ns of data discarded prior to analysis. The long-range electrostatics were evaluated with the particle mesh Ewald (PME) method.55,56 A cutoff of 10 Å was used for non-bonded interactions, including the direct space PME terms and particles interacting through softcore potentials. Only the bonds involving hydrogen were constrained with the SHAKE algorithm63,64 except the atoms of ligands, and all simulations were performed using a 1 fs integration time step.
3.4. Benchmark reference calculations using alchemical enhanced sampling (ACES)
To generate the benchmark reference number for test systems, we introduced the alchemical enhanced sampling method (ACES) that will be described in detail elsewhere.13,54 Initial structures and the equilibration procedure were performed in the same way as for relative binding free energy simulations, but were repeated 16 independent runs and with non-uniform λ scheduling which led to 25 λ windows (0, 0.176834, 0.229764, 0.269379, 0.302697, 0.33229, 0.359436, 0.384886, 0.40913, 0.432518, 0.455318, 0.477748, 0.5, 0.522252, 0.544682, 0.567482, 0.59087, 0.615114, 0.640564, 0.66771, 0.697303, 0.730621, 0.770236, 0.823166, 1). These 25 λ points correspond to uniform spacing of the S2(λ) smoothstep function (eq 7) that is used for the non-linear mixing weights in eq 6. As the S2(λ) function has vanishing gradients at the λ=0 and 1 end-points, this schedule has greatest density of points at λ=0.5 rather than at the end-points. Optimal λ spacing for the new alchemical transformation pathway will be explored in more detail in future work. The benchmark reference calculations were sampled with 4 times as many independent trials as for the other production calculations (16 as opposed to 4 independent trials). There are two main requirements to perform efficient ACES calculations in AMBER22. The first requirement is the targeted conformational barriers are reduced or eliminated in the “dummy state”, which can be achieved by the use of the “gti_add_sc” control flag equal to 5. The second requirement is the conformations in the “dummy state” need to be efficiently propagated to the real state endpoint, which can be achieved by using the Hamiltonian replica exchange73-77 framework in AMBER. Alchemical free energy calculations were performed using concerted transformations in 25 alchemical states. Each window was run in NPT ensemble at 300 K through Langevin thermostat with a friction constant of 2.0 ps−1 for 5 ns with the first half of data discarded prior to analysis. The long-range electrostatics were evaluated with the particle mesh Ewald (PME) method.55,56 A cutoff of 10 Å was used for non-bonded interactions, including the direct space PME terms and particles interacting through softcore potentials. Only the bonds involving hydrogen were constrained with the SHAKE algorithm63,64 except the atoms of ligands, and all simulations were performed using a 1 fs integration time step.
3.5. Simulations to examine stability and energy conservation
We examine the alchemical transformation from Mg2+ to Ca2+ in aqueous solution. The system was prepared using the AMBER ff14SB,69 GAFF force field,11,59 and solvated using TIP3P62 waters with initial buffer size of 20 Å. Any remaining net charge of the system was first neutralized and then solvated as 0.15 M ion concentration by addition of Na+ or Cl− as appropriate. Alchemical free energy calculations were performed for different softcore potential methods using single-step concerted transformations in a series of 21 alchemical states equally spaced along the λ dimension ranging from 0 to 1 (Δλ = 0.05). The system for each λ window was first energy minimized with 1000 steps which the steepest descent method was used, then followed by 5 ps heating stage. After the heating, the 2 ns pre-equilibration with NPT ensemble at 298 K through Langevin thermostat with a friction constant of 5.0 ps−1 was performed. Each window was run in the NVE ensemble at 298 K for 5.2 ns with the first 0.2 ns discarded prior to analysis to get 5 ns of production sampling. A cutoff of 10 Å was used for non-bonded interactions, including the direct space PME terms and particles interacting through softcore potentials. All simulations were performed using a 1 fs integration time step, and only the bonds and angle involving hydrogens of water molecules were constrained with the SHAKE algorithm.63,64 The SHAKE tolerance was set to 10−8.
4. Results and Discussion
We present results for the development and validation of a new framework for improved alchemical transformation pathways in AMBER, and provide discussion in the context of comparisons with other existing methods and identification new directions for further advance. The next section (section 4.1) uses simple 2-particle models to illustrate examples of the endpoint catastrophe, particle collapse and large gradient-jumps that the new softcore potential developed in Section 4.2 is designed to address. Section 4.3 compares the methods developed in the current work to several established methods in the literature using three example molecular systems in solution. Section 4.4 provides validation tests against RSFE and RBFE calculations for a set of 4 ligands that target the protein tyrosine phosphatase 1B (PTP1B), and another validation tests against ASFE calculations for 4 small molecules that represent more stringent edge cases, with focus on comparison to highly converged benchmark reference calculations and theoretical cycle closure conditions. Section 4.5 ends the results and discussion with an analysis of energy fluctuations and conservation in the simulations using different alchemical transformation pathways. Finally, the manuscript concludes with a summary of key results, and outlook for the future.
Notation for specifying alternative alchemical transformation pathways.
Through the remainder of the manuscript, we will make comparisons to several alternative alchemical transformation pathways (eq 2) that differ by their λ-dependent weight functions (section 2.2) and softcore potentials (section 2.3). The notation will take the general form: SX[n,m,α,β], where “X” indicates the order of the smoothstep function used in the λ-dependent weight function (i.e., mixing term). Specifically, S0 indicates linear (i.e., 0th-order smoothstep function) and S2 indicates a 2nd-order smoothstep weight functions/mixing terms, respectively. The integers n and m are positive integers and α and β are adjustable positive semi-definite parameters that control the behavior of the separation-shifted scaling of the effective interaction distance for the Lennard-Jones and Coulomb interactions in eqs 18 and 19. In the present work, we introduce a new functional form for the softcore potential that uses separation-shifted scaling of eqs 20 and 21 that contain unitless αLJ and αCoul parameters, and we will distinguish this softcore potential form by the label “S2*”. The 5 alchemical transformation pathways compared in the current work are thus designated as: S0 Linear, S0[6,2,0.5,12], S0[6,2,0.2,17.3], S2[6,2,0.2,50] and S2*[2,2,0.5,1] (present work), and are summarized in Table 3.
Table 3:
Abbreviations and associated forms of the alchemical transformation pathways. Indicated are the form of the dependent weight functions (in terms of smoothstep function SX, where X indicates the order of the smoothstep function); and n, m , α and β parameters of eqs 18 and 19 or n, m, αLJ and αCoul parameters of eqs 20 and 21. All α parameters are unitless, whereas the β parameter has units of Å2. The S2*[2,2,0.5,1] softcore potential differs in functional form from the others, using Eqns 20/21 for the separation-shifted scaling of the effective interaction distance with unitless αLJ and αCoul parameters rather than the more conventional form shown in eqs 18 and 19.
| Abbreviation | W(λ) | n | m | α/αLJ | β/αCoul | Eqns. | Ref. | Comment |
|---|---|---|---|---|---|---|---|---|
| S0 Linear | S0 | - | - | - | - | - | - | Linear mixing/no softcore |
| S0[6, 2, 0.5, 12] | S0 | 6 | 2 | 0.5 | 12 | 18/19 | 24 | Default in AMBER18 |
| S0[6, 2, 0.2, 17.3] | S0 | 6 | 2 | 0.2 | 17.3 | 18/19 | 57 | Modified for improved stability |
| S2[6, 2, 0.2, 50] | S2 | 6 | 2 | 0.2 | 50 | 18/19 | 41 | Default in AMBER20 |
| S2*[2, 2, 0.5, 1] | S2 | 2 | 2 | 0.5 | 1.0 | 20/21 | - | Present work, new form |
4.1. Endpoint catastrophes, particle collapses, and large gradient-jumps
We examine three problems that commonly occur in alchemical simulations with concerted transformations that involve simultaneous changes in both nonbonded Lennard-Jones and Coulombic electrostatic interactions: endpoint catastrophe, particle collapse, and large gradient-jump. These problems have been discussed elsewhere.13,41 The endpoint catastrophe is the sharp divergence of the free energy that is prone to occur at the thermodynamic endpoints (λ becomes close to 0 or 1) and can largely be avoided by use of appropriate softcore potentials.23,24 However, under certain circumstances, the use of softcore potentials can lead to large amplitude fluctuations or phase transition behavior along the λ dimension and result in new artificial minimum at intermediate λ states29 due to an imbalance of Coulomb attraction and exchange repulsion.24 This is referred to as the particle collapse problem, and can be treated by increasing the softcore exchange repulsions and/or decreasing the the Coulomb attractions at short distances across the range of λ values to correct for unstable imbalance. Nonetheless, this treatment for particle collapse can lead to large gradient-jumps, i.e., large amplitude fluctuations of the thermodynamic derivatives that are sensitive to the parameters that control the balance of Coulomb attraction and exchange repulsion.41 Note that while the behavior of endpoint catastrophe and large gradient-jumps might appear similar, their origins are different. The endpoint catastrophes are due to poor phase space overlap and often occur with linear alchemical transformations, and usually can be corrected with the use of softcore potentials. The large gradient-jumps can occur even with the use of softcore potentials, and often happen when large β values are required to adjust the softcore parameter ratio to solve the Coulomb-exchange imbalance problem. As will be seen later, the proposed non-linear mixing and new functional form of the softcore potential alleviates all of these problems.
In order to provide simple illustrative examples, we examine transformations involving 2-body model systems for which accurate 1D profiles can be computed (integrated) numerically. Specifically, we consider cases of the annihilation of a Na+ ion interacting with a TIP3P water oxygen, the transformation of a Li+/Cl− ion pair into a Cs+/Cl− ion pair, and the annihilation of a large spherical hydrophobic R group interacting with a TIP3P water oxygen. These are designated as “Na+ → 0”, “Li+ → Cs+”, and “R → 0”, respectively. Interactions were constrained to remain with a 10 Å interaction distance, and the interaction parameters for each model are summarized in Table 4.
Table 4:
Summary of parameters used in transformations of illustrative 2-body model systems (taken from Joung and Cheatham ion monovalent parameters78 and TIP3P water62). The 1-body parameters (Q in units of ∣e∣, σ in units of Å, and ε in units of kcal/mol) for atoms are: Cs+ (Q=1.0, σ=1.888, ε=0.3944318); Li+ (Q=1.0, σ=0.808, ε=0.103984); Cl− (Q=−1.0, σ = 2.760, ε=0.0116615); Na+ (Q=1.0, σ=1.226, ε=0.1684375); OW (Q=−0.834, σ=1.57535, ε=0.1521). The hydrophobic R group model was chosen as a LJ sphere of σij=5.0 Å and εij=1.0 kcal/mol, and Coulomb interaction between a OW atom and a R group charge Q=0.1∣e∣. For the annihilation models, and additional quadratic “surface tension” term of the form (1/2)k-r2 was added (force constant k in units of kcal/mol·Å2) to capture the effect that a real solution would resist formation of an empty cavity. Particles were constrained to remain with a 10 Å range.
| λ=0 state | → | λ=1 state | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Transformation | Qi·Qj | σij | εij | k | Qi·Qj | σij | εij | k | |
| Na+ → 0 | −0.834 | 2.80135 | 0.16006 | 1.0 | → | - | - | - | 1.0 |
| Li+ → Cs+ | −1.0 | 3.568 | 0.03482 | - | → | −1.0 | 4.648 | 0.06782 | - |
| R → 0 | −0.0834 | 5.0 | 1.0 | 1.0 | → | - | - | - | 1.0 |
For the annihilation models, an additional quadratic “surface tension” term (1/2)k · r2 is added (k=1.0 kcal/mol/Å2) to capture the effect that a real solution opposes formation of an empty cavity. Note that the purely heuristic value of k chosen for illustration here for 2-particle systems is much different than those used in conjunction with implicit solvent models of many-particle systems that are typically two orders of magnitude smaller.79 As these are 2-body interaction models, this allows a simple 1D representation of the λ-dependent potential energy, U(r; λ), and it’s derivative with respect to λ, dU(r; λ)/dλ, as well as the Boltzmann probability distribution, P(r; λ) ~ Exp[−βU(r; λ)] at T=298.15 K. Examination of the probability distribution, it’s sensitivity to λ and overlap with dU(r; λ)/dλ provides insight into the stability of the transformation pathway and its integration. The illustrative examples are shown in Fig. 3, and examine specific λ states where problems are observed to occur, and compare results for three transformation pathways (see Table 3): S0 Linear, or “linear mixing” (no softcore potential), as well as a traditional softcore potential S0[6,2,0.5,12]24 and with updated/modified parameters S0[6,2,0.2,17.3].57 Also shown for completeness is the new softcore potential and non-linear mixing scheme, designated S2*[2,2,0.5,1], that will be developed below in the sections that follow.
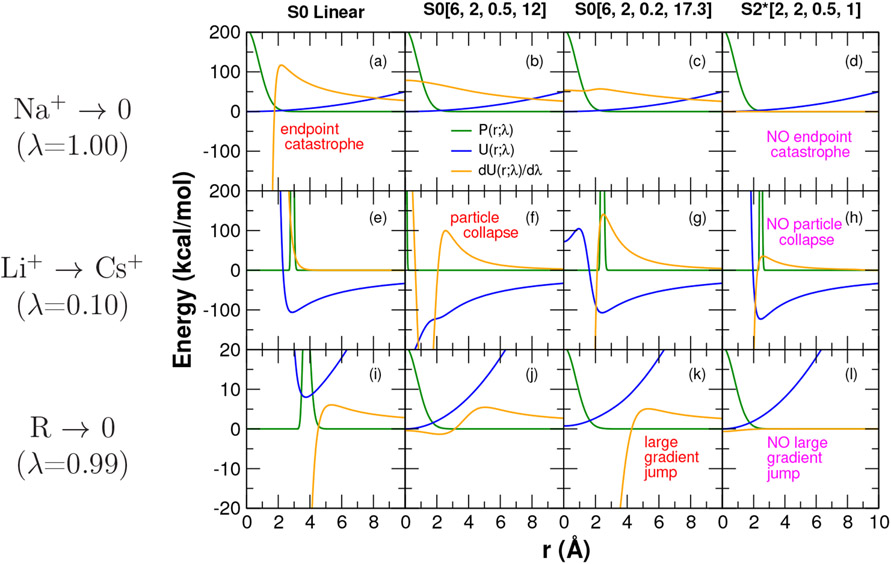
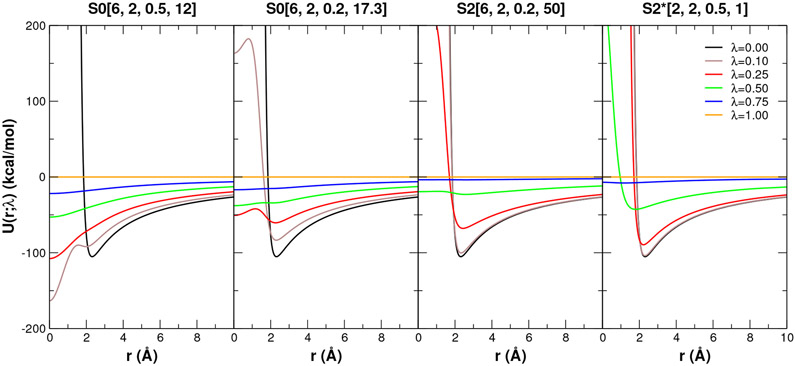
Figure 3:
Illustrative examples of endpoint catastrophe, particle collapse, and large gradient-jump in transformations of the 2-particle model systems summarized in Table 4. The 2-particle nature of the models facilitates comparison using 1D plots as a function of interparticle separation r. Shown are the potential energy U(r; λ) (blue), derivative dU(r; λ)/dλ (gold) and Boltzmann probability P(r; λ) (green) scaled so as to be easier to view on the same plot. For the annihilation models (Na+ →0, and R→0), and additional quadratic “surface tension” term was added (see Table 4). This surface tension term is meant to capture the effect that a real solution would resist formation of an empty cavity, and acts as a weak confining potential to keep particles in close proximity in the limit their interactions become very weak or vanish. Particles were further constrained to remain with a 10 Å range. These 2-particle models were designed to qualitatively mimic the behavior of the three example alchemical free energy simulations presented later in the discussion. Top row: Annihilation of Na+ ion (interacting with a TIP3P water oxygen) at λ=1.00 illustrating endpoint catastrophe. At λ=1.00, the Na+ Coulomb and LJ interactions vanish, and only the weak confining potential remains and is shown as the blue curve, as in this case it is the same as U(r; 1). In a real condensed phase simulation, the annihilated Na+ would be immersed in the water bath and unable to avoid passing on top of the many space-filling water molecules so as to produce an endpoint catastrophe. In this simple illustrative 2-particle model, the surface tension term produces the same qualitative effect. Middle row: Li+→Cs+ transformation with the ions interacting with a TIP3P water oxygen at λ=0.10 illustrating particle collapse. Bottom row: Annihilation of large R group (interacting with a TIP3P water oxygen) at λ=0.99 illustrating large gradient-jump. The R group is modeled as a 5.0-Å LJ sphere with partial charge of 0.1∣e∣, and also uses the same surface tension term as for the annihilation of Na+ above. Note: the scale of the y-axis differs for this model by a factor of 10 relative to the ion models above.
The endpoint catastrophe is illustrated in Fig. 3(a) for the Na+ → 0 transformation at λ=1 using the linear mixing scheme. In the linear mixing scheme, the dU(r; λ)/dλ is independent of λ (although it does depend on r, it is the same function of r for all λ values), and blows up at the origin (r=0); however, at the λ=1 endpoint (with the Na+ fully annihilated), the probability of OW is at a maximum at the origin, causing the ⟨∂U/∂λ⟩λ to diverge. This behavior is easily handled by the use of a softcore potential that results in a dU(r; λ)/dλ profile that stably approaches a constant value at r=0, as shown in Fig. 3(b,c).
However, the use of softcore potentials can also become problematic under different circumstances, as illustrated by the Li+ → Cs+ transformation at λ=0.1 in Fig. 3(e,f,g). Unlike the linear mixing scheme shown in Fig. 3(d), the S0[6,2,0.5,12] softcore potential forms an intermediate λ potential that produces a deep artificial minima at r=0 causing the Cl− probability to collapse on the Li+/Cs+ transforming particle (Fig. 3f). This produces a spike in ⟨∂U/∂λ⟩λ. The origin of this particle collapse (which is exhibited over the range 0.1 ≤ λ ≤ 0.9) is that the Coulomb attraction is able to overcome the exchange-repulsion at these intermediate λ points. Adjustment of the relative α and β parameters so as to make the Lennard-Jones exchange-repulsion “harder’ (i.e., soften more slowly) by lowering the α value from 0.5 to 0.2, while at the same time making the Coulomb attraction term “softer” by raising the β value from 12 to 17.3 Å2 leads to the S0[6,2,0.2,17.3] curve in Fig. 3(g), which does not exhibit particle collapse. As will be shown later, this softcore potential does not guarantee elimination of particle collapse in all cases, but does reduce the occurrence in practice.
Unfortunately, the re-balancing of the exchange and Coulomb terms can lead to other adverse effects, as illustrated in Fig. 3(i,j,k) for the annihilation of the bulky R group. This transformation is dominated by the exchange-repulsion term, which is sensitive to the α parameter, especially with softcore potentials that have a large value of n=6 in eq 18. Whereas the S0[6,2,0.5,12] softcore potential is reasonably well-behaved near the endpoint at λ=0.99 (Fig. 3j), the decrease in the α parameter for the S0[6,2,0.2,17.3] softcore potential leads to large values of the dU(r; λ)/dλ for small r and a resulting sharp increase in the magnitude of ⟨∂U/∂λ⟩λ as λ → 1 (Fig. 3k). This is known as a large gradient-jump, and although less severe, has similarities to the endpoint catastrophe that can occur with the S0 Linear transformation (Fig. 3i) despite that the S0[6,2,0.2,17.3] transformation uses a softcore potential.
In this way, the form of the traditional S0 alchemical transformations cannot simultaneously eliminate the endpoint catastrophe, particle collapse and large gradient-jump problems. Recent work to extend the alchemical transformation to use a smoothstep softcore potential,41 S2[6,2,0.2,50] further improves the ability to handle these problems, but does not eliminate them for some edge cases. As is illustrated in Fig. 3(d,h,l) and will be shown more extensively below, the new form of the alchemical transformation pathway S2*[2,2,0.5,1] developed in the sections that follow has been designed to overcome these and other issues in a highly robust fashion, and has resolved the instability issues of all edge cases encountered thus far for the previous smoothstep softcore potential.41 Nonetheless, there will likely be cases that are found where the new alchemical transformation is not well-suited, and recourse must be taken into more conservative approaches that involve λ-scheduling or stepwise decoupling of electrostatic and LJ terms, possibly with additional restraints.
4.2. New smoothstep softcore potential with balanced Coulomb and exchange
We recently reported a new form of softcore potential that utilized a smoothstep function to enable stabilization of alchemical transformations,41 while otherwise maintaining the functional form of the more traditional softcore potential of eqs 18 and 19. In the current work, we revise the functional form to introduce a new form of the softcore potential in eqs 20 and 21. Two features of the new functional form are: 1) a pairwise σij term is introduced to both Coulomb and LJ terms, and are controlled by unitless α parameters, and 2) smooth switching of and at the cut-off boundary is introduced so as to eliminate discontinuities of the energy and forces and improve the stability of simulations.
One of the main considerations was to introduce a balanced scaling of the Coulomb and LJ exchange terms throughout the range of λ [0 to 1]. In this way, if the real particle-particle interaction potential at λ=0, before scaling, is able to prevent the particles from collapsing onto one another, then by ensuring that the the separation-shifted scaling of the exchange interaction is less than or equal to that of the Coulomb interaction, collapse at small r values can generally be prevented. This implies the condition:
| (26) |
One of the issues with the original softcore potential was that both the functional form in eqs 18 and 19 and the n and m scaling powers were different, making it the case that at some intermediate λ values the and curves would cross (Fig. 4), allowing the possibility that Coulomb attraction could overcome the exchange repulsion. In the new softcore potential developed in this work, the functional form of the the separation-shifted scaling for LJ and Coulomb interactions of eqs 20 and 21 are the same when n=m. For this case, the only requirement is that
| (27) |
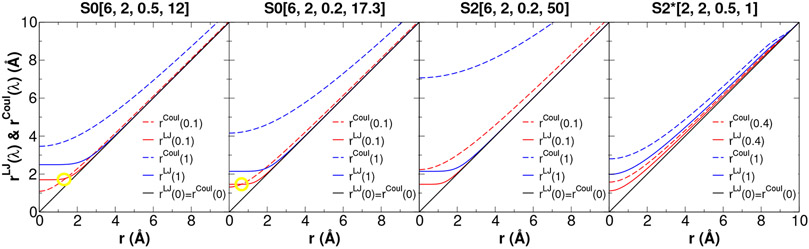
Figure 4:
Separation-shifted scaling, rCoul(λ) and rLJ(λ), of Coulomb/LJ non-bonded interactions used in eqs 18 and 19 and eqs 20 and 21 shown for each of the softcore potentials summarized in Table 3. In addition to the endpoints (λ=0, 1), an intermediate value of λ is selected to illustrate if/when the curves cross as indicated by a yellow circle. For the new S2*[2,2,0.5,1] softcore potential, the rCoul(λ)/rLJ(λ) are non-intersecting over the entire range of λ [0,1].
We experimented extensively with several values of n = m and combinations of the unitless αLJ and αCoul parameters, and found that a very robust balance was achieved with n = m = 2 and αLJ = 0.5 and αCoul = 1.0 (see Figure S1 and Tables S1-S3 of the Supporting Information for comparisons). For these values of the parameters, rCout*(λ) > rLJ*(λ) (and are non-intersecting) over the entire range of λ [0,1] (Fig. 4, rightmost panel). We designate this softcore potential S2*[2,2,0.5,1].
Figure 5 illustrates the potential energy curves for the interaction of a Na+ ion with a TIP3P water oxygen as a function of separation distance r for several values of λ in the Na+ → 0 transformation (Table 4). With the S0[6,2,0.5,12] softcore potential, there are deep minima at the origin for even small λ values that exacerbate the particle collapse problem. With the modified S0[6,2,0.2,17.3] softcore potential, the potential is more repulsive for small values of λ, but still may have spurious minima that arise at the origin for λ=0.25. The original smoothstep softcore potential S2[6,2,0.2,50] remains repulsive to slightly larger values of λ, but has behavior somewhat similar to the S0[6,2,0.2,17.3] potential, again producing spurious minima, which is due to the introduction of the softcore potential, at intermediate λ=0.5 values and a deep minimum at r=0. The new smoothstep softcore potential introduced in the current work, S2*[2,2,0.5,1], eliminates these spurious and deep minimum at the origin, having a much more gradual reduction of the repulsive exchange interactions. In following sections we compare the behavior of the 4 softcore potentials in alchemical free energy simulations of increasing complexity using various assessment metrics discussed in the next section.
Figure 5:
U(r; λ) potential energy curve for the interaction of a Na+ ion with a TIP3P water oxygen as a function of separation distance r for several values of λ in the Na+ → 0 transformation (Table 4). U(r; λ) curves are shown for the alchemical transformation pathways/softcore potentials summarized in Table 3.
4.3. Comparison of ⟨∂U/∂λ⟩λ profiles for different alchemical transformation pathways
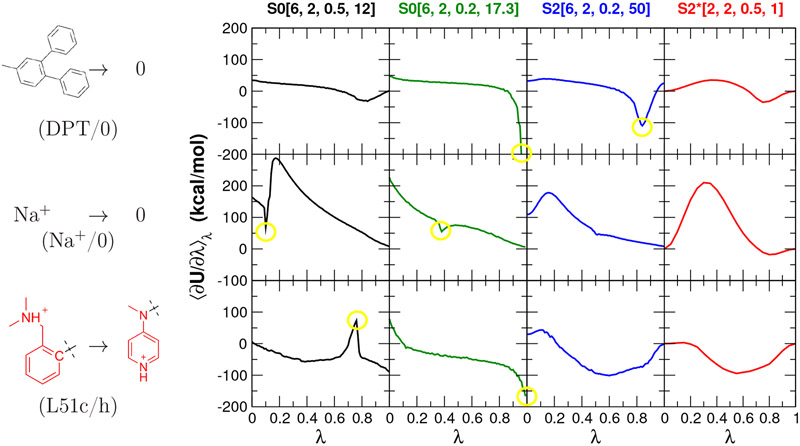
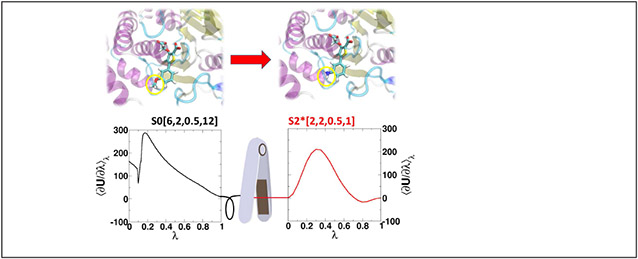
Figure 6 ⟨∂U/∂λ⟩λ compares profiles for alchemical free energy simulations of three example molecular systems in aqueous solution using the concerted scheme and the alchemical transformation pathways summarized in Table 3: the annihilation of a bulky hydrophobic molecule (diphenyltoluene), the annihilation of a small ion (Na+), and the transformation of a charged region in a large ligand (Factor Xa ligand80 L51c to L51h). These are abbreviated DPT/0, Na+/0 and L51c/h, respectively. These real systems loosely mirror, in a very qualitative sense, the simple 2-particle model systems used for illustration purposes in section 4.1.
Figure 6:
The ⟨∂U/∂λ⟩λ profiles for alchemical free energy simulations of three molecular systems in aqueous solution using the concerted scheme and the alchemical transformation pathways summarized in Table 3: the annihilation of diphenyltoluene (DPT/0, upper rows), the annihilation of Na+ ion (Na+/0, middle rows), and the transformation between Factor Xa ligand80 L51c to L51h (L51c/h, bottom rows). The L51c ligand has 65 atoms and L51h has 58 atoms, and the red-colored atoms shown are the defined softcore regions, whereas the atoms common to both ligands are not shown except the connecting carbon shown in black. Highlighted by yellow circles are unstable points that are discussed in the text.
Overall, the S0[6,2,0.5,12] pathway performs worst for the Na+/0 transformation, since there is strong Coulomb attraction that overpowers the poorly balanced exchange interactions, similar to the particle collapse observed for the 2-particle Li+ → Cs+ model system in Fig. 3(e). The S0[6,2,0.2,17.3], on the other hand, better balances the Coulomb and exchange, but at the consequence of exhibiting large gradient-jumps for the DPT/0 transformation, similar to problems observed in the 2-particle R → 0 model system in Fig. 3(i).
In addition, there are several instances where the ⟨∂U/∂λ⟩λ profiles exhibit instabilities at intermediate or end points, as indicated in Fig. 6 by the yellow circles. These instabilities arise from intervals for which there is anomalously poor phase space overlap19 and large standard error of the free energy estimate per λ-interval. An additional consideration for TI is the ability to accurately integrate the ⟨∂U/∂λ⟩λ profiles, and this can be estimated using quadrature stability analysis, and in particular the estimated quadrature RMSE index QRMSE that measures the sensitivity of the free energy to numerical integration using fewer discrete points (see Supporting Information for detailed discussion of quadrature stability). Specifically, QRMSE estimates the error of integrating the ⟨∂U/∂λ⟩λ profile using a cubic spline representation with roughly 1/e (~36.8%) fewer points. The larger the value of QRMSE, the greater the estimated thermodynamic integration error of the ⟨∂U/∂λ⟩λ profile. Table 5 compares the TI standard errors and quadrature stability indexes for each transformation pathway (Table 3) for the the DPT/0, Na+/0 and L51c/h model transformations. In all cases except one, the standard error estimates were below 0.2 kcal/mol (the exception being the L51c/h transformation using S0[6,2,0.5,12] with std. err. of 0.95 kcal/mol). The quadrature stability indexes, QRMSE, on the other hand, with the new S2*[2,2,0.5,1] softcore potential/transformation pathway having universally the smallest values, ranging from 0.21-0.7 kcal/mol, whereas the other transformation pathways ranged from 0.5-7.6 kcal/mol. The smaller quadrature stability indexes for S2*[2,2,0.5,1] qualitatively reflect the generally improved smoothness of the ⟨∂U/∂λ⟩λ profiles in Fig. 6. In the following section, the various transformation pathways will be examined in the context of relative solvation and binding free energies of ligand networks.
Table 5:
Examination of standard errors for TI free energy estimates and quadrature stability indexes for ⟨∂U/∂λ⟩λ profiles for DPT/0, Na+/0 and L51c/h model transformations. For each index, the smallest/largest value for a given transformation is highlighted in boldface/italics. All units are in kcal/mol.
| S0[6, 2, 0.5, 12] | S0[6, 2, 0.2, 17.3] | S2[6, 2, 0.2, 50] | S2*[2, 2, 0.5, 1] | |
|---|---|---|---|---|
| Transformation | Std. Err/QRMSE | Std. Err/QRMSE | Std. Err/QRMSE | Std. Err/QRMSE |
| DPT/0 | 0.06 / 0.50 | 0.14 / 2.44 | 0.08/2.38 | 0.09/ 0.44 |
| Na+/0 | 0.05/7.33 | 0.08 /7.59 | 0.05 / 2.29 | 0.07/ 0.21 |
| L51c/h | 0.95 / 3.36 | 0.18/2.01 | 0.12 / 2.17 | 0.18 /0.70 |
4.4. Validation against solvation and relative binding free energies
In the previous sections, we analyzed in detail both 2-particle numerical models as well as a set of real model transformations in aqueous solution. Here we turn toward more complex systems and real-world applications. The goal here is not to evaluate the accuracy of the force field or to address challenging sampling issues (the examples were chosen so as to avoid such issues), but rather how the alchemical transformation pathway itself affects the accuracy of the free energy estimate. To achieve this goal, we will focus attention on comparisons to benchmark reference calculations to assess the reliability of different alchemical transformation pathways. We first establish a baseline by examining a well-studied set of ligand transformations in gaseous, aqueous and complex environments for which the established methods typically do not fail, in order to establish that the new methods also perform well. Next we examine more challenging transformations that involve absolute hydration free energies of bulky hydrophobic, polar, and anionic/cationic systems where other methods are observed to break down.
Well-studied ligand transformations in gaseous, aqueous and protein complex environments
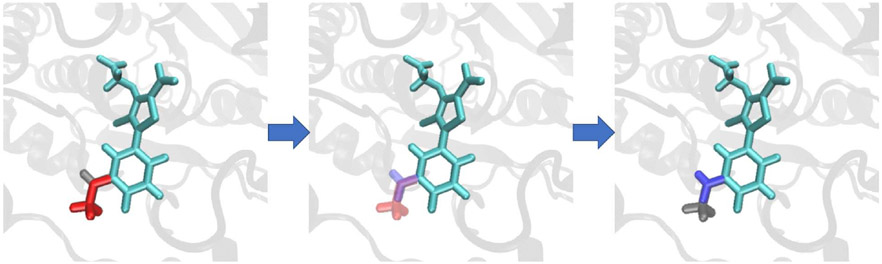
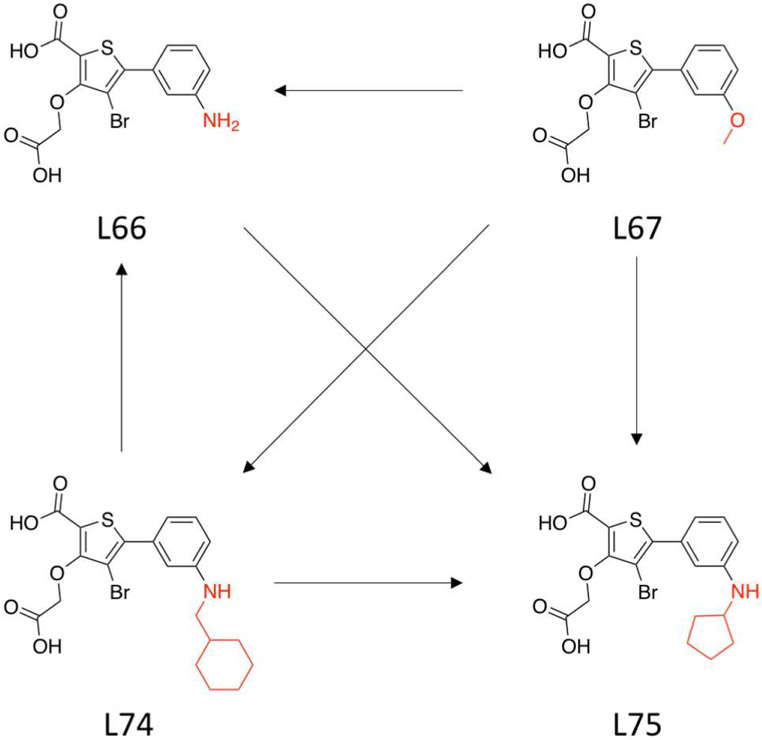
We first examine transformations between four ligands (L66, L67, L74 and L75) that target the protein tyrosine phosphatase 1B (PTP1B)65,66 (Fig. 7). A thermodynamic graph is constructed that involves all 6 possible alchemical transformation between ligands, producing 6 edges to the complete thermodynamic graph (Fig. 7). We will consider transformations within this thermodynamic graph in three different environments: gas phase, aqueous solution, and complexed to PTP1B. This will enable cycles to be constructed for both RSFE and RBFE (Fig. 1). In addition, we perform benchmark reference calculations using new alchemical advanced enhanced sampling techniques, as well as increased number of λ sampling windows and number of independent runs in order to increase the level of precision of the TI/BAR/MBAR free energy estimates (see Methods for details). Note that we report our benchmark reference data using the BAR analysis method as we find this to be generally the most robust protocol for the data set considered here, and avoids errors that arise from numerical quadrature with TI.
Figure 7:
Illustration of a thermodynamic graph which involves 4 ligands (L66, L67, L74, and L75) that target the PTP1B.65,66 The thermodynamic graph is constructed that involves all 6 possible alchemical transformation between ligands. The red-colored atoms shown are the defined softcore regions chosen in accord with the MCS-Enw atom-mapping algorithm described in the Methods section.
Table 6 summarizes relative hydration free energy values from TI for 6 alchemical transformations between ligands. All of the error estimates are quite small with respect to the reference calculations (less than 0.2 kcal/mol), and all except for the S0[6,2,0.2,17.3] pathway have errors below 0.1 kcal/mol. The situation is overall similar for the relative binding free energy values shown in Table 7, with TI error estimates all below 0.2 kcal/mol. An independent assessment of reliability of the calculations can be ascertained through analysis of theoretical cycle closure conditions that the exact results must strictly obey. The cycle closure errors for the RSFE calculations using TI are around 0.1 kcal/mol or less for all methods with the exception of S0[6,2,0.2,17.3] which has TI cycle closure errors greater than 0.3 kcal/mol. The corresponding cycle closure errors for the RBFE calculations using TI are generally less than 0.3 kcal/mol, with the S2[6,2,0.2,50] being particularly small (less than 0.1 kcal/mol). In general, the cycle closure errors are even smaller with BAR and MBAR analysis (see Tables S4 and S5 of the Supporting Information for further details). Table 8 compares the TI standard errors and quadrature stability indexes for each transformation pathways for the 6 transformations. In most cases, the standard error estimates are below 0.2 kcal/mol, except the L67→L74 and L67→L75 using the S0[6,2,0.5,12] pathway. The S2*[2,2,0.5,1] pathway generally has the smallest quadrature stability indexes, in particular QRMSE, ranging from 0.06-0.38 kcal/mol, whereas the other alchemical transformation pathways ranged from 0.21-5.17 kcal/mol. Overall, the new S2*[2,2,0.5,1] performs very well and appears to be stable and robust for these transformations.
Table 6:
Relative hydration free energy values (kcal/mol)a for four alchemical transformation pathways/softcore potentials
| Transformation | S0[6, 2, 0.5, 12] | S0[6, 2, 0.2, 17.3] | S2[6, 2, 0.2, 50] | S2*[2, 2, 0.5, 1] | Ref. |
|---|---|---|---|---|---|
| L66→L75 | 2.34(07) | 2.20(08) | 2.40(07) | 2.39(06) | 2.31(04) |
| L67→L66 | −8.17(07) | −8.08(06) | −8.07(07) | −7.98(08) | −8.00(03) |
| L67→L74 | −6.29(07) | −6.49(16) | −6.21(12) | −6.28(10) | −6.22(05) |
| L67→L75 | −5.74(08) | −5.55(12) | −5.80(07) | −5.59(10) | −5.70(04) |
| L74→L66 | −1.72(06) | −1.56(14) | −1.76(10) | −1.87(10) | −1.72(05) |
| L74→L75 | 0.51(11) | 0.35(19) | 0.55(15) | 0.59(13) | 0.59(05) |
| MUE | 0.07 | 0.17 | 0.06 | 0.06 | |
| RMSE | 0.08 | 0.17 | 0.06 | 0.08 |
The relative hydration free energy values are obtained by concerted scheme and analyzed using the TI method. Standard errors are shown in parentheses (multiplied by 102). Accurate reference values (Ref.) were obtained from ACES calculations, sampled with 16 independent trials (as opposed to 4 for other calculations) and 25 λ windows (as opposed to 21 for other calculations), and analyzed with BAR method (see Methods section 3.4 for details).
Table 7:
Relative binding free energy values (kcal/mol) for four alchemical transformation pathways/softcore potentials
| Transformation | S0[6, 2, 0.5, 12] | S0[6, 2, 0.2, 17.3] | S2[6, 2, 0.2, 50] | S2*[2, 2, 0.5, 1] | Ref. |
|---|---|---|---|---|---|
| L66→L75 | −0.72(09) | −0.77(12) | −0.82(09) | −0.69(17) | −0.84(05) |
| L67→L66 | 0.83(05) | 0.75(06) | 0.78(05) | 0.72(05) | 0.74(03) |
| L67→L74 | −0.24(26) | −0.17(18) | −0.04(12) | 0.15(10) | −0.08(06) |
| L67→L75 | −0.32(28) | −0.17(14) | −0.12(09) | −0.05(13) | −0.06(05) |
| L74→L66 | 0.77(08) | 0.84(19) | 0.92(14) | 0.81(16) | 0.88(06) |
| L74→L75 | 0.19(15) | −0.27(51) | 0.01(16) | 0.21(14) | 0.01(06) |
| MUE | 0.15 | 0.10 | 0.03 | 0.11 | |
| RMSE | 0.15 | 0.12 | 0.04 | 0.13 |
Relative binding free energy values are obtained by concerted scheme and analyzed using the TI method. Standard errors are shown in parentheses (multiplied by 102). Accurate reference values (Ref.) were obtained from ACES calculations, sampled with 16 independent trials (as opposed to 4 for other calculations) and 25 A windows (as opposed to 21 for other calculations), and analyzed with BAR method (see Methods section 3.4 for details).
Table 8:
Examination of standard errors for TI free energy estimates and quadrature stability indexes for ⟨∂U/∂λ⟩λ profiles for PTP1B model transformations in the complex. For each index, the smallest/largest value for a given transformation is highlighted in boldface/italics. All units are in kcal/mol.
| S0[6, 2, 0.5, 12] | S0[6, 2, 0.2, 17.3] | S2[6, 2, 0.2, 50] | S2*[2, 2, 0.5, 1] | |
|---|---|---|---|---|
| Transformation | Std. Err/QRMSE | Std. Err/QRMSE | Std. Err/QRMSE | Std. Err/QRMSE |
| L66 → L75 | 0.07/0.42 | 0.10/0.83 | 0.06/0.94 | 0.16/0.13 |
| L67 → L66 | 0.04/0.34 | 0.05/1.03 | 0.04/0.68 | 0.04/0.06 |
| L67 → L74 | 0.25/0.21 | 0.13/0.99 | 0.09/1.16 | 0.07/0.25 |
| L67 → L75 | 0.28/0.25 | 0.10/1.40 | 0.08/0.87 | 0.12/0.08 |
| L74 → L66 | 0.07/0.47 | 0.13/1.11 | 0.11/1.21 | 0.14/0.38 |
| L74 → L75 | 0.11/0.25 | 0.48/5.17 | 0.11/1.62 | 0.08/0.14 |
Absolute hydration free energies of bulky hydrophobic, polar, and anionic/cationic systems
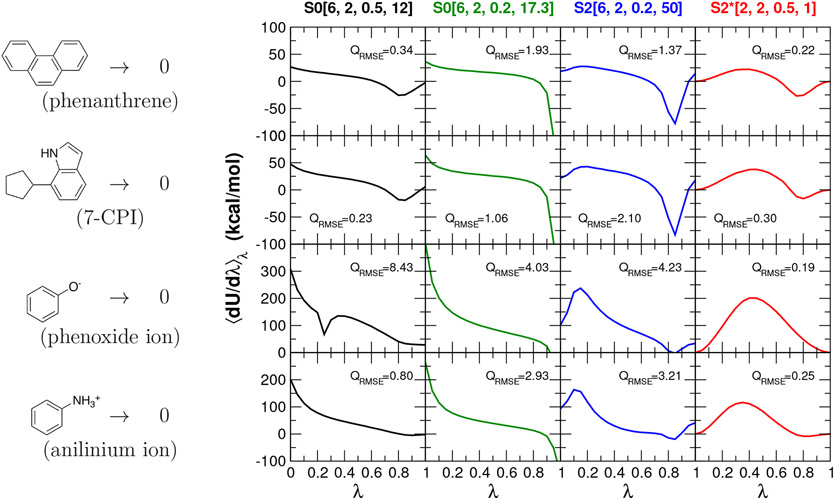
Next, we examine the absolute hydration free energies for phenanthrene, 7-cyclopentanylindole (7-CPI), phenoxide ion and anilinium ion. These systems represent more stringent edge cases that combine large steric annihilation with neutral, negative and positive charged systems. Similarly to the PTP1B ligands, we also perform benchmark reference calculation in order to make error estimates using new alchemical enhanced sampling techniques, as well as increased number of λ sampling windows and number of independent trials.
Figure 8 compares ⟨∂U/∂λ⟩λ profiles for alchemical free energy simulations of these four molecular systems in solution using the concerted scheme and the alchemical transformation pathways summarized in Table 3. Overall, the S0[6,2,0.5,12] pathway performs worst for the annihilation of phenoxide ion, similar to the particle collapse observed for the 2-particle Li+ → Cs+ model system in Fig. 3(e). Specifically, for the phenoxide ion, the profile is not smooth for λ values around 0.25. The origin of this issue is the particle collapse problem, where the softened exchange repulsions cannot balance the attractive softcore Coulomb attractions of the charged particles, causing them to collapse on top of one another. The S0[6,2,0.2,17.3] causes large gradient-jumps particularly for the larger phenanthrene and 7-cyclopentanylindole transformations, similar to problems observed in the 2-particle R → 0 model system in Fig. 3(i). The S2[6,2,0.2,50] exhibits instabilities between intermediate λ=0.90 and 0.95 for the annihilation of phenanthrene and 7-cyclopentanylindole due to poor phase space overlap. The S2*[2,2,0.5,1] overall performs best and achieve stable ⟨∂U/∂λ⟩λ curves, as reflected also by improved quadrature stability (QRMSE is smallest, with the minor exception of the 7-CPI case where S0[6,2,0.5,12] is slightly lower).
Figure 8:
The ⟨∂U/∂λ⟩λ profiles for alchemical free energy simulations of four molecular systems in aqueous solution using the concerted scheme and the alchemical transformation pathways summarized in Table 3: the annihilation of phenanthrene (upper rows), the annihilation of 7-cyclopentanylindole (7-CPI) (the second rows), the annihilation of phenoxide ion (the third rows), and the annihilation of anilinium ion (bottom rows).
Table 9 summarizes absolute hydration free energy values for four molecular systems calculated with different alchemical transformation pathways. The bold numbers are the error estimates between the free energy values with respect to the ACES reference results. The annihilation of phenoxide ion shows by far the largest error (8.01 kcal/mol) with S0[6,2,0.5,12]. The large difference matches the irregularity of the ⟨∂U/∂λ⟩λ profile, which has a sharp kink around λ=0.25. The S0[6,2,0.5,12] results are overall the worst, with average estimates error of 2.03 kcal/mol. The S0[6,2,0.2,17.3] has the next highest average estimated error of 0.49 kcal/mol, followed by S2[6,2,0.2,50] which is significantly reduced (0.09 kcal/mol). The S2*[2,2,0.5,1] has the smallest estimated error of 0.05 kcal/mol, with the highest value (0.07 kcal/mol) being for phenanthrene. This suggests that the new S2*[2,2,0.5,1] is robust in its ability to stably carry out these more challenging absolute hydration free energy simulations and provide reliable free energy estimates.
Table 9:
Absolute hydration free energy values (kcal/mol)a for four alchemical transformation pathways. The bold numbers are the differences between the free energy values with respect to the reference numbers.
| Transformation | S0[6, 2, 0.5, 12] | S0[6, 2, 0.2, 17.3] | S2[6, 2, 0.2, 50] | S2*[2, 2, 0.5, 1] | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| phenanthrene → 0 | 5.91(02) | 0.01 | 6.36(07) | 0.44 | 5.70(16) | 0.22 | 5.85(05) | 0.07 | 5.92(03) |
| 7CPIb → 0 | 7.40(06) | 0.05 | 8.20(06) | 0.75 | 7.41(08) | 0.04 | 7.50(05) | 0.05 | 7.45(03) |
| phenoxide ion → 0 | 79.50(09) | 8.01 | 71.95(08) | 0.46 | 71.56(05) | 0.07 | 71.51(07) | 0.05 | 71.49(02) |
| anilinium ion → 0 | 50.89(06) | 0.04 | 51.14(07) | 0.29 | 50.84(06) | 0.01 | 50.81(06) | 0.04 | 50.85(03) |
| Avg. Δc | 2.03 | 0.49 | 0.09 | 0.05 | |||||
The absolute hydration free energy values are obtained by concerted scheme and analyzed using the TI method. Standard errors are shown in parentheses (multiplied by 102). Ref. is the values obtained from ACES calculations, sampled 4X greater with more independent trials and λ windows, and analyzed with BAR method (see Methods section 3.4 for details).
7-cyclopentanylindole
The average free energy differences with respect to the reference,
4.5. Energy stability and conservation
In order to examine the stability of the simulations (i.e., total energy fluctuations and conservation) using different functional forms and parameters for the various softcore potentials, we perform simulations for Mg2+ → Ca2+ (both ions treated using softcore potentials) with single precision model (SPFP) and the NVE ensemble at λ =0.5 using four different softcore potentials. Note that for λ=0.5, the value of the λ-dependent weight functions W(λ) in eq 2 are all the same (0.5). The time evolution of the total energy and 1-ps energy drift is compared in Fig 9. In the 1-ps time domain, the distributions of energy drift values are normal (symmetric about the mean, unimodal and Gaussian-like) for all of the softcore potentials, and also similar to the end state simulations (data not shown). A statistically significant difference, however, is that the mean value is considerably larger for the S0[6,2,0.5,12] and S0[6,2,0.2,17.3] softcore potentials (0.19 and 0.12 kcal/mol, respectively) with respect to the smoothstep softcore potentials that have mean values of 0.01 kcal/mol or less. These differences are more evident by looking at the time evolution of the total energy, which illustrates there is a persistent, steady energy drift over 5 ns that gives rise to the mean values in the 1-ps histograms. This drift persists for simulations extended to 20 ns with very similar slope (data not shown). Formally, only the new S2*[2,2,0.5,1] softcore potential is rigorously smooth at the cut-off boundary and conserves energy. However, it appears that for the present example, the S2[6,2,0.2,50] simulation also conserves energy quite well. A more detailed preliminary analysis indicates that the origin of the trends in energy conservation derives mainly from short-ranged interactions, and relatively minimally from the lack of continuity (in cases other than S2*[2,2,0.5,1]) of the softcore potentials at the cut-off boundary. Specifically, instabilities can arise when “hard” collisions that occur for potentials where the short-ranged LJ are steeply changing due to the large exponent n=6 in eq 18, and this behavior is exacerbated when these repulsions are countered by strong Coulomb interactions (i.e., smaller β values in eq 19). Thus, the magnitude of the energy drift is negligible for the new S2*[2,2,0.5,1] softcore potential, and for the other softcore potentials follows the trend S0[6,2,0.5,12] > S0[6,2,0.5,17.3] > S2[6,2,0.2,50] in accord with the increasing β values. It should be noted that none of the energy drifts are severe, and do not greatly impact results when used with an appropriate thermostat. Nonetheless, it is important to examine closely these issues, and engineer stable softcore potentials from the start in the design of next-generation alchemical transformation pathways. As a final comment, we note that we observed virtually no performance difference using the various softcore potentials discussed in the current work (see Table S6 of the Supporting Information).
Figure 9:
The potential energy drift in the relative hydration free energy calculations for Mg2+ → Ca2+ with single precision model (SPFP) and the NVE ensemble at λ = 0.5 for the alchemical transformation pathways/softcore potentials summarized in Table 3. The left column shows the time evolution of the total energy (dashed line indicates the average value in 103 kcal/mol, and slope is in kcal/mol/ps), whereas the right column shows the 1-ps energy drift histograms with mean values and standard deviations in kcal/mol.
5. Conclusion
The current work develops a robust framework for the design of alchemical transformation pathways using a new form for the λ-dependent mixing weight functions and smoothstep softcore potential. The latter is distinct from previous softcore potentials available in AMBER in that it uses smoothstep functions to stabilize behavior near the λ=0 and 1 end points, consistent power scaling of Coulomb and LJ interactions with unitless control parameters to maintain balance of electrostatic attractions and exchange repulsions, pairwise form based on the LJ contact radius for the effective interaction distance with separation-shifted scaling, and rigorous smoothing of the potential at the non-bonded cut-off boundary. The new alchemical transformation pathway is illustrated to overcome commonly encountered endpoint catastrophe, particle collapse and large gradient-jump problems in free energy simulations, and represents a considerable advance with respect to other alchemical transformations and softcore potentials. The current work provides the foundation for more robust free energy simulations, including the development of new alchemical enhanced sampling methods and new streamlined workflows for high-throughput simulation and analysis of ligand libraries and thermodynamic graph networks.
Supplementary Material
Acknowledgments
The authors are grateful for financial support provided by the National Institutes of Health (No. GM107485 to DMY). Computational resources were provided by the Office of Advanced Research Computing (OARC) at Rutgers, and by the MSU HPC. The State University of New Jersey, the National Institutes of Health under Grant No. S10OD012346, the Blue Waters sustained-petascale computing project (NSF OCI 07-25070, PRAC OCI-1515572), and by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (No. ACI-1548562 and No. OCI-1053575). We gratefully acknowledge the support of the nVidia Corporation with the donation of several Pascal and Volta GPUs and the GPU-time of a GPU-cluster where the reported benchmark results were performed.
References
- (1).Cournia Z; Chipot C; Roux B; York DM; Sherman W In Free Energy Methods in Drug Discovery—Introduction; Armacost KA, Thompson DC, Eds.; ACS Symposium Series; 2021; Vol. 1397; pp 1–38. [Google Scholar]
- (2).Mey ASJS; Allen BK; Macdonald HEB; Chodera JD; Hahn DF; Kuhn M; Michel J; Mobley DL; Naden LN; Prasad S; Rizzi A; Scheen J; Shirts MR; Tresadern G; Xu H Best Practices for Alchemical Free Energy Calculations [Article v1.0]. Living Journal of Computational Molecular Science 2020, 2, 18378–18429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Cournia Z; Allen B; Sherman W Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model 2017, 57, 2911–2937. [DOI] [PubMed] [Google Scholar]
- (4).Lee T-S; Allen BK; Giese TJ; Guo Z; Li P; Lin C; T. D. M Jr.; Pearlman DA; Radak BK; Tao Y; Tsai H-C; Xu H; Sherman W; York DM Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery. J. Chem. Inf. Model 2020, 60, 5595–5623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Mobley DL; Klimovich PV Perspective: Alchemical free energy calculations for drug discovery. J. Chem. Phys 2012, 137, 230901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Aldeghi M; Heifetz A; Bodkin MJ; Knapp S; Biggin PC Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J. Am. Chem. Soc. 2017, 139, 946–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Chodera J; Mobley D; Shirts M; Dixon R; Branson K; Pande V Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol 2011, 21, 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Jorgensen WL Efficient drug lead discovery and optimization. Acc. Chem. Res 2009, 42, 724–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Abel R; Wang L; Harder ED; Berne BJ; Friesner RA Advancing Drug Discovery through Enhanced Free Energy Calculations. Acc. Chem. Res 2017, 50, 1625–1632. [DOI] [PubMed] [Google Scholar]
- (10).Lee T-S; Hu Y; Sherborne B; Guo Z; York DM Toward Fast and Accurate Binding Affinity Prediction with pmemdGTI: An Efficient Implementation of GPU-Accelerated Thermodynamic Integration. J. Chem. Theory Comput 2017, 13, 3077–3084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Lee T-S; Cerutti DS; Mermelstein D; Lin C; LeGrand S; Giese TJ; Roitberg A; Case DA; Walker RC; York DM GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model 2018, 58, 2043–2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Mermelstein DJ; Lin C; Nelson G; Kretsch R; McCammon JA; Walker RC Fast and flexible gpu accelerated binding free energy calculations within the amber molecular dynamics package. J. Comput. Chem 2018, 39, 1354–1358. [DOI] [PubMed] [Google Scholar]
- (13).Lee T-S; Tsai H-C; Ganguly A; Giese TJ; York DM In Robust, Efficient and Automated Methods for Accurate Prediction of Protein-Ligand Binding Affinities in AMBER Drug Discovery Boost; Armacost KA, Thompson DC, Eds.; ACS Symposium Series; 2021; Vol. 1397; pp 161–204. [Google Scholar]
- (14).Heinzelmann G; Henriksen NM; Gilson MK Attach-Pull-Release Calculations of Ligand Binding and Conformational Changes on the First BRD4 Bromodomain. J. Chem. Theory Comput 2017, 13, 3260–3275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Henriksen NM; Fenley AT; Gilson MK Computational Calorimetry: High-Precision Calculation of Host-Guest Binding Thermodynamics. J. Chem. Theory Comput 2015, 11, 4377–4394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Yin J; Henriksen NM; Slochower DR; Gilson MK The SAMPL5 host-guest challenge: computing binding free energies and enthalpies from explicit solvent simulations by the attach-pull-release (APR) metho. J. Comput.-Aided Mol. Des 2017, 31, 133–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Tembre BL; McCammon JA Ligand-receptor interactions. Comput. Chem 1984, 8, 281–283. [Google Scholar]
- (18).Fleck M; Wieder M; Boresch S Dummy Atoms in Alchemical Free Energy Calculations. J. Chem. Theory Comput 2021, 17, 4403–4419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Giese TJ; York DM Development of a Robust Indirect Approach for MM → QM Free Energy Calculations That Combines Force-Matched Reference Potential and Bennett’s Acceptance Ratio Methods. J. Chem. Theory Comput 2019, 15, 5543–5562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).König G; Brooks BR; Thiel W; York DM On the convergence of multi-scale free energy simulations. Mol. Simul 2018, 44, 1062–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Wu D; Kofke DA Phase-space overlap measures. I. Fail-safe bias detection in free energies calculated by molecular simulation. J. Chem. Phys 2005, 123, 54103. [DOI] [PubMed] [Google Scholar]
- (22).Wu D; Kofke DA Phase-space overlap measures. II. Design and implementation of staging methods for free-energy calculations. J. Chem. Phys 2005, 123, 84109. [DOI] [PubMed] [Google Scholar]
- (23).Beutler TC; Mark AE; René C van Schaik and Paul R. Gerber and Wilfred F. van Gunsteren, Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett 1994, 222, 529–539. [Google Scholar]
- (24).Steinbrecher T; Joung I; Case DA Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem 2011, 32, 3253–3263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Hornak V; Simmerling C Development of softcore potential functions for overcoming steric barriers in molecular dynamics simulations. J. Mol. Graphics Model 2004, 22, 405–413. [DOI] [PubMed] [Google Scholar]
- (26).Giese TJ; York DM A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput 2018, 14, 1564–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Gapsys V; Seeliger D; de Groot BL New Soft-Core Potential Function for Molecular Dynamics Based Alchemical Free Energy Calculations. J. Chem. Theory Comput 2012, 8, 2373–2382. [DOI] [PubMed] [Google Scholar]
- (28).Buelens FP; Grubmüller H Linear-scaling soft-core scheme for alchemical free energy calculations. J. Comput. Chem 2012, 33, 25–33. [DOI] [PubMed] [Google Scholar]
- (29).Pal RK; Gallicchio E Perturbation potentials to overcome order/disorder transitions in alchemical binding free energy calculations. J. Chem. Phys 2019, 151, 124116. [DOI] [PubMed] [Google Scholar]
- (30).Mezei M Polynomial path for the calculation of liquid state free energies from computer simulations tested on liquid water. J. Comput. Chem 1992, 13, 651–656. [Google Scholar]
- (31).Resat H; Mezei M Studies on free energy calculations. I. Thermodynamic integration using a polynomial path. J. Chem. Phys 1993, 99, 6052–6061. [Google Scholar]
- (32).Simonson T Free energy of particle insertion. Mol. Phys 1993, 80, 441–447. [Google Scholar]
- (33).Steinbrecher T; Mobley DL; Case DA Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys 2007, 127, 214108. [DOI] [PubMed] [Google Scholar]
- (34).Jiang W; Chipot C; Roux B Computing Relative Binding Affinity of Ligands to Receptor: An Effective Hybrid Single-Dual-Topology Free-Energy Perturbation Approach in NAMD. J. Chem. Inf. Model 2019, 59, 3794–3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).König G; Glaser N; Schroeder B; Kubincová A; Hünenberger PH; Riniker S An Alternative to Conventional λ-Intermediate States in Alchemical Free Energy Calculations: λ-Enveloping Distribution Sampling. J. Chem. Inf. Model 2020, 60, 5407–5423. [DOI] [PubMed] [Google Scholar]
- (36).König G; Ries B; Hünenberger PH; Riniker S Efficient Alchemical Intermediate States in Free Energy Calculations Using λ-Enveloping Distribution Sampling. J. Chem. Theory Comput 2021, 17, 5805–5815. [DOI] [PubMed] [Google Scholar]
- (37).de Ruiter A; Petrov D; Oostenbrink C Optimization of Alchemical Pathways Using Extended Thermodynamic Integration. J. Chem. Theory Comput 2021, 17, 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Reinhardt M; Grubmuller H Determining Free-Energy Differences Through Variationally Derived Intermediates. J. Chem. Theory Comput 2020, 16, 3504–3512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Blondel A Ensemble Variance in Free Energy Calculations by Thermodynamic Integration: Theory, Optimal "Alchemical" Path, and Practical Solutions. J. Comput. Chem 2004, 25, 985–993. [DOI] [PubMed] [Google Scholar]
- (40).Pham TT; Shirts MR Optimal pairwise and non-pairwise alchemical pathways for free energy calculations of molecular transformation in solution phase. J. Chem. Phys 2012, 136, 124120. [DOI] [PubMed] [Google Scholar]
- (41).Lee T-S; Lin Z; Allen BK; Lin C; Radak BK; Tao Y; Tsai H-C; Sherman W; York DM Improved Alchemical Free Energy Calculations with Optimized Smoothstep Softcore Potentials. J. Chem. Theory Comput 2020, 16, 5512–5525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Kirkwood JG Statistical mechanics of fluid mixtures. J. Chem. Phys 1935, 3, 300–313. [Google Scholar]
- (43).Straatsma TP; Berendsen HJ Free energy of ionic hydration: Analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys 1988, 89, 5876–5886. [Google Scholar]
- (44).Bennett CH Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys 1976, 22, 245–268. [Google Scholar]
- (45).Torrie GM; Valleau JP Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys 1977, 23, 187–199. [Google Scholar]
- (46).Shirts MR; Pande VS Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J Chem Phys 2005, 122, 144107. [DOI] [PubMed] [Google Scholar]
- (47).Shirts MR; Chodera JD Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Tan Z; Gallicchio E; Lapelosa M; Levy RM Theory of binless multi-state free energy estimation with applications to protein-ligand binding. J. Chem. Phys 2012, 136, 144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Giese TJ; York DM Variational Method for Networkwide Analysis of Relative Ligand Binding Free Energies with Loop Closure and Experimental Constraints. J. Chem. Theory Comput 2021, 17, 1326–1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Case DA; Aktulga HM; Belfon K; Ben-Shalom IY; Berryman J; Brozell SR; Cerutti DS; Cheatham III TE; Cruzeiro VWD; Darden TA; Duke RE; Giambasu G; Gilson MK; Gohlke H; Goetz AW; Harris R; Izadi S; Izmailov SA; Kasavajhala K; Kaymak MC; King E; Kovalenko A; Kurtzman T; Lee TS; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Machado M; Man V; Manathunga M; Merz KM; Miao Y; Mikhailovskii O; Monard G; Nguyen H; O’Hearn KA; Onufriev A; Pan F; Pantano S; Qi R; Rahnamoun A; Roe D; Roitberg A; Sagui C; Schott-Verdugo S; Shajan A; Shen J; Simmerling CL; Skrynnikov NR; Smith J; Swails J; Walker RC; Wang J; Wang J; Wei H; Wolf RM; Wu X; Xiong Y; Xue Y; York DM; Zhao S; Kollman PA AMBER22. University of California, San Francisco: San Francisco, CA, 2022. [Google Scholar]
- (51).Meng Y; Dashti D; Roitberg AE Computing alchemical free energy differences with Hamiltonian replica exchange molecular dynamics (H-REMD) simulations. J. Chem. Theory Comput 2011, 7, 2721–2727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Roe DR; Bergonzo C; Cheatham TE Evaluation of enhanced sampling provided by accelerated molecular dynamics with Hamiltonian replica exchange methods. J. Phys. Chem. B 2014, 118, 3543–3552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Hahn DF; König G; Hünenberger PH Overcoming Orthogonal Barriers in Alchemical Free Energy Calculations: On the Relative Merits of λ-Variations, λ-Extrapolations, and Biasing. J. Chem. Theory Comput 2020, 16, 1630–1645. [DOI] [PubMed] [Google Scholar]
- (54).Lee T-S; Tsai H-C; Ganguly A; York DM ACES: Alchemically Enhanced Sampling. J. Chem. Theory Comput 2022, submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Darden T; York D; Pedersen L Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (56).Essmann U; Perera L; Berkowitz ML; Darden T; Hsing L; Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (57).Labute P; Ebert M In Optimizing Simulations Protocols for Relative Free Energy Calculations; Armacost KA, Thompson DC, Eds.; ACS Symposium Series; 2021; Vol. 1397; pp 227–245. [Google Scholar]
- (58).Lee Y-K; Parks DJ; Lu T; Thieu TV; Markotan T; Pan W; McComsey DF; Milkiewicz KL; Crysler CS; Ninan N; Abad MC; Giardino EC; Maryanoff BE; Damiano BP; Player MR 7-fluoroindazoles as potent and selective inhibitors of factor Xa. J. Med. Chem 2008, 51, 282–297. [DOI] [PubMed] [Google Scholar]
- (59).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (60).Jakalian A; Bush BL; Jack DB; Bayly CI Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. method. J. Comput. Chem 2000, 21, 132–146. [DOI] [PubMed] [Google Scholar]
- (61).Jakalian A; Jack DB; Bayly CI Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. parameterization and validation. J. Comput. Chem 2002, 23, 1623–1641. [DOI] [PubMed] [Google Scholar]
- (62).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (63).Miyamoto S; Kollman PA SETTLE: An analytic version of the SHAKE and RATTLE algorithms for rigid water models. J. Comput. Chem 1992, 13, 952–962. [Google Scholar]
- (64).Ryckaert JP; Ciccotti G; Berendsen HJC Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- (65).Wilson DP; Wan Z-K; Xu W-X; Kirincich SJ; Follows BC; Joseph-McCarthy D; Foreman K; Moretto A; Wu J; Zhu M; Binnun E; Zhang Y-L; Tam M; Erbe DV; Tobin J; Xu X; Leung L; Shilling A; Tam SY; Mansour TS; Lee J Structure-Based Optimization of Protein Tyrosine Phosphatase 1B Inhibitors: From the Active Site to the Second Phophotyrosine Binding Site. J. Med. Chem 2007, 50, 4681–4698. [DOI] [PubMed] [Google Scholar]
- (66).Wang L; Wu Y; Deng Y; Kim B; Pierce L; Krilov G; Lupyan D; Robinson S; Dahlgren MK; Greenwood J; Romero DL; Masse C; Knight JL; Steinbrecher T; Beuming T; Damm W; Harder E; Sherman W; Brewer M; Wester R; Murcko M; Frye L; Farid R; Lin T; Mobley DL; Jorgensen WL; Berne BJ; Friesner RA; Abel R Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (67).Raymond JW; Gardiner EJ; Willett P RASCAL: Calculation of Graph Similarity using Maximum Common Edge Subgraphs. Comput J 2002, 45, 631–644. [DOI] [PubMed] [Google Scholar]
- (68).http://www.rdkit.org, RDKit: Open-source cheminformatics. Accessed Oct. 26th, 2022.
- (69).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).He X; Man VH; Yang W; Lee T-S; Wang J A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys 2020, 153, 114502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Horn HW; Swope WC; Pitera JW; Madura JD; Dick TJ; Hura GL; Head-Gordon T Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys 2004, 120, 9665–9678. [DOI] [PubMed] [Google Scholar]
- (72).Mobley DL; Guthrie JP FreeSolv: a database of experimental and calculated hydration free energies, with input files. J. Comput.-Aided Mol. Des 2014, 28, 711–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Hritz J; Oostenbrink C Hamiltonian replica exchange molecular dynamics using softcore interactions. J. Chem. Phys 2008, 128, 144121. [DOI] [PubMed] [Google Scholar]
- (74).Jiang W; Roux B Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J. Chem. Theory Comput 2010, 6, 2559–2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Arrar M; de Oliveira CAF; Fajer M; Sinko W; McCammon JA w-REXAMD: A Hamiltonian replica exchange approach to improve free energy calculations for systems with kinetically trapped conformations. J. Chem. Theory Comput 2013, 9, 18–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Itoh SG; Okumura H Hamiltonian replica-permutation method and its applications to an alanine dipeptide and amyloid-β(29-42) peptides. J. Comput. Chem 2013, 34, 2493–2497. [DOI] [PubMed] [Google Scholar]
- (77).Yang M; Huang J; MacKerell AD Jr. Enhanced Conformational Sampling Using Replica Exchange with Concurrent Solute Scaling and Hamiltonian Biasing Realized in One Dimension. J. Chem. Theory Comput 2015, 11, 2855–2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Joung IS; Cheatham TE III Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Genheden S; Ryde U The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Hu Y; Sherborne B; Lee T-S; Case DA; York DM; Guo Z The importance of protonation and tautomerization in relative binding affinity prediction: a comparison of AMBER TI and Schrödinger FEP. J. Comput.-Aided Mol. Des 2016, 30, 533–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.