Methods for Large-scale Single Mediator Hypothesis Testing: Possible Choices and Comparisons

Abstract

Mediation hypothesis testing for a large number of mediators is challenging due to the composite structure of the null hypothesis, $H_0:\alpha \beta =0(\alpha$: effect of the exposure on the mediator after adjusting for confounders; $\beta$: effect of the mediator on the outcome after adjusting for exposure and confounders). In this paper, we reviewed three classes of methods for large-scale one at a time mediation hypothesis testing. These methods are commonly used for continuous outcomes and continuous mediators assuming there is no exposure-mediator interaction so that the product $\alpha \beta$ has a causal interpretation as the indirect effect. The first class of methods ignores the impact of different structures under the composite null hypothesis, namely, 1) $\alpha =0,\beta \ne 0$; 2) $\alpha \ne 0,\beta =0$; and 3) $\alpha =\beta =0$. The second class of methods weights the reference distribution under each case of the null to form a mixture reference distribution. The third class constructs a composite test statistic using the three p-values obtained under each case of the null so that the reference distribution of the composite statistic is approximately $U\left(\mathrm{0,1}\right)$. In addition to these existing methods, we developed the Sobel-comp method belonging to the second class, which uses a corrected mixture reference distribution for Sobel’s test statistic. We performed extensive simulation studies to compare all six methods belonging to these three classes in terms of the false positive rates under the null hypothesis and the true positive rates under the alternative hypothesis. We found that the second class of methods which uses a mixture reference distribution could best maintain the false positive rates at the nominal level under the null hypothesis and had the greatest true positive rates under the alternative hypothesis. We applied all methods to study the mediation mechanism of DNA methylation sites in the pathway from adult socioeconomic status to glycated hemoglobin level using data from the Multi-Ethnic Study of Atherosclerosis (MESA). We provide guidelines for choosing the optimal mediation hypothesis testing method in practice and develop an R package medScan available at https://github.com/umich-cphds/medScan for implementing all the six methods.

1. Introduction

Mediation analysis is often used to identify potential mechanistic pathways of the effect of an exposure on an outcome through a mediator or sets of mediators. It has become increasingly popular in epidemiology (Z. Chen, Wen, et al., 2020; Huang et al., 2015; Pierce et al., 2014; VanderWeele, 2015; Yang et al., 2017). With the advances in high-throughput technologies, mediation analysis often requires analyzing a large number of potential mediators (Zeng et al., 2021; Zhang et al., 2016). These agnostic explorations of high-dimensional mediators allow researchers to investigate molecular traits associated with complex diseases that may be a result of socioeconomic inequalities, environmental pollution, or other exogenous factors. In particular, molecular epidemiological research has frequently considered the mediating role of DNA methylation (DNAm), and mounting studies have identified methylation differences at $\mathrm{CpG}$ sites as important mediators for diseases such as cancer (Kulis & Esteller, 2010; VanderWeele et al., 2012; Wu et al., 2018), cardiovascular disease (Richardson et al., 2017) and diabetes (Grant et al., 2017).

Suppose there is a total number of $J$ candidate mediators potentially mediating the effect of an exposure $X$ on the outcome $Y$. Let $M_j$ denote the $\mathrm{j}-\mathrm{th}$ mediator where $j\in \{\mathrm{1,2},\dots ,J\}$. To identify which $M_j$’s are truly in the mediating pathways, one can jointly model $M_1,M_2,\dots ,M_J$ (Chén et al., 2018; Huang, 2019; Song, Zhou, Zhang, et al., 2020). However, the computational burden may be too great and the solution may not be robust for large $J$ but with modest sample sizes. Therefore, practitioners may use a scan with the simpler single-mediator analysis, which examines one mediator at a time. Such agnostic searches for active mediators are often based on the parametric models in traditional mediation analysis (Baron & Kenny, 1986). The two regression models typically involved in mediation analysis with the continuous outcome and the continuous mediators are:

$$Y={\beta }_{0,j}+{\beta }_{X,j}X+{\beta }_j{M}_j+{\mathit{\beta }}_{C,j}^{\top }\mathit{C}+{ϵ}_{Y,j};$$ (1)

$$M_j={\alpha }_{0,j}+{\alpha }_{j}X+{\mathit{\alpha }}_{C,j}^{\top }\mathit{C}+{ϵ}_{M,j},$$ (2)

for $j\in \{\mathrm{1,2},\dots ,J\}$, where $\mathit{C}$ is the set of potential confounders and ${ϵ}_{Y,j}\sim N\left(0,{\sigma }_{Y,j}^2\right)$ and ${ϵ}_{M,j}\sim N\left(0,{\sigma }_{M,j}^2\right)$ are independent. In the traditional mediation analysis, ${\alpha }_j{\beta }_j$ is the mediation effect (also called the indirect effect) from $X$ to $Y$ through $M_j$ (MacKinnon et al., 2002; MacKinnon et al., 2020).

An important development in mediation analysis in the last decade is causal mediation analysis using the counterfactual framework (Rubin, 1978; VanderWeele, 2015). Conditional on $C$, the counterfactual framework considers $M_j$ as a function of $X$, and $Y$ as a function of $X$ and $M_j$. That is, $M_j\left(x\right)$ indicates the potential mediator that would be observed had $X$ been set as $x$; and $Y(x,m)$ indicates the potential outcome that would be observed had $X$ and $M_j$ been set as $x$ and $m$, respectively. The following four no-unmeasured-confounding assumptions are needed to establish the causal interpretation of the indirect effect (Pearl, 2022; VanderWeele & Vansteelandt, 2009): A.1(1) $Y(x,m)⫫X\mid C$, no unmeasured confounders for the exposure-outcome relationship conditional on $C$; A.1(2) $Y(x,m)\perp M_j\mid X,C$, no unmeasured confounders for the mediator-outcome relationship conditional on $C;A.1\left(3\right)M_j\left(x\right)\perp X\mid C$, no unmeasured confounders for the exposure-mediator relationship conditional on $C$; A.1(4) $Y(x,m)⫫M_j\left(x^{\mathrm{*}}\right)\mid C$, no unmeasured confounders for the mediator-outcome relationship that is affected by the exposure conditional on $C$. In addition, we assume that (A.2) there is no exposure-mediator interaction affecting the outcome.

A causal diagram for illustrating the role of the $\mathrm{j}-\mathrm{th}$ mediator is presented in Figure 1. Under assumptions $A.1$ and $A.2$, the causal mediation effect is expressed as:

$$E\left[Y\left(x^{\text{*}},M_j\left(x^{\text{*}}\right)\right)\mid C\right]-E\left[Y\left(x^{\text{*}},M_j(x)\right)\mid C\right]={\alpha }_j{\beta }_j\left(x^{\text{*}}-x\right).$$

In terms of hypothesis testing for the mediation effect, the traditional approach is equivalent to the modern causal approach for continuous outcomes and continuous mediators if assumptions $A.1$ and A.2 hold (MacKinnon et al., 2020). However, the causal framework offers more flexibility in deriving causally interpretable mediation effects for different types of outcomes and mediators with accompanying software (Y. Li et al., 2022; Shi et al., 2021; Steen et al., 2020; Tingley et al., 2014). MacKinnon et al. (2020) compares the traditional and causal approaches for continuous outcomes and mediators in terms of bias, type I error, power, and coverage of the indirect effect. A detailed discussion and review of the connection between traditional and counterfactual methods are presented in section S1 of the supplementary materials.

Figure 1:

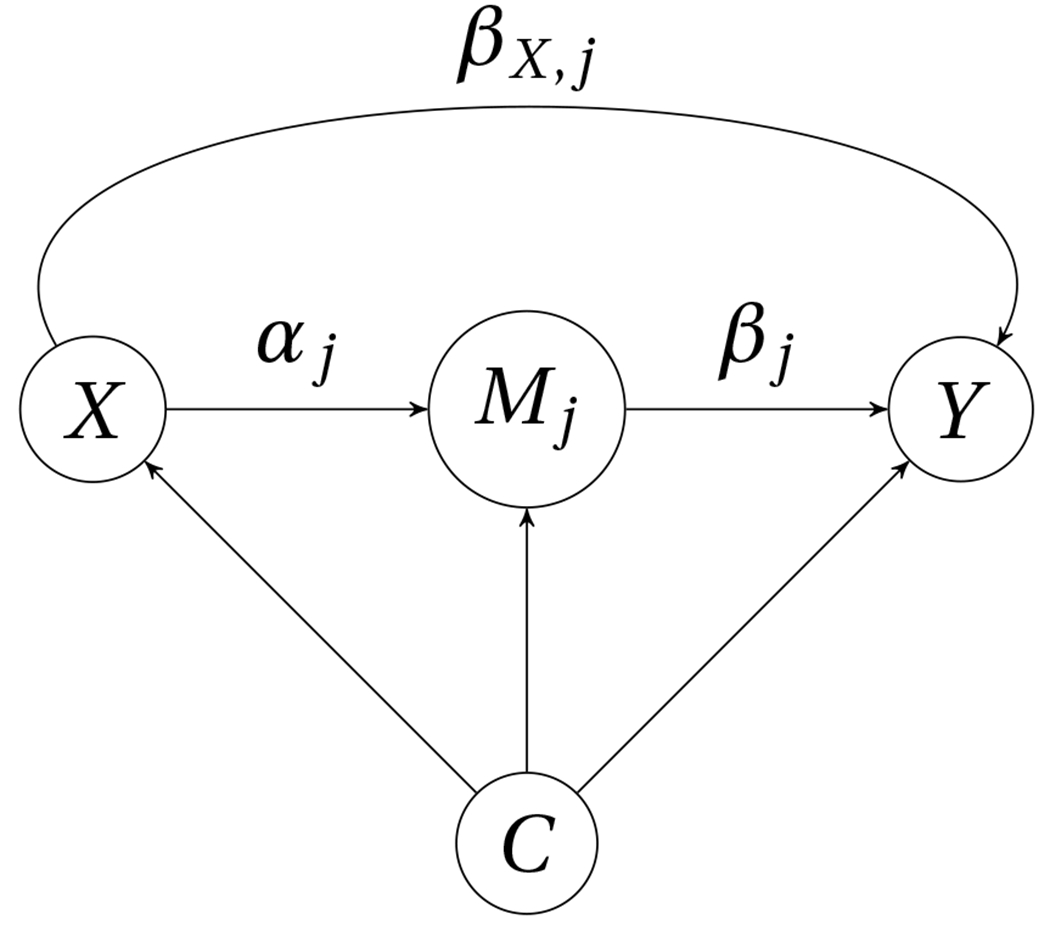
A causal diagram for mediation analysis. For $j=\mathrm{1,2},\dots ,J,X$ is the exposure, $M_j$ is the j-th mediator, $Y$ is the outcome, $C$ is the set of confounders. ${\alpha }_j$ is the effect of $X$ on $M_j$ after adjusting for $C.{\beta }_j$ is the effect of $M_j$ on $Y$ after adjusting for $(X,C).{\beta }_{X,j}$ is the direct effect of $X$ on $Y$ after adjusting for $M_j$ and $C$.

The three classes of methods we will review for mediation hypothesis testing are designed under assumptions A.1 and A.2 for continuous outcomes and continuous mediators. It is inappropriate to use them in a causal framework if the product $\alpha \beta$ does not correspond to a causally interpretable indirect effect. Examples of this include common situations like if the outcome or mediator is binary (VanderWeele, 2015), or if there is exposure-mediator interaction affecting the outcome (MacKinnon et al., 2020). Under assumptions $A.1$ and $A.2$ with continuous outcomes and continuous mediators, to test whether $M_j$ is mediating the effect of $X$ on $Y$, the underlying null and alternative hypotheses can be stated as:

$$H_{0,j}:{\alpha }_j{\beta }_j=0vs.H_{1,j}:{\alpha }_j{\beta }_j\ne 0,forj=1,2,\dots ,J.$$

Since $H_{\mathrm{0,1}},\dots ,H_{0,J}$ are tested in a similar manner, we drop the subscript $j$ for now. The first class of hypothesis testing methods contains Sobel’s test (Sobel, 1982) and the MaxP test (MacKinnon et al., 2002). The null hypothesis involving the product of parameters is composite (Barfield et al., 2017) and consists of three cases, namely, 1) $H_{01}:\alpha =0,\beta \ne 0$; 2) $H_{10}:\alpha \ne 0,\beta =0$; and 3) $H_{00}:\alpha =\beta =0$. Since the commonly used reference distributions $\left(\mathrm{N}\right(\mathrm{0,1}\left)\right)$ for Sobel’s test statistic and MaxP test statistic $\left(\mathrm{U}\right(\mathrm{0,1}\left)\right)$ are incorrect under $H_{00}$, they are often conservative (Barfield et al., 2017; Liu et al., 2022) in high-dimensional settings where the majority of mediators are likely to have no mediation effect, namely, a sparse situation.

Many recent studies have developed single-mediator hypothesis testing methods to produce calibrated p-values that specifically consider the composite null structure. Huang et al. (2019) proposed the joint significance test under the composite null hypothesis (JT-comp) that uses the product of two normally distributed variables as the test statistic. Dai et al. (2022) developed a procedure for high-dimensional mediation hypotheses testing (HDMT) which considered the correct reference distribution for the MaxP statistic. A common feature of these two methods is to weight the reference distribution under $H_{01},H_{10},H_{00}$ to form a mixture null distribution corresponding to the test statistic. We group these two methods into the second class.

The third class contains the Divide-Aggregate Composite-null Test (DACT) method proposed by Liu et al. (2022). In contrast to the second class which forms a mixture reference distribution, this method constructs a composite test statistic using the three p-values obtained under $H_{01},H_{10}$ and $H_{00}$.

However, no study has numerically compared the performance of the above-mentioned methods. It remains unclear how these methods would be affected by various factors with high-dimensional mediators, in particular, by the sample size, the proportion of $H_{01},H_{10},H_{00},H_1$ being true, the variation of non-zero $\alpha$ and $\beta$ across $J$ tests, and the $R^2$ in the data generating models, i.e. models (1) and (2). Our contribution in this paper is twofold. First, in addition to the existing methods, we develop a new method, called Sobel-comp, which is a variant of HDMT. Sobel-comp uses a corrected mixture reference distribution for Sobel’s test statistic utilizing the composite structure of the null. Second, we perform extensive simulation studies to compare all six methods in terms of false positive rates under the null hypothesis and true positive rates under the alternative hypothesis.

This paper is organized as follows: In Section 2.1, we first describe the five existing mediation hypothesis testing methods, including Sobel’s test, MaxP, JT-comp, HDMT, and DACT. We then propose our new method, Sobel-comp. In Section 2.2, we describe the simulation setup to compare the testing performance of the six methods. In Section 2.3, we describe the analysis steps for studying the mediation mechanism of DNAm in the pathway from adult socioeconomic status (SES) to glycated hemoglobin (HbA1c) level using data from the Multi-Ethnic Study of Atherosclerosis (MESA). Numerical results of both simulation and data example are presented in Section 3. We summarize the key strengths and limitations of each method and provide recommendations for applying these methods in practical settings in Section 4.

2. Methods and Materials

2.1. Methods for mediation hypothesis testing

Mediation hypothesis testing methods are often based on the Wald test statistics obtained from models (1) and (2). Denote $Z_{\beta }$ as the test statistic for testing $H_0:\beta =0$ in model (1) and $Z_{\alpha }$ as the test statistic for testing $H_0:\alpha =0$ in model (2), respectively. Under the respective null hypotheses, we have:

$$Z_{\beta }=\frac{\widehat{\beta }-\beta }{{\widehat{\sigma }}_{\beta }}\sim N(0,1);Z_{\alpha }=\frac{\widehat{\alpha }-\alpha }{{\widehat{\sigma }}_{\alpha }}\sim N(0,1),$$

where $\widehat{\beta }$ and $\widehat{\alpha }$ are the maximum likelihood estimates for $\beta$ and $\alpha$, respectively. ${\hat{\sigma }}_{\beta }$ and ${\hat{\sigma }}_{\alpha }$ are the estimated standard error of $\widehat{\beta }$ and $\widehat{\alpha }$, respectively. Let the two-sided p-value for $Z_{\beta }$ be $p_{\beta }$ and for $Z_{\alpha }$ be $p_{\alpha }$.

2.1.1. Sobel’s test

Sobel’s test statistic (Sobel, 1982) uses the first-order multivariate delta method to find the standard error of $\hat{\alpha }\hat{\beta }$, which is $\sqrt{\widehat{{\beta }^2}\widehat{{\sigma }_{\alpha }^2}+\widehat{{\alpha }^2}\widehat{{\sigma }_{\beta }^2}}$. Since $\widehat{\alpha }$ and $\widehat{\beta }$ derived from models (1) and (2) are independent (MacKinnon et al., 1995; Sobel, 1982), Sobel’s test statistic is defined as:

$$T_{\mathit{\text{sobel}}}=\frac{\hat{\beta }\hat{\alpha }}{\sqrt{\widehat{{\beta }^2}\widehat{{\sigma }_{\alpha }^2}+\widehat{{\alpha }^2}\widehat{{\sigma }_{\beta }^2}}}=\frac{Z_{\alpha }}{\sqrt{1+{\left(Z_{\alpha }/Z_{\beta }\right)}^2}}.$$ (3)

$T_{\mathit{\text{Sobel}}}$ is typically compared to $N\left(\mathrm{0,1}\right)$ to determine the p-value. However, the $N\left(\mathrm{0,1}\right)$ reference distribution is incorrect because the product of two normally distributed random variables $\hat{\alpha }$ and $\hat{\beta }$ is not always well approximated by a normal distribution (MacKinnon et al., 2004). This result can be also explained from the composite null perspective. The reference distribution is correct asymptotically under $H_{01}$ and $H_{10}$, but is incorrect under $H_{00}$. Under $H_{01},T_{\mathit{\text{sobel}}}$ is asymptotically equivalent to $Z_{\alpha }$ because $Z_{\beta }^{-1}$ converges to zero and $Z_{\alpha }$ is bounded in probability so that $Z_{\alpha }/Z_{\beta }$ in the denominator converges to zero in probability (Liu et al., 2022). Thus, $T_{\mathit{\text{sobel}}}\sim N\left(\mathrm{0,1}\right)$ under $H_{01}$. Likewise, $T_{\mathit{\text{sobel}}}\sim N\left(\mathrm{0,1}\right)$ under $H_{10}$. However, under $H_{00}$, the multivariate delta method for calculating the standard error of $\hat{\alpha }\hat{\beta }$ fails when $\alpha =\beta =0.T_{\mathit{\text{sobel}}}$ does not follow $N\left(\mathrm{0,1}\right)$ asymptotically since $Z_{\alpha }/Z_{\beta }$ (or $Z_{\beta }/Z_{\alpha }$) does not converge to 0 in probability. Liu et al. (2022) shows that $T_{\mathit{\text{sobel}}}$ follows $N(\mathrm{0,1}/4)$ under $H_{00}$. Therefore, using $N\left(\mathrm{0,1}\right)$ as the reference distribution for every null case for Sobel’s test is incorrect.

2.1.2. MaxP test

The MaxP test, also called the joint significance test (MacKinnon et al., 2002), has been developed based on the idea that if we want to reject $H_0$ at level $t$, we should reject two separate hypothesis tests of $\alpha =0$ and $\beta =0$ at level $t$ simultaneously. The MaxP test statistic is defined as:

$$p_{\mathit{\text{max}}}=\mathit{\text{max}}\left(p_{\alpha },p_{\beta }\right).$$ (4)

$p_{\mathit{max}}$ is compared to $U\left(\mathrm{0,1}\right)$ to determine the p-value. Equivalently, $p_{\mathit{\text{max}}}$ is determined by the smaller $\left|Z_{\alpha }\right|$ or $\left|Z_{\beta }\right|$. Since $\mathit{min}\left(\left|Z_{\alpha }\right|,\left|Z_{\beta }\right|\right)>\left|T_{\mathit{\text{Sobel}}}\right|$ in a finite sample, the MaxP p-value is always smaller than that from Sobel’s test and thus is more powerful. However, the reference distribution of $U\left(\mathrm{0,1}\right)$ is incorrect under $H_{00}$. Since $P\left(p_{\mathit{max}}<t\right)=P\left(p_{\alpha }<t\right)\cdot P\left(p_{\beta }<t\right)=t^2$, the correct reference distribution for $p_{\mathit{max}}$ under $H_{00}$ is $\mathit{Beta}\left(\mathrm{2,1}\right)$ (Dai et al., 2022; Liu et al., 2022). Since the p-value under $H_{00}$ determined by $U\left(\mathrm{0,1}\right)$ will be larger than that by Beta $\left(\mathrm{2,1}\right)$, the MaxP test is conservative.

2.1.3. Joint significance test under the composite null hypothesis (JT-comp)

We now resume to use the subscript $j$ corresponding to the $j$-th hypothesis test for $j=\mathrm{1,2},\dots ,J$. The test statistic for JT-comp is the product of two normally distributed random variables, $Z_{\alpha ,j}{Z}_{\beta ,j}$ (Huang et al., 2019). Unlike Sobel’s test and the MaxP test, JT-comp distinguishes the null distributions for its test statistic under $H_{01,j},H_{10,j}$ and $H_{00,j}$ to obtain case-specific p-values. Specifically, let $w_{01,j},w_{10,j},w_{00,j}$ be the probability of $H_{01,j},H_{10,j}$ and $H_{00,j}$ being true, respectively. Denote $F\left(t\right)$ as the two-sided tail probability of the standard normal product distribution evaluated at $t$. Under $H_{00,j}$, since $Z_{\alpha ,j}\sim N\left(\mathrm{0,1}\right)$ and $Z_{\beta ,j}\sim N\left(\mathrm{0,1}\right)$, the case-specific p-value is $F\left(Z_{\alpha ,j}{Z}_{\beta ,j}\right)$. Under $H_{01,j},Z_{\alpha ,j}\sim N\left(\mathrm{0,1}\right)$ and $Z_{\beta ,j}\sim N\left({\mu }_{\beta ,j},1\right)$, where ${\mu }_{\beta ,j}={\beta }_j/{\widehat{\sigma }}_{\beta ,j}\ne 0$. Huang et al. (2019) further assumes that ${\mu }_{\beta ,j}$ follows a symmetric distribution with mean 0 and variance ${\delta }_{\beta ,j}^2$, e.g. ${\mu }_{\beta ,j}\sim N\left(0,{\delta }_{\beta ,j}^2\right)$. By integrating out ${\mu }_{\beta ,j}$, the p-value under $H_{01,j}$ is obtained by using the same $F(\cdot )$ function as if under $H_{00,j}$, but only differs by a scaling factor of $1/\sqrt{1+{\delta }_{\beta ,j}^2}$. That is, the p-value under $H_{01,j}$ is $F\left(Z_{\alpha ,j}{Z}_{\beta ,j}/\sqrt{1+{\delta }_{\beta ,j}^2}\right)$. Similarly, the p-value under $H_{10,j}$ is $F\left(Z_{\alpha ,j}{Z}_{\beta ,j}/\sqrt{1+{\delta }_{\alpha ,j}^2}\right)$, where ${\delta }_{\alpha ,j}^2$ is the assumed variance of the mean of $Z_{\alpha ,j}$ under $H_{10,j}$. The final composite p-value is aggregated as:

$$p_{JT-comp,j}=w_{01,j}F\left(\frac{Z_{\alpha ,j}{Z}_{\beta ,j}}{\sqrt{1+{\delta }_{\beta ,j}^2}}\right)+w_{10,j}F\left(\frac{Z_{\alpha ,j}{Z}_{\beta ,j}}{\sqrt{1+{\delta }_{\alpha ,j}^2}}\right)+w_{00,j}F\left(Z_{\alpha ,j}{Z}_{\beta ,j}\right).$$

$p_{JT-comp,j}$ is then approximated by the Taylor series:

$${\hat{p}}_{JT-\mathit{\text{comp}},j}=F\left(\frac{Z_{\alpha ,j}{Z}_{\beta ,j}}{\sqrt{\mathit{\text{Var}}\left(Z_{\beta ,j}\right)}}\right)+F\left(\frac{Z_{\alpha ,j}{Z}_{\beta ,j}}{\sqrt{\mathit{\text{Var}}\left(Z_{\alpha ,j}\right)}}\right)-F\left(Z_{\alpha ,j}{Z}_{\beta ,j}\right).$$ (5)

where $\mathit{Var}\left(Z_{\beta ,j}\right)=1+w_{01,j}{\delta }_{\beta ,j}^2$ and $\mathit{Var}\left(Z_{\alpha ,j}\right)=1+w_{10,j}{\delta }_{\alpha ,j}^2$. Sample variances of $Z_{\alpha ,j}$ and $Z_{\beta ,j}$ across all tests are used to estimate $\mathit{Var}\left(Z_{\alpha ,j}\right)$ and $\mathit{Var}\left(Z_{\beta ,j}\right)$. The advantage of using the approximated p-value is to avoid estimating $w_{01,j},w_{10,j},w_{00,j}$. Since the reference distribution of $Z_{\alpha ,j}{Z}_{\beta ,j}$ is correct under $H_{01,j},H_{10,j}$ and $H_{00,j}$, JT-comp is more powerful than Sobel’s and MaxP tests.

However, the accuracy of $p_{JT-comp,j}$ approximated by ${\hat{p}}_{JT-comp,j}$ depends on the residual error from Taylor series expansion in (5). The error relative to the p-value becomes larger when the p-value becomes smaller, suggesting that JT-comp cannot maintain the family-wise-error-rate at small significance thresholds. A good approximation requires that ${\delta }_{\alpha ,j}^2$ and ${\delta }_{\beta ,j}^2$ are close to 0. Namely, the approximation works well when ${\mu }_{\alpha ,j}$ is concentrated near zero (similar for ${\mu }_{\beta ,j}$). Since ${\mu }_{\alpha ,j}=$ ${\alpha }_j/{\widehat{\sigma }}_{\alpha ,j}$, this condition is violated if ${\alpha }_j$ is large or if the sample size is large so that ${\widehat{\sigma }}_{\alpha ,j}$ is small. A practical suggestion given by Huang et al. (2019) is to check whether the sample variance of $Z_{\alpha ,j}$ and $Z_{\beta ,j}$ are less than 1.5. Since JT-comp only works well for small ${\delta }_{\alpha ,j}^2$ and ${\delta }_{\beta ,j}^2$, its applicability is limited to the settings with small samples and small ${\alpha }_j$’s and ${\beta }_j$’s.

2.1.4. High dimensional mediation testing (HDMT)

Another method which uses the correct reference distribution is HDMT (Dai et al., 2022). Let ${\pi }_{01},{\pi }_{10},{\pi }_{00}$ be the proportion of $\left({\alpha }_j=0,{\beta }_j\ne 0\right),\left({\alpha }_j\ne 0,{\beta }_j=0\right)$ and $\left({\alpha }_j={\beta }_j=0\right)$ among all $J$ tests. The test statistic for the HDMT method is the MaxP statistic. Under $H_{01,j}$ and $H_{10,j},p_{\mathit{max},j}\sim U\left(\mathrm{0,1}\right)$ asymptotically. Under $H_{00,j},p_{\mathit{max},j}\sim \mathit{Beta}\left(\mathrm{2,1}\right)$. The reference distribution for $p_{\mathit{max},j}$ is:

$$\left({\hat{\pi }}_{01}+{\hat{\pi }}_{10}\right)U(0,1)+{\hat{\pi }}_{00}\mathit{\text{Beta}}(2,1),$$

where ${\hat{\pi }}_{01},{\hat{\pi }}_{10}$ and ${\hat{\pi }}_{00}$ are obtained by non-parametric methods for estimating the proportion of nulls (Storey, 2002). HDMT further proposes improving the power under finite samples. Under $H_{01,j}$, the p-value determined by $U\left(\mathrm{0,1}\right)$ is accurate asymptotically when the power of rejecting ${\beta }_j=0$ goes to 1. Namely, $P\left(p_{\beta ,j}<t\mid H_{01,j}\right)\stackrel{n\to \mathrm{\infty }}{⟶}1$ for any $t>0$. However, this condition is difficult to hold when $t$ is extremely small in a finite sample, resulting in a noticeably larger p-value than the truth. In such cases, HDMT uses the Grenander estimator to estimate $P\left(p_{\beta ,j}<t\mid H_{01,j}\right)$ and $P\left(p_{\alpha ,j}<t\mid H_{10,j}\right)$.

Overall, since the mixture null distribution of $p_{\mathit{max},j}$ statistic is asymptotically correct, HDMT is robust to any choices of ${\pi }_{01},{\pi }_{10},{\pi }_{00}$. However, since the rejection rule of HDMT is determined by empirically estimating the significance thresholds and false discovery rates, it is difficult to compare it with other methods in terms of p-values. We make the following modifications to obtain p-values from HDMT using the asymptotic mixture reference distribution:

$$p_{HDMT,j}=\left({\hat{\pi }}_{01}+{\hat{\pi }}_{10}\right)p_{\mathit{\text{max}},j}+{\hat{\pi }}_{00}{p}_{\mathit{\text{max}},j}^2.$$

with finite samples, we estimate $P\left(p_{\alpha ,j}<p_{\mathit{max},j}\mid H_{10,j}\right)$ and $P\left(p_{\beta ,j}<p_{\mathit{max},j}\mid H_{01,j}\right)$ by the Grenander estimator as described in Dai et al. (2022). The adjusted p-value is:

$${\tilde{p}}_{HDMT,j}={\hat{\pi }}_{01}{p}_{\mathit{\text{max}},j}\hat{P}\left(p_{\beta ,j}<p_{\mathit{\text{max}},j}\mid H_{01,j}\right)+{\hat{\pi }}_{10}{p}_{\mathit{\text{max}},j}\hat{P}\left(p_{\alpha ,j}<p_{\mathit{\text{max}},j}\mid H_{10,j}\right)+{\hat{\pi }}_{00}{p}_{\mathit{max},j}^2.$$

2.1.5. Divide-Aggregate Composite-null Test (DACT)

The test statistic for DACT is a composite p-value obtained by averaging the three case-specific p-values weighted by ${\pi }_{01},{\pi }_{10},{\pi }_{00}$, respectively (Liu et al., 2022). Under $H_{01,j}$, the p-value is $p_{\alpha ,j}$ since ${\beta }_j$ is known to be non-zero. Similarly, the p-value under $H_{10,j}$ is $p_{\beta ,j}$. Under $H_{00,j}$, the p-value is $p_{\mathit{\text{max}},j}^2$ using the MaxP statistic, which follows $\mathit{Beta}\left(\mathrm{2,1}\right)$. The DACT test statistic is defined as:

$$DAC{T}_j={\hat{\pi }}_{01}{p}_{\alpha ,j}+{\hat{\pi }}_{10}{p}_{\beta ,j}+{\hat{\pi }}_{00}{p}_{\mathit{\text{max}},j}^2,$$ (6)

where ${\hat{\pi }}_{01},{\hat{\pi }}_{10}$ and ${\hat{\pi }}_{00}$ are obtained based on the empirical characteristic function and Fourier analysis (Jin & Cai, 2007). If any of ${\hat{\pi }}_{00},{\hat{\pi }}_{10},{\hat{\pi }}_{01}$ is close to 1, DACT then follows $U\left(\mathrm{0,1}\right)$ approximately. Otherwise, the DACT statistic deviates from $U\left(\mathrm{0,1}\right)$. Under this scenario, the DACT method adapts Efron’s empirical null framework (Efron et al., 2001) to estimate the null distribution of the transformed DACT statistic. The final p-value is calibrated using the empirical null distribution.

The reference distribution for the DACT test statistic can only be approximated or empirically estimated while the exact reference distribution has not been established. When none of ${\pi }_{00},{\pi }_{10},{\pi }_{01}$ is close to 1, it remains unclear how close the empirical estimation using Efron’s method is to the truth. In fact, the cumulative distribution function for the DACT statistic is complicated, because the third term $p_{\mathit{\text{max}},j}^2$, in (6) depends on the larger of the first two terms such that the three terms are dependent. Therefore, DACT should be used cautiously when ${\pi }_{00},{\pi }_{01},{\pi }_{10}$ are all far from 1.

2.1.6. A new variant of HDMT: Sobel-comp

We propose a variant of HDMT using Sobel’s test statistic, called Sobel-comp. Under $H_{01,j}$ and $H_{10,j},T_{\mathit{\text{sobel}},j}\sim N\left(\mathrm{0,1}\right)$. Under $H_{00,j},T_{\mathit{\text{sobel}},j}\sim N(\mathrm{0,1}/4)$. The reference distribution for $T_{\mathit{\text{sobel}},j}$ is:

$$\left({\hat{\pi }}_{01}+{\hat{\pi }}_{10}\right)N(0,1)+{\hat{\pi }}_{00}N(0,1/4),$$

where ${\widehat{\pi }}_{01},{\widehat{\pi }}_{10},{\widehat{\pi }}_{00}$ are obtained from the HDMT method. When $\left|Z_{\beta ,j}\right|>\left|Z_{\alpha ,j}\right|$, the p-value for HDMT under $H_{00,j}$ is identical no matter how large $\left|Z_{\beta ,j}\right|$ is. Therefore, the HDMT method loses power since a stronger effect of the mediator on the outcome does not increase the power to detect the mediation effect if the exposure has a relatively weak effect on the mediator. In contrast, the p-value for Sobel-comp under $H_{00,j}$ decreases as $\left|Z_{\beta ,j}\right|$ increases. In particular,

Proposition 1. Suppose $\left|Z_{\beta ,j}\right|>\left|Z_{\alpha ,j}\right|\ge 0$. The case-specific p-value under $H_{00,j}$ from Sobel-comp is smaller than that from HDMT if $\left|Z_{\beta ,j}\right|>\mathit{max}\left(\left|Z_{\alpha ,j}\right|,{\left\{4{\left({\mathrm{\Phi }}^{-1}\left(2\mathrm{\Phi }{\left(\left|Z_{\alpha ,j}\right|\right)}^2\right)\right)}^{-2}-Z_{\alpha ,j}^{-2}\right\}}^{-1/2}\right)$, where $\mathrm{\Phi }(\cdot )$ is the cumulative distribution function of a standard normal random variable.

Proposition 1 is also true when we interchange $\left|Z_{\beta ,j}\right|$ and $\left|Z_{\alpha ,j}\right|$. The proof of Proposition 1 is provided in section S2 in the supplementary materials. However, in addition to the conditions in Proposition 1, Sobel-comp requires ${\pi }_{00}$ close to 1 to be more powerful than HDMT. On the other hand, unlike HDMT which can estimate $P\left(p_{\alpha ,j}<p_{\mathit{max},j}\mid H_{10,j}\right)$ and $P\left(p_{\beta ,j}<p_{\mathit{max},j}\mid H_{01,j}\right)$ to further increase power with finite samples, it is difficult to extend Sobel-comp using similar technique because $Z_{\alpha ,j}$ and $Z_{\beta ,j}$ in the Sobel’s statistic are not separable.

2.2. Simulation setup

We evaluate the performance of Sobel’s test, MaxP, JT-comp, HDMT, Sobel-comp and DACT in terms of false positive rate (FPR) under the null hypothesis and true positive rate (TPR) under the alternative hypothesis in simulation scenarios by varying 1) the proportion of the null and the alternative components, denoted as ${\pi }_{00},{\pi }_{01},{\pi }_{10},{\pi }_{11};2$) the sample size $\left.n;3\right)$ the variation of the non-zero parameters $\alpha ,\beta$ across mediators; and 4) $R^2$ in the outcome and mediator models. Here, $R^2$ is the proportion of variation explained by the regression model. We assess the mediation effect of $J=\mathrm{100,000}$ mediators (denoted as $M_j$ where $j\in \{\mathrm{1,2},\dots ,J\}$) from the exposure $\left(X\right)$ to the outcome $\left(Y\right)$. For the j-th pair of models, we first generate the covariate $C\sim N\left(\mathrm{0,1}\right)$ and the exposure $X\sim N\left(\mathrm{0,1}\right)$. We then generate $M_j$ and $Y$ from:

$$M_j={\alpha }_{j}X+{\alpha }_{C}C+{ϵ}_{M_j},$$ (7)

$$Y={\beta }_j{M}_j+{\beta }_{X}X+{\beta }_{C}C+{ϵ}_Y,$$ (8)

where ${ϵ}_{M_j}\sim N\left(0,{\sigma }_{M_j}^2\right),{ϵ}_Y\sim N\left(0,{\sigma }_Y^2\right)$ and ${\alpha }_C={\beta }_C={\beta }_X=1$. For $J$ pairs of models, with probability ${\pi }_{00},{\alpha }_j={\beta }_j=0$; with probability ${\pi }_{01},{\alpha }_j=0,{\beta }_j\sim N\left(0,{\tau }^2\right);$ with probability ${\pi }_{10},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right),{\beta }_j=0$; and with probability ${\pi }_{11},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right),{\beta }_j\sim N\left(0,{\tau }^2\right)$. The parameter $\tau$ controls the dispersion of the non-zero coefficients.

To evaluate the FPR for the six methods under the composite null hypothesis, ${\pi }_{11}$ is set as 0. We construct six classes of scenarios (Table 1). In Null 1 scenarios, ${\sigma }_{M_j}^2={\sigma }_Y^2=1$. In contrast to Null 1 scenarios where $R^2$ varies across mediators, Null 2 scenarios control $R^2$ at the same level. In model (7), $R^2=\left({\alpha }_j^2+{\alpha }_A^2\right)/\left({\alpha }_j^2+{\alpha }_A^2+{\sigma }_{M_j}^2\right)$ and in model (8), $R^2=\left({\beta }_j^2\left({\alpha }_j^2+{\alpha }_A^2+{\sigma }_{M_j}^2\right)+{\beta }_X^2+{\beta }_A^2\right)/\left({\beta }_j^2\left({\alpha }_j^2+\right.\right.\left.\left.{\alpha }_A^2+{\sigma }_{M_j}^2\right)+{\beta }_X^2+{\beta }_A^2+{\sigma }_Y^2\right)$. After generating data, we fit linear regression models adjusted for the confounder to obtain $z_{\alpha ,j}$ for ${\alpha }_j$ in model (7) and $z_{\beta ,j}$ for ${\beta }_j$ in model (8) for all $j$. We then apply the six mediation methods to obtain p-values for testing the mediation effect. We calculate the FPR at the nominal significance levels of ${10}^{-3},{10}^{-4},{10}^{-5},{10}^{-6}$, and $5\times {10}^{-7}$, where $5\times {10}^{-7}$ corresponds to controlling the overall family-wise-error-rate (FWER) at 0.05. Under the null hypothesis, the FPR given a significance level is calculated as the proportion of p-values among 100,000 tests below this level. We repeat this process 2,000 times $(\mathrm{R}=2000)$ and average FPRs over 2,000 replicates. More specifically, the empirical FPR is calculated as

$$\widehat{FPR}=R^{-1}\sum _{r=1}^R\left[J^{-1}\sum _{j=1}^{J}I\left({\text{reject H}}_{0,\text{j}}^{(\text{r})}\mid {\text{H}}_{0,1}^{(\text{r})},\dots ,{\text{H}}_{0,\text{J}}^{(\text{r})}\text{are true}\right)\right].$$

Table 1:

Simulation scenarios for comparing false positive rates. In total, we simulate 100,000 mediators. For the j-th mediator, with probability ${\pi }_{01},{\alpha }_j=0$ and ${\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{10},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right)$ and ${\beta }_j=0$; with probability ${\pi }_{00},{\alpha }_j={\beta }_j=0$, where ${\alpha }_j$ is the effect of the exposure on the outcome conditional on $C$ and ${\beta }_j$ is the effect of the mediator on the outcome conditional on $C$ and $X$. The last column refers to the $R^2$ in the outcome model $\left(R_Y^2\right)$ and in the mediator model $\left(R_M^2\right)$, where $R^2$ is the ratio of variation explained by the regression model to the total variation.

Case	${\mathit{\pi }}_{11},{\mathit{\pi }}_{01},{\mathit{\pi }}_{10},{\mathit{\pi }}_{00}$	Sample size	$\mathit{\tau }$	${\mathit{R}}^2={\mathit{R}}_{\mathit{Y}}^2={\mathit{R}}_{\mathit{M}}^2$
Null 1(a)	$\mathrm{0,0.001,0.001,0.998}$	$\left(\mathrm{200,500,1000}\right)$	$\left(\mathrm{0.1,0.3,0.7}\right)$	Not controlled
Null 1(b)	$\mathrm{0,0.33,0.33,0.34}$	$\left(\mathrm{200,500,1000}\right)$	$\left(\mathrm{0.1,0.3,0.7}\right)$	Not controlled
Null 1(c)	$\mathrm{0,0.5,0.5,0}$	$\left(\mathrm{200,500,1000}\right)$	$\left(\mathrm{0.1,0.3,0.7}\right)$	Not controlled
Null 2(a)	$\mathrm{0,0.001,0.001,0.998}$	$\left(\mathrm{200,500,1000}\right)$	$\left(0.3\right)$	$\left(\mathrm{0.1,0.15,0.2}\right)$
Null 2(b)	$\mathrm{0,0.33,0.33,0.34}$	$\left(\mathrm{200,500,1000}\right)$	$\left(0.3\right)$	$\left(\mathrm{0.1,0.15,0.2}\right)$
Null 2(c)	$\mathrm{0,0.5,0.5,0}$	$\left(\mathrm{200,500,1000}\right)$	$\left(0.3\right)$	$\left(\mathrm{0.1,0.15,0.2}\right)$

For power comparison, we follow the same data generation process described above except that we also simulate data under the alternative hypothesis. We have six classes of scenarios in Table 2. Under the control of the true false discovery rate (FDR) at 0.05, we evaluate the TPR for each method by calculating the number of observed rejections under which the alternative hypothesis is true to the total number of true non-null signals. Calculating the true FDR is possible in simulation studies since the underlying truth is known. We repeat the process $200(\mathrm{R}=200)$ times, and the TPR is averaged over all 200 replicates. More specifically, the TPR is calculated as

$$\widehat{TPR}=R^{-1}\sum _{r=1}^R\left[J^{-1}\sum _{j=1}^{J}I\left({\text{reject H}}_{0,\text{j}}^{(\text{r})}\mid {\text{H}}_{0,\text{j}}^{(\text{r})}\text{is not true}\right)\right]\text{.}$$

Table 2:

Simulation scenarios for comparing true positive rates. In total, we simulate 100,000 mediators. For the $\mathrm{j-th}$ mediator, with probability ${\pi }_{11},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right),{\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{01},{\alpha }_j=0$ and ${\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{10},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right)$ and ${\beta }_j=0$; with probability ${\pi }_{00},{\alpha }_j={\beta }_j=0$, where ${\alpha }_j$ is the effect of the exposure on the outcome conditional on $C$ and ${\beta }_j$ is the effect of the mediator on the outcome conditional on $C$ and $X$. The last column refers to the $R^2$ in the outcome model $\left(R_Y^2\right)$ and in the mediator model $\left(R_M^2\right)$, where $R^2$ is the ratio of variation explained by the regression model to the total variation.

Case	${\mathit{\pi }}_{11},{\mathit{\pi }}_{01},{\mathit{\pi }}_{10},{\mathit{\pi }}_{00}$	Sample size	$\mathit{\tau }$	${\mathit{R}}^2={\mathit{R}}_{\mathit{Y}}^2={\mathit{R}}_{\mathit{M}}^2$
Alternative 1(a)	$\mathrm{0.001,0.001,0.001,0.997}$	$\left(\mathrm{200,500,1000}\right)$	$\left(\mathrm{0.1,0.3,0.7}\right)$	Not controlled
Alternative 1(b)	$\mathrm{0.2,0.2,0.2,0.4}$	$\left(\mathrm{200,500,1000}\right)$	$\left(\mathrm{0.1,0.3,0.7}\right)$	Not controlled
Alternative 1(c)	$\mathrm{0.2,0.4,0.4,0}$	$\left(\mathrm{200,500,1000}\right)$	$\left(\mathrm{0.1,0.3,0.7}\right)$	Not controlled
Alternative 2(a)	$\mathrm{0.001,0.001,0.001,0.997}$	$\left(\mathrm{200,500,1000}\right)$	$\left(0.3\right)$	$\left(\mathrm{0.1,0.15,0.2}\right)$
Alternative 2(b)	$\mathrm{0.2,0.2,0.2,0.4}$	$\left(\mathrm{200,500,1000}\right)$	$\left(0.3\right)$	$\left(\mathrm{0.1,0.15,0.2}\right)$
Alternative 2(c)	$\mathrm{0.2,0.4,0.4,0}$	$\left(\mathrm{200,500,1000}\right)$	$\left(0.3\right)$	$\left(\mathrm{0.1,0.15,0.2}\right)$

We use existing R software and packages to implement JT-comp (Huang et al., 2019), DACT (Liu et al., 2022) and HDMT (Dai et al., 2022).

2.3. Data example using MESA: study design and methods

We apply all six methods (Sobel’s test, the MaxP test, JT-comp, HDMT, Sobel-comp, and DACT) to study the mediation mechanism of DNA methylation levels at $\mathrm{CpG}$ sites in the pathway from adult SES to HbA1c using data from MESA (Bild et al., 2002). Our exposure, adult SES, defined by educational attainment, is a risk factor for cardiovascular disease and diabetes (Telfair & Shelton, 2012; Whitaker et al., 2014). Our outcome, HbA1c, which reflects the three-month average blood sugar level, is a critical measurement in the diagnosis of diabetes and is a known risk factor for cardiovascular disease (Sakurai et al., 2013; Singer et al., 1992; Yeung et al., 2018). We assume that the effect direction is from educational attainment to HbA1c level since the exposure has remained unchanged during the study and was collected before measuring HbA1c. Previous research has reported potential causality between educational attainment and type 2 diabetes (Liang et al., 2021). Since educational attainment is associated with DNAm (van Dongen et al., 2018), and DNAm is associated with HbA1c (Z. Chen, Miao, et al., 2020), it is thus of interest to study the mediating role of DNAm from educational attainment to $\mathrm{HbA}1\mathrm{c}$.

Since correlated mediators may lead to inflated Type I error rates and spurious signals, we selected a subset of 228,088 potentially mediating $\mathrm{C}\mathrm{p}\mathrm{G}$ sites that were, at most, only weakly correlated with one another. We provide details for processing MESA data in section S3 in the supplementary materials. For each CpG site, we obtained $z_{\alpha ,j}$ and $z_{\beta ,j}$ from linear models for testing ${\alpha }_j=0$ (effect of the exposure on the $\mathrm{j}$-th mediator) and ${\beta }_j=0$ (effect of the $\mathrm{j}$-th mediator on the outcome). In both models, we adjusted for age, sex, and race as potential confounders and adjusted for the estimated proportions of residual non-monocytes (neutrophils, B cells, T cells, and natural killer cells) to account for potential contamination by non-monocyte cell proportions. In addition, we adjusted for the exposure in the outcome model. We applied the six mediation methods to the selected 228,088 $\mathrm{C}\mathrm{p}\mathrm{G}$ sites, and obtained p-values for testing the mediation effect. $\mathrm{C}\mathrm{p}\mathrm{G}$ sites with significant mediation effects are determined by the p-value threshold of $2.19\times {10}^{-7}$, which corresponds to controlling FWER at 0.05.

Sensitivity analysis methods.

To evaluate the robustness of our findings toward the assumptions defined above, we performed three sensitivity analyses focusing on the top $\mathrm{C}\mathrm{p}\mathrm{G}$ sites in our global scan. (a) Presence of exposure-mediator interaction: Since the no-exposure-mediator interaction assumption is critical to using the six hypothesis testing methods, in addition to the traditional methods, we estimated the causal mediation effects with and without including the exposure-mediator interaction term in the outcome model. The causal mediation analysis was performed using $\mathrm{R}$ package mediate (Tingley et al., 2014) with 1,000 bootstrap draws. (b) Choice of measured confounders and unmeasured confounding: For the measured confounders, we evaluated the mediation effect with the agnostic combination of all covariates. In total, we had $128\left(2^7\right)$ combinations for seven measured confounders, including age, sex, race, and residual white blood cell proportions (neutrophils, B cells, T cells, and natural killer cells). For unmeasured confounders, we calculated the mediation E-value (VanderWeele & Ding, 2017), which quantifies the minimum strength of associations that an unmeasured confounder would need to have with both the exposure and the outcome to fully explain away the mediation effect. The E-value for continuous outcomes is based on the risk ratio transformation of the standardized mediation effect. To calculate this parameter, we used R package EValue (Mathur et al., 2021). (c) Fitting a multivariate model with all mediators: Since the correlation among mediators may distort the single-mediator results, we performed a multivariate mediation analysis method, HIMA (Zhang et al., 2016). In the screening step, we include the top $n/\log n\mathrm{CpG}$ sites in the exposure-mediator path to increase the possibility of finding significant mediating signals, where $n=963$ is the sample size. The threshold $n/\log n$ is chosen for reducing the data dimension while maintaining the accuracy of the sure independence screening (Fan & Lv, 2008; Zhang et al., 2016). In addition, since it is difficult to determine the causal direction between DNA methylation and HbA1c which were measured concurrently in MESA, we performed bidirectional causal mediation analysis to compare the $SES\to DNAm\to HbA1c$ and $SES\to HbA1c\to DNAm$ pathways.

3. Results

3.1. Simulation results

3.1.1. False positive rates under the composite null hypothesis

In Table S1, we present FPR from six methods under the Null 1(a) scenario, where $\left({\pi }_{01},{\pi }_{10},{\pi }_{00}\right)=$ $\left(\mathrm{0.001,0.001,0.998}\right)$, the sample size $n\in \left(\mathrm{200,500,1000}\right)$ and $\tau \in \left(\mathrm{0.1,0.3,0.7}\right)$. To better illustrate the distributions of p-values, we provide QQ plots from one replication in Figure 2. For all nine cases, Sobel’s test is the most conservative test, followed by the MaxP test. P-values from both tests are uniformly larger than the expected ones due to large ${\pi }_{00}$. R package DACT fails in certain cases, e.g. when $\tau =0.7$ or when $n=1000$. When $n=200$ and $\tau =0.1$, the FPRs from HDMT and Sobel-comp are close to expected values at the cut-off higher than ${10}^{-6}$, but are inflated at lower cut-offs. In comparison, FPRs from JT-comp and DACT are greatly inflated, especially when the cut-off is lower than ${10}^{-6}$. At the $5\times {10}^{-7}$ level, the ratio of the FPR to the corresponding level for JT-comp, DACT, Sobel-comp, and HDMT is 15.2, 1.8, 2.3 and 22.7, respectively. When increasing $n$ from 200 to 1000 with $\tau =0.1$, the FPR for JT-comp dramatically increases. In comparison, Sobel-comp is less inflated and HDMT almost keeps the same level of FPR. Similar trends are observed with an increasing $\tau$.

Figure 2:

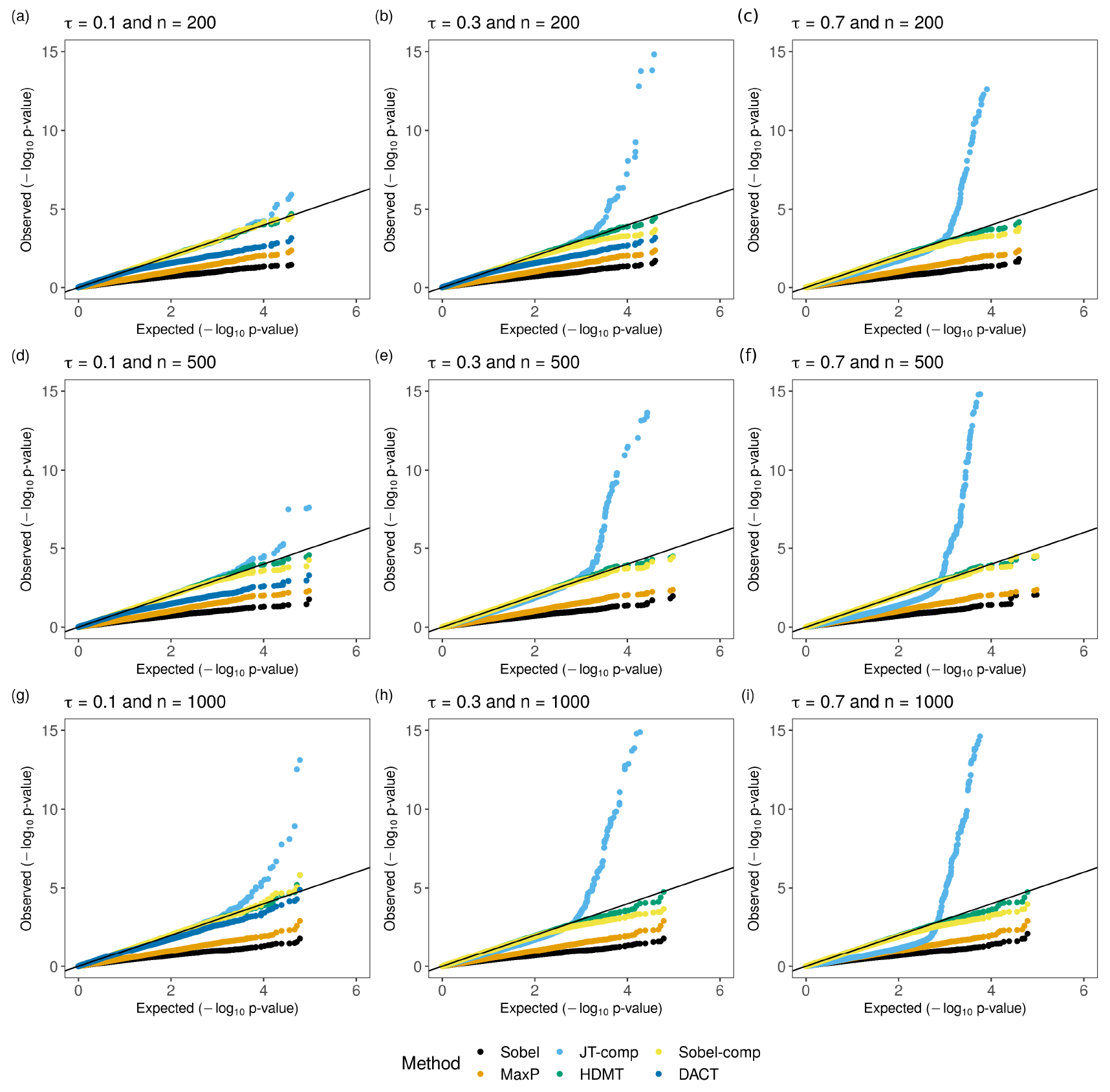
QQ plots for p-values from Sobel’s test, the MaxP test, JT-comp, HDMT, Sobel-comp and DACT under the Null $1\left(a\right)$ scenario. $n$ is the sample size. The total number of mediators is 100,000. For $j=\mathrm{1,2},\dots ,\mathrm{100,000}$, with probability ${\pi }_{01}=0.001,{\alpha }_j=0$ and ${\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{10}=0.001,{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right)$ and ${\beta }_j=0$; with probability ${\pi }_{00}=0.998,{\alpha }_j={\beta }_j=0$.

When the non-zero coefficients are dense in the Null 1(b) scenario (Figure 3 and Table S2), HDMT is the only method that maintains the FPR at the nominal level in all scenarios, and is robust to the change of $n$ or $\tau$. HDMT also works well when ${\pi }_{00}=0$ in the Null 1(c) scenario (Table S3). As expected, the MaxP method performs similar to the HDMT method in this case with moderate or large $\tau$, since $N\left(\mathrm{0,1}\right)$ is the correct reference distribution for the p-value under $H_{01}$ and $H_{10}$.

Figure 3:

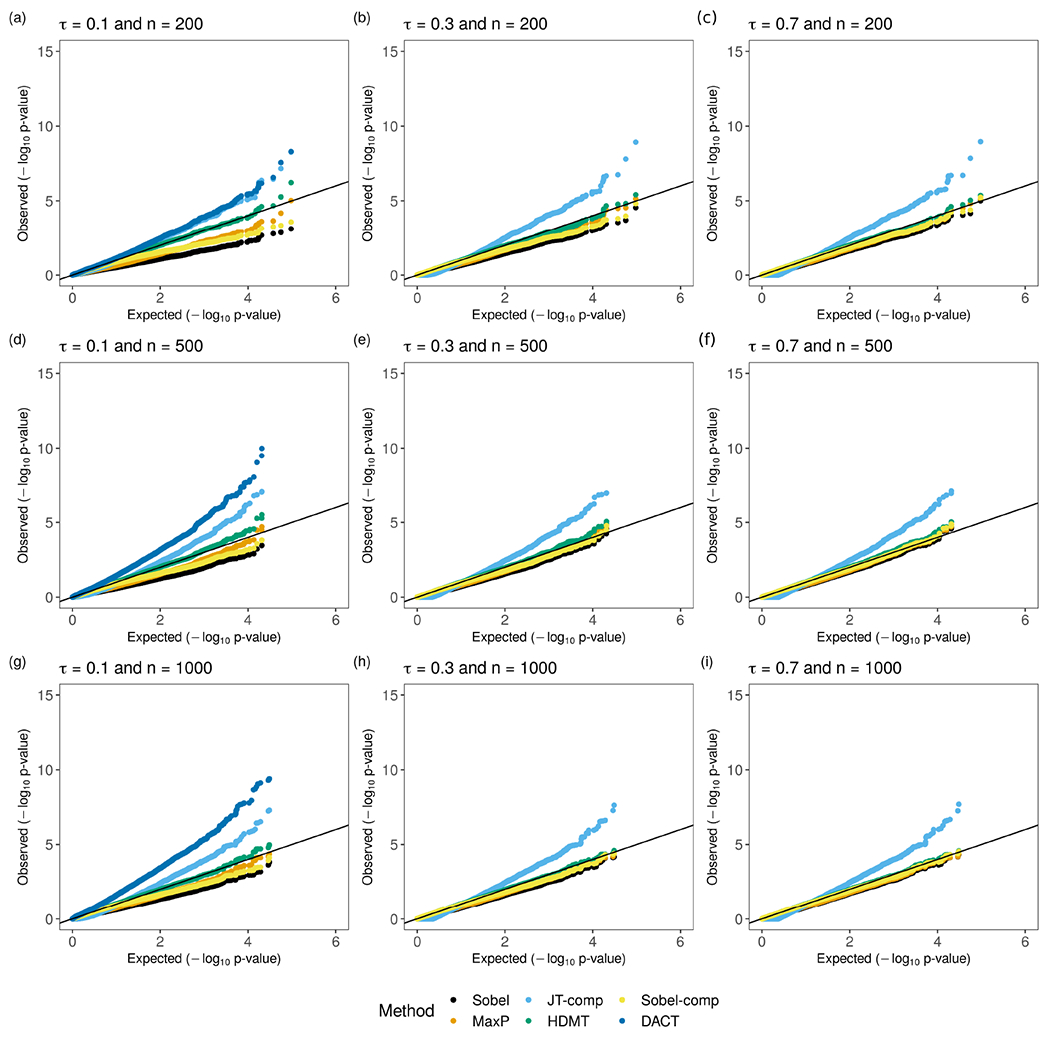
QQ plots for p-values from Sobel’s test, the MaxP test, JT-comp, HDMT, Sobel-comp and DACT under the Null 1(b) scenario. $n$ is the sample size. The total number of mediators is 100,000. For $j=\mathrm{1,2},\dots ,\mathrm{100,000}$, with probability ${\pi }_{01}=0.33,{\alpha }_j=0$ and ${\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{10}=$ $0.33,{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right)$ and ${\beta }_j=0$; with probability ${\pi }_{00}=0.34,{\alpha }_j={\beta }_j=0$.

In Tables S4–S6, we present the FPR for Null 2 scenarios, where $R^2\in \left(\mathrm{0.1,0.15,0.2}\right)$ is controlled across $J$ tests. Overall, the FPRs are inflated for DACT in all three classes of scenarios. When the non-zero coefficients are sparse (Null 2(a)), the impact of $R^2$ is similar to $\tau$ in the Null 1(a) scenario for JT-comp, HDMT and Sobel-comp. In Null 2(b) and Null 2(c) scenarios, where ${\pi }_{00}$ is much smaller than 1, HDMT is the only method that maintains the FPR at the nominal level. In the Null 2(c) scenario where ${\pi }_{00}=0$, the FPR for MaxP is smaller than the nominal level due to the small $R^2$.

3.1.2. True positive rates under the alternative hypothesis

Results of the TPRs for the Alternative 1(a) and Alternative 1(b) scenarios are shown in Figure 4 and for the Alternative 1(c) are shown in Figure S1. R package DACT fails when $\tau >0.1$. Under the Alternative $1\left(a\right)$ scenario, where ${\pi }_{11},{\pi }_{10},{\pi }_{01},{\pi }_{00}$ are $\mathrm{0.001,0.001,0.001,0.997}$, respectively, JT-comp has lower TPR than the four other methods in general, except when $\tau$ is small (e.g. $\tau =0.1$) and the sample size is small (e.g. $n=200$). Sobel’s test and Sobel-comp have the highest TPRs, closely followed by HDMT and MaxP. The TPR increases for all methods when the sample size increases. Sobel’s test and Sobel-comp perform the same because the rank of the weighted composite p-values is unchanged and so are the MaxP test and HDMT. Under the Alternative 1(b) scenario, where ${\pi }_{11},{\pi }_{10},{\pi }_{01},{\pi }_{00}$ are $\mathrm{0.2,0.2,0.2,0.4}$, respectively, the TPR of Sobel’s test, MaxP, HDMT and Sobel-comp is the same under the control of FDR. JT-comp has the lowest TPR among all methods. Results for the average TPR in Alternative 2 scenarios are shown in Figures S2 and S3. The impact of an increasing $R^2$ on the power of each method is similar to $\tau$ and the main observations are similar to Alternative 1 scenarios.

Figure 4:

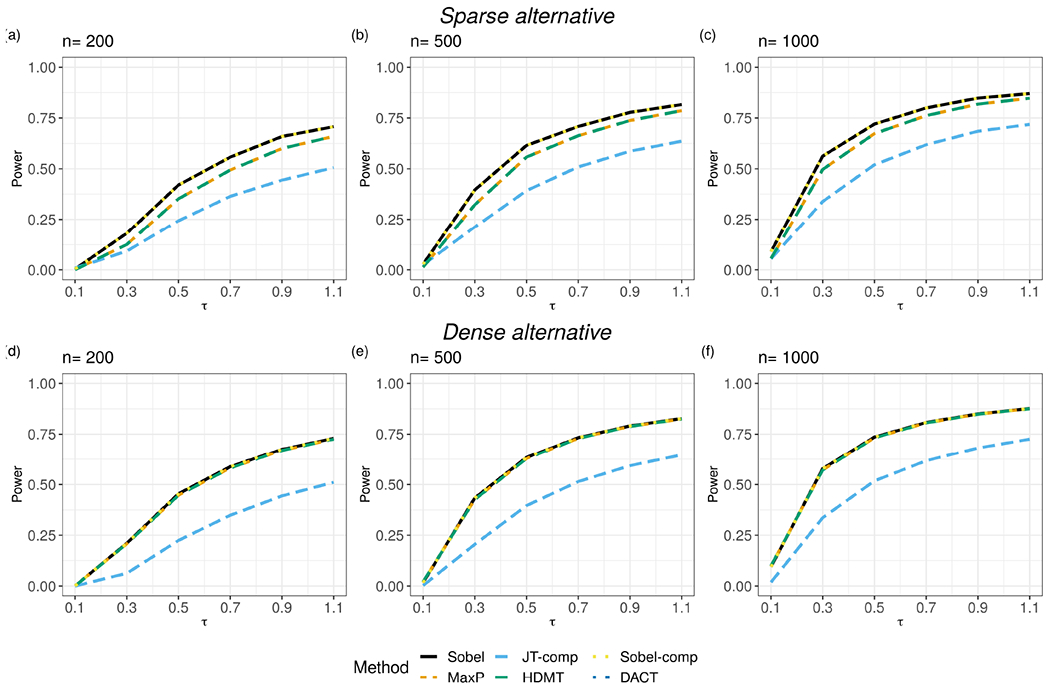
The average true positive rate over 200 replicates when controlling the true false discovery rate (FDR) at 0.05 for Sobel’s test, MaxP, JT-comp, HDMT, Sobel-comp and DACT under the Alternative $1\left(a\right)$ and Alternative $1\left(b\right)$ scenarios. The total number of mediators is 100,000. $n$ is the sample size. For $j=\mathrm{1,2},\dots ,\mathrm{100,000}$, with probability ${\pi }_{11},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right),{\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{01},{\alpha }_j=0$ and ${\beta }_j\sim N\left(0,{\tau }^2\right)$; with probability ${\pi }_{10},{\alpha }_j\sim N\left(\mathrm{0,5}{\tau }^2\right)$ and ${\beta }_j=0$; with probability ${\pi }_{00},{\alpha }_j={\beta }_j=0$. Under the Alternative $1\left(a\right)$ scenario, ${\pi }_{11},{\pi }_{10},{\pi }_{01},{\pi }_{00}$ are set as $\mathrm{0.001,0.001,0.001,0.997}$ and under the Alternative $1\left(b\right)$ scenario, ${\pi }_{11},{\pi }_{10},{\pi }_{01},{\pi }_{00}$ are set as $\mathrm{0.2,0.2,0.2,0.4}$.

3.2. Results from MESA

In Figure 5, we present the QQ plot for p-values of all 228,088 $\mathrm{C}\mathrm{p}\mathrm{G}$ sites from six methods, including Sobel’s test, the MaxP test, JT-comp, HDMT, Sobel-comp and DACT. As expected, p-values from Sobel’s test and the MaxP test were deflated, potentially due to a large number of zero ${\alpha }_j$ and ${\beta }_j$. JT-comp identified two significant $\mathrm{C}\mathrm{p}\mathrm{G}$ sites and HDMT identified three significant $\mathrm{C}\mathrm{p}\mathrm{G}$ sites (Table S7). Two CpG sites, cg10508317 and $\mathrm{c}\mathrm{g}01288337$, were significant from both methods (Table 3). In contrast, Sobel-comp detected no significant mediation effects probably because ${\hat{\pi }}_{00}$ is bounded away from $1\left({\hat{\pi }}_{00}=0.884,{\hat{\pi }}_{01}=0.029,{\hat{\pi }}_{10}=0.040\right)$.

Figure 5:

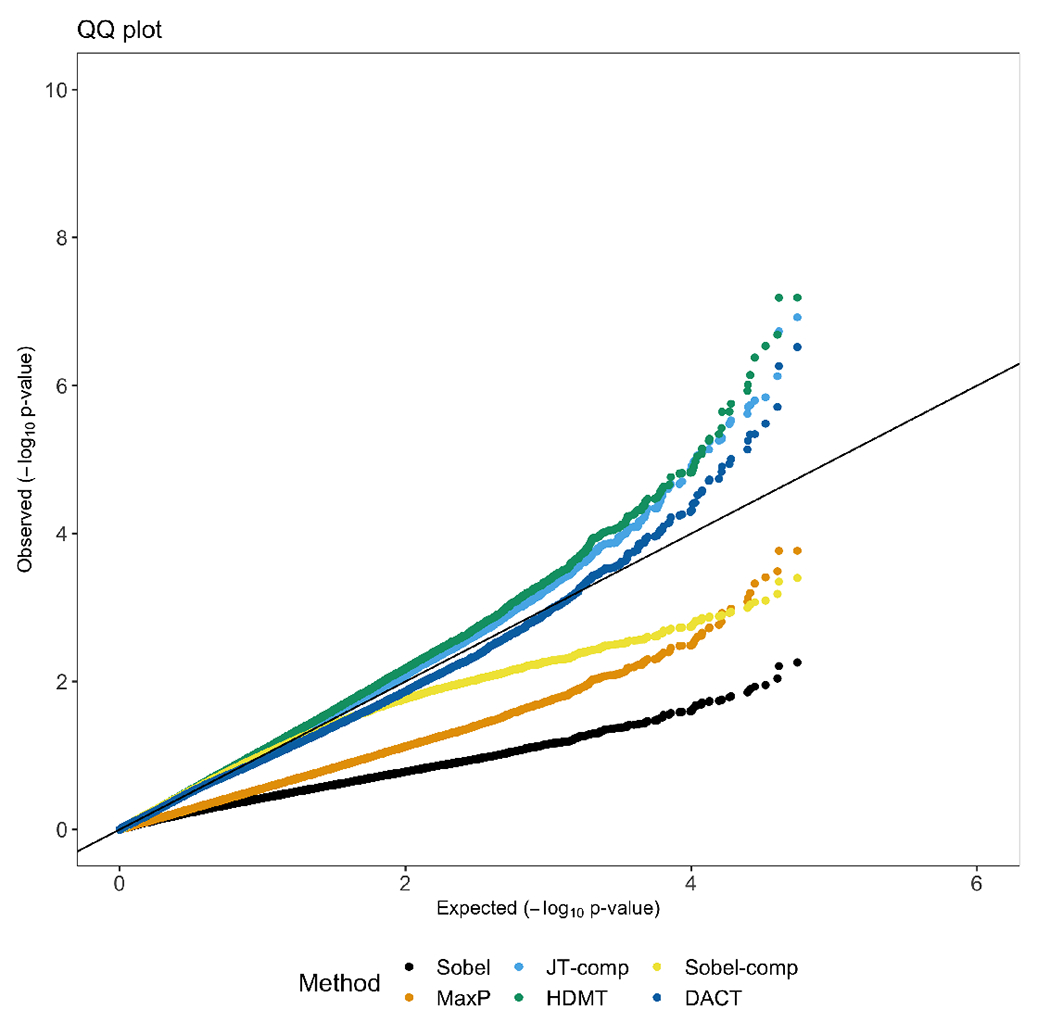
QQ plot for the six mediation hypothesis testing methods, including Sobel’s test, MaxP, JT-comp, HDMT, Sobel-comp and DACT with 963 observations. The outcome is the continuous HbA1c level, the exposure is the binary adult SES, and the mediators are 228,088 CpG sites. In the mediator and outcome models, we adjust for age, sex, race and residual white blood cell proportions (neutrophils, B cells, T cells, and natural killer cells). In addition, we adjust for the exposure in the outcome model.

Table 3:

Two mediation pathways identified by JT-comp and HDMT after controlling the family-wise-error-rate at 0.05. The exposure is adult SES and the outcome is HbA1c. The total number of mediators is 228,088. In both models, we adjust for age, sex, race and residual white blood cell proportions (neutrophils, B cells, T cells, and natural killer cells). In addition, we adjust for the exposure in the outcome model. $\hat{\alpha }$ is the estimated effect of the exposure on the mediator and $\hat{\beta }$ is the estimated effect of the mediator on the outcome, conditional on other covariates. The estimated mediation effect is $\hat{\alpha }\hat{\beta }$ and the proportion of mediation effect is provided in the parenthesis. The $95\mathrm{\%}$ confidence interval $\left(\mathrm{C}\mathrm{I}\right)$ for the mediation effect is calculated based on 1,000 bootstrap samples.

CpG	Chr	Gene	$\text{UCSC RefGene Group}$	$\stackrel{\mathit{ˆ}}{\mathit{\alpha }}$	$\stackrel{\mathit{ˆ}}{\mathit{\beta }}$	$\text{Mediation effect (proportion)}$	95% CI	${\mathit{p}}_{\mathit{J}\mathit{T}–\text{comp}}$	${\mathit{p}}_{\mathit{H}\mathit{D}\mathit{M}\mathit{T}}$
cg10508317	17	SOCS3	Body	−0.28	−0.12	$0.035\left(0.18\right)$	$\left(\mathrm{0.013,0.064}\right)$	$1.19\mathrm{E}-07$	$6.49\mathrm{E}-08$
cg01288337	14	RIN3	Body	0.23	0.15	$0.034\left(0.17\right)$	$\left(\mathrm{0.013,0.061}\right)$	$1.85\mathrm{E}-07$	$6.47\mathrm{E}-08$

The CpG site cg10508317 in the SOCS3 gene on chromosome 17 encodes a protein that is involved in the signaling pathways of key hormones such as insulin (Pedroso et al., 2019). It has been found that increased SOCS3 expression is associated with insulin resistance (Pedroso et al., 2019), which is directly related to HbA1c. The CpG site $\mathrm{c}\mathrm{g}01288337$ is in the RIN3 gene on chromosome 14. The RIN3 gene encodes a member of the RIN family of Ras interaction-interference proteins and is next to the SLC24A4 gene. Recent studies showed that SLC24A4/RIN3 is significantly associated with brain glucose metabolism in humans (Stage et al., 2016) and SLC24A4 knockout mice revealed brain glucose hypometabolism (X.-F. Li & Lytton, 2014).

Results of the sensitivity analysis.

For (a) presence of exposure-mediator interaction: there was no evidence of exposure-mediator interaction affecting the outcome (Table S8). For (b) choice of measured confounders and unmeasured confounding: the mediation effects through cg10508317 and $\mathrm{c}\mathrm{g}01288337$ were significant in all combinations of covariates, indicating that the mediating role of the two $\mathrm{C}\mathrm{p}\mathrm{G}$ sites is robust to the measured confounders (Figure 6). For unmeasured confounders, the E-value for $\mathrm{c}\mathrm{g}10508317$ was 1.33 (lower bound: 1.15) and for $\mathrm{c}\mathrm{g}01288337$ was 1.32 (lower bound 1.15). In other words, to completely explain away the mediation effect, an unmeasured confounder beyond the variables adjusted for in our model would need to have a risk ratio of 1.33 for cg10508317, and 1.32 for $\mathrm{c}\mathrm{g}01288337$, in association with adult SES and HbA1c. For (c) fitting a multivariate model with all mediators: the two $\mathrm{C}\mathrm{p}\mathrm{G}$ sites, which were significant from the single-mediator hypothesis testing methods (HDMT and JT-comp), were also significant from the multivariate mediation analysis method, HIMA (Table S9).

Figure 6:

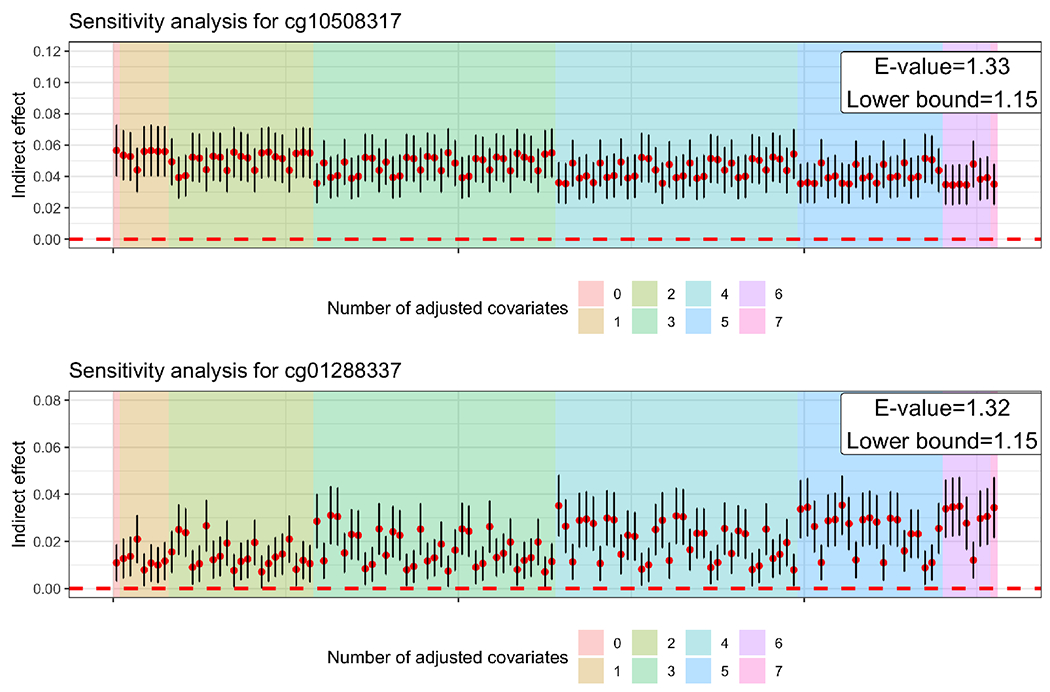
Estimates of the indirect effects through cg10508317 (upper panel) and $\mathrm{c}\mathrm{g}01288337$ (lower panel) with $95\mathrm{\%}\mathrm{C}\mathrm{I}$ for all possible combinations of seven covariates: age, sex, race and residual white blood cell proportions (neutrophils, B cells, T cells, and natural killer cells). E-value estimation is based on the approximation of risk ratio transformation of the standardized mediation effect estimate.

4. Discussion

We reviewed and compared the testing performance of six mediation methods (Sobel’s test, MaxP, JT-comp, HDMT, DACT and Sobel-comp). Our study indicates that the methods which use the mixture reference distribution (HDMT, Sobel-comp) can better control false positive rates (FPRs) and yield larger true positive rates (TPRs). However, there is no uniform dominance of one method over the others across all simulation scenarios. Their performances differ according to ${\pi }_{00},{\pi }_{01},{\pi }_{10},{\pi }_{11}$, the sample size and the strength of independent variables explaining the variation of the dependent variable, as captured by the variance of non-zero $\alpha ,\beta$ or $R^2$ in the outcome and mediator models.

Under the null hypothesis, the distribution of p-values is strongly affected by the three proportions, ${\pi }_{00},{\pi }_{01},{\pi }_{10}$, for all methods except HDMT. Sobel’s test and the MaxP test overly control the FPR, especially when ${\pi }_{00}$ is large. The fundamental problem with Sobel’s test and the MaxP test is that the reference distribution when $\alpha =\beta =0$ is incorrect. However, if a screening step is performed to select mediators associated with either the outcome or the exposure so that after screening ${\pi }_{00}\approx 0$, the reference distributions for Sobel’s test $\left(\mathrm{N}\right(\mathrm{0,1}\left)\right)$ and for the MaxP test $\left(\mathrm{U}\right(\mathrm{0,1}\left)\right)$ under the null are asymptotically correct. In this case, the MaxP test maintains the FPR at the nominal level.

Under the null when non-zero $\alpha$ and $\beta$ coefficients are sparse, i.e., ${\pi }_{10}$ and ${\pi }_{01}$ are small, Sobel-comp and HDMT maintain the FPR at the nominal level for any $n$ or $\tau$. JT-comp maintains the nominal level of FPR only when $n$ and $\tau$ (or $R^2$) are small and thus, the application of JT-comp is valid only in sparse settings with small samples and small non-zero coefficients. But under the null with dense coefficients, i.e., ${\pi }_{01}$ and ${\pi }_{10}$ are large, HDMT is the only method that maintains the nominal level of FPR.

Under the alternative hypothesis with sparse signals, all methods perform similarly with small $n$ and $\tau$. As $n$ and $\tau$ increase, Sobel-comp is the most powerful method with the greatest TPR, followed by HDMT. However, Sobel-comp requires ${\pi }_{00}$ close to 1 to have such optimal properties, the choice of Sobel-comp depends on the screening strategy before the mediation analysis. Presented with a large number of mediators, if one separately uses large $\left|Z_{\alpha }\right|$ and/or $\left|Z_{\beta }\right|$ as screening steps, ${\pi }_{00}$ may be bounded away from 1. However, if one only restricts the analyses to exposures associated with the outcome, ${\pi }_{00}$ could still be near 1 since a significant total effect can lead to nearly all indirect effects being zero, with most of the exposure effect coming through direct effects. In practice, we recommend to choose the method based on ${\hat{\pi }}_{01},{\hat{\pi }}_{10},{\hat{\pi }}_{00}$ obtained from R package HDMT (Dai et al., 2022). Sobel-comp is preferred when ${\pi }_{00}$ is close to 1. Although we do not provide strict guidelines, our simulation studies show that when ${\pi }_{00}=0.997$ and ${\pi }_{01}={\pi }_{10}={\pi }_{11}=0.001$, Sobel-comp is the most powerful method in almost all scenarios. Under the alternative hypothesis with dense signals, HDMT and Sobel-comp have the same TPR under the control of the false discovery rate.

We summarize key features, advantages and limitations for all the six methods based on our simulation studies in Table 4 and provide a decision tree for choosing an appropriate method in Figure 7. Since MaxP is always more powerful than the Sobel test and DACT fails in many simulation scenarios, these two methods do not appear as preferred methods in Figure 7. We develop an $\mathrm{R}$ package medScan available at https://github.com/umich-cphds/medScan for implementing all the six methods.

Table 4:

A summary of methods with key advantages and limitations. For $J$ tests, ${\pi }_{11},{\pi }_{01},{\pi }_{10},{\pi }_{00}$ are the true proportion of ($\left.\alpha \ne 0,\beta \ne 0\right),(\alpha =$ $0,\beta \ne 0),(\alpha \ne 0,\beta =0)$, and $(\alpha =\beta =0)$, respectively. ${\tau }^2$ is the variance for the non-zero $\alpha ,\beta .p_{\alpha }$ and $p_{\beta }$ are the two-sided p-value for $Z_{\alpha }$ and $Z_{\beta }$, respectively.

Method	First Author Year	R package (package name)	Test statistic	Reference Distribution	Advantages	Limitations
Sobel’s test	Sobel, 1982	✗	$\frac{Z_{\alpha }}{\sqrt{1+{\left(Z_{\alpha }/Z_{\beta }\right)}^2}}$	N(0,1)	Protect the false positive rate (FPR) at the nominal level under the null hypothesis. Robust for any value of π00, π01, π10 and τ.	Conservative since the multivariate delta method fails when α and β are zero.
MaxP	Mackinnon, 2002	✗	$\mathit{max}\left(p_{\alpha },p_{\beta }\right)$	U(0,1)	Protect the FPR at the nominal level under the null hypothesis. Robust for any value of π00, π01, π10 and τ. Uniformly more powerful than Sobel’s test.	Conservative because of using the incorrect reference distribution when α and β are zero.
JT-comp	Huang, 2019	✓	$Z_{\alpha }{Z}_{\beta }$	H00: Standard normal product distribution. H01, H10: Normal product distribution with non-zero mean.	Correct mixture reference distribution for ZαZβ. No need to estimate π00, π01, π10. Keeping the FPR close to the nominal level when the sample size and τ are small.	Inflated FPR at a small significance threshold. Inflated FPR when the sample size or τ increases. Only works with small samples and relatively weak signals.
HDMT	Dai, 2022	✓(HDMT)	$\mathit{max}\left(p_{\alpha },p_{\beta }\right)$	H00 : Beta(2,1). H01, H10: U(0,1).	Correct mixture reference distribution for the MaxP test statistic. Maintaining the FPR close to the nominal level for any value of π00, π01, π10 and τ. More powerful than Sobel’s test and the MaxP test. Provides finite-sample size adjustment for p-values to increase power.	Power lose when pβ is much smaller than pα and vice versa.
Sobel-comp	-	✗	$\frac{Z_{\alpha }}{\sqrt{1+{\left(Z_{\alpha }/Z_{\beta }\right)}^2}}$	H00 : N(0,1/4). H01, H10: N(0,1)	Correct mixture reference distribution for Sobel’s test statistic. Maintaining the FPR close to the nominal level and more powerful than HDMT when π01 and π10 are close to 0.	Conservative if π01 or π10 is far from 0 due to the use of the asymptotic reference distribution under H01 and H10.
DACT	Liu, 2022	✓(DACT)	${\hat{\pi }}_{01}{p}_{\alpha }+{\hat{\pi }}_{10}{p}_{\beta }+{\hat{\pi }}_{00}{p}_{\mathit{max}}^2$	U(0,1) approximately.	Weights the case-specific p-values to construct a composite test statistic to accommodate the composite nature of the null hypothesis.	Approximation of the reference distribution is often inaccurate, causing the FPR to deviate from the nominal level, while the exact reference distribution of DACT statistic is not established.

Figure 7:

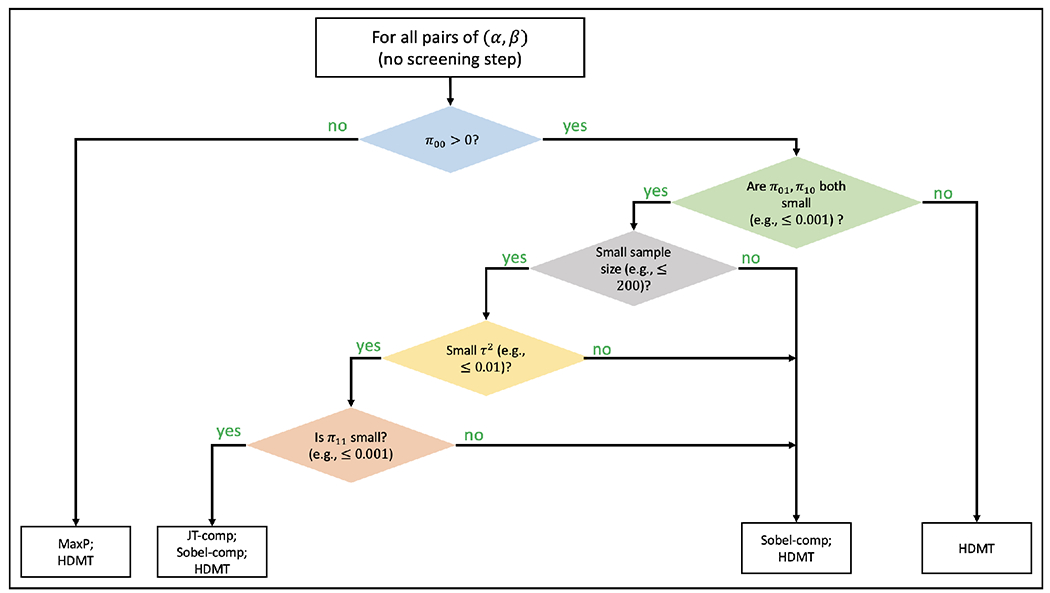
Decision tree for choosing the optimal mediation hypothesis testing method based on the simulation studies for the normally-distributed outcomes and mediators. ${\pi }_{11},{\pi }_{01},{\pi }_{10},{\pi }_{00}$ are the proportion of $(\alpha \ne 0,\beta \ne 0),(\alpha =0,\beta \ne 0),(\alpha \ne 0,\beta =0)$, and ($\alpha =\beta =0)$, respectively. In practice, estimates of ${\pi }_{11},{\pi }_{01},{\pi }_{10},{\pi }_{00}$ can be obtained from the HDMT method.

There are two common limitations of all the six methods. Firstly, it is inappropriate to use any of the six methods if the outcome or mediator is binary (VanderWeele, 2015), or if there is exposure-mediator interaction affecting the outcome (assumption A.2 mentioned in Section 1 is violated) (MacKinnon et al., 2020) so that $\alpha \beta$ does not correspond to the indirect effect. In this case, the causal mediation analysis offers a flexible framework and provides valid quantification of the causally interpretable mediation effect. However, since causal mediation analysis methods with accompanying software largely focus on point and interval estimation, hypothesis testing at a small alpha level relevant to large-scale association testing has not been well studied. Due to the unknown null distribution, most of the existing R packages, e.g., mediation (Tingley et al., 2014), medflex (Steen et al., 2020), CMAverse (Shi et al., 2021), regmedint (Y. Li et al., 2022), recommend using the bootstrap technique to determine the p-value of the indirect effect. In epigenetic studies, bootstrapped samples need to be large enough for a good approximation to the tail probability of the null distribution, which, in turn, could be computationally expensive for a large number of mediators. It is of future interest to investigate the composite null hypothesis in large-scale mediator testing from the counterfactual framework. Secondly, none of the six methods has desirable properties of FPR and TPR when mediators are correlated. Presented with correlated mediators, single-mediator analysis does not adjust for all the mediator-outcome confounders affected by the exposure, resulting in a violation of assumption A.1(4). In this case, it is necessary to extend the mediation analysis models to jointly account for multiple correlated mediators (Song, Zhou, Kang, et al., 2020; Song, Zhou, Zhang, et al., 2020; Zhang et al., 2016). For computational reasons, we only explore a range of parameters. Parameter values beyond this range combined with correlated mediators are of interest for future analysis.

The two significant CpG sites we identified in the SOCS3 and RIN3 genes from MESA add to a growing body of literature on the mediating role of DNA methylation between socioeconomic status and disease risk factors associated with HbA1c (Giurgescu et al., 2019; Song, Zhou, Zhang, et al., 2020). However, a limitation of our analysis is that our mediator (methylation) and outcome (HbA1c) were measured concurrently. Therefore, we identify statistical mediation, but are unable to formally determine the causal direction (Table S10). More studies are needed to fully understand the underlying biological mechanisms that link socioeconomic disadvantage to HbA1c-associated diseases.

Data Availability Statement

Data used in this analysis can be obtained through the MESA Data Coordinating Center (https://www.mesanhlbi.org/).