THE WIN RATIO METHOD IN HEART FAILURE TRIALS: LESSONS LEARNT FROM EMPULSE

Abstract

Aims

The EMPULSE trial evaluated the clinical benefit of empagliflozin versus placebo using the stratified win ratio approach in 530 patients with acute heart failure (HF) after initial stabilization. We aim to elucidate how this method works and what it means, thereby giving guidance for use of the win ratio in future trials.

Methods and Results

The primary trial outcome is a hierarchical composite of death, number of heart failure (HF) events, time-to-first HF event, or a 5-point + difference in KCCQ-TSS change at 90 days. In an overall (unstratified) analysis we show how comparison of all 265 × 265 patients pairs contribute to “wins” for empagliflozin and placebo at all four levels of the hierarchy, leading to an unstratified win ratio of 1.38 (95% CI 1.11, 1.71) P = 0.0036. How such a win ratio should (and should not) be interpreted is then described.

The more complex primary analysis using a stratified win ratio is then presented in detail leading to a very similar overall result. Win ratios for de novo acute HF and decompensated chronic HF patients were 1.29 and 1.39 respectively, their weighted combination yielding an overall stratified win ratio of 1.36 (95% CI 1.09, 1.68) P = 0.0054.

Alternative ways of including HF events and KCCQ scores in the clinical hierarchy are presented, leading to recommendations for their use in future trials. Specifically, inclusion of both number of HF events and time-to-first HF event appears an unnecessary complication. Also, the use of a 5-point margin for KCCQ score paired comparisons is not statistically necessary.

Conclusions

The EMPULSE trial findings illustrate how deaths, clinical events and patient-reported outcomes can be integrated into a win ratio analysis strategy that yields clinically meaningful findings of patient benefit. This has implications for future trial designs that recognize the clinical priorities of patient evaluation and the need for efficient progress towards approval of new treatments.

Graphical Abstract

INTRODUCTION

EMPULSE was a double-blind placebo-controlled trial to evaluate the efficacy and safety of empagliflozin 10mg once daily in patients with a primary diagnosis of acute de novo or decompensated chronic heart failure (HF).¹ The primary outcome was clinical benefit, defined as a hierarchical composite of death, number of HF events, time to first HF event, and change from baseline in Kansas City Cardiomyopathy Questionnaire Total Symptom Score (KCCQ-TSS) at 90 days, as assessed using the win ratio.

There was strong evidence of clinical benefit of empagliflozin compared with placebo, based on a highly significant result from the stratified win ratio analysis. This led to the conclusion that initiation of empagliflozin as part of usual care in patients hospitalized for acute heart failure will result in a clinically meaningful benefit in 90 days without safety concerns.

The win ratio approach^2,3 has been increasingly used as a means of recognizing the clinical priorities amongst components of a composite outcome. In this case a hierarchy was formed covering three fundamental goals of patient care: improvement of survival, then reduction of heart failure events, and lastly improvement of symptoms. But since the win ratio is a relatively new method, how it works is not fully understood by cardiologists and other researchers. Hence, the first goal of this article is to explain what the win ratio means, using EMPULSE as our prime example.

We then go on to explore some of the more subtle issues in how to implement the win ratio. Specifically, 1) is it useful to stratify patients in the analysis (e.g., decompensated vs acute de novo)? 2) for heart failure events should one use the frequency, the time-to-first event, or both? 3) for symptom score, does one need a margin, e.g., patient difference of at least 5 points on KCCQ-TSS change, or can smaller differences also be used?

In addition to a better understanding of the EMPULSE findings, our intention is to help the design, analysis, reporting, and interpretation of future trials that intend to adopt the win ratio approach.

METHODS

The EMPULSE trial design has been reported previously.⁴ In brief, it was a randomized double-blind trial comparing once daily oral empagliflozin 10 mg with placebo as regards clinical benefit, safety and tolerability over 90 days follow-up. Participants were hospitalized with a primary diagnosis of acute heart failure with randomization as early as possible after stabilization between 1 to 5 days after admission. Efficacy and safety parameters were assessed during follow-up visits at 3 and 5 (if still in hospital) and 15, 30, and 90 days after randomization.

The primary outcome was defined as a hierarchical composite of time to all-cause death, the number of HF events, time to first HF event, and a 5-point or greater difference in change from baseline in KCCQ-TSS after 90 days of treatment. HF events included HF hospitalization, urgent HF visits, and unplanned outpatient HF visits.

A sample size of 500 patients was estimated to provide 87% power at one-sided alpha 0.025 under a set of assumptions previously published. An unstratified win ratio analysis of the primary hierarchical outcome uses the unmatched pairs approach of Pocock et al ², and is described in the Results section below. The pre-defined primary analysis is a stratified win ratio approach using the method of Dong et al ^5,6 the two strata being acute de novo or decompensated chronic heart failure. All analyses were performed according to the intention-to-treat principle.

Sensitivity analyses were performed by making several changes to the hierarchical primary outcome as follows: 1) removing the time-to-first HF events from the hierarchy, 2) removing the number of HF events over 90 days from the hierarchy, or 3) substituting the 5-point difference in KCCQ-TSS change with either any difference or a difference of 2, 10, or 15 points, respectively. Throughout, a multiple imputation approach was used to impute missing data for the KCCQ-TSS.¹ The impact of not doing this is explored. All analyses were performed with SAS version 9.4 or higher.

RESULTS

The primary endpoint in EMPULSE is hierarchical with 4 components: death, number of heart failure events, time to first heart failure event, and change in KCCQ-TSS from baseline to 90 days. The most straightforward win ratio analysis compares every patient on empagliflozin with every patient on placebo, i.e., 265 × 265 = 70225 pairs of patients are compared to see which one “won”. The pre-defined primary analysis was stratified, but let us first consider their overall (unstratified) win ratio analysis, which is easier to explain.

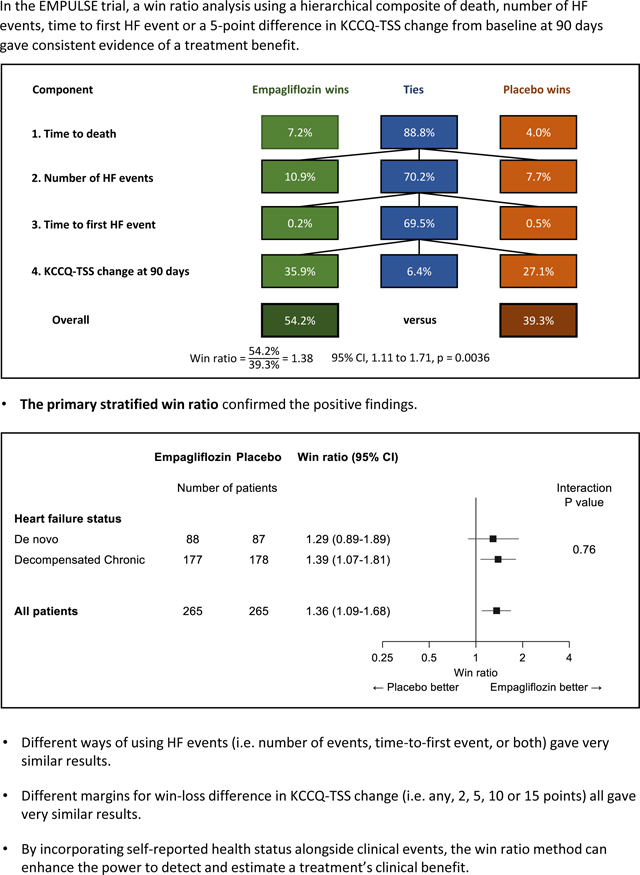
Figure 1 presents this unstratified win ratio analysis, with the following hierarchical rules for determining who won in every patient pair:

Figure 1:

Win Ratio in EMPULSE trial (unstratified⁺): all paired comparisons of empagliflozin and placebo: 265 × 265 pairs.

The Win Ratio in EMPULSE trial (unstratified): Figure 1 shows the distribution of wins and ties for each of the 70,225 (265 × 265 pairs) empagliflozin versus placebo paired comparisons at each level of the hierarchy of the primary composite endpoint. Note that the primary analysis in EMPULSE was a stratified win ratio. HF = heart failure; KCCQ-TSS = Kansas City Cardiomyopathy Questionnaire Total Symptom Score.

Step 1: death.

Over the pair’s common follow-up time: death is worse than no death, earlier death is worse than later death, tied if neither patient died.

Of the 70225 patient pairs, 7.2% had a win for empagliflozin, 4.0% had a win for placebo. The remaining 88.8% tied and move to step 2.

Step 2: number of heart failure events (HF events).

Over common follow-up time: more HF events is worse, tied if same number of HF events.

This led to 10.9% wins for empagliflozin, 7.7% wins for placebo, leaving 70.2% of pairs still tied.

Step 3: time to first HF event.

Over common follow-up time: earlier HF event is worse, tied if neither patient had an HF event. This led to 0.2% wins for empagliflozin, 0.5% wins for placebo, leaving 69.5% of pairs still tied.

Step 4: KCCQ-TSS change from baseline at 90 days.

A more positive change from baseline is better, with a threshold of ≥5 points better to declare a win, otherwise tied if the pair’s difference in 90-day change is less than 5 points. On this basis there were 35.9% wins for empagliflozin, 27.1% wins for placebo, and 6.4% of pairs stayed tied right through all 4 steps of the hierarchy.

Thus, for empagliflozin the total % pairs with a win are 7.2% + 10.9% + 0.2% + 35.9% = 54.2% compared to 4.0% + 7.7% + 0.5% + 27.1% = 39.3% wins for placebo. Hence, the win ratio is 54.2% ÷ 39.3% = 1.38.

How can we interpret this result? One way is to declare for any randomly chosen pair of patients, one on empagliflozin and the other on placebo, for whom there was not a tie, then the estimated odds that the empagliflozin patient won is 1.38. One can go on to state the estimated probability that the empagliflozin patient wins is 1.38 / (1 + 1.38) = 0.58.

Like for any estimate from a randomized trial, one needs to express the uncertainty around it, hence the 95% confidence interval for the win ratio is 1.11 to 1.71. The fact that the whole interval is substantially above 1 means we have a highly significant result: P = 0.0036 using a generalized analytical solution⁶, which is based on the Finkelstein-Schoenfeld test.⁷ This test was established before the win ratio concept was created, and one of its first uses was in the PARTNER trial in 2010 comparing TAVR versus control for the hierarchical composite of death or repeat hospitalization ⁸. This example stimulated the wish to provide an estimate (and CI) for the treatment effect in this setting of a hierarchical composite outcome, and hence the win ratio came into existence to satisfy this need.²

Most uses of the win ratio method have been with just two steps in the hierarchy, whereas EMPULSE has four steps. This affects how one interprets later steps in the hierarchy. For instance, the third step, time to first HF event, had only 0.2% and 0.5% wins on empagliflozin and placebo respectively with 69.5% tied. This is because it is only applied to patient pairs with the same number of HF events (i.e. those who tied in step 2) and the great majority of these had no HF events. This brings into question whether in hindsight this third step was worth including.

We note that the fourth step, based on KCCQ-TSS change from baseline to 90 days, made the biggest contribution to the win ratio estimate (35.9% versus 27.1% wins) whereas steps 1 to 3 combined contributed less (18.3% versus 12.2%). The latter has a win ratio 18.3 ÷ 12.2 = 1.50 with 95% CI 0.99 to 2.26 and P = 0.055. Thus, a win ratio analysis of deaths and HF events alone is consistent with the overall win ratio analysis that also includes symptom score, but is underpowered to reach a definitive conclusion. The same lack of power arises if one does a time-to-first event analysis for the conventional composite of CV death and HF event which yields hazard ratio 0.69 (95% CI 0.45, 1.08) P = 0.10. Details of this analysis are in Table 2. We see that the composite ignores 6 cardiovascular deaths (which occurred after a HF event) and 21 repeat HF events. In contrast, the win ratio analysis incorporates all this information.

Table 2:

Composite endpoints: time to CV death or HF event and time to all-cause death or HF event.

Outcome	Empagliflozin (n=265)	Placebo (n=265)	Hazard Ratio	(95% CI)
CV death or HF Event	34	49	0.69	(0.45, 1.08)
All-cause death or HF Event	37	57	0.65	(0.43, 0.99)
CV death	8	14
All-cause death	11	22
≥1 HF event	28	39
Total HF events	36	52

Table 2 shows the results of time to first event analyses for the composite outcomes of (i) CV death or HF event and (ii) all cause death or heart failure event. We see that the composite ignores 6 cardiovascular deaths (which occurred after a HF event) and 21 repeat HF events. In contrast, the win ratio analysis incorporates all this information. HFE = heart failure event; CV = cardiovascular; CI = confidence interval.

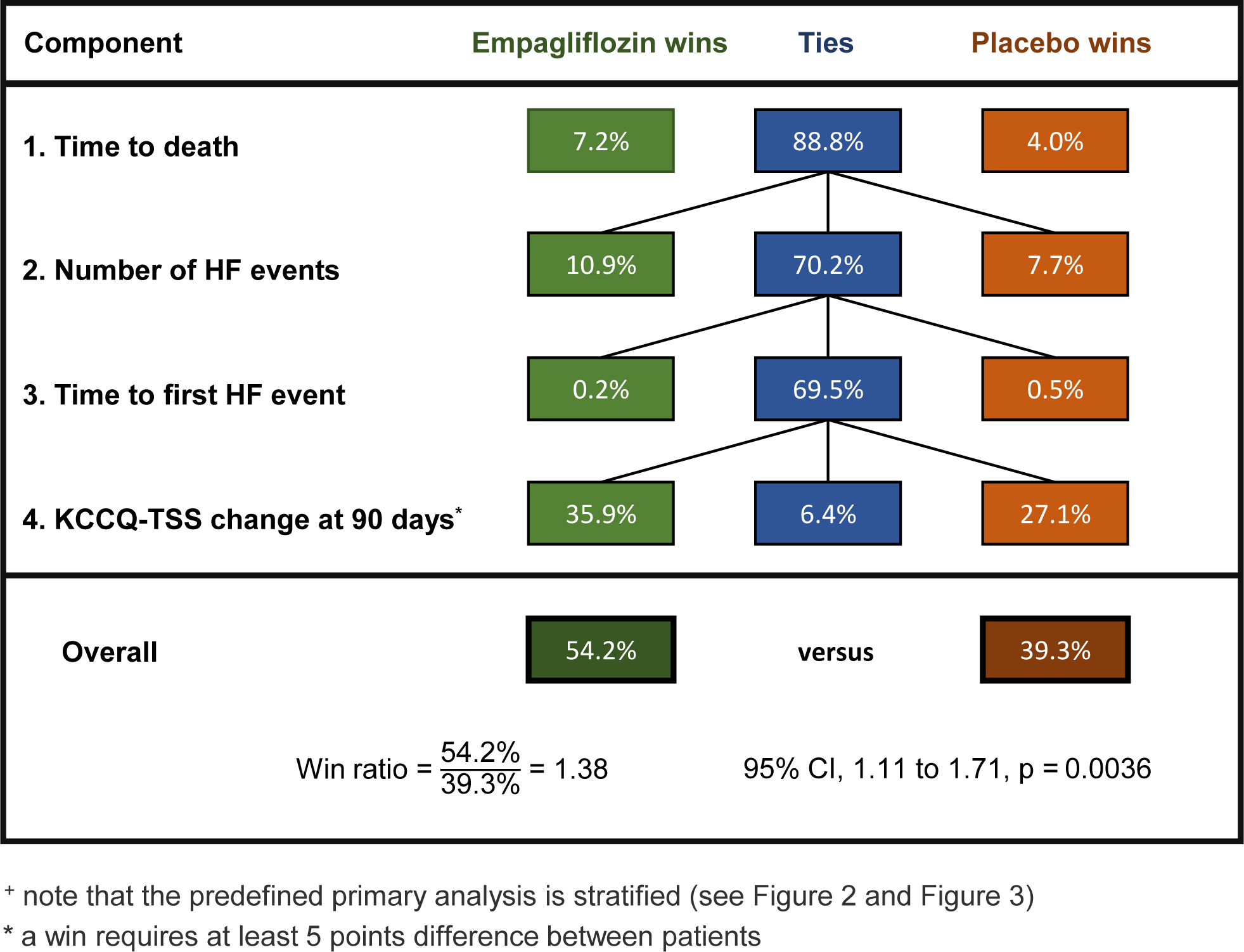
The Stratified Win Ratio

The pre-defined primary win ratio analysis in EMPULSE was stratified ^5,6 according to whether the diagnosis was acute do novo (88 empagliflozin, 87 placebo) or decompensated chronic HF (177 empagliflozin, 178 placebo). This means one separately estimates the win ratio for each of the two strata, and then combines them into an overall weighted estimate (see Figure 2). A more detailed breakdown of wins and losses is in Figure 3.

Figure 2:

The Stratified Win Ratio in the EMPULSE trial: combining win ratio estimates for the two strata into an overall win ratio estimate.

The primary analysis in the EMPULSE trial was the stratified win ratio, with two strata, (i) de novo heart failure patients and (ii) decompensated chronic heart failure patients. Figure 2 shows the win ratio and 95% CI in each stratum and the overall stratified win ratio and 95% CI. CI = confidence interval.

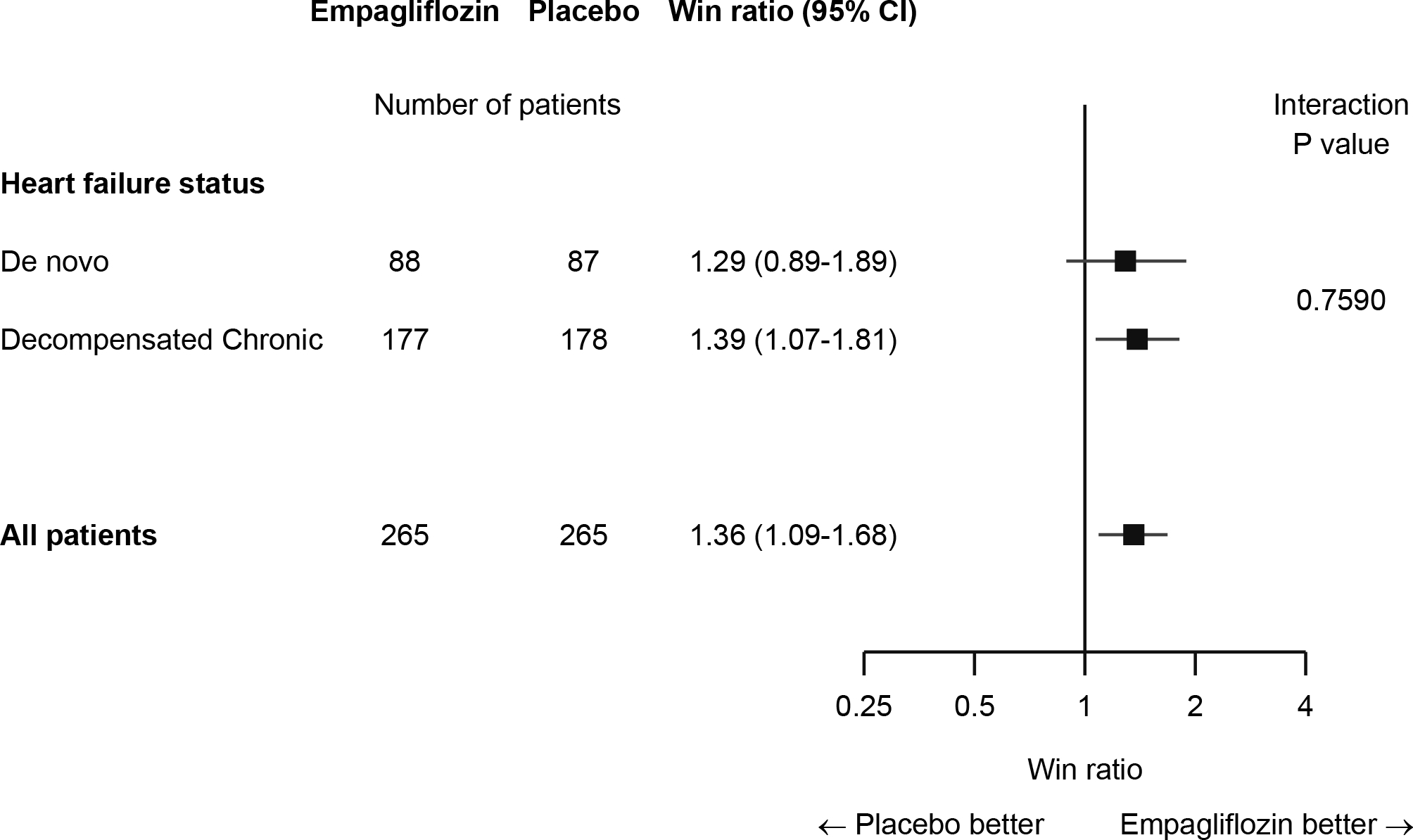
Figure 3.

Detailed Results of the Stratified Win Ratio in EMPULSE.

Detailed results for the stratified win ratio in EMPULSE. Figure 3 shows the number of wins for empagliflozin, wins for placebo or ties at each level of the hierarchy in each of the two strata (de novo patients and decompensated chronic patients). The figure also shows the total number of wins in each stratum, the stratum specific win ratios and 95% CIs and the overall stratified win ratio and 95% CI. HF = heart failure; KCCQ-TSS = Kansas City Cardiomyopathy Questionnaire - Total Symptom Score; CI = Confidence Interval.

For both acute de novo and decompensated chronic HF, the subgroup win ratio estimates were similar, 1.29 and 1.39 respectively. The former had a wider CI due to the smaller number of patients involved. The overall combined win ratio estimate was 1.36 with 95% CI 1.09 to 1.68 with P = 0.0054 which is very similar to the unstratified result shown in Figure 1.

Note the weighting here is according to the number of patients in each stratum. If instead one were to just add up the numbers of wins and losses in each stratum this would give too much weight to the larger stratum, yielding a win ratio of 1.37. For instance, if one stratum is twice the size of the other, it has four times as many patient pairs.

One complexity in the analysis of KCCQ is the occurrence of missing data at day 90. A multiple imputation algorithm was used (see Supplementary Appendix of Voors et al¹ for full details). The consequence is that all win ratio results in Figures 1 and 2 are averages based on 100 imputations.

Sensitivity Analyses

It is of interest to see whether the win ratio results depend on the specific criteria for declaring a win at the different levels of the hierarchical composite. For instance, the primary stratified analysis had HF events at both steps 2 and 3 of the hierarchy: first declaring a win in any pair based on the number of HF events and then, if that number was the same, declaring a win based on the time-to-first HF event. One could have simplified this by only using one of the two criteria. Table 1A shows that results stay virtually identical whichever of these options is adopted. Thus, in future trials using the win ratio with HF events, the better strategy might be to base this step of the hierarchy on the number of HF events. However, we note that calculations are easier using time to first HF event.

Table 1.

Sensitivity Analysis for the EMPULSE trial Win Ratio Approach

A. Different Ways of Handling HF Events
Criterion to Declare a Win	% of Wins using HF Events		Overall Result
	on empa	on placebo	Win Ratio (95% CI)	P	% tied
Number of HF events	10.59%	7.65%	1.36 (1.10, 1.69)	0.0051	6.5%
Time to First HF event	10.79%	8.25%	1.36 (1.09, 1.68)	0.0057	6.4%
Both in Sequence*	10.83%	8.21%	1.36 (1.09, 1.68)	0.0054	6.4%
B. Different Ways of Handling KCCQ-TSS change in 90 days
Criterion to Declare a Win	% of Wins using KCCQ		Overall Result
	on empa	on placebo	Win Ratio (95% CI)	P	% tied
any difference	38.94%	30.35%	1.34 (1.09, 1.64)	0.0051	0.5%
≥2 points	38.16%	29.54%	1.34 (1.09, 1.65)	0.0050	2.1%
≥5 points*	35.91%	27.48%	1.36 (1.09, 1.68)	0.0054	6.4%
≥10 points	32.39%	24.06%	1.39 (1.10, 1.75)	0.0050	13.3%
≥15 points	28.83%	20.70%	1.42 (1.11, 1.81)	0.0046	20.3%
KCCQ-TSS not used	0%	0%	1.50 (0.99, 2.26)	0.055	69.5%

^*the pre-specified primary analysis

all analyses are stratified, with multiple imputation for missing KCCQ at 90 days

Table 1A and 1B shows how the win ratio results are affected by a variety of sensitivity analyses. Table 1A shows that the win ratio is virtually unchanged if we use either (i) number of HF events, or (ii) the time to first HF event, or (iii) both in sequence (the pre-specified primary analysis in EMPULSE). Table 1B shows how the win ratio is affected by varying the winning margin required for the KCCQ-TSS or by omitting this level completely. The win ratio increases with larger margins though the p-value remains fairly unchanged.

Our logic, supported by the EMPULSE data, is that when a pair of patients have the same number of HF events, differences in their time sequence, i.e., which came first, may carry little insight as to who had the better outcome. A better alternative might be to untie on the number of days in hospital. It would be helpful to explore this issue in HF trials with longer follow up. Also, simulations of alternative scenarios might be useful when planning future trials with the win ratio. ⁹

The handling of change in KCCQ-TSS change at 90 days as the last step of the hierarchy can have several alternative options, as shown in Table 1B. The primary analysis required a difference of 5 points or more to declare a win amongst any pair of patients, the underlying clinical rationale being that one patient must be performing substantially better than the other for a “win” to be declared. But statistically there is no need for such a margin of 5 points, and this is often the case in other types on non-parametric statistical testing. Thus, if any difference counts as a win, then the % of ties is reduced from 6.4% to 0.5%. The % of wins using KCCQ on empagliflozin and on placebo respectively increase from 35.9% vs 27.5% with a 5-point margin to 38.9% vs 30.4% respectively with no margin at all. The win ratio is reduced slightly from 1.36 to 1.34 but the strength of evidence for a treatment benefit is virtually unchanged, P = 0.0054 becoming P = 0.0051.

Figure 1B also includes other choices of margin for a win, i.e. 2 points, 10 points, and 15 points. A clear pattern emerges: a bigger choice of margin inevitably increases the number of ties, the estimated win ratio increases slightly while the P-value remains consistent, around P = 0.005.

The multiple imputation algorithm for handling missing KCCQ values is quite complex ¹, and hence it is useful to see how alternative simpler approaches would affect the results.

Relevant are the numbers of patients with missing KCCQ-TSS at baseline and/or day 90 who enter level 4 of the hierarchical win ratio analysis, i.e. are alive at day 90 and had no HF event: these are 18 (6.8%) on placebo and 23 (8.7%) on empagliflozin. The simplest analysis counts all pairs involving such missing KCCQ values as ties. Redoing the stratified analysis in Figure 3 on that basis substantially increases the number of ties from 6.1% to 18.7%. The consequent win ratio is 1.43 (95% CI 1.14, 1.78) P=0.0018, which is slightly increased but with a wider CI. To reduce the number of ties due to missing values, one further sensitivity analysis substituted the day 30 KCCQ (or day 15 KCCQ) changes for both patients in such otherwise tied pairs. The number of ties was then reduced to 13.4% and the stratified win ratio became 1.39 (95% CI 1.12, 1.72) P=0.0029, a very similar finding.

One could consider a conventional mixed model for repeated measures (MMRM) analysis of mean KCCQ-TSS change at 90 days only including patients for which this was recorded. This leads to a treatment difference in means in favour of empagliflozin of 6.76 (95% CI 1.59, 11.93) P = 0.0105. It is customary to take account of the baseline value in this MMRM, in which case the difference in means becomes 4.45 (95% CI 0.32, 8.59) P = 0.035.

The logic here is that patients with a poorer initial symptom score have more scope to improve than those not so affected at baseline. We note that this issue of regression to the mean¹⁰ is not currently accounted for in the win ratio method. Thus, some form of baseline-adjusted change over time may be warranted in future trials with KCCQ or any other quantitative outcome as a component of the win ratio hierarchy.

But these analyses of mean KCCQ change alone fail to consider the competing risk of death and the possible influence of HF events. An option here is a non-parametric ranked-based analysis in which death is included as the worst symptom score. A consequent win ratio analysis of this non-normal outcome ¹¹ can then be performed, as recently illustrated as a secondary analysis in the DELIVER trial.¹²

DISCUSSION

We have presented an interesting case study of how the win ratio approach which facilitated the integration of data on mortality, clinical events and patient-reported health status into an overall assessment of whether clinical benefit was successfully applied in a randomized controlled trial. Until now it has been common practice to evaluate separately any influence of treatment on event outcomes, with patient-reported outcomes, e.g. KCCQ analyzed as secondary endpoints. This practice requires the trial to be adequately powered for event outcomes and often such a large sample size is unachievable. For instance, EMPULSE would have needed to be many times larger than the 530 patients actually recruited.

An alternative convention is to concentrate on the symptoms outcome as primary, but this usually fails to take account of the competing risk of death and ignores the importance of clinical events, such as hospitalizations. Hence, there is considerable merit in recognizing the clinical priorities amongst outcomes, e.g. death is a more impactful outcome than hospitalizations, which in turn are given greater priority than changes in KCCQ. The win ratio method was developed as a means of capturing this hierarchy amongst different types of outcomes. Since its creation in 2012 most uses of the win ratio in cardiology trials focused on just two levels in the hierarchy: death (all cause or cardiovascular) followed by hospitalizations (either all, cardiovascular or specifically due to heart failure). One high-profile example is the ATTR-ACT placebo-controlled trial of tafamidis treatment for transthyretin amyloid cardiomyopathy:¹³ It had all-cause death as the first step followed by the number of cardiovascular hospitalizations (including repeats) as the second. The consequent win ratio was 1.70 (95% CI 1.26, 2.29) P = 0.0006, stronger evidence of a treatment benefit than was obtained by separate analyses of deaths and of hospitalizations.

Now EMPULSE is one of the growing selection of randomized trials extending the win ratio to three (or more) hierarchical types of outcome, particularly relevant to cardiovascular device trials. For instance, TRILUMINATE is an ongoing trial of the TriClip device versus medical therapy in tricuspid valve repair: ¹⁴ the primary hierarchical composite outcome is all-cause death, tricuspid valve surgery, heart failure hospitalizations, and change in KCCQ score over 12 months.

For an open (unblinded) trial, as is often the case for medical devices, there may be concern about potential bias in a subjective symptoms outcome in which case alternatives such as biomarkers (e.g. NT-proBNP) or functional outcomes (e.g. 6-minute walk test) could be the last step in the clinical hierarchy, though the latter may still be perceived as similarly subjective.

The win ratio approach works best when there is a directional consistency of observed treatment difference at every level of the clinical hierarchy. For instance, the positive EMPULSE trial finding of clinical benefit is reinforced by the greater number of wins (versus losses) for deaths, number of hospitalizations, and KCCQ change. If this consistency were not observed, then the interpretation of an overall positive win ratio result, which say rested solely on improved symptoms with no matching reduction in clinical events, would be more challenging. But the same issue applies to any conventional composite primary outcome in which the components show disparate results.

In the EMPULSE trial the primary analysis was stratified by type of heart failure (acute de novo or decompensated chronic), though we show that a simpler unstratified analysis gave a very similar result. The ATTR-ACT trial had four strata in its win ratio analysis.¹⁵ We have seen more extensive use of strata, e.g. analysis stratified by centre. At present we advocate caution in doing stratified win ratio analyses since their statistical pros and cons need further exploration. For instance, the number of paired comparisons is greatly reduced, roughly inversely proportional to the number of strata and this potentially weakens the precision of the win ratio estimate. We recommend only to stratify on a patient factor known to strongly influence prognosis.

There is an ongoing debate when analyzing data on hospitalizations or other non-fatal events whether it is better to use time-to-first event or perform more complex analyses of all events, including repeats.¹⁶ In the EMPULSE win ratio hierarchy patient pairs were untied on the number of HF events and only if that was equal in any pair was the time-to-first event then used. In hindsight this appears an unnecessary complication since virtually identical results were obtained using one or the other (see Table 1A). In EMPULSE follow-up was relatively short: perhaps if a study has longer follow-up, e.g. 2 years, then repeat HF events would be more common, making the number of events a more informative choice, as in the ATTR-ACT trial.¹²

In EMPULSE the pre-defined primary analysis adopted a rule whereby for any pair of patients one had to have a change in KCCQ-TSS at 90 days at least 5 points better than the other for that to be counted as a “win”, while smaller differences between a patient pair counted as a “tie”. This 5-point margin is somewhat arbitrary, being mainly based on the acceptance that 5 points or more is a clinically meaningful difference. Our sensitivity analyses in Table 1B explore alternative margins including the option that any difference no matter how small counts as a win. The pattern is clear: a smaller margin reduces the % of ties and slightly reduces the estimated win ratio while the strength of evidence (P-value) for benefit is essentially unaltered. Therefore, on statistical grounds we see no need in future trials to introduce a 5-point margin, i.e. any difference counts as a win. But it would be interesting to explore this issue in other trial databases. The statistical logic is that the win ratio is analogous to other non-parametric tests. The ranking of patients from highest to lowest value takes into account the closeness of some pairs of values but does not consider them equal. Thus, imposing a margin is contrary to the principle of rank based statistical testing.³ Indeed, simulation studies have shown a potential loss of statistical power if the chosen margin is substantial.¹⁷

From our experience in presenting and discussing win ratio analysis with other trialists, we have encountered a few common misperceptions:

Win ratio = 1.36 does not mean that patients are 36% more likely to benefit on empagliflozin than on placebo, though such a statement is not seriously misleading.

Nor does it mean that 36% of patients benefitted from empagliflozin.

The precise meaning is that of all patient pairs for which there was a preference (i.e. ignoring ties) there were 36% more wins on empagliflozin than on placebo.

Alternatively, win ratio = 1.36 means that for any untied pair of patients, the odds that the winner is empagliflozin (rather than placebo) is 1.36.

One also needs to recognize that looking at components of the win ratio at any level other than the first level is no longer comparing all patients and therefore needs careful interpretation. That is why level 3 in the EMPULSE trial, time-to-first HF events is largely ties because it only applies to patients who tied at level 2, the number of HF events. In the sensitivity analysis that removed level 2 (see Table 1A), time-to first HF event then had more wins on empagliflozin than on placebo, a more logical finding.

Note that level 4 of the hierarchy is looking at KCCQ wins and losses for patient pairs who were both event-free in levels 1, 2 and 3. Furthermore, the 5-point threshold for declaring a win is not a “responder” threshold. For instance, if a pair of patients had KCCQ increases of 20 and 30 both would be “responders”, but it is the latter that is the “winner” for that specific pairing.

The win odds is a modification of the win ratio which takes ties into account.¹⁸ It is defined as win odds = (#wins + ½ #ties)/(#losses + ½ #ties). In our unstratified analysis in Figure 1 the win odds is 1.35 inevitably smaller than the win ratio of 1.38. In this case the rate of ties 6.4% was low, whereas in examples with a higher rate of ties the the win odds would be even closer to the null value of 1.0. Proponents of the win odds advocate certain theoretical advantages¹⁸, but we feel it would add further challenges in interpretation which inhibit a wider understanding. Another alternative to the win ratio is the win difference¹⁹ defined as % wins minus % losses, which from our unstratified case in Figure 1 is 54.2% - 39.3% = 14.9%. This has also been called the net treatment benefit. We see the win difference as a useful complement to the win ratio, by providing a measure of absolute treatment benefit alongside the relative benefit. In other examples with a higher proportion of ties, for any estimated win ratio the corresponding win difference will be smaller. Note all three estimates (win ratio, win odds and win difference) result in approximately the same p-value.

The win ratio is analogous to the hazard ratio for time-to-event analyses in providing a measure of relative treatment benefit, whereas measures of absolute benefit are also of value. Hence it is useful in practice for any win ratio analysis to also include the win difference and/or win odds estimates.

When follow-up is the same for all patients and there are no missing values, one can rank all patients from worst to best outcome based on the clinical hierarchy of endpoints e.g., in EMPULSE the worst outcome would be the earliest death after randomization and the best would be the patient who lived to 90 days with no HF event and the greatest improvement from baseline in KCCQ-TSS. One could then perform a non-parametric Mann-Whitney test. The estimated treatment effect can be quantified in the same way as for the Finklestein-Schoenfeld test. That is, the win ratio approach to estimation (including win odds and win difference) seems most appropriate for any comparison of an ordered outcome (comparing pairs with respect to a single outcome rather than a hierarchy of outcomes) including a global rank score.¹¹

The win ratio approach to analysis and reporting of composite outcomes does have some limitations. Being a relatively new method, the interpretation of what a win ratio actually means has not been clear to many researchers, and we hope this article goes some way to alleviating that sense of mystery. A recent perspective article also helps clarify the relevance and meaning of the win ratio.²⁰

In EMPULSE the finding of significant clinical benefit for empagliflozin versus placebo rests substantially on the observed superior symptoms score at 90 days. Numerically, around two thirds of the “wins” for empagliflozin were because of superior KCCQ-TSS change at 90 days. While death and HF events did contribute meaningfully, they were not the driving force behind the positive conclusion. Hence acceptance of the win ratio approach as clinically meaningful depends on a realization that the majority of patients survive event-free, so that patient-reported outcomes necessarily are an integral part of treatment evaluation.

In conclusion, the EMPULSE trial is an important contribution to understanding how deaths, clinical events and patient-reported outcomes can all be integrated into an overall assessment of treatment benefit. The win ratio approach responds to the existence of such clinical priorities (i.e. a hierarchy of outcomes) in providing a robust method to estimate the magnitude of treatment benefit across such disparate outcomes. It has the advantage of reducing trial size compared to event-driven trials, thereby facilitating earlier evidence of clinical benefit for any new intervention. Our findings are summarized in the Graphical Abstract.