Determining air-water interfacial areas for the retention and transport of PFAS and other interfacially active solutes in unsaturated porous media

Abstract

The objective of this work was to determine the methods that produce the most representative measurements and estimations of air-water interfacial area specifically for the retention and transport of PFAS and other interfacially active solutes in unsaturated porous media. Published data sets of air-water interfacial areas obtained with multiple measurement and prediction methods were compared for paired sets of porous media comprising similar median grain diameters, but one with solid-surface roughness (sand) and one without roughness (glass beads). All interfacial areas produced with the multiple diverse methods were coincident for the glass beads, providing validation of the aqueous interfacial tracer-test methods. The results of this and other benchmarking analyses demonstrated that the differences in interfacial areas measured for sands and soil by different methods are not due to errors or artifacts in the methods but rather the result of method-dependent differential contributions of solid-surface roughness. The contributions of roughness to interfacial areas measured by interfacial tracer-test methods were quantified and shown to be consistent with prior theoretical and experiment-based investigations of air-water interface configurations on rough solid surfaces. Three new methods for estimating air-water interfacial areas were developed, one based on the scaling of thermodynamic-determined values and the other two comprising empirical correlations incorporating grain diameter or NBET solid surface area. All three were developed based on measured aqueous interfacial tracer-test data. The three new and three existing estimation methods was tested using independent data sets of PFAS retention and transport. The results showed that the method based on treating air-water interfaces as smooth surfaces as well as the standard thermodynamic method produced inaccurate air-water interfacial areas that failed to reproduce the multiple measured PFAS retention and transport data sets. In contrast, the new estimation methods produced interfacial areas that accurately represented air-water interfacial adsorption of PFAS and associated retention and transport. The measurement and estimation of air-water interfacial areas for field-scale applications is discussed in light of these results.

GRAPHICAL ABSTRACT

1. Introduction

The air-water interface plays a critical role in numerous processes in the environment. This includes the subsurface environment, for which the air-water interface is central to fluid distributions and flow, to inter-phase mass and energy transfer, and to the adsorption and retention of matter. The latter aspect has become a particular focus of attention recently, with the advent of per and polyfluoroalkyl substances (PFAS) as emerging contaminants of critical concern. This study is focused on the role of the air-water interface in the retention and transport of PFAS and other interfacially active solutes in unsaturated porous media.

Recent research has demonstrated that adsorption at the air-water interface can significantly impact the retention and transport of PFAS in unsaturated porous media. These studies include laboratory miscible-displacement experiments (e.g., Lyu et al., 2018, 2022; Lyu and Brusseau, 2020; Lyu et al., 2020; Brusseau et al., 2019, 2021; Yan et al., 2020; Li et al., 2021), model-based analyses (Brusseau, 2018, 2020; Brusseau et al., 2019; Guo et al., 2020, 2022; Silva et al., 2020; Newell et al., 2021; Zeng et al., 2021; Gnesda et al., 2022; Wallis et al., 2022), and field-scale investigations (Brusseau and Guo, 2022; Schaefer et al., 2022). The results of prior studies have demonstrated that adsorption at the air-water interface can also influence the retention and transport of other solutes, including hydrocarbon surfactants (e.g., Kimetal.,1997; Allred and Brown, 2001; Brusseau et al., 2007; Costanza-Robinson and Henry, 2017), hydrophobic organic compounds (e.g., Brusseau et al., 1997; Kim et al., 1998, 2001, 2005; Popovicova and Brusseau, 1998), and pharmaceuticals (e.g., Dai et al., 2020; Hamdollahi et al., 2022). Characterizing and quantifying the impact of air-water interfacial adsorption on the retention of PFAS and other interfacially active solutes requires knowledge of the amount of air-water interfacial area present in the porous medium. Concomitantly, measurements or estimates of air-water interfacial area are needed to parameterize models to simulate the transport of PFAS and other interfacially active solutes in unsaturated media.

Multiple approaches are available to determine air-water interfacial areas for unsaturated porous media. Several measurement methods have been developed, including gas-phase interfacial tracer tests, various aqueous-phase advective interfacial tracer tests, various aqueous batch-mode mass-balance interfacial tracer tests, and several imaging methods such as X-ray microtomography. Alternatives to these measurement methods include thermodynamic analyses of soil-water characteristic data and the application of pore-scale models. In addition to these six measurement and prediction methods, interfacial areas can also be estimated based on empirical correlations. While a detailed review of these methods is beyond the scope of this study, a brief overview is presented in the Supplemental Information (SI, Section 1). Initial discussions of methods for measuring and estimating air-water interfacial areas specifically for PFAS applications have been recently presented (Brusseau, 2018; Brusseau et al., 2019; Brusseau and Guo, 2021; Silva et al., 2022).

Ideally, interfacial areas would be measured directly for the porous medium of interest using one of the several methods that have been developed. However, this is often not practical, particularly for field-scale applications. Hence, methods are needed to estimate air-water interfacial areas. Efforts to estimate interfacial areas between immiscible fluids have been employed for several different applications, including the dissolution of nonaqueous-phase liquids (NAPL), colloid transport, mass transfer in packed-bed reactors, oxygen transport and attendant biological activity, and the retention of interfacially active solutes. The focus of the present study will be on the latter application.

The above-cited modeling and field studies that investigated the distribution, retention, and transport of PFAS employed different methods for determining air-water interfacial areas. Some studies used measured values (Brusseau, 2018, 2020; Guoetal., 2020), others employed thermodynamic-determined values (Silva et al., 2020), and still others used empirical estimates based on a variety of approaches (Brusseau et al., 2019; Zeng et al., 2021; Brusseau and Guo, 2022; Gnesda et al., 2022; Guo et al., 2022; Newell et al., 2021; Schaefer et al., 2022; Wallis et al., 2022). The use of the different methods is complicated by the fact that they can produce different interfacial areas for the same medium (e.g., Brusseau et al., 2007; Brusseau and Guo, 2021). These differences can significantly impact the calculated magnitudes of retention by air-water interfacial adsorption, which can for example lead to large differences in predicted travel times for PFAS transport (Brusseau and Guo, 2021). Uncertainty as to which methods produce the most representative air-water interfacial areas specific to the air-water interfacial adsorption of PFAS and other interfacially active solutes engenders uncertainty in analyzing, interpreting, and modeling retention and transport. Resolving this issue is particularly critical now given that research studies and site investigations are being implemented to characterize the distribution, retention, and transport of PFAS in the vadose zone.

Estimation methods are based on specific underlying methods of measurement or prediction. To be robust, the estimation method must be based on a measurement or prediction method that produces representative interfacial areas for the relevant application. There is current uncertainty as to which methods produce the most representative air-water interfacial areas specific to the air-water interfacial adsorption of PFAS and other interfacially active solutes. Three primary factors contribute to uncertainty in determining the most relevant measurement or prediction methods. The first is uncertainty in the sources of the disparities in interfacial areas produced with the different measurement and prediction methods noted above. These disparities have been attributed by some investigators to method-specific differences in the extents to which the contributions of different interfacial domains are characterized due to method design or implementation. Other investigators have speculated that the differences are due primarily to errors or artifacts associated with certain methods, particularly the aqueous advective interfacial tracer-test method. Resolving this issue has been impeded by the fact that few specific investigations have compared multiple methods at once for the same porous medium, and none to date have simultaneously investigated all six primary measurement and prediction methods.

The second contributing factor is uncertainty in delineating which interfacial-area domains impact retention. It is well established that the air-water interface is comprised of multiple domains. One domain consists of the interfaces that exist between the bulk wetting and non-wetting fluids, in this case water and air, which are typically referred to as meniscus or capillary interfacial area. There is also air-water interface associated with water that is wetting the surfaces of the solids, which is typically referred to as film- or surface-associated interfacial area. A critical aspect of film-associated area is the potential contribution of solid-surface roughness, which can greatly increase total magnitudes. For any estimation method to produce robust results for the intended application, it is critical that it represent the contributions of all interfacial-domains that are relevant for that application, in this case interfacial adsorption of solutes. However, the specific contributions of the different interfacial domains to the retention of interfacially active solutes have received minimal investigation. The third factor is uncertainty in the governing relationship between interfacial area and water saturation. Estimation methods need to produce values that are consistent with this governing relationship, which notably has been represented by both linear and nonlinear functions. There has been no comprehensive assessment to date of which is correct.

The objective of this work is to determine the methods that produce the most representative measurements and estimations of air-water interfacial area specifically for the retention and transport of PFAS and other interface-active solutes in unsaturated porous media. Prior measurements and pore-scale model simulations of air-water interfacial areas are examined to determine the sources of the disparities in interfacial areas produced with different measurement and prediction methods, to delineate the contributions of different interfacial-area domains to the interfacial areas relevant to air-water interfacial adsorption, and to elucidate the inherent governing relationship between air-water interfacial area and water saturation. Interfacial areas obtained with multiple measurement and prediction methods are compared for paired sets of porous media comprising similar median grain diameters, but one with solid-surface roughness (sand) and one without roughness (glass beads). These comparisons are used to critically examine the robustness and validity of the various methods. For the first time, the specific contribution of air-water interface associated with solid-surface roughness is quantified with respect to interrelationships between the interfacial areas produced with different measurement methods and the absolute-maximum interfacial area that is present in the medium. The outcomes of these novel investigations are used to evaluate the efficacy of existing estimation methods and to inform the development of new estimation methods. The existing and new estimation methods are tested and compared using independent data sets for PFAS retention and transport to determine which approach is most representative for characterizing and quantifying the air-water interfacial adsorption of PFAS. Finally, issues associated with determining air-water interfacial areas for field-scale applications are discussed.

2. Materials and methods

Prior measurements and pore-scale model simulations of air-water interfacial area were aggregated from the literature. Multiple literature searches were conducted using Web of Science, Scopus, and Google Scholar. A variety of search terms were employed. Data sets were obtained for several measurement methods, including the gas-phase interfacial tracer test (GPITT), various aqueous interfacial tracer tests (AQITT), and X-ray microtomography (XMT). The measured data sets were digitized from the original works and brought into excel to allow for processing and replotting. The Engauge free ware program was used for the digitization (Mitchell et al., 2022). Several tests were conducted to ensure the accuracy of the digitization process, including (1) digitizing data from figures for comparison to the same data sets presented in tabular form and (2) comparing digitization results of the same data sets obtained by multiple people.

The data sets were fit with linear and nonlinear (polynomial) functions to assess the operative relationship between air-water interfacial area and water saturation. The best-fit nonlinear function was used to determine the effective maximum air-water interfacial area for each data set. Specific focus is placed on the maximums obtained for the AQITT data, which is designated as ${\text{A}}_{\text{aw}}^{\text{Max}}$ (see Fig. 1 for an example). Regression analyses were conducted to examine potential correlations between air-water interfacial area and porous-medium properties including median grain diameter and solid surface area. Information reported in the original studies served as the source of the property data. All data processing was conducted in Excel using standard statistical methods.

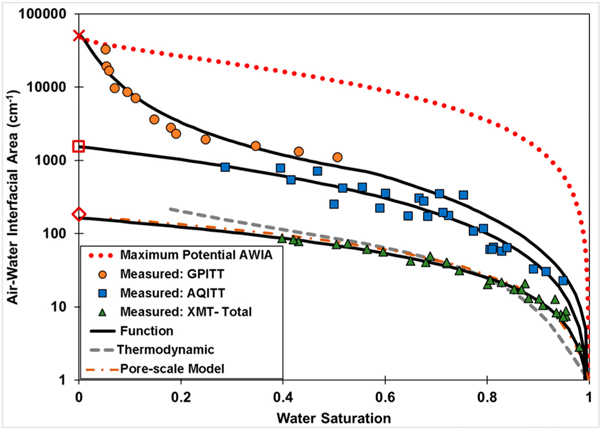
Fig. 1.

Measured and predicted air-water interfacial areas obtained with different methods for Vinton soil. Also included is the absolute-maximum interfacial area (red dotted curve) as described in the text. The large red diamond, square, and cross on the y-axis represent the geometric (smooth-surface) solid-surface area (GSSA), the AQITT-related maximum interfacial area (${\text{A}}_{\text{aw}}^{\text{Max}}$), and the NBET specific solid surface area (NBSSA), respectively. AWIA is air-water interfacial area; GPITT represents the gas-phase interfacial tracer-test method; AQITT represents various aqueous interfacial tracer-test methods; XMT represents the x-ray microtomography method. The measured data sources are presented in Section 2 of the SI.

Air-water interfacial areas are presented for three paired sets of two media with similar median grain diameters, but one is as and with solid surface roughness and one is a glass-bead medium with minimal roughness. The three sets comprise median grain diameters of approximately 0.35, 0.75, and 1.2 mm. Note that while these values will be used when referring to the data sets, the actual diameters may vary somewhat. Measured data sets reported by Brusseau and colleagues for Vinton soil, 0.35-mm sand, and 1.2-mm sand are used as training data to develop new estimation methods to determine air-water interfacial areas. The sources of all data sets are reported in Section 2 of the SI. All measured and predicted air-water interfacial areas are determined for primary drainage conditions, unless otherwise noted in the SI. Note that the pore-scale model simulations are based on the assumption that the solid surfaces are smooth (SI, Section 1.6). Hence, the simulated interfacial areas do not incorporate the contributions of solid-surface roughness.

Solid surface areas are often used as reference areas. The geometric smooth-surface specific solid surface area (GSSA) is one such area, determined as:$\text{GSSA}\left({\text{cm}}^{-1}\right)=6(1-\text{n})/{\text{d}}_{50}$, where n is porosity and d₅₀ (cm) is the median grain diameter of the porous medium. The nitrogen-Brunauer-Emmett-Teller (NBET) solid surface area (NBSSA) is another relevant surface area. A significant difference between the two is that the NBSSA incorporates the contributions of solid-surface roughness whereas the GSSA does not. The latter in effect represents equivalent smooth-surface areas.

Three existing methods for estimating air-water interfacial areas (${\text{A}}_{\text{aw}},{\text{cm}}^2/{\text{cm}}^3{\text{or}\text{cm}}^{-1}$) will be compared to methods newly developed in this study. The first is based on two assumptions, one that the GSSA defines the maximum possible interfacial area and the second that air-water interfacial area is a linear function of water saturation(Costanza-Robinson etal., 2008; Wallis et al., 2022):

$${\text{A}}_{\text{aw}(\text{Sw})}=\left(1-{\text{S}}_{\text{w}}\right)\times \text{GSSA}$$ (1)

The second is based on the use of maximum interfacial areas determined from linear extrapolation of ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ data measured by aqueous interfacial tracer tests, and an assumption of a linear relationship between air-water interfacial area and water saturation (Lyu et al., 2018). The maximum interfacial areas are estimated from a correlation to the median grain diameter, which results in the following combined equation:

$${\text{A}}_{\text{aw}(\text{Sw})}=\left(1-{\text{S}}_{\text{w}}\right)\times 3.9\times {\text{d}}_{50}-1.2$$ (2)

This function was originally developed for application to only higher water-saturation conditions under there cognition that measured interfacial areas are typically nonlinear functions of water saturation. The third, thermodynamic-based method employs an analysis of soil-water characteristic (SWC) data and is given by Leverett (1941):

$${\text{A}}_{\text{aw}(\text{Sw})}=\frac{n}{\sigma }{\int }_{Sw}^{1}CP{\text{dS}}_{\text{w}}$$ (3)

where $\sigma$ is surface tension and CP is capillary pressure. The van Genuchten function was applied to the measured SWC data to assist in the determination of interfacial areas with Eq. (3).

3. Results and discussion

3.1. Comparison of measured and predicted air-water interfacial areas

Multiple methods have been used to measure or predict air-water interfacial areas in porous media. Brief overviews of the methods are presented in Section 1 of the SI. Several studies have demonstrated that the different methods can produce different magnitudes of air-water interfacial area for the same porous medium. This disparity is illustrated in Fig. 1 for a soil and in Fig. 2 for a sand. Additional comparisons for two other sands are presented in Figs. SI–1 and SI–2 (Section 3 of the SI). The GPITT method produces the largest magnitudes of air-water interfacial area, significantly greater than those produced with the AQITT methods at lower water saturations. The GPITT- and AQITT-measured interfacial areas are much larger than the total interfacial areas measured by XMT. Note that while not shown, capillary-only interfacial areas measured by XMT are typically substantially smaller than XMT-measured total interfacial areas (e.g., Brusseau et al., 2007; Porter et al., 2010; Araujo and Brusseau, 2020). The interfacial areas determined with the thermodynamic and pore-scale modeling methods are similar to those measured by XMT, but are much smaller than those measured by the GPITT and AQITT methods. The potential reasons for the disparities in interfacial areas produced with the different methods have been discussed in only a few studies. Two primary potential reasons have been proposed.

Fig. 2.

Measured and predicted air-water interfacial areas obtained with different methods for the 0.35-mm sand. The large red diamond on the y-axis represents the geometric (smooth-surface) solid-surface area (GSSA). The measured data sources are presented in Section 2 of the SI. The measured AQITT data labeled Li-Lyu are from a separate research group (Lyu et al., 2020; Li et al., 2021). For these data, the points at the higher and lower water saturations represent the mean of 12 and 2 experiments, respectively.

Some investigators have speculated that the differences observed between AQITT measurements versus XMT and thermodynamic-based values are due primarily to errors or artifacts associated with the AQITT method. Deviations between XMT-based interfacial-area estimates and literature AQITT data were attributed in part to possible issues with the AQITT method, including tracer accessibility and mass-transfer limitations, uncertainties in quantifying solid-phase sorption of the tracer, and surfactant-induced flow (Costanza-Robinson et al., 2008). Subsequent work focused on surfactant-induced flow as a source of error for the advective AQITT method (Costanza-Robinson et al., 2012; Costanza-Robinson and Henry, 2017). Thermodynamic-determined air-water interfacial areas were observed by Kibbey and Chen (2012) to be larger than, similar to, or smaller than measured literature data depending upon the medium and measurement method (Section 4 of the SI). The observation that advective AQITT-measured interfacial areas for a soil were larger than the thermodynamic values was speculated to result from some “unidentified experimental artifact” impacting the AQITT measurements, with foam formation, surfactant-induced flow, and uncertainty in determining the air-water interfacial adsorption coefficient three possible sources of error mentioned. Based on the speculation that the AQITT measurements were erroneous, the investigators concluded that air-water interfacial area can be represented by the smooth-surface solid surface area (Costanza-Robinson et al., 2008; Kibbey and Chen, 2012; Kibbey, 2013). Differences between AQITT-measured interfacial areas and thermodynamic-derived values have also been conjectured to result from changes in the configuration of the air-water interface caused by the presence of the interfacial tracer (Silva et al., 2022). In addition to the preceding, Kim et al. (1999) hypothesized that observed differences between GPITT- and AQITT-determined interfacial areas may in part have been due to the interfaces being mobile to some degree for the advective AQITT system. It is important to recognize that with the exception of surfactant-induced flow, none of the conjectured sources of error or artifacts were specifically investigated, much less demonstrated, in any of the cited studies. Additionally, the assessments were based on a few select literature data sets rather than comprehensive evaluations, and were focused solely on the AQITT method and did not include air-water data sets measured by GPITT methods nor NAPL-water interfacial-area data sets measured by AQITT.

The significantly greater interfacial areas measured by the GPITT method versus the AQITT methods, and by AQITT compared to XMT and thermodynamic methods have been hypothesized by other investigators to result from the contribution of solid-surface roughness to film-associated interfacial area. The potential contributions of roughness to fluid-fluid interfacial areas have been proposed and discussed in several studies following four different approaches. In the first approach, observations that GPITT- or AQITT-measured interfacial areas were larger than GSSAs, which do not account for roughness contributions, were attributed to the impact of solid-surface roughness (Kim et al., 1999; Schaefer et al., 2000; Costanza-Robinson and Brusseau, 2002). In a second approach, GPITT- and AQITT-measured interfacial areas were observed to be significantly larger than XMT-measured values for the same porous medium, which was attributed to the impact of roughness (Brusseau et al., 2006, 2007, 2010, 2020; McDonald et al., 2016). Additionally, a correlation was demonstrated between the maximum interfacial area and the NBET solid surface area (Brusseau et al., 2010). In the third approach, interfacial areas measured by the advective AQITT method were compared for two porous media with the same or similar median grain diameters (i.e., similar GSSA) but different magnitudes of NBSSAs due to differences in solid-surface roughness. The interfacial areas measured for the medium with greater roughness were larger than the areas measured for the medium with lesser or no roughness for all three cases, which was attributed to the impact of roughness (Brusseau et al., 2010; Brusseau, 2019; Lyu et al., 2020). In the fourth approach, Jiang et al. (2020a) developed a pore-scale mathematical model to simulate fluid-fluid interfacial area in variably saturated porous media, with a specific focus on incorporating the effects of solid-surface roughness. The model simulations demonstrated that the contributions of surface roughness cause interfacial areas to be greater for media with roughness compared to media comprising smooth surfaces, and that the degree to which fluid-fluid interfacial area is influenced by roughness is a function of fluid-retention characteristics, the nature of the rough surfaces, and masking due to the formation of thick wetting films.

The cause of the observed disparities in interfacial areas determined with the different methods is investigated by comparing interfacial-area data sets obtained with the different methods for paired sets of porous media comprising the same or similar median grain diameters. Because the grain diameters are similar, the two paired media have essentially identical GSSAs. However, one set of media comprise glass beads that have minimal solid-surface roughness and effectively smooth surfaces, as demonstrated by the fact that the measured NBSSAs are the same as the GSSAs. Conversely, the second set of media is sands that have significant surface roughness, with NBSSAs that are much greater than the GSSAs. The glass-beads data sets allow direct examination of the consistency between different measurement and prediction methods in the absence of surface roughness, which serves as a means to test the validity of the two proposed sources of disparity. These data sets represent the first time that interfacial areas obtained with all of these methods have been compared simultaneously for the same media. Details of the sources of the data sets are presented in Section 2 of the SI.

Data for the 0.35-mm glass beads are presented in Fig. 2. The air-water interfacial areas measured with the AQITT and XMT methods are coincident. The interfacial areas simulated with the pore-scale models, which assume smooth surfaces, match the AQITT and XMT measurements for the glass beads. Additionally, the thermodynamic-determined interfacial areas for the glass beads match the values determined with all of the other methods. Similar results showing excellent consistency among interfacial areas determined with AQITT, XMT, pore-scale modeling, and thermodynamic methods are obtained for the 1.2-mm glass beads (Fig. 3) and the 0.75-mm glass beads (Fig. SI–1, Section 3 of the SI). It is observed that the XMT data for all three sets of glass beads extrapolate at low water saturation to the GSSA, which represents the smooth-surface area. Furthermore, the pore-scale modeling and thermodynamic-based values for all three media extrapolate to the GSSA as well. Notably, the AQITT data for all three sets of glass beads also extrapolate to the GSSA.

Fig. 3.

Measured and predicted air-water interfacial areas obtained with different methods for the 1.2-mm sand. The large red diamond on they-axis represents the geometric (smooth-surface) solid-surface area (GSSA). The measured data sources are presented in Section 2 of the SI.

The consistency among all of the sets of interfacial areas for all three glass-beads media demonstrates that the different methods are capable of producing the same values despite the fact that they are based on greatly different approaches and attendant implementation conditions. This demonstrates that any differences in the method-specific approaches or systems used for interfacial-area determinations have no measurable impact on the resultant values produced, and do not prevent consistency among the methods. These results represent an interdependent validation of the different methods. Critically, the fact that the measurements obtained with the AQITT methods match those produced by all of the other methods provides incontrovertible validation of the AQITT methods.

As noted above, some investigators have speculated that differences in air-water interfacial areas produced with AQITT methods versus other methods are due to errors or artifacts associated with the AQITT methods (Costanza-Robinson et al., 2008, 2012; Kibbey and Chen, 2012; Costanza-Robinson and Henry, 2017; Silva et al., 2022). Several potential sources of errors or artifacts have been mentioned, all of which are related in some manner to the presence of the interfacial tracer. The XMT measurements reported above serve as a key benchmark for evaluating the validity of the AQITT methods. The robustness of the XMT method has been validated in prior studies (see Section 1 of the SI).

The XMT method directly images the phases within the sample under conditions of static fluid distributions, and no interfacial tracers are used. Hence, issues associated with the presence of an interfacial tracer are not relevant. Similarly, interfacial-tracer issues are not relevant for the pore-scale modeling and thermodynamic methods. The fact that interfacial areas measured with the AQITT methods perfectly match those obtained with XMT, pore-scale modeling, and thermodynamic methods for the different sets of glass beads clearly shows that the presence of the interfacial tracer does not impact the capability of the AQITT methods to produce accurate measurements of fluid-fluid interfacial areas. This proves that tracer-related factors such as surfactant-induced flow, changes in airwater interface configuration, foam formation, and uncertainties in determining solid-phase or air-water interfacial adsorption coefficients are not relevant for the AQITT methods as employed for the measured data sets used in this study. Significantly, these results demonstrate that if pore-scale configurations of the air-water interface differ between the different measurement systems, any such differences have negligible impact on the measured interfacial areas. Additionally, as noted, the XMT method is based on measurements of interfacial area conducted for static fluid distributions. The measurements therefore are not impacted by interface mobility, mass-transfer limitations, or other issues related to dynamic flow and tracer-transport conditions potentially present for the advective AQITT method. This is similarly true for the pore-scale model simulations. The consistency of the AQITT measurements with those of XMT and the pore-scale modeling shows that issues of interface mobility, tracer mass-transfer limitations, and other flow and transport related factors are either irrelevant or inconsequential for the AQITT method. Hence, water flow and tracer transport can be treated as ideal, mass transfer can be considered an effectively equilibrium process, and interfaces can be assumed immobile under the conditions used for the AQITT applications reported herein. In total, these results demonstrate that the AQITT methods as employed in the studies reported herein produce accurate and representative measurements of air-water interfacial area.

In contrast to the glass beads, the air-water interfacial areas measured by AQITT for the 0.35-mm sand are much greater than the XMT-measured interfacial areas (Fig. 2). The GPITT-measured interfacial areas are even greater. Similar results are observed for Vinton soil (Fig. 1), the 1.2-mm sand (Fig. 3), the 0.75-mm sand (Fig. SI–1), and the 0.17-mm sand (Fig. SI–2, Section 3 of the SI). Notably, the XMT-measured interfacial areas for the sand match the XMT values for the glass beads. As discussed, the XMT method produces interfacial-area measurements that are equivalent to smooth surfaces. The sand and glass beads for each paired set have essentially identical GSSAs, meaning that their equivalent smooth-surface areas are the same. This explains why the XMT-measured interfacial areas for the sand are the same as those measured for the glass beads. Additionally, it is observed that the XMT data for the sands extrapolate at low water saturation to the GSSA, which supports the hypothesis that the XMT method does not measure interfacial area associated with solid-surface roughness as noted in prior works (Brusseau et al., 2006, 2007; Costanza-Robinson et al., 2008). Conversely, the GPITT- and AQITT-measured interfacial areas for the soil and all sands are much greater than the respective GSSAs at lower water saturations.

The interfacial areas determined with the thermodynamic method for the 0.35-mm sand are much smaller than the GPITT and AQITT measured values. Similar results are observed for Vinton soil (Fig. 1) and the other sands (Fig. 3, Fig. SI–1, Fig. SI–2). This difference is also observed for data sets reported by other investigators, as discussed in Sections 3 and 4 of the SI. For example, interfacial areas measured for two sands using variations of the mass-balance AQITT method are observed to be larger than the values determined with the thermodynamic method (Figs. SI–3 and SI–4 in Section 3 of the SI). The results of this and prior studies demonstrate that measured interfacial areas for all GPITT data sets and the great majority of AQITT data sets exceed the respective thermodynamic-determined interfacial areas for sands and soils. Notably, these data sets comprise measurements produced with several different methods and by different investigators.

Whereas the thermodynamic-determined interfacial areas for all of the sands and the soil are much smaller than the GPITT and AQITT values, they match those measured by XMT and simulated by the pore-scale models. In addition, the thermodynamic values for the sands are essentially identical to the thermodynamic values of the glass beads. Furthermore, the thermodynamic-based interfacial areas for the sands and soil extrapolate to the GSSA. These results strongly indicate that the thermodynamic method does not fully capture the contribution of solid-surface roughness to interfacial areas. Rather, the method appears to produce estimates consistent with smooth-surface areas. This would explain the observation that the thermodynamic-determined interfacial areas are much smaller than those measured with AQITT and GPITT for the sands and soil, as both methods characterize to some extent the contributions of solid-surface roughness, whereas the thermodynamic-determined values match the AQITT-measured interfacial areas for the glass beads which have no appreciable roughness.

The data sets presented for Vinton soil, 0.17-mm sand, 0.35-mm sand, and 0.75-mm sand comprise only air-water interfacial areas. Conversely, the data sets presented for the 1.2-mm sand include NAPL-water and air-water interfacial areas. The two sets of interfacial areas are plotted together for each respective method. Inspection of Fig. 3 shows that the two sets of interfacial areas are indistinguishable for each of the methods. It is also observed that the thermodynamic-determined NAPL-water interfacial area, produced from a NAPL-water SWC, is similar to the thermodynamic-determined air-water interfacial area. The comparisons between the AQ-ITT, XMT, and thermodynamic-determined interfacial areas for the NAPL-water systems are consistent with those discussed for the air-water systems.

The AQITT data sets reported for the glass beads were obtained with the advective AQITT and solution-recirculation mass-balance AQITT methods, which were proven to produce accurate measurements of air-water interfacial area. These same validated methods were used for the measurements reported for the sands and Vinton soil. The robustness of the AQITT methods specific to the 0.35-mm sand and Vinton soil training data sets is further demonstrated by several additional factors. First, the aggregated AQITT data for the 0.35-mm sand and Vinton soil each comprise measurements obtained with four different methods (Section 2, SI), which all produced comparable results. Second, the AQITT data reported by a separate research group are consistent with the data from Brusseau and colleagues (Fig. 2).Third, a measured value obtained with the GPITT method is consistent with the AQITT data (Fig. 2). The robustness of the advective AQITT method has also been demonstrated in a prior study in which tracer transport, water flux, and changes in water saturation were accurately predicted with a mathematical model for which all input parameters were determined independently (El Ouni et al., 2021). The robustness of the data is further demonstrated by the successful use of AQITT-measured interfacial areas in several studies characterizing and modelling the retention, distribution, and transport of PFAS, as discussed in Section 5 of the SI.

The glass-beads results demonstrated that the AQITT methods as employed for the reported data sets were not affected by potential method-associated errors or artifacts. The potential impacts of conjectured errors or artifacts can be further investigated specifically for the sands and soil. One possible error source mentioned is surfactant-induced flow. As noted, the aggregated AQITT data comprise measurements obtained with multiple methods, all of which were demonstrated to mitigate issues associated with surfactant-induced flow (Section 1, SI). Another potential concern mentioned is uncertainty in determination of air-water interfacial adsorption coefficients. El Ouni et al. (2021) and Brusseau (2021) showed excellent consistency among four and 10 separate surface-tension data sets, respectively, used to determine the air-water interfacial adsorption coefficients for interfacial tracers. In addition, air-water interfacial adsorption coefficients determined from surface-tension data were shown to match those measured by neutron reflectometry (Brusseau,2021), which is an advanced high-resolution direct-measurement method. The impact of tracer mass-transfer limitations is another potential concern mentioned specifically for the advective AQ-ITT method. The air-water interfacial adsorption coefficients measured with AQITT were demonstrated to also match those determined by neutron reflectometry, which measures equilibrium values (Brusseau, 2021). Additionally, the interfacial areas measured with the advective AQITT method are consistent with those measured with the mass-balance AQITT method, which represent equilibrium conditions. A detailed analysis of rate-limited air-water interfacial adsorption was conducted by Brusseau (2020), who showed that equilibrium conditions effectively prevail under the conditions of the AQITT. This is supported by the fact that the studies discussed in the SI (Section 5) that quantified and modeled PFAS retention and transport all employed the local equilibrium assumption for air-water interfacial adsorption.

The only differences between the sands and glass beads for the paired-media comparisons are that the sands may sorb the interfacial tracer whereas measurements show negligible tracer sorption for the glass beads, and that the sands have significant solid-surface roughness and the glass beads donot. Uncertainty in measurements of solid-phase sorption coefficients for the interfacial tracer is a potential error source mentioned. Brusseau and Taghap (2020) reported the results of 12 separate sorption measurements for SDBS by the sand, the primary tracer used in the AQITT methods. The sorption coefficient was quite small (0.04 cm³/g), with a coefficient of variation of 10 %. In addition, the sands used by the separate research group (Lyu et al., 2020; Li et al., 2021) were pre-treated to minimize solid-phase sorption. This was also done by Schaefer et al. (2000) for their AQITT measurements. These results demonstrate that uncertainty in measuring solid-phase sorption of the tracer is not a source of error for these AQITT measurements.

One could hypothesize that the impacts of potential method-specific differences in interface configuration, which was demonstrated to be insignificant for the glass beads, may be greater for the sands and soil because of the roughness. This issue can be illuminated by examining air-water interfacial area data measured by the GPITT method. As discussed in Section 1.3 of the SI, the GPITT method has been benchmarked by comparisons to the NBSSA. Several theoretical and experiment-based studies have demonstrated that the topography of the air-water interface duplicates that of the solid surface when wetting films are very thin (high capillary pressures and low water saturations). In such cases, the magnitude of air water interfacial area will be similar to that of the solid surface area. All reported GPITT data sets are observed to extrapolate to the respective NBSSAs, which confirms that the method produces accurate measurements of air-water interfacial area. This indicates that the presence of the interfacial tracer has no discernable influence on measured interfacial areas, and hencehas negligible apparent impact on interface configuration. The insensitivity of measured air-water interfacial areas to potential differences in interface configuration is demonstrated by the results of Peng and Brusseau (2005) who reported that GPITT-measured interfacial areas for a sand were similar under conditions of primary imbibition and pre-mixing water with the medium (Fig. SI–2). This suggests that either the two methods produced similar interface configurations or that the measurements are insensitive to any differences produced. Similar results were reported for AQITT-measured interfacial areas wherein values were similar for drainage and imbibition conditions (Brusseau et al., 2007, 2015; El Ouni et al., 2021). These results are supported by measurements of water-film thicknesses on rough surfaces that showed no differences between drainage and imbibition conditions, indicating minimal change in wetting-film configuration (Tokunaga et al., 2003; Kim et al., 2012). They are also supported by pore-scale modeling investigations that showed no difference in simulated total interfacial areas between drainage and imbibition (Reeves, 1997; Chan and Govindaraju, 2011), and by XMT measurements that have shown no difference in interfacial areas for sands or Vinton soil wherein water was pre-mixed versus drainage conditions (Brusseau et al., 2006; Costanza-Robinson et al., 2008) and no measurable impact of interfacial-tracer presence on interface configuration or magnitude (Brusseau et al., 2007).

The results presented in the preceding paragraphs, in combination with the results for the glass beads, validate the efficacy of the AQITT methods to produce accurate and representative interfacial areas. Consequently, the disparities between interfacial areas measured by AQITT and those determined by XMT and thermodynamic methods for the data sets presented herein cannot logically be ascribed to uncertainties or errors in the AQITT methods. This in turn provides compelling support to the hypothesis that the disparities are due to the contributions of solid-surface roughness to fluid-fluid interfacial areas. The degree to which the different measurement methods characterize the contribution of roughness to interfacial area is investigated in the following section.

3.2. Contributions of interface domains to total interfacial area

This and prior studies have demonstrated that different methods can in some cases produce different magnitudes of air-water interfacial area for the same porous medium. The results in the preceding section indicate that this is caused primarily by the differential contributions of solid-surface roughness to the interfacial areas characterized by the different methods. This phenomenon is demonstrated by comparing measured ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ data sets reported for Vinton soil to the theoretical absolute-maximum interfacial area present in the system(Fig. 1).The absolute-maximum interfacial area (${\text{A}}_{\text{Max}}$) is determined from application of the pore-scale model developed by Jiang et al. (2020a), which was developed to explicitly account for the contributions of solid-surface roughness. The absolute-maximum interfacial area represents the total theoretically-possible interfacial area present for a given wetting-fluid saturation based on the assumption that the wetting films remain sufficiently thin such that the contribution of solid-surface roughness to film-associated interface remains at its maximum (i.e., there is no wetting-film masking). The ${\text{A}}_{\text{Max}}$ for a specific wetting-fluid saturation is equivalent to the solid surface area that is available at that saturation.

Inspection of Fig. 1 shows that all of the measured air-water interfacial areas are much smaller than the absolute-maximum air-water interfacial area. The measurements obtained with GPITT produce the largest measured interfacial areas as discussed previously. These areas in most cases will likely represent the maximum effective interfacial area potentially available to interfacially active solutes. These areas represent on average approximately 9 % of the absolute-maximum area across the 0.5 to 0.2 range of water saturation. The primary reason that the measured interfacial areas represent such small proportions of the absolute-maximum interfacial area is the impact of masking, where in wetting film sare sufficiently thick to reduce the contribution of solid-surface roughness (Philip, 1978; Sweeney et al., 1993; Costanza-Robinson and Brusseau, 2002; Kibbey, 2013; Jiang et al., 2020a). The specific percentage increases significantly at the lowest water saturations (<0.2), approaching for example ~50 % at a water saturation of 0.05. Based on the model simulations, this occurs because the great majority of pores are drained at this point and because the water films have decreased in thickness such that the degree of masking has decreased significantly. The interfacial areas measured with the AQITT methods represent an even smaller fraction of the absolute-maximum interfacial area, comprising only ~3.4 % on average over the measured range of saturation and increasing from 2.6 % to 3.9 % as water saturation decreases. Notably, the interfacial areas measured with XMT are approximately 0.5 % of the absolute-maximum area.

The primary reason for the great disparity in measured values obtained between the tracer and XMT methods in comparison to the absolute-maximum interfacial area is the differential contributions of solid-surface roughness. The relative contribution of roughness-associated interfacial area to the total air-water interfacial area measured by each of the methods can be assessed by comparing the interfacial areas measured by GPITT and AQITT to those measured by XMT. It is important to recall for this comparison that the XMT-measured interfacial areas include the contribution of both capillary and film-associated interfacial areas, but not the contribution of solid-surface roughness. Hence, the XMT totals represent smooth-surface equivalent interfacial areas. The XMT interfacial areas are approximately 10 to 30 % of the AQITT interfacial areas for Vinton soil. Hence, film-associated interfacial area contributed by solid-surface roughness is determined by difference to comprise approximately 70 to 90 % of the total interfacial area measured by the AQITT methods. Similarly, the contribution of roughness-associated interfacial area to the interfacial areas measured by the GPITT method is approximately 90% or greater, given that the XMT measurements are ~10% or less of the GPITT measurements. Interestingly, the difference between the tracer-and XMT-measured areas increases as water saturation decreases. This indicates that the contribution of roughness is greater at lower water saturations, which is consistent with the model-based results of Jiang et al. (2020a, 2020b).

The preceding results highlight the fact that the contribution of solid-surface roughness to film-associated interfacial area comprisesa significant portion of the total effective air-water interfacial area accessible to interfacially active solutes. However, it is critical to note that the magnitudes of interfacial area contributed by solid-surface roughness as measured by the AQITT methods in particular represent just a very small fraction of the total roughness-associated area that is present in the soil. This result is consistent with the hypothesis of Costanza-Robinson and Brusseau (2002) that the interfacial area measured by AQITT comprises a small fraction of the total potential film-associated area. To our knowledge, the present study represents the first demonstration of this functional interrelationship between interfacial areas obtained with different measurement methods and the absolute-maximum potential interfacial area. These results have significant implications for characterizing PFAS retention, given that the AQITT methods were demonstrated to produce the most representative interfacial areas for the air-water interfacial adsorption of PFAS (Section 5 of the SI). The following analyses will therefore focus on comparisons of the AQITT results to theoretical and experiment-based pore-scale investigations.

The observations that the interfacial areas measured with AQITT are significantly greater than XMT-measured interfacial areas as well as the respective GSSAs indicate that the air-water interfaces as characterized by the interfacial tracer are rough rather than smooth. The AQITT-related maximum air-water interfacial area ${\text{A}}_{\text{aw}}^{\text{Max}}$ can be compared to the GSSA to define a roughness index as${\text{R}}_{\text{smooth}}^{AWI}={\text{A}}_{\text{aw}}^{\text{Max}}/\text{GSSA}$, which represents the comparative roughness of the tracer-characterized interface versus the equivalent smooth surface. The values range between 2.4 and 5.8 for the three sands of similar diameter (Figs. 2, SI–3, and SI–4) and is 8.3 for Vinton soil, consistent with the greater solid-surface roughness of Vinton. However, the fact that the AQITT-measured interfacial areas represent small proportions of the absolute-maximum interfacial area indicates that the tracer-characterized air-water interfaces are considerably smoother than the underlying solid surfaces. Comparison of ${\text{A}}_{\text{aw}}^{\text{Max}}$ to the NBSSA provides a means to evaluate the effective roughness of the air-water interface, as characterized by the interfacial tracer, relative to the solid-surface roughness. The smooth-surface interfacial and surface areas (i.e., GSSA) are subtracted from the ${\text{A}}_{\text{aw}}^{\text{Max}}$ and NBSSA, respectively, to scale the comparisons specifically to the roughness-associated solid-surface area. The ratio of these two differences produces what can be considered an index of the relative roughness of the air-water interface in comparison to the actual solid surface:${\text{R}}_{\text{rough}}^{AWI}=\left({\text{A}}_{\text{aw}}^{\text{Max}}-\text{GSSA}\right)/(\text{NBSSA}-\text{GSSA})$. The ${\text{R}}_{\text{rough}}^{AWI}$ is ~0.03 for Vinton and ranges from 0.14 to 0.22 for the three sands. The small values confirm that the air-water interfaces are much smoother than the solid surfaces. The observed increases in the contribution of roughness to air-water interfacial area for lower water saturations suggest that the roughness of the interface increases at lower saturations. The Vinton soil has a much greater magnitude of solid-surface roughness compared to the sands, with an NBSSA that is >10-times greater. The smaller proportional contribution of roughness for Vinton in conjunction with its much greater magnitude of roughness suggests that relative film thickness is in general greater for Vinton.

The results presented above can be compared to the seminal work of Philip (1978), who presented an initial quantitative analysis of the configuration of wetting fluid on rough surfaces and the impacts on film thickness and the fluid-fluid interface. The analysis considered both adsorption and capillary contributions to wetting and included an illustrative example for a water-solid system. The results showed that the air-water interface is rough for a rough solid surface, and that the interface roughness is a function of film thickness. The air-water interface mimics the rough solid surface for very thin films, and becomes smoother as film thickness increases. It was also shown that film thicknesses were greater for rougher surfaces. Sweeney et al. (1993) also conducted a theoretical analysis of wetting-fluid configuration on rough solid surfaces and the impact on film thickness and the fluid-fluid interface. They similarly showed that the fluid-fluid interface transitions from smoother to rougher as capillary pressure increases, and that the surface of the interface is similar to that of the rough solid surface at high pressures. The results of another theoretical analysis similarly showed that the roughness of the air-water interface is similar to that of the solid surface for thin films (Bazrafshan et al., 2018). Investigations employing direct measurements of wetting films on rough surfaces conclusively demonstrate that fluid-fluid interfaces are rough, and that the interface is similar to that of the solid surface for thin films (Zhao and Cerro, 1992; Sun et al., 2021). Additionally, studies reporting direct measurements of film thicknesses have shown that films are thicker for rough versus smooth surfaces and that the films thin as capillary pressure is increased (Tokunaga et al., 2000, 2003; Kim et al., 2012, 2013). The results presented herein indicating that tracer-characterized air-water interfaces are rough, that they are smoother than the solid surfaces, that the interface roughness increases at lower saturations, and that film thickness is greater for the medium with greater roughness are consistent with the results of all of these prior studies.

The present results can additionally be compared to the study by Kibbey (2013), who also conducted a theoretical analysis of water configuration on rough surfaces and impacts to film thickness and the air-water interface. The results demonstrated that the air-water interfaces exhibited roughness even at very low capillary pressures. The fact that the air-water interfaces exhibited roughness was reflected in the observation that the calculated air-water interfacial areas were greater than the smooth-surface solid-surface area for all capillary pressures examined. Additionally, the roughness of the air-water interface was shown to increase at greater capillary pressures as the films thinned. Consequently, the difference between the air-water interfacial area and the smooth-surface solid-surface area also increased. These outcomes clearly illustrate that solid-surface roughness causes air-water interfaces to be rough, and that this results in air-water interfacial areas exceeding those equivalent to smooth surfaces. This is consistent with the results presented in the studies discussed in the preceding paragraph.

Analysis of the configurations and thicknesses of the water films indicated that only a small proportion of the actual solid-surface roughness was manifest in the air-water interfacial areas (Kibbey, 2013). In other words, the air-water interfaces were smoother than the underlying solid surfaces. This is also consistent with the results presented in the studies discussed in the preceding paragraph. A ${\text{R}}_{\text{rough}}^{AWI}$ can be calculated for the illustrative example provided for a sand (Table 1 and Fig. 8, Kibbey, 2013), which is ~0.28 for the highest capillary pressure. Hence, the air-water interface is approximately one quarter as rough as the solid surface at that pressure. The muted impact of roughness was attributed to the relative thicknesses of the water layers. For example, it was estimated that at the highest capillary pressure only 5 % of the surface-associated water would be considered adsorbed water for the sand (Kibbey, 2013).

Table 1.

Comparison of estimated air-water interfacial areas to measured values.

Method	0.75–0.85 sand	0.35–0.45 sand
	${\text{A}}_{\text{aw}}\left({\text{cm}}^{-1}\right)$	${\text{A}}_{\text{aw}}\left({\text{cm}}^{-1}\right)$
Measured (Lyu et al., 2020)	161	272
GSSA-based linear	26	50
AQITT-based linear	45	102
Thermodynamic	24	45
AQITT-based nonlinear	191	203
Corrected AQITT-based linear	104	237
Scaled thermodynamic	125	233

Recall from above that only a very small fraction (~3.5 %) of the total solid-surface roughness contributed to the air-water interfacial areas measured by the AQITT methods for Vinton soil. Additionally, ${\text{R}}_{\text{rough}}^{AWI}$values ranging between 0.14 and 0.22 were calculated for the sands. These relatively small proportional contributions of solid surface roughness are in complete agreement with the Kibbey results. Additionally, the results herein indicated that the tracer-characterized air-water interfaces were significantly smoother than the solid surfaces and that the contribution of solid-surface roughness to air-water interfacial area increased at lower water saturations. These observations are also fully consistent with the Kibbey results.

While the two sets of results are congruent, the conclusions reached differ significantly. Kibbey concluded that the relatively small proportional contributions of roughness to air-water interfacial area are of inconsequential importance, and therefore proposed that air-water interfacial area is reasonably well represented by the smooth-surface solid surface area. However, the GPITT- and AQITT-measured interfacial areas reported in the present study for the soil and sands, which have been independently validated, greatly exceed the respective GSSAs. Additionally, the smooth-surface assumption will be demonstrated in Section 3.4 to produce inaccurate air-water interfacial areas that fail to reproduce multiple measured PFAS retention and transport data sets. Conversely, the results presented herein demonstrate that the relatively small proportional contributions of solid-surface roughness provide a very significant impact to measured air-water interfacial areas. Methods to characterize solid-surface roughness in relation to fluid-fluid interfacial areas, the relationship between roughness and medium properties, and methods to quantify its impact were discussed in detail in Jiang et al. (2020b).

3.3. Estimating air-water interfacial areas

To be robust, the estimation method should be based on measurement or prediction methods that produce representative interfacial areas for the relevant application. The results presented in Section 5 of the SI indicate that the AQITT methods provide the most representative air-water interfacial areas for air-water interfacial adsorption of PFAS in unsaturated porous media, consistent with the conclusion of Brusseauand Guo (2021). This is a logical outcome given that these methods produce measurements of an effective total air-water interfacial area that is accessible to the interfacial tracer, which is typically a surfactant or other interfacially active solute. Hence, the measurements of air-water interfacial area are conducted under conditions similar to those relevant for PFAS transport in unsaturated media.

Another important criterion for robust estimation methods is that they produce representative interfacial areas for the full range of water saturation. It has been widely demonstrated that water saturation is a critical factor mediating the magnitude of air-water interfacial area present in a given porous medium. The relationship between air-water interfacial area and water saturation has been represented with both linear and nonlinear functions, depending in part upon which measurement method was employed as well as which media were used for the measurements. A comprehensive discussion of this issue is presented in Section 6 of the SI, the results of which support the conclusion that the ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ relationship is inherently nonlinear. The degree of nonlinearity that will be manifest in measurements for a given porous medium will depend upon properties of the medium (e.g., pore-size distribution, solid surface area magnitude and structure) and the measurement method employed (e.g., the degree to which the method characterizes roughness contributions), as demonstrated and discussed in detail in Jiang et al. (2020a). Any relevant estimation method needs to reflect the nonlinear nature of the ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ relationship to produce reasonable and representative interfacial areas.

Several methods have been used to estimate air-water interfacial areas (see Section 1.7 in the SI). Three primary ones are presented in Eqs. (1)–(3). As discussed in the SI, none of the three existing methods are anticipated to be adequate for producing estimates representative of the air-water interfaces relevant for air-water interfacial adsorption of PFAS and other interfacially active solutes. This will be further demonstrated in the following section. In addition, the empirical correlation reported by Peng and Brusseau (2005) based on measured GPITT data should not be used because interfacial areas measured with the method greatly exceed those measured by AQITT methods at lower water saturations. Therefore, new estimation methods are needed. Three new estimation methods are developed here in based on the outcomes of the preceding investigations. Measured data sets reported by Brusseau and colleagues for Vinton soil, 0.35-mmsand, and 1.2-mm sand are used astraining data to develop the new estimation methods. These data sets have been validated in multiple ways as discussed above.

The first method is termed the AQITT-based nonlinear method. A three-step procedure was employed in the development. First, a nonlinear polynomial function was fit to each individual ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ data set to obtain an effective maximum air-water interfacial area (${\text{A}}_{\text{aw}}^{\text{Max}}$). The three sets of training ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ were then plotted with their measured interfacial areas normalized by their respective maximum interfacial areas to establish a master ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ function. Finally, the normalized literature data sets were plotted with the training data to test the generality of the master function.

Inspection of the resultant plot reveals that a single nonlinear function provides a reasonably good representation of all the measured data sets, recognizing that significant data scatter exists for some of the data sets (Fig. SI–5 in Section 7 of the SI). It is important to emphasize that only the three training data sets were used to establish the master function. The ability of this function to represent the literature test data reasonably well indicates that the master function is relatively robust. Hence, this function serves as a means to determine an estimated normalized air-water interfacial area for a given porous medium as a function of water saturation. Knowledge of the ${\text{A}}_{\text{aw}}^{\text{Max}}$ is required to employ this method to determine specific interfacial areas. A correlation to the NBET specific solid surface area was determined, based on all data sets for which NBSSAs were available, as: A^Max_aw = 761 × logNBSSA – 2025; r² = 0.986, where A^Max_aw and NBSSA both have units of cm⁻¹. Combining this with the equation presented in Fig. SI–5 produces the combined function to estimate air-water interfacial area:

$$\begin{gathered} {\text{A}}_{\text{aw}(\text{Sw})}=\left[0.83{\left(1-{\text{S}}_{\text{w}}\right)}^2+0.16\left(1-{\text{S}}_{\text{w}}\right)\right] \\ \times [761\times \log \text{NBSSA}-2025] \end{gathered}$$ (4)

It should be noted that the great majority of measured data sets used to establish the estimation method comprise relatively ideal media. Additional measurements need to be conducted using soils comprising a range of physical and geochemical properties to further develop the method.

This new estimation method requires measured NBET solid surface areas, which is a standard measurement available at select commercial laboratories. Hence, it is anticipated that this approach can be readily applied in many cases. There may be instances however where such data are not available. A second empirical estimation method is developed as an alternative for such cases. The estimation method presented by Lyu et al. (2018) has an advantage in that the required correlation input parameter, median grain diameter, is a simple and commonly reported measure. However, the method does not represent the nonlinear nature of the ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ relationship. This estimation method can be revised to address this limitation by developing a correction factor. This revised method is termed the corrected AQITT-based linear method.

The air-water interfacial-area ratios of the nonlinear-function values (polynomial fits) and the linear-based estimates are plotted in Fig. SI–6 (Section 7 of the SI) for the three training data sets. The ratios are observed to be linear inverse functions of water saturation. Additionally, the values for the three media are comparatively similar. The mean of the three functions is selected for use as a representative correction factor to translate air-water interfacial areas estimated with the linear estimation method to equivalent nonlinear-based values. The combined function to estimate air-water interfacial area is given by:

$$\begin{gathered} {\text{A}}_{\text{aw}(\text{Sw})}=\left[-2.85\times {\text{S}}_{\text{w}}+3.6\right] \\ \times \left[\left(1-{\text{S}}_{\text{w}}\right)\times 3.9\times {\text{d}}_{50}^{-1.2}\right] \end{gathered}$$ (5)

This estimation approach can be used for cases wherein soil texture and grain-size distribution data are the only relevant soil-property information available.

The two new empirical estimation methods as well as the existing estimation methods represented by Eqs. (1) and (2) all involve determining a maximum air-water interfacial area for the selected porous medium, and then applying a linear or nonlinear ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ function to estimate an ${\text{A}}_{\text{aw}}$ for a specific water saturation. Costanza-Robinson and Brusseau (2002) introduced the concept of using solid surface areas to scale measured air-water interfacial areas, and investigated the use of GSSA and NBET solid-surface areas for the scaling. The estimation methods presented by Costanza-Robinson et al. (2008) and Wallis et al., 2022 use the GSSA, whereas the first new method presented above uses the NBSSA. This latter approach is consistent with prior work that developed correlations for estimating air-water or NAPL-water interfacial areas based on the NBSSA to account for the contributions of solid-surface roughness (Peng and Brusseau, 2005; Brusseau et al., 2010). Of the two specific solid surface areas typically used as reference, it is likely that the NBET-measured area will be more relevant for the air-water interfacial adsorption of PFAS and other interfacially active solutes given the significant contributions provided by solid-surface roughness demonstrated in Section 3.2. Therefore, it is anticipated that the new empirical estimation methods, which account directly or indirectly for roughness contributions, will produce more representative estimates in comparis on to methods based on scaling to the GSSA. This will be evaluated in Section 3.4.

The thermodynamic method is a convenient approach that has been used as an alternative to determine air-water interfacial areas in lieu of direct measurement (SI, Section 1.5). However, the results presented in this and prior studies clearly demonstrate that this method does not produce representative air-water interfacial areas for characterizing air-water interfacial adsorption ofPFAS. While thermodynamic-determined values should not be used directly, they may be used with the application of a scaling procedure. Guo and Brusseau introduced the concept of scaling thermodynamic-determined air-water interfacial areas to values that would be representative for the retention and transport of PFAS (Zeng etal., 2021; Guo etal., 2022).This was accomplished by developing a functional relationship between air-water interfacial areas determined with the thermodynamic method and values measured for the same porous medium with the AQITT method (Zeng et al., 2021). The scaling function can then be applied to thermodynamic values produced for other media for which measured SWC data are available. This approach can also be used with SWC data obtained from means other than measurement. Guo et al. (2022) developed scaled thermodynamic estimates of air-water interfacial area for several soils, with the SWC parameters obtained from the Rosetta pedotransfer model (Zhang and Schaap, 2017). Hence, this approach can be used even in the absence of measured SWC data. In this case, surrogate soil properties such as those representing texture can be characterized for the soil, and the resultant measurements used to obtainestimates of soil hydraulic parameters that are then employed to produce air-water interfacial areas with the thermodynamic method. The scaling procedure is then applied to these values to produce interfacial areas representative for air-water interfacial adsorption. Silva et al. (2022) presented an estimation method employing the same approach as Zeng et al. (2021) that scaled thermodynamic-determined interfacial areas to AQITT-measured values, using the measured ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ data sets of Brusseau and colleagues for the Vinton soil (Fig. 1) and 0.35-sand (Fig. 2). However, they incorrectly excluded portions of the measured data sets, which resulted in significantly smaller scaling factors compared to those of Zeng et al. and those reported below (see Section 1.7 of the SI). Silva et al. did not test their estimation method against independent data sets, but the smaller scaling factors they obtained may likely lead to underestimates of representative air-water interfacial areas.

The approach developed by Guo and Brusseau is expanded up on herein, which constitutes the third new estimation method. AQITT-measured and thermodynamic-determined air-water interfacial areas are compared for the three training media (Vinton soil, 0.35-mm sand, and 1.2-mm sand). Note that the mean of 5 separate SWC measurements, spanning a range of porosities and bulk densities, was used for the Vinton soil to account for the inherent variability of soils. The ratios of the two sets of interfacial areas for each of the three media are presented in Fig. SI–7 Top (Section 7 of the SI). It is observed that the ratios vary over a relatively narrow range as a function of water saturation, as was reported previously (Zeng etal., 2021).In addition, the ratios for all three media are relatively similar. The specific profiles differ somewhat among the three, likely due at least in part to their respective grain/pore-size distributions. These ratios can be used as scaling factors (SF) for translating thermodynamic-determined values to interfacial areas consistent with those measured by the AQITT methods.

Mean ratios determined for the data sets are 4.5 (4 %), 4.8 (6 %), and 4.9(3%) for the 1.2-mms and, 0.35-mms and, and Vinton soil, respectively, across a water-saturation range of 0.2–0.8. The values in parentheses are the coefficients of variation for the 95 % confidence intervals. The selected water-saturation range is used to eliminate some of the extreme changes in the ratio, and represents a typical range of saturations encountered in the field. Given the similarity in mean ratios, the simplest approach for applying this scaling-factor estimation would be to use a standard fixed value for all soils and saturations (Zeng et al., 2021). Alternatively, the moderate impact of grain size can be accounted for to determine a medium-specific scaling factor. The mean ratios are a function of the median grain diameter, with a correlation equation of ${\text{SF}}_{\text{mean}}=-0.45\times {\text{d}}_{50}+5$,${\text{r}}^2=0.989$.

The preceding equation produces scaling factors averaged across the entire range of water saturation. An additional function can be applied to account for the water-saturation dependency observed in Fig. SI–7 Top. The ratios of AQITT-measured and thermodynamic-determined air-water interfacial areas normalized by the respective mean ratios are plotted in Fig. SI–7 Bottom (Section 7 of the SI). Also presented is the mean of the three sets of normalized ratios. It is observed that the mean can be approximated reasonably well with a linear function. This function can be combined with the prior scaling-factor equation to produce the following:

$${\text{SF}}_{(\text{Sw})}=\left[-0.65{\text{S}}_{\text{w}}+1.33\right]\times \left[-0.45{\text{d}}_{50}+5\right]$$ (6)

This equation can be used to calculate a scaling factor for a given porous medium and specific water saturation. It is critical to note that this correlation is based on only three datasets. Therefore, there is inherent uncertainty in its applicability beyond sands and sandy soils. Additional characterization is needed with a range of soils to further test the correlation.

3.4. Comparison and testing of estimation methods

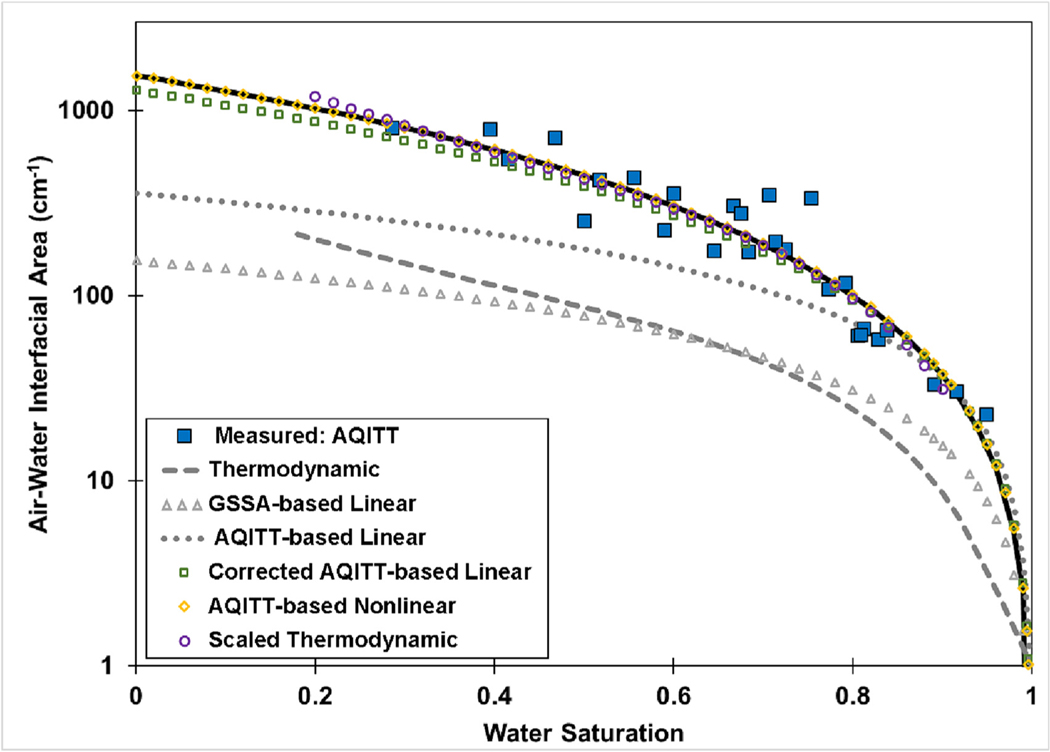
The significant differences in estimated interfacial areas produced with the new versus the existing methods are illustrated for Vinton soil in Fig. 4. The interfacial areas estimated with the GSSA-based linear approach (Eq. (1)), wherein the maximum possible interfacial area is equal to the GSSA, are significantly smaller than the measured values. The GSSA-based interfacial areas approach a factor of 10 smaller for low saturations. The non-representativeness of the AQITT-based linear method (Eq. (2)) for moderate and lower water saturations is clearly illustrated, wherein the estimated interfacial areas begin to deviate from the measured areas at water saturations of approximately 0.88. As the water saturation decreases below this range, the deviation increases greatly, with the estimated interfacial areas several factors smaller than the measured at the lowest saturations. Similar results are observed for the 0.35-mms and, with deviations beginning at ~0.7 water saturation (data not shown). The specific water saturation below which significant deviations begin may vary somewhat based on soil properties. The inadequacy of the thermodynamic approach (Eq. (3)) is also illustrated in Fig. 4, wherein the interfacial areas are several times smaller than the measured values as noted previously. In contrast to the existing methods, the interfacial areas produced with the three new estimation methods (AQITT-based nonlinear, corrected AQITT-based linear, and scaled thermodynamic) all reproduce the measured data very well.

Fig. 4.

Comparison of air-water interfacial areas estimated with existing and new methods to measured data for Vinton soil.

The effectiveness of the different existing and new estimation methods for producing representative air-water interfacial areas is evaluated by testing with four independent PFAS retention and transport data sets. The first test uses data for PFOA transport in unsaturated commercial sand (Unimin Corp.) reported by a separate research group (Lyu et al., 2020). They determined retardation factors from the breakthrough curves measured for PFOA transport in two sands with different median diameters. They then determined air-water interfacial areas from the measured retardation factors, with measured values known for all other parameters. The SWC and NBET data (Schroth et al., 1996; Peng and Brusseau, 2005; Brusseau and Guo, 2021) used to parameterize the estimation methods comprise measurements conducted for sands of similar size obtained from the same source (Unimin Corp).

The measured interfacial areas are presented in Table 1, along with interfacial areas estimated with the different methods. The estimated interfacial areas obtained with the GSSA-based linear and standard-thermodynamic methods are approximately 6 times smaller than the measured areas, while those estimated with the AQITT-based linear method are roughly 3 times smaller. Conversely, the estimated interfacial areas obtained with the three new methods are all significantly closer to the measured values. While the measured data set comprises only two values and measurement uncertainty needs to be kept in mind, these results further illustrate the large differences in estimated values obtained with the new versus existing methods, and that the former are clearly more representative of the measured data.

The second test employs data reported by Li et al. (2021) for PFOA transport in the same sand as used in the Lyu et al. (2020) study discussed above. A representative measured breakthrough curve is presented in Fig. 5, along with simulated breakthrough curves obtained using interfacial areas determined from the different estimation methods. It is clear that the measured retardation is greatly underpredicted when using interfacial areas produced with the three existing estimation methods, indicating that the respective estimated interfacial areas are too small. Conversely, the simulations produced using interfacial areas from the three new methods produce much better matches to the measured data, particularly the corrected AQITT linear and scaled-thermodynamic methods. This congruency indicates that these methods produced estimated air-water interfacial areas that are representative of the measured PFOA air-water interfacial adsorption.

Fig. 5.

Measured and simulated transport of PFOA in unsaturated sand (${\text{S}}_{\text{w}}=\text{0.64}$; input concentration = ~7 μg/L; 30 mM CaCl₂ solution). Measured data from Li et al., 2021. Simulations produced with the model of Brusseau (2020). All input parameters are constant except for the air-water interfacial area, which is estimated using the methods discussed in the main text. The estimated values range from 24 to119 cm⁻¹. Values for the equilibrium sorption coefficient, air-water interfacial adsorption coefficient, bulk density, and porosity are reported in the source paper.

The third test employs measured PFAS porewater-concentration data reported by Schaefer et al. (2022), who conducted a pilot field study at a site impacted by aqueous film-forming foam to investigate PFAS distribution in the vadose zone (see Section 5 of the SI for details). They compared predicted and measured porewater concentrations for PFOA, PFOS, and perfluoroheptanesulfonate (PFHpS), with the latter two reported to be significantly impacted by air-water interfacial adsorption. The measured data for those two are presented in Table 2 along with estimated concentrations obtained using air-water interfacial areas from the different estimation methods presented herein. No SWC data were reported for the site media. Therefore, data measured for the 0.35-mm sand are used as a surrogate. This is anticipated to be a reasonable proxy given the similar grain diameters and the fact that the site medium comprises 90–92 % sand. The porewater concentrations were calculated using the comprehensive-distribution model developed for PFAS (Brusseau and Guo, 2022). The sources of the required input parameters are noted in Table 2.

Table 2.

Comparison of estimated PFAS porewater concentrations obtained with different air-water interfacial areas to measured values.

Method	Porewater concentration (ng/L)
	PFOS	PFHPS
Measured (Schaefer et al., 2022)	10,000	410
GSSA-based linear	28,280	1000
AQITT-based linear	20,940	860
Thermodynamic	29,930	1025
Corrected AQITT-based linear	11,690	597
Scaled thermodynamic	12,480	620

Parameter sources: mean grain diameter (Schaefer et al., 2022); mean water saturation (Schaefer et al., 2022, Fig. 2); equilibrium sorption coefficients, ${\text{K}}_{\text{d}}$(Schaefer et al., 2022); air-water interfacial adsorption coefficients (Brusseau and Van Glubt, 2021); SWC (Brusseau and Guo, 2021).

The estimated porewater concentrations obtained with the GSSA-based linear correlation and the standard-thermodynamic method are approximately 28,000 and 30,000 ng/L respectively, which are roughly three times larger than the measured porewater concentration of 10,000 ng/L. The similarity of the two estimates supports the use of the surrogate SWC data for the thermodynamic determination, given that GSSA-based and thermodynamic-based results were shown to be very similar in the prior assessments (Figs. 4, 5 and Table 1). The AQITT-based linear method produces an estimate of ~21,000, approximately double that of the measured concentration. Similar results are observed for PFHpS, wherein the estimated porewater concentrations obtained with the three existing methods are 2–2.5 times larger than the measured concentration. These results demonstrate that the air-water interfacial areas obtained with the existing estimation methods are too small to adequately quantify the magnitude of air-water interfacial adsorption that is mediating the measured porewater concentrations. Conversely, the estimated porewater concentrations obtained with the corrected AQITT-based method and the scaled thermodynamic method are much closer to the measured values for both PFOS and PFHpS. While this analysis does not directly account for uncertainty in the measured or predicted porewater concentrations, their potential impacts are mitigated by the use of the same set of values for all input parameters except for the ${\text{A}}_{\text{aw}}$ estimates. These results again illustrate the significant differences in interfacial areas estimated with the existing and new methods, and provide support for the robustness of the new methods for estimating air-water interfacial areas that are representative for quantifying the air-water interfacial adsorption of PFAS.

The fourth test employs measured PFAS porewater and soil concentrations obtained from an outdoor lysimeter experiment. The raw data reported in Felizeter et al. (2021) were analyzed by Brusseau and Guo (2022) using the newly developed PFAS mass-distribution model to compare predicted versus measured soil-to-porewater concentration ratios. Comparisons of predicted concentration ratios obtained using interfacial areas estimated with two estimation methods, one existing and one new, are compared to the measured data in Table 3 for the most surface-active PFAS. SWC data are not available to use the thermodynamic-based methods. It is observed that the predicted ratios produced with corrected AQITT-based method are closer to the measured data compared to the GSSA-based linear method. This is consistent with the prior tests.

Table 3.

Comparison of estimated PFAS soil-porewater concentration ratios obtained with different air-water interfacial areas to measured values.

Method	PFOS	PFNA	PFDA	PFUnDA	PFTDA
Measured (Brusseau and Guo, 2022)	28.9	7.9	37.5	128	233
GSSA-based linear	10	3.8	13.8	41	175
Corrected AQITT-based linear	27.2	8.7	37.8	94	259

PFOS = perfluoroctane sulfonic acid; PFNA = Perfluorononanoic acid; PFDA = Perfluorodecanoicacid; PFUnDA=perfluoroundecanoic acid; perfluorotridecanoic acid (PFTDA). Details on parameters used for the calculations are presented in Brusseau and Guo (2022).

The preceding analyses support the conclusion that the three existing estimation methods tested are inadequate for producing estimated air-water interfacial areas that are relevant for air-water interfacial adsorption of PFAS. Conversely, the results of the testing demonstrate that the new estimation methods are capable of producing representative interfacial areas that adequately quantify the adsorption of PFAS at the air-water interface and the resultant impact on PFAS retention and transport in unsaturated porous media. This difference in efficacy is due to two primary factors. One is that the new methods in some manner account for the contribution of solid-surface roughness to interfacial area, which was demonstrated in Section 3.2 to be greatly significant. This is accomplished either directly by determining maximum interfacial areas from correlation to the NBSSA, or indirectly by scaling interfacial areas to be consistent with AQITT-measured values, which implicitly account for roughness. The other major factor is that the new methods account in some manner for the nonlinear relationship between air-water interfacial area and water saturation.

The results presented in this section have critical implications for characterizing and quantifying the air-water interfacial adsorption of PFAS and other interfacially active solutes, and the concomitant impacts to retention and transport. This is illustrated by the results presented in Brusseau and Guo (2021), who conducted mathematical modeling to investigate the impact of estimated versus measured air-water interfacial areas on simulated PFOA leaching in the vadose zone for a representative fire-training scenario. The predicted travel times for PFOA migration to groundwater varied from 3 to 20 years depending on the respective air-water interfacial area used in the simulation (all other parameters were constant). The predicted travel time was 6 years for the simulation that used an interfacial area obtained from XMT data, which is equivalent to the GSSA-based linear estimation method. The predicted travel time was also 6 years for the simulation using the interfacial area obtained with the thermodynamic method. The predicted travel time was 20 years for the simulation that used an interfacial area obtained from measured AQITT data. Similar under-predictions of PFAS retention and travel times obtained using interfacial areas produced with the existing estimation methods are evident in the independent-data testing results.

The preceding illustrates how differences in estimated interfacial areas can translate to significant differences in predicted PFAS retention and transport in unsaturated media. Hence, it is critical to employ estimation methods that produce representative magnitudes of air-water interfacial area. The results suggest that PFAS studies that have used one of the existing methods to estimate interfacial areas have the potential to under-predict the contributions of air-water interfacial adsorption to PFAS retention. For example, interfacial areas estimated with the standard-thermodynamic method and the GSSA-based linear method were used in the PFAS modeling studies reported by Silva et al. (2020) and Wallis et al., 2022, respectively. The resultant estimated interfacial areas are much smaller than the values measured herein for the sand and soil. Conversely, Gnesda et al. (2022) used the empirical correlation from Peng and Brusseau (2005) that is based on measured GPITT data. Hence, the estimated interfacial areas for low water saturations are likely to be greater than those determined herein to be representative of PFAS retention.

3.5. Determining air-water interfacial areas for field applications

A critical issue for characterizing and modelling the retention and transport of PFAS and other interfacially active solutes in vadose zones at field sites is the determination of representative air-water interfacial areas. The GPITT and AQITT methods can be employed at the field scale to produce in-situ measurements of air-water interfacial area. A notable aspect of the GPITT method is that a suite of tracers can be used to characterize different retention domains (Brusseauetal., 1997). For example, a water-partitioning tracer can be used to measure water saturation. Costanza-Robinson et al. (2013) demonstrated a pilot field-scale application of the GPITT for measuring water saturations and air-water interfacial areas to successfully predict retardation and vapor-phase transport of trichloroethene. The air-water interfacial areas measured with the GPITT will need to be scaled to be representative for characterizing the aqueous-phase transport of PFAS and other interfacially active solutes. Details of the method and issues for field-scale applications are presented in Brusseau et al. (2003). While it is feasible to conduct interfacial tracer tests at the field scale, they represent non-standard methods that may not be practical for routine application in many cases. Another approach would be to collect soil samples from the site of interest and measure air-water interfacial areas in the laboratory, using preferably an AQITT method. This site-specific ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ relationship would then be used along with measured water saturations to determine air-water interfacial areas for the conditions present at the site. Again, however, this approach may not be possible in many cases as most commercial laboratories do not conduct measurements of air-water interfacial area. The alternative is to employ a robust estimation method, wherein surrogate soil properties are characterized either in-situ or in the laboratory and water saturations are measured to support the application of the estimation method.

A number of factors need to be considered when measuring and estimating air-water interfacial areas for field-scale applications. First, it is critical to note that measurements of water saturation are required for establishing measured ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ relationships and for determining representative estimates. Such measurements are not routinely conducted at most sites, particularly periodically over long time frames. Multiple methods are available to measure water saturations at the field scale. Efforts should be made to incorporate measurements of water saturation as a routine method of investigation for PFAS-impacted sites.

Another critical factor to consider is the potential spatial variability of air-water interfacial area due to soil heterogeneity. Interfacial area can vary across a site due to variability in the inherent maximum interfacial areas of different soils. For example, interfacial areas for a medium with large fractions of silt and clay are typically much larger than for a coarse sand for a given water saturation (e.g., Peng and Brusseau, 2005). Interfacial area can also vary due to spatial variability in water saturations, which are also a function of soil properties. More research is needed to determine the degree to which air-water interfacial area is spatially variable at sites, and the scale and resolution to which such variability needs to be characterized and quantified.

Other factors to consider involve the dynamic aspects of water movement and distribution in the vadose zone and their impacts on air-water interfaces. One aspect to consider is potential hysteresis of the air-water interface as the vadose zone undergoes cycling through infiltration, redistribution, and drainage events. Prior research has demonstrated that total interfacial areas as measured by interfacial tracer tests exhibit minimal impacts of hysteresis (Brusseau et al., 2007, 2015; El Ouni et al., 2021). The results of XMT measurements (Brusseau et al., 2007, 2009; Porter et al., 2010; Landry et al., 2011) and pore-scale modeling investigations (Reeves, 1997; Chanand Govindaraju, 2011) support this observation. This is a result of film-associated area typically comprising a major fraction of total interfacial area, especially at moderate and lower water saturations. However, capillary interfacial area is influenced by hysteresis (e.g., Culligan et al., 2004). This could influence the status of pore-scale flow and transport pathways, which in turn could affect the accessibility of air-water interfaces. In addition, potential interface-accessibility and mass-transfer limitations could be exacerbated in heterogeneous or structured soils for which preferential flow phenomena are prevalent.

Another aspect relevant during infiltration and drainage cycles is the change in air-water interfacial area due to temporal changes in water saturation. Changes in water saturation will clearly cause changes in the magnitude of air-water interfacial areas as a function of the governing ${\text{A}}_{\text{aw}}-{\text{S}}_{\text{w}}$ relationship. If characterizing the temporal variability of air-water interfacial area is an objective of a project, the monitoring of water saturations at the site will need to be of sufficient frequency to characterize the temporal changes in water saturation. The use of automated measurement instrumentation would facilitate the collection of such data.

An additional aspect is the movement of air-water interfaces under non-steady flow conditions prevalent during infiltration and drainage cycles. It is typically assumed that air-water interfaces are effectively immobile during steady-state flow. The successful independent-prediction simulations of measured surfactant transport data with this assumption employed for both hydrocarbon surfactants and PFAS indicates that air-water interfaces can be treated as effectively immobile under relevant conditions. This is also supported by the results presented in Section 3.1. Conversely, some, primarily capillary, air-water interfaces will be mobile during nonsteady flow, which can translocate matter that is adsorbed at the mobile interfaces (e.g., Lazouskaya et al., 2011; Chahal et al., 2016).

In considering the dynamic aspects discussed in the preceding paragraphs, it is important to distinguish between short-term events and long-term conditions and how the two impact the relevant status of air-water interfacial areas. The impacts of individual infiltration/drainage events are typically dampened with depth (e.g., Turkeltaub et al., 2014; Dickinson and Ferré, 2018; Zhou et al., 2018). As a result, the systems are generally treated as quasi-steady state for analyses focusing on extensive time scales. The adequacy of assuming steady-state conditions for assessing long-term leaching behavior of PFAS in the vadose zone was demonstrated by Guo et al. (2022). Hence, measurements or estimates of air-water interfacial area under quasi-steady state conditions are anticipated to be adequate for site-characterization projects focused on longer-term applications. In these cases, a representative long-term average water saturation would be determined, along with a corresponding representative air-water interfacial area. Conversely, projects focused specifically on the impacts of infiltration and recharge should consider the dynamics-related factors discussed above.

4. Conclusion

This study produced several key outcomes relevant to the determination of air-water interfacial areas in general, and specifically for applications focused on air-water interfacial adsorption of PFAS and other interfacially active solutes. The first key outcome is the determination of the reason for the differences in air-water interfacial areas measured with AQITT methods versus those determined with XMT and thermodynamic methods. Some investigators have speculated that these differences were due to errors or artifacts of the AQITT method, whereas others have hypothesized that the disparities are related to the impact of solid-surface roughness on interfacial area. It was demonstrated that the multiple diverse methods produced consistent interfacial areas for glass beads that have minimal surface roughness. This concurrence provides validation of the AQITT methods, and clearly negates the speculation that the differences are due to errors or artifacts in the AQITT method. Consequently, the results indicate the role of solid-surface roughness in the disparities.

A second relevant outcome was that a comparison of measured interfacial areas to the absolute-maximum potential interfacial area indicated that roughness contributions are a major component of GPITT- and AQITT-measured interfacial areas. However, these contributions represent a very small proportion of the total solid-surface roughness. The analyses indicated that the air-water interface as characterized by tracer tests is rough, but significantly smoother than the solid surface. In addition, the results indicated that interface roughness increases at lower saturations. These results are fully consistent with outcomes of both theoretical and experiment-based studies that have investigated the configuration of wetting films on rough surfaces and related impacts to film thickness and interfacial area, all of which demonstrate that fluid-fluid interfaces are rough for rough solids. There is no question that solid-surface roughness causes interfacial areas to exceed equivalent smooth-surface areas. The question is to what magnitude does roughness-associated area manifest for a particular medium and system conditions, and to what extent it is accessible and measurable by any specific measurement method.

A third important outcome is the identification of methods that do and do not produce representative air-water interfacial areas for characterizing the air-water interfacial adsorption of PFAS. Some investigators have proposed that air-water interfacial areas are equivalent to the smooth-surface solid surface area (GSSA). However, the results presented herein over-whelming show that GPITT- and AQITT-measured interfacial areas for sands and a soil are significantly greater than the respective GSSAs. This is consistent with the results of prior the oretical and experiment-based studies demonstrating fluid-fluid interfaces are rough. The results also clearly demonstrate that air-water interfacial areas measured by GPITT and AQITT for sands and a soil are significantly greater than interfacial areas determined with the thermodynamic method. The many measured data sets presented herein comprise data measured by multiple investigators with several different methods. Critically, it was demonstrated in Section 3.4 that both the smooth-surface assumption and standard thermodynamic method produced inaccurate air-water interfacial areas that failed to reproduce multiple measured PFAS retention and transport data sets. Based on these results, it is recommended that the GSSA- and thermodynamic-based methods should not be used to estimate interfacial areas for applications involving the air-water interfacial adsorption of PFAS and other interfacially active solutes. In contrast, the results showed that interfacial areas measured with AQITT methods accurately represent that air-water interfacial adsorption of PFAS and associated retention and transport.

Fourth, three new estimation methods were presented and successfully tested against independent data sets for PFAS retention measured from miscible-displacement experiments and field porewater concentrations. The three new estimation methods have different input requirements, which provides flexibility to account for different data availability. The use of these or any estimation method should consider the potential impact of inherent soil-property variability as well as measurement uncertainty on estimated values. This can be addressed by determining estimated values with multiple robust approaches when possible and by using a range of values obtained with a single method. Further testing and development of these approaches is needed, employing soils comprising a range of physical and geochemical properties.

Differences in estimated interfacial areas can translate to significant differences in predicted PFAS retention and transport. Hence, it is critical to employ estimation methods that provide representative magnitudes of air water interfacial area to produce accurate characterizations and simulations of PFAS retention and transport for unsaturated systems. Robust estimation of air-water interfacial areas at the field scale will typically require the measurement of soil properties such as the grain-size distribution, which is relatively standard, and the soil-water characteristic and NBET solid surface area, which have not been routinely measured for field investigations. Additionally, characterization of air-water interfacial areas at sites will require monitoring of water saturations, which also is not a routine measurement. It is therefore recommended that such measurements be conducted for PFAS-impacted sites for which vadose-zone sources are important.

HIGHLIGHTS.

• The relationship between air-water interfacial area and water saturation is nonlinear

• Aqueous tracer-test methods produce the most representative interfacial areas

• Thermodynamic estimates need to be scaled to produce reasonable values

• New estimation methods are introduced and tested against independent data sets

Data availability

The data used are obtained from prior published works and therefore are available in the literature