Neurons in human pre-supplementary motor area encode key computations for value-based choice

Abstract

Adaptive behaviour in real-world environments requires that choices integrate several variables, including the novelty of the options under consideration, their expected value and uncertainty in value estimation. Here, to probe how integration over decision variables occurs during decision-making, we recorded neurons from the human pre-supplementary motor area (preSMA), ventromedial prefrontal cortex and dorsal anterior cingulate. Unlike the other areas, preSMA neurons not only represented separate pre-decision variables for each choice option but also encoded an integrated utility signal for each choice option and, subsequently, the decision itself. Post-decision encoding of variables for the chosen option was more widely distributed and especially prominent in the ventromedial prefrontal cortex. Our findings position the human preSMA as central to the implementation of value-based decisions.

Humans and other animals can make decisions in a manner that maximizes the chance of obtaining rewards. Computational theories of decision-making suggest that doing so relies on a number of variables¹. Most studied among these is the expected value (EV) associated with an option. By comparing options with varying EVs, it is possible to guide behaviour towards higher expected future rewards. However, in the real-world, the relationship between actions and their subsequent outcomes is often uncertain; as such, one needs to consider not only the expected reward but also its estimation uncertainty, which quantifies an agent’s current lack of information about the outcome probability distribution^2-4. Another relevant feature is the novelty of an option—new options can potentially provide new opportunities to gain rewards⁵. These features can be used to resolve an often-encountered dilemma in decision-making: whether to explore uncertain options that could yield richer rewards or exploit familiar options with known rewards^6,7.

How does the human brain represent the decision variables associated with the available options and how are they integrated to make a decision? One possibility is that neurons encode a utility signal that integrates over relevant decision variables for each given option and that this integrated utility is then used as an input to the decision process. Alternatively, these variables could be encoded in non-overlapping neuronal populations and be integrated at the population level to inform action selection. Studies in rodents and non-human primates have reported neurons throughout the prefrontal cortex that correlate with EV^8-13, uncertainty^14-17 and novelty^18-20. Most human studies have been restricted to non-invasive methods, such as functional magnetic resonance imaging (fMRI), revealing roles in value-based decision-making for the ventromedial prefrontal cortex (vmPFC)^21-24, dorsal anterior cingulate cortex (dACC)²⁵ and pre-supplementary motor area (preSMA)^22,26. Overall, these areas encode decision variables such as EV^{10,21,22,24,26}, uncertainty^24,27,28 and outcomes^10,29, while novelty-related effects have also been found in the dopaminergic midbrain and striatum^5,30-32. Some studies reported signatures of value computations in the prefrontal cortex using intracranial electroencephalography from depth and grid electrodes^33,34. While this approach affords greater temporal resolution than fMRI, intracranial electroencephalography reflects pooled synaptic activity across large numbers of neurons with a similar lack of spatial selectivity as fMRI. In particular, while previous studies^22,26 demonstrated correlations with action-value in the pre-supplementary motor cortex with fMRI, they did not show whether value-related signals precede decision-related signals and how these two signals interact. Despite its nomenclature, which associates this brain area with motor processes, preSMA is also anatomically and functionally connected to other areas of the prefrontal cortex, notably the dorsolateral prefrontal cortex; its role has been tied to executive control, action planning, decision-making and sequence learning^35-38.

We sought to determine how single neurons in these three brain areas are recruited during decision-related computations, to address whether these variables are integrated into a utility signal at the level of single neurons and to probe how these signals might be used for informing choice. For this, we recorded single neurons in preSMA, dACC and vmPFC while human patients with drug-resistant epilepsy undergoing invasive electrophysiological monitoring performed a decision-making task specifically designed to dissociate EV, novelty and estimation uncertainty, which we interchangeably refer to as ‘uncertainty’ in this work. Additionally, we aimed to distinguish neurons that encode stimulus features and choice from those that evaluate the consequences of the decision. Finally, we identified neurons encoding outcomes and prediction errors to ascertain how these regions contribute to updating decision information after feedback at the neuronal level. Thus, this study afforded us an unparalleled opportunity to investigate the role of human prefrontal neurons across multiple stages of value-based decision-making: from the representation of individual decision variables, through to the integration of these variables into a putative utility signal, up to choice and ultimately feedback.

Results

Task and behaviour

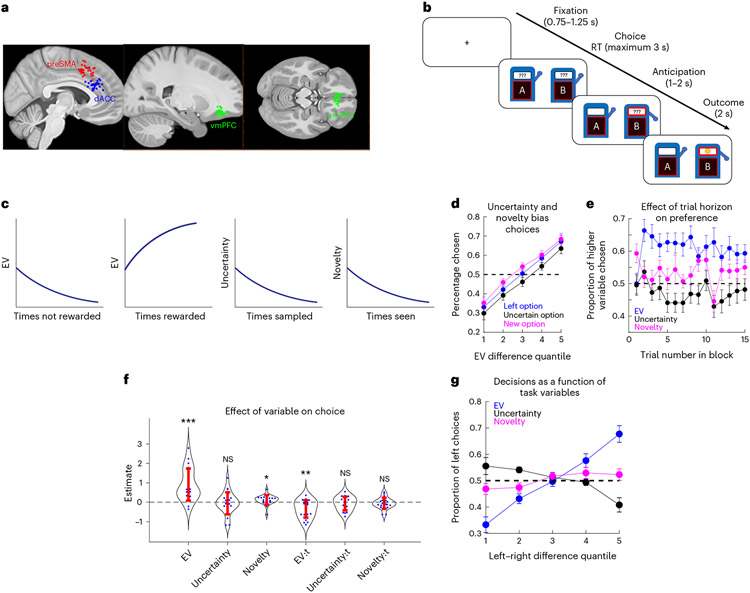
We recorded 191 vmPFC, 137 preSMA and 108 dACC single neurons (436 in total) in 22 sessions from 20 patients chronically implanted with hybrid macro- and microelectrodes for epilepsy monitoring (Fig. 1a). Patients performed a two-armed bandit task³⁹ designed to separate the influence of EV, uncertainty and novelty on decision-making, divided into 20 blocks consisting of 15 binary choices each. On each trial, participants used a button box to decide between two uniquely identifiable bandits presented on the left or right of the screen (Fig. 1b). Across all trials, mean reaction time (RT) was 1.47 s ± 0.02 s (relative to the onset of the choice screen; Fig. 2b), with a 95% confidence interval (CI) from 0.43 s to 3.55 s. After a time delay, a feedback screen announced the binary outcome (win or no win). The experimental design included two critical features. First, participants were informed that the probability of each bandit delivering a reward was fixed for the duration of each block but randomized across blocks. Second, both new and familiar stimuli were systematically incorporated into the set from which options could be drawn during a block, resulting in pairs of bandits that varied in terms of EV, uncertainty and novelty.

Fig. 1 ∣. Electrode positions, exploration task and behaviour.

a, Electrode positioning. Each dot indicates the location of a microwire bundle in the preSMA (red), dACC (blue) or vmPFC (green). b, Trials were structured according to fixation, decision, anticipation and feedback stages. In the actual task, slot machines were distinguished by artistic paintings displayed in front of them, represented in this figure by distinct letter labels. c, Schematic indicating how $Q$ values, uncertainty and novelty of stimuli vary as a function of the past history of rewards, choices (‘sampled’) and exposures. d,e, Behaviour. d, EV correlates with choice, biased by novelty and uncertainty. Patients chose the left option (blue), the more uncertain option (black) or the newer option (magenta) as a function of chosen minus unchosen EV. n = 22 sessions. e, Proportion of trials in which patients chose the option with higher EV (blue), uncertainty (black) or novelty (magenta), as a function of trial number. The dots and bars indicate the mean and s.e.m., respectively. n = 22 sessions. f, Logistic regression coefficients for EV (P < 0.001), uncertainty (P = 0.639), novelty (P = 0.034) and interactions with trial number (EV:t, P = 0.001; uncertainty:t, P = 0.352; novelty:t, P = 0.369). The dots and bars indicate the fits for each patient and s.e.m., respectively (*P < 0.05; **P < 0.01; ***P < 0.001, two-sided t-test). Positive values indicate seeking behaviour. g, Decision as a function of task variables. The lines indicate the proportion of left choices as a function of the difference in the variable of interest between left and right stimuli (EV: blue; uncertainty: black; novelty: magenta). All error bars indicate the s.e.m.

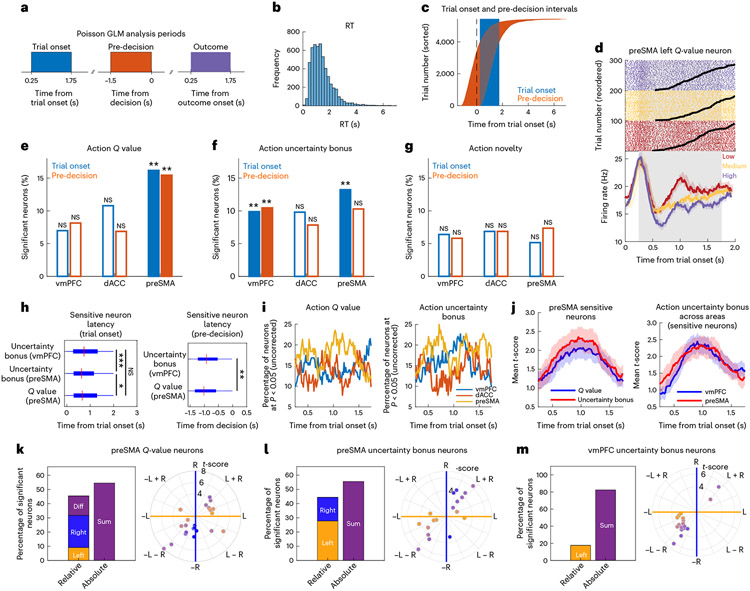
Fig. 2 ∣. Encoding of action utility components in the preSMA and vmPFC.

a, Time windows used for all analyses (trial onset, pre-decision and outcome). b, Reaction times in all trials. c, Relationship between trial onset and pre-decision periods across all trials, relative to trial onset, reordering trials by reaction time. d, Example left $Q$-value preSMA neuron. Top, spike raster plots. The black lines indicate RT. Trials sorted by $Q$-value tertile (purple: high; yellow: medium; red: low). Bottom, peristimulus time histogram (PSTH) (bin size = 0.2 s, step size = 0.0625 s). Data are presented as mean values ± s.e.m. e, Percentage of neurons sensitive to action $Q$ value in the trial onset (blue, preSMA: P = 0.002) and pre-decision (orange, preSMA: P = 0.002) periods (**P < 0.01, one-sided permutation test). The unfilled bars indicate non-significant counts. f, Same but for action uncertainty (vmPFC, trial onset: P = 0.002; vmPFC, pre-decision: P = 0.004; preSMA, trial onset: P = 0.002). g, Same but for action novelty. h, Box plots of latency time across trials for sensitive neurons at trial onset (left) or pre-decision (right) (*P < 0.05; **P < 0.01; ***P < 0.001, two-sided Wilcoxon rank-sum test). P values as follows: P < 0.001 for preSMA versus vmPFC uncertainty bonus; P = 0.036 for $Q$ value versus uncertainty bonus in preSMA. The red mark indicates the median and the box extends between the 25th and 75th centiles of latency times. The bar whiskers extend to the most extreme data points not labelled as outliers, defined as values that are more than 1.5 times the interquartile length away from the edges of the box. i, Significant neuron percentages (uncorrected) for action $Q$ value or uncertainty bonus in vmPFC (blue), dACC (orange) or preSMA (yellow). j, Timing in sensitive neurons of absolute t-score from the Poisson GLM. Left, $Q$ values (blue) versus uncertainty bonus (red) in the preSMA. n = 22 $Q$-value neurons, n = 18 uncertainty bonus neurons. Right, uncertainty bonus in vmPFC (blue) versus preSMA (red). n = 18 preSMA neurons, n = 17 vmPFC neurons. k, Left versus right coding in sensitive preSMA $Q$-value neurons. Left, percentage of neurons coding left and right, difference or sum values. Right, polar plot for left (yellow), right (blue) and mixed (purple) $Q$-value coding. The radial lines indicate the separation used for neuron classification as right, left, sum or difference. The hues indicate the degree of left (yellow), right (blue) or mixed (purple) coding. l, Same but for preSMA uncertainty bonus neurons. m, Same but for vmPFC uncertainty bonus neurons.

We first assessed how EV, uncertainty and novelty related to behaviour. Within each block of trials, EV and uncertainty were quantified as the average proportion of wins and the total number of times a given stimulus was chosen thus far in a given block of trials, respectively. To do this in a model-agnostic manner, we defined $Q$ values as the mean of a $\beta$ distribution that estimates the probability of receiving a reward from a bandit, as determined by the history of wins and losses. Similarly, we defined an uncertainty value as the variance of the same $\beta$ distribution. Finally, we defined novelty as the variance of a $\beta$ distribution in which $\beta =1$ = 1 and the $\alpha$ parameter is the number of times patients were exposed to a stimulus in the entire session. This formulation means that novelty is a monotonically decreasing function of the number of times a stimulus is seen, regardless of its sampling or outcome history (Fig. 1c).

Uncertainty- and novelty-biased value-based decisions in distinct directions: while on average patients preferred options with higher EVs over options with lower EVs (P < 0.001, t = 18.2, linear regression), they sought them more often if they were also the newest option than if they were also the more uncertain option (P = 0.006, t = 2.73, two-sided t-test) (Fig. 1d). This was not the result of changing preferences over time because trial number did not correlate with how often patients sought the option with higher uncertainty (P = 0.31, t = −1.00, linear regression) or higher novelty (P = 0.76, t = −0.29, linear regression) (Fig. 1e). We then used logistic regression to correlate decision variables and choices (see the Methods section for details of the logistic regression analysis) with EVs, uncertainty and novelty as predictors. A positive model coefficient for a variable indicates that patients tended to choose a stimulus more often if the value of that variable was higher (for example, a positive logistic regression coefficient for EV indicates that the patient was EV-seeking). Model coefficients (Fig. 1f) indicated that patients were EV-seeking (P < 0.001, t = 5.15, t-test) and novelty-seeking (P = 0.034, t = 2.26, t-test), with a negative effect of the interaction between EV and trial number (P = 0.001, t = −3.67, t-test), suggesting a deviation from optimal outcome integration. This can be summarized by plotting the proportion of left choices as a function of the difference between left and right EVs, uncertainties and novelties (Fig. 1g). Importantly, we also confirmed that patient behaviour reflected value reset at the start of each block (Supplementary Information), indicating that patients understood the task structure and learned how to choose the more advantageous options based on their past experiences. Additionally, novelty and uncertainty correlated with behaviour in a separable manner: while patients were novelty-seeking overall, some patients avoided uncertainty whereas others were uncertainty-seeking. Because we did not observe a change in how uncertainty is valued from the beginning to the end of trial blocks, this result also indicates a departure from previously observed exploration behaviour^28,39, which includes a switch from exploration to exploitation as the trial horizon approaches. A possible reason for this is that the task reported in this study did not offer the sensitivity required to probe for the interaction between novelty and uncertainty reported in ref. ³⁹ due to the shorter task horizon and reduced stimulus set being learned (see Methods for details of the task and model specification).

Theoretically, optimal behaviour in a general multi-armed bandit problem has a tractable solution under the constraints of a Markov decision process with infinite time steps and geometrically discounted future rewards⁴⁰. The solution relies on computing a Gittins index for each bandit and always selecting the one with the highest value, which essentially reflects the known value of the bandit plus the value of the uncertainty in unexplored stimuli. Computing the Gittins index is less tractable under the constraint of finite trial horizons, as is the case in this manuscript, but algorithmic approximations have been proposed⁴¹. Despite the lack of a change in how much uncertainty is valued through the extension of a trial block, we investigated whether behaviour is driven by the concept of uncertainty bonuses for exploration, as is also proposed by the upper confidence bound class of exploration algorithms⁴².

We compared four nested candidate computational models to explain patient behaviour (Supplementary Material, model comparison). All models relied on $Q$ values to construct stimulus utilities and included learning rates $\alpha$ for value updates and inverse temperature parameters $\beta$ for the softmax in the stimulus utility comparison step. Additionally, we tested the effect of adding an uncertainty bonus to the utility of stimuli, with an individualized weight uI to the value of uncertainty, which reflected each patient’s tendency to avoid or seek uncertain stimuli. We adapted this concept from the upper confidence bound class of models, which use information gain as a mechanism for exploration in uncertain environments^39,42. Finally, we tested the effect of novelty-based optimistic initiation⁵, which is another separate mechanism through which novelty can influence exploration. In our models, we added a novelty bias nI to the initial $Q$ values to reflect the intrinsic value of novelty regardless of a stimulus’s uncertainty. We hypothesized that these two mechanisms are ways through which novelty and uncertainty may separably influence patients’ decisions in the task. To summarize the nested model comparison approach, models 1–4 respectively included the following parameter sets: $(\alpha ,\beta )$; $(\alpha ,\beta ,ul)$; $(\alpha ,\beta ,nl)$; and $(\alpha ,\beta ,ul,nl)$.

Using hierarchical Bayesian inference on patients’ behavioural data⁴³, we determined that model responsibilities (that is, the estimated percentage of sessions that were better explained by each model) for models 1–4 were (0.6, 55.8, 0.1 and 43.8%). This indicates that while most patient behaviour was better explained by a simple uncertainty bonus, a considerable portion of patients had their behaviour better explained by a combination of an uncertainty bonus and an optimistic novelty initiation bonus. Our approach for the following neural analyses was to use the model with the highest responsibility score obtained with the hierarchical Bayesian inference for each individual session to generate regressors ($Q$ values, uncertainty bonus, stimulus utilities) for that session. Concretely, in 13 of 22 sessions, model 2 was the prevailing explanation, while the remaining 9 of 22 sessions were better explained by model 4 (see Supplementary Fig. 1 for model parameters and posterior predictive checks). Note that tuning to novelty was analysed across all sessions, regardless of whether model 2 or 4 best explained a given individual’s behaviour. This is because while individuals for which model 2 fitted best, there was no novelty initiation bias; whether a stimulus was new or not was nevertheless a relevant variable to decide the explore–exploit trade-off.

PreSMA neurons represent features of individual options

We next probed the neural representation of stimulus features by examining whether the $Q$ value, uncertainty or novelty of each option presented on the screen was represented by neurons in our regions of interest using a Poisson generalized linear model (GLM), named ‘action-value model’, with these features as regressors (for a complete list of encoding models, see Supplementary Table 2). Because these variables pertain to each stimulus being considered on a given trial and are not contingent on the choice of option that is subsequently made, they are candidate variables for acting as an input to the decision process.

We then grouped neurons according to their sensitivity to features associated with the left or right option, which we refer to as action $Q$ value, action uncertainty bonus and action novelty neurons, respectively (see Fig. 2d for an example). To determine whether activity in a brain area significantly correlated with these action-based stimulus features, we tested whether the selected number of neurons were larger than expected by chance (Fig. 2e-g). All our tests were performed in the subset of neurons from each brain area separately; subsequent neuron count results were Bonferroni-corrected for the number of time windows and brain areas in which we tested for a significant neuron count.

This analysis revealed prominent encoding of action $Q$ value and uncertainty bonus during the trial onset period (16.1%, P = 0.002 and 13.2%, P = 0.002, respectively, permutation test) and encoding of action $Q$ value during the pre-decision period in the preSMA (15.4%, P = 0.002, permutation test). On the other hand, neurons in the vmPFC encoded the action uncertainty bonus during the two periods (9.88%, P = 0.002 and 10.4%, P = 0.004, respectively, permutation test). This indicates that preSMA and vmPFC neurons encode the components of stimulus utility that can serve as input to the decision process. Additionally, action novelty encoding was not significant and none of the selected cell counts were significant in dACC (Fig. 2e-g).

Given the role of the preSMA and vmPFC in encoding components of value, we investigated the temporal activity patterns for the selected neurons in these two areas. For qualitative results, we repeated the Poisson GLM analysis described above in sliding time windows and we report on the time courses for uncorrected percentages of neurons at P < 0.05 for each action $Q$ value and action uncertainty bonus neurons in the Poisson GLM (Fig. 2I). For quantitative results, we performed a Poisson latency analysis in neurons that were exclusively sensitive to one of the tested variables (Fig. 2h)⁴⁴ to compare their onset latencies (Methods). In the preSMA, action uncertainty bonus neurons were active first relative to stimulus onset (median time: 0.63 s), followed by action $Q$-value neurons (median time: 0.66 s, P < 0.03, two-sided Wilcoxon rank-sum test). Action uncertainty bonus neurons were also active earlier in the preSMA than in the vmPFC (median time: 0.80 s, P < 0.001, two-sided Wilcoxon rank-sum test) Additionally, in the pre-decision period, preSMA $Q$-value neurons (median time: −1.01 s) were active before the vmPFC uncertainty bonus neurons (median time: −0.92 s, P < 0.01, two-sided Wilcoxon rank-sum test). These results indicate that the preSMA encoded the components of value earlier than the vmPFC after stimulus presentation.

For the subset of selected (sensitive) neurons, we plotted their sensitivity for the left and right action-value components along a polar coordinate plane to obtain an unbiased classification⁴⁵ (Methods) for neurons that coded exclusively for one spatial position or both of them (Fig. 2k-m). The polar angle between the left and right t-scores indicates whether a neuron was classified as coding for the left component, right component, the difference between the components or their sum (see Supplementary Fig. 2 for the classification diagram). Neurons that were classified as coding for the left value, right value or their difference, were grouped as ‘relative’ coding neurons because in these three cases, these values could be used to support relative value comparisons between the two stimuli. Neurons that coded for the sum of values, on the other hand, were grouped as ‘absolute’ coding neurons because the information about individual stimuli is lost if only the total value is represented. In the preSMA, we found that 54.5% of $Q$-value sensitive neurons performed absolute $Q$-value coding at trial onset, while 45.4% performed relative coding (9.1% left, 22.7% right, 13.6% difference). Similarly, for the action uncertainty bonus at trial onset, 55.5% of selected preSMA neurons performed absolute coding, while 44.3% performed relative coding (27.7% left, 16.6% right). Finally, in the vmPFC, absolute uncertainty coding was more prominent (82.3% sum versus 17.7% left of selected neurons). These results indicate that preSMA neural activity supports both relative and absolute action-value component representation, for both $Q$ values and uncertainty bonuses, while the vmPFC had a more specific role in coding absolute uncertainty bonuses regardless of action.

We also tested whether neurons coded stimulus features positively (that is, higher firing rates for higher variable values) or negatively more than expected by chance (Supplementary Table 1), using a two-tailed binomial test for neuron count, assuming a null probability of 0.5 for positive or negative coding. Among the variables that had a significant neuron count, we only found a bias for action uncertainty bonus coding in the vmPFC, which had a bias towards negative coding. Only 11% of significant neurons coded it positively in the trial onset period (P = 0.002, two-tailed binomial test).

Taken together, these findings suggest that the preSMA encodes action-value components both based on the past history of rewards and the past history of sampled options. While both the preSMA and vmPFC encoded uncertainty bonuses, thereby reflecting the tendency to seek out or avoid uncertain stimuli, the preSMA did so earlier than the vmPFC. Finally, in the preSMA this encoding was in the form of signalling stimulus features for one and both options, indicating that these signals can serve as an input to the decision process.

PreSMA neurons encode an integrated stimulus utility signal

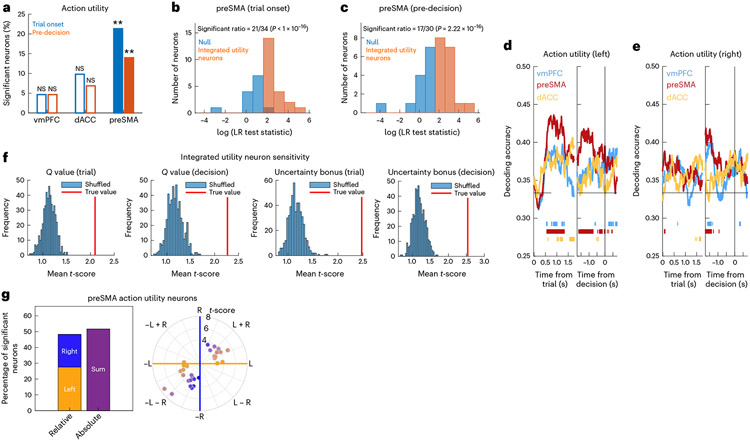
To determine whether neurons represented an integrated utility for each decision option (incorporating EV, uncertainty and novelty), we used the utility signal derived from our computational models. We performed a Poisson GLM encoding analysis (Fig. 3a) with left utility, right utility and decision as regressors (decision and utility model). We found that a significant number of preSMA neurons encoded action utility after trial onset (21.3%, P = 0.002, permutation test) and in the pre-decision period (13.9%, P = 0.002, permutation test). One interpretation is that single neurons in the preSMA encode an integrated utility signal for individual choice options. Alternatively, it is possible that neurons correlating with utility in our regression analysis are mostly reflecting the effects of $Q$ values per se as these variables are correlated (Supplementary Fig. 2).

Fig. 3 ∣. Neurons in the preSMA encode integrated utility.

a, Percentage of action utility neurons in the vmPFC, dACC and preSMA at the trial onset (blue, preSMA: P = 0.002) and pre-decision (orange, preSMA: P = 0.002) periods (**P < 0.01, one-sided permutation test). The unfilled bars indicate non-significant counts. b, LR test statistics across candidate preSMA integrated action utility neurons at the trial onset period. Neurons whose activity was better explained by a model containing $Q$ values and uncertainty bonuses were classified as integrated utility neurons (orange). For the remaining neurons (blue), the null model restricted to $Q$ values was not rejected. c, Same but for the pre-decision period. d, dPCA population decoding performance for the left action utility for the vmPFC (blue), preSMA (red) and dACC (yellow). The bars indicate periods of time where decoding accuracy was significantly above chance. The horizontal line indicates chance. Left, trial onset period. Right, pre-decision period. e, Same but for the right action utility. f, Integrated utility preSMA neuron sensitivity to $Q$ values. The red lines indicate the mean absolute t-score across integrated utility neurons. The histograms include the mean absolute t-scores for 500 iterations of bootstrapped null models with shuffled firing rates. Tested variables (from left to right): $Q$ value (trial onset); $Q$ value (decision); uncertainty bonus (trial); uncertainty bonus (decision). g, Left versus right coding in sensitive preSMA action utility neurons. Left, percentage of neurons coding left, right or sum values. Right, polar plot for left (yellow), right (blue) and mixed (purple) $Q$-value coding. The colours indicate the degree of left (yellow), right (blue) or mixed (purple) coding. The radial lines indicate the separation used for neuron classification as right, left, sum or difference.

To test this hypothesis, we defined the subpopulations of preSMA neurons previously identified either as $Q$-value or utility neurons as candidate neurons for an integrated utility signal. To determine whether they encoded an integrated utility signal versus $q$ alone, we performed a likelihood ratio (LR) test (with a threshold at P < 0.05) comparing the performance of a model containing $q$, uncertainty and decision regressors versus a restricted model containing only $q$ and decision (Methods), while predicting each candidate neuron’s spike count. The restricted model was rejected for 61% (21 of 34) of preSMA candidate neurons at trial onset and for 56% (17 of 30) of preSMA candidate neurons in the pre-decision window (Fig. 3b,c). Therefore, a significant portion of candidate neurons in the preSMA qualified as integrated utility neurons (trial onset: P < 0.001; pre-decision: P < 0.001, binomial test). These integrated utility neurons collectively encoded the main components of utility ($Q$ values and uncertainty bonuses) at a higher level than expected by chance (P < 0.001 in all instances, permutation test), further confirming their role in computing an integrated signal (Fig. 3f).

Like the action-based stimulus feature analysis, for the subset of sensitive action utility neurons, we plotted their sensitivity for left and right utility components along a polar coordinate plane to obtain an unbiased classification⁴⁵ (Methods) for neurons that coded exclusively for one spatial position or both of them (Fig. 3g). In the preSMA, we found that 51.7% of action utility sensitive neurons performed absolute utility coding at trial onset, while 48.2% performed relative coding (27.5% left, 20.7% right).

Population decoding of utility as an input to decisions

Building on these results demonstrating that single neurons in the preSMA and vmPFC encode stimulus features that could support the decision-making process, we next tested when and where it was possible to decode an integrated stimulus utility value from neural populations. To do so, we considered the firing patterns of all recorded neurons from each brain region across all trials, using demixed principal component analysis⁴⁶ (dPCA) to reduce data dimensionality (using pseudopopulations; Methods).

We performed two separate analyses for left and right utilities, including the decision itself (that is, left versus right choice) as a marginalization in both analyses (Fig. 3d,e). Action utilities were decodable in the preSMA, both after trial onset and before the button press (Fig. 3d-e; significant time periods are indicated in the figure). Thus, these results suggest that the preSMA encodes an integrated utility signal that encompasses both $Q$ values and uncertainty. At the population level, the utility for each decision option was decodable in the preSMA even after demixing utility from the decision, indicating that the utility for each of the two possible decision options is represented at the population level. Together, these findings suggest that preSMA neurons represent the signals needed as an input to the decision-making process.

Decision is represented later than stimulus utility

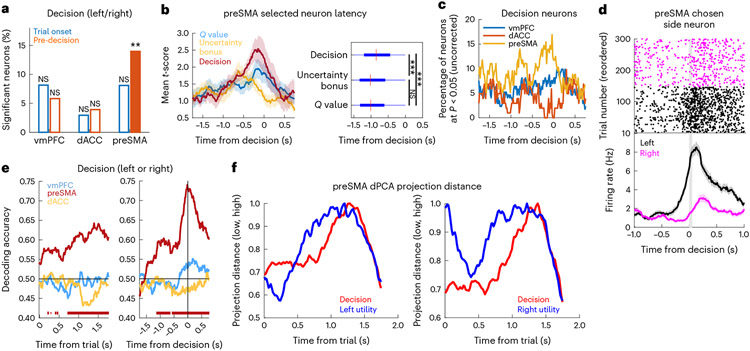
At the level of single neurons, we used a decision and utility GLM (Supplementary Table 2) and determined that the decision to select the left or the right slot machine was encoded only in the preSMA and only in the pre-decision period (Fig. 4a). In this time window, 14.0% (P = 0.002, permutation test) of neurons encoded the decision to choose the left or the right option (Fig. 4d shows an example). We determined whether decision neurons and action utility neurons encoded these variables jointly or separately by measuring their angle in the polar plane defined by their t-scores for decision and utility (see the Methods for the polar coordinate analysis). We then tested whether the number of overlapping neurons was larger than expected by chance by performing a binomial test, assuming a uniform probability for neurons to be in each polar plane sector. In the preSMA, neurons that encoded action utility had no significant overlap with those encoding the decision (P = 0.830, binomial test). Neither at the single-neuron (Fig. 4a) nor at the population level was the decision represented in the vmPFC or dACC (Fig. 4e). Therefore, we restricted the following analysis to the preSMA.

Fig. 4 ∣. The PreSMA encodes decisions.

a, Percentage of decision neurons (left versus right choice) in the vmPFC, dACC and preSMA at the trial onset (blue) and pre-decision (orange, preSMA: P = 0.002) periods (**P < 0.01, one-sided permutation test). The unfilled bars indicate non-significant counts. b, Sensitive preSMA neuron timing during the pre-decision period. Left, mean absolute t-score for the $Q$ value (blue, n = 21 neurons), uncertainty bonus (yellow, n = 14 neurons) and decision (red, n = 19 neurons). The shaded areas indicate the s.e.m. Right, latency time box plots for all $Q$-value, uncertainty bonus or decision neurons (***P < 0.001, two-sided Wilcoxon rank-sum test). P values are as follows: P < 0.001 for decision versus uncertainty bonus; P < 0.001 for decision versus $Q$. The red mark indicates the median and the box extends between the 25th and 75th centiles of latency times. The bar whiskers extend to the most extreme data points not labelled as outliers, defined as values that are more than 1.5 times the interquartile length away from the edges of the box. c, Percentage of significant decision neurons in the vmPFC (blue), dACC (orange) or preSMA (yellow). d, Example preSMA decision neuron. Top, raster plot. For plotting, we sorted trials into left (black) and right (magenta) decisions. Bottom, PSTH (bin size = 0.2 s, step size = 0.0625 s). The grey bar indicates the button press. Data are presented as mean values ± s.e.m. e, dPCA decision decoding for vmPFC (blue), preSMA (red) and dACC (yellow). The bars indicate significant times compared to a bootstrapped null distribution. The horizontal line indicates chance. Left, trial onset period. Right, pre-decision period. f, Normalized Euclidean distance between dPCA projections onto principal utility components (blue), between low- and high-utility trials and decision components (red) and between left and right decision trials, with left (left) or right (right) utility marginalizations.

Relative to the time of response, a single-unit analysis showed that preSMA $Q$-value neurons responded first at −1.00 s, not significantly later than uncertainty bonus neurons at −1.01 s (P = 0.731, two-sided Wilcoxon rank-sum test). Decision neurons (median time: −0.84 s); however, they responded later than both $Q$-value neurons (P < 0.001, two-sided Wilcoxon rank-sum test) and uncertainty bonus neurons (P < 0.001, two-sided Wilcoxon rank-sum test). At the population level, we projected neural data onto the dPCA demixed principal components separately for low- and high-utility trials and for left and right decisions. We then examined the Euclidean distances between these trajectories as a function of time. This showed that the distance in state space was maximal for action utility earlier than for decisions (Fig. 4f). Relative to trial onset, this latency difference was apparent for both left utility (1.20 s versus 1.28 s) and right utility (1.21 s versus 1.37 s).

Therefore, in the preSMA, decisions and stimulus values are encoded by largely separate groups of neurons, with utility encoding appearing earlier than the decision. This time course and encoding scheme suggests that preSMA encodes pertinent stimulus features pre-decision, thereby revealing a potential substrate for value-based decision-making.

vmPFC neurons represent decision-conditioned variables

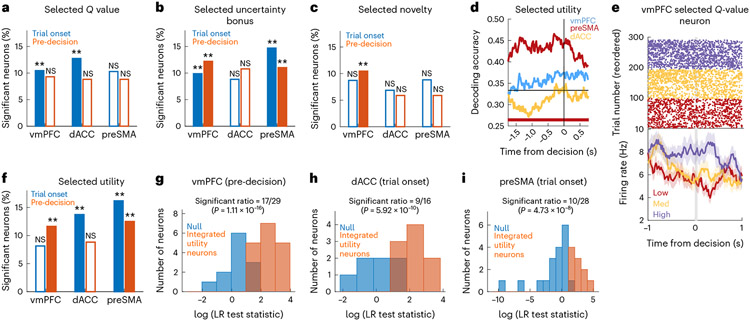
Representing the expected outcome of a choice is a critical step in decision-making because it facilitates learning by way of comparison of the expected outcome to the actual outcome received. Therefore, we next examined the neuronal representation of the selected option’s utility and its components (see the selection-based model and selection-based utility model in Supplementary Table 2). In the vmPFC, selected $Q$ values, uncertainty and novelty were encoded (Fig. 5a-c,e shows an example). In the dACC, selected $Q$ values were represented, while the preSMA also encoded selected uncertainty bonuses. Furthermore, we examined the encoding of value for the rejected option and for the option that was not offered in a trial (in this case, only for patients who performed the longer task with three stimuli per block) (Supplementary Fig. 3). We found significant coding of rejected $Q$ values and uncertainty bonuses in the vmPFC and preSMA, as well as unseen $Q$ values in the vmPFC. We also found that selected uncertainty bonus neurons were active significantly earlier in the preSMA than in the vmPFC, which is consistent with action-values (−0.91 s versus −1.02 s, P < 0.001, Wilcoxon rank-sum test) (Supplementary Fig. 3). Additionally, a significant proportion of preSMA-selected uncertainty neurons signalled whether a trial was exploratory or not before button press (Supplementary Fig. 3). Overall, these findings indicated widespread coding of value components that are contingent on the decision that was made.

Fig. 5 ∣. Encoding selected stimulus properties.

a, Percentage of selected $Q$-value neurons in the vmPFC, dACC and preSMA at the trial onset (blue, P = 0.002 for the vmPFC and dACC) and pre-decision (orange) periods (**P < 0.01, one-sided permutation test). The unfilled bars indicate non-sensitive counts. b, Same but for selected uncertainty. P = 0.002 for the vmPFC and preSMA, both periods. c, Same but for selected novelty. P = 0.002 for the preSMA, pre-decision. d, dPCA selected utility decoding in the pre-decision period for the vmPFC (blue), preSMA (red) and dACC (yellow). The bars indicate significant decoding accuracies for each brain region, compared to a bootstrapped null distribution. e, Example selected $Q$-value neuron in the vmPFC. Top, raster plots. For plotting, we sorted trials by $Q$-value tertiles (purple: high; yellow: medium; red: low). Bottom, PSTH (bin size = 0.2 s, step size = 0.0625 s). The grey bar indicates the button press. Data are presented as mean values ± s.e.m. f, Same as in a but for selected utility. P = 0.002 for vmPFC, pre-decision, dACC, trial onset and preSMA, both periods. g, Histogram of LR test statistics across candidate vmPFC integrated selected utility neurons (orange) in the pre-decision period. For the remaining neurons (blue), a null model containing only selected $Q$ values was not rejected. h, Same as in g but for dACC. i, Same as in g but for the preSMA.

Like the integrated action utility analysis, we defined a group of candidate integrated selected utility neurons as the subset of units that correlated with the selected option’s $Q$ value or utility (Fig. 5a,f), as determined with the selection-based GLM or the selection-based utility GLM, respectively (Supplementary Table 2). We determined that, in all brain areas, the number of neurons selected this way was larger than expected by chance (Fig. 5g-i) (vmPFC: P < 0.001; dACC: P < 0.001; preSMA: P < 0.001). The activity of this subset of neurons was therefore indicative of the integrated utility of the selected option.

Finally, we examined the points in time at which the selected option’s integrated utility could be decoded from pooled activity across all neurons in the regions of interest (using dPCA; Methods). This analysis revealed robust decoding of selected utility in the preSMA (Fig. 5d). Motivated by the earlier utility decoding in the preSMA, we tested whether selected utility neuron latency times were also shorter in the preSMA than in the other areas. A Poisson latency analysis at trial onset revealed a median onset time in the preSMA of 0.67 s, which was significantly earlier than in the dACC (0.87 s, P < 0.001, one-sided Wilcoxon rank-sum test). Similarly, although both vmPFC and preSMA had significant neuron counts for the selected utility, sensitive neurons had earlier latencies in the pre-decision window in the preSMA (−1.02 s) than in the vmPFC (−0.87 s, P < 0.001, one-sided Wilcoxon rank-sum test).

Like the analysis we performed with action-based stimulus features, we also tested whether neurons coded decision-conditioned variables positively or negatively more than expected by chance (Supplementary Table 1). Among the variables that had a significant neuron count, we found that selected uncertainty bonus coding in the vmPFC had a bias towards negative coding. Only 23% of significant neurons coded it positively during the trial onset period (P = 0.049, two-tailed binomial test), with 22% in the pre-decision period (P = 0.010, two-tailed binomial test). Together with negative action uncertainty coding in the vmPFC, this result indicates a general negative bias towards uncertainty coding in the vmPFC. Additionally, selected utility coding in preSMA also had a negative bias in the preSMA: only 21% of significant neurons coded it positively during the trial onset period (P = 0.041, two-tailed binomial test).

Taken together, these findings establish widespread value coding specific to the chosen option in all tested brain areas. One interpretation of these findings is that features of selected stimuli are monitored after the decision in the time window that immediately precedes the button press. While all areas displayed evidence of integrated selected utility coding, the preSMA represented this signal earlier than the other regions, which is consistent with the possibility that the preSMA is more closely involved in the actual choice process.

After feedback neuronal responses

The consequences of decisions offer information that can be leveraged to make better decisions in the future. We tested for neurons encoding reward information, probing for representations of outcome and reward prediction error (RPE) during the feedback period (Supplementary Figs. 4a-c; see the outcome model in Supplementary Table 2). Outcome (win or lose) was robustly encoded in the dACC, preSMA and vmPFC (percentage of neurons selected 34.3%, P = 0.002; 34.5%, P = 0.002; and 21.5%, P = 0.002, respectively, permutation test). The $Q$ value of the selected stimulus was also encoded in the preSMA (15.4%, P = 0.002, permutation test). We also probed absolute RPEs, which track surprise irrespective of valence. Absolute RPE was also encoded in the preSMA (11.6%, P = 0.002, permutation test; Supplementary Fig. 4).

Latency analysis revealed that contrary to the error signals we studied previously⁴⁷, dACC neurons encoded outcome significantly earlier than both preSMA and vmPFC (Supplementary Fig. 6; outcome-aligned median latency: 0.62 s versus 0.78 s, P < 0.001 and versus 0.87 s, P < 0.001, two-sided Wilcoxon rank-sum test). There was no difference between the onset of outcome signals in the preSMA and vmPFC (P = 0.267, Wilcoxon rank-sum test). Lastly, outcome neurons were active earlier than selected $Q$-value neurons in the preSMA (0.86 s, P = 0.008, Wilcoxon rank-sum test), suggesting that selected $Q$-value representations were not persistently maintained from the choice period.

To probe signed RPEs, we tested whether a significant number of neurons positively encoded outcomes and negatively encoded selected $Q$ values, or vice-versa. A neuron that encodes both of these values in opposite directions has sufficient information to support the computation of RPEs. We found that only seven of 58 preSMA neurons that encoded outcomes or selected $Q$ values at the time of the outcome did so in opposite directions. This number was not significantly larger than expected by chance assuming a null uniform distribution along the polar plane defined by outcomes and selected $Q$ values (12.0%, P = 0.987, binomial test).

Discussion

We investigated value-based decision-making at the level of human single neurons, while manipulating variables relevant to resolution of the explore–exploit dilemma, specifically, stimulus value, uncertainty and novelty. By recording from three areas of the frontal cortex implicated in decision-making across humans and other animals^{10,12,22,26,34,48-52}, we identified how these variables are encoded and addressed how they are integrated to inform decisions. Our findings highlight a particularly important role for the human preSMA in value-based decisions.

We found evidence for separate representations of the EV, uncertainty and novelty associated with options under consideration in human single neurons in both the preSMA and vmPFC, supporting the separable encoding of each of these decision variables across these areas. Crucially, we also found that a subset of EV-coding neurons were better explained by an integrated utility signal, in which the option’s EV was combined with uncertainty and novelty. This signal was most robustly represented in the preSMA, where it was encoded both at the single-neuron and population levels. These findings provide a proof of principle for the existence of an integrated utility signal in human frontal neurons. Importantly, the role of vmPFC in value coding was more strongly tied to post-decisional monitoring, unlike the preSMA, in which a significant portion of neurons tracked action-value and its components. Furthermore, we provide correlational evidence that preSMA neurons encode sufficient information to integrate the components of value utility.

Specifically, we identified a distinct population of preSMA neurons encoding the decision itself above and beyond stimulus utility, expanding on previous findings linking preSMA to volitional decision-making^53,54. Thus, unlike the dACC or vmPFC, the preSMA represented not only the key utility signal that informs choice but also the decision itself. These results for value-based decisions expand on previous work that reported choice signalling in categorization and memory tasks in the preSMA and dACC⁵⁵. We found robust outcome tracking in the dACC and preSMA, in agreement with previous findings in the human dorsomedial prefrontal cortex⁵⁶. While the preSMA and SMA⁵⁷ have been shown to monitor internally generated error responses, preceding dACC error neurons temporally⁴⁷, we observed that value-based feedback elicited earlier outcome responses in the dACC than in the preSMA. RPE, on the other hand, was more robustly encoded in the preSMA than in the dACC. Taken together, these results position the preSMA as having a central role in value-based decision-making in humans, particularly in decision tasks that elicit the integration of multiple stimulus features as required to balance the explore–exploit trade-off. Although we found that the preSMA has a privileged role in encoding decision variables, we expect that these computations are probably supported by a broader cortico-striatal network beyond the preSMA alone^58-64.

We note that while the human fMRI literature on value-based decision-making has tended to focus on the role of the vmPFC, orbitofrontal cortex and ACC in encoding value-related responses and choice as opposed to the preSMA, the preSMA emerges in meta-analyses focused on positive and negative correlates of value⁶⁵. However, the relatively poor spatiotemporal resolution of the fMRI signal makes it difficult to ascertain the precise role of the preSMA and indeed of each of these other regions in value-based decision-making from fMRI studies alone. Additionally, the action-specific utility signals or other action-specific decision variables that we found in the preSMA and elsewhere are unlikely to be accounted for by autonomic and skeleto-motor effects associated with generally anticipating a reward as noted in previous discussions on subjective value signalling⁶⁶. However, the chosen utility signals or other chosen decision variables reported in this study could potentially involve contributions of such non-specific valuation concomitants.

Note that our focus on manipulating uncertainty and novelty implied that this experimental design was not optimal for testing stimulus-based hypotheses, such as the value tied to a specific stimulus identity, as previously reported in the literature⁶⁷. In our current design, we frequently replaced old stimuli with new ones; consequently, each individual stimulus was shown for a relatively low number of trials. Additionally, a relatively high number of stimulus identities was used per session, decreasing the power of stimulus-based analyses. Therefore, a future study direction is to understand how human neurons encode the dynamic transformation between identity-based stimulus values and action-values, which fMRI evidence indicates is tied to a vmPFC-dorsomedial prefrontal cortex circuitry²².

Our findings support a distinction between dorsal and ventral areas of the frontal cortex, whereby dorsal regions contribute to action-based decisions while more ventral areas, such as the vmPFC, are involved in valuation but not in decisions over actions^34,49,68-72. In this study, we found that a similar organization applies at the level of human single neurons. However, we also found a degree of specificity in the dorsal human frontal cortex, where integrated utility and the decision itself are encoded: in the preSMA but not as robustly in the dACC. These findings situate the human preSMA as more prominently involved in the computations directly required for value-based decision-making than the subregion of the dACC from which we recorded. Thus, the present findings contribute to a more fine-grained understanding of functional specificity in the dorsomedial frontal cortex.

We also looked for the representation of variables pertinent to the selected option and thus contingent on the decision made. The integrated utility for the option that was ultimately chosen was widely encoded throughout all three of the brain regions we recorded from. It is noteworthy that this signal emerged markedly earlier in the preSMA than in the vmPFC, which is consistent with the possibility that the preSMA is more proximal to the generation of the decision itself than the vmPFC. Single neuron activity in the vmPFC also correlated with individual decision variables for the value, uncertainty and novelty of those stimuli that had been selected on a given trial. When taken together, these findings suggest a role for vmPFC neurons in post-decisional monitoring of option features, especially in the context of exploratory decision-making.

We found widespread outcome encoding across all three regions, in agreement with a vast literature implicating the prefrontal cortex in signalling outcomes in rodents^73-76, monkeys^77-80 and humans^50,81. We further found evidence for concurrent encoding of outcomes and selected EVs in the preSMA after feedback, which together constitute the two main components of RPEs^1,82,83. These findings suggest that preSMA neurons can support learning of reward expectations.

In conclusion, our results situate the human preSMA as an important centre for value-based decision-making, with a robust encoding of decision variables and, most crucially, an integrated utility signal at the single-neuron level that can be leveraged to inform choice. While vmPFC neurons encoded pre-decision and post-decision variables contingent on choice, neither this region nor the dACC showed an equivalently robust encoding of pre-decision integrated utilities or the choice itself. These findings suggest that value-based decision-making during exploration depends on highly specialized computations performed in distinct areas of the prefrontal cortex. Furthermore, the existence of an integrated utility at the level of single neurons that could serve as the input to the choice process suggests that relevant decision variables such as EV, uncertainty and novelty are first integrated into a unified neuronal representation before being entered into a decision comparison, shedding light on how subjective utility-based choices are implemented in the human brain.

Methods

Electrophysiology and recording

We used Behnke-Fried hybrid depth electrodes (AdTech Medical), positioned exclusively according to clinical criteria (Supplementary Table 3). Broadband extracellular recordings were performed with a sampling rate of 32 kHz and a bandpass of 0.1–9,000 Hz (ATLAS System, Neuralynx). The dataset reported in this study was obtained bilaterally from the vmPFC, dACC and preSMA with one macroelectrode on each side. Each macroelectrode contained eight 40-μm microelectrodes. Recordings were bipolar, using one microelectrode in each bundle of eight microelectrodes as a local reference.

Patients

Twenty patients (14 females) were implanted with depth electrodes for seizure monitoring before potential surgery for treatment of drug-resistant epilepsy. Patient age and sex information is included in Supplementary Table 3. Two of the patients performed the task twice, totalling 22 recorded sessions. Electrode location was determined based on preoperative and postoperative T1 scans obtained for each patient. All patients received a gift card containing US$50 at the end of their recording period regardless of task performance as compensation for their time. Patients were aware that task performance did not factor into compensation.

Task

Patients performed a two-armed bandit task (Fig. 1b). The task contained 20 blocks of 15 trials, for a total of 300 trials. The 20 blocks were split into two recording sessions with ten blocks each, with a 5-min break in between sessions. Each trial began with a baseline period (sampled randomly from a uniform distribution of 0.75–1.25 s), followed by a choice screen showing the two available slot machines presented on the left or on the right of the screen. The identity of each slot machine was uniquely identifiable by a painting displayed on the centre of each slot machine. After the button press, the chosen slot machine was shown for a period of 1–2 s (sampled randomly from a uniform distribution), followed by the outcome screen shown for 2 s. The outcome screen showed either a golden coin to represent winning a reward or a crossed out coin to represent not winning (both shown on top of the chosen slot machine).

To shape the novelty and uncertainty of the presented stimuli, we manipulated which stimuli would appear in each block and each trial according to the rules described as follows. For each block, the identity of the two slot machines that appeared in each trial was drawn randomly from a set of three possible options, selected specifically for each block. In the first block, the three options were selected randomly from a set of 200 paintings. In every subsequent block, one out of the three stimuli from the previous block was chosen to be replaced, substituting it for a new, unused stimulus out of the 200 paintings.

To manipulate the interaction between stimulus novelty and trial horizon, in every block after the first one, we chose stimuli to be held out and only presented after a minimum trial threshold, selected randomly for each block, between seven and 15 trials. For every block after the first one, we alternated whether the held-out stimulus would be one of the familiar ones or the new stimulus for that block.

The probabilities of receiving a reward from each slot machine were reset at the beginning of every block and determined according to the chosen difficulty of each block, which alternated between easy and hard conditions. Crucially, these reward probabilities did not change in each block. In the easy condition, reward probabilities were more widely spaced out between different slot machines and chosen from the values (0.2, 0.5, 0.8). In the hard condition, the possible probabilities were (0.2, 0.5, 0.6).

Some patients performed a shorter variant of the task, which consisted of 206 trials across ten blocks (Supplementary Table 4). In this version, the set of possible stimuli in each block contained five options; in each block, after the first one, two new options were introduced, one of which composed the held-out set along with one out of the three familiar options from the previous blocks. Bandit win probabilities were sampled from the linearly spaced interval (0.2, 0.8) in the easy blocks and from (0.4, 0.6) in the hard blocks. In the long version of the task, patients had to decide between the left or the right option by pressing a button in less than 3 s or the trial would be considered missed and no reward would be accrued. In the short variant of the task, no time limit was enforced. We pooled data from the two task variants together for all analyses.

Behavioural analysis and computational modelling

Logistic regression for value components and decisions.

We used a logistic regression model to describe how the past history of rewards, sampling history, stimulus exposure history and their interactions with trial number correlated with decisions (Fig. 1f). For this, we defined $Q$ values (denoted as $Q_s$) as the mean of a $\beta$ distribution that estimates the probability of receiving a reward from a bandit, as determined by the history of wins and losses after sampling a stimulus $s$, as well as $\delta Q=Q_{\text{left}}-Q_{\text{right}}$, the difference between left and right $Q$ values. Similarly, we defined an uncertainty value $U$ as the variance of the same $\beta$ distribution, as well as its corresponding differential $\delta U=U_{\text{left}}-U_{\text{right}}$. Finally, we defined novelty ($N$) as the variance of a $\beta$ distribution in which $\beta =1$ and the $\alpha$ parameter is the number of times patients were exposed to a stimulus $s$ in the entire session, as well as its corresponding differential $\delta N=N_{\text{left}}-N_{\text{right}}$.

We then performed a logistic regression using the MATLAB’s function mnrfit to model the probability $P_{\text{left}}$ of a left decision based on these regressors, as well as their interaction with the trial number $t$ within a block:

$$\log \frac{P_{\text{left}}}{1-P_{\text{left}}}={\beta }_0+{\beta }_1\delta Q+{\beta }_2\delta U+{\beta }_3\delta N+{\beta }_4\delta Q\times t+{\beta }_5\delta U\times t+{\beta }_6\delta N\times t$$ (1)

Uncertainty and novelty-based models of exploration.

We compared four nested computational models fitted to patients’ behaviour. Individualized model fits and model comparisons were obtained across the patient population through hierarchical Bayesian inference⁴³. This method yielded model parameters for each individual in the dataset, for each of the tested models, as well as exceedance probabilities, which expressed the probability that either model was the most frequent in the behavioural dataset⁸⁴.

We performed model comparison in a nested manner, which meant that the smaller models incorporated subsets of free parameters from the full model. As such, we describe the full model, which incorporated a learning rate, an inverse temperature parameter, an uncertainty bonus to be added to stimulus utilities and a novelty initiation bias. Notably, the task reported in this study did not offer the sensitivity required to probe for the interaction between novelty and uncertainty reported in ref.³⁹ because of the shorter task horizon and reduced stimulus set being learned. As such, we did not pursue an investigation of the relationship between these exploratory drives in the patient data. For completeness, the simplest model included only the learning rate and the inverse temperature, parameters that were included in all models; the second model also had the uncertainty bonus but no novelty initiation bias; and the third model had a novelty initiation bias but no uncertainty bonus.

The fourth (full) model we tested included an uncertainty bonus and a novelty initiation bias as mechanisms to support exploratory decision-making. In this model, the choice probability for a decision $d$ in a trial $t$ was estimated using the utilities assigned to the left ($U_{\mathrm{L}}$) and right ($U_{\mathrm{R}}$) options, through a softmax function:

$$P_t(d=\text{LEFT})=\frac{1}{1+e^{\beta (U_{\mathrm{R},t}-U_{\mathrm{L},t})}}$$ (2)

In this equation, $\beta$ is the inverse temperature free parameter. To balance incentives to explore and exploit different stimuli, the utilities assigned to each stimulus $s$ on a trial $t$ were defined to be the sum of its weighted $Q$ values and an uncertainty bonus $B$, depending on the past history of rewards received from the slot machine and how often the slot machine had been sampled, respectively:

$$U_{s,t}=Q_{s,t}+B_{s,t}$$ (3)

Our definition of $Q$ values relies on a Bayesian representation of the probability of receiving rewards from a slot machine. If the probability $P$ of receiving rewards from a slot machine is itself an unknown variable that patients must attempt to learn, then a simple assumption is that $P\beta (a,b)$, where $a$ is the number of wins plus one and $b$ is the number of no wins minus one. This distribution ranges between 0 and 1 and is initially a uniform when $a=b=1$. In the limit of infinite gambles, this distribution converges onto a $\delta$ centred around the true probability of receiving a reward from that slot machine.

Therefore, the $Q$ value was defined similarly to the EV of a $\beta$ distribution, as a function of the past history of wins and losses received from a slot machine, modified to account for the effect of recency over stimulus preferences:

$$Q_{s,t}=\frac{{\alpha }_{s,t}}{{\alpha }_{s,t}+{\beta }_{s,t}}$$ (4)

In this equation, ${\alpha }_{s,t}$ and ${\beta }_{s,t}$ describe the effect of previous wins and previous losses, respectively, received from the slot machine s before trial $t$.

The $\alpha$ term is defined as follows, where $H_{s,t}^W$ is how many times sampling slot machine $s$ has resulted in a win before trial $t$ and $w$ is an exponentially decaying effect of recency. The main role of the learning in this model is to mediate the importance of recent versus old trials in the assessment of $Q$ values. This effect has been previously illustrated for different learning rates in this class of models³⁹. The timescale of this exponential decay is determined by a learning rate free parameter $\lambda$, fitted in the interval (0,1):

$${\alpha }_{s,t}=1+\sum _{i=1}^{t-1}{w}_{i,t}{H}_{s,t}^W$$ (5)

$$w_{i,t}=(1-\lambda {)}^{(t-i)}$$ (6)

Similarly, the $\beta$ term is defined as follows, where $H_{s,t}^L$ is how many times sampling slot machine $s$ has resulted in a no win before trial $t$:

$${\beta }_{s,t}=1+\sum _{i=1}^{t-1}{w}_{i,t}{H}_{s,t}^L$$ (7)

We also allowed novelty to bias the initialization of the learning rate and inverse temperature parameters, to include an optimistic initialization strategy⁵ for exploration. This was done by including a novelty initialization bias-free parameter $n_I$, which was modulated by the same exponential decay $w_{0,t}$, creating the novelty bias $n_I{w}_{0,t}$. If $n_I{w}_{0,t}>0$, we would add this quantity to ${\alpha }_{s,t}$, resulting in a novelty-seeking bias; if $n_I{w}_{0,t}<0$, we added this quantity to ${\beta }_{s,t}$, resulting in a novelty avoidance bias.

The uncertainty bonus term in equation (3) was defined as a function of raw stimulus uncertainty, weighed by each patient’s uncertainty preferences, according to the uncertainty intercept parameter $u_I$:

$$B_{s,t}=V_{s,t}{u}_I$$ (8)

Raw stimulus uncertainty $V_{s,t}$ was defined as the variance of the $\beta$ distribution representing the option’s reward history as a function of how many times a stimulus has been sampled, using the previously defined ${\alpha }_{s,t}$ and ${\beta }_{s,t}$ terms:

$$V_{s,t}=12\frac{{\alpha }_{s,t}{\beta }_{s,t}}{({\alpha }_{s,t}+{\beta }_{s,t}{)}^2({\alpha }_{s,t}+{\beta }_{s,t}+1)}$$ (9)

We introduced a normalizing factor of 12 to the raw stimulus uncertainty equation to ensure that maximal uncertainty, obtained when ${\alpha }_{s,t}+{\beta }_{s,t}=1$, was equal to 1.

Neural data preprocessing

We performed spike detection and sorting with the semiautomatic template-matching algorithm OSort⁸⁵. Channels with interictal epileptic activity were excluded. Across all 22 sessions, we obtained 191 vmPFC, 137 preSMA and 108 dACC putative single units (436 in total). In this article, we refer to these isolated putative single units as ‘neuron’ and ‘cell’ interchangeably. For the single-neuron encoding analyses in this study, we preselected only neurons with more than a 0.5-Hz average firing rate across all trials, resulting in 172 vmPFC, 136 preSMA and 102 dACC putative single units (410 total).

Poisson GLM encoding analysis

We used Poisson regression GLMs to select for neurons, with spike counts as the dependent variables and different subsets of model variables as the independent variables. We computed the spike counts in every trial in four windows of interest (trial onset, from 0.25 s to 1.75 s, aligned to trial onset; pre-decision, from −1 s to 0 s, aligned to button press; and outcome, from 0.25 s to 1.75 s, aligned to the outcome onset). For visualization purposes, we also fitted the same models with 0.5-s time windows, sliding by 16-ms steps, within the same time limits. We then tested hypotheses about how the spike count of each neuron was correlated with left and right utility ($U_{\mathrm{L}}$, $U_{\mathrm{R}}$), chosen side (Side), left and right $Q$ value ($Q_L$, $Q_R$), left and right uncertainty bonus ($B_{\mathrm{L}}$, $B_{\mathrm{R}}$), left and right novelty ($N_{\mathrm{L}}$, $N_{\mathrm{R}}$), as well as their selected and rejected counterparts, outcome ($O$) and absolute RPE. For a summary of GLM variable abbreviations, see Supplementary Table 5.

In the analyses with action-value components (see Supplementary Table 2 for a list of models), we aimed to determine whether each neuron significantly encoded the left or right components, or their respective sums or differences. Previous work indicated that the proportion of neurons classified as coding for both the left and right components of value may be biased by model specification, especially if the adopted criterion uses independent significance thresholds for the left and right value regressors⁴⁵. Therefore, we suggest an adaptation of a classification procedure proposed by the authors to mitigate such biases, described as follows. Broadly, we first determined which neurons are generally coding for each variable of interest, then we determined whether they code left and right action-values jointly or separately. Specifically, we first fitted the full action-value GLM to each neuron’s spike rate, with left and right components. Second, we fitted a restricted model containing every pair of left and right action-value components, except the pair we intended to test (for example, when testing for $Q$-value neurons, the restricted model would only contain left and right uncertainty and left and right novelty values). Third, we determined which neurons are generally coding for each action-value component with a model comparison approach, by performing an LR hypothesis test between the full and unrestricted models. Fourth, to classify a neuron as significant or not, we compared their test statistic with a bootstrapped null distribution, obtained with a session permutation procedure described further. Fifth, for each neuron considered significant in the LR test, we determined its position in a two-dimensional polar coordinate space of the regression coefficients for the left and right action-value components. For this, we used the t-scores for the left and right action-value components obtained from fitting the full action-value GLM. The polar radius of each neuron for each action-value component ($Q$ value, uncertainty or novelty) in polar coordinates is given by $\rho =\sqrt{t_{\text{left}}^2+t_{\text{right}}^2}$, whereas the polar angle of each neuron depends on the relationship between the $t$-scores for the left and right regressors:

$$\theta =\text{arctan}\frac{t_{\text{right}}}{t_{\text{left}}}$$ (10)

Finally, we used the angle $\theta$ to classify each significant neuron as coding for left or right values exclusively, or their sum or differences. As illustrated in Supplementary Figure 2e, neurons in the ($-\pi ∕8$, $\pi ∕8$), ($7\pi ∕8$, $\pi$) or ($-\pi$, $-7\pi ∕8$) intervals were classified as left value neurons; neurons in the ($3\pi ∕8$, $5\pi ∕8$) or ($-5\pi ∕8$, $-3\pi ∕8$) intervals were classified as right value neurons; neurons in the ($5\pi ∕8$, $7\pi ∕8$) or ($-3\pi ∕8$, $-\pi ∕8$) intervals were classified as difference neurons; and neurons in the ($\pi ∕8$, $3\pi ∕8$) or ($-7\pi ∕8$, $-5\pi ∕8$) intervals were classified as sum neurons.

To create a null distribution for the LR test statistics and mitigate the effect of ’nonsense’ correlations that might arise due to incorrectly classifying random-walk neurons as coding for one of the time series of interest, we adopted a session permutation method. This issue may arise in our case because of the correlations across time steps in the temporal series of regressors and firing rates^86,87. Specifically, to generate a null distribution, we assumed that in a neuron truly coding for a regressor, the regressor time series should be better explained by that neuron than by a randomly selected neuron from another session. Therefore, we generated 500 random permutations in which the spike rate time series of each neuron was replaced with the time series of another eligible neuron from another session. Eligibility was determined by whether the random neuron was recorded in at least as many trials as the neuron to be replaced, to guarantee time series of equivalent size. We then obtained LR test statistics from each null random permutation and obtained a P value for the true LR test statistic by measuring which quantile of the null distribution it belonged to, the lowest P value possible being $P=1∕500$. Additionally, we sought to determine whether the significant neuron count was larger in a brain area than expected by chance by performing a permutation test. For this, we repeated the same classification procedure for each of the 500 permutations and obtained the significant neuron count. Then, we obtained the null distribution of significant neuron counts in each permutation and compared it with the true count to obtain a $P$ value. The lowest possible $P$ value occurs when the true neuron count is larger than all the null neuron counts, resulting in $P=1∕500=0.002$. For a summary of significant neuron counts obtained with this method, see Supplementary Table 6.

We also tested whether neuronal activity in the pre-decision period correlated with whether a trial was classified as an explore or a non-explore trial, correcting for selected uncertainty bonus. We defined explore trials as those in which $Q_{\text{sel}}<Q_{\text{rej}}$ and $U_{\text{sel}}>U_{\text{rej}}$, defining the explore flag Explore = 1 for those trials and Explore = 0 for all others. For all encoding analyses, we specified the models described in Supplementary Table 2 and fitted them with the MATLAB function fitglm.

Binomial test

After labelling each neuron as coding for a variable of interest (such as integrated utilities), another way to determine whether neuron counts in each brain area were larger than expected by chance were binomial tests on the number of significant neurons, relative to the size of the tested population of each brain area. Concretely, assuming a false positive rate of 5% and a Bernoulli process to generate significant neurons at this rate, the number of neurons $S$ falsely classified as significant within a population of size $N$ is given by a binomial distribution of $S\sim \text{binomial}(N,0.05)$. Accordingly, we derived a binomial $P$ value for the probability of obtaining an observed sensitive neuron count $K$ larger than expected by chance, using the cumulative binomial distribution: $P=1-\text{binomialCDF}(K,N,0.05)$.

Poisson latency analysis

To determine when individual neurons were active at a single-trial level, we performed Poisson latency analyses⁴⁴ for preselected groups of neurons sensitive to the variable of interest in the encoding analyses (Figs. 2h,4b and Supplementary Fig. 4I). This method detects the first point in time in which interspike intervals significantly differ from what would be expected from a constant firing rate Poisson point process, using the neuron’s average firing rate as the rate parameter. We used a significance parameter of $P<0.05$ as our burst detection threshold for all analyses.

Jaccard index test

After performing the Poisson GLM encoding analyses, we tested whether the subpopulations of neurons that were sensitive to two variables of interest had significant overlap. For this, we computed the Jaccard index⁸⁸ of overlap between neurons sensitive to each of the variables $X$ and $Y$, where $N_X$ and $N_Y$ indicate the number of neurons sensitive to the variables $X$ and $Y$, respectively, and $N_{X,Y}$ indicates the number of neurons concurrently sensitive to both variables:

$$J=\frac{N_{X,Y}}{N_X+N_Y-N_{X,Y}}$$ (11)

To compute $P$ values for each comparison between two variables, we bootstrapped a null distribution of Jaccard indexes using 1,000 reshuffles, considering that $X$ and $Y$ are independent variables with a false positive rate of $P=0.05$.

LR hypothesis testing

We tested whether neurons in action $Q$ value or action utility sensitive subpopulations had their activity better explained by an unrestricted model including the main additive components of utility ($Q$ value and uncertainty bonus) or by a restricted model including only $Q$ values, given the correlations we observed between $Q$ values and integrated utility values. Neurons that had their activity better explained by the unrestricted model were defined as true integrated utility neurons.

Before constructing the unrestricted and restricted models, we determined the preferred side of each neuron by fitting their activity with the utility and decision model, including left utility, right utility and decision as regressors (Supplementary Table 2) and defining the preferred side as the one in which its utility regressor has the highest absolute $t$-score.

Then, using the spike count $Y$ of each neuron, we fitted an unrestricted GLM including $Q$ values and uncertainty bonuses. We performed the model fitting and obtained a log-likelihood $L_u$ using MATLAB’s function fitglm:

$$\log (E(Y\mid x))=b_0+b_1{Q}_{\text{preferred}}+b_2{B}_{\text{preferred}}+b_3\text{decision}$$ (12)

To each neuron in this subpopulation we also fitted a restricted GLM including $Q$ values but not uncertainty bonuses and obtained its log-likelihood $L_r$:

$$\log (E(Y\mid x))=b_0+b_1{Q}_{\text{preferred}}+b_2\text{decision}$$ (13)

We also performed this analysis including novelty regressors into the restricted and unrestricted models and obtained qualitatively equivalent results in all instances. Specifically, adding novelty to the GLM yielded 50% of preSMA neurons($P=9.8\times {10}^{-11}$, binomial test) at trial onset and 55% during the decision period ($P=1.1\times {10}^{-14}$, binomial test) being better explained by the unrestricted model, which is a similar proportion to what we report without novelty. Finally, we performed LR tests with the MATLAB’s function lratiotest between the unrestricted and restricted models, by computing the LR test statistic $\text{LR}=2(L_u-L_r)$ and comparing it to a chi-squared null distribution for LR with one degree of freedom, stemming from one variable restriction. Neurons that rejected the null restricted model at a significance level of $\alpha =0.05$ were defined as integrated utility neurons.

For the subpopulation of integrated utility neurons, we used their fits from the unrestricted models to determine whether activity in these neurons correlated with $Q$ values and uncertainty bonuses individually more than expected by chance. We averaged absolute $t$-scores for $Q$ value and uncertainty bonus across integrated utility neurons to measure their collective degree of correlation regardless of excitation or inhibition. We then compared these values with average absolute $t$-scores obtained from bootstrapping 500 iterations of unrestricted model fits shuffling spike counts $Y$. We derived $P$ values from the number of times the true average absolute $t$-score surpassed the bootstrapped iterations.

Similarly, we performed an LR test to test whether neurons encoded an integrated selected utility signal in the pre-decision period by fitting the following unrestricted model:

$$\log (E(Y\mid x))=b_0+b_1{Q}_{\text{selected}}+b_2{B}_{\text{selected}}$$ (14)

Subsequently, we compared the unrestricted model with the following null restricted model:

$$\log (E(Y\mid x))=b_0+b_1{Q}_{\text{selected}}$$ (15)

We then followed the same likelihood test protocol described above to determine whether neurons would be classified as integrated utility neurons or not.

Dimensionality reduction and decoding with dPCA

To decompose the contribution of variables of interest and decisions to the neural population data and decode these variables interest from patterns of neural activity, we used dPCA⁴⁶.

For each variable of interest, and each brain area, we created a pseudopopulation aggregating trials from all patients to generate a full data matrix $X$, with dimensions $(N,SQTK)$, where $N$ is the total number of neurons recorded in that brain area, $S$ is the number of stimulus quantiles used to partition trials (low, medium and high), $Q$ is the number of possible decisions (left and right), $T$ is the number of time bins and $K$ is the number of trials used to construct the pseudopopulation as described further. First, we binned spike counts into 500-ms bins, with a 16-ms time window step. We repeated the binning procedure in two different time periods: the trial onset period (0 s, 2 s), aligned to trial onset; and the pre-decision period (−2 s, 1 s), aligned to button press.

Constructing pseudopopulations

To create neural pseudopopulations for dPCA, we pooled trials from all sessions and treated them as if they had been recorded simultaneously. To allow for trials from different sessions to be grouped together, despite having continuous variables of interest, we pooled groups of trials into three quantiles with the same number of trials, dividing the full range of each variable for each session into low, medium and high levels. After obtaining these quantiles, we assigned every trial in each session to one out of 3 × 2 = 6 categories, to account for all possible combination of quantile levels and decisions, and randomly sampled an equal number $k$ of trials from each category, for each session, such that ${\Sigma }_{\text{sesslons}}k=K$. We chose $k=15$ for it to be small enough to allow sampling an equal number of trials from each of the six categories for every session, while including as many training examples as possible.

To mitigate biases introduced during the random trial sampling procedure, we repeated these steps ten times, yielding ten pseudopopulations on which the dimensionality reduction and decoding procedures were repeated independently.

dPCA dimensionality reduction

For dPCA dimensionality reduction, the full data matrix $X$ is centred over each neuron and decomposed as a factorial analysis of variance where $t$, $s$ and $d$ are labels to indicate the time, stimulus and decision marginalizations, respectively:

$$X=X_t+X_{ts}+X_{td}+X_{tsd}+X_{\text{noise}}=\sum _{\varphi }{X}_{\varphi }+X_{\text{noise}}$$ (16)

The goal of dPCA is to minimize the regularized loss function, where $F$ indicates the Frobenius norm and $\mu$ is the ridge regression regularization parameter, determined optimally through cross-validation:

$$L=\sum _{\varphi }(\Vert X_{\varphi }-F_{\varphi }{D}_{\varphi }X{\Vert }_F^2+\mu \Vert F_{\varphi }{D}_{\varphi }{\Vert }_F^2)$$ (17)

$F_{\varphi }$ and $D_{\varphi }$ are the non-orthogonal encoder and decoder matrices, respectively, arbitrarily chosen to have three components for each marginalization. Therefore, dPCA aims to reduce the distance between each marginalized dataset and their reconstructed version obtained by projecting the full data matrix onto a low-dimensional space with the decoders $D$ and reconstructing it with the encoders $F$.

dPCA decoding

We used the same dPCA framework to perform population decoding of the variables of interest. The dPCA linear decoding pipeline has been previously described in detail⁴⁶, but we briefly discuss it in this article.

First, the pseudopopulation data matrix $X$ of dimensions $(N,SQTK)$ is divided into training and test datasets by leaving out one random trial for each of the $SQ$ possible combinations of stimulus levels and chosen side, for all neurons and time points, to form $X_{\text{test}}$ of dimensions $(N,SQT)$ and $X_{\text{training}}$ with the remaining data points. We performed this random trial sampling procedure 100 times for each of the ten random pseudopopulations, resulting in a total of 1,000 random resamples.

We performed the aforementioned dPCA steps with the training data matrix $X_{\text{training}}$ to obtain a decoder matrix $D_{\varphi }$, with $i=(1,2,3)$ representing each of the three demixed principal components for each marginalization $\varphi$.

To perform stimulus decoding, we iterated over the three components $i=(1,2,3)$ to obtain the mean projections over all training trials, for each stimulus class $s=(1,\dots ,S$ pertaining to the current marginalization, and the vectors of decoded projections for test trials, for each unique test trial $k=1,\dots ,SQ$, representing all the possible stimulus-decision combinations:

$$P_{\varphi ,s}^{\text{training}}=\left[\begin{array}{c}\hfill <D_{\varphi ,1}{X}_{\text{training}}{>}_s\hfill \\ \hfill <D_{\varphi ,2}{X}_{\text{training}}{>}_s\hfill \\ \hfill <D_{\varphi ,3}{X}_{\text{training}}{>}_s\hfill \end{array}\right],P_{\varphi }^{\text{test},k}=\left[\begin{array}{c}\hfill D_{\varphi ,1}{X}_{\text{test},k}\hfill \\ \hfill D_{\varphi ,2}{X}_{\text{test},k}\hfill \\ \hfill D_{\varphi ,3}{X}_{\text{test},k}\hfill \end{array}\right]$$ (18)

We then defined the decoded class $C_k$ to be the one that minimizes the three-dimensional Euclidean distance between the test projection and the mean training projections:

$$C_k=\text{arg}\underset{s}{\text{min}}\Vert P_{\varphi ,s}^{\text{training}}-P_{\varphi }^{\text{test},k}\Vert$$ (19)

We obtained classification accuracy values for each trial resample by counting how many test trials were correctly labelled and averaged classification accuracy values over the 100 random test trial resamples, as well as the ten pseudopopulation resamples.

Equivalently, to perform decision decoding, we followed the same steps, except that we obtained mean projections over all training trials for each decision class $Q=(1,\dots ,Q)$ to compare with the test trial projections.

Significance scores for each time bin were determined by obtaining the distribution of null scores from the random test trial reshuffles and computing the quantile placement of the true decoding accuracy, assuming an approximate normal distribution for reshuffled decoding accuracies. We subsequently Bonferroni-corrected significance scores for multiple comparisons across time bins.

dPCA component projection distance

To summarize how dPCA representations of utility and decision differ for low- and high-utility trials, as well as left and right decisions (Fig. 4f), for every time bin, we projected data $X_{\text{subset}}$ from each trial subset (low-utility trials, high-utility trials, left-decision trials and right-decision trials) onto the demixed principal components, expressed by the decoder matrix $D$, obtaining $D{X}_{\text{subset}}$. Note that each row of $D$ represents one demixed principal component for the dataset. We then computed Euclidean distances between projections $D_{\text{decision}}=\Vert D{X}_{\text{left}}-D{X}_{\text{right}}{\Vert }^2$ and $D_{\text{utility}}=\Vert D{X}_{\text{high}}-D{X}_{\text{low}}{\Vert }^2$. We subsequently normalized projection distances into the (0, 1) range.

Statistical test assumptions

For two-sample comparison tests reported in the behavioural analysis (Fig. 1d), we tested for equal variances with an F-test, using the MATLAB function vartest2 and for sample normality with a Kolmogorov–Smirnov test, using the MATLAB function kstest. In all samples, we did not reject the equal variance and normality null hypotheses. Therefore, we performed two-sample t-tests with the MATLAB function ttest2. Similarly, we tested for normality before performing one-sample t-tests on model fits (Fig. 1f and Supplementary Information; additional behavioural analysis) with the MATLAB function ttest and found no deviation from normality. To compare neural temporal latencies across variables or brain areas, we did not assume data normality and performed non-parametric Wilcoxon rank-sum tests. Finally, permutation tests for neural counts did not require any additional assumptions on data distributions.

Data availability

Behavioural and neural data have been deposited in the OSF platform: https://osf.io/34b9f/?view_only=be3c529466fa444d8b97a2bab8951435.

Code availability

The code for data analysis can be found at: https://github.com/43technetium/casino_task_analysis.