Cell protrusions and contractions generate long-range membrane tension propagation

Summary:

Membrane tension is thought to be a long-range integrator of cell physiology. During migration, membrane tension has been proposed to enable cell polarity through front-back coordination and long-range protrusion competition. These roles necessitate effective tension transmission across the cell. However, conflicting observations have left the field divided as to whether cell membranes support or resist tension propagation. This discrepancy likely originates from the use of exogenous forces that may not accurately mimic endogenous forces. We overcome this complication by leveraging optogenetics to directly control localized actin-based protrusions or actomyosin contractions while simultaneously monitoring the propagation of membrane tension using dual-trap optical tweezers. Surprisingly, actin-driven protrusions and actomyosin contractions both elicit rapid global membrane tension propagation, while forces applied to cell membranes alone do not. We present a simple unifying mechanical model in which mechanical forces that engage the actin cortex drive rapid, robust membrane tension propagation through long-range membrane flows.

Graphical Abstract

IN BRIEF:

Experiments and modelling reveal the requirements for rapid and robust membrane tension propagation

Introduction:

For proper physiology, cells need a way to link short-range biochemical signaling events with long-range integration of cell-wide behaviors. Membrane tension is thought to serve as this global coordinator during cell migration. Membrane tension is the resistance of membrane to deformations. In cells membrane tension is thought to be a combination of in-plane tension and adhesion between the membrane and the underlying actin cytoskeleton^1,2. It has been proposed that membrane tension guides shape determination in motile cells by relaying actin-based protrusive forces at the front to the disassembly and contraction of the rear^1,3–14. Conversely, the retraction of the trailing edge appears to modulate actin organization in the cell front through propagated membrane tension changes¹⁵. Long-range membrane tension propagation may similarly enable protrusions to communicate with one another for the winner-take-all that establishes the axis of cell movement^16–19. Membrane tension is thought to serve as a central regulator in many other facets of cell and tissue physiology, including cell spreading and membrane trafficking^11,20–25, immune response^26,27, cell fate^28,29, cell division³⁰, and organ homeostasis^31–33.

To operate as a long-range integrator of cell shape and movement, membrane tension needs to propagate rapidly and efficiently across the cell. However, the actin cortex’s attachment to the plasma membrane appears to inhibit membrane flow and tension propagation when external forces are applied to the plasma membrane^26,34–36. It remains a source of significant debate as to whether cell membranes support or resist long-range membrane tension propagation. This is a crucial point to resolve for understanding the role of membrane tension as a global integrator of cell shape and movement.

Several factors could potentially underlie the discrepancies among these conflicting studies of membrane tension propagation. For instance, tension propagation could be cell-type dependent, perhaps more efficient in migrating cells than non-motile cells^35,37,38. Alternatively, the origin of discrepancies could stem from limitations of traditional tools to manipulate and analyze membrane tension. For example, exogenously-applied mechanical perturbations of the plasma membrane may elicit different tension responses than the endogenously-generated mechanical forces that are exerted during cell migration. To overcome these limitations, we implemented optogenetics to control localized actin-based cell protrusions or actomyosin contractions while simultaneously monitoring membrane tension response at multiple locations around the cell using high-precision force measurements with dual-trap optical tweezers. We find that optogenetically-activated cell protrusions and actomyosin contractions both induce long-range membrane tension propagation within seconds. In contrast, perturbations affecting only the plasma membrane fail to elicit propagation of membrane tension—consistent with previous results^34,35,37. We propose a simple unifying mechanical model in which the cortex resists membrane flow when forces are applied to the plasma membrane alone. In contrast, when forces engage the cortex, the membrane and cortex act as an integrated system to efficiently transmit membrane tension throughout the cell. Our work demonstrates that membrane tension has the properties expected for a long-range integrator of cell physiology, critical for its role in regulating cell shape and movement.

Results:

Local cell protrusions elicit a rapid long-range increase in membrane tension.

To investigate membrane tension propagation upon endogenous force generation, we employed an optogenetic approach (Opto-PI3K)^39,40 to activate localized actin-driven membrane protrusions in neutrophil-like HL-60 cells (Figure 1A, B, Figure S1A-E; video S1) and increase membrane tension at the protruding site^9,16,41. The propagation of membrane tension can be probed via a membrane tether pulled out on the opposite side of cell body using a bead (coated with lectin to bind carbohydrate groups on the membrane) and held by an optical trap (a.k.a. trap-based tether pulling assay; Figure 1C; see Methods). To verify that our optical trap experiments measure forces exerted by the plasma membrane as opposed to potential actin polymerization within or along the membrane tether^42,43, we ensured that trapped beads linking to a membrane tether snap back to the cell within seconds upon release of the optical trap at the end of our experimental measurements (Figure 1D, video S1; this was a standard control in our operation protocol for all sets of optical trap experiments; see Methods). In response to light-induced actin-driven protrusions, we observed a rapid long-range increase in membrane tension (Figure 1E,F, Figure S1F-K, video S2). The long-range rise in tension within ~5–15s of light activation is in stark contrast to the conclusion arrived at in recent studies³⁴ that “cell membranes resist flow.” We also verified that the observed increase in tension correlates with the local activation of the actin regulator, Rac GTPase, which is downstream of phosphoinositide 3-kinase (PI3K) activation and precedes actin-driven protrusion (Figure S1A-E). As an additional control, we treated the cells with the actin inhibitor latrunculin B and observed a lack of membrane tension increase following light activation (Figure 1F,G, Figure S1L, O). These results demonstrate that actin-based protrusions elicit a rapid long-range propagation of membrane tension.

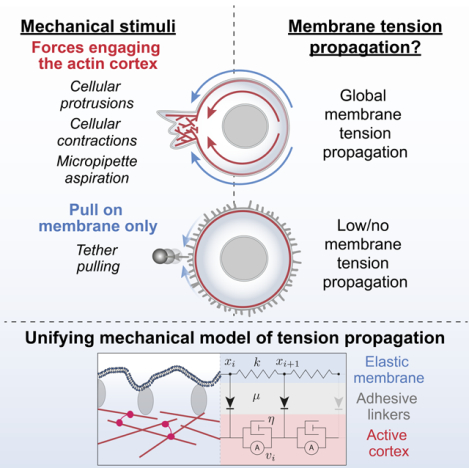
Figure 1. Local cell protrusions elicit a sharp increase in membrane tension on the opposite side of the cell within seconds.

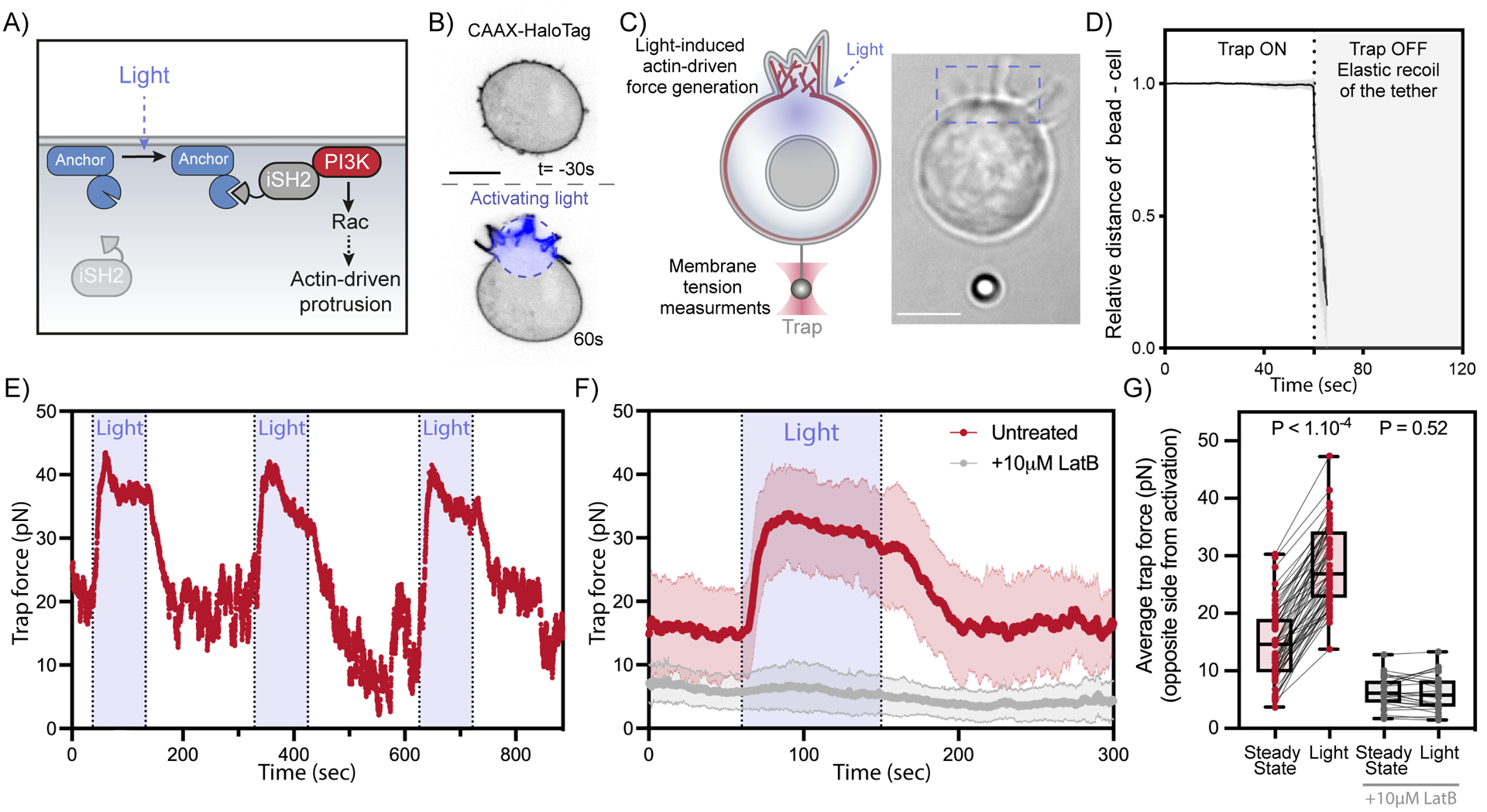
(A) Optogenetic control for light-induced activation of phosphoinositide 3-kinase (PI3K) via localized recruitment of inter SH2 domain (iSH2), resulting in Rac GTPase activation that initiates actin-driven cell protrusions (see Methods). (B) Time-lapse confocal images of a neutrophil-like HL-60 cell expressing opto-construct (Opto-PI3K) and membrane marker (CAAX-HaloTag) showing localized membrane protrusion upon light activation. (C) Following light-activated protrusion on one side of the cell (top of frame), changes in membrane tension on the opposite side (bottom of frame) are measured via a membrane tether held by an optical trap. Right, brightfield image of a protruding cell during tether pulling assay. (D) After tether pulling measurements, the trapping laser is turned off and the elastic recoil of the bead toward the cell is observed to confirm the absence of cytoskeleton in the tether. (means ± SD; n>15, N=5) (E) Representative time trace of trap force (a direct readout of cell membrane tension change) reveals robust and sharp increase in membrane tension over repeating cycles of light-activated protrusion on the opposite end of the cell (as in panel C); light: 90s on (shaded area). (F) Red: averaged time trace of trap force before (Steady-state), during (Light), and after activating cell protrusion (means ± SD; n>60, N=8). Grey: as a control, averaged trace from cells treated with actin polymerization inhibitor (10 μM latrunculin B) shows little membrane tension change upon optogenetic activation. (G) Averaged trap force before (Steady-state) and during activation. Box and whiskers: median and min to max; p values from Wilcoxon paired Student’s t test. Scale bars: 5μm. See also Figure S1 and Video S1.

Actin-driven protrusions stimulate global, unattenuated, membrane tension propagation.

To examine the dynamics of membrane tension propagation in more detail, we performed a dual-tether pulling assay and simultaneously monitored membrane tension on the side and the back of the cell (at 90° and 180° from the site of illumination, respectively) throughout multiple cycles of light-induced protrusion (Figure 2A–C, Figure S2, video S2). Interestingly, the two membrane tethers exhibit a near-simultaneous increase in tension, with a delay on average of 1.2 ± 1.2s between the two (Figure 2D). Readouts on both tethers plateau towards similar tension levels (Figure 2B, E, Figure S2A-C). Furthermore, membrane tension measurements of the two tethers remain highly correlated during light-activated protrusion and during recovery (Figure 2F). Our experiments indicate that endogenous actin-based protrusions generate a long-range increase in membrane tension that is transmitted virtually undampened across the cell within seconds.

Figure 2. Actin-driven protrusions stimulate global, nearly undampened, membrane tension propagation.

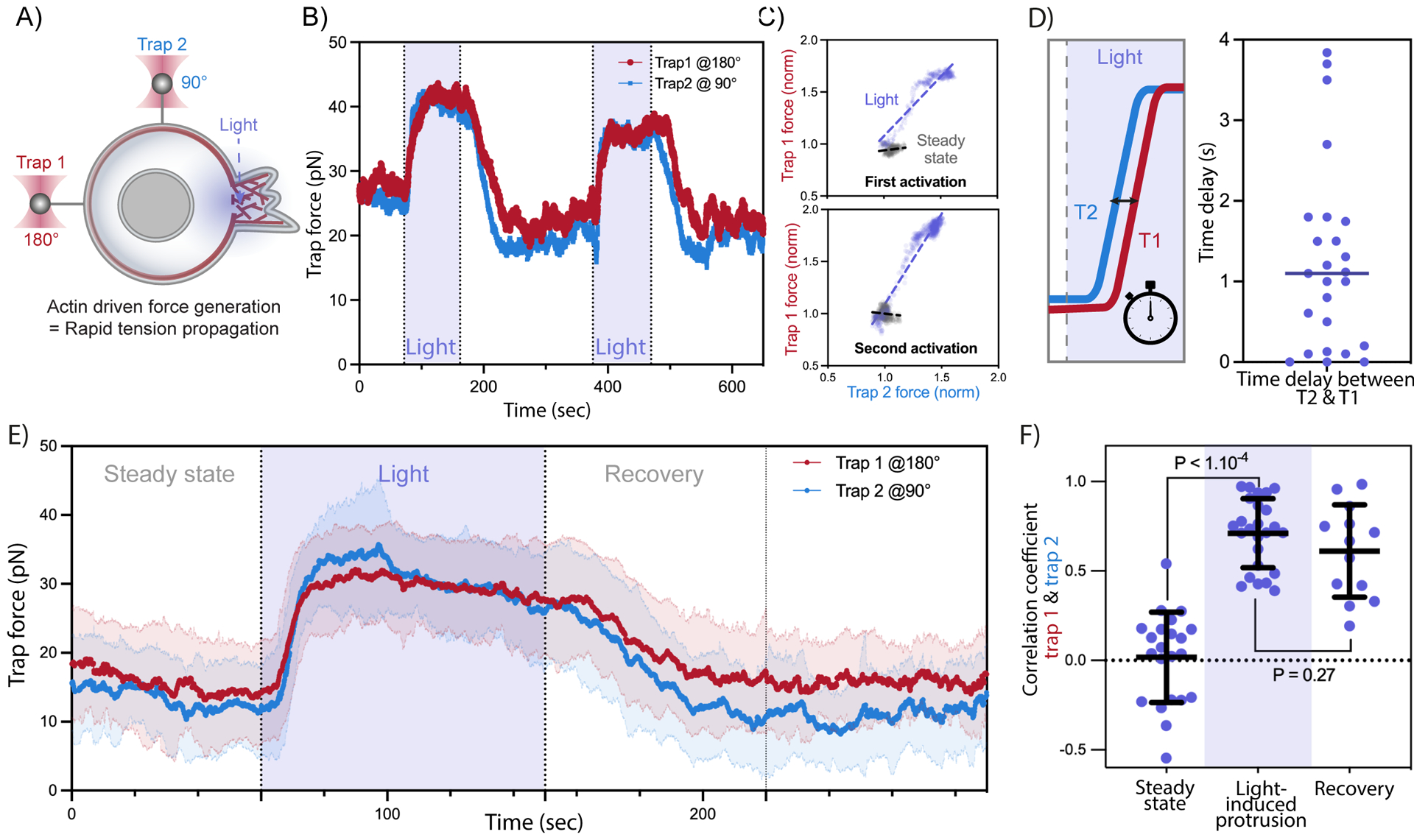
(A) A dual-tether pulling assay to simultaneously monitor membrane tension on the far-end (left, trap 1 at 180°) and on the side of the cell (top, trap 2 at 90°) during light-activated protrusion. (B) Representative time traces of dual trap forces over successive cycles of light-activated protrusion show coinciding tension increases on both membrane tethers adjacent to (trap 2) and at the opposite cell surface from (trap 1) protrusion; light: 90s on (shaded area), 180s off. (C) Correlation between trap forces at the two tether positions during activation (blue) remains robust from first activation cycle to the next; for comparison, minimal correlation is seen between the two tethers before optogenetic activation (grey). Dashed line: linear regression. (D) Left: time delay measured between tension rise on membrane tethers adjacent to (trap 2 at 90°, blue) and opposite from (trap 1 at 180°, red) cell protrusion. Right: in most cells, the traps detect membrane tension increase on both tethers within a second or less of one another, indicating a rapid propagation of tension across the cell. (E) Averaged traces of dual trap forces before, during (Light), and after activation (n>25, N=4). (F) Pearson correlation coefficient between dual trap forces measured at steady state, during light activation, and recovery afterwards (70s post light). Error bar: means ± SD; p values from Welch’s unpaired Student’s t test (n>10, N>4). See also Figure S2 and Video S2.

The actin cortex resists membrane tension propagation when external forces are applied to the membrane alone.

The contradictory observations between our current work and previous studies^34,35,37,38 may originate from how a mechanical perturbation is applied to cell membranes. Here, we optogenetically induce cellular membrane protrusion (i.e., endogenous actin-driven), eliciting rapid global membrane tension propagation. In this approach, the forces of actin polymerization are potentially applied to both the cortex as well as the plasma membrane. In contrast, previous studies concluding that membrane tension is locally constrained by the actin cytoskeleton³⁴ used a pair of membrane tethers to pull on the cell membrane (i.e., exogenous bead-pulling), thereby applying forces to the plasma membrane alone. To test whether the membrane tether-induced forces also fail to propagate in our cells, we repurposed our dual-tether assay to dynamically pull one tether by actively moving the first trap while measuring membrane tension on a nearby membrane tether held in place by the second trap (i.e., Figure 2A vs. Figure 3A). In line with analogous experiments performed in epithelial cells, we observe no propagation of membrane tension from the extending tether to the static one (Figure 3A–C, J, K, Figure S3A, E; video S2)—even with the two tethers in close proximity (<2μm apart). In contrast, when we performed the same dual-tether assay on cellular blebs (membrane detached from actin cortex, achieved in latrunculin-treated cells), tension propagates almost instantly (<100μs, i.e., below the temporal resolution of the optical tweezers instrument; Figure 3D–F,J,K, Figure S3B-D, F; video S2), in agreement with similar measurements in epithelial cells³⁴. These bleb-based experiments can only test tension propagation at the size scale of cellular blebs (<4μm). To test whether tension can propagate for longer distances, we performed tether experiments in cells treated with inhibitors that efficiently disassemble the actin cytoskeleton. Because latrunculin does not suffice to depolymerize a population of latrunculin-resistant actin filaments, we used a combination of latrunculin treatment and osmotic shock, which has previously been shown to be effective at more fully depolymerizing the actin cortex⁴⁴, as we verify in our cells (Figure S3G). These cortex-free cells exhibited rapid long range propagation of membrane tension, both for traps at 90° (Figure 3G–I), and for traps at opposite ends of the cell (Figure S3H-J, video S2). Both blebs and cortically depolymerized cells propagate tension when forces are applied to the plasma membrane alone, but cells with an intact cortex do not (Figure 3J,K). Our observations that effective membrane tension propagation depends on how mechanical perturbations are exerted within the context of the same cell type (Figures 2, 3, S2, S3) suggest that existing disagreements in the field are at least partially methodological in nature. While mechanical perturbations via exogenous tether pulling fail to elicit membrane tension propagation (consistent with the ‘picket fence’ model of cortex adhesion to the plasma membrane^34,38), endogenous actin-based force generation efficiently promotes membrane tension propagation across the cell.

Figure 3. Membrane tension does not propagate upon direct mechanical pulling on the cell membrane.

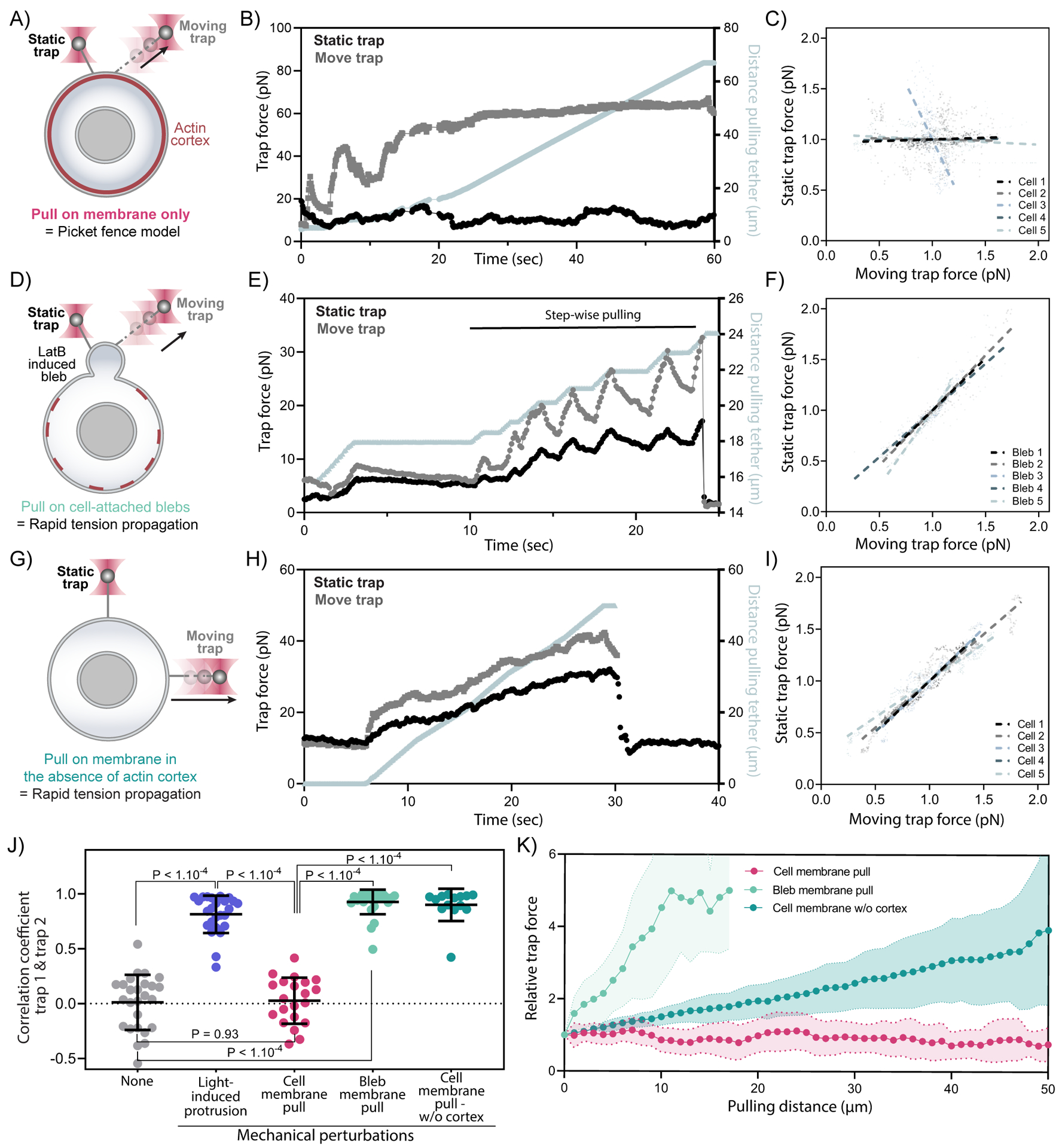
(A) A dual-tether assay to detect tension propagation (static tether, left) while a nearby force is exerted through the use of an optically trapped bead to pull on the membrane ~2-um away (moving tether, right). (B) An example time trace of trap force for dual membrane tension measurements, where one moving trap (T2, grey) dynamically pulls on the cell membrane by continuously pulling and extending the membrane tether, while the other trap controls a second static membrane tether (T1, black) to monitor nearby changes in membrane tension. The increase in length of the extending tether from the cell body is plotted in grey along the right y-axis. (C) Correlation plots of normalized trap forces between the moving and static tethers. Five representative measurements from different cells are shown; dashed lines: linear regression. (D)(E)(F) Similar to (A)(B)(C) but probing tension in blebs (membrane detached from actin cortex generated by using latrunculin B treatment to weaken the actin cortex); here a high correlation is observed between static and moving tethers. (G)(H)(I) Similar to (A)(B)(C) but probing tension in cells where the actin cortex has been significantly disassembled using a combination of latrunculin B treatment and osmotic shock; a high correlation is observed between static and moving tethers even at a significant distance from one another (here 90 degrees, but in supplement S3H-J 180 degrees. (J) Pearson correlation coefficient between dual trap forces measured before perturbations (None; light gray), upon light-activated protrusions (purple; Figure 2), during cell membrane pulling (pink; panel A-C), during membrane pulling on a bleb (light green; panel D-F), and during cell membrane pulling in cells with heavily disassembled actin cortex (Dark green; panel G-I). Error bar: means ± SD; p values from Welch’s unpaired Student’s t test (n>15, N>3). (K) Relative force changes (y-axis) for membrane tension monitored on the static tether as a function of the extending tether length (x-axis) upon continuous pulling. In the case of blebs or cells with heavily disassembled actin cortex (light and dark green), the tension on static tether increases as the extending tether lengthens; however, there are no perceptible tension changes on the static tether tension from the cell body (pink, intact cortex) even when the other tether has extended by more than 60 μm (n>14, N>3). Graphical data represent means ± SDs. See also Figure S3 and Video S2.

Long-range tension propagation coincides with directed membrane and actin flows toward the protrusion.

Next, we investigated the mechanism of tension propagation from the site of protrusion to the rest of the cell. We observed enrichment of our plasma probe in the opto-induced protrusions (Figure 1B; video S3) on a similar timescale to the cellular deformation and tension increase (10–15s) following optogenetic protrusion generation (Figure S1C-E). We hypothesized that membrane and cortical flows could underlie the rapid propagation of membrane tension from the protrusion to the rest of the cell. To resolve the time-dependent flow of the plasma membrane and actin cytoskeleton relative to light-activated protrusions, we used fluorescent markers of the plasma membrane (CAAX-HaloTag) and actin cytoskeleton (Actin-HaloTag); these markers were individually examined in separate cells. During protrusion formation, the intensity of the plasma membrane probe is increased at the site of protrusion while decreasing elsewhere (Figure 4A, B, Figure S4A-G; video S3). Since the true width of the plasma membrane is likely to be constant during our experiments, these apparent shifts in intensity presumably represent bunching and unfolding of sub-resolution plasma membrane folds⁴⁵. Neutrophils have more than twice the amount of plasma membrane needed to cover their surface, and this excess is held in wrinkled plasma membrane reservoirs^46–48. The actin probe similarly accumulated at the site of protrusion and decreased on the side of the cell opposite from the protrusion (video S3).

Figure 4. Long-range tension propagation is accompanied by directed membrane and actin flows toward the protrusion.

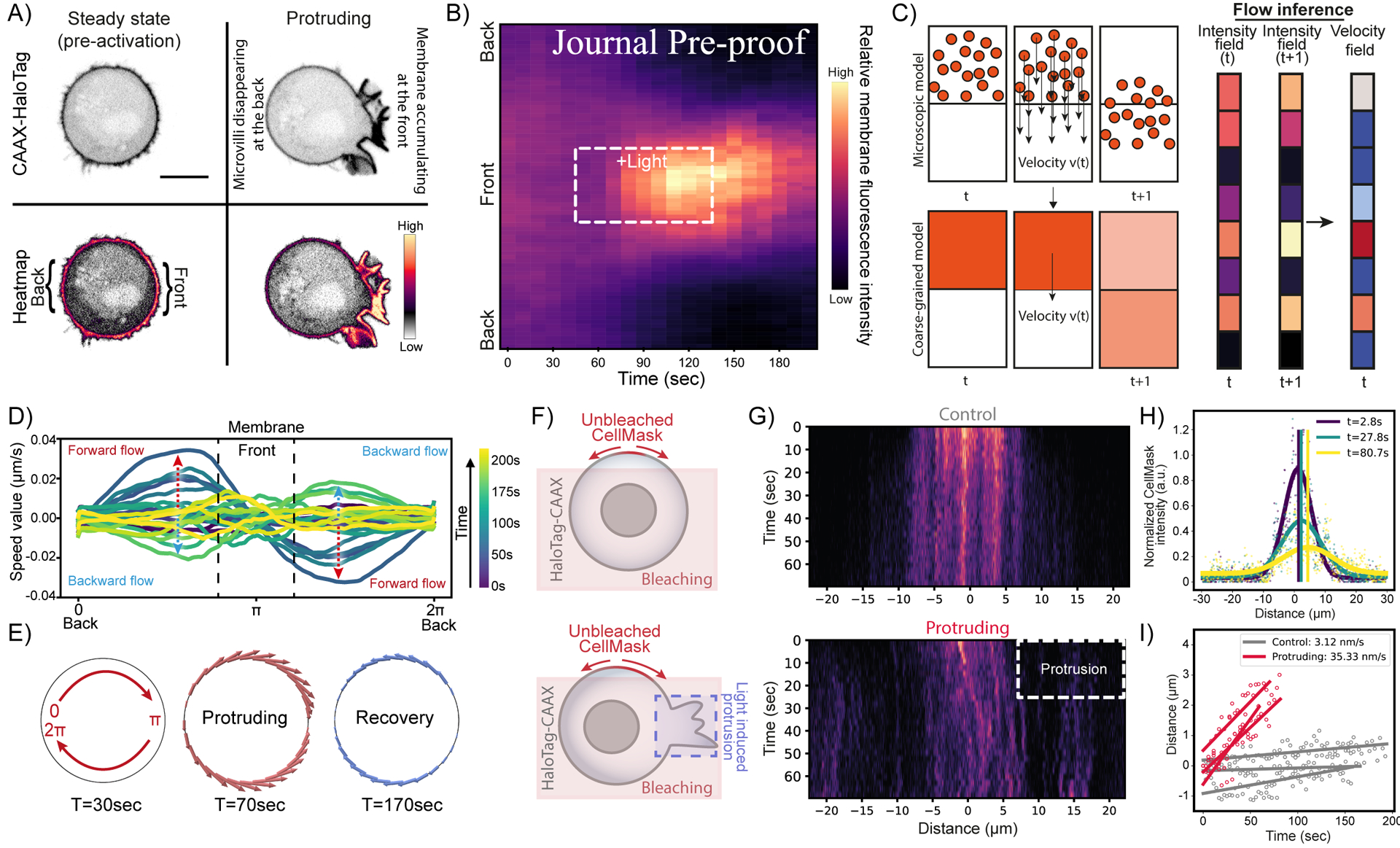
(A) Confocal images of opto-PI3K cells expressing membrane marker (CAAX-HaloTag): before and during light-activated protrusion. Scale bars: 5 μm. (B) Kymographs of membrane fluorescence along the normalized cell circumference (y-axis) show that over time (x-axis) membrane accumulates towards the protruding cell front and is depleted from the back (n>50, N=6; Figure S4; see Methods). (C) Flows of membrane and actin during protrusion are calculated assuming optimal transport (see Methods). (D) Membrane flow field inferred using optimal transport from kymograph intensity changes over time: shortly after activation begins (t=70s, dark teal traces), the magnitude of membrane flow speed increases (red dashed arrows), with positive speed for clockwise flow along the cell upper half and negative speed for counterclockwise flow along the bottom half (panel G), all moving towards the cell protruding front (π). During recovery (t=170s, light green traces), the direction of membrane flow reverses (blue dashed arrows). (E) Membrane flow around the cell before, during, and after (t=30, 70, 170s) right-side protrusion; the flow magnitude is denoted by the arrow size (red: forward flow, blue: backward). Membrane flows toward the protrusion in the protruding phase and away from the protrusion during the recovery phase. (F) Alternative membrane diffusion assay where we bleach the membrane marker CellMask across a wide section of the cell (sparing a small section of the membrane maker) opto-activate a portion of the cell angled 90° from the unbleached area (or use no light as control) and monitor the diffusion pattern of the unbleached area over time. (G) Top, example kymograph of unbiased diffusion in a control cell (no activating light). Bottom, same as top but in a protruding cell, showing biased diffusion and bulk flow of the unbleached membrane signal toward the protrusion. Heatmap similar as in (B). (H) Sample fits of individual timepoints of kymograph data (points colored by respective timepoints) with a gaussian equation (thick curves, colored by respective timepoints). Shifts in the means of the gaussian fits, quantified bulk membrane flow, are shown as vertical lines (colored by respective timepoints). (I) Quantification of mean shifts fit by linear regression to quantify membrane flow rate in control cells (grey, no apparent flow, u=3.34 nm/s) and protruding cells (red, biased flow toward side of protrusion, u=35.51 nm/s) (N=3, n=3). See also Figure S4 and Video S3.

To characterize the flows of membrane and actin over time, we developed a novel flow inference method based on kymographs to predict a flow field that can explain the spatiotemporal redistribution of membrane (or actin) intensity (Figure 4C). A model to rationalize our experimental observations is that the protrusion resulting from the actin polymerization pulls the actin cortex towards the protrusion front, which in turns drags the membrane around the cell at each point to which it is connected. In this case, it is reasonable to assume that the flows resulting from the actin-driven protrusions are accompanied by dissipation generated by the friction between the membrane and its underlying cortex. Under these conditions, the observed flow reduces to a case of optimal transport^49,50 that minimizes the dissipation. Thus, it is possible to infer membrane and cortical velocity fields from the experimental kymographs using optimal transport theory (see Methods S1; Figure S4H, I). We verified that our inference method is able to recover velocity fields from various simulated kymographs with high accuracy (Figure S4J and Methods S1). Our analysis revealed the presence of a cell-wide flow of both plasma membrane and actin cortex toward the protruding front during light-induced protrusion and reversing in direction during recovery (Figure 4D, E, Figure S4F,G, K; video S3). We used membrane photobleaching (Figure 4F–I, Figure S4L-P) and tracking of microvilli movement (Figure S4Q; videos S3) to further validate plasma membrane flows towards the protrusion. These directed membrane and cortex flows provide a potential mechanism to mediate tension propagation following cell protrusion.

Actomyosin contractions also generate rapid long-range membrane tension propagation and membrane flows.

Because actin-based protrusions elicit membrane and actin flows (Figure 4), but forces applied to the membrane alone do not (Figures 3, S3, video S4), our data suggest that forces applied to the actin cortex could be central to membrane tension propagation. As optogenetically-activated protrusions exert forces on both the cortex and plasma membrane, we next sought to investigate the consequences of applying forces directly to the actin cortex. For this purpose, we leveraged an optogenetic approach to induce local actomyosin contractility by local recruitment of the Rho activating domain of LARG (Leukemia-associated Rho guanine nucleotide exchange factor) (Figure 5A–C)⁵¹. Focal Rho activation elicited local flattening of the cell (Figure 5B), as expected for local myosin activation;^52,53. Similar to light-activated protrusions (Figures 1,2), light activated actomyosin contractility also generated long-range propagation of membrane tension (Figure 5D,E video S4) that rapidly propagated virtually unattenuated across the cell (Figure 5F–H). As we observed for actin-based protrusions, local generation of actomyosin contractility also generated flows of both plasma membrane (Figure 5I–L, video S4) and actin cortex (Figure S5E-H, video S4) toward the site of contractions. As an additional control, we also used speckle tracking of focal enrichments of the actin cortex to demonstrate cortical flows towards the site of contractions (Figure S5I, video S4). These data suggest that forces applied to the actin cortex suffice for efficient membrane flows and membrane tension propagation in cells.

Figure 5. Optogenetically-induced actomyosin contractions generate rapid long-range membrane tension propagation and membrane flows.

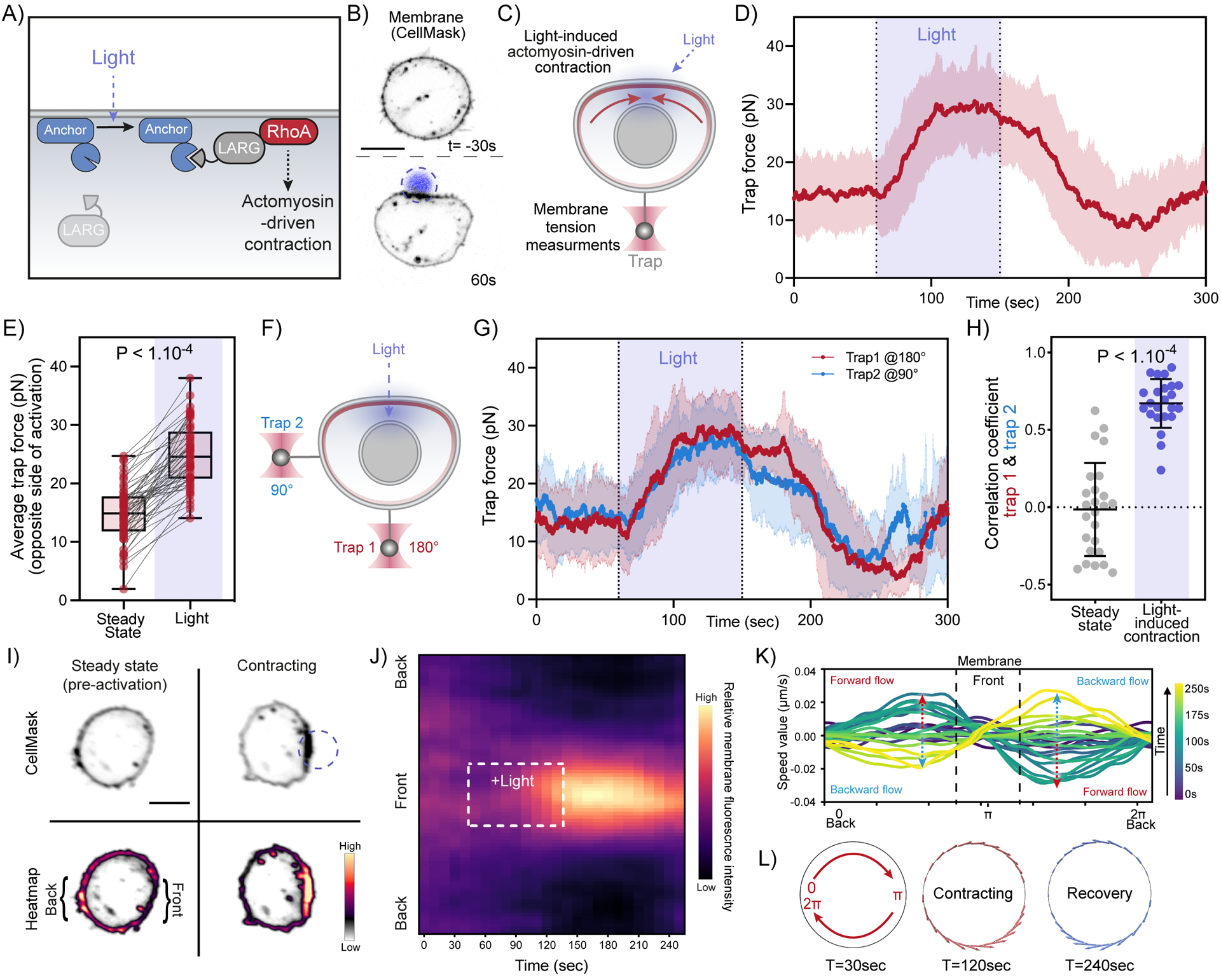
(A) Optogenetic approach for light-induced activation of leukemia-associated Rho guanine nucleotide exchange factor (LARG), resulting in Rho GTPase activation to initiate actomyosin-driven cell contraction (see Methods). (B) Time-lapse confocal images of a neutrophil-like HL-60 cell expressing opto-construct (Opto-LARG) and membrane marker (CellMask) showing localized membrane contraction and cell flattening upon light activation. (C) Following light-activated contraction on one side of the cell (top), changes in membrane tension on the opposite side (bottom) are measured via a membrane tether held by an optical trap. (D) Averaged time trace of trap force before (Steady-state), during (Light), and after activating cell contraction (means ± SD; n>55, N=7). (E) Averaged trap force before (Steady-state) and during activation. Box and whiskers: median and min to max; p values from Wilcoxon paired Student’s t test. (F) A dual-tether pulling assay to simultaneously monitor membrane tension on the far-end (left, trap 1 at 180°) and on the side of the cell (top, trap 2 at 90°) during light-activated contraction. (G) Averaged traces of dual trap forces before, during (Light), and after activation showing coinciding tension increases on both membrane tethers adjacent to (trap 2) and at the opposite cell surface from (trap 1) contraction (n=25, N=4). (H) Pearson correlation coefficient between dual trap forces measured at steady state and during light activation. Error bar: means ± SD; p values from Welch’s unpaired Student’s t test (n>20, N>4). (I) Confocal images of opto-LARG cells stained with membrane marker (CellMask) before and during light-activated contraction. Scale bars: 5 μm. (J) Kymographs of membrane fluorescence along the normalized cell circumference (y-axis) show that over time (x-axis) membrane accumulates towards the contracting cell front and is depleted from the back (n=40, N=3; see Methods). (K) Membrane flow field inferred using optimal transport from kymograph intensity changes over time: shortly after activation begins (t=120s, teal traces), the magnitude of membrane flow speed increases (red dashed arrows), with positive speed for clockwise flow along the cell upper half and negative speed for counterclockwise flow along the bottom half, all moving towards the site of cell contraction (π). During recovery (t=200s, light green traces), the direction of membrane flow reverses (blue dashed arrows). (L) Membrane flow around the cell before, during, and after (t=30, 120, 240s) right-side contraction; the flow magnitude is denoted by the arrow size (red: forward flow, blue: backward). Membrane flows toward the contraction in the contracting phase and away from the contraction during the recovery phase. Scale bars: 5μm. See also Figure S5 and Video S4.

Mechanical forces engaging the actin cortex drive robust membrane tension propagation in cells.

To infer the critical requirements for cellular membrane tension propagation, we constructed a simple composite mechanical model in which an elastic plasma membrane is coupled to a viscous and contractile gel-like actomyosin cortex⁵² via adhesive linkers (Figure 6A; see Methods S1). The tension of a 2D membrane is overall of entropic origin and corresponds to the unfolding of membrane fluctuations. In such entropic regime, membrane tension is proportional to the exponential of the area strain, as found experimentally⁵⁴ and predicted theoretically⁵⁵. Our model assumes small strains, where this exponential behaves approximately as an affine function and where the membrane can be considered as linearly elastic.

Figure 6. Mechanical forces acting on the actin cortex drive rapid long-range membrane tension propagation in cells.

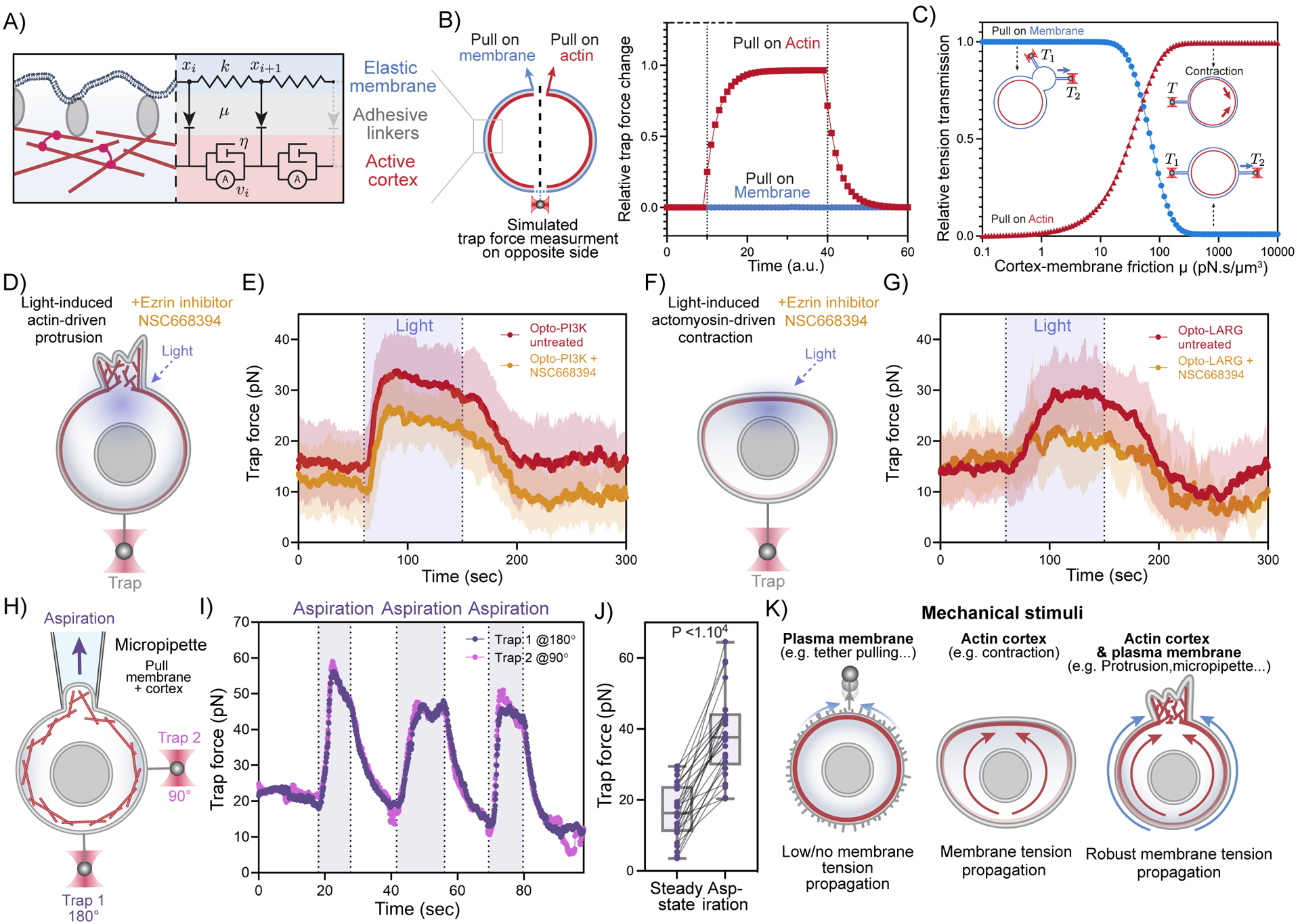
(A) A three-tier composite model for membrane tension propagation in cells: membrane displacements (x_i) as a readout for tension propagation upon cortical flows (v_i) depend on the membrane elasticity (k) and the membrane-cortex friction μ imposed through the adhesive linkers. (B) Model predictions of membrane tension response at moderate membrane-cortex friction (see Methods S1): only actin-based pulling leads to tension increase and propagation (red rectangles); external pulling on the membrane alone is inefficient (blue circles). (C) Predicted membrane tension transmission as a function of membrane-cortex friction (x-axis) for different targets of force application: plasma membrane only (blue) and actin cortex only (red). (D) Membrane tension measurements during light-induced protrusions in cells with decreased MCA by using 25μM of Ezrin inhibitor NSC668394. (E) Red: averaged time trace of trap force before (Steady-state), during (Light), and after activating cell protrusion in control cells (same data as Figure 1F). Orange: averaged trace from cells with decreased MCA by using 25μM of Ezrin inhibitor NSC668394, showing slight defects in membrane tension propagation during light activated protrusions (n>25, N=3). (F)(G) Similar to (D)(E) but using light-induced actomyosin contractions, in which decreases in MCA lead to severe defects in membrane tension propagation across the cell. (Red: same data as Figure 5D; n>25, N=4). (H) A dual-tether assay to simultaneously monitor membrane tension on the far-end (bottom, trap 1 at 180°) and on the side of the cell (right, trap 2 at 90°) during micropipette aspiration (top), which mechanically pulls on both the membrane and underlying actin cortex. (I) Representative time traces of dual trap forces over successive cycles of aspiration (shaded area) show coinciding tension increases and decreases on both membrane tethers, similar to that in Figure 2B. (J) Averaged trap forces measured before (Steady-state) and during aspiration. The robust increase in membrane tension upon aspiration on both membrane and cortex is consistent with our model prediction (panel B). Box and whiskers: median and min to max; p values from Wilcoxon paired Student’s t test (n>25, N=5). (K) Schematic of requirements for effective membrane tension propagation: in the presence of membrane-to-cortex attachments, force application to plasma membrane alone does not generate tension propagation, in agreement with the picket fence model. However, mechanical stimuli acting on actin cortex such as contraction, lead to rapid, long-range membrane tension propagation in the presence of significant membrane-to-cortex attachments. Perturbations affecting both actin cortex and plasma membrane (such as protrusions or micropipette aspiration) lead to robust long-range membrane tension propagation regardless of membrane to cortex attachment levels. See also Figure S6, Methods S1, and Video S5.

For the simplicity of our model, we neglected the contribution of membrane reservoirs, as we do not envision that these dominate tension propagation. The presence of multiple membrane reservoirs that can unfold above a given tension threshold would simply limit the ability of tension to increase above this value. Our experimental data is consistent with reservoirs being accessed at the plateau phase (max tension values) of tension propagation. At early, pre-plateau phases of protrusion extension, membrane tension increases rapidly even for relatively small protrusions and then plateaus at a maximum even as the protrusion continues to expand (Figure S1F). Neutrophils have much larger plasma membrane reservoirs than other cells such as fibroblasts (Figure S6A,B;⁵⁶), making it unlikely that we are exhausting local reservoirs during early, pre-plateau phases of protrusion/contraction or during our tether-pulling experiments. Intriguingly, both optogenetically-induced protrusions and optogenetically-induced contractions reach similar maximal membrane tension values, likely reflecting the threshold of accessing membrane tension buffers (Figures 2 and 5). Therefore, membrane tension propagation observed in the pre-plateau phases—the focus of our study here—is unlikely to be affected by the presence of folded membrane tension buffers, which manifest mostly in the plateau phase.

In our model, the membrane displacement (x_i)— upon cortical flows (v_i)—is determined by the overall friction imposed through the interconnecting layer of adhesive linkers (e.g., membrane-to-cortex attachment proteins (MCA), such as Ezrin). This friction μ exerts a drag force on the cell membrane with a magnitude that is proportional to the relative tangential velocity between the cortex and the membrane. Given a moderate membrane-cortex friction, this model adequately captures the known tension responses upon different types of mechanical perturbations (Figure 6B, C), including the absence of tension transmission when only the membrane is pulled (e.g., exogenous tether pulling) and rapid propagation of tension upon actin-driven cell protrusion (e.g., endogenous force generation). Furthermore, the model suggests that perturbations engaging both membrane and cortex not only lead to tension propagation but also exhibit a robust tension transmission over a much wider range of membrane-cortex coupling conditions than perturbing either component alone. To test how membrane tension propagation is affected by weakening membrane-to-cortex attachment, we utilized NSC668394, an inhibitor of Ezrin phosphorylation and Ezrin-actin binding. In accordance with the predictions of our model (Figure 6C), this ezrin inhibitor only gave mild defects for protrusion-mediated tension propagation (Figures 6D,E, S6C) and elicited more significant defects in tension propagation for contraction-mediated tension propagation (Figures 6F,G, S6C).

Our modeling suggests that the key determinant of long-range membrane response is not the endogenous or exogenous application of force but rather whether the mechanical forces directly engage the actin cortex, and whether the cortex is sufficiently attached to the membrane (i.e., sufficient friction/coupling) to effectively transmit forces to produce membrane displacement upon cortex displacement. To test whether exogenously applied forces can mediate membrane tension propagation, we implemented micropipette aspiration to apply mechanical pulling on both the actin cortex and plasma membrane and monitored tension propagation using our dual-tether assay (Figure 6H). We detected a rapid, robust, and global increase in membrane tension with little to no attenuation across the cell (Figure 6I,J, Figure S6D-L; video S5). Our unifying model indicates that the plasma membrane and actin cortex act as an integrated system for robust membrane tension propagation.

Discussion:

By combining optogenetics for local endogenous control of cell protrusion/contraction and optical trapping for direct membrane tension measurements in tether pulling assays, we demonstrate that local mechanical force generation such as cellular protrusions and contractions elicit rapid long-range propagation of membrane tension throughout the cell. In addition, our findings resolve the long-standing dispute as to whether the actin cortex facilitates or impedes tension propagation. When forces are applied to membranes alone (e.g., tether pulling), the actin cortex opposes membrane flow and tension propagation. However, when forces engage the actin cortex underneath the membrane—either upon optogenetically-induced actin polymerization or actomyosin contraction, or upon micropipette aspiration, tension rapidly propagates nearly undampened across the cell through the generation of actin-driven membrane flows (Figure 6K).

It is noteworthy that the propagation of membrane tension following cell protrusion/contraction is not only rapid but also unattenuated, an optimal behavior to coordinate processes at the scale of the entire cell. Our experiments and modeling suggest that one essential prerequisite for this efficient tension propagation is that the force transmits through the cortex. Accordingly, we propose that the cortical propagation of tension across the cell is supported by a continuous cortical network, and that interactions between the cortex and cellular substrates other than the low-stiffness, highly compliant plasma membrane must be sufficiently weak so as to minimize dissipative losses in tension propagation. Any discontinuities in the cortex or physical barriers that disrupt cortical flow (e.g., the division between the apical versus basolateral portions of epithelia cells) would be expected to impede tension propagation. Consistent with this idea, we observe more robust membrane flows toward the protrusion for the portions of the cell away from the surface compared to the substrate-adhered ventral region of the cell (Fig S6M-P).

Actin-based protrusions and actomyosin contractions both mediate long-range membrane tension propagation and flows of both actin and membrane towards the site of protrusion/contraction (Figures 4, 5, S4, S5). For actomyosin contraction, the primary force is myosin contractility that generates the actin flows. In this case, the flow of the plasma membrane and propagation of membrane tension depend on high membrane-to-cortex attachment (MCA) (Figure 6C, F,G). Compared to actomyosin contraction, we have less of an understanding why the cortex flows toward the protrusion. We speculate that the newly polymerized actin at the leading edge both generates a pushing force on the membrane while also generating a pulling force on the preexisting actin cortex. Future high-resolution electron microscopy images of protrusive and cortical actin could help reveal the relative organization of these actin networks during motility^15,57.

Our modeling suggests that forces that engage both the cortex and plasma membrane could ensure robust membrane tension over a wide range of membrane-to-cortex adhesion strengths (Figure 6C–E). During light-activated cell protrusions, forces from actin polymerization are exerted on both the plasma membrane and actin cortex, as can be observed by the flow of membrane and cortex towards the site of protrusion (Figure 4). Membrane flows enable membrane tension propagation in regions of low membrane-to-cortex attachment, cortical flows permit membrane tension propagation in areas of high membrane-to-cortex attachment, and forces applied to both networks should propagate tension in both settings. The ability of protrusions to engage both the plasma membrane and cortex may be particularly important for long-range tension propagation in motile cells with discontinuous membrane-to-cortex attachments⁵⁸. We envision that actin polymerization at the leading edge, which has low attachment between the cortex and the plasma membrane^58,59 would extend the plasma membrane perpendicular to actin assembly and cause the plasma membrane to flow towards the protrusion; while at the periphery of the cells (where MCA goes back up), membrane tension would be propagated via pulling forces from the actin cortex.

Our work indicates that membrane tension has the properties expected for a long-range integrator of cell physiology. Long-range propagation of membrane tension could mediate the competition among multiple protrusion sites for a ‘winner-take-all’ establishment of a dominant front^16,18,60 and could enable the front-back coordination that maintains cell shape and movement^5,7,9,14,15. In contrast, cellular processes that do not apply significant forces to actin cortex may be more dependent on local membrane reservoirs; this property could explain why filopodia can coexist in adjacent regions of the cell without substantially affecting one another^61,62. In future work, it will be critical to examine how cells modulate the dynamic range of membrane tension propagation based on the origin of the forces as well as the continuity and mechanical properties of the cortex.

Limitations of the study.

In this study, we leverage multiple modes of force generation (optogenetic protrusion formation, optogenetic cell contractility, optical-trap-based tether pulling, micropipette aspiration) to probe the requirements for membrane tension propagation in cells. Our model system for this work is neutrophil-like HL60 cells. The mechanical model we propose explains our experimental results, correctly predicts the effects of MCA perturbations, and is consistent with both our experimental observations and those from other groups. Therefore, our general conclusions on membrane tension propagation are likely to translate to other cellular settings. But it is likely that some of the quantitative features we observe in our cells, in particular the nearly unattenuated propagation of tension across the cell and the precise speed of tension propagation, may differ in other cells with different mechanical properties of the cortex or active mechanosensory-based regulation of the membrane or cortex. Therefore, it will be important to extend our approach—in particular the optogenetic engagement of endogenous membrane/cortex forces and direct measurement of membrane tension propagation—to a broader diversity of cell types.

STAR Methods

Resource Availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Orion Weiner (Orion.Weiner@ucsf.edu)

Materials availability

All unique/stable reagents generated in this study are available from the Lead Contact without restriction.

Data and Code Availability

• All data reported in this paper will be shared by the lead contact upon request.

• All original code has been deposited on GitHub and Zenodo and is publicly available as of the date of publication.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Experimental model and subject details

HL-60 cells are from the laboratory of Henry Bourne and were recently verified via STR profiling in³⁹. HL-60s were cultured in R10 growth medium, which is RPMI 1640 supplemented with L-glutamine and 25 mM HEPES (Corning; Corning, NY) and containing 10% (v/v) heat-inactivated fetal bovine serum (Gibco; Waltham, MA). Cultures were kept at a density of 0.2–1.0 million cells/mL at 37°C/5% CO_2.

HEK293T cells (used to make lentivirus for transduction of HL-60s) are from UCSF cell culture facility (CCLZR076) and were grown in DMEM (Corning; Corning, NY) containing 10% (v/v) heat-inactivated fetal bovine serum (Gibco; Waltham, MA) and maintained at 37°C/5% CO₂. All media were 0.22-um filtered.

Opto-PI3K cells (iLid-BFP-CAAX, iSH2-GFP, Pak-PBD-mCherry) were obtained from³⁹. Plasmids used to generate Opto-LARG cells (iLid-BFP-CAAX, DHPH-ARHGEF1-GFP, AnillinRBD-mCherry), Opto-PI3K expressing CAAX-HaloTag, and Actin-HaloTag were assembled using a Golden-Gate-based modular cloning toolkit⁶³.

3T3-Swiss Albino were obtained from UCSF cell culture facility (CCLZR083) and were cultured in DMEM (Corning; Corning, NY) supplemented with 10% Bovine Calf Serum (Sigma; St. Louis, MO, 12138C) and maintained at 37°C/5% CO₂

Method details

Transduction of HL-60 cells

HEK293T cells were used to generate lentivirus and were seeded into 6-well plates until approximately 80% confluent. For each transduction, 1.5 μg pHR vector (containing the appropriate transgene), 0.167 μg vesicular stomatitis virus-G vector, and 1.2 μg cytomegalovirus 8.91 vector were prepared for transfection using TransIT-293 Transfection Reagent (Mirus Bio; Madison, WI). Three days post transduction virus-containing supernatants were harvested and concentrated approximately 40-fold using Lenti-X Concentrator (Clontech; Mountainview, CA). Concentrated viruses were frozen and stored at −80°C until needed. For all transductions, thawed virus was mixed with approximately 0.3 million cells in growth media supplemented with polybrene (8 μg/mL) and incubated overnight. Cells expressing desired transgenes were isolated using fluorescence-activated cell sorting (FACS) as appropriate (FACSAria2; BD Biosciences; Franklin Lakes, NJ).

Microscopy hardware

Imaging depicted in Figure 1B; 4B, 5B; S4A, S4D, S4F, S5E, S5I, S6N and Video S1, S3, S4 were performed at 37°C on a Nikon Eclipse Ti inverted microscope equipped with a Borealis beam conditioning unit (Andor), a CSU-W1 Yokogawa spinning disk (Andor; Belfast, Northern Ireland), a 100X PlanApo TIRF 1.49 numerical aperture (NA) objective (Nikon; Toyko, Japan), an iXon Ultra EMCCD camera (Andor), and a laser merge module (LMM5, Spectral Applied Research; Exton, PA) equipped with 405, 440, 488, and 561-nm laser lines. All hardware was controlled using Micro-Manager (UCSF).

Optogenetic activation was performed using a LED (470-nm) via a custom DMD (Andor Technology). Illumination intensities were varied by connecting the LEDs to the analog outputs of a digital-to-analogue converter and setting the LED voltages using serial commands via custom Python code. The microscope is equipped with two stacked dichroic turrets such that samples can be simultaneously illuminated with LEDs and imaged using a 488-nm long-pass dichroic filter (Chroma Technology Corp.)

Preparation of Opto-PI3K and Opto-LARG cells for confocal imaging

For experiments in which we monitored cells by confocal imaging, cells were seeded in a 96-well #1.5 glass-bottom plates (Azenta Life Sciences) in R+B imaging media, which is RPMI 1640 supplemented with L-glutamine and 25 mM HEPES (Corning; Corning, NY) and containing 0.2% Bovine Serum Albumin (BSA, endotoxin-free, fatty acid free; A8806, Sigma; St. Louis, MO). For optogenetic activation, cells were illuminated using DMD (see above) at a chosen location (using custom Python code) in a circular pattern of varying size (~2 microns radius for Opto-PIK, ~1 micron radius for Opto-LARG) for a duration of 90 seconds. For figure S6M–P, we imaged the cells using a two-step Z-stack of the ventral side (~TIRF plane) and mid-section of the cell.

For plasma membrane and actin imaging using HaloTag (Figure 1B, 4A, S4F, S4M–Q, S6N), cells were stained with 100nM of JF646X for 10 min before being pelleted at 300g for 3 min and resuspended in R+B imaging media (RPMI+0.2% BSA).

For plasma membrane imaging using the membrane dye CellMask (Figure S4D; 5B, 5I), cells were first incubated with ~2–5μg/ml of CellMask^™ Deep Red (C10046, Thermofisher) for 3 minutes at 37°C/5% CO₂. Cells were then pelleted at 300g for 3 min and resuspended in R+B imaging media (RPMI+0.2% BSA).

For actin imaging of Opto-LARG (Figure S5E, S5I), cells were incubated with the actin dye SPY650-FastAct^™ (CY-SC505) for 1h at 37 C/5% CO_2. Cells were then pelleted at 300g for 3 min and resuspended in R+B imaging media (RPMI+0.2% BSA).

Preparation, settings, and operation procedures for membrane tethering pulling experiments on C-trap^® optical tweezers with confocal imaging Cell preparation

Opto-PI3K & Opto-LARG: 1–1.5 ml cells (from culture at density of 0.6–0.8 million cells/mL) were stained (with 0.5 μl of CellMask^™ Deep Red or 100nM of JF646X), then pelleted down and resuspended in either R+B imaging medium (RPMI+0.2% BSA) or R10 medium (all media 0.22-um filtered) in the absence or presence of actin inhibitor (10 μM Latrunculin B) for samples used in tether pulling assay.

To heavily depolymerize the cortex (Figure 3G–K & Figure S3G–J) Cells were resuspended in a hypotonic media 60% H2O and 40% R10) containing 10 μM Latrunculin B.

To decreases membrane-to-cortex attachment (Figure 6D–G & Figure S6C), cells were resuspended in media (R10) containing 25μM of Ezrin inhibitor NSC668394 (Sigma-Aldrich, 341216).

Bead preparation

In a 1.7 ml Eppendorf tube, the following solutions were added: 9 μl of ultrapure water (Corning, 46–000-CM), 9 μl of carboxyl latex bead (4% w/v, 2 μm; Invitrogen, C37278), and 2 μl of Concanavalin A (1 mg/ml; Sigma-Aldrich, C2272); sample was vortexed at low speed at room temperature for 45–60 min; 1–2 μl of this bead mixture stock was added into 1 ml of RPMI 1640 buffer (0.22-um filtered) for samples used in tether pulling assay.

Microfluidics

An u-Flux^™ flow cell (70-mm chips; Lumicks, C1), installed on an heat-insulating PVC holder, was passivated with R+B imaging media (0.22-um filtered) and pre-warmed at 35–37°C for 1–2 hours. A custom-made microchamber integrated with micropipettes (descriptions on the assembly provided at the end) was used in place of u-Flux^™ flow cell to apply aspiration in tether pulling assay performed on C-trap^® (instrument operation procedures in the next section). During the assay, an air-pressured microfluidics flow system (u-Flux^™, Lumicks), with pre-cleaned and proper dimensions of tubing connections, was used to deliver cell samples, bead solutions, and blank media/buffers (for flushing) into the flow cell or microchamber. Specifically, a tubing with large ID (1/32 inch; Idex, 1520L) was used to deliver cells at the lowest pressure setting (0.04–0.12 mbar, or sometimes just gravity flow) so as to minimize the shear force exerted to the cells during delivery. The delivery of beads and media was made with a narrower tubing (ID 0.004 inch; Upchurch Scientific, PM-1148-F). After flowing ~200–500 μl (sufficient to displace dead volumes combined within the microfluidics system) of cells into the C-trap^® system pre-warmed at ~36°C, incubated for 15–20 min so that the cells settle and stably attach to the bottom surface of the u-Flux^™ flow cell. Cell locations were then marked prior to the subsequent tether pulling experiments with optical traps. The cell samples were replenished every 1.5–2 hours, with abundant flushing of R+B imaging medium in between (which ensures the flow cell surface remains properly passivated).

Optical trapping – setting and operations

A commercial dual-trap optical tweezers with 3-color confocal imaging, aka C-trap^®, from Lumicks was used to perform the tether pulling assay with concurrent fluorescence imaging. The flow cell, or microchamber, held paralleled to the table surface was aligned perpendicular between a water objective (60x, NA 1.2; Nikon, MRD07602) coming from the bottom and a matching condenser (60x, NA 1.4, used with Type A immersion oil; Leica) coming from the top. The flow cell was positioned in between the two such the IR laser beams (1064 nm) focused down by the objective were formed inside the flow cell ~10–20 μm above the inner bottom surface (with the flow cell nano-stage set at the middle position). After the flow cell, the condenser can adequately collect photons from the IR trapping beams and project on to position-sensitive detectors (PSDs) for accurate trap force measurement (data acquisition at a rate of 78125 Hz and later down sampled to 10 Hz for analysis). The objective also directs fluorescence excitations in the visible wavelength range (488, 532, and 642 nm respectively for opto-tool, Rac/RhoA biosensor, and CellMask/HaloTag) into the flow cell (or microchamber). The two set of light sources (IR and visible) were controlled by separate telescopes and mirror-steering systems upstream from the objective. The same objective collected the emission photons from the imaging/optical trapping sample plane inside the flow cell for fluorescence imaging (bandpass filters: 512/25, 582/75, and 680/42; camera pixel size: 100 nm; frame rate depends on confocal scanning area size), whereas the condenser provided bright field imaging (850 nm LED light source) recorded at 10 Hz.

Both the objective and the condenser were pre-warmed to 35–37°C (temperature control unit, Lumicks) for at least 2–3 hours prior to cell experiments. The IR trapping power was typically set at 100% trapping laser, 10% overall power, and 50–50 split between trap 1 (T1) and trap 2 (T2), which is about ~175 mW per trap (measured at the objective front) and ~0.2 pN/nm in trap stiffness for a 2 ~m bead (bead corner frequency ~2500 Hz). Low settings of excitation laser were sufficient for fluorescence imaging (typically ~2–5% of total power gives ~0.02–0.04 μW measured at the objective front), minimizing the photo-toxicity to the cell during experiments.

At the beginning of each cell recording in the tether pulling assay, 2- ~m Concanavalin-coated beads were flowed into the microchamber (e.g., at 0.4 mbar via channel 5 in u-Flux^™ C1 flow cell) and single beads were captured in either one or both traps; we then moved the flow cell stage to bring the beads to a cell location marked after incubation (as described earlier). With beads in the vicinity of the cell, i.e., in z-axis at the same confocal imaging plane for the cell (~2–6 μm from the flow cell bottom surface) and ~4–6 μm away from the cell body in the x-y plane, the trap stiffness was calibrated, and any residual force readout were zeroed before engaging the bead with the cell body to form membrane tethers. Region of interest (ROI) was cropped for bright field imaging (typically an area of 35×45 μm), and continuous recording at 10 Hz was initiated.

1. Tether pulling assay with light-activated cell protrusions: as seen from the bright field camera, we approached beads to position them in direct contact with the cell body (even pressing a little, judging from the counter force acted on the bead in the trap), then we waited for several seconds before carefully (slowly) pulling out membrane tethers (~4–10 μm in length) at the desired con Figuration (e.g., two tethers right angle from each other). We monitored steady state tension for at least 1 min (Figure S1G) before local 488-nm excitation (ROI: 6×10 μm) continuously for 90 sec on the opposite site of (or right angle from) the membrane tether. Upon localized 488-nm illumination, the local recruitment of opto-controls (iSH2 labelled with EGFP) to trigger cell protrusions was also imaged simultaneously (~1–1.3 sec/frame scanned). Post protrusion activation, we monitored cell membrane tension recovery for 180 sec and repeated activation cycles for as long as the tethers last (see Video S2). At desired time points, i.e., before, during, or after 488-nm light activation, the activated Rac was specifically imaged via 532-nm illumination to visualize the distribution of the Rac biosensor (Pak-PDB-mCherry) inside the cell (see Figure S1B–E; Video S1). Similarly, the changes in cell membrane morphology were imaged over time with 642-nm illumination (for CellMask Deep Red or Halo-tag 660 if cells were stained earlier).

2. Other experimental conditions in tether pulling assay, including controls: following the same bead engagement procedure described above, membrane tethers were pulled out from the cell body or from small patches of vesicle-like, outward budding membrane blebs that are detached from actin cortex upon Latrunculin treatment. Specifically, after the first membrane tether was formed, the second tether was pulled from a nearby location ~2 μm away. The membrane tension was recorded in the same fashion as detailed earlier but for the following conditions: light activation on wild-type cells or drug-treated opto-PI3K cells; in the absence of any light illumination, we moved one trap to extend the length of one tether on the cell body (or bleb) and monitor the tension response on the other (see Video S2); or instead of 488-nm illumination (which triggers actin-driven cell protrusion), the cell was engaged with micropipette aspiration, which exerts mechanical pulling on both membrane and cortex, and the membrane tension was recorded over cycles of aspiration and relaxation (see below; Video S5). For Figure S6A–B, we pulled tethers from either HL60s or 3T3 cells at a constant rate until eventual tether breakage (following method from⁵⁶). We then measured distance bead to cell using force measurement as a readout of tether rupture.

At the end of each measurement, and unless tethers had already broken on their own or by debris flying in the trap, trapping lasers were turned off to observe the tether & bead elastic recoil toward the cell as a control of the absence of cytoskeleton in the tethers (Figure 1D; S3C, J & Video S1).

Micropipette aspiration

A custom-made microchamber was used to implement micropipette aspiration on the C-trap^® system. Specifically, a micropipette of 2–6 um tip diameter was prepared by gravity pulling a thin glass capillary tube (ID 0.040 +/− 0.010 mm, OD 0.080 +/− 0.010 mm, length 150 mm; King Precision Glass, KG-33) that was threaded through a heated platinum coil (~2 mm in diam.; Pt wire is 0.3 mm in diam., Alfa Aesar) upon application of a desired voltage. The micropipette tip size generally correlates with the heating time required to pull the glass tube apart; the faster heating, the more rapid the pull, giving micropipette tips in smaller diameters.

The micropipette was then sandwiched between a 1-mm glass cover slide (3”x1”x 1 mm; VWR) and a #1.5 glass cover slip (24×60 mm; VWR), held together with two pieces of melted Nescofilm (100 um in thickness; Karlan) as sealant and spacer in the microchamber. 6 holes were drilled prior on the glass slide to provide inlets, which are connected to valves and uFlex^™ pressurized syringe reservoirs (for cell and bead samples delivery as well as buffer flushing), and outlets towards the waste collection. The micropipette was connected to a separated microfluidic pressurized system (MFCS^™-EZ from Fluigent; input: −600 mbar, output: −69 to 0 mbar) powered by a small floor pump (KNF, model: N86KN.18, with manual regulator) to provide aspiration control in the tether pulling assay on C-trap^®. The aspiration pressure zero point for each micropipette was carefully calibrated and set to have no outward nor inward flow detectable to a laser trapped bead that was placed at the tip opening of the micropipette. During the experiments, cells were delivered into the microchamber at the same gentle flow rate (0.04–0.12 mbar, or sometimes just gravity flow) and captured by the optical trap, which quickly brings the cell to the micropipette tip. A minute amount of suction was applied to keep the cell stably engage with the tip (so it neither floats away from the tip nor falls back into the optical trap) but without any visible deformation of the cell morphology (as seen in bright field camera). Then following the same bead calibration procedure and membrane tether pulling process as described earlier, consecutive rounds of aspiration and relaxation were performed on the cell for as long as the membrane tethers persist (see Video S5).

Quantification and statistical analysis

Image and membrane tension analysis

Fiji (NIH)⁶⁴, Excel (Microsoft; Redmond, WA), custom Python code, and Prism (Graphpad software, Inc) were used for image and membrane tension analysis. Average trap force plots (Figure 1F, 2E, 5D, 5G, 6E, 6G, S1J, S2A–B, S5C) were obtained by aligning trap force traces at time of light induction.

Average linked trap force plots were made using Prism Graphpad (software, Inc). In Figure 1G & 5E, average trace trap force was measured for 60 seconds before light induction (steady state) and for the duration of the light induction (90 seconds, Light). For Figure 6J, average trace trap force shown here for 30 seconds before aspiration (steady state), for the duration of aspiration (15–30 seconds), and for intervening recovery periods.

Pearson correlation coefficients between T1 and T2 were calculated using Prism Graphpad software, Inc) (Figure 2F, 3J, 5H, S6K). For Figure 2F and 3H, we used 30 seconds before activation for steady state, 30 seconds of light induction for opto-activated protrusion, and ~10–30 seconds of active tether pulling on cell membrane (tether length >30 μm) and on blebs. In Figure 2F, for ‘+Light’ we used the full duration of light activation (90sec) and for ‘Recovery’ 70sec post light induction. In Figure S6K we used 15–30 sec pre-aspiration for steady state value and full duration of aspiration (~15–30sec) for aspiration.

Delay between T2 and T1 during light induced protrusion (Figure 2D, S5D, S6J) was calculated by measuring the time difference between light induction and change in trap force slope for each trap. Of note, measuring time difference from light induction to plateau in force increase yields similar results (i.e., delay time between the two traps is still of ~ 1 sec).

For measurement of relative tether force over distance of moving tether (Figure 3K), we normalized the trap force of static tether by its average when the extending tether was at distance <1 μm (namely, before any active pulling).

For Figure S5E–F, we observed that FastAct (see above) intensity linearly increases during imaging. To make sure that these increases did not interfere with our quantifications, we used a set of ~40 unstimulated cells, acquired in parallel of every Opto-LARG experiments using FastAct and corrected our measured fluorescence intensity to compensate for this passive intensity increase.

For Figure S1F, in combination to trap forces measurements (see above), cell diameter at the long axis was measured using a custom Fiji plugin and brightfield imaging from optical trap setup as a proxy to roughly approximate cell shape changes during light-induced protrusions.

For Figure S4Q, microvilli tracking was achieved by manually tracking microvilli over consecutive time frames using HaloTag-CAAX (see above) as membrane marker.

For Figure S5I, Actin speckle tracking was achieved by using actin dye FastAct (see above) and by manually tracking distinct actin features (e.g., high intensity points) over consecutive time frames.

For tether length tracking (Figure 1D, 3B, 3E, 3H, 3K, S3A–C, S3I, J), we used a custom-made Fiji macro tracking the position of the bead overtime using brightfield recordings during optical trapping experiments. The timestamps for turning the trap off were also recorded.

In Figure 4G, kymographs were generated by segmenting the cell body through the HT-CAAX (JFX-549) channel and finding the three-pixel wide boundary pixels that best capture the membrane of the CellMask channel. This segmented cell outline is unraveled and averaged over every three values to provide 1 × N arrays which are stacked to show the evolution of membrane signal over time. Image segmentation code utilized the Python package Scikit-Image⁶⁵.

In Figure 4H ,CellMask signal along the membrane is fitted with the parametric extension of the gaussian equation defined as:

$$f\left(x\right)=m\cdot e{}^{\left(-\frac{{(x-c)}^2}{2r_0^2}\right)}+o$$

where × is the distance along the cell’s perimeter in μm, m is the peak of the CellMask signal, r0 is the width of the CellMask signal, c position of the peak CellMask signal, and o is the offset of the CellMask signal from zero. The shift in the peak CellMask signal along the membrane was quantified over time for both control and protruding cells in Figure 4I. Membrane flow rates were calculated by taking the slope of the fitted linear regression lines and averaging the flow rates within the control and protruding groups. Code for gaussian and linear regression fitting utilized the curve_fit and linregress functions in the Python package Scipy⁶⁶. Image analysis and gaussian fitting code in available on Github and Zenodo.

Statistical analysis

For all statistical analysis, PRISM 9 (Graphpad software, Inc) was used. Statistical details can be found in the legend of each figure. N represents number of independent biological replicates. Pooled independent experiments are used in dot plots. Error bars always represent SD.

Supplementary Material

2

video S1. Controls of optogenetically-induced protrusions and of tether pulling experiments. Related to Figure 1 & Figure S1. First movie: time-lapse confocal images of HL-60 cells expressing opto-construct (Opto-PI3K) and membrane marker (CAAX-HaloTag) showing localized membrane protrusion upon light activation. Related to Figure 1B. Scale bar: 5μm.

Second movie: time-lapse (confocal) of Opto-PI3K HL-60 cell expressing Rac biosensor Pak-PBD-mCherry undergoing light-induced protrusions, confirming active Rac recruitment at the site of light-induction. Related to Figure S1B. Scale bar: 5μm.

Third movie: time-lapse (confocal, taken on C-Trap) of Opto-PI3K HL-60 cell expressing iSH2-GFP. Heatmap represents fluorescence signal intensity showing iSH2 recruitment from the cytoplasm to the plasma membrane shortly after light induction. Related to Figure S1C–E.

Fourth movie: brightfield imaging of tether & bead snapping back toward the cell once the trapping laser is turned off at the end of measurements across different conditions (Untreated, Latrunculin B, Latrunculin B + Osmotic shock). This shows the elastic recoil of the bead toward the cell and is used to confirm the absence of cytoskeleton in the tether. Related to Figures 1–3.

3

Video S2. Membrane tension measurements of cells undergoing optogenetically-induced protrusions or external membrane pulling. Related to Figure 1, 2, 3. First movie: brightfield imaging and time trace of trap force measurement of a protruding cell exhibiting sharp increase in membrane tension during light-activated protrusion on the opposite end of the cell Related to Figure 1E–F.

Second movie: Brightfield imaging and time trace of dual trap force measurements of a protruding cell showing nearly coinciding tension increases on both membrane tethers adjacent to (trap 2) and at the opposite cell surface from (trap 1) protrusion. Related to Figure 2B,E. Scale bar: 5μm.

Third movie: brightfield imaging and time trace of measurements of a dual-tether assay to detect tension propagation between two tethers closely pulled out from the cell body membrane. The bead on the right continuously extends the tether on the right, thereby applying mechanical force to the cell membrane. Trap force (as tension responses readout) from the static tether remain uncorrelated to that of the moving tether Related to Figure 3A–C.

Fourth movie: brightfield imaging and time trace of measurements of a dual-tether assay performed on a bleb to detect tension propagation between two tethers closely pulled out from the bleb membrane. The bead on the right continuously extends the tether on the right, thereby applying mechanical force to the bleb membrane. Related to Figure 3D–F.

Fifth movie: brightfield imaging and time trace of measurements of a dual-tether assay performed on a cell with heavily disassembled actin cytoskeleton by using a combination of latrunculin B and osmotic shock. The bead on the left continuously extends the tether on the left, thereby applying mechanical force to the cell membrane, which is simultaneously felt by the static tether on the opposite side of the cell. Related to Figure 3G–I. Scale bar: 5μm.

4

Video S3. Long-range tension propagation coincides with directed membrane and actin flows toward the protrusion. Related to Figure 4 & Figure S4. First movie: time-lapse (confocal) of Opto-PI3K cells expressing membrane marker (CAAX-HaloTag) undergoing light-induced protrusions, related to Figure 4A. Scale bar: 5μm.

Second movie: time-lapse (confocal) of Opto-PI3K cells expressing actin marker (ActinHaloTag) undergoing light-induced protrusions, related to Figure S4D. Scale bar: 5μm.

Third movie: membrane flow around the cell before, during, and after right-side protrusion; the flow magnitude is denoted by the arrow size (red: forward flow, blue: backward). Membrane flows toward the protrusion in the protruding phase and away from the protrusion at the recovery phase. Related to Figure 4C–E.

Fourth movie: actin flow around the cell before, during, and after right-side protrusion; the flow magnitude is denoted by the arrow size (red: forward flow, blue: backward). Actin flows toward the protrusion in the protruding phase and away from the protrusion at the recovery phase. Related to Figure S4K. Third movie: three examples of microvilli tracking during light-induced cell protrusion. Tracked microvilli are circled in red and their trajectory is represented by lines of different colors. Related to Figure S4Q.

5

Video S4. Optogenetically-induced contractions lead to global membrane tension porpagation which coincide with actin and membrane flows toward the contraction. Related to Figure 5 & Figure S5. First movie: brightfield imaging and time trace of trap force measurement of a contracting cell exhibiting sharp increase in membrane tension during light-activated contraction on the opposite end of the cell. Related to Figure 5 C,D.

Second movie: time-lapse (confocal) imaging of Opto-LARG cell expressing membrane marker (CellMask) undergoing light-induced contraction. Related to Figure 5I.

Third movie: membrane flow as inferred by Optimal Transport around the cell before, during, and after right-side contraction; the flow magnitude is denoted by the arrow size (red: forward flow, blue: backward). Membrane flows toward the contraction in the contracting phase and away from the contraction at the recovery phase. Related to Figure 5K.

Fourth movie: similar as previous but for Actin. Related to Figure S5E. Fourth movie: timelapse (confocal) imaging of Opto-LARG cell expressing actin marker (FastAct) undergoing light-induced contraction. Actin speckles are tracked over time, displaying flow toward the site of contraction. Related to Figure S5G. Scale bar: 5μm.

6

Video S5. Mechanical pull on both membrane and actin via micropipette aspiration lead to global membrane tension propagation. Related to Figure 6 & Figure S6. First movie: brightfield imaging and time trace of trap force measurements during micropipette aspiration, which mechanically pulls on both the membrane and underlying actin cortex.

Second movie: brightfield imaging and time trace of dual trap force measurements during micropipette aspiration, which mechanically pulls on both the membrane and underlying actin cortex. Scale bar: 5μm. Related to Figure 6H–J. Scale bar: 5μm.

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
RPMI 11640 supplemented with L-glutamine and 25 mM HEPES	Corning	10-041-CM
Bovine Serum Albumin (endotoxin-free, fatty acid free)	Sigma-Aldrich	A8806
Heat-inactivated fetal bovine serum	Gibco	16140071
DMEM	Corning	10-017-CV
Bovine Calf Serum	Sigma-Aldrich	12138C
Latrunculin B	Sigma-Aldrich	76343-94-7
NSC668394	Sigma-Aldrich	341216
Carboxyl latex bead	Invitrogen	C37278
Concanavalin A	Sigma-Aldrich	C2272
SPY650-FastAct™	Cytoskeleton	CY-SC505
CellMask™ Deep Red	Thermofisher	C10046
Janelia Fluor 646	Janelia	JF646X
Lenti-X Concentrator	Clontech	631231
TransIT-293 Transfection Reagent	Mirus Bio	MIR2705
96-well #1.5 glass-bottom plates	Azenta Life Sciences	4ti-0223
u-Flux™ flow cell (70-mm chips)	Lumicks	C1
Glass capillary tube	King Precision Glass	KG-33
Deposited data
Optimal transport and model	GitHub	https://github.com/VirtualEmbryo/membrane-cortex-tension
	Zenodo	10.5281/zenodo.7894202
Bleaching & gaussian fitting	GitHub	https://github.com/weinerlab/Inverse_Photobleach_Flow
	Zenodo	10.5281/zenodo.7894212
Experimental models: Cell lines
HL60s	Bourne lab	N/A
Opto-PI3K HL60s	Weiner lab	N/A
Opto-LARG HL60s	Weiner lab	N/A
3T3-Swiss Albino	UCSF cell culture facility	CCLZR083
HEK293T	UCSF cell culture facility	CCLZR076
Software and algorithms
Fiji	64	N/A
Prism 9	Graphpad software, Inc	N/A
Adobe Illustrator	Adobe	N/A
Excel	Microsoft	N/A
Napari	67	N/A

HIGHLIGHTS:

• Forces engaging actin cortex generate rapid long-range membrane tension propagation

• Forces applied to cell membrane alone fail to propagate membrane tension

• Unifying mechanical model explains the requirements for membrane tension propagation

• Membrane tension is consistent with a long-range integrator of cell physiology

Inclusion and diversity

We support inclusive, diverse, and equitable conduct of research.

Data and materials availability:

All data are available upon request