A Non-Perturbative, Low-Noise Surface Coating for Sensitive Force-Gradient Detection of Electron Spin Resonance in Thin Films

Abstract

The sensitivity of magnetic resonance force microscopy (MRFM) is limited by surface noise. Coating a thin-film polymer sample with metal has been shown to decrease, by orders of magnitude, sample-related force noise and frequency noise in MRFM experiments. Using both MRFM and inductively detected measurements of electron-spin resonance, we show that thermally evaporating a 12 nm gold layer on a 40 nm nitroxide-doped polystyrene film inactivates the nitroxide spin labels to a depth of 20 nm, making single-spin measurements difficult or impossible. We introduce a “laminated sample” protocol in which the gold layer is first evaporated on a sacrificial polymer. The sample is deposited on the room-temperature gold layer, removed using solvent lift-off, and placed manually on a coplanar waveguide. Electron spin resonance (ESR) of such a laminated sample was detected via MRFM at cryogenic temperatures using a high-compliance cantilever with an integrated 100-nm-scale cobalt tip. A 20-fold increase of spin signal was observed relative to a thin-film sample prepared instead with an evaporated metal coating. The observed signal is still somewhat smaller than expected, and we discuss possible remaining sources of signal loss.

Graphical Abstract

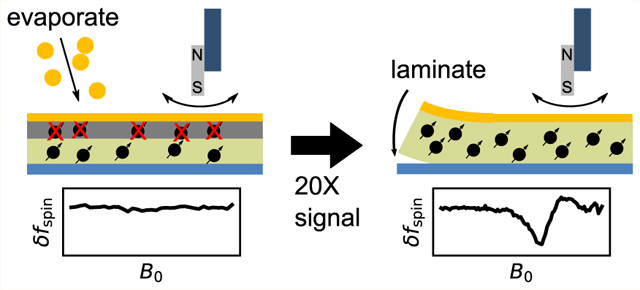
Imaging individual electron spins at atomic resolution is a long-sought goal in the physical sciences.^1–13 Reaching this goal is driven by needs ranging from imaging molecular assemblies in frozen cells to understanding spin dynamics in quantum computers. Labeling biomolecules with nitroxides and imaging the locations of the individual nitroxides, for example, would enable the determination of the three-dimensional structure of protein and nucleic-acid assemblies at the single-copy level, in situ, in flash-frozen samples.^7,13

Frustratingly, prior attempts to image individual electron spins with generally applicable techniques like magnetic resonance force microscopy (MRFM)⁵ or nitrogen-vacancy center magnetometry¹⁰ have fallen short of atomic resolution and have required more than 45 min of signal averaging per data point. MRFM has the 20 nm depth of view required to study frozen cell membranes, but the force detection protocol used to observe a single unpaired electron spin in quartz⁵ is inapplicable to nitroxides because of their short spin-relaxation times.⁷ Nitroxides can be detected via MRFM using a force-gradient protocol,^7,14–16 registering spin flips in a sample as a change in the mechanical oscillation frequency of a magnet-tipped cantilever.

Reducing the size of the MRFM experiment’s magnetic tip increases the tip’s magnetic field gradient and increases the resulting frequency shift per spin. Performing the experiment with the magnetic tip affixed to the cantilever enables the study of a wide range of as-fabricated samples. Hickman et al. were the first to detect magnetic resonance using a cantilever with a lithographically defined magnetic tip.¹⁵ Longenecker and co-workers created cantilevers with nanomagnet tips producing record-large magnetic field gradients¹⁷ and used them to observe proton nuclear magnetic resonance in a spin-cast polymer film via force detection with an equivalent electron sensitivity of 0.8 ${\mu }_{\text{B}}$ in 12.5 min of signal averaging.¹⁶ The spin sensitivity of this experiment was limited by deleterious surface-related force noise and force-gradient noise. The source of this noise at low temperature is debated; possible noise sources include dielectric fluctuations (in organic or polymeric samples),^18–21 thermal current fluctuations (in metallic samples),^22–27 and the thermal rotation and diffusion of polar surface adsorbates.^27–31

Isaac et al. significantly reduced surface-related force noise and force-gradient noise over a nitroxide-doped polymer film by coating the film with a ~10-nm-thick metal layer.³² Electron spin resonance experiments were carried out on the film at a temperature of $T=4.2\text{K}$ and a magnetic field of $B_0=1.4\text{T}$ with high-gradient cantilevers capable of achieving single-electron-spin sensitivity in less than a minute of signal averaging. Yet the observed electron-spin signals were disappointingly small,³³ raising the possibility that metal coating the film had rendered the nitroxide spins inactive.

Here we carry out MRFM experiments, inductively detected ESR experiments, and signal simulations to quantify the damage to sample spins in a polymer film caused by applying an evaporated metal coating. Moreover, we introduce a laminated sample-preparation protocol that obviates this damage and increases the ESR-MRFM signal 20-fold.

RESULTS

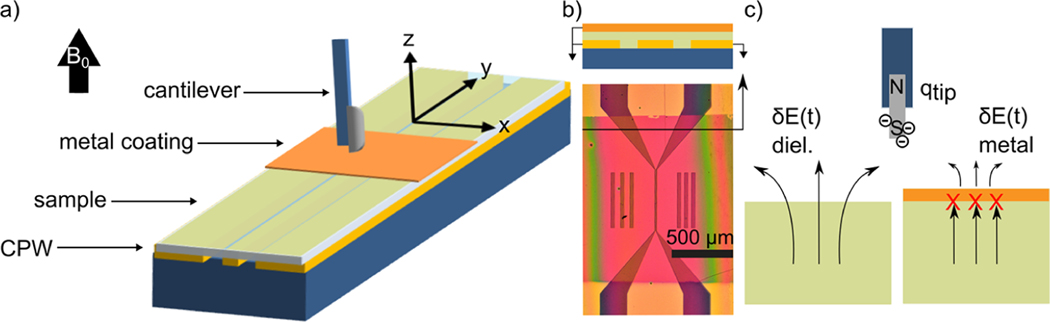
The MRFM experiment is sketched in Figure 1, and cantilever parameters are summarized in Table 1. See the Methods section below for experimental details. Briefly, a magnet-tipped, attonewton-sensitivity cantilever with an integrated ~100-nm-diameter cobalt nanorod tip was brought near a sample surface at a temperature of $T=4.2\text{K}$ and a magnetic field of $B_0=0.5$ or 1.4 T. The sample was a nitroxide-doped polymer film, spun-cast onto a coplanar waveguide (CPW) delivering up to $100\mu \text{T}$ of transverse magnetic field oscillating at 20 to 40 GHz. Experiments were carried out on films with and without a metal coating. This sample platform has been used to detect electron spin resonance (ESR), to detect nuclear magnetic resonance, and to demonstrate transfer of magnetization from electrons to protons in MRFM experiments performed with micron-scale nickel tips.^34,35 We previously described in detail methods for aligning magnet-tipped cantilevers with the centerline of the coplanar waveguide buried beneath a metal-coated sample.³² The application of resonant microwaves saturated sample spins, leading to a detectable shift in the mechanical oscillation frequency of the cantilever due to the CERMIT effect (cantilever-enabled readout of magnetization inversion transients;^7,14 see Methods). Observing magnetic resonance as a frequency shift requires electrons with a spin–lattice relaxation time $T_1\ge T_c$, with $T_{\text{c}}\le 180\mu \text{s}$ the cantilever period. At $T=4.2\text{K}$ and $B_0=0.6\text{T}$, 4-amino-TEMPO dissolved in polystyrene at a concentration of 40 mM has $T_1=1300\mu \text{s}$, satisfying this requirement. Absent additional fluctuating magnetic fields, we expect the nitroxide spins in our experiment to satisfy the $T_1\ge T_{\text{c}}$ requirement.

Figure 1.

Magnetic resonance force microscope schematic. A coplanar waveguide (CPW) was produced by depositing 200 nm Cu and 5 nm Au on top of a high-resistivity silicon substrate ($1\times {10}^4\text{Ω cm}$). A 200 to 500 nm layer of polystyrene ($\text{MW}=2\times {10}^6$), doped to 40 mM with 4-amino-TEMPO radicals, was spin-coated on top of the CPW. A 12 nm antistatic layer of gold was then deposited on top via electron beam evaporation. (a) Isometric view showing waveguide, sample, and cantilever. The external field $B_0$ is along the $z$ direction, current moves through the waveguide in $y$, and the cantilever oscillates in $x$. (b) Top-down optical image of the waveguide showing dimensions. The CPW center line narrows to a $500\mu \text{m}\times 10\mu \text{m}$ region, where the transverse magnetic field is large enough to invert spins. The metallic antistatic coating is optically transparent and appears red. (c) The antistatic coating blocks stochastic electric fields arising from both thermal fluctuations in the metallic CPW and dielectric fluctuations in the sample.

Table 1.

Cantilever Parameters^a

			cantilever
parameter	symbol	unit	A	B
frequency	$f_0$	Hz	7280	6550
spring constant	$k_0$	${\text{mN m}}^{-1}$	0.8	1.0
quality factor	$Q$	$\times {10}^4$	2.4	7.0
dissipation const.	$\text{Γ}$	${\text{pN s m}}^{-1}$	1.5	0.52
force noise	$\sqrt{P_{\delta F}}$	$\text{aN}/\sqrt{\text{Hz}}$	18	11
magnet thickness	$l_x$	nm	100	80
magnet width	$l_y$	nm	70	135
magnetic length	$l_z$	nm	1500	1500
sample thickness	$t$	nm	470	200

^aMagnet dimensions are indexed with respect to the $(x,y,z)$ coordinates defined in Figure 1. Magnetometry measurements were used to confirm the spring constants of cantilevers A and B (see Tables S2 and S3).

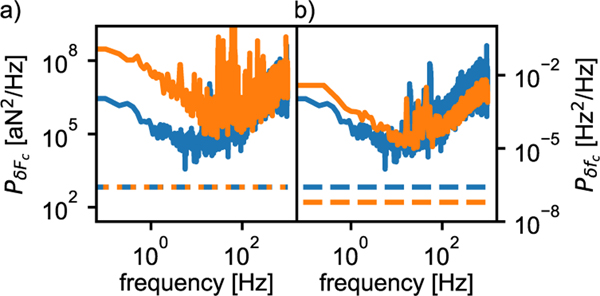
In order to dramatically reduce cantilever frequency noise, a 12-nm-thick, antistatic gold coating was applied to the sample surface (Figure 1). Electric field gradient fluctuations arising from thermal motions of charges and molecular dipoles in the sample and CPW couple to cantilever tip charges to create force-gradient noise (and therefore cantilever frequency noise).^20,21 The gold coating shields the tip from seeing these fluctuations, decreasing the cantilever frequency-noise power spectrum by 2 to 3 orders of magnitude (Figure 2(a)). The reduction was essentially independent of how the metal coating was deposited, whether via electron beam (e-beam) evaporation or by the gentler lamination procedure described below (Figure 2(b)).

Figure 2.

Metal coating the polymer-film sample decreased frequency noise significantly. Spectrum of cantilever frequency fluctuations observed experimentally (right-hand axis) and the equivalent power spectral density of force fluctuations (left-hand axis, calculated using eq 1). (a) Force fluctuation spectrum over a gold-coated film prepared by lamination (blue, tip–sample separation $h=37\text{nm}$; see Figure 6) and over bare polystyrene (orange, $h=41\text{nm}$). (b) Force fluctuation spectrum over gold-coated film prepared by lamination (blue, $h=37\text{nm}$; see Figure 6) and by e-beam evaporation (orange, $h=40\text{nm}$). All data were taken at a temperature of $T=4.2\text{K}$ and an external magnetic field of $B_0=0\text{T}$. The gold thickness was 12 nm. The zero-to-peak cantilever amplitude was $x_{0_{\text{p}}}=164\text{nm}$. The data in (a) and the blue data in (b) were acquired using cantilever A (Table 1), while the orange data in (b) were acquired using cantilever B. The dashed lines are the thermomechanical force noise, eq 2, and the corresponding thermally limited frequency noise.

ESR-MRFM measurements were conducted over metal-coated films using micron-scale nickel tips,^7,34 where the tip’s magnetic field gradient falls off slowly with tip–sample separation. We observed an ESR signal whose amplitude and microwave (MW) frequency dependence agreed well with theory for samples with⁷ and without³⁴ a metallic coating. Furthermore, we measured the electron spin–lattice relaxation time $T_1$ and found that it matched closely the value expected from bulk measurements^7,34 (see Figure S5).

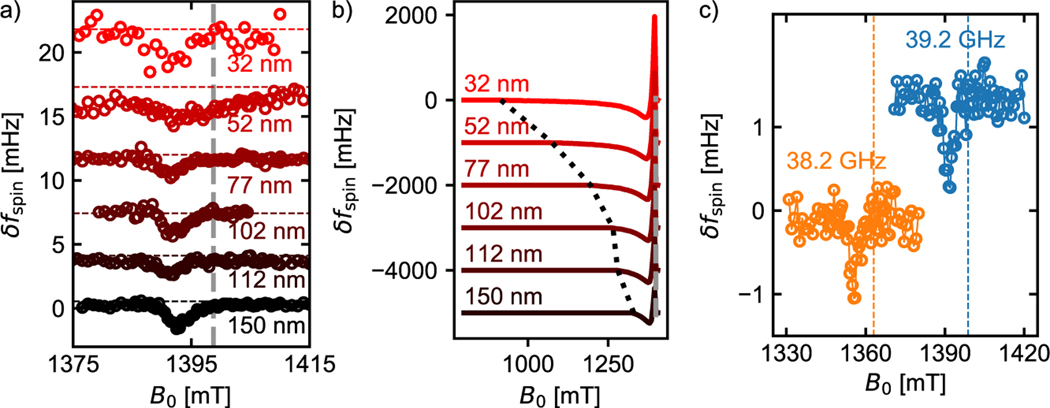
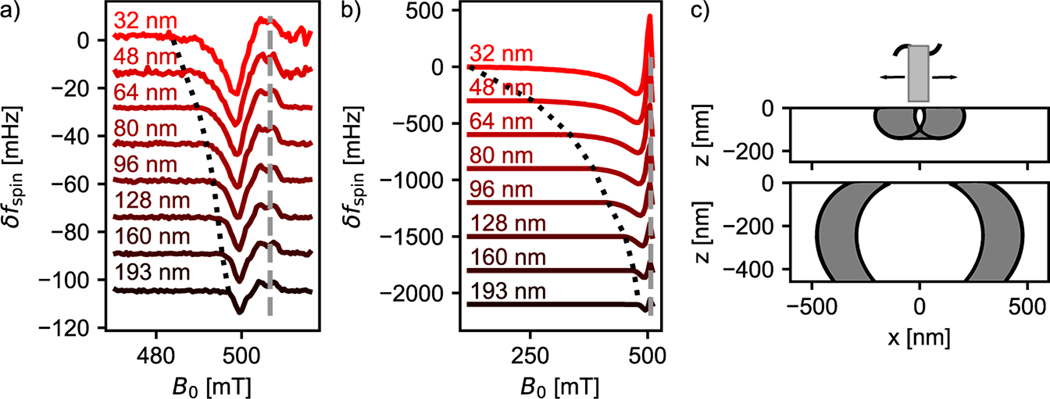
Samples whose metal coating was deposited by e-beam evaporation were then examined using ~100 nm diameter cobalt tips (Table 1). ESR signal was observed, but the signal amplitude and inferred tip magnetic field were 1 to 2 orders of magnitude smaller than expected. Figure 3 shows this disparity for a 135 nm × 80 nm × 1500 nm cobalt tip, cantilever B. Figure 3(a) shows the modulated cantilever frequency-shift signal vs external field detected at tip–sample separations between 30 and 150 nm. The dashed line shows the bulk resonance frequency we expect based on the 39.2 GHz excitation frequency. Measuring the separation between the bulk frequency and the low field edge of the signal tells us the tip-field experienced by those spins most proximal to the tip. We can see that this tip-field changes by at most a few mT over the 120 nm scan range.

Figure 3.

Poor agreement between observed and calculated electron-spin resonance signal vs magnetic field, tip–sample separation, and irradiation frequency for a film with an evaporated gold overlayer. (a) Modulated CERMIT electron-spin resonance signal vs magnetic field $B_0$ at microwave irradiation frequency $f_{\text{MW}}=39.2\text{GHz}$ at various tip–sample separations $h$; the dashed gray line shows the expected field for bulk resonance. (b) Simulation of (a) assuming no magnet damage (${\mu }_0{M}_{\text{s}}=1800\text{mT}$), no sample damage, accounting for incomplete spin saturation due to tip motion for $B_1=24\mu \text{T}$ (see Methods), and accounting for tip motion when calculating the frequency shift (eq 20 in ref 36). The dotted black line represents the tip field at the indicated height $h$. (c) Electron-spin resonance signal vs microwave irradiation frequency at $h=112\text{nm}$.

Figure 3(b) shows a simulation of the same signal assuming a uniformly magnetized tip with dimensions 135 nm × 80 nm × 1500 nm using the numerical integral of eq 20 in Lee et al.³⁶ Based on the simulations in Figure 3(b), we expect the local peak—the negative signal peak at low external field, representing spins close to the tip—to have a magnitude larger than 250 mHz; we expect a positive bulk peak larger than 1300 mHz. We observe instead ~2 mHz shift at 32 nm tip–sample separation and no obvious bulk peak. Yet from Figure 3(c) we can see that the observed signal is a spin-resonance phenomenon because the peak changes locations when we alter the transverse field frequency.

Prior hypotheses for an MRFM signal being smaller than expected include (1) oxidation damage to the leading edge of the cantilever’s nanomagnet^15,16 and (2) shortened sample $T_1$ caused by stochastic magnetic fields arising from thermomagnetic fluctuations^37–39 or thermal current fluctuations^26,37,40 in the magnetic (and metallic) tip. Shortened $T_1$ is a concern for CERMIT experiments because the spin-induced frequency shift is attenuated when spins relax faster than a cantilever period ($T_1\le 150\mu \text{s}$).

We should also consider that the e-beam evaporation of metallic electrodes onto organic samples can create a damage layer 10’s of nanometers thick.^41–46 During electron beam evaporation, gold is vaporized in a $P=1\times {10}^{-6}$ mbar vacuum chamber at temperatures nearing 3000 °C. The vaporized gold atoms travel through the vacuum chamber, largely unperturbed, until they make contact with the sample surface. Upon collision with the sample surface, the heat and kinetic energy of the gold molecules is transferred to the sample, which can cause significant damage. It has been found that gold atoms readily diffuse through ordered, organic films and can congregate into subsurface clusters.⁴⁶ (2,2,6,6-Tetramethylpiperidin-1-yl)oxyl (TEMPO) nitroxide radicals have been shown, by ESR spectroscopy, to thermally decompose in only 10 to 20 s at 550 K.⁴⁷

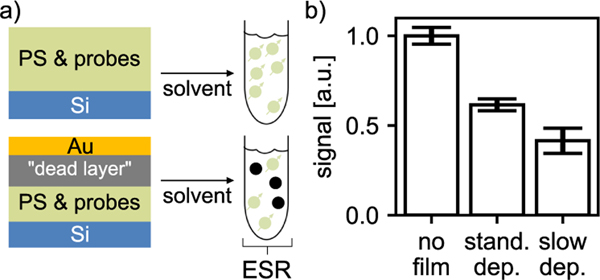
Interested in the possibility of a spin-inactive, “dead” layer at the top of the sample, we used inductively detected ESR to make a comparison of the number of active spin radicals in the polystyrene film with and without gold deposition. The deposited gold layer presents a possible difficulty for inductively detecting magnetic resonance. We avoided this difficulty by redissolving the polymer and performing spin-resonance measurements on the decanted solution (Figure 4). The experiment showed a loss of about half of the ESR signal after gold deposition on a 40-nm-thick sample, consistent with a dead layer of 20 nm.

Figure 4.

Inductively detected electron-spin resonance measurement of dead-layer thickness. (a) Preparation of sample. 40 nm of polystyrene, doped to 40 mM with 4-oxo-TEMPO, was spin-coated on top of a silicon substrate. 12 nm of gold was deposited at a rate of $1\text{Å}{\text{s}}^{-1}$ for the standard deposition treatment and $0.1\text{Å}{\text{s}}^{-1}$ for the slow deposition treatment (“stand. dep.” and “slow dep.”, respectively); for comparison, a film with no metal was prepared (“no film”). The films were dissolved in toluene to produce a solution, $0.6\mu \text{M}$ in 4-oxo-TEMPO, for study by inductively detected electron spin resonance (ESR). Damaged spins resulted in a reduced signal amplitude. (b) Signal and standard errors for the three treatments.

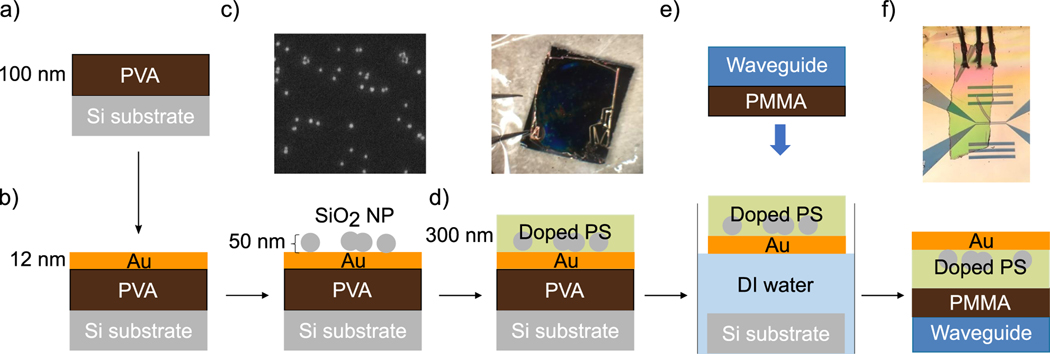
We then developed a laminate procedure for preparing doped polymer samples with metal overlayers that obviated the need to expose sample nitroxide radicals to e-beam deposition (Figure 5). Instead of depositing the gold on the polystyrene, we first deposited a sacrificial poly(vinyl alcohol) polymer (PVA; Figure 5(a–c)). The electron-beam deposition occurred without any spin radicals in the sample, so there was no risk of damaging the sample spins from heat or exposure to the beam. We then spin-coated the doped polymer over the film (Figure 5(d)). When the sample substrate was submerged in water, the PVA quickly dissolved and the doped polymer film floated to the surface and was pulled flat by surface tension (Figure 5(e)).

Figure 5.

Laminated sample preparation recipe: (a) spin-coat poly(vinyl alcohol) (PVA); (b) electron-beam deposit gold overlayer, let cool; (c) disperse SiO₂ nanoparticles (NP) in isopropanol, spin-coat over gold (see SEM); (d) spin-coat polystyrene (PS) doped to 40 mM with 4-amino-TEMPO (see optical micrograph, upper panel); and (e) submerge substrate in distilled water. The PVA dissolves and the gold-coated, doped PS film floats to the surface. Stamping downward with a waveguide coated in protective poly(methyl methacrylate) (PMMA) layer, the Au/PS film attaches to the waveguide. Finally, wire bond the gold overlayer to the waveguide’s ground plane (see optical image).

Two methods were developed for placing the resulting sample film on the waveguide. Stamping: The waveguides were stamped downward from above, with the conductive surface of the coplanar waveguide pointed downward and the gold coating of the sample film facing the water as in Figure 5(e). Scooping: The gold-coated polymer film was inverted so the gold was on top; the waveguide was submerged in the water with the conductive surface pointing upward; and the submerged waveguide was used to scoop the film from the surface of the water.

Both methods have advantages. The stamping method is simpler, because it does not require the polymer film to be flipped once it separates from the sacrificial polymer substrate. The stamping method furthermore allows the film to float with the hydrophobic polymer away from the water, so that less water gets trapped between the top of the waveguide and the polymer film, resulting in a smoother film. If the gold-coated film was machine-patterned before liftoff and aligned mechanically, a stamping approach would be superior. On the other hand, for the manual process used to produce the Figure 5(f) film studied experimentally, scooping the film from below facilitated aligning the film to the narrow portion of the waveguide’s centerline by eye.

Typically we coated the waveguide in a protective layer of poly(methyl methacrylate) (PMMA) before applying the gold-laminated thin-film sample. This additional layer protected the fragile CPW from scratching and significantly reduced the probability of the sample’s gold coating electrically shorting to the waveguide. For this experiment we coated the waveguide in doped polymer. This film had the same protective effect as PMMA and allowed us to collect signal over the portion of the waveguide without a top contact. Another advantage of the laminate approach is that it allows us to introduce a layer of nanoparticles between the gold and the doped polymer (Figure 5(c)). In future experiments we plan to image these nanoparticles by detecting a reduction in thin-film signal in the voids where no spin labels are present.

We were able to transfer the film with minimal tearing. The film conformed to the CPW with only a few wrinkles. We measured a surface roughness of ~1 nm rms over small areas via atomic force microscopy (Figure S12). The $T_1$ of sample spins, measured with a 4 μm nickel tip using the protocol of Moore et al.,⁷ was $T_1=1.22\pm 0.08\text{ms}$ (Figure S5), within the margin of error of inductive measurements of similar samples.

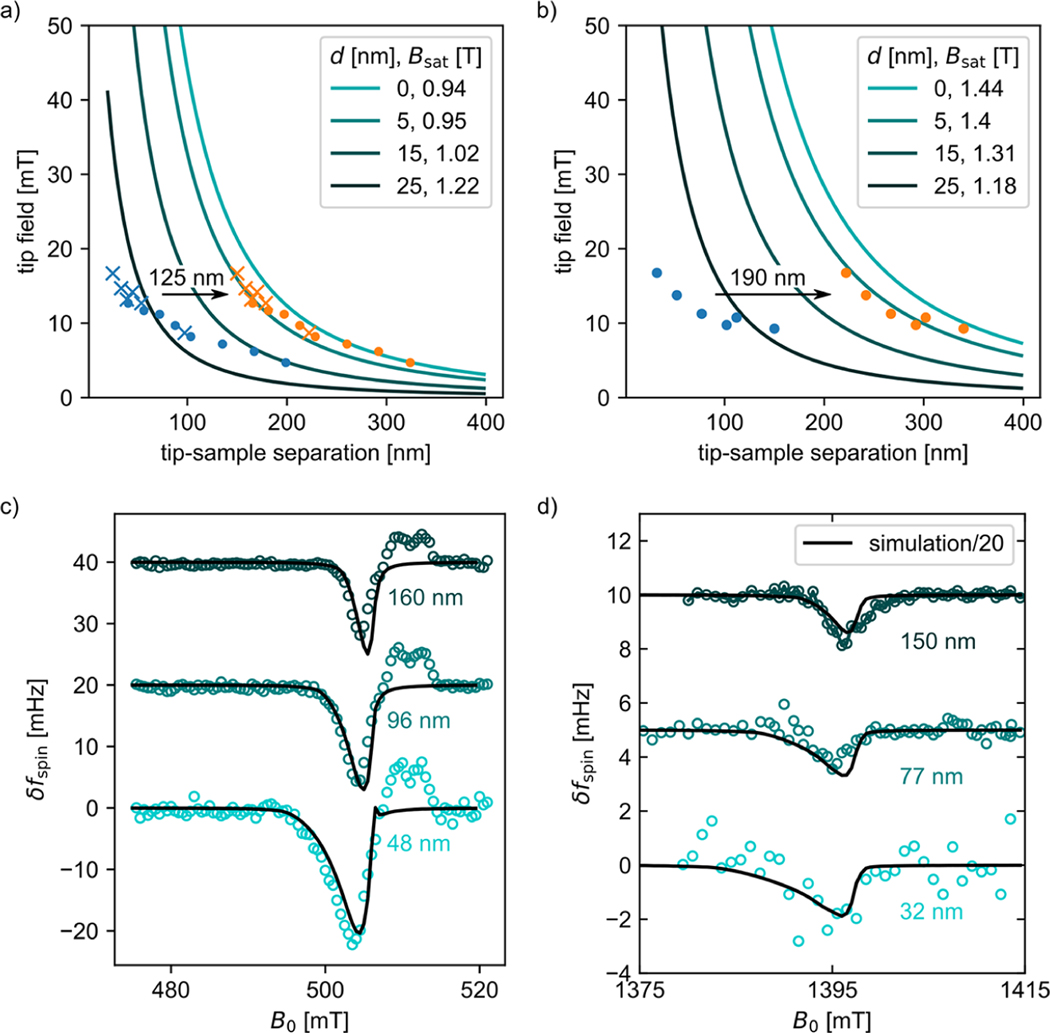
We measured MRFM ESR signal in the laminate film with the same apparatus used to examine the film prepared with a directly deposited gold overlayer. Figure 6(a) shows the spin signal vs external field $B_0$ measured at a number of different tip–sample separations. The dashed gray line shows the expected bulk resonance at the applied microwave frequency of $f_{\text{MW}}=14.2\text{GHz}$. The black dotted line shows the low-field edge of the measured signal. The difference, measured to be 22.7 mT at a 32 nm tip–sample separation, represents the additional magnetic field experienced by those spins most proximal to the magnetic tip. Figure 6(b) shows the results of simulations assuming the tip is fully magnetized with a saturation magnetization $B_{\text{sat}}=1800\text{mT}$ and accounting for the fact that the microwave pulse only occurred over part of the cantilever motion. Figure 6(c) shows the region of the sample swept out by the resonant slice at the maximum of the local peak, 470 mT (upper), and at the minimum of the bulk peak, 504 mT (lower). We can see that the top 10 to 30 nm of the sample contains a significant fraction of the spins contributing to the local peak.

Figure 6.

Significantly improved agreement between observed and calculated electron-spin resonance signal vs magnetic field, tip–sample separation, and irradiation frequency for a film with a laminated gold overlayer (Figure 5). (a) Modulated CERMIT electron-spin resonance signal vs magnetic field $B_0$ at microwave irradiation frequency $f_{\text{MW}}=14.2\text{GHz}$ at various tip–sample separations $h$. The dashed gray line shows the expected field for bulk resonance. The dotted black line is used to obtain the tip field. Experimental parameters: cantilever A, $x_{0\text{p}}=164\text{nm}$, and $t_{\text{pulse}}=25\mu \text{s}$. (b) Simulation of (a) assuming no magnet damage (${\mu }_0{M}_{\text{s}}=1800\text{mT}$), no sample damage, accounting for incomplete spin saturation due to tip motion for $B_1=40\mu \text{T}$ (see Supporting Information), and accounting for tip motion when calculating the frequency shift (eq 20 in ref 36). (c) Schematic showing saturated spins from the simulation in (b) at a tip–sample separation of $h=32\text{nm}$. Top: 470 mT, $1.5\times {10}^5$ active spins. Bottom: 504 mT, $2.7\times {10}^6$ active spins.

The simulated tip field, 386.1 mT at 32 nm tip–sample separation, is 17-fold larger than we observe experimentally. While the tip used in the experiment was produced similarly to the tip used to obtain the Figure 3 data, cantilever magnetometry data suggest reduced saturation magnetization (Figure S10); this observation could explain part of the discrepancy between simulation and experiment. Nevertheless, we observe a 20-fold increase in signal size when compared with similar measurements on samples with directly deposited gold films (Figure 6)—a promising improvement in spin sensitivity.

CONCLUSIONS

Let us begin by contrasting our findings with those of the three prior MRFM experiments detecting magnetic resonance with cantilevers having a lithographically defined magnetic tip.

The ESR signals from Hickman etal.’s batch-fabricated nickel tip¹⁵ and from the serially focused ion beam (FIB)-fabricated cobalt tip in Figure 3 were surprisingly similar. The tips in the Hickman and Figure 3 experiment both appeared well magnetized in cantilever magnetometry measurements, although it must be realized that drawing firm conclusions about the tip magnetic moment from the size of the magnetic-field-induced frequency shift alone is challenging. In our apparatus, there is uncertainty in the fiber interferometer’s position with respect to the cantilever tip, leading to a 40% uncertainty in the cantilever spring constant $k_0$ when estimating $k_0$ from cantilever thermomechanical position fluctuations. Allowing $k_0$ to vary over reasonable values, the magnetometry data were consistent with the expected demagnetization factors and a fully magnetized tip in both experiments. Hickman etal.’s sample was coated with 20 nm of gold deposited by electron-beam evaporation. The ESR signals in ref 15 and Figure 3 were each 1 to 2 orders of magnitude smaller than expected and exhibited a field dependence (i.e., line shape) in very poor agreement with numerical simulations. Hickman’s signal was only observable over a narrow range of tip–sample separations, so it was not possible to study the signal’s height dependence. The cobalt-tip signal of Figure 3 was somewhat easier to observe, but still failed to show an obvious systematic dependence on tip–sample separation.

In contrast, the nuclear magnetic resonance (NMR) signals from Longenecker etal.’s serially FIB-fabricated cobalt tips¹⁶ had a size and signal line shape vs tip–sample separation in very good agreement with theory, although 51 nm of magnet damage had to be introduced into the signal model to describe the observed line shape quantitatively. The ref 16 cantilever magnetometry data were consistent with a fully magnetized cobalt tip. The ref 16 sample was uncoated.

The Figure 6 ESR signal was acquired with a serially FIB-fabricated cobalt tip similar to Longenecker’s and exhibited a line shape that varied systematically with tip–sample separation, in stark contrast with prior small-tip ESR experiments. Comparing the ref 15 and Figure 3 signals to the Figure 6 signal, we see that the laminated sample improves the ESR signal size 20-fold. Considering our Figure 4 findings, this improvement suggests to us that the low signal in prior ESR experiments was in part due to deactivation of the sample’s nitroxide spins by the evaporated metal coating applied to reduce sample-related friction and frequency noise.

The laminated sample-preparation protocol of Figure 5 relied on the difference in solubility between the hydrophobic doped-polystyrene sample and the sacrificial hydrophilic poly(vinyl alcohol). We believe that lift-off can likewise be achieved with a hydrophilic sample by using a hydrophobic sacrificial layer instead, making the Figure 5 protocol a quite general approach to non-perturbatively creating low-noise metal-coated samples for spin resonance experiments.

What accounts for the remaining 17-fold discrepancy between the observed and calculated signals in Figure 6? Hypotheses for the observed small signal include

1. oxidation damage to the leading edge of the nanomagnet affixed to the cantilever;^15,16

2. shortened sample $T_1$ caused by stochastic magnetic fields arising from

   1. thermal current fluctuations^26,37,40 in the metallic tip or the metal overlayer, or
   2. thermomagnetic fluctuations in the magnetic tip;^37–39

3. fewer electron spin radicals present in the sample due to damage from the sample preparation process; or

4. inability to fully saturate sample spins because the magnetic field is changing rapidly, due to tip motion, during the microwave pulse.

Shortened $T_1$ is a concern for CERMIT experiments because the spin-induced frequency shift is attenuated when spins relax faster than a cantilever period ($T_1\le 150\mu \text{s}$).

To evaluate Hypothesis 4, we created an analytic theory describing the breakdown of saturation in a time-dependent magnetic field. This theory predicts that saturation losses due to tip motion depend on $B_1^2$ and the time derivative of the tip field. See the Supporting Information for a summary of the theory. This theory was incorporated into the signal simulations in Figures 3, 6, 7, and 8. At the applied $B_1$ of $24\mu \text{T}$ and $40\mu \text{T}$ (in Figures 3 and 6, respectively), the predicted breakdown of saturation due to tip motion was modest. Simulations of the Figure 6 experiment presented in the Supporting Information, Figure S2, show that breakdown of saturation leads to a factor of 2 loss in peak signal. Additional experiments presented in the Supporting Information show that low $B_1$ does not explain the reduction in signal width (Figure S7) and that increasing the MW power does little to increase signal size or width (Figure S8(c)). Taken together, these observations indicate that Hypothesis 4 is a noticeable but not major source of signal loss.

Figure 7.

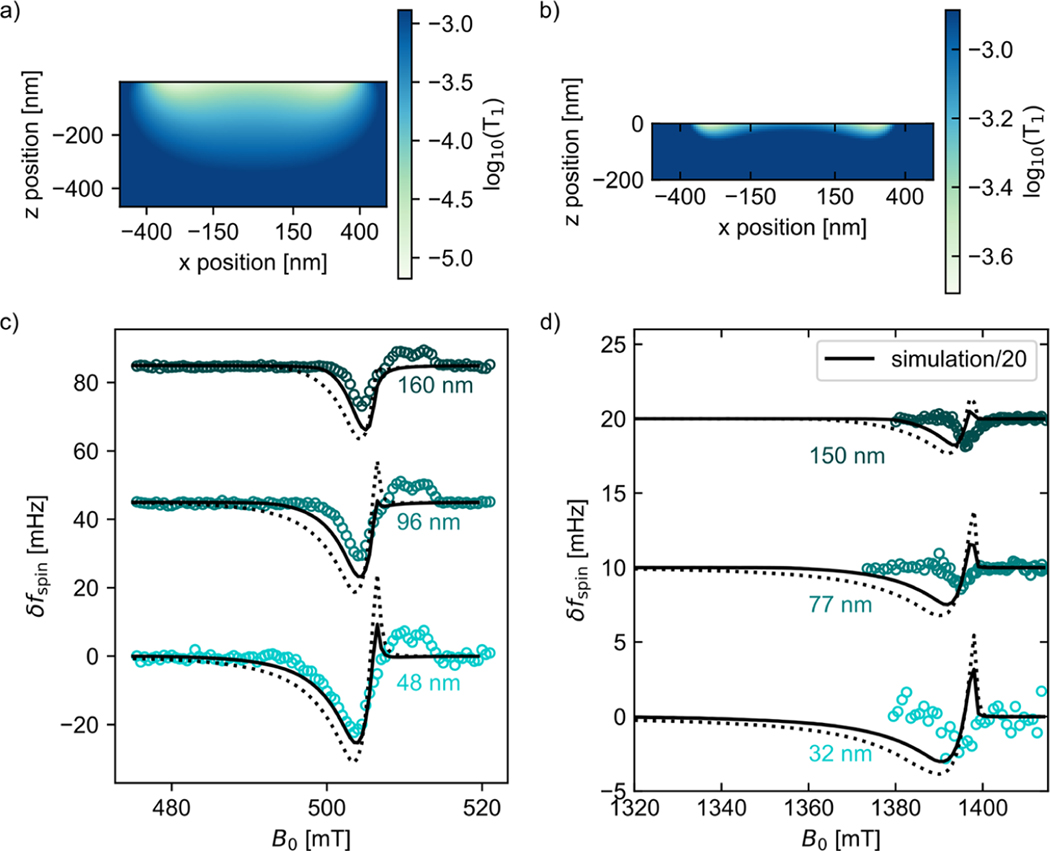
A damage layer partially explains the electron-spin resonance signal’s dependence on tip–sample separation and magnetic field. Measured magnet tip field vs tip–sample separation for the experiment in (a) Figure 6(a) and (b) Figure 3(a). Solid lines are tip-field models obtained from analysis of magnetometry data, Figure S1 and Tables S2 and S3, with the assumed uniform magnet damage layer thickness $d$ and tip saturation magnetization $B_{\text{sat}}$ indicated. Blue circles and crosses are measured data. Orange circles and crosses are the data expected for $h_{\text{damage}}=125\text{nm}$ in (a) and $h_{\text{damage}}=190\text{nm}$ in (b). (c, d) Measured (circles) and calculated (lines) electron-spin resonance signal vs magnetic field at various tip–sample separations, assuming $d=5\text{nm}$ and $h_{\text{damage}}=125\text{nm}$ in (c) and $h_{\text{damage}}=190\text{nm}$ in (d). The simulation in (d) was divided by a factor of 20 to match the experimental signal.

Figure 8.

A spatially dependent sample $T_1$, due to tip magnetization fluctuations, partially explains the electron-spin resonance signal’s dependence on tip–sample separation and magnetic field. Cross-sectional plot of sample $T_1$ calculated for (a) the Figure 6(a) experiment at $h=48\text{nm}$ (cantilever A, assuming $d=5\text{nm}$ and $B_{\text{sat}}=0.95\text{T}$) and (b) the Figure 3(a) experiment at $h=32\text{nm}$ (cantilever B, assuming $d=5\text{nm}$ and $B_{\text{sat}}=1.4\text{T}$). (c, d) Observed (circles) and calculated (lines) electron-spin resonance signal vs magnetic field. The dotted-line calculation assumes no damage layer. The solid-line calculation assumes $h_{\text{damage}}=60\text{nm}$. The simulation in (d) was divided by a factor of 20 to match the experimental signal.

To evaluate Hypotheses 1 and 3, we carried out additional signal simulations. Magnet oxidation, Hypothesis 1, could occur uniformly, over the entire magnet surface, or primarily at the leading edge. Uniform oxidation alters the tip’s demagnetization factors and magnetic moment, which affect the cantilever magnetometry signal (Figure S1). Based on an analysis of the cantilever magnetometry signals (see Supporting Information), we estimate a uniform magnetic dead layer of $d\le 5$ nm for both magnets. As long as the damage thickness is small compared to the sample thickness, both leading-edge damage, Hypothesis 1, and sample surface damage, Hypothesis 3, appear in the experiment as an increased tip–sample separation. To evaluate Hypotheses 1 and 3, we carried out simulations using a combination of a damaged magnet and increased tip–sample separation, $h_{\text{damage}}$.

The simulation results are shown in Figure 7. A measured tip field was extracted from the Figure 6(a) and Figure 3(a) data and plotted vs tip–sample separation (Figure 7(a,b) circles and crosses). A predicted tip field was calculated for various uniform damage layer thicknesses $d$ and saturation magnetization $B_{\text{sat}}$ consistent with cantilever magnetometry data (Figure 7(a,b) lines). The agreement between the measured tip field and the various predictions is poor. However, the measured and predicted tip field vs tip–sample separation data are in excellent agreement if we assume $d=5\text{nm}$ in both experiments and $h_{\text{damage}}=125\text{nm}$ in Figure 7(a) and $h_{\text{damage}}=190\text{nm}$ in Figure 7(b). In this damage model, the thickness $h_{\text{damage}}$ represents the sum of leading-edge magnet damage and sample surface damage. In qualitative agreement with our Figure 4 findings, $h_{\text{damage}}$ is lower for the laminated sample. The damage models were used to predict the full electron spin-resonance signal vs magnetic field (Figure 7(c,d)). For the laminated sample, Figure 7(c), the prediction captures the line shape of the local peak nearly quantitatively but predicts essentially no bulk peak, in disagreement with experiment. For the unlaminated sample, Figure 7(d), the prediction overestimates the measured signal by 20-fold, although the line shape is well predicted.

To evaluate Hypothesis 2, it is instructive to compare the Longenecker NMR experiment¹⁶ to the Figure 6 ESR experiment. The experiments used similarly fabricated cobalt tips, but the Longenecker experiment lacked a metal coating and observed nuclear spins. The rate of spin relaxation due to stochastic magnetic fields is $k_1=1/T_1={\gamma }^2{P}_{\delta B}\left(f_{\text{L}}\right)$ with $\gamma$ the gyromagnetic ratio, $P_{\delta B}$ the spectral density of magnetic field fluctuations, and $f_{\text{L}}=\gamma B_0/2\pi$ the relevant Larmor frequency. The proton gyromagnetic ratio is 650 times smaller than the electron gyromagnetic ratio, making protons $4.2\times {10}^5$-fold less sensitive to magnetic field fluctuations. If magnetic field fluctuations were affecting the spin signal, we would expect ESR experiments to be affected more strongly than NMR experiments. In ref 16, $f_{\text{L}}=120\text{MHz}$, while in Figure 6, $f_{\text{L}}=39.2\text{GHz}$. We expect conductivity fluctuations to yield a $P_{\delta B}$ that is essentially frequency independent below 100’s of GHz.^23,25,26 The thermomagnetic fluctuation spectrum, in contrast, will exhibit peaks at the tip’s ferromagnetic resonance frequencies, which could well include peaks near 39.2 GHz. For these reasons, nanoscale magnetic field fluctuations are a plausible explanation for the simultaneous loss of ESR signal in the Figure 6 ESR experiment and the retention of NMR signal in the ref 16 experiment.

To independently evaluate Hypothesis 2(a) losses from the metal overlayer, we measured the resistivity of the top contact down to 4 K and used a model enumerated by Ariyaratne etal.²⁶ to estimate the $T_1$ relaxation induced by thermal current fluctuations (Figure S9). Based on that model and the measured resistivity, we expect $T_1$ times to remain longer than the cantilever period for spins further than just a few nm from the gold film. This analysis rules out Hypothesis 2(a) losses from the metal overlayer.

Additional signal simulations were carried out to evaluate Hypothesis 2 contributions from the magnetic tip. The power spectral density of transverse magnetization fluctuations for each tip was estimated from the magnetic dissipation measured in cantilever magnetometry experiments (see Methods and Figures S10 and S11). Using this fluctuating transverse magnetization we modeled the fluctuating magnetic field at each point in the sample and computed a local $T_1$. Signal simulations were carried out using the resulting locally varying $T_1$. Lowering a spin’s $T_1$ reduces its contribution to the signal. In this model, spins near the magnet have a reduced $T_1$ due to their proximity to the magnet. This reduction qualitatively accounts for the missing local-spin signal.

The results of these simulations are shown in Figure 8. A cross-sectional plot of the computed sample $T_1$ is shown in Figure 8(a) for the laminated-sample experiment (cantilever A) and in Figure 8(b) for the unlaminated-sample experiment (cantilever B). In cantilever magnetometry experiments, the inferred transverse magnetization fluctuations were much larger for cantilever A’s tip than for cantilever B’s tip. Consequently, the estimated reduction in sample $T_1$ is much more significant near the sample surface for cantilever A compared to cantilever B. Spin signal was recomputed for the Figure 6(a) and Figure 3(a) experiments using the spatially dependent $T_1$ of Figure 8(a,b). The resulting predictions are compared to the observed electron-spin resonance signal vs magnetic field in Figure 8(c,d). Two sets of predictions are shown: no damage layer (dotted line) and a $h_{\text{damage}}=60\text{nm}$ (solid line); here $h_{\text{damage}}$ was adjusted to reproduce the height of the bulk peak in Figure 8(c). We can see in Figure 8(c) that a tip-fluctuation reduction of $T_1$, by itself, predicts the local-peak signal height and line shape in the cantilever A, laminated-sample experiment quite well; however, the bulk-peak height is overestimated and the bulk-peak width is again underestimated. The predicted local-peak line shape and bulk-peak height are improved somewhat by introducing a damage layer of $h_{\text{damage}}=60\text{nm}$, comparable to the 51 nm magnet damage layer inferred by Longenecker etal.¹⁶ in their protonspin MRFM experiments. In contrast, the tip-fluctuation reduction of $T_1$ fails to even qualitatively predict the observed signal in the cantilever B, unlaminated-sample experiment, Figure 8(d); again the prediction overestimates the measured signal by 20-fold.

Let us now draw some overarching conclusions from these simulations. Two signal models were considered: Model 1 probed both Hypotheses 1 and 3 (magnet damage and sample damage, Figure 7), while Model 2 probed Hypothesis 2 (tip-induced $T_1$ reduction, Figure 8). Both models required some uniform magnet damage and a reduced tip saturation magnetization to describe the measured signal well. Model 1 required the additional ad-hoc assumption of leading-edge tip damage or sample damage. In Model 2, in contrast, tip magnetization fluctuations inferred from experimental cantilever magnetometry data were used to compute the local $T_1$.

Consider first the cantilever A experiment carried out on a sample with a laminated metal coating. Model 1 did a slightly better job than Model 2 in explaining the size and line shape of the local peak. For reasons not understood, both models failed to predict the height or width of the bulk peak. Whether magnet and sample damage or tip-induced $T_1$ reduction is the dominant source of local-peak signal loss will require further experiments carried out over a larger number of tip–sample separations. Nevertheless, the success of Model 2 forces us to conclude that tip magnetization fluctuations could be a major source of signal loss in the cantilever A experiment.

Now consider the cantilever B experiment carried out on a sample with a directly deposited metal coating. The failure of Model 2 forces us to conclude that the small signal in the cantilever B experiment is due primarily to a combination of magnet damage and sample damage. For simplicity, in Model 2 we approximated the effect of sample damage as an increase in the tip–sample separation. However, the required $h_{\text{damage}}=190\text{nm}$ was comparable to the sample thickness of 200 nm; if attributed solely to sample damage, the estimated $h_{\text{damage}}$ would result in a thickness for the undamaged remainder of the sample of only 10 nm, wildly inconsistent with the size and width of the observed spin signal. We conclude that most of the damage in the cantilever B experiment is leading-edge magnet damage.

While Model 1 predicted the correct width of the local peak in the cantilever B experiment, the predicted signal size was 20-fold larger than the observed signal. An additional hypothesis is required to explain this signal loss, such as an anomalously low $B_1$. A low $B_1$ is at odds with the observation that the coplanar waveguide transmission losses were similar in both the cantilever A and B experiments. However, we know from bulk ESR measurements that gold atoms infiltrated the sample in the directly deposited metal coating experiments. We propose that this infiltration leads to a reduced $B_1$ and a loss of signal for near-surface spins.

Our overall conclusion is that the ESR signal in a small-tip MRFM experiment is extremely sensitive to both the magnetic properties of the tip and how the sample is prepared. Both the cantilever A and cantilever B tips were prepared in nominally the same way, yet the tips had very different magnetization fluctuations. The laminated-sample protocol introduced here clearly led to a 20-fold improvement in the ESR-MRFM signal. This improvement was achieved in spite of the laminated-sample experiment being conducted with a comparatively worse magnetic tip, whose fluctuations likely contributed to signal loss. Bulk ESR measurements indicated a reduction in sample damage of at least 20 nm, which will certainly aid in future single-spin experiments but did not fully explain the signal improvement. Future work should focus on preparing cantilever tips with less leading-edge damage and reduced magnetization fluctuations.

Loss of force-gradient signal in a small-tip ESR experiment can be studied, in future work, by performing force experiments. If $T_1\ll T_c$, a detectable Curie-law spin signal can be created by cyclically saturating electron spins to create a modulated sample magnetization oscillating in resonance with the cantilever. The net force between a magnet-tipped cantilever operating in the Figure 1 geometry and a semi-infinite sheet of spins is zero. To achieve a net force requires breaking the sample’s lateral symmetry. This can be accomplished by introducing spin-free voids into the film—the SiO₂ particles shown in Figure 5.

Further theory and numerical simulations will be required to assess stochastic magnetic field due to thermal current and magnetization fluctuations. Magnetic fields arising from current fluctuations can be calculated for a semi-infinite film of finite thickness^{23,25,26,37,40} but not yet for a rectangular metal object. We know of only one numerical simulation of the magnetic fields arising from thermomagnetic fluctuations in an MRFM experiment; this simulation was carried out using custom-written code.⁴⁸ Recently it has become possible to model these fluctuating fields using the National Institute of Standards and Technology’s open-source micromagnetics package OOMMF (The Object Oriented MicroMagnetic Framework).⁴⁹

METHODS

Coplanar Waveguide.

A coplanar waveguide⁵⁰ was produced on a high-resistivity silicon substrate (University Wafer, ⟨100⟩ orientation, $1\times {10}^4\text{Ω cm}$, Float Zone). Layers of Ti (5 nm), Cu (200 nm), and Au (30 nm) were electron-beam deposited on top of the substrate and patterned via a liftoff process. The entire CPW including ground planes covers $2\text{mm}\times 10\text{mm}$. As can be seen in Figure 1(b), the patterned center line of the CPW tapered down to a $5\mu \text{m}\times 500\mu \text{m}$ or $10\mu \text{m}\times 500\mu \text{m}$ wire where the current was concentrated to maximize $B_1$ for a given input power. The wire was flanked on both sides by a ground plane with a gap size equal to 3/5 of the wire width (i.e., 3 or $6\mu \text{m}$, respectively). The ends of the CPW were connected by wire bonds ($(38\mu \text{m}$ diameter, Al) to an Arlon board, which couples the microwaves in from a coaxial cable with SMA connections. A hole was cut into the Arlon board and the CPW placed into the hole; the Arlon board and CPW edges were within $\sim 200\mu \text{m}$ of each other. Each Arlon–CPW connection was made with three wire bonds, and additional wire bonds were used to connect the ground planes (over 21 wire bonds were used in total).

At $T=4\text{K}$, cable-conduction losses through the microscope to the CPW were on the order of −17 dB between 10 and 20 GHz and −35 dB between 25 and 40 GHz (Figure S5(a)). In the Supporting Information we calculate $B_1$ using these measured losses and the known input power (Figure S6). Additionally, we simulate the expected signal vs MW power for a past experiment performed with a micron-scale Ni tip and use the simulations to estimate the coil constant. Our most conservative estimate from these simulations was $B_1=40\mu \text{T}$ between 10 and 20 GHz and $B_1=4\mu \text{T}$ near 40 GHz, for $P_{\text{MW}}=10\text{mW}$ applied at top of the microscope. These $B_1$’s are well in excess of the $0.24\mu \text{T}$ needed to saturate electrons ($T_1=1.3\text{ms}$ and $T_2=450\text{ns}$⁷). Consistent with this estimate, we observed signal even at 40 GHz.

In the simulations of Figure 3(b) we use a $B_1$ value of $24\mu \text{T}$. To arrive at this number, we account for the 100 mW of power used and the −31 dB of losses measured to the centerline at 39.2 GHz and assume a doubled current density from using a centerline with a $5\mu \text{m}$ width instead of $10\mu \text{m}$.

Sample Preparation and Direct Deposition of Metal Overlayer.

The test sample for MRFM ESR experiments was produced by codissolving polystyrene (Fluka Analytical, lot 900711010, $M_n=1.735\times {10}^6$, $M_{\text{w}}/M_{\text{n}}=1.22$) and 4-amino-TEMPO (Sigma-Aldrich, batch 60483) in deuterated toluene (Cambridge Isotope Laboratories, lot 17E-405). The dissolved sample was spin-coated on the surface of the CPW at 5000 rpm, producing a 200 to 300 nm thick film. The thickness of the film was measured via stylus profilometry (Tencor AlphaStep 500). A silicon shadow mask was placed over the CPW, leaving only the center, narrow, microwire region exposed. Then the 12 nm gold overlayer was e-beam deposited at a rate of 1 Å s⁻¹ using the CVC SC4500 Egun Evaporation System at the Cornell Nanoscale Facility. The CPW center line, ground planes, and the overlayer were then wire-bonded across a $\sim 200\mu \text{m}$ gap to the Arlon substrate. The scattering parameters S₁₁ and S₂₁ were measured between 10 MHz and 40 GHz to ensure that the device was not shorted and that MW power would be sufficient to saturate electron spins.

Laminate Sample Preparation.

A 100-nm-thick layer of poly(vinyl alcohol) (Sigma-Aldrich, 99% hydrolyzed, $M_w=8.9\times {10}^4$) was spin-coated on the surface of a 1.5 cm × 1.5 cm Si substrate. A 12-nm-thick layer of gold was electron-beam deposited on top at 1 Å s⁻¹ in the same manner as the direct deposition. The solution of codissolved polystyrene and 4-amino-TEMPO (Sigma-Aldrich, lot 07610EH) in deuterated toluene (Cambridge Isotope Laboratories, 99.5%, lot 17E-405) was spin-coated on top of the deposited metal layer. We performed a static dispense and spread the liquid so it covered most of the PVA/Au, but not quite to the edges of the Si substrate. The thickness of the polystyrene layer was measured with profilometry. Thicker films were more durable and had less of a tendency to wrinkle. The polystyrene film was allowed to dry overnight in a nitrogen glovebox. A 100 nm thick layer of poly(methyl methacrylate) (Scientific Polymer, $M_w=1.47\times {10}^5$, $M_{\text{w}}/M_{\text{n}}=1.05$, lot 890708001) was spin-coated onto the waveguide to act as a protective layer. This layer reduced the incidence of shorting between the centerline and ground plane upon application of the laminate film and helped the film adhere to the surface of the waveguide.

Two Petri dishes were filled with deionized water and covered. The substrate was submerged in the first dish. The PVA dissolved within a minute, leading to a noticeable change in the appearance of the film and peeling away of the edges from the surface of the substrate. Bits of gold film without polystyrene were removed, and the sample was rinsed in the first Petri dish before being transferred. The sharp end of a dental pick was used to carve out a rectangular region of the sample long enough to cross the CPW over its narrow dimension (~3 mm) and wide enough to cover the narrow part of the center line (~0.3 mm). If the overlayer covered the center line outside of the tapered region, the transmitted MW power and therefore $B_1$ were reduced dramatically. The carved-out region gently started to peel up at the edges and then float to the surface of the water, where it was pulled flat by surface tension. The piece of film was gently flipped over so that the gold was on top.

The CPW was submerged in the water and then raised to the surface. A dental pick was used to hold the film in place on the surface, and alignment was maintained manually as the film attached to the CPW. The extra film folded around the edge of the CPW and could be scraped off the side. The film was allowed to dry overnight in a nitrogen glovebox. The CPW was wire-bonded to the Arlon board as in the direct deposition approach, and the scattering parameters were measured.

Assessing Sample Damage Layer via Inductively Detected ESR.

We performed inductively detected ESR at Cornell University’s National Biomedical Research Center for AdvanCed ESR Technology (ACERT). The pulse ESR measurements were carried out at 17.3 GHz by accurate detection of primary electron spin–echo (ESE) amplitudes to compare the number of active spin radicals with and without gold deposition, to infer a dead-layer depth. The deposited gold layer presents a possible difficulty for detection, further complicated by the too high spin concentration of 40 mM. These problems were avoided by redissolving the polymer and using the decanted solution. ESE amplitude measurements were made at 60 K on glassy toluene solutions by setting detection at the low-field side of the nitroxide spectrum and using 1.25 μs microwave pulse separation. Polystyrene and 4-oxo-TEMPO (Sigma-Aldrich, lot 07610EH) were codissolved in deuterated toluene and spun to form a 40 mM film with a thickness of about 40 nm on a square, 1.5 cm × 1.5 cm piece of polished silicon. Thin-film interference was quite noticeable on silicon and helped confirm the uniform thickness as well as aid in the redissolving step by assuring that all of the polymer had been removed. Toluene almost instantly redissolved polystyrene with no top contact. All of the pieces were sonicated to ensure that the film was fully dissolved and to remove more stubborn flecks underneath the deposited gold. The weight of toluene used to dissolve the film was measured and used to adjust the final calculation.

The radical concentration of the solution was approximately 0.6 μM. This was sufficient to produce spin–echoes with signal-to-noise on the order of 100 in minutes. Fused silica capillary tubes (Vitrocom 2024-CFQ, 2.0 mm i.d.) were used as the sample tube. The inner diameters of the tubes were measured by weighing the water required to fill the bottom two centimeters. Care was taken to work with round tubes prescreened for the same diameter (±0.01 mm) for each experiment. After the samples were dissolved in toluene, the resulting solutions were placed in the capillary tubes, the tubes were immersed in liquid nitrogen, and the ESR signal was measured. Signal response was checked in every measurement by obtaining a spin–echo from the Cr³⁺ ions in the resonator dielectrics. These reference echo amplitudes were consistent within 5% throughout all measurements. The repeat substrate preparations without gold layer and repeat sample reinsertion were consistent within 5%. Several trials were run, and the samples with gold deposited were compared against control samples with no deposited gold. Measurements showed essentially complete and uniform coverage of substrates with a <1 nm difference between center and edge thicknesses by profilometry and similar repeatability of thickness between spin trials. Trials with uneven coats had noticeable unevenness in thin-film interference color and were respun. After spinning, each wafer had its thickness tested by profilometry, and the average value allowed for more accurate comparison between control and test samples.

We performed trials on films with gold deposited at 1 $\text{Å}{\text{s}}^{-1}$ and 0.1 $\text{Å}{\text{s}}^{-1}$ and a control with no film. We compared the integral of the pulse ESR signal for each of the trials and made small adjustments to account for slight differences in thickness. We observed reduced signal size for the films with gold top contacts, a roughly 50% reduction for a 40-nm-thick sample.

Magnetic Resonance Force Microscopy.

Magnetic resonance force microscopy measurements were performed at a pressure of $P=5\times {10}^{-6}$ mbar and a temperature of $T=4.2\text{K}$ using silicon cantilevers custom-fabricated as described in Jenkins etal.⁵¹ and Hickman etal.¹⁵ With the uncoated sample, a small tip bias voltage was applied to minimize cantilever frequency noise; with metal-coated samples, the optimal tip bias was found to be near zero volts, so the tip was grounded. Cantilevers were $200\mu \text{m}$ long, $4\mu \text{m}$ wide, and 340 nm thick, with a pad centered $70\mu \text{m}$ from the tip. Experiments performed over the directly deposited sample and the laminate sample used cantilevers from the same batch with magnets produced and attached via the same process with similar magnet dimensions. Following Longenecker etal., cobalt magnets were electron-beam deposited onto a silicon chip, which was then transferred to the fabricated cantilevers in an FEI Strata 400 STEM FIB system.^16,17,52 A complete description of the attachment process is given in ref 52. Cantilever and magnet properties are summarized in Table 1. The laminated sample was studied using cantilever A, while the directly deposited sample was studied using cantilever B.

Cantilever tip position was read out using a temperature-tuned⁵³ Fabry-Pérot fiber-optic interferometer⁵⁴ (wavelength $\lambda =1310\text{nm}$) and a commercial photodetector. During experiments where the tip position or $B_0$ was varied, a National Instruments PXI-7952 field programmable gate array (FPGA) calculated a lock-in signal at the second harmonic of the cantilever resonance and used it to temperature-tune the interferometer’s wavelength so the interferometer continuously operated at fringe center. The cantilever’s thermal position fluctuations were recorded, and the spring constant $k_{\text{c}}$ was calculated from the integrated power spectrum and temperature using the equipartition theorem;⁵⁵ due to uncertainty in the location of the laser reflection on the cantilever pad, the error in $k_{\text{c}}$ could be as large as 44%.¹⁶ To measure the cantilever frequency, the photodetector output was filtered and fed into the FPGA, which phase-shifted the cantilever signal and transmitted a fixed-amplitude copy to a piezoceramic element at the cantilever base, driving the cantilever into self-oscillation. Cantilever frequency $f_{0}vs$ time $t$ data were obtained from a digitized record of cantilever position vs time using a software frequency demodulator;⁵⁶ the mean cantilever frequency and power spectrum of cantilever frequency fluctuations $P_{\delta f_0}(f)$ were calculated from the inferred $f_{0}vs$ $t$ data. The cantilever’s decay time ${\tau }_{\text{c}}$ was obtained via a ringdown measurement and used to calculate the cantilever quality factor $Q=\pi f_0{\tau }_{\text{c}}$. A dissipation constant was calculated using $\text{Γ}=k_0/\left(2\pi f_{0}Q\right)$, and the power spectral density of force fluctuations calculated from $P_{\delta \text{F}}=4\text{Γ}{k}_{\text{B}}{T}_0$, with $T_0$ the cantilever temperature, assumed to be $T_0=4.2\text{K}$. From the power spectrum of cantilever frequency fluctuations an equivalent power spectrum of force fluctuations⁵ was calculated from

$$P_{\delta F}\left(f_0-f\right)=\frac{4k_0^2{x}_{\text{rms}}^2}{f_0^2}{P}_{\delta f_0}(f)$$ (1)

with $k_0$ the cantilever spring constant, $f_0$ the cantilever frequency, and $x_{\text{rms}}=x_{0\text{p}}/\sqrt{2}$ the cantilever root-mean-square oscillation amplitude. For comparison, the (frequency-independent) power spectrum of thermomechanical force fluctuations is computed from

$$P_{\delta F}^{\text{therm}}=\frac{2k_{\text{B}}{T}_0{k}_0}{{\pi }^2{f}_0^2{\tau }_{\text{c}}}$$ (2)

with $k_{\text{B}}$ Boltzmann’s constant.

Cantilever A and B tip magnets were characterized in situ using frequency-shift cantilever magnetometry.^38,57 The magnetic field was stepped and the cantilever self-oscillation frequency and quality factor were measured at each step. The observed frequency vs field data were fit to eq 1 in Ng etal.³⁹ to yield the tip’s magnetic moment and demagnetization factors (see Supporting Information).

ESR signal was detected as a Curie-law force-gradient signal using a modulated version of the CERMIT protocol,¹⁴ following Moore etal.⁷ MW irradiation was supplied by an Anritsu-Wiltron source (model 6814B) and modulated by an American Microwave Corporation switch (model SWN-218–2DT). For experiments with $f_{\text{MW}}$ between 10 and 20 GHz, the signal was amplified by a Narda microwave amplifier (model DBP-0618N830). For experiments with $f_{\text{MW}}$ between 20 and 40 GHz, a Marki microwave frequency doubler (model ADA1020) was used to mix the microwaves up to the desired frequency. For the experiment over the directly deposited sample, microwave irradiation was timed to last for half a cantilever cycle and start at the apex of cantilever motion. After each cantilever cycle with MW irradiation, there were two cycles with the MW off to prevent cantilever heating. As with Moore’s original experiment, this on/off modulation sequence was interspersed with periods of no irradiation to produce a square wave modulation of $f_0$ with a modulation frequency between 1 and 20 Hz. The modulation frequency was chosen to avoid $1/f$ frequency noise from dielectric fluctuations and $f^2$ noise from interferometer circuitry.^20,21 The amplitude of the resulting modulated frequency shift signal could be determined by a software frequency demodulator and lock-in detector.⁵⁶ For the data taken over the laminate sample, microwaves were applied twice per cycle instead of once, on both zero crossings; this microwave timing was found to reduce spurious excitation of the cantilever at the modulation frequency. To reduce heating without decreasing signal size, the irradiation duration was reduced from one-half cantilever cycle to 25 μs.

Signal Simulation.

The simulated cantilever frequency-shift signals of Figure 3 and Figure 6 were calculated by numerically evaluating eq 20 in ref 36 over a simulation sample grid. Briefly, the component of the tip magnetic field in the z direction, $B_z^{\text{tip}}$, and its first derivative in the direction of cantilever motion, $B_{zx}^{\text{tip}}$, were calculated analytically using formulas for a rectangular prism from ref 58. The magnet was assumed to be uniformly and fully magnetized with $B_{\text{sat}}=1.8\text{T}$. The sample was treated as a square prism with extent $L_x$ and $L_y=1000\text{nm}$ and $L_z=200\text{nm}$ (or 470 nm for the laminate film simulation) with grid points spaced 10 nm apart in $x$ and $y$ and spaced 5 nm apart in $z$. An approximation of the Bloch equations result for the case of a moving tip with $B_1=40\mu \text{T}$ was used to determine partial saturation of spins that pass through resonance during the application of microwaves. The equations used are briefly derived in the Supporting Information, with a more complete description in a forthcoming manuscript. The assumptions made apply most accurately when $B_1<6.3\mu \text{T}$ and where the magnetic field is linear in time as spins pass through resonance. In Figure S3 we show how our simulation performs at larger $B_1$ and for grid points that experience nonlinear change in field vs time. Finally, the frequency shift contribution from each grid point was evaluated using the numerical integral of eq 20 in ref 36 at each of 32 cantilever displacements and summed together to compute a total cantilever frequency shift from the force vs displacement data.

In figures where a comparison was made between experimental data and simulation (Figures 7 and 8), a +5 mT adjustment had to be made to match experimental data to simulations. We believe this is due to a calibration error in our Antritsu-Wiltron microwave source.

For the simulations in Figure 8 we incorporate the effects of tip-magnetic field fluctuations on sample $T_1$. The estimated sample $T_1$ values, when used to calculate average magnetization according to eq 7 of the Supporting Information, lead to a reduction in signal contribution from spins near the cantilever tip. First, the magnetic dissipation was calculated by measuring the cantilever dissipation as the external field B₀ was varied and then subtracting off the dissipation at $B_0=0\text{T}$. The magnetic dissipation was then used to calculate the spectral density of transverse tip magnetic moment fluctuations at the cantilever frequency, $S_{\mu }\left(f_c\right)$. We calculated the fluctuating magnetic field due to the tip according to $S_B=S_{\mu }{B}_{\text{tip}}^2/4{\mu }^2$, and for $B_{\text{tip}}$ we calculated the value at each grid point assuming the undamaged tip from Table S3. The electron-spin relaxation rate can be calculated from the spectral density of transverse magnetic field fluctuations at the Larmor frequency, $T_1^{-1}={\gamma }_{\text{e}}^2{S}_B\left(f_{\text{L}}\right)$. For this calculation, we assumed $S_B\left(f_{\text{L}}\right)\approx S_B\left(f_{\text{c}}\right)$. For further details, see Figure S10 in the Supporting Information and also ref 39. In Figure 8(a) and (b), $T_1$ was calculated at each sample grid point using the magnetic dissipation obtained from the data in Figures S10 and S11, respectively, and the average $B_{\text{tip}}$ calculated over the cantilever cycle computed using the magnet model from Tables S3 and S2, respectively. Spin saturation was then calculated for $B_1=40\mu \text{T}$ and $B_1=24\mu \text{T}$, respectively, accounting for the resonance offset’s time-dependence as described in the Supporting Information.