Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2023 Jul 10.
Published in final edited form as: Comput Methods Biomech Biomed Engin. 2020 Oct 5;24(3):278–288. doi: 10.1080/10255842.2020.1826457

Finite element simulation of head impacts in mixed martial arts

Stephen Tiernan a, Aidan Meagher a, David O’Sullivan b, Eoin O’Kelly c
PMCID: PMC10330963  NIHMSID: NIHMS1913781  PMID: 33017178

Abstract

Thirteen MMA athletes were fitted with the MiG2.0 Stanford instrumented mouthguard. 451 video confirmed impacts were recoded during sparring sessions and competitive events. The competitive events resulted in five concussions. The impact with the highest angular acceleration from each event was simulated using the GHBMC head model. Average strain in the corpus callosum of concussed fighters was 0.27, which was 87.9% higher than uninjured fighters and was the best strain indicator of concussion. The best overall predictor of concussion found in this study was shear stress in the corpus callosum which differed by 111.4% between concussed and uninjured athletes.

Keywords: Concussion, maximum principal strain, corpus callosum

Introduction

Concussion in sport is very prevalent with between 1.6 and 3.8 million sports-related concussions in the United States each year (Langlois et al. 2006). The diagnosis of concussion is particularly difficult with many studies reporting that approximately 50% of concussions go unreported (Elliott et al. 2015).

The relationship between head kinematics and concussion in US football has been extensively studied as it has been possible to mount sensors within the helmet to capture acceleration data. The Head Impact Telemetry System (HITS), Simbex, Lebanon, NH, USA, was developed in 2002 and uses an array of accelerometers to measure linear and rotational accelerations. The alternative to measure head accelerations in vivo is to recreate the impact using video data in a laboratory or with kinematic software. Several video angles are required for this to be successful and it is a difficult and time consuming task with up to 25% angular acceleration errors (Newman et al. 2005).

To address these errors and to enable the measurement of head accelerations in vivo instrumented mouthguards have been developed. Hernandez et al. recorded two concussions in US football using an instrumented mouthguard, one case involved a loss of consciousness and the other was self-reported (Hernandez et al. 2015). King et al. used the X2 BioSystems mouthguard to record over 20,000 impacts above 10 g in amateur rugby but no head injuries were sustained (King et al. 2014). One of the few studies to report concussions in an unhelmeted sport was carried out by McIntosh et al. who used simulation software to recreate impacts in Australian rules football and rugby (McIntosh et al. 2014). The study recreated 27 concussive impacts and determined that the mean linear and angular accelerations for the injury cases were 103.4 g (±29.5 g) and 7951 rad/s2 (±3562 rad/s2), respectively.

The only known studies to report in vivo unhelmeted head accelerations that have resulted in a concussion have used data from the study of head impacts in Mixed Martial Arts (MMA) reported in this paper. The first of these studies included rugby players and MMA athletes and investigated the correlation of strain with disruption to the blood brain barrier (O’Keeffe et al. 2019). The second developed a multi-directional dynamic model of the head and investigated its reliability in predicting head injury (Laksari et al. 2019). Laksari’s study found that peak angular acceleration was the best predictor of head injury in cases of high angular acceleration and low velocity.

In 1943 Holburn first proposed that concussion was caused by angular velocity and acceleration rather than linear acceleration (Holbourn 1943). Since then animal studies have found that linear head accelerations are important for focal trauma but angular accelerations cause inertial loading of the brain and correlate with brain trauma severity (Ommaya and Gennarelli 1974; Gennarellie 1983; Raghupathi et al. 2004). In a study of 300,977 impacts in US football which included 57 concussions an angular acceleration of 6383 rad/s2 was found to represent a 50% risk of concussion (Rowson et al. 2012). The magnitude of the change in angular velocity, and hence high angular acceleration has been shown to correlate with brain strain (Kleiven 2005).

Simulation studies play a unique role in head impact investigations as they enable the determination of brain tissue stress and strain resulting from trauma. The Wayne state head model is one of the most detailed head models and is capable of simulating impacts up to 200 g and 12 krad/s2 (Zhang et al. 2001). This model was used to investigate concussion and determined that the largest strains occurred in the fornix, mid-brain and corpus callosum and that there was a significant correlation between strain and concussive symptoms (Viano, Casson, Pellman, Zhang, et al. 2005). Kleiven found lateral angular accelerations (in the coronal plane) gave rise to higher strains than impacts from other directions (Kleiven 2005). Generally, kinematic data are used to define the boundary conditions for simulation models. In order to quantify the kinematics of head impacts in US football Newman et al. recreated 27 impacts in a laboratory (Newman et al. 2000). Several researchers have used these data with simulation models to find the average strain in various brain regions of concussed players or the strain that related to a 50% probability of concussion. A 50% probability of concussion in US football has been reported for strains in the corpus callosum of 0.13 (Giordano and Kleiven 2014) to 0.21 (Kleiven 2007). The average strain in the corpus callosum of concussed Australian rules football and rugby players was 0.31 (Patton et al. 2013; McIntosh et al. 2014). High strains in the corpus callosum are thought to be due to lateral distortions of the falx, caused by high coronal angular accelerations (Ho et al. 2017).

Strain rate has also been found to be associated with the risk of concussion. Strain rates of 48.5 s−1 (Kleiven 2007) and 60 s−1 (Zhang et al. 2003) have been related to a 50% probability of concussion.

Mixed martial arts

Mixed martial arts (MMA) is a competitive, full-contact sport that involves an amalgamation of elements drawn from boxing, wrestling, karate, taekwondo, jujitsu, muay thai, judo, and kickboxing (Hutchison et al. 2014). The fighters wear 110–170 g gloves and do not wear head protection. Competitive bouts consist of three rounds of 5 min each, provided the referee does not stop the fight. Fights are ended by the referee either due to a knockout (KO), where there is a loss of consciousness, or more commonly a technical KO (TKO), where a fighter appears unable to defend themselves. The fight may also end by submission. A 10-year review of injuries in MMA found that head trauma was the most common reason for match stoppages (28.3%) (Buse 2006).

Method

Thirteen adult MMA fighters took part in the study, 12 professional or semi-professional and one amateur. Fighters took part in both sparring and competitive events, as shown in Table 1. The fighters were fitted with the Stanford instrumented mouthguard (MiG2.0) and ethical approval was granted by the Technological University Dublin, Tallaght Campus, Ethics committee REC-STF1–201819.

Table 1.

Study participants.

No. of events Weight class Max weight (kg) Gender Level
Sparring Competition
Fighter 1 1 Lightweight 70.3 Male Pro
Fighter 2 2 1 Lightweight 70.3 Male Pro
Fighter 3 3 2 Middleweight 83.9 Male Pro
Fighter 4 1 2 Lightweight 70.3 Male Pro
Fighter 5 4 1 Lightweight 70.3 Male Pro
Fighter 6 1 1 Flyweight 56.7 Female Pro
Fighter 7 1 Strawweight 52.2 Female Pro
Fighter 8 1 Bantamweight 61.2 Male Amateur
Fighter 9 3 1 Featherweight 65.9 Male Pro
Fighter 10 1 1 Bantamweight 61.2 Male Semi-Pro
Fighter 11 1 Lightweight 70.3 Male Semi-Pro
Fighter 12 1 Strawweight 52.2 Female Pro
Fighter 13 1 Welterweight 77 Male Semi - Pro
Open in a new tab

The Stanford instrumented mouthguard has previously been used in studies of head impacts primarily in US football (Hernandez et al. 2015). The mouthguard has a triaxial accelerometer and a triaxial gyro-scope to measure angular rate. The sensors, processor and battery are completely sealed in three layers of ethylene vinyl acetate in a dental moulded mouthguard. Data are downloaded from the device post-event via Bluetooth (Kuo et al. 2016). In this study impacts were recorded when linear accelerations exceeded the 10 g threshold established in previously published studies (King et al. 2015). The acquisition window was 50 ms pre-trigger and 150 ms post-trigger. Linear acceleration and angular velocity were sampled at 1000 Hz and all data were filtered using a 4fourth-order Butterworth low-pass filter with a cut-off frequency of 300 Hz. Angular acceleration was estimated using a five-point stencil derivative of the measured angular velocity (Wu et al. 2016). The accelerations were transformed to the centre of gravity using the offsets for a 50th percentile human head. A normalised root mean square error of 15% has been reported for the kinematic measurements recorded by the Stanford mouthguard (Kuo et al. 2016). A sample of the data from one impact recorded during a sparring session is shown in Figure 1.

Figure 1.

Figure 1.

Open in a new tab

The co-ordinate system and head and neck of the GHBMC model.

In order to validate the mouthguard data each event was video recorded by two cameras at 60 frames per second. The cameras were placed around the arena at approximately 90° to each other. In addition, TV coverage was available for the competitive events. The time on the mouthguard data was aligned with the video time line and the video was examined frame by frame by two researchers using Kinovea video analysis software. The video data were used to confirm that a head impact had occurred and that the direction of the impact conformed to the direction indicated by the mouthguard. If an impact could not be confirmed using the video data, it was removed from the data set.

The MMA athletes were medically examined before the study commenced, immediately after competitive bouts and again approximately 48 h after the competitive events. The impact with the highest resultant angular acceleration from each event was simulated.

Simulation

The Global Human Body Model Consortium (GHBMC) is a multi-institutional organisation created in 2006 that includes six universities and eight automotive manufacturers. The organisation aims to produce the most biofidelic simulation body model. The model head was developed by Wayne State University, the neck by the University of Waterloo, and the thorax and pelvis by the University of Virginia. The model is available to researchers under license from Elemance Ltd., USA. This study used the head and neck portion of the GHBMC which consists of 532,608 elements and 426 parts. The head portion of this model has 246,831 elements and 71 parts, as shown in Figures 2 and 3. This model has been validated against number of cadaver experiments (Mao et al. 2013). Brain and ventricle pressure were validated from instrumented cadaver experiments (Nahum et al. 1977; Trosseille et al. 1992). Intracranial brain motion was validated using Hardy et al.’s experiments which tracked embedded neutral density targets in cadaver heads (Kleiven and Hardy 2002; Hardy et al. 2008).

Figure 2.

Figure 2.

Open in a new tab

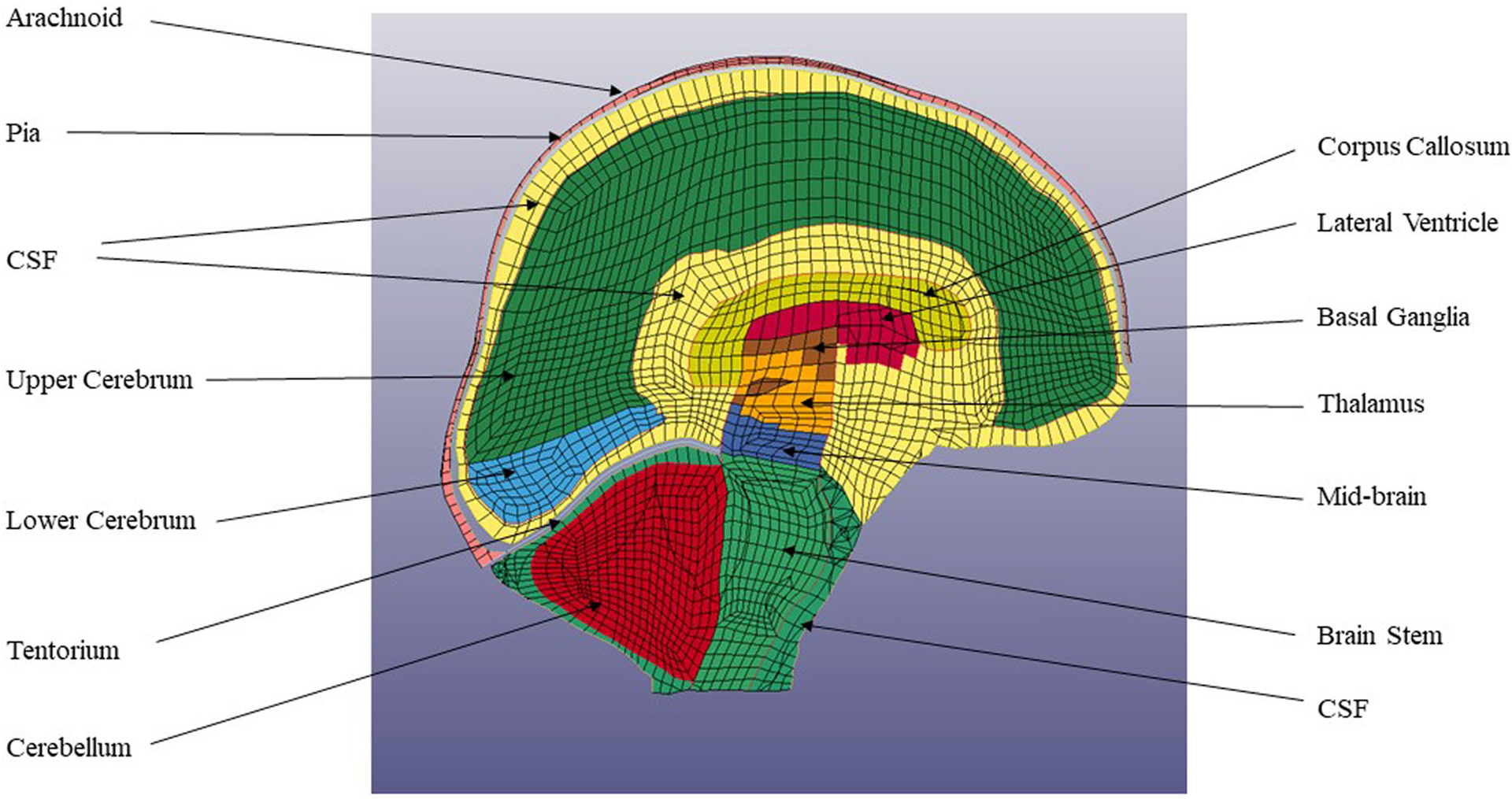
Brain parts in the GHBMC model.

Figure 3.

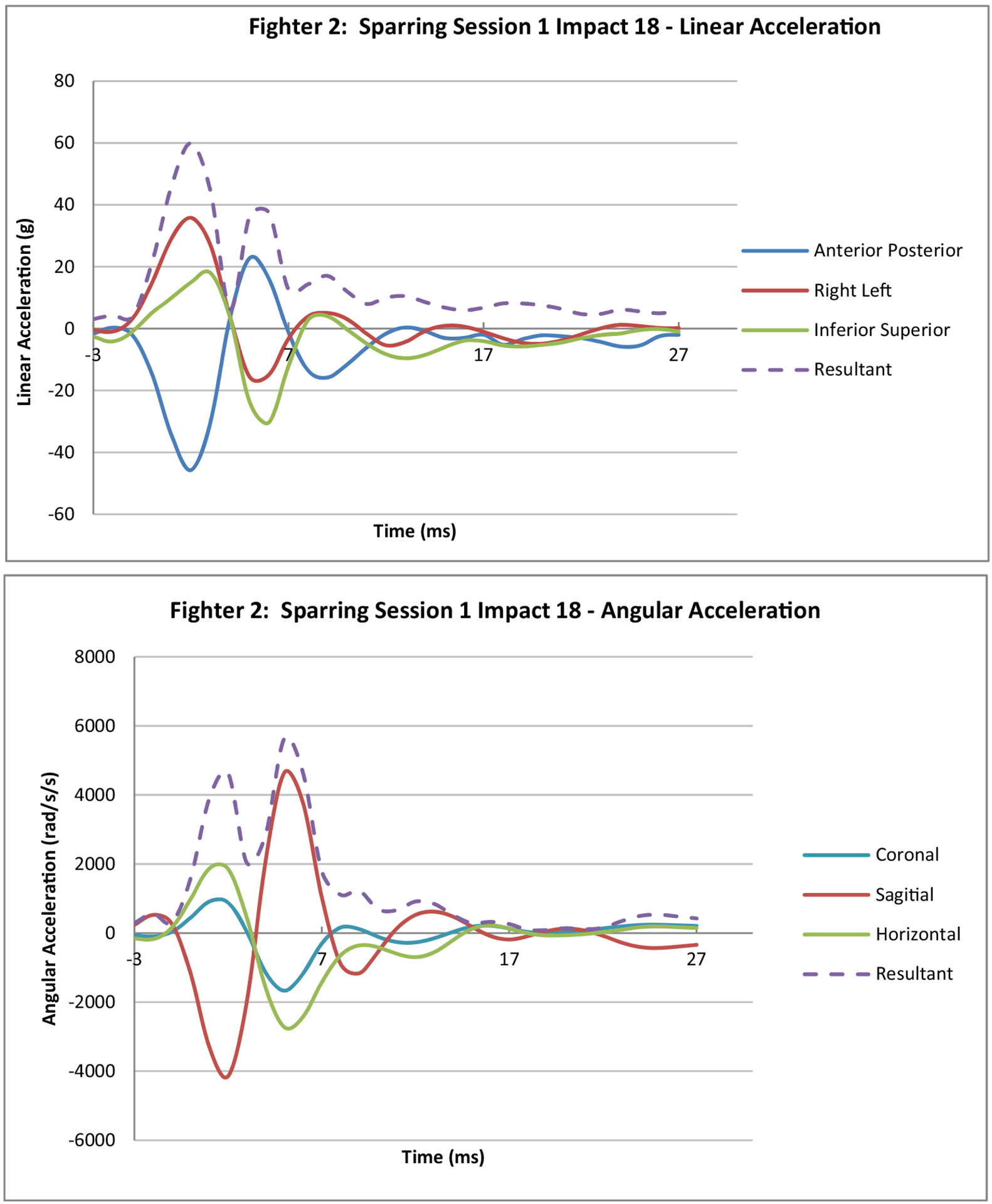
Figure 3.

Open in a new tab

Sample data from sparring session.

(Note: 3ms pre trigger and 27ms post trigger is displayed)

The brain tissue including the cerebrum, cerebellum, corpus callosum, thalamus and brain stem are modelled as non-linear viscoelastic materials (Table 2). The viscoelastic materials are modelled using a Kelvin Maxwell model.

Table 2.

Material properties of principal brain parts.

Description Number of elements Density ρ (kg/m3) Bulk modulus K (MPa) Shear modulus Decay constant s−1
Short term GO (kPa) Long term GI (kPa)
Cerebellum grey matter and thalamus 14,540 1060 2190 3.00 0.60 200
Cerebrum, mid-brain and brain stem 25,484 1060 2190 6.00 0.60 200
Corpus callosum 980 1060 2190 3.75 0.75 200
Cerebrospinal fluid 10,828 1040 2190 0.50 0.01 200
Cerebellum-white matter 23,340 1060 2190 3.75 0.75 200
Open in a new tab

The simulations were performed by applying orthogonal linear acceleration components, and angular accelerations around each of the three axes, to the local co-ordinate system at the centre of gravity of the GHBMC head model. The simulations were run on LS-Dyna, Livermore Software Tech. Corp. for 50 ms using Amazon Cloud Computing Services with 72 cores and 144 Gbytes of memory. Simulations of 30 ms have been found to be insufficient as maximum strain may not been reached (Sanchez et al. 2019), thus 50 ms was selected to enable the total strain to be recorded and yet have a reasonable simulation run-time of 4 h. The first principal Green Lagrange strain was determined by locating the maximum within a region and averaging the strain around the adjacent elements, thus avoiding unrealistic singularities. The shear stress (Tresca) in the corpus callosum was found in a similar manner. The impact with the highest angular acceleration in each event was simulated. Simulation results were divided into the two categories: concussed and uninjured. The acceleration, strain and shear stress results in each category were then averaged.

Statistical analysis

Descriptive statistics including means, standard deviations and t-tests were processed using MiniTab (Version 19.2020). A two sample independent t-test was used to compare concussive and uninjured data. The dependent variable was concussion/uninjured while the continuous variables were: resultant linear acceleration, resultant angular velocity, resultant angular acceleration, strain in the corpus callosum, thalamus, midbrain and brain stem, Tresca shear stress in the corpus callosum, and strain rate in the corpus callosum. A statistical significance of p < .05 was used to reject the null hypothesis. Cohen’s effect sizes were calculated to quantify the magnitude of the differences between the concussion injury data and the uninjured data. Cohen’s number (d) defines the effect sizes as d < 0.01 very small, d < 0.2 small, d < 0.5 medium, d < 0.8, large, d < 1.2 very large and d > 2.0 huge (Sawilowsky 2009).

Results

Data were recorded during 19 sparring sessions and 11 competitive events. Above 10 g, 298 confirmed head impacts were recorded during the sparring sessions and 153 impacts at the competitive events. The average number of impacts above 10 g in the sparring sessions was 15.7. No injuries occurred during the sparring sessions. Five of the competitive events resulted in the fighter sustaining a concussion, all five fighters were professional or semi-professional and were in weight categories above 70 kg. The concussions were diagnosed by a medical doctor either immediately after the event or at a 48 h check-up. Symptoms reported included: a very short loss of consciousness (< 1 s), persistent headaches in the days following the event, visual disturbance and imbalance. The number of impacts in the events that ended with a concussion ranged from 4 to 26. The average number of impacts that ended with a concussive impact was 16.0 while the average number of impacts in competitive events that had no injury was 12.2.

A simulation was performed of the impact with the highest resultant angular acceleration from each of the 30 events. Maximum strain in the corpus callosum, thalamus, mid-brain, brain stem and overall (any brain region) were recorded from the simulations. Also recorded were the shear stress (Tresca), Von Mises distortion stress and strain rate within the corpus callosum. Maximum principal strain and stress results were averaged and are plotted in Figures 4 and 5.

Figure 4.

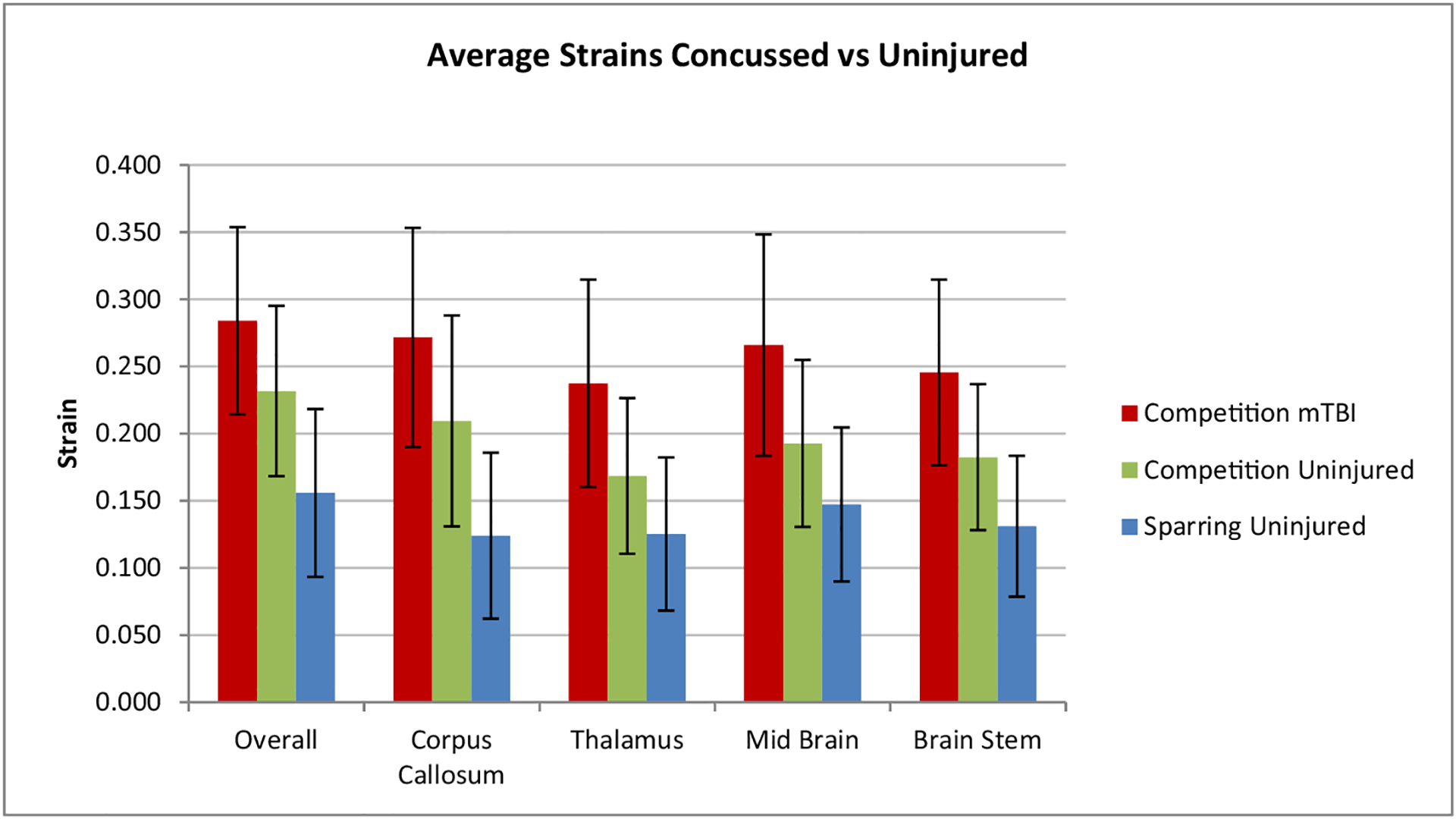
Figure 4.

Open in a new tab

Average strains with standard deviation in various brain regions.

Figure 5.

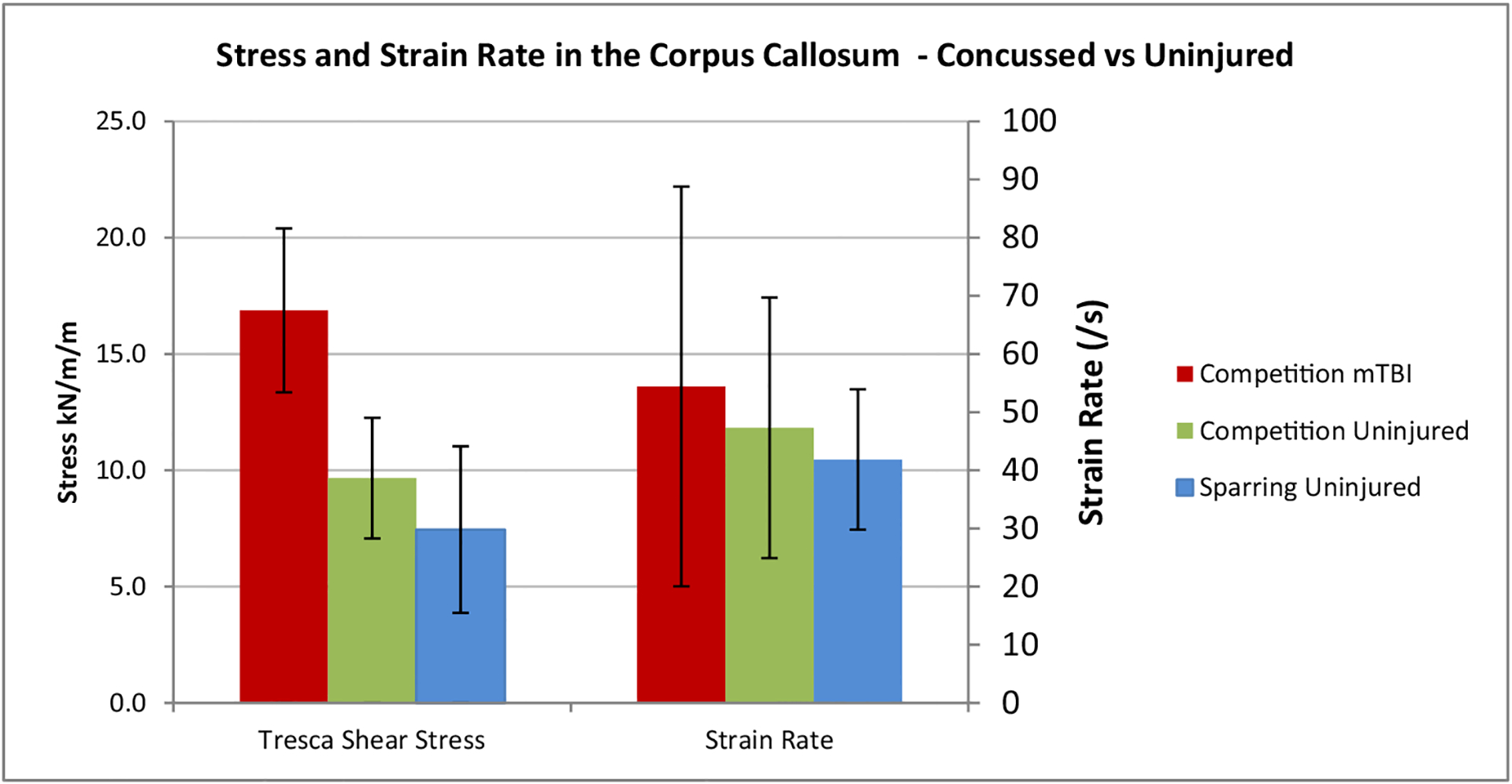
Figure 5.

Open in a new tab

Stress and strain rate with standard deviation in the corpus callosum.

The statistical differences between the concussed and uninjured athletes were investigated using independent sample t-tests (shown in Table 3). The t-tests showed significant differences in the resultant linear acceleration, t(4) = 2.9, p < .05, d = 1.4 (very large effect size), strain in the corpus callosum t(4) = 2.9, p < .05, d = 1.51 (very large effect size), strain in the brain stem t(4) = 2.8, p < .05, d = 1.49 (very large effect size) and the Tresca shear stress in the corpus callosum t(5) = 4.7, p < .05, d = 2.36 (huge effect size). The effect size is quoted as per Sawilowsky (2009). There was no other significant difference between concussed and uninjured athletes in the resultant angular velocity, resultant angular acceleration, strain in the thalamus and mid brain, and the strain rate in the corpus callosum.

Table 3.

Results of statistical t tests between concussed and uninjured athletes.

Resultant linear Acceleration (g) Resultant angular Velocity (rad/s) Resultant Angular acceleration (rad/s2) Corpus Callosum Thalamus Mid Brain Brain Stem Tresca shear stress in corpus callosum kPa Strain rate in corpus callosum s−1
Strain
Competition concussed 86.7 24.0 7561 0.27 0.24 0.27 0.25 16.87 54.40
Standard deviation concussed 21.0 4.7 1825 0.08 0.06 0.06 0.06 3.57 13.70
Average uninjured 56.8 13.6 5169 0.14 0.14 0.16 0.14 7.98 45.05
Standard deviation uninjured 21.6 10.7 3843 0.09 0.09 0.09 0.08 3.94 38.40
Difference in averages 52.7% 76.7% 46.3% 87.9% 75.0% 68.1% 71.2% 111.4% 20.8%
T value 2.9 2.1 1.4 2.9 2.5 2.5 2.8 4.7 0.5
p value .034 .1 .245 .033 .066 .067 .049 .005 .619
Effect size (d) 1.40 1.26 0.80 1.51 1.36 1.37 1.49 2.36 0.32
Open in a new tab

NB: Significant differences (p < .05) are bolded

Figure 6 shows sample transverse and sagittal cross sections of the simulated brain strain of Fighter 5, Bout 1, impact 21 who was concussed. High strains are evident in the corpus callosum and thalamus. The high strains on the periphery of the brain are in the cerebrospinal fluid (CSF), hence they are not actual strains in the brain tissue. The strains in the CSF due to the fluid being modelled with solid elements with the bulk modulus of water. Figure 7 shows cross sections of an uninjured athlete (Fighter 10, Bout 1 impact 50).

Figure 6.

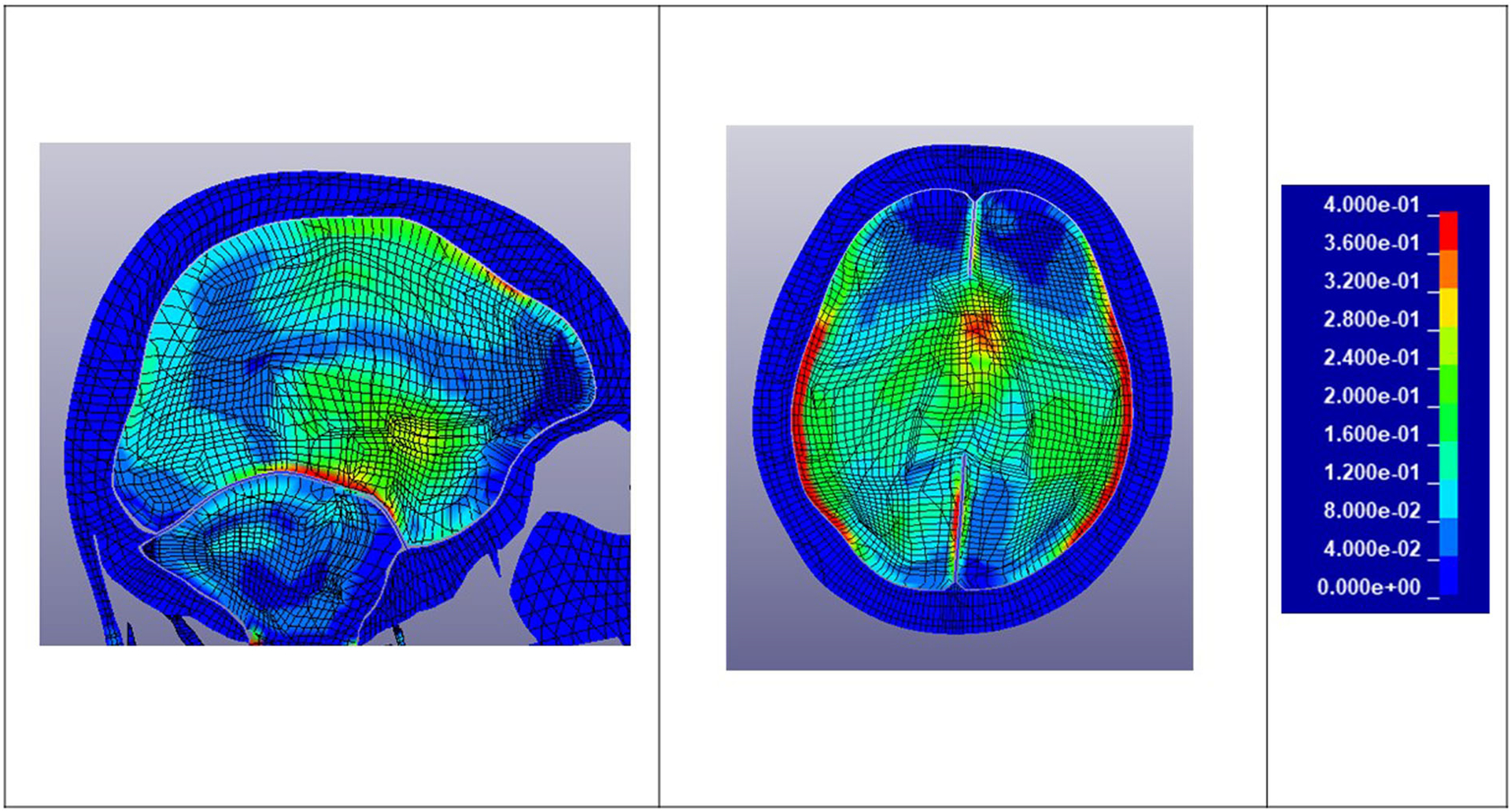
Figure 6.

Open in a new tab

Transverse and sagittal brain cross sections: Strain plots – Fighter 5 Bout 1 Impact 21 – Concussed.

Figure 7.

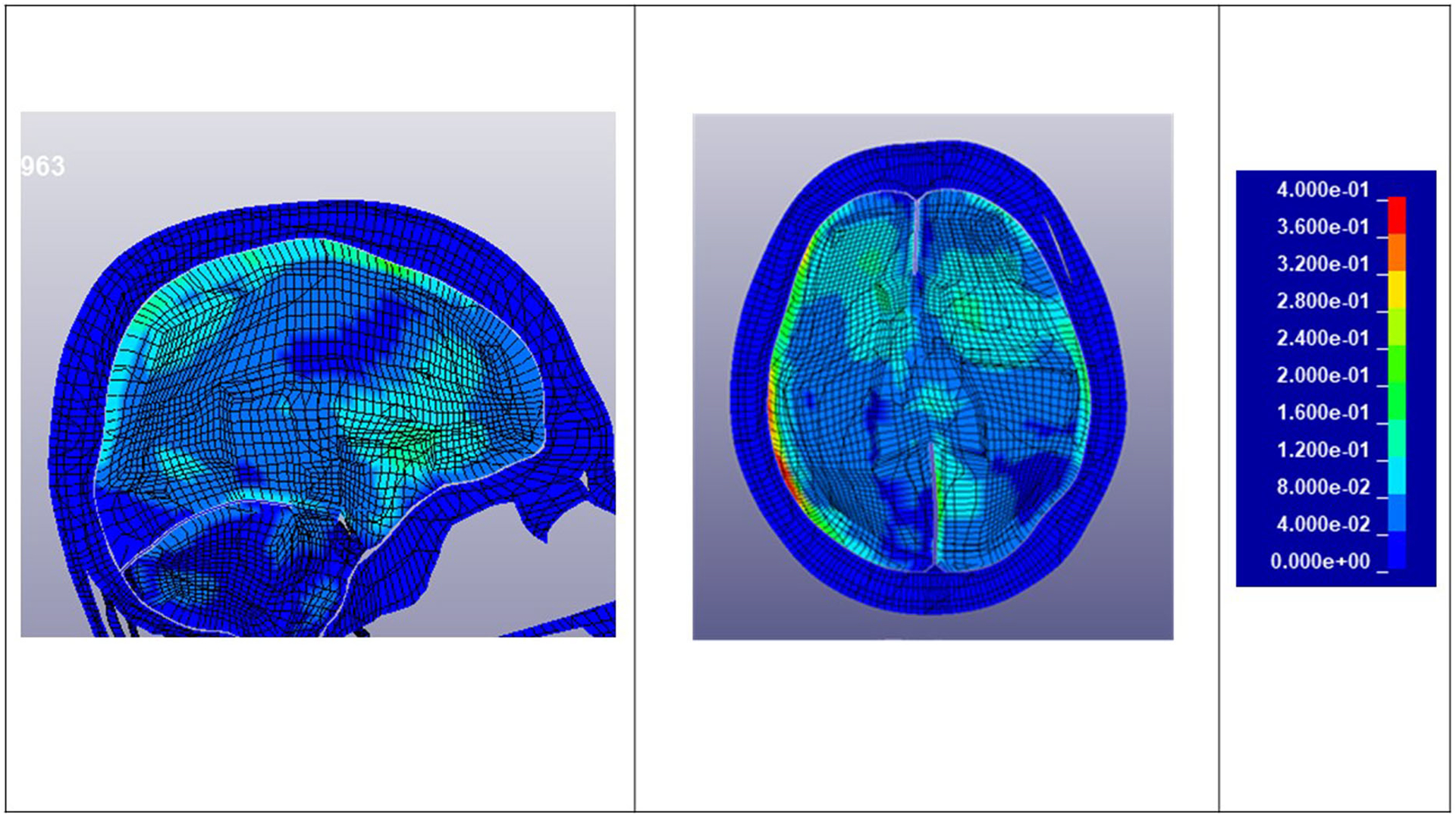
Figure 7.

Open in a new tab

Transverse and sagittal brain cross sections: Strain – Fighter 10 Bout 1 Impact 50 – Uninjured.

NOTE: Figures 3, 4, and 5 follow and are left in editable form. Figures 1, 2, 6 and 7 uploaded as separate files.

Discussion

Head acceleration data were recorded from 451 video confirmed impacts in MMA at 30 events. This is the only known study to measure head accelerations in vivo that have resulted in a concussive injury in an unhelmeted sport. The impact with the highest resultant angular acceleration from each event was simulated using the GHBMC head model. Linear accelerations to the side of the head (Y-direction) were 62.2% higher in impacts that resulted in a concussive injury. Punches to the jaw create high lateral accelerations and due to the offset from the co-ordinate system this leads to high angular accelerations about the X-axis (coronal plane). Viano et al. studied boxers punching a Hybrid III head and found that ‘hook’ type punches lead to high moments about the X-axis and very high angular accelerations (Viano, Casson, Pellman, Bir, et al. 2005). Impacts to the side of the head have been found to correlate with concussive injuries (Zhang et al. 2001; McIntosh et al. 2014; Hernandez et al. 2019).

In this study, linear acceleration, strain in the corpus callosum and brain stem and shear stress in the corpus callosum were significantly different (p < .05) between concussed and uninjured athletes. In this study, the strain in the corpus callosum differed by 87.9% (p < .05) between concussed and uninjured athletes. This difference in strain in the corpus callosum was greater than any other brain region indicating that it may be the best strain indicator for concussion. The average strain in the corpus callosum of the concussed athletes in this study was 0.27, this compares well with the strain of 0.3 found by Hernandez et al. in US football, although it should be noted that that study only included two cases of concussion (Hernandez et al. 2015). Newman et al. reconstructed 58 impacts in US football and determined that the average linear and angular accelerations of concussed players was 97.8 g and 6432 rad/s2 (Newman et al. 2000, 2005). Kleiven simulated Newman’s impacts and determined that the average strain in the corpus callosum of the concussed players was approximately 0.23 and predicted a 50% probability of concussion for strains of 0.21 (Kleiven 2007). Kleiven reported an average strain in the corpus callosum which was 28.6% lower than that found in this study but also reported an average angular acceleration which was 17.6% lower. Sanchez et al. found that there was an error in some of the accelerometer data in Newman et al.’s study which may have resulted in an average error in the maximum principal strain of 23%.

In a simulation study of concussion in an unhelmeted sport, kinematic data from computer reconstructions were used to simulate impacts in Australian rugby and football (Patton et al. 2013). Patton et al. found that the average angular acceleration in concussive impacts was 7951 rad/s2 which is similar to the average angular acceleration of 7561 rad/s2 found in this study. Although the angular acceleration was similar Patton’s average strain of 0.31 ± 0.16 in the corpus callosum was 14.8% higher than in this study. Patton et al.’s study had a wider spread of data than this study as indicated by his standard deviation of 0.16. The greater spread of data in Patton’s study may be due to the variation in magnitude and direction of impacts inherent in football as opposed to MMA and the methods employed in the re-creation of the impacts.

Tresca shear stress in the corpus callosum differed between concussed and uninjured athletes by 111.4% with a huge effect size (2.36) (Sawilowsky 2009). Indicating that shear stress, in this study, was the best parameter to predict a concussive injury, followed by the strain in the corpus callosum (1.51). Shear stress has been reported in very few studies of concussion. A US football study (Zhang et al. 2004) reported that the shear stress in the mid-brain was the best predictor of concussion. They found that shear stress in the thalamus differed by 58.5% between concussed and uninjured athletes, but they did not report on the magnitude of the shear stress in the corpus callosum.

Conclusion

This is the first known study to measure head accelerations in vivo in an unhelmeted sport, which included five concussions. The study found significant differences (p < .05) in the strain in the corpus callosum and brain stem of concussed athletes compared to uninjured. The magnitude of the strain in the corpus callosum was higher than in concussed athletes in a US football study due to a higher average angular acceleration. The single best predictor of concussion in this study was shear stress in the corpus callosum (t(5) = 4.7, p < .05, d = 2.36). The high strains and shear stresses in the core brain regions were primarily due to lateral impacts which resulted in high angular accelerations in the coronal plane.

Limitations

The number of fighters and events in this study was limited; a greater number of impacts are required to improve the robustness of these findings. The mouthguard has been validated for indirect impacts but further validation is required for impacts directly to the sensors. Impacts that could not be video verified and also impacts that appeared to be direct hits to the mouthguard were removed; this may have resulted in some valid data not being included. The GHBMC head model has limitations inherent in finite element models and the material properties are approximations for brain tissue and assume homogeneous and isotropic behaviour. One of the criteria used to validate the GHBMC head model is relative brain–skull motion (Mao et al. 2013). Zhou et al. have suggested that this may not be sufficient for models intended for strain prediction (Zhou et al. 2018).

The CSF in the brain was modelled with solid elements with the bulk modulus of water. The concussed fighters received multiple impacts during their bouts therefore it is not possible to identify which impact caused the injury.

Funding

This work was in part supported by CADFEM Ireland and UK Ltd.

Footnotes

Disclosure statement

The authors declare that they have no conflicts of interest.

References

  1. Buse GJ. 2006. No holds barred sport fighting: a 10 year review of mixed martial arts competition. Br J Sports Med. 40(2):169–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Elliott MR, Margulies SS, Maltese MR, Arbogast KB. 2015. Accounting for sampling variability, injury under-reporting, and sensor error in concussion injury risk curves. J Biomech. 48(12):3059–3065. 10.1016/j.jbiomech.2015.07.026. [DOI] [PubMed] [Google Scholar]
  3. Gennarelli TA. 1983. Head injury in man and experimental animals: neuropathology. Acta Neurochir Suppl (Wien). 32:15–30. [DOI] [PubMed] [Google Scholar]
  4. Giordano C, Kleiven S. 2014. Evaluation of axonal strain as a predictor for mild traumatic brain injuries using finite element modeling. Stapp Car Crash J. 58(14):29–61. [DOI] [PubMed] [Google Scholar]
  5. Hardy WN, Mason MJ, Foster CD, Shah CS, Kopacz JM, Yang H, King AI, Bishop J, Bey M. 2008. A study of the response of the human cadaver head to impact. Stapp Car Crash J. 51:17–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hernandez F, Giordano C, Goubran M, Parivash S, Grant G, Zeineh M, Camarillo D. 2019. Lateral impacts correlate with falx cerebri displacement and corpus callosum trauma in sports-related concussions. Biomech Model Mechanobiol. 18(3):631–649.(0123456789).. [DOI] [PubMed] [Google Scholar]
  7. Hernandez F, Wu L, Yip MC, Laksari K, Hoffman AR, Lopez JR, Grant GA, Kleiven S, Camarillo D. 2015. Six degree-of-freedom measurements of human mild traumatic brain injury. Ann Biomed Eng. 43(8):1918–1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ho J, Zhou Z, Li X, Kleiven S. 2017. Jun. The peculiar properties of the falx and tentorium in brain injury biomechanics. J Biomech. 60:243–247. 10.1016/j.jbiomech.2017.06.023. [DOI] [PubMed] [Google Scholar]
  9. Holbourn AHS. 1943. Mechanics of head injuries. Lancet. 242(6267):438–441. [Google Scholar]
  10. Hutchison MG, Lawrence DW, Cusimano MD, Schweizer TA. 2014. Head trauma in mixed martial arts. Am J Sports Med. 42(6):1352–1358. [DOI] [PubMed] [Google Scholar]
  11. King D, Hume P. a, Brughelli M, Gissane C. 2014. Instrumented mouthguard acceleration analyses for head impacts in amateur rugby union players over a season of matches. Am J Sport Med. 43(3). http://www.ncbi.nlm.nih.gov/pubmed/25535096. [DOI] [PubMed] [Google Scholar]
  12. King D, Hume P, Gissane C, Brughelli M, Clark T. 2015. The influence of head impact threshold for reporting data in contact and collision sports: systematic review and original data analysis. Sport Med http://link.springer.com/10.1007/s40279-015-0423-7. [DOI] [PubMed] [Google Scholar]
  13. Kleiven S 2005. Influence of direction and duration of impacts to the human head evaluated using the finite element method. Proceedings of the IRCOBI Conference; September; Prague, Czech Republic.p. 41–57. http://www.ircobi.org/wordpress/downloads/irc0111/2005/Session1/13.pdf. [Google Scholar]
  14. Kleiven S 2007. Oct. Predictors for traumatic brain injuries evaluated through accident reconstructions. SAE Technical Paper. p. 81–114. http://www.ncbi.nlm.nih.gov/pubmed/18278592. [DOI] [PubMed] [Google Scholar]
  15. Kleiven S, Hardy WN. 2002. Correlation of an FE model of the human head with local brain motion – consequences for injury prediction. Stapp Car Crash J. 46:123–144. http://www.ncbi.nlm.nih.gov/pubmed/17096222. [DOI] [PubMed] [Google Scholar]
  16. Kuo C, Wu L, Hammoor BT, Luck JF, Cutcliffe HC, Lynall RC, Kait JR, Campbell KR, Mihalik JP, Bass CR, et al. 2016. Effect of the mandible on mouthguard measurements of head kinematics. J Biomech. 49(9):1845–1853. 10.1016/j.jbiomech.2016.04.017. [DOI] [PubMed] [Google Scholar]
  17. Laksari K, Fanton M, Wu L, Nguyen T, Kurt M, Giordano C, Kelly E, O’Keeffe E, Wallace E, Doherty C. 2019. Multi-directional dynamic model for traumatic brain injury detection. J Neurotrauma. 37(7):1–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Langlois JA, Rutland-Brown W, Wald MM, ET. 2006. The epidemiology and impact of traumatic brain injury: a brief overview. J Head Trauma Rehabil. 21(5):375–378. http://www.ncbi.nlm.nih.gov/pubmed/16983222. [DOI] [PubMed] [Google Scholar]
  19. Mao H, Zhang L, Jiang B, Genthikatti VV, Jin X, Zhu F, Makwana R, Gill A, Jandir G, Singh A, et al. 2013. Development of a finite element human head model partially validated with thirty five experimental cases. J Biomech Eng. 135(11):111002. http://biomechanical.asmedigitalcollection.asme.org/article.aspx?doi=10.1115/1.4025101. [DOI] [PubMed] [Google Scholar]
  20. McIntosh AS, Patton D. a, Fréchède B, Pierré P-A, Ferry E, Barthels T. 2014. The biomechanics of concussion in unhelmeted football players in Australia: a case-control study. BMJ Open. 4(5):e005078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Nahum AM, Smith R, Ward CC. 1977. Intracranial pressure dynamics during head impact. http://papers.sae.org/770922/.
  22. Newman J, Barr C, Beusenberg M, Fournier E, Shewchenko N, Welbourne E, Withnall C. 2000. A new biomechanical assessment of mild traumatic brain injury, part 2: results and conclusions. Proceedings of the 2000 International Conference on the Biomechanics of Impact. p. 223–233. [Google Scholar]
  23. Newman J, Beusenberg MC, Shewchenko N, Withnall C, Fournier E. 2005. Verification of biomechanical methods employed in a comprehensive study of mild traumatic brain injury and the effectiveness of American football helmets. J Biomech. 38(7):1469–1481. [DOI] [PubMed] [Google Scholar]
  24. O’Keeffe E, Kelly E, Liu Y, Giordano C, Wallace E, Hynes M, Tiernan S, Meagher A, Greene C, Hughes S, et al. 2019. Dynamic blood brain barrier regulation in mild head trauma. J Neurotrauma. 1–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ommaya AK, Gennarelli TA. 1974. Cerebral concussion and traumatic unconsciousness. Correlation of experimental and clinical observations of blunt head injuries. Brain. 97(4):633–654. [DOI] [PubMed] [Google Scholar]
  26. Patton DA, McIntosh AS, Kleiven S, ET. 2013. The biomechanical determinants of concussion: finite element simulations to investigate brain tissue deformations during sporting impacts to the unprotected head. J Appl Biomech. 29(6):721–730. [DOI] [PubMed] [Google Scholar]
  27. Raghupathi R, Mehr MF, Helfaer MA, Margulies SS. 2004. Traumatic axonal injury is exacerbated following repetitive closed head injury in the neonatal pig. J Neurotrauma. 21(3):307–316. [DOI] [PubMed] [Google Scholar]
  28. Rowson S, Duma SM, Beckwith JG, Chu JJ, Greenwald RM, Crisco JJ, Brolinson PG, Duhaime A-C, McAllister TW, Maerlender AC. 2012. Rotational head kinematics in football impacts: an injury risk function for concussion. Ann Biomed Eng. 40(1):1–13. . http://link.springer.com/10.1007/s10439-011-0392-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Sanchez EJ, Gabler LF, Good AB, Funk JR, Crandall JR, Panzer MB. 2019. Feb. A reanalysis of football impact reconstructions for head kinematics and finite element modeling. Clin Biomech (Bristol, Avon)). 64:82–89. [DOI] [PubMed] [Google Scholar]
  30. Sawilowsky SS. 2009. New effect size rules of thumb. J Mod App Stat Meth. 8(2):597–599. [Google Scholar]
  31. Trosseille X, Tarriére C, Lavaste F, Guillon F, Domont A. 1992. Development of a F.E.M. of the human head according to a specific test protocol. SAE Technical Paper. [Google Scholar]
  32. Viano DC, Casson IR, Pellman EJ, Zhang L, King AI, Yang KH. 2005. Concussion in professional football: brain responses by finite element analysis: part 9. Neurosurgery. 57(5):891–915. [DOI] [PubMed] [Google Scholar]
  33. Viano D, Casson I, Pellman E, Bir C, Zhang L, Sherman D, Boitano M. 2005. Concussion in professional football: comparison with boxing head impacts-part 10. Neurosurgery. 57(6):1154–1170. [DOI] [PubMed] [Google Scholar]
  34. Wu LC, Nangia V, Bui K, Hammoor B, Kurt M, Hernandez F, Kuo C, Camarillo DB. 2016. In vivo evaluation of wearable head impact sensors. Ann Biomed Eng. 44(4):1234–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Zhang L, Yang K, King A. 2001. Comparison of brain responses between frontal and lateral impacts by finite element modeling. J Neurotrauma. 18(1):21–30. http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=11200247. [DOI] [PubMed] [Google Scholar]
  36. Zhang L, Yang KH, King AI. 2004. A proposed injury threshold for mild traumatic brain injury. J Biomech Eng. 126(2):226–236. http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15179853. [DOI] [PubMed] [Google Scholar]
  37. Zhang L, Yang K, King A, Viano D. 2003. A new biomechanical predictor for traumatic brain injury – a preliminary finding. Proceedings of the 2003 Summer Bioengineering Conference Vol. 1. p. 1–2. http://www.tulane.edu/~sbc2003/pdfdocs/0137.PDF. [Google Scholar]
  38. Zhang L, Yang KH, Dwarampudi R, Omori K, Li T, Chang K, Hardy WN, Khalil TB, King AI. 2001. Recent advances in brain injury research: a new human head model development and validation. Stapp Car Crash J. 45(11): 369–394. [DOI] [PubMed] [Google Scholar]
  39. Zhou Z, Li X, Kleiven S, Shah CS, Hardy WN. 2018. A reanalysis of experimental brain strain data: implication for finite element head model validation. SAE Technical Paper. 2019-Novem(November). [DOI] [PubMed] [Google Scholar]

RESOURCES