Excluded Volume and Weak Interactions in Crowded Solutions Modulate Conformations and RNA Binding of an Intrinsically Disordered Tail

Abstract

The cellular milieu is a solution crowded with a significant concentration of different components (proteins, nucleic acids, metabolites, etc.). Such a crowded environment affects protein conformations, dynamics, and interactions. Intrinsically disordered proteins and regions are particularly sensitive to these effects. Here, we investigate the impact on an intrinsically disordered tail that flanks a folded domain, the N-terminal domain, and the RNA-binding domain of the SARS-CoV-2 nucleocapsid protein. We mimic the crowded environment of the cell using polyethylene glycol (PEG) and study its impact on protein conformations using single-molecule Förster resonance energy transfer. We found that high-molecular-weight PEG induces a collapse of the disordered N-terminal tail, whereas low-molecular-weight PEG induces a chain expansion. Our data can be explained by accounting for two opposing contributions: favorable interactions between the protein and crowder molecules and screening of excluded volume interactions. We further characterized the interaction between protein and RNA in the presence of crowding agents. While for all PEG molecules tested, we observed an increase in the binding affinity, the trend is not monotonic as a function of the degree of PEG polymerization. This points to the role of nonspecific protein–PEG interactions on binding in addition to the entropic effects due to crowding. To separate the enthalpic and entropic components of the effects, we investigated the temperature dependence of the association constants in the absence and presence of crowders. Finally, we compared the effects of crowding across mutations in the disordered region and found that the threefold difference in association constants for two naturally occurring variants of the SARS-CoV-2 nucleocapsid protein is reduced to almost identical affinities in the presence of crowders. Overall, our data provide new insights into understanding and modeling the contribution of crowding effects on disordered regions, including the impact of interactions between proteins and crowders and their interplay when binding a ligand.

At variance with the dilute conditions in which the majority of biochemical experiments and simulations are conducted, proteins perform their function within crowded cells amid a myriad of other molecules. In eukaryotic cells, the total concentration of molecules can account for ∼10–25% of the overall volume,¹⁻⁴ significantly reducing the available space that each molecule can explore. This phenomenon is commonly referred to as crowding. In addition to pure excluded volume effects, the high concentration of components within the cell gives rise to non-negligible “weak” interaction effects, often referred to as quinary interactions.⁵⁻⁸ As a result of these effects, the crowded cellular environment impacts protein folding stability, conformations, dynamics, diffusion, and interactions with ligands.^5,9−13 Moreover, both crowding effects and quinary interactions are likely crucial within the context of biomolecular condensates, which select and concentrate a specific subset of components to very high concentrations (if not for the scaffolding elements, at least for the host components).^5,14−16 Quantifying and modeling such contributions is essential to better understand how protein function and interactions are modulated by the cellular environment.

Lacking a stable 3D structure, intrinsically disordered proteins (IDPs) and regions (IDRs) are particularly susceptible to changes in the surrounding milieu.¹⁴ Studies with synthetic crowders have revealed that IDP conformations tend to adopt more compact ensembles in denser environments.^14,17−19 The precise degree of compaction depends on the specific polymer properties of the protein and of the synthetic crowder.¹⁴ Similar observations were made also in the context of simulations.^17,20,21 Crowding effects apply not only to the conformations of disordered proteins but also to their interactions with ligands, where entropic forces modulate both equilibrium and kinetics of binding.²² The same effects can be observed in vitro, using synthetic crowders²² or cell extract,^23,24 and in living cells.^18,19 As for conformations, these effects have been rationalized using polymer theories that account for screening of excluded volume and depletion effects.²⁵⁻²⁸

Previous efforts have contributed to building a general theoretical framework for understanding the impact of crowding on disordered proteins, linking the protein response to fundamental properties of the sequence, such as the scaling exponent. While the scaling exponent reflects the monomer–solvent and monomer–monomer interactions, and therefore depends on the primary structure of the protein, different disordered proteins may attain the same scaling exponent through completely different sequence compositions.²⁹⁻³¹ Sequence-specific effects are relatively unexplored, but they can encode for nonspecific affinities for crowding agents, modulate conformations across different length scales, and even introduce transient secondary structure motifs. Furthermore, the contribution of macromolecular crowding has been previously tested only for full-length IDPs. Little is known about the impact of crowding on disordered regions flanking folded domains: different effects may occur when a disordered region is attached to one or more folded domains, including stabilization of interactions between the disordered region and the folded interface.

Here, we studied the effects of crowding on the disordered N-terminal domain (NTD) of the SARS-CoV-2 nucleocapsid protein (Wuhan-Hu-1 variant) when attached to the contiguous RNA-binding domain (RBD) (Figure 1; Tables S1 and S2). This is a well-characterized system where we previously found that the N-terminal tail is disordered, flexible, and retains its dynamics even when complexed with nucleic acids.^32,33 In particular, when compared to the RBD in the absence of the NTD, the disordered tail significantly increases the binding affinity of the RBD for RNA, alters the mode of binding, and mutations in the disordered sequence result in modulation of the binding affinity.³³ Overall, these data point to an essential role of the disordered in the interactions of the protein. To investigate the effects of crowding on the NTD–RBD, we opted for single-molecule Förster resonance energy transfer (FRET), which provides a powerful toolbox to quantify the impact of crowding on protein conformations, dynamics, and diffusion, both in the presence and in the absence of ligands.^{14,18,22,34,35} To monitor the conformational changes in the disordered tail, we used a previously designed construct^32,33 that comprises both NTD and RBD and carries cysteine mutations for introducing fluorescent dyes at positions 1 and 68 (Figure 1, Table S2). Because the labeling positions probe the NTD, we will refer to the construct as NTD_L–RBD. The construct has been labeled with Alexa Fluor 488 and 594, as previously described.^32,33 Using polyethylene glycol (PEG) as a model synthetic crowder, we set out to investigate how the presence of crowder molecules impacts protein conformations and its binding to RNA.

Figure 1.

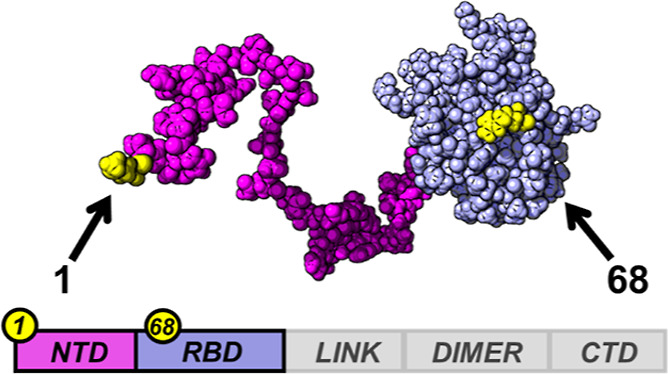
NTD of SARS-CoV-2 and RNA-binding domain (NTD–RBD). SARS-CoV-2 nucleocapsid protein comprises an NTD (in magenta), an RBD (in lilac), a linker region (LINK, in gray), a dimerization domain (DIMER, in gray), and a C-terminal domain (CTD, in gray). In the present study, we focus on an NTD–RBD truncation variant (magenta and lilac domains). Positions of fluorophores are reported in yellow over an all-atom van der Waals surface representation of the NTD–RBD construct.

Methods

All single-molecule FRET experiments have been performed in a 50 mM N-(2-hydroxyethyl)piperazine-N′-ethanesulfonic acid (HEPES) buffer pH 7.4 at a temperature of 23 °C, unless differently specified, with addition of 200 mM β-mercaptoethanol and 0.001% v/v Tween 20. Single-molecule measurements were performed on a modified PicoQuant MT200, as previously described.^32,36 Volume fractions of PEG solutions have been computed by converting from the weight/volume (w/v) fraction using the density of PEG molecules, as previously reported.^14,22 Further experimental and theoretical details are reported in the Supporting Information.

Results

We started by investigating the conformations of the protein under dilute conditions (no crowding). Single-molecule FRET measurements of the NTD_L–RBD protein in HEPES buffer (see Methods) provided a distribution of transfer efficiencies characterized by a single shot-noise-limited population with a mean value of 0.698 ± 0.006 at 23 °C, consistent with the previously reported value of 0.709 ± 0.009 obtained in Tris buffer under analogous solution conditions.^32,33 As previously discussed, this single population represents a flexible and dynamic tail. Having determined a reference state of the protein structural ensemble under dilute solution conditions, we set to quantify the impact of crowding on protein conformations. To this end, we studied the effects as a function of polymer concentration and length, which previously have been shown to provide a robust tool to discriminate across theoretical frameworks.^14,15 In particular, polymer “length” determines the type of response that a test chain (e.g., our protein) will perceive in a bath of other chains (e.g., PEG). When the degree of polymerization (number of monomers) P of the crowders is larger than the degree of polymerization N of the test chain, the test chain compacts and adopts conformations close to the one of the ideal state. Flory’s criterion³⁷ provides a quantitative reference for this crossover regime, which is P > N^1/2. For the system in this study, this threshold approximately coincides with PEG 1000 (see the Supporting Information). With this criterion in mind, we started quantifying the impact of large and small crowders on protein conformations.

Large Crowders Compact Protein Conformations

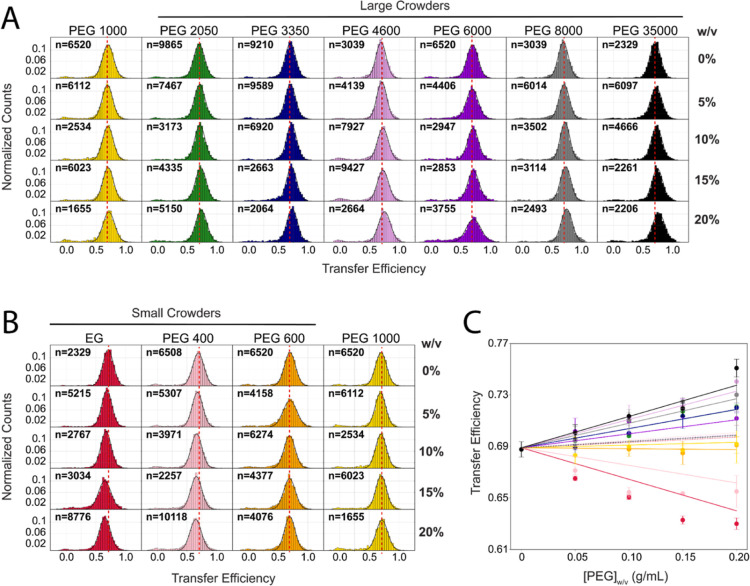
First, we investigated the contribution of high-molecular-weight PEG polymers. We identified a series of PEG molecules with average molecular weight equal to or larger than 1000 Da and with sufficient purity (lack of fluorescent contaminants) to allow for single-molecule detection: PEG 1000, PEG 2050, PEG 3350, PEG 4600, PEG 6000, PEG 8000, and PEG 35000 (see Table S3). For each molecular weight, we explored the impact of increasing concentrations of PEG up to 20% of weight per volume (w/v), a similar concentration to the volume fraction occupied in a crowded cellular environment.¹⁵

Inspection of the transfer efficiency distributions, after selection of the donor–acceptor population (see the Supporting Information), reveals under all conditions one single population (Figure 2A,B). Changes in mean transfer efficiency with increasing crowding concentrations reflect conformational changes occurring in the protein. Interestingly, for PEG 1000, we detected no substantial shift in the mean transfer efficiency at any of the concentrations tested. In contrast, for all the other high molecular weights of PEG (PEG 2050, PEG 3350, PEG 4600, PEG 6000, PEG 8000, and PEG 35000), we observed a clear shift of the mean transfer efficiency toward higher values (Figure 2A,C), indicating compaction of the IDR. Note that the change in the refractive index of the solution can contribute to a shift toward lower transfer efficiencies, de facto counteracting the collapsing effect of the crowding agents. However, this effect is negligible compared to the measured shifts in transfer efficiency (see dotted lines in Figure 2C). Corresponding changes in terms of root-mean-square interdye distance computed from the mean transfer efficiency (see the Supporting Information) are reported in Figure 3A.

Figure 2.

Impact of crowders on IDR conformations. (A) Transfer efficiency distributions as a function of crowder concentrations (weight per volume, w/v, in g/mL) for large crowders (average molecular weight larger than 600 Da). n indicates the number of bursts per histogram. (B) Transfer efficiency distributions as a function of crowder concentrations (weight per volume, w/v, in g/mL) for small crowders (average molecular weight smaller than 1000 Da). PEG 1000 is shown as a reference for comparison with the case of larger crowders. n indicates the number of bursts per histogram. (C) Plot of measured transfer efficiencies for the NTD_L–RBD in the range between 0 and 20% (w/v). Each point represents the mean and standard deviation from at least two independent replicates. The dotted lines represent the expected variation in transfer efficiency if there were only a change in the refractive index rather than a change in distance. Solid lines are guides for the eyes.

Figure 3.

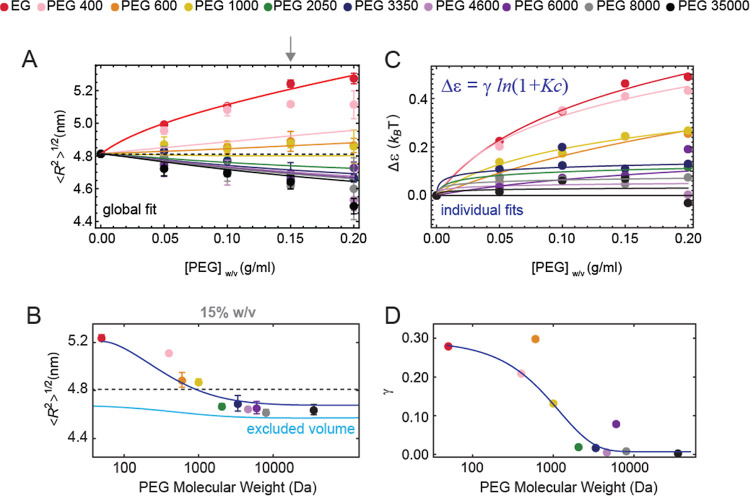
Degree of compaction as a function of crowding concentration. (A) Conversion of the mean transfer efficiencies in root-mean-square interdye distance for all the molecules. Each point represents the mean and standard deviation of at least two independent replicates. The dashed line represents the value in the absence of crowders. Solid lines are the global fit to the model described in the Supporting Information. (B) Dependence of the interdye root-mean-square distance at a fixed concentration (15% w/v) as a function of the PEG molecular weight. Each point represents the mean and standard deviation of at least two independent replicates. The dashed line represents the value in the absence of crowders. The solid cyan line is the expectation of conformational changes at this concentration of PEG for the effect of pure excluded volume screening. The measured values depart from the predicted trend, suggesting the occurrence of additional interactions. The blue line is a fit to the model described in the Supporting Information and reported in (C,D). (C) Estimate of the excess interaction not accounted for by the pure excluded volume screening as a function of the PEG concentration. The trend is fitted to the Schellman weak binding model (as previously proposed for small solvent molecules). (D) Number of binding sites associated with the Schellman weak binding model (γ) decreases with increased polymer molecular weight, with a characteristic molecular weight of approximately 1200 ± 100 Da. This observation is qualitatively consistent with previous observations from the Record lab, where the PEG ends are found to have different preferential interactions than the backbone of PEG.⁴⁹

We further compared the degree of compaction and its dependence on the molecular weight of PEG. This is best captured by contrasting the variation in transfer efficiency (or distance) at a constant concentration of crowders such that the number of PEG monomers in solution is approximately constant, and all the differences in conformations are due to the changes in the PEG chain length. Analysis of the changes in transfer efficiency (Figure S1) and root-mean-square interdye distance (Figure 3B) at 15% w/v shows that increasing the molecular weight of PEG above 1000 Da results in compaction of the disordered tail, approaching a saturation limit of the degree of compaction at molecular weights higher than 8000 Da (Figures S1 and 3C). This is consistent with previous observations for other disordered proteins.¹⁴

Small Crowding Agents Expand Protein Conformations

One notable difference from previous results,¹⁴ where a monotonic increase in the strength of compaction was found with increasing molecular weight, is that we do not observe any change in transfer efficiency for PEG 1000. This observation suggests that small crowding agents (≤1000 Da) may have no impact on the compaction of the NTD region. Therefore, we investigated this case scenario by measuring the impact of ethylene glycol (EG), PEG 400, and PEG 600. Here, we observed that PEG 600 behaves similarly to PEG 1000, whereas for all crowding agents smaller than PEG 600, the mean transfer efficiency does not shift toward higher values but instead moves toward lower ones (Figure 2B). The lower the molecular weight, the larger the shift toward lower transfer efficiencies. A shift toward lower values of this extent exceeds the changes due to the refractive index of the solution and implies an expansion of the tail. Corresponding changes in chain dimensions are reported in Figure 3A. This observation implies that smaller PEG molecules interact with the disordered tail. We further compared the change in mean transfer efficiency at a 15% w/v concentration (Figures 2C and S1), and we noticed that the smallest-molecular-weight molecule, EG (the constitutive monomer of PEG), has the largest impact and expansion on the chain, whereas increasing the molecular weight leads to a decrease of chain expansion (Figure 3B). This further supports the idea that two different forces are at balance: one attractive that leads to chain expansion for low molecular weights and one repulsive that leads to chain compaction for high molecular weights of PEG. The length of the polymeric crowder seems to determine one scenario or the other.

Disordered Tail Remains Dynamic under Crowded Conditions

To rule out that the observed compaction or expansion is due to folding of the IDR or specific interactions between the IDR and the folded RBD, we performed nanosecond fluorescence correlation spectroscopy (nsFCS) measurements, which report on chain dynamics.³⁸ Based on previous observations,³³ we expect anticorrelated behavior in the cross-correlation of donor–acceptor photons over time due to fast chain dynamics in the 100 ns time scale. This anticorrelated behavior reflects the intrinsic anticorrelated nature of FRET, where an increase in acceptor emission requires a decrease in donor emission and vice versa. Measurements for PEG 400 and PEG 3350 at 15% w/v are reported in Figure S2. For all measured samples, we found that the donor–acceptor cross-correlation is anticorrelated, confirming fast conformational dynamics in the disordered region between the fluorophores. The donor–donor and acceptor–acceptor correlations and the donor–acceptor cross-correlation can be described by a global fit where the correlation time is shared (Table S4), supporting that the same dynamics are captured across the three correlations. The correlation time is approximately 120 ns, in agreement with previously reported values in the absence of crowders.³³ Overall, our data confirm that in both scenarios, whether the crowding agents cause a shift toward higher or lower transfer efficiencies, the NTD remains disordered and flexible.

Balancing Excluded Volume Screening and Local Interactions

To try to make sense of the experimental observations, we conceptualized the observed phenomenon in terms of a polymer model.

The theory of coil-to-globule transition³⁹ is a useful model to compute the impact of solution conditions on the conformation of a disordered protein.⁴⁰⁻⁴² We used this model to quantify the solvation free energy change upon mixing of the IDR with each crowded solution.

Previous experiments¹⁴ have also supported the use of a renormalized-group polymer theory²⁵⁻²⁷ of ternary solutions to capture the compaction of IDPs in the presence of crowding polymers. The model accounts for screening of a single-chain excluded volume (the one associated with the protein) by the excluded volume of other chains (the PEG molecules). It is called renormalized because it accounts for the different length scales at play, including the characteristic size of the protein and the one of the crowding polymers. We used this model to estimate the excluded volume screening contribution to the free energy of solvation.

Finally, we accounted for the polymeric nature of PEG molecules and for the fact that above a critical concentration, PEG molecules start to overlap (overlap concentration,⁴³ see Figure S3). The characteristic length scale of the polymer solution is no longer represented by the radius of gyration of PEG but by the mesh size of the solution, due to overlapping PEG molecules. This regime is commonly referred to as the semidilute regime, and PEG molecules longer than 50 monomers (∼2500 Da) can easily enter such a regime at volume fractions lower than 5%¹⁵ (Figure S3).

A detailed mathematical description of the model is provided in the Supporting Information but can be summarized as

1

where R_g0 is the radius of gyration of the protein in the absence of PEG, N and P are the degree of polymerization of protein and PEG, respectively, ϕ is the volume fraction occupied by the polymer, and ε is the effective interaction energy between monomers after subtracting the contribution of excluded volume screening effects. The term effective is used to highlight that ε accounts for several factors, including the contribution of the solvent and cosolutes.

Since R_g0, N, P, and ϕ can be derived from known parameters (the length of the protein sequence, the conformations adopted by the protein in the absence of PEG, and PEG solution concentrations), we can use the model to directly extract the ε parameter as a function of PEG concentration and molecular weight (Figure 3C). The change in the interaction parameter between any crowded condition and the uncrowded reference state, Δε = ε – ε₀, is directly related to the change in the solvation free energy.⁴² Δε can be fitted to the Schellman weak binding model^44,45 according to Δε = γ ln(1 + Kc), where γ is the average number of binding sites, K is a binding constant, and c is the molar concentration of PEG monomers in solution. Fitting results are reported in Table S5. A plot of γ as a function of PEG molecular weight (Figure 3D) reveals two interesting features. First, the number of binding sites associated with the larger PEG molecules is negligible (close to zero), which suggests that the renormalization group theory well captures this regime. Second, Δε is the largest for EG and decreases with increasing molecular weight (Figure 3C). Data can be fitted to an empirical exponential decay, γ = Δγ exp(−P/P_c) + γ_∞, with P_c representing a “correlation molecular weight” (900 ± 200 Da) over which the effect of chemical interaction between the protein and the PEG end groups becomes negligible.

Alternatively, we can assume that the terminal ends and the backbone of PEG interact differently with the protein and account for the fact that at a constant volume fraction, the concentration of PEG terminal groups decreases with an increasing degree of polymerization (eq S15 in the Supporting Information). The resulting fit captures the trend of experimental data across all concentrations (Figure 3A) and provides a global quantification of the corresponding interactions (Table S6). Our observations further support that the end groups of PEG interact with different residues compared to the backbone of PEG and result in a stronger conformational change.

Crowder Effects on Binding Affinity Equilibrium

With the observation that the NTD–RBD sequence encodes for interactions with the crowder molecule and that this effect can be counterbalanced by excluded volume screening, we turn to investigate how these effects will be reflected in binding equilibria. We have previously shown that single-molecule FRET can be used to quantify the binding of the NTD_L–RBD to RNA because it is accompanied by a shift in transfer efficiency, which reflects conformational changes of the tail.³³ Here, we monitored the effects of crowding on the binding of NTD_L–RBD to (rU)₄₀. The specific length of the oligonucleotide has been chosen based on previous experiments to maximize the sensitivity of the transfer efficiency change for determining both protein affinity and conformations. For each molecular weight of PEG, we studied the change in binding affinity at a fixed concentration of 15% w/v by titrating NTD_L–RBD with increasing concentrations of (rU)₄₀ in the presence and absence of the crowder (Figure 4A). The change in binding affinity is expressed as K_A/K_A,0 and the corresponding change in binding free energy ΔΔG (Figure 4C)

2

Figure 4.

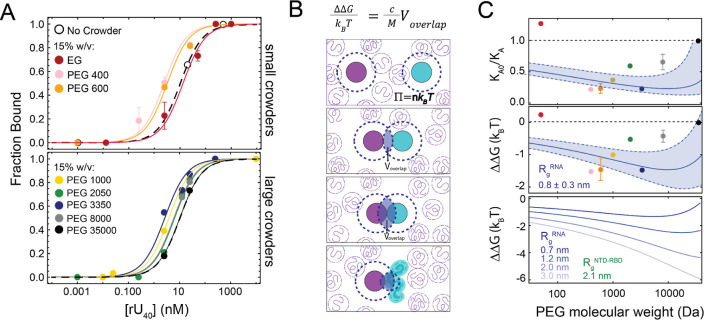
Crowding impact on the NTD–RBD and (rU)₄₀ association constant. (A) Examples of titrations of (rU)₄₀ on NTD_L–RBD as a function of a fixed concentration of PEG (15% weight/volume) for different PEG molecular weights. The color scheme is provided in the legend. Each point represents an independent measurement. Mean and standard deviation are shown for independent replicates of the same concentration. Note that measurements of the bound fraction strongly constrain the estimate of the binding affinity for (rU)₄₀. (B) Schematic of depletion theory. Two colloidal particles (purple and cyan circles) in a polymer solution are surrounded by a depletion layer (dashed blue line), where polymers (purple coils) do not enter. Bringing the two colloidal particles together gives rise to an overlap between the two depletion layers, which is maximized when colloidal particles are in contact. The larger the overlapping volume of the depletion layers, the stronger the attractive entropic force between the two particles. For the case treated in this work, the NTD–RBD is described as a colloidal particle (accounting for the presence of a folded domain), whereas RNA is represented by a smaller effective radius since PEG and RNA can interpenetrate, resulting in a significantly smaller depletion layer than the colloidal particle. (C) Upper panel. Association constant K_A0 (in the absence of crowding) divided for the measured value K_A in the presence of 15% w/v PEG. The blue band is the estimate based on depletion theory when assuming a radius of gyration of the RNA equal to 0.8 ± 0.3 nm. The dashed line is the reference state. Central panel. Conversion of the association constant ratio to the corresponding ΔΔG as a function of the PEG molecular weight. Colored points represent measurements. Error bars are standard deviations of two independent sample repeats (see Table S6). The blue band is the estimate based on depletion theory when assuming a radius of gyration of the RNA equal to 0.8 ± 0.3 nm. The dashed line is the reference state. Lower panel. Expected values for the theory when assuming a fixed radius of gyration (as estimated for the protein in the absence of crowding from simulations,³³R_g = 2.1 nm) and increasing molecular weight of PEG molecules that adopt a radius of gyration between 0.7 and 3.0 nm.

In particular, we are interested in understanding what happens to binding affinity with respect to PEG 1000, which acts as the divider between the regimes where attractive or screening interactions dominate. We found that for crowding agents smaller than PEG 1000, there is an increase of the association constant (tighter binding) with increasing molecular weight of PEG, until reaching a maximum at approximately the molecular weight of PEG 600 (Figure 4C and Table S7). For molecules larger than PEG 600, the trend reverts, and the association constant decreases (weaker binding) with increasing polymer molecular weight. However, it does not decrease below the value measured in the absence of crowding agents. Our experimental observations suggest a nontrivial relation between protein conformations and binding. To better understand the source of this behavior, we turned to established models that have previously captured analogous behavior for disordered proteins and nucleic acids.^22,35

Depletion Effects Can Describe Binding Affinities

From the equilibrium constant, we estimated the ΔΔG associated with the crowding process and compared it to predictions from the depletion theory.^22,28 We used a model where depletion forces are estimated for two colloidal particles in a solution crowded by one type of polymer (Figure 4B).²⁸ In this framework, the polymers in the solution are depleted from the surface of the colloidal particle within a given layer that is commonly referred to as the depletion layer. This layer reflects the fact that polymers cannot interpenetrate with the colloidal particle. When the two colloidal particles are brought in proximity, the depletion layers start to overlap, leading to an increase in the volume that the polymers can explore or, in other words, an increase in the entropy of the solution. As a result, the two colloidal particles in a polymer solution experience an attractive entropic force that depends on the radius of the colloidal particles, the radius of gyration of the polymers, and the concentration of polymers

3

where n is the concentration of the polymer expressed in number density, V_overlap represents the overlapping volume of depletion layers, and R_g, R_g^RNA, and R_g are the radius of gyration of the protein, RNA, and PEG, respectively. As for the case of protein conformations, we also accounted for overlapping of polymers under semidilute conditions. Mathematical details are presented in the Supporting Information (eqs S19–S22).

We assigned the radius of gyration of one particle to be equal to the value obtained from the simulations of the NTD–RBD.³³ Note that the radius of gyration of the NTD–RBD reflects both the content of the folded domain as well as the disordered conformations adopted by the tail. In this respect, the colloidal particle representing the NTD–RBD is regarded as a “soft sphere”. We further rescaled the radius as a function of crowder size and concentration to account for the small change in size observed with increasing molecular weight of PEG. Finally, we used the radius of gyration of the RNA as a model parameter and computed the case of a purely entropic contribution of PEG. We plot our predictions as a function of the molecular weight at a constant concentration of crowding agents of 15% w/v (Figure 4C). For a large R_g^RNA (3.0 nm), we found that ΔΔG is expected to decrease monotonically with increasing molecular weight; however, when decreasing the R_g, we recover a nonmonotonic trend that is qualitatively compatible with our experimental observations. The experimental trend is better captured assuming an effective radius of the RNA in the range of 0.8 ± 0.3 nm. The reduced size of RNA is consistent with previous treatment of binding between two disordered proteins with the same theory,²² where only a segment of the disordered protein was proposed to sense depletion interactions. This can be explained by accounting for the fact that polymer crowders and disordered proteins (or RNA, in the current case) can interpenetrate in the solution. Small effective radii of the RNA and PEG molecules (due to the mesh size) reduce the depletion layers and corresponding overlap volume, consequently reducing the entropic forces and resulting in the nonmonotonic trend for long PEG molecules.

Temperature Effects on Protein Conformations in the Absence of Crowders

The emerging picture from our experiments is of a balance of enthalpic and entropic forces that determine protein conformations. However, depletion theory suggests that entropic contributions alone can be sufficient to qualitatively describe the trend of association constants for binding to RNA. To better quantify the contribution of the entropic and enthalpic components on the binding of NTD–RBD to RNA, we determined changes in the association constant as a function of temperature. To this end, we used a temperature-controlled cuvette holder, analogous to previous studies,⁴⁶⁻⁴⁸ which allowed us to monitor the conformations of the NTD, in the context of NTD_L–RBD, at temperatures from 10 to 56 °C. Similar to other studies of the temperature dependence of disordered proteins,⁴⁶⁻⁴⁸ we found that the FRET efficiency of NTD_L–RBD shifts toward higher values with increasing temperature from 10 to 37 °C, indicating a compaction of the disordered tail. Above 37 °C, we additionally observe a broadening of the distribution of transfer efficiencies, revealing another conformational change in the NTD_L–RBD. Measurements performed on the RBD_L construct (Figure S4) reveal a small deviation in transfer efficiencies that is not compatible with a complete unfolding of the RBD. Together with the conformational changes observed for NTD_L–RBD above 37 °C, which indicate compaction of the probed segment, we reason that this transfer efficiency change reflects the formation of an intermediate configuration of the RBD.

Enthalpic and Entropic Contributions to RNA Binding in the Absence of Crowders

Having established a range of temperatures where the NTD_L–RBD shows a single population (10–37 °C), we then proceed to study the temperature dependence of RNA binding in the absence of PEG. At saturating concentrations of (rU)₄₀, we observe a single population up to 44 °C and the appearance of a second population, shifted to higher transfer efficiencies, only above that temperature. This implies that RNA stabilizes the “low temperature” conformation of the NTD–RBD (Figures 5A–C and S5). In addition, the mean transfer efficiency of the new population does not change upon addition of RNA, independently from the concentration, suggesting that the new conformational state is noncompetent for RNA binding and dissociation of RNA is required to adopt that conformation. To avoid the complications associated with this conformational change, we restricted our analysis of the association constant to temperatures equal to and below 37 °C (Table S8). According to the van’t Hoff equation, if in a given range of temperatures, the enthalpy of a reaction does not change, the logarithm of the association constant K_A is a linear function of the reciprocal of absolute temperature T, where the slope reports about the enthalpy ΔH and the intercept reports about the entropy ΔS of binding

4

where R is the gas constant.

Figure 5.

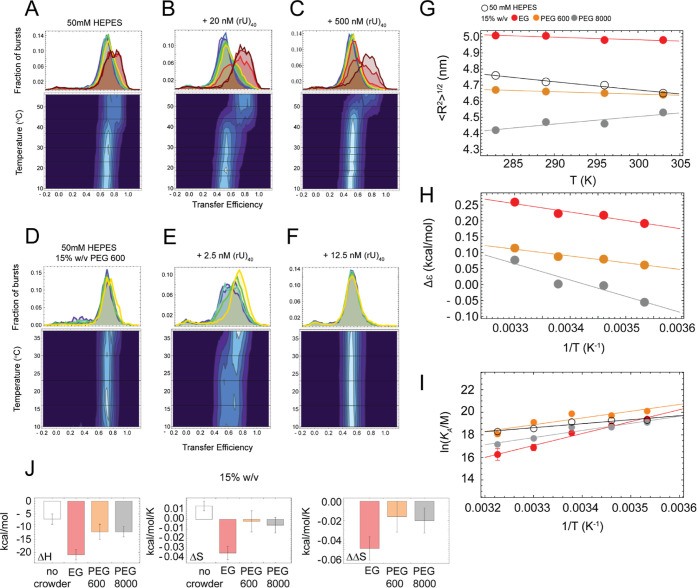
NTD–RBD conformations and binding of (rU)₄₀ as a function of temperature. (A–C) Upper panels. Representative transfer efficiency distributions of the NTD_L–RBD in 50 mM HEPES buffer (A), with addition of 20 nM (rU)₄₀ (B), and with addition of 500 nM (rU)₄₀ (C) as a function of temperature from 10 to 56 °C. Lower panels. Contour plots of the transfer efficiency distributions of NTD_L–RBD as a function of temperature. (D–F) Upper panels. Representative transfer efficiency distributions of the NTD_L–RBD in 50 mM HEPES buffer supplemented with 15% w/v PEG 600 in the absence of RNA (D) and in the presence of 2.5 nM (rU)₄₀ (E) and 12.5 nM (rU)₄₀ (F), as a function of temperature from 10 to 37 °C. Lower panels. Contour plots of the transfer efficiency distributions of NTD_L–RBD as a function of temperature for the corresponding experimental conditions in the upper panels. (G) Temperature dependence of the interdye distance in the absence of PEG (black) and with EG (red), PEG 600 (orange), and PEG 8000 (gray). (H) Dependence of Δε(T) = ε(T) – ε₀(T) on the reciprocal of temperature. (I) Plot of ln(K_A/M) as a function of 1/T (K^–1) in the absence of PEG (black) and in the presence of 15% w/v EG (red), PEG 600 (orange), and PEG 8000 (gray). Error bars represent errors of the fit. The linear fit reports the enthalpy (slope) and entropy (intercept) of binding according to eq 4. (J) ΔH, ΔS, and ΔΔS obtained from the fit of the data in panel I.

We observed a linear increase of ln K_A as a function of 1/T in the range of temperatures from 10 to 37 °C. Fitting of eq 4 provides a ΔH and ΔS of −7 ± 2 kcal/mol and 0.014 ± 0.005 kcal/mol/K, respectively, for the binding of NTD_L–RBD to (rU)₄₀ in the absence of crowding agents (see Table S9), indicating that the binding reaction is mildly exothermic and mostly enthalpically driven under this experimental condition (Figure 5I). These values provide the reference for understanding the impact of crowding agents on the entropy and enthalpy of binding.

Temperature Dependence of Protein Conformations in Crowded Conditions

As a next step, we characterized the temperature response of the protein in the presence of three archetypal crowders (EG, PEG 600, and PEG 8000) at a fixed concentration (15% w/v) (Figures 5D–F, S6–S8). These specific molecular weights have been chosen because they reflect three distinct regimes: low molecular weight and no significant effect on K_A (EG), low molecular weight and significant effect on K_A (PEG 600), and high molecular weight and no significant effect on K_A (PEG 8000).

We found that, at a fixed volume fraction of crowding agents of 15% w/v, the protein conformations exhibit different temperature responses depending on the type of crowding agent (Figure 5G). For the case of EG and PEG 600, the presence of the crowder appears to limit the extent of the conformational collapse of the protein, resulting in an almost unchanged protein configuration. For PEG 8000, we observed an opposite trend, with the protein conformations expanding with increasing temperature instead of collapsing. These results are apparently discordant, with the overall protein conformation expanding or collapsing as a function of the crowding degree of polymerization.

To better understand the contribution of the forces at play, we estimated Δε(T) = ε(T) – ε₀(T) from eq 1, which separates the contribution of solvent and crowder interactions from excluded-volume screening effects. We found that Δε increases with increasing temperature for all three crowding agents (Figure 5H), indicating that the specific temperature response of chain dimensions for the different degrees of polymerization of PEG is due to excluded-volume screening effects. We note that the temperature dependence of Δε is not surprising and does reflect the change in the interaction of PEG and water molecules with the protein (number of sites on the protein and binding constant), as implied by the Schellman weak binding model. The exact quantification of these effects would require a comparison of different sequence compositions for the disordered tail, which is beyond the scope of this work.

Having characterized the effect of temperature on the conformations of the protein in the presence of crowders, we proceeded to study how the association constant for RNA binding depends on temperature.

Enthalpic and Entropic Components to RNA Binding in the Presence of Crowders

For all three crowding agents (EG, PEG 600, and PEG 8000), we found a linear dependence of the logarithm of the association constant as a function of the reciprocal of the temperature. As mentioned before, the slope of this linear dependence reports the enthalpic contribution to binding. In this respect, while binding remained exothermic in the presence of all three crowders at 15% w/v, there were clear differences in the magnitude of their effects (Figure 5I,J). Interestingly, although PEG 600 favors binding more than EG and PEG 8000, it exerts a negligible effect on the enthalpy (ΔΔH_exp = −5 ± 5 kcal/mol, Table S9), indicating that the contribution introduced by this crowding agent to binding is purely of entropic nature. The experimental change in the entropy of binding induced by addition of PEG 600, ΔΔS_exp = −0.02 ± 0.02 kcal/mol/K (Table S9), is compatible with the large error with the value from depletion theory (assuming an effective radius of gyration of 0.8 ± 0.3 nm for RNA, see Depletion Effects Can Describe Binding Affinities), ΔΔS_dt = 0.002 (±0.006) kcal/mol/K. PEG 8000, on the other hand, the crowder of the three that impacts binding the least, presents a more significant change in enthalpy (ΔΔH_exp = −6 ± 4 kcal/mol, Table S9), but this favorable effect on binding is completely compensated by a negative change in the entropy of binding ΔΔS_exp, −0.02 ± 0.01 kcal/mol/K. In this case, the measured change in entropy is of the opposite sign and greater in absolute value than what is predicted by depletion theory, ΔΔS_dt = 0.0029 (+0.001, −0.0014) kcal/mol/K. Lastly, at variance with PEG 600 and PEG 8000, EG shows a significant change in both enthalpy and entropy, with a ΔΔH_exp = −14 ± 3 kcal/mol and ΔΔS_exp = −0.05 ± 0.01 kcal/mol/K (Table S9), also in the opposite direction to the estimated value from depletion theory of ΔΔS_dt = 0.0014 (±0.0003) kcal/mol/K, displaying a strong compensation between enthalpic and entropic components of their effects on the binding of NTD–RBD to (rU)₄₀ (Figure S10). The result is robust with respect to the fitting procedure used to estimate the association constants as a function of temperature (Figure S11 and Table S10). Overall, our data suggest that whereas depletion theory can capture the overall trend of the equilibrium constants for this system, the origin of the observed phenomenon is more complicated than the entropic explanation proposed by the model.

Sequence Specificity

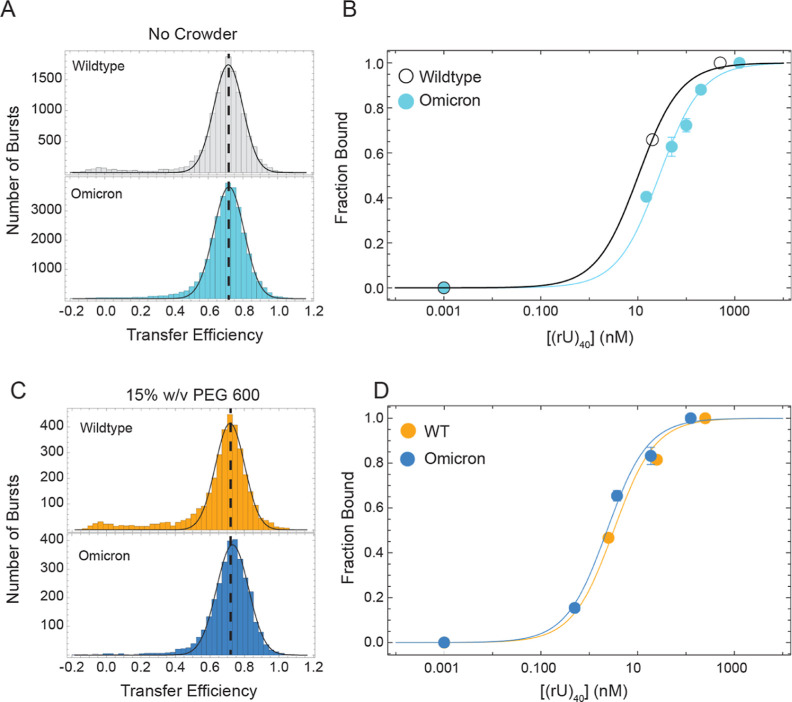
We have previously shown that mutations characteristic to the Omicron variant of SARS-CoV-2 do not alter the conformations of the disordered tail, compared to the Wuhan-Hu-1 variant, but lead to a fourfold change in binding affinity for poly(rU).³³ Here, we asked whether crowding effects can modulate the binding affinity of these two different variants. In other words, we asked whether the “functional” differences encoded in the sequence are maintained under crowded conditions. While this in first approximation seems a reasonable assumption, there is the possibility that conformational changes and depletion effects induced by crowders may normalize the contribution of mutations.

To this end, we compared the binding of the two variants in the absence and presence of 15% w/v PEG 600 (Figures 6 and S12). We selected PEG 600 because, in our previous binding experiments, this crowding agent showed the strongest effect on K_A. In the HEPES buffer and no-crowder condition, we found that the association constants for (rU)₄₀ of the Wuhan variant were 2.7 ± 0.3 times the value for the Omicron variant, with the K_A^WUHAN and K_A^Omicron equal to 0.097 ± 0.006 and 0.036 ± 0.004 nM^–1, respectively. Interestingly, when measured in the presence of 15% w/v PEG 600, K_A^WUHAN is equal to 0.32 ± 0.04 nM^–1 and K_A^Omicron is 0.46 ± 0.06 nM^–1. Therefore, addition of crowding reduces the change of affinity between the two variants to a factor of 0.7 ± 0.1. This suggests that crowding effects can effectively “normalize” some of the interactions encoded in disordered regions and that the chain response will be effectively different depending on the environmental context.

Figure 6.

Effects of crowding on the Omicron variant. (A) Distribution of transfer efficiencies for wildtype (Wuhan-Hu-1) and Omicron variants in the absence of crowding. The vertical dashed line provides a reference for comparing the mean transfer efficiency. (B) Corresponding fraction bound and unbound based on titrations of (rU)₄₀ in the absence of crowding and fit to eq S17. Errors are from multiple independent repeats of the same condition. (C) Distribution of transfer efficiencies for wildtype (Wuhan-Hu-1) and Omicron variants in the presence of crowding. The vertical dashed line provides a reference for comparing the mean transfer efficiency. (D) Corresponding fraction bound and unbound based on titrations of (rU)₄₀ in the presence of 15% w/v PEG 600 and fit to eq S17. Errors are from multiple independent repeats of the same condition.

Discussion

Crowding and IDR Conformations

Our results expand on previous investigations of full-length IDPs by studying the impact of crowding on a disordered tail attached to a folded domain.

To mimic the effect of the crowded cell, we used PEG molecules with molecular weights that span from 50 to 35,000 Da. Previous in-cell experiments suggest that PEG 35000 mimics, in first approximation, the average distribution of crowders within the cell.¹⁸ Smaller PEG molecules serve as a model for the effect of small solutes in the cell, which can impact not only in terms of crowding but also in terms of weak interactions with the protein of interest. It is important to note that the investigation of multiple molecular weights of PEG enables proper accounting of the polymeric properties of PEG across different solution regimes (dilute and semidilute). Larger PEG molecules would not result in significantly different effects because, under the studied experimental conditions, the crowded environment is described no longer by the radius of gyration of the individual crowder but by the mesh size of the semidilute solution, which has a negligible dependence on the degree of polymerization of PEG.¹⁵

Concerning our specific system, the disordered N-terminal tail of SARS-CoV-2, within the range of crowders and volume fractions that we explored in this work, we did not observe stabilization of contacts with the folded domain, as confirmed by nsFCS measurements. While a stable rigid conformation is not adopted, the disordered region definitely was found to be sensitive to the surrounding environment. The emerging picture is of a competition between weak binding interactions that alter the free energy of solvation of the protein and the excluded volume screening effects due to the spatial hindrance of other crowders. The key parameters controlling protein conformations are the degree of expansion of the protein, the “size” (degree of polymerization and scaling exponent) of the crowding agents, and the extent of interactions between crowding agents and protein. The degree of expansion (or compaction) of the protein is measured with reference to the dimensions of the “ideal state” of the protein, which can be estimated based on scaling exponent measurements or simulations. The Flory criterion provides the reference to define large (P > N^1/2) and small (P < N^1/2) crowders when compared to the length of the disordered protein. This is consistent with approximately the size of PEG 1000 (Supporting Information). In this framework, the protein conformations in the presence of small polymeric crowders sense a small-to-negligible contribution of the screening-excluded volume effect. If there are weak attractive interactions of the protein to the crowders, they can modulate the conformations of the protein. This modulation can occur in one of two ways where either the interaction with the crowders can increase the solvation free energy of the chain, therefore leading to an expansion (as in the case studied here), or decrease the solvation free energy and therefore lead to a collapse. Another scenario can occur if there are weak repulsive interactions between the protein and the crowders. Repulsive interactions between the protein and the crowder will result in an amplification of the excluded volume screening effects, as predicted by polymer theories of ternary solutions²⁵⁻²⁷ and shown in previous experiments.¹⁴ In the case of large polymeric crowders, the contribution of excluded volume screening becomes significant and can drive compaction of the chain if the chain is more expanded than its ideal state conformation.²⁵⁻²⁷ Weak attractive interactions can counterbalance in some measure the effect of screening if the protein–crowder local interactions favor better solvation of the polymer chain, which is the case for the system in this study.

Crowding and IDR Interactions

In our experiment, we tested the impact of a fixed concentration of crowding on binding when modulating the degree of polymerization of PEG. We found a nonmonotonic behavior of the association constant of NTD–RBD for RNA (Figure 4), with the strongest effect (favoring association) detected for PEG 400 and PEG 600. We compared experimental estimates of the change in free energy with expectations from depletion theory and found that a purely entropic contribution can explain the nonmonotonic trend. We took a step forward and verified whether this interpretation holds true by quantifying the enthalpic and entropic contributions to binding from the van’t Hoff analysis of the temperature dependence of the association constant. We found that the predicted entropic changes, based on the depletion theory, are smaller than the ones observed in the experiments. This is not completely surprising, given that the version of the model adopted here operates various simplifications in the description of the protein and, in particular, of the RNA. The enthalpic contribution is truly negligible only for PEG 600 and, within errors, for PEG 8000, whereas it becomes dominant for EG. We speculate that this is due to the interactions of EG with both the protein and RNA, bridging the two molecules together. While all these effects point to a prevalent contribution of crowding to the disordered tail, we further tested how crowding impacts binding of the same RNA to the RBD in the absence of NTD. We compared the case of EG and PEG 600. We found that EG has a smaller impact (in relative terms) on binding when compared to the decrease in binding affinity observed in the presence of the NTD (see Figure S13 and Table S11). Similarly, while PEG 600 affects binding in the opposite direction of EG for both the RBD and NTD–RBD, suggesting that the RBD itself perceives weak interactions with PEG, we observed smaller relative changes for the RBD compared to the NTD–RBD. Overall, our data indicates that the observed effects of crowding on the binding of RNA are not exclusively attributable to modulations in the affinity of the RBD alone. The difference in binding affinity of Wuhan-Hu-1 and Omicron variants in a 15% w/v PEG 600 solution further suggests that few mutations in the sequence are sufficient to alter the entropic and enthalpic contributions to binding, pointing to sequence-specific encoded interactions in the IDR.

PEG Interactions

Our results reveal weak attractive interactions between the disordered tail and low-molecular-weight PEG molecules. The existence of interactions between protein (or nucleic acids) and PEG has been reported before in the literature,^9,13,49,50 leading even to recommendations against the use of PEG as a crowding agent because it is not inert.⁹ Indeed, weak interactions complicate the interpretation of ensemble experiments, where different protein (or nucleic acid) conformations cannot be resolved. However, single-molecule measurements^14,22,34,35 and carefully designed ensemble experiments^5,51 can leverage such interactions to explore the interplay between purely entropic effects and enthalpic contributions. In this respect, the use of cytomimetic solutions based on polymers and other solutes can provide physical insights into the properties of the cellular medium.⁵² Different from previous single-molecule experiments focused on the folding of nucleic acids,^34,35 we observed enthalpic contributions on both conformations of the proteins and interactions of the protein with RNA that could not be simply described in terms of depletion effects. The dependence of the interaction on the molecular weight of PEG molecules was similar to recent determinations of enthalpic and entropic crowding effects on a foldable protein,⁵¹ with enthalpic effects dominating low molecular weights of PEG. Interestingly, we found compensating effects of enthalpic and entropic effects on RNA binding, which counterbalance each other. We speculate that the dynamic nature of the complex facilitates a trade-off between increased enthalpic interactions, for example, mediated by short PEG, and entropic changes. Finally, it is worth mentioning that the use of the Schellman weak binding model implicitly accounts for the dynamic exchange of water molecules with crowding agents in the proximity of the protein. Indeed, addition of osmolytes is known to alter the water activity and contribute entropically to protein conformations, interactions, and folding.^53,54

Implications for SARS-CoV-2

Finally, it is interesting to consider the implications of our experiments in the context of SARS-CoV-2. We found that the nucleocapsid NTD_L–RBD and RBD_L undergo a cooperative conformational change in the absence of RNA above 37 °C, with NTD_L–RBD adopting a more compact conformation and RBD_L slightly expanding. By comparison with previous states identified in denaturation experiments,³³ we reason that this change is linked to interactions of the tail with an intermediate (partially unfolded) state of RBD. Interestingly, binding of single-stranded nucleic acid favors the stability of the open configuration (folded RBD) and the transition toward the intermediate state is shifted toward higher temperatures. This supports a picture where the NTD–RBD region of the SARS-CoV-2 nucleocapsid protein not only has a preference for the binding of single-stranded RNA but the binding of RNA also stabilizes specific conformations. The comparison between variants provides further insights into the impact of evolutionary mutations in the protein sequence. The small (yet measurable) difference in the association constants between the Wuhan-Hu-1 and the Omicron variants in the presence of PEG suggests that the specific mutations are largely tolerated by the virus because, under crowded conditions, they result in a similar affinity. However, our observations open the door to a more complex interpretation of the role of disordered regions in the cellular environment, where the function (here represented by RNA binding affinity) can become context-dependent: in an uncrowded environment, the two variants may bind to RNA differently than in a crowded environment. For what concerns the crowding conditions of the N protein in the context of the virus life cycle, it is plausible to consider that the protein may experience different crowding when it is in the cytoplasm of the infected cell compared to when it is inside the virion. Indeed, within the virion, we expect a volume fraction occupancy of about 1–2% (based on a rough estimate of about 1000 nucleocapsid protein in a virion⁵⁵ bound to a 30,000-base viral genome) vs the 10–20% of volume fraction occupied inside of the cytoplasm.

Conclusions

Our experiments and theoretical modeling provide new insights into the balance between weak interactions and excluded volume screening effects on disordered regions, in particular in the context of disordered tails (Figure 7). We found weak attractive interactions, previously not observed, which reveal a sequence specificity in the interaction with PEG. While interpretations of ensemble studies are complicated by attractive interactions, single-molecule FRET enables quantification of these impacts on both conformations and binding. These quantifications are essential elements for rigorously testing current polymer models. In this respect, the theory presented here helps quantify the role of excluded volume screening and weak interactions. However, more work is needed to establish quantitative models capable of capturing the role of entropic and enthalpic interactions of crowders on IDR conformations and binding. Future work will focus on studying effects from the perspective of RNA, testing the contribution of cellular crowding, as well as exploring sequence compositional effects within the conformation–affinity–crowding space.

Figure 7.

Weak interactions and excluded volume screening effects on disordered tails. Schematic summary of the competition between weak interactions and excluded volume screening as a function of the degree of polymerization (or molecular weight) of PEG molecules.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.3c02356.

• Reagents, instrumentation and data analysis, theory, and characterization results (PDF)

Author Present Address

^§ Instituto de Química y Fisicoquímica Biológicas, Universidad de Buenos Aires—CONICET, Junín 956–1113, Ciudad de Buenos Aires, Argentina

Author Contributions

^# M.A.S. and J.C. contributed equally to the work. M.A.S. and J.C. performed the experiments. D.R. and J.J.I. provided research tools. M.A.S., J.C., J.J.I., and A.S. analyzed the data. M.D.S.-B., K.B.H., and A.S. supervised the experiments. A.S. designed the research. M.A.S., J.C., J.J.I., K.B.H., M.D.S.-B., and A.S. wrote the manuscript.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Early-Career and Emerging Researchers in Physical Chemistry Volume 2”.