ABSTRACT
Pancreatic islets are mini-organs composed of hundreds or thousands of ɑ, β and δ-cells, which, respectively, secrete glucagon, insulin and somatostatin, key hormones for the regulation of blood glucose. In pancreatic islets, hormone secretion is tightly regulated by both internal and external mechanisms, including electrical communication and paracrine signaling between islet cells. Given its complexity, the experimental study of pancreatic islets has been complemented with computational modeling as a tool to gain a better understanding about how all the mechanisms involved at different levels of organization interact. In this review, we describe how multicellular models of pancreatic cells have evolved from the early models of electrically coupled β-cells to models in which experimentally derived architectures and both electrical and paracrine signals have been considered.
KEYWORDS: Computational model, mathematical model, islets, gap-junctions, paracrine, diabetes mellitus
GRAPHICAL ABSTRACT

Introduction
Pancreatic islets, also known as islets of Langerhans, are mainly composed of ɑ, β and δ-cells, endocrine cells that secrete glucagon, insulin and somatostatin, respectively, critical hormones for the regulation of blood glucose. Insulin, the only hormone capable of reducing glucose levels directly, is secreted when blood glucose rises, producing its hypoglycemic effect by promoting the uptake of glucose by hepatic, muscular and adipose tissues. On the contrary, glucagon is secreted when blood glucose decreases, promoting the release of the stored glucose (i.e., glycogen) mainly from the liver to restore the normal glucose levels. Finally, somatostatin, secreted by δ-cells, is not involved in the regulation of blood glucose directly, although it has a relevant indirect role by inhibiting the secretion of both glucagon and insulin from ɑ and β-cells, respectively.1
Pancreatic ɑ, β and δ-cells share a common secretion mechanism involving glucose transport, metabolism and electrical activity, which, by driving the entry of Ca2+ to the intracellular space, ultimately promotes exocytosis. Despite this, ɑ, β and δ-cells have particularities that make them secrete their respective hormone in a finely tuned fashion following the body’s needs (for details see refs.2–4). In addition, glucagon, insulin and somatostatin also serve as paracrine and autocrine signals, forming regulatory loops that shape the secretory behavior of the islet in response to the dynamic changes in blood glucose.5,6 On the other hand, it is also well known that β-cells in close contact can communicate via gap-junctions, thus allowing the flow of ions and small molecules between the connected cells.7 Moreover, it has been demonstrated that gap-junctions also connect neighbor β and δ-cells.8,9 All these communication pathways within the islets, in addition to the external endocrine, nutritional and neural inputs, conform an extremely complex dynamical system and as such has been widely studied both experimentally and theoretically.
Experimentally, the study of isolated pancreatic cells and pancreatic islets has grown in complexity following the technological advances. For instance, electrophysiological measurements of the electrical activity of single β-cells was first performed using the intracellular recording technique.10–12 Then, the patch clamp techniques13 allowed researchers to characterize the properties of the ionic channels involved and their role on the electrical response of the cells (see for instance refs.14–19). The recordings of the electrical activity of β-cells were eventually complemented with measurements of intracellular Ca2+ 20,21 and metabolism,22–25 thus making it possible to delineate the relationship between cellular mechanisms leading to the exocytosis of insulin, which has been described extensively in more recent years owing to the use of advanced microscopy techniques.26–28 Afterward, the simultaneous recording of two neighbor β-cells (separated by 20–50 μm) suggested the possibility of electrical coupling between β-cells in intact islets.29,30 Moreover, fluorescence and electrophysiological techniques, along with the use of specifical chemical blockers and genetic knockout of gap-junctions have allowed to elucidate how electrical signals propagate throughout intact islets.31,32 On the other hand, paracrine interactions between islet cells have been studied experimentally,33–37,37–40 thus allowing us to gain a better understanding of how glucose is regulated at the islet level considering the hormonal crosstalk. Similarly, optogenetic techniques have been adopted to evaluate whether a small population of specialized hub β-cells could act as pacemakers within the islets.41 Recently, RNA sequencing has been combined with electrophysiology to identify genes associated with cell function in health and disease.42,43
As a complement, theoretical models of the electrical activity of ɑ,44,45 β46–48 and δ-cells49 have been extensively used to explain the experimental observations at the single-cell level. Similarly, mathematical and computational models of clusters of communicating β-cells and recently, of pancreatic islets including ɑ, β and δ-cells, have been proposed with the objective of evaluating plausible hypotheses to explain the collective behavior observed experimentally.
In this review, we describe how multicellular models of pancreatic cells have evolved along the years, briefly explaining how they are constructed in terms of its components, their geometrical configuration, the modeling approaches adopted and the underlying physiological hypotheses. The characteristics of all the multicellular models of pancreatic cells reviewed are summarized in the table provided as Supplementary Material.
Modeling strategies in multicellular models of pancreatic cells
The presence of gap-junctions between neighbor β-cells was demonstrated by Orci et al.50 in 1973 using electron microscopy images of rat islets. A few years later, functional electrophysiological evidence obtained by the simultaneous measurement of the electrical activity of two neighbor β-cells in mouse islets by Eddlestone et al.,29 Meissner30 and Meda et al.51 demonstrated that they are electrically coupled, as indicated by the synchronized electrical response following a glucose stimulus. After the proposal of the paradigmatic mathematical model of the electrical activity of the pancreatic β-cell by Chay and Keizer,52 it was a matter of time before theoretical studies of electrical coupling between β-cells were developed, recently followed by models of paracrine signaling between islet cells, as growing evidence has emerged about its importance for the regulation of the secretion of pancreatic hormones. Throughout the years, several multicellular models of clusters of β-cells and pancreatic islets have been proposed using different modeling strategies, briefly described in the following.
Dynamical models of electrically coupled cells and paracrine signaling
As the great majority of single-cell models (for a review see refs.46–48), most of the multicellular models of pancreatic cells are dynamical models, in which all the variables of interest (e.g. membrane potential, intracellular Ca2+, etc.) change over time and therefore are represented by a system of coupled differential equations.
The first theoretical study of a pair of coupled β-cells was proposed by Banghman et al.53 in 1986 using the classical dynamical model of Chay and Keizer,52 where it was shown that electrical coupling was capable of synchronizing the electrical activity of the pair of cells. Since the beginning, most of the dynamical models of coupled β-cells included a coupling current between cells i and j, which only depends on the difference between the membrane potentials of the coupled cells ( and ) and the conductance of the gap-junctions (see Figure 1a):
| (1) |
Figure 1.
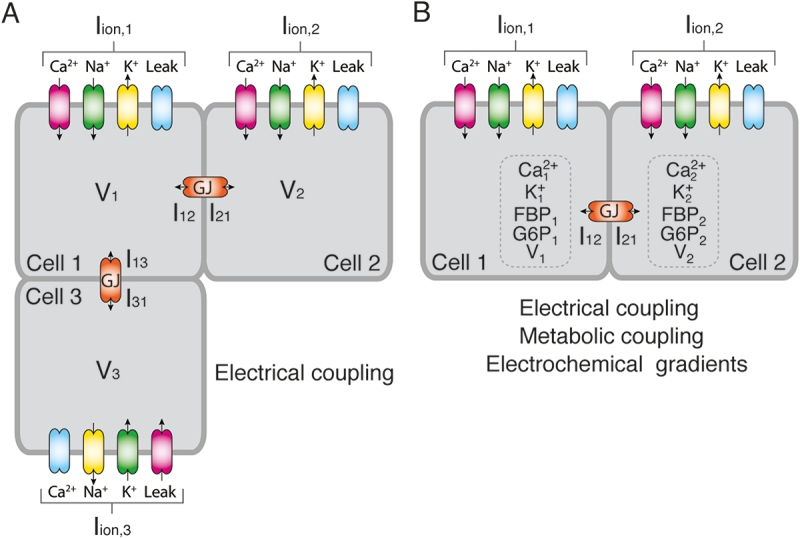
A. Electrical coupling through gap-junctions between three hypothetical β-cells can be modeled using Eq. 2 where represents the currents through the ionic channels and the coupling currents , (and , ) are described by Eq. 1. B. Other models considered the changes in concentration and flow of ions (e.g., Ca2+ and K+) and metabolites (e.g., FBP, G6P) through gap-junctions (GJ) in addition to the voltage differences between connected cells.
In practice, Eq. 1 means that whenever the membrane potentials of the coupled cells are different, there will be a current flowing between them, either inward or outward, in addition to the currents produced by the populations of ionic channels located in the cell membrane, thus contributing to shape the electrical response of the cells. In mathematical terms, a typical dynamical model of coupled β-cells can be described as:
| (2) |
where is the membrane potential of cell i, is the membrane capacitance, which is used in models of excitable cells as an indirect measure of cell size, includes all the currents flowing through the populations of ionic channels in the cell membrane and the last term, , represents the currents flowing through the gap-junctions connecting cell i with its neighbors, j. In Figure 1a, an example considering three β-cells (i = 1,2,3) where cell 1 is connected to both cells 2 and 3 is shown. In this hypothetical case, assuming that β-cells have populations of Na+, K+, Ca2+ and leak channels, the first term of the right-hand side of Eq. 2 would be for the three cells, while the respective coupling terms , , and would be given by Eq. 1.
A minority of dynamical models (see for instance refs.54,55) adopted the slightly more complex approach proposed by Kitagawa et al.54 to simulate the gap junction currents. Their proposal was based on the Goldman-Hodgkin-Katz approximation and considered the flow of K+ and Ca2+ ions through the gap-junctions (see Figure 1b). In mathematical terms:
| (3) |
where is the junctional current between coupled cells (second term of Eq. 2), and are the mobilities of K+ and Ca2+, and are the corresponding valences, and represent the area and length of the gap-junctions, respectively, , , and are the intracellular concentrations of K+ and Ca2+ of cells i and j, and F, R and T are the Faraday constant, the gas constant and the absolute temperature, respectively.
This representation of gap-junctions in models of coupled β-cells allowed the simulation of more detailed scenarios, although inevitably increasing the complexity of the models since a mathematical representation of the changes in the intracellular ionic concentrations (Ki and Cai in Eq. 3) and several additional parameters are needed in comparison to the basic representation of gap-junctions given by Eq. 1.
In addition to electrical coupling and the diffusion of K+ and Ca2+ through gap junctions, other models explored the effect of gap-junctional diffusion of metabolites, such as fructose 1–6-biphosphate and glucose 6-phosphate, on the coordination of β-cells56–58 (see Figure 1b). The diffusion of metabolites through the gap-junctions adopted a similar form than that used to simulate electrical coupling between two cells, i.e. , where represents the flux of X = Ca2+, FBP or G6P through the gap junctions between the cell i and cells j in its neighborhood , is the gap-junctional permeability, and Xi and Xj are the corresponding intracellular concentrations.
The modeling approach described in this section is, by far, the most popular strategy to develop multicellular models of pancreatic cells, since it allows a relatively detailed description of all the variables of interest. However, it must be noted that the computational cost involved in solving a dynamical model composed of hundreds or thousands of cells, each described by tens of coupled differential equations, is considerably high, thus requiring the use of specialized computer clusters or parallel computing.
Discrete models based on percolation theory
Discrete models of communicating β-cells, in contrast to the complex dynamical models, do not require a detailed description of all the cellular mechanisms included, which reduces the computational power required to perform simulations significantly, with the drawback that physiological interpretability, in terms of the subcellular processes involved, is completely lost.
In short, according to this approach, coupled β-cells form a network where each cell is a node and linked nodes or cells are assumed to be functionally coupled (e.g., if a cell is active, all the other cells coupled to it are also active). Coupling between cells is determined using a probabilistic approach, where p is the probability of being open for coupling and the complement, 1 – p, is the probability of not being coupled. According to percolation theory, there is a critical probability value pc that determines if the network is formed by disconnected clusters (p < pc) or a large predominant cluster is formed (p > pc). An additional parameter Sp, representing the percentage of excitable and non-excitable cells, can be included in the model to simulate, using the same probabilistic approach, how coupling (given by the parameter p) and the proportion of the different subpopulations included in the model would influence the collective behavior of the cluster of cells. An example of this can be seen in Figure 2c-e, where both the connectivity between cells (represented by the gray links) and the proportions of active and inactive cells (green and black cells, respectively) have been determined probabilistically.
Figure 2.
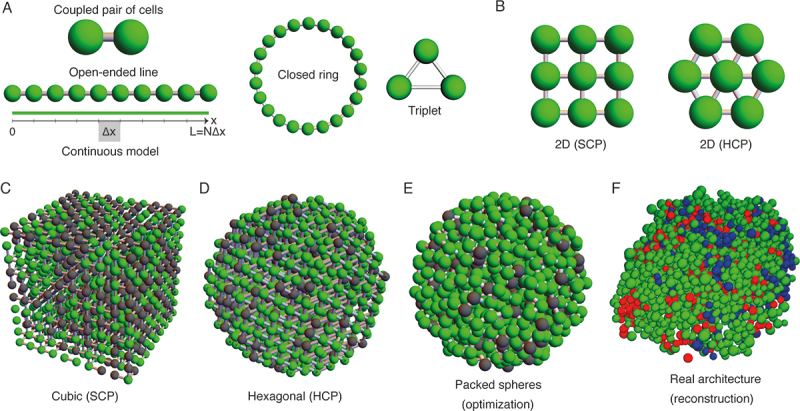
A. One-dimensional arrangement of clusters of cells including a coupled pair of cells and an open-ended line composed of 10 coupled cells. According to the continuous approximation, the propagation of electrical signals through a linear arrangement of cells can be approximated by Eq. 5 where it is assumed that each cell contributes with ∆x to the length of the continuous line (see main text for details). B. Bi-dimensional arrangement of cells including the simple and hexagonal cubic packing (SCP and HCP, respectively). C-F. Three-dimensional structures used in multicellular models of pancreatic cells. In C-E, green and black cells represent active and inactive cells, respectively, as modeled using the discrete probabilistic approach based on percolation theory. In F, red, green and blue cells represent the ɑ, β and δ-cells, respectively.
As will be described in more detail below (see Section Applications of multicellular models of pancreatic cells), discrete models have been used to study how gap-junction coupling affects synchronization and wave propagation,31 to explain the effects of the cluster architecture (size and shape) on the functionality of both 2D and 3D cell aggregates,59 to predict the effect of the proportion of excitable and non-excitable cells and coupling on the cluster activity,60 and to determine the critical value of β-cell loss where an islet is not functional,61 which proves the usefulness of this modeling approach in spite of its relative simplicity.
Model of coupled oscillators
Another simplified approach that does not consider explicitly the cellular mechanisms involved in electrical activity, electrical coupling and paracrine signaling was adopted by Hoang et al.,62 who reinterpreted the Kuramoto model of coupled oscillators63,64 to represent the pulsatile secretory behavior of ɑ, β and δ-cells and the corresponding paracrine interactions (see Figure 4c). This model is based on the following differential equation describing the oscillation phase (θi) of cell i, assumed to interact with cells j in its neighborhood :
| (4) |
Figure 4.

A. Diagram of the communication signals included in the multicellular model of Briant et al.8 When active, β-cells promote the activity of δ-cells due to the electrical communication between them via gap-junctions. Somatostatin secretion then inhibits the secretion of glucagon from ɑ-cells. B. The model by Watts et al.125 includes paracrine signals between the three types of cells. C. Model of coupled oscillators used by Hoang et al.62 to simulate the paracrine interactions between the ɑ, β and δ-cells. Note that only one cell of each type is shown while the model included hundreds or thousands of cells. ATP: adenosine triphosphate, KATP: ATP-dependent K+ channels, VDCC: voltage-dependent Ca2+ channels, GJ: gap-junctions, GIRK: G-protein coupled inwardly-rectifying K+ channel.
where represents the intrinsic frequency of cell i, and indicate if cells i and j are either ɑ, β or δ, and is an interaction parameter that determines the strength of the interaction between communicating cells. In simple terms, each cell oscillates at a given frequency with an oscillation phase influenced by the phases of the neighbor cells (see Figure 4c). Although relatively simple, by varying the sign and value of the interaction parameter in Eq. 4, this type of model is suitable for simulating both excitatory or inhibitory effects between cells and to evaluate the degree of synchronization of the islet. On the other hand, the main disadvantage of this approach is that cellular mechanisms are not considered explicitly, thus limiting the interpretation of the simulation results from a physiological viewpoint.
Continuous propagation models
In other works, in order to study the propagation of excitation waves through clusters of coupled β-cells,65–68 the system of equations for a one-dimensional cluster of β-cells was simplified to a single equation by treating the cluster as a continuous medium formed by the connected cells. For instance, for a cluster of β-cells in 1-D, the continuous approximation can be described mathematically as:
| (5) |
where V is the propagating voltage through the line of N cells located along the x coordinate, each located at (i = 0 … N), being the length of the continuous medium (see the bottom panel of Figure 2a), Cm the cell capacitance and includes all the membrane currents as in the dynamical models described previously (e.g. as in the example used above). This approach was also used to simulate the propagation of waves across a bi-dimensional array of cells in rectangular coordinates,67 as well as in spherical coordinates, assuming that an islet can be morphologically represented by a sphere.66
Since a continuous approximation implies a reduction of the mathematical complexity of the model, the computational power needed to solve it is considerably low when compared to that required to solve a multicellular dynamical model, with the drawback that the resolution at the cellular and subcellular levels is lost.
Geometry of clusters of β-cells and islet architectures
Including electrical and paracrine communication between islet cells in multicellular models implies that a geometrical representation of the cluster of cells or islet must be defined in advance in order to determine how cells communicate with each other. Along the years, the geometry of the multicellular models of islet cells has increased in complexity, aiming to adopt the most realistic representation of the actual islet architecture.
As explained before, the first model of coupled cells only considered the interaction between two β-cells53 (Figure 2a), a basic geometrical configuration that, in spite of its simplicity, has been continuously used to describe how a pair of coupled cells interact before exploring a more complex multicellular system (see for instance refs.53,56,69,70). As an example of this, even very recently, Ren et al.71 proposed a model with only two cells to simulate the interactions between α and β cells where, instead of gap-junctions, communication between the pair of cells relies on paracrine mechanisms.
Next in complexity are the 1-D arrays of more than two β-cells, ranging in size from triplets72 to open-ended lines67,68 or closed rings73 including tens or hundreds of cells (see Figure 2a). The main drawback of the 1D models is that each cell has only two neighbors, and, therefore, the number of interactions between cells is considerably limited.
Bi-dimensional clusters of β-cells have adopted squared (2D-Simple Cubic Packing, SCP),54,59,67,74,75 hexagonal76 (2D Hexagonal Closest Packing, HCP) and rectangular geometries77 thus increasing the number of possible interactions between cells to four in the case of the 2D SCP and rectangular structures and six for the case of the 2D HCP geometry (see Figure 2b).
Finally, three-dimensional models have adopted a variety of geometries, including the 3D SCP and HCP structures (see Figure 2c, d), as well as more complex three-dimensional structures generated using sphere-packing algorithms (Figure 2e). Other recent models have used real islet architectures obtained via confocal microscopy and immunofluorescence techniques, aiming to develop more realistic models in terms of the composition and organization of the simulated islets (see Figure 2f). Regarding the connectivity between islet cells, 3D SCP and HCP structures have a pre-defined maximum number of interactions of 6 and 12, respectively. On the other hand, the architectures based on sphere packing (Figure 2e) and reconstructed architectures (Figure 2f) have relied on a threshold-based criteria to determine the intercellular contacts in the simulated islets, using the Euclidean distance between the coordinates of the center of the cell as the main factor to determine the intercellular interactions taking place in the simulations. A minority of models have adopted a probabilistic approach based on percolation theory to determine the connectivity of clusters of β-cells (briefly explained above; see also Figures 2c, d).60 While these are reasonable assumptions, there are some aspects that are worth being considered. Firstly, the electrical interactions between β-cells via gap-junctions require that the membranes of the interacting cells are in close contact, and, therefore, it could be easy to overestimate the number of cells interacting locally if a large distance threshold is used. On the other hand, paracrine crosstalk within the islet might involve interactions between more distant cells, which could be also wrongly implemented if an incorrect threshold is selected. Recently, an optimization algorithm was proposed to reconstruct three-dimensional islets composed of non-overlapping ɑ, β and δ spherical cells with varying sizes assigned randomly in accordance with the capacitance distributions obtained via electrophysiological experiments.78–80 Along with the mechanisms considered in the multicellular model at the single-cell level, the geometrical configuration of the multicellular model, and therefore its connectivity, is a key aspect with important functional implications.
Applications of multicellular models of pancreatic cells
Role of noise and heterogeneity in the electrical activity of coupled β-cells
The origin of mathematical models of clusters of β-cells is closely related to the need for a plausible explanation of the experimental observations of the heterogeneous electrical behavior of isolated β-cells and β-cells in intact islets; that is, irregular spiking or bursting in single β-cells,81 and robust synchronized bursting in intact islets.29,51 The main goal of early models of clusters of β-cells was to elucidate whether bursting is produced intrinsically at the cellular level or is a property emerging as a result of cell coupling, a hypothesis based on the simultaneous measurement of both the electrical activity21,29 and intracellular Ca2+ of neighbor cells,82–85 which showed an apparent perfect synchronization.
One of the main hypotheses proposed to explain these observations was the channel sharing hypothesis, originally proposed by Atwater et al.,86 postulating that the stochastic gating of “shared” ionic channels due to cell-to-cell coupling via gap-junctions, prevents single β-cells from bursting, which can be recovered when cells are electrically coupled87–89 (see Figure 3a). Representative models of the channel sharing hypothesis are those proposed by Sherman et al.88 and Chay and Kang,87 who considered the stochastic nature of the gating of the ionic channels as the source of the irregular and noisy electrical activity observed in isolated β-cells, which was gradually counteracted as the number of electrically coupled cells increased, thus leading to an organized bursting activity throughout the islet. In Figure 3a, simulations of the electrical activity of single and clusters of increasing number of cells are shown. When the number of cells in the cluster increases, and therefore the number of shared channels, robust bursting is observed (top panel of Figure 3A), which contrasts with the electrical behavior observed in isolated cells and small clusters (middle and lower panels in Figure 3a). The main assumption of these models, that is, an infinite gap-junction conductance (or zero resistance), produced that the whole ensemble of cells behaves as a single cell with a higher number of channels (hence these models received the name of “supercell” models). Models by Carroll and Sherman et al.90,91 modified the previous supercell model by Sherman et al.88 to introduce a finite coupling conductance based on the experimental observations by Pérez-Armendariz et al.92 in isolated pairs of β-cells from mice. The updated multicellular model90 showed that only moderate coupling (not infinite as suggested by the previous models) was required to synchronize the bursts of action potentials. Other models considered different sources of noise and stochasticity. For instance, Kang et al.93 and Jo et al.94 modified Eq. 2 by adding a random (additive) noise term to represent the effect of thermal fluctuations on membrane voltage; that is:
| (6) |
Figure 3.
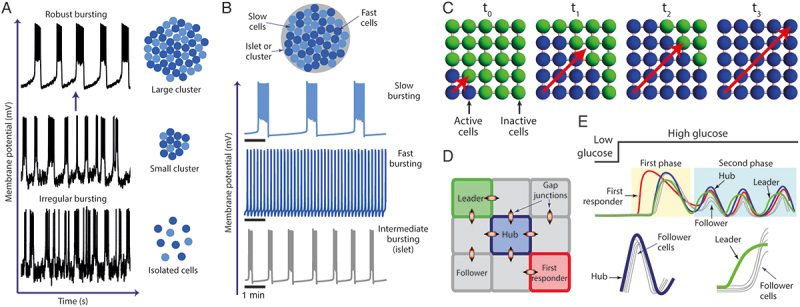
A. According to the channel sharing and heterogeneity hypothesis, robust bursting observed in β-cells of intact islets (top panel) is a result of coupling of a large number of cells, while in small clusters (middle panel) and isolated cells (bottom panel), irregular bursting is regularly observed. B. A simulated islet composed of heterogeneous β-cells (i.e., slow and fast bursting cells) show intermediate bursting as a result of cell coupling. C. The origin and propagation of waves in clusters of β-cells has been an aspect extensively studied using computational models. D. Multicellular models have been used to evaluate the existence and role of hubs, leader and first responder β-cells. E. Following a glucose challenge, first responder cells participate during the first phase of oscillations while hub and leader cells are thought to be relevant during the second phase.
where is the noise term randomly added at each time step of the simulation. As an alternative, they also explored adding a voltage-dependent (multiplicative) noise term to Eq. 2 to simulate channel gating stochasticity:
| (7) |
where represents, for instance, the randomly varying conductance of the open channels and is the driving force of the stochastic current depending on the membrane voltage of cell i ( and the reversal potential () of the permeating ion. Another example of stochasticity in ionic channels is the model by Meyer-Hermann and Benninger,95 who included, in addition to stochastic variations in the gap-junction currents, stochasticity in the expression of ATP-dependent K+ channels (KATP) aiming to explain the origin of active and inactive regions observed experimentally by Rocheleau et al.96 in an islet subject to a glucose gradient.
The heterogeneity hypothesis, on the other hand, postulates that a population of electrically coupled β-cells, with heterogeneous properties such as ionic channel conductance (or channel density), membrane capacitance (cell size), gap-junction conductance, metabolism, etc., is capable of producing robust bursting in spite of the variety of electrical behaviors produced individually (i.e., continuous spiking, bursting with different periodicities, etc.). In contrast to the channel sharing hypothesis, based on the inclusion of stochastic terms in the models, heterogeneity is achieved by assigning different values to certain model parameters to generate different electrical behaviors among the simulated cells (e.g., fast or slow bursting) without the need of stochastic terms. A representative example of this hypothesis is the model by Zimliki et al.97 who used the phantom burster model of the pancreatic β-cell proposed by Bertram et al.,98,99 which is based on the idea that the heterogeneous periodicity of the electrical behavior of β-cells is a result of the interaction of slow and fast oscillatory variables, as shown schematically in Figure 3b. Following this proposal, Zimliki et al.97 simulated heterogeneous clusters of cells composed of fast and slow β-cells with the main objective of explaining why β-cells in intact islets generally show bursting with an intermediate period between 10 and 60 s, while isolated cells showed a wide range of bursting periods, from <10 s (fast) or >60 s (slow). From their simulations, they concluded that bursting of intermediate periodicity could be obtained if islets are composed either by all fast or slow cells or by a combination of the two.
An alternative hypothesis explored by early models of clusters of β-cells was based on the experiments performed by Pérez-Armendariz et al.,100,101 who proposed a role for the intercellular K+ concentration in the synchronization of bursting among islet cells via depolarization of adjacent cells due to the efflux of K+ from neighbor cells in conjunction with a “long distance” effect caused by the diffusion of K+ throughout the intercellular space. This hypothesis was explored theoretically by Stokes and Rinzel102 in an islet model composed of concentric shells of uncoupled β-cells surrounded by non-β-cells, thus resembling the organization of rodent islets. A model of K+ diffusion was also incorporated into their model to calculate the local K+ concentrations affecting the K+ currents through the effect on the K+ reversal potential. As a result, in spite of the lack of direct electrical communication between adjacent β-cells (i.e. gap-junctions), their simulations showed that β-cells could synchronize by the solely effect of K+ accumulation and diffusion in the intercellular space, as proposed by Pérez-Armendariz et al.100,101 although this mechanism alone was not capable of reproducing experiments in which current injection in one cell produced a corresponding voltage change in an impaled adjacent cell.29,48 The authors concluded that both coupling through gap junctions as well as diffusion of ions in the intercellular space could be participating in the synchronized response of islet cells. Additional theoretical support to this hypothesis was provided by Rinzel et al.103 An interesting result obtained by Stokes and Rinzel102 when heterogeneity was considered in their model, is the idea of groups of β-cells leading the electrical behavior of the islet, which can be related to recent observations suggesting the existence of a subpopulation of leader β-cells41,104 (see Section Hubs, leaders and first responders below).
Since the first experimental reports of cellular heterogeneity in pancreatic islets published at the time by D. Pipeleers,105 it has been an aspect included in practically all the multicellular models developed throughout the years. In contrast, noise (in any of its forms) and concentration gradients have not been widely considered, although early models have shown the possibility that both mechanisms could partially dictate the behavior of islet cells as members of interacting cell populations.
Wave propagation
Simultaneous recordings of the electrical activity of neighbor β-cells in intact islets showed that the electrical signals of both cells were similar both in shape and periodicity, which led to believe that the connectivity between β-cells via gap-junctions would produce a perfect synchronized response of the islet β-cells.21,29 Similarly, the first experimental measurements of the oscillations of intracellular Ca2+ in rodent islets suggested that β-cells synchronized perfectly (probably due to the low time resolution of the recordings).82–84 Other groups, based on Ca2+ measurements and electrophysiological measurements, suggested the possibility of wave propagation throughout the islets85,106,107 as a synchronizing mechanism in response to glucose stimulation (described schematically in Figure 3c). For instance, Palti et al.85 concluded, based on external measurements of the electrical signal produced by intact islets, that waves were originated from pacemaker cells with special properties such as high excitability and/or high firing frequency. On the other hand, Bertuzzi et al.,106,107 using fluorescence techniques to measure the changes in cytosolic Ca2+ in isolated islets from both mouse and pigs, found that the propagation of Ca2+ signals involved both electrical communication and extracellular mechanisms such as the diffusion of molecules throughout the intercellular space, conclusion reached after observing that Ca2+ waves elicited by a mechanical stimulus rely on functional gap-junctions, while waves produced by glucose stimulation propagate independently of gap-junction communication, as indicated by the minor effect of a specific inhibitor of gap-junctions (AGA, ɑ-glycyrrhetinic acid) on the propagation of the oscillatory Ca2+ signals, as well as the fact that depletion of extracellular Ca2+ produced the blockade of the Ca2+ oscillations.106
Following these experimental observations, theoretical models were developed to elucidate how the connectivity and properties of the coupled β-cells could be related to both the origin and propagation of electrical and Ca2+ waves. The first model to investigate wave propagation was proposed by Aslanidi et al.,65 who demonstrated that Ca2+ oscillations are mostly asynchronous, thus appearing as periodic propagating waves. Their simulations of a linear cluster of β-cells supported the hypothesis postulating that the Ca2+ waves observed experimentally are produced by the propagation of electric impulses through the cluster of electrically coupled cells. From the modeling perspective, the authors proposed the continuous approximation of the propagation of Ca2+ waves described before (Eq. 5), later adopted by Pedersen67 to model 1D and 2D clusters of β-cells to show that the wave propagation speed decreases as the heterogeneity of the coupling conductance increases. In a later work, Aslanidi et al.66 reformulated their continuous model using spherical coordinates and complemented it with a diffusion model to account for the extracellular distribution of glucose, as proposed previously by a model by Bertram and Pernarowski108 based on the experiments of Bennett et al.109 who measured the metabolic activity (i.e. NAD(P)H) elicited by the penetration of glucose into an intact islet. Their results indicated that extracellular glucose gradients could initiate the Ca2+ waves observed experimentally; that is, waves initiated at the periphery, then spreading throughout the islet as a result of the diffusion of glucose into the islet.
Experiments by Rocheleau et al.96 showed that Ca2+ waves elicited by a glucose gradient in mice islets, propagated only through islet regions where the glucose concentration was above the activation threshold and was halted in regions below that threshold. In contrast to the proposal of pacemaker cells initiating the propagation of waves, their results led them to hypothesize that Ca2+ waves were propagated as a result of the strength of coupling and the activity of KATP channels. Based on these experiments, Pedersen and Sørensen68 showed, using both discrete and continuous models, that this phenomena could be in fact produced by the spatial variation of the ATP-dependent K+ channels, as hypothesized by Rocheleau et al.96 In a different model, Meyer-Hermann and Benninger95 proposed that a stochastic variation of gap-junction currents and the expression of KATP channels could be behind the observations by Rocheleau et al.96
In a detailed study involving both experiments and computational modeling, Benninger et al.31 measured the velocity of the Ca2+ waves in mouse islets and evaluated the effects of reducing the electrical coupling between β-cells. They found that chemical blocking of gap-junctions slowed the propagation of the Ca2+ waves, and that gap-junction knockout completely disrupted both the propagation of Ca2+ waves, as well as the synchronization of Ca2+ oscillations. They reproduced these experimental observations using a computational model of a cubic cluster of heterogeneous β-cells, concluding that cellular heterogeneity is sufficient to produce propagating Ca2+ waves. In a follow-up study by the same group,55 they demonstrated experimentally that in an islet subject to a glucose gradient, waves originate in regions where cells are highly excitable in comparison with the average excitability of the islet β-cells, being the direction of propagation determined by the intrinsic heterogeneity of the islet β-cells, while the extent of propagation across the islet is regulated by the glucose-dependent gap junction coupling. The authors concluded that including the electrochemical gradients in the junctional currents (as in Eq. 3) was needed to reproduce the experimental observations. From these results, it was suggested that islets could have a pacemaker region randomly determined by the location of highly excitable cells, although they did not discard a possible role for islet development in the distribution of the pacemaker region.
A different approach based on network theory was adopted by Stozer et al.110 to analyze the functional connectivity of β-cells in slices of mouse islets based on the correlation between Ca2+ signals recorded experimentally at different locations of the islet slices. They found that functional networks with small-world properties (i.e. high local coupling with shortcuts to distant cells) were formed (see the works by Stozer et al. and Markovic et al.110–112 for details). Since the mechanism of communication between distant regions of the islets is still unknown, following these observations, Cappon and Pedersen113 developed a three-dimensional model aiming to elucidate how the functional networks observed experimentally could be formed in pancreatic islets. Their simulations showed that the small-world networks in pancreatic islets are not necessarily produced as a result of a long-range mechanism or signal communicating distant cells, but they can arise as a result of heterogeneity and wave propagation throughout the islet via gap-junction coupling, without discarding a potential contribution of intra-islet neurons or paracrine signals.
Given the importance of wave propagation as a reflection of the structural and functional properties of the islets, it is key to understand how they originate and propagate in order to determine their functional implications. What is clear is that gap-junction coupling, excitability, expression of KATP channels and intercellular gradients of glucose or other molecules are likely to have a relevant role in the origin and propagation of waves throughout the islets. Pacemaker cells, on the other hand, although still controversial, could participate to some extent, aspect that has also been explored using multicellular models, as described in the next section.
Hubs, leaders and first responders
Throughout the years, different functional subpopulations of β-cells have been identified and characterized by the prolific combination of experiments and computational modeling (Figure 3d, e). Johnston et al.41 proposed, based on experimental observations, that highly functionally connected β-cells, called hub cells (see Figure 3e), a term firstly used in 2013 by Stozer et al.110 in the context of pancreatic islets, are required to maintain islet oscillations and are key for the coordinated islet response to high glucose and insulin release. According to this proposal, the highly connected hub cells are responsible for coordination of the Ca2+ activity of the beta cell network.41 Although the authors suggested that hub cells could have pacemaker properties, their firing activity, although preceding the activity of the follower cells, also outlasts it, which differs greatly from the typical pacemaker activity (e.g. cardiac pacemaker cells). Hub cells showed no preference regarding their location within the islets and were characterized by a particular metabolic signature (i.e., increased proton pumping in the mitochondria, ATP synthase activity and ATP generation) and a reduced number of insulin granules. On the other hand, Salem et al.114 identified a subpopulation of “leader cells” that currently are known to lead the oscillations during the second phase (see Figure 3e). Although at first, leader cells were thought to be similar to hub cells, as suggested by the high number of functional links, recent experimental studies115,116 have concluded that they constitute a different subpopulation of β-cells. In addition to hub and leader cells, Kravets et al.115 described a different sub-population of cells denoted as “first responders,” defined as those β-cells showing the fastest response to a glucose stimulus (see Figure 3e), likely to be characterized by a high membrane excitability and lower coupling with its neighbors, as suggested by simulations performed using a multicellular model. In contrast to hub and leader cells, which seem to be relevant for the regulation and coordination of the second phase of secretion, the so-called first responders seem to participate mainly during the first phase of secretion (Figure 3e). Recent studies have confirmed that hubs, leaders and first responders are in fact different subpopulations (see for instance refs.115,116), thus clarifying the functional organization of β-cells within the islets.
Hogan and Peercy117 implemented a multicellular model to evaluate the feasibility of the hypothesis postulating the existence of hub cells. While they were not able to reproduce the behavior and properties of hub and leader cells as described by Johnston et al.41 and Salem et al.,114 they found that certain cells, called switch cells, have the ability of switch off the islet activity when they are silenced. Dwulet et al.118 performed computational simulations using a multicellular model to test if small populations of β-cells could have a disproportionate control of the islet Ca2+ dynamics. According to their results, there was not a particular type of cell capable of exerting a disproportionate control of the islet Ca2+ via direct electrical coupling, which contradicted the hypothesis of hub cells acting as pacemakers. However, as the authors acknowledge, other mechanisms not considered in their model, such as paracrine signaling or the diffusion of intermediate metabolites through gap junctions, cannot be discarded and must be evaluated in future works.
Models of human islets have also been developed aiming to predict how hubs of β-cells could delineate the global islet activity while considering the important differences between rodents and humans, both at the single-cell and islet levels. Loppini and Chiodo119 evaluated the effects of hub cells on the synchronization of human β-cells for the three electrical regimes observed experimentally; that is, action potential spiking and fast and slow bursting.14,120 Interestingly, their simulations indicated that for the spiking and fast bursting regimes, the presence of hub cells could have a negative effect on the cells’ synchronization. In contrast, for the slow bursting regime, the presence of hub cells enhanced the synchronization of coupled human β-cells. A different model by Lei et al.104 predicted that the coordinated oscillatory response both in human and mouse islets can be dictated by hub cells, although according to their simulations, human islets could be more susceptible to the inhibition of hubs than mouse islets.
In a recent review, Peercy and Sherman121 discussed the experimental and theoretical evidence for the existence of hubs of β-cells acting as pacemakers. Although they agree that some β-cells may have a disproportionate influence on the islet behavior, according to their view, the available evidence does not support the existence of pacemaker cells. Other voices (i.e. Korosak et al.122 have proposed a reconciled scheme in which hubs of β-cells are generated not by differences in the cellular mechanisms in some “special” β-cells, but as a result of intercellular communication. According to this proposal, if a hub fails at some point, other cells will take over as a new commanding hub as long as communication between β-cells remains possible. Simulations performed by Scialla and Loppini123 supported this proposal by predicting that cells that are not hubs can turn into hubs and vice versa in response to changing stimuli.
Undoubtedly, multicellular models have been useful to identify the characteristics of these subpopulations of β-cells, as well as to evaluate how these subpopulations would influence the islet response, both in humans and rodents. Despite this, further work, both theoretical and experimental, is necessary to detail the mechanisms of action of these populations on the islet function.
Functional implications of the islet architecture
While previous models had focused mainly on synchronization, noise, cellular heterogeneity, wave propagation and hub cells, Nittala et al.76 focused on investigating the functional implications of cytoarchitecture (i.e. number of β -cells, connectivity and coupling strength), a relevant aspect not considered in detail in previous models. They proposed the HCP geometry for models of pancreatic islets and evaluated how the cytoarchitecture influenced the fraction of bursting β-cells, the bursting period, plateau fraction and synchronization, as well as the amplitude of intracellular Ca2+ oscillations. In a latter work, the same group,124 based on extensive simulations, proposed a cytoarchitectural integrity descriptor denominated cluster coupling index as a measure of morphological and structural integrity of the islet.
Hraha et al.59 studied the role of cytoarchitecture and coupling in the islet function by forming 2D and 3D aggregates of MIN6 β-cells to determine the effect of dimensionality (2D or 3D) and size on the synchronization of excitability. They showed that in 3D aggregates at high glucose, a greater proportion of cells synchronizes, and that the velocity of Ca2+ waves is greater in comparison to the 2D aggregates. Interestingly, 2D aggregates showed spontaneous Ca2+ transients at low glucose, which were not observed in the 3D aggregates, although large 2D aggregates also showed a quiescent behavior at low glucose. The authors then used a probabilistic model based on percolation theory (previously used by Benninger et al.)31 to explain these observations. In a later work,60 they evaluated the capacity of a network of coupled β-cells to generate a robust response when there is a subpopulation of non-excitable cells. Their simulations indicated that there could be an excitability threshold where there is a rapid transition between the active and inactive state of the islet, determined by the proportions of excitable and non-excitable cells with a relevant role of gap-junction coupling. These models highlighted the importance of cytoarchitecture for the functionality of clusters of β-cells, an important aspect that must be considered in future models of pancreatic islets.
Models of paracrine signaling
From all the multicellular models developed so far, only the dynamical model by Briant et al.8 has considered the electrical communication between neighbor β-cells and β and δ-cells, as well as the paracrine interactions between δ and ɑ-cells (see Figure 4a) in a multicellular model in which actual architectures of human islets were used to determine the structural and connectivity properties of the islets. With their model, Briant et al.8 investigated how activation of δ-cells by electrically coupled β-cells could mediate the inhibition of glucagon secretion. In addition to an electrical model mathematically described by Eq. 2, the authors included minimal secretion models to estimate the concentration of glucagon, insulin and somatostatin. The concentration of somatostatin was then used to regulate the activity of ɑ-cells via a somatostatin-dependent ionic current, as depicted in Figure 4a. Previously, Watts et al.125 had used a similar approach in a model of the paracrine interactions between islet cells where only one cell of each type (ɑ, β and δ) represented the average behavior of the corresponding populations. In contrast to the multicellular model by Briant et al.,8 the model by Watts125 included paracrine interactions between the three types of cells, as described graphically in Figure 4b.
A different approach to simulate the paracrine interactions between ɑ, β and δ-cells in real islet architectures was adopted by Hoang et al.62 in a model of coupled oscillators, mathematically and graphically described by Eq. 4 and Figure 4c, respectively. In this model, each cell is represented by an oscillating function with an intrinsic frequency and phase (ω and θ in Eq. 4 and Figure 4c), depending on the type of cell (ɑ, β and δ) where paracrine signals are described by positive and negative interaction terms of variable strength (parameter K in Eq. 4 and Figure 4c). As a result, depending on the value and sign of the corresponding interaction term and the phase difference between the interacting cells, oscillation phases are affected between neighbor cells following Eq. 4. In spite of the oversimplified representation of the physiological mechanisms involved, the model of coupled oscillators by Hoang et al.62 was useful to evaluate how synchronization of hormone pulses can be controlled at different glucose regimens.
Including paracrine signaling in multicellular models of pancreatic islets, in addition to electrical coupling, is crucial to capture the complexity of the regulatory mechanisms involved in the control of blood glucose. However, building such a complete model is still challenging. Despite this, recent models including paracrine and electrical communication have laid the foundations for the development of increasingly realistic models.
Discussion
As described throughout this article, multicellular models of pancreatic islets are composed of a myriad of elements at different levels of organization. Firstly, a mathematical representation of the physiological behavior at the cellular level must be adopted, which implies selecting 1) a model for each type of cell considered in the model and 2) a modeling strategy (i.e., dynamical, continuous, probabilistic or oscillators). Secondly, a geometrical representation of the model must be selected, including its dimensionality (1, 2 or 3 dimensions) and configuration; that is, open or closed ended for 1-D, cubic, hexagonal (for 2 or 3-D), sphere-packed or reconstructed realistic architecture (3D). Implicitly, this determines the connectivity of the model, of great importance for the global behavior of the cluster or islet model. Thirdly, the communication pathways to be included in the model must be selected; that is, electrical and/or paracrine signaling. Once the components of the model have been determined, researchers can determine if a pathological scenario will be simulated, either by inducing alterations at the cellular level (e.g., ionic channels, metabolism, secretion), at the communication mechanisms such as gap-junctions or paracrine signaling or at the architecture level (e.g., loss of β-cell mass).
By definition, a model is a representation of a real system with a certain degree of approximation. As such, models have limitations that extend from its constituents. In this case, approximations are made practically at every stage of the process described above. For instance, different models of the β-cells have been proposed in the last decades, each based on a different physiological hypothesis (reviewed extensively in 46–48). Then, when a particular β-cell model is selected as the building block of a multicellular model, the simulation results are delineated by the cellular mechanisms included and the underlying physiological hypothesis. In addition, although important advances have been achieved, there are still open questions about the physiology of the ɑ, β and δ-cells. On the other hand, the selection of the geometrical representation greatly determines the connectivity of the model that could be either under or overestimated. Moreover, if paracrine signals are not included in the multicellular model, as in most of the models described in this review, the simulated scenarios will not reflect the physiological behavior of the islet. In fact, even considering the paracrine interactions, models of islets proposed so far lack a representation of relevant aspects such as the islet vasculature, hormone diffusion through the intercellular space, the irregular shape of δ-cells that, according to some reports, show long neurite-like processes which can greatly influence the connectivity of the islet cells.3
Despite these limitations, in our view, models of pancreatic islets, as challenging as they are, along with all the advanced experimental techniques available to date, will keep contributing greatly to gain a better understanding about how all the cellular mechanisms involved in the regulation of glucose interact at the islet level and importantly, to predict how this coordinated behavior would be affected by functional and structural alterations.
Supplementary Material
Acknowledgments
GJFM thanks CONACYT (Consejo Nacional de Ciencia y Tecnología, México) for the support given to this project (CVU 302514, Proyecto 829 del Programa “Investigadoras e Investigadores por México”). GJFM and JRGF thanks the Division of Basic Sciences and the Department of Electrical Engineering for the support given to this work.
Funding Statement
The author(s) reported that there is no funding associated with the work featured in this article.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Supplementary material
Supplemental data for this article can be accessed online at https://doi.org/10.1080/19382014.2023.2231609
References
- 1.Liao EP, Brass B, Abelev Z, Poretsky L.. Endocrine Pancreas. In: Poretsky L, editor. Principles of diabetes mellitus. Cham, Switzerland: Springer International Publishing; 2017. pp. 23–20. doi: 10.1007/978-3-319-18741-9_3. [DOI] [Google Scholar]
- 2.Rorsman P, Ashcroft FM.. Pancreatic β-Cell electrical activity and insulin secretion: of mice and men. Physiol Rev. 2018;98(1):117–214. doi: 10.1152/physrev.00008.2017. PMID:22974438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rorsman P, Huising MO. The somatostatin-secreting pancreatic δ-cell in health and disease. Nat Rev Endocrinol. 2018;14(7):404–414. doi: 10.1038/s41574-018-0020-6. PMID:29773871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gromada J, Chabosseau P, Rutter GA. The α-cell in diabetes mellitus. Nat Rev Endocrinol. 2018;14(12):694–704. doi: 10.1038/s41574-018-0097-y. PMID:30310153. [DOI] [PubMed] [Google Scholar]
- 5.Noguchi GM, Huising MO. Integrating the inputs that shape pancreatic islet hormone release. Nat Metab. 2019;1(12):1189–1201. doi: 10.1038/s42255-019-0148-2. PMID: 32694675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Caicedo A. Paracrine and autocrine interactions in the human islet: more than meets the eye. Semin Cell Dev Biol. 2013;24(1):11–21. doi: 10.1016/j.semcdb.2012.09.007. PMID:23022232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Benninger RKP, Head WS, Zhang M, Satin LS, Piston DW. Gap junctions and other mechanisms of cell–cell communication regulate basal insulin secretion in the pancreatic islet. J Physiol. 2011;589(22):5453–5466. doi: 10.1113/jphysiol.2011.218909. PMID: 21930600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Briant LJB, Reinbothe TM, Spiliotis I, Miranda C, Rodriguez B, Rorsman P. δ-cells and β-cells are electrically coupled and regulate α-cell activity via somatostatin. J Physiol. 2018;596(2):197–215. doi: 10.1113/JP274581. PMID: 28975620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Miranda C, Begum M, Vergari E, Briant LJB. Gap junction coupling and islet delta-cell function in health and disease. Peptides. 2022;147:170704. doi: 10.1016/j.peptides.2021.170704. PMID: 34826505. [DOI] [PubMed] [Google Scholar]
- 10.Dean PM, Matthews EK. Electrical activity in pancreatic islet cells. Nature. 1968;219:389–390. doi: 10.1038/219389a05152. PMID: 4873864. [DOI] [PubMed] [Google Scholar]
- 11.Dean P, Matthews E. Glucose-induced electrical activity in pancreatic islet cells. J Physiol1970. 1970;210(2):255–264. doi: 10.1113/jphysiol.1970.sp009207. PMID: 5501259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dean P, Matthews E. Electrical activity in pancreatic islet cells: effect of ions. J Physiol. 1970;210(2):265–275. doi: 10.1113/jphysiol.1970.sp009208. PMID: 5501260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sakmann B, Neher E. Patch clamp techniques for studying ionic channels in excitable membranes. Annu Rev Physiol. 1984;46:455–472. doi: 10.1146/annurev.ph.46.030184.002323. PMID: 6143532. [DOI] [PubMed] [Google Scholar]
- 14.Braun M, Ramracheya R, Bengtsson M, Zhang Q, Karanauskaite J, Partridge C, Johnson PR, Rorsman P. Voltage-gated ion channels in human pancreatic β-cells: electrophysiological characterization and role in insulin secretion. Diabetes. 2008;57(6):1618–1628. doi: 10.2337/db07-0991. PMID: 18390794. [DOI] [PubMed] [Google Scholar]
- 15.Braun M, Ramracheya R, Amisten S, Bengtsson M, Moritoh Y, Zhang Q, Johnson PR, Rorsman P. Somatostatin release, electrical activity, membrane currents and exocytosis in human pancreatic delta cells. Diabetologia. 2009;52(8):1566–1578. doi: 10.1007/s00125-009-1382-z. PMID: 19440689. [DOI] [PubMed] [Google Scholar]
- 16.Ramracheya R, Ward C, Shigeto M, Walker JN, Amisten S, Zhang Q, Johnson PR, Rorsman P, Braun M. Membrane potential-dependent inactivation of voltage-gated ion channels in α-cells inhibits glucagon secretion from human islets. Diabetes. 2010;59(9):2198–2208. doi: 10.2337/db09-1505. PMID: 20547976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ashcroft FM, Kakei M, Kelly RP, Sutton R. ATP-sensitive K+ channels in human isolated pancreatic B-cells. FEBS Lett. 1987;215(1):9–12. doi: 10.1016/0014-5793(87)80103-5. PMID: 2436949. [DOI] [PubMed] [Google Scholar]
- 18.Ashcroft FM, Rorsman P. Electrophysiology of the pancreatic β-cell. Prog Biophys Mol Biol. 1989;54(2):87–143. doi: 10.1016/0079-6107(89)90013-8. PMID: 2484976. [DOI] [PubMed] [Google Scholar]
- 19.Smith PA, Ashcroft FM, Rorsman P. Simultaneous recordings of glucose dependent electrical activity and ATP-regulated K+-currents in isolated mouse pancreatic β-cells. FEBS Lett. 1990;261(1):187–190. doi: 10.1016/0014-5793(90)80667-8. PMID: 2407553. [DOI] [PubMed] [Google Scholar]
- 20.Valdeolmillos M, Santos RM, Contreras D, Soria B, Rosario LM. Glucose-induced oscillations of intracellular Ca2+ concentration resembling bursting electrical activity in single mouse islets of Langerhans. FEBS Lett. 1989;259(1):19–23. doi: 10.1016/0014-5793(89)81484-x. PMID:2689228. [DOI] [PubMed] [Google Scholar]
- 21.Santos RM, Rosario LM, Nadal A, Garcia-Sancho J, Soria B, Valdeolmillos M. Widespread synchronous [Ca2+]i oscillations due to bursting electrical activity in single pancreatic islets. Pflugers Arch. 1991;418(4):417–422. doi: 10.1007/BF00550880. PMID:1876486. [DOI] [PubMed] [Google Scholar]
- 22.Tarasov AI, Semplici F, Ravier MA, Bellomo EA, Pullen TJ, Gilon P, Sekler I, Rizzuto R, Rutter GA, Saks V. The mitochondrial Ca2+ uniporter MCU is essential for glucose-induced ATP increases in pancreatic β-cells. PLoS One. 2012;7(7):e39722. doi: 10.1371/journal.pone.0039722. PMID:22829870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wiederkehr A, Szanda G, Akhmedov D, Mataki C, Heizmann CW, Schoonjans K, Pozzan T, Spät A, Wollheim CB. Mitochondrial matrix calcium is an activating signal for hormone secretion. Cell Metab. 2011;13(5):601–611. doi: 10.1016/j.cmet.2011.03.015. PMID:21531342. [DOI] [PubMed] [Google Scholar]
- 24.Li J, Shuai HY, Gylfe E, Tengholm A. Oscillations of sub-membrane ATP in glucose-stimulated beta cells depend on negative feedback from Ca2+. Diabetologia. 2013;56(7):1577–1586. doi: 10.1007/s00125-013-2894-0. PMID:23536115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Krippeit-Drews P, Düfer M, Drews G. Parallel oscillations of intracellular calcium activity and mitochondrial membrane potential in mouse pancreatic B-cells. Biochem Biophys Res Commun. 2000;267(1):179–183. doi: 10.1006/bbrc.1999.1921. PMID:10623595. [DOI] [PubMed] [Google Scholar]
- 26.Ohara-Imaizumi M, Fujiwara T, Nakamichi Y, Okamura T, Akimoto Y, Kawai J, Matsushima S, Kawakami H, Watanabe T, Akagawa K, et al. Imaging analysis reveals mechanistic differences between first- and second-phase insulin exocytosis. J Cell Biol. 2007;177(4):695–705. doi: 10.1083/jcb.200608132. PMID:17502420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hanna ST, Pigeau GM, Galvanovskis J, Clark A, Rorsman P, MacDonald PE. Kiss-and-run exocytosis and fusion pores of secretory vesicles in human β-cells. Pflugers Arch - Eur J Physiol. 2009;457(6):1343–1350. doi: 10.1007/s00424-008-0588-0. PMID:18795319. [DOI] [PubMed] [Google Scholar]
- 28.Lam AD, Ismail S, Wu R, Yizhar O, Passmore DR, Ernst SA, Stuenkel EL. Mapping dynamic protein interactions to insulin secretory granule behavior with TIRF-FRET. Biophys J. 2010;99(4):1311–1320. doi: 10.1016/j.bpj.2010.06.014. PMID:20713017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Eddlestone GT, Gonçalves A, Bangham JA, Rojas E. Electrical coupling between cells in islets of Langerhans from mouse. J Membr Biol. 1984;77(1):1–14. doi: 10.1007/BF01871095. PMID:6321740. [DOI] [PubMed] [Google Scholar]
- 30.Meissner HP. Electrophysiological evidence for coupling between β cells of pancreatic islets. Nature. 1976;262(5568):502–504. doi: 10.1038/262502a0. PMID:785280. [DOI] [PubMed] [Google Scholar]
- 31.Benninger RKP, Zhang M, Head WS, Satin LS, Piston DW. Gap junction coupling and calcium waves in the pancreatic islet. Biophys J. 2008;95(11):5048–5061. doi: 10.1529/biophysj.108.140863. PMID:18805925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ravier MA, Güldenagel M, Charollais A, Gjinovci A, Caille D, Söhl G, Wollheim CB, Willecke K, Henquin J-C, Meda P. Loss of connexin36 channels alters beta-cell coupling, islet synchronization of glucose-induced Ca2+ and insulin oscillations, and basal insulin release. Diabetes. 2005;54(6):1798–1807. doi: 10.2337/diabetes.54.6.1798. PMID:15919803. [DOI] [PubMed] [Google Scholar]
- 33.Ravier MA, Rutter GA. Glucose or insulin, but not zinc ions, inhibit glucagon secretion from mouse pancreatic α-Cells. Diabetes. 2005;54(6):1789–1797. doi: 10.2337/diabetes.54.6.1789. PMID:15919801. [DOI] [PubMed] [Google Scholar]
- 34.Vergari E, Knudsen JG, Ramracheya R, Salehi A, Zhang Q, Adam J, Asterholm IW, Benrick A, Briant LJB, Chibalina MV, et al. Insulin inhibits glucagon release by SGLT2-induced stimulation of somatostatin secretion. Nat Comms. 2019;10(1):139. doi: 10.1038/s41467-018-08193-8. PMID:30635569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cabrera O, Ficorilli J, Shaw J, Echeverri F, Schwede F, Chepurny OG, Leech CA, Holz GG. Intra-islet glucagon confers β-cell glucose competence for first-phase insulin secretion and favors GLP-1R stimulation by exogenous glucagon. J Biol Chem. 2022;298(2):101484. doi: 10.1016/j.jbc.2021.101484. PMID:34896391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cejvan K, Coy DH, Efendic S. Intra-islet somatostatin regulates glucagon release via type 2 somatostatin receptors in rats. Diabetes. 2003;52(5):1176–1181. doi: 10.2337/diabetes.52.5.1176. PMID:12716749. [DOI] [PubMed] [Google Scholar]
- 37.Hauge-Evans AC, King AJ, Carmignac D, Richardson CC, Robinson ICAF, Low MJ, Christie MR, Persaud SJ, Jones PM. Somatostatin secreted by islet δ-cells fulfills multiple roles as a paracrine regulator of islet function. Diabetes. 2009;58(2):403–411. doi: 10.2337/db08-0792. PMID:18984743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hauge-Evans AC, Anderson RL, Persaud SJ, Jones PM. Delta cell secretory responses to insulin secretagogues are not mediated indirectly by insulin. Diabetologia. 2012;55(7):1995–2004. doi: 10.1007/s00125-012-2546-9. PMID:22526610. [DOI] [PubMed] [Google Scholar]
- 39.Svendsen B, Holst JJ. Paracrine regulation of somatostatin secretion by insulin and glucagon in mouse pancreatic islets. Diabetologia. 2020;64(1):142–151. doi: 10.1007/s00125-020-05288-0. PMID:33043402. [DOI] [PubMed] [Google Scholar]
- 40.Kellard JA, Rorsman NJG, Hill TG, Armour SL, van de Bunt M, Rorsman P, Knudsen JG, Briant LJB. Reduced somatostatin signalling leads to hypersecretion of glucagon in mice fed a high-fat diet. Mol Metab. 2020;40:101021. doi: 10.1016/j.molmet.2020.101021. PMID:32446876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Johnston NR, Mitchell RK, Haythorne E, Pessoa MP, Semplici F, Ferrer J, Piemonti L, Marchetti P, Bugliani M, Bosco D, et al. Beta cell hubs dictate pancreatic islet responses to glucose. Cell Metab. 2016;24(3):389–401. doi: 10.1016/j.cmet.2016.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Camunas-Soler J, Dai X-Q, Hang Y, Bautista A, Lyon J, Suzuki K, Kim SK, Quake SR, MacDonald PE. Patch-seq links single-cell transcriptomes to human islet dysfunction in diabetes. Cell Metab. 2020;31(5):1017–1031.e4. doi: 10.1016/j.cmet.2020.04.005. PMID:32302527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dai X-Q, Camunas-Soler J, Briant LJB, dos Santos T, Spigelman A F, Walker E M, e Drigo, R A, Bautista A, Jones R C, Avrahami D, et al. Heterogenous impairment of α cell function in type 2 diabetes is linked to cell maturation state. Cell Metab. 2022;34(2):256–268.e5. doi: 10.1016/j.cmet.2021.12.021. PMID:35108513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Diderichsen PM, Göpel SO. Modelling the electrical activity of pancreatic α-cells based on experimental data from intact mouse islets. J Biol Phys. 2006;32(3–4):209–229. doi: 10.1007/s10867-006-9013-0. PMID:19669464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Watts M, Sherman A. Modeling the pancreatic α-cell: dual mechanisms of glucose suppression of glucagon secretion. Biophys J. 2014;106(3):741–751. doi: 10.1007/s10867-006-9013-0. PMID:19669464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Félix-Martinez GJ, Godínez-Fernández JR. Mathematical models of electrical activity of the pancreatic β-cell: a physiological review. Islets. 2014;6(3):e949195. doi: 10.4161/19382014.2014.949195. PMID:25322829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pedersen MG. Contributions of mathematical modeling of beta cells to the understanding of beta-cell oscillations and insulin secretion. J Of Diabetes Sci And Tech. 2009;3(1):12–20. doi: 10.1177/193229680900300103. PMID:20046647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sherman A. Contributions of modeling to understanding stimulus-secretion coupling in pancreatic beta-cells. Am J Physiol Endocrinol Metab. 1996;271(2):E362–72. doi: 10.1152/ajpendo.1996.271.2.E362. PMID:8770032. [DOI] [PubMed] [Google Scholar]
- 49.Félix‐Martínez GJ, González‐Vélez V, Godínez‐Fernández JR, Gil A. Electrophysiological models of the human pancreatic δ‐cell: from single channels to the firing of action potentials. Int J Numer Meth Biomed Eng. 2020;36(2):e3296. doi: 10.1002/cnm.3296. PMID:31833669. [DOI] [PubMed] [Google Scholar]
- 50.Orci L, Unger RH, Renold AE. Structural coupling between pancreatic islet cells. Experientia. 1973;29(8):1015–1018. doi: 10.1007/BF01930436. PMID: 4582082. [DOI] [PubMed] [Google Scholar]
- 51.Meda P, Orci L, Atwater I, Bangham A, Rojas E, Gonçalves A. The topography of electrical synchrony among beta-cells in the mouse islet of Langerhans. Q J Exp Physiol. 1984;69(4):716–735. doi: 10.1113/expphysiol.1984.sp002864. PMID:6440208. [DOI] [PubMed] [Google Scholar]
- 52.Chay TR, Keizer J. Minimal model for membrane oscillations in the pancreatic beta-cell. Biophys J. 1983;42(2):181–190. doi: 10.1016/S0006-3495(83)84384-7. PMID:6305437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bangham JA, Smith PA, Croghan PC. Modelling the β-cell electrical activity. In: Atwater I, Rojas ESoria B, editors. Biophysics of the Pancreatic β-Cell. Boston, MA: Springer US; 1986. pp. 265–278. doi: 10.1007/978-1-4684-5314-0_24. [DOI] [Google Scholar]
- 54.Kitagawa T, Murakami N, Nagano S. Modeling of the gap junction of pancreatic β-cells and the robustness of insulin secretion. Biophysics. 2010;6:37–51. doi: 10.2142/biophysics.6.37. PMID:27857584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Benninger RKP, Hutchens T, Head WS, McCaughey MJ, Zhang M, Le Marchand SJ, Satin LS, Piston DW. Intrinsic islet heterogeneity and gap junction coupling determine spatiotemporal Ca2+ wave dynamics. Biophys J. 2014;107(11):2723–2733. doi: 10.1016/j.bpj.2014.10.048. PMID:25468351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Tsaneva-Atanasova K, Zimliki CL, Bertram R, Sherman A. Diffusion of calcium and metabolites in pancreatic islets: killing oscillations with a pitchfork. Biophys J. 2006;90(10):3434–3446. doi: 10.1529/biophysj.105.078360. PMID:16500973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Loppini A, Braun M, Filippi S, Pedersen MG. Mathematical modeling of gap junction coupling and electrical activity in human β-cells. Phys Biol. 2015;12(6):066002. doi: 10.1088/1478-3975/12/6/066002. PMID:26403477. [DOI] [PubMed] [Google Scholar]
- 58.Saadati M, Jamali Y. The effects of beta-cell mass and function, intercellular coupling, and islet synchrony on ${\text {Ca}}^{2+}$ dynamics. Sci Rep. 2021;11(1):10268. doi: 10.1038/s41598-021-89333-x. PMID:33986325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hraha TH, Bernard AB, Nguyen LM, Anseth KS, Benninger RKP. Dimensionality and size scaling of coordinated Ca2+ dynamics in MIN6 β-cell clusters. Biophys J. 2014;106:299–309. doi: 10.1016/j.bpj.2013.11.026. PMID:24411262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hraha TH, Westacott MJ, Pozzoli M, Notary AM, McClatchey PM, Benninger RKP. Phase transitions in the multi-cellular regulatory behavior of pancreatic islet excitability. PLOS Comp Biol. 2014;10(9):e1003819. doi: 10.1371/journal.pcbi.1003819. PMID:25188228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Stamper IJ, Jackson E, Wang X. Phase transitions in pancreatic islet cellular networks and implications for type-1 diabetes. Phys Rev E. 2014;89(1):012719. doi: 10.1103/PhysRevE.89.012719. PMID:25580269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hoang D-T, Hara M, Jo J, von Herrath MG. Design principles of pancreatic islets: glucose-dependent coordination of hormone pulses. PLoS One. 2016;11(4):e0152446. doi: 10.1371/journal.pone.0152446. PMID:27035570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kuramoto Y. Self-entrainment of a population of coupled non-linear oscillators. In: Araki H, editor. International symposium on mathematical problems in theoretical physics. Berlin/Heidelberg: Springer-Verlag; 1975. pp. 420–422. doi: 10.1007/BFb0013365. [DOI] [Google Scholar]
- 64.Acebrón JA, Bonilla LL, Pérez Vicente CJ, Ritort F, Spigler R. The Kuramoto model: a simple paradigm for synchronization phenomena. Rev Mod Phys. 2005;77(1):137–185. doi: 10.1103/RevModPhys.77.137. [DOI] [Google Scholar]
- 65.Aslanidi OV, Mornev OA, Skyggebjerg O, Arkhammar P, Thastrup O, Sørensen MP, Christiansen PL, Conradsen K, Scott AC. Excitation wave propagation as a possible mechanism for signal transmission in pancreatic islets of Langerhans. Biophys J. 2001;80(3):1195–1209. doi: 10.1016/S0006-3495(01)76096-1. PMID:11222284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Aslanidi OV, Mornev OA, Vesterager M, Sørensen MP, Christiansen PL. A model for glucose-induced wave propagation in pancreatic islets of Langerhans. J Theor Biol. 2002;215(3):273–286. doi: 10.1006/jtbi.2001.2517. PMID:12054836. [DOI] [PubMed] [Google Scholar]
- 67.Pedersen MG. Homogenization of heterogeneously coupled bistable ODE’s—applied to excitation waves in pancreatic islets of Langerhans. J Biol Phys. 2004;30(3):285–303. doi: 10.1023/B:JOBP.0000046727.28337.f4. PMID:23345873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Pedersen MG, Sørensen MP. Wave-block due to a threshold gradient underlies limited coordination in pancreatic islets. J Biol Phys. 2008;34(3–4):425–432. doi: 10.1007/s10867-008-9069-0. PMID:19669486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sherman A. Anti-phase, asymmetric and aperiodic oscillations in excitable cells—I. coupled bursters. Bull Math Biol. 1994;56(5):811–835. doi: 10.1016/S0092-8240(05)80292-7. PMID:7920266. [DOI] [PubMed] [Google Scholar]
- 70.Pedersen MG, Bertram R, Sherman A. Intra-and inter-islet synchronization of metabolically driven insulin secretion. Biophys J. 2005;89(1):107–119. doi: 10.1529/biophysj.104.055681. PMID:15834002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ren H, Li Y, Han C, Yu Y, Shi B, Peng X, Zhang T, Wu S, Yang X, Kim S, et al. Pancreatic α and β cells are globally phase-locked. Nat Commun. 2022;13(1):3721. doi: 10.1038/s41467-022-31373-6. PMID:35764654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Loppini A, Pedersen MG, Braun M, Filippi S. Gap-junction coupling and ATP-sensitive potassium channels in human β -cell clusters: effects on emergent dynamics. Phys Rev E. 2017;96(3):032403. doi: 10.1103/PhysRevE.96.032403. PMID:29346932. [DOI] [PubMed] [Google Scholar]
- 73.Shahriari Z, Parastesh F, Jalili M, Berec V, Ma J, Jafari S. The role of coupling factors on the emergence of synchronization and chimera patterns in network of non-locally coupled pancreatic β-cells. EPL. 2019;125(6):60001. doi: 10.1209/0295-5075/125/60001. [DOI] [Google Scholar]
- 74.Giugliano M, Bove M, Grattarola M. Insulin release at the molecular level: metabolic-electrophysiological modeling of the pancreatic beta-cells. IEEE Trans Biomed Eng. 2000;47(5):611–623. doi: 10.1109/10.841333. PMID:10851805. [DOI] [PubMed] [Google Scholar]
- 75.Stožer A, Markovič R, Dolenšek J, Perc M, Marhl M, Slak Rupnik M, Gosak M. Heterogeneity and delayed activation as hallmarks of self-organization and criticality in excitable tissue. Front Physiol. 2019;10:869. doi: 10.3389/fphys.2019.00869. PMID:31333504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Nittala A, Ghosh S, Wang X. Investigating the role of islet cytoarchitecture in its oscillation using a new beta-cell cluster model. PLoS One. 2007;2(10):e983. doi: 10.1371/journal.pone.0000983. PMID:17912360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Montaseri G, Meyer-Hermann M. Diversity of coupled oscillators can enhance their synchronization. Phys Rev E. 2016;94(4):042213. doi: 10.1103/PhysRevE.94.042213. PMID:27841630. [DOI] [PubMed] [Google Scholar]
- 78.Félix-Martínez GJ, Mata AN, Godínez-Fernández JR. Reconstructing human pancreatic islet architectures using computational optimization. Islets. 2020;12(6):121–133. doi: 10.1080/19382014.2020.1823178. PMID:33090076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Félix-Martínez GJ, Nicolás-Mata A, Godínez-Fernández JR. Computational reconstruction of pancreatic islets as a tool for structural and functional analysis. J Vis Exp. 2022;181. doi: 10.3791/63351. PMID:35343963. [DOI] [PubMed] [Google Scholar]
- 80.Félix-Martínez GJ. IsletLab: an application to reconstruct and analyze islet architectures. Islets. 2022;14(1):36–39. doi: 10.1080/19382014.2021.2008742. PMID:34875977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Rorsman P, Trube G. Calcium and delayed potassium currents in mouse pancreatic beta-cells under voltage-clamp conditions. J Physiol. 1986;374:531–550. doi: 10.1113/jphysiol.1986.sp016096. PMID:2427706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bergsten P, Grapengiesser E, Gylfe E, Tengholm A, Hellman B. Synchronous oscillations of cytoplasmic Ca2+ and insulin release in glucose-stimulated pancreatic islets. J Biol Chem. 1994;269(12):8749–8753. doi: 10.1016/S0021-9258(17)37032-1. PMID:8132606. [DOI] [PubMed] [Google Scholar]
- 83.Henquin JC, Jonas JC, Gilon P. Functional significance of Ca2+ oscillations in pancreatic beta cells. Diabetes Metab. 1998;24(1):30–36. PMID:9534006. [PubMed] [Google Scholar]
- 84.Gilon P, Henquin JC. Distinct effects of glucose on the synchronous oscillations of insulin release and cytoplasmic Ca2+ concentration measured simultaneously in single mouse islets. Endocrinology. 1995;136(12):5725–5730. doi: 10.1210/endo.136.12.7588329. PMID:7588329. [DOI] [PubMed] [Google Scholar]
- 85.Palti Y, David GB, Lachov E, Mika YH, Omri G, Schatzberger R. Islets of Langerhans generate wavelike electric activity modulated by glucose concentration. Diabetes. 1996;45(5):595–601. doi: 10.2337/diab.45.5.595. PMID:8621009. [DOI] [PubMed] [Google Scholar]
- 86.Atwater I, Rosario L, Rojas E. Properties of the Ca-activated K+ channel in pancreatic β-cells. Cell Calcium. 1983;4:451–461. doi: 10.1016/0143-4160(83)90021-05-6. PMID:6323007. [DOI] [PubMed] [Google Scholar]
- 87.Chay TR, Kang HS. Role of single-channel stochastic noise on bursting clusters of pancreatic β-cells. Biophys J. 1988;54(3):427–435. doi: 10.1016/S0006-3495(88)82976-X. PMID:2850030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Sherman A, Rinzel J, Keizer J. Emergence of organized bursting in clusters of pancreatic β-cells by channel sharing. Biophys J. 1988;54(3):411–425. doi: 10.1016/S0006-3495(88)82975-8. PMID:2850029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.De Vries G, Sherman A. Channel sharing in pancreatic β-cells revisited: enhancement of emergent bursting by noise. J Theor Biol. 2000;207(4):513–530. doi: 10.1006/jtbi.2000.2193. PMID:11093836. [DOI] [PubMed] [Google Scholar]
- 90.Sherman A, Rinzel J. Model for synchronization of pancreatic beta-cells by gap junction coupling. Biophys J. 1991;59(3):547–559. doi: 10.1016/S0006-3495(91)82271-8. PMID:1646657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Carroll PB, Sherman A, Ferrer R, Boschero AC, Rinzel J, Atwater I. Modulation of the frequency of glucose-dependent bursts of electrical activity by HCO3/CO2 in rodent pancreatic B-cells: experimental and theoretical results. Eur Biophys J. 1990;18(2):71–77. doi: 10.1007/BF00183265. PMID:2108857. [DOI] [PubMed] [Google Scholar]
- 92.Pérez-Armendariz M, Roy C, Spray DC, Bennett MV. Biophysical properties of gap junctions between freshly dispersed pairs of mouse pancreatic beta cells. Biophys J. 1991;59(1):76–92. doi: 10.1016/S0006-3495(91)82200-7. PMID:2015391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Kang H. Systems of pancreatic beta-cells and glucose regulation. Front Biosci. 2008;13(13):6421–6431. doi: 10.2741/3163. PMID:18508669. [DOI] [PubMed] [Google Scholar]
- 94.Jo J, Kang H, Choi MY, Koh D-S. How noise and coupling induce bursting action potentials in pancreatic β-cells. Biophys J. 2005;89(3):1534–1542. doi: 10.1529/biophysj.104.053181. PMID:15994889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Meyer‐Hermann M, Benninger RKP. A mathematical model of β‐cells in an islet of Langerhans sensing a glucose gradient. Hfsp J. 2010;4(2):61–71. doi: 10.2976/1.3354862. PMID:20885774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Rocheleau JV, Walker GM, Head WS, McGuinness OP, Piston DW. Microfluidic glucose stimulation reveals limited coordination of intracellular Ca2+ activity oscillations in pancreatic islets. Proc Natl Acad Sci U S A. 2004;101(35):12899–12903. doi: 10.1073/pnas.0405149101. PMID:15317941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Zimliki CL, Mears D, Sherman A. Three roads to islet bursting: emergent oscillations in coupled phantom bursters. Biophys J. 2004;87(1):193–206. doi: 10.1529/biophysj.103.038471. PMID:15240457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Bertram R, Previte J, Sherman A, Kinard TA, Satin LS. The phantom burster model for pancreatic β-cells. Biophys J. 2000;79(6):2880–2892. doi: 10.1016/S0006-3495(00)76525-8. PMID:11106595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Bertram R, Sherman A. A calcium-based phantom bursting model for pancreatic islets. Bull Math Biol. 2004;66(5):1313–1344. doi: 10.1016/j.bulm.2003.12.005. PMID:15294427. [DOI] [PubMed] [Google Scholar]
- 100.Perez-Armendariz E, Atwater I, Rojas E. Glucose-induced oscillatory changes in extracellular ionized potassium concentration in mouse islets of Langerhans. Biophys J. 1985;48(5):741–749. doi: 10.1016/S0006-3495(85)83832-7. PMID:3907727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Perez-Armendariz E, Atwater I. Glucose-evoked changes in [K+] and [Ca2+] in the intercellular spaces of the mouse islet of Langerhans. Adv Exp Med Biol. 1986;211:31–51. doi: 10.1007/978-1-4684-5314-0_3. PMID:3300189. [DOI] [PubMed] [Google Scholar]
- 102.Stokes CL, Rinzel J. Diffusion of extracellular K+ can synchronize bursting oscillations in a model islet of Langerhans. Biophys J. 1993;65(2):597–607. doi: 10.1016/S0006-3495(93)81092-0. PMID:8218890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Rinzel J, Sherman A, Stokes CL. Channels, coupling, and synchronized rhythmic bursting activity. In: Eeckman F, editor. Analysis and modeling of neural systems. Boston, MA: Springer US; 1992. pp. 29–46. doi: 10.1007/978-1-4615-4010-6_3. [DOI] [Google Scholar]
- 104.Lei CL, Kellard JA, Hara M, Johnson JD, Rodriguez B, Briant LJB. Beta-cell hubs maintain Ca2+ oscillations in human and mouse islet simulations. Islets. 2018;10(4):151–167. doi: 10.1080/19382014.2018.1493316. PMID.30142036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Pipeleers D. The biosociology of pancreatic B cells. Diabetologia. 1987;30(5):277–291. doi: 10.1007/BF00299019. PMID:3301479. [DOI] [PubMed] [Google Scholar]
- 106.Bertuzzi F, Davalli AM, Nano R, Socci C, Codazzi F, Fesce R, Di Carlo V, Pozza G, Grohovaz F. Mechanisms of coordination of Ca2+ signals in pancreatic islet cells. Diabetes. 1999;48(10):1971–1978. doi: 10.2337/diabetes.48.10.1971. PMID:10512361. [DOI] [PubMed] [Google Scholar]
- 107.Bertuzzi F, Zacchetti D, Berra C, Socci C, Pozza G, Pontiroli AE, Grohovaz F. Intercellular Ca2+ waves sustain coordinate insulin secretion in pig islets of Langerhans. FEBS Lett. 1996;379(1):21–25. doi: 10.1016/0014-5793(95)01422-5. PMID:8566222. [DOI] [PubMed] [Google Scholar]
- 108.Bertram R, Pernarowski M. Glucose diffusion in pancreatic islets of Langerhans. Biophys J. 1998;74(4):1722–1731. doi: 10.1016/S0006-3495(98)77883-X. PMID:9545035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Bennett BD, Jetton TL, Ying G, Magnuson MA, Piston DW. Quantitative subcellular imaging of glucose metabolism within intact pancreatic islets. J Biol Chem. 1996;271(7):3647–3651. doi: 10.1074/jbc.271.7.3647. PMID:8631975. [DOI] [PubMed] [Google Scholar]
- 110.Stožer A, Gosak M, Dolenšek J, Perc M, Marhl M, Rupnik MS, Korošak D, Shvartsman S. Functional connectivity in islets of Langerhans from mouse pancreas tissue slices. PLOS Comp Biol. 2013;9(2):e1002923. doi: 10.1371/journal.pcbi.1002923. PMID:23468610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Markovič R, Stožer A, Gosak M, Dolenšek J, Marhl M, Rupnik MS. Progressive glucose stimulation of islet beta cells reveals a transition from segregated to integrated modular functional connectivity patterns. Sci Rep. 2015;5(1):1–10. doi: 10.1038/srep07845. PMID:25598507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Stožer A, Šterk M, Paradiž Leitgeb E, Markovič R, Skelin Klemen M, Ellis CE, Križančić Bombek L, Dolenšek J, MacDonald PE, Gosak M. From isles of Königsberg to islets of Langerhans: examining the function of the endocrine pancreas through network science. Front Endocrinol. 2022;13:922640. doi: 10.3389/fendo.2022.922640. PMID:35784543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Cappon G, Pedersen MG. Heterogeneity and nearest-neighbor coupling can explain small-worldness and wave properties in pancreatic islets. Chaos. 2016;26(5):053103. doi: 10.1063/1.4949020. PMID:27249943. [DOI] [PubMed] [Google Scholar]
- 114.Salem V, Silva LD, Suba K, Georgiadou E, Neda Mousavy Gharavy S, Akhtar N, Martin-Alonso A, Gaboriau DCA, Rothery SM, Stylianides T, et al. Leader β-cells coordinate Ca2+ dynamics across pancreatic islets in vivo. Nat Metab. 2019;1(6):615–629. doi: 10.1038/s42255-019-0075-2. PMID:32694805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Kravets V, Dwulet JM, Schleicher WE, Hodson DJ, Davis AM, Pyle L, Piscopio RA, Sticco-Ivins M, Benninger RKP, Mandrup S. Functional architecture of pancreatic islets identifies a population of first responder cells that drive the first-phase calcium response. PLoS Biol. 2022;20(9):e3001761. doi: 10.1371/journal.pbio.3001761. PMID:36099294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Gosak M, Yan-Do R, Lin H, MacDonald PE, Stožer A. Ca2+ oscillations, waves, and networks in islets from human donors with and without type 2 diabetes. Diabetes. 2022;71(12):2584–2596. doi: 10.2337/db22-0004. PMID: 36084321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Hogan JP, Peercy BE, Satin LS. Flipping the switch on the hub cell: islet desynchronization through cell silencing. PLoS One. 2021;16(4):e0248974. doi: 10.1371/journal.pone.0248974. PMID:33831017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Dwulet JM, Briggs JK, Benninger RKP. Small subpopulations of β-cells do not drive islet oscillatory [Ca2+] dynamics via gap junction communication. PLOS Computa Biol. 2021;17(5):e1008948. doi: 10.1371/journal.pcbi.1008948. PMID:33939712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Loppini A, Chiodo L. Biophysical modeling of β-cells networks: realistic architectures and heterogeneity effects. Biophys Chem. 2019;254:106247. doi: 10.1016/j.bpc.2019.106247. PMID:31472460. [DOI] [PubMed] [Google Scholar]
- 120.Riz M, Braun M, Pedersen MG. Mathematical modeling of heterogeneous electrophysiological responses in human β-cells. PLOS Comp Biol. 2014;10(1):e1003389. doi: 10.1371/journal.pcbi.1003389. PMID:24391482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Peercy BE, Sherman AS. Do oscillations in pancreatic islets require pacemaker cells? J Biosci. 2022;47(1):14. doi: 10.1007/s12038-021-00251-6. PMID: 35212266. [DOI] [PubMed] [Google Scholar]
- 122.Korošak D, Jusup M, Podobnik B, Stožer A, Dolenšek J, Holme P, Rupnik MS. Autopoietic Influence Hierarchies in Pancreatic β Cells. Phys Rev Lett. 2021;127(16):168101. doi: 10.1103/PhysRevLett.127.168101. PMID:34723613. [DOI] [PubMed] [Google Scholar]
- 123.Scialla S, Loppini A, Patriarca M, Heinsalu E. Hubs, diversity, and synchronization in FitzHugh-Nagumo oscillator networks: resonance effects and biophysical implications. Phys Rev E. 2021;103(5):052211. doi: 10.1103/PhysRevE.103.052211. PMID:34134340. [DOI] [PubMed] [Google Scholar]
- 124.Nittala A, Wang X. The hyperbolic effect of density and strength of inter beta-cell coupling on islet bursting: a theoretical investigation. Theor Biol Med Model. 2008;5(1):17. doi: 10.1186/1742-4682-5-17. PMID:18673579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Watts M, Ha J, Kimchi O, Sherman A. Paracrine regulation of glucagon secretion: the β/α/δ model. Am J Physiol Endocrinol Metab. 2016;310(8):E597–611. doi: 10.1152/ajpendo.00415.2015. PMID:26837808. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


