The efficient design of Nested Group Testing algorithms for disease identification in clustered data

Abstract

Group testing study designs have been used since the 1940s to reduce screening costs for uncommon diseases; for rare diseases, all cases are identifiable with substantially fewer tests than the population size. Substantial research has identified efficient designs under this paradigm. However, little work has focused on the important problem of disease screening among clustered data, such as geographic heterogeneity in HIV prevalence. We evaluated designs where we first estimate disease prevalence and then apply efficient group testing algorithms using these estimates. Specifically, we evaluate prevalence using individual testing on a fixed-size subset of each cluster and use these prevalence estimates to choose group sizes that minimize the corresponding estimated average number of tests per subject. We compare designs where we estimate cluster-specific prevalences as well as a common prevalence across clusters, use different group testing algorithms, construct groups from individuals within and in different clusters, and consider misclassification. For diseases with low prevalence, our results suggest that accounting for clustering is unnecessary. However, for diseases with higher prevalence and sizeable between-cluster heterogeneity, accounting for clustering in study design and implementation improves efficiency. We consider the practical aspects of our design recommendations with two examples with strong clustering effects: (1) Identification of HIV carriers in the US population and (2) Laboratory screening of anti-cancer compounds using cell lines.

1. Introduction

Group testing has been used since the 1940s to reduce the cost of screening a population for disease, among other medical, industrial, and agricultural applications. One simple design [1] pools and tests individuals’ samples in groups; individual samples are then only tested if their pool is positive overall. For rare diseases, this procedure allows all cases in the population to be identified, using far fewer tests than the population size. Substantial research has introduced more sophisticated (and efficient) designs and improved the efficiency of established designs, e.g. through optimization of group sizes, under both frequentist and Bayesian paradigms [2–6]. A large body of research has addressed the impact of misclassification on group testing [7–10].

Although a number of researchers have examined the impact of data clustering when using group testing to estimate prevalence [11–14], little research has focused on the important question of group testing design for screening individuals who are observed in clusters. The motivating examples for our design methodology come from two diverse areas of biological science. The first one is the identification of HIV carriers in the United States, where there is substantial geographic heterogeneity in prevalence across states, across counties, or within cities. The second is testing of novel anti-cancer compounds on the NCI-60 cell lines, where there is heterogeneity in the effectiveness of the compound between tumor types. In this setting, the compounds may be difficult to produce or otherwise expensive and pooling cells from lines of the same tumor type may conserve resources.

Screening for SARS-CoV-2 infection is another area where clusters may plausibly arise, and where group testing may be used to increase screening efficiency. Reverse-transcription polymerase chain reaction (RT–PCR) tests are sensitive and specific for detection of SARS-CoV-2 infection, and it is established that RT–PCR testing can be used on pooled samples, potentially with group sizes as large as 100 individuals [15]. Pooled RT–PCR testing with the Dorfman algorithm has been implemented successfully [16], and more complex designs have been proposed for low-prevalence settings [15]. COVID-19 infections have a potential for clustering on several levels. In addition to broad geographic heterogeneity in community infection rates, clustering may occur on a much smaller scale. For example, if all students at an elementary school are tested weekly, the classes and grade levels form potential clusters due to the potential for transmission: a large proportion of one class may be infected due to close contact within that group, while another class may be entirely free from infection.

Lendle, Hudgens, and Qaqish [17] showed that for hierarchical and matrix group testing procedures, arranging positively correlated data in the same pool results in increased efficiency. Their paper assumed that the mean disease prevalence as well as the between-cluster heterogeneity is known and does not factor their estimation into design considerations. Our focus is on the practical problem of designing a screening procedure when little is known about the distribution of cluster prevalences. While we estimate cluster prevalences, these estimates are used only to choose the group sizes for subsequent group testing; our focus is on identification of cases, not prevalence estimation overall.

In this paper, we focus on efficient designs, where efficiency is determined by the expected number of tests per subject, using group testing procedures for screening when participants are clustered. We consider a set of efficient practical designs where the group size is determined either overall or for each cluster, requiring either overall or cluster-specific prevalence estimation. In either case, we assume that a small number of tests in each cluster are used to estimate prevalence and corresponding group size based on that prevalence. In Section 2, we formally introduce the data structure and briefly review the group testing algorithms under consideration. Section 3 addresses optimization of the number of cluster members individually tested to estimate the cluster-specific prevalences, by cluster size and distribution of the true cluster-specific prevalences. In Section 4, we compare group testing algorithms for clustered data using simulation studies, as a function of overall disease prevalence, variability of prevalence across clusters, cluster size, and number of clusters. Section 5 additionally incorporates misclassification affecting test sensitivity (dilution). Section 6 considers the practical aspects of our design recommendations with two examples with strong clustering effects: (1) Identification of HIV carriers in the US population and (2) Laboratory screening of anti-cancer compounds using cell lines. In Section 7, we discuss the implications of our results for practical applications.

2. Methods

2.1. Notation and assumptions

Suppose that our data consist of $n$ clusters, with disease prevalences $P_i,i=1,\dots ,n$, where the $P_i$ are i.i.d. Beta random variables with parameters $\alpha$ and $\mathrm{\text{β}}$ and mean $p=\alpha /\phantom{\alpha \alpha +\mathrm{\text{β}}}\alpha +\mathrm{\text{β}}$. Each cluster contains $m_i$ individuals with a single binary trait $X_{ij},i=1,\dots ,n,j=1,\dots ,m_i$, where the $X_{ij}$ are Bernoulli random variables, conditionally independent given $P_i$. This is the standard Beta-Binomial model used by Lendle et al.[17].

We consider a series of different two-step procedure designs where we first estimate $P_i,i=1,\dots ,n$, by individually testing a subset of each cluster, and then choose an efficient group testing design given these estimates. For the estimation step of this procedure, we assume that $l_i$ $(l_i<m_i\mathrm{\forall }i=1,\dots ,n)$ individuals are drawn from each cluster and individual testing is done in order to estimate $P_i.$The random variable $X_i$, denoting the number of cases in this subsample, is assumed to also follow a Binomial distribution given $P_i$. We use four methods to estimate $P_i$:

$${\hat{p}}_i\text{ = }\frac{X_i\text{ + 1}}{l_i\text{ + 2}}$$ (1)

$${\tilde{p}}_i=\frac{X_i+\alpha }{l_i+\alpha +\mathrm{\text{β}}}$$ (2)

$${\widehat{\stackrel{~}{p}}}_i=\frac{X_i+\hat{\alpha }}{l_i+\hat{\alpha }+\widehat{\mathrm{\text{β}}}}$$ (3)

$${\hat{p}}_i=\hat{p}=\frac{1+{\sum }_{j=1}^n{X}_j}{2+{\sum }_{j=1}^n{l}_j}\mathrm{\forall }i=1,\dots ,n$$ (4)

Under the Beta-Binomial distribution, ${\hat{p}}_i$ is the posterior mean under a Uniform $\left(0,1\right)$ (Beta $\left(1,1\right)$) prior for $P_i$, ${\tilde{p}}_i$ is the posterior mean under a Beta prior with known parameters $\alpha$ and $\mathrm{\text{β}}$, and ${\widehat{\stackrel{~}{p}}}_i$ is the posterior mean under a Beta prior where $\alpha$ and $\mathrm{\text{β}}$ are replaced by their maximum-likelihood estimates $\hat{\alpha }$ and $\widehat{\mathrm{\text{β}}}$, respectively. The estimator $\hat{p}$ is the maximum-likelihood estimator of $P_i$ under the assumption of a constant prevalence across participants $(P_i=P)$. A cluster-specific group size is chosen based on $P_i$ estimated in Step 1 and using optimality results presented in Malinovsky and Albert [3] and references within.

In the second step of the two-step procedure, we apply the estimated group sizes from Step 1 to identify cases in the remaining $m_i-l_i$ individuals from each of the n clusters. We examine the expected number of tests under several group testing algorithms, presented in Section 2.2. Specifically, we focus on three members of the class of nested group testing algorithms [5], where once a group tests positive, the next subgroup tested is a proper subset of that group.

2.2. Group testing algorithms

The Dorfman procedure (Procedure D) was introduced by Robert Dorfman [1] for the administration of syphilis blood testing of Army draftees during World War II. It is the simplest and most easily implementable group testing algorithm. A single test is first applied to pooled samples from a group of size $k$. If this test is negative, all $k$ group members are classified negative; otherwise, each group member is tested individually to identify cases within these $k$. Given disease prevalence $p\left(q=1-p\right)$ and a perfect test (sensitivity and specificity of 100%), the expected number of tests per individual ${\mathbb{E}}_D\left(T\right)$ may be calculated:

$${\mathbb{E}}_D\left(T|k,p\right)=\{\begin{array}{c}1-q^k+\frac{1}{k}\\ 1\end{array}\begin{array}{c}k\ge 2\\ k=1\end{array},$$ (5)

with the optimal group size $k_D^{\ast }\equiv k_D^{\ast }\left(p\right)$ [18]; $k_D^{\ast }=1$ for $p\ge 1-{\left(\frac{1}{3}\right)}^{\frac{1}{3}}$.

Procedure D´ improves upon Procedure D with a simple adaptation: If a group of size $k$ is positive overall and the first $k-1$ individual tests are negative, the final group member is not tested and is classified as positive. As with Procedure D, we may calculate the expected number of tests per individual:

$${\mathbb{E}}_{D^{\mathrm{\prime }}}\left(T|k,p\right)=1-q^k+\frac{1}{k}-\frac{1}{k}p{q}^{k-1}.$$ (6)

A derived closed-form expression for the optimal group size $k_{D^{\mathrm{\prime }}}^{\ast }$ is unavailable, but $k_{D^{\mathrm{\prime }}}^{\ast }\le k_D^{\ast }$ for $p<1-{\left(\frac{1}{3}\right)}^{\frac{1}{3}}$, and a conjectured closed-form expression has been verified numerically [3].

An algorithm introduced by Sterrett [19] (Procedure S) improves further upon D´ [3]; if a group is positive overall, its members are tested sequentially one-by-one until the first case is found. The remaining group members are then pooled and re-tested; if this subgroup tests negative, all its members are classified as negative, and if it is positive, the procedure is repeated. These steps are repeated until all group members are classified. Although more logistically challenging in practice, Procedure S provides an improvement in efficiency over D and D´:

$${\mathbb{E}}_S\left(T|k,p\right)=\frac{1}{k}\left[2k-\left(k-2\right)q-\frac{1-q^{k+1}}{p}\right].$$ (7)

An expression for the optimal group size under this design, $k_S^{\ast }$, is presented by Malinovsky and Albert [3]. Procedure S has been empirically shown to dominate D´, although this has not been proven in general [20].

The generalized group testing problem (GGTP) arises when designing a group testing procedure for $w$ individuals, with corresponding probabilities $\mathit{p}=p_1,\dots ,p_w$ of being positive ( $q_i=1-p_i$). Clustered data are a subset of this general scenario, in which the set of $w$ individuals is partitioned into $m$ subsets defined by the clusters and all individuals within a given subset have a common probability of being positive. We may use GGTP results to calculate the expected number of tests in our setting; Equations S1-S3 in the online supplement give the expected number of tests per individual under D, D´, and S, respectively, for any subset of size $k\ge 1$.

2.3. Group testing with dilution

Test misclassification is an important practical concern for group testing, particularly dilution effects in which increasing the group size reduces the assay sensitivity. Hwang [8] introduced a function to model this dilution effect (Eq. S4). Although the literature contains research pertaining to other forms of misclassification in a GGTP setting [21, 22], Hwang’s dilution function does not have a straightforward adaptation for the GGTP setting; we assume that groups are comprised of individuals with a common $p_i$. Hwang also introduced an expected-cost function for the Dorfman procedure in a setting in which the total number of individuals is divisible by the group size (no-residual setting). This cost function may be optimized for $k$ in place of the expected number of tests, based on the unit test cost $c$ (Equations S5, S6), to serve as an alternative objective function to minimize when selecting the group size. As, in the presence of dilution, group sizes obtained by optimizing $\mathbb{E}\left(T\right)$ without consideration of test accuracy measures are anti-conservative, we introduce two additional quantities: The ratio of the expected number of correct classifications to the total expected number of tests $\left(\frac{\mathbb{E}\left(T_C\right)}{\mathbb{E}\left(T_T\right)}\right)$ and the ratio of the expected number of missed cases to the total expected number of cases $\left(\frac{\mathbb{E}\left(M\right)}{\mathbb{E}\left(D\right)}\right)$ (Equations (S7)–(S10)).

3. Choice of $l$

In the absence of test misclassification and for a given number of resolved individuals used to estimate cluster prevalence $l_i$, cluster size $m_i$, and Beta distribution parameters $\alpha$ and $\mathrm{\text{β}}$, we can obtain the expected number of tests per individual, $\mathbb{E}\left(T\right),$ through successive use of the Law of Total Expectation. In general, selecting such an $l_i$ is a balancing act; a larger $l_i$ allows for more precise estimation of $P_i$ within a cluster, at the cost of increasing the number of individuals resolved prior to group testing. Additionally, our estimates ${\hat{p}}_i,{\tilde{p}}_i$, and ${\widehat{\stackrel{~}{p}}}_i$ are bounded; their minimum values are $\frac{1}{l_i+2},\frac{\alpha }{l_i+\alpha +\mathrm{\text{β}}},$ and $\frac{\hat{\alpha }}{l_i+\hat{\alpha }+\widehat{\mathrm{\text{β}}}}$, respectively, all of which may be much larger than $p_i$.

We denote the observed number of cases among the $l_i$ resolved individuals by $x_i$ and the true case prevalence in the cluster by $p_i$, realizations of the random variables $X_i$ and $P_i$ respectively. For simplicity, in this section, we assume that the $m_i-l_i$ is divisible by the estimated optimal group size $\widehat{k_i^{\ast }}\equiv \widehat{k_i^{\ast }}\left(x_i\right)$. Without loss of generality, we may calculate the expected number of tests per individual for a single cluster of size $m_i$. Additionally, the below expressions are in terms of ${\hat{p}}_i$ although ${\tilde{p}}_i$ or ${\widehat{\stackrel{~}{p}}}_i$ may be substituted. Using the properties of conditional  expectation, we calculate the expected number of tests under Procedure D, D´, or S:

$$\mathbb{E}\left(T\right)=\underset{0}{\overset{1}{\int }}\sum _{x_i=0}^{l_i}\underbrace{{\underbrace{{\mathbb{E}{\left(T|\widehat{k_i^{\ast }}\left(x_i\right),p_i\right)}_{}}_{\mathfrak{B}}}}_{\mathfrak{A}}{f}_{X|P}\left(x_i|p_i\right)}{f}_P\left(p_i\right)d{p}_i.$$ (8)

In evaluating expression $\mathfrak{B}$ from Equation (8), we must take care: This term is the expectation under the true $P_i=p_i$; Procedure D, D´, or S; and respectively using groups of size ${\hat{k}}_D^{\ast }\left(x_i\right),{\hat{k}}_{D^{\mathrm{\prime }}}^{\ast }\left(x_i\right),$ or ${\hat{k}}_S^{\ast }\left(x_i\right)$ estimated using $x_i,$ ${\hat{p}}_i,$ and $q_i=1-p_i$ as described in Section 2.2. For example, under Procedure D,

$${\mathfrak{B}}_D=\{\begin{array}{c}\frac{1}{m_i}\left[l_i+\left(m_i-l_i\right)\left(1-q_i^{{\hat{k}}_D^{\ast }\left(x_i\right)}+\frac{1}{{\hat{k}}_D^{\ast }\left(x_i\right)}\right)\right],{\hat{p}}_i<1-{\left(\frac{1}{3}\right)}^{\frac{1}{3}}\\ 1,{\hat{p}}_i\ge 1-{\left(\frac{1}{3}\right)}^{\frac{1}{3}}\end{array}.$$ (9)

Notably, the design elements of Equation (9) are defined by ${\hat{p}}_i$ as estimated from $x_i$, while the expectation is taken relative to the true prevalence $p_i$.

Given $P_i=p_i$, $X_i$ is a Binomial $\left(l_i,p_i\right)$ random variable, and so we can evaluate expression $\mathfrak{A}$ from Equation (8), the expected number of tests under procedure D, given $P_i=p_i$.

$$\mathfrak{A}=\mathfrak{B}\times \left(\begin{array}{c}{l}_i\\ x_i\end{array}\right)p_i^{x_i}{q}_i^{l_i-x_i}.$$ (10)

Finally, $P_i$ is a Beta $\left(\alpha ,\mathrm{\text{β}}\right)$ random variable and we may find the overall expected number of tests given $\alpha ,\mathrm{\text{β}},$ the cluster size $m_i$, and the number of resolved individuals $l_i$:

$$\mathbb{E}\left[T\right]=\underset{0}{\overset{1}{\int }}\mathfrak{A}\times \frac{p_i^{\alpha -1}{q}_i^{\mathrm{\text{β}}-1}}{B\left(\alpha ,\mathrm{\text{β}}\right)}d{p}_i.$$ (11)

For our results, we used numerical techniques to obtain values of $\mathbb{E}\left(T\right)$; namely, we took $0=p_0<p_1<\dots <p_{200}=1$ to be a sequence of evenly spaced points and calculated:

$$\mathbb{E}\left(T\right)\approx \sum _{j=1}^{200}\mathfrak{A}\times P(p_{j-1}<P_i<p_j).$$ (12)

For a given $\alpha ,\mathrm{\text{β}},$ and $m_i$, a local optimum of $l_i$ can be obtained by calculating $\mathbb{E}\left(T\right)$ for a series of candidate values of $l_i$, say $\left\{2,3,\dots ,30\right\}$, and taking $l_i^{\ast }$ to be the value of $l_i$ which minimizes $\mathbb{E}\left(T\right)$. Empirically, $l_i^{\ast }$ was a unique minimum of $\mathbb{E}\left(T\right)$ in all simulations.

These calculations may also be performed under Procedures D´ and S; in Equation (8) above, $\widehat{k_i^{\ast }}$ may be replaced by the estimated group size and $\left(1-q_i^{\widehat{k_i^{\ast }}}+\frac{1}{\widehat{k_i^{\ast }}}\right)$ by the appropriate expected number of tests, under D´ or S, where $q_i=1-p_i$.

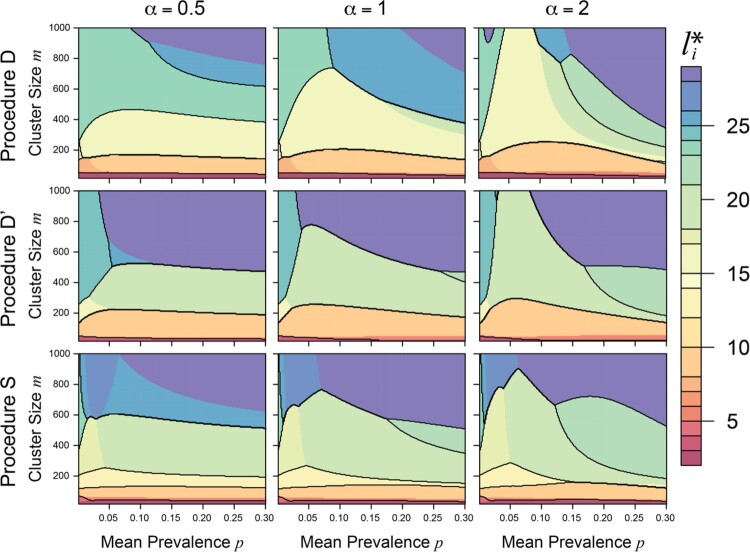
We calculated $l_i^{\ast }$ for Procedures D, D´, and S and estimators ${\hat{p}}_i$, ${\tilde{p}}_i$, and ${\widehat{\stackrel{~}{p}}}_i$, as described above for $\alpha \in \left\{0.5,0.625,0.75,0.875,1,1.25,1.5,1.75,2\right\}$ and 200 evenly spaced values of each of $p\in \left(0,0.3\right)$ and $m_i\in \left(10,1000\right)$. Figure 1 provides contour plots of $l_i^{\ast }$ for $\alpha \in \left\{0.5,1,2\right\}$ (columns) and for Procedures D, D´, and S (rows) using ${\hat{p}}_i$, with highlighted contours $l_i^{\ast }=\left\{5,10,15,20,25\right\}$. Across all values of $\alpha$ and for all three procedures (and for each of ${\hat{p}}_i$, ${\tilde{p}}_i$, and ${\widehat{\stackrel{~}{p}}}_i$), we found that for small-to-moderate cluster sizes (approximately $m_i\le 200$), the optimum $l_i^{\ast }$ in our setting was nearly invariant to the true mean prevalence. This is reassuring from a design standpoint; in practice, it’s unlikely that $\alpha$ and $\mathrm{\text{β}}$ will be known precisely by researchers, while cluster sizes are likely to be known, indicating that an acceptable number of individuals to resolve may be chosen based on the cluster size and group testing procedure alone. Results were comparable for ${\tilde{p}}_i$ and ${\widehat{\stackrel{~}{p}}}_i$. Averaging across a range of Beta distributions, we found that for different estimates of $p_i$ and group testing procedures, $l_i=8$ performs well (Figure S1 in the online supplement).

Figure 1.

Filled contour plot of optimum number of individuals to test per cluster, $l^{\ast }$, by mean prevalence $p=\frac{\alpha }{\alpha +\mathrm{\text{β}}}\in \left[0.001,0.3\right]$ and cluster size $m\in \left[2,32\right]$, for $\alpha \in \left\{0.5,1,2\right\}$ (columns) and Procedures D, D´, and S (rows), using ${\hat{p}}_i$. Contour lines are drawn at $l^{\ast }=\left\{5,10,15,20,25\right\}$.

While the above calculations are performed for a single cluster, the results hold for multiple clusters of the same size or differing sizes; under the former, each cluster has the same value of $l^{\ast }$, while under the latter, each cluster has an optimum $l_i^{\ast }$ computed based on its size $m_i$.

The calculations above assume that the size of the remaining cluster is divisible by the estimated group size $\widehat{k_i^{\ast }}$. However, in practice this assumption is unlikely to hold, and the overall partition of groups within each cluster must be adjusted to distribute residual cluster members among groups (finite-sample algorithm adjustment). Using the algorithm adjustment established for the standard setting, the groups in the adjusted partition differ in size from $\widehat{k_i^{\ast }}$ by at most one individual. We assessed the impact of this assumption through simulations and find that the optimality results for $l_i^{\ast }$ are only minimally affected by cluster residuals (Figure S2). Section A3 of the supplementary material and Figure S3 examine the choice of $l_i$ when using $\hat{p}$.

4. Comparison of group testing algorithms

4.1. Methods

4.1.1. Group construction and cluster integrity

In addition to comparing group testing algorithms and prevalence estimators, we also investigate the handling of individuals during construction of the group testing partition; Lendle, Hudgens, and Qaqish [17] showed that arranging positively correlated data in the same pool results in increased efficiency, but in applications this may add logistical challenges as described below. To investigate the amount of efficiency gain, we use simulations to consider four possibilities, illustrated by the following example (as well as Table S1). Suppose that biological samples are being assessed to identify cases of HIV infection, with clustering formed by geographic region (e.g. state or county). The lab analyzing these samples could then:

1. Estimate HIV prevalence within each region ( ${\hat{p}}_i$, ${\tilde{p}}_i$, or ${\widehat{\stackrel{~}{p}}}_i$) and test groups each of which consists exclusively of samples from a single region.

2. Estimate HIV prevalence within each region and test groups that consist of samples from regions with the same prevalence estimate ( ${\hat{p}}_i$, ${\tilde{p}}_i$, or ${\widehat{\stackrel{~}{p}}}_i$).

3. Estimate a common HIV prevalence across all regions ( $\hat{p}$) and test groups each of which consists exclusively of samples from a single region.

4. Estimate a common HIV prevalence across all regions and test groups without regard to region.

We may consider these scenarios as using the cluster structure in both design and implementation, in design only, in implementation only, and in neither. Scenarios 1 and 3 pose more logistical challenges than 2 and 4: As samples arrive at the lab for testing, the lab must wait for sufficient samples from each region to accrue before conducting a test for that region, while in Scenario 2 samples may accrue into a group from multiple regions simultaneously and in Scenario 4 they may accrue from all regions simultaneously.

For our simulations, we refer to this implementation-level sample handling as ‘individual handling’ and refer to scenarios 1 and 3 as maintaining clustering and 2 and 4 as ignoring clustering. In practice, Scenarios 1 and 3 may combine some samples across clusters, within a supercluster (1) or overall (3), to reduce the number of residuals within each cluster.

4.1.2. Simulation design

Using simulations, we assessed the differences between a number of group testing algorithms for clustered data. Broadly, we may categorize the algorithms used based on (1) individual handling (cluster structure ‘maintained’ vs ‘ignored’), (2) group testing procedure, and (3) estimation of $P_i$, as summarized in Table S1. We estimate $P_i$ as ${\hat{p}}_i$ (Equation (1)), ${\tilde{p}}_i$ (Equation (2)), ${\widehat{\stackrel{~}{p}}}_i$ (Equation (3)), or $\hat{p}$ (Equation (4)).

Using cluster-specific prevalence estimates ${\hat{p}}_i$ (or ${\tilde{p}}_i$ or ${\widehat{\stackrel{~}{p}}}_i$), we may apply a group testing algorithm with finite-sample adjustment to group sizes when the cluster size is not evenly divisible by the group size (Procedures D, D´, S) to superclusters comprised of all clusters with the same ${\hat{p}}_i$ (individals $X_{wj}$ from clusters $w$ such that ${\hat{p}}_w={\hat{p}}_i)$, for each unique ${\hat{p}}_i$, using ${\hat{p}}_i$ to estimate the group sizes $\widehat{k_i^{\ast }}$. Under $\hat{p}$, we apply Procedure D, D´, or S to all individuals, with finite-sample adjustment, with an estimated group size $\widehat{k^{\ast }}$ calculated using $\hat{p}$.

For the 24 group testing designs summarized above and in Table S1, we calculated $\mathbb{E}\left(T\right)$ and $\text{Var}\left(T\right)$ for $n$ clusters of size $m$, with prevalences following a $\text{Beta}\left(\alpha ,\mathrm{\text{β}}\right)$ distribution through simulations. Using Procedures D, D´, and S on superclusters (18 designs), we followed the following procedure:

1. Calculate $l^{\ast }$ for $m$, $\alpha$, $\mathrm{\text{β}}$, the procedure (D, D´, or S), and the prevalence estimator ( ${\hat{P}}_i$, ${\tilde{P}}_i$, or ${\widehat{\stackrel{~}{P}}}_i$). As all clusters were the same size, we calculated a common $l_i^{\ast }=l^{\ast }$.

2. For each of $w$ simulated cohorts with parameters $n,m$, $\alpha$, $\mathrm{\text{β}}$:

   1. Construct a vector of disease prevalence estimates ( ${\hat{p}}_i$, ${\tilde{p}}_i$, ${\widehat{\stackrel{~}{p}}}_i,$ or $\hat{p}$) from the first $l^{\ast }$ individuals from each cluster (and corresponding vector $\mathit{x}$ of cluster-specific observed counts of defectives), simulating individual testing of these individuals.
   2. For individual handling ignoring cluster structure only (Section 4.1.1): randomize the vector of true simulated prevalences ${\mathit{p}}_j$ within each supercluster of individuals with a common ${\hat{p}}_i$ (or ${\tilde{p}}_i$, ${\widehat{\stackrel{~}{p}}}_i,$ or $\hat{p}$). In other words, for a commonly estimated prevalence, we randomized across all clusters, and for cluster-specific prevalence estimates, we randomized across all clusters that share a common estimated prevalence.
   3. Construct a partition of groups for each supercluster using its prevalence estimate and corresponding optimal group size $\widehat{{\mathit{k}}^{\ast }}\left({\mathit{x}}_{\mathit{j}}\right)$.
   4. Evaluate $\mathbb{E}\left(T|\widehat{{\mathit{k}}^{\ast }}\left(\mathit{x}\right),{\mathit{p}}_j\right)$ on the combined partition of the $n\left(m-l^{\ast }\right)$ individuals, under the true simulated prevalences ${\mathit{p}}_j$ and estimated optimal group sizes $\widehat{{\mathit{k}}^{\ast }}\left(\mathit{x}\right)$, applying Equation (5) (D), 6 (D´), or 7 (S) to each group in the partition and summing across groups.

3. Take the overall $\mathbb{E}\left(T\right)$ as the empirical average of, and $\sigma \left(T\right)$ as the empirical standard deviation of, the values of $\frac{1}{m}\left[l^{\ast }+\left(m-l^{\ast }\right)\mathbb{E}\left(T|\widehat{{\mathit{k}}^{\ast }}\left(\mathit{x}\right),{\mathit{p}}_j\right)\right]$ calculated from the $w$ simulated cohorts.

For Procedures D, D´, and S using $\hat{p}$ (6 designs), we follow the steps above, using $l^{\ast }$ calculated for each procedure under $\hat{P}$; Step 2 proceeds with all $n$ clusters combined in a single supercluster with estimated prevalence $\hat{p}$.

In addition to the 24 group testing designs summarized above and in Table S1(b-c), we varied the overall size of the data set ( $n\times m\approx \left\{500,1000,2000\right\}$), number and size of the clusters (10 clusters; clusters of size 10; $n\approx m$), mean prevalence $p=\frac{\alpha }{\alpha +\mathrm{\text{β}}}\in \left\{0.01,0.05,0.1,0.2,0.3\right\}$, and $\alpha \in \left\{0.5,0.75,1,1.5,2\right\}$. In all cases, we simulated 100,000 cohorts.

4.2. Results

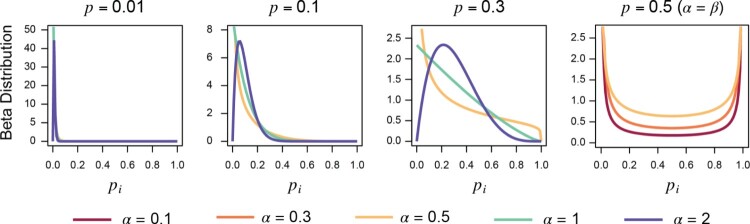
Table 1 provides an overview of the simulation results most relevant to practical study design: use of cluster structure in the design and in implementation of the group testing procedure (Section 4.1.1). This table presents the expected number of tests per subject for small ( $p=0.01$), moderate ( $p=0.1$), large ( $p=0.3$), and very large $(p=0.5$, bimodal Beta distributions) mean prevalences, three Beta shape parameters ( $\alpha =0.5,1,2$), and a variety of study designs (procedures D, D´, and S; $\hat{p}$ and ${\hat{p}}_i$; cluster structure maintained or ignored during group construction). Simulated prevalence distributions are illustrated in Figure 2. Across all three algorithms, estimating cluster-specific prevalences improved efficiency ( $\mathbb{E}\left[T\right]$) for high overall prevalence or a bimodal prevalence distribution; otherwise, the boundedness and imprecision of ${\hat{p}}_i$ outweigh the ability to calculate group size based on clusters’ individual estimated prevalences. Maintaining cluster structure when constructing groups increases efficiency in every scenario for Procedures D and D´, while Procedure S occasionally is more efficient when cluster structure is ignored setting due to the asymmetry in its expected number of tests. Overall, however, efficiency was nearly equivalent between the two implementation paradigms.

Table 1.

Expectation $\mathbb{E}\left(T\right)$of the number of tests per subject, overall by use of cluster structure in the design (use of ${\hat{\mathit{p}}}_i$ vs. $\hat{\mathit{p}}$) and use of cluster structure in implementation (‘Maintained’ vs. ‘Ignored’), mean prevalence $p$, and Beta shape parameter $\alpha$, for Procedures D, D´ and S, $n=31,m=32$.

			$\mathit{p}$	0.01			0.1			0.3			0.5
Alg.	Design	Implementation Cluster Handling	$\mathit{\alpha }$	0.5	1	2	0.5	1	2	0.5	1	2	0.1	0.3	0.5
D	${\hat{p}}_i$	Maintained		0.46	0.46	0.46	0.64	0.65	0.67	0.81	0.92	0.87	0.77	0.85	0.89
		Ignored		0.46	0.46	0.46	0.65	0.66	0.68	0.82	0.93	0.88	0.78	0.85	0.90
	$\hat{p}$	Maintained		0.30	0.30	0.30	0.61	0.60	0.61	0.91	0.96	0.94	1.00	1.00	1.00
		Ignored		0.30	0.30	0.30	0.66	0.62	0.62	0.97	0.98	0.98	1.00	1.00	1.00
D´	${\hat{p}}_i$	Maintained		0.55	0.55	0.55	0.69	0.71	0.72	0.83	0.90	0.85	0.81	0.87	0.90
		Ignored		0.55	0.55	0.55	0.69	0.71	0.72	0.84	0.90	0.86	0.81	0.87	0.91
	$\hat{p}$	Maintained		0.26	0.26	0.26	0.56	0.58	0.59	0.88	0.91	0.90	0.99	1.00	1.00
		Ignored		0.26	0.26	0.26	0.60	0.60	0.60	0.91	0.92	0.92	1.00	1.00	1.00
S	${\hat{p}}_i$	Maintained		0.38	0.38	0.38	0.60	0.63	0.64	0.78	0.89	0.84	0.74	0.82	0.87
		Ignored		0.38	0.38	0.38	0.59	0.62	0.63	0.78	0.88	0.84	0.74	0.82	0.87
	$\hat{p}$	Maintained		0.26	0.26	0.26	0.57	0.54	0.55	0.88	0.91	0.90	0.99	1.00	1.00
		Ignored		0.25	0.25	0.26	0.58	0.54	0.54	0.86	0.89	0.88	0.99	0.99	1.00

Notes: The number of initial individual tests $l_i^{\ast }$ is optimized for each $p$, $m$, and procedure (D, D´, or S); For common parameters, results for $\hat{p}$ and ${\hat{p}}_i$ share a common $l^{\ast }$. Cells with the minimum $\mathbb{E}\left[T\right]$ for each $p$, $\alpha$, and algorithm combination are highlighted.

Figure 2.

Illustration of Beta distributions included in Table 1.

Tables S2–S9 expand the results of Table 1 to a wider range of values and provide the results of additional simulations, varying the overall size or composition of the simulated data, varying the cluster prevalence estimator, and examining specific extreme distributions. Applying the group testing algorithms using the true $p$ or $p_i$ (Table S2), we observe the established efficiency rankings between procedures. Substituting $\hat{p}$ for $p$ reduces efficiency overall (Table S3), and estimating cluster-specific prevalences with ${\hat{p}}_i$ further reduces efficiency due to imprecision and boundedness of this estimate (Table S4). For equal values of $p$, differences in $\mathbb{E}\left(T\right)$ across varying Beta distribution parameters were small, indicating that the choice of study design can be made using knowledge of $p$ but without precise values of $\alpha$ and $\mathrm{\text{β}}$ (Table S5). Performance is roughly equivalent regardless of individual handling during group construction, across a wide range of parameter values (Table S6). Increasing $n$ for fixed $m$ does not measurably improve $\mathbb{E}\left(T\right)$ but does reduce $\sigma \left(T\right)$, while increasing $m$ for fixed $n$ improves $\mathbb{E}\left(T\right)$ but not $\sigma \left(T\right)$ (Table S7). Comparing cluster prevalence estimators, ${\tilde{p}}_i$ is more efficient than ${\hat{p}}_i$ and $\widehat{{\stackrel{~}{p}}_i}$,which perform equivalently (Table S8). For $\alpha =\mathrm{\text{β}}\le 1$, group testing using ${\hat{p}}_i$ is more efficient than single-unit testing, as we can categorize such clusters as either very high or low prevalence (Table S9a). These results hold for mixture distributions with higher heterogeneity than standard Beta distributions and for bimodal mixture distributions with modes at values other than 0 and 1 (Table S9c), and when varying $\mathrm{\text{β}}$ rather than $\alpha$ (data not shown).

5. Dilution simulations

We used simulations similar to those described in Section 4.1 to evaluate the impact of dilution on Dorfman group testing designs with clustering; full details on these simulations are given in Section A4 of the supplementary material. Table 2 and Tables S10–S14 provide the results of these simulations.

Table 2.

Total expected number of tests per subject $\mathbb{E}\left(T_T\right)$ and percentage of cases expected to be missed $(100\times \mathbb{E}(M\left)/\mathbb{E}\right(D\left)\right)$, by amount of dilution penalization (None: dilution not accounted for in group size calculation; Low, Moderate High: $\mathit{c}=50,100,200$ respectively) and use of cluster structure in the design (use of ${\hat{\mathit{p}}}_i$ vs. $\hat{\mathit{p}}$), mean prevalence $p$, and dilution parameter $d$, for $n=31,m=32$. For common parameters, results for $\hat{p}$ and ${\hat{p}}_i$ share a common $l^{\ast }$, which is optimized for each $p$ and $m$.

			$\mathit{p}$	0.01			0.05			0.1
Dilution Penalization	Performance Metric	Cluster Structure in GT Design	$\mathit{d}$	0.05	0.1	0.2	0.05	0.1	0.2	0.05	0.1	0.2
None	Expected # Tests	No		0.26	0.26	0.25	0.44	0.42	0.40	0.58	0.56	0.54
		Yes		0.41	0.41	0.41	0.54	0.53	0.52	0.64	0.64	0.62
	% Expected Missed Cases	No		8.4	16.0	29.2	6.8	13.0	24.2	5.4	10.5	19.7
		Yes		4.8	9.3	17.6	4.0	7.7	14.6	3.2	6.2	11.7
Low	Expected # Tests	No		0.29	0.30	0.35	0.54	0.63	0.81	0.81	0.91	0.98
		Yes		1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	% Expected Missed Cases	No		7.6	13.5	22.4	4.4	6.7	6.2	1.9	1.7	0.7
		Yes		0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Moderate	Expected # Tests	No		0.35	0.47	0.68	0.73	0.92	0.98	0.96	0.99	1.00
		Yes		1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	% Expected Missed Cases	No		6.3	9.5	9.8	2.3	1.4	0.8	0.4	0.1	0.0
		Yes		0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
High	Expected # Tests	No		0.48	0.68	1.00	0.92	0.98	1.00	0.99	1.00	1.00
		Yes		1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	% Expected Missed Cases	No		4.6	5.2	0.0	7.0	0.4	0.0	0.0	0.0	0.0
		Yes		0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

Briefly, introducing dilution without accounting for it in the choice of group size nominally increases efficiency by reducing the total number of expected tests. However, this reduction is due to missing cases during screening. Using ${\hat{p}}_i$ rather than $\hat{p}$ reduces efficiency, for small $p$, but may provide a more tolerable rate of missed cases (Table S10). Accounting for dilution reduces group size, with smaller groups for a higher unit test cost parameter $c$ (Equation S5, S6) (Table S11), correspondingly increasing the number of tests but decreasing the proportion of missed cases. When using ${\hat{p}}_i$, the relative proportion of missed cases decreases with cluster size, but no clear relationship holds for $\hat{p}$ (Table S12). The proportion of missed cases was consistent across different choices of $\alpha$ (Table S13). For $\alpha =\mathrm{\text{β}}\le 1$, not only is group testing using ${\hat{p}}_i$ more efficient than single-unit testing, but few cases are missed as they are concentrated within high-prevalence clusters that receive individual testing (Table S14).

6. Applications

6.1. HIV prevalence

We used data tabulating HIV prevalence rates by state (including Washington DC), county, and ZIP code in a simulation study using observed clusters to examine the performance of our algorithms in a large-scale public health setting. Identification of HIV-positive people, particularly while they are asymptomatic, has immense public health value, as HIV-positive individuals can receive anti-retroviral therapy to manage the infection, and individuals’ knowledge of their HIV status helps to reduce the spread of the disease. Currently, the US Preventive Services Task Force recommends that clinicians screen for HIV infection in adolescents and adults aged 15–65 years and in all pregnant women. Pooled blood samples have previously been used to reduce the cost of screening for acute HIV infection in low-prevalence populations and of screening for failure of anti-retroviral therapy [23, 24]. Additionally, standard rapid serum antibody assays have been shown to retain their high sensitivity when diluted to 1:20; false negatives from pooled samples would have been false negatives in individual testing by the same assay [25].

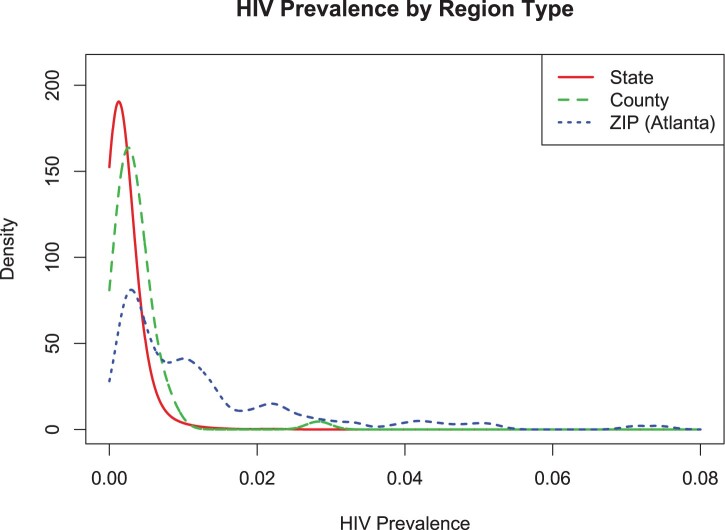
HIV prevalence rates from 2016 were obtained from the AIDSVu interactive online mapping tool, which compiles state and county HIV prevalence rates from the CDC Division of HIV/AIDS Prevention and ZIP code prevalence rates directly from state and local health departments [26]. The CDC estimated rates include people with unknown HIV infections, while the local rates include known diagnoses only. Statewide HIV prevalence rates are highly variable, ranging from 74.4 per 100,000 individuals in Wyoming to 2831.6 per 100,000 in Washington DC. Similarly, available data from counties range from 14 to 2306 per 100,000 (in Butler County, PA, and Union County, FL, respectively). For our analysis by ZIP code, we used data from Atlanta, GA, which range from 105 per to 7464 per 100,000 (ZIP codes 30,041 and 30,303, respectively) (Figure 3).

Figure 3.

Density plot of HIV prevalence by type of geographic division (state, county, ZIP code within Atlanta).

Since the AIDSVu database contains HIV prevalences by region, but not individual-level data, we used the 2016 prevalences to simulate cohorts and then applied the simulation methods described in Section 4.1.2 to obtain $\mathbb{E}\left(T\right)$. We obtained $l^{\ast }$ by estimating $\alpha$ and $\mathrm{\text{β}}$ from the respective data sets; in a real-world HIV screening situation, researchers would likely be able to estimate the overall distribution of HIV prevalence rates from recent geographic prevalence data despite not knowing the exact present location-specific prevalences, as drastic and sudden shifts in the overall prevalence distribution are unlikely. For each geographic grouping, we simulated 50,000 cohorts, with clusters of size $m=5000$ for the states, $m=500$ for the counties, and $m=50$ for the ZIP code regions. For Procedures D, D´, and S, using $\hat{p}$ was more efficient than using ${\hat{p}}_i$; despite the heterogeneity in HIV prevalences by region, prevalence is still low enough overall to favor group testing algorithms that do not account for clustering (Table 3).

Table 3.

Expectation $\mathbb{E}\left(T\right)$ of the number of tests per subject using reported HIV prevalence data for simulation of 5000 cohorts.

		$\hat{p}$	${\hat{p}}_i$
State	D	0.125	0.165
	D´	0.126	0.166
	S	0.097	0.127
County	D	0.146	0.216
	D´	0.148	0.217
	S	0.105	0.177
ZIP	D	0.324	0.404
	D´	0.339	0.414
	S	0.234	0.354

6.2. Cell lines

The NCI-60 cell lines encompass 60 different human tumor cell lines that are used to identify and characterize novel compounds for anti-cancer activity, as measured by growth inhibition or killing of tumor cells [27]. These data are publicly available using the online COMPARE database provided by the National Cancer Institute (NCI) Division of Cancer Treatment and Diagnosis (DCTD) Developmental Therapeutics Program (DTP) [28]. Group testing could plausibly be used in this setting as the compounds tested can be rare and difficult to harvest and/or manufacture; it may be feasible to test compounds on groups comprised of pooled cells from lines of the same tumor tissue type (e.g. breast), measure the anti-cancer activity within that pool, and retest individual lines if any activity is seen overall. As heterogeneity is expected across tumor types, we can consider this to be a clustered data setting, where the clusters are defined by the nine types of tumor present in the NCI-60 lines (Breast, Central Nervous System (CNS), Colon, Leukemia, Melanoma, Non-Small-Cell Lung Cancer (NSCLC), Ovarian, Prostate, and Renal).

As a binary measure of anti-cancer activity, we used GI50 data recorded on the NCI-60 lines, which measure the concentration that causes 50% growth inhibition [29], dichotomized such that log₁₀ of concentration values ≤−6 indicated the presence of activity, while >−6 indicated the absence. We investigated three compounds: bulbophyllanthrone (NSC-708791), ethoxycurcumin trithiadiazolaminomethylcarbonte (NSC-742020), and carboxyphthalato platinum (NSC-271674). In each case, due to the small size of the clusters (range 2-9, median 7 cell lines), we used $l=2$ and estimated ${\hat{p}}_i$ for each cluster and $\hat{p}$ across all clusters. We then applied Procedures D, D´, and S to the remaining data, using estimated optimal group sizes based on ${\hat{p}}_i$ and $\hat{p}$, and recorded the observed number of tests (and corresponding observed average number of tests per subject). Due to the potential for interaction between cell lines, we did not group cell lines from different tumor types. In this example, exact cluster sizes and individual testing results were available for each cluster, compound, and cell line, and there is no inherent ordering to the individuals within the clusters. In order to assess overall algorithm performance for these data, we repeated our calculations across 5000 randomized orderings of the individuals within the clusters and present the average across these permutations of the data.

Table 4 shows the observed rates of anti-cancer activity for these compounds across the nine tumor types and the average number of tests per subject across these 5000 permutations of the data. For NSC-708791, $\hat{p}$ was more efficient than ${\hat{p}}_i$ for all three algorithms; despite the heterogeneity between cell lines, the overall proportion of cell lines for which the compound is active is low. ${\hat{p}}_i$ provided higher efficiency for Procedure D and both NSC-742020 and NSC-271674, due to the high heterogeneity for both compounds, but $\hat{p}$ was more efficient for D´ and S.

Table 4.

Results of NCI-60 Cell Lines data analysis: Observed rate of anti-cancer activity (% of cell lines observed to have GI50 < −6) and average number of tests per cell line across 5000 permutations of the individual cell lines within the clusters.

		Compound Name
	Tissue Type (# Cell Lines)	NSC-708791	NSC-271674	NSC-742020
Anti-Cancer Activity (% of cell lines with GI50 < −6)	Breast (6)	0%	0%	20%
	CNS (6)	0%	0%	17%
	Colon (7)	0%	14%	28%
	Leukemia (6)	33%	83%	100%
	Melanoma (9)	11%	0%	11%
	NSCLC (9)	11%	11%	0%
	Ovarian (7)	0%	0%	0%
	Prostate (2)	0%	0%	0%
	Renal (8)	0%	0%	0%
Algorithm	Prev. Est.	Average Number of Tests per Cell Line
D	$\hat{\mathit{p}}$	0.601	0.707	0.719
	${\hat{\mathit{p}}}_{\mathit{i}}$	0.682	0.696	0.710
D´	$\hat{\mathit{p}}$	0.601	0.679	0.730
	${\hat{\mathit{p}}}_{\mathit{i}}$	0.713	0.717	0.756
S	$\hat{\mathit{p}}$	0.531	0.681	0.724
	${\hat{\mathit{p}}}_{\mathit{i}}$	0.669	0.700	0.729

7. Discussion

In this paper, we have proposed different design strategies for disease screening using group testing when the population of interest has clustering. Using two motivating examples that cover a broad range of applications in the biosciences, we show the importance of our design results in practical situations. We considered different group testing algorithms, different approaches to estimating cluster prevalences, different ways to combine the individual samples into groups, and dilution effects.

Counter to our intuition, we found that in most situations, under our framework, estimating individual prevalences for determining group sizes did not result in increased efficiency relative to obtaining and using an overall estimate of prevalence. This is particularly true when the disease prevalence is small (<0.20) and the cluster variation is not extreme. However, when the prevalence and variability between clusters are high, there can be sizeable efficiency gains, relative to single-unit testing, from accounting for cluster structure in both design and implementation. Group testing is currently rarely used in practice when disease prevalence is high, but an approach incorporating cluster structure may still improve efficiency when both the overall disease prevalence and inter-cluster heterogeneity are high, allowing for single-unit testing on clusters with high prevalence and group testing on clusters with low prevalence.

In order to address the scenario where test sensitivity varies with group size, we incorporated dilution in simulations for the Dorfman design; we considered only this design due to its practical and simple approach, which is easily implemented in real-world scenarios. Dilution introduces an additional consideration in comparing designs; in addition to minimizing the number of tests, one can consider reducing the number of missed cases. This may be done by changing the objective function for the choice of the group size. However, if one does not want to specify additional parameters, using cluster-specific prevalence estimates for the choice of group sizes can provide this reduction as, on average, the boundedness of the prevalence estimates reduces the group sizes. This may provide a ‘balancing act’ in design selection; by the results discussed above, estimating cluster-specific prevalences often reduces efficiency in terms of number of tests, but it may also reduce the number of missed cases in a setting with dilution. For example, if a small amount of dilution ( $d=0.05$) is present but unknown or unaccounted for, using cluster-specific prevalence estimates can nearly halve the number of missed cases (Table S12b).

There exist complex dynamic programming algorithms to find optimal and efficient groupings in the GGTP setting if the individual prevalences are known (Procedure D: Hwang [30]; Procedure S: Malinovsky [31]). These methods perform equivalently to simply applying Procedures D and S on superclusters, due to the discreteness of the distribution of ${\hat{p}}_i$. There also exists an optimal nested group testing procedure for unclustered data (Sobel and Groll [5]), but it is not optimal for clustered data. Our work assumes that nothing is known a priori regarding the exact cluster prevalences, although the distribution of cluster prevalences may be known. This is not necessarily the case in all settings; for example, historical data may provide limited information about prevalence for some or all clusters. In such a situation, it may be possible to use this information to estimate $l_i^{\ast }$ as well as the current cluster prevalence, or to use group testing when estimating cluster prevalence.

We considered different ways to formulate groups, including composing groups from members of the same cluster, composing groups from individuals with the same estimated cluster-specific prevalence (i.e. within a supercluster), and disregarding clustering entirely. Similar to the issue of cluster prevalence estimation (i.e. cluster specific versus population), disregarding clustering when formulating groups does not result in substantial efficiency loss when the disease prevalence is small and the heterogeneity is not enormous.

We considered a design where we estimate the prevalence (either cluster specific or common) based on a small number of individual tests taken on each cluster, followed by applying group testing procedures to the remaining individual tests for each cluster. This test was chosen for its practical simplicity. However, Bayesian adaptive group testing designs could be developed where design choices (e.g. group size) are updated with increasing amounts of information as more testing is done in each cluster [6]. In order to calculate the optimal number of individual tests to perform on each cluster, we assume that the cluster prevalences follow a Beta distribution. However, the group testing may be conducted using nonparametric prevalence estimates. For a non-Beta prevalence distribution, the number of individual tests $l$ used for estimation may no longer be optimal, but Figure S1 indicates that this value is primarily dependent on cluster size and group testing procedure, and thus even a non-optimal $l$ for the appropriate procedure and cluster size is likely reasonable despite distribution misspecification.

Overall, our recommendation is that in most scenarios it is not necessary to account for clustering when performing group testing on clustered data; it is sufficient to estimate a single overall prevalence across all clusters and use this estimate for the choice of group size. The boundedness of the prevalence estimator distribution result in inaccurate estimation of low cluster prevalences (and corresponding optimum group sizes) when using a reasonable number of observations for estimation. Further, its discreteness results in even non-negligible amounts of between-cluster heterogeneity being represented by a limited number of possible (and more limited number of probable) group sizes. However, there may be efficiency gain in incorporating cluster-specific prevalence estimation into the design under extreme heterogeneity between clusters with not too small overall prevalence (i.e. a non-negligible fraction of clusters with prevalences on either side of the threshold for favoring single-unit vs. group testing), and if one suspects the presence of dilution, estimating prevalence cluster-by-cluster may provide a reduced number of missed cases.

Funding Statement

This work was supported by the Intramural Research Program of the National Cancer Institute. The views presented in this article are those of the authors and should not be viewed as official opinions or positions of the National Cancer Institute, National Institutes of Health, or US Department of Health and Human Services. The research of YM was supported by grant number 2020063 from the United States-Israel Binational Science Foundation (BSF), Jerusalem, Israel.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data that support the findings of this study are openly available from the AIDSVu web portal at https://aidsvu.org and the National Cancer Institute Division of Cancer Treatment and Diagnosis Developmental Therapeutics Program Public COMPARE portal at https://dtp.cancer.gov/databases_tools/compare.htm.