Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jun 26;127(26):5789–5798. doi: 10.1021/acs.jpcb.3c01804

Molecular Simulations of Conformational Transitions within the Insulin Receptor Kinase Reveal Consensus Features in a Multistep Activation Pathway

Kwangho Nam †,*, Yunwen Tao †, Victor Ovchinnikov ‡
PMCID: PMC10332359  PMID: 37363953

Abstract

graphic file with name jp3c01804_0006.jpg

Modulating the transitions between active and inactive conformations of protein kinases is the primary means of regulating their catalytic activity, achieved by phosphorylation of the activation loop (A-loop). To elucidate the mechanism of this conformational activation, we applied the string method to determine the conformational transition path of insulin receptor kinase between the active and inactive conformations and the corresponding free-energy profiles with and without A-loop phosphorylation. The conformational change was found to proceed in three sequential steps: first, the flipping of the DFG motif of the active site; second, rotation of the A-loop; finally, the inward movement of the αC helix. The main energetic bottleneck corresponds to the conformational change in the A-loop, while changes in the DFG motif and αC helix occur before and after A-loop conformational change, respectively. In accordance with this, two intermediate states are identified, the first state just after the DFG flipping and the second state after the A-loop rotation. These intermediates exhibit structural features characteristic of the corresponding inactive and active conformations of other protein kinases. To understand the impact of A-loop phosphorylation on kinase conformation, the free energies of A-loop phosphorylation were determined at several states along the conformational transition path using the free-energy perturbation simulations. The calculated free energies reveal that while the unphosphorylated kinase interconverts between the inactive and active conformations, A-loop phosphorylation restricts access to the inactive conformation, thereby increasing the active conformation population. Overall, this study suggests a consensus mechanism of conformational activation between different protein kinases.

Introduction

Protein kinases are key enzymes in signal transduction pathways that regulate cell growth, proliferation, metabolism, differentiation, and migration.1,2 Despite their different functions within the cell, they are structurally very similar and catalyze the same chemical reaction, i.e., the transfer of a phosphoryl group from adenosine triphosphate (ATP) to a target residue.3 Thus, normal cells precisely regulate their catalytic activity, and when dysregulated, many diseases, such as cancer, develop.4−7 Insulin receptor kinase (IRK) is a member of the tyrosine kinase superfamily and is the first enzyme in insulin signaling to transmit an extracellular insulin signal into the cell through dimerization-mediated activation of the kinase domain.8−11 The activated kinase domain then phosphorylates key tyrosine residues on downstream protein substrates, thereby activating the insulin signaling cascade. In the remainder of this paper, we will use IRK to refer to the kinase domain, for brevity.

Like other protein kinases, IRK is found with two major conformations: active and inactive (Figure 1a,b).7,12,13 The hallmarks that differentiate the two conformations are the orientation of the activation loop (A-loop), the αC helix, and the Asp-Phe-Gly (DFG) motif.12,13 In the inactive conformation, also called the autoinhibited conformation, the activation loop adopts an orientation that sterically blocks the active site of the enzyme.12 Activation of the enzyme is achieved by post-translational phosphorylation of three tyrosine residues (Tyr 1158, 1162, and 1163) within the A-loop. This leads to the transition of the activation loop to an open active conformation that permits the binding of ATP, Mg2+ ions, and target protein. This conformational transition, together with the rotation of the DFG motif and αC helix toward the active site, characterizes the major conformational change of IRK.13 These changes also accompany the formation of the so-called catalytic and regulatory spines (C- and R-spines, respectively).14,15 In particular, the adenine base of ATP binds into the hydrophobic pocket of the C-spine and the Phe 1151 (F1151) residue of the DFG motif inserts into the R-spine. In addition, the inward rotation of the αC helix brings Glu 1047 (E1047) close to Lys 1030 (K1030) to form a salt bridge with it.

Figure 1.

Figure 1

Open in a new tab

(a) Inactive12 and (b) active conformations of IRK.13 In the figure, αC-helix is shown in green cartoon, activation loop in (a) red and (b) salmon cartoons, DFG motif in orange, HRD motif in blue, C- and R-spine residues in yellow and violet spheres, and M1076 gatekeeper residue in green sphere. The remainder of the kinase is shown in white cartoon. (c) Free-energy profiles of IRK conformational change determined by the string method in collective variables (SMCV): black for the fully phosphorylated IRK (3P-IRK) and red for the unphosphorylated IRK (0P-IRK), respectively. The conformational change is described by the normalized reaction coordinate, α, between 0 for the inactive conformation and 1 for the active conformation. The state “I” refers to the inactive-state conformation shown in (a), the state “A” the active-state conformation of (b), and the state “I′” the DFG-in inactive conformation. Key events along the conformational change are indicated at the top of the figure.

While the A-loop, DFG motif, and αC helix form similar conformations in the active conformation between different protein kinases, their inactive conformations show notable differences.5,16 For example, in the cSrc kinase family, the DFG motif adopts an orientation characteristic of the active conformation, called DFG-in orientation (Figure S1a), in its inactive state.17 The IRK-like inactive DFG orientation, i.e., DFG-out orientation, is also observed for cSrc in the presence of certain drug molecules, such as imatinib (Figure S1b).18,19 In contrast, for cyclin-dependent kinase 2 (CDK2), only the DFG-in orientation has so far been reported for the inactive conformation (Figure S1c),20 and for IRK, only the DFG-out inactive conformation has been known.12 These conformational differences raise the question of whether their conformational changes to the active conformation occur through similar or different mechanisms. To this end, computational studies have played a significant role in advancing our understanding of this topic.21−27 For example, the Roux group has conducted extensive investigations on the conformational change of cSrc, focusing on the transitions between the DFG-in inactive conformation and the active conformation.24,26 Their findings revealed that the A-loop conformational change occur prior to the inward rotation of the αC helix, and both transitions occur with relatively small free-energy barriers. In a separate study, the same group examined DFG flipping in the inactive conformation and compared it with the Abl kinase.28 Interestingly, they observed a preference for the DFG-in conformation in cSrc, while the opposite was true for Abl, which aligns with previously reported X-ray structures.18,19 Based on their results, the Roux group proposed a role for the DFG’s Asp residue protonation in controlling the energetics of DFG-flipping, a concept also suggested by Shan et al. based on the MD simulations of epidermal growth factor receptor (EGFR) kinase.23 More recently, this hypothesis was further investigated by Tsai et al., who explored the protonation-dependent DFG flip in cSrc activation.27 This study confirmed that DFG-Asp protonation promotes the flipping of the motif, with the deprotonated Asp favoring the DFG-in conformation and the protonated Asp favoring the DFG-out conformation. However, despite these interesting findings, it is important to note that the X-ray structures used in these studies included ligands in their active site, which could perturb the actual orientation of the DFG motif and the A-loop, particularly when compared to IRK and IGF-1RK.

Upon full activation, IRK’s catalytic activity increases approximately 200-fold, which can be broken down into a 5–8-fold decrease in KM and a 36-fold increase in kcat (i.e., catalytic efficiency).29 Although the relationship between kinase conformation and catalytic activity has been well established, the actual mechanism underlying kinase activation is more complex.29−31 For instance, the basal-level catalytic activity displayed by unphosphorylated enzymes requires that the enzyme transiently adopts the active conformation to allow substrate binding and catalysis, rather than remaining in the inactive conformation, which cannot bind substrates due to blockage of the active site by the A-loop. To explain this and the allosteric effect of A-loop phosphorylation on kinase activity and substrate binding, we recently proposed a free-energy landscape of kinase activation based on the calculated free energies of A-loop phosphorylation of insulin-like growth factor 1 kinase (IGF-1RK), a close homologue of IRK, and other existing computational and experimental data.32 However, that study did not directly investigate the mechanism of kinase conformational change. To establish a connection between kinase conformation and experimental kinetic data, it is therefore necessary to determine the mechanisms of kinase conformational activation between fully phosphorylated and unphosphorylated forms of the kinase.

In the present study, we investigated the mechanism of IRK conformational change and its free-energy profile. Unlike that in Src, IRK activation involves the flipping out of the DFG-motif toward in-orientation, the swinging away of the A-loop from its inactive-state conformation to the active-state conformation and the inward rotation of the αC helix.13 During this conformational change, several residues near the active site rearrange to form new interactions, such as the K1030–E1047 salt-bridge and the R-spine interactions mentioned above. To achieve this complex conformational change, we have applied the string method (SM)33,34 together with the self-guided (SG)35 and targeted molecular dynamics (TMD) simulation techniques.36 Our simulations reveal that the kinase conformational change occurs roughly in three steps. First, the DFG-motif flips toward the in-orientation, while the A-loop remains in the inactive orientation. Then, the A-loop swings away from the ATP binding pocket and extends toward the orientation of the active conformation, which occurs with the highest free-energy barrier. Finally, the αC helix moves inward with the completion of the A-loop conformation change. Below, we provide a detailed comparison of the conformational change paths and their free-energy profiles between the fully phosphorylated and unphosphorylated IRKs. Furthermore, we compare the intermediates identified from the present study to the structures available for IRK and other protein kinases toward establishing a consensus of the kinase activation process. Finally, free-energy perturbation (FEP) simulations37−39 are performed to determine the impacts of A-loop phosphorylation on the free-energy values along the conformational change path determined by the SM simulations.

Methods

System Preparation and Equilibrium MD Simulations

The systems for the phosphorylated IRK were prepared based on the X-ray structures of IRK in the inactive (PDB ID: 1irk(12)) and active (PDB ID: 1ir3(13)) conformations. For each system, only the protein atoms were included, and protonation states of all ionizable side chains were determined based on their pKa values in water and interactions within the protein. The systems were then neutralized with 0.15 M NaCl and solvated with a 80 Å cubic box of TIP3P waters,40 resulting in a total of 48,925 atoms. For the unphosphorylated system, we mutated the phosphorylated Tyr residues back to the original Tyr residues.

Each system was first energy-minimized for 2500 steps, in which the first 1000 steps had harmonic restraints applied to protein backbone atoms and the remaining steps without any restraints. The resulting system was heated to 300.0 K over 12 ps and equilibrated for 88 ps with restraints on protein backbone atoms, followed by 200 ps MD simulations at 300 K without any restraints. Then, 1 μs MD simulations were performed at 300 K and 1 bar with 2 fs time integration step, and SHAKE41 was applied to all bonds involving hydrogen atoms. The temperature and pressure of the system were maintained using the Nose–Hoover thermostat42 and an extended system barostat,43 respectively. The particle mesh Ewald (PME) summation method44 was used for the electrostatic interactions, and the van der Waals (vdW) interactions were switched to zero between 10 and 12 Å. The all-atom CHARMM27 force fields45,46 were used for the protein, Na+ and Cl– ions, and the water molecules were represented by the TIP3P water potential. For the protein backbone dihedrals, the CMAP correction was applied.47,48 All simulations were performed using the CHARMM program (version c45a2)49 utilizing the DOMDEC-GPU module50 for GPU acceleration.

String Method in Collective Variables (SMCV) Simulation

The initial path for the conformational change between the inactive and active conformations of IRK was generated by applying the generalized self-guided molecular dynamics (SGMD) simulation method35 in the inactive and active conformations, respectively. The atoms to which the SGMD guiding force was applied included the backbone atoms of K1030, the αC helix residues between 1037 and 1055, and the A-loop between 1152 and 1175, as well as the heavy atoms of the DFG residues. A total of 100 ns SGMD simulation was performed for each of the inactive and the active-state conformations. All other details of the simulation were identical to the equilibrium MD simulations described above. Then, TMD simulations36 were performed from the DFG-flipped inactive conformation to the active conformation as well as to the (DFG-out) inactive conformation, in which the same set of atoms as in the SGMD simulation was selected to apply the TMD perturbation. The perturbation was applied to decrease the root-mean-square displacement (rmsd) from the target structure at the rate of 1 Å for every 200 ps MD simulation. During the TMD simulation, a total of 28 snapshots and restart files were saved and relaxed for 5 ns for each saved snapshot using MD without any restraints.

Starting from the initial path, SMCV path optimization was performed for 40 ns (for each SM replica and a total of 30 replicas to represent the entire conformational change pathway) in an iterative manner.34,51 Each iteration consisted of a 2 ps MD simulation (for each SM replica), during which the forces on each collective variable were evaluated as the local free-energy gradient, evolution of the path following the local free-energy gradient, and finally, reparameterization of the path to redistribute each collective variable along the updated path. The convergence of the paths during 40 ns path optimization simulation is shown for selected SM replicas in Figure S2. Then, the potential of mean force SM simulations were performed for 80 ns for each replica without the conformational change path update, and the free-energy value as a function of α was computed by the thermodynamic integration scheme, using

graphic file with name jp3c01804_m001.jpg 1

where ΔF refers to the free energy at α relative to the free energy at α = 0.0, and dF/dα is the free-energy gradient computed as a time average of the force acting on the path. For the 0P-IRK system, the path optimization was carried out starting from the initial path of the 3P-IRK system after removing the phosphoryl group from each A-loop Tyr residue. The overall procedure was the same as for the 3P-IRK system. For each system, the total lengths of the SM simulations were 3.6 μs.

In the SM simulations, the following collective variables (CVs) were used to describe the conformational change path: (1) the center of mass (COM) of the backbone heavy atoms of K1030, the αC helix residues between 1939 and 1052, V1074, H1130, DFG motif, and the A-loop residues between 1154 and 1175 and (2) the center of mass of the side chain heavy atoms of K1030, αC helix residues between 1039 and 1052, V1074, H1130, DFG motif’s D1150 and F1151, and A-loop residues between 1154 and 1175. In addition to these residues, the backbone of the αE and F helices (residues 1106–1125 for αE and residues 1188–1205 for αF) were used to define the relative orientation for each COM position of the collective variables. Thus, a total of 80 COM collective variable positions were used as CVs and 38 COM positions for relative orientation, respectively. Here, these CVs were selected with the goal to understand the interplay between the three structural elements that underlie the transition (i.e., αC helix, A-loop, and the DFG motif). However, it is important to note that the string method implicitly considers a coarse-grained landscape within the selected CV space, and as a result, the computed paths and free energies are implicitly dependent on this landscape.34 Therefore, the challenge lies in finding a unique set of CVs that accurately characterizes a conformational transition. In principle, different sets of CVs could be tested posteriorly using commitment analysis.52 This analysis involves initiating numerous unbiased simulations from a putative transition state identified from the free-energy landscape and computing the probability of “committing” to the reactant state vs the product state. For true transition states, this probability should exhibit a sharply peaked density around 0.5. However, conducting the commitment test becomes computationally intractable for complex systems,34 as it typically requires very long MD trajectories. Enhanced sampling methods have been developed specifically to avoid such lengthy simulations. In the present case, due to the high computational cost involved, we have not validated the choice of CV using the committor test; in fact, even MD simulations of 10 ns performed at each SM image did not show significant changes in the conformation. Nevertheless, although each individual free-energy profile may be considered a subjective function of the chosen CV set, we believe it is still valid to compare the free-energy profiles of phosphorylated and unphosphorylated systems using the same CV set. Furthermore, within a single profile, certain features are physically meaningful, such as the relative depth of different minima. Additionally, since the employed CVs are essentially Cartesian coordinates, their corresponding metric tensors are close to diagonal mass matrices, which suggests that entropic contributions due to coordinate transformation to CV space are the same between different minima.53

FEP Simulation

Free-energy differences between the phosphorylated and unphosphorylated IRK were calculated with the FEP simulation method.37,54,55 These simulations were conducted by alchemically mutating each tyrosine to phosphor-tyrosine (and vice versa) at four different conformational states of IRK (at α = 0.0, 0.2, 0.8, and 1.0, respectively). As a reference, the FEP simulations were also performed for the dephosphorylation of hexapeptide pYETDpYpY (segment of the A-loop and pY refers to the phosphor-Tyr) in water.

Each phosphor-Tyr → Tyr mutation simulation was performed with the dual topology approach,56 i.e., the side chain of the Tyr and phosphor-Tyr (pTyr) residues co-existed throughout the entire transformation, with phosphor-Tyr modeled as doubly negatively charged, and the total charge of the system has changed, e.g., from −3 to 3 during the dephosphorylation transformation. These end-state charges were selected to minimize the charge correction needed. The nonbonded interactions (i.e., electrostatic and vdW interactions) of the pTyr side chain with the protein/water environment were gradually scaled to zero with λ as the coupling parameter between the start and end-state potentials. At the same time, the nonbonded interactions between the Tyr side chain and the environment were gradually turned on. The intramolecular nonbonded (self-) interactions for Tyr and pTyr were also scaled (i.e., turned on or off) accordingly. In all transformation simulations, the interaction between Tyr and pTyr side chains was excluded and a soft-core potential55 was applied to avoid end-point singularities. Each transformation was accomplished in 34 λ steps (i.e., λ = 0.00, 0.01, 0.02, 0.06, 0.09, 0.13, 0.16, 0.19, 0.22, 0.26, 0.29, 0.33, 0.36, 0.39, 0.42, 0.46, 0.49, 0.53, 0.56, 0.59, 0.62, 0.66, 0.69, 0.73, 0.76, 0.79, 0.82, 0.86, 0.89, 0.93, 0.96, 0.98, 0.99, and 1.00). At each λ, a total of 9 ns MD simulation was performed and the 4000 coordinate sets saved from the last 8 ns were used for free-energy calculations by the Bennett acceptance ratio method (BAR).57 To estimate the error in the free-energy values, the bootstrap strategy58,59 was employed by resampling the 4000 snapshots, and this process was repeated 1000 times. A histogram with a bin size of 0.05 kcal/mol was created for these 1000 free-energy values, and a Gaussian function was fitted against this histogram to determine the 95% confidence interval. Additionally, we determined the free energy of the (intramolecular) bonded interactions of pTyr and Tyr to complete the transformation, where bonded terms such as bond, angle, and torsional energies of both Tyr and pTyr were not scaled in the above simulations. These values were used as a correction for the free energies of A-loop phosphorylation, reported in Table 1.

Table 1. Free-Energy (FE) Values of A-Loop Phosphorylation Determined from the FEP Simulations at Selected Points Along the Kinase Conformational Change of IRK. All Free Energy Values Are Given in kcal/mol.

  IRK
 water (reference)
  α = 0.0 α = 0.2 α = 0.8 α = 1.0  
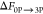Inline graphic a –601.9 ± 0.6 –600.9 ± 0.6 –609.0 ± 0.4 –608.1 ± 0.5 –603.7 ± 0.4
relative FEb 1.8 2.8 –5.3 –4.4  
Open in a new tab
a

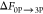The Inline graphic value is the negative of the free energy determined for 3P → 0P dephosphorylation simulation performed for 3P-IRK.

b

The relative FE value is the FE difference from the reference value in water.

All FEP simulations were performed using the BLaDE program60 interfaced with the CHARMM program (version c47a2).49 In addition, 50 ns MD simulations were performed starting from each of the end-state conformations of the alchemical transformation for the analysis of their conformational overlap between the different end states.

Results and Discussion

Determination of Conformational Change Pathway

Our efforts to determine the mechanism of IRK conformational change began with the TMD simulations36,61 applied to drive the conformational change between the inactive and active conformations. Our original plan was to use the TMD-generated pathways as the input/initial path for path optimization using the SMCV.34 Recently, this combined TMD/SM simulation approach was applied to study the conformational change mechanism of human 8-oxoguanine DNA glycosylase upon recognition of damage nucleotide in base excision repair.51 In the present study, we first performed the TMD simulation starting from the inactive conformation to the active conformation and then the simulation in the reverse direction, i.e., active-to-inactive conformational change, to check the consistency between the TMD-generated paths. However, both simulations generated two different paths where the A-loop conformation change occurred as the first event and the DFG-motif flipping as the last event. This inconsistency in the sequence of events between forward and reverse paths is a well-known issue with the TMD simulation method.61,62 In particular, since A-loop contributes the most to the order parameter of TMD, i.e., the rmsd with respect to the target structure, its change occurs as the earliest event during TMD. Moreover, the sequence of events did not change during subsequent SMCV path optimization.

We therefore modified our approach and performed SGMD simulation35 to examine the early events of the conformational change in a collective-variable independent manner. The (100 ns) SGMD simulation in the inactive conformation showed a transition of the DFG motif from out- to in-conformation, after which no significant change was observed in A-loop. In the DFG-flipped conformation, the D1150 residue of the DFG motif, which now faces the active site, forms a salt bridge with K1030 of the catalytic domain’s β3 sheet, and the flipped F1151 contacts M1051 and H1130 R-spine residues (Figure S3). [This interaction pattern differs from that of the holo-state (active conformation) enzyme, where D1150 coordinates with two bound Mg2+ ions and K1030 forms a salt bridge with E1047 of αC helix.13] In contrast, in the (apo-state) active conformation, both A-loop and DFG motif remained unchanged during the 100 ns SGMD simulation. Based on the result, we propose that the first event in the inactive-to-active conformational change is the flipping of the DFG motif, followed by the A-loop conformational change, and the inward rotation of the αC helix as the last event. This sequence of events is supported by X-ray crystallographic structures determined for different protein kinases. For example, the X-ray structure of cSrc in the inactive state has its DFG flipped to that of the active conformation, i.e., DFG-in.17 This DFG orientation is comparable to the DFG-in orientation of the SGMD simulation in the inactive conformation (Figure S1a). cSrc has also been shown to adopt the DFG-out conformation in the presence of an inhibitor molecule (Figure S1b).18 The two inactive conformations, i.e., DFG-in and -out, have also been reported for cAbl kinase.21 In CDK2, the apo-state enzyme only showed the DFG-in orientation (Figure S1c), in which F146 (of the DFG motif) contacted H125,20 similar to our DFG-flipped conformation. Additionally, in both cSrc and CDK2, the DFG-in inactive conformation has the salt-bridge interaction between the flipped aspartate residue and the lysine residue of the catalytic domain (i.e., in cSrc between D404 and K295 and in CDK2 between D127 and K33).

Starting from the DFG-in inactive conformation, we resumed the search of the conformational change path with the TMD simulations to drive the conformational change of A-loop and αC helix to the active conformation as well as the DFG-out to in conformational change. Then, for each of the 28 selected conformations along the TMD generated pathways, unbiased MD simulations were performed to equilibrate the structures. The resulting structures, along with the (DFG-out) inactive and active conformation structures, were used as the input pathway for the path optimization and free-energy calculation using the string method. All of the above simulations were performed with fully phosphorylated A-loop (i.e., triply phosphorylated A-loop), hereafter denoted by 3P-IRK. For the unphosphorylated state IRK (i.e., 0P-IRK), we removed the phosphoryl groups from the A-loop of 3P-IRK and starting from the 3P-IRK path, performed the SMCV path reoptimization and free-energy calculation. The details of the SM simulations are provided in the Methods section.

Free-Energy Landscape of IRK Conformational Change

The free-energy profiles thus determined are presented in Figure 1c, in which the entire conformational change can be divided into three separate steps as annotated at the top of the FE profile. Key conformations along the SM-optimized conformational change path of 3P-IRK are shown in Figure 2, and the entire paths are shown in the Supporting Information Movie. Figure 1c shows that the free-energy barrier of DFG flipping is relatively low in both the 0P and 3P state IRK (2.8 kcal/mol for 0P-IRK and 4.8 kcal/mol for 3P-IRK) and that the DFG-in inactive conformation forms a stable minimum at α = 0.2. During flipping, F1151 of DFG rotates away from C-spine residues V1010 and M1139 (Figure 2a,b), which sandwiches F1151 in the (DFG-out) inactive conformation and also the adenine base of ATP in the active conformation. In the DFG-in inactive conformation (at α = 0.2), the flipped DFG motif is stabilized by two interactions: first the salt-bridge interaction between D1150 of DFG and K1030 (Figure 3a) and the π-stacking formed between flipped F1151 and H1130 (Figure 2b). The insertion of F1151 into the R-spine (between M1051 of αC and H1130 of the HRD motif) takes place during the subsequent steps (Figure 2c).

Figure 2.

Figure 2

Open in a new tab

Snapshots along the conformational change pathway of 3P-IRK, showing the change of A-loop, αC helix, DFG motif, K1030-E1047 interaction, and insertion of F1151 to the R-spine. The bottom figure is the close-up view showing the change of F1151 orientation relative to C-spine, H1130, and R-spine residues along the conformational change pathway. The color scheme is as in Figure 1.

Figure 3.

Figure 3

Open in a new tab

(a) K1030–E1047 (black) and K1030–D1150 (orange) salt-bridge interaction distances along the conformational change pathway of 3P-IRK. (b) Distribution of rmsd values with respect to the active (X-axis) and inactive conformations (Y-axis), along the SM conformational change pathway of 3P-IRK. The figure is color-coded according to α between 0 and 1. The rmsd values are computed for protein backbone atoms excluding the flexible N- and C-terminal regions. The top-right insert shows the rmsd of the αC helix, and the bottom-left insert shows the rmsd of the A-loop. The green arrows indicate the rmsd distribution at α = 0.63. (c) Cumulative sum of projection square for the inactive (lower panel) and active conformation MD simulations (upper panel) relative to the principal component analysis (PCA) modes. The cumulative sum was calculated as 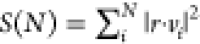Inline graphic, where r and vi denote the displacement vector for each sampled coordinates relative to the average structure and the ith PCA mode vector, respectively, and the PCA modes were determined to N = 5, i.e., up to the 5th slowest mode. For each MD system, the S(N) values and their running averages are determined relative to both the inactive (solid-black) and active PCA modes (solid-red). In the upper panel, the protein coordinates are from the MD simulations of the active conformation and in the bottom panel, from the inactive conformation MD simulations. Thus, both simulations show a large overlap relative to their respective PCA modes while a small overlap is obtained relative to the other PCA modes. (d) Cumulative sum S(N) for each sampled coordinate from SM simulations: the gray points are relative to the inactive-state PCA modes, and the color-coded points are relative to the active-state PCA modes. At each α value, the average and standard deviations are also shown. The color-coding is the same as in (b). As a reference, the S(N) values are shown for the MD simulations performed for (c): black for the inactive conformation and red for the active conformation MD simulations.

The DFG-flipped inactive conformation (the IApo′ state at α = 0.2 in Figure 1c) has a lower free energy than the DFG-out inactive conformation (the IApo state), by 7.1 kcal/mol for 0P-IRK and 1.7 kcal/mol for 3P-IRK. This result proposes that the two conformations exist as an equilibrium in solution, where the DFG-in inactive conformation is dominant. Importantly, except for the DFG-out vs -in difference, both conformations (i.e., IApo and IApo) share a very similar overall structure (Figure 3b), including their A-loop and αC helix orientations. We further characterized the two states by projecting protein configurations saved from SM simulations onto the five slowest protein motions determined at the DFG-out inactive conformation (Figure 3c,d). Between α = 0.0 and 0.2, the cumulative projection decreases from 0.56 ± 0.05 to 0.45 ± 0.03. It remains near the value until α = 0.3 and gradually decreases with the change of A-loop conformation. This suggests that the two conformations have similar intrinsic protein motions, and also that protein motions associated with the low-frequency PCA modes likely contribute to the DFG-flipping conformational change, as evidenced by the diminished cumulative protection above. The opposite trend is observed from the projection to the protein motions of the active conformation. Namely, the last event in conformational change is consistent with the intrinsic protein motions of the active conformation. To provide a reference data, Figure 3c compares the projections of the MD simulations performed at the (DFG-out) inactive and active conformations, which shows little overlap of intrinsic protein motions between the two conformations. These results suggest that the driving forces for the first and last events are different from that of the A-loop conformational change, which is consistent with the three-step conformational change mechanism proposed from Figure 1c.

As mentioned above, the DFG-in inactive conformation is stabilized by two interactions, i.e., salt bridge between D1150 and K1030 and π-stacking between F1151 and H1130 (Figure 2b). The D1150-K1030 salt-bridge is also observed in the X-ray structure of the DFG-in inactive conformation of cSrc between D404 and K295 (PDB ID: 2src; Figure S1a).17 However, this structure was crystallized in the presence of an ATP analogue, adenyl-5′-yl imidodiphosphate (AMP-PNP). In this case, since the adenine base of AMP-PNP binds in the space that F405 (equivalent to IRK F1151) would have occupied in its out-orientation state, it is possible that the DFG motif is forced to flip and that F405 is partly inserted into the R-spine of the kinase. Here, we describe this orientation to be “partly inserted” to distinguish it from the full insertion as seen in the active conformation (e.g., 3dqw(63)). In addition, the bound ligand and the DFG flipping push the A-loop away from the A-loop orientation of the imatinib-bound complex (Figure S1b) or that of the inactive conformation of IRK (Figure 1a), toward the orientation observed in the 2src X-ray structure. Consistent with this, this conformation is similar to our simulated IRK structure near α = 0.5, where F1151 is partly inserted into the R-spine and A-loop is significantly rotated toward the active conformation (Figure 4a,b). Moreover, K1030 retains its salt-bridge interaction with D1150, while E1047 is away from K1030. The K1030–E1047 salt-bridge begins to form with the rotation of the αC helix toward its in-orientation near α = 0.6. This interaction pattern (i.e., the K1030–D1150 salt-bridge and no interaction with E1047) is also observed in the inactive conformation of CDK2 (Figure S1c),20 and our conformation at α = 0.4 (Figure 2c) is comparable to the inactive conformation of CDK2. This similarity suggests that our simulated structures capture the inactive conformations observed in other kinases and that these X-ray structures represent the kinase conformation later in the conformational activation process of IRK.

Figure 4.

Figure 4

Open in a new tab

(a,b) DFG-in (orange ball-and-stick) and partly rotated A-loop (red cartoon) orientations of IRK at α ≈ 0.5 and (c,d) autoinhibited state structure of cSrc (PDB ID: 2src(17)), whose A-loop orientation is comparable to that of IRK near α ≈ 0.5. In comparison with the A-loop of the imatinib-bound cSrc structure (PDB ID: 2oiq;18Figure S1b), the A-loop orientation of 2src likely represents an intermediate of A-loop conformational change to the active conformation. In both figures, the phenylalanine of the DFG motif is shown in orange spheres, and the salt-bridge between the catalytic lysine (K1030 of IRK and K295 of cSrc) and the DFG’s aspartate residue is shown with dotted line.

The step in the conformational transition with the highest free-energy barrier is the change in the A-loop orientation between α = 0.2 and 0.8, which is predicted to be the rate-determining step and proceeds through 2–3 meta-stable substates (Figure 1c). This is reasonable, given that the A-loop rotates through nearly 180°. Thus, the change in the rmsd along the conformational change path is dominated by the change in A-loop orientation (lower insert of Figure 3b); the αC helix begins to rotate inward only for α > 0.6 (upper insert of Figure 3b). The A-loop tyrosines continuously form new interactions and break existing ones along the conformational transition pathway (Supporting Information, Movie). Therefore, except for the increase of the free energy between α = 0.2–0.3, the free-energy landscape of 0P-IRK is relatively flat during the A-loop conformational transition. In contrast, 3P-IRK shows larger free-energy changes during this step, likely because phosphorylated A-loop tyrosines (phosphor-Tyr’s) can form stronger interactions with neighboring residues; in some cases, buffer Na+ ions form bridged interactions with A-loop phosphor-Tyr’s and nearby charged residues. Consistent with these differences between Tyr and phosphor-Tyr, the location of the transition state is different between the two kinases, i.e., α = 0.33 for 3P-IRK and 0.67 for 0P-IRK. Nevertheless, their free-energy barriers are similar: 13.6 kcal/mol for 3P-IRK and 15.8 kcal/mol for 0P-IRK. As the A-loop settles into the orientation close to that of the active conformation, the free energy drops, forming the second intermediate state around α = 0.8 (Figure 1c). The conformation at this state can be characterized by the full insertion of F1151 into the R-spine, the three-way salt bridge between K1030, E1047, and D1150, and the near-complete conformational change of A-loop (Figure 2e). For 3P-IRK, this state has the lowest free energy over the entire conformational change pathway (by −21.4 kcal/mol relative to the DFG-out inactive conformation and by −19.7 kcal/mol versus the DFG-in inactive conformation). For 0P-IRK, this state is also a stable state. However, it is not the most stable state, and its free energy is higher than that of the DFG-in inactive conformation by 3.2 kcal/mol.

Finally, the αC helix rotates inward with the completion of the A-loop conformational change between α = 0.8 and 1.0 (Figures 2d–f and 3b). This step is energetically uphill in both the 0P and 3P kinases, but the free-energy change is significantly smaller in 3P-IRK than in 0P-IRK (Figure 1c). This change in free energy may be due to the absence of ligands (e.g., ATP, Mg2+ ions, and/or target protein). In other words, substrate binding would be necessary to make the inward rotation of the αC helix energetically favorable. This interpretation is consistent with the observed collapse of the glycine-rich loop of N-lobe toward the C-lobe at α = 1.0, which is driven by the hydrophobic contact formed between V1010 (C-spine), M1076 (gatekeeper residue), and M1139 (Figure 2f). Additionally, two arginine residues, Arg 1039 (R1039) of the αC helix and Arg 1155 (R1155) of the A-loop, which interact with phosphor-Tyr 1163 in 3P-IRK, form salt-bridge interactions with Glu 1043 (E1043) of the αC helix in 0P-IRK. The interaction with R1155, in particular, physically blocks the inward rotation of the αC helix and must be broken to achieve the catalytically competent active conformation. In our recent study of IGF-1RK, we highlighted the importance of the salt-bridge interactions formed between the A-loop and αC helix residues to the inward motion of the αC helix.32

Based on our findings and the fact that the active conformation of IRK was crystallized with substrates, we hypothesize that the completion of the conformation change occurs with substrate binding or after substrate binding, possibly in an induced-fit manner. Then, the conformation at α = 0.8 can be considered as an open active site for substrate binding, and the free-energy difference between α = 0.8 and 1.0 is overcome by the binding of ATP, Mg2+(s), and substrate protein. Based on this hypothesis, the relatively small free-energy difference between the active (α = 0.8) and inactive conformations (α = 0.0 and/or 0.2) of 0P-IRK can explain the basal level catalytic activity of the enzyme. As we discussed in our study of IRK catalysis,31 the unphosphorylated kinase (0P-IRK) must transiently adopt the active conformation to perform the basal level catalytic activity. For this, the two conformations must have a relatively small free-energy difference, as shown in Figure 1c for 0P-IRK.

Free Energy of A-Loop Phosphorylation

To gain further insight into the free-energy landscape of IRK conformational transition, we performed FEP simulation39,55 to determine the free energy of A-loop phosphorylation at Y1158, Y1162, and Y1163. The dephosphorylation simulation (i.e., 3P → 0P) was initiated starting from the DFG-out inactive conformation (α = 0.0) of 3P-IRK, and the negative of the free energy was used as the free energy of A-loop phosphorylation (i.e., 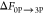Inline graphic) in Table 1. In the table, the large negative free energies are due to the solvation of three phosphor-Tyr residues. For a reference, we also performed the same simulation on a short A-loop peptide containing all three Tyr residues in water, which serves as a representation of the unfolded protein. By comparing the results, we can access the impact of A-loop phosphorylation on protein stability between different conformational states, relative to the unfolded protein.

The computed free-energy values indicate that A-loop phosphorylation destabilizes the (DFG-out) inactive conformation by 1.8 kcal/mol and stabilizes the active conformation by 5.3 kcal/mol (at α = 0.8). This leads to a shift of 7.1 kcal/mol in the free energy of the inactive conformation relative to the active conformation (between α = 0.0 and 0.8), making the inactive conformation thermodynamically inaccessible for 3P-IRK enzyme; between α = 0.2 and 0.8, the free-energy gap increases to 8.1 kcal/mol. This result is consistent with our previous IGF-1RK study.32 However, based on the SM simulation results (Figure 1c), we expected much larger stabilization of the α = 0.8 and 1.0 states for 3P-IRK relative to the value in water. We suspect that this discrepancy might be due to differences in IRK conformations between the 0P and 3P systems, at each α value. For example, in the 0P-IRK system near α = 1.0, the R1155–E1043 salt-bridge formation blocked the inward rotation of the αC helix. This disparity in the conformation and interaction network between the 0P and 3P-IRK systems may not have been fully captured in the FEP simulations. To check this possibility, we performed 50 ns MD simulations from the end state of the 3P → 0P transformation simulations and compared their rmsd values relative to the 0P-IRK end state MD simulations. However, despite both simulations corresponding to the same unphosphorylated A-loop systems, the sampled configurations did not overlap in all simulated states (Figure S4), suggesting that the free energies of the alchemical transformation were not fully converged in terms of protein conformation and would require significantly longer simulations. Therefore, while the trends of the FEP simulation results are consistent with the SM simulation results, we must be cautious in quantitatively interpreting the values from the FEP simulations.

Conclusions

The present study reveals interesting details on the conformational change mechanism and their differences between IRK with unphosphorylated and fully phosphorylated activation loops (A-loop). First, the conformational activation of IRK can be described as a three-step process that involves two intermediates and multiple meta-stable states. Energetically, kinase phosphorylation significantly stabilizes the active conformation relative to the inactive conformation. In particular, for the fully phosphorylated IRK (3P-IRK), the active conformation is favored by 21.4 kcal/mol (between α = 0 and 0.8). The slowest step is observed during the A-loop conformational change with a 13.6 kcal/mol barrier. For the unphosphorylated kinase (0P-IRK), the free energy of the active conformation at α = 0.8 is within the sampling error of the (DFG-out) inactive conformation and is 3.2 kcal/mol higher than that of the DFG-in inactive conformation. Second, while the increase in free energy at the onset of the A-loop conformational change (between α = 0.2 and 0.3) is similar between 0P and 3P-IRKs, the decrease in free energy during the A-loop rotation is greater for 3P kinase, especially, between α = 0.65 and 0.8. This decrease in free energy can be attributed to the favorable and stronger interactions formed between the phosphorylated tyrosine residues of A-loop and surrounding residues, which are more pronounced as A-loop adopts the active conformation. In contrast, the phosphorylation of A-loop in the inactive conformation is unfavored. Third, the large free-energy difference in the conformational change suggests that the inactive conformation is essentially inaccessible by the fully phosphorylated kinase, while the inactive-state kinase (i.e., unphosphorylated kinase) accesses both the active and inactive conformations. Finally, the similarity of the two identified intermediates to existing structures of other kinases suggests a common mechanism of kinase conformational activation.

Acknowledgments

This research was supported by the National Institute of General Medical Sciences of the National Institute of Health (R01GM132481 to K.N.). Computer resources were provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N) and by the National Energy Research Scientific Computing (NERSC) Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231.

Data Availability Statement

Initial PDB coordinates of all systems were obtained from the RCSB Protein Data Bank (https://www.rcsb.org/). The CHARMM program, parameters, and topologies are available from the CHARMM homepage (https://www.charmm.org/). Data (MD trajectories) obtained in this work, systems, and input files for MD and SM simulations can be obtained from the authors of the manuscript upon request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.3c01804.

  • Comparison of X-ray structures of Src and CDK2, CV rmsd convergence, SGMD snapshot, and rmsd analysis of free-energy perturbation simulations (PDF)

  • Entire path of conformations along the SM-optimized conformational change of 3P-IRK (MPG)

The authors declare no competing financial interest.

Supplementary Material

jp3c01804_si_001.pdf (591.5KB, pdf)
jp3c01804_si_002.mpg (23.2MB, mpg)

References

  1. Blume-Jensen P.; Hunter T. Oncogenic kinase signalling. Nature 2001, 411, 355–365. 10.1038/35077225. [DOI] [PubMed] [Google Scholar]
  2. Cohen P. Protein kinases - the major drug targets of the twenty-first century?. Nat. Rev. Drug Discov. 2002, 1, 309–315. 10.1038/nrd773. [DOI] [PubMed] [Google Scholar]
  3. Adams J. A. Kinetic and catalytic mechanisms of protein kinases. Chem. Rev. 2001, 101, 2271–2290. 10.1021/cr000230w. [DOI] [PubMed] [Google Scholar]
  4. Endicott J. A.; Noble M. E. M.; Johnson L. N. The Structural Basis for Control of Eukaryotic Protein Kinases. Annu. Rev. Biochem. 2012, 81, 587–613. 10.1146/annurev-biochem-052410-090317. [DOI] [PubMed] [Google Scholar]
  5. Nolen B.; Taylor S.; Ghosh G. Regulation of Protein Kinases: Controlling Activity Through Activation Segment Conformation. Mol. Cell 2004, 15, 661–675. 10.1016/j.molcel.2004.08.024. [DOI] [PubMed] [Google Scholar]
  6. Lengyel E.; Sawada K.; Salgia R. Tyrosine Kinase Mutations in Human Cancer. Curr. Mol. Med. 2007, 7, 77–84. 10.2174/156652407779940486. [DOI] [PubMed] [Google Scholar]
  7. Hubbard S. R.; Till J. H. Protein Tyrosine Kinase Structure and Function. Annu. Rev. Biochem. 2000, 69, 373–398. 10.1146/annurev.biochem.69.1.373. [DOI] [PubMed] [Google Scholar]
  8. Haeusler R. A.; McGraw T. E.; Accili D. Biochemical and cellular properties of insulin receptor signalling. Nat. Rev. Mol. Cell Biol. 2018, 19, 31–44. 10.1038/nrm.2017.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hubbard S. R.; Miller W. T. Receptor tyrosine kinases: mechanisms of activation and signaling. Curr. Opin. Cell Biol. 2007, 19, 117–123. 10.1016/j.ceb.2007.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cabail M. Z.; Li S.; Lemmon E.; Bowen M. E.; Hubbard S. R.; Miller T. The insulin and IGF1 receptor kinase domains are functional dimers in the activated state. Nat. Commun. 2015, 6, 6406. 10.1038/ncomms7406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Youngren J. F. Regulation of insulin receptor function. Cell. Mol. Life Sci. 2007, 64, 873–891. 10.1007/s00018-007-6359-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hubbard S. R.; Wei L.; Hendrickson W. A. Crystal structure of the tyrosine kinase domain of the human insulin receptor. Nature 1994, 372, 746–754. 10.1038/372746a0. [DOI] [PubMed] [Google Scholar]
  13. Hubbard S. R. Crystal structure of the activated insulin receptor tyrosine kinase in complex with peptide substrate and ATP analog. EMBO J. 1997, 16, 5572–5581. 10.1093/emboj/16.18.5572. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Taylor S. S.; Kornev A. Protein kinases: evolution of dynamic regulatory proteins. Trends Biochem. Sci. 2011, 36, 65–77. 10.1016/j.tibs.2010.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Meharena H. S.; Chang P.; Keshwani M. M.; Oruganty K.; Nene A. K.; Kannan N.; Taylor S. S.; Kornev A. P. Deciphering the Structural Basis of Eukaryotic Protein Kinase Regulation. PLoS Biol. 2013, 11, e1001680 10.1371/journal.pbio.1001680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Tong M.; Seeliger M. A. Targeting Conformational Plasticity of Protein Kinases. ACS Chem. Biol. 2015, 10, 190–200. 10.1021/cb500870a. [DOI] [PubMed] [Google Scholar]
  17. Xu W.; Doshi A.; Lei M.; Eck M. J.; Harrison S. C. Crystal Structures of c-Src Reveal Features of Its Autoinhibitory Mechanism. Mol. Cell 1999, 3, 629–638. 10.1016/s1097-2765(00)80356-1. [DOI] [PubMed] [Google Scholar]
  18. Seeliger M. A.; Nagar B.; Frank F.; Cao X.; Henderson M. N.; Kuriyan J. c-Src Binds to the Cancer Drug Imatinib with an Inactive Abl/c-Kit Conformation and a Distributed Thermodynamic Penalty. Structure 2007, 15, 299–311. 10.1016/j.str.2007.01.015. [DOI] [PubMed] [Google Scholar]
  19. Seeliger M. A.; Ranjitkar P.; Kasap C.; Shan Y.; Shaw D. E.; Shah N. P.; Kuriyan J.; Maly D. J. Equally Potent Inhibition of c-Src and Abl by Compounds that Recognize Inactive Kinase Conformations. Cancer Res. 2009, 69, 2384–2392. 10.1158/0008-5472.can-08-3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Schulze-Gahmen U.; De Bondt H. L.; Kim S.-H. High-Resolution Crystal Structures of Human Cyclin-Dependent Kinase 2 with and without ATP: Bound Waters and Natural Ligand as Guides for Inhibitor Design. J. Med. Chem. 1996, 39, 4540–4546. 10.1021/jm960402a. [DOI] [PubMed] [Google Scholar]
  21. Levinson N. M.; Kuchment O.; Shen K.; Young M. A.; Koldobskiy M.; Karplus M.; Cole P. A.; Kuriyan J. A Src-Like Inactive Conformation in the Abl Tyrosine Kinase Domain. PLoS Biol. 2006, 4, e144 10.1371/journal.pbio.0040144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Huang H.; Zhao R.; Dickson B. M.; Skeel R. D.; Post C. B. αC Helix as a Switch in the Conformational Transition of Src/CDK-like Kinase Domains. J. Phys. Chem. B 2012, 116, 4465–4475. 10.1021/jp301628r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Shan Y.; Arkhipov A.; Kim E. T.; Pan A. C.; Shaw D. E. Transitions to catalytically inactive conformations in EGFR kinase. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 7270–7275. 10.1073/pnas.1220843110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Shukla D.; Meng Y.; Roux B.; Pande V. S. Activation pathway of Src kinase reveals intermediate states as targets for drug design. Nat. Commun. 2014, 5, 3397. 10.1038/ncomms4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Zang Y.; Wang H.; Hao D.; Kang Y.; Zhang J.; Li X.; Zhang L.; Yang Z.; Zhang S. p38α Kinase Auto-Activation through Its Conformational Transition Induced by Tyr323 Phosphorylation. J. Chem. Inf. Model. 2022, 62, 6639–6648. 10.1021/acs.jcim.2c00236. [DOI] [PubMed] [Google Scholar]
  26. Meng Y.; Roux B. Locking the Active Conformation of c-Src Kinase through the Phosphorylation of the Activation Loop. J. Mol. Biol. 2014, 426, 423–435. 10.1016/j.jmb.2013.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Tsai C.-C.; Yue Z.; Shen J. How Electrostatic Coupling Enables Conformational Plasticity in a Tyrosine Kinase. J. Am. Chem. Soc. 2019, 141, 15092–15101. 10.1021/jacs.9b06064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Meng Y.; Lin Y.-l.; Roux B. Computational Study of the “DFG-Flip” Conformational Transition in c-Abl and c-Src Tyrosine Kinases. J. Phys. Chem. B 2015, 119, 1443–1456. 10.1021/jp511792a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ablooglu A. J.; Kohanski R. A. Activation of the insulin receptor’s kinase domain changes the rate-determining step of substrate phosphorylation. Biochemistry 2001, 40, 504–513. 10.1021/bi002292m. [DOI] [PubMed] [Google Scholar]
  30. Favelyukis S.; Till J. H.; Hubbard S. R.; Miller W. T. Structure and autoregulation of the insulin-like growth factor 1 receptor kinase. Nat. Struct. Biol. 2001, 8, 1058–1063. 10.1038/nsb721. [DOI] [PubMed] [Google Scholar]
  31. Ojeda-May P.; Li Y.; Ovchinnikov V.; Nam K. Role of Protein Dynamics in Allosteric Control of the Catalytic Phosphoryl Transfer of Insulin Receptor Kinase. J. Am. Chem. Soc. 2015, 137, 12454–12457. 10.1021/jacs.5b07996. [DOI] [PubMed] [Google Scholar]
  32. Li Y.; Nam K. Dynamic, structural, and thermodynamic basis of insulin-like growth factor 1 kinase allostery mediated by activation loop phosphorylation. Chem. Sci. 2017, 8, 3453–3464. 10.1039/c7sc00055c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vanden-Eijnden E.; Venturoli M. Revisiting the finite temperature string method for the calculation of reaction tubes and free energies. J. Chem. Phys. 2009, 130, 194103. 10.1063/1.3130083. [DOI] [PubMed] [Google Scholar]
  34. Ovchinnikov V.; Karplus M.; Vanden-Eijnden E. Free energy of conformational transition paths in biomolecules: The string method and its application to myosin VI. J. Chem. Phys. 2011, 134, 085103. 10.1063/1.3544209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wu X.; Brooks B. R.; Vanden-Eijnden E. Self-Guided Langevin Dynamics via Generalized Langevin Equation. J. Comput. Chem. 2016, 37, 595–601. 10.1002/jcc.24015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Schlitter J.; Engels M.; Krüger P.; Jacoby E.; Wollmer A. Targeted Molecular Dynamics Simulation of Conformational Change-Application to the T ↔ R Transition in Insulin. Mol. Simul. 1993, 10, 291–308. 10.1080/08927029308022170. [DOI] [Google Scholar]
  37. Kollman P. A. Free energy calculations: applications to chemical and biochemical phenomena. Chem. Rev. 1993, 93, 2395–2417. 10.1021/cr00023a004. [DOI] [Google Scholar]
  38. Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
  39. Li Y.; Nam K. Repulsive Soft-Core Potentials for Efficient Alchemical Free Energy Calculations. J. Chem. Theory Comput. 2020, 16, 4776–4789. 10.1021/acs.jctc.0c00163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  41. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  42. Hoover W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
  43. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  44. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  45. MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  46. Foloppe N.; MacKerell A. D. Jr. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000, 21, 86–104. . [DOI] [Google Scholar]
  47. MacKerell A. D. Jr.; Feig M.; Brooks C. L. III Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
  48. MacKerell A. D. Jr.; Feig M.; Brooks C. L. III Improved Treatment of the Protein Backbone in Empirical Force Fields. J. Am. Chem. Soc. 2004, 126, 698–699. 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
  49. Brooks B. R.; Brooks C. L.; MacKerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Hynninen A.-P.; Crowley M. F. New faster CHARMM molecular dynamics engine. J. Comput. Chem. 2014, 35, 406–413. 10.1002/jcc.23501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Shigdel U. K.; Ovchinnikov V.; Lee S.-J.; Shih J. A.; Karplus M.; Nam K.; Verdine G. L. The trajectory of intrahelical lesion recognition and extrusion by the human 8-oxoguanine DNA glycosylase. Nat. Commun. 2020, 11, 4437. 10.1038/s41467-020-18290-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Dellago C.; Bolhuis P. G.; Geissler P. L.. Transition Path Sampling. Advances in Chemical Physics; Wiley, 2002; Vol. 123, pp 1–78. [Google Scholar]
  53. Ovchinnikov V.; Karplus M. Investigations of α-helix↔β-sheet transition pathways in a miniprotein using the finite-temperature string method. J. Chem. Phys. 2014, 140, 175103. 10.1063/1.4871685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Chodera J. D.; Mobley D. L.; Shirts M. R.; Dixon R. W.; Branson K.; Pande V. S. Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Hayes R. L.; Armacost K. A.; Vilseck J. Z.; Brooks C. L. III Adaptive Landscape Flattening Accelerates Sampling of Alchemical Space in Multisite λ Dynamics. J. Phys. Chem. B 2017, 121, 3626–3635. 10.1021/acs.jpcb.6b09656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Bruckner S.; Boresch S. Efficiency of alchemical free energy simulations. I. A practical comparison of the exponential formula, thermodynamic integration, and Bennett’s acceptance ratio method. J. Comput. Chem. 2011, 32, 1303–1319. 10.1002/jcc.21713. [DOI] [PubMed] [Google Scholar]
  57. Bennett C. H. Efficient estimation of free-energy differences from Monte-Carlo data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  58. Boyce S. E.; Mobley D. L.; Rocklin G. J.; Graves A. P.; Dill K. A.; Shoichet B. K. Predicting Ligand Binding Affinity with Alchemical Free Energy Methods in a Polar Model Binding Site. J. Mol. Biol. 2009, 394, 747–763. 10.1016/j.jmb.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Hanson S. M.; Ekins S.; Chodera J. D. Modeling error in experimental assays using the bootstrap principle: understanding discrepancies between assays using different dispensing technologies. J. Comput. Aided Mol. Des. 2015, 29, 1073–1086. 10.1007/s10822-015-9888-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Hayes R. L.; Buckner J.; Brooks C. L. III BLaDE: A Basic Lambda Dynamics Engine for GPU-Accelerated Molecular Dynamics Free Energy Calculations. J. Chem. Theory Comput. 2021, 17, 6799–6807. 10.1021/acs.jctc.1c00833. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. van der Vaart A.; Karplus M. Simulation of conformational transitions by the restricted perturbation-targeted molecular dynamics method. J. Chem. Phys. 2005, 122, 114903. 10.1063/1.1861885. [DOI] [PubMed] [Google Scholar]
  62. Ovchinnikov V.; Karplus M. Analysis and Elimination of a Bias in Targeted Molecular Dynamics Simulations of Conformational Transitions: Application to Calmodulin. J. Phys. Chem. B 2012, 116, 8584–8603. 10.1021/jp212634z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Azam M.; Seeliger M. A.; Gray N. S.; Kuriyan J.; Daley G. Q. Activation of tyrosine kinases by mutation of the gatekeeper threonine. Nat. Struct. Mol. Biol. 2008, 15, 1109–1118. 10.1038/nsmb.1486. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp3c01804_si_001.pdf (591.5KB, pdf)
jp3c01804_si_002.mpg (23.2MB, mpg)

Data Availability Statement

Initial PDB coordinates of all systems were obtained from the RCSB Protein Data Bank (https://www.rcsb.org/). The CHARMM program, parameters, and topologies are available from the CHARMM homepage (https://www.charmm.org/). Data (MD trajectories) obtained in this work, systems, and input files for MD and SM simulations can be obtained from the authors of the manuscript upon request.

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES