Longitudinal Canonical Correlation Analysis

Summary.

This paper considers canonical correlation analysis for two longitudinal variables that are possibly sampled at different time resolutions with irregular grids. We modeled trajectories of the multivariate variables using random effects and found the most correlated sets of linear combinations in the latent space. Our numerical simulations showed that the longitudinal canonical correlation analysis (LCCA) effectively recovers underlying correlation patterns between two high-dimensional longitudinal data sets. We applied the proposed LCCA to data from the Alzheimer’s Disease Neuroimaging Initiative and identified the longitudinal profiles of morphological brain changes and amyloid cumulation.

1. Introduction

Canonical correlation analysis (CCA) aims to find the correlation structures between two sets of multivariate variables. CCA seeks linear combinations within each set, such that the resulting linear combinations from variables are maximally correlated, but orthogonal with all other linear combinations in either set. Recently, CCA has been applied to high-dimensional multivariate variables via dimension reduction (Song et al., 2016), penalization (Avants et al., 2010; Bao et al., 2019; Fang et al., 2016; Gossmann et al., 2018; Lin et al., 2014; Wilms and Croux, 2016; Witten et al., 2009) and combining multiple datasets (Deleus and Van Hulle, 2011; Zhang et al., 2014; Kim et al., 2019).

CCA has been used frequently in medical applications to identify associations between clinical/behavior/imaging/genetic variables. For example, CCA has been applied to explore the associations between clinical symptoms and behavioral measures (Mihalik et al., 2019), functional connections in the brain and cognitive deficits (Adhikari et al., 2019) or clinical symptoms (Kang et al., 2016; Grosenick et al., 2019), two sets of imaging data (Avants et al., 2010), and gene-imaging associations (Lin et al., 2014; Kim et al., 2019).

When one of the multivariate variables is measured over time, CCA can be extended using a multi-set sparse canonical correlation approach via group lasso penalization (Hao et al., 2017) and temporal multi-task SCCA (T-MTSCCA) (Du et al., 2019). However, existing methods cannot handle missing values, irregular temporal sampling, and temporal misalignment between two variables.

To address this gap, we propose a new LCCA method that identifies the patterns of canonical variates that maximize the association between longitudinal trajectories. We model the longitudinal trajectory of each variable using random effects (e.g. random intercept and random slope). Then we find the linear combinations of the random effects that maximize the correlations. Since the dimensions of the two multivariate variables can be greater than the sample size, we employ dimension reduction via eigen decomposition. We implement estimation in the longitudinal principal component analysis framework. We conduct extensive simulation experiments to evaluate the performance of LCCA. We also apply LCCA to data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) cohort (Mueller et al., 2005; Weiner et al., 2012). The ADNI data include longitudinal ¹⁸F-AV45 (florbetapir) Positron emission tomography (PET) images to quantify brain amyloid loads over eight years and structural MRI data during the same follow-up. Our LCCA method shows stable performance in terms of dimension selection and yields accurate signal identification, and the method identifies distinct AD- related brain patterns in the ADNI data.

2. Method

2.1. Longitudinal Canonical Correlation Analysis

For each subject $i=1,\dots ,n$ and visits $j=1,\dots ,J_i$, we observe the $p$-dimensional vector ${\mathbf{X}}_{ij}$ at time $t_{ij}$. Similarly, for the visits $k=1,\dots ,K_i$, we observe a $q$-dimensional vector ${\mathbf{Y}}_{ik}$ at time $s_{ik}$. For illustration, we consider the linear trajectories for each variable and later we generalize to the nonlinear trajectories via spline regression. We model each observation using a random intercept and slope model:

$$X_{ij}={\mu }_{ij}^X+Z_{i,0}^X+t_{ij}{Z}_{i,1}^X+{ϵ}_{ij}^X,$$ (1)

$$Y_{ik}={\mu }_{ik}^Y+Z_{i,0}^Y+s_{ik}{Z}_{i,1}^Y+{ϵ}_{ik}^Y,$$ (2)

where ${\mu }_{ij}^X$ and ${\mu }_{ik}^Y$ are fixed effects; ${\mathbf{Z}}_{i,0}^X$ and ${\mathbf{Z}}_{i,0}^Y$ are random intercepts; ${\mathbf{Z}}_{i,1}^X$ and ${\mathbf{Z}}_{i,1}^Y$ are random slopes; ${\mathit{ϵ}}_{ij}^X$ and ${\mathit{ϵ}}_{ik}^Y$ are errors. The random effects are stacked to a $2p$-dimensional vector ${\mathbf{Z}}_i^X:={\left({\mathbf{Z}}_{i,0}^{X^{\text{'}}},{\mathbf{Z}}_{i,1}^{X^{\text{'}}}\right)}^{\text{'}}\in {\mathbb{R}}^{2p}$, and a $2q$-dimensional vector ${\mathbf{Z}}_i^Y:={\left({\mathbf{Z}}_{i,0}^{Y^{\text{'}}},{\mathbf{Z}}_{i,1}^{Y^{\text{'}}}\right)}^{\text{'}}\in {\mathbb{R}}^{2q}$, and are assumed to be distributed with zero mean and a covariance ${\mathbf{\Sigma }}_c=\left[\begin{array}{ll}{\mathbf{\Sigma }}_c^{\left(\mathrm{0,0}\right)}& {\mathbf{\Sigma }}_c^{\left(\mathrm{0,1}\right)}\\ {\mathbf{\Sigma }}_c^{\left(\mathrm{1,0}\right)}& {\mathbf{\Sigma }}_c^{\left(\mathrm{1,1}\right)}\end{array}\right]$, where ${\mathbf{\Sigma }}_c^{(a,b)}=\mathbb{E}\left({\mathbf{Z}}_{i,a}^c{\mathbf{Z}}_{i,b}^c{}^{\text{'}}\right),a,b\in \left\{\mathrm{0,1}\right\},c\in \{X,Y\}$ and uncorrelated with ${\mathit{ϵ}}_{ij}^X$ and ${\mathit{ϵ}}_{ik}^Y$. The random intercepts, slopes and errors are assume to follow a Gaussian distribution.

Then, the objective function defining the canonical correlation is

$$r_m^{XY}={\mathit{\text{max}}}_{u_m\in {ℛ}^{2p},v_m\in {ℛ}^{2q}}\langle u_m^{\prime }{Z}_i^X,v_m^{\prime }{Z}_i^Y\rangle .$$ (3)

When $p$ is greater than $n/2$, we can employ principal component analysis to represent ${\mathbf{Z}}_i^X\approx {\mathbf{\Phi }}_X{\mathit{\xi }}_i^X$, where ${\mathbf{\Phi }}_X={\left({\mathbf{\Phi }}_0^{X^{\text{'}}},{\mathbf{\Phi }}_1^{X^{\text{'}}}\right)}^{\text{'}}$ is a $2p\times N_X$ matrix of the leading $N_X$ eigenvectors of ${\mathbf{\Sigma }}_X=Var \left({\mathbf{Z}}_i^X\right)$ and ${\mathit{\xi }}_i^X={\left({\xi }_{i1}^X,\dots ,{\xi }_{i{N}_X}^X\right)}^{\text{'}}\in {\mathbb{R}}^{N_X}$ are the associated subject $i$-specific eigenscores. Using longitudinal principal component analysis (LPCA) (Greven et al., 2011; Zipunnikov et al., 2014; Lee et al., 2015), each term is expressed as

$${\mathbf{X}}_{ij}\approx {\mu }_{ij}^X+\sum _{l=1}^{N_X} {\xi }_{il}^X\left({\Phi }_l^{X,0}+t_{ij}{\Phi }_l^{X,1}\right)+{ϵ}_{ij}^X,$$ (4)

where $\left({\xi }_{i{l}_1}^X,{\xi }_{i{l}_2}^X\right)~\left(\mathrm{0,0};{\lambda }_X^{l_1},{\lambda }_X^{l_2};0\right)$, in which “. $~\left({\mu }_1,{\mu }_2;{\sigma }_1^2,{\sigma }_2^2;\rho \right)$ “ represents that a pair of gaussian variables has a distribution with mean $\left({\mu }_1,{\mu }_2\right)$, variance $\left({\sigma }_1^2,{\sigma }_2^2\right)$, and correlation $\rho$. Similarly, ${\mathbf{Y}}_{ik}$ are expressed as

$${\mathbf{Y}}_{ik}\approx {\mu }_{ik}^Y+\sum _{l=1}^{N_Y} {\xi }_{il}^Y\left({\Phi }_l^{Y,0}+s_{ik}{\Phi }_l^{Y,1}\right)+{ϵ}_{ik}^Y,$$ (5)

where $\left({\xi }_{i{l}_1}^Y,{\xi }_{i{l}_2}^Y\right)~\left(\mathrm{0,0};{\lambda }_Y^{l_1},{\lambda }_Y^{l_2};0\right)$. The eigenvectors of (4) and (5) can be obtained by the least-squares estimation of the covariance matrices. Without loss of generality, we assume ${\mathbf{X}}_{ij}$ is demeaned to have mean zero. The $p\times p$-covariance of ${\mathbf{X}}_{i{j}_1}$ and ${\mathbf{X}}_{i{j}_2}$ is given by

$$E{\mathbf{X}}_{i{j}_1}{\mathbf{X}}_{i{j}_2}^{\top }={\mathbf{\Sigma }}_X^{\left(\mathrm{0,0}\right)}+t_{i{j}_2}{\mathbf{\Sigma }}_X^{\left(\mathrm{0,1}\right)}+t_{i{j}_1}{\mathbf{\Sigma }}_X^{\left(\mathrm{1,0}\right)}+t_{i{j}_1}{t}_{i{j}_2}{\mathbf{\Sigma }}_X^{\left(\mathrm{1,1}\right)}+{\delta }_{j_1,j_2}{\mathbf{\Sigma }}_X^{ϵ},$$ (6)

where ${\Sigma }_X^{ϵ}$ is the covariance matrix of ${ϵ}_{ij}^X$ and ${\delta }_{j_1,j_2}=1$ if $j_1=j_2$ and ${\delta }_{j_1,j_2}=0$ otherwise. Denote $vec (\cdot )$ as the vectorization of a matrix by stacking columns of the matrix on top of one another. Then, we can form a matrix ${\mathbf{K}}_X=\left\{vec \left({\mathbf{\Sigma }}_X^{\left(\mathrm{0,0}\right)}\right),vec \left({\mathbf{\Sigma }}_X^{\left(\mathrm{0,1}\right)}\right),vec \left({\mathbf{\Sigma }}_X^{\left(\mathrm{1,0}\right)}\right),vec \left({\mathbf{\Sigma }}_X^{\left(\mathrm{1,1}\right)}\right)\right.,\left.vec \left({\mathbf{\Sigma }}_X^{ϵ}\right)\right\}$ and ${\mathbf{f}}_{i{j}_1{j}_2}={\left(1,t_{i{j}_2},t_{i{j}_1},t_{i{j}_1}{t}_{i{j}_2},{\delta }_{j_1,j_2}\right)}^{\top }$ such that $\mathit{\text{Evec}} \left({\mathbf{X}}_{i{j}_1}{\mathbf{X}}_{i{j}_2}^{\top }\right)={\mathbf{K}}_X{\mathbf{f}}_{i{j}_1{j}_2}$. By concatenating all vectors across all subjects and visits, we obtain a moment matrix identity for the $p^2\times J$ matrix $\mathbf{X}:\mathbf{X}={\mathbf{K}}_X\mathbf{F}$, where $J={\sum }_{i=1}^N J_i^2$. Then covariance parameters ${\mathbf{K}}_X$ can be unbiasedly estimated by using ordinary least squares $\left(OLS\right):{\widehat{\mathbf{K}}}_X=\mathbf{X}\mathbf{F}{\mathbf{F}}^{\top }{\left({\mathbf{F}\mathbf{F}}^{\top }\right)}^{-1}$. Given the estimated covariance matrix, the eigenvectors are computed via eigen decomposition. Given the eigenvectors, the eigenscores are estimated by the best linear unbiased predictors (BLUP) from the equations (4) and (5) as discussed in Greven et al. (2011); Zipunnikov et al. (2014).

Denote the $N\times N_X$ matrix ${\mathit{\xi }}^X={\left\{{\xi }_{il}^X\right\}}_{i=1,\dots ,N;l=1,\dots ,N_X}$ and $N\times N_Y$ matrix ${\mathit{\xi }}^Y={\left\{{\xi }_{il}^Y\right\}}_{i=1,\dots ,N;l=1,\dots ,N_Y}$. Then, the objective function defining the canonical correlation is

$$r_m^{XY}={\mathit{\text{max}}}_{u_m\in {ℛ}^{N_X,v_m}\in {ℛ}^{N_Y}}\langle {\xi }^X{u}_m,{\xi }^Y{v}_m\rangle$$ (7)

The objective function in (7) is maximized under the restriction that each ${\mathbf{u}}_m$ is orthogonal to the lower order ${\mathbf{u}}_{m^{\text{'}}}$, with $1\le m<m^{\text{'}}\le min\left(N_X,N_Y\right)$. Same restriction is applied for ${\mathbf{v}}_m$ of the second set of variates. For identification purpose, we require a normalization condition for the canonical variates, ${\mathbf{u}}_m^{\top }{\mathit{\xi }}_i^X,{\mathbf{v}}_m^{\top }{\mathit{\xi }}_i^Y,m=1,\dots ,min\left(N_X,N_Y\right)$, to have unit variance. The canonical vectors are estimated in the lower-dimensional space, and the $m$-th longitudinal canonical vectors are computed as $\left({\mathbf{\Phi }}_0^X+t_{ij}{\mathbf{\Phi }}_1^X\right){\mathbf{u}}_m$ and $\left({\mathbf{\Phi }}_0^Y+s_{ik}{\mathbf{\Phi }}_1^Y\right){\mathbf{v}}_m$ for $m=1,\dots ,min\left(N_X,N_Y\right)$.

Depending on the availability of time points, this formation can be naturally extended to higher-order trends or modeled via B-spline basis expansion. Assume that the trajectory of the imaging measure at location $v$ is represented by a spline function with fixed knot sequence ${\tau }_1<\cdots <{\tau }_D$ and fixed degree $d$.

$${\mathbf{X}}_{ij}\left(v\right)={\mu }^X\left(v\right)+\sum _{r=1}^{D+d+1} Z_{i,r}\left(v\right)b_r\left(t_{ij}\right)+{ϵ}_{ij}^X,$$ (8)

where the $b_r$ are a set of basis functions and $Z_{i,r}\left(v\right)$ are the associated spline coefficients. The $(D+d+1)V$-dimensional stacked vector of ${\mathbf{Z}}_{\mathbf{i}}={\left({\mathbf{Z}}_{i,1}^{\top },\dots ,{\mathbf{Z}}_{i,D+d+1}^{\top }\right)}^{\top }$ can be approximated by the principal component analysis: ${\mathbf{Z}}_{\mathbf{i}}\approx {\sum }_{l=1}^{N_X} {\xi }_{il}^X{\mathbf{\Phi }}_l^X$ with each element expressed as $Z_{i,r}\left(v\right)\approx {\sum }_{l=1}^{N_X} {\xi }_{il}^X{\Phi }_l^{X,r}\left(v\right)$, for $r=1,\dots ,D+d+1$. Then, (8) is reorganized as

$${\mathbf{X}}_{ij}\left(v\right)={\mu }^X\left(v\right)+\sum _{l=1}^{N_X} {\xi }_{il}^X\sum _{r=1}^{D+d+1} {\Phi }_l^{X,r}\left(v\right)b_r\left(t_{ij}\right)+{ϵ}_{ij}^X.$$ (9)

Similarly, $Y$ is modeled as

$${\mathbf{Y}}_{ik}\left(v\right)={\mu }^Y\left(v\right)+\sum _{l=1}^{N_Y} {\xi }_{il}^Y\sum _{r=1}^{D+d+1} {\Phi }_l^{Y,r}\left(v\right)b_r\left(s_{ik}\right)+{ϵ}_{ik}^Y.$$ (10)

This method does not require that $X$‘s and $Y$ ‘s are observed at the same time. As long as they are observed within a time frame that the research question asks, the proposed method can extract association patterns.

2.2. The number of canonical covariates

To determine the dimension of the CCA, we employ a traditional likelihood ratio testbased approach in the latent space. Starting with $m=0$, we test the null hypothesis $H_0:d=m$ versus the alternative hypothesis $H_1:d>m$. If $H_0$ is rejected, $m$ is incremented and a new test is conducted. This proceeds until $H_0$ is not rejected or $m$ reaches $M=\mathit{\text{min}}\left(N_X,N_Y\right)$. For a given number of canonical variates, $m$, the Wilk’s test statistics (Wilks, 1935; Bartlett, 1947; Friederichs and Hense, 2003) is given by

$${\Lambda }_m={\Pi }_{j=m+1}^{min\left(N_X,N_Y\right)}\left(1-{\hat{r}}_j^2\right).$$ (11)

Based on Rao’s F-approximation (Rao et al., 1973), $F=d{f}_2/d{f}_1{\left(1-{\Lambda }_m/\left({\Lambda }_m\right)\right)}^{1/\nu }$ follows asymptotically $F_{d{f}_1,d{f}_2}$, where $\nu =\sqrt{\left(d{f}_1^2-4\right)/\left({\left(N_X-m\right)}^2+{\left(N_Y-m\right)}^2-5\right)},d{f}_1=\left(N_X-m\right)*\left(N_Y-m\right)$, and $d{f}_2=\left(n-1.5-\left(N_X+N_Y\right)/2\right)\nu -d{f}_1/2+1$.

The performance of LCCA depends on the selection of $N_X$ and $N_Y$. Previous works suggested using 80% threshold of the variance explained by the number of individual components (Greven et al., 2011; Lee et al., 2015) or pre-specified numbers (Zipunnikov et al., 2014). In practice, the performance depends on the signal-to-noise ratio, which is particularly relevant for imaging applications. Our numerical experiments show good performance using a threshold of 80–90% as a rule of thumb. The algorithms are implemented as an R package LCCA and available in github (https://seonjoo.github.io/lcca/).

3. Alzheimer’s Disease Neuroimaging Data Analysis

3.1. Participants

We apply our LCCA method to the ADNI data to identify longitudinal associations between brain morphometry and amyloid deposition. The data were downloaded from the ADNI database (http://adni.loni.usc.edu). The initial phase (ADNI-1) recruited 800 participants, including approximately 200 healthy controls, 400 patients with late mild cognitive impairment (MCI), and 200 patients clinically diagnosed with probable AD over 50 sites across the United States and Canada and followed up at 6- to 12-month intervals for 2–3 years. ADNI has been followed by ADNI-GO and ADNI-2 for existing participants and enrolled additional individuals, including early MCI. To be classified as MCI in ADNI, a subject needed an inclusive Mini-Mental State Examination score of between 24 and 30, subjective memory complaint, objective evidence of impaired memory calculated by scores of the Wechsler Memory Scale Logical Memory II adjusted for education, a score of 0.5 on the Global Clinical Dementia Rating, absence of significant confounding conditions such as current major depression, normal or near-normal daily activities, and absence of clinical dementia.

All studies were approved by their respective institutional review boards and all subjects or their surrogates provided informed consent compliant with HIPAA regulations. In total, the analysis included PET-MRI scan pairs of 680 subjects on average $2.7(\pm 0.79)$ visits over $3.7(\pm 1.66)$ years on average. There are 291 cognitively normal (CN), 365 mild cognitive impairment (MCI), and 24 AD participants at baseline. Detailed characteristics of these individuals are given in Table 1.

Table 1.

Demographic characteristics at baseline and 5 year conversion rate.

	AD (N=24)	MCI (N=365)	CN (N=291)	Total (N=680)	p value
Sex, Female, n (%)	10 (41.7)	162 (44.4)	147 (50.5)	319 (46.9)	0.257
Age, years, Mean (SD)	76.75 (7.15)	71.88 (7.74)	74.62 (6.47)	73.23 (7.35)	<0.001
Non-hispanic, n (%)	22 (91.7)	351 (96.2)	279 (95.9)	652 (95.9)	0.245
Race , White, n (%)	23 (95.8)	342 (93.7)	267 (91.8)	632 (92.9)	0.713
MMSE1, Mean (SD)	18.83 (4.90)	26.89 (3.34)	28.81 (1.63)	27.43 (3.39)	< 0.001
ADAS2, Mean (SD)	37.35 (13.75)	16.64 (11.06)	9.05 (5.71)	14.10 (10.93)	< 0.001
5 Yr AD Transition3, n (%)	N/A	104 (28.5)	16 (5.5)	120 (18.3)	< 0.001

¹Eight participants has missing values.

²Nine participants had missing values.

³Only non-demented participants at baseline were analyzed.

3.2. Structural imaging processing

For internal consistency, 3.0 MPRAGE T1-weighted MR images were used. Cross-sectional image processing was performed using FreeSurfer Version 6. Region of interest (ROI)-specific cortical thickness and volume measures were extracted from the automated FreeSurfer v6 anatomical parcellation using the Desikan-Killiany Atlas (Desikan et al., 2006) for cortical regions; there were 68 ROIs (34 each on the left and right hemispheres), in which the longitudinal cortical thickness and volume measures were collected. The volume measures from 28 subcortical regions (Fischl et al., 2002) were computed, including Lateral Ventricle, Inferior Lateral Ventricle, Thalamus, Caudate, Putamen, Pallidum, Hippocampus, Amygdala, Accumbens area, Third Ventricle, Fourth Ventricle, and five corpus callosum subregions. In addition, the total intracranial volume was included.

We computed amyloid SUVR levels using the PetSurfer pipeline (Greve et al., 2014, 2016), which is available with Freesurfer version 6. The PetSurferpipeline first registers the PET image with the corresponding MRI scan, then applies Partial Volume Correction, and finally resamples the voxel-wise SUVR values onto the cortical surface. The 81 ROI-level summary was computed based on Desikan Atlas for the cortical and subcortical regions.

3.3. Naive approach

There are no existing CCA methods to handle the longitudinal data’s missing and irregular temporal sampling. Thus, we consider the following approach. First, we computed the intercept and slope of each variable for each subject. Then, within each modality, the vectors of intercepts and slopes were stacked, and we performed a canonical correlation analysis. Finally, the number of canonical variates was estimated in the same principles described in Section 2.2. We named this approach the naive approach.

3.4. Results

The longitudinal CCA identified 7 canonical variates. The significant canonical correlation coefficients are displayed in Figure 1. The longitudinal canonical vectors were reorganized as a function of time $\left({\mathbf{\Phi }}_0^X+t{\mathbf{\Phi }}_1^X\right){\mathbf{u}}_m$ and $\left({\mathbf{\Phi }}_0^Y+s{\mathbf{\Phi }}_1^Y\right){\mathbf{v}}_m$ for $m=1,\dots ,min\left(N_X,N_Y\right)$ are displayed in Figures 2 at $\mathit{\text{time}}=0,1,2,3,4$. For visualization, the vectors are standardized with the total variance of the vectors, and the ROIs with at least one element of the vector over 1.64 are included in the heatmaps. Figures 2 and 3 include the longitudinal canonical (LC) vectors of the longitudinal canonical variates of T1 and PET. The LC vectors are presented separately by volumetric (Vol) and cortical thickness (CT) measures. For better interpretation, the rows of the matrix are sorted by the Braak staging (Braak et al., 2006), a semi-quantitative measure of the severity of neurofibrillary tangle (NFT) pathology used in Alzheimer’s disease. The order of stage consists of transentorhinal regions (B1, B2, initial stage), limbic regions (B3, B4, incipient AD stage), and neocortical regions (B5-B6, fully developed AD stage) by order of severity. Additional brain regions not included on the Braak staging were also included (NA). We also performed the Naive approach and compared its performance. The longitudinal canonical vectors of the naive methods are displayed in Figures 4 and 5. We only present the LCVs that are significantly associated with either baseline diagnosis or AD transition.

Fig. 1.

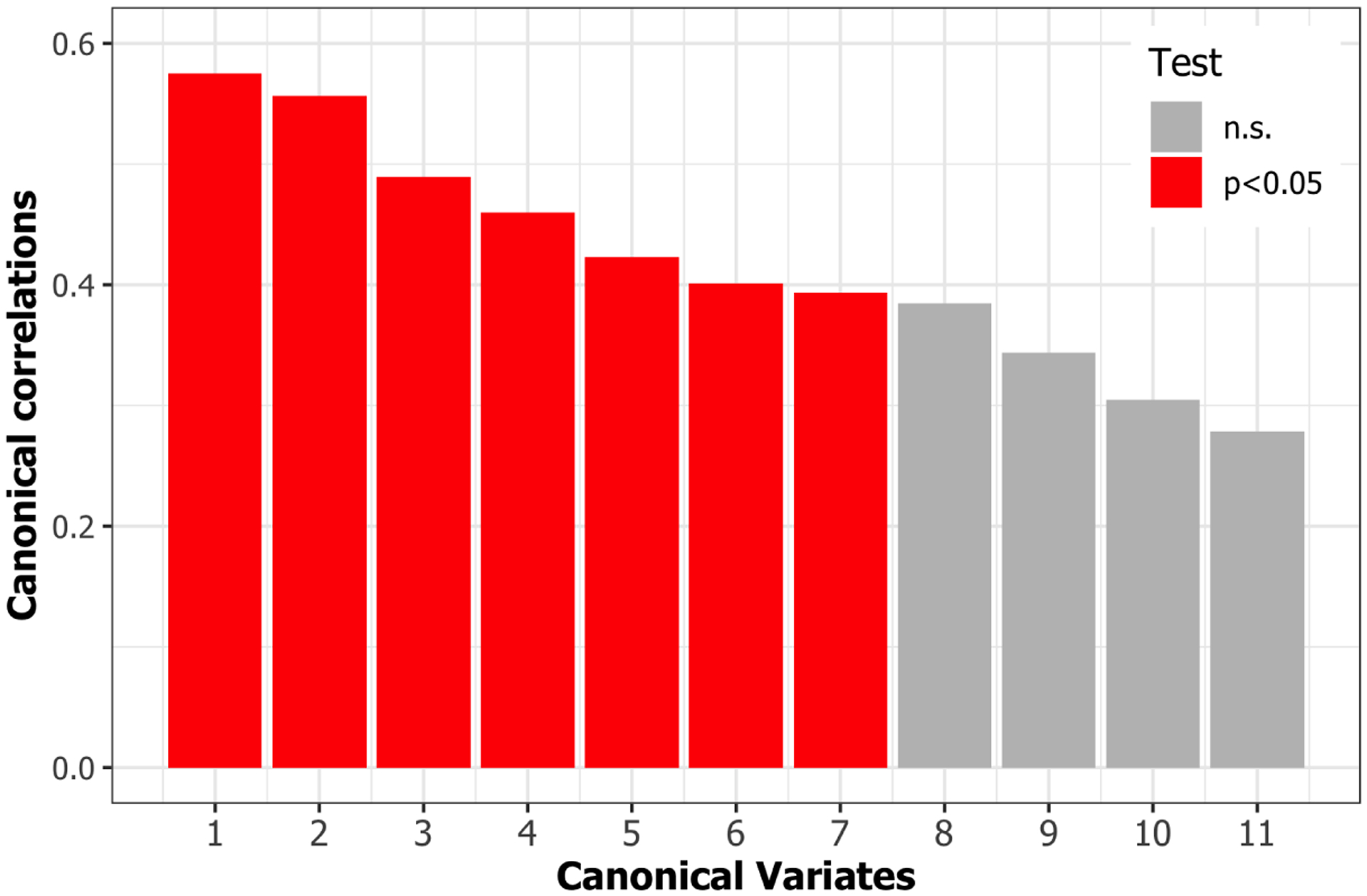
Canonical correlation coefficients. Seven canonical correlation coefficients were significant $(p<0.05)$ using F-test based on Rao’s F-approximation of Wilk’s Lambda.

Fig. 2.

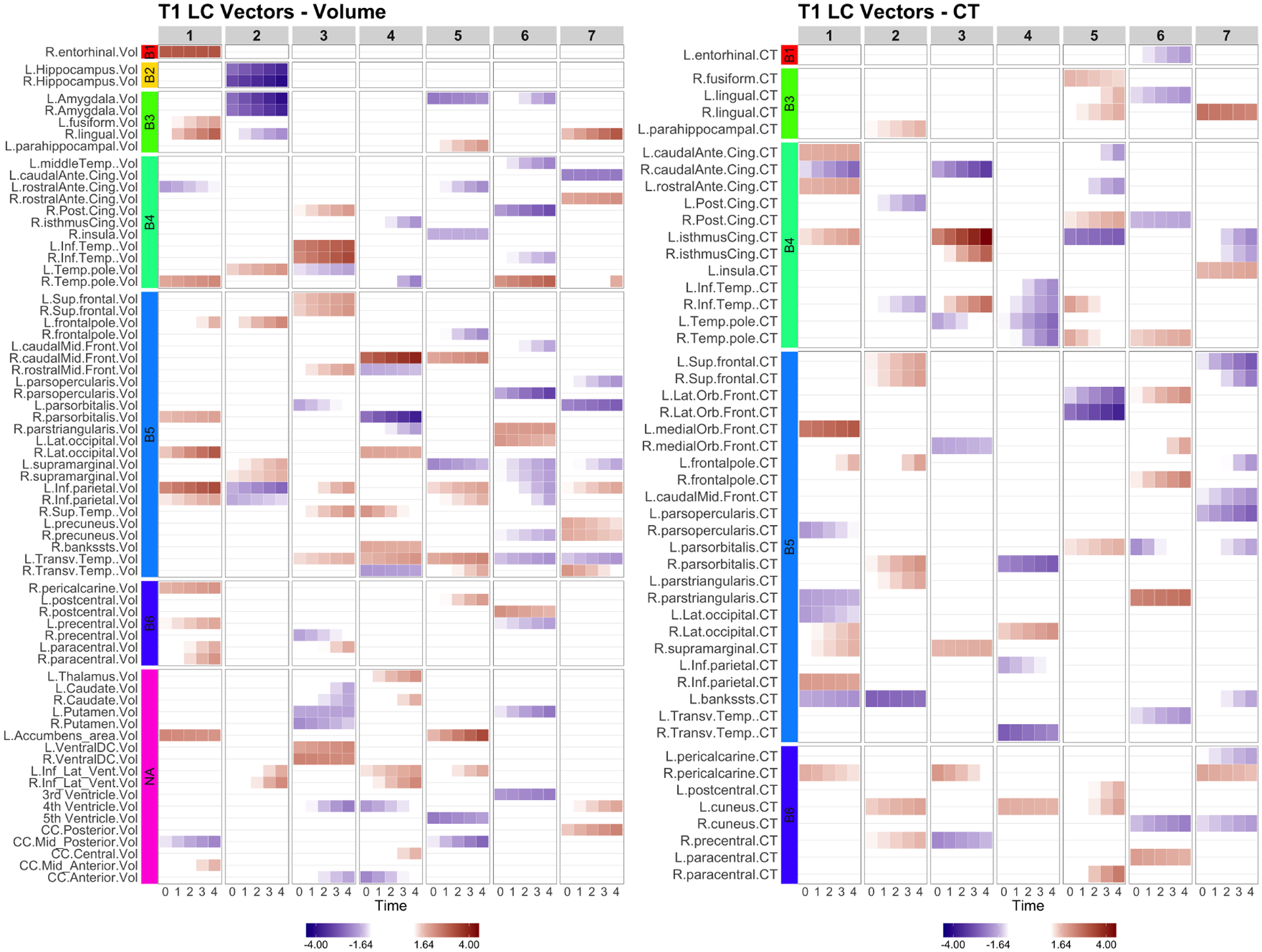
LCCA: the longitudinal canonical vectors for T1 are displayed at $\mathit{\text{time}}=0,1,2,3,4$. We separately present the LC vectors by volumetric (Vol) and cortical thickness (CT) measures. The rows are sorted by the Braak staging (B1-B6, NA). T1 measures have higher vectors at baseline with little longitudinal changes in the earlier Braak staging brain regions such as entorhinal (LCV1), Hippocampus and Amygdala (LCV2). Later Braak staging brain regions show longitudinal changes.

Fig. 3.

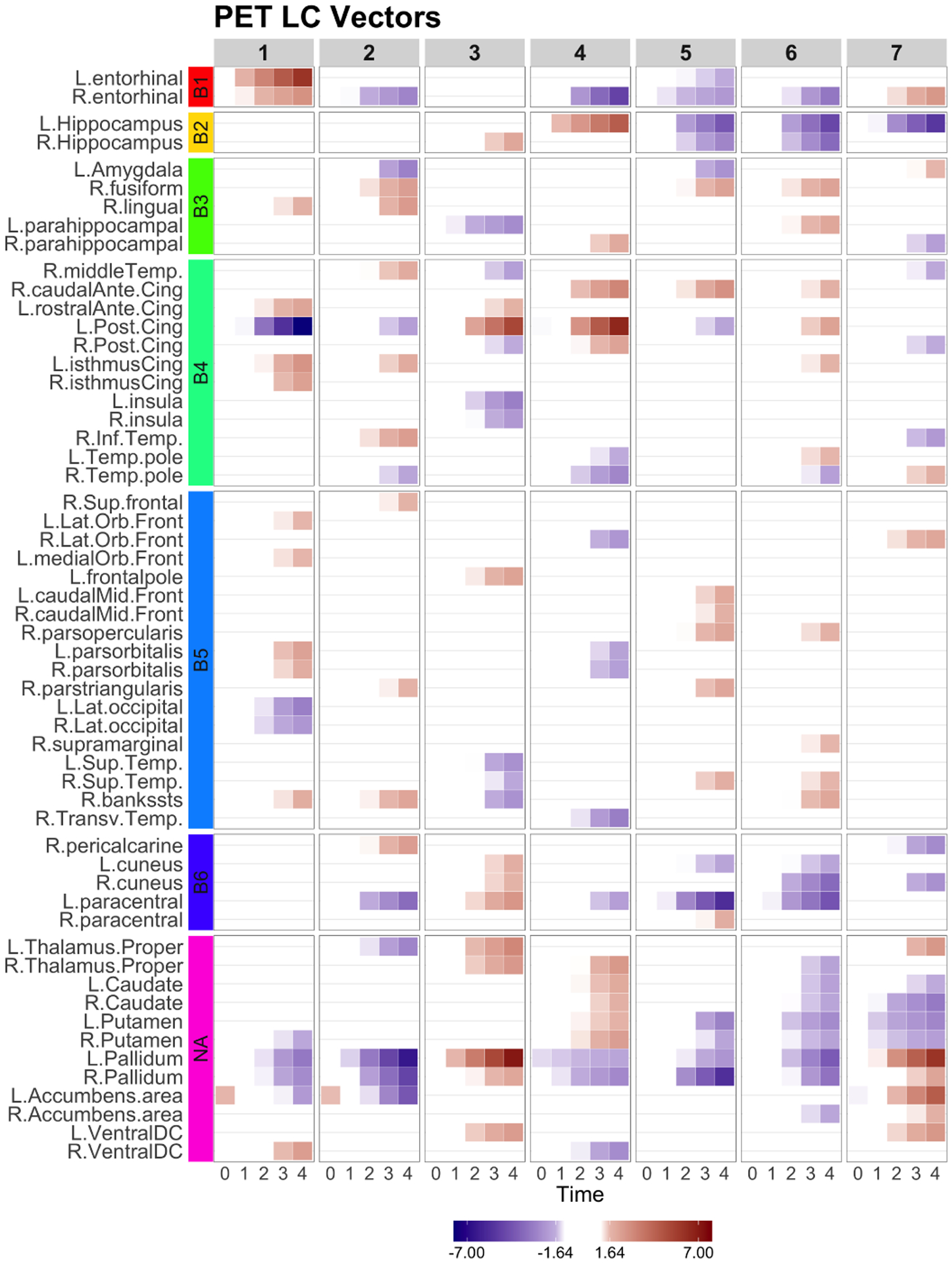
LCCA: the longitudinal canonical vectors for PET are displayed at $\mathit{\text{time}}=0,1,2,3,4$. The rows were sorted by the Braak staging (B1-B6, NA). All LCVs represent longitudinal changes over time.

Fig. 4.

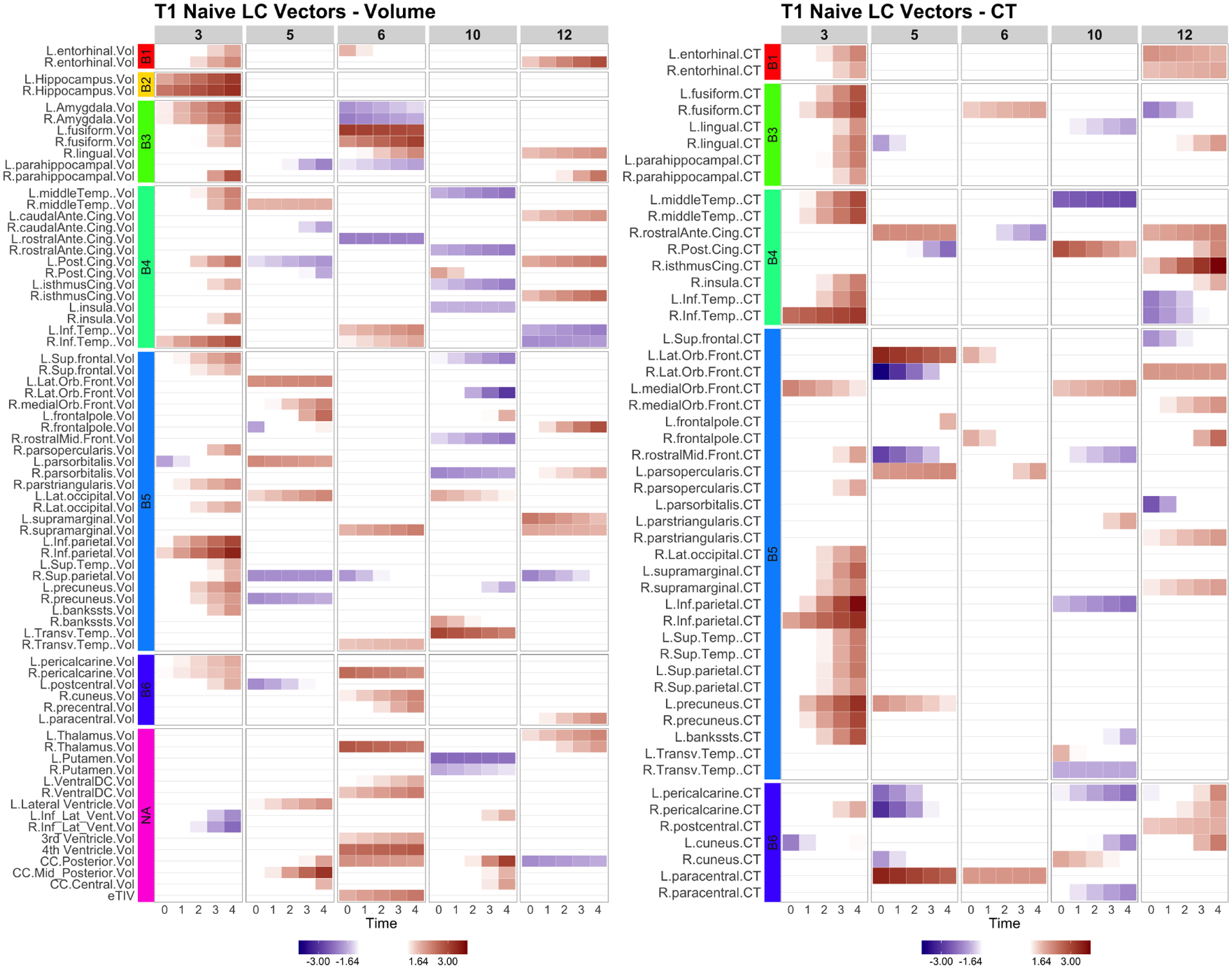
Naive: the longitudinal canonical vectors for T1 are displayed at $\mathit{\text{time}}=0,1,2,3,4$. We separately present the LC vectors by volumetric (Vol) and cortical thickness (CT) measures. The rows were sorted by the Braak staging (B1-B6, NA). The Naive LCV 3 represents a global longitudinal patterns in volumes and cortical thickness.

Fig. 5.

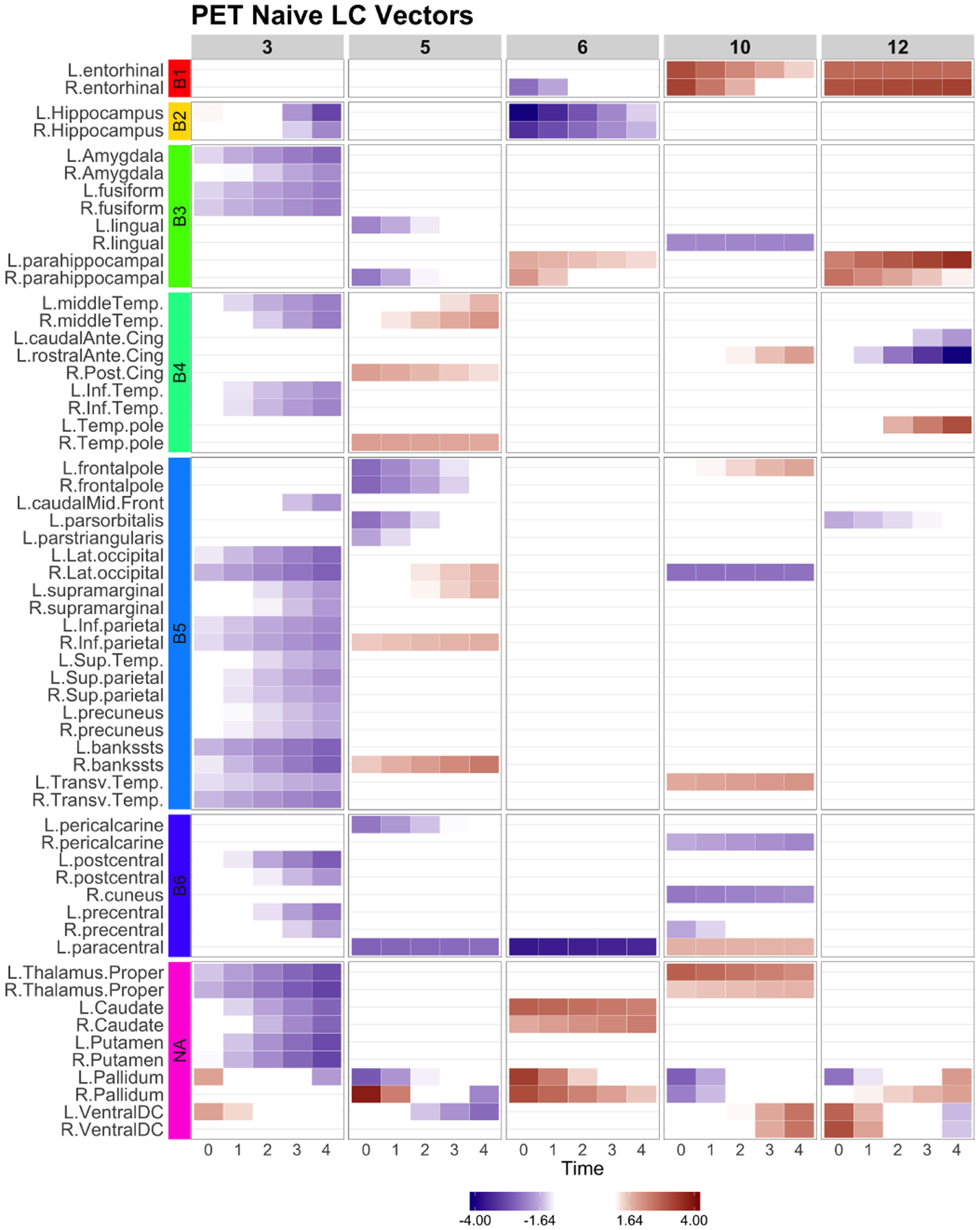
Naive: the longitudinal canonical vectors for PET are displayed at $\mathit{\text{time}}=\mathrm{0,1},\mathrm{2,3},4$. The rows were sorted by the Braak staging (B1-B6, NA). The Naive LCV 3 represents a global longitudinal changes in amyloid accumulation.

Further, we investigated the longitudinal canonical variates (CV). First, we compared CVs by each subject’s baseline clinical status. For group comparison, linear regression was conducted with age, sex and years of education as covariates, followed by multiple comparison correction controlling for false discovery rate (Benjamini and Hochberg, 1995). Table 2 reports the F-statistics, unadjusted p-values and multiple comparison corrected p-values. For all analyses, we excluded extreme outliers beyond 3 IQR from the first and third quartiles. For post-hoc pair-wise group comparison, least squared mean differences were computed. Figure 6 shows jittered boxplots and pair-wise comparison results with unadjusted p-values for the CVs with significant group difference after multiple comparison correction.

Table 2.

ANOVA of diagnosis group comparison and AD conversion with age, sex and education adjusted for LCCA.

		T1				PET
	LCV	F	p	${\eta }_p^2$	outliers	F	p	${\eta }_p^2$	outliers
Group Comparison	1	3.47	0.032	0.010	0	0.57	0.566	0.002	1
	2	19.83	<0.001 *	0.056	0	38.73	<0.001 *	0.103	0
	3	2.13	0.120	0.006	1	1.08	0.342	0.003	2
	4	4.86	0.008 *	0.014	1	3.34	0.036	0.010	2
	5	0.95	0.386	0.003	0	11.60	<0.001 *	0.033	2
	6	2.42	0.090	0.007	0	2.46	0.086	0.007	1
	7	8.26	<0.001 *	0.024	0	3.86	0.022	0.011	2
AD Conversion	1	11.74	0.001 *	0.018	0	5.76	0.017 *	0.009	1
	2	102.21	<0.001 *	0.136	0	164.90	<0.001 *	0.202	0
	3	1.51	0.220	0.002	0	0.08	0.773	0.000	1
	4	6.11	0.014 *	0.009	0	7.70	0.006 *	0.012	1
	5	0.00	0.972	0.000	0	0.75	0.386	0.001	1
	6	3.19	0.074	0.005	0	7.05	0.008 *	0.011	0
	7	2.80	0.095	0.004	0	3.44	0.064	0.005	2

Fig. 6.

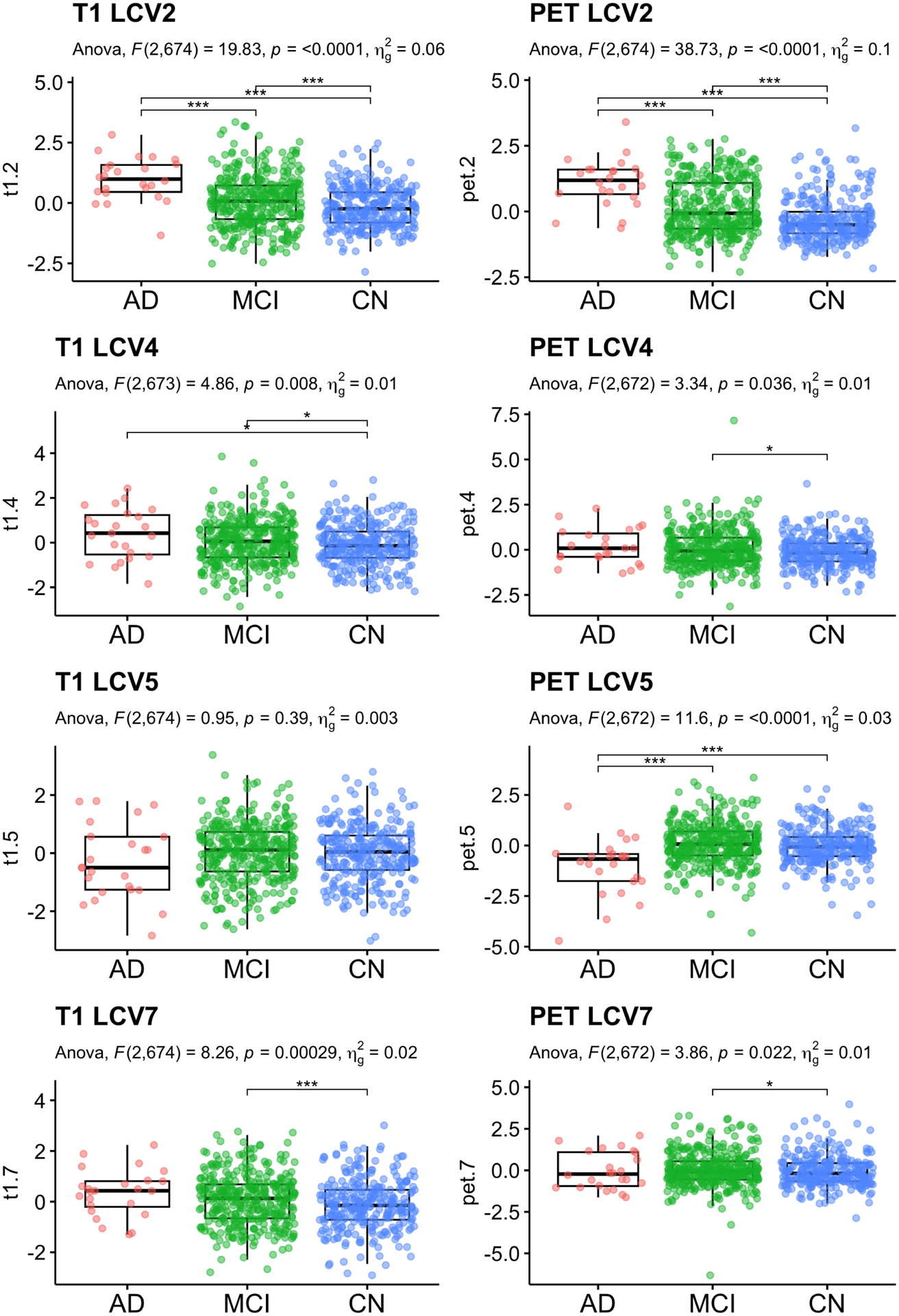
LCCA: Baseline diagnosis status comparison. Significant CVs are reported. Age, sex and education were adjusted for statistical testing. For post-hoc pair-wise group comparison, least squared mean differences were computed, and unadjusted p-values are reported.

The CV 2, 4, and 7 of T1 and CVs 2 and 5 of PET showed group differences after multiple comparison correction. The CV2 indicates that AD patients at baseline showed atrophy in bilateral hippocampus and amygdala (B1 and B2 regions). The amyloid deposition showed a decreased pattern in bilateral Pallidum (no Braak staging regions), and increasing amyloid deposition in the cortical areas (right lingual, right pericalcarine, right fusiform, and inferior temporal cortices, B3-B5 regions). The CV4 of T1 showed the enlarged volume in right caudal middle frontal gyus and longitudinal atrophy in right pars orbitalis in AD and MCI comparing to CN, while PET did not showed any differences. The CV5 of T1 did not show differences across baseline clinical status. The AD patients showed brain atrophy in the left Accumbens area volume, and right paracentral thickness, smaller volume in the left temporal transverse volume and right caudal middle frontal volume, while thicker thickness in the left isthmus cingulate and right lateral orbitofrontal gyrus. The CV5 of av45 showed a longitudinal increase in the left hippocampus and right Pallidum and left paracentral area in AD participants, while MCI and CN participants did not show that pattern on average. CV7 showed enlarged volumes in right lingual gyrus, but atrophy in left caudal ACC and pars orbitals, while no significant difference in amyloid deposition. The naive method identified CV 3 and 5 with significant T1 differences and CVs 9 and 12 for PET. Unlike LCCA, naive method did not identify CVs showed group differences between diagnosis status in both T1 and PET. For AD transition, only CV3 T1 and CV9 PET showed significant group difference.

Secondly, among the non-demented participants at baseline, we compared CVs between the participants who translated to AD within 5 years and those who remained non-demented. Among 656 non-demented participants, 120 participants (18.3%) converted to AD in 5 years. Table 2 reports the F-statistics, unadjusted p-values and multiple comparison corrected p-values. For post-hoc pair-wise group comparison, least squared mean differences were computed. Figure 8 shows jittered boxplots and pair-wise comparison results with unadjusted p-values for the CVs with significant group difference after multiple comparison correction. The CVs 1, 2 and 4 for T1 and CVs 1, 2, 4 and 6 of PET showed a significant difference between those who converted to AD and those who did not.

Fig. 8.

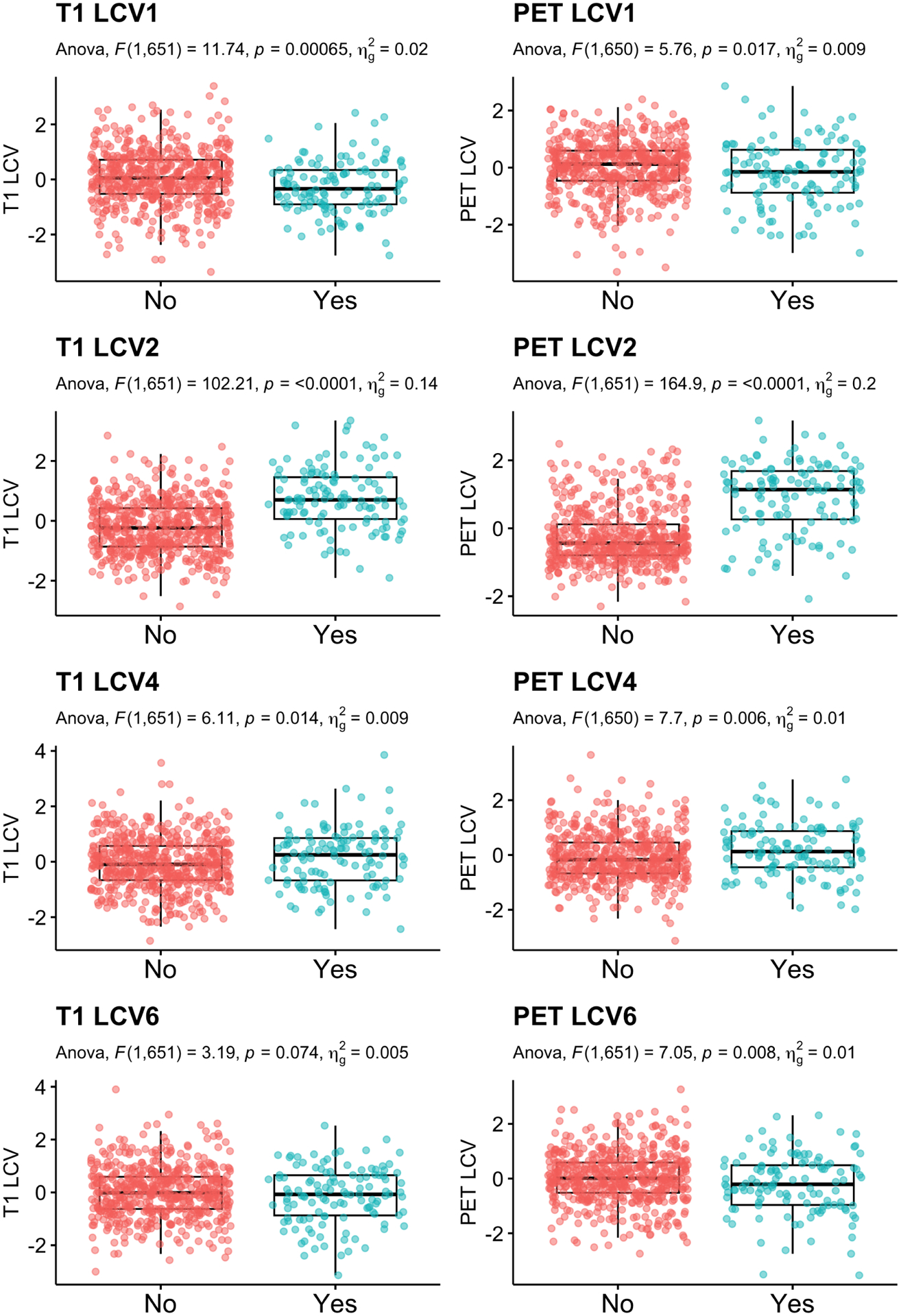
LCCA: Group comparison of the canonical variates between participants who transition to dementia within 5 years compared to those who did not. Age, sex and education were adjusted.

4. Simulations

We conducted extensive numerical experiments to evaluate the performance of the LCCA comparing to the naive approach. The first simulation setting was designed to evaluate general performance of LCCA when the data were generated from the LCCA model. The second simulation was designed when the data were generated with a low signal-to-noise ratio. We also conducted a third simulation to determine the ability of LCCA to recover subgroups across a range of sample sizes and a varied degree of subgroup imbalance.

For all simulation settings, we generated 100 independent datasets and compared the performance of LCCA according to the following criteria: (1) number of estimated canonical variates;(2) bias of the estimated canonical correlation coefficients; (3) accuracy of the estimated canonical loading using cosine similarity. For the third simulation, we report the correlation between the true and estimated canonical variates in the place of (2). Since the true number of canonical variates is one, we compared the first canonical variate’s performance even if the LCCA or the naive approach selected different numbers of canonical variates.

4.1. Simulation Setting 1.

Data were generated from the model 4 setting $N_X$ and $N_Y$ to 3. The LPC loadings were generated as depicted in Figure 10; we set $p=144$ and $q=81$. The LPC scores ${\xi }_{ik}^X$ and ${\xi }_{ik}^Y$ were generated from the $N\left(0,{\lambda }_k\right),{\lambda }_1=8,{\lambda }_2=4,{\lambda }_3=2$, where $Cor \left({\xi }_{i2}^X,{\xi }_{i2}^Y\right)=r$. We note that we correlated the second pairs of the LPCs to evaluate LCCA’s performance when the correlated signals explain more minor variances. For each subject, the number of visits were generated from Poisson(1) followed by adding 3 such that each subject has on average 4 time points. The time intervals between visits were generated from $U$[1, 2]. Figure 11 shows examples of the time variables $t_{ij}$ and $s_{ik}$ from the first 10 subjects from a simulation setting. The time points between $X$ and $Y$ variables are not aligned, and the numbers of visits differ. We conducted simulations for $r=\mathrm{0.1,0.3,0.5}$, at $n=100,200,400$, and different threshold for LPC dimension selection (80% or 90%). For each scenario, 100 independent datasets were generated.

Fig. 10.

Simulation 1. LFPCA models for simulation.

Fig. 11.

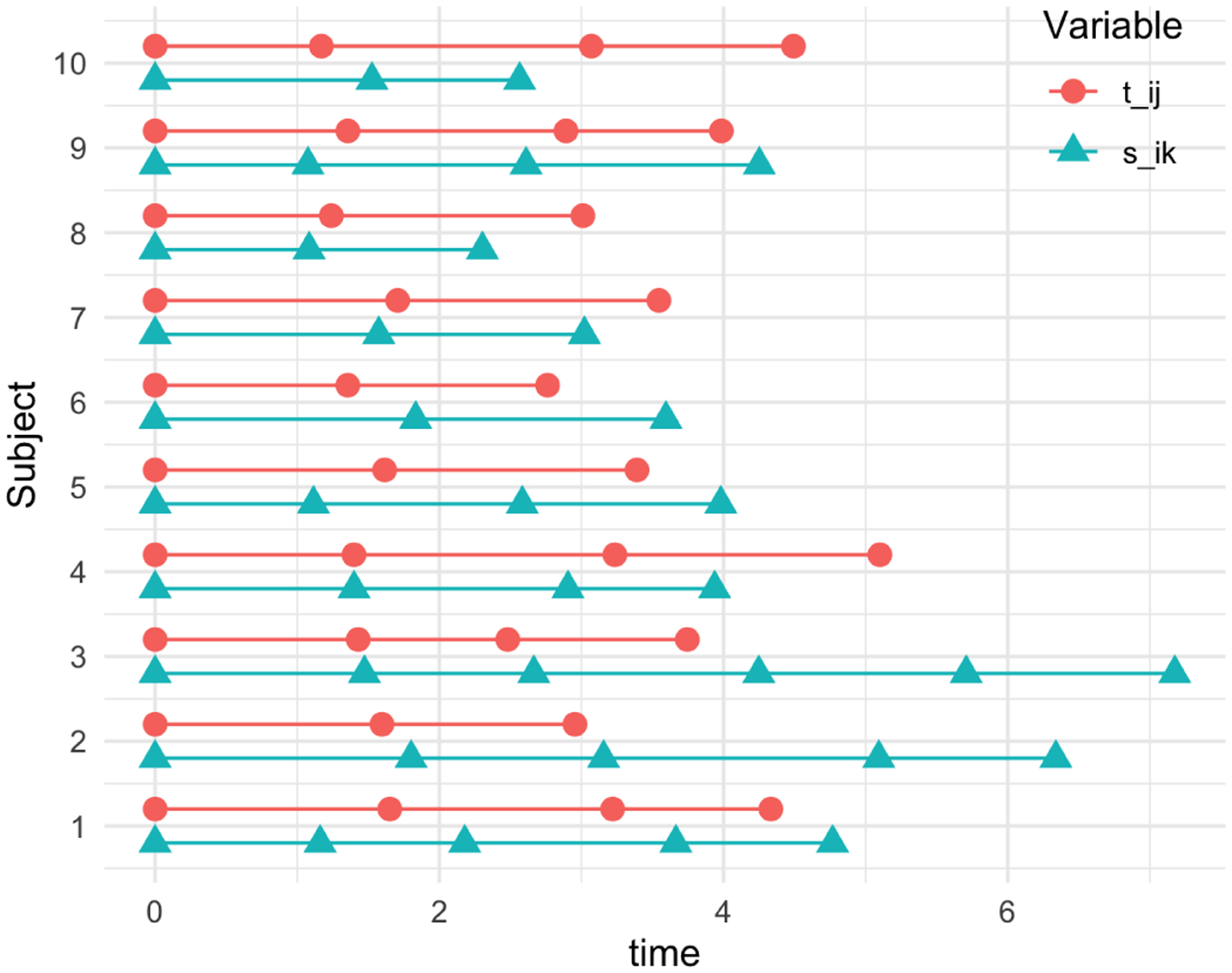
Example of the time variables $t_{ij}$ and $s_{ik}$ from the first 10 subjects from a simulation setting. The time points between $X$ and $Y$ variables are not aligned, and the numbers of visits differ.

Overall, LCCA outperforms the naive approach in the three criteria. Figure 12 shows that both LCCA and the naive approach tend to overestimate canonical correlation when the sample size is small and the true canonical correlation is smaller, while LCCA performs better than the naive approach. The results show that the approximation-based CV dimension estimation performs better as the sample size increases, and the underlying true canonical correlation is larger. LCCA identifies the number of canonical variates more accurately than the naive approach. Similar patterns were found in the cosine similarity measures. The cosine similarity between estimated LCV loadings performs better as the sample size increases, and the underlying true canonical correlation is larger.

Fig. 12.

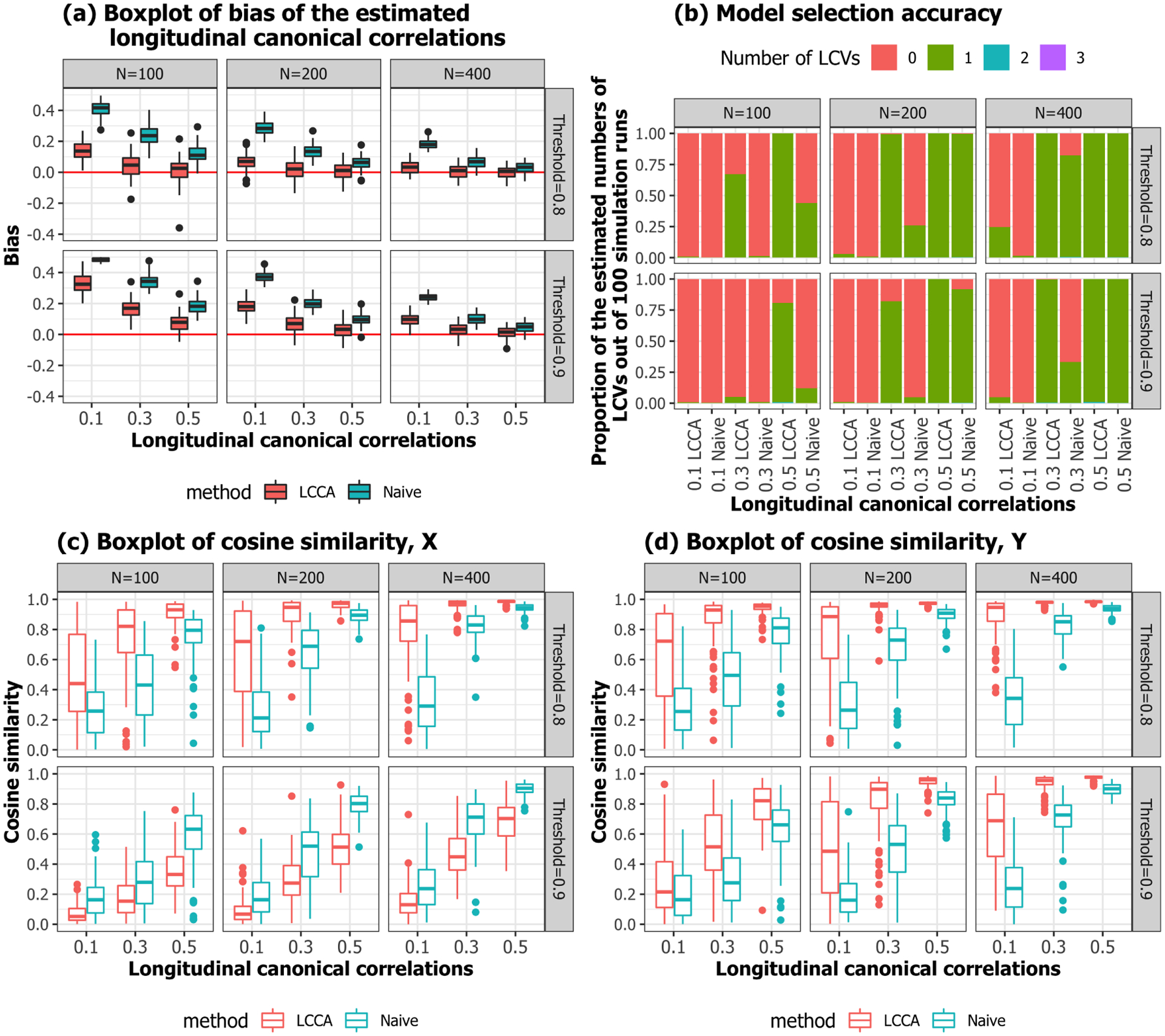
Simulation 1. Performance evaluation.

4.2. Simulation Setting 2.

Data were generated similarly to the first simulation, except the first five LPC loadings were taken from ADNI data from Section 3 (Figure 13). The LPC scores ${\xi }_{ik}^X$ and ${\xi }_{ik}^Y$ were generated from the $N\left(0,{\lambda }_k\right),{\lambda }_1=45.4,{\lambda }_2=17.2,{\lambda }_3=7.0,{\lambda }_4=\mathrm{4,1},{\lambda }_5=3.8$, where $Cor \left({\xi }_{i2}^X,{\xi }_{i2}^Y\right)=r$. For each subject, the number of visits were generated from Poisson(1) followed by adding 3 such that each subject has on average 4 time points. The time intervals between visits were generated from $U$[1, 2]. We conducted simulations for $r=0.1,0.3,0.5$, at $n=100,200,400$, and different threshold for LPC dimension selection (80% or 90%). For each scenario, 100 independent datasets were generated. We found very similar results as Simulation 1 (Figure 14, assuring our data analysis results in Section 3 have less bias in estimating canonical weights and correlations. The both methods tend to underestimate canonical correlation when the threshold $(=0.8)$ is smaller, while this issue does not persist when the threshold is more lenient.

Fig. 13.

Simulation 2. LFPCA models for simulation.

Fig. 14.

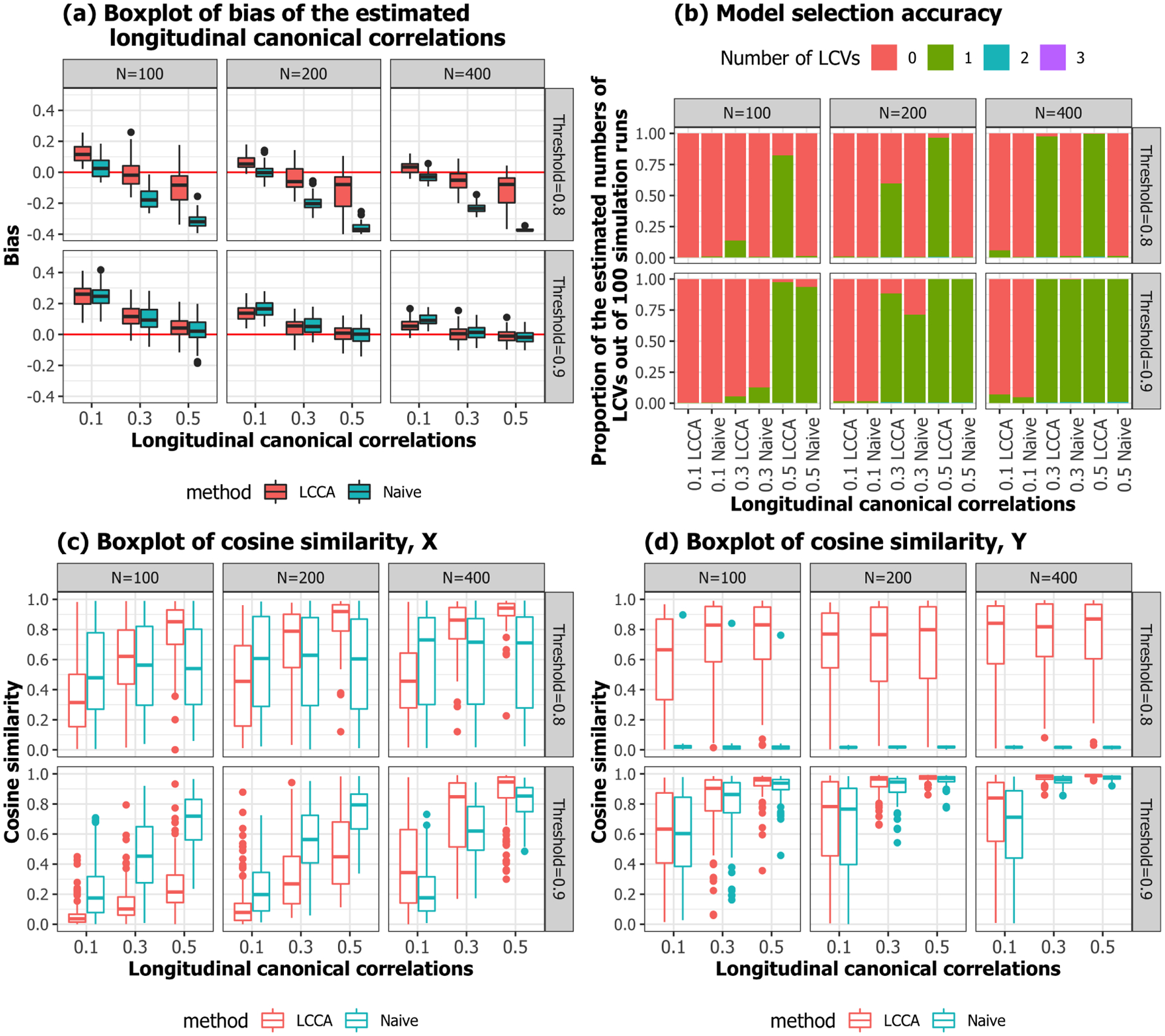
Simulation 2. Performance evaluation.

4.3. Simulation Setting 3.

We also examined whether the LCCA can recover subgroups. We employed the same simulation settings from Simulation 2, except longitudinal canonical variates (LCVs). Instead of generating the LCVs from a multivariate normal distribution, we imposed two subgroups. One group was generated from $MVN\left(0,\lambda {\mathbf{I}}_2\right)$ and the other group was generated from $N\left(\mu 1_2,{\mathbf{I}}_2\right)$ as shown in Figure 15. We varied the proportion of subsamples from 0.1 to 0.5 and evaluated whether the LCCA can identify subgroups.

Fig. 15.

Simulation 3. An example of the longitudinal canonical variates (LCVs) at the different ratios of subgroups.

To evaluate whether LCCA recovers the true LCVs with subgroups, the correlations between the true and estimated LCVs were calculated. Figure 16 shows that the LCCA identified LCVs, LC vectors, and the number of LCVs well, even with smaller sample sizes and a highly unbalanced subgroups $(subsampleproportion=0.1)$.

Fig. 16.

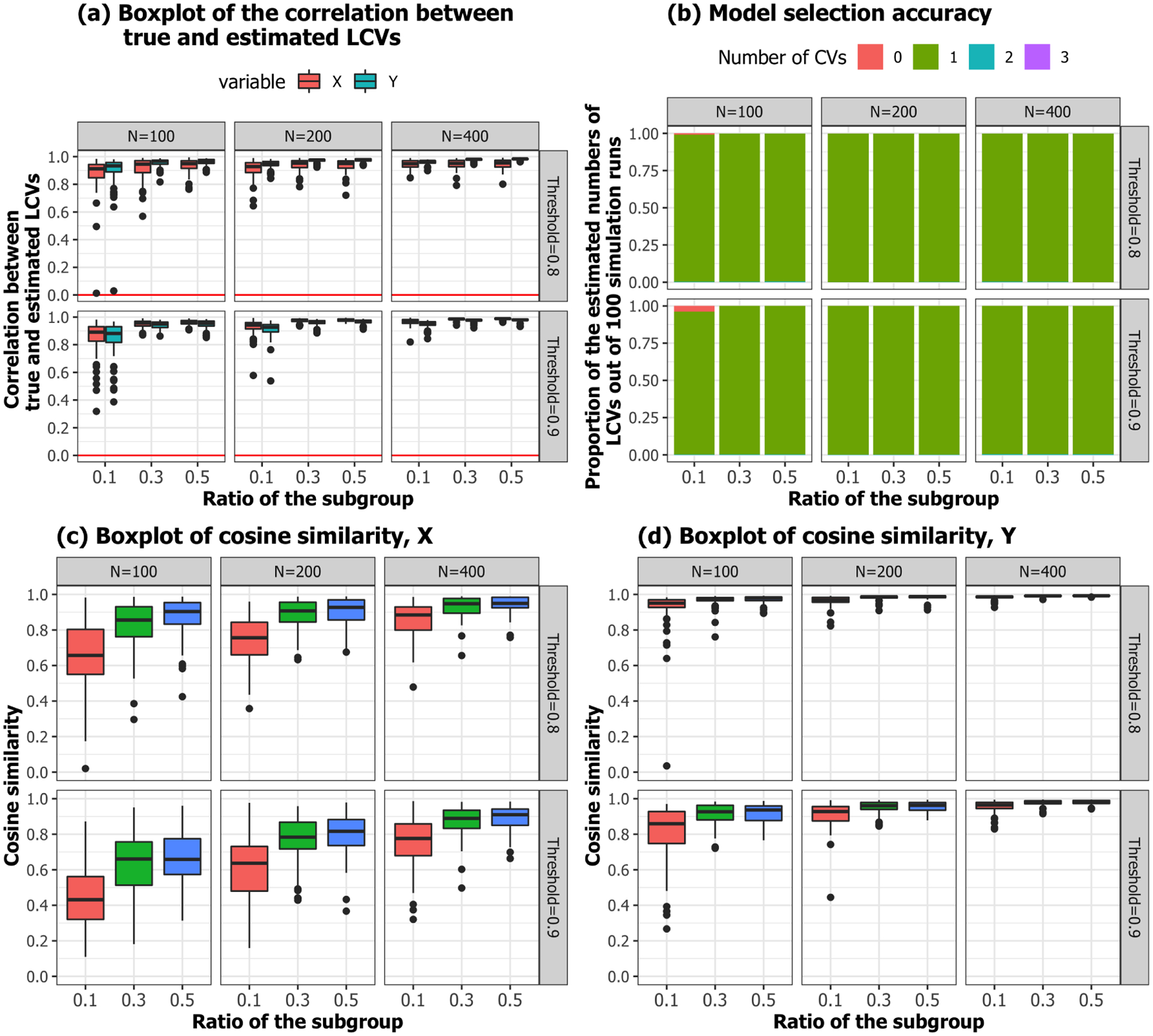
Simulation 3. Performance evaluation.

5. Conclusion

In this manuscript, we proposed a new longitudinal CCA method that can handle different temporal samplings and missing values that often occur in longitudinal data. The proposed method is very flexible in its ability to handle linear and nonlinear trajectories. The application to ADNI data, the longitudinal CCA revealed the most relevant patterns between Amyloid deposition associated neuronal loss measured as cortical thickness and subcortical volume. The canonical variates are associated with the baseline clinical status and predicted AD transition. The numerical experiments showed that LCCA outperformed the naive approach, also showing the performance of LCCA is not very sensitive to the selection of the threshold but requires adequate sample size or an effect size of the correlation.

Our two-stage approach is computationally fast, and our numerical experiments showed good performance using a threshold of 80–90% as a rule of thumb. However, the dimension reduction step using the LPCA possibly removes small but important biological signals in other neuroimaging modalities such as functional magnetic resonance imaging (fMRI). Furthermore, the two-step approach does not optimize both dimension reduction and dimension selection for CCA simultaneously, unlike the unified estimation approach for cross-sectional high-dimensional data (Song et al., 2016). Nonetheless, our novel LCCA approach offers a computationally efficient and well performing tool that could have important applications in neuroimaging and other settings producing high-dimensional, longitudinal, multivariate data.

Fig. 7.

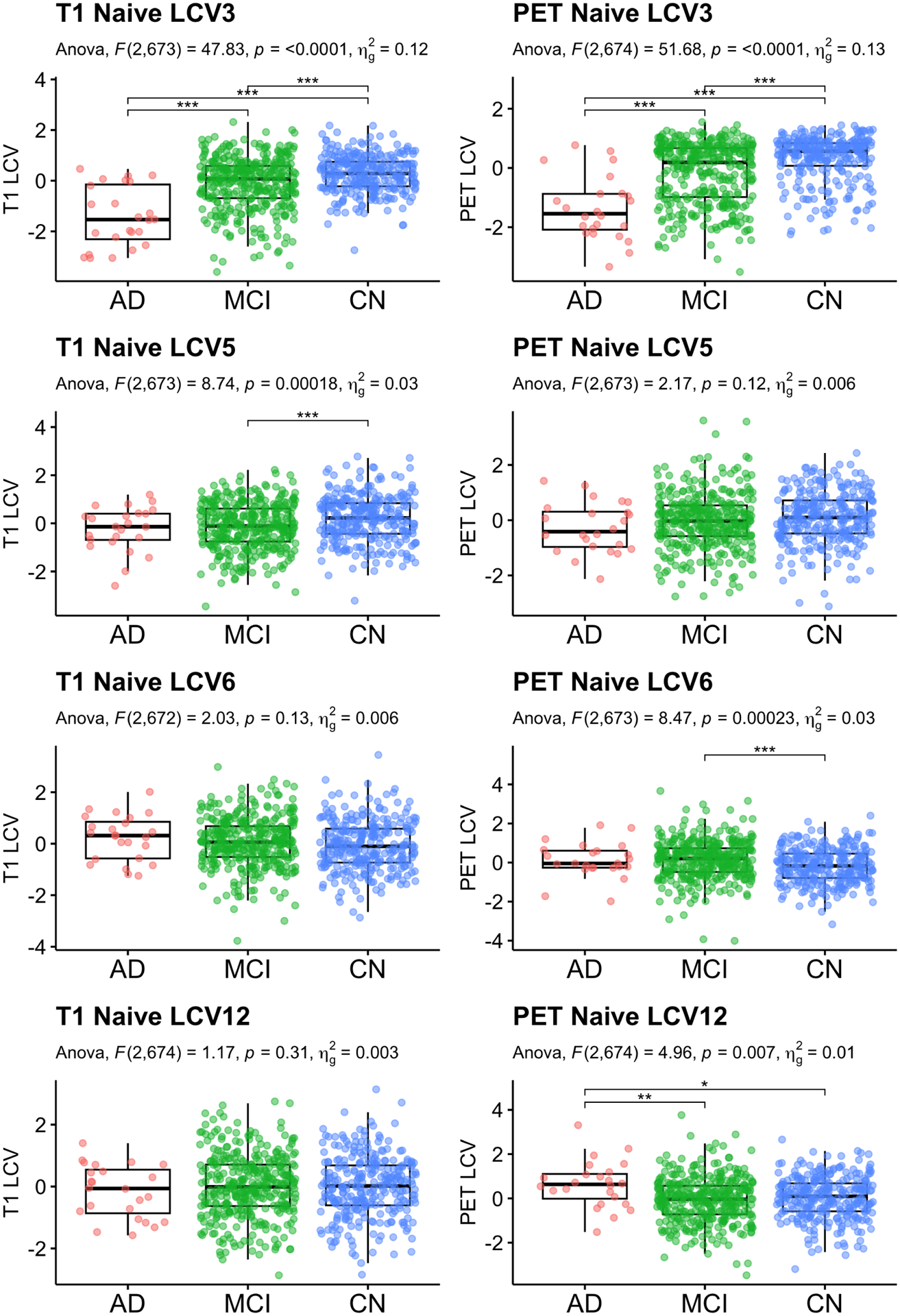
Naive: Baseline diagnosis status comparison. Significant CVs are reported. Age, sex and education were adjusted for statistical testing. For post-hoc pair-wise group comparison, least squared mean differences were computed, and unadjusted p-values are reported.

Fig. 9.

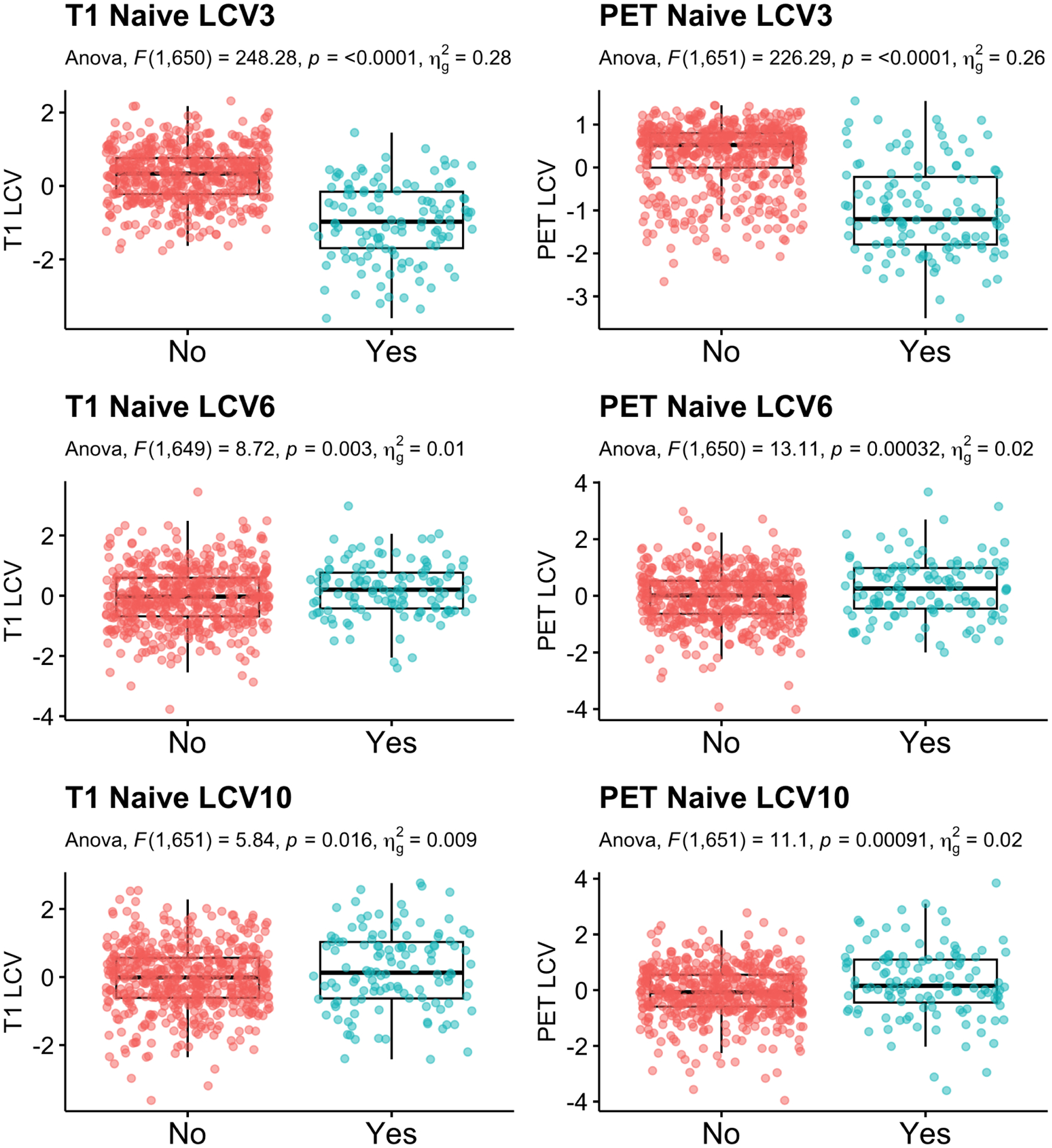
Naive: Group comparison of the canonical variates between participants who transition to dementia within 5 years compared to those who did not. Age, sex and education were adjusted.

Table 3.

ANOVA of diagnosis group comparison and AD conversion with age, sex and education adjusted for the Naive approach.

		T1				PET
	CV	F	p	${\eta }_p^2$	outliers	F	p	${\eta }_p^2$	outliers
Group Comparison	1	0.02	0.984	0.000	3	3.23	0.040	0.010	4
	2	4.24	0.015	0.012	3	1.18	0.308	0.004	4
	3	47.83	<0.001 *	0.124	1	51.68	<0.001 *	0.133	0
	4	0.75	0.472	0.002	0	1.92	0.148	0.006	1
	5	8.74	<0.001 *	0.025	1	2.17	0.115	0.006	1
	6	2.03	0.132	0.006	2	8.47	<0.001 *	0.025	1
	7	0.24	0.787	0.001	1	1.19	0.304	0.004	3
	8	0.78	0.458	0.002	0	1.60	0.202	0.005	1
	9	0.53	0.589	0.002	0	1.71	0.183	0.005	2
	10	0.25	0.780	0.001	0	1.47	0.230	0.004	0
	11	1.00	0.367	0.003	0	1.71	0.182	0.005	2
	12	1.17	0.310	0.003	0	4.96	0.007 *	0.015	0
AD Conversion	1	0.64	0.424	0.001	2	1.89	0.170	0.003	3
	2	0.80	0.372	0.001	2	0.94	0.334	0.001	3
	3	248.28	<0.001 *	0.276	1	226.29	<0.001 *	0.258	0
	4	0.47	0.494	0.001	0	1.00	0.317	0.002	1
	5	0.23	0.635	0.000	1	0.03	0.874	0.000	1
	6	8.72	0.003 *	0.013	2	13.11	<0.001 *	0.020	1
	7	0.38	0.541	0.001	1	0.81	0.368	0.001	3
	8	0.02	0.886	0.000	0	3.43	0.064	0.005	1
	9	0.09	0.769	0.000	0	1.16	0.282	0.002	2
	10	5.84	0.016	0.009	0	11.10	0.001 *	0.017	0
	11	0.01	0.910	0.000	0	0.14	0.713	0.000	2
	12	0.31	0.578	0.001	0	1.21	0.271	0.002	0

^*:adjusted $p<0.05$.