Programming the morphology of DNA origami crystals by magnesium ion strength

Significance

DNA origami is a technique that involves folding a bacteriophage DNA into a prescribed nanostructure using short oligonucleotides. This technique has found great utility in crystal engineering, where DNA origami constructs are assembled into crystalline materials via DNA hybridization. However, accessing distinct structural outcomes is difficult without an intricate set of DNA designs. The limited DNA design space over which DNA origami can crystallize hampers achieving this goal. Here, a facile approach is used to tune the crystallization pathways of DNA origami building blocks. Therein, changes in the strength of allosteric factor lead to distinct equilibrium phases and crystals. This approach promises access to engineering a library of crystalline materials with tunable features and properties via environmental variables.

Abstract

Harnessing the programmable nature of DNA origami for controlling structural features in crystalline materials affords opportunities to bring crystal engineering to a remarkable level. However, the challenge of crystallizing a single type of DNA origami unit into varied structural outcomes remains, given the requirement for specific DNA designs for each targeted structure. Here, we show that crystals with distinct equilibrium phases and shapes can be realized using a single DNA origami morphology with an allosteric factor to modulate the binding coordination. As a result, origami crystals undergo phase transitions from a simple cubic lattice to a simple hexagonal (SH) lattice and eventually to a face-centered cubic (FCC) lattice. After selectively removing internal nanoparticles from DNA origami building blocks, the body-centered tetragonal and chalcopyrite lattice are derived from the SH and FCC lattices, respectively, revealing another phase transition involving crystal system conversions. The rich phase space was realized through the de novo synthesis of crystals under varying solution environments, followed by the individual characterizations of the resulting products. Such phase transitions can lead to associated transitions in the shape of the resulting products. Hexagonal prism crystals, crystals characterized by triangular facets, and twinned crystals are observed to form from SH and FCC systems, which have not previously been experimentally realized by DNA origami crystallization. These findings open a promising pathway toward accessing a rich phase space with a single type of building block and wielding other instructions as tools to develop crystalline materials with tunable properties.

DNA origami technique has developed into a reliable methodology for manufacturing a variety of materials with exotic structures (1–6). Such DNA origami can serve as a platform to impart controllability to the spatial organization of hosted objects (7–12) and enable the informed design of emergent properties (13–20). Moreover, recent strides have proven the vast potential of this technique in the fabrication of metamaterials, in which DNA origami architectures are utilized as templates that can imbue functional materials with structural features (21–29). The realization of a customizable structure shows the ability to define the binding specificity between DNA origami and other components, which is particularly attractive for DNA origami–based crystal engineering (30–33). Leveraging sequence-specific DNA hybridization achieves exquisite control over the characteristics of the resultant crystalline materials, including the lattice parameters (34), crystal symmetries (35, 36), and macroscopic shapes (37). Integral to any approach to adding binding specificity into the assembly of DNA origami building blocks is the ability to program the directional interactions among building blocks. This requirement necessitates the position-selective functionalization of DNA origami; that is, to introduce recognition sites to the exterior of DNA origami. Therein, it is possible to direct the crystallization pathway of building blocks to form prescribed organizations that are impractical via conventional strategies. Nevertheless, in the context of DNA origami–based crystal engineering, access to an arbitrarily customized structure is partly hampered by the constraints of the crystallization process, despite the fully designed layout of recognition sites on the building blocks. These constraints pertain to the electrostatic and steric repulsion inherent in the assembly process of DNA origami, which imposes restrictions on designing recognition sites of a given building block. Given these limitations, accessing multiple crystalline arrangements and macroscopic shapes remains challenging under the finite design space of recognition sites.

Herein, we describe a facile approach for accessing crystals with diverse equilibrium phases and shapes using morphologically identical octahedral DNA origami frames (DOFs). Through the utilization of chemical makeup as a tool to modulate the binding coordination of DOFs, phase behavior of DOFs can be tuned. Specifically, octahedral DOFs assemble into a simple cubic (SC) lattice, a simple hexagonal (SH) lattice, and a face-centered cubic (FCC) lattice at low, intermediate, and high ambient magnesium ion (Mg²⁺) strengths, respectively, as the result of the Mg²⁺-dictated phase transition in DOF crystallization. Previous studies have investigated the impact of the Mg²⁺ strength and other environmental cues on various DNA nanostructures. For instance, the interplay between Mg²⁺ and four-way Holliday junctions has been shown to influence their electrophoretic mobilities (38) and resolution process (39). In crystallization of DNA tensegrity triangles, changes in the Mg²⁺ strength impact the structure of resulting crystals by affecting the monomer arrangement propensities (40), and additionally, can dynamically induce the crystal expansion and contraction (41). Furthermore, related studies have elucidated the role of Mg²⁺ and ethidium bromide (EB) in the complete formation and heterogeneous polymerization of DNA origami constructs (42, 43). Building upon these studies, our work shows that Mg²⁺-dictated phase transitions impart allosterism on the shape of the DOF crystals, wherein SH and FCC lattices externally express hexagonal prism (HP) crystals and crystals characterized by triangular facets (CCTF), respectively. Furthermore, selectively incorporating nanoparticles into DOFs arranged in SH and FCC lattices derives a body-centered tetragonal (BCT) and a chalcopyrite lattice, respectively, which creates a phase transition path that changes the crystal system. In contrast to investigations related to dynamic phase transitions, this study yields a rich phase diagram where each sample is synthesized de novo by prealtering the Mg²⁺ strength in the buffer environment. Products obtained in this manner cannot experience lattice rearrangement through continuous dynamic modulations, and the ability to trigger interconversion between different crystalline symmetries and shapes remains unattainable. Importantly, the contributing element behind structural transitions is the increased Mg²⁺ strength, which effectively neutralizes the electrostatic repulsion between DOFs exerted by the negatively charged phosphate backbone. This allows mutually repelled DOFs to be in closer proximity to one another and engage in denser packing arrangements. Hence, this approach can tune the assembly behavior of DOFs and, in turn, the crystalline phase and shape of the resulting products, without the need to design varied types of DOF building blocks. Our findings shed light on the role of the chemical makeup–assisted modulation of binding coordination in the crystallization of DNA origami and unlock access to a diverse set of crystalline products consisting of a single type of DNA origami building block.

Results and Discussion

Crystallization of DOFs and Phase Transitions of AuNP Lattices.

To probe how the chemical makeup impacts the crystallization behaviors, we first investigated a binary system in which DOFs are divided into two groups based on their sticky ends. Experimentally, DOFs are functionalized by the position-selective introduction of sticky ends, whereby internally bound gold nanoparticles (AuNPs) are engineered to encode the binding valence on the surface (step 1, Fig. 1A and SI Appendix, Figs. S1 and S2). Incorporation of AuNPs with DOFs allows assigning the identity of the AuNP lattice as a proxy for determining the packing arrangement of DOFs. In our previous report, discrete DOFs can crystallize into a lattice with an SC symmetry and a cubic shape via slow annealing under conventional chemical makeups (37). Here, we found that the introduction of the allosteric factor (e.g., Mg²⁺ strength) is able to modulate the binding coordination of DOFs, resulting in distinct crystalline products (step 2). As the Mg²⁺ strength increases, electrostatic repulsion between DOFs is substantially shielded, allowing them to be spatially closer. Consequently, the layout of the DOF recognition sites converging at a single position shifts to new modes, and the vertex-to-vertex arrangement for the DOF alignment becomes unfavored. This results in the generation of SH and FCC lattices upon crystallization, which yields HP-shaped crystals and CCTF, respectively (Fig. 1B and SI Appendix, Fig. S3). This chemically fueled modulation of DNA origami crystallization was discovered from small-angle X-ray scattering (SAXS) and was systematically investigated by further studies.

Fig. 1.

Chemical makeup–dictated phase transitions of DOF crystals. (A) Schematics for overwriting the binding valence of AuNPs (step 1), wherein AuNP is embedded in an octahedral DOF to yield an AuNP with predefined binding valence. The engineered AuNPs are subdivided into two groups according to the exterior recognition sites. Two types of recognition sites composed of complementary DNA strands are color coded as purple and turquoise, respectively. (B) DOF crystals undergo phase transitions due to tuning the DOF binding coordination (step 2). The premodulated strength of the allosteric factor (in this work, Mg²⁺) results in progressive transitions of the local binding coordination of DOF monomers, and thus the phase transitions of the resulting crystals. Cubic crystals (light blue), HP-shaped crystals (medium blue), and octahedral crystals (dark blue) form from lattices with SC, SH, and FCC symmetries, respectively, as a function of the Mg²⁺ strength. For a typical system with a DOF monomer concentration of ~20 nM, the low Mg²⁺ strength spans from 12.5 to 32.5 mM, the moderate Mg²⁺ strength spans from 32.5 to 52.5 mM, and the high Mg²⁺ strength is above 52.5 mM.

SAXS was employed to interrogate the lattice structures of AuNPs as a function of the Mg²⁺ strength. At Mg²⁺ strengths of 12.5, 32.5, and 82.5 mM, the scattering pattern indexes to an SC (space group: Pm$\overline{3}$m), an SH (space group: P6/mmm), and an FCC (space group: Fm$\overline{3}$m) lattice, respectively, indicating that phase transitions occur with an increased Mg²⁺ strength (Fig. 2A). The results are corroborated via scanning transmission electron microscopy (STEM) at local levels, where the DOF–AuNP lattices were encapsulated in silica to better visualize the positions of AuNPs. The observations are in agreement with modeled lattice projections viewed along specific crystallographic orientations (Fig. 2B and SI Appendix, Fig. S6). Meanwhile, the SAXS analysis indicates that the nearest neighbor distances between AuNPs within the SH and FCC lattice are 38.3 nm and 44.6 nm, respectively, compared to the 58.8 nm for the SC lattice. Variations in this parameter predict the emergence of unusual packing arrangements where DOFs are in closer proximity. For high Mg²⁺ strengths, excessive Mg²⁺ exhibits a Debye screening effect on the electrostatic repulsive forces between phosphate groups (44, 45), allowing DOFs to overcome electrostatic repulsion and steric repulsion and move into closer proximity. Thus, DOFs can pack into denser arrangements through unusual binding coordination. Moreover, we explored the effect of the DOF monomer concentration on the phase behavior via SAXS experiments and determined a phase diagram for DOFs as a function of the Mg²⁺ strength and monomer concentration of DOFs (Fig. 2C). As observed with experiments, AuNP lattices assembled from 10, 20, and 40 nM DOFs gradually transitioned to the FCC phase with the elevation of Mg²⁺ strength, while an increased DOF monomer concentration resulted in a lower Mg²⁺ strength required for inducing phase transitions. In other words, the phase behavior of DOFs is susceptible to the monomer concentration (SI Appendix, Figs. S8–S10). This behavior is likely due to the closer proximity of DOFs in the system with higher DOF monomer concentration, which lowers the Mg²⁺ strength capable of inducing phase transitions. This enables one to tune the location of phase transitions by modifying the assembly environment. It is noted that a lattice is evaluated as possessing FCC symmetry so long as the emergence of scattering peaks related to the FCC structure, regardless of intensities of these peaks (full details are provided in SI Appendix, Text). The phase diagram was determined following this criterion to unambiguously demarcate phase boundaries.

Fig. 2.

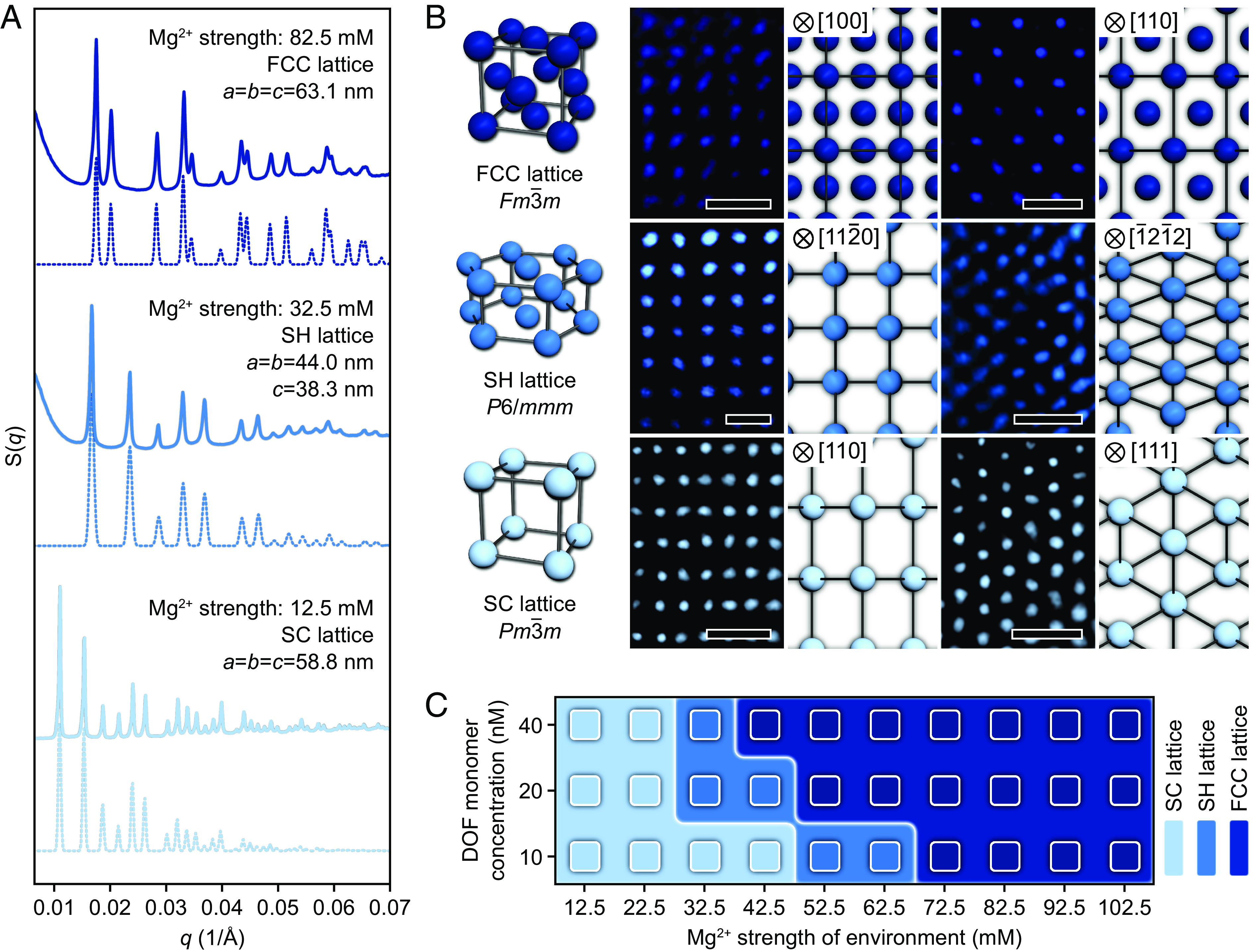
Structural transformation of crystalline phases. (A) SAXS patterns for three distinct equilibrium phases. Lattices undergo phase transitions from SC via SH to FCC due to an increasing Mg²⁺ strength in the environment from 12.5 mM to 82.5 mM. Simulated SAXS data (dashed lines) are shown beneath the experimental data (solid lines). (B) STEM images of silica-encapsulated lattices observed along specific orientations. Images of the modeled projections are shown to the right of the corresponding STEM images. Images are false-colored for clarity. (Scale bars: 50 nm.) (C) Phase diagram for the AuNP lattices is shown as a function of the Mg²⁺ strength and DOF monomer concentration, where phase behaviors are determined by SAXS. The SAXS (A) and STEM (B) experiments were performed on AuNP lattices that formed at a DOF monomer concentration of ~20 nM.

Morphological Transitions of DOF Crystals.

Our prior study opens the ability to tailor macroscopic crystal shapes by modifying the morphology of the DOF building blocks (37). We found that modulations in the Mg²⁺ strength also enable crystal shapes to be controlled, as proven by scanning electron microscopy (SEM) characterizations. Images indicate that an evolution of crystal shapes is concurrent with the phase transition, where the SC, SH, and FCC lattices externally exhibit a cubic shape (Figs. 3 A and B and SI Appendix, Figs. S11 and S12), an HP shape (Figs. 3 D and E and SI Appendix, Figs. S13–S15), and an octahedral shape (Fig. 3 G and H), respectively. We stress that it is more appropriate to classify most of the crystals formed from FCC lattices into CCTF due to the low yield of octahedral crystals with structural integrity (SI Appendix, Figs. S16 and S17). A well-defined equilibrium shape is governed by exposed facets that are dependent upon the packing arrangement of DOFs. Evidently, the packing arrangement adopted by DOFs varies based on the raising of Mg²⁺ strength, as the result of the modulation of binding coordination of DOFs. Within the SC lattice, DOFs pack with an efficiency of ~15.47% and each DOF connects to six neighboring DOFs in a vertex-to-vertex fashion along the three mutually orthogonal orientations to yield a cubic crystal bound by six (100) facets (Fig. 3C and SI Appendix, Figs. S18 and S19). While an SH lattice results from the stacking of planar, hexagonally close-packed layers, in which each DOF aligns its edge with its neighbors, and DOFs within adjacent layers orientate oppositely and arrange in a complete face-to-face manner. In this case, each DOF is surrounded by eight neighbors, resulting in a coordination number of 8 and an increased packing efficiency (~48.98%). This organization produces a crystal bound by six equivalent rectangular (10$\overline{\mathrm{1}}$ 0) facets and two equivalent hexagonal (0001) facets (Fig. 3F and SI Appendix, Figs. S20 and S21). For the CCTF, the emergence of (111) and (100) facets stems from the dense DOF packing within the underlying FCC lattice, where each DOF is closely surrounded by twelve neighbors through an edge-to-edge contact (Fig. 3I and SI Appendix, Figs. S22 and S23); namely, the coordination number is 12. DOFs arranged in an FCC symmetry take on the highest packing efficiency (~50.08%) among the three structures (SI Appendix, Fig. S24). Within the phase transition system, the elevation of cationic strength not only drives DOFs to be in more proximity by reducing the Debye length of DOFs, but also significantly influences the conformation of short single-stranded sticky ends which are well described by the worm-like chain (WLC) model (46). At lower Mg²⁺ strengths, the sticky ends tend to adopt a stretched-out conformation (47). Conversely, increased Mg²⁺ strengths impart greater flexibility and space available to the sticky ends, attributed to the Mg²⁺ binding on DNA molecules, which reduces the stiffness and end-to-end distance of DNA strands (48). Thus, the original extension direction of sticky ends becomes uncertain with increased Mg²⁺ strengths. This raises the possibility of extending in more flexible directions and interconnecting DOFs through manners beyond the vertex-to-vertex fashion.

Fig. 3.

Evolution of the crystal morphology. Schematics and whole-view/magnified SEM images showing DOFs assembled into cubic (A–C), HP-shaped (D–F), and octahedral (G–I) crystals with SC, SH, and FCC symmetries, respectively. (Scale bars: 1 μm for B, E, and H; and 25 nm for C, F, and I.) For clarity, crystals in whole-view SEM images (B, E, and H) are false-colored, and AuNPs are omitted in the structure models shown in C, F, and I. Besides, some of the edges of DNA octahedra are color coded to highlight the structural features of exposed crystal facets. It should be stressed that while the octahedron is the ideal final shape of crystals formed from FCC lattices, octahedral crystals with shape integrity (shown in H) were experimentally produced with a low yield.

Formation of Derived AuNP Lattices.

For the association of DOFs within HP crystals and CCTF, however, the binding modality of sticky ends remains unknown compared with its counterpart within cubic crystals. Deciphering this problem entails determining the subtypes of the DOFs at given sites within the SH and FCC lattices. To this end, we investigated the phase behaviors of a derived binary system, where one of two types of DOFs was filled with AuNPs, while the other was selectively unfilled. The distribution of two DOF types within a cubic crystal is highly certain. The crystallization of DOFs in the derived system should form AuNP lattices with an FCC symmetry at an Mg²⁺ strength of 12.5 mM, as proven in a previous study (33). Subsequently, AuNPs are mediated by DOFs to assemble into a BCT lattice (space group: I4/mmm) and a chalcopyrite-type lattice (space group: I$\overline{4}$m2) at Mg²⁺ strengths of 42.5 and 72.5 mM (Fig. 4 A and B and SI Appendix, Figs. S25–S27), while the DOF building blocks retain the SH and FCC orders, respectively (SI Appendix, Figs. S28 and S29). Although the distribution of two types of DOFs may deviate from expectations at some local domains, the BCT and chalcopyrite-type lattices are generated predominantly over the others upon crystallization. These observations reveal another form of phase transition of AuNP lattices that occurs with the toggling of the DOF system between different states and involves changes in the crystal system. More importantly, this design-by-selective deletion approach provides access to a broader phase space and is informative in identifying how two types of DOFs distribute within SH and FCC lattices (SI Appendix, Fig. S30, and full details are provided in SI Appendix).

Fig. 4.

Type expansion of AuNP lattice and theoretical analysis for the formation of HP-shaped crystals. (A and B) Two derived AuNP lattices are obtained due to the selective removal of AuNPs from crystals consisting of DOFs arranged in an SH and an FCC lattice. Shown are (A) SAXS patterns, (B) models and STEM images of silica-encapsulated lattices. The Insets in the STEM images are simulated projections viewed along specific orientations, and the STEM images are false-colored for clarity. (Scale bars: 50 nm.) (C) Schematics for the three types of polyhedra that can form from DOFs packed in an SH arrangement. (D) Theoretical molar surface energies (E_s) for TP, QP, and HP crystals are shown as a function of the aspect ratio (AR) of the corresponding crystals.

Given these results, we therefore proposed several possible binding formats for DOFs within the SH and FCC lattices (full details are provided in SI Appendix, section 2), and sought to gain a fuller understanding of how binding format affects the formation of crystalline shapes by a theoretical study on HP-shaped crystals. We hypothesized that the packing arrangement adopted by DOFs within an SH lattice should also permit the generation of the triangular prism (TP) and quadrangular prism (QP) equilibrium shapes, where both are enclosed by (10$\overline{1}$ 0) and (0001) facets. This hypothesis builds upon the geometrical perspective that TP and QP are the only two possible regular prismatic shapes allowed to form from an SH lattice of DOFs as these two shapes contain the angles of 60° and can minimize the anisotropy of surface energy (Fig. 4C, and full details are provided in SI Appendix). Theoretical calculations reveal that the surface energy of an equilibrium crystal varies with the aspect ratio (AR) under a given binding format of DOF monomers. In an ideal SH system containing 20 nM DOFs, the HP-shaped crystals are enclosed by the lowest surface energies when possessing a mean AR of 1.81, which is very close to the AR of 1.66 obtained from experiments. Furthermore, the lowest surface energies for HP, QP, and TP crystals exhibit a ratio of γ_HP:γ_QP:γ_TP = 1:1.10:1.14, manifesting a thermodynamic condition favoring preferential growth of HP-shaped crystals (Fig. 4D, and full details are provided in SI Appendix). While not excluding the likelihood of other binding formats existing within HP-shaped crystals, the theoretical arguments, to some extent, suggest that the crystallization system spontaneously circumvents the DOF binding formats that lead to thermodynamically unstable products.

Formation of DOF Crystals with Exotic Shapes.

In contrast to SC and SH systems, in which well-defined cubic and HP crystals form in high yield, FCC systems suffered from frustration in yielding uniform octahedral crystals that are expected to be obtained. The grains shown in Fig. 3H and SI Appendix, Fig. S17 represent a type of faceted crystals which was formed from the FCC lattice and quite close to perfect octahedron in shape, but was seldom observed among the resulting products. Indeed, a vast majority of the practically obtained products is CCTF and its variants. To monitor the structural evolution of crystals throughout the transition process from SH to FCC, we examined the assemblies generated at a series of intermediate Mg²⁺ concentrations using SAXS. The spectra show that with the raising of Mg²⁺ concentration, scattering peaks related to the FCC symmetry gradually emerge and sharpen, accompanied by a marked decrease in the intensity of the SH scattering peaks. It is important to note that the peaks associated with the SH symmetry remain observable throughout the SAXS experiments, albeit their constantly diminishing intensities, which reflects that the SH domain persists in assemblies generated under all conditions (Fig. 5A and SI Appendix, Fig. S31). Subsequently, samples used for SAXS experiments were characterized via SEM imaging after silica encapsulation to visualize changes in the macroscopic structural features of the resulting products. As the Mg²⁺ strength raises, FCC phase gradually increases in domain size and develops into CCTF of high crystallinity, while HP-shaped crystals obviously shrink and integrate into CCTF, as observed from the SEM images (SI Appendix, Figs. S32–S36). For example, we routinely observed heterostructured crystals formed at an Mg²⁺ strength of 72.5 mM, where crystals contain coexisting SH and FCC phases, and visible phase boundaries are flanked by pure SH and FCC domains (Fig. 5B). The formation of this mixed-composition phase is based on the premise that the SH and FCC structures share a hexagonally close-packed plane through which both phase domains can interconnect with each other (SI Appendix, Fig. S37). Moreover, we sought to eliminate phase boundaries to obtain single crystals by further increasing the Mg²⁺ strength and annealing the as-synthesized products for another cycle. However, these attempts did not result in an appreciable increase in the yield of the uniform octahedral crystals. This is probably reflective of the insignificant difference in surface energy between the FCC(111) and SH(10$\overline{1}$ 0) facets, which causes the lack of driving force for the growth of a uniform crystal shape.

Fig. 5.

Shape diversity of the multiphase DOF crystals. (A) SAXS patterns revealing the structural evolution from SH to FCC states, wherein gradual phase transitions are observed. The red arrow points to the location of the SH (10$\overline{1}$ 0) scattering peak. (B) Whole-view SEM image of the crystals that possess multiple coexisting domains (Left) and the zoomed-in image on a multidomain region with identifiable grain boundaries (Right, positions of phase boundaries are outlined by white dashed lines). (Scale bars: zoom out, 0.5 μm; zoom in, 200 nm.) (C) SEM image and schematics of a twinned crystal, which consists of two separate subunits related by a symmetry operation based on a twin plane (denoted by a green slab). (Scale bar: 1 μm.) (D and E) SEM images (D) and schematics (E) of an FTC, which is characterized by a star-like shape and two pentagonal dimples at the emergence of the fivefold axis. (Scale bars: zoom out, 1 μm; zoom in, 200 nm.) Note that the SAXS data are obtained based on systems with a DOF monomer concentration of ~20 nM, where crystals formed in a solution with a 72.5 mM Mg²⁺ strength are encapsulated in silica for SEM imaging.

Within this context, the similar surface energy between these two facets is prone to produce a lower energy barrier for the growth of defect structures, which is validated by the emergence of twinned crystals (Fig. 5C). Structurally, a twinned crystal is composed of two equivalent subunits related by a symmetry operation based on a twin plane (SI Appendix, Figs. S38 and S39). The subunits are architectures with octahedral features generated from an FCC lattice or mixed lattices containing small amounts of SH domains. The symmetrical orientation causes DOFs at the junction of two subunits to form an SH-structured segment where the twin plane passes through the middle (SI Appendix, Fig. S40). Another intriguing observation of the twinning phenomenon is the presence of fivefold twinned crystals (FTCs), where five twin planes intersect and cyclically arrange around an axis with D_5h symmetry, yielding a star-like-shaped FTC with a pentagonal dimple (Fig. 5D and SI Appendix, Fig. S42). Considering the slight faceting at the dimples, each subunit is terminated by six (111) facets and a (100) facet (Fig. 5E and SI Appendix, Fig. S43). According to the spinel twin law, in an ideal FTC with an FCC structure, two adjacent twin planes enclose an angle of ~70.53°. In theory, repeated twinning of subunits cannot form a complete space-filling structure and creates an angular misfit of ~7.35° (SI Appendix, Fig. S44) (49, 50). However, no gaps were observed in the obtained FTCs. We project that such an angular gap, in practical, can be accommodated by long, soft sticky ends on the exterior of DOFs (51), resulting in a deviation from the theoretical structure.

Conclusion

This work underscores the notion that the tuning of Mg²⁺ strength in the environment can be employed as a tool to tune the binding coordination of DOFs in crystallization. Such manner influences the crystallization pathway of DOF building blocks and results in unexpected structural transitions of the structural outcomes. Increasing the Mg²⁺ strength directs DOF monomers to engage in dense packing arrangements, where association of DOFs is maintained by unusual interconnections of sticky ends, therefore the formation of faceted crystals that were previously unachieved in DNA origami crystallization. As such, the capability to manipulate phase behaviors by changing the chemical makeup represents an approach to build various crystals with a single type of origami. Looking forward, one can imagine pushing current understanding toward other environmental variables to map a widely applicable strategy to engineer assembly pathways of structural units for the manufacture of a library of crystalline materials unattainable under conventional conditions. Such materials can be used to exploit properties and functionalities dominated by environmental variables while being fully user defined.

Materials and Methods

Detailed materials and methods are provided in SI Appendix.

Synthesis of DNA–AuNP Compounds.

The DOFs were synthesized by mixing M13mp18 DNA strands, staple oligonucleotides, inner anchoring strands, and sticky end strands in a 1× TAE buffer (PH = 8.0 at 20 °C) containing 40 mM Tris-acetate, 1 mM EDTA, and 12.5 mM magnesium acetate. The final concentration of M13mp18 DNA strands was typically 10 nM in a total volume of 100 μL. The mixture was subject to a predetermined thermal annealing procedure over a course of 20 h in a PCR thermocycler. Subsequently, anchoring ssDNA-grafted AuNPs inside the DOFs was fulfilled by adding a specific volume of functionalized AuNPs into the as-synthesized DOFs followed by heating the mixture to 50 °C and then slowly cooling to 20 °C at a rate of 0.04 °C/min.

Modification of Crystallization Medium for DOF–AuNP Compounds.

The obtained DOF–AuNP compounds were first purified from excessive staple strands before subsequent crystallization (details in SI Appendix, schematically shown in SI Appendix, Fig. S4) (52). The operation was initiated by mixing DNA–AuNP compounds with a PEG buffer [20% w/v PEG, 40 mM Tris-acetate, 1 mM EDTA, and 12.5 mM Mg(CH₃COO)₂] at a volumetric ratio of 1:1. Then, the compounds were precipitated into a pellet via centrifugation at 15,000 × g for 2 h. The supernatant was removed, and a specific volume of fresh buffer with an Mg²⁺ concentration of 12.5 mM was filled into the centrifuge tube. The solution was shaken (37.5 °C, 750 rpm) on a thermal shaker for 20 h to allow for the permeation of buffer into the compact precipitate of aggregative DNA–AuNP compounds and the even dissolution of the DOF–AuNP compound. In the final step, a specific volume of freshly prepared buffer containing a high Mg²⁺ concentration was dropwise added to the solution containing well-dispersed DOF–AuNP compounds, and the mixture was vigorously shaken (25 °C, 1,000 rpm) for 30 min before crystallization.

Crystallization of DOF–AuNP Compounds.

The crystallization process was initiated by mixing two types of purified DOF–AuNP compounds dispersed in a media with varying Mg²⁺ strengths. In a typical experiment, two types of compounds were mixed in a volumetric ratio of 1:1 to a total volume of 100 μL. Then, the mixed solutions were incubated at 50 °C for 30 min and allowed to cool to 20 °C in a thermal incubator at a cooling rate of 0.2 °C/h.

Silica Encapsulation of Crystals.

The obtained crystals were encapsulated in a silica matrix following the procedure described in previous works (37, 53, 54). The formed crystals were first washed through removing the supernatant and filling the freshly prepared 1× TAE buffer containing 7 mM MgCl₂. After several rounds of treatment, the buffer exchange was fulfilled, and the Mg²⁺ strength in the surrounding environment of crystals drastically decreased. Then, the samples were incubated with TMAPS, during which the mixtures were shaken on a thermal shaker (500 rpm, 30 min) at room temperature. The TMAPS can attach to DNA strands via electrostatic interactions between the cationic end of the TMAPS and the negatively charged phosphate backbone of the DNA, thereby providing cocondensation sites for silica growth. Subsequently, the TEOS was added followed by shaking for another 30 min at the same rate. After these steps, the samples were left static on the thermal shaker for over 10 h at room temperature, resulting in the formation of whitish-red precipitates at the bottom of the centrifuge tubes, indicating the solidification of DOF crystals. The solidified crystals were rinsed and isolated, wherein the samples were centrifuged for 10 s at a rate of 3,000 rpm. The supernatant was removed, and the samples were resuspended in ethanol. This step was repeated for several rounds to maximize the removal of silica debris generated during encapsulation process and excess silica sources as possible.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.