Abstract
For a general cubic fourfold with Fano variety F, we compute the Hodge numbers of the locus of lines of second type and the class of the locus of triple lines, using the description of the latter in terms of flag varieties. We also give an upper bound of 6 for the degree of irrationality of the Fano scheme of lines of any smooth cubic hypersurface.
Keywords: Cubic fourfold, Fano scheme, Second type locus, Invariants
Introduction
Let be a general cubic fourfold and its Fano scheme of lines, which is a four-dimensional hyperkähler variety. The normal bundle of a line decomposes as one of the following two:
and is called of first or second type respectively. The locus of second type lines is a smooth projective irreducible surface which has drawn considerable interest since the landmark paper [5] of Clemens–Griffiths. The aim of this paper is to study some invariants of S and F.
In Sect. 2 we summarise what is known about S and F and fix notation. In Sect. 4 we use Amerik’s description of the second type locus S as the degeneracy locus of the universal Gauss map
the Harris–Tu formula as well as Borel–Bott–Weil computations on the Grassmannian from Sect. 3 to compute the Hodge numbers of S.
Theorem A
If is a general cubic then the second type locus is a smooth irreducible surface whose Hodge numbers are as follows:
whereas contains a non-trivial element of order 2.
The order of the torsion element in the above theorem was pointed out to us by Huybrechts (see Remark 4.4), who also independently calculated the above invariants in his lecture notes on cubic hypersurfaces, although our approach using Borel–Bott–Weil directly on F leads to a more refined analysis of the projective embedding S in the Plücker space.
In the final Sect. 6 we extend results from [11] to prove the following
Theorem B
Let be a smooth cubic hypersurface and F(X) its Fano scheme of lines. Then degree of irrationality of F(X), i.e., the minimal degree of a dominant, generically finite, rational map to , satisfies
Background and notation
As the notation surrounding cubic fourfolds is substantial, we devote this section to fixing that used in the paper and recalling some basic properties, so that it acts as a reference for later sections.
For a vector bundle E we denote by  , so that projective space parametrises one-dimensional subspaces. We denote by the space of k-dimensional subspaces of , with universal bundle of rank k and universal quotient bundle of rank . We will denote by the standard Schubert cycles for an index I so that, e.g., for .
, so that projective space parametrises one-dimensional subspaces. We denote by the space of k-dimensional subspaces of , with universal bundle of rank k and universal quotient bundle of rank . We will denote by the standard Schubert cycles for an index I so that, e.g., for .
Throughout, will be a smooth cubic fourfold with and the Fano scheme of lines contained in X which is a hyperkähler fourfold [3]. To unburden notation, we will often be sloppy in distinguishing a line and the point that it defines. We denote by the restrictions of to F.
The subvariety is given by a section of the rank four bundle where p, q are the projections from the universal family . In fact it is the section induced, under this isomorphism, by whose vanishing is X (see [6, Proposition 6.4]) and its cohomology class in the Grassmannian is given by which can be computed as follows (see [9, Example 14.7.13]):
| 1 |
Following [5], there are two types of lines , depending on the decomposition of the normal bundle .
Definition 2.1
We say that a line is
of first type if
 ,
,of second type if
 .
.
An equivalent geometric description is as follows: is of
first type if there is a unique tangent to X along ,
second type if there is a family , , of 2-planes tangent to X along .
Denote by
the locus of second type lines.
Denote by the Plücker ample line bundle on F and by the restriction on S. The following is a combination of [1, Lemma 1], [19, Section 3] and [14, Proposition 6.4.9].
Theorem 2.2
If is a cubic fourfold then S is 2-dimensional and is the degeneracy locus of the Gauss map, i.e., the following morphism of vector bundles:
In particular in and the class of S in is given by
If X is general, S is a smooth projective irreducible surface.
We motivate now the study of S. Consider the Voisin map of [22] , taking a general line and giving the residual line in the tangent 2-plane to , i.e., . Note that this is not defined on S nor on any lines contained in a plane contained inside X. Containing a plane is a divisorial condition, so for X outside this locus, we can resolve this map with one blowup along the surface S. The map has been used in various contexts (see, e.g., [2, 21]), so it is important to understand its locus of indeterminacy. See also [14, Sections 2, 6] for further references and motivation.
As another example, [19, Theorem 0.2] proves that if X is very general then for every rational curve of class , the generator of , there exists a unique so that . In [18] this is used to count the number of arithmetic genus 1 curves of fixed general j-invariant in F of class , and in [12] to count the number of nodal rational curves of class respectively.
Cohomology of
This section contains some ancillary computations necessary for the next section. We briefly recall the necessary notation for the Borel–Weil–Bott Theorem used to compute various cohomology groups of tautological bundles on the Grassmannian with universal sub and quotient bundle respectively. For a quick introduction we found [4, Appendix A] and [17] helpful, although a more thorough reference is [23].
Denote by ,  respectively and the standard Weyl module. If is regular, i.e., all its components are distinct integers, then the BWB Theorem states that
respectively and the standard Weyl module. If is regular, i.e., all its components are distinct integers, then the BWB Theorem states that
is the only non-trivial cohomology group of this sheaf. In the above, is the unique element of the symmetric group which permutes the components of so that they are non-increasing, i.e., with , and is defined as the length of in the sense of the number of transpositions of the form that constitutes of. If on the other hand is not regular, then all cohomology groups are zero.
We recall the formula, e.g., from [7, Theorem 6.3], that if is such that then
whereas for an arbitrary non-increasing sequence , we may twist by some large weight (e.g., ) to make all components positive — this has the effect of tensoring the representation by a 1-dimensional one which does not change the dimension.
The first task is to decompose various tautological sheaves into irreducible representations. Here are some examples of irreducible representations
Proposition 3.1
The non-zero cohomology groups of 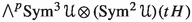 and
and  on for are
on for are
whereas for they are
 |
Proof
Using the following code in the SchurRing package of Macaulay2,  we compute the weights of the irreducible components of the representation
we compute the weights of the irreducible components of the representation
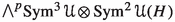 as follows:
as follows:
| p | |||
|---|---|---|---|
| 0 | (1,−1) | (7, 4, 4, 3, 2, 1) | −1 |
| 1 | 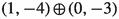 |
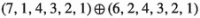 |
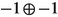 |
 |
 |
 |
|
| 2 |  |
 |
 |
 |
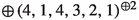 |
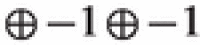 |
|
| 3 |  |
 |
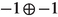 |
 |
 |
 |
|
| 4 | (−5,−7) | −1 |
since for example a decomposition into irreducibles for is
In the table, signifies that the weight w is not regular. From the Borel–Weil–Bott Theorem, we obtain
For , as
we obtain
Similarly, the table for 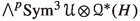 is as follows:
is as follows:
| p | |||
|---|---|---|---|
| 0 | (0, 0) | (6, 5, 4, 2, 1, 0) | 0 |
| 1 | (6, 2, 4, 2, 1, 0) | − 1 | |
| 2 | 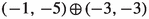 |
 |
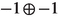 |
| 3 | 5 | ||
| 4 | − 1 |
so the only non-zero cohomology groups occur for . Using the same formulas as above we compute
The table for  is as follows
is as follows
| p | |||
|---|---|---|---|
| 0 | (4, 1, 4, 3, 2, 1) | − 1 | |
| 1 |  |
 |
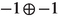 |
 |
 |
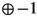 |
|
| 2 | 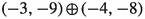 |
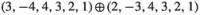 |
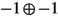 |
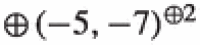 |
 |
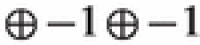 |
|
| 3 | 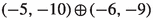 |
 |
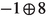 |
 |
 |
 |
|
| 4 | 8 |
giving
Similarly, the table for 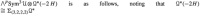 .
.
| p | |||
|---|---|---|---|
| 0 | (0, 0) | (6, 5, 7, 5, 4, 3) | −1 |
| 1 | (0,−3) | (6, 2, 7, 5, 4, 3) | 5 |
| 2 |  |
 |
 |
| 3 | (−3,−6) | −1 | |
| 4 | (−6,−6) | 8 |
giving
Hodge numbers of S
In Theorem 2.2, we described how S is given as the degeneracy locus of the map
Restricting to S we thus have the following sequence of vector bundles:
| 2 |
where K is a line bundle and C of rank 2. Note that there is a formula for the normal bundle of a degeneracy locus in [13, Section 3] giving
The map f is generically injective when considered on F, hence injective, and Amerik [1, Section 2] has constructed the following resolution of the ideal sheaf of :
| 3 |
A short explanation is in order concerning the above. The cokernel of f is torsion-free by noting that the degeneracy locus S does not have any divisorial components (see the local computations of [8, pp. 32–33]). From this one obtains  for some line bundle M, and an Euler characteristic computation in [1] gives .
for some line bundle M, and an Euler characteristic computation in [1] gives .
Proposition 4.1
For S the surface parametrising lines of second type on a cubic fourfold X we have
,
.
Proof
As and from Theorem 2.2, we compute that . To simplify notation for this proof we denote by
To compute we compute first the Chern numbers of K and C. For this we use the Harris–Tu formula [13], although we follow the notation of [20]. We denote the Segre polynomial
where are the Segre and Chern polynomials of and respectively. Written in terms of the standard Schubert cycles  on we have
on we have
and in what follows we denote by  . For a partition we denote by
. For a partition we denote by
so now [20, Example 5.4] (note there are some typos fixed in a later paper) gives the following intersection numbers, all taking place on F, i.e., intersected with [F] from (1):
From the tangent sequence of and the fact that we obtain
from which 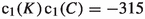 and hence . On the other hand from the tangent sequence of
and hence . On the other hand from the tangent sequence of
we have , giving
From the Noether formula we compute now
Remark 4.2
Using the fact that S is isomorphic to a section of the vector bundle  on , we have from [10, p. 54] the formula
on , we have from [10, p. 54] the formula
which can also be used to compute . In fact, recently Huybrechts [14, Proposition 6.4.9] has studied the ideal sheaf , proving that sequence (2) on S is
| 4 |
for a line bundle L satisfying . From this one can, by taking Euler characteristics, also obtain that . Studying cohomological vanishing on he also obtains like we do in what follows.
Our aim now is to compute or , noting that
so one determines the other from the above computation. This will be achieved by computing cohomology from sequence (3). As F is the vanishing of a section of , we can consider the Koszul resolution
| 5 |
from which it becomes clear that in order to compute groups such as
we will need to compute the groups
which was achieved using the Borel–Weil–Bott Theorem in Sect. 3.
Theorem 4.3
The Hodge numbers of S are as follows:
Also, and , i.e., S has torsion in the Néron–Severi group and has non-trivial fundamental group.
Proof
Tensoring sequence (5) with and and using the hypercohomology spectral sequence [15, B.1.5], we obtain the following second quadrant spectral sequences:
From Proposition 3.1 for and the first spectral sequence, we have that
is the only non-trivial differential between the only two non-trivial terms of the -page. Since as , it must be that and so that is surjective. This gives that and hence that is the only non-zero cohomology group of this sheaf. Similarly, the second spectral sequence gives that
From sequence (3) we obtain now immediately that
The sequence
and the fact that is 1, 0, 1, 0, 1 for respectively give that . From we immediately obtain . As , so are the Betti numbers . Since S is connected, . Note that , giving that and hence from the Hodge decomposition and Hodge duality that .
For , the first spectral sequence and Proposition 3.1 give as the only non-zero term. Hence
is the only non-zero cohomology group of this sheaf. The second spectral sequence for gives that
are the only two non-trivial cohomology groups.
The resolution of the ideal sheaf twisted by 3H
and the computations above give that . Kodaira vanishing gives for all so the sequence
induces . If and were linearly equivalent and not just equal in the group , then which is a contradiction to the computation above giving .
Since is the tangent space to the abelian variety , this must be zero, giving . Since and are cohomologically but not linearly equivalent, there must be torsion in cohomology, or in other words .
Remark 4.4
In [14, Remark 6.4.10], it is shown that there is a degree 2 étale cover of S trivialising the above torsion element, which is, from (4), the difference . This cover can be realised as the surface in parametrising the two distinct ramification points of the Gauss map when restricted to a line.
The surface V and its invariants
Let be a smooth cubic, and denote by  the surface of triple lines, i.e., lines so that there exists a 2-plane so that . Denote also by , the strict transform of V. In [12, 4.3–4.4] we prove that if X is general, then V is an irreducible surface and is its smooth normalisation, and we prove that the class of V in the cohomology of F is . In this section we will give a different geometric interpretation of than the one in [12] and use this to compute the class of V again and some of the invariants of . After setting up the geometric construction, we will perform the computations using Macaulay2 as they are similar to the ones in previous sections.
the surface of triple lines, i.e., lines so that there exists a 2-plane so that . Denote also by , the strict transform of V. In [12, 4.3–4.4] we prove that if X is general, then V is an irreducible surface and is its smooth normalisation, and we prove that the class of V in the cohomology of F is . In this section we will give a different geometric interpretation of than the one in [12] and use this to compute the class of V again and some of the invariants of . After setting up the geometric construction, we will perform the computations using Macaulay2 as they are similar to the ones in previous sections.
We will need the following construction, suggested to us by Kuznetsov. Let  be the 11-dimensional Flag variety parametrising tuples
be the 11-dimensional Flag variety parametrising tuples  so that , and let be the universal bundles on and L the kernel of the surjection . Denote by E the rank 9 quotient of the following natural inclusion:
so that , and let be the universal bundles on and L the kernel of the surjection . Denote by E the rank 9 quotient of the following natural inclusion:
| 6 |
which is a vector bundle as the inclusion of 3L is of full rank at every point. The equation of the cubic X induces a section , and hence a section . Denote by the vanishing locus of this section. Note that
| 7 |
by the usual Leray argument (in the latter two groups is now considered as the universal bundle on ), and these vector spaces also agree with the 56-dimensional since the pullback of to the universal family is . As is globally generated, so is E, so V(s) has dimension 2 and a general section of induces a section of E whose zero locus is generically reduced (see [6, Lemma 5.2]).
Note that the set consists of pairs so that or . To see this, note that if is already a zero of t then the equation of X vanishes on from equation (7). For the remaining zeros of s, note that L parametrises linear forms on which vanish on , so that from sequence (6) such a point is an so that .
If X is a general cubic, then S is smooth and the blowup of F at S parametrises planes tangent to lines in X as it is known (see [14, Remark 2.2.19]) that it is isomorphic to the incidence variety
Under the genericity assumption, X does not contain any ’s and V(s) is necessarily reduced, so the discussion above gives.
Proposition 5.1
If X is a general cubic, then V(s) is isomorphic to .
We give now another proof of the following fact, using the above construction, that was obtained by a different geometric construction in [12, Theorem 4.7].
Lemma 5.2
The class of V in the cohomology of F is given by
Proof
This can be obtained as a consequence of the construction of Proposition 5.1, and as it involves Schubert calculus computations very similar to the ones of sections above, we perform it directly in Macaulay2 in the following code, which sets up etc, computes the class of V(s) in as the top Chern class of E, pushes it forward to the Grassmannian , and then compares it with :
Note that as V(s) is the vanishing of a section of the vector bundle E, its ideal sheaf has a Koszul resolution
Computing using Grothendieck–Riemann–Roch and Schubert calculus we obtain that
e.g., via the following Macaulay2 code ![]() On the other hand, as the normal bundle of in is given by (as and V(s) are isomorphic), we can compute that , for H the pullback of the Plücker polarisation restricted to , using
On the other hand, as the normal bundle of in is given by (as and V(s) are isomorphic), we can compute that , for H the pullback of the Plücker polarisation restricted to , using ![]() which we also computed differently in [12, Proposition 4.6] by expressing as a section of a rank two bundle in . We can now easily compute as follows
which we also computed differently in [12, Proposition 4.6] by expressing as a section of a rank two bundle in . We can now easily compute as follows ![]()
What remains in terms of the invariants of are the geometric genus and the irregularity q, which satisfy . As E involves indecomposable bundles on the Flag variety, the Borel–Weil–Bott computations necessary to compute either of these invariants is much more involved. Nevertheless, very recently, Mboro [16] computed that and by computing the Hodge numbers of the Fano scheme of 2-planes in the cyclic cover cubic 5-fold associated to X and proving this is an étale 3-1 cover of , so all the Hodge number of are now also known.
A bound on the degree of irrationality of F
We recently proved in [11] that if is a smooth cubic threefold and F(Y) its Fano surface of lines, then the degree of irrationality , i.e., the minimal degree of a dominant rational map , satisfies
with equality if Y is general. In this section we extend the construction of a degree 6 map to the Fano scheme of lines of any smooth cubic hypersurface. Whether this upper bound is optimal for a general hypersurface remains to be proven.
We recall first the construction in the case of threefolds, and elaborate on the linear system it is induced by.
Lemma 6.1
Let be a smooth cubic threefold and 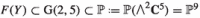 its Fano surface of lines. For any hyperplane there is a degree 6 rational map
its Fano surface of lines. For any hyperplane there is a degree 6 rational map
which is the restriction of the rational map given by the sublinear-system of sections corresponding to Schubert cycles for a hyperplane in H.
Proof
The map takes and gives . Consider now a . Its pullback , which corresponds to lines meeting , is of class and so a section of the Plücker line bundle . Observe that this section contains all lines contained inside H. In other words, if
then the base locus is equal to . Projecting now from the which is the span of in onto we obtain the map whose restriction to is . The map has degree 6 as there are 6 lines through a general point of Y.
Remark 6.2
In particular, is the projection from the containing the Plücker embedding of .
Proposition 6.3
Let be a smooth cubic hypersurface for and its Fano scheme of lines. Then
More precisely, we have a degree 6 rational map
where , for , is a hyperplane section of X with one node and hence rational and is general. The map is the restriction of the map
where is given by the sections of cutting out the projective space 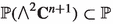 containing the Plücker embedding of and is given by the space of sections of which correspond to Schubert cycles
containing the Plücker embedding of and is given by the space of sections of which correspond to Schubert cycles
for some fixed and T runs over all hyperplanes in R.
Proof
Let be a hyperplane section with exactly one node. Note that by projecting from the node inside , we obtain a birational map .
Fix now and general inside . We will construct a degree 6 map  . Consider a general point . For the following two points:
. Consider a general point . For the following two points:
define now . For any , there is a subvariety of dimension parametrising lines so that passes through q. This variety in fact embeds in the original as a complete intersection of type (1, 1, 2, 3). Fix a . The lines through q are parametrised by the space we just described. Note now that, the points so that are precisely the six points of the intersection . In other words has degree six and we can compose with a birational map 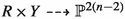 to obtain a degree six map .
to obtain a degree six map .
Acknowledgements
We would like to thank Olof Bergvall, Daniel Huybrechts and Fabio Tanturri for helpful correspondence, and Alexander Kuznetsov for suggesting the construction in Sect. 5. The first author was partially supported by the ERC Consolidator Grant 681838 “K3CRYSTAL”.
Funding Information
Open Access funding enabled and organized by Projekt DEAL.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Frank Gounelas, Email: gounelas@mathematik.uni-goettingen.de.
Alexis Kouvidakis, Email: kouvid@uoc.gr.
References
- 1.Amerik E. A computation of invariants of a rational self-map. Ann. Fac. Sci. Toulouse Math. 2009;18(3):445–457. [Google Scholar]
- 2.Amerik, E., Voisin, C.: Potential density of rational points on the variety of lines of a cubic fourfold. Duke Math. J. 145(2), 379–408 (2008)
- 3.Beauville, A., Donagi, R.: La variété des droites d’une hypersurface cubique de dimension . C. R. Acad. Sci. Paris Sér. I. Math. 301(14), 703–706 (1985)
- 4.Borisov, L.A., Căldăraru, A., Perry, A.: Intersections of two Grassmannians in . J. Reine Angew. Math. 760, 133–162 (2020)
- 5.Clemens, C.H., Griffiths, P.A.: The intermediate Jacobian of the cubic threefold. Ann. Math. 95, 281–356 (1972)
- 6.Eisenbud, D., Harris, J.: 3264 and All That—A Second Course in Algebraic Geometry. Cambridge University Press, Cambridge (2016)
- 7.Fulton W, Harris J. Representation Theory Graduate Texts in Mathematics, New York: Springer; 1991. [Google Scholar]
- 8.Friedman R. Algebraic Surfaces and Holomorphic Vector Bundles. New York: Universitext. Springer; 1998. [Google Scholar]
- 9.Fulton, W.: Intersection Theory. 2nd edn. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 2. Springer, Berlin (1998)
- 10.Fulton W, Pragacz P. Schubert Varieties and Degeneracy Loci Lecture Notes in Mathematics, Berlin: Springer; 1998. [Google Scholar]
- 11.Gounelas F, Kouvidakis A. Measures of irrationality of the Fano surface of a cubic threefold. Trans. Amer. Math. Soc. 2019;371(10):7111–7133. doi: 10.1090/tran/7565. [DOI] [Google Scholar]
- 12.Gounelas, F., Kouvidakis, A.: Geometry of lines on a cubic four-fold. Int. Math. Res. Not. IMRN. (2021). 10.1093/imrn/rnac160
- 13.Harris J, Tu L. Chern numbers of kernel and cokernel bundles. Invent. Math. 1984;75(3):467–475. doi: 10.1007/BF01388639. [DOI] [Google Scholar]
- 14.Huybrechts D. The Geometry of Cubic Hypersurfaces. Cambridge Studies in Advanced Mathematics. Cambridge: Cambridge University Press; 2023. [Google Scholar]
- 15.Lazarsfeld, R.: Positivity in Algebraic Geometry. Vol. I. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 48. Springer, Berlin (2004)
- 16.Mboro, R.: Remarks on the geometry of the variety of planes of a cubic fivefold (2023). arXiv:2301.04997
- 17.Mukai S, et al. Polarized surfaces of genus thirteen. In: Mukai S, et al., editors. Moduli Spaces and Arithmetic Geometry. Tokyo: Mathematical Society of Japan; 2006. pp. 315–326. [Google Scholar]
- 18.Nesterov D, Oberdieck G. Elliptic curves in hyper-Kähler varieties. Int. Math. Res. Not. IMRN. 2021;2021(4):2962–2990. doi: 10.1093/imrn/rnaa016. [DOI] [Google Scholar]
- 19.Oberdieck, G., Shen, J., Yin, Q.: Rational curves in holomorphic symplectic varieties and Gromov–Witten invariants. Adv. Math. 357, Art. No. 106829 (2019)
- 20.Pragacz P. Enumerative geometry of degeneracy loci. Ann. Sci. École Norm. Sup. 1988;21(3):413–454. doi: 10.24033/asens.1563. [DOI] [Google Scholar]
- 21.Shen, M., Vial, C.: The Fourier Transform for Certain Hyperkähler Fourfolds. Memoirs of the American Mathematical Society, vol. 240(1139). American Mathematical Society, Providence (2016)
- 22.Voisin C, et al. Intrinsic pseudo-volume forms and -correspondences. In: Collino A, et al., editors. The Fano Conference. Turin: Università di Torino; 2004. pp. 761–792. [Google Scholar]
- 23.Weyman J. Cohomology of Vector Bundles and Syzygies. Cambridge Tracts in Mathematics. Cambridge: Cambridge University Press; 2003. [Google Scholar]


