Harnessing the potential of CsPbBr₃-based perovskite solar cells using efficient charge transport materials and global optimization

Abstract

Perovskite solar cells (PSCs) have become a possible alternative to traditional photovoltaic devices for their high performance, low cost, and ease of fabrication. Here in this study, the SCAPS-1D simulator numerically simulates and optimizes CsPbBr₃-based PSCs under the optimum illumination situation. We explore the impact of different back metal contacts (BMCs), including Cu, Ag, Fe, C, Au, W, Pt, Se, Ni, and Pd combined with the TiO₂ electron transport layer (ETL) and CFTS hole transport layer (HTL), on the performance of the devices. After optimization, the ITO/TiO₂/CsPbBr₃/CFTS/Ni structure showed a maximum power conversion efficiency (PCE or η) of 13.86%, with Ni as a more cost-effective alternative to Au. After the optimization of the BMC the rest of the investigation is conducted both with and without HTL mode. We investigate the impact of changing the thickness and the comparison with acceptor and defect densities (with and without HTL) of the CsPbBr₃ perovskite absorber layer on the PSC performance. Finally, we optimized the thickness, charge carrier densities, and defect densities of the absorber, ETL, and HTL, along with the interfacial defect densities at HTL/absorber and absorber/ETL interfaces to improve the PCE of the device; and the effect of variation of these parameters is also investigated both with and without HTL connected. The final optimized configuration achieved a V_OC of 0.87 V, J_SC of 27.57 mA cm⁻², FF of 85.93%, and PCE of 20.73%. To further investigate the performance of the optimized device, we explore the impact of the temperature, shunt resistance, series resistance, capacitance, generation rate, recombination rate, Mott–Schottky, JV, and QE features of both with and without HTL connected. The optimized device offers the best thermal stability at a temperature of 300 K. Our study highlights the potential of CsPbBr₃-based PSCs and provides valuable insights for their optimization and future development.

Here we have done SCAPS simulation for optimizing the performance of CsPbBr₃-based PSC. We first optimized the BMC with HTL connected mode and then optimized the CsPbBr₃, TiO₂, & CFTS layers' various parameters in both with-HTL and without-HTL modes.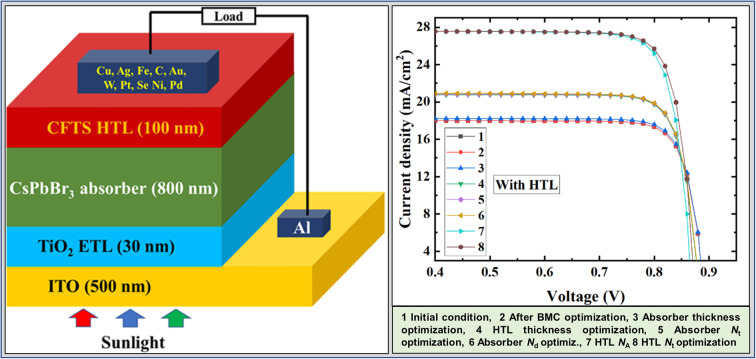

1. Introduction

In recent years, the exponential increase in demand for conventional energy sources, coupled with the rapid depletion of fossil fuels due to extensive industrialization, has led to serious environmental and economic concerns.^1–5 In response, photovoltaic (PV) solar cells appear to be one of the most promising solutions for sustainable energy production, offering both environmental benefits and cost-effectiveness.^6–8 Among the various types of PV solar cells, thin film solar cells (TFSCs) have gained widespread consideration due to their fast growth and potential for high performance.^9–14 However, the efficiency of TFSCs is strongly influenced by the choice of semiconductor materials and growth methods employed. Despite incremental gains in efficiency since the invention of the first modern silicon solar cell in 1954, significant progress has been made, with modules developed by 2010 capable of converting up to 18% of solar energy into electricity.¹⁵

The TFSCs have gained significant consideration in recent years, particularly organic-inorganic metal halide perovskite solar cells, owing to their remarkable optoelectronic features, such as improved absorption coefficients, customizable band gaps, longer electron and hole diffusion lengths, low cost, efficient charge separation, and solution processability.^16–19 Perovskite compounds with the chemical formula PQX₃ (^XIIP^2+VIQ⁴⁺X₃²⁻), consisting of an organic cation P (e.g., methylammonium or formamidinium), a divalent metal B (e.g., Pb or Sn), and a halide X (e.g., Br or I),²⁰ are of particular interest for the lower cost and easier manufacturing.^21,22 The efficiency of PSCs has increased dramatically, from an initial maximum PCE or η of 3.8% in 2009 to a remarkable PCE of 25.2% in 2019,^23,24 with current overall PCE on PSCs reaching up to 23%,²⁵ similar to CIGS based solar cells and commercialized silicon-based solar cells.²⁶ Regardless of their superior performance, the instability of PSCs, caused by the presence of organic elements, has been a major concern. To address this issue, researchers have investigated the use of alternative inorganic ions (such as Cs⁺) with organic ions. In 2012, the very first Cs-based perovskite i.e. CsSnI₃ with Schottky solar cells was reported, with a PCE of 0.88 percent.²⁷ There onwards extensive work has been going on to enhance the performance of the CsPbI₃-based PSC device. Although CsPbI₃ has an appropriate energy band gap of 1.73 eV and an efficiency of 13.21%,²⁸ its phase stability at ambient temperature is poor, degrading rapidly to a non-perovskite yellow phase δ-CsPbI₃.^28,29 Recently, researchers have focused on developing dual-halide inorganic perovskite CsPbI_xBr_3−x to enhance the stability as well as the efficiency of all-inorganic perovskite. The best efficiency of any inorganic perovskite solar cell recorded so far is achieved by the SnO₂/ZnO bi-layer electron transport layer-based CsPbI₂Br PSC with a high PCE of 14.6%.^30,31 However, the overall sustainability of the dual-halide perovskite remains inadequate. Although most efficient CsPbBr₃ PSC described are mesostructured, requiring a high-temperature treatment for the electron transport layers,³² Liang et al. have produced a hole-conductor-free PSC with a compact TiO₂/m-TiO₂/CsPbBr₃/carbon structure, that achieved a PCE of 6.7%.³³

In the field of PSCs, carrier transport materials, or electron transport layers (ETLs), play a crucial role in achieving high efficiency.^34–38 Titanium dioxide (TiO₂) is one of the most commonly used ETLs due to its popularity and ease of processing.³⁹ However, it's high resistance and limited carrier mobility compared to the perovskite layer can limit the device's performance.⁴⁰ To address this, TiO₂ must be doped to increase its energy bands and conductivity.⁴¹ Additionally, while high efficiency has been achieved, there is still a need to develop PSCs using earth-abundant, nontoxic, and affordable materials. Several compounds, including FeS₂, Bi₂S₃, Cu₂S, and SnS, have been studied in this regard.^42–44 Quaternary chalcogenides, specifically Cu₂ZnSn(S, Se)₄ known as CZTSSe, have shown promise in this area.⁴⁵ Various vacuum and non-vacuum-based techniques for producing Cu₂FeSnS₄ (CFTS), a p-type material with an acceptable band gap (1.28–1.50 eV) and high optical absorption coefficients (>10⁴ cm⁻¹), have also been established.^46,47 CFTS is composed of abundant and affordable elements that are relatively non-toxic. Replacing Zn with Fe in CZTS thin films further lowers its optical energy band gap and enhances conductivity, leading to improved solar-to-electrical conversion efficiency.⁴⁸

This research is the extension of our previous study⁴⁹ where we studied about nine HTLs and six ETL-associated 54 combinations of PSCs configuration where the best six structures performance studies are conducted. In this study, we optimized the optoelectronic parameters of CsPbBr₃-based PSCs utilizing SCAPS-1D simulation software. This paper is divided into four different sections, 1–4. Introduction Section 1 is followed by device modeling Section 2 where a detailed description of simulation methodology is provided along with the device and material parameters considered during simulations. Results are reported in Section 3, which is started by optimizing the BMC of the ITO/TiO₂/CsPbBr₃/CFTS/Au solar cell device structure. We further investigated the impact of absorber layer thickness, charge carrier density, as well as defect density with and without HTL-connected conditions. Additionally, we optimized the thickness of the ETL and HTL, charge carrier density, and interface defect density in both with and without HTL-connected modes. Finally, we observed the optimized device's quantum efficiency, J–V characteristics, generation recombination rate, capacitance, and Mott–Schottky characteristics in both HTL and non-HTL modes. The results of the finding are concluded in the conclusion Section 4. Our study provides a cost-effective and unique approach to designing and constructing high-performance PSCs.

2. Device modeling

2.1. Simulation

In the present study, SCAPS-1D simulation software^50–59 is used to study the CsPbBr₃-based solar cell configuration. The simulator program employs 3-coupled differential equations: i.e. Poisson's equation (eqn (1)), the equation of continuity for electrons (eqn (2)), and the equation of continuity for holes (eqn (3)). These equations are shown below.⁶⁰

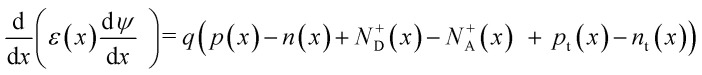1

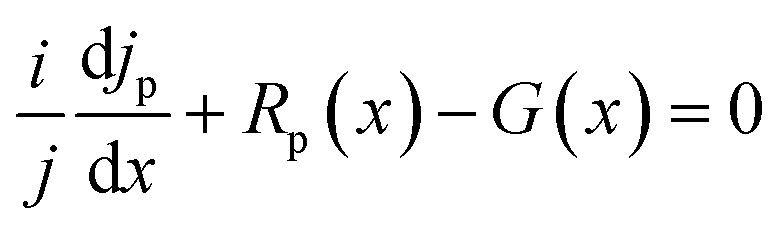2

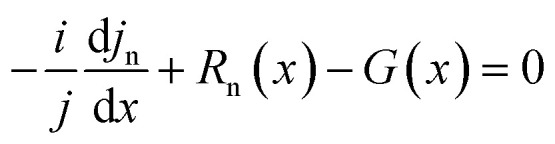3

Here, q is the electron charge, ε is the dielectric permittivity, ψ is the electrostatic potential, n is the electron concentration, p is the concentration of the free hole, n_t is the density of trapped electron, p_t is the density of trapped hole, N⁺_D is the ionized shallow uniform donor doping concentration, and N⁻_A is the ionized shallow uniform doping concentration of the acceptor. R_n(x) and R_p(x) are the rates of electron and hole recombination, respectively, G(x) is the rate of charge carrier production, and J_n and J_p are the electron and hole current densities.⁶⁰ The effect of thickness, doping concentration, defect density, interface defect density, series and shunt resistance, temperature as well as front and back contact on V_OC, J_SC, FF, and efficiency has been analyzed by SCAPS-1D, which was developed by the University of Gent in Belgium.

2.2. Device structure

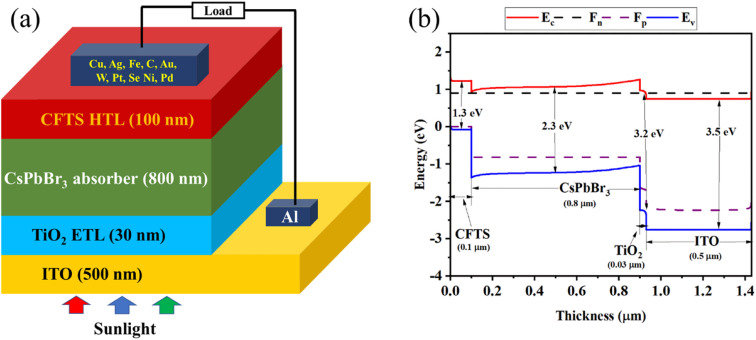
In this research optimization of optoelectronic parameters of CsPbBr₃-based PSC is mainly conducted where TiO₂ is taken as ETL, CFTS is taken as HTL, and Au as BMC initially. Whereas, the optoelectronic parameters of different materials are taken from previous studies which are listed in Tables 1 and 2. To find out the optimized structure for different combinations of ETL and HTL is performed through SCAPS-1D to determine the most efficient structure. From Table 1, it is seen that TiO₂ is taken as ETL and their optoelectronic parameters are also included in Table 1. Also from Table 1, it is seen that CFTS is taken as HTL and their optoelectronic parameters are also included. In Table 2, the interface layer's parameters are listed. In addition, CsPbBr₃ absorber layer optoelectronic parameters are also included in Table 1 and sequentially simulate different structure configurations and evaluate the photovoltaic features like open-circuit voltage (V_OC), short circuit current density (J_SC), fill Factor (FF), and PCE to find out the primarily optimized PSC's configuration before the variation of parameters. After many trials and errors, ITO/TiO₂/CsPbBr₃/CFTS/Au structure finds out to be an efficient primary structure. To increase the efficiency, many variations of optoelectronic parameters are also done. Fig. 1(a) gives an illustrative observation of the working strategy of this study. Here in Fig. 1(a), it is seen in the middle there is light-absorbing material as CsPbBr₃ and it is sandwiched between TiO₂ ETL and CFTS HTL. Fig. 1(b) gives an idea about the energy band diagram of the proposed solar cell structure. Where on the x-axis is the thickness and on the y-axis energy (eV), HTL's valence band Fermi-level is higher than that of the CsPbBr₃ absorber layer.

Parameters of TCO, ETLs, and absorber layer⁴⁹.

Parameters	TCO	TiO2	CFTS	CsPbBr3
Thickness (μm)	0.5	0.03	0.1	0.8a
Band gap, Eg (eV)	3.5	3.2	1.3	2.3
Electron affinity, χ (eV)	4	3.9	3.3	3.6
Dielectric permittivity (relative), εr	9	9	9	6.5
CB effective density of states, NC (cm−3)	2.2 × 1018	2 × 1018	2.2 × 1018	4.94 × 1017
VB effective density of states, NV (cm−3)	1.8 × 1019	1.8 × 1019	1.8 × 1019	8.47 × 1018
Electron mobility, μn (cm2 V−1 s−1)	20	20	21.98	4500
Hole mobility, μh (cm2 V−1 s−1)	10	10	21.98	4500
Shallow uniform acceptor density, NA (cm−3)	0	0	1 × 1018	0
Shallow uniform donor density, ND (cm−3)	1 × 1021	9 × 1016	0	1 × 1015
Defect density, Nt (cm−3)	1 × 1015a	1 × 1015a	1 × 1015a	1 × 1015a

^aIn this study CsPbBr₃ absorber layer's thickness makes a constant of 800 nm primarily also the constant defect density of 1 × 10¹⁵ cm⁻³ at the initial condition. After the optimization process begins then variation will perform.

Parameters of interface layer⁴⁹.

Interface	Defect type	Capture cross section: electrons/holes (cm2)	Energetic distribution	Reference for defect energy level	Total density (cm−2) (integrated over all energies)
ETL/CsPbBr3	Neutral	1.0 × 10−17	Single	Above the VB maximum	1.0 × 1010
		1.0 × 10−18
CsPbBr3/HTL	Neutral	1.0 × 10−18	Single	Above the VB maximum	1.0 × 1010
		1.0 × 10−19

Fig. 1. (a) Schematic structure, and (b) energy band diagram of CsPbBr_3-based PSC.

3. Result and discussion

3.1. BMC optimization

In this section, we emphasized the optimization of the BMC of the ITO/TiO₂/CsPbBr₃/CFTS/BMC solar cell structure. To increase the output parameters of the PSC, various BMC's work function variation is also done. Metals are arranged according to their work function values. It is widely known that when the work-function of the contact metal declines, the devices' shunt resistance and performance also fall. Specifically, when using Ag as BMC the performance is lower compared to the rest of the metals. Besides the low work function, Ag present also has a serious stability problem. The use of Cu and Fe as BMCs with high work function leads to favorable band bending at the perovskite-HTM-BMC interfaces, providing an efficient barrier to electron transfer from perovskite to metal and to high R_SH which reduces the alternative current path created previously by the low R_SH value. Besides, these metals form low interfacial resistance with the HTM. However, the solar cell performance remains almost constant with back contact work function higher than that of the aforementioned BMCs. This is due to the fact that a further rise in the work function enhances R_SH and remove completely the alternate current route for the light-generated current. The decline of reverse saturation current causes a higher value of FF for a low work function. Finally, Ni, as a back contact seems to be more efficient because it is cost-effective, and using Ni as a back contact, the solar cell configuration seems to be more efficient than the others. Finally, the optimized solar cell structure is ITO/TiO₂/CsPbBr_3/CFTS/Ni, whose performance parameters are V_OC nearly 0.890 V, J_SC nearly 17.98 mA cm⁻², FF nearly 86.59%, while an improved PCE of 13.86% (Table 3).

The detailed analysis of PV parameters of CsPbI₃-based solar cells for different BMCs.

BMC	Work function61 (eV)	V OC (V)	J SC (mA cm−2)	FF (%)	PCE (%)
Ag	4.26	0.85	13.11	85.95	9.57
Cu	4.65	0.87	16.25	86.27	12.22
Fe	4.81	0.89	17.97	86.59	13.85
C	5	0.89	17.98	86.59	13.86
Au	5.1	0.89	17.98	86.59	13.86
W	5.22	0.89	17.98	86.59	13.86
Ni	5.5	0.89	17.98	86.59	13.86
Pd	5.6	0.89	17.98	86.59	13.86
Pt	5.7	0.89	17.98	86.59	13.86
Se	5.9	0.89	17.98	86.59	13.86

For the proper collection of holes via the rear contact, an ohmic contact must be created.⁶² The simulation is firstly done with Au as a back contact, but due to the adjustment of the back contact, there are some significant changes observed in performance parameters in the energy band diagram because there exists a Schottky barrier.

3.2. Combined influence of absorber thickness and the acceptor density

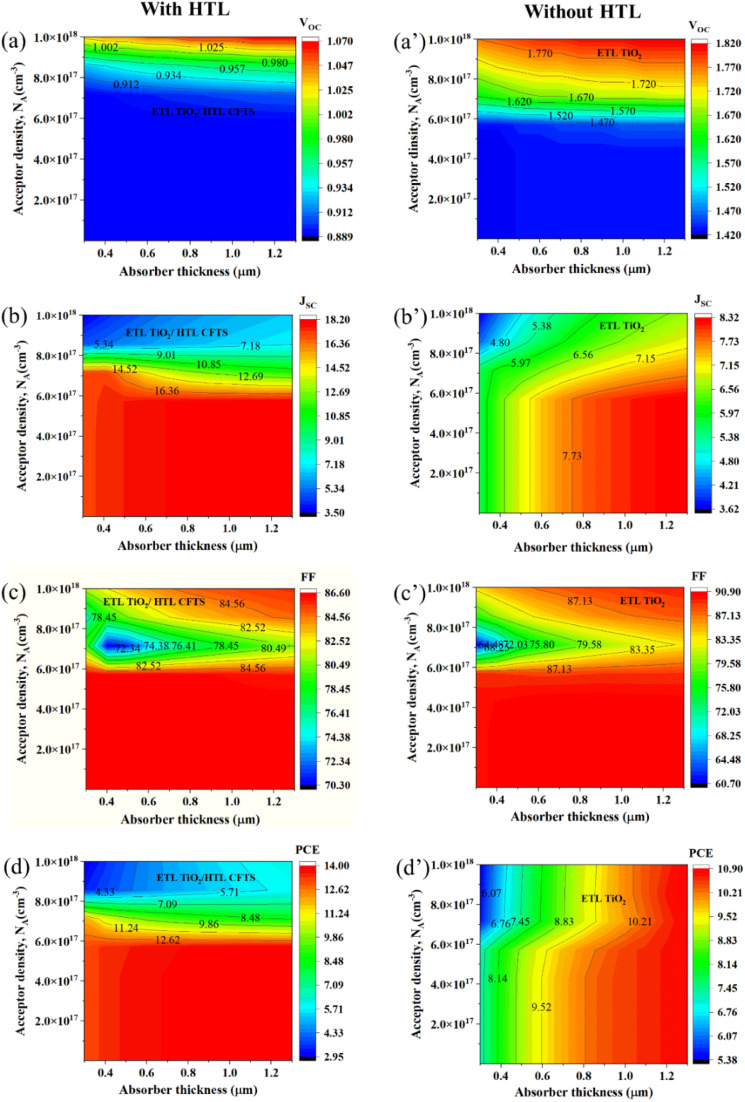
In this section, the impact of changing absorber layer thickness with absorber acceptor density variation simultaneously on TiO₂ as ETL and CFTS as HTL and CsPbBr₃ as absorber-based PSC's performance is observed through contour mapping in both HTL and without HTL connected mode. According to Fig. 2, the case without HTL connected structure shows the highest V_OC which is 1.82 V. This increase is mainly attributed to both HTL-related series resistance and eliminated interface traps. Similarly, in the case of higher N_A conditions and also absorber thickness increasing may increase the V_OC. However, J_SC shows differences, as compared to V_OC, here with HTL connected structure, shows the highest J_SC of 18.20 mA cm⁻² in case of both high value of absorber thickness and N_A condition, but N_A has limitation up to 7 × 10¹⁷ cm⁻³ FF shows a 90.9% value in the case of without HTL connected mode and the parameters nature is exactly as similar as J_SC's. However, the case of PCE with HTL connected structure shows the highest PCE which is 14% when the absorber thickness varies from 0.3 μm to 1.3 μm.

Fig. 2. Contour mapping of performance parameters when ETL as TiO₂. (a)–(d) with HTL, and (a′)–(d′) without HTL.

The presence of HTL and the associated HTL/absorber interface can be a source of charge carrier recombination, which can reduce the V_OC. In HTL-free devices, the charge carriers are transported directly from the perovskite layer to the anode, which reduces the opportunity for recombination. In addition, the carrier mobility in the HTL is typically lower than the carrier mobility in the perovskite layer. This means that the holes in the HTL can move more slowly, which can reduce the V_OC. In HTL-free devices, the holes can move more quickly through the perovskite layer, which increases the V_OC.

3.3. Combined impact of absorber thickness with defect density

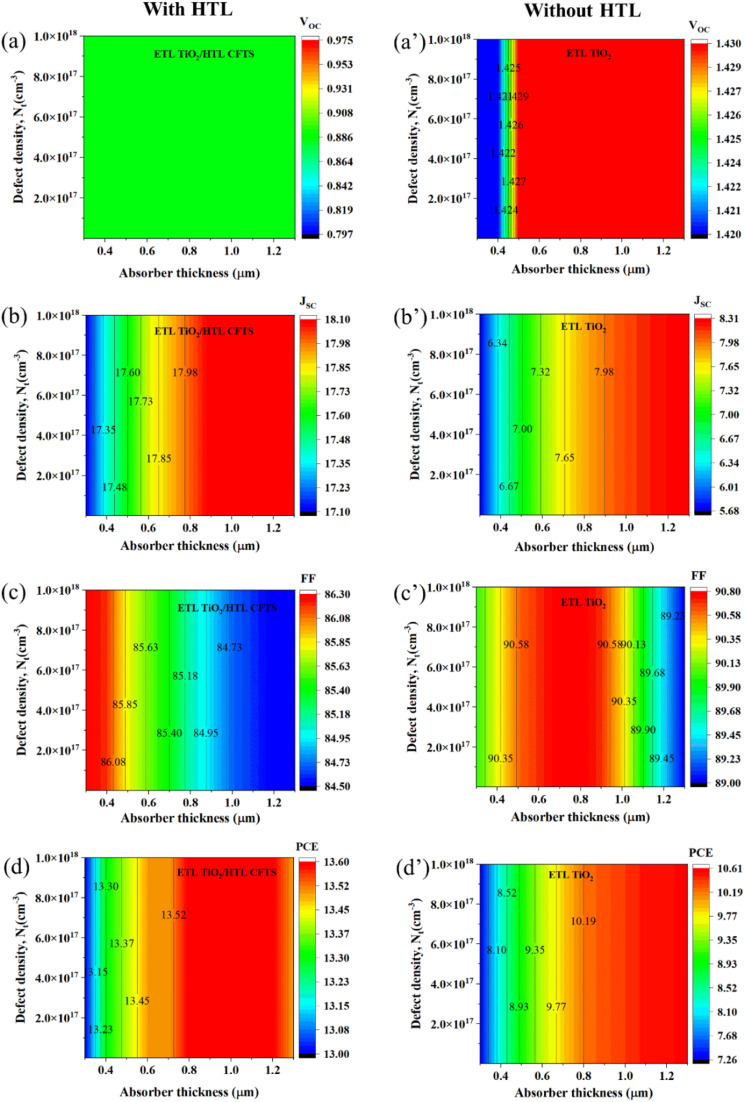
The impact of changing the thickness of the absorber and defect density on solar cell outputs is discussed in this section. Where TiO₂ is taken as well as the performance associated with ETL and CFTS as HTL. Both HTL and without HTL-Associated Mode (HTL-AM) performance are evaluated in this section. Fig. 3 shows the optimized solar cell performances where a higher V_OC of 0.886 V is achieved in the case of HTL-AM when the thickness of the absorber ranges from 0.3 μm to 1.3 μm, and N_t ranges from 1 × 10¹¹ cm⁻³ to 1 × 10¹⁸ cm⁻³. Where without HTL-AM shows a V_OC of 1.43 V when the thickness of the absorber ranges from 0.3 μm to 1.3 μm regardless of N_t. The case of J_SC with HTL-AM shows a J_SC of 18.10 mA cm²; whereas without HTL-AM shows 8.31 mA cm⁻² of J_SC. But with HTL-AM shows 86.30% of FF when N_t ranges from 1 × 10¹¹ to 1 × 10¹⁸ cm⁻³, respectively. Whereas without HTL-AM shows 90.8% of FF when the thickness of the absorber ranges from 0.5 μm to 0.9 μm. Finally, HTL-AM shows 13.60% of PCE while the thickness of the absorber ranges from 0.8 to 1.2 μm whereas without HTL-AM shows 10.63% of PCE when the thickness of the absorber is greater than 1 μm as depicted in Fig. 3.

Fig. 3. Contour mapping of performance parameters using TiO₂ as ETL. (a)–(d) with HTL, and (a′)–(d′) without HTL.

3.4. Optimization of absorber, ETL and HTL thickness

3.4.1. Optimization of absorber layer thickness

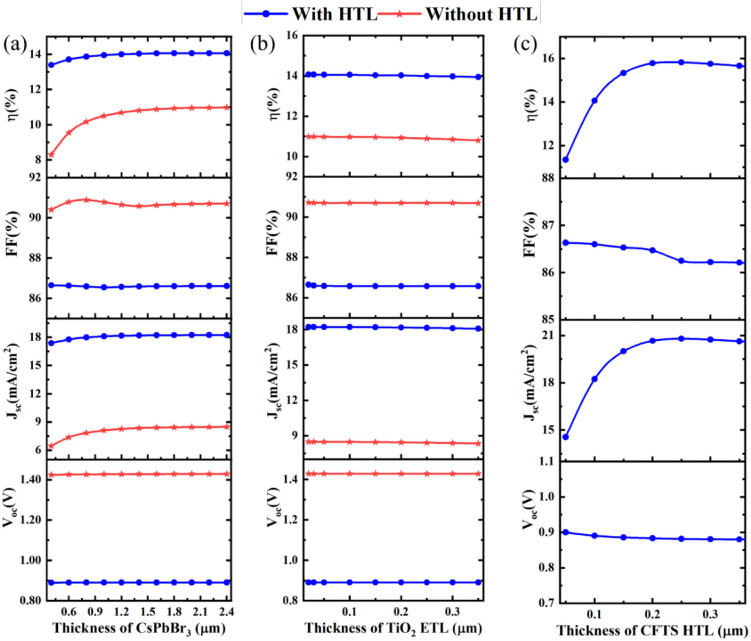
Variation of the absorber layer thickness is also studied with HTL and without HTL conditions. Initially, the absorber thickness is fixed at 0.8 μm. Some impacts on performance parameters are observed whenever the thickness of the absorber layer is varied from 0.4 μm to 2.4 μm. From Fig. 4(a), it is clear that the V_OC is almost constant for both cases but with HTL V_OC (0.89 V) is lower than without HTL (1.43 V) condition. Also, for the J_SC, it is observed that up to 0.9 μm of the absorber thickness, the J_SC enhances, and after that, it remains almost constant. In this case, J_SC is higher with HTL than without HTL architecture. For the case of FF, when HTL is connected then it suddenly drops up to 1.2 μm absorber thickness due to the increased series resistance and then shows a minor increment initially, after that, it shows a constant profile. The FF is mainly influenced by the series resistance of the devices which encompasses resistances of all the layers and corresponding interfaces. The absorber layer with higher thickness resulted in higher resistance and hence reduces the FF. However, without HTL condition it is observed from Fig. 4(a) that a minimal increase can be observed from 0.8 μm thickness of absorber layer, and then a decreasing profile is observed up to 1.8 μm absorber thickness and a constant FF r profile is observed up to 2.4 μm. In addition, an incremental PCE profile is observed in Fig. 4(a) for both conditions, with HTL and without HTL up to 1.8 μm of the absorber thickness and after that, it shows an almost constant profile. The PCE was observed (14.06%) and (10.93%) with HTL and without HTL respectively.

Fig. 4. Thickness variation of (a) CsPbBr₃, (b) TiO₂, (c) CFTS.

As the photon collection capacity rises with the enhancement of the absorber layer thickness, the rate of charge carrier creation also increases that's why V_OC increases.⁴⁶ Also from Fig. 4(a), it can be seen that J_SC also enhances with the increase of thickness of the absorber. Because the spectral sensitivity at higher wavelengths increases with an increase in the thickness of the absorber.⁶³ The series resistance (R_s) increases with increasing the thickness of the cell, so FF suddenly drops after a certain thickness of the absorber.⁶⁴ Because of the supremacy of carrier recombination and the prevalence of parasitic resistance losses, this might be the case.⁶⁵ The PCE grew with thickness at first, peaking at 14.06% at 1.8 μm, which was determined to be the ultimate optimal absorber thickness. Then it started to go down with a thickening of the absorber. The enhancement in the creation of electron–hole pairs with higher thickness can be linked to the first rise in PCE. The decrease in PCE as absorber thickness increases are due to increased charge route resistance as well as radiative recombination.

In this section, at 1.8 μm absorber layer thickness, the optimum PCE is found. So, the next evaluation is conducted by adjusting the absorber layer thickness to 1.8 μm.

3.4.2. Optimization of the thickness of ETL

Fig. 4(b) represents the performance parameters variation at the thickness change of TiO₂ ETL from 0.02 μm to 0.35 μm. It is observed that the V_OC, J_SC, FF, and PCE for both with HTL and without HTL are almost constant but the open-circuit voltage without HTL is highest, i.e. 1.429 V than with HTL, i.e. 0.891 V. In the case of short circuit current density with HTL, it shows a higher J_SC of 18.23 mA cm⁻² than without HTL 8.48 mA cm⁻². In addition, the FF without HTL shows a higher value than with HTL. But in the case of PCE with HTL, it shows higher (14.06%) PCE than (10.99%) without HTL.

Charge transport layer characteristics should be carefully selected when developing highly efficient PSCs. In PSCs, a good ETL can assist reduce recombination currents and boost transmittance.⁶⁶ In this work, after finding the optimum thickness (1.8 μm) of the absorber, the thickness variation of ETL is conducted and the optimum thickness of ETL is 0.03 μm find out which is the same as earlier.⁶⁷ Although with the thickness variation of TiO₂, the value of V_OC, FF, J_SC, and PCE stayed nearly constant. The little drop in J_SC and PCE might be attributed to partial light absorption by a thicker ETL, resulting in a slower rate of charge creation and collection.⁶⁰ According to,⁶⁰ the performance loss is caused by increased ETL thickness as the transmittance decreases.⁶⁰Eqn (4) depicts the relationship between thickness and transmittance.⁶⁸

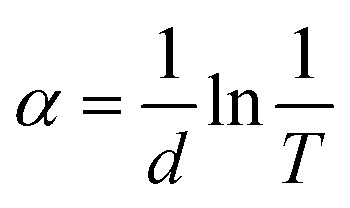4

Here, the absorption coefficient is α, the layer thickness is d, and the transmittance is T.

Here ETL optimum thickness is 0.03 μm for the best PCE. Further evaluation of other parameters is done after fixing the ETL thickness as 0.03 μm.

3.4.3. Optimization of the thickness of HTL

Fig. 4(c) depicts the impact of HTL thickness on overall performance parameters. From Fig. 4(c), it is observed that the V_OC reduces from (0.9 V) to (0.88 V) with increasing the thickness of HTL from 0.04 μm to 0.25 μm, and then it remains constant. Also, short circuit current density increases up to 0.25 μm and then constant up to 0.36 μm and also decreases FF at almost 0.2 μm HTL thickness and then shows an almost constant fill factor. Finally, the PCE and J_SC increased (from 11.35% to 15.82%) up to 0.25 μm of HTL thickness and then constant, so the optimum thickness of HTL is 0.25 μm is chosen for optimized performance.

Here we used CFTS as HTL, which has a bandgap (E_g) of 1.3 eV (Table 1). This bandgap value falls within the appropriate range for an absorber layer in a solar cell.⁴⁶ It should be noted that CsPbBr₃ (E_g = 2.3 eV) exhibits a cut-off wavelength of λ_CsPbBr3 = 1.24/E_g (539 nm), while CFTS has a cut-off wavelength of λ_CFTS = 1.24/E_g (954 nm) for photon absorption. Thus, the perovskite layer absorbs photons with wavelengths shorter than 539 nm, while longer wavelengths are transmitted through the perovskite and utilized by the CFTS layer. Consequently, the absorption of photons leads to the generation of electron–hole pairs in both the perovskite and CFTS layers, contributing to the overall J_SC. Increasing the thickness of the CFTS layer results in a higher generation of electron–hole pairs and an increased J_SC, leading to improved PCE. However, a slight reduction in FF is observed with a higher thickness of the HTL due to increased series resistance.

In the earlier section, it can be seen that with the increment in the ETL thickness, there is less effect on the overall performance of PSCs. From Fig. 4(c), it can be observed that the thickness increment of the CFTS HTL layer slightly increases its PCE but slightly reduced the FF. At a certain thickness of about 0.25 μm, it shows the optimized performance. According to the available literature, the PCE rose as the HTL thickness grew.⁶⁹ HTL should have a thickness that is more than ETL thickness (0.03 μm). As a result, the optimal depth of HTL was chosen to be 0.25 μm, as the PCE improvement beyond that was negligible. The absorption of photons upon that light-harvesting layer is reinforced by the increasing thickness of HTL. In general, an n-type layer is ought to be thinner than a p-type layer for reducing the odds of recombination. As it allows an equal amount of electric charge to be transported to the terminal at the same time.⁷⁰

After study and simulation in this section, the minimum HTL thickness is found 0.25 μm. Also, further evaluation is conducted after setting up the HTL thickness as 0.25 μm.

3.5. Optimization of perovskite layers properties

3.5.1. Effect of acceptor density of the perovskite layer

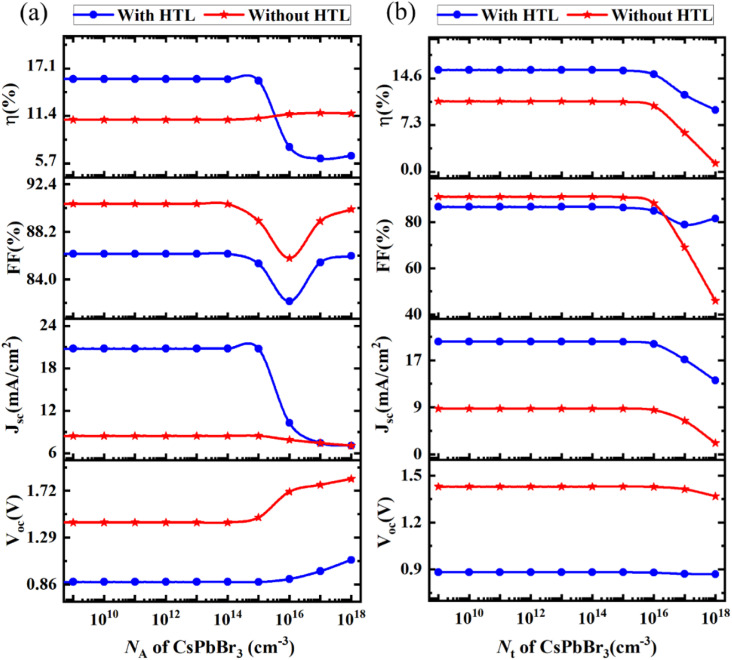
Fig. 5(a) gives illustrative observations about the performance parameters after N_A variation. V_OC is increasing in nature both with HTL and without HTL; but specifically, without HTL PSC architecture shows a higher value than with HTL PSC architecture. As the J_SC is constant up to 1 × 10¹⁵ cm⁻³ with HTL and then J_SC is decreasing in nature and without HTL, J_SC is almost constant but shows a little bit of decrease in nature after 1 × 10¹⁵ cm⁻³. Also, HTL shows a higher J_SC than without HTL. The FF is almost the same in nature for both cases but FF is almost constant up to the N_A of the absorber is 1 × 10¹⁴ cm⁻³ and then it shows decreasing nature. The PCE is almost constant up to 1 × 10¹⁵ cm⁻³ for both cases after that PCE slightly increases without HTL and decreases with HTL. The incoming light photons are absorbed by the perovskite layer, resulting in the formation of electron–hole pairs. A tiny quantity of n-type or p-type doping can thus be added to a perovskite absorber layer to improve the solar cell's performance.⁷¹ Here, the N_A of the perovskite layer (CsPbBr₃) changed from 10⁹ cm⁻³ to 10¹⁸ cm⁻³. But at 0 cm⁻³ it shows the optimum performance parameters, which is the desired N_A of the absorber for showing the best PCE. Also, from Fig. 5(a) it is seen that a certain value of the N_A of the absorber performs less impact on the performance parameter of the PSC in this study.

Fig. 5. (a) The effect of acceptor density, and (b) defect density variation of the absorber layer.

3.5.2. Optimization of defect density of the perovskite absorber

The device architecture and the quality of light-absorbing materials play a trivial impact on the PCE of the PSCs. Since the photoelectrons are generated while the light of the sun is irradiated on the absorber layer. Inadequate coverage of the perovskite layer on the ETL is caused for poor morphology. Because of the lower film quality, there is a larger defect density, which leads to more recombination.⁷² In this work, the perovskite layer N_t variation was performed from 10⁹ cm⁻³ to 10¹⁸ cm⁻³ and shown in Fig. 5(b). Within the perovskite layer, many operations of recombination, generation, and absorption occur, which are dependent on the perovskite layer's quality and N_t.⁷³ The PSC's performance began to deteriorate as the defect density value crossed a particular threshold. This decrease can be attributed to non-radiative recombination Shockley–Read–Hall (SRH) recombination, which is a vital root of lifetime reduction, carrier recombination, and a considerable decrease in device performance. The trap-aided SRH recombination model may be used to compute the diffusion length. Since SRH recombination is the most typical kind of recombination in PSCs. SRH recombination can be illustrated by the following two eqn (5) and (6).⁷⁴

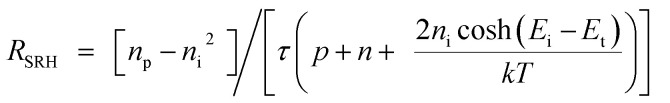5

τ = 1/[σ × N_t × V_th] 6

where σ is the charge carrier capture cross-section, τ is the charge carrier lifetime, V_th is the charge carrier thermal velocity, and N_t is the perovskite absorber layer defect density.

Here 10¹⁴ cm⁻³ is the N_t of the perovskite layer is the reason for showing the best PCE in the evaluating process. So, by setting up this as defect density of absorber then further evaluating process is done so far.

3.5.3. Absorber's donor density optimization

In this study donor density (N_D) of absorbers varied from 10⁹ cm⁻³ to 10¹⁸ cm⁻³. The N_D of the absorber valued at 10¹⁶ cm⁻³ shows the optimum performance parameter. Before this step, the optimized N_t of the absorber is set up then this variation performs. And after performing the simulation 10¹⁶ cm⁻³ is an optimized N_D of the absorber, which would be used for the following sections' optimization of various parameters.

3.6. Optimization of ETL's features

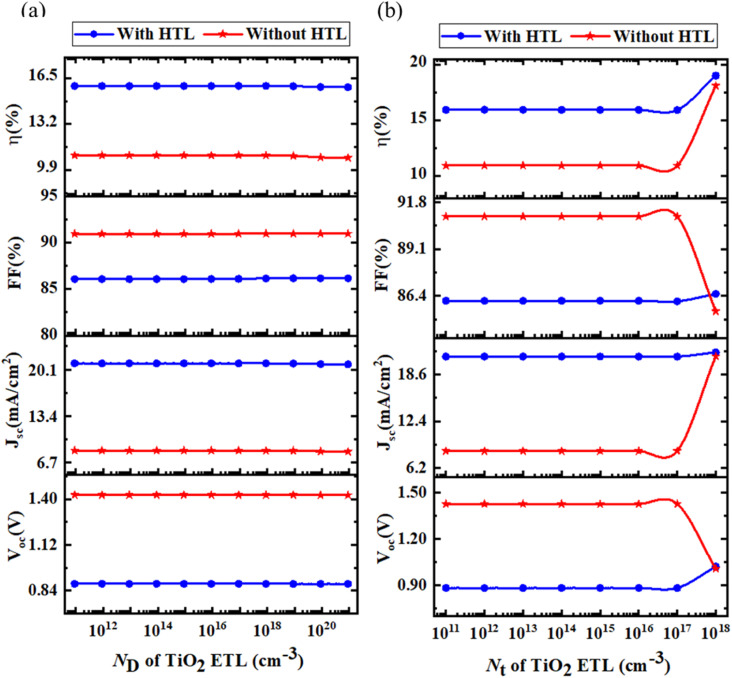
3.6.1. Optimization of ETL's donor density

Fig. 6(a) gives a glimpse that there is no significant influence on the output parameters of PSCs by varying the doping density (N_D) of ETL. It shows almost constant performance parameters but little increase in FF and PCE. Also, it is observed that without the inclusion of HTL shows a higher V_OC and FF than with HTL which is attributed to the absence of absorber/HTL interface traps and series resistance. The addition of HTL shows higher J_SC and PCE than without HTL because the creation of a depletion zone at the interface absorber/HTL will boost the separation mechanism of the photogenerated carriers.

Fig. 6. The effect of the (a) donor, and (b) defect density variation of ETL.

In this section, the N_D of the ETL (TiO₂) layer is varied from 9 × 10¹⁰ cm⁻³ to 9 × 10²⁰ cm⁻³, and also observed the output parameters, i.e. J_SC, V_OC, FF, and PCE of PSC are to find the optimum performance. At an N_D of 9 × 10¹⁶ cm⁻³, the PSC shows the best performance. By setting the N_D of ETL as 9 × 10¹⁶ cm⁻³ next evaluation process is conducted. Also from Fig. 6(a), it is identified that in the variation of N_D of ETL, there is no significant change of V_OC, J_SC. Also, the FF and PCE are almost significantly increased to it show the optimum performance. Because a larger ETL's N_D value makes carrier extraction and transmission easier at the ETL/perovskite interface. The recombination rate is unaffected because V_OC is constant and independent of doping density. This indicates that recombination has remained constant.⁷⁵ The electric behavior of a layer, which may be changed by adding a dopant, has a big impact on the PV performance of solar cells. ETL and HTL doping increases the performance by increasing the electric field of the interface which enhances the separation mechanism.⁷⁶ The interface electric field is created by the difference in the Fermi levels of the ETL/absorber and absorber/HTL materials. When the ETL and HTL are doped, the Fermi levels of the materials are shifted and create a higher built-in potential at the interface. This creates a larger electric field at the interface, which helps to drive the charge carriers away from the interface and prevent recombination. The doping of the ETL and HTL increases the concentration of charge carriers in the materials and creates a larger difference in the Fermi levels of the materials, which in turn creates a larger electric field at the interface. The doping of the ETL and HTL can also change the band alignment at the interface. This can further increase the electric field at the interface.

3.6.2. Optimization of defect density of ETL

Fig. 6(b) shows almost constant performance parameters for changing the N_t of the ETL material. Specifically, for both the simulated devices, in the case of V_OC, it is seen that with HTL almost constant profile but when ETL's N_t is almost 1 × 10¹⁷ cm⁻³ is seen that increasing nature, also without HTL constant nature of V_OC shown but at N_t of ETL when 10¹⁷ cm⁻³ it shows decreasing in nature. Also without HTL, it shows higher V_OC than with HTL. Similarly, a constant J_SC is depicted in Fig. 6(b) while at the N_t of almost 10¹⁶ cm⁻³ without HTL condition it shows increasing J_SC nature and a very small increase in J_SC with HTL condition. For comparison, with HTL condition shows higher J_SC than without HTL as can be well depicted in Fig. 6. Also, a constant FF profile is seen but without HTL it shows higher FF at the defect density of ETL when 10¹⁷ cm⁻³ shows decreasing FF for without HTL condition and increasing profile for with HTL condition. Also, a similar PCE profile is observed both with HTL and without HTL condition but with HTL shows higher PCE than without HTL. In addition, the 10¹⁵ cm⁻³N_t of ETL shows the optimized performance of PSCs and by setting up the N_t further evaluation is conducted.

3.7. Optimization of properties of the HTL

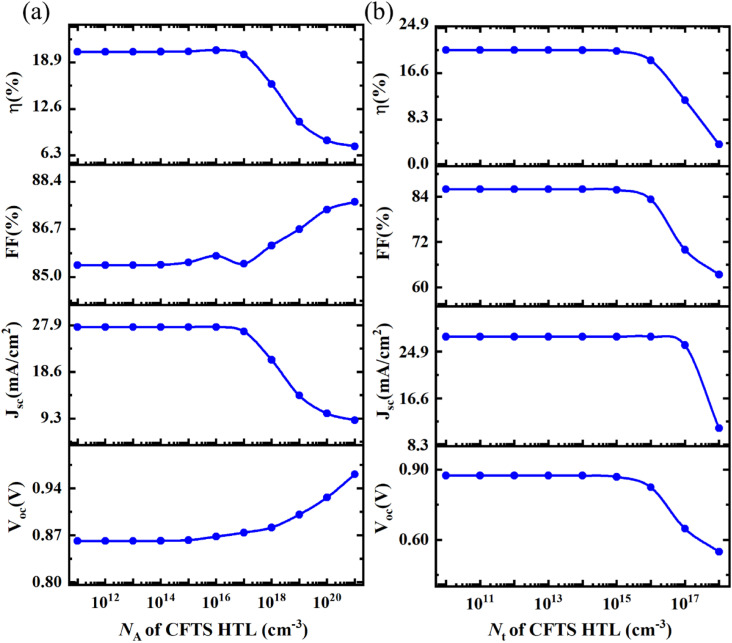
3.7.1. Optimization of doping density of HTL

Fig. 7(a) depicts the variation of N_A from 10¹¹ cm⁻³ to 10²¹ cm⁻³ of CFTS as HTL when all the other optoelectronic parameters are constant. Since all the parameters are almost constant up to 10¹⁷ cm⁻³ doping density, after that V_OC and FF increase but J_SC and PCE decrease. The doping density of HTL 10¹⁶ cm⁻³ is the optimized value because it shows the best PCE. By setting up this optimization, a further evaluation process is being conducted.

Fig. 7. Effect of (a) acceptor density and (b) defect density variation of HTL.

The ETL and HTL doping can be performed in one of two ways. Firstly, it can be done using minority carriers, but the photovoltaic characteristics are substantially reduced. On the other hand, the majority of carriers may achieve this greatly by increasing the PV parameters. The PSCs will perform better if doping density is kept at a moderate level.⁶³ As the N_A of HTL increases, the V_OC also increases. The greater value of V_OC at greater N_A can be attributed to an enhancement in the built-in voltages at the HTL/perovskite interface⁷⁷ which results in increasing electric potential. This improves the PCE of the PSC by reinforcing charge carrier separation with lower recombination.⁷⁸

3.7.2. Optimization of defect density of HTL

Here, due to the consequence of the previous sections by fixing the optimized previous parameters, HTL's N_t variation is done from 10¹⁰ cm⁻³ to 10¹⁸ cm⁻³. Fig. 7(b) represents the change of N_t of HTL and it is observed that all the parameters are constant up to 10¹⁵ cm⁻³ defect density of HTL, after that all parameters are gradually decreased. Therefore, the optimized value of the N_t of HTL is kept at 10¹³ cm⁻³.

Finally, 10¹³ cm⁻³ is the N_t of HTL, which was the optimized one for the best PCE and set up for the next evaluation purpose.

3.8. Optimization of the interface layer's defect density

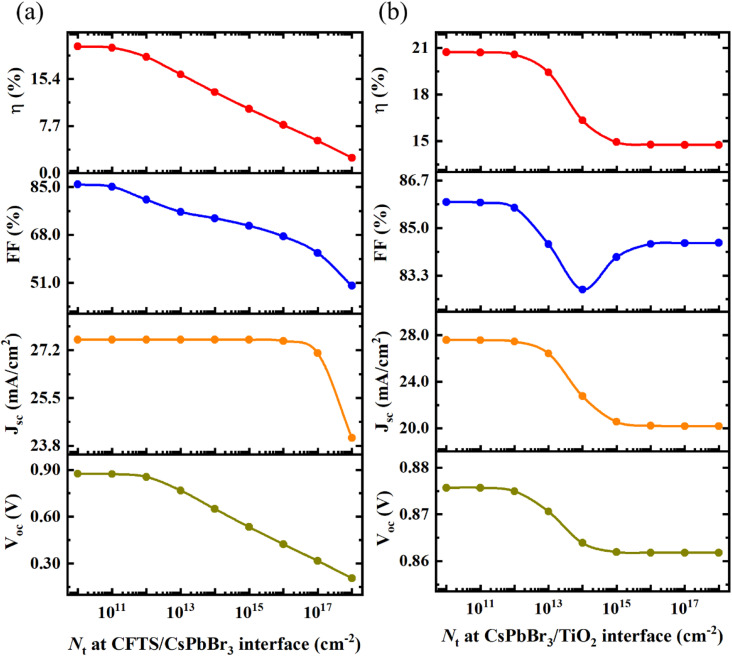
3.8.1. Optimization of HTL/absorber interface layer defect density

To investigate the impact of the HTL/absorber interface, the defect density is varied from 10¹⁰ cm⁻² to 10¹⁸ cm⁻² which is depicted in Fig. 8(a). From this figure, it is observed that the decreasing pattern of V_OC, J_SC, FF, and PCE after increasing the N_t from 10¹⁰ cm⁻². This is the minimum defect density that causes the best performance of PSCs in this study and that is set up for the next step of evaluation. The recombination rate improves with increased N_t, which causes a lowers PCE. The higher defect densities at both interfaces result in additional trap and recombination centers, lowering cell performance. As a consequence of the simulation, it is clear that an interface defect density of 10¹⁰ cm⁻² is optimal for device simulation.⁷⁹

Fig. 8. Effect of (a) CFTS/CsPbBr₃, and (b) CsPbBr₃/TiO₂ interface defect density variation.

3.8.2. Optimization of absorber/ETL interface layer defect density

Absorber/ETL interface layers N_t is varying from 10¹⁰ cm⁻² to 10¹⁸ cm⁻² and as indicated in Fig. 8(b). From this figure, it can be seen that with the enhancement in the N_t the performance parameters of perovskite are decreased because the recombination rate improves with enhancing N_t, which causes in lowering the PCE. Also in this case the best outputs of the PSC are found at a defect density value of 10¹⁰ cm⁻² and set as an optimized parameter for the next step of evaluation. The N_t range was chosen for V_OC because it is much more sensitive to N_t than J_SC. The following formula eqn (7) can be used to define the interface recombination V_OC limit.⁸⁰

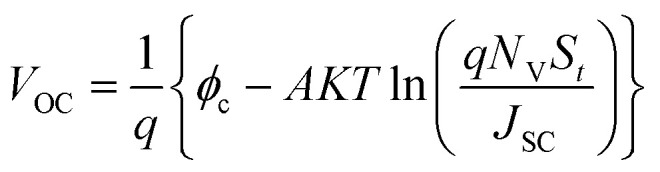7

where S_t is the recombination velocity at the interface, A denotes the ideality factor, and ϕ_c denotes an effective barrier height.

3.9. Impact of shunt resistance, series resistance, and temperature

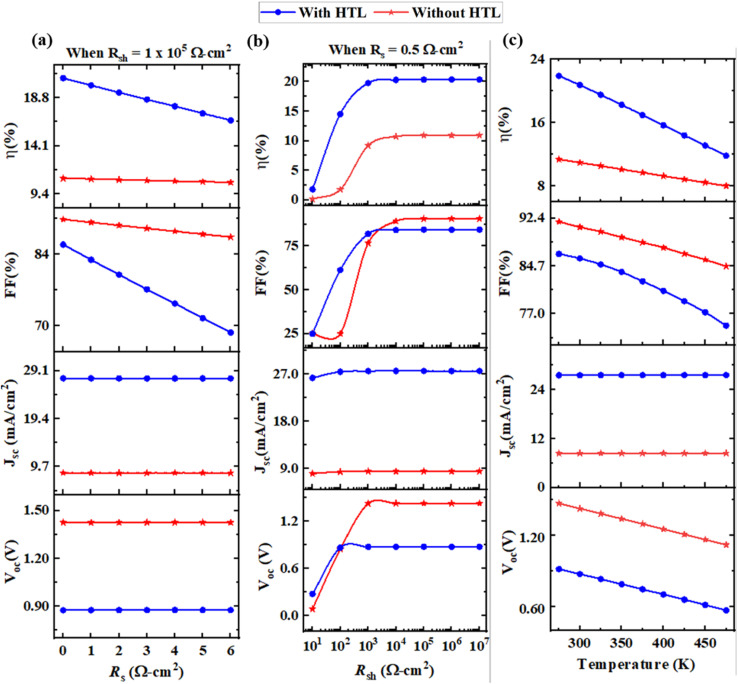
3.9.1. Impact of series resistance

Fig. 9(a) shows the variations of R_s from 0 Ω cm² to 6 Ω cm² when shunt resistance (R_SH) is constant at 10⁵ Ω cm². From Fig. 9(a), it is observed that the V_OC and J_SC are almost constant for both cases but V_OC (0.9 V) is lower than without HTL V_OC (1.5 V) and J_SC (27 mA cm⁻²) is higher than without HTL J_SC (9 mA cm⁻²). The FF and PCE are reduced for the higher value of R_s because the device's series resistance is determined by numerous internal resistances, while the R_SH is chosen by various loss processes.⁸¹ In the case of FF without HTL shows higher FF than with HTL. Finally, the addition of HTL shows higher PCE than without HTL structure.

Fig. 9. Impact of (a) series resistance, (b) shunt resistance, and (c) temperature variation.

3.9.2. Effect of shunt resistance

In this section, the value of R_SH is changed from the range of 10¹ Ω cm² to 10⁷ Ω cm² when the R_s is constant at 0.5 Ω cm². The variation of shunt resistance is performed for both the addition of the HTL and without HTL architecture. It can be seen from Fig. 9(b) that the V_OC, FF, and PCE monotonically increased with increasing shunt resistance. But it is also observed that the addition of the HTL has a higher value of shunt resistance than without HTL and there isn't any significant impact on J_SC. As the J_SC is almost constant entire the variation of shunt resistance.

3.9.3. Effect of operating temperature

Temperatures have made some effect on PSCs, because solar cells are normally installed outside, and they are constantly illuminated by AM1.5G of the sun. As a result, their temperature can quickly rise over room temperature.⁸² Recent publications on optoelectronics based on perovskites have demonstrated success in increasing the device's performance stability at high temperatures.^83–85 To show the influence of the temperature on the output parameters of PSCs, the temperature is varied from 275 K to 475 K. The value of V_OC is decreasing with increasing temperature, because of the increase in reversed saturating current (J₀) at higher temperatures and the inverse connection between V_OC and J₀. Eqn (8) illustrates the relationship between them.

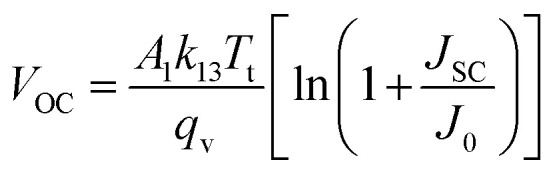8

The ideality factor is denoted by A₁, while the thermal voltage is denoted by 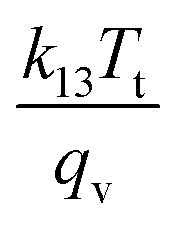. Furthermore, when the temperature rises, the flaws defect increases, resulting in a reduction in V_OC. However, when the temperature rises, the FF and PCE values decrease, possibly due to a decrease in shunt resistance.⁸² Also from Fig. 9(c), it is depicted that the optimum PCE is finding out at 300 K temperature which is room temperature. This optimal temperature was similar to those found in prior studies.⁸⁶

3.10. Effect of capacitance, Mott–Schottky, generation and recombination rates

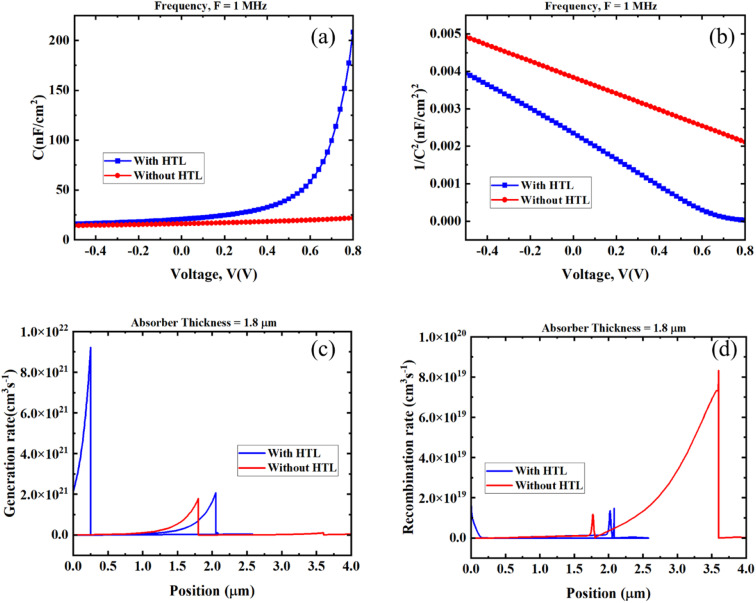
In the case of capacitance and the Mott–Schottky effect Fig. 10(a) and (b) show the pattern whenever voltage is changed from −0.5 to 0.8 V in the case of both optimized with HTL and without HTL anointed devices. In both cases, the frequency is considered as 1 MHz. From Fig. 10(a) it is clearly visible that with HTL connected device shows an exponentially increasing capacitance pattern, after 0.4 V it shows drastically increasing capacitance and at the terminating point it shows 200 nF cm⁻². Whereas, without HTL connected mode shows almost constant capacitance as depicted in Fig. 10.

Fig. 10. (a) Capacitance, (b) Mott–Schottky plot, (c) generation rate, (d) recombination rate for PSC.

Fig. 10(c) and (d) show the generation and recombination rate of TiO₂ as ETL, and CFTS as HTL-associated CsPbBr₃-based solar cell structure. Fig. 10(c) with HTL-connected structure shows the highest generation rate. Whereas in the case of recombination rate according to Fig. 10(d) without HTL connected mode shows the highest recombination rate.

3.11. Output parameters of the simulated final PSC

3.11.1. J–V characteristics

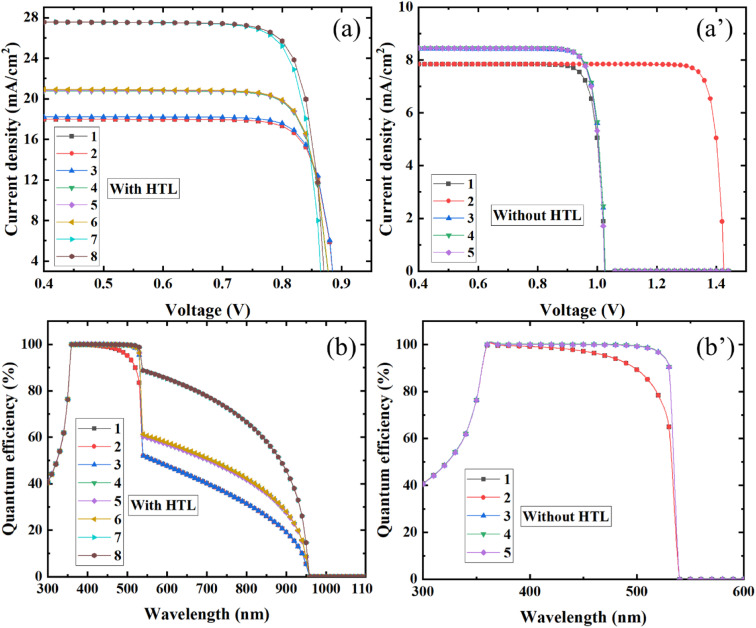
The J_SC concerning the variation of voltage range is observed in this study. Fig. 11(a) and a′) shows the graphical representation of J_SC's change concerning the variation of voltage at ranges of 0 V to 0.9 V. This is done in eight (1 initial condition, 2 after BMC optimization, 3 absorber thickness optimization, 4 HTL thickness optimization, 5 absorber N_t optimization, 6 absorber N_d optimization, 7 HTL N_A, and 8 HTL N_t optimization during with HTL condition and during without HTL condition 1 initial condition, 2 BMC optimization, 3 absorber thickness optimization, 4 absorbers N_t optimization, 5 absorber N_d optimization) steps to show the variation or change in current density. Similar to the optimization steps of PSCs, here we have also observed the J_SC variation concerning the electrostatic potential from 0 V to −0.9 V in the initial mode. Apart from that as back contact connected mode, then optimized ETL thickness associated mode, optimized HTL thickness associated mode, optimized acceptor density associated mode, optimized absorber defect density associated mode, optimized ETL donor density associated mode, and finally optimized ETL defect density associated mode are depicted in Fig. 11(a) and a′ at both with HTL and without HTL associated condition.

Fig. 11. (a, a′) J–V characteristics curve for with and without HTL, and (b, b′) quantum efficiency curve for with and without HTL.

Because the photoelectrons are generated in the layers and the recombination of the electron–hole can become dominant in describing the PV performance of the device. The quantity of defects in perovskite films plays a substantial role in deciding the PSCs output. The J–V curve and V_OC in a perovskite film are plotted in Fig. 11(a) and a′, as a function of bulk trap density and so on. The presence of defect states in the perovskite layer is lower than all PV metrics significantly. This is in line with the finding that perovskites' strong crystalline helps to reduce recombination of the charge and so allows for great performance.⁸⁷

3.11.2. Quantum efficiency (QE)

Fig. 11(b) and (b′) provide illustrative observations about the QE curve of PSCs with the different conditioned modes. Firstly, the optimized structure with Au as back contact associated structure's quantum efficiency curve is illustrated. Consequently, for the methodological purpose, Ni as back contact associated optimized structure's QE curve is shown. Then similarly optimized ETL thickness, optimized HTL thickness, optimized acceptor density of absorber, the optimized defect density of absorber, optimized donor density of ETL, and optimized defect density of ETL associated structure's quantum efficiency's curve are illustrated in Fig. 11(b) and (b′), with HTL and without HTL respectively.

3.12. Assessment of SCAPS-1D results with earlier work

A comparison of optimized solar cell structures is conducted in this section. Here, in Table 4 improved parameters of the PSC's HTL, the absorber layer, and ETL data are given. After many trials and errors, the optimized solar cell structure is found to be ITO/TiO₂/CsPbBr₃/CFTS/Ni, which shows the best performance. The V_OC of 0.875 V, J_SC of 27.57 mA cm⁻², FF of 85.93%, and PCE of 20.73%, respectively, for the proposed cell.

Optimized parameters of CFTS, CsPbBr₃, TiO₂.

Parameters	CFTS	CsPbBr3	TiO2
Thickness (μm)	0.25	1.8	0.03
E g (eV)	1.3	2.3	3.2
χ (eV)	3.3	3.6	3.9
ε r	9	6.5	9
N C (cm−3)	2.2 × 1018	4.94 × 1017	2 × 1018
N V (cm−3)	1.8 × 1019	8.47 × 1018	1.8 × 1019
μ n (cm2 V−1 s−1)	21.98	4500	20
μ h (cm2 V−1 s−1)	21.98	4500	10
N A (cm−3)	1 × 1016	0	0
N D (cm−3)	0	1 × 1016	9 × 1016
N t (cm−3)	1.0 × 1013	1.0 × 1014	1.0 × 1015

Several CsPbBr₃ absorber layer-based devices published during the year 2016–2023 are compared and listed in Table 5. Experimental and theoretical works are categorized as types 1 and 2, respectively. Table 5 shows that different device architectures based on distinct ETL and HTL materials are proposed and investigated but the conversion efficiency remained below 12% due to low J_SC values as shown in Table 5. Lower J_SC values are attributed to the wide bandgap of CsPbBr₃ resulting in low cutoff wavelength and inefficient spectrum utilization. However, the addition of CFTS significantly increased the spectrum utilization which resulted in improved J_SC (17.98 mA cm⁻²) and PCE (13.86%).⁴⁹ Further optimization reported in this work improved the performance of the CFTS-based device by delivering J_SC (27.57 mA cm⁻²) and PCE (20.73%) as shown in Table 5.

Literature study of CsPbBr₃ absorber layer⁴⁹.

Typea	Device structure	V OC (V)	J SC (mA cm−2)	FF (%)	PCE (%)	Year	Ref.
1	m-TiO2/CsPbBr3/carbon	1.24	7.4	73.0	6.70	2016	33
1	m-TiO2/CQD/CsPbBr3 IO/spiro/Ag	1.06	11.34	69.0	8.29	2017	88
1	FTO/TiO2/CsPbBr3/MoS2 QDs	1.31	6.55	79.4	6.80	2018	89
1	FTO/c-TiO2/m-TiO2/CsPbBr3/NiOx/C	1.40	6.84	76.1	7.29	2018	90
1	TiO2/CsPbBr3/CuPc/carbon	1.26	6.62	74.0	6.21	2018	91
1	m-TiO2/GQDs/CsPbBr3/CISZ-QDs/C	1.52	7.35	84.0	9.43	2018	92
1	m-TiO2/GQDs/CsPbBr3/C	1.46	8.12	82.0	9.72	2018	93
1	FTO/GQDs/CsPbBr3/PQDs/carbon	5.08	1.21	66.7	4.10	2018	94
2	FTO/TiO2/CsPbBr3/NiO/Au	1.11	8.65	42.0	4.04	2019	95
1	FTO/TiO2/I-CsPbBr3/carbon	1.29	7.07	59.0	5.38	2019	96
1	FTO/a-Nb2O5/CsPbBr3/CuPc/carbon	1.45	5.64	70.0	5.74	2019	97
1	FTO/TiO2/CsPbBr3/spiro-MeOTAD/Ag	1.12	7.04	68.1	5.36	2019	98
1	m-TiO2/CsPbBr3/PTAA/Au	1.28	6.24	74.0	5.95	2020	99
1	FTO/mp-TiO2/CsPbBr3	1.27	6.13	56.7	4.43	2020	100
1	FTO/TiO2/CsPbBr3 + 3% l-lysine/carbon	1.56	7.64	81.0	9.68	2020	101
1	FTO/c-TiO2/Sn doped CsPbBr3/carbon	1.36	9.27	71.0	8.95	2021	102
2	FTO/TiO2/CsPbBr3/spiro-MeOTAD	1.68	8.17	84.4	11.58	2020	103
2	ITO/GO/CsPbBr3/PEDOT:PSS/Au	1.57	8.50	77.4	10.34	2021	104
2	ITO/TiO2/CsPbBr3/CFTS/Ni	0.89	17.98	87.0	13.86	2023	49
2	ITO/TiO2/CsPbBr3/CFTS/Ni	0.87	27.57	85.9	20.73	2023	b

^a1 - experimental, 2 - theoretical.

^bThis work.

This concludes that the TiO₂ as ETL, CFTS as HTL, and Finally CsPbBr₃ as the light-absorbing layer offers the best possible output parameters. This combination of solar cells makes the highly efficient than the other solar cell structures. The light-absorbing layer plays a crucial role in solar cell efficiency. Many other researchers are also working on the CsPbBr₃ light absorber layer. But in this work by trial and error choosing appropriate ETL, HTL and their optoelectronic parameters make the solar cell structure more effective and efficient than the other with a PCE of 20.73%.

4. Conclusion

In summary, we have demonstrated a comprehensive simulation approach for optimizing the performance of CsPbBr₃-based PSCs. We first optimized the BMC with HTL connected mode and then optimized the CsPbBr₃, TiO₂, and CFTS layers thickness, charge carrier density, defect density, and interface defect densities as well in both additions of HTL and deduction of the HTL connected conditions. Our optimization process led to the following results:

1. The ITO/TiO₂/CsPbBr₃/CFTS/Ni structure with optimized BMC showed a PCE of 13.86% with HTL-connected condition.

2. We evaluated the impact of absorber thickness concerning absorber defect density and acceptor density on the ITO/TiO₂/CsPbBr₃/CFTS/Ni structure and achieved a maximum PCE of 14%.

3. The optimized final thickness of the CsPbBr₃ absorber, TiO₂ ETL, and CFTS HTL were found to be 1.8, 0.03, and 0.25 μm, respectively, in both with and without HTL-connected conditions.

4. We determined the optimized absorber acceptor, defect, and donor densities, as well as the optimized defect density and doping density of the ETL and HTL layers. The final optimized device showed a PCE of 20.73%, with the optimized HTL/absorber and absorber/ETL interface defect densities at 1 × 10¹⁰ cm⁻². Here, in most cases, with HTL-connected mode shows the best performance.

5. Interfacial defect density remained unchanged during the optimization process and showed the best performance with the initial condition.

Moreover, we investigated the impact of temperature, series and shunt resistance, capacitance, Mott–Schottky, recombination and generation rates, J–V and QE features of the optimized devices both with and without HTL connected conditions. Our study provides valuable insights for designing and constructing high-performance PSCs.

Data availability

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.

Author contributions

M. K. Hossain: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – original draft, and writing – review & editing; S. Bhattarai, A. A. Arnab, M. K. A. Mohammed, and R. Pandey: data curation, formal analysis, investigation, software, validation, visualization, and writing – original draft; M. H. Ali, M. F. Rahman, M. R. Islam, D. P. Samajdar, J. Madan, and H. Bencherif, D. K. Dwivedi, and Mongi Amami: data curation, formal analysis, investigation, validation, visualization, and writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.