Abstract
Potential evapotranspiration (PET) is a crucial component of the hydrological cycle and energy balance. Although the Penman-Monteith (PM) model is the most widely used method to estimate daily PET, it requires temperature, relative humidity, solar radiation, and wind speed. In Thailand, the number of potential weather stations to provide the required data is limited, which resulted in the absence of some input variables in many locations. The objective of this study is to develop the revised potential evapotranspiration (RPET) model to estimate daily PET using Global Navigation Satellite System-derived Precipitable Water Vapor (GNSS-PWV) and temperature data. The multiple linear regression analysis was used to develop and validate the RPET model. The performance of the RPET model along with the Global Land Evaporation Amsterdam Model (GLEAM v3.2 b) and the European Centre for Medium-Range Weather Forecasts Reanalysis-5 (ERA5-Land) products was investigated using the PM model. The results revealed that the RPET model showed a strong correlation with the PM model (r = 0.85, RMSE = 0.97 mm day−1, RSR = 0.53, NSE = 0.72) under limited meteorological inputs. The RPET model performance was superior when compared to GLEAM and ERA5-Land (r = 0.80, RMSE = 1.06 mm day−1). Therefore, the proposed model is greatly suitable for daily PET estimation with only required GNSS-PWV and temperature data, and this can be implemented for drought assessment and water resources management.
Keywords: Potential evapotranspiration, Global navigation satellite system, Precipitable water vapor, Penman-monteith model
1. Introduction
Evapotranspiration (ET) is one of the essential components of the water cycle, which is the combination of two processes such as evaporation and transpiration [1,2]. Evaporation is converting water into water vapor and remove from the evaporating surface. Moreover, transpiration includes the vaporization of water in plant tissues and the vapor removal to the atmosphere. Potential evapotranspiration (PET) is the process of water loss from the surface with good water status in the soil profile, which is affected by temperature, humidity, wind, and solar radiation. It has great supporting information for comprehending climate change because it affects both surface runoff and water storage in the catchment. When the rates of evapotranspiration are extremely high and similar to the amount of precipitation, it can lead to a deficiency of water for crops [3]. Additionally, PET is also applied in water management and crop production [4], improving irrigation scheduling [5], and drought monitoring [[6], [7], [8]]. Thus, the estimation of PET is a crucial process for application in various research works.
To estimate PET, several studies have investigated PET estimation using different techniques such as the eddy covariance method [9,10], the Penman-Monteith model [11] and satellite remote sensing [12]. The eddy covariance (EC) method is used to study energy, carbon dioxide and water vapor fluxes on the regional scale, which employ to estimate the PET with high temporal resolution and great precision. However, the instruments used for this measurement are costly and only installed in selected few locations. Thus, it is limited spatially, and restricted in some areas with complex terrain [13,14]. Moreover, the instrument failure and poor maintenance of the EC approach also resulted in missing data in long-term observations [15]. Because of these issues, the Penman-Monteith (PM) model is recommended as a standard and reliable method by the Food and Agriculture Organization (FAO). Although the PM model commonly used meteorological data, it has revealed weaknesses in the spatial coverage and required several meteorological parameters [2]. Satellite remote sensing has been utilized to estimate the PET in large areas by several researchers [[16], [17], [18], [19], [20]]. However, it has been limited by cloud cover during the wet season, moderate accuracy, and relatively low spatial and temporal resolutions [[21], [22], [23], [24], [25]]. For example, the MODIS Global Evapotranspiration is based on the PM equation and provided the MOD16 global evapotranspiration (ET), latent heat flux (LE), potential ET (PET) and potential LE (PLE) datasets in extensive areas. However, these MOD16 products have some drawbacks such as cloud cover, and low spatial resolution (500 m spatial resolution) [26,27].
The PM model is the most widely used approach, which is used to estimate the PET for water resources management [28,29], crop modeling [30], and drought assessment [31,32]. However, it required various meteorological parameters such as temperature, humidity, radiation, and wind speed. In some cases, the lack of input parameters limits the use of the PM model because of the non-availability of data in many locations, particularly solar radiation, and wind speed [33]. For instance, the PET showed overestimation in Canada when the solar radiation data was unavailable with RMSE between 0.8 and 1.1 mm day−1 [34]. In Thailand, this method has also been applied to evaluate PET. For instance, the spatial and temporal distributions of PET were analyzed to monitor drought conditions and study climate change at the regional level [[35], [36], [37]]. However, it remains the main limitation for obtaining all required parameters due to the number of potential weather stations restriction. In particular, solar radiation data are restricted in some weather stations. Therefore, this shortcoming needs to be addressed mainly in constrained meteorological data.
Global Navigation Satellite System (GNSS) is the technology that uses signals from satellites to find locations on Earth's surface [38]. Because of the development of GNSS, the GNSS network has operated to permanently acquire the GNSS signals continuously with high precision, known as Continuously Operating Reference Station or GNSS CORS [39]. GNSS CORS has been analyzed to retrieve the precipitable water vapor (PWV) by tropospheric delay in the GNSS signal [[40], [41], [42], [43]]. This delay is one of the important error sources for GNSS positioning, e.g. satellite and receiver clock errors, which require the GNSS processing techniques to eliminate these errors [38]. There are basically two approaches to estimate high precision position of GNSS such as baseline positioning and Precise Point Positioning (PPP) [44]. In this research, the PPP method was selected to achieve the centimeter level positioning accuracy with required precise orbit and clock data [45,46]. The International GNSS Service (IGS) is responsible for providing the precise orbit and clock products [47]. Precipitable Water Vapor (PWV) is the vertically integrated amount of water vapor, and it is a key factor of the atmosphere that affects the global water cycle. GNSS-derived PWV (GNSS-PWV) has been widely applied in climate research and water vapor determination. In addition, it is an alternative technology that is efficiently utilized to obtain water vapor with continuous data and high temporal resolutions in all-weather. Furthermore, it has been applied in various research works such as hydrological application [48], forecasting precipitation [[49], [50], [51]], monitoring and estimating snow evaporation [52], predicting flash floods [53], assessing the PET [54,55] and evaluating the drought index [56]. In Thailand, the previous studies found the study of spatial and temporal variability and the validation of PWV value from GNSS observations [[57], [58], [59]]. The vertical distribution of water vapor and its spatiotemporal distribution is important in hydrological and climatological studies. However, the ground based PWV receivers are limited in most parts of the world. This makes challenging to apply GNSS-PWV on water balance research and related applications.
Recently, the GNSS-derived PWV has been applied to improve the PET acquisition approach for calculating the drought monitoring index such as standardized precipitation evapotranspiration index (SPEI) [[54], [55], [56]]. Previous studies proposed models to enhance the accuracy of PET using the Thornthwaite (TH) and PM models difference and temperature data, e.g. revised TH (RTH) model, the site-based RTH (S-RTH) model, a novel ETp model over China (C-RTH) model, the high-precision PET (HPET) model and diurnal-provided PET values (DTH-PET). Additionally, these models were developed to overcome the accuracy of PET derived from the TH model and the requirement of various meteorological parameters of the PM model. However, the mentioned models were shown highly accurate values at specific locations. Such procedures have required evaluation in different geographic locations to fit the model coefficients. Consequently, this study highlights the benefit of the developed model in fitting the coefficients of the model and overcoming the limitations of current models to cope with the meteorological data constraint. This study aims to develop the revised potential evapotranspiration (RPET) model using GNSS-PWV and temperature data. The GNSS-PWV was evaluated in the one full year of hourly GNSS-PWV in 2020. These results were used to develop the model to estimate the PET using GNSS-PWV and temperature. Furthermore, the relationship among PET, PWV and temperature was analyzed to obtain the new model coefficients and evaluated the model performance for estimating the PET in other stations with limited meteorological data.
2. Materials and methods
2.1. Study area
The study area is located in the northeast region of Thailand (14–19 °N latitude, 101–106°E longitude), a plateau from the northwest to the eastward. This region covers an area of 168,845 km2 that consists of 20 provinces such as Amnat Charoen, Bueng Kan, Buri Rum, Chaiyaphum, Kalasin, Khon Kaen, Loei, Maha Sarakham, Mukdahan, Nakhon Phanom, Nakhon Ratchasima, Nong Bua Lam Phu, Nong Khai, Roi Et, Sakon Nakhon, Sisaket, Surin, Ubon Ratchathani, Udon Thani and Yasothon (Fig. 1). The elevation ranges between 74 and 1800 m, and the prominent soil texture is sandy soil and distributed saline soils with extremely low soil fertility [60]. Moreover, the climate of this region is tropical. The region experiences dry weather from November to April due to the northeast monsoon and higher rainfall from May to October caused by the southwest monsoon. The annual precipitation is uneven from 1250 to 2500 mm, with an average rainfall of about 1384 mm during the rainy season [61]. The annual average temperature is approximately 26.8 °C [62]. The potential evapotranspiration in this region ranges between 1 and 6 mm day−1 [63] or 1200 to 1250 mm year−1 [35]. Regarding these conditions, the northeast region of Thailand was selected as the case study. Furthermore, the positions and details of GNSS CORS and meteorological stations used in this study were also shown in Fig. 1 and Table 1.
Fig. 1.
Study area.
Table 1.
List of GNSS and meteorological stations with geographic location information.
| Station codes | Provinces | GNSS CORS stations | Coordinates | Altitude (m) | Weather stations code | Coordinates |
|---|---|---|---|---|---|---|
| 1 | Amnat Charoen | DACR | 15.944, 104.632 | 153 | BNYM | 15.862, 104.516 |
| 2 | Buriram | DBRM | 14.555, 102.932 | 185 | BSKJ | 14.396, 102.847 |
| 3 | Chaiyaphum | PCPM | 16.083, 101.803 | 231 | NNKO | 16.199, 101.932 |
| 4 | Kalasin | AKSN | 16.798, 104.045 | 173 | NAKU | 16.798, 104.045 |
| 5 | Khon Kaen | TKK1 | 16.838, 102.913 | 382 | KPEM | 16.748, 102.923 |
| 6 | Khon Kaen | TKK2 | 15.895, 102.649 | 197 | BNPI | 16.117, 102.707 |
| 7 | Loei | DLEI | 17.421, 101.933 | 282 | NNPT | 17.321, 102.025 |
| 8 | Loei | LLEI | 16.885, 101.885 | 237 | PHKD | 16.877, 101.861 |
| 9 | Mukdahan | LMDH | 16.547, 104.726 | 121 | KAHN | 16.497, 104.669 |
| 10 | Nakhon Phanom | DNPM | 16.955, 104.451 | 134 | DMKH | 17.079, 104.326 |
| 11 | Nakhon Ratchasima | ENMA | 14.597, 102.002 | 205 | UDMS | 14.538, 101.969 |
| 12 | Nakhon Ratchasima | LNMA | 15.348, 102.742 | 122 | NGCH | 15.279, 102.639 |
| 13 | Nong Bua Lamphu | LNBP | 17.224, 102.425 | 209 | VLGE32 | 17.147, 102.332 |
| 14 | Nong Khai | LNKI | 17.880, 102.742 | 145 | PTWY | 17.877, 102.727 |
| 15 | Sakon Nakhon | DSNK | 17.305, 103.839 | 156 | BBUA | 17.373, 103.984 |
| 16 | Sisaket | DSSK | 15.176, 104.156 | 135 | BNLG | 15.122, 104.241 |
| 17 | Sisaket | TSSK | 15.105, 104.569 | 119 | MKTR | 15.105, 104.569 |
2.2. Data descriptions
In this study, the datasets of GNSS CORS and meteorological parameters of Northeastern Thailand were collected in 2020 as shown in Table 2. The GNSS observations were obtained from 17 permanent GNSS CORS stations of the Royal Thai Survey Development (RTSD), which include the original RINEX (Receiver-Independent Exchange) files with 30-s interval data. Moreover, the meteorological datasets were collected from the Hydro-Informatics Institute (HII) and the Thai Meteorological Department (TMD). Surface pressure, temperature and relative humidity were obtained from HII, and the sunshine duration and wind speed were collected from TMD. These data have been checked rigorously before the analysis. Therefore, there are six GNSS CORS of RSTD, six weather stations of HII and four weather stations of TMD selected from nearby GNSS CORS stations and sufficient data for model development and performance evaluation.
Table 2.
Detailed information of the datasets used in this study.
| Name | Source | Format | Spatial coverage | Temporal resolution | Temporal coverage |
|---|---|---|---|---|---|
| GNSS CORS | RTSD | Point | 17 stations | 30-s | 2020 |
| Surface pressure, Temperature, Relative humidity | HII | Point | 17 stations | Hourly | 2020 |
| Sunshine duration, Wind speed | TMD | Point | 4 stations | Daily | 2020 |
| PET | GLEAM | Grid | 0.25° | Daily | 2020 |
| PET | ERA5 | Grid | 0.1° | Hourly | 2020 |
List of abbreviations. ERA5 is the European Centre for Medium-Range Weather Forecasts Reanalysis-5. GLEAM is the Global Land Evaporation Amsterdam Model. HII is the Hydro-Informatics Institute. RTSD is the Royal Thai Survey Development. TMD is the Thai Meteorological Department.
2.3. Methodology
Fig. 2 showed the overall methodology for the estimation of daily potential evapotranspiration. This research was divided into three parts. First, The GNSS observations and meteorological data were analyzed in the Precise Point Positioning (PPP) mode to obtain the Precipitable Water Vapor (PWV). Second, six weather stations of HII and four weather stations of TMD were selected to estimate daily PET as reference data using the PM model because of the limitation of solar radiation data in some weather stations. Finally, the multiple linear regression analysis was used to develop and validate the revised potential evapotranspiration (RPET) model. After that, the daily PET was calculated for the 11 different stations of the region using the RPET model. The model performance was also evaluated by comparing it to the other existing datasets.
Fig. 2.
Overall methodology.
2.3.1. Estimation of GNSS-based precipitable water vapor
The GNSS CORS and weather stations were selected for analyzing the PWV with a distance between them less than 20 km as shown in Fig. 1. In this research, the GNSS CORS were processed in Precise Point Positioning (PPP) approach to estimate Zenith Total Delay (ZTD) using goGPS v1.0 in MATLAB software. The goGPS-MATLAB is an advanced software for processing GNSS observations [64,65], which uses the PPP processing to remove the errors and provide an exact position [57,66]. The PPP method were applied to estimate the ZTD parameter because of the highly accurate orbit and clock products provided by the International GNSS Service (IGS) [45,47]. Table 3 showed the configuration for goGPS-MATLAB software in this study [67,68].
Table 3.
The configuration parameters for goGPS.
| Parameters | Feature/Models |
|---|---|
| GNSS Observations | GPS: L1&L2, GLONASS: G1&G2 |
| Sampling interval | 30-s |
| Antenna correction (ATX) | I14.ATX |
| Ocean loading | FES2004 model |
| Orbits and satellite clocks | ESOC final products |
| Ionospheric correction | Ionospheric-free combination |
| Tropospheric modeling | Saastamoinen model from meteorological data |
| Tropospheric mapping function | GMF (Global Mapping Function) + MacMillan |
| Satellite elevation cut-off | 10° |
The Zenith Hydrostatic Delay (ZHD) was calculated by the Saastamoinen model [69] as Equation (1).
| (1) |
where Ps is the pressure temperature (millibar), is the station latitude (radius), and H is the height of the station above sea level (meter). After that, the Zenith Wet Delay (ZWD) is calculated by subtracting ZTD and ZHD (ZWD = ZTD – ZHD). In addition, the ZWD is converted into PWV at 30s intervals by the conversion factor [40,70] as Equations (2), (3)).
| (2) |
| (3) |
where is the conversion factor computed by the mean of temperature (Tm) in Kelvin unit, the density of liquid water (ρw, 999.97 kg m−3) and the constant of water vapor (Rv, 461.525 J kg K−1). The k3 and k′2 are the physical constant with values of 3739 k2 mbar−1 and 22.1 k2 mbar−1, respectively. Tm was calculated by the surface temperature (Ts) in Kelvin unit: , which is specified in the tropical zone [40,57,67]. Ts is the surface temperature (°C) obtained from the meteorological stations. Moreover, meteorological data required the conversion of GMT (UTC+7) to the UTC time zone before the analysis. After the PWV was analyzed, the PWV data were averaged to obtain the hourly mean PWV and then converted the UTC into local time (UTC+7) for model development.
2.3.2. Potential evapotranspiration estimation by Penman-Monteith model
Potential evapotranspiration (PET) was calculated based on the Penman-Monteith (PM) model by CROPWAT 8.0 for windows. CROPWAT 8.0 software is a computer program for calculating crop water requirements and irrigation requirements based on soil, climate, and crop data. Therefore, this software is selected to calculate the PET as reference data based on the PM model. The PM model requires five meteorological parameters such as maximum air temperature (°C), minimum air temperature (°C), relative humidity (%), sunshine duration (hours), and wind speed (m s−1). The maximum air temperature, minimum air temperature, and relative humidity were collected from six HII weather stations (BBUA, BNPI, DMKH, KPEM, NAKU and NNPT) at hourly intervals. These data have then averaged the value from 6:00 to 12:00 h to represent the daily value matching the overpass time of Landsat-8 images. In addition, the daily wind speed and sunshine duration belonging to four TMD meteorological stations (353201, 356301, 381201 and 381301) were also used to calculate the PET. The PM model can be calculated the daily PET as Equation (4) [2,29].
| (4) |
where Rn is net radiation at the crop surface (MJ m−2 day−1), G is soil heat flux density (MJ m−2 day−1), is the psychometric constant (kPa °C−1), T is the air temperature at 2 m height (°C), u2 is the average wind speed at 2-m height (m s−1), es is saturated vapor pressure (kPa), ea is the actual vapor pressure (kPa), (es – ea) is saturated vapor pressure deficit (kPa), and is a slope vapor pressure curve (kPa °C−1).
2.3.3. Model development and performance evaluation
In this study, the new model for the estimation of PET is developed by GNSS-PWV and temperature. GNSS-PWV is similar to surface evapotranspiration, and temperature is a key parameter affecting the PET [54,56]. Six GNSS CORS stations and nearby weather stations were selected to estimate the PET (n = 2035). These data were divided into two groups for model development and performance evaluation. After that, the functional relationship among PET, PWV and temperature was analyzed to fit the model coefficients by 673 data (1/3) using multiple linear regression. Consequently, this paper proposed a revised potential evapotranspiration (RPET) model as Equation (5).
| RPET = f(PWV,T) = b0 + b1 × PWV + b2 × T | (5) |
where b0, b1 and b2 are the model coefficients, which can be estimated using multiple linear regression. PWV is the daily mean PWV (mm). T is the daily mean temperature (°C), and RPET is the daily potential evapotranspiration.
The performance of the proposed RPET model was evaluated using the 1362 other PET, PWV and temperature data (2/3). Performance evaluation is analyzed to know the reliability of the proposed model. The correlation coefficient (r), the root mean square error (RMSE), the RMSE-observations of the standard deviation ratio (RSR) and the Nash-Sutcliffe efficiency (NSE) were selected as statistical indicators to evaluate the strength of relationship and model performance in this study [71,72] as Equations (6), (7), (8), (9)).
| (6) |
| (7) |
| (8) |
| (9) |
where are the observed PET, the simulated PET, and the mean of observed PET data, respectively, and n is the total number of observations.
After the proposed RPET model had evaluated the performance, the estimation of PET was calculated for 11 other GNSS CORS stations with local meteorological data. These could apply the RPET model using GNSS-PWV and the temperature data. Finally, the outputs showed the daily PET of the 17 GNSS CORS stations in 2020 in the case study of Northeastern Thailand. Furthermore, the performance evaluation of the predicted RPET and other existing satellite data was studied to fit in context with the others proposed at different spatial scales and formulations. The Global Land Evaporation Amsterdam Model (GLEAM v3.2 b) and the European Centre for Medium-Range Weather Forecasts Reanalysis-5 (ERA5-Land) products were selected because of well performance in estimating the gridded PET [73]. Both products are gridded PET datasets, which are used to estimate the daily PET with spatial resolutions of 0.25° for GLEAM and 0.1° for ERA5-Land. Moreover, the Priestly-Taylor (PT) and Penman-Monteith (PM) approaches are used to estimate the PET of the GLEAM and ERA5-Land, respectively. The PET data of GLEAM (v3.2 b) was downloaded from the website (https://www.gleam.eu/) with daily temporal resolution, and the PET data of ERA5-Land was derived from the website with hourly temporal resolution (https://data.bris.ac.uk/data/dataset/qb8ujazzda0s2aykkv0oq0ctp). In this paper, the specific locations of three GNSS CORS stations (DSSK, LMDH, and TSSK) were used to extract the corresponding satellite pixels. The comparison of the different datasets with the daily PET estimated by PM model was evaluated the performance of the proposed model. In addition, the evaluation was conducted based on the correlation coefficient (r) and the estimated error (RMSE).
3. Results
3.1. PWV characteristics
Fig. 3 showed the GNSS-derived PWV between January and December 2020 from 17 stations in Northeastern Thailand. The time series of GNSS-PWV were averaged at the daily interval. The results showed that the PWV varied from 4.2 to 68.5 mm for 2020. The overall mean daily PWV was 42.9 mm day−1. The PWV showed fluctuating values throughout the year. The maximum PWV peaked in mid-May to mid-October (rainy season), and the minimum PWV occurred from mid-October to mid-May (winter and summer seasons). In addition, the PWV data were missing in some periods, which could be caused by the absence of GNSS observations and meteorological parameters. Therefore, the missing data were not used in the model development. Furthermore, the daily PWV at the TKK1 and DSNK stations were found to have relatively low PWV values (average PWV = 35.4 mm) compared to other stations. This is influenced by the elevation of the station location. The average PWV values decrease when the altitude rises [67]. However, the mean daily PWV was high (average PWV = 45.2 mm) at the LMDH, LNMA and TSSK stations with altitude decreases (less than 130 m). In addition, the other stations were shown relatively high PWV with 43.6 mm of average PWV, which include the AKSN, DACR, DBRM, DLEI, DNPM, DSSK, ENMA, LLEI, LNBP, LNKI, PCPM and TKK2 stations. Moreover, GNSS-PWV and surface evapotranspiration are related. Thus, GNSS-PWV is utilized for the estimation of PET. GNSS-PWV of six GNSS CORS stations were selected for developing the model and performance evaluation because of the sufficient data in these stations. In addition, the PWV of 11 different stations were used to estimate the PET of 11 other stations.
Fig. 3.
Daily precipitable water vapor at different GNSS CORS stations of Northeastern Thailand in 2020.
3.2. Revised potential evapotranspiration (RPET) model development and performance evaluation
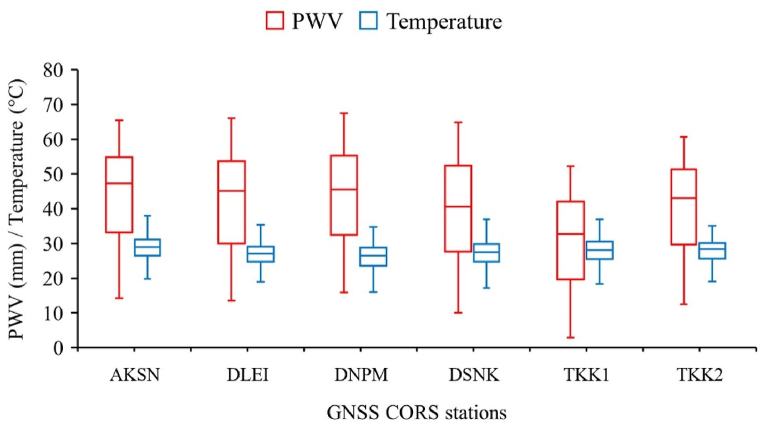
When some meteorological variables were missing because of the limited number of potential weather stations for daily PET estimation, the revised potential ET (RPET) model was developed in this study and evaluated the model performance. Six GNSS CORS of RSTD, six weather stations of HII and four weather stations of TMD were chosen from nearby GNSS CORS stations for model development. The PWV and temperature used in this study were shown in Fig. 4. The PWV varied at each individual station, which showed the ranges between 2.9 and 67.5 mm for PWV and 16.0–38.7 °C for temperature. The mean PWV and temperature was 40.1 mm and 27.5 °C, respectively. The relationship between PET, PWV and temperature was investigated at six GNSS CORS stations as depicted in Fig. 5a and b. It could be observed that a negative correlation between PWV and PET (r = −0.35), and a positive correlation between temperature and PET (r = 0.58). It was noted, however, that the contribution of PWV to PET was relatively small compared to that of temperature. Nevertheless, the PWV should not be overlooked in the estimation of PET, as it may play a role in determining the relative influence of the two variables. Therefore, multiple linear regression was used to analyze the model coefficients by the daily PET based on PM model, PWV and temperature data. The revised potential evapotranspiration (RPET) model is proposed in this paper with R2 = 0.83 as the following equation: RPET = −4.345 – 0.099 × PWV + 0.498 × T, where PWV is the mean precipitable water vapor during 6:00 to 12:00 h (mm) and T is the mean temperature during 6:00 to 12:00 h (°C). The RPET model, which is used to estimate PET in a specific region, may not be applicable or accurate in other geographic locations. Therefore, it is important to modify the PET estimation model when considering different regions.
Fig. 4.
Box plots of the PWV and temperature data at six selected stations for model development.
Fig. 5.
Relationship between (a) PWV and PET and (b) temperature and PET at six GNSS CORS stations of Northeastern Thailand in 2020.
Apart from the model development, the performance of the proposed RPET model was evaluated using other PET, PWV and temperature data (two-thirds). The time-series of the observed PM model and predicted RPET model for daily PET were plotted against the day of the year (DOY) at different GNSS CORS stations (Fig. 6a–f). The results revealed that the relationship between PET derived from the RPET and the PM models showed a strong correlation (r = 0.85) and good accuracy with RSR = 0.53 and NSE = 0.72. In addition, the statistical result found that the error of the RPET model was 0.97 mm day−1 as shown in Fig. 7 and Table 4. Therefore, the results confirmed that the proposed RPET model showed satisfactory performance and had great potential for estimating the daily PET of other regional stations.
Fig. 6.
Comparison of observed PM model and predicted RPET model time-series for daily PET at different GNSS CORS stations: (a) AKSN, (b) DLEI, (c) DNPM, (d) DSNK, (e) TKK1, and (f) TKK2.
Fig. 7.
Scatter plot of daily PET derived from the PM and RPET model.
Table 4.
Model performance of the RPET model.
| Number of Sample (n) | r | RMSE (mm d−1) | RSR | NSE | |
|---|---|---|---|---|---|
| Value | 1362 | 0.85 | 0.97 | 0.53 | 0.72 |
| Performance | – | strong | – | good | good |
3.3. Daily potential evapotranspiration estimation by RPET model
Fig. 8 showed the variation of daily PET from 17 GNSS CORS stations in Northeastern Thailand in 2020. Daily PET was evaluated from two methods. GNSS-PWV of six GNSS CORS stations were derived from the PM model (AKSN, DLEI, DNPM, DSNK, TKK1 and TKK2), whereas the PWV of 11 other GNSS CORS stations were estimated from the RPET model (DACR, DBRM, DSSK, ENMA, LLEI, LMDH, LNBP, LNKI, LNMA, PCPM and TSSK). The variation trends of daily PET from the RPET model showed similarities to the PM model. Therefore, the RPET model developed in this study was greatly suitable for estimating daily PET. The PET showed fluctuation throughout the year, which was affected by the seasonal variation [74] and elevation of GNSS CORS station locations [75,76]. These components directly affected the environmental and biological factors for PET estimation such as net radiation, vapor pressure deficit, surface conductance, leaf area index, air temperature and soil water content [77]. The maximum daily PET was 13.2 mm day−1, found in July at the TKK1 station. The minimum daily PET was 0.3 mm day−1, which occurred in March at the LMDH station. In addition, the overall mean daily PET was 5.4 mm day−1. The PET showed gradually increased from January to the highest value in April (summer) and then decreased to the lowest value in December (winter). Such results of PET were also similar to the findings of Vudhivanich and Zheng [35,63].
Fig. 8.
Daily potential evapotranspiration of 17 GNSS CORS stations in Northeastern Thailand.
To investigate the performance of the RPET model, the daily PET of three datasets (RPET model, GLEAM, and ERA5-Land) was compared as the input of the PM model at different GNSS CORS stations as shown in Fig. 9a–c. The results demonstrated that the PET values estimated by the RPET model showed relatively corresponding to the PM model, GLEAM and ERA5-Land. The PET values were high during the summer and winter seasons and low in the rainy season. However, both GLEAM and ERA5-Land products showed an underestimation of PET values in all stations. Fig. 10 showed the scatter plot of the three datasets against the PM model. The RPET model estimated PET was closer to the PM model than the other datasets. In addition, it had good performance with r = 0.80 and RMSE 1.06 mm day−1 (n = 1008, Fig. 10a) and performed greater than the ERA5-Land products (r = 0.74, RMSE = 1.73, n = 1008) and the GLEAM dataset (r = 0.69, RMSE = 2.57, n = 1008). However, the ERA5-Land products perform better than the GLEAM dataset in term of r and RMSE values as shown in Fig. 10b and c.
Fig. 9.
Comparison of daily PET predicted by RPET model, GLEAM, ERA5-Land and PM model at three GNSS CORS stations: (a) DSSK, (b) LMDH, and (c) TSSK.
Fig. 10.
Scatter plot of daily PET derived from predicted RPET (a), GLEAM (b) and ERA5-Land (c) datasets against the PM model.
4. Discussions
In this study, the revised PET (RPET) model is proposed to overcome the PET estimation in the case of lacking meteorological data in some weather stations. The RPET model is evaluated by GNSS-based PWV and temperature since both parameters are closely related to surface evapotranspiration [54,56]. Therefore, the GNSS-PWV were evaluated as the initial value for the RPET model and then confirmed the variation trends by comparing the other studies in different years. The average PWV was high in mid-May to mid-October (rainy season) and low in mid-October to mid-May (summer and winter seasons); a similar finding was reported by Meunram and Satirapod [57], and Buntoung et al. [78]. Meunram and Satirapod reported that the amount of PWV increased between the day of year 100–150 because of the effect of transforming the season from the northeast monsoon season to the southwest monsoon season. However, a low amount of PWV was shown in the summer and winter seasons (dry season) due to the influence of the northeast monsoon that resulted in the cool and dry weather [57].
In the PET estimation model, GNSS-PWV has been applied rapidly for PET estimation and drought monitoring. Several researchers developed models for estimating PET and drought monitoring. Zhao et al. proposed the revised Thornwaite (RTH) and a high-precision PET (HPET) models using the PWV and temperature data for calculating the PET and improving the drought monitoring index over the Loess Plateau of China [55,56]. In addition, Ma et al. developed the site-based revised Thornwaite (S-RTH) model and an RTH model over China (C-RTH) with high spatial resolution over the whole of China [54]. The mentioned models used the PET difference or ET residual as reference data to develop the models. The PET difference was calculated by subtraction of the TH and PM models to overcome the low precision of the Thornwaite (TH) model and the several input parameters of the Penman-Monteith (PM) model [[54], [55], [56]]. These previous models have shown satisfactory performance for estimating monthly PET difference in China with the average root mean square (RMS) of 12.3 mm for the RTH model, 10.7 mm for the S-RTH model and 8.0 mm for the HPET model. However, the previous models were proposed in the specific GNSS CORS stations and related to the height of each GNSS CORS station. As a result, the PET estimation model should be improved when the geographical locations are changed [55]. This study proposed a new approach named the revised potential evapotranspiration (RPET) model to estimate daily PET for tropical regions using GNSS-PWV and temperature, which is a similar approach to the prior studies. The previous finding relied on the PET difference to develop the models, while this study utilized only the PET derived from the PM model as reference data to address the issue of missing meteorological parameters. The study found a moderate positive correlation between PET and temperature and a weak correlation between PET and GNSS-PWV. However, the use of both GNSS-PWV and temperature showed good performance for estimating daily PET with the RMSE of 1.06 mm day−1 when compared to the PM model.
To evaluate the RPET model performance in comparison to the others proposed at multiple scales and formulations, the predicted RPET and other available satellite data were compared. Although both GLEAM and ERA-5 Land datasets could estimate the gridded PET with high temporal resolution and moderate accuracy, these gridded PET datasets may not ensure reliability to represent the specific geographical locations. The influences of heterogeneity on the PET grid data and the restrictions of geography, climate and satellite inversion algorithms could be the main cause of the uncertainty in the gridded PET estimation [79,80]. Therefore, a grid-based model should be developed using the proposed RPET model as ground-based GNSS observations-driven method for improving the accuracy of gridded PET datasets in the regional scale.
5. Conclusion
In this research, the daily potential evapotranspiration (PET) was estimated through Precipitable Water Vapor (PWV) derived from the GNSS CORS in the case study of the northeast region of Thailand. The PWV values were obtained by analyzing GNSS CORS, which was evaluated by surface pressure, temperature, and humidity. The PET was assessed and considered as reference data using the PM model by humidity, temperature, wind speed and solar radiation in some meteorological stations with sufficient data. The revised PET (RPET) model was developed to fit the model coefficients by the PWV, PET and temperature data using multiple linear regression analysis. The performance of the proposed model was evaluated using statistical indicators and then calculated the daily PET of other stations by the RPET model. The results reveal that the RPET model was satisfactory for estimating the daily PET with an error of 0.97 mm day−1. The PM model-based daily PET showed similar trends compared with the estimated PET by the RPET model. These results indicated that the proposed RPET model has the potential to evaluate the daily PET with high temporal resolution in all weather conditions. This technique can overcome the meteorological data constraint in some weather stations [34,81,82]. Moreover, it performs very well using only the GNSS-PWV and temperature data when compared to the PM method with the correlation coefficient higher than 0.85. However, such a model can be utilized for specific GNSS CORS stations. The application of this model for spatial PET is recommended. In a further study, the grid-based PET can be analyzed to obtain high spatial and temporal resolutions by the interpolation and extrapolation techniques [80,83]. Additionally, it is possible to apply the presented model in various research areas such as climate research, agricultural water management, irrigation scheduling and drought assessment. The study on agricultural drought indices can be performed based on the proposed model for improving the accuracy and spatial-temporal resolutions of drought monitoring. Furthermore, more datasets of GNSS-PWV and meteorological data are required to develop near real-time applications for flood and drought monitoring [53,84]. Therefore, the developed model is a potential alternative approach to estimate the daily PET and beneficial to climate and agricultural research works for alleviating the adverse impacts by global warming and extreme weather events.
Author contribution statement
Piyanan Pipatsitee; Sarawut Ninsawat: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Nitin Kumar Tripathi; Mohanasundaram Shanmugam: Conceived and designed the experiments; Analyzed and interpreted the data.
Patsharawadee Chitsutti: Contributed reagents, materials, analysis tools or data.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors would like to acknowledge Remote Sensing and GIS Program, Asian Institute of Technology (AIT), the Royal Thai Survey Development, the Hydro-Informatics Institute, and the Thai Meteorological Department for providing the GNSS CORS and meteorological data for this research study.
Contributor Information
Piyanan Pipatsitee, Email: st121454@ait.ac.th.
Sarawut Ninsawat, Email: sarawutn@ait.ac.th.
References
- 1.Novak V. Springer; Dordrecht: 2012. Evapotranspiration in the Soil-Plant-Atmosphere System Progress in Soil Science. [DOI] [Google Scholar]
- 2.Allen R.G., Pereira L.S., Raes D., Smith M. 1998. FAO Irrigation and Drainage Paper No. 56 - Crop Evapotranspiration, Rome, Italy. [Google Scholar]
- 3.Macek U., Bezak N., Sraj M. Reference evapotranspiration changes in Slovenia, Europe. Agric. For. Meteorol. 2018;260–261:183–192. doi: 10.1016/j.agrformet.2018.06.014. [DOI] [Google Scholar]
- 4.Bennett D.R., Harms T.E. Crop yield and water requirement relationships for major irrigated crops in Southern Alberta. Can. Water Resour. J. 2011;36:159–170. doi: 10.4296/cwrj3602853. [DOI] [Google Scholar]
- 5.Davis S.L., Dukes M.D. Irrigation scheduling performance by evapotranspiration-based controllers. Agric. Water Manag. 2010;98:19–28. doi: 10.1016/j.agwat.2010.07.006. [DOI] [Google Scholar]
- 6.Wu R., Liu Y., Xing X. Evaluation of evapotranspiration deficit index for agricultural drought monitoring in North China. J. Hydrol. 2021;596 doi: 10.1016/j.jhydrol.2021.126057. [DOI] [Google Scholar]
- 7.Wang Q., Zeng J., Qi J., Zhang X., Zeng Y., Shui W., Xu Z., Zhang R., Wu X., Cong J. A multi-scale daily SPEI dataset for drought characterization at observation stations over mainland China from 1961 to 2018. Earth Syst. Sci. Data. 2021;13:331–341. doi: 10.5194/essd-13-331-2021. [DOI] [Google Scholar]
- 8.Vicente-Serrano S.M., Begueria S., Lopez-Moreno J.I. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 2010;23:1696–1718. doi: 10.1175/2009JCLI2909.1. [DOI] [Google Scholar]
- 9.Anapalli S.S., Fisher D.K., Reddy K.N., Wagle P., Gowda P.H., Sui R. Quantifying soybean evapotranspiration using an eddy covariance approach. Agric. Water Manag. 2018;209:228–239. doi: 10.1016/j.agwat.2018.07.023. [DOI] [Google Scholar]
- 10.Anapalli S.S., Fisher D.K., Pinnamaneni S.R., Reddy K.N. Quantifying evapotranspiration and crop coefficients for cotton (Gossypium hirsutum L.) using an eddy covariance approach. Agric. Water Manag. 2020;233 doi: 10.1016/j.agwat.2020.106091. [DOI] [Google Scholar]
- 11.Song X., Lu F., Xiao W., Zhu K., Zhou Y., Xie Z. Performance of 12 reference evapotranspiration estimation methods compared with the Penman–Monteith method and the potential influences in northeast China. Meteorol. Appl. 2019;26:83–96. doi: 10.1002/met.1739. [DOI] [Google Scholar]
- 12.Herman M.R., Nejadhashemi A.P., Abouali M., Hernandez-Suarez J.S., Daneshvar F., Zhang Z., Anderson M.C., Sadeghi A.M., Hain C.R., Sharifi A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018;556:39–49. doi: 10.1016/j.jhydrol.2017.11.009. [DOI] [Google Scholar]
- 13.Wilson K.B., Hanson P.J., Mulholland P.J., Baldocchi D.D., Wullschleger S.D. A comparison of methods for determining forest evapotranspiration and its components: sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001;106:153–168. doi: 10.1016/S0168-1923(00)00199-4. [DOI] [Google Scholar]
- 14.Moorhead J.E., Marek G.W., Gowda P.H., Lin X., Colaizzi P.D., Evett S.R., Kutikoff S. Evaluation of evapotranspiration from eddy covariance using large weighing lysimeters. Agronomy. 2019;9:1–17. doi: 10.3390/agronomy9020099. [DOI] [Google Scholar]
- 15.Liu S.M., Xu Z.W., Zhu Z.L., Jia Z.Z., Zhu M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013;487:24–38. doi: 10.1016/j.jhydrol.2013.02.025. [DOI] [Google Scholar]
- 16.Degano M.F., Rivas R.E., Sanchez J.M., Carmona F., Niclos R. 2018 IEEE Bienn. Congr. Argentina, ARGENCON 2018. IEEE; 2018. Assessment of the potential evapotranspiration MODIS product using ground measurements in the pampas; pp. 1–5. [DOI] [Google Scholar]
- 17.Knipper K.R., Kustas W.P., Anderson M.C., Alfieri J.G., Prueger J.H., Hain C.R., Gao F., Yang Y., McKee L.G., Nieto H., Hipps L.E., Alsina M.M., Sanchez L. Evapotranspiration estimates derived using thermal-based satellite remote sensing and data fusion for irrigation management in California vineyards. Irrigat. Sci. 2019;37:431–449. doi: 10.1007/s00271-018-0591-y. [DOI] [Google Scholar]
- 18.He M., Kimball J.S., Yi Y., Running S.W., Guan K., Moreno A., Wu X., Maneta M. Satellite data-driven modeling of field scale evapotranspiration in croplands using the MOD16 algorithm framework. Remote Sens. Environ. 2019;230 doi: 10.1016/j.rse.2019.05.020. [DOI] [Google Scholar]
- 19.Cao M., Wang W., Xing W., Wei J., Chen X., Li J., Shao Q. Multiple sources of uncertainties in satellite retrieval of terrestrial actual evapotranspiration. J. Hydrol. 2021;601 doi: 10.1016/j.jhydrol.2021.126642. [DOI] [Google Scholar]
- 20.Salazar-Martinez D., Holwerda F., Holmes T.R.H., Yepez E.A., Hain C.R., Alvarado-Barrientos S., Angeles-Perez G., Arredondo-Moreno T., Delgado-Balbuena J., Figueroa-Espinoza B., Garatuza-Payan J., Gonzalez del Castillo E., Rodriguez J.C., Rojas-Robles N.E., Uuh-Sonda J.M., Vivoni E.R. Evaluation of remote sensing-based evapotranspiration products at low-latitude eddy covariance sites. J. Hydrol. 2022;610 doi: 10.1016/j.jhydrol.2022.127786. [DOI] [Google Scholar]
- 21.Ruhoff A.L., Paz A.R., Aragao L.E.O.C., Mu Q., Malhi Y., Collischonn W., Rocha H.R., Running S.W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Hydrol. Sci. J. 2013;58:1658–1676. doi: 10.1080/02626667.2013.837578. [DOI] [Google Scholar]
- 22.Moran M.S., Inoue Y., Barnes E.M. Opportunities and limitations for image-based remote sensing in precision crop management. Remote Sens. Environ. 1997;61:319–346. doi: 10.1016/S0034-4257(97)00045-X. [DOI] [Google Scholar]
- 23.Li X., Long D., Han Z., Scanlon B.R., Sun Z., Han P., Hou A. Evapotranspiration estimation for Tibetan plateau headwaters using conjoint terrestrial and atmospheric water balances and multisource remote sensing. Water Resour. Res. 2019;55:8608–8630. doi: 10.1029/2019WR025196. [DOI] [Google Scholar]
- 24.Wang Y., Li R., Hu J., Wang X., Kabeja C., Min Q., Wang Y. Evaluations of MODIS and microwave based satellite evapotranspiration products under varied cloud conditions over East Asia forests. Remote Sens. Environ. 2021;264 doi: 10.1016/j.rse.2021.112606. [DOI] [Google Scholar]
- 25.Kumar U., Srivastava A., Kumari N., Rashmi, Sahoo B., Chatterjee C., Raghuwanshi N.S. Evaluation of spatio-temporal evapotranspiration using satellite-based approach and lysimeter in the agriculture dominated catchment. J. Indian Soc. Remote Sens. 2021;49:1939–1950. doi: 10.1007/s12524-021-01367-w. [DOI] [Google Scholar]
- 26.Running S.W., Mu Q., Zhao M., Moreno A. User's guide MODIS global terrestrial evapotranspiration (ET) product (MOD16A2/A3 and year-end gap-filled mod16a2gf/A3GF) 2019. https://lpdaac.usgs.gov/documents/494/MOD16_User_Guide_V6.pdf 1–37.
- 27.Mu Q., Heinsch F.A., Zhao M., Running S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007;106:519–536. doi: 10.1016/j.rse.2006.07.007. [DOI] [Google Scholar]
- 28.Lang D., Zheng J., Shi J., Liao F., Ma X., Wang W., Chen X., Zhang M. vol. 9. 2017. (A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China, Water (Switzerland)). [DOI] [Google Scholar]
- 29.Li Y., Qin Y., Rong P. Evolution of potential evapotranspiration and its sensitivity to climate change based on the Thornthwaite, Hargreaves, and Penman–Monteith equation in environmental sensitive areas of China. Atmos. Res. 2022;273 doi: 10.1016/j.atmosres.2022.106178. [DOI] [Google Scholar]
- 30.Akumaga U., Alderman P.D. Comparison of penman–monteith and priestley-Taylor evapotranspiration methods for crop modeling in Oklahoma. Agron. J. 2019;111:1171–1180. doi: 10.2134/agronj2018.10.0694. [DOI] [Google Scholar]
- 31.Ficklin D.L., Letsinger S.L., Gholizadeh H., Maxwell J.T. Incorporation of the penman-monteith potential evapotranspiration method into a palmer drought severity index tool. Comput. Geosci. 2015;85:136–141. doi: 10.1016/j.cageo.2015.09.013. [DOI] [Google Scholar]
- 32.Zhou J., Wang Y., Su B., Wang A., Tao H., Zhai J., Kundzewicz Z.W., Jiang T. Choice of potential evapotranspiration formulas influences drought assessment: a case study in China. Atmos. Res. 2020;242 doi: 10.1016/j.atmosres.2020.104979. [DOI] [Google Scholar]
- 33.Majidi M., Alizadeh A., Vazifedoust M., Farid A., Ahmadi T. Analysis of the effect of missing weather data on estimating daily reference evapotranspiration under different climatic conditions. Water Resour. Manag. 2015;29:2107–2124. doi: 10.1007/s11269-014-0782-0. [DOI] [Google Scholar]
- 34.Sentelhas P.C., Gillespie T.J., Santos E.A. Evaluation of FAO Penman-Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010;97:635–644. doi: 10.1016/j.agwat.2009.12.001. [DOI] [Google Scholar]
- 35.Vudhivanich V. Monthly potential evapotranspiration of Thailand. Kasetsart J./Nat. Sci. 1996;30:392–399. https://li01.tci-thaijo.org/index.php/anres/article/view/241176 [Google Scholar]
- 36.Kosa P., Pongput K. Evaluation of spatial and temporal reference evapotranspiration in the chao phraya river basin, Thailand. Sci. Asia. 2007;33:245–252. doi: 10.2306/scienceasia1513-1874.2007.33.245. [DOI] [Google Scholar]
- 37.Homdee T., Pongput K., Kanae S. A comparative performance analysis of three standardized climatic drought indices in the Chi River basin, Thailand. Agric. Nat. Resour. 2016;50:211–219. doi: 10.1016/j.anres.2016.02.002. [DOI] [Google Scholar]
- 38.Jin S., Cardellach E., Xie F. 2014. GNSS Remote Sensing: Theory, Methods and Applications. [DOI] [Google Scholar]
- 39.Ogaja C.A. 2022. Introduction to GNSS Geodesy. [DOI] [Google Scholar]
- 40.Bevis M., Businger S., Chiswell S. GPS meteorology: mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994;33:379–386. [Google Scholar]
- 41.Tregoning P., Boers R., O'Brien D., Hendy M. Accuracy of absolute Precipitable Water vapor estimates from GPS observations. J. Geophys. Res. Atmos. 1998;103:28701–28710. doi: 10.1029/98JD02516. [DOI] [Google Scholar]
- 42.Liang H., Cao Y., Wan X., Xu Z., Wang H., Hu H. Meteorological applications of precipitable water vapor measurements retrieved by the national GNSS network of China, Geod. Geodyn. 2015;6:135–142. doi: 10.1016/j.geog.2015.03.001. [DOI] [Google Scholar]
- 43.Lu C., Li X., Ge M., Heinkelmann R., Nilsson T., Soja B., Dick G., Schuh H. Estimation and evaluation of real-time precipitable water vapor from GLONASS and GPS. GPS Solut. 2016;20:703–713. doi: 10.1007/s10291-015-0479-8. [DOI] [Google Scholar]
- 44.Awange J.L. Springer Berlin; Heidelberg: 2011. Environmental Monitoring Using GNSS. [DOI] [Google Scholar]
- 45.Zumberge J.F., Heflin M.B., Jefferson D.C., Watkins M.M., Webb F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth. 1997;102:5005–5017. doi: 10.1029/96jb03860. [DOI] [Google Scholar]
- 46.Charoenphon C., Satirapod C. Improving the accuracy of real-time precipitable water vapour using country-wide meteorological model with precise point positioning in Thailand. J. Spat. Sci. 2022;67:313–329. doi: 10.1080/14498596.2020.1758969. [DOI] [Google Scholar]
- 47.Kouba J.A.N., Heroux P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001;5:12–28. [Google Scholar]
- 48.Bordi I., Raziei T., Pereira L.S., Sutera A. Ground-based GPS measurements of precipitable water vapor and their usefulness for hydrological applications, water resour. OR Manag. 2015;29:471–486. doi: 10.1007/s11269-014-0672-5. [DOI] [Google Scholar]
- 49.Yeh T.K., Shih H.C., Wang C.S., Choy S., Chen C.H., Hong J.S. Determining the precipitable water vapor thresholds under different rainfall strengths in Taiwan. Adv. Space Res. 2018;61:941–950. doi: 10.1016/j.asr.2017.11.002. [DOI] [Google Scholar]
- 50.Zhao Q., Yao Y., Yao W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Sol. Terr. Phys. 2018;167:124–133. doi: 10.1016/j.jastp.2017.11.013. [DOI] [Google Scholar]
- 51.Yao Y., Shan L., Zhao Q. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017;7:1–11. doi: 10.1038/s41598-017-12593-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Valeo C., Skone S.H., Ho C.L.I., Poon S.K.M., Shrestha S.M. Estimating snow evaporation with GPS derived precipitable water vapour. J. Hydrol. 2005;307:196–203. doi: 10.1016/j.jhydrol.2004.10.009. [DOI] [Google Scholar]
- 53.Ziv S.Z., Reuveni Y. Flash floods prediction using precipitable water vapor derived from GPS tropospheric path delays over the eastern mediterranean. IEEE Trans. Geosci. Rem. Sens. 2022;60:1–17. doi: 10.1109/TGRS.2022.3201146. [DOI] [Google Scholar]
- 54.Ma X., Zhao Q., Yao Y., Yao W. A novel method of retrieving potential ET in China. J. Hydrol. 2021;598 doi: 10.1016/j.jhydrol.2021.126271. [DOI] [Google Scholar]
- 55.Zhao Q., Sun T., Zhang T., He L., Zhang Z., Shen Z., Xiong S. High-precision potential evapotranspiration model using GNSS observation. Rem. Sens. 2021;13 doi: 10.3390/rs13234848. [DOI] [Google Scholar]
- 56.Zhao Q., Ma X., Yao W., Liu Y., Du Z., Yang P., Yao Y. Improved drought monitoring index using GNSS-derived precipitable water vapor over the Loess Plateau Area. Sensors. 2019;19:3–5. doi: 10.3390/s19245566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Meunram P., Satirapod C. Spatial variation of precipitable water vapor derived from GNSS CORS in Thailand. Geod. Geodyn. 2019;10:140–145. doi: 10.1016/j.geog.2019.01.003. [DOI] [Google Scholar]
- 58.Trakolkul C., Satirapod C. Variations of precipitable water vapor using GNSS CORS in Thailand. Surv. Rev. 2021;53:90–96. doi: 10.1080/00396265.2020.1713611. [DOI] [Google Scholar]
- 59.Satirapod C., Anonglekha S., Choi Y.S., Lee H.K. Performance assessment of GPS-sensed precipitable water vapor using IGS ultra-rapid orbits: a preliminary study in Thailand. Eng. J. 2011;15:1–8. doi: 10.4186/ej.2011.15.1.1. [DOI] [Google Scholar]
- 60.Mitsuchi M., Wichaidit P., Jeungnijnirund S. Soils of the northeast plateau, Thailand. 1989. https://www.jircas.go.jp/sites/default/files/publication/techtarc/techtarc25-_1-66.pdf
- 61.Hydro-Informatics Institute Thailand water situation in 2018. 2018. https://tiwrm.hii.or.th/current/YearlyReport2018/rain.html (accessed December 8, 2022)
- 62.Thai Meteorological Department The climate of Thailand (1981-2010) 2015. http://climate.tmd.go.th/content/file/75 1–7. (accessed December 8, 2022)
- 63.Zheng C., Jia L., Hu G., Lu J. Earth observations-based evapotranspiration in Northeastern Thailand. Rem. Sens. 2019;11 doi: 10.3390/rs11020138. [DOI] [Google Scholar]
- 64.Herrera A.M., Suhandri H.F., Realini E., Reguzzoni M., de Lacy M.C., goGPS open-source MATLAB software. GPS Solut. 2016;20:595–603. doi: 10.1007/s10291-015-0469-x. [DOI] [Google Scholar]
- 65.Realini E., Reguzzoni M. GoGPS: open source software for enhancing the accuracy of low-cost receivers by single-frequency relative kinematic positioning. Meas. Sci. Technol. 2013;24 doi: 10.1088/0957-0233/24/11/115010. [DOI] [Google Scholar]
- 66.Liu J., Chen X., Sun J., Liu Q. An analysis of GPT2/GPT2w+Saastamoinen models for estimating zenith tropospheric delay over Asian area. Adv. Space Res. 2017;59:824–832. doi: 10.1016/j.asr.2016.09.019. [DOI] [Google Scholar]
- 67.Ssenyunzi R.C., Oruru B., D’ujanga F.M., Realini E., Barindelli S., Tagliaferro G., von Engeln A., van de Giesen N. Performance of ERA5 data in retrieving precipitable water vapour over east african tropical region. Adv. Space Res. 2020;65:1877–1893. doi: 10.1016/j.asr.2020.02.003. [DOI] [Google Scholar]
- 68.Wang E., Yang T., Wang Z., Zhang Y., Guo J., Shu W., Qu P. Performance evaluation of precise point positioning for beidou-3 b1c/b2a signals in the global range. Sensors. 2021;21 doi: 10.3390/s21175780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Saastamoinen J. Contributions to the theory of atmospheric refraction. Bull. Geod. 1973;107:13–34. doi: 10.1007/BF02522083. [DOI] [Google Scholar]
- 70.baba shaeb Kannemadugu H., Ranganathan K., Gharai B., Seshasai M.V.R. GNSS-GPS derived integrated water vapor and performance assessment of ERA-5 data over India. J. Atmos. Sol. Terr. Phys. 2022;227 doi: 10.1016/j.jastp.2021.105807. [DOI] [Google Scholar]
- 71.Moriasi D.N., Arnold J.G., Van Liew M.W., Bingner R.L., Harmel R.D., Veith T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE (Am. Soc. Agric. Biol. Eng.) 2007;50:885–900. doi: 10.13031/2013.23153. [DOI] [Google Scholar]
- 72.Schober P., Schwarte L.A. Correlation coefficients: appropriate use and interpretation. Anesth. Analg. 2018;126:1763–1768. doi: 10.1213/ANE.0000000000002864. [DOI] [PubMed] [Google Scholar]
- 73.Wang C., Si J., Li Z., Zhao C., Jia B., Celestin S., He X., Zhou D., Qin J., Zhu X. Evaluation of three gridded potential evapotranspiration datasets for streamflow simulation in three inland river basins in the arid Hexi Corridor, Northwest China. J. Hydrol. Reg. Stud. 2022;44 doi: 10.1016/j.ejrh.2022.101234. [DOI] [Google Scholar]
- 74.Tanaka N., Kume T., Yoshifuji N., Tanaka K., Takizawa H., Shiraki K., Tantasirin C., Tangtham N., Suzuki M. A review of evapotranspiration estimates from tropical forests in Thailand and adjacent regions. Agric. For. Meteorol. 2008;148:807–819. doi: 10.1016/j.agrformet.2008.01.011. [DOI] [Google Scholar]
- 75.Goulden M.L., Anderson R.G., Bales R.C., Kelly A.E., Meadows M., Winston G.C. Evapotranspiration along an elevation gradient in California's Sierra Nevada. J. Geophys. Res. Biogeosciences. 2012;117:1–13. doi: 10.1029/2012JG002027. [DOI] [Google Scholar]
- 76.Hu Z., Wang G., Sun X., Zhu M., Song C., Huang K., Chen X. Spatial-temporal patterns of evapotranspiration along an elevation gradient on mount gongga, southwest China, water resour. Res. 2018;54:4180–4192. doi: 10.1029/2018WR022645. [DOI] [Google Scholar]
- 77.Wang Y., Zou Y., Cai H., Zeng Y., He J., Yu L., Zhang C., Saddique Q., Peng X., Siddique K.H.M., Yu Q., Su Z. Seasonal variation and controlling factors of evapotranspiration over dry semi-humid cropland in Guanzhong Plain, China. Agric. Water Manag. 2022;259 doi: 10.1016/j.agwat.2021.107242. [DOI] [Google Scholar]
- 78.Buntoung S., Janjai S., Pariyothon J., Nunez M. Distribution of precipitable water over Thailand using mtsat-1r satellite data. Sci. Eng. Heal. Stud. 2021;15:1–6. [Google Scholar]
- 79.Jiang S., Wei L., Ren L., Xu C.Y., Zhong F., Wang M., Zhang L., Yuan F., Liu Y. Utility of integrated IMERG precipitation and GLEAM potential evapotranspiration products for drought monitoring over mainland China. Atmos. Res. 2021;247 doi: 10.1016/j.atmosres.2020.105141. [DOI] [Google Scholar]
- 80.Shanmugam M., Mekonnen M.M., Ray C. Grid-based model for estimating evapotranspiration rates of heterogeneous Land surface. J. Irrigat. Drain. Eng. 2020;146:1–12. doi: 10.1061/(asce)ir.1943-4774.0001436. [DOI] [Google Scholar]
- 81.Djaman K., O'Neill M., Diop L., Bodian A., Allen S., Koudahe K., Lombard K. Evaluation of the Penman-Monteith and other 34 reference evapotranspiration equations under limited data in a semiarid dry climate. Theor. Appl. Climatol. 2019;137:729–743. doi: 10.1007/s00704-018-2624-0. [DOI] [Google Scholar]
- 82.Koudahe K., Djaman K., Adewumi J.K. Evaluation of the Penman–Monteith reference evapotranspiration under limited data and its sensitivity to key climatic variables under humid and semiarid conditions. Model. Earth Syst. Environ. 2018;4:1239–1257. doi: 10.1007/s40808-018-0497-y. [DOI] [Google Scholar]
- 83.Chavez J.L., Neale C.M.U., Prueger J.H., Kustas W.P. Daily evapotranspiration estimates from extrapolating instantaneous airborne remote sensing et values. Irrigat. Sci. 2008;27:67–81. doi: 10.1007/s00271-008-0122-3. [DOI] [Google Scholar]
- 84.Ninsawat S., Chitsutti P., Chaudhary S., Jindasee P., Khamyai T. Development of near real-time PWV estimation System for monitoring the meteorological events in Thailand. Int. J. Geoinformatics. 2022;18:38–53. doi: 10.52939/ijg.v18i3.2201. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.