Hydration layer structure modulates superlubrication by trivalent La³⁺ electrolytes

Abstract

Water-based lubricants provide lubrication of rubbing surfaces in many technical, biological, and physiological applications. The structure of hydrated ion layers adsorbed on solid surfaces that determine the lubricating properties of aqueous lubricants is thought to be invariable in hydration lubrication. However, we prove that the ion surface coverage dictates the roughness of the hydration layer and its lubricating properties, especially under subnanometer confinement. We characterize different hydration layer structures on surfaces lubricated by aqueous trivalent electrolytes. Two superlubrication regimes are observed with friction coefficients of 10⁻⁴ and 10⁻³, depending on the structure and thickness of the hydration layer. Each regime exhibits a distinct energy dissipation pathway and a different dependence to the hydration layer structure. Our analysis supports the idea of an intimate relationship between the dynamic structure of a boundary lubricant film and its tribological properties and offers a framework to study such relationship at the molecular level.

The structure of the hydration shell of adsorbed ions dictates their lubricating properties.

INTRODUCTION

Lubrication of rubbing surfaces using water-based lubricants has a substantial technological value due to the outstanding lubricating properties of water (1, 2) and a potential environmental impact by decreasing our dependence on synthetic lubricating oils (3). Lubrication mediated by hydration layers is known as hydration lubrication (HL) (4–6) and is often considered as one of the most efficient lubrication mechanism found in nature to achieve superlubrication (7–9), that is, lubrication with friction coefficients lower than 10⁻³. Multiple technical fields such as biomedical materials (10), biolubricating materials (11), marine antifouling coatings (12), anti-adhesive coatings (13), and other engineering applications (14–16) rely on highly hydrated interfaces.

It is agreed that the core concept defining the HL mechanism is the presence of a surface-bound hydration layer, which can support high normal pressures and exhibits low shear resistance under compression, at the macroscopic (17, 18) or microscopic (4, 19, 20) scales. HL is known to be sensitive to surface commensuration (21) and, therefore, to the crystallographic properties of the surfaces (22, 23). However, establishing a relationship between the boundary hydration layer structure and its associated tribological properties has still been elusive. The frictional energy dissipation mechanism of HL has been extensively studied in the presence of monovalent ions as hydrophilic moieties promoting the hydration layer formation (19, 24, 25) and, to lesser extent, in the presence of multivalent ions (9). It is generally accepted that the structure of hydrated ions remains constant in HL (4, 24) simply because the effect of salt concentration on lubricating properties was largely neglected. Strongly coordinated water layer and homogeneous interfacial water structure between two charged surfaces were reported to support hydration force and ease sliding friction by sum frequency generation spectroscopy (2, 26). With ionic strength increasing, an accumulation of ions at the interface was more effective at disrupting the hydrogen bond network, resulting in a breakdown in the ordered interfacial water and a decrease in water coordination, which led to a notable change of the interfacial lubrication properties (26–29). Recent imaging studies using frequency-modulation atomic force microscopy (AFM) have demonstrated the existence of different types of adsorbed hydrated structures depending on ion concentrations (30–32). However, analyzing the structure of a single hydrated ion at the atomic scale (33), especially under subnanometer confinement, still remains challenging.

To address these challenges, we conducted a nanoscale tribological study of aqueous solutions of La³⁺ ions at concentrations ranging from 25 to 2000 mM using the surface force apparatus (SFA) complemented with molecular dynamics (MD) simulations and high-resolution AFM (HR-AFM) imaging. We identified two different lubrication regimes corresponding to different hydration layer structures. In each regime, the energy dissipation mechanism was characterized and linked to the hydration layer structure. These evidences confirm that ion concentration is a strong determinant of the hydration layer structure, confirming their central role in tribological properties under subnanometer confinement. The impact of the hydration layer structure was evident only when the boundary film thickness was less than a nanometer thick, well in the regime where frictional energy dissipation is described as a rate-activated process.

RESULTS

Boundary superlubrication in the presence of trivalent hydration layers

Evidence of a hydration layer induced by the adsorption of La³⁺ ions on mica surfaces was obtained by measuring the interaction forces between two facing mica surfaces. The normal interaction force profiles, F_n/R, versus the separation distance, D, between two surfaces positioned in a cross-cylindrical configuration (radius of curvature R ≈ 2 cm) are shown in Fig. 1A and figs. S1 and S2 at different concentrations of La(NO₃)₃ salt. In the long-range regime (D = 5 to 50 nm), a repulsive exponentially decaying force is observed. The characteristic decay length of this repulsive force, λ_d, deviates notably from the theoretical Debye length, λ_D, especially at high electrolyte concentrations (λ_d = 3.1 ± 0.7 nm and λ_D = 0.78 nm at C_s = 25 mM; λ_d = 10.5 ± 1.1 nm and λ_D = 0.07 nm at C_s = 2 M; see section S1), a phenomenon that has been explained by the presence of strong ion correlation at high concentrations (16, 34, 35). Previous studies on monovalent ions showed that λ_d/λ_D ~ (d/λ_D)³ at high concentrations where d/λ_D > 1 (d being the ion diameter) while λ_d ≈ λ_D at low concentrations where d/λ_D < 1 (34, 35). These reports showed that in monovalent electrolyte solutions, the critical concentration delimiting these two regimes is around 1 M, while in pure protic and aprotic ionic liquids, the critical concentration was below 0.7 M. Our data show that in trivalent electrolyte solutions, the frontier is situated below 25 mM. To confirm this difference, we carried out additional experiments and compiled the results with reported values obtained from the literature, as shown in fig. S3. The compilation shows that the decay length decreased monotonically with increasing ion concentration because of effective screening of surface charges over short distances at dilute electrolyte solutions at C_s < 10 mM where d/λ_D = 1.2 (which is close to the transition observed for monovalent ions). However, at C_s > 10 mM, the decay length increased anomalously with increasing ion concentration. The data reported in monovalent electrolyte and the present compilation in trivalent electrolyte demonstrate that the transition concentration appears to depend on the electrolyte valency but the transition point at d/λ_D ≈ 1 is still preserved.

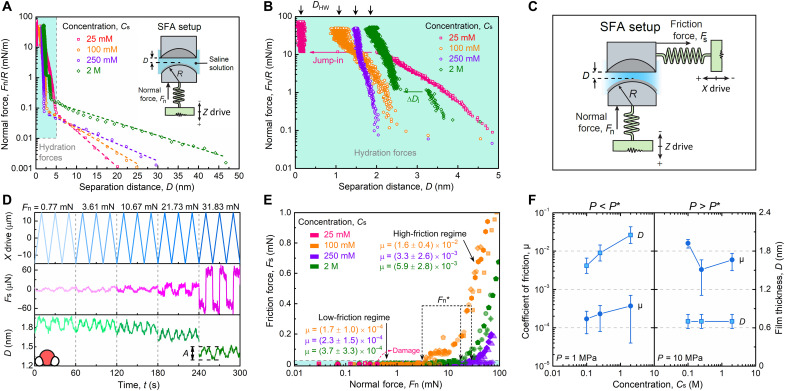
Fig. 1. Hydration forces and lubrication regimes in lanthanide ion solutions.

(A) Normal force profile between two curved mica surfaces across La(NO₃)₃ solutions at 25 mM, 100 mM, 250 mM, and 2 M concentrations. The dashed curves are the exponential fitting, F_n/R ~ exp(−λ_d⁻¹ D), of the long-range electrostatic repulsion data, with the decay length, λ_d, of 3.3, 4.5, 6.3, and 10.7 nm with increasing concentrations. The inset represents the SFA setup for normal force measurement. The maximum applied force F_n/R in (A) was smaller than 80 mN/m, which corresponds to F_n < 1.6 mN in the tribological tests. (B) Magnification of the blue area in (A) highlighting the short-range hydration repulsion forces. The experimental decay length of the exponential force law associated with the hydration forces (D < 3 nm) is λ_hd = 0.24 ± 0.11, 0.12 ± 0.02, and 0.18 ± 0.08 nm at C_s = 0.1, 0.25, and 2 M, respectively. (C) Schematic representation of the SFA setup for measuring normal and friction forces. In this setup, all experimental parameters, F_s, F_n, and D, are measured continuously and simultaneously. (D) Friction traces and the separation distance fluctuations in response to the reciprocating motion of the lower surface across 2 M La(NO₃)₃ solution at increasing normal loads and a fixed velocity of 3 μm s⁻¹. (E) Friction force measurements recorded at different normal loads across 25 to 2000 mM La(NO₃)₃ solutions. Different symbols represent independent experiments (different mica pairs and contact points). (F) Evolution of the coefficient of friction and film thickness in the low- and high-friction regimes.

In the short-range regime (D < ~5 nm), a strong exponential repulsive force is measured whose magnitude depends on C_s (Fig. 1B). This regime is associated with the compression of layers of hydrated ions (which will be referred to as hydration layers from now on) adsorbed on the mica surface. At C_s = 25 mM, ion layers appeared to be weakly bound to the mica surfaces as evidenced by the sudden jump-in of the surfaces at F_n/R = 9.8 ± 1.5 mN m⁻¹ and D = 2.0 ± 0.3 nm, which corresponds to the squeezing out of the confined ions. When increasing the electrolyte concentration to C_s = 100 and 250 mM, the hydration forces were notably changed and appeared to be purely repulsive and monotonic. The thickness of the hydrated ion layer, which corresponds to the separation distance measured at the highest applied force, was 1.1 ± 0.1 nm at C_s = 100 and increased to 1.5 ± 0.1 nm at 250 mM. At higher electrolyte concentrations, C_s = 2 M, a small jump-in instability, similar to the one recorded at C_s = 25 mM was observed between D = 3.3 ± 0.5 and 2.5 ± 0.3 nm. The amplitude of the jump-in distance, ΔD_j = 0.93 ± 0.23 nm, is in good agreement with the hydrated diameter of a La³⁺ ion (~0.90 nm). Therefore, the instability was attributed to the squeezing out of a single layer of hydrated cations confined between two strongly mica-bound hydrated ion layers.

Therefore, it appears that the mechanical properties and structure of the hydration layers strongly depend on C_s, which, in turn, should affect their lubricating properties. To evaluate the nanotribological properties of the hydration layers, we used the SFA as schematically represented in Fig. 1C. In this setup, the shear force and film thickness are recorded during the back-and-forth motion of one surface. Figure 1D and fig. S4 show the time evolution of the shear force, F_s, and the corresponding separation distance, D, at different C_s under increasing normal load, F_n, and at a constant sliding velocity, v_s = 3 μm s⁻¹. No sign of stiction nor stick-slip in the range of applied normal force was observed during these experiments. As can be seen, the film thickness at the contact exhibited periodic oscillations with amplitudes, A, in the range of A = 1.7 to 2.1 Å, which is smaller than the diameter of a water molecule (2.8 Å) or of a dehydrated NO₃⁻ (5.3 Å) or a La³⁺ (2.1 Å) ion (36). These angstrom-level oscillations of the film thickness most likely arise from mechanical perturbation linked to the bimorph slider motion (and change of direction), which can create a minute shift in the optical fringe position. Measurements of F_s versus F_n (Fig. 1E and figs. S5 and S6) revealed the presence of two friction regimes: a low-friction regime below a concentration-dependent critical normal force F_n* (or compressive pressure P*), where the friction coefficient was the smallest μ ~ 10⁻⁴, and a high-friction regime at F_n > F_n*, where μ suddenly increased to μ ~ 10⁻³. Notably, in the low-friction regime, μ was weakly increasing with C_s, while in the high-friction regime, μ decreased from μ = 0.016 ± 0.004 at C_s = 100 mM to μ = 0.0033 ± 0.0026 and μ = 0.0059 ± 0.0028 at C_s = 250 mM and 2 M, respectively (Fig. 1F). The results show that the critical normal force, F_n*, increases from ~3 to ~30 mN, corresponding to an increase of P* from ~1 to 6 to 7 MPa, when C_s increases from 100 to 250 mM, and remains constant above C_s = 250 mM (fig. S7). It should be emphasized that the data shown throughout the manuscript were obtained with no sign of damage. At C_s = 25 mM, damage was systematically observed at F_n > 0.3 ± 0.1 mN, and therefore, friction force, friction coefficient, and film thickness were not shown in Fig. 1 (E and F).

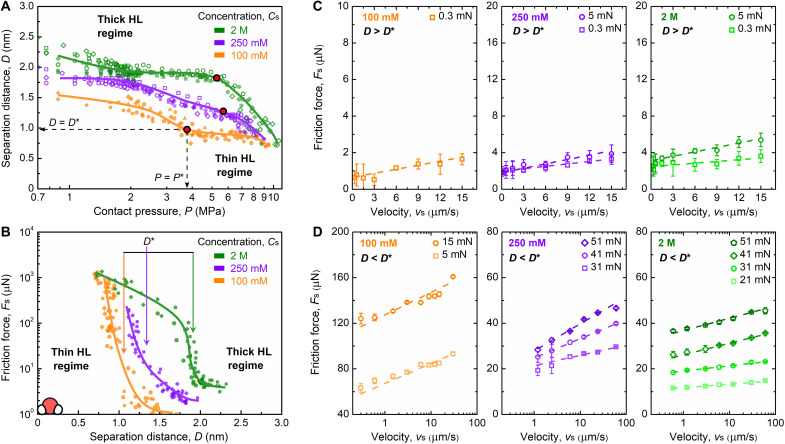
To gain more insights into the origin of the two friction regimes, shear force and film thickness values were recorded against the normal pressure P (Fig. 2, A and B). The normal pressure was extracted from the normal force data and contact area measurements (figs. S8 and S9). At C_s = 100 mM, the evolution of D with P (Fig. 2A) reveals that D tends to decrease continuously in a stepwise manner with P and reaches a constant value at D = 0.75 to 0.80 nm at P = 9 to 10 MPa. At C_s = 250 mM, a similar trend was observed, although starting at separation distances that were slightly larger at low pressures. As for C_s = 2 M, the separation distance remained constant when increasing the pressure up to P = 5 to 6 MPa, above which a sharp decrease from D = 1.9 nm to D = 0.8 nm was observed. The coordinates of the critical transition points (D*, P*) are also indicated in Fig. 2A, marking the boundaries between the low- and high-friction regimes. It appears that each transition point is systematically located in a region where the hydration layer is thinning and therefore marks the boundary between thick and thin HL regimes, which corresponds to low- and high-friction regimes, respectively. In these two regimes, two very different tribological behaviors are observed (Figs. 1E and 2B). In the thick HL regime, the friction force increases slightly with C_s and the friction coefficient, while in the thin HL regime, the film thickness does not change notably and the friction coefficient decreases obviously from low concentration, C_s = 100 mM, to high concentration, C_s = 250 mM and 2 M. The data shown in Fig. 2A also reveal that at P = 9 to 10 MPa, the film thickness of the hydration layer converges toward D = 0.8 nm independently of C_s. As shown in Fig. 2B, a slight change in film thickness at C_s = 100 mM caused a significant change in friction force, while a large change in film thickness at C_s = 2 M only caused a slight friction change. As will be discussed later, this phenomenon is reminiscent of the differences in structure of the hydration layers at different C_s.

Fig. 2. Thick and thin HL regimes have different energy dissipation mechanisms.

(A) Evolution of the separation distance with the normal pressure and (B) the friction force with the separation distance across confined La(NO₃)₃ solutions at different salt concentrations at v_s = 3 μm s⁻¹. Velocity-dependent friction forces at different concentrations and at increasing normal loads in the thick (C) and thin (D) HL regimes. In the thick HL regime, the existence of nonzero friction force at zero sliding speed is expected because of weak mechanical coupling between the sliding surface and the spring used to measure the friction force, as reported in previous research (1, 4, 24, 50). Measurements located at the intersection between both regimes seem to be better presented on a logarithmic scale (fig. S10).

To identify the main energy dissipation mechanism occurring during thin and thick HL regimes, we performed further tests to assess the speed dependence of the shear force. In the thick HL regime (Fig. 2C), where D (=1.5 to 2.1 nm) > D* at C_s = 0.1 to 2 M, F_s depends linearly on the shearing speed, v_s, suggesting a viscous dissipation of the frictional energy. In this regime, the speed dependence can be described by the following expression assuming Couette flow between the surfaces (37)

$$F_{\mathrm{s}}\sim A\mathrm{\eta }\frac{v_{\mathrm{s}}}{D}$$ (1)

where A is the contact area, η is the viscosity, and v_s/D is the shear rate. In the thin HL regime (Fig. 2D), where D (=0.7 to 1.5 nm) < D* for all C_s, the variation of F_s with v_s is logarithmic, suggesting a distinct dissipation mechanism arising from shear-induced thermally activated sliding, and can be described by the following equation, which was inspired by the rate-activated sliding theory (24, 25, 38, 39)

$$F_{\mathrm{s}}=\frac{\text{Δ}E}{\mathrm{\lambda }}+\frac{k_{\mathrm{B}}T}{\mathrm{\lambda }}\ln \frac{v_{\mathrm{s}}}{v_0}$$ (2)

where ΔE is the energy barrier, λ is the stress-activated length, v₀ is a reference velocity, k_B is the Boltzmann constant, and T is the absolute temperature. In this model, the energy barrier originates from the overlapping of the hydration shells of facing adsorbed ions during the sliding motion. Similar conclusions concerning a linear and a logarithmic regime were reached earlier in a study of a monovalent Na⁺ ion at C_s = 100 mM (24).

Hydration layer structure tunes lubrication mechanisms

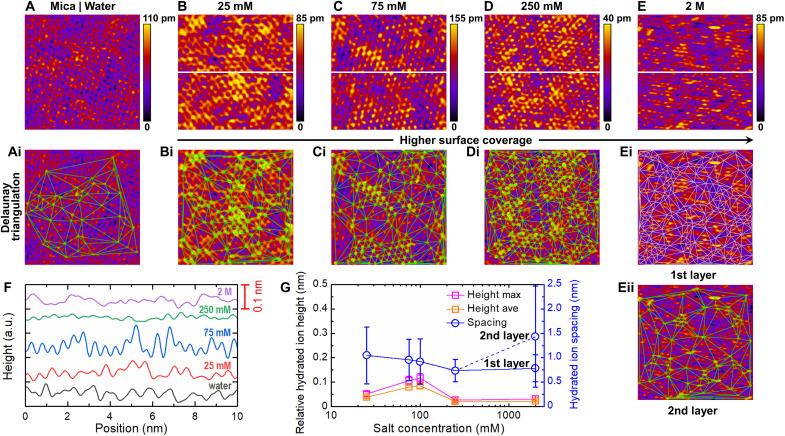
To gain more insights into the hydration layer structure at different C_s, the organization of adsorbed La³⁺ ions on mica surfaces was evaluated by HR-AFM (Fig. 3) and MD simulations (fig. S11). Both MD simulations and HR-AFM imaging showed a gradual increase of the surface coverage of La³⁺ ions on the mica surface at increasing concentrations, C_s. Figure 3A shows the surface of bare mica imaged in ultrapure deionized water (C_s = 0 mM). As highlighted in the inset of fig. S12A, a honeycomb-like pattern with hexagonal array structure is visible and is characteristic of the (100) plane of cleaved mica (40). Such hexagonal arrangement is also well defined in the corresponding fast Fourier transform map (fig. S12B). Figure 3 (B to E) shows the AFM topographies of cleaved mica surfaces immersed in La³⁺ solutions at different C_s with different height scales to visually enhance features appearing on mica surfaces as C_s increases. Figure 3F shows the height profile measured for each La³⁺ concentration across the white line in Fig. 3 (B to E). Figure 3G displays the measured relative hydrated ion height and hydrated ion spacing as a function of C_s, where ion positions were identified systematically and independently of the height scale using Delaunay triangulation analysis (see section S2). The individual ions can be identified as bright yellow spots and green or white intersections at all concentrations (Fig. 3, Bi to Eii).

Fig. 3. Evolution of structural changes at the surface of the hydration layer.

(A) HR-AFM topography of cleaved muscovite mica (100) surface in ultrapure water. (B to E) AFM images of mica surfaces in contact with LaNO₃ solutions at concentrations ranging from 25 mM to 2 M. (i and ii) The Delaunay triangulation analysis used to analyze the AFM images, identify ion positions, and calculate closest neighbor distance (see section S2). (F) Height fluctuation of hydrated ions at different concentrations across the white line in (B to E). (G) Relative hydrated ion height (representing the average height between the peak and bottom, where Height max and Height ave mean the maximum and average of the height data, respectively) and hydrated ion spacing (representing the average distance between two peaks) as a function of LaNO₃ concentration. Error bars represent the SD averaged over five different line profiles (for height data) and each AFM image (for spacing data). The length and width of each AFM image was 10 nm by 10 nm. a.u., arbitrary units.

From C_s = 25 to 250 mM, the number of features corresponding to adsorbed ions (i.e., green intersections; Fig. 3, Bi to Di) and the corresponding decrease in spacing between them (Fig. 3G) both show that ion surface coverage increases. At C_s = 2 M, applying the feature identification protocol used for the other lower concentrations led us to identify very few ions on the surface (Fig. 3Eii, labeled second layer). Because, at C_s = 250 mM, the mica surface was almost fully covered with ions (with the lowest height and spacing; Fig. 3G), it can be indicated that a second layer of ions is forming at C_s = 2 M. Because only a few ions were spotted on the second layer, the first layer is still quite visible, and therefore, we modified the filtering scheme (see section S2) to focus on features present on the first layer (Fig. 3Ei, labeled first layer); then, both ion layers were distinguished. It appeared that the number of adsorbed ions and the average ion-ion distance in the first layer were close to the values obtained at C_s = 250 mM (Fig. 3G). The apparent distortion of the shape of the ions at 2 M (Fig. 3E) is linked to their weaker affinity to the surface (and increased lateral mobility stimulated by the presence of the scanning tip), which is a consequence of the formation of multilayers of ions on the mica surface. As the AFM tip scans the surface, ions are transiently laterally displaced around their equilibrium position in a direction close to the scanning direction, creating a distorted image of the ions. As a comparison, mica in water shows an average ion distance of 1.5 ± 1.0 nm (Fig. 3Ai), reflecting the K⁺ ion spacing.

These high-resolution images have shown that the surface coverage of adsorbed ions depends strongly on the bulk concentration. Although water molecules could not be individually resolved in the images, the observed fluctuation of the ion layer height (Fig. 3, F and G) suggested potential differences in the hydration states or vertical position of the ions, which could translate into differences in hydration shell structure. The low concentration of adsorbed ions at C_s = 25 mM (Fig. 3B) correlates with SFA experiments where low compressive pressures (P < 1 to 2 MPa) led to squeezing out of the hydration layer and solid-solid contact. At this concentration, mica damage was systematically observed during sliding because of the lack of hydrated ions at the surfaces (Fig. 1, B and E) and weak repulsive hydration forces. As C_s increases up to C_s = 75 to 250 mM (Fig. 3, C and D), higher surface coverage of ions is expected to contain higher amount of hydration water molecules. This observation also correlates with the SFA experiments, which showed an increase of the hydration film thickness D with C_s (Fig. 1B). As C_s increases even further (C_s = 2 M; Fig. 3E), multilayers of ions start to form with distal ion layers weakly adsorbed. The SFA experiments also show an increase of the hydration film thickness D with C_s and the formation of multilayers that could be squeezed out of the contact area by increasing the applied load (Fig. 1B). The combination of distal weakly bound hydrated layers and strongly attached proximal layer provides effective superlubrication as shown in Fig. 1E.

Ion-induced structural changes in the hydration layer

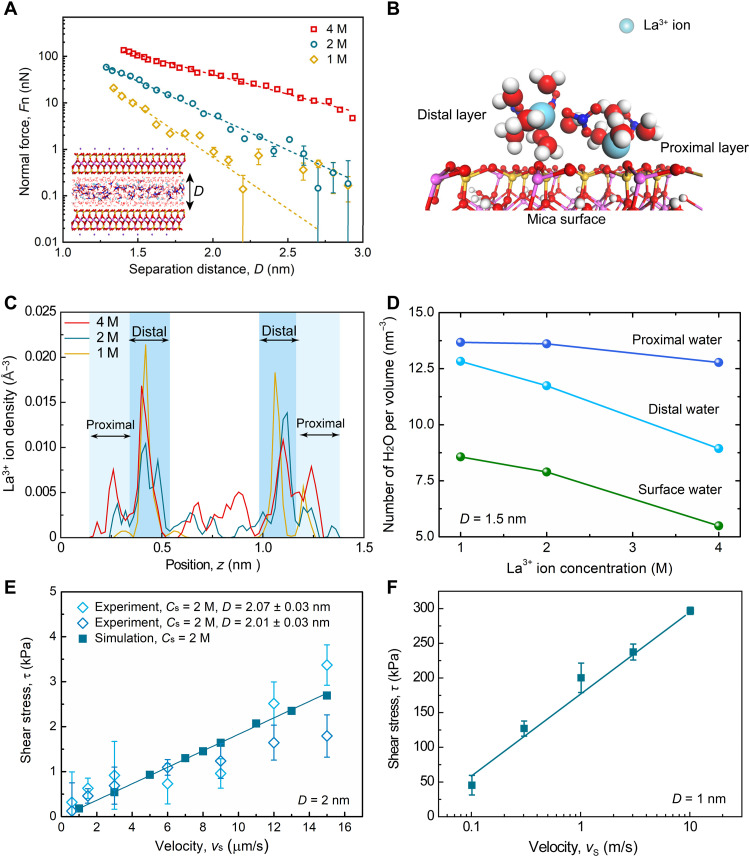
MD simulations were performed in the confined configuration, similarly to those in SFA experiments, to corroborate the insights gained from HR-AFM and MD simulations obtained in the open configuration. An atomistic model was used, which allowed for exchange of molecules between the two shear planes and the bulk phase (41). A first series of simulations aimed to reproduce the evolution of the normal force with the separation distance at different concentrations (C_s = 1 to 4 M) was realized (Fig. 4A). Only simulations at high C_s values were possible to ensure sufficient ions in a nanometer-thick space. The simulation results revealed an exponential relationship between F_n and D. Both simulations (Fig. 4A) and experiments (Fig. 1B) show decay lengths of 0.1 to 0.3 nm at C_s < 2 M in the hydration repulsion regime (D < 3 nm), confirming the common origin of the strong repulsive forces in this confinement regime.

Fig. 4. MD simulation of confined trivalent electrolytes.

(A) Variation of F_n with respect to D for La(NO₃)₃ aqueous solution confined between mica surfaces at 1 to 4 M concentrations. The short dashed curves are exponential fittings using F_n ~ exp(−λ_h⁻¹ D), where λ_h = 0.20 ± 0.01, 0.29 ± 0.01, and 0.51 ± 0.01 nm at C_s = 1, 2, and 4 M. The model represents La(NO₃)₃ aqueous solution between two mica slabs at D = 1.3 nm and C_s = 2 M at equilibrium condition. (B) The local structure of the La³⁺ hydration shells adsorbed on the mica surface. (C) The La³⁺ ion density profiles (number of ions per volume) along the normal direction to the mica surfaces at C_s = 1 to 4 M and D = 1.5 nm. (D) The number of water molecules per volume for proximal, distal, and surface water with respect to C_s at D = 1.5 nm. Proximal and distal water molecules are meant to distinguish between molecules forming the hydration shells of ions that are close or further away from the mica surface, respectively, and surface water refers to the molecules in direct contact with the mica surface and not involved in the hydration shell of ions. (E) Comparison between the variation of shear stress τ versus v_s = 1 to 15 μm s⁻¹ in SFA experiments (details are in Materials and Methods; F_n = 0.3 mN) and MD simulations at D = 2 nm and C_s = 2 M. (F) Variation of τ with v_s = 0.1 to 10 m/s at D = 1 nm and C_s = 2 M.

Analysis of the ion density distribution shows that the hydrated La³⁺ ions form two layers on each mica surface independently of the separation distance between the surfaces (Fig. 4B and fig. S13). The proximal layer is located at z = 0.26 nm (with z = 0 nm being the position of the mica surface), while the distal layer was higher at z = 0.42 nm (Fig. 4B). The bilayer structure of hydrated La³⁺ on mica persists in both the thick and thin HL regimes (fig. S13) at high C_s, but the number density of hydrated ions populating the proximal layer is notably increased at high electrolyte concentrations (Fig. 4C). Simulations also show that the number density of water molecules bound to La³⁺ in the proximal layer weakly depends on C_s (Fig. 4D and table S2), while it decreases sharply with C_s in the distal layer and at the mica surface because of an increased number of La³⁺ ions in these positions (water molecules in direct contact with the surface but not with any ions).

In addition to the experimental tribo-tests, a recently proposed auxiliary path method (APM; see Materials and Methods) (42) was used to calculate the friction force in the thick HL regime (D = 2 nm) at C_s = 2 M. By increasing the statistical efficiency over 10 orders of magnitude, the APM can study the frictional properties at sliding speeds matching the experimental conditions. A good quantitative agreement between SFA experiments and MD simulations was obtained (Fig. 4E), indicating that the simulations capture the essence of the mechanisms, where the viscous dissipation within the solution accounts for the linear dependence of friction on sliding speed.

In the thin HL regime (D = 1 nm), simulations using the APM were not conclusive because of the rare event nature of the erratic frictional behavior (Fig. 1D). Alternatively, we used the steered MD method, performed at a sliding speed far higher than experimental values (43). Simulation results corroborated the logarithmic relationship between shear stress and sliding velocity observed experimentally (Fig. 4F).

DISCUSSION

Trivalent La³⁺ ions are known to be chemically stable in aqueous solution and do not hydrolyze nor form polynuclear complexes (44). The series of experiments and simulations presented revealed both the effect of concentration and confinement on the lubricating behavior of multivalent electrolytes. A transition from thick to thin HL regime was observed and characterized by a drastic increase in friction coefficient μ from ~10⁻⁴ to ~10⁻³. The value of critical pressure P*, delimiting the boundary between the two regimes, was found to depend on C_s up to C_s = 250 mM, above which it remained constant. Previous reports have also shown a similar transition for monovalent ions but with a transition pressure far smaller than the values that we report for the trivalent ions (21, 24, 45). AFM imaging of the adsorbed ions on mica surfaces revealed that at C_s = 250 mM, the maximum surface coverage was reached. In the same line, SFA force profiles showed that at C_s > 250 mM, mobile layers of ions started to form on a more strongly adsorbed layer of ions. Therefore, P* appears to be entirely controlled by the surface coverage of the strongly adsorbed ions layer.

In the thick HL regime (D > D*, P < P*), SFA experiments showed that the thickness of the lubricating film varied between 1.2 and 2.3 nm (Fig. 2A), depending on C_s that is comparable to two to four times the primary hydrated diameter of La³⁺ ions (46). MD simulations showed that water molecules coexist in different states: bound to La³⁺ ions, bound to the mica surface, or unbound and freely diffusing. The number of water molecules forming the first hydration shell of La³⁺ ions is around n_h = 8 to 10 (46). The number density of La³⁺ ions trapped between two charged mica surfaces is given by ρ_La = [2(σ* − σ₋)/3e]/D (47, 48), where σ* is the effective surface charge density, σ₋ = −2e nm⁻² is the areal density of ionizable lattice sites on the mica surface, and e is the electronic charge. Streaming current measurements (48) and numerical calculations (47) have shown that σ* ≈ −0.3σ₋ at C_s = 2 M, indicating that more than one-third of the ionizable surface site is occupied by La³⁺ ions because of charge inversion (fig. S14). Therefore, the number ratio of water molecules to La³⁺ ions in a lubricating film of D = 2 nm, n_w, is equal to n_w = ρ_w/ρ_La ≈ 38, where ρ_w ≈ 33 nm⁻³ is the number density of water molecules, and is about four times higher than n_h [note that three to four La³⁺ layers are present at D = 2 nm (Fig. 4C), leading to smaller n_w < 38 due to larger ρ_La] (46), which is a result that is consistent with our MD simulations as well (table S2). Therefore, we can estimate that more than one-quarter of the water molecules are bound to La³⁺ ions, while the rest are adsorbed on the mica surfaces or freely diffusing at C_s = 2 M under nanoconfinement (D = 2 nm). The large amount of free water molecules in the lubricating film is correlated with the viscous dissipation mechanism identified experimentally in this regime. The measured friction coefficient slightly increasing with C_s (Fig. 1F) indicated that the effective viscosity η_eff of the lubricating film is increasing as well, which was estimated using Eq. 1 and led to η_eff = 460 ± 76 mPa·s at C_s = 100 mM and increased up to η_eff = 737 ± 87 mPa·s at C_s = 2 M at P = 1.3 to 1.6 MPa (table S3), more than two orders of magnitude larger than the bulk values measured with the SFA using the oscillation technique (fig. S15). Similar trends were found from MD simulations. Calculations of the effective diffusion coefficient D_eff of the water molecules showed that in the thick HL, D_eff decreases notably with C_s, indicating an increase of the Stoke-Einstein effective viscosity (η_eff ≈ 1/D_eff; see fig. S16).

In the thin HL regime, the trends identified in the thick HL regime did not hold anymore. MD simulations showed that in the thin HL regime, D_eff is independent of C_s (fig. S16), while SFA results demonstrated that the coefficient of friction μ was decreasing with C_s (Fig. 1F). In this regime, the number of water molecules per La³⁺ ion estimated as before or via MD simulations (table S2) is ~1.8 for a film thickness D ≈ 1 nm, comparable to approximately twice the hydrated diameter of La³⁺. μ at C_s = 100 mM is nearly one order of magnitude larger than that at C_s = 250 mM and 2 M (Fig. 1, E and F). Similar results were found with monovalent electrolytes at C_s = 200 mM and 4 M using an AFM silicon tip and a mica surface (49). As mentioned, when the applied pressure reached the value of P = 9 to 10 MPa, well into the thin HL regime, the film thickness was found to be independent of C_s at constant sliding speed (Fig. 2A), but the friction forces (and associated μ) were still strongly dependent on C_s (Fig. 1F). Such behavior is intimately linked to changes in the hydration layer composition and structure. MD simulations showed that as C_s increases, the proximal layer of La³⁺ ions are gradually more populated, as well as the associated water proximal layer (Fig. 4, C and D). This shift of ions and water molecule distribution is correlated to a decrease of the atomic roughness of the surfaces as seen by AFM imaging (Fig. 3, G and H). Manifestations of such subtle structural changes are seen in the evolution of the friction force with the sliding speed. Because the frictional energy dissipation mechanism identified in this regime can be described by Eq. 2, experimental data obtained from SFA allow us to extract the energy barrier ΔE and normalized stress activation length λ/λ₀ and evaluate their dependence to C_s (fig. S17). The obtained values of ΔE were found to strongly depend on C_s and decreased by ¹/₄ to ¹/₃ from C_s = 100 mM to C_s = 250 mM and 2 M (fig. S17A). This decrease in ΔE is correlated to the evolution of the atomic roughness of mica surfaces coated with La³⁺ hydrated ions obtained from AFM imaging (Fig. 3), where the relative hydrated ion height and the hydrated ion spacing were notably lower at C_s = 250 mM compared to 75 and 100 mM. Similarly, the extracted values for λ/λ₀ were notably affected by C_s and far less by the normal force (fig. S17B). High values of λ/λ₀ were measured at C_s = 250 mM and 2 M, which were approximately one order of magnitude larger than that at C_s = 100 mM, reflecting the enhanced fluidity or mobility of the confined hydration layers at high C_s.

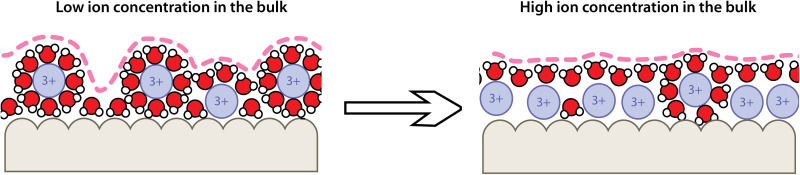
The present study offers fundamental insights regarding the HL in the thin film regime modulated by the “roughness” of the hydration layer (Fig. 5). The fine structural changes occurring in the adsorbed ions layers (proximal and distal) as C_s increases lead to changes in hydration water distribution. At low C_s, the predominance of two layers of adsorbed ions creates a rough hydration layer on the surfaces, while at increasing C_s, the number of ions in the proximal layer increases and smoothens the hydration layer. We revealed that ion concentration plays different roles depending on the lubrication regime and is a strong determinant of the hydration layer structure at high concentration. This evidence supports the idea of an intimate relationship between the dynamic structure of a boundary lubricant film and its tribological properties and offers a framework to study such relationship at the molecular level.

Fig. 5. Evolution of the hydration layer structure.

Schematic representation of the ion distribution in the hydration layer and its evolution with the bulk ion concentration.

MATERIALS AND METHODS

Materials

Ruby mica sheets were commercial products from S&J Trading Inc. (USA). La(NO₃)₃·6H₂O with 99.999% purity was purchased from Sigma-Aldrich (USA) and used as received. The pure water was produced using a Milli-Q integral water purification system (Millipore Corporation, USA) with resistivity of 18.2 megohm·cm and total organic carbon ≤2 parts per billion. Ultraviolet (UV)–curable glue (Norland Optical Adhesive 83H) was used to glue the back silvered mica surfaces onto the cylindrical glass discs.

Surface force measurements

Surface preparation

All experiments were conducted using an SFA (SFA2000, SurForce LLC, USA). Surfaces were prepared following the previously reported standard procedure (41). Briefly, freshly cleaved mica sheets with thicknesses of 1 to 3 μm were cut into pieces by a hot platinum wire; then, mica pieces were placed on the backing mica sheet for silvering (55-nm silver layer thickness). Two back silvered mica pieces with the same thickness were glued onto the cylindrical glass discs with a curvature radius (R) of 2 cm. We used strong UV irradiation to cure the UV-curable glue, fix the mica surfaces on the glass disks, and burn any organic deposit on the surfaces. UV exposure time was about 2 hours and took place under a laminar flow hood. During that time, the temperature close to the surfaces could rise as high as 70°C, which helps the decontamination process (which is similar to a UV-ozone cleaning procedure). Once the UV treatment is finished, the surfaces are immediately transferred to the SFA chamber where they cool down under dry Ar atmosphere for 30 min. Then, surfaces were approached until adhesive contact using coarse and fine differential micrometers and a DC motor to measure the reference point of mica-mica contact in air. After a slight deformation of surfaces, the position of fringes of equal chromatic order (FECO) and Hg reference was recorded using a spectrometer. Control measurements indicated that the separation distance of mica-mica contact was almost the same before and after adding pure water when prepared via the UV treatment method. Previous surface force measurements have shown that there is a contaminant layer adsorbed from air on mica, which can be removed under pure water (1, 4). Using a UV cleaning method, the air-adsorbed contaminants can also be removed effectively as UV radiation induces rapid degradation of organic materials through the reduction of organic contaminants into harmless H₂O, CO₂, and NO_x desorbing from the surfaces (see section S3). After the calibration, the surfaces were separated to a distance above 1 mm, and about 50 μl of salt solution was injected between two surfaces. Water was deposited randomly onto the bottom of the chamber to humidify the chamber and limit the evaporation of salt solution during the experiments. Surfaces were then left to equilibrate for 30 min before the measurements. All subsequent experiments were performed at 23° ± 1°C, and the relative humidity in the SFA chamber was close to 100%.

Normal force measurements

The normal interaction force was determined by measuring the deflection of the spring cantilever with a spring constant of 482 N/m that supports the lower surface. The separation distance between two surfaces was measured by multiple-beam interferometry and calculated using the FECO fringes by MATLAB software. The normal interaction forces as a function of separation distance between two surfaces in La(NO₃)₃ solutions at four different concentrations (25 mM, 100 mM, 250 mM, and 2 M) were measured through approaching the surfaces at a speed of 1 nm/s while simultaneously acquiring the FECO fringes every 0.5 s. For each concentration, the independent experiments (with different mica pairs and contact points) were repeated at least three times.

Friction force measurements

The friction force was measured by moving the lower surface horizontally and determined by measuring the response of the upper surface using semiconductive strain gauges. All friction measurements were performed by driving the lower surface back and forth at a motion amplitude of 30 μm and a sliding frequency of 5 to 500 mHz (controlled by a function generator, corresponding to a sliding velocity of 0.3 to 30 μm/s) while continuously recording the FECO fringes every 0.5 s. Acquired data (including motion of the upper surface, load, and friction force) were analyzed by Origin software. Two or three cycles of normal compression/decompression were performed at the same contact position before friction measurements. Because the relative orientation of the mica surfaces was not controlled, the small variability of coefficient of friction from one pair of surfaces to another at a given salt concentration suggests that surface commensurability had little to no effect on the measurements.

Thin film viscosity measurements

Thin film viscosity (η) can be obtained directly as a function of film thickness using a dynamic technique, where a piezoelectric crystal was used to oscillate the upper surface using an applied square wave with an amplitude (A₀) by applying an AC voltage (2.5 and 10 V) and a frequency of 0.1 Hz and then using an applied sine wave with the same amplitude and a higher frequency (v) of 0.5 Hz for the response amplitude (A) (42, 43). When the separation distance (D) between two mica surfaces is large enough (typically larger than 200 nm), the lower surface does not oscillate with the upper surface because of weak viscous coupling between the two surfaces. While oscillating, the surfaces are brought closer gradually in a stepwise manner, and the lower surface starts to oscillate at a response amplitude (A) because of the viscous force induced by the oscillation of the upper surface. The response amplitudes (A) with varying separation distances (D) were measured during oscillation. The thin film viscosity (η) at any separation distance (D) in terms of v, A₀, A, R, and the spring stiffness (K) of a cantilever spring supporting the lower surface is expressed as

$$\mathrm{\eta }=\frac{KD}{12{\mathrm{\pi }}^2{R}^{2}v}{[{\left(\frac{A_0}{A}\right)}^2-1]}^{1/2}(\mathrm{for}A\ll D)$$

where K = 482 N/m, R = 2 cm, v = 0.5 Hz, and A₀ = 120 ± 3 and 451 ± 23 Å at the voltage of 2.5 and 10 V, respectively.

Evaluation of contact pressures

The contact diameter on mica surfaces under different normal loads was measured through measuring the length of the flat parts of FECO fringes (with a calibration of 0.38 μm per pixel), which gave the contact area (A), as illustrated in figs. S8 and S9. The Hertzian contact theory or Johnson-Kendall-Roberts (JKR) theory was also used to calculate the contact area for the flattened circular contact of two crossed cylinders under a load (F_n), A = π(F_nR/k)^2/3, where k is an effective mean modulus of the mica/glue layer, which was determined separately from several independent experiments and had a value of k = (11 ± 2) × 10⁹ N/m² (fig. S8). The mean contact pressure was evaluated as P = F_n/A. At low-load (<~4 mN) regime, the contact pressure calculated according to Hertzian or JKR model was more accurate because the contact area was too small to be measured accurately through the FECO fringes. At high-load regime (>~4 mN), the calculated contact pressure was in good accordance with the measured pressure. The uncertainty of the calculated contact pressure arising from uncertainties in k and R was estimated to be lower than 30%.

HR-AFM imaging

AFM topographies were recorded with a Cypher ES (Asylum Research, Oxford Instruments, Santa Barbara, CA, USA) using Arrow headed UHF-AuD cantilevers (NanoWorld, CH). Photothermal excitation with amplitude modulation was used as driving mode, with a typical oscillation amplitude of 3 to 5 Å, and the scan rate was set between 8 and 10 Hz per line. Mica was freshly cleaved before imaging. The collected data were reprocessed by applying a low-pass filter that removes high-frequency noise (i.e., above ¹/₅ of the Nyquist frequency). To achieve an even better resolution of the filtered images, an upper threshold corresponding to 80% of the (Gaussian) pixels’ intensity distribution was applied, which leads to a hue saturation of the pixels lying above such 80% threshold. These saturated pixels also correspond to the highest features detected. However, unsaturated images were still used to extract quantitative data from the line profiles such as height and relative hydrated ion height (Fig. 3, F and G). To calculate the hydrated ion spacing (Fig. 3G), we first increased the lower threshold of the pixels’ distribution histogram (≥65 to 70% of the Gaussian distribution) so that a mask is created with only the brightest and highest features of the topographies selected (i.e., the hydrated ions). The mask (a binary black and white image) was then transferred to ImageJ, where the positions of the ions were identified by means of the automated particle counter (“Analyze Particles” in ImageJ) and saved as a region of interest. Last, the distances between nearest neighbors were calculated as Delaunay triangulations across the whole scanned surface (10 nm by 10 nm). The code for triangulations is already embedded in ImageJ (it is thereby open source). More details can be found in section S2.

MD simulations

To explore the approaching of two mica surfaces within salt solution, MD simulations were performed. The well-defined liquid-vapor MD model (figs. S18 and S19) was applied to model squeezing during normal compression (35). In this model, the liquid molecules are allowed to exchange between the confined area (between two mica surfaces) and the bulk area (between two hydrophobic surfaces). The mica surface was built from the Muscovite mica crystal. A smooth mica surface with a side length of ~5 nm was built as the two surface models, where the K⁺ on the side of the confined space was deleted, to mimic the surface properties found in experiments. Some of the K⁺ on the outside was deleted randomly to sustain a surface charge density of ~2e/nm² that is consistent with the value of ~33 μC/cm⁻² from experiments. Mica was rigid in the simulations. Very long (~40 nm) hydrophobic walls were extended along the x direction of the mica, also to prevent the interaction between periodic images of liquid molecules. Periodic boundary condition was applied to the y direction.

The force field of mica was taken from the CLAYFF potential that has been applied to study the water-mica interactions (44). Simple point charge/extended (SPC/E) model was used to describe the water molecules (45). The interaction between NO₃⁻ and NO₃⁻ was described by the optimized potentials for liquid simulations (OPLS) force field (46), where specific interaction between La³⁺ and oxygen in NO₃⁻ was optimized to get accurate structure (47). The interaction between La³⁺ and La³⁺, as well as between La³⁺and water, was taken from the parameter reported in the literature (48). All the van der Waals (vdW) interactions were calculated on the basis of the Lenard-Jones 12-6 equation, with a cutoff of 1.2 nm. vdW interactions between different molecules were obtained by the Lorentz-Berthelot mixing rule. The long-range columbic interaction was computed from the Ewald method (49). By performing equilibrium simulations for the La(NO₃)₃ in bulk water, we get a consistent first-shell hydration radius (0.26 nm) and a hydration number (9.45) of La³⁺ with the experiments (48). The radial distribution function of La³⁺ in water is depicted in figs. S18C and S19.

All the calculations were performed by LAMMPS packages (50). In the model shown in fig. S18, the upper solid part was coupled to springs along all the three directions. The spring constants are k_x = k_z = 150 N/m and k_y = 0.1 N/m. The normal force during the compression was estimated from the normal spring. First, the normal spring was moved close to the substrate in a low velocity (v = 0.01 Å/ps), from an interlayer distance of D = 3 nm until the slider dropped into contact. Then, continuum configurations were taken to be minimized further to get equilibrium normal force at a certain interlayer distance. After equilibrium, the liquid structures within the mica area are analyzed, as shown in Fig. 4 (B and C). Here, the interlayer distance D is defined by the distance between two closest oxygen layers that belong to two separated mica slabs. The concentration C_s in the simulations could differ from that used in the experiments because of the simplified protocol compared to real SFA measurements.

Shear simulations

Nonequilibrium MD simulations were conducted for hydrated La³⁺ layers sheared by the mica surface. Salt concentrations of C_s = 2 M in the SFA geometry were used to investigate the shear velocity, v_s, dependence on friction in the thick (D = 2 nm) and thin (D = 1 nm) HL regime. An APM was proposed to increase statistical efficiency in nonequilibrium MD simulations to overcome the large noise-to-signal ratio of dynamical quantities. The APM method constructs extra auxiliary paths of the real paths in trajectory phase space to increase the accuracy of the estimate; the dynamics of the system remains unchanged. With the help of this method, we conduct MD simulations under the same v_s in experiments in the thick HL regime (Fig. 4E). Notably, the offset friction force by extrapolating the data to v_s = 0 was estimated, and we obtained a remnant force F_s0 = 2.7 μN at C_s = 2 M. Because F_s0 is expected to depend on the shearing amplitude, it is expected that our values are larger than already reported values, as our sliding amplitude is Δx₀ = 30 μm compared to F_s0 ≈ 0.2 μN at Δx₀ = 200 nm (1, 4) and F_s0 ≈ 0.3 to 0.4 μN at Δx₀ = 600 and 800 nm (24). The shear stress data obtained from SFA experiments were calculated using the equation τ = (F_s − F_s0)/A at F_n = 0.3 and 5 mN.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S21

Tables S1 to S4

References