Abstract
Discharging livestock manure slurry without proper treatment causes various environmental and sociological problems. Chemical coagulation is a widely used and easily applicable method for treating such wastewater. However, the technique requires optimization to enhance coagulation efficiency while minimizing chemical usage. In this study, we propose an efficient, low-cost, and environmentally safe chemical coagulation method for solid–liquid separation of dairy manure slurry. Experiments were conducted in laboratory jar tests using dairy manure slurry to investigate the impact of coagulants, specifically polyaluminum chloride (PAC) and cationic polyacrylamide (CPAM), as well as pH, on the process of solid-liquid separation. Preliminary ranges of PAC, CPAM, and pH were estimated through single-factor experiments. Coagulation optimization and modeling were performed using the response surface methodology (RSM) with the Box-Behnken design (BBD), wherein the desired goal of each parameter was set to maximize solid–liquid separation efficiency while reducing chemical dosage to maintain residual aluminum (Al) concentrations below water quality standards. Numerical optimization predicted that the optimal dosages were 75 mg/L of PAC and 35 mg/L of CPAM at pH 7. Under these conditions, removal efficiencies of 99% for turbidity and 97% for chemical oxygen demand (COD) were achieved, with a minimal residual Al concentration of 0.045 mg/L. Positive zeta potential values in the treated water confirmed complete separation of negatively charged solids in the dairy manure slurry. The response values predicted by BBD aligned with the experimental results, and the analysis of variance (ANOVA) demonstrated the predictability and accuracy of the response models. Consequently, this study highlights the practical application of RSM with BBD in optimizing chemical coagulation using PAC and CPAM to achieve efficient solid–liquid separation in livestock wastewater while maintaining low residual Al concentrations.
Keywords: Dairy manure slurry, Solid–liquid separation, Chemical coagulation, Polyaluminum chloride, Cationic polyacrylamide, Surface response methodology, Box–Behnken design
Highlights
-
•
Chemical coagulants, PAC and CPAM, were utilized for treating dairy manure slurry.
-
•
The method was optimized using RSM based on Box-Behnken design.
-
•
The model predicted a solid separation efficiency of 99% under optimal conditions.
-
•
The optimal concentrations were 75 mg/L of PAC and 35 mg/L of CPAM, at pH 7.
-
•
The residual Al concentration (0.045 mg/L) ensured the safe reuse of treated water.
1. Introduction
Livestock farming activities have rapidly increased in recent decades worldwide to fulfill the dietary requirements of the increasing human population [1]. According to recent statistics from the Food and Agriculture Organization (FAO), there are 270 million dairy cows and 677 million pigs worldwide [1]. A mature milking cow normally produces roughly 7.3 kg of dry manure mass per day, which is about 7–8% of its body weight. In the USA, about 24 billion tons of dry weight of dairy manure is produced per year [2]. In the UK, the annual dairy manure output as undiluted slurry is 17.73 million tones [3]. Improper management of livestock wastes is associated with many negative environmental effects such as excess nutrients in adjacent lands and the production of greenhouse gases such as methane (CH4) [[2], [3], [4]]. Livestock manure dilution by urine and wash water turns the manure into a slurry form. Slurry and solid manure are spread directly onto land as fertilizers in traditional farming practices, which may be potential sources of water and air pollution.
Water pollution mainly occurs owing to the leakage of stored slurry or discharge of slurry without adequate treatment, which can increase biochemical oxygen demand (BOD), chemical oxygen demand (COD), dissolved ammonia, and phosphorous in water, causing algal blooms in freshwater systems [2]. Especially, improper treatment of manure slurry is becoming a critical problem worldwide.
Therefore, it is necessary to recognize sustainable livestock and manure management practices including acceptable manure treatment technologies to avoid negative environmental impacts and enhance the growth of industry [1]. Recently, there has been a huge demand for proper livestock farming practices with manure and nutrient management.
Manure management is carried out in two different ways: anaerobic digestion and solid–liquid separation. Bioremediation of dairy wastewater, mechanical treatments using membranes, chemical treatments, windrow composting, separators, and anaerobic digestion are commonly used commercial technologies to treat cattle manure and slurries.
Solid–liquid separation of livestock manure yields two resources; the liquid fraction contains a high concentration of soluble nitrogen, which is a fertilizer source used in farming activities, whereas the separated solid fraction containing organic matter, phosphorus, and solids can be used for the manufacturing of fertilizer and generation of energy [3,5]. The often used solid–liquid separation methods include physical methods such as sedimentation, centrifugation, screw pressing, screening, and filtering. However, some of these require a large amount of energy.
In chemical treatments, 75% of the water from manure is separated, which results in clean water and dry solids consisting of phosphorus, organic nitrogen, stable ammonium, and potassium [2]. Coagulation is one of the cost-effective and easily applicable solutions for the solid–liquid separation of manure slurry [3].
In coagulation, as a result of adding coagulants and/or organic polymers, dispersed and colloidal particles in a solution aggregate and form settable flocs. Most suspended particles in wastewater with a pH greater than 4 have a negative charge. Therefore, inorganic salts with multivalent cations such as aluminum (Al), iron (Fe), and calcium (Ca) are used as coagulants. Al coagulants are widely used for water and wastewater treatment because of their high cationic charge and efficiency in the removal of suspended solids. Polyaluminum chloride (PAC), which is a pre-hydrolyzed coagulant, shows distinct and efficient behavior in the coagulation of suspended solids when compared with other Al-based coagulants [[4], [5], [6]]. PAC has many advantages; in particular, PAC treatment requires a smaller dosage than other coagulants, which leads to the generation of smaller sludge volume, high positive overall charge, less impact from temperature, and effectivity in a wide pH range because PAC contains pre-polymerized forms of Al [[7], [8], [9]]. In addition, flocculation is known as the agglomeration of coagulated solids into larger flocs, which leads to rapidly settling flocs. Coagulant aids are natural or synthetic polymer macromolecules containing different molecular weights with positive, negative, or neutral charges. These long polymer molecules contribute to the attachment of suspended particles to form flocs, which subsequently settle because of gravity [7]. Cationic polyacrylamide (CPAM) is considered more effective for the removal of solids [10]. However, it is important to optimize the coagulation and flocculation process to improve the efficiency of solid–liquid separation in livestock manure slurry while reducing chemical use, thereby minimizing the residual chemicals in treated water. Overdosing of PAC increases the residual Al concentration of treated water, and discharging of treated water with residual Al is associated with numerous environmental and health problems [8]. Moreover, the effect of CPAM-based flocculants on human and environmental health has recently become a concern [11].
Response surface methodology (RSM) is an optimization procedure, which represents empirical modeling, that can be used to develop a relationship between process factors and experimental output [12]. The individual and combined effect of independent variables on desired response parameters were measured to build a mathematical model [13]. RSM has many advantages over the traditional time-consuming approach of analyzing one variable at a time: cost-effective and time-saving approach with less number of experimental runs, assessing the interaction effect of the independent variables on desired response, and modeling of the selected responses [13,14]. Therefore, the RSM is widely applied for the optimization of process parameters in water and wastewater treatment to maximize the treatment performance, thereby the best treatment conditions can be identified with a minimum number of experiments [15]. The central composite design (CCD) and Box–Behnken design (BBD) are the most common design types of RSM [13,16]. The CCD method is made of a two-level factor design and each factor has five different levels. CCDs usually have axial points outside the “cube”, which tests at extreme conditions and those points may not be in the region of interest. On the other hand, in the BBD method, each factor has three different levels and no axial points outside the specified limits. The BBD method is more practical because it often requires fewer design points to fall within the operating range and the number of experiments in the BBD method is usually less than that in CCD [[17], [18], [19]].
To the best of our knowledge, there is limited information available on the optimization of chemical coagulation treatment using PAC and CPAM for solid–liquid separation in dairy manure slurry through the application of RSM based on a BBD. In this study, we conducted single-factor experiments followed by RSM based on BBD to optimize the dosages of PAC, CPAM, and the initial pH for solid–liquid separation in dairy manure slurry. The quality of the treated water was assessed in terms of turbidity removal efficiency, COD removal efficiency, zeta potential, and residual Al concentration, with the ultimate objectives being the safe discharge and reuse of the treated water.
2. Materials and methods
2.1. Materials
Dairy manure was collected from a dairy farm located in Ageo, Japan. Solid manure was sieved using a 0.5 mm mesh to remove coarse particles and diluted 20 times with deionized water to obtain the slurry form of dairy manure. The characteristics of diluted dairy manure slurry are presented in Table 1.
Table 1.
Characteristics of 20-fold-diluted dairy manure slurry (n = 3).
| Parameter | Average (S.D.) |
|---|---|
| pH | 7.2 (0.15) |
| Electrical conductivity (κ) (μS/cm) | 710 (50) |
| Dissolved oxygen (DO) (mg/L) | 0.12 (0.02) |
| Turbidity (NTU) | 2070 (40) |
| Suspended solids (SS) (mg/L) | 1513 (26) |
| Chemical oxygen demand (COD) (mg/L) | 2565 (55) |
| Dissolved organic carbon (mg/L) | 106 (12) |
| Zeta potential (mV) | −19.45 (0.43) |
PAC was purchased from Nitto Chemical Industries, Ltd., Kanagawa, Japan. CPAM was obtained from MT Aqua Polymer, Inc., Tokyo, Japan. Table 2 shows the characteristics of CPAM.
Table 2.
Characteristics of CPAMa.
| Parameter | Description/value |
|---|---|
| Polyacrylamide polymer type | C-512 |
| Principal component | Polyacrylic acid ester type |
| Ionic characteristics | Medium/high cationic |
| Molecular weight | 4 million |
| Viscosity (mPas at 25 °C) | 230 |
Product safety information of ARONFLOC and ACCOFLOC. Obtained from the revised fertilizer regulation act of special fertilizers.
2.2. Methods
2.2.1. Experimental design and modeling
In this study, we investigated the effects of PAC, CPAM, and pH on the solid–liquid separation of dairy manure slurry. Our previous study showed that PAC was the best coagulant among the Al coagulants evaluated for the separation of the solid and liquid components of dairy manure slurry [4]. Accordingly, in this study, we selected PAC as the coagulant. Jar tests were performed using a programmable jar testing apparatus (JMD-6E, Miyamoto Riken Ind. Co., Ltd., Osaka, Japan).
2.2.1.1. Single-factor experiments
The preliminary ranges of PAC dosage, CPAM dosage, and pH for the solid–liquid separation of dairy manure slurry were determined by single-factor experiments. Jar tests were carried out separately for PAC, CPAM, and pH in the ranges of 0–100 mg/L, 0–60 mg/L, and 4–8, respectively.
2.2.1.2. Box–Behnken experimental design
After identifying the preliminary ranges of PAC, CPAM, and pH, RSM based on BBD was applied to investigate the best combination of those for achieving the maximum solid–liquid separation efficiency with minimum chemical usage. RSM is a statistical and mathematical technique that is used to determine the relationship between independent factors and response [20]. In other words, RSM is used to fit the polynomial equation to the experimental results [21]. The analyses were carried out using Design Expert software 13 (Trial Version, State-Ease Inc., Minneapolis, USA).
RSM based on Box–Behnken was designed as listed in Table 3. A three-factor three-level BBD model was used to optimize the coagulation and flocculation of dairy manure slurry. Three independent variables, namely, PAC dosage (A), CPAM dosage (B), and pH (C) were selected. The three levels (−1, 0, and +1) of A (PAC dosage), B (CPAM dosage), and C (pH) represented 50, 70, and 90 mg/L, 20, 30, and 40 mg/L, and 5.5, 6.5, and 7.5, respectively.
Table 3.
Different variables and their respective levels of BBD.
| Independent variables (Unit) | Symbol | Coded levels |
||
|---|---|---|---|---|
| Lower limit (–1) | Center (0) | Upper limit (+1) | ||
| PAC dosage (mg/L) | A | 50 | 70 | 90 |
| CPAM dosage (mg/L) | B | 20 | 30 | 40 |
| pH |
C |
5.5 |
6.5 |
7.5 |
| Response variables (Unit) | Constraints | |||
| Turbidity removal efficiency (%) | Y1 | Maximize | ||
| COD removal efficiency (%) | Y2 | Maximize | ||
| Zeta potential (mV) | Y3 | Target is zero | ||
| Residual Al concentration (mg/L) | Y4 | Minimize | ||
Turbidity and COD removal efficiency, zeta potential, and residual Al concentration were designated as the responses for the optimization.
The following Eq. (1) was used to calculate the total number of experiments [22,23].
| (1) |
here, is the number of independent variables and is the number of central points.
A total of 17 experimental runs, including five center points, were performed. Average values from triplicate measurements were used to represent the observed response under each condition. The following widely used second-order polynomial equation (Eq. 2) [24,25] was employed to fit the observed response data (experimental data). The effect of the independent variables (linear, quadratic, and interactive) on response was examined.
| (2) |
Here, is the predicted response variable for the model input independent variables (, ). , , , are regression coefficients for intercept, linear, quadratic, and interaction coefficients, respectively. is the random error of the different variability sources.
The statistical significance of model equations was tested using analysis of variance (ANOVA) with F-test values and respective p-values of each response. A model fit was revealed using the coefficient of determination (R2), adjusted R2, and adequate precision. 3D response surface plots were used to identify the optimum interaction and regions. Upon numerical optimization with the desirability function, the optimum treatment conditions were determined by fixing the desired goals for the highest turbidity and COD removal, the lowest Al concentration, and the zeta potential is equal to zero (Table 3). The numerical model was validated by carrying out experimental runs under optimum conditions.
2.2.2. Jar test procedure
Each set of experiments was conducted with 1 L of 20-fold-diluted dairy manure slurry samples. As the first step, PAC was added to the manure slurry and the solution was rapidly stirred at 200 rpm for 1 min. Secondly, CPAM was added and the slurry was stirred at a moderate speed of 100 rpm for 3 min, followed by slow stirring at 30 rpm for 5 min. After 30 min of settling, treated water samples were collected from 5 cm below the surface.
2.2.3. Analytical techniques
Treated water samples were collected from 5 cm below the surface using a pipette after settling. The physicochemical parameters of water samples were determined in accordance with standard methods for the examination of water and wastewater [26]. Turbidity, COD, and zeta potential were used to investigate the efficiency of chemical coagulation and flocculation to treat dairy manure slurry.
2.2.3.1. Turbidity
Turbidity was measured using a laboratory turbidity meter (2100 N, HACH Company, Colorado, USA).
2.2.3.2. Chemical oxygen demand
The reactor digestion method was used. Samples were homogenized and 2 mL of each sample was added to individual 5–500 mg/L range CODCr test vials, and then they were incubated in a COD reactor (45600, HACH, Colorado, USA) at 150 °C to digest the samples. After 2 h, the CODCr test vials with samples were taken out and allowed to cool to room temperature, and the COD readings were taken in mg/L using a photometer (Spectroquant NOVA 60, Merck, Darmstadt Germany) at 445 nm.
The removal efficiency of turbidity and COD was calculated using Eq. (3).
| (3) |
here, is the initial turbidity and COD concentration prior to the start of the experiment. is the final turbidity and COD concentration after chemical treatment.
2.2.3.3. Zeta potential
The zeta potential was analyzed using a zeta potential and particle size analyzer (ELSZ-2000, Otsuka Electronics Co., Ltd., Osaka, Japan).
Other physicochemical parameters such as pH, electrical conductivity (κ), and oxidation-reduction potential (ORP) were measured using a portable digital meter (HM-40P, DKK-TOA, Tokyo, Japan), a portable conductivity meter (AS710, AS ONE Corporation, Osaka, Japan), and a digital ORP meter (MM-41DP, DKK-TOA, Tokyo, Japan), respectively.
2.2.3.4. Soluble aluminum analysis
The residual Al of the treated water samples was analyzed by a photometric method. The treated water samples were filtered through 0.45 μm nylon syringe hydrophilic filters, and 6 mL of homogenized samples were pipetted into reaction cells. One level of blue microspoon of the reagent Al–1K was added to each sample, and it was vigorously shaken until the reagent was completely dissolved. Then 0.25 mL of reagent Al–2K was added and mixed. The readings were obtained in mg/L using a photometer (Spectroquant NOVA 60) after allowing 5 min for the reaction. The detection limit was 0.02 mg/L.
3. Results and discussion
3.1. Single-factor experiments
3.1.1. Effect of PAC dosage on solid–liquid separation of dairy manure slurry
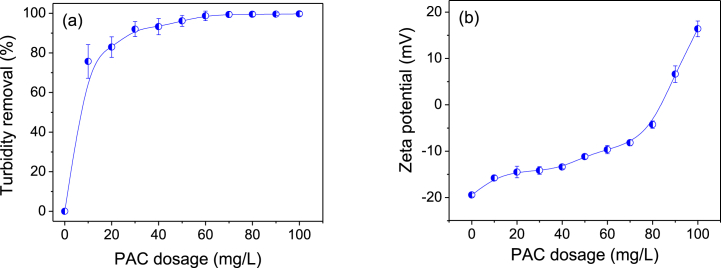
PAC in the range of 0–100 mg/L was tested to identify the preliminary PAC dosage range for the solid–liquid separation of dairy manure slurry. CPAM dosage and pH were kept constant at 30 mg/L and 7, respectively, for each set of PAC experiments. The initial average turbidity and zeta potential of the dairy manure slurry were measured as 2070 ± 40 NTU and −19.45 ± 0.43 mV, respectively.
As shown in Fig. 1a, the turbidity removal efficiency increased when the PAC dosage was increased. However, turbidity removal efficiency was nearly constant at a PAC dosage of 70 mg/L. The average residual turbidity at a PAC dosage of 70 mg/L of was 13 ± 4 NTU. Despite increasing the PAC dosage, no significant further reduction in turbidity was observed. However, the zeta potential at a PAC dosage of 70 mg/L was −8.2 ± 0.63 mV (Fig. 1b). Zeta potential is a key parameter utilized to evaluate coagulation efficiency, providing a precise measure of charge neutralization. When the zeta potential approaches zero, it indicates optimal conditions for the aggregation of solids. Colloidal particles carrying the same electrical charge experience electrostatic repulsion, which causes them to repel each other, resulting in a stable colloidal system [27]. External energy is required to overcome this repulsion between the particles leading to the destabilization of the colloidal system [28]. In this study, as the PAC dosage was increased progressively, the zeta potential increased as a result of the decrease in the strength of the repulsive force between the particles. As shown in Fig. 1b, the zeta potential increased to zero at a PAC dosage between 80 and 90 mg/L as a consequence of the charge neutralization [9].
Fig. 1.
Variations of (a) turbidity removal efficiency and (b) zeta potential of dairy manure slurry as functions of PAC dosage. Error bars represent the standard deviation (n = 3). CPAM dosage and pH were maintained constant at 30 mg/L and 7, respectively.
3.1.2. Effect of CPAM dosage on solid–liquid separation of dairy manure slurry
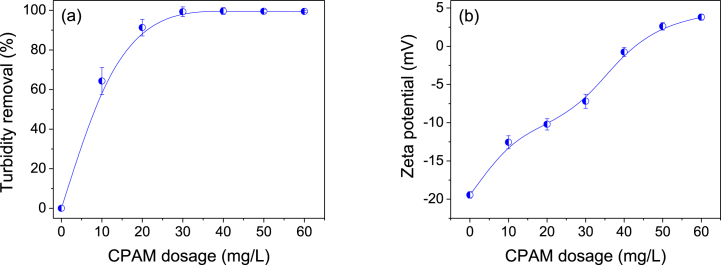
CPAM concentration in the range of 0–60 mg/L was tested to investigate the effect of CPAM dosage on dairy manure slurry treatment. The PAC dosage and pH were kept constant at 70 mg/L and 7, respectively. Fig. 2a reveals that the turbidity removal efficiency remained relatively constant when the CPAM dosage was maintained at 30 mg/L.
Fig. 2.
Variations of (a) turbidity and (b) zeta potential of dairy manure slurry as functions of CPAM dosage. Error bars represent the standard deviation (n = 3). The PAC dosage and pH were maintained constant at 70 mg/L and 7, respectively.
It was found that the optimal dosage of CPAM for achieving maximum turbidity removal was 30 mg/L (Fig. 2a), resulting in a residual turbidity measurement of 15.5 ± 10 NTU. Fig. 2b shows that the zeta potential increased towards the positive side when the CPAM dosage was increased. The zeta potential results clearly demonstrate that CPAM, with its high cationic charge, plays a dominant role in the charge neutralization mechanism for flocculating suspended particles. This dominance is observed over other mechanisms such as hydrogen bonding, bridging, and electrostatic adsorption [29].
3.1.3. Effect of pH on solid–liquid separation of dairy manure slurry
In this section, the effect of pH on the solid–liquid separation of dairy manure slurry was determined. pH in the range of 4–8 was examined while PAC and CPAM dosages were kept constant at 70 and 30 mg/L, respectively, at each set of experiments. A pH of 4 exhibited the maximum turbidity removal efficiency, reaching 97%. There was no significant difference among pH levels from 4 to 7 in terms of turbidity removal (F (8,18) = 62.548, p < 0.001) (Fig. 3). In acidic pHs, highly charged polynuclear Al hydrolysis products are dominant [30]. As the pH became more alkaline, the turbidity removal gradually decreased. The lowest turbidity removal efficiency, reported at pH 8, was measured to be 80%. Furthermore, the zeta potential of the liquid fraction displayed highly negative values at basic pH levels, indicating inadequate destabilization of negatively charged colloids present in the dairy manure slurry. As the pH decreased, the zeta potential approached zero, indicating an increase in H+ concentration [31].
Fig. 3.

Turbidity removal efficiency and final zeta potential of dairy manure slurry as functions of pH. Error bars represent the standard deviation (n = 3). PAC and CPAM dosages were maintained constant at 70 and 30 mg/L, respectively.
3.2. Optimization of solid–liquid separation of dairy manure slurry using BBD
RSM based on BBD was designed for three independent variables and five central points with 17 runs. Table 4 summarizes the BBD matrix with real and coded values of three independent variables and actual (experimental) and predicted responses. The effect of each independent variable and their interaction on response were determined.
Table 4.
Box–Behnken design matrix with actual and predicted responses.
| Run | Experimental conditions |
Response |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Turbidity removal (%) |
COD removal (%) |
Zeta potential (mV) |
Residual Al concentration (mg/L) |
||||||||
| PAC dosage (mg/L) (A) | CPAM dosage (mg/L) (B) | pH (C) | Actual | Predicted | Actual | Predicted | Actual | Predicted | Actual | Predicted | |
| 1 | 70 (0) | 30 (0) | 6.5 (0) | 99.2 | 99.0 | 97.1 | 96.9 | −6.08 | −4.59 | 0.040 | 0.036 |
| 2 | 70 (0) | 40 (+1) | 5.5 (−1) | 99.7 | 99.9 | 96.3 | 96.5 | −1.66 | 1.83 | 0.050 | 0.049 |
| 3 | 90 (+1) | 30 (0) | 7.5 (+1) | 99.8 | 100 | 97.6 | 97.6 | −5.6 | −3.67 | 0.070 | 0.068 |
| 4 | 70 (0) | 30 (0) | 6.5 (0) | 98.7 | 99.0 | 96.7 | 96.9 | −9.6 | −4.59 | 0.040 | 0.036 |
| 5 | 90 (+1) | 40 (+1) | 6.5 (0) | 97.1 | 96.9 | 95.6 | 95.5 | 20.51 | 14.85 | 0.080 | 0.081 |
| 6 | 50 (−1) | 40 (+1) | 6.5 (0) | 99.6 | 99.5 | 97.7 | 97.6 | −5.21 | −10.73 | 0.020 | 0.019 |
| 7 | 70 (0) | 30 (0) | 6.5 (0) | 98.9 | 99.0 | 96.8 | 96.9 | −6.67 | −4.59 | 0.030 | 0.036 |
| 8 | 70 (0) | 30 (0) | 6.5 (0) | 99.3 | 99.0 | 97.3 | 96.9 | −5.14 | −4.59 | 0.040 | 0.036 |
| 9 | 50 (−1) | 30 (0) | 7.5 (+1) | 97.9 | 98.0 | 95.4 | 95.5 | −14.06 | −12.27 | 0.020 | 0.020 |
| 10 | 70 (0) | 40 (+1) | 7.5 (+1) | 99.8 | 99.8 | 97.4 | 97.4 | 1.73 | 2.28 | 0.040 | 0.041 |
| 11 | 70 (0) | 20 (−1) | 7.5 (+1) | 98.7 | 98.5 | 94.7 | 94.5 | −10.88 | −18.23 | 0.030 | 0.031 |
| 12 | 90 (+1) | 30 (0) | 5.5 (−1) | 99.8 | 99.7 | 96.5 | 96.5 | 11.98 | 10.97 | 0.080 | 0.080 |
| 13 | 90 (+1) | 20 (−1) | 6.5 (0) | 99.6 | 99.7 | 96.5 | 96.6 | −9.79 | −7.55 | 0.060 | 0.061 |
| 14 | 50 (−1) | 20 (−1) | 6.5 (0) | 94.5 | 94.7 | 93.4 | 93.4 | −17.31 | −14.93 | 0.020 | 0.019 |
| 15 | 70 (0) | 20 (−1) | 5.5 (−1) | 99.2 | 99.2 | 96.3 | 96.2 | 0.17 | −4.25 | 0.040 | 0.039 |
| 16 | 50 (−1) | 30 (0) | 5.5 (−1) | 99.3 | 99.2 | 97.5 | 97.4 | −12.24 | −13.39 | 0.020 | 0.023 |
| 17 | 70 (0) | 30 (0) | 6.5 (0) | 98.8 | 99.0 | 96.8 | 96.9 | −8.22 | −4.59 | 0.030 | 0.036 |
3.2.1. Model development
Three independent variables (, , and ) and response variable are presented in the following second-order polynomial coded regression model (Eq. (4)) [23,32].
| (4) |
Here, is the regression coefficient. , , and are linear coefficients. , , and are interaction effect coefficients. , , and are quadratic coefficients.
The second-order response variables representing turbidity removal efficiency , COD removal efficiency , zeta potential , and residual Al concentration can be expressed as a function of independent variables using the coded quadratic equations given in Eqs. (5), (6), (7), (8)), which is employed by multiple regression analysis of the experimental data listed in Table 4.
| (5) |
| (6) |
| (7) |
| (8) |
in this study, coefficients of the full equation were used without removing insignificant terms to predict responses [[33], [34], [35]]. The response values can be calculated within the range of BBD. According to Table 4, the predicted results obtained from the models closely matched the experimental data for turbidity, COD, and Al concentration. However, some runs indicated that there was a deviation between predicted and experimental data for the zeta potential. The diagnostic plots show the relationship between predicted data generated by models and actual data (Fig. 4a–d). The data points are located close to the diagonal line, which confirmed that there is a good agreement between experimental and predicted data [22].
Fig. 4.
Relationship between predicted and actual data of responses for (a) turbidity removal, (b) COD removal, (c) zeta potential, and (d) residual Al concentration.
3.2.2. Model verification by ANOVA
The significance and adequacy of the models were tested using ANOVA. Table 5, Table 6, Table 7, Table 8 represent the statistical significance of linear, interaction, and quadratic terms of each model. The model is significant if at least one of the model terms in the equation is significantly correlated to responses [36]. According to the model fit statistics, the quadratic model is suggested to be highly significant among linear, 2-factor interactions (2FI), and quadratic models for turbidity (p = 0.0001), COD (p = 0.0004) removal, and residual Al (p = 0.0274) implying high correlation coefficient (R2) values, 0.9831, 0.9838, and 0.9775, respectively. However, the 2FI model was suggested for the zeta potential (p = 0.0493).
Table 5.
ANOVA statistical results of the response surface quadratic model for turbidity removal.
| Source | Sum of Squares | df | Mean Square | F-value | p-value | |
|---|---|---|---|---|---|---|
| Model (Quadratic) | 27.16 | 9 | 3.02 | 45.26 | <0.0001 | significant |
| A-PAC dosage | 2.98 | 1 | 2.98 | 44.64 | 0.0003 | |
| B-CPAM dosage | 2.1 | 1 | 2.1 | 31.51 | 0.0008 | |
| C-pH | 0.3784 | 1 | 0.3784 | 5.67 | 0.0487 | |
| AB | 14.14 | 1 | 14.14 | 211.99 | <0.0001 | |
| AC | 0.5041 | 1 | 0.5041 | 7.56 | 0.0285 | |
| BC | 0.09 | 1 | 0.09 | 1.35 | 0.2834 | |
| A2 | 2.27 | 1 | 2.27 | 34.06 | 0.0006 | |
| B2 | 1.39 | 1 | 1.39 | 20.84 | 0.0026 | |
| C2 | 3.65 | 1 | 3.65 | 54.67 | 0.0002 | |
| Residual | 0.4668 | 7 | 0.0667 | |||
| Lack of Fit | 0.2125 | 3 | 0.0708 | 1.11 | 0.4419 | not significant |
| Pure Error | 0.2543 | 4 | 0.0636 | |||
| Corrected Total Sum of Squares | 27.63 | 16 | ||||
| Coefficient of variance (CV, %) | 0.26 | |||||
| R2 | 0.9831 | |||||
| Adjusted R2 | 0.9614 | |||||
| Predicted R2 | 0.8626 | |||||
| Adequate precision | 26.53 |
Table 6.
ANOVA statistical results of the response surface quadratic model for COD removal.
| Source | Sum of Squares | df | Mean Square | F-value | p-value | |
|---|---|---|---|---|---|---|
| Model (Quadratic) | 20.13 | 9 | 2.24 | 47.2 | <0.0001 | significant |
| A-PAC dosage | 0.5995 | 1 | 0.5995 | 12.65 | 0.0093 | |
| B-CPAM dosage | 4.9 | 1 | 4.9 | 103.38 | <0.0001 | |
| C-pH | 0.285 | 1 | 0.285 | 6.01 | 0.0439 | |
| AB | 6.71 | 1 | 6.71 | 141.57 | <0.0001 | |
| AC | 2.33 | 1 | 2.33 | 49.08 | 0.0002 | |
| BC | 1.74 | 1 | 1.74 | 36.77 | 0.0005 | |
| A2 | 0.326 | 1 | 0.326 | 6.88 | 0.0343 | |
| B2 | 3.12 | 1 | 3.12 | 65.83 | <0.0001 | |
| C2 | 0.0526 | 1 | 0.0526 | 1.11 | 0.3272 | |
| Residual | 0.3317 | 7 | 0.0474 | |||
| Lack of Fit | 0.0842 | 3 | 0.0281 | 0.4534 | 0.7291 | not significant |
| Pure Error | 0.2475 | 4 | 0.0619 | |||
| Corrected Total Sum of Squares | 20.46 | 16 | ||||
| Coefficient of variance (CV, %) | 0.23 | |||||
| R2 | 0.9838 | |||||
| Adjusted R2 | 0.9629 | |||||
| Predicted R2 | 0.9153 | |||||
| Adequate precision | 24.98 |
Table 7.
ANOVA statistical results of the response surface two-factor interaction model for zeta potential variation.
| Source | Sum of Squares | df | Mean Square | F-value | p-value | |
|---|---|---|---|---|---|---|
| Model (two-factor interaction) | 1211.83 | 6 | 201.97 | 10.45 | 0.0008 | significant |
| A-PAC dosage | 576.64 | 1 | 576.64 | 29.83 | 0.0003 | |
| B-CPAM dosage | 327.42 | 1 | 327.42 | 16.94 | 0.0021 | |
| C-pH | 91.53 | 1 | 91.53 | 4.74 | 0.0546 | |
| AB | 102.01 | 1 | 102.01 | 5.28 | 0.0445 | |
| AC | 62.09 | 1 | 62.09 | 3.21 | 0.1033 | |
| BC | 52.13 | 1 | 52.13 | 2.7 | 0.1316 | |
| Residual | 193.3 | 10 | 19.33 | |||
| Lack of Fit | 180.74 | 6 | 30.12 | 9.59 | 0.0232 | significant |
| Pure Error | 12.56 | 4 | 3.14 | |||
| Corrected Total Sum of Squares | 1405.13 | 16 | ||||
| Coefficient of variance (CV, %) | 93.35 | |||||
| R2 | 0.8624 | |||||
| Adjusted R2 | 0.7799 | |||||
| Predicted R2 | 0.4134 | |||||
| Adequate precision | 11.81 |
Table 8.
ANOVA statistical results of the response surface quadratic model for the variation of residual Al concentration.
| Source | Sum of Squares | df | Mean Square | F-value | p-value | |
|---|---|---|---|---|---|---|
| Model (Quadratic) | 0.0063 | 9 | 0.0007 | 33.8 | <0.0001 | significant |
| A-PAC dosage | 0.0055 | 1 | 0.0055 | 266.12 | <0.0001 | |
| B-CPAM dosage | 0.0002 | 1 | 0.0002 | 9.66 | 0.0171 | |
| C-pH | 0.0001 | 1 | 0.0001 | 5.43 | 0.0526 | |
| AB | 0.0001 | 1 | 0.0001 | 4.83 | 0.0640 | |
| AC | 0 | 1 | 0 | 1.21 | 0.3083 | |
| BC | 0 | 1 | 0 | 0 | 1 | |
| A2 | 0.0003 | 1 | 0.0003 | 13.83 | 0.0075 | |
| B2 | 2.37E-06 | 1 | 2.37E-06 | 0.1143 | 0.7452 | |
| C2 | 0 | 1 | 0 | 2.15 | 0.1863 | |
| Residual | 0.0001 | 7 | 0 | |||
| Lack of Fit | 0 | 3 | 8.33E-06 | 0.2778 | 0.8395 | not significant |
| Pure Error | 0.0001 | 4 | 0 | |||
| Corrected Total Sum of Squares | 0.0064 | 16 | ||||
| Coefficient of variance (CV, %) | 10.90 | |||||
| R2 | 0.9775 | |||||
| Adjusted R2 | 0.9486 | |||||
| Predicted R2 | 0.9089 | |||||
| Adequate precision | 17.90 |
The response models of turbidity and COD removal, and residual Al showed high F values (45.26, 47.2, and 33.8, respectively) with very low p values (<0.0001), which indicated the suitability of the model for analyzing and predicting the results. Smaller p-values indicate that their corresponding coefficients are more significant in terms of predicting [37] and insignificant results from the “Lack of Fit” model justify the significance of the models. However, the model developed for zeta potential exhibited a relatively low F value of 10.45.
The R2 shows changes in the dependent variable owing to the changes in the independent variable. R2 is a measure of goodness of fit to the model, which indicates the degree of correlation between actual and predicted results [32]. High R2 values indicate that the model has acceptable accuracy. The R2 values of turbidity and COD quadratic models were 0.9831 and 0.9838, respectively (Table 5, Table 6), which indicate that the sample variation is attributed to the independent variables within 98% of a confidence interval for turbidity and COD removal efficiency and only about 2% of the total variance cannot be explained by the model [34]. However, the R2 of the two-factor interaction model for zeta potential was 86%, which was lower than the R2 values reported by other quadratic models. The difference between the adjusted R2 and the predicted R2 was <0.2 for turbidity, COD, and residual Al models, which indicates a reasonable agreement between adjusted and predicted R2 values [38]. Furthermore, adequate precision indicates the signal to noise ratio. In other words, adequate precision is represented by the range in predicted data relative to its associated error, if the adequate ratio is greater than four, it is desirable [38]. In this study, all the response models exhibited adequate precision ratios higher than 4 (Table 5, Table 6, Table 7, Table 8), which proved that the predicted data by the models are reliable and thus the models can be used to predict data within the design range. The coefficient of variance (CV) is the ratio of the standard error to the mean value of the response, a measure of the reproducibility of the model. CV less than 10% indicates that the model can be considered reproducible [32]. The very low CV values for turbidity (0.26%) and COD (0.23%) models proved the accuracy and reliability of the results. However, CV values of zeta potential and residual Al models were higher than 10.
3.2.3. Interactive effect of independent factors on solid–liquid separation
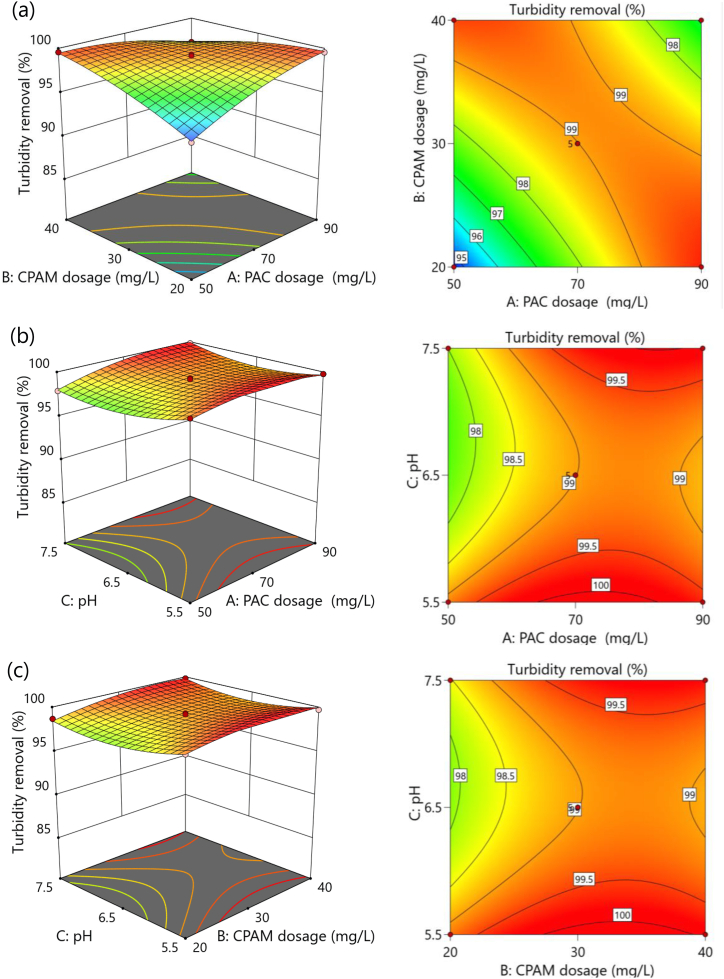
3D surface plots and corresponding contour plots (Fig. 5, Fig. 6, Fig. 7, Fig. 8) are helpful for visualizing the interaction effect of two factors on solid–liquid separation of dairy manure slurry. These plots represent interactions as a function of two factors, while other parameters are fixed at a constant level. The constant levels are central points of the BBD; PAC = 70 mg/L, CPAM dosage = 30 mg/L, and pH = 6.5. The color variation on the 3D surface plots and corresponding contour plots represents the maximum (Red color) and minimum (Blue color) value response variables. The smallest ellipse in the contour plots indicates the maximum predicted response [39].
Fig. 5.
3D response surface plots and two-dimensional contour plots showing the effects of PAC dosage (A), CPAM dosage (B), and pH (C) on the turbidity removal efficiency of dairy manure slurry treatment. (a) Response surface and contour plots of residual turbidity as a function of A and B. (b) Response surface and contour plots of residual turbidity as a function of A and C. (c) Response surface and contour plots of residual turbidity as functions of B and C.
Fig. 6.
3D response surface plots and two-dimensional contour plots showing the effects of PAC dosage (A), CPAM dosage (B), and pH (C) on the COD removal efficiency of dairy manure slurry treatment. (a) Response surface and contour plots of COD removal % as functions of A and B. (b) Response surface and contour plots of COD removal % as functions of A and C. (c) Response surface and contour plots of COD removal % as functions of B and C.
Fig. 7.
3D response surface plots and two-dimensional contour plots showing the effects of PAC dosage (A), CPAM dosage (B), and pH (C) on the zeta potential of the liquid fraction of treated dairy manure slurry. (a) Response surface and contour plots of zeta potential as functions of A and B. (b) Response surface and contour plots of zeta potential as functions of A and C. (c) Response surface and contour plots of zeta potential as functions of B and C.
Fig. 8.
3D response surface plots and two-dimensional contour plots showing the effects of PAC dosage (A), CPAM dosage (B), and pH (C) on the residual Al concentration of the liquid fraction of treated dairy manure slurry. (a) Response surface and contour plots of residual Al concentration as functions of A and B. (b) Response surface and contour plots of residual Al concentration as functions of A and C. (c) Response surface and contour plots of residual Al concentration as functions of B and C.
Fig. 5a–c depict 3D response surface plots and two-dimensional contour plots illustrating the impact of PAC dosage, CPAM dosage, and pH on the turbidity removal efficiency during dairy manure slurry treatment. As shown in Fig. 5a, the turbidity removal efficiency increased when both PAC and CPAM dosages were increased. Optimal conditions for responses were exactly located within the design range as an obvious trough located on the response surface [38]. Significant interaction was observed between PAC and CPAM dosages regarding turbidity removal in the liquid fraction of dairy manure slurry (p < 0.0001) (Table 5). However, it was found that at high concentrations of both PAC and CPAM, the presence of residual chemicals in the treated water resulted in an increase in residual turbidity, leading to a decrease in turbidity removal efficiency. The interaction effect of PAC dosage and pH was significant at p-values of 0.0285. However, ANOVA results revealed that there is no interaction effect of pH on CPAM dosage (p = 0.2834) for the removal of turbidity (Table 5).
Fig. 6a–c shows the interaction effects of PAC, CPAM, and pH on COD removal efficiency. The COD removal efficiency increased with increasing chemical dosage (Fig. 6a). There was a significant interaction effect of PAC and CPAM dosage on COD removal (p < 0.0001) (Table 6). As the pH shifted towards basic conditions, the efficiency of COD removal decreased (Fig. 6b and c). ANOVA results for the interaction effect of pH and PAC on COD removal proved that there is significant interaction between pH and PAC on COD removal (p = 0.0002). Similarly, the COD removal efficiency was reduced at basic pHs when CPAM was used (p = 0.0005) (Table 6). At high chemical dosages compared to the optimum conditions, no significant impact of pH on COD removal was observed. This can be attributed to the dominant sweep coagulation mechanism at basic pH [40], which requires a higher chemical dosage to achieve effective removal.
The zeta potential plots (Fig. 7a–c) showed that there is a positive impact of both PAC and CPAM on increasing the zeta potential towards the positive side (Fig. 7a). This is because the addition of chemicals with a high positive charge and cationic properties enhances the solid–liquid separation of dairy manure by neutralizing the negatively charged solids and facilitating their flocculation. ANOVA results showed that there is an interaction effect between PAC and CPAM dosage on the variation of zeta potential (p = 0.0445) (Table 7). The pH of the solution also affected the zeta potential as H+ ions neutralize the negatively charged ions in the solution. However, statistical results indicated that there is less impact of pH on PAC (p = 0.1033) or CPAM (p = 0.1316) in terms of the variation of zeta potential (Table 7).
Fig. 8a–c presents 3D response surface plots and two-dimensional contour plots depicting the influence of PAC dosage, CPAM dosage, and pH on the residual aluminum (Al) concentration in the treated water. As shown in Fig. 8a and b, the residual Al concentration increased when the PAC dosage was increased. There was no interaction effect of PAC and CPAM on residual Al concentrations in the treated liquid fraction (p = 0.0640) (Table 8). Particularly at low pH levels, the soluble Al concentration increased (Fig. 8b). This is because the amphoteric behavior of Al(OH)3 at acidic pHs enhanced the production of soluble Al species such as Al3+, Al(OH)2+, and Al(OH)2+ [41].
3.2.4. Numerical optimization using the desirability function
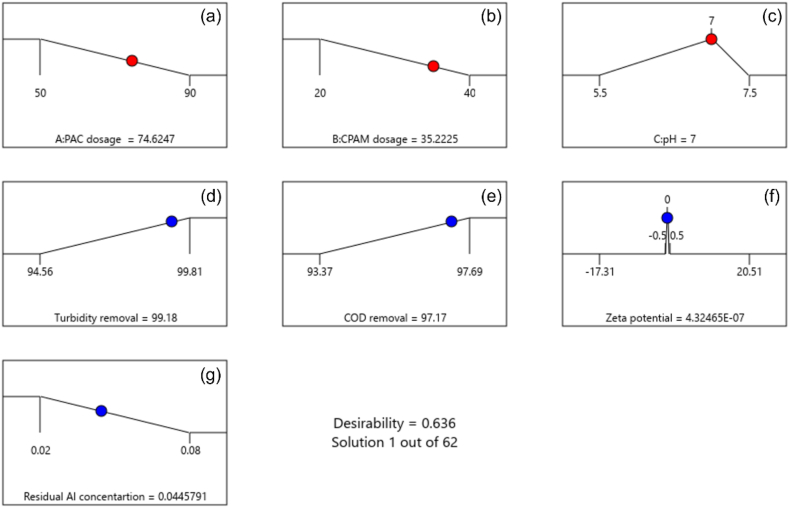
In this section, the desirability function was employed to simultaneously optimize the independent variables that achieved the maximum solid–liquid separation in dairy manure slurry. Desirability is an objective function ranging from 0 to 1 [42]. Close to zero means the value of the response is outside the required acceptable range, and close to “1” indicates the expected goal [42]. The numerical optimum conditions were obtained by setting the goals of independent variables such as PAC dosage “minimize”, CPAM dosage “minimize” and pH “target in 7” to minimize the cost and residual Al concentration in treated water. Goals on responses were set as turbidity removal “maximize”, COD removal “maximize”, zeta potential “target is zero”, and residual Al concentration “minimize”.
Ramp plots show the optimized parameters and corresponding response obtained through numerical optimization (Fig. 9a–g). As shown in Fig. 9a–c, the optimum conditions of PAC, CPAM, and pH were ∼75 mg/L, 35 mg/L, and 7, respectively, with a model desirability of 0.636. When several factors and responses are used, all the goals become associated with combined desirability (Fig. 10). Hence, achieving a very high desirability value is challenging since it depends on the proximity of each optimum condition to its upper and lower limits established at the outset. In this optimization, we found a comprehensive set of conditions of independent variables, resulting in a maximized efficiency while concurrently minimizing the residual Al concentration. The predicted turbidity and COD removal efficiency were 99.2% (Figs. 9d) and 97.2% (Fig. 9e), respectively, at 0.045 mg/L of residual Al concentration (Fig. 9g).
Fig. 9.
Ramp plots of numerically optimized parameters and conditions. (a) PAC dosage, (b) CPAM dosage, (c) pH, (d) turbidity removal efficiency, (e) COD removal efficiency, (f) zeta potential, and (g) residual Al concentration.
Fig. 10.
Individual and combined disabilities of different parameters.
3.2.5. Model validation by experiments
The validity and predictability of models developed at numerical optimization (Fig. 9) were verified by experimental runs.
To validate the predicted results from the model, triplicate experiment runs were conducted under the optimal conditions. The comparison between the experimental and predicted values, as presented in Table 9, revealed no significant difference. This finding confirms the predictability of the model developed using RSM based on the BBD. Consequently, the proposed model in this study can be deemed reliable and applicable for reuse within the designated range of the design.
Table 9.
Validation of predicted results with experimental results under optimum conditions.
| Response | Mean (SD) |
|
|---|---|---|
| Actual | Predicted | |
| Turbidity removal (%) | 99.5 (1.3) | 99.18 |
| COD removal (%) | 96.8 (0.9) | 97.17 |
| Zeta potential (mV) | 1.2 (1.4) | 0 |
| Residual Al concentration (mg/L) | 0.04 (0.02) | 0.045 |
4. Conclusions
In this study, the solid-liquid separation of dairy manure slurry was optimized using PAC and CPAM through RSM based on BBD. The responses obtained from the quadratic models developed for turbidity and COD removal, as well as residual Al concentration, were statistically significant (p < 0.05) at a 95% confidence level. This confirms the validity, accuracy, and acceptability of the proposed models. Numerical optimization with the desirability function predicted that the optimal combination of PAC and CPAM dosages at pH 7 was 75 mg/L and 35 mg/L, respectively, resulting in maximum turbidity (99%) and COD removal efficiency (97%). The experimental results closely aligned with the predicted values from the models, and it was verified that the treated water met the discharge water quality standards in terms of residual turbidity and Al concentration. Hence, the application of PAC and CPAM in combination, under optimized conditions, is a highly recommended approach for achieving efficient, cost-effective, and environmentally safe solid–liquid separation in livestock manure slurry.
Author contribution statement
Kasun Meetiyagoda, Toshinori Takahashi, Takeshi Fujino: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Data availability statement
Data included in article/supp. material/referenced in article.
Additional information
No additional information is available for this paper.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This study was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (22K12472) and a research grant from the Strategic Research Area for Sustainable Development in East Asia (SRASDEA), Saitama University.
Contributor Information
Thenuwara Arachchige Omila Kasun Meetiyagoda, Email: 822kasun@gmail.com.
Toshinori Takahashi, Email: t.takahashi.091@ms.saitama-u.ac.jp.
Takeshi Fujino, Email: fujino@mail.saitama-u.ac.jp.
References
- 1.Varma V.S., Parajuli R., Scott E., Canter T., Lim T.T., Popp J., Thoma G. Dairy and swine manure management – challenges and perspectives for sustainable treatment technology. Sci. Total Environ. 2021;778 doi: 10.1016/J.SCITOTENV.2021.146319. [DOI] [PubMed] [Google Scholar]
- 2.Font-Palma C. Methods for the Treatment of Cattle Manure—A Review, C. 2019;5:27. doi: 10.3390/c5020027. [DOI] [Google Scholar]
- 3.Smith K.A., Williams A.G. Production and management of cattle manure in the UK and implications for land application practice. Soil Use Manag. 2016;32:73–82. doi: 10.1111/sum.12247. [DOI] [Google Scholar]
- 4.Science E. 2022. Solid – Liquid Separation of Dairy Barn by Electrocoagulation with Cationic Polymer Coagulant Solid – Liquid Separation of Dairy Barn by Electrocoagulation with Cationic Polymer Coagulant. [DOI] [Google Scholar]
- 5.Liu Z., Zhou L., Liu F., Gao M., Wang J., Zhang A., Liu Y. Impact of Al-based coagulants on the formation of aerobic granules: comparison between poly aluminum chloride (PAC) and aluminum sulfate (AS) Sci. Total Environ. 2019;685:74–84. doi: 10.1016/J.SCITOTENV.2019.05.306. [DOI] [PubMed] [Google Scholar]
- 6.Wu X., Ge X., Wang D., Tang H. Distinct mechanisms of particle aggregation induced by alum and PACl: floc structure and DLVO evaluation. Colloids Surfaces A Physicochem. Eng. Asp. 2009;347:56–63. doi: 10.1016/J.COLSURFA.2008.12.005. [DOI] [Google Scholar]
- 7.Srivastava V.C., Mall I.D., Mishra I.M. Treatment of pulp and paper mill wastewaters with poly aluminium chloride and bagasse fly ash. Colloids Surfaces A Physicochem. Eng. Asp. 2005;260:17–28. doi: 10.1016/J.COLSURFA.2005.02.027. [DOI] [Google Scholar]
- 8.Zouboulis A., Traskas G., Samaras P. Comparison of efficiency between poly-aluminium chloride and aluminium sulphate coagulants during full-scale experiments in a drinking water treatment plant. Separ. Sci. Technol. 2008;43:1507–1519. doi: 10.1080/01496390801940903. [DOI] [Google Scholar]
- 9.Wei N., Zhang Z., Liu D., Wu Y., Wang J., Wang Q. Coagulation behavior of polyaluminum chloride: effects of pH and coagulant dosage. Chin. J. Chem. Eng. 2015;23:1041–1046. doi: 10.1016/J.CJCHE.2015.02.003. [DOI] [Google Scholar]
- 10.Rico C., Rico J.L., García H., García P.A. Solid – liquid separation of dairy manure: distribution of components and methane production. Biomass Bioenergy. 2012;39:370–377. doi: 10.1016/J.BIOMBIOE.2012.01.031. [DOI] [Google Scholar]
- 11.Duggan K.L., Morris M., Bhatia S.K., Khachan M.M., Lewis K.E. Effects of cationic polyacrylamide and cationic starch on aquatic life. J. Hazardous, Toxic, Radioact. Waste. 2019;23 doi: 10.1061/(asce)hz.2153-5515.0000467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Abdulhameed A.S., Firdaus Hum N.N.M., Rangabhashiyam S., Jawad A.H., Wilson L.D., Yaseen Z.M., Al-Kahtani A.A., Alothman Z.A. Statistical modeling and mechanistic pathway for methylene blue dye removal by high surface area and mesoporous grass-based activated carbon using K2CO3 activator. J. Environ. Chem. Eng. 2021;9 doi: 10.1016/J.JECE.2021.105530. [DOI] [Google Scholar]
- 13.Ebba M., Asaithambi P., Alemayehu E. Development of electrocoagulation process for wastewater treatment: optimization by response surface methodology. Heliyon. 2022;8 doi: 10.1016/J.HELIYON.2022.E09383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ghelich R., Jahannama M.R., Abdizadeh H., Torknik F.S., Vaezi M.R. Central composite design (CCD)-Response surface methodology (RSM) of effective electrospinning parameters on PVP-B-Hf hybrid nanofibrous composites for synthesis of HfB2-based composite nanofibers. Compos. B Eng. 2019;166:527–541. doi: 10.1016/J.COMPOSITESB.2019.01.094. [DOI] [Google Scholar]
- 15.Bashir M.J.K., Amr S.S.A., Aziz S.Q., Aun N.C., Sethupathi S., Technology G., Tunku U., Rahman A. Wastewater treatment processes optimization using response surface methodology (RSM) compared with conventional methods : review and comparative study department of environmental engineering, faculty of engineering School of civil engineering, enginee, middle-east. J. Sci. Res. 2015;23:244–252. doi: 10.5829/idosi.mejsr.2015.23.02.52. [DOI] [Google Scholar]
- 16.Somayajula A., Asaithambi P., Susree M., Matheswaran M. Sonoelectrochemical oxidation for decolorization of reactive red 195. Ultrason. Sonochem. 2012;19:803–811. doi: 10.1016/J.ULTSONCH.2011.12.019. [DOI] [PubMed] [Google Scholar]
- 17.Salari M., Nikoo M.R., Al-Mamun A., Rakhshandehroo G.R., Mooselu M.G. Optimizing Fenton-like process, homogeneous at neutral pH for ciprofloxacin degradation: comparing RSM-CCD and ANN-GA. J. Environ. Manag. 2022;317 doi: 10.1016/J.JENVMAN.2022.115469. [DOI] [PubMed] [Google Scholar]
- 18.Ngan C.L., Basri M., Lye F.F., Fard Masoumi H.R., Tripathy M., Abedi Karjiban R., Abdul-Malek E. Comparison of Box–Behnken and central composite designs in optimization of fullerene loaded palm-based nano-emulsions for cosmeceutical application. Ind. Crop. Prod. 2014;59:309–317. doi: 10.1016/J.INDCROP.2014.05.042. [DOI] [Google Scholar]
- 19.Huang X., Lv Z., Zhao B., Zhang H., Yao X., Shuai Y. Optimization of operating parameters for methane steam reforming thermochemical process using Response Surface Methodology. Int. J. Hydrogen Energy. 2022;47:28313–28321. doi: 10.1016/J.IJHYDENE.2022.06.166. [DOI] [Google Scholar]
- 20.Bhattacharya S.S., Banerjee R. Laccase mediated biodegradation of 2,4-dichlorophenol using response surface methodology. Chemosphere. 2008;73:81–85. doi: 10.1016/J.CHEMOSPHERE.2008.05.005. [DOI] [PubMed] [Google Scholar]
- 21.Peng X., Yang G., Shi Y., Zhou Y., Zhang M., Li S. Box–Behnken design based statistical modeling for the extraction and physicochemical properties of pectin from sunflower heads and the comparison with commercial low-methoxyl pectin. Sci. Rep. 2020;10:1–10. doi: 10.1038/s41598-020-60339-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thirugnanasambandham K., Karri R.R. Preparation and characterization of Azadirachta indica A. Juss. plant based natural coagulant for the application of urban sewage treatment: modelling and cost assessment. Environ. Technol. Innov. 2021;23 doi: 10.1016/J.ETI.2021.101733. [DOI] [Google Scholar]
- 23.Akar S.T., Sayin F., Turkyilmaz S., Akar T. Multivariate optimization of the decolorization process by surface modified biomaterial: Box–Behnken design and mechanism analysis. Environ. Sci. Pollut. Res. 2014;21:13055–13068. doi: 10.1007/s11356-014-3245-5. [DOI] [PubMed] [Google Scholar]
- 24.Huzir N.M., Aziz M.M.A., Ismail S.B., Mahmood N.A.N., Umor N.A., Faua’ad Syed Muhammad S.A. Optimization of coagulation-flocculation process for the palm oil mill effluent treatment by using rice husk ash. Ind. Crop. Prod. 2019;139 doi: 10.1016/J.INDCROP.2019.111482. [DOI] [Google Scholar]
- 25.Kang C., Zhao Y., Tang C., Addo-Bankas O. Use of aluminum-based water treatment sludge as coagulant for animal farm wastewater treatment. J. Water Process Eng. 2022;46 doi: 10.1016/J.JWPE.2022.102645. [DOI] [Google Scholar]
- 26.AWWA-American Water Works Association . American Public Health Association; 1995. Standard Methods for the Examination of Water and Wastewater. [Google Scholar]
- 27.Singh D., Malik K., Sindhu M., Kumari N., Rani V., Mehta S., Malik K., Ranga P., Sharma K., Dhull N., Malik S., Arya N. Biostimulation of anaerobic digestion using iron oxide nanoparticles (IONPs) for increasing biogas production from cattle manure. Nanomaterials. 2022;12 doi: 10.3390/nano12030497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Razali M.A.A., Ahmad Z., Ahmad M.S.B., Ariffin A. Treatment of pulp and paper mill wastewater with various molecular weight of polyDADMAC induced flocculation. Chem. Eng. J. 2011;166:529–535. doi: 10.1016/J.CEJ.2010.11.011. [DOI] [Google Scholar]
- 29.Ren B., Min F., Chen J., Fang F., Liu C. Adsorption mechanism insights into CPAM structural units on kaolinite surfaces: a DFT simulation. Appl. Clay Sci. 2020;197 doi: 10.1016/J.CLAY.2020.105719. [DOI] [Google Scholar]
- 30.Klimiuk E., Filipkowska U., Korzeniowska A. Effects of pH and coagulant dosage on effectiveness of coagulation of reactive dyes from model wastewater by polyaluminium chloride (PAC) Pol. J. Environ. Stud. 1999;8:73–79. [Google Scholar]
- 31.Yan M., Wang D., Yu J., Ni J., Edwards M., Qu J. Enhanced coagulation with polyaluminum chlorides: role of pH/Alkalinity and speciation. Chemosphere. 2008;71:1665–1673. doi: 10.1016/J.CHEMOSPHERE.2008.01.019. [DOI] [PubMed] [Google Scholar]
- 32.Agarry S.E., Ogunleye O.O. Box-Behnken design application to study enhanced bioremediation of soil artificially contaminated with spent engine oil using biostimulation strategy. Int. J. Energy Environ. Eng. 2012;3:1–14. doi: 10.1186/2251-6832-3-31. [DOI] [Google Scholar]
- 33.López-López J.A., Borrego-Corchado C., Mánuel M.P., Espada-Bellido E. A simple and economical spectrofluorimetric alternative for Al routine analysis in seafood. Talanta. 2018;182:210–217. doi: 10.1016/J.TALANTA.2018.01.092. [DOI] [PubMed] [Google Scholar]
- 34.Bae S., Shoda M. Statistical optimization of culture conditions for bacterial cellulose production using Box-Behnken design. Biotechnol. Bioeng. 2005;90:20–28. doi: 10.1002/bit.20325. [DOI] [PubMed] [Google Scholar]
- 35.Nikerel I.E., Öner E.T., Kirdar B., Yildirim R. Optimization of medium composition for biomass production of recombinant Escherichia coli cells using response surface methodology. Biochem. Eng. J. 2006;32:1–6. doi: 10.1016/J.BEJ.2006.08.009. [DOI] [Google Scholar]
- 36.Sibiya N.P., Amo-Duodu G., Kweinor Tetteh E., Rathilal S. Response surface optimisation of a magnetic coagulation process for wastewater treatment via Box-Behnken. Mater. Today Proc. 2022;62 doi: 10.1016/J.MATPR.2022.02.098. S122–S126. [DOI] [Google Scholar]
- 37.Dadban Shahamat Y., Masihpour M., Borghei P., Hoda Rahmati S. Removal of azo red-60 dye by advanced oxidation process O3/UV from textile wastewaters using Box-Behnken design. Inorg. Chem. Commun. 2022;143 doi: 10.1016/J.INOCHE.2022.109785. [DOI] [Google Scholar]
- 38.Kumar S.S., Bishnoi N.R. Coagulation of landfill leachate by FeCl3: process optimization using Box–Behnken design (RSM) Appl. Water Sci. 2017;7:1943–1953. doi: 10.1007/s13201-015-0372-1. [DOI] [Google Scholar]
- 39.Dwivedi G., Sharma M.P. Application of Box–Behnken design in optimization of biodiesel yield from Pongamia oil and its stability analysis. Fuel. 2015;145:256–262. doi: 10.1016/J.FUEL.2014.12.063. [DOI] [Google Scholar]
- 40.Meetiyagoda T.A.O.K., Fujino T. Optimization of electrocoagulation–flotation treatment with an aluminum anode to enhance Microcystis aeruginosa cell removal efficiency. J. Water Process Eng. 2022;48 doi: 10.1016/J.JWPE.2022.102871. [DOI] [Google Scholar]
- 41.Maldhure A., Khadse G., Labhasetwar P. Effect of clariflocculator and pulsator based sedimentation technology and poly-aluminium chloride coagulant type on the efficiency of the water treatment plant. Water Supply. 2022;22:2793–2802. doi: 10.2166/WS.2021.434. [DOI] [Google Scholar]
- 42.Trigueros D.E.G., Braun L., Hinterholz C.L. Environmental and economic feasibility of the treatment of dairy industry wastewater by photo-Fenton and electrocoagulation process: multicriteria optimization by desirability function. J. Photochem. Photobiol. Chem. 2022;427 doi: 10.1016/J.JPHOTOCHEM.2022.113820. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. material/referenced in article.