Abstract
The main objective of this work was to study the effects of carbon nanotubes (CNTs) on the strength and electrical properties of cement mortar. Molecular dynamic simulations (MDSs) were carried out to determine the mechanical and electrical properties of a cementitious composite and its associated mechanisms. To model the atomic structure of a calcium silicate hydrate (C-S-H) gel, tobermorite 11Å was chosen. Single-walled carbon nanotubes (SWCNTs) embedded in a tobermorite structure were tested numerically. In particular, it was concluded that a piezoelectric effect can be effectively simulated by varying the concentration levels of carbon nanotubes. The deformation characteristics were analyzed by subjecting a sample to an electrical field of 250 MV/m in the z-direction in a simulation box. The results indicated a progressively stronger converse piezoelectric response with an increasing proportion of carbon nanotubes. Additionally, it was observed that the piezoelectric constant in the z-direction, denoted by d33, also increased correspondingly, thereby validating the potential for generating an electrical current during sample deformation. An innovative experiment was developed for the electrical characterization of a cementitious composite of carbon nanotubes. The results showed that the electrostatic current measurements exhibited a higher electric sensitivity for samples with a higher concentration of CNTs.
Keywords: carbon nanotubes, tobermorite, cement mortar, electrical and mechanical properties, molecular dynamics
1. Introduction
Concrete, a very old material, has been widely used since the 19th century. It is the most commonly used material in the construction of civil engineering structures. Since climatic warming is a hard fact, its use is questioned because of its significant carbon footprint. Today, researchers are working to improve its physical and mechanical characteristics, as well as its durability, by mixing cement paste with different additive powders or nanoparticles. These nanoadded substances are generally used with superplasticizers. One of the most useful nanoadditives these days is carbon nanotubes (CNTs). The exceptional mechanical, electrical, and thermal properties of carbon nanotubes (CNTs) [1,2,3] make them beneficial for applications in various areas of civil engineering. The use of CNTs improves the mechanical properties of concretes, as reported in the literature [4,5]. However, objective of recent research is not only to focus on improving the mechanical properties but also to view CNTs as an adaptive and evolving material. Inducing the piezoresistive effect in cementitious materials to monitor structures can be achieved via the use of conductive fillers such as carbon nanofibers, carbon nanotubes, and graphene [6,7,8,9,10]. Azhari, F. et al. [8] considered cement-based sensors, including carbon nanofibers or carbon nanotubes, to change the resistivity, with good results for sensors with both nanotubes and nanofibers. Zhao, P. et al. [9] showed an improvement in the piezoelectric properties when carbon nanotubes were dispersed in cement-based composites in the range of 0 to 0.9 vol% (volume percentage). Gong et al. 2011 [10] created composites using Portland cement and PZT powders with the inclusion of modified CNTs ranging from 0 to 1.3 vol%. The best outcome was achieved when the concentration of the modified CNTs was 0.6 vol%. The results showed that the highest constant d33 (see Equation (2) below) was equal to 62 pC/N for a 0.3 vol% CNT.
Electrical conductivity is one of the properties that the microstructure of cement cannot naturally develop. The resistivity of concrete varies from 105 Ω/mm to a range of 1012 Ω/mm between wet and dry concrete, respectively, changing from a semiconductor to an insulator in these two phases, thereby allowing evaporable water to be considered as having an important role in electrical conductivity. The ion concentration in water induces an ionic association that leads to the formation of C-S-H gel, consequently decreasing the mobility of the ions due to the electrical insulation layer in the cement grains. After modeling a concrete sample, the conductivity of the aqueous phase, facilitated by the dissolved ions, was significant. So, the resistivity was very low; however, this resistivity increased with the hydration of the concrete, indicating a proportionality between the evolution of resistivity and the evolution of strength. This variation in resistivity could help predict the performance and thus indicate the age factor of structures [1]. At this point, the modification of concrete to obtain electrical properties is very promising for structural health monitoring applications, for example. In this study, we combined experimental and numerical research to investigate the effects on mechanical and electrical properties caused by the modification of cement with carbon nanotubes. The first part of our study focuses on numerical simulations. In these simulations, the dynamics occur through discrete interactions; in our case, this occurs with atoms, which are called particles. The number of particles used in the simulations in this study varied depending on the number of carbon nanotubes incorporated into the tobermorite structure. These simulations were made possible by the ongoing development of the LAMMPS program for molecular modeling, which is a computational tool that continuously improves its ability to accurately represent the physical, chemical, and biological characteristics of systems composed of interacting molecules and atoms [11].
In addition, innovative experimental tests were conducted to measure the electrical currents in prismatic mortar samples of 40 × 40 × 80 mm with carbon nanotubes in weight percentages (wt.%) by weights of cement of 0.00 wt.%, 0.006 wt.%, and 0.018 wt.%. The effectiveness of CNTs in modifying the properties of concrete is largely determined by their level of dispersion [12]. There is a general consensus that standard mixing or manual mixing methods are insufficient for achieving the uniform dispersion of CNTs [13]. Consequently, various dispersion techniques, such as sonication and CNT functionalization, have been devised to achieve stable and uniform aqueous CNT dispersions [14]. It should be noted, however, that the CNT dispersion obtained through sonication tends to re-agglomerate over time, resulting in a decrease in the dispersion quality. For the experimental test, we utilized a Masterbatch CW2-45, which was produced by Arkema Group Co. To disperse the premix, we employed a high-speed bead mill mixer with 55% carboxymethylcellulose and 45% MWCNT. This Masterbatch can be used directly in the water needed to prepare the cement paste, which helps to avoid the coagulation of carbon nanotubes in the dispersion. This technology has been patented for use in cement systems [15].
Therefore, the aim of this paper was to focus on the modification of the cement paste structure via the addition of CNTs. To achieve this, we aimed to determine the atomic structure of the C-S-H/CNT composite and simulate it.
2. Molecular Dynamics Simulation
To elucidate the initiation of electrical conductivity and strength improvement in the cementitious composite with CNTs, an understanding of the interaction processes between nanoadditives and cement paste is needed. The electrical and mechanical properties of the cement paste containing CNTs were determined using a molecular dynamics study. The piezoelectric effect can be obtained using applied strains. Under compression or tension, the atoms change position in the crystal structure and generate a voltage. The polarization along the r-axis can be obtained via the following process:
| (1) |
where qi is the charge of the ith atom, ri is the r-coordinate of the ith atom, N is the number of atoms, and V is volume.
When an electric field is applied to generate deformations, the piezoelectric effect is simulated. It can be represented by matrices [11] to obtain the strain resulting from the elastic, thermal, electric, and magnetic phenomena. The tensors for variables such as the stress , electric field , magnetic field , and temperature differential can be represented as follows:
| (2) |
where is the elastic compliance, is piezo-electric, is piezo-magnetic, and is the thermal expansion tensor.
Apart from the aforementioned equation, we can represent the effects of interest in this study using another equation that eliminates the magnetic effect. This can be expressed as:
| (3) |
where is the electric displacement field, is the piezo-electric tensor, is the material electric permittivity, and is the pyro-electric tensor.
For this study, we selected tobermorite as the main constituent of cement after hydration, as it has a similar structure to that of the C-S-H gel. Tobermorite is a crystalline and natural mineral with the chemical formula Ca5Si6016(OH)24H2O. There are different subspecies of tobermorite categorized by their interlayer spacing, with tobermorite 11Å being the most commonly used model to describe cement paste in MD simulations [16,17,18]. Its initial structure is monoclinic and has vectors a = 6.735Å, b = 7.385Å, and c = 22.487Å, and angles between vectors α = 90°, β = 90°, and γ = 123.25°, as determined by Merlino in 1999 [19].
To create the initial configuration system, a Python code was utilized. The triclinic unit cell basis can be expressed in a matrix format using the following formula:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
The vector format was used to include the fractional positions and the positions were extended in the three cartesian dimensions using three loops based on the system size to create a supercell, as shown in Figure 1. We employed tobermorite 11Å supercells of size 5 × 5 × 3(Å), containing a total of 9683 to 9899 atoms in this project.
Figure 1.
The process used to generate the configuration of the tobermorite 11Å system.
We opted for a single-wall carbon nanotube, specifically the armchair (3,3)-type with a diameter of 4.073Å and length of around 70Å, due to its ideal diameter-to-insertion ratio within the tobermorite structure. The nanotubes were inserted into the tobermorite structure along the z-axis (Figure 1) after establishing a vacuum in the structure. In the context of this investigation, the word “vacuum” denotes the empty space generated to accommodate the nanotube insertion into the tobermorite structure while preserving the system’s neutral charge. This was accomplished by refraining from allocating unit cells to a specific location in the xy plane, resulting in the absence of atoms within the simulation box. In Figure 2, to create a void in the xy plane and along the z-direction for the 5 × 5 × 3 supercell to insert one CNT, unit cells U331, U332, and U333 were not considered in the code. As a result, the code created unit cells around the nanotube. When the unit cell’s geometry, particularly its cross-sectional dimensions, closely matches the targeted hole diameter, the ensuing vacuum within the monoclinic-shaped tobermorite 11Å exhibits a cylindrical appearance after the minimization procedure, as illustrated in Figure 2. Therefore, it could be advantageous to consider the dimensions of the unit cell during the creation of the hole to obtain the desired shape of the void. There are alternative approaches to incorporating CNTs into tobermorite, apart from the method mentioned previously. For example, in a study by Eftekhari M. et al. [20], a cylindrical diameter of a hole, which was initially zero, was incrementally increased using the “fix ident cylinder” command of LAMMPS [21]. Generating a vacuum is also possible by removing the less stable atoms while keeping the molecular neutral following the verification of the charge [22]. Plassard C. et al. [23] noted the absence of silica tetrahedral in tobermorite like C-S-H and accordingly identified the silicon atoms with lower stability within the silicon chains. By eliminating the less stable silicon atoms, the system’s charge can remain neutral while altering the geometry of the silica tetrahedron to a silica trigonal pyramidal structure.
Figure 2.
The procedural steps for incorporating a CNT within the tobermorite 11Å unit cell.
To govern the interaction between the carbon atoms of CNT, we adopted the Tersoff potential [24]. The cumulative energy associated with the interatomic forces between all the atoms within the tobermorite structure is derived from the summation of all the various types of atomic interactions. Such interactions between the atoms of tobermorite and CNT are described in numerous studies, such as in [25,26].
To examine the incidence of the concentration of CNT in the cement paste, systems without CNT and one, two, and three CNTs that yield 0.00%, 1.22%, 2.55%, and 4.00% of CNTs by weight (wt.%) of tobermorite were prepared (Figure 3). To determine the concentrations, one can calculate the product of the total number of atoms present in the system and their respective atomic masses.
Figure 3.
Four different systems comprising the minimized CNT-reinforced tobermorite structures were employed in the simulations.
The simulation employed periodic boundary conditions to simulate a larger system and prevent the boundary effect. After minimization, an NPT ensemble was utilized with a time step of 1 femtosecond at a temperature of 300 K and zero pressure to regulate the temperature and pressure of the simulation box.
3. Experimental Program
3.1. Materials
3.1.1. Carbon Nanotubes
Multi-wall carbon nanotubes (MWCNT) from Arkema company were used in this study. The product used for this experiment was Graphistrength® CW 2-45, which is a masterbatch with a high concentration of 45% by weight of pre-dispersed carbon nanotubes Graphistrength® C100 (Figure 4) with the typical properties presented in Table 1, perfectly dispersed in carboxyl methyl cellulose (CMC).
Figure 4.
Graphistrength® C100 at different scales [27].
Table 1.
Properties of multi-walled carbon nanotubes (MWCNTs).
| Description | MWCNT Graphistrength C100 | |
|---|---|---|
| Production process | Catalytic chemical vapor deposition (CCVD) | |
| Powder characteristics | Apparent density | 50–150 kg/m3 |
| Mean agglomerate size | 200–500 μm | |
| Weight loss at 105 °C | <1% | |
| MWNT characteristics | C content | >90 wt.% |
| Free amorphous carbon | No detectable (SEM/TEM) | |
| Mean number of walls | 5–15 nm | |
| Outer mean diameter | 10–15 nm | |
| Length | 0.1–10 μm |
Graphistrength® CW 2-45 is presented in the form of pellets with the key characteristics given in Table 2.
Table 2.
Main characteristics of Graphistrength® CW 2-45.
| Characteristic | Unit | Typical Value |
|---|---|---|
| Aspect | Black Pellets | |
| MWCNT with purity > 90% content | wt.% | 55 |
| CMC content | wt.% | 45 |
3.1.2. Cement, Sand, and Mortar
PERFORMAT® CEM I 52,5 N CE PM-CP2 NF was used to produce the mortar. Table 3 summarises the composition of clinker and some physical properties of the cement used in this work, provided by the Vicat group, France.
Table 3.
Composition of clinker and some physical properties of source cement.
| Mineralogical phases of clinker | C3S (%) | 60.0 |
| C2S (%) | 15.5 | |
| C3A (%) | 7.1 | |
| C4AF (%) | 10.8 | |
| Physical characteristics | Density (g/cm3) | 3.17 |
| Blaine number (cm2/g) | 4150 | |
| Setting start time (min) | 150 | |
| equivalent diameter (μm) | 11.8 |
Standard sand (ISO standard sand) was certified in accordance with EN 196-1, which is siliceous, and its finest fractions with the grading given in Table 4 were used.
Table 4.
Grading of the source sand.
| Square Mesh Size (mm) | Cumulative Retained (%) |
|---|---|
| 0.08 | 99 ± 1 |
| 0.16 | 87 ± 5 |
| 0.50 | 67 ± 5 |
| 1.00 | 33 ± 5 |
| 1.60 | 7 ± 5 |
| 2.00 | 0 |
Mortar mix with 0.006 wt.% of MWCNTs was chosen as a principle mix based on the results of [28] that show the best concentration of CNT in cement concrete using the same carbon nanotubes from Arkema. We hypothesized that this represents 1.22% of the CNTs by weight of tobermorite. To obtain the proportionality of the nanotube concentration compared to the simulation and obtain additional results, we prepared a mix with 0.018 wt.% of MWCNTs that represent 4.00% of CNTs by weight of tobermorite.
Thus, mortar mixes with 0.00 wt.%, 0.006 wt.%, and 0.018 wt.% of MWCNTs were prepared. The samples were mixed using a laboratory mixer.
We used 40 × 40 × 160 cm3 prismatic molds to prepare the samples with two 2D inox meshes 2 × 2 cm placed in the normal axis 2 cm apart from each other to simulate the electrodes of the capacitor (see Figure 5 and Figure 6) and homogenizing via a vibrating table. Table 5 shows the mixing proportions. After curing for 28 days, the samples were cut into two parts to obtain 6 of each concentration of MWCNTs of size 40 × 40 × 80 cm3 (see Figure 5).
Figure 5.
Samples 40 × 40 × 80 cm3 and temperature measurement by a thermal camera. Picture samples with and without MWCNTs.
Figure 6.
Samples 40 × 40 × 80 cm3 with MWCNTs and electric field measurement.
Table 5.
Materials proportion for mortar mixing.
| Reference | MWCNTs Content (g) | Cement (g) | Water (g) | Sand (g) |
|---|---|---|---|---|
| Control | 0.0 | 450 | 225 | 1350 |
| CEM/CNT-0.006 | 2.7 | 450 | 225 | 1350 |
| CEM/CNT-0.018 | 8.1 | 450 | 225 | 1350 |
3.2. Testing Procedure
The samples were heated by an infra-red lamp to simulate the sun, and the corresponding electrostatic current was measured with a Keithley model 6482 dual-channel picoammeter. The temperatures were measured using a thermal camera FLIR Systems AB model 60b × 1.0 (Figure 5). As shown in Figure 5, the samples with and without MWCNTs look identical. Only a scanning electron microscope (SEM) analysis can be used to differentiate them.
The Keithley model 6482 dual-channel picoammeter was connected to the two electrodes of the capacitor (Figure 6). The leakage current was measured when the sample was subjected to a temperature field.
4. Results and Discussion
4.1. Dynamic Molecular Study
The Young’s modulus of the built model was evaluated and compared with previous research using Table 6 and Table 7. The system was equilibrated before undergoing deformation via a uniaxial tension by fixing one side of the structure and stretching the other side at a strain rate of 0.00001/fs. The initial length of the simulation box in the z-direction, as shown in Figure 3, was saved before this process.
Table 6.
Results of the computed Young’s modulus of tobermorite 11Å.
Table 7.
Results of determinate Young’s modulus of SWCNT.
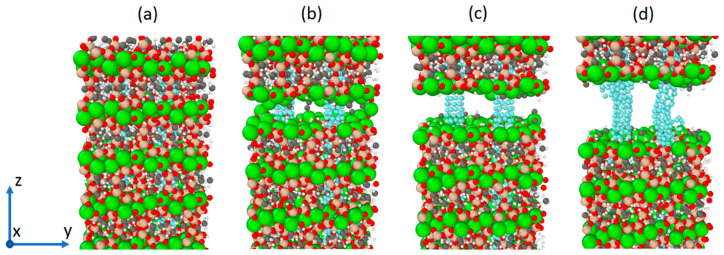
After carrying out separate tensile tests on tobermorite 11Å and CNT (3,3), the combination of tobermorite 11Å + CNT was subjected to the same test to determine the effect of CNT concentration on the tensile resistance of tobermorite 11Å. Table 8 and Figure 7 present the results for Young’s modulus, tensile strength, and stress evolution due to applied strain for the tobermorite-CNT models. The initial stress peak at 0.1 strain (Figure 7) indicates bond breaking in the tobermorite atoms (Figure 8b), followed by an increase in stress as only the CNTs were strained (Figure 8c) until the CNTs ruptured at around 0.25 strain (Figure 8d).
Table 8.
Results of Young’s modulus and tensile strength values of tobermorite-CNT samples.
| Model | Young’s Modulus (GPa) | Tensile Strength (GPa) |
|---|---|---|
| Tobermorite 11Å | 114.05 | 14.07 |
| Tob-CNT(1.22 wt.%) | 139.98 | 12.49 |
| Tob-CNT(2.55 wt.%) | 148.76 | 13.03 |
| Tob-CNT(4.00 wt.%) | 165.46 | 14.27 |
Figure 7.
Tensile stress vs. strain for the tobermorite-CNT sample in the z-orientation.
Figure 8.
Tobermorite 11Å containing 2.55 wt.% of CNTs under uniaxial tension in the longitudinal direction is shown in four different stages: (a) at zero strain, (b) at a strain of 0.125, (c) at a strain of 0.15, and (d) at a strain of 0.25.
Subsequently, the piezoelectric effect was simulated. The system was first equilibrated, and then the lengths of the simulation box were monitored while an external electric field of 250 MV/m was applied in the z-direction (as shown in Figure 3). The evolution of the box length in the z-direction for the four systems is compared and presented in Figure 9.
Figure 9.
Simulation of the changing of cell size in z-orientation with varying CNT concentrations under an external electric field.
The strain tensor was determined between simulation steps 4000 and 10,000, resulting from an electric field of 250 MV/m applied in the z-direction (refer to Figure 3). As there was no external stress or temperature change, Equation (2) for the converse piezoelectric effect in a triclinic structure could be expressed as follows:
| (11) |
This can be solved for , yielding:
| (12) |
The piezoelectric constant calculated for each of the samples is shown in Table 9.
Table 9.
Piezoelectric constant for each of the four samples.
| Sample | 0.00 wt.% | 1.22 wt.% | 2.55 wt.% | 4.00 wt.% |
|---|---|---|---|---|
| d33 (pC/N) | 1.12 | 6.48 | 8.62 | 6.14 |
The tobermorite 11Å structure alone displays a higher ultimate tensile strength than the models Tob-CNT (1.22 wt.%) and Tob-CNT (2.55 wt.%). However, the Tob-CNT model (4.00 wt.%) has the highest tensile strength of 14.27 GPa and the highest Young’s modulus of 165.46 GPa, as shown in Table 8. It is observed that the models Tob-CNT (1.22 wt.%) and Tob-CNT (2.55 wt.%) exhibit a decreased maximum tensile strength. In all cases where CNTs were incorporated into tobermorite, a higher Young’s modulus was observed. The initial stress peak, which is associated with the collapse of the tobermorite structure, occurs at a strain of 0.1. Figure 9 shows multiple stress peaks, which indicate that collapse occurs for strains ranging from 0.25 to 0.3 when CNTs are present. Despite a discontinuous collapse in the modeling when translating reality, cracking should not be separated. This numerical result can be interpreted as a discontinuity in the overall strain. Under the application of an electric field, the samples follow displacements, and the sample oriented in the same direction (z) of the electric field is analyzed. The piezoelectric constant is aligned in this direction, and the highest strain of 0.002155 was observed in Tob-CNT (2.55 wt.%). The samples with 1.22 wt.% and 4.00 wt.% displayed similar results. Without CNTs, the response to the applied electrical field is weak. By taking into account these numerical considerations, it should be experimentally possible to cause the deformation of a mortar sample containing CNT by a strain field (temperature field, for example), and thus generate an electric field. That is what we have tested in the following section.
4.2. Experimental Study
A total of 137 measurements of current were carried out on 6 samples of size 40 × 40 × 80 cm3 (see Figure 5) with 0.00 wt.% of MWCNTs. For 0.006 wt.% and 0.018 wt.% of MWCNTs, 6 samples were prepared and 109 measurements of current were carried out on each mixture. A solar lamp was used to simulate these materials. It can produce UVA or UVA-UVB. This infrared lamp was chosen to simulate sun exposure. The temperatures were measured using a thermal camera (Figure 5). The values of the current obtained from the experimental test in with respect to the temperature for all the samples are displayed in Figure 10. Only the measurements where the temperature was stabilized at 20 °C (ambient temperature), 30 °C, 35 °C, 45 °C, and 50 °C were retained in the range of ±2 °C. The results show great dispersion (see Figure 10) because electrical measurements at such low levels are very sensitive to the environment. An electrically neutral enclosure, controlled by temperature and humidity, should have been used. This is planned as the next step of this research. Nevertheless, the tendencies (see Figure 10) show that the current increases for the same temperature when the percentage of wt.% of MWCNTs increases in the mixture, which was expected, given the dynamic molecular study.
Figure 10.
Measured values of current (nano-ampere) vs. temperature (°C) for mortar samples with three different concentrations of carbon nanotubes.
As shown in Equation (2), the strain of a material can be expressed as the change in temperature multiplied by the coefficient of thermal expansion . For mortar, the coefficient of thermal expansion is in the order of /°C [36]. Table 10 uses to express the increment of the measured current concerning the strain by averaging the samples that have the same CNT concentration. The average electrostatic current increment for a strain of and = 10 °C increases between 1.28 ( and 1.51 ( when the percentage increases between 0.000 wt.% and 0.018 wt.%.
Table 10.
Average electrostatic current increment for mortar samples with three different concentrations of carbon nanotubes for a strain of and = 10 °C.
| Concentration | 0.00 wt.% | 0.006 wt.% | 0.018 wt.% |
|---|---|---|---|
| Δi (ηA) | 1.28 | 1.38 | 1.51 |
Dynamic molecular and experimental studies demonstrated that the piezoelectric effect can be obtained in a mortar containing MWCNTs. As in certain ceramics, piezoelectricity is the electric charge that accumulates in solid materials in response to applied stresses and reciprocally. This electricity, resulting from the displacement caused by an increase in temperature, can be capped. The piezoelectric phenomenon arises due to the interdependent relationship between the mechanical and electrical properties of materials. By including MWCNTs in a mortar, we can achieve a piezoelectric effect. This piezoelectric effect can be used as a sensor to analyze the field of stress detection caused by loads or temperature.
5. Conclusions
This study examined how the inclusion of carbon nanotubes affects the electrical properties of cement composites. To investigate this, a molecular dynamics simulation was performed using tobermorite 11Å as a representative of calcium silicate hydrate gel, combined with armchair (3,3)-type single-wall carbon nanotubes. Thus, numerical simulations of tobermorite mixtures with different percentages of carbon nanotubes were prepared. First, the molecular dynamics study showed that the piezoelectric effect can be simulated for four different concentrations. The deformation in the simulation box was then analyzed by subjecting it to an electrical field of 250 MV/m in the z-direction, The results showed a stronger converse piezoelectric response when the percentage of carbon nanotubes was increased. The deducted piezoelectric constant in the z-direction d33 increased in the same manner, proving in theory that current can be generated when samples are subjected to strains.
The experimental investigation was conducted using samples of mortar reinforced with different amounts (0.00 wt.%, 0.006 wt.%, 0.018 wt.%) of tangled multi-walled carbon nanotubes from Arkema. The samples were heated by an infra-red lamp to simulate the sun, and the corresponding electrostatic current was measured with a Keithley model 6482 dual-channel picoammeter. In parallel, the temperatures were measured using a thermal camera with a precision of ±2 °C. The results showed that electrostatic current measurements exhibited a higher electric sensitivity for samples with a higher concentration of CNTs. These experimental results are very promising when compared with molecular dynamics studies, and such effects can be used for analyses of stress detection caused by loads or temperatures in concrete structural elements.
Acknowledgments
The authors would like to thank Arkema for providing multi-walled carbon nanotubes to conduct this study and the laboratory LOCIE for financially supporting this project. The authors also acknowledge IUT Chambéry and Polytech for providing facilities to access laboratories and technical assistance.
Author Contributions
Conceptualization, A.L. and O.P.; methodology, Y.D.S.G.; software, Y.D.S.G.; validation, A.L., O.P., X.J. and W.Y.; writing—original draft preparation, A.L. and O.P.; writing—review and editing, A.L. and O.P.; visualization, X.J. and W.Y.; supervision, O.P.; project administration, O.P. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data are contained in the present manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
This research received no external funding.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Cerro-Prada E., Pacheco-Torres R., Varela F. Effect of multi-walled carbon nanotubes on strength and electrical properties of cement mortar. Materials. 2020;14:79. doi: 10.3390/ma14010079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Falcao E.H., Wudl F. Carbon allotropes: Beyond graphite and diamond. J. Chem. Technol. Biotechnol. 2007;82:524–531. doi: 10.1002/jctb.1693. [DOI] [Google Scholar]
- 3.Danoglidis P.A., Konsta-Gdoutos M.S., Gdoutos E.E., Shah S.P. Strength, energy absorption and self-sensing properties of multifunctional carbon nanotube reinforced mortars. Constr. Build. Mater. 2016;120:256–274. doi: 10.1016/j.conbuildmat.2016.05.049. [DOI] [Google Scholar]
- 4.Konsta-Gdoutos M.S., Metaxa Z.S., Shah S.P. Highly dispersed carbon nanotube reinforced cement based materials. Cem. Concr. Res. 2010;40:1052–1059. doi: 10.1016/j.cemconres.2010.02.015. [DOI] [Google Scholar]
- 5.Li G.Y., Wang P.M., Zhao X. Mechanical Behavior and Microstructure of Cement Composites Incorporating Surface-Treated Multi- Walled Carbon Nanotubes. Carbon. 2005;43:1239–1245. doi: 10.1016/j.carbon.2004.12.017. [DOI] [Google Scholar]
- 6.Yu X., Kwon E. A carbon nanotube/cement composite with piezoresistive properties. Smart Mater. Struct. 2009;18:055010. doi: 10.1088/0964-1726/18/5/055010. [DOI] [Google Scholar]
- 7.Saafi M., Gullane A., Huang B., Sadeghi H., Ye J., Sadeghi F. Inherently multifunctional geopolymeric cementitious composite as electrical energy storage and self-sensing structural material. Compos. Struct. 2018;201:766–778. doi: 10.1016/j.compstruct.2018.06.101. [DOI] [Google Scholar]
- 8.Azhari F., Banthia N. Cement-based sensors with carbon fibers and carbon nanotubes for piezoresistive sensing. Cem. Concr. Compos. 2012;34:866–873. doi: 10.1016/j.cemconcomp.2012.04.007. [DOI] [Google Scholar]
- 9.Zhao P., Wang S., Kadlec A., Li Z., Wang X. Properties of cement–sand-based piezoelectric composites with carbon nanotubes modification. Ceram. Int. 2016;42:15030–15034. doi: 10.1016/j.ceramint.2016.06.153. [DOI] [Google Scholar]
- 10.Gong H., Zhang Y., Quan J., Che S. Preparation and properties of cement based piezoelectric composites modified by CNTs. Curr. Appl.Phys. 2011;11:653–656. doi: 10.1016/j.cap.2010.10.021. [DOI] [Google Scholar]
- 11.Thompson A.P., Aktulga H.M., Berger R., Bolintineanu D.S., Brown W.M., Crozier P.S., in’t Veld P.J., Kohlmeyer A., Moore S.G., Nguyen T.D., et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022;271:108171. doi: 10.1016/j.cpc.2021.108171. [DOI] [Google Scholar]
- 12.Ramezani M., Kim Y.H., Sun Z. Mechanical properties of carbon-nanotube-reinforced cementitious materials: Database and statistical analysis. Mag. Concr. Res. 2019;72:1047–1071. doi: 10.1680/jmacr.19.00093. [DOI] [Google Scholar]
- 13.Zhang D., Huang Y., Chia L. Effect of carbon nanotube (CNT) geometries on the dispersion characterizations and adhesion properties of CNT reinforced epoxy composites. Compos. Struct. 2022;296:115942. doi: 10.1016/j.compstruct.2022.115942. [DOI] [Google Scholar]
- 14.Parveen S., Rana S., Fangueiro R. A Review on Nanomaterial Dispersion, Microstructure, and Mechanical Properties of Carbon Nanotube and Nanofiber Reinforced Cementitious Composite. J. Nanomater. 2013:19. doi: 10.1155/2013/710175. [DOI] [Google Scholar]
- 15.Korzhenko A., Vincendeau C., Lushnikova A., Yakovlev G.I., Pervushin G.N., Suau J.M., Platel D. Method for Producing a Master Mixture Based on Carbonaceous Nanofillers and Superplasticiser, and the Use Thereof in Hardenable Inorganic Systems. No. EP2922801A1. U.S. Patent. 2017 December 26;
- 16.Zaoui A. Insight into elastic behavior of calcium silicate hydrated oxide (C-S-H) under pressure and composition effect. Cem. Concr. Res. 2012;42:306–312. doi: 10.1016/j.cemconres.2011.10.003. [DOI] [Google Scholar]
- 17.Hou D., Li Z. Molecular dynamics study of water and ions transport in nano-pore of layered structure: A case study of tobermorite. Microporous Mesoporous Meter. 2014;195:9–20. doi: 10.1016/j.micromeso.2014.04.011. [DOI] [Google Scholar]
- 18.Wang S., Peng X., Tang L., Zeng L., Lan C. Influence of inorganic admixtures on the 11 Å -tobermorite formation prepared from steel slags: XDR and FTIR analysis. Constr. Build. Mater. 2014;60:42–47. doi: 10.1016/j.conbuildmat.2014.03.002. [DOI] [Google Scholar]
- 19.Merlino S., Bonaccorsi E., Armbruster T. Tobermorites: Their real structure and order-disorder (OD) character. Am. Mineral. 1999;84:1613–1621. doi: 10.2138/am-1999-1015. [DOI] [Google Scholar]
- 20.Eftekhari M., Mohammadi S. Molecular dynamics simulation of the nonlinear behavior of the CNT-reinforced calcium silicate hydrate (C-S-H) composite. Compos. Part A Appl. Sci. 2016;82:78–87. doi: 10.1016/j.compositesa.2015.11.039. [DOI] [Google Scholar]
- 21.LAMMPS Molecular Dynamic Simulator. [(accessed on 15 May 2023)]; Available online: http://lammps.sandia.gov/
- 22.Lushnikova A., Zaoui A. Influence of single-walled carbon nantotubes structure and density on the ductility of cement paste. Constr. Build. Mater. 2018;172:86–97. doi: 10.1016/j.conbuildmat.2018.03.244. [DOI] [Google Scholar]
- 23.Plassard C., Lesniewska E., Pochard I., Nonat A. Investigation of the surface structure and elastic properties of calcium silicate hydrates at the nanoscale. Ultramicroscopy. 2004;100:331–338. doi: 10.1016/j.ultramic.2003.11.012. [DOI] [PubMed] [Google Scholar]
- 24.Tersoff J. Empirical interatomic potential for carbon, with application to amorphous carbon. Phys. Rev. Lett. 61. 1988;25:2879–2882. doi: 10.1103/PhysRevLett.61.2879. [DOI] [PubMed] [Google Scholar]
- 25.Leach A.R. Molecular Modelling: Principles and Applications. Prentice Hall; Harlow, UK: New York, NY, USA: 2001. [Google Scholar]
- 26.Satoh A. Introduction to Practice of Molecular Simulation: Molecular Dynamics, Monte Carlo, Brownian Dynamics, Lattice Boltzmann and Dissipative Particle Dynamics. Elsevier; Amsterdam, The Netherlands: 2010. Kindle Edition. [Google Scholar]
- 27.McAndrew T.P., Havel M., Korzhenko A., Delprat P. Composites with Multi-Walled Carbon Nanotubes. Arkema Inc.; King of Prussia, PA, USA: 1940. [Google Scholar]
- 28.Yakovlev G., Bazhenov Y., Buryanov A., Pudov I. Increased durability concrete for generation of pillars power lines. MATEC Web Conf. 2016;86:04013. doi: 10.1051/matecconf/20168604013. [DOI] [Google Scholar]
- 29.Dharmawardhana C.C., Misra A., Aryal S., Rulis P., Ching W.Y. Role of interatomic bonding in the mechanical anisotropy and interlayer cohesion of CSH crystals. Cem. Concr. Res. 2013;52:123–130. doi: 10.1016/j.cemconres.2013.05.009. [DOI] [Google Scholar]
- 30.Lushnikova A., Zaoui A. Improving mechanical properties of C-S-H from inserted carbon nanotubes. J. Phys. Chem. Solids. 2017;105:72–80. doi: 10.1016/j.jpcs.2017.02.010. [DOI] [Google Scholar]
- 31.Shahsavari R., Buehler M.J., Pellenq R.J.-M., Ulm F.-J. First-principles study of elastic constants and interlayer interactions of complex hydrated oxides: Case study of tobermorite and jennite. J. Am. Ceram. Soc. 2009;92:2323–2330. doi: 10.1111/j.1551-2916.2009.03199.x. [DOI] [Google Scholar]
- 32.Wang Y., Wang X.-X., Ni X.-G., Wu H.-A. Simulation of the elastic response and the buckling modes of single-walled carbon nanotubes. Comput. Mater. Sci. 2005;32:141–146. doi: 10.1016/j.commatsci.2004.08.005. [DOI] [Google Scholar]
- 33.Lushnikova A. Ph.D. Thesis. Laboratoire Génie Civil et Géo-Environnement; Lille, France: 2017. Improving Mechanical Properties of Concrete from Inserted Carbon Nanotubes: A Molecular Dynamics Study. [Google Scholar]
- 34.Lu X., Hu Z. Mechanical property evaluation of single-walled carbon nanotubes by finite element modeling. Compos. Part B Eng. 2012;43:1902–1913. doi: 10.1016/j.compositesb.2012.02.002. [DOI] [Google Scholar]
- 35.Rao P.S., Anandatheertha S., Naik G.N., Gopalakrishnan S. Estimation of mechanical properties of single wall carbon nanotubes using molecular mechanics approach. Sadhana. 2015;40:1301–1311. doi: 10.1007/s12046-015-0367-5. [DOI] [Google Scholar]
- 36.Zeng Q., Li K., Fen-Chong T., Dangla P. Effect of porosity on thermal expansion coefficient of cement pastes and mortars. Constr. Build. Mater. 2012;28:468–475. doi: 10.1016/j.conbuildmat.2011.09.010. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are contained in the present manuscript.