99m-Tc TRODAT Single-Photon Emission Computerized Tomography Scan Image Compression using Singular Value Decomposition

Abstract

Introduction:

The objective of the study was to compress 99m-Tc TRODAT single-photon emission computerized tomography (SPECT) scan image using Singular Value Decomposition (SVD) into an acceptable compressed image and then calculate the compression factor.

Materials and Methods:

The SVD of every image from the image dataset of 2256 images (of forty-eight 99m-Tc TRODAT SPECT studies [48 studies X 47 trans-axial images = 2256 trans-axial images]) was computed and after truncating singular values smaller than a threshold, the compressed image was reconstructed. The SVD computation time and percentage compression achieved were calculated for each image. Two nuclear medicine physicians visually compared compressed image with its original image, and labeled it as either acceptable or unacceptable. Compressed image having loss of clinical details or presence of compression artifact was labeled unacceptable. The quality of compressed image was also assessed objectively using the following image quality metrics: Error, structural similarity (SSIM), brightness, global contrast factor (GCF), contrast per pixel (CPP), and blur. We also compared the TRODAT uptake in basal ganglia estimated from the compressed image and original image.

Results:

Nuclear Medicine Physician labeled each image acceptable, as they found compressed image identical to its original image. The values of brightness, GCF, CPP, and blur metrics show that compressed images are less noisy, brighter, and sharper than its original image. The median values of error (0.0006) and SSIM (0.93) indicate that the compressed images were approximately identical to its original image. In 39 out of 48 studies, the percentage difference in TRODAT uptake (in basal ganglia from compressed and original image) was negligible (approximately equal to zero). In remaining 9 studies, the maximum percentage difference was 13%. The SVD computation time and percentage compression achieved for a TRODAT study were 0.17398 s and up to 54.61%, respectively.

Conclusions:

The compression factor up to 54.61% was achieved during 99m-Tc TRODAT SPECT scan image compression using SVD, for an acceptable compressed image.

Introduction

The image compression reduces the storage space and also the transmission time of an image over the network. The lossy image compression techniques in which usually some of the image data are discarded provide better image compression compared to lossless image compression technique. The more data we discard, the higher compression we achieve. However, with higher compression, the compressed image might have artifacts or the compressed image might not be acceptable for the diagnostic purpose. Thus, the parameters of an image compression technique need to be adjusted to get an acceptable compressed image with a better compression. There are several image compression techniques and still the new one is being explored for better compression.[1-4]

The singular value decomposition (SVD) factors an image matrix into three matrices namely: Left singular vectors, the singular values matrix, and right singular vectors; and from these three factors, we can again reconstruct the image matrix.[5] The quality of information contained in the singular values depends on the magnitude of the singular values; larger singular values contain dominant information of the image while smaller singular values contain less important or insignificant information. The smaller singular values can be safely discarded to achieve the compression. The challenge here is to decide a threshold for truncating the singular values that can result in an acceptable compressed image.

Gavish and Donoho has developed an algorithm for the optimum threshold of singular values and has demonstrated that with this optimum threshold, the compressed image quality is approximately equal to its original image.[6] However, this algorithm has not been evaluated for 99m-Tc TRODAT single-photon emission computerized tomography (SPECT) scan images.

In the objective of this study was to compress 99m-Tc TRODAT SPECT scan image using SVD into an acceptable compressed image and then calculate the compression factor. We have used the Gavish and Donoho algorithm to determine the threshold for truncating the singular values that can result in an acceptable compressed image.

Materials and Methods

Singular value decomposition

A TRODAT SPECT study is acquired as a set of two-dimensional projection image of spatial distribution of radiopharmaceutical inside the human body at the time of acquisition. Then from the projection images, the two-dimensional trans-axial slices are reconstructed. Thus, TRODAT SPECT study data can be stored as projection images or as reconstructed trans-axial image or as both projection image and reconstructed image.

The two-dimensional projection or trans-axial images is stored as matrix; we denote this matrix as (A).

The matrix (A) can be represented in a space defined by orthogonal matrices (U) and (V) as:

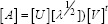
Where [λ] is a diagonal matrix, whose entries are the singular values of (A), (U) is the row eigenvector system of (A) and (V) is the column eigenvector system of (A).[7] The expansion of the matrix (A) can be represented in vector outer product notation as:

Where u_i, v_i, and λ_i respectively are the column vectors of (U), (V), and diagonal terms of [λ]. The limit of the summation K represents the rank (number of nonzero singular values) of (A). If (A) is nonsingular, K will equal N, the dimension of (A).

The value of K depends on the image the distribution of recorded counts at each pixel; thus, the value of K might be different for different trans-axial image slices.

Estimation of compressed images

The SVD of each image was computed using the SVD function with economy option,[7] and the computation time was recorded for each image. To determine the value of K (the optimum threshold for truncating smaller singular values), we have used the algorithm developed by Gavish and Donoho; the error between the reconstructed and original image was calculated using the nuclear norm during the process of finding the optimum value.[6] Singular values smaller than the threshold were truncated. After truncation of singular values, the compressed image was reconstructed with the remaining larger singular values containing the dominant patterns of the image.

Image data

This is a retrospective study. The Ethical Committee of our Institute has approved this Study (Approval Number: IECPG-711/November 25, 2021).

The image data consist of attenuation corrected and nonattenuation corrected trans-axial images of TRODAT SPECT study. There were total 48 TRODAT studies (38 attenuation corrected and 10 nonattenuated corrected SPECT studies), each study had 47 trans-axial images. These studies were transferred from the image processing terminal in DICOM format.

The SVD of each trans-axial slice was computed and the optimum threshold for truncating insignificant singular values was determined using Gavish and Donoho algorithm. After truncating insignificant singular values, the compressed trans-axial image was reconstructed. SVD computation time for each trans-axial image was determined.

The experiments were performed on a LAPTOP-568R779P having a Microsoft Windows 10 Home Basic 64-bit operating system, 16GB of random-accessed memory, and an Intel (R) Core (TM) i7-10870H CPU @ 2.20GHz 2.21GHz.

Compression ratio

For an image matrix [A] of size m × n, and K being the rank of the matrix, the compression ratio (CR) for each trans-axial slice was calculated using the following formula:

Moreover, percentage compression was calculated using the following equation

TRODAT uptake quantification in basal ganglia

We inspected all trans-axial slices and selected the one slice in which size of the basal ganglia was largest. Then, we draw irregular region of interest (ROI) around the basal ganglia and copied the ROI on all the trans-axial slices in which basal ganglia was clearly visible. Then, extracted pixel counts (from each slice) were summed to get the TRODAT uptake in basal ganglia. This process was repeated to estimate TRODAT uptake from compressed and original image.

The split basal ganglia uptake was computed by using the following equations:

The split basal ganglia uptake was computed by using the following equations: 1

The percentage difference in split basal ganglia TRODAT uptake estimated from compressed and original image was calculated using the following equation:

Image quality assessment

Nuclear medicine physician visually compared the compressed image with its original image and labeled the compressed image as unacceptable if there was loss of clinical information or there was the presence of any compression artifact. We also evaluated the quality of the compressed images using the following image quality metrics: Error, structural similarity (SSIM),[8] blur,[9] brightness, global contrast factor (GCF),[10] and contrast per pixel (CPP).[11] The error and SSIM for compressed image were calculated with respect to its original image. Error was calculating using this formula:

2^nd norm was calculated using MATLAB function.[7]

Statistical analysis

It is to be remembered that each TRODAT SPECT study contains 47 trans-axial images. The estimated value of CR, percentage compression, SVD computation time, Blur, GCF, CPP, SSIM, and Brightness for each trans-axial image of a given study was averaged to a get the average value of CR, percentage compression, SVD computation time, Blur, GCF, CPP, SSIM, and brightness of the study. The process was repeated for all the 48 TRODAT SPECT study. From the averaged value of CR, percentage compression, SVD computation time, Blur, GCF, CPP, SSIM, and Brightness of the entire data set (i.e., 48 TRODAT SPECT study); the summary statistics was calculated.

For finding significant difference in the value of Blur, GCF, CPP and Brightness between the compressed and original image, Wilcoxon signed-rank sum test was applied. For statistical analysis, the open source statistical software R was used.[12]

Results

Figure 1 shows four sets of 99m-Tc TRODAT images (original and its compressed). It is to be noticed that uptake in basal ganglia of the original image is present in its compressed images and compressed image looks identical to its original image.

Figure 1.

Four sets of 99m-Tc TRODAT original images with its corresponding compressed images. Compressed images look identical to its original image

Figure 2 shows plot of SVD computation time, percentage compression, error and SSIM for a TRODAT study. It is obvious from the Figure 2 that SVD computation time, percentage compression, error, and SSIM value for each trans-axial slice were different. One can also notice that the maximum percentage compression achieved was up to 35% (ranging from 10% to 35%); the error between the compressed image and the original image was very minimum (in the range of 10e-4–10e-5); the SSIM value was above 0.85; in this particular study.’

Figure 2.

Shows plot of Percentage compression (Top left), SVD computation time (Bottom left), Error (Top right), and SSIM (Bottom right) for each trans axial 99m-Tc TRODAT images. SVD: Singular value decomposition, SSIM: structural SImilarity

The summary statistics of averaged CR, SVD computation time, percentage compression, error and SSIM are given in Table 1. Average CR per study was found to be up to 2.20 (54%). After inspecting summary statistics of SSIM given in Table 1, it is obvious that the compressed images were closer to its original images (majority of images has SSIM value equal to or >0.88). The SVD computation time per study was <1 s, and the error between the compressed and original image was negligible (maximum error: 0.015).

Table 1.

Summary statistics of compression ratio, singular value decomposition computation time, percentage compression, error, and SSIM

	Summary statistics
	Minimum	1st quartile	Median	Mean	3rd quartile	Maximum
Compression ratio	1.14	1.19	1.22	1.39	1.28	2.20
SVD computation time	0.05	0.06	0.07	0.07	0.07	0.17
Percentage compression	12.53	15.99	18.10	24.78	22.07	54.61
Error	0.0003	0.0005	0.0006	0.0027	0.0008	0.0156
SSIM	0.44	0.91	0.93	0.93	0.94	0.96

SVD: Singular value decomposition, SSIM: Structural similarity index measure

The uptake in left and right basal ganglia calculated using equation[1] is listed in Table 2. In 39 out of 48 studies; the uptake in left and right basal ganglia calculated from compressed images were equal to the corresponding uptakes in the left and right basal ganglia calculated form it original images. The remaining nine studies, in which the difference was noticed, are shown in bold italic fonts. In these nine studies; seven studies were non-computed tomography (CT)-based attenuation corrected studies, and two studies were CT-based attenuation corrected studies. In seven studies which were non-CT based attenuation corrected, the maximum difference in uptake was found to be 13%. In two studies which were CT-based attenuation corrected, the maximum uptake difference was 3%. There were also three non-CT based attenuation corrected studies in which there was no difference in the uptake calculated from the compressed and original image.

Table 2.

Trodat uptake in left and right basal ganglia calculated from compressed and original images

Lt_O	Lt_C	Rt_O	Rt_C
70.67234	70.67234	29.32766	29.32766
56.80226	56.80226	43.19774	43.19774
58.84494	58.84494	41.15506	41.15506
46.60338	46.60338	53.39662	53.39662
46.11414	46.11414	53.88586	53.88586
44.58673	44.58673	55.41327	55.41327
59.75937	59.75937	40.24063	40.24063
79.58791	79.58791	20.41209	20.41209
54.16633	54.16633	45.83367	45.83367
42.60088	42.60088	57.39912	57.39912
37.49669	37.49669	62.50331	62.50331
48.10532	48.10532	51.89468	51.89468
45.52245	45.52245	54.47755	54.47755
61.46488	61.46488	38.53512	38.53512
55.21501	55.21501	44.78499	44.78499
59.44687	59.44687	40.55313	40.55313
77.36909	77.36909	22.63091	22.63091
47.82352	47.82352	52.17648	52.17648
53.69945	53.69945	46.30055	46.30055
64.72252	64.72252	35.27748	35.27748
59.34789	59.34789	40.65211	40.65211
56.13698	56.13698	43.86302	43.86302
54.94483	54.94483	45.05517	45.05517
55.58942	58.60249	44.41058	41.39751
58.29581	61.91325	41.70419	38.08675
63.1034	63.1034	36.8966	36.8966
57.00708	57.00708	42.99292	42.99292
55.64801	55.64801	44.35199	44.35199
54.93311	54.93311	45.06689	45.06689
41.0934	41.0934	58.9066	58.9066
45.30055	45.30055	54.69945	54.69945
61.72837	61.72837	38.27163	38.27163
49.75728	49.75728	50.24272	50.24272
54.03727	54.03727	45.96273	45.96273
37.19771	37.19771	62.80229	62.80229
57.37908	57.37908	42.62092	42.62092
45.90211	45.90211	54.09789	54.09789
44.7782	44.7782	55.2218	55.2218
57.75955	57.75955	42.24045	42.24045
55.75756	46.62528	44.24244	53.37472
46.30181	59.12516	53.69819	40.87484
57.11798	33.23283	42.88202	66.76717
31.42047	44.96008	68.57953	55.03992
46.87443	50.14404	53.12557	49.85596
49.72773	46.01104	50.27227	53.98896
50.83983	60.26406	49.16017	39.73594
60.43608	60.43608	39.56392	39.56392
56.43082	56.43082	43.56918	43.56918

Lt_O: Left basal ganglia uptake calculated from the original image, Lt_C: Left basal ganglia uptake calculated from the compressed image, Rt_O: Right basal ganglia uptake calculated from the original image, RT_C: Right basal ganglia uptake calculated from the compressed image

We found significant difference in the value of blur, GCF, CPP, and brightness of compressed image and the corresponding value of blur, GCF, CPP, and brightness of original image at P < 0.001 [Table 3]. The compressed images were less blurred (median value of blur of compressed image [0.46] is smaller than that of median blur of original image [0.47]). The compressed images had both local and global contrast better than its corresponding original images (median value of GCF of compressed image (2341.3) is greater than that of median GCF of original image [2339.7]). The compressed image had also better CPP (median value of CPP of compressed image [2.2475] is greater than that of median CPP of original image [2.1263]), and were brighter than that of original image (median value of brightness of compressed image [17.855] is greater than that of median brightness of original image [17.01]).

Table 3.

Statistical summary of blur, global contrast factor, contrast per pixel, and brightness for objective image quality assessment of compressed image and original image

Summary statistics
	I	II	III	IV	V	VI	P
Blur
Original	0.4360	0.4662	0.4739	0.4905	0.5035	0.6500	<3.4e-06
Compressed	0.4224	0.4525	0.4633	0.4770	0.4975	0.6095
GCF
Original	367.9	1772.9	2339.7	2120.4	2544.1	2957.6	0.00037
Compressed	377.9	1778.4	2341.3	2123.3	3545.3	2956.3
CPP
Original	0.353	1.524	2.126	1.969	2.383	2.763	<1.4e-14
Compressed	0.469	1.585	2.247	2.062	2.503	2.880
Brightness
Original	2.83	12.20	17.01	15.76	19.07	22.11	<1.4e-14
Compressed	3.628	12.618	17.855	16.406	19.901	22.917

I: Minimum, II: 1^st quartile, III: Median, IV: Mean, V: 3^rd quartile, VI: Maximum. GCF: Global contrast factor, CPP: Contrast per pixel

Discussion

In this study, we have compressed the trans-axial images of 99m-Tc TRODAT studies using SVD into an acceptable compressed image and then calculated the compression factor. The compression was achieved by approximating the trans-axial images with larger singular values. The smaller singular value usually contains insignificant information was discarded. The threshold for truncating singular values was determined using Gavish and Donoho algorithm. Two nuclear medicine (NM) physicians compared the compressed image with its original image to label compressed image as either acceptable or unacceptable. They found compressed image identical to its original image (i.e., no loss of clinical details) and also absence of compression artifacts in the compressed image. Based on objective assessment, the compressed images were found to be brighter, less noisy, and also have better local and global contrast and CPP. The percentage compression achieved was up to 54.61%. The maximum SVD computation time per study was 0.17398 s.

The uptake in basal ganglia calculated from compressed and original image was found to be equal in 39 TRODAT studies and different in 9 TRODAT studies. In these nine studies, the maximum difference of 13% was found in one of the no-attenuation corrected TRODAT study. In CT-based attenuation corrected image, the maximum difference of 3% was observed. Thus, the uptake difference can occur in either attenuation corrected image or nonattenuation corrected images. Since the study data are not sufficiently large, we do not have sufficient evidence to conclude that large uptake can exist in a TRODAT study with no attenuation correction applied.

99m-Tc TRODAT SPECT study is performed for the evaluation of Parkinson’s disease (PD).[13] The reduction of TRODAT uptake in striatum indicates the loss of dopaminergic neurons in the striatum.[14,15] Dopamine transporter (DAT) is a protein present on the membrane of the presynaptic terminal of dopaminergic cells. In normal healthy volunteers, there is no loss of dopaminergic neurons, while in PD, there is a progressive degeneration of dopaminergic neurons.[13,16] NM Physician visually inspects every trans-axial image of the TRODAT SPECT study and looks for the pattern of loss of TRODAT uptake in the basal ganglia. By correlating the loss of TRODAT uptake with the associated clinical symptoms, they guide the referring neurologist regarding whether the referred patient is likely to have been suffering from PD. Although mostly they heavily rely on their visual assessment, some of the NM physicians also quantify the TRODAT uptake; provided the software tools are available and incorporate the quantitative information in making their final diagnosis.

Usually, the uptake in basal ganglia is calculated from the current study (the uncompressed TRODAT study) and will be compared with the previous study (intended to be stored as a compressed study); in this case 13% uptake difference (if not accounted in the respective clinical decision) might lead to error in the diagnosis. Thus, we recommend the error between the uptake calculated on compressed and original image, if it exists, be documented, so that it can be referenced at the time of comparison for appropriate consideration.

The difference of TRODAT uptake calculated from compressed image and original image can possibly be explained on account of the amount of noise present in the input image. Figure 3a shows two representative images of a study (from the group of original-compressed images; in which TRODAT uptake was equal) and another two representative images of a study (from the group of original-compressed images; in which TRODAT uptake was different), [Figure 3b]. After visual inspection of Figure 3, the difference in original images can be noticed – the original image appears noisier [Figure 3a and b] in the group of images where the TRODAT uptake was different when calculated from original and its compressed image. The percentage compression achieved is comparatively higher for the group of images in which TRODAT uptake was different [Figure 3c and d]. Larger CR indicates compressed images were reconstructed with relatively smaller number of singular values and thus larger difference (comparatively large error) in basal ganglia uptake calculated from the compressed image and from the original image.

Figure 3.

(a) Two sets of original and compressed images from the group of studies in which no uptake difference was noticed up to four decimal places, (b) Two sets of original and compressed images in which uptake difference was noticed. (c) Boxplot of percentage compression of the study (two sets of images shown in a), and (d) Boxplot of percentage compression of the study (two sets of images shown in b)

Research paper related to nuclear medicine image compression using SVD is very few. Wack and Badgaiyan have used complex SVD to reduce noise in Dynamic positron emission tomography (PET) images.[17] “They have also quantified the uptake value and estimated the error between quantified and original value of uptake.” They have found that error between the uptake quantified on denoised image and original image was within approximately 5% and greater in case of noisy image. They have used complex SVD in dynamic PET images and we have used real SVD on TRODAT SPECT study.

In general, several image compression techniques exist in the literature. There is continuous research going on in this field to achieve higher and higher compression. Rebelo et. al. have compressed images of cardiac nuclear medicine using the discrete cosine transform algorithm. They applied DCT compression algorithm on the group of 23 normal sequence images and calculated ejection fraction before and after compression. They have found no significant difference in the value of ejection fraction before and after compression.[18]

Zhou et al. investigated the usefulness of JPEG2000 compression for NM image, normal and abnormal static images were compressed using a JPEG2000 plug-in. For lossless algorithm, they have calculated CR and for lossy algorithm, images were visually analyzed by NM physicians and receiver operating characteristic curves were generated. On comparing the original and the compressed image, there was no significant difference for 10:1 CR but significant difference for bigger CRs. They have concluded that lossless compression has little usefulness for NM image because of very low CR.[19]

This study had focused on the image compression of 99m-Tc TRODAT scan using SVD and experimented on 2256 images (48 TRODAT study consisting of 47 image slices in each study). The software implementation (MATLAB code for image compression, MATLAB code for objective image quality evaluation, visual image quality assessments, R code for generating plots, and for statistical analysis) was performed on the personal computer. This is the uniqueness of the study.

The significance of this study is that this study demonstrates that image compression research can be performed on personal computer. Usual practice in nuclear medicine is to use the vendors provided image processing computers for image processing research. Computers provided by vendors are costly compared to the personal computer (with similar processing capability) and are also highly occupied because of clinical overloads.

The limitation of the examined SVD-based image compression technique is that amount of compression as they achieved is not excellent. However, it is also possible to achieve further more compression by using pipelines of another image compression schemes. In future, we would like to develop and evaluate one such pipeline of image compression schemes for its clinical acceptability by nuclear medicine physician specifically for 99m-Tc TRODAT study.

Conclusions

The investigated image compression techniques using SVD provide acceptable compressed trans-axial images of TRODAT SPECT study having 54.61% compression.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.