Deep Learning Coordinate-Free Quantum Chemistry

Abstract

Computing quantum chemical properties of small molecules and polymers can provide insights valuable into physicists, chemists, and biologists when designing new materials, catalysts, biological probes, and drugs. Deep learning can compute quantum chemical properties accurately in a fraction of time required by commonly used methods such as density functional theory. Most current approaches to deep learning in quantum chemistry begin with geometric information from experimentally derived molecular structures or pre-calculated atom coordinates. These approaches have many useful applications, but they can be costly in time and computational resources. In this study, we demonstrate that accurate quantum chemical computations can be performed without geometric information by operating in the coordinate-free domain using deep learning on graph encodings. Coordinate-free methods rely only on molecular graphs, the connectivity of atoms and bonds, without atom coordinates or bond distances. We also find that the choice of graph-encoding architecture substantially affects the performance of these methods. The structures of these graph-encoding architectures provide an opportunity to probe an important, outstanding question in quantum mechanics: what types of quantum chemical properties can be represented by local variable models? We find that Wave, a local variable model, accurately calculates the quantum chemical properties, while graph convolutional architectures require global variables. Furthermore, local variable Wave models outperform global variable graph convolution models on complex molecules with large, correlated systems.

Graphical Abstract

INTRODUCTION

Efforts to develop artificial intelligence, culminating in recent advances in deep learning, are bringing us closer to solving significant problems in medicinal chemistry,¹ dermatology,² radiology,³ genomics,^4,5 protein folding,⁶ and other industrial and scientific fields. There has been substantial interest in deep learning among chemistry researchers, who are using these technologies on small molecules to reduce drug toxicity,^7–9 identify biological probes,¹⁰ predict chemical reactions,¹¹ and compute basic properties.¹²

The observed behavior of small molecules arises from electronic interactions described by quantum mechanics. Often, in practice, approximations of quantum mechanics for chemistry are made with simplified density functional theory (DFT),¹³ and higher level ab initio¹⁴ methods, combined with quantitative structure–activity relation models, are invaluable tools for understanding relationships between chemical structure and activity with applications in the design of materials,¹⁵ catalysts,¹⁶ and drugs.^17,18 Unfortunately, these methods often require minutes or hours to compute the properties of small molecules. Computational chemists have been using deep learning to compute quantum chemical (QC) properties of molecular systems in a fraction of time required by standard methods. Deep learning has been successfully applied for computing the total energy of molecular systems,¹⁹ bond energies,²⁰ orbital energies,²¹ site-level (atom- and bond-level) properties,²² and molecular dynamics.²³ This success raises the possibility of using deep-learning-derived QC calculations to quickly screen large molecular databases or design new molecules using automated de novo or evolutionary algorithms suitable for applications in photovoltaic panels,^24–26 materials design,²⁷ chemistry,²⁸ biology, and medicine.^27,29

There are two key limitations of current deep learning approaches to quantum chemistry that limit their practicality for screening tasks. First, most quantum chemistry deep learning studies have focused on very small molecules, with fewer than 10 heavy atoms, whereas many commonly used biological probes, drugs, and catalysts are substantially larger. Second, many of the standard benchmark datasets in this field, such as QM9,³⁰ provide molecular geometries optimized at the same level of theory used for the reference quantum calculations. Alternatively, other benchmarks may use experimentally derived structures.³¹ Deep learning models trained on these data often require coordinate or distance data derived from these structures as input and thus, for application to new data, structures must be obtained through similar methods as the original datasets. This can be a computationally or time-intensive process. For example, given a structural formula for a compound, a three-dimensional structure could be generated by application of a force field or by deriving a structure experimentally. Some groups have even shown that optimized structures at high levels of theory can be generated by deep learning via gradient descent. However, generating structures computationally in this manner has only been studied with very small molecules, and optimization still incurs a significant computational cost.³²

Identifying a deep learning architecture with the greatest efficiency—with respect to the number of variables, training data requirements, and generalizability of learned representations of quantum chemistry—is another area of active inquiry in this field. Numerous architectures have been proposed that leverage different feature sets and molecular representations and different internal structures. Past approaches have included matrices of inter-atomic distances,³³ empirical force fields,³⁴ empirical potentials,^32,35 and derived features from lower levels of theory.³⁶ The innovation of convolutional neural networks provided a tool for deep learning networks to natively process input molecular systems with varying size.^19,37–41 These convolutional networks operate either on pairs of atoms or molecular graphs derived from atomic spatial relationships or structural formulas and process data at the atom level, aggregating empirically derived atom-level representations to compute QC properties at the atom, bond, and molecule levels. Input representations often include inter-atomic distances or coordinates^19,31,38 but can also operate solely on non-spatial features such as atomic number.^22,40,42 Because they operate on a principal of aggregation of local information in atom neighborhoods, convolutional networks may not be the most efficient way to represent long-range information in chemical systems.^40,43 Graph recursive networks such as Wave are an alternative to convolutional networks designed to specifically address this issue.^12,40,44

The varying deep learning architectures used for chemistry also raise the possibility of constructing local variable models of quantum chemistry.⁴⁵ The existence of local variables of quantum mechanics is a subject of a long-standing debate.^46,47 Some deep learning architectures describe molecular systems with local variables assigned to each atom, while other deep learning architectures may also utilize global variables. The performance differences between local and global models may shed empirical light on this question, determining empirically which aspects of quantum chemistry can, in practice, be represented by local variables alone, and which may require global variables.

METHODS

Dataset Selection and Processing.

This work included QC calculations of total energy, gap energy (difference of lowest unoccupied and highest occupied molecular orbital energies), atom valence, bond order, and bond lengths by DFT from two datasets: QM9³⁰ and PubChemQC.⁴⁸ In addition, we included polarizability calculations from a combinatorial oligomer dataset. In the following paragraphs, we describe the details of the data and calculations performed for each of these datasets.

The QM9 dataset and reference total energy calculations for free atoms of each of the five included atomic species (H, C, N, O, and F) were obtained from the figshare QM9 repository.³⁰ One-fifth of the molecules (26,650) were randomly chosen as a test set, and the remainder were retained for model training. The QM9 dataset consists of 13 QC properties for 1,34,000 molecules calculated using DFT at the B3LYP/6–31G(2df,p) level.

To improve the diversity of compounds included in this study, a subset of the PubChemQC dataset, a repository of 3.9 million DFT calculations on PubChem molecules,⁴⁸ was obtained with the permission of the PubChemQC authors by scraping the content of the PubChemQC project website (pubchemqc.riken.jp). PubChemQC aggregates minimum energy structures and QC properties computed using DFT at the B3LYP 6–31 + G* level. We selected a subset of molecules in three steps. First, we excluded molecules that met the following criteria: contained atom types not supported by the 6–31 + G* basis set used in the calculations (atomic numbers 1–18 are supported), were mixtures of two or more compounds, had partial charges larger in magnitude than two, had more than 10 rings, or had spin values greater than triplet. Second, we narrowed our selection to 1.5 million molecules by sampling from a joint probability distribution over aromatic system size, conjugated system size, number of heavy atoms, charge, spin, and number of rings. Rare compounds (e.g., large number of rings and large aromatic system sizes) were more likely to be selected than compounds with more commonly occurring properties. Finally, we selected a topologically diverse subset from this filtered list of compounds by iterating over the filtered list and including compounds with a Tanimoto similarity less than 0.7 to any compound already included. Tanimoto similarity was computed using path-based fingerprints with a depth of 8 and a bit vector size of 2¹⁶.⁴⁹ The final dataset contained 5,10,010 compounds. For these compounds, we extracted total energies, molecular orbital energies, atom valences, bond orders, and bond lengths from PubChemQC calculations. Atom valences and bond orders were computed with the Mayer valence analysis.⁵⁰ Gap energy was computed as the difference between the lowest unoccupied and highest occupied molecular orbital energies (LUMO–HOMO).

To improve on the QM9 data’s limited range of polarizability values, we collected a set of 9505 oligomers with a larger range of polarizability values (Figure S1). Each oligomer was constructed from a pre-defined set of 91 monomers and consisted of between one and six monomer subunits.⁵¹ Polarizability values were calculated by DFT using the Gaussian 09 software with the ωB97X-D functional⁵² and the cc-pVTZ basis set,^53–55 which have proven to have good accuracy for predicting static polarizabilities.⁵⁶

Total energy calculations (in both QM9 and PubChemQC) and polarizability calculations showed strong correlations with molecule size (Figure S2). Normalization to remove these correlations improved the performance of the tested QC models (data not shown) and is commonly performed in the literature on deep learning in quantum chemistry.³³ Models were trained against normalized targets, but accuracy values were computed by denormalizing model output and comparing to the original calculated values. Total energy calculations from both the QM9 and PubChemQC datasets were normalized by subtracting the sum of free atom energies of the constituent atoms (computed in the ground state at neutral charge) and dividing by the number of atoms (Figure S2A,C). Polarizability calculations were normalized by simply dividing by the number of atoms (Figure S2B).

Conjugated Systems and Rotable Bonds.

We computed the number of atoms in conjugated systems and the number of rotable bonds within molecules using the RDKit software.⁵⁷ RDKit uses a topological algorithm to assess whether bonds belong to conjugated systems. An atom was defined as belonging to a conjugated system if any of its bonds was marked with the is Conjugated flag by RDKit. The number of rotable bonds was calculated with the RDKit CalcNumRotatableBonds method.

Matched Pair Analysis.

As coordinate-free methods are based on graph topology, we evaluated the effect of topological similarity by selecting matched pairs of molecules from additional PubChemQC data. For each molecule in PubChemQC that met our initial filtering criteria, we identified the most similar molecule from the training set by Tanimoto similarity (path-based fingerprints, depth 8, bit vector size 2¹⁶). These were then considered a matched pair if their Tanimoto similarity was at least 0.5. The majority of matched pairs (17,48,733 of 23,86,889 or 73%) had Tanimoto similarity greater than 0.8.

Model Structure and Training.

To evaluate the performance of each graph-encoding architecture on the six QC calculation tasks examined in this work, we used a fixed input architecture, fixed decoder architecture, and fixed training protocol for all models. Only the architecture used at the graph encoder step was allowed to vary between models (Figure 3A).

Figure 3.

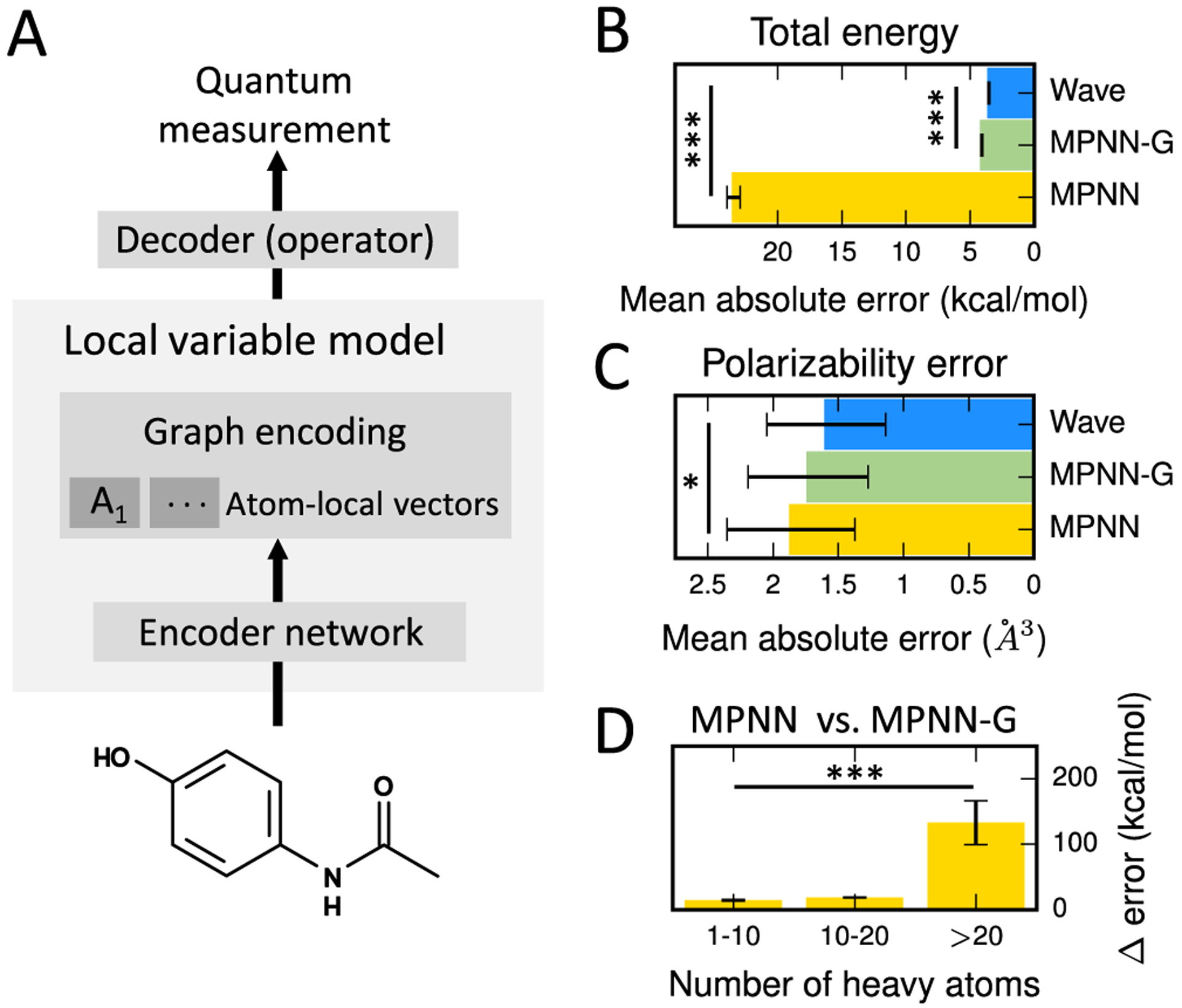
Wave represents QC systems accurately with a local variable model, while convolution requires global variables. (A) Graph-based deep learning methods can be used to learn an atom-local variable model of quantum chemistry. This intermediate representation can then be decoded to a quantum measurement. Wave is an atom-local variable model, while MPNN-G, which includes a global variable, is a mixed local variable model. (B) Removing the global variable from MPNN-G (MPNN) results in substantially higher error on total energy and (C) polarizability. Both methods exhibit higher error than Wave. (D) Increase in total energy error of MPNN vs MPNN-G. MPNN exhibits a statistically significant increase in error for all molecules, but substantially larger error increases for large molecules. Statistical tests were performed by paired t-test. *: p < 0.05, ***: p < 0.001.

The input architecture first generated an initial vector of atom features containing a one-hot encoding of element type and formal charge. This input representation was transformed by a single layer of neighborhood convolution with a depth of three bonds⁴⁰ with an output vector size of 128 and exponential linear unit (eLU) activation.⁵⁸ These computed representations were used to initiate the state of each atom-local variable.

The graph encoders tested in this work included two variants of the graph convolutional network that use message passing neural networks (MPNN and MPNN-G) and a breadth-first graph recurrent network (Wave). Input atom state variables were processed by five passes with either algorithm. MPNN and MPNN-G networks were implemented with the DeepMind Graph Nets python library.⁵⁹ MPNN-G used global, node, and edge update blocks. The recurrent unit was a single-layer neural network with eLU activation. In practice, this worked substantially better than more sophisticated recurrent units, such as gated recurrent units (data not shown). Global and edge states were initialized to zero for the first pass. MPNN did not use the global block or global state variable. For the Wave network, we used the reference implementation provided by the Teflon deep learning API.⁶⁰ Wave used the gated recurrent unit (GRU) with tanh activation,⁶¹ a softsign-weighted mix-gate,⁴⁰ and layer normalization at both the mix-gate and GRU output layers.

To calculate the quantum properties, different architectures were used at the atom, bond, and molecule levels. At the atom level, each atom variable was passed to a neural network consisting of two hidden layers (sizes 64 and 32) with an exponential linear unit or eLU activation and a linear output layer. At the bond level, atom variables for each bond were concatenated to form input to a two hidden layer neural network (sizes 64 and 32) with eLU activation and linear output. The first layer of this neural network performed a weave operation to compute a vector representation of each bond that was order invariant.³⁷ Given vector-valued atom variables A₁, A₂, and hidden layer f, the weave operation calculated f([A₁A₂]) + f([A₂A₁]), where the brackets indicate vector concatenation. At the molecule level, the complete collection of atom variables was passed to a decoder based on the set2set network architecture,⁶² which generated a single molecule-level vector representation. The set2set decoder has been used to achieve state-of-the-art performance on the QM9 benchmark with the MPNN architecture.³⁸ Briefly, the decoder reduces atom variables to a single-molecule-level vector by several passes of weighted summation over the atom variables and subsequent transformation with a recurrent neural network. The decoder performed five passes with a long short-term memory recurrent network⁶³ and a single hidden layer attention network with eLU activation. The molecule-level vector was then passed to a neural network consisting of one hidden layer size of 32 with eLU hidden layer activation and an output layer with linear activation.

All the models were constructed and trained using TensorFlow,⁶⁴ DeepMind Graph Nets, and the Teflon deep learning toolkit. Models were trained by batch gradient descent on the mean-squared error loss using the Adam optimizer⁶⁵ with a learning rate of 10⁻³, a continuous learning rate decay of 0.98, a batch size of 64 molecules, and 1,00,000 training iterations.

Statistical Analysis.

Because all methods were evaluated against the same test sets, all statistical tests were calculated by two-sided, paired Student’s t-test.

Data and Code Availability.

Sample python code and pre-trained models of total energy using the Wave and MPNNG architectures are available at our Bitbucket Git repository: https://bitbucket.org/mkmatlock/coordinate_free_quantum_chemistry. The repository provides sample code for generating predictions on new molecules and training new models. It also contains a pre-processed copy of the training and test data used to evaluate the models in our paper. PubChem compound IDs for each compound in the training, test, and external validation data are also included, and the raw data are available via the PubChemQC project (pubchemqc.riken.jp). The pre-processed extended test data used in Figure 2F,G is too large for repository storage but is available on request. The implementations of basic operations required by the Wave and MPNN-G architectures are contained in the Teflon (https://bitbucket.org/mkmatlock/tflon) and graph_nets (https://github.com/deepmind/graph_nets) python packages, respectively. To facilitate experimentation with the software, the Bitbucket repository includes a docker recipe with the required dependencies.

Figure 2.

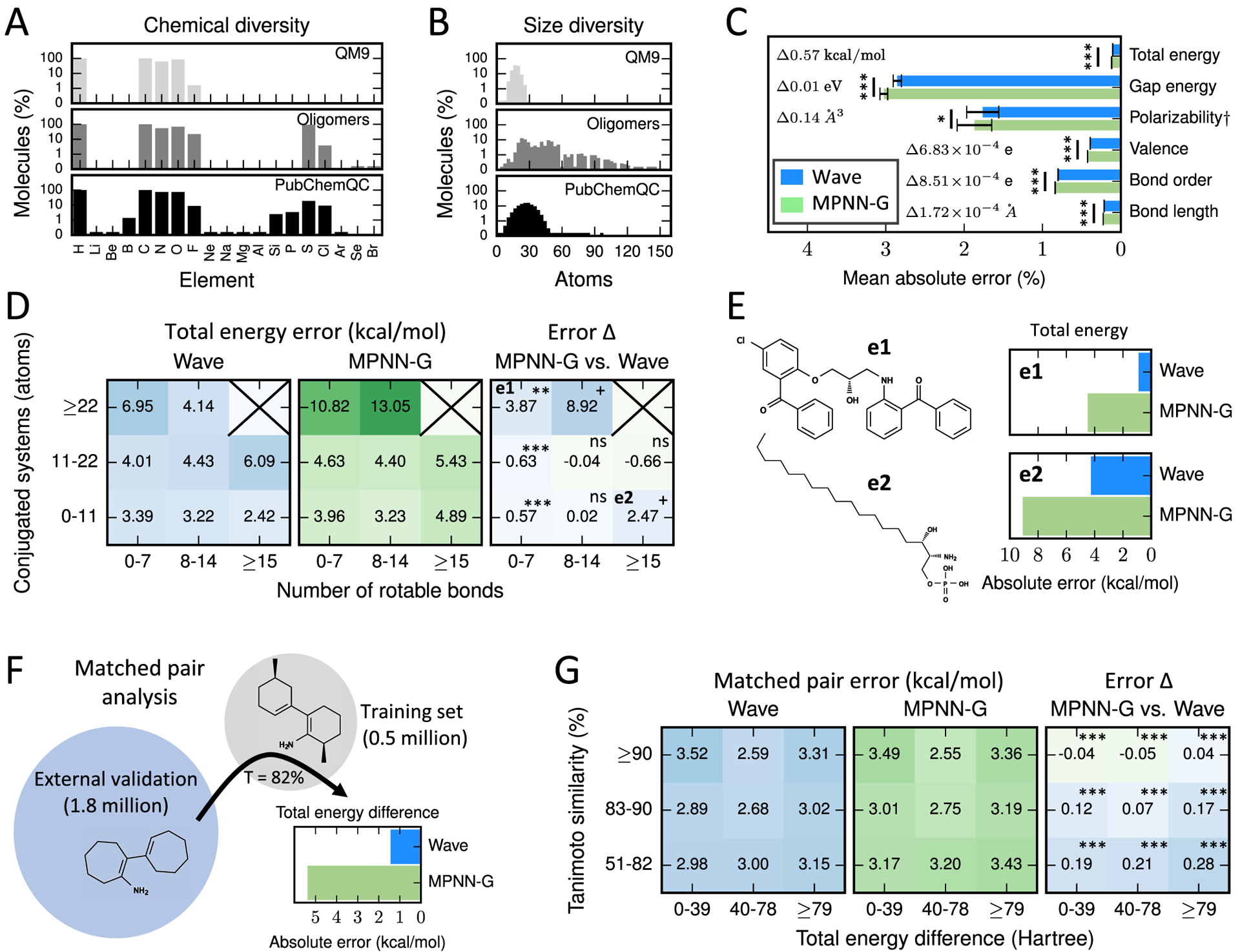
Wave enables more accurate coordinate-free calculation of QC properties across diverse molecules. (A) PubChemQC and Oligomer datasets used in this study cover a substantially larger number of atom types and (B) include substantially larger molecules than QM9. (C) Wave was slightly more accurate than MPNN-G on the six QC properties included in this study. (D) Wave exhibits substantially lower error compared to MPNN-G when calculating total energy for molecules with large conjugated systems and also outperformed MPNN-G on large, flexible molecules. (E) Example molecules on which Wave achieves lower absolute error on total energy (kcal/mol) compared to MPNN-G with (e1) many atoms in conjugated systems and (e2) many rotable bonds. (F) Matched pairs were selected by choosing topologically similar molecules from a large external validation set. (G) Coordinate-free methods exhibit a small increase in error when computing the difference in total energy between matched pairs of molecules. Wave slightly outperformed MPNN-G on this task. Statistical tests were performed by paired t-test. +: p < 0.1, *: p < 0.05, **: p < 0.01, and ***: p < 0.001.

RESULTS AND DISCUSSION

Graph-Based and Coordinate-Free Quantum Chemistry.

With these considerations in mind, we constructed coordinate-free, local variable models of quantum chemistry capable of computing QC properties of molecules in energy-minimized states without explicitly computing optimized geometries. Our coordinate-free deep learning models utilize a graph-based intermediate representation of molecules. This approach is inspired by organic chemists, who often reason about the molecular behavior by representing molecules as graphs in a coordinate-free domain, with atoms represented by nodes and bonds by edges. This construction enables us to bypass time-consuming molecular geometry optimization and energy minimization steps and derive QC properties directly from molecular structures (Figure 1A). In this work, we present results from two major classes of graph neural network: graph convolution and breadth-first recurrent (Wave) networks. Graph convolution, as implemented by message passing neural networks (MPNN),³⁸ computes state variables, local to each atom in a molecular system, by aggregating features of the atom and the atom’s local neighbors (Figure 1B). In addition to local aggregation, MPNN allows for global variables (MPNN-G), which exchange information with each atom in the molecule during each aggregation step. These global variables may help in contexts where long-range information is important, such as large aromatic and conjugated systems.⁴⁵ In contrast, Wave networks use only local variables and propagate information by ordering atom variable updates by a breadth-first search (Figure 1C). In Wave, atom variable updates depend only on ancestors in a breadth-first search. This ordering of updates allows Wave to achieve high accuracy and efficiency compared to graph convolution on tasks requiring long-range information.^43,45 In particular, to ensure that long-range information is propagated between all pairs of nodes, in the worst case, graph convolution requires as many convolutional passes as there are atoms in the molecule. However, Wave is designed to propagate information between all the atoms in a molecule within a small, constant number of passes, regardless of molecule size.

Figure 1.

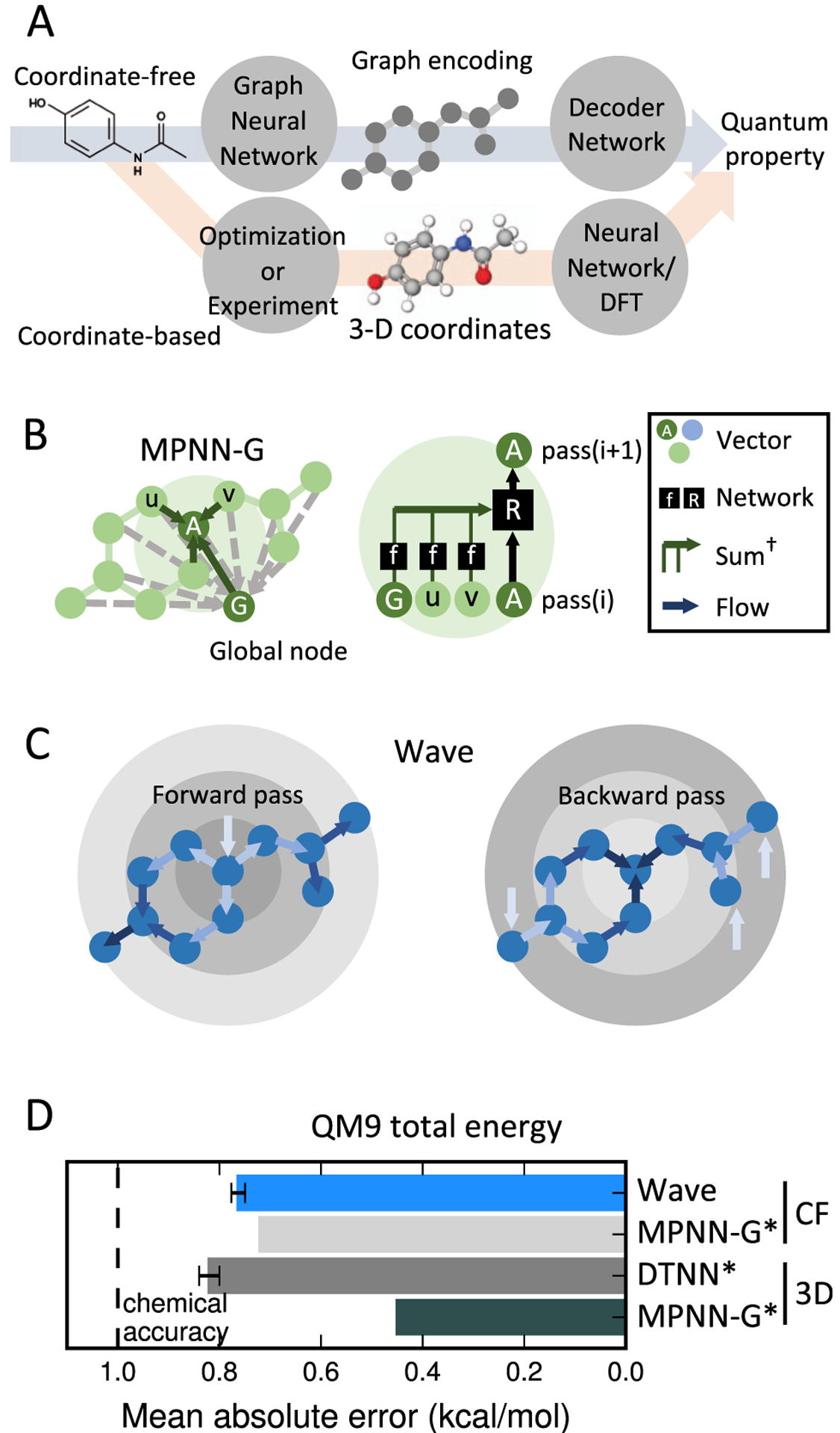
Coordinate-free methods leverage deep learning to compute QC properties. (A) Many deep-learning-based QC calculation methods require coordinates from experiment or computational optimization, which can be time-consuming to obtain. Coordinate-free methods operate directly on structural formulas without the need for coordinates. (B) Many graph-based deep learning methods describe atoms by aggregating features from other atoms in their local environment. Atoms may also exchange information with global variables, as in message passing neural networks (MPNN-G). (C) Wave deep learning architecture describes atoms based only on their ancestors as defined by a breadth-first search. Information is propagated in Waves, forward and backward across a molecule. (D) Wave achieves better than chemical accuracy when predicting total energy on QM9, a standard benchmark dataset. This result is comparable to the published, coordinate-based methods. CF: Coordinate-free 3D: 3D coordinates used as input features, *value from published results.^19,38

Coordinate-free methods achieve results comparable to other literature reports on QM9 (Figure 1D).^19,38 Wave achieved a mean absolute error of 0.76 kcal/mol when trained on approximately 1,10,000 DFT calculations of total energy at zero kelvin. Most importantly, this value is below the benchmark standard of “chemical accuracy”, which is close to the accuracy of experimental measurements. Coordinate-free MPNN-G has also been studied in the literature and achieves a mean absolute error of 0.72 kcal/mol, which is comparable to our results using Wave.³⁸ In comparison, deep tensor neural networks, a deep neural network that calculates atom features based on their relative spatial proximity to other atoms, achieves a mean absolute error of 0.82 kcal/mol.¹⁹ Graph-based neural networks have also been investigated in a coordinate-based framework. A variant of MPNN-G that used bond lengths from optimized molecular structures as a feature achieved a mean absolute error of 0.45 kcal/mol.³⁸ Standard errors were not available for these literature-derived estimates of MPNN-G accuracy, so a direct statistical comparison is not possible. Furthermore, while this evaluation holds the molecule set (QM9), calculation methods (total energy), and evaluation metric (mean absolute error) constant, there are variations in training protocols, hyperparameter optimization, and selection of training and test subsets that may affect the comparability of these values.

Wave Improves the Accuracy on Complex Molecules.

To investigate the feasibility of constructing accurate, coordinate-free quantum chemistry models useful in screening applications, we used two benchmark datasets more chemically diverse than QM9 (Figure 2A,B). The first benchmark dataset was derived from the PubChemQC project, a repository of 3.9 million DFT calculations on PubChem molecules. We selected a subset of 5,10,010 molecules with a wide range of atom types for our study (Methods). From this dataset, we extracted key properties of molecular systems including calculations of total energy, gap energy (difference between the highest occupied and lowest unoccupied molecular orbital energy), Mayer atom valence and bond order, and bond length. The second benchmark dataset addresses the limited range of polarizability values in QM9. Polarizability is a critical property for evaluating non-bonding interactions in the design of metal catalysts.⁶⁶ We collected a set of 9505 π-conjugated oligomers with polarizability ranging from 3 to 515 ų (Methods). These molecules demonstrated a considerably larger range of atom types (19), compared to QM9 (5), as well as a larger range of molecule sizes (146 atoms vs 29 atoms), ring counts (20 vs 6), aromatic system sizes (76 atoms vs 9 atoms), and conjugated system sizes (84 atoms vs 9 atoms) (Figure S3). In addition, calculated QC properties exhibited considerably wider ranges compared to QM9 including total energy (3,170,000 kcal/mol vs 423,000 kcal/mol due to increased size of molecular systems), polarizability (512 ų vs 28.2 ų), and molecular orbital energy (42.6 eV vs 16.9 eV) (Figure S1). This large range of molecular orbital energies arises from PubChemQC’s diversity of molecular structures from single atoms and salts to large organic compounds.

Coordinate-free methods perform well on these complex benchmarks (Figures 2C, S4, and S5). Both Wave and MPNNG achieve less than 3% error on all six QC properties included in this study. However, Wave exhibited small but consistent improvements on all targets (using paired t-test on the mean absolute error, p < 1 × 10^–8 for total energy, gap energy, atom valence, bond order, and bond length and p = 0.028 for polarizability). Coordinate-free methods can accurately predict spatial measurements like bond length with a mean absolute error of 0.003 ų, which is less than 1% of the typical range of carbon–carbon bond lengths. The deviation of coordinate-free methods from DFT predictions is substantially lower than the error of most DFT methods.⁶⁷ Furthermore, this performance is consistent across different types of carbon–carbon bonds (Figure S6A), and across bonds between different atom types (Figure S6B). Interestingly, Wave outperforms MPNN-G on less common bond types, such as carbon–carbon triple bonds and sulfur–hydrogen bonds, with a 40 and 16% decrease in error compared to MPNN-G, respectively (p < 0.01, paired t-test). It should be noted that these datasets are biased toward carbon, nitrogen, oxygen, sulfur, and hydrogen atom types and may not exhaustively represent the diversity of bond chemistries among the supported atom types.

Coordinate-free methods perform well even on flexible molecules with many rotational degrees of freedom, and Wave exhibits increased accuracy on large, chemically complex molecules (Figure 2D,E). We binned molecules by conjugated system size and number of rotable bonds and assessed total energy prediction performance. Large conjugated systems typically suggest delocalized electrons which can increase the molecular rigidity by constraining bond rotation, while many rotable bonds suggest high flexibility. Both coordinate-free methods exhibit good performance on flexible and rigid molecules (Figure 2D). However, error decreased by 50% with Wave compared to MPNN-G on molecules with a large number of rotable bonds (p < 0.1, paired t-test). In addition, Wave performed significantly better than MPNN-G on molecules with large conjugated systems, with a 36% decrease in error (p < 0.01, paired t-test). To determine whether these increases in error could be attributed to increased molecular size alone, we binned by conjugated system size and number of heavy atoms. Error increased with increasing conjugated system size even within each molecular size bin (Figure S7). For the largest molecules with the largest conjugated systems, Wave achieved a 46% decrease in error compared to MPNN-G (p = 0.01, paired t-test). These data support our hypothesis that the Wave architecture enables accurate, coordinate-free calculations of QC properties for chemically diverse molecules.

Coordinate-Free Methods Discern between Similar Molecules.

Coordinate-free methods accurately predict differences in QC properties between similar small molecules. Graph topology-based predictive algorithms have a long history in chemistry, but some literature suggests that algorithms relying primarily on topological features may fail to identify property differences between topologically similar molecules.⁶⁸ When designing drugs and biological probes, medicinal chemists often test many variants of the same core molecular scaffold with different substituted functional groups, which results in a series of topologically similar molecules. Matched pairs of molecules were collected from PubChemQC to test whether graph-based ML methods were able to identify property differences between topologically similar molecules (Figure 2F). For each molecule in the PubChemQC database matching our selection criteria, we identified the closest matched molecule in our training data by fingerprint similarity (Methods). The dataset contained 1.8 million matched pairs. Both Wave and MPNN-G accurately predict the difference in total energy between these matched pairs (Figure 2G). Mean error increases less than 0.15 kcal/mol between pairs more or less than 90% similar. These data suggest that graph-based deep learning algorithms are able to correctly discern QC differences between similar molecules.

Wave Enables Local Variable Models of Quantum Chemistry.

Whether it is possible to construct local variable models that describe quantum mechanics is a subject of longstanding debate in physics. With the architectural flexibility of deep learning, it is possible to investigate how choices in the representation of molecular systems affect the accuracy of QC calculations. In this work, graph-based encodings are used to build accurate representations of molecular systems from simple input descriptions. These learned representations are then passed to a decoder, which can compute QC properties (Figure 3A). Wave and MPNN-G achieve similar performance on the datasets in this study, but Wave is a local variable model, while MPNN-G is a mixed local and global variable model. When the global variables are removed from MPNN-G (MPNN), total energy and polarizability error increase by an average of 473 and 7.6% (Figure 3B,C). Importantly, MPNN-G and Wave exhibit a similar behavior insofar as their errors are strongly correlated (Pearson correlation R² = 0.56, Figure S8B). However, MPNN behaves differently, exhibiting a low error correlation with MPNN-G and very large errors on molecules accurately predicted by MPNN-G (R² = 0.04, Pearson correlation, Figure S8A). Furthermore, MPNN exhibits a substantial 22-fold increase in error on total energy for large molecules compared to MPNNG (Figure 3D). This suggests that, without global variables, graph convolutional methods such as MPNN have difficulty representing long-range information. In contrast, Wave is a local variable model and outperforms both methods both total energy and polarizability. This suggests that local variable deep learning models can predict non-local quantum mechanical properties such as polarizability and that propagating information in a Wave-like pattern improves these local variable models.

CONCLUSIONS

Recently, there has been a substantial growth of interest in the applications of high-throughput, in silico screening and automated de novo design of small molecules for a wide range of applications including new materials, catalysts, biological probes, and drugs. For these tasks, it is valuable to avoid the time-consuming computations of optimized molecular geometries or numerical approximations to the Schrödinger equation. In this study, we have demonstrated that coordinate-free methods can be used to compute QC properties of complex molecules in energy-minimized states, while bypassing the significant computational costs incurred by other methods. These coordinate-free methods achieve parity with coordinate-based methods on benchmark data. Coordinate-free methods also succeed when computing geometric properties, such as bond lengths, and when computing properties of highly flexible molecules. Using the Wave graph encoding improves predictions for large molecules and for molecules with delocalized electrons (conjugated systems). Importantly, these graph-based algorithms are able to discern QC differences between topologically similar molecules, which is critically important for successfully identifying optimal chemical structures in many applications.

While we have focused primarily on analyzing coordinate-free methods for quantum chemistry, work on deep learning and quantum chemistry has broader implications. Deep learning architectures may provide a new approach to investigate a broader question in physics: what types of quantum mechanical systems can be represented by local variable models? In this study, we show that Wave, a local variable model, can represent quantum chemistry equally well when compared to MPNN-G, a state-of-the-art graph convolutional architecture, which requires global variables for similar performance. With a better algorithm, which propagates information in Waves, it is possible to construct local variable models of quantum chemistry for diverse molecules. Enumerating and studying which QC systems can or cannot be accurately represented with local variables remains an open question. Several groups working in this field are extending quantum chemistry to very large molecular systems. Furthermore, developing an understanding of how quantum chemistry is being internally represented by these algorithms may shed light on the generalizability of deep learning in quantum chemistry. Can deep learning represent all the information in a quantum system, similar to a Wave function? This ongoing work presents an opportunity to generate empirical data that may shed light on this fundamental question.