The computational and neural bases of context-dependent learning

Abstract

Flexible behavior requires the creation, updating and expression of memories to depend on context. While the neural underpinning of each of these processes have been intensively studied, recent advances in computational modeling revealed a key challenge in context-dependent learning that had been largely ignored previously: under naturalistic conditions, context is typically uncertain, necessitating contextual inference. We review a theoretical approach to formalizing context-dependent learning in the face of contextual uncertainty, and the core computations it requires. We show how this approach begins to organize a large body of disparate experimental observations, from multiple levels of brain organization (including cells, circuits, systems, and behavior) and multiple brain regions (most prominently the prefrontal cortex, the hippocampus, and motor cortices) into a coherent framework. We argue that contextual inference may also be key to understanding continual learning in the brain. This theory-driven perspective places contextual inference as a core component of learning.

1. INTRODUCTION

The flexibility of human behavior relies on our ability to lay down memories across a number of domains, including for episodic events, motor skills and decision-making. Research on learning and memory has, for the most part, studied how individual memories are laid down, recalled, and modified, one at a time. These studies use carefully controlled laboratory experiments, in which salient events and unambiguous stimuli cue when a memory needs to be stored, and when and which memory needs to be recalled, or modified. For example, studies of animal learning typically use easily discriminable stimuli for conditioning, or study spatial memory for the location of a single platform in a water maze. However, in the real world, we experience a continuous stream of sensorimotor experience and need to lay down multiple distinct memories. This leads to the problem of how to manage our growing repertoire of memories, when to create a new memory and how to express and update existing memories such that old memories are not (necessarily) forgotten as new memories are acquired.

There have been recent developments that place the idea of context central to the management of such repertoires. Rooted in so-called mixture models that have long been pursued in machine learning (Jacobs et al. 1991, Singh 1991), a number of theories have argued that the brain organizes memories according to discrete internally constructed contexts (Wolpert & Kawato 1998, Wolpert et al. 1998, Haruno et al. 2001, Gershman et al. 2010, Collins & Koechlin 2012, Collins & Frank 2013, Gershman et al. 2014, Heald et al. 2021). As such, context serves to tag or index memories for subsequent recall and updating. The effects of context on memory have been demonstrated in a diverse set of cognitive domains including classical conditioning (Redish et al. 2007, Gershman et al. 2010), episodic memory (Howard & Kahana 2002, Zacks et al. 2007, Gershman et al. 2014), economic decision making (Collins & Koechlin 2012, Collins & Frank 2013), spatial memory (Gulli et al. 2020, Plitt & Giocomo 2021, Julian & Doeller 2021), and motor learning (Heald et al. 2018, Oh & Schweighofer 2019, Heald et al. 2021). These results suggest that successfully managing a repertoire of memories hinges on our ability to determine which contexts are appropriate at different points in time.

Although context is unambiguously defined in most laboratory experiments (at least from the experimenter’s point of view), in the wild (and in general, from the animal’s perspective), it is anything but (Heald et al. 2022 in press). Thus, determining, or inferring, the currently appropriate context is a core computational challenge in context-dependent learning. We start by reviewing a theoretical framework for formalizing contextual inference and how it controls memory expression, updating and creation. We then use this framework to organize our understanding of the neural bases of context-dependent learning. Finally, we review recent advances in training artificial neural networks on continual learning tasks, i.e. tasks that require managing multiple, potentially interfering memories. We discuss how such models may inform the study of the neural bases of context-dependent learning, and conversely, how a better understanding of the way the brain solves contextual inference may provide useful clues for constructing more efficient artificial continual learning systems.

2. A COMPUTATIONAL FRAMEWORK FOR CONTEXT-DEPENDENT LEARNING

In order to study the neural bases of context-dependent learning we introduce a normative approach that starts from a ‘generative model’ that summarizes the causal and statistical relationships between relevant quantities in the environment, such as contexts, sensory cues, and actions – including the ways they may change over time. Some of these quantities, such as sensory cues and actions, are directly observed by the brain, while others, such as contexts and reward contingencies, are ‘hidden’ as they cannot be observed directly. While there has been a number of different proposals for the precise form of the generative model (Wolpert & Kawato 1998, Wolpert et al. 1998, Haruno et al. 2001, Gershman et al. 2010, Collins & Koechlin 2012, Collins & Frank 2013, Gershman et al. 2014, Sanders et al. 2020, Heald et al. 2021), here we focus on one particular, recent example, the COIN (COntextual INference) model of motor learning (Heald et al. 2021), because it unifies a number of aspects of previous models, and it has been particularly successful in accounting for behavioral data. Although, in its original form, the COIN model was developed to understand the principles of motor adaptation, its foundational concepts are domain-general.

Once the generative model is defined, learning amounts to the process of inferring the hidden variables of the environment based on the observed variables, and in particular to inferring those hidden variables that are assumed to change only slowly, or not at all, over time.¹ Below, we describe this computational framework in formal detail, but the uninitiated reader is welcome to skip forward to Section 3, where we begin by summarizing the main properties and predictions of this framework more informally.

2.1. Generative model

The generative model of the environment that is relevant for contextual learning is a variant of the standard ‘Markov decision process’ or, more generally, ‘partially observable Markov decision process’) that forms the basis of reinforcement learning (Sutton & Barto 2018; see also below) and its applications to neuroscience (Dayan & Abbott 2005). We illustrate the generative model with respect to a mouse in a maze seeking food. In this framework, the (biological or artificial) agent has a ‘state’ at time t, s_t (Fig. 1a, orange; the mouse’s location in the maze) and can generate an action, a_t (Fig. 1a, green; the mouse turning left or right). The mouse then receives ‘sensory feedback’, r_t (Fig. 1a, purple; the absence or presence of a food reward) and experiences a state transition (the mouse moves to a new location). Therefore, according to this generative model, the (distribution of) r_t as well as the (distribution of the) next state, s_t+1, depends on the current state, s_t, together with the agent’s action, a_t in a manner defined by a set of ‘primary’ contingencies (e.g. the current configuration of walls in the maze and the location of food inside it). In addition, there may exist ‘sensory cues’, q_t (Fig. 1a, pink; the general appearance of the room containing the maze) that are unrelated to states, actions, and feedback and depend on additional primary contingencies.² The primary contingencies may themselves change over time (some passageways become obstructed or new ones may open), controlled by some other (‘secondary’) contingencies (e.g. the volatility of the environment; Piray & Daw 2020).

Figure 1. A normative model of context-dependent learning.

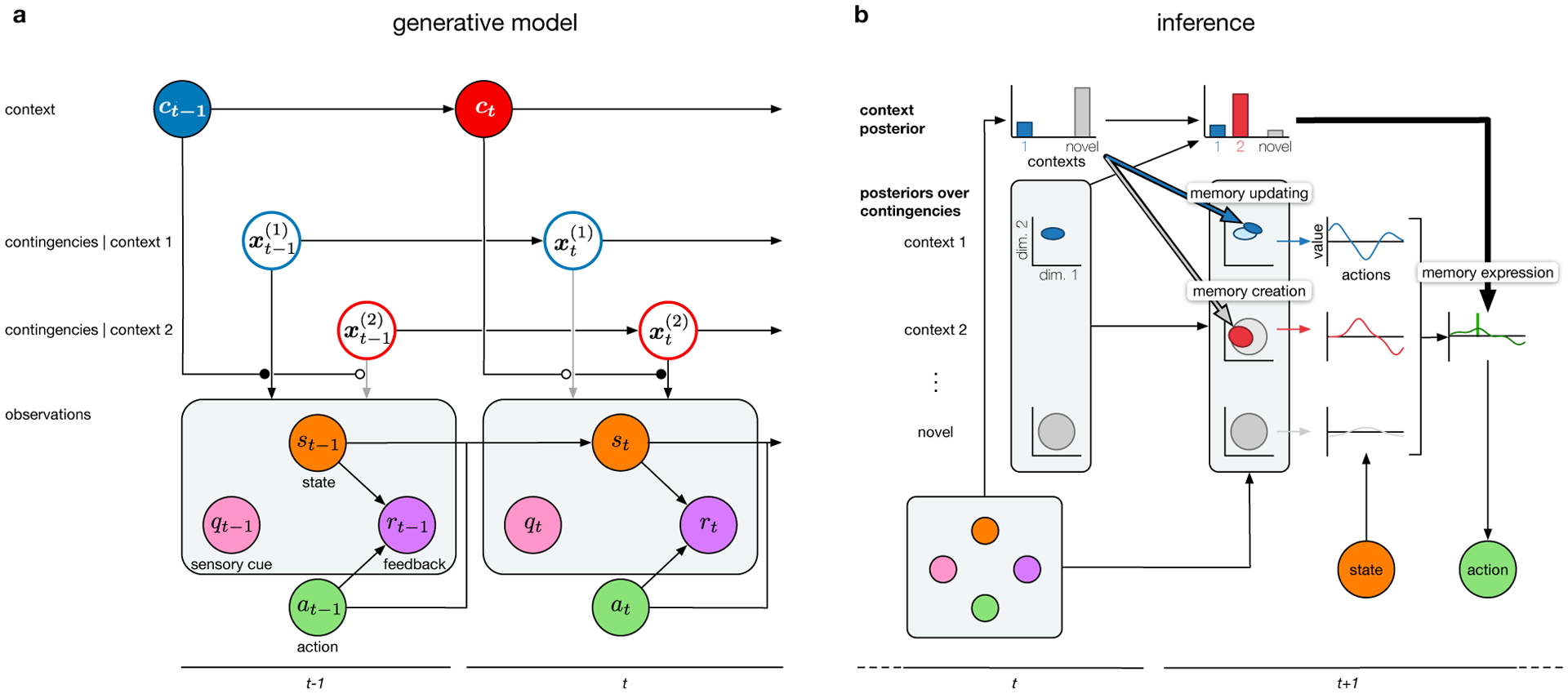
a. Generative model, showing two consecutive time steps, t − 1 and t. Context, c_t, evolves over time (color represents the identity of the active context). Each context j is associated with a set of contingencies, $x_t^{\left(j\right)}$, that may also evolve in time, independent of the contingencies of the other contexts. (Only two contexts are shown for simplicity; in general, the number of contexts and sets of contingencies can be unbounded). The contingencies of the currently active context (filled vs. empty circle respectively gating black vs. gray arrows) determine what sensory cue is received, q_t (pink), and how the agent’s action, a_t (green), change its state, s_t (orange), and lead to sensory feedback, r_t (purple). In general, the contingencies of the active context can also affect the next context transition (not shown for clarity), and states may not be directly observable. b. Inference, showing two consecutive time steps. The agent infers contexts (top, inferred posterior distributions shown as histograms) and context-specific contingencies (middle, inferred posterior distributions in a multi-dimensional space of contingencies illustrated with covariance ellipses, dimensions [dim.] 1 and 2 shown) based on observed states, sensory cues, sensory feedback, and its own actions (bottom, colors as in a). Contexts are color coded in top and middle as in panel a. Note that the probability that a yet-unseen, novel context with ‘default’ contingencies is encountered is also always computed (gray). Columns 1 and 2: the context posterior at time t (column 1, top) is computed by fusing prior expectations (propagated context posterior from time t − 1, not shown) with information about the current observations (column 1, bottom). This posterior determines the degree to which information from the current observations is used to update the inferred context-specific contingencies at time t + 1 (column 2, middle, memory updating, pale blue distribution updated to bright blue distribution) and whether a new memory is instantiated (column 2, middle, memory creation, the red posterior over contingencies updated from the gray posterior over contingencies of a novel context). Column 3: for each represented context, the expected values of actions (curves in context-specific colors) are computed based on the inferred contingencies of that context. Column 4: the final expected values of actions (green curve) are the weighted sum of their context-specific values, with the weighting determined by the posterior probabilities of the corresponding contexts (memory expression). The action with the highest final expected value is chosen (vertical green line; potentially with some decision or motor noise, not shown). Note that memory creation, expression and updating can all occur on the same time step, but they are shown here on separate time steps to avoid visual clutter.

Critically, central to context-dependent learning is the assumption that there may exist several such sets of (primary and secondary) contingencies in parallel, $x_t^{\left(j\right)}$ (j = 1, 2,…; Fig. 1a, blue and red open circles), and the identity of the currently active one (i.e. the one that gets to control state transitions and feedback) is determined by the current context, c_t (Fig. 1a, colored filled circles on top; e.g. the maze identity). Note that it is because there are multiple contexts that sensory cues become relevant: they can be informative as to the context (different mazes may be associated with different looking rooms). However, as opposed to states, once the context is known, sensory cues are no longer informative as to the relation between actions and feedback.

Finally, context can also change over time (depending on context-specific transition probabilities, which can be regarded as further secondary contingencies), and when it does, it is thought to instantaneously switch which set of contingencies is active (Fig. 1a; modulatory connections from context nodes, with filled and empty circle heads, to the black and gray arrows of the active vs. non-active context-specific contingencies, respectively, expressing their control, or lack of control, of observations). One important aspect by which previous and more recent models of contextual learning differ is the extent to which they allow context transition probabilities to be structured, i.e. whether and how much transition probabilities depend on (or conversely, generalize across) ‘from’ contexts, ‘to’ contexts, both, or neither (for a review, see Heald et al. 2022 in press; for a more general comparison beyond transition probabilities see Section 7 of the Supplementary information and Extended Data Table 1 in Heald et al. 2021).

Note that, theoretically, the distinction between contexts and states need not be as clear cut as we depict it here. States (rather than just contexts) may also be hidden, sensory cues may also depend on states (rather than just on contexts), and transitions between contexts (rather than just those between states) may also depend on actions and states. In this more general framework, contexts may simply correspond to higher level, more slowly changing components of a high-dimensional, hierarchical hidden state representation. For example, although in typical experiments contexts may be naturally operationalized by different experimental rooms, and states as positions within a maze situated in a room, the mouse may actually integrate all these into a single multiresolution map of its environment. Nevertheless, it may be computationally advantageous to distinguish between high-level contexts (often referred to as ‘tasks’, Xie et al. 2021) and low-level states. Moreover, there is both behavioral and neural evidence suggesting that (the internal representations of) contexts may have a special status (see below), and so for the purposes of this review, we maintain a qualitative distinction between contexts and states.

2.2. Contextual learning as recursive inference

The ultimate goal of a reinforcement learning agent, and arguably also of the brain, is to choose actions, a_t, adaptively so as to maximize (cumulative) rewards (that are included in our notion of sensory feedback, r_t). Although there are many algorithmic strategies that can be used for this (Sutton & Barto 2018), the most flexible class of algorithms that makes the best use of limited experience with the environment (i.e. most data-efficient) is based on a generative model of the environment (i.e. it is model-based). Thus, the task for the brain in context-dependent learning can be formalized as the inference of the hidden variables of the generative model described in Section 2.1, based on the observed sensory inputs and motor outputs (actions). To reduce the computational complexity of learning, and especially of choosing actions (i.e. expressing memories, albeit at the cost of reduced data-efficiency and behavioral flexibility), the brain may also combine model-based inference of context with model-free strategies for learning within individual contexts (Singh 1991). Although below we consider the fully model-based setting, our focus will be on the inference of context, which thus remains relevant even in such a hybrid learning system.

2.2.1. The targets of inference: environmental contingencies and context.

The key hidden variables to be inferred are the contingencies specific to each context that has been encountered so far, $x_t^{\left(j\right)}$, and the identity of the current context, c_t (Fig. 1a, top half). In our example with the mouse foraging for food, it needs to infer the layout (and other features, such as the volatility, see below) of each maze it has encountered (the contingencies), and the identity of the maze it is currently in (the context). The observations that can be used for this are the state, s_t, the sensory feedback, r_t, the sensory cue, q_t, and the agent’s own action, a_t (Fig. 1a, bottom half)³. While treating the contingencies of the environment as hidden variables has been a common feature of formal theories of learning, treating the current context as an additional hidden variable is a relatively recent innovation (Gershman et al. 2010, Collins & Koechlin 2012, Gershman et al. 2014, Heald et al. 2021) that has far reaching consequences, as we will see below. This choice is motivated by a simple fact we already highlighted in the Introduction: that – from an animal’s perspective – context is only defined ambiguously in most situations, especially in ecologically relevant ones.

2.2.2. The result of inference: the posterior distribution.

Optimally, the result of inference should be a posterior probability distribution defining the joint probability of all possible combinations of the current values of all hidden variables given the history of all previous observations, $\text{P}\left(c_t,x_t^{\left(j=1,\dots \right)}|s_{0:t},a_{0:t},r_{0:t},q_{0:t}\right)$. This distribution can be computed recursively, incorporating the most recent observations into the posterior computed in the previous time step. The joint posterior over all hidden variables at any point in time can be conceptually separated into two components: the posterior distribution over the current context (Fig. 1b, top row with histograms), and the posterior distributions over the contingencies of each possible context (Fig. 1b, middle three rows with covariance ellipses). In particular, it is sufficient to represent posterior context probabilities and posteriors over contingencies for only those contexts inferred to have been encountered so far (Fig. 1b, top row, blue and red bars in histograms, and top two of middle rows, blue and red covariance ellipses). Beside these, the novel context probability, i.e. the total probability of all yet-unseen contexts, also always needs to be represented (Fig. 1b, top row, gray bar at the end of each histogram), together with an additional set of ‘default’ contingencies for all such contexts (lowest middle row, gray covariance ellipses).

Critically, all the agent’s experience pertinent to a given context is captured by the corresponding posterior over contingencies. In other words, in this framework, the posterior over contingencies specific to a given context constitutes the memory of that context. Alternatively, to reduce computational and representational complexity, instead of inferring a full posterior distribution, most theories posit that only single estimates of contingencies are learned (but see Section 4.3). Yet other, altogether model-free strategies may not try to infer or estimate the contingencies of the environment at all, and instead learn other kinds of representations (such as value functions, or policies). Whatever the precise nature of the context-specific representations being learned, we will henceforth refer to them as “memories”. Importantly, the principles of contextual learning we describe in the next section apply to all kinds of memories, regardless of their representational content.

In contrast to inferring the values of hidden variables based only on past and present observations (Fig. 1b), in some situations, it may be desirable to retrospectively refine inferences made in the past based on subsequent observations, such as when recalling an episodic memory (Gershman et al. 2014). In Bayesian inference, this type of retrospective inference is known as smoothing and is a computationally challenging operation that requires storing the entire history of observations in memory. How the brain might approximate the fully Bayesian solution to smoothing is unknown, though consolidation-like processes that replay previous experiences (Pfeiffer 2020) are likely to be involved.

3. COMPUTATIONAL PRINCIPLES FOR MANAGING MULTIPLE MEMORIES

The unique challenge of contextual learning is that it requires the agent to manage multiple memories, each corresponding to a different context. In particular, it needs to ensure that at all times it expresses and updates existing memories, and keeps creating new memories, as appropriate. The normative theory developed in Section 2 reveals the computational principles governing how these processes should optimally be organized. In particular, it highlights that memory expression, updating, and creation needs to be graded, or probabilistic, rather than all-or-none and deterministic, as in standard conceptualizations of these processes. It also specifies how the current context needs to be continually inferred, and how this contextual inference needs to control each of these graded processes. In this section, we describe these computational principles in more detail. These principles will provide a set of important constraints on the putative neural mechanisms of contextual learning, reviewed in Section 4. To aid intuition about the computational principles underlying the managing of multiple memories, we will continue to use the ‘mouse in a maze’ example. We will also briefly refer to relevant work demonstrating these effects behaviorally in specific experimental paradigms (see Heald et al. 2022 in press for a recent more comprehensive review on behavioral effects).

3.1. Contextual inference

In order for memory expression, creation and updating to be optimal, these operations should be performed in a graded or probabilistic manner. This in turn requires the full distribution over contexts, expressing the probability that each known context or a yet-unknown novel context is currently active, and hence context uncertainty, to be represented at each point in time. This contrasts with alternative approaches that ignore context uncertainty by only estimating the most probable context. The distribution over contexts should not be independent at each point in time (a priori) but should take into account the previous context distribution and the context transition probabilities (or more generally, the dependence of the current context on the history of past contexts).

The generative model described above (Section 2.1) is, perhaps, the simplest form of contextual inference as it assumes that exactly one discrete context (a hidden cause) is active at each point in time. There are three major extensions to such a model in terms of compositional, continuous and hierarchical representations of contexts, which can each contribute to more powerful generalization. In compositional models, multiple hidden causes can be active at each point in time, and hence a context is formalized as a unique combination of hidden causes. For example, when navigating a maze to find a reward, it can be beneficial to represent the reward function (goal location) and state transition function (mapping from states and actions to next states) as two separate hidden causes so that they can be combined in novel ways to solve new tasks (Franklin & Frank 2020). Continuous representations of context allow the contingencies associated with different contexts to vary along a continuum. For example, when manipulating objects, it may be beneficial to consider different objects within a class (e.g. different cups) to lie on a manifold of contexts, defined by continuously varying contingencies (such as their weight and visual size; Braun et al. 2009). Finally, contexts may also be hierarchically organized, e.g. because different mazes in the same room may have different configurations but still share many of their sensory cues, while mazes in different rooms will even differ in their sensory cues. In the following, we focus on how the posterior distribution over contexts controls memory expression, memory updating and memory creation.

3.2. Memory expression

The ultimate goal of having memories is to express them in behavior. The simplest form of how contextual inference can control this is when the current context is known to the learner with absolute certainty, that is, when the posterior distribution over contexts is all-or-none. In this case, behavior is driven by a single memory: that corresponding to the current context. The normative strategy for choosing an action in a given context is to compute the value of every available action in terms of the cumulative reward the agent expects to receive in the future after choosing that action now – depending, of course, on its current state (Fig. 1b, Column 3, arrow from state in the bottom to context-specific value functions in the middle) and its context-specific memories (Fig. 1b, Column 3, colored arrows from the posteriors over contingencies to the value functions in the middle). Then, the action with the highest value can be chosen.

In general, as there will often be uncertainty about the current context, in principle the memories for all contexts need to be “mixed” (Haruno et al. 2001, Gershman et al. 2017a, Heald et al. 2021). In this case, once the context-specific action values have been computed (see above), according to the rules of Bayesian decision theory, the final expected value of each action is computed by averaging its value across contexts⁴, weighted by the posterior context probabilities, and the action with the highest expected value can be chosen (Fig. 1b, Column 4, thick black arrow pointing from the context posterior of Column 2 to the green action-value function). Thus, a key feature of the model is that contextual inference controls the expression of memories in the actions the agent chooses. In particular, the contents of several memories (those associated with contexts that have a non-zero posterior probability) need to be mixed for optimal behavior. This is notably different from classical accounts of memory recall that focus on how a single memory is retrieved at a time (Hopfield 1982).

The graded mixing of memories provides an alternative account to even such a basic process as memory extinction. Classical (Rescorla & Wagner 1972) and even more modern accounts (Smith et al. 2006) treat extinction as the overwriting (or erasure) of some previously established memory trace, and as such related to memory updating (see also below). In contrast, when viewed through the lens of contextual learning, extinction may instead be due to the gradual re-expression of the memory for the original context preceding the beginning of acquisition (Gershman et al. 2010), as the newly acquired memory (associated with the acquisition context) has no reason to be expressed. This naturally explains ubiquitous post-extinction phenomena that are widely regarded as difficult to reconcile with a simple overwriting-based account, such as the slow spontaneous recovery of the extinguished memory with the passage of time (Rescorla 2004), its fast evoked recovery in response to context-specific sensory cues (as in ABA renewal; Bouton & King 1983) or sensory feedback (reinstatement or evoked recovery; Rescorla & Heth 1975, Heald et al. 2021), or its rapid reacquisition (compared to the speed of its original acquisition; Napier et al. 1992).

3.3. Memory updating

On each time step, the context posterior and the memories are updated by fusing information from the past with information arriving in the current time step (Fig. 1b, transition from Column 1 to Column 2, respectively corresponding to time step t − 1 and t). For example, imagine that a passageway that the mouse found to be open on previous trials, now appears to be closed. In principle, this experience in the current time step will require updating its existing memories, representing information from the past (that the passageway used to be open). The extent of this updating fundamentally depends on the balance between the reliability (or relevance) of present versus past information. In principle, the higher the reliability of current information relative to that of past information, the more memories should be updated in light of this new experience.

The key question then becomes: what determines the relative reliabilities of these two sources of information? The reliability of existing memories (i.e. the relevance of past information they store for the present), depends on the context-specific secondary contingencies describing how (and how much) the primary contingencies are expected to change over time. If, based on previous experience, the mouse has inferred that the maze configuration in a room tends to remain the same for long periods of time, the new information about the passageway being closed may be chalked up to happenchance and as such largely ignored. However, if previous experience tells the mouse that the maze in a room is often reconfigured by some malevolent power (i.e. the experimenter), then this same information will be used to update the mouse’s cognitive map of the maze. This predicts higher effective learning rates in more volatile environments—an effect that has been confirmed experimentally (Burge et al. 2008). Note that, however, this prediction changes when the volatility of the environment is at the level of contexts rather than the level of contingencies (i.e. across-rather than within-context volatility), for example if the mouse is often transported to an altogether different maze. In this case, rather than changes in the rate of adaptation being driven by memory updating (proper learning), they may be due to changes in memory expression (apparent learning, so called because from behavior alone it may appear as though proper learning has taken place; Heald et al. 2021, 2022 in press).

The reliability/relevance of currently incoming information is determined by two factors. First, the better the quality of evidence it supplies, the more relevant it is for updating memories. For example, if the mouse only saw the passageway to be closed from a distance, this observation may be attributed to poor visibility, and as such ignored again. If, however, the mouse went all the way to the end of the passageway to confirm it was closed, this strong evidence is worth registering in memory. Second, specific to contextual learning, a given memory should only be updated inasmuch as the current information comes from the same context as that associated with that memory. More precisely, contextual inference should gate and modulate the updating of memories, such that the extent that memories are updated is proportional to the posterior probabilities of the contexts to which they belong. Again, in contrast to classical notions of memory updating (e.g. via reconsolidation), this implies that when there is uncertainty about the current context (so that several context probabilities are non-zero), multiple memories need to be updated in parallel. That is, if the mouse is unsure which of two mazes it is currently navigating, the information about the closed passageway needs to be incorporated into both memories. Consistent with this idea, studies of single-trial motor learning have shown that under experimentally-controlled contextual uncertainty, multiple memories are updated in proportion to their posterior probabilities (Heald et al. 2021).

3.4. Memory creation

The notion of memory creation is naturally captured by Bayesian nonparametric models, such as the so-called “Chinese restaurant process” (and its hierarchical extension, the “Chinese restaurant franchise”; Teh et al. 2006). These models assume that the number of contexts in the environment are unknown and unbounded (i.e. can be infinite), such that when a new context is inferred, a new memory is created. These models have been used to account for a wide range of context-dependent phenomena in a variety of domains, including classical conditioning (Gershman et al. 2010), episodic memory (Gershman et al. 2014), economic decision making (Collins & Koechlin 2012) and motor learning (Heald et al. 2021; for a more comprehensive overview of Bayesian nonparametric models in context-dependent learning, see Heald et al. 2022 in press).

According to these models, in each time step, with some probability, a hitherto unseen context is inferred to have been encountered, and a new memory for this context is added to the repertoire of existing memories (Fig. 1b, thick gray arrow with black outline). The probability for this is given by the probability of a novel context in the previous time step (Fig. 1b, Column 1, top row, gray context probability). The memory associated with this newly encountered context is an updated version of the default posterior over contingencies of a novel, yet-unseen context (Fig. 1b, Column 2, middle row, creation of the red posterior and its updating starting from the gray posterior). As all contexts are assumed to have existed indefinitely before they are first encountered, the contingencies for a novel context have a stationary state distribution that is never updated (Fig. 1b, Column 2, lowest middle row, the gray covariance ellipse remains unchanged). For the mouse, this means that if no familiar mazes are consistent with a set of observations (so that the probabilities of existing contexts are all low, and consequently – as probabilities add to one – the probability of the novel context is high), it probably means that there is a new maze in place, and it is time to create a new memory for it. Thus, contextual inference also controls memory creation.

Memory creation in the model is unlikely when small changes occur in the environment as errors will be small and current memories will be able to explain sensory cues and feedback. In contrast, abrupt changes in the environment will increase the probability of a new memory being created. Consistent with this, de-adaptation in motor control is slower after the removal of a gradually, versus abruptly, introduced perturbation. The gradual introduction leads to the adaptation of an existing memory which then needs to de-adapt back to the unperturbed situation (a slow process). In contrast, the abrupt perturbation leads to a new memory being created, allowing preservation of the original memory for the unperturbed situation and subsequently rapid switching back to the unperturbed memory (a rapid process; Heald et al. 2021). Analogous phenomena have also been described in a variety of other domains of learning (Heald et al. 2022 in press).

4. NEURAL BASES OF CONTEXTUAL LEARNING

The computational principles of contextual learning reviewed above (Section 3) provide a useful framework for organizing the large body of data on its neural bases. At present, there is no unified circuit-level understanding of contextual inference and learning as described above. In this section, we highlight studies implicating specific circuits and mechanisms underlying different aspects of contextual inference and learning. As contextual inference is critical for controlling all aspects of contextual learning, we begin by reviewing experimental data about its neural underpinning. We then review data relevant for each of the main operations that contextual inference controls – memory expression, updating, and creation – focusing on their aspects that are relevant when multiple context-dependent memories need to be managed.

4.1. Contextual inference

Although many brain areas have been implicated in some aspect of context-dependent learning, here we focus on three areas that have been most extensively studied in paradigms tapping into contextual inference: prefrontal cortex, hippocampus and the thalamus.

4.1.1. Prefrontal cortex.

The prefrontal cortex (PFC) is thought to play a key role in representing contextual information (Donoso et al. 2014, Botvinick 2008, Soltani & Koechlin 2022). In our terminology, PFC may be involved in both computing context probabilities and updating them based on context transitions and sensory cues. This is broadly consistent with multiple areas within PFC encoding abstract task rules (Wallis et al. 2001, Saez et al. 2015), and medial PFC being necessary for switching between different rules based on sensory cues (Marton et al. 2018).

Implementation-level models of PFC corroborate its role in contextual inference. Collins & Frank (2013) developed a neurobiologically explicit network model consisting of multiple modules corresponding to distinct areas within the corticobasal ganglia loop. When the network was trained on an instrumental learning task with multiple hidden contexts (by pure reinforcement learning), the module corresponding to PFC developed activations consistent with contextual inference. This network model also provided an approximate implementation of a Bayesian nonparametric model of contextual learning, similar to the one described in Section 2, which itself explained a wealth of behavioral data from humans performing the same task.

If PFC is involved in computing context probabilities, then lesioning it, or interfering with its function, should impair behaviors that rely on the maintenance and updating of context probabilities. This is broadly consistent with a large body of neuropsychological literature, describing how patients with PFC lesions have difficulties maintaining behavioral flexibility between contexts (Shallice & Cipolotti 2018). Going beyond simple behavioral impairments, perturbing (by transcranial magnetic stimulation) the dorsolateral PFC led to the directed forgetting of episodic memories – a process that is thought to be based on the suppression or substitution of the representation of the context relevant to those memories (Anderson & Hulbert 2021).

In animal learning experiments with rats, lesioning the medial orbitofrontal cortex (OFC), a major subdivision of PFC, resulted in a pattern of decision making impairments (diminished Pavlovian-instrumental transfer and outcome devaluation) that was mostly well accounted for by the putative role of OFC in contextual inference (bar a lack of effects on reinstatement; Bradfield et al. 2015). In addition, as we saw above, extinction and subsequent savings on re-learning are behavioral effects that bear the signatures of contextual inference. In particular, they reflect the increasing expression of the memory of the pre- or post-acquisition context, respectively, driven by the growing probability that each of these contexts is active. Indeed, lesions of OFC slow down extinction (or the relearning of a previous set of contingencies) in classical conditioning (Butter 1969). This may be because, rather than re-expressing a previous memory (a potentially rapid process), OFC-lesioned animals need to update their current memory (a relatively slow process) (Wilson et al. 2014).

Spontaneous recovery has been suggested to be another behavioral signature of memory expression driven by contextual inference (Heald et al. 2021, see also Section 3.2). Here, introducing a working memory task, which is known to tax PFC resources, led to a boosting of spontaneous recovery (Keisler & Shadmehr 2010). This seemingly paradoxical effect (interference makes a behavioral effect greater, rather than smaller) has been explained by a model in which the working memory task specifically affects the active maintenance of current context probabilities (Heald et al. 2021). According to this explanation, when context probabilities are not actively maintained and updated, they revert to a set of default values that are stored in long-term memory (instead of working memory) that favor the acquisition context as it has been experienced for a long time.

Functional imaging studies have shown that OFC represents the abstract state of the task (see e.g. Wilson et al. 2014), especially when it is hidden and must be inferred (Schuck et al. 2016, Schuck & Niv 2019, Nassar et al. 2019). One prominent demonstration of this used a paradigm in which participants had to judge the age (in our terminology: the state; old or young) of one of two simultaneously displayed categories (house or face) on each trial (Schuck et al. 2016, Schuck & Niv 2019). The relevant category (in our terminology: the context) was not indicated directly to participants but depended on the relevant category of the previous trial, as well as on the age on the previous two trials. To fully account for these dependencies, the authors defined the ‘task state’ as a conjunction of the current and previous category and age. Interestingly, three out of these four variables (previous and current category, and previous age) were represented in OFC, but not the current age. The authors argued that this was because the current age was directly observable, whereas the other variables were hidden. However, Bayesian models of perception suggest that stimulus features such as age are also hidden and must be inferred. Instead, we suggest that the previous age and previous category (together with the age on two trials earlier, which was untested) are sufficient statistics of the posterior distribution over the current context, while the current age is not. Thus, if OFC is involved in contextual inference, we would expect the combination of these variables to be decodable in OFC—just as has been found (Schuck et al. 2016). This interpretation makes the prediction that the age on two trials earlier should also be decodable, which remains to be tested.

More direct evidence for the role of PFC in contextual inference comes from studies that combine functional imaging with Bayesian multiple-context models. Such studies suggest that PFC does not represent a single context at a time (e.g. the most likely active one) but represents multiple contexts and the probability that each of them is currently active. For example, in an economic decision making task in which state-action-feedback contingencies could switch based on a hidden context, anterior regions of PFC, and ventromedial PFC in particular, were shown to encode the current reliability of different context-specific behavioral strategies (Donoso et al. 2014) (Fig. 2a). These ‘reliability’ signals are formally analogous to the posterior context probabilities (often termed responsibilities) of Bayesian multiple-context models (Heald et al. 2021).

Figure 2. Neural basis of contextual learning.

a. Prefrontal cortex encodes context probabilities. Participants learned strategies that involved choosing an action (correct button press) in response to a state observation (number displayed on a screen). The state-action contingencies occasionally switched between three possibilities, necessitating different context-specific strategies. Brain activations (fMRI) that correlated with the probability (strategy ‘reliability’, derived from a behavioral model) of the context associated with either the participants’ current strategy (magenta), or with alternative strategies (cyan). Reproduced from Donoso et al. 2014. b. Hippocampal activity samples from context-specific maps under context uncertainty. Hippocampal activity was recorded as rats navigated one of two spatial environments. Occasionally, animals would be “teleported” between the environments by instantaneously switching sensory cues. Left: time series (columns show successive theta cycles) of correlations between current neural population activity and reference activity associated with each location in environment A (top, red) and environment B (bottom, blue). A teleportation from environment A to B took place shortly before this series. The correlation shows evidence of spontaneous flickering between the hippocampal place-field maps associated with each environment despite no change in the environment during this period (green cross shows current location). Right: histogram shows a temporary increase in the number of flickers after a change in the environment. Reproduced from Jezek et al. 2011. c. Hippocampal representation of a prior distribution over contexts. Hippocampal activity was recorded as mice navigated through virtual reality environments that could morph between two extremes by continuously varying the frequency of a sinusoidal grating on the walls, thus giving rise to a continuum of contexts. Mice experienced one of two different distributions of contexts, characterized by different distributions of the morphs (“rare” vs. “frequent” morph distributions, respectively red vs. blue thick lines). Thin lines show the prior reconstructed from the hippocampal activity of individual mice exposed to the rare (left) and frequent (right) distributions. The prior approximated the true distribution for each condition. Reproduced from Plitt & Giocomo 2021. d. Context-dependent motor learning. Nonhuman primates reached to targets under two possible force perturbations applied to the hand (forces applied by a robotic interface that act in clockwise, CW, or counter-clockwise directions, CCW) or unperturbed. Neural state space show preparatory activity (after dimensionality reduction) in dorsal premotor and primary motor cortex for movements to the same 12 targets (points) under the three possible contexts: before learning (black), CW perturbation (red), and CCW (blue) perturbations. Projections of the neural state space are shown on the ‘floor’ and ‘wall’. Figure plotted from data in Sun et al. 2022. e. Neural representation of extinction in the mouse amygdala during fear conditioning. Change in a distance measure between the neural representation of the CS during training (conditioning and extinction) and the pre-learning representation of the US (red) or CS (blue). Negative values mean the representations become more similar. Reproduced from Grewe et al. 2017.

The aforementioned studies demonstrated the representation of inferred contexts in PFC even in the absence of explicit information about the existence of different contexts, and when contextual inference needed to combine information about context transitions as well as action-outcome contingencies. However, they did not specifically test whether full posterior distributions are represented over contexts, as would be required theoretically. More direct evidence for this comes from an experiment in which participants had to infer the current context (which sector of a safari park they are in) after viewing a sample of animals from that context. OFC responses were best explained as representing the (log-transformed) posterior distribution over contexts given those stimuli, outperforming alternative representations, such as the most probable context or the uncertainty over contexts (Chan et al. 2016). However, the paradigm used in this study was specifically designed so that full context posteriors needed to be represented to perform well, while–compared to some of the previous studies—only requiring relatively impoverished context-specific information to be learned (the distribution of animals in each context, but no actions or structured context transitions). Therefore, it remains an open question whether these results generalize to richer, more challenging contextual inference settings.

Direct neural recordings from monkey OFC (and other prefrontal cortical areas) confirmed a neural representation of context in the PFC, even on trials when context was hidden, and as such had to be inferred (Saez et al. 2015, Bernardi et al. 2020). Nevertheless, similar context-encoding representations were also found in other brain areas, including the hippocampus and amygdala. These studies indicate that context is encoded in an abstract way in prefrontal (and hippocampal) areas, orthogonal to other task-relevant variables (e.g. stimulus identity; Bernardi et al. 2020). Such abstraction allows flexible generalization to novel combinations of context and other variables. Interestingly, when assessed using a simple condition-specific linear decoder, only activities in the amygdala, but not those in OFC or other cortical areas, were predictive of behavioral errors (Saez et al. 2015). However, the level of ‘abstraction’ of neural representations, assessed using a decoder that was required to generalize across conditions, was predictive of behavioral errors in prefrontal (and other cortical) areas (Bernardi et al. 2020). More importantly, although the tasks used in these studies often required the animals to infer context from past observations, without providing unambiguous sensory cues on a given trial, only the representation of the experimentally defined veridical context was tested. Thus, whether and how probabilistic inferences are reflected in neural activities in these tasks remains unknown.

At the level of neural circuits, the evidence for the causal role of PFC in contextual inference is somewhat mixed – at least in the relatively simple behavioral paradigms used so far. Optogenetic suppression of PFC (anterior cingulate) projections to primary visual cortex (V1) in an odd-ball paradigm (in which deviant stimuli ostensibly lead to the inference of a novel context) have shown that contextually appropriate responses (larger responses to deviants) depend on an intact PFC input (Hamm et al. 2021). Another study used an olfactory delayed match-to-sample paradigm (Wu et al. 2020) that can also be seen as engaging contextual inference, such that the sample stimulus acts as a sensory cue indicating the context, which in turn determines the mapping from the test stimulus to the correct response. In this study, although context could be decoded from OFC, other relevant cortical areas also carried such signals, including a primary sensory cortical area (the piriform cortex), and a premotor area (the anterolateral motor cortex, ALM). More importantly, optogenetic inactivation of OFC did not impair context-dependent behavior in this case (effects on neural responses were not studied), while that of ALM did.

4.1.2. Hippocampus.

Information stored in the hippocampus has long been considered to serve as indices to patterns of neocortical activity produced by particular episodes (Teyler & Rudy 2007, Káli & Dayan 2004). This is broadly consistent with a role in contextual inference, inasmuch as context probabilities are essentially indexing which memories need to be expressed and updated.

More specifically, several lines of evidence point to the hippocampus as a key brain region that represents information about context, and in particular spatially defined contexts (which undoubtedly have special ecological relevance for most animals). Indeed, the hippocampus has been implicated in maintaining a cognitive map of the environment (O’Keefe & Nadel 1978). Moreover, like the OFC (see Section 4.1.1), it has been suggested to encode cognitive maps in the broad sense, capturing the relationships between sensory cues, states, actions, and feedback (Wikenheiser & Schoenbaum 2016) – much like the relationships governed by the context variable in our model (Fig. 1a).

Classical work on fear conditioning demonstrated that pairing a foot-shock with an auditory tone in a particular chamber (i.e. spatial context) leads to occasional fear responses (behavioral freezing) in the same chamber even in the absence of the tone, and conversely, to the conditioned auditory tone even when in a different chamber. Critically, lesioning the hippocampus selectively dampens fear to the context (but not to the tone) previously associated with the shock, albeit this role seems to be time limited (Kim & Fanselow 1992). In some cases, inactivating the hippocampus may also dampen fear renewal when the tone is presented outside of the extinction context (Holt & Maren 1999).

The neural representation of spatial context is widely thought to rely on the activity of place cells. As place cells have place fields (the region of physical space that needs to be occupied by the animal in order for a given cell to become active), their joint population activity provides a neural representation of the animal’s location (see e.g. Fig. 2b, left, leftmost bottom frame, blue heat map vs. green cross). Critically, due to “remapping” (a change in relative place field locations with a change in environment), the activity of place cells also encodes the environment, or the spatial context (Fig. 2b, left, leftmost top vs. bottom frame, red vs. blue heat map). While remapping is most often induced by placing animals in a different environment, and thus changing the combination of sensory cues available, remapping has also been observed when the animal’s behavioral policy needed to be different in the same environment (Markus et al. 1995). This is in line with context not only determining sensory cues but also the mapping of states and actions to feedback, and thus ultimately the policy that is best for acquiring rewards (Fig. 1a). Indeed, a formal mathematical model of contextual inference very similar to the one we propose here (Fig. 1b; but without a concept of context transitions) has been able to account for a number of different (and sometimes puzzling) features of remapping, such as its dependence on sensory cues (including their variability), training and testing protocol, and its variability across animals (Sanders et al. 2020).

Contextual inference requires that probability distributions over contexts are represented, rather than just inferring a single context at a time (see Section 2.2). One proposal for how hippocampal responses might encode probability distributions is based on probabilistic sampling (Savin et al. 2014). This predicts that context representations in the hippocampus should dynamically alternate over time even under constant experimental conditions. Evidence for this proposal comes from experiments showing that the context encoded by hippocampal activity can “flicker” between representing two different spatial environments, such that in each cycle of the hippocampal theta oscillation (lasting for ~125 ms) a single context is represented coherently across the population, but the represented context occasionally changes across subsequent theta cycles spontaneously, without changes in sensory cues (Jezek et al. 2011; Fig. 2b, left). Moreover, also in line with sampling-based inference, the frequency of flickers was shown to increase following a switch in sensory cues (Fig. 2b, right), which – under a suitable model of context transitions – are ostensibly periods of time with increased contextual uncertainty.

Contextual inference, as a form of Bayesian inference, involves the combination of current sensory information with prior expectations to make inferences about the current context. In particular, prior expectations should reflect the probability distribution over contexts experienced during training. In accordance with this, recent recordings of large neural populations showed that hippocampal ensembles encode context in an experience-dependent manner (Plitt & Giocomo 2021). More specifically, the particular prior distribution of contexts (defined over a spectrum of continuously morphed environments) used for training could be decoded from hippocampal activity (Fig. 2c).

The hippocampus may also contribute to contextual inference more indirectly via its effects on OFC. During periods of rest, an fMRI study found that the human hippocampus replayed sequences of previously experienced ‘task states’ (Schuck & Niv 2019) that embody our notion of context (see Section 4.1.1). Moreover, the more faithfully the statistics of these sequences reflected the transition structure of task states, as defined by the task, the more accurately task states could be decoded from OFC during task performance. In turn, decoding accuracy in OFC was positively correlated with task performance. As long as there is a causal relationship underlying these correlations, these results suggest that hippocampal replay may play a role in constructing the task-relevant representations in OFC that underlie contextual inference.

4.1.3. Thalamus.

The PFC has reciprocal connections with thalamus, which in turn receives strong inputs from the basal ganglia, a brain structure that has been implicated in context-dependent action selection (Hikosaka et al. 2000, Klaus et al. 2019, Collins & Frank 2013). By integrating inputs from many different cortical areas, thalamic circuits are well situated to compute contextual signals that can rapidly reconfigure cortical representations. Indeed, it has been suggested that the thalamus acts as an optimal Bayesian observer of context, computing likelihoods that update posterior context probabilities in cortex (Rikhye et al. 2018). Consistent with this view, inhibition of mediodorsal thalamus in mice leads to perseveration of actions appropriate for a previous context following a change in context, such as a reversal of action-outcome contingencies (Parnaudeau et al. 2013, 2015).

4.2. Memory expression

An emerging view of how memories are recalled by networks of recurrently connected neurons is based on a dynamical systems perspective. This perspective was anticipated by classical theories (Hopfield 1982), and it has recently gained experimental support particularly in the field of motor control, that is, in the context of the expression of motor memories (Vyas et al. 2020). According to this perspective, the evolution of the state of a neural population is best understood in terms of the dynamical rules that govern how the next neural state is caused by the current neural state and inputs. In general, inputs can either be transient, such as those that set the initial (“preparatory”) state of motor cortex before movement offset, or tonic, persisting while the neural trajectory unfolds, or even longer, across many consecutive movements. Transient inputs are ideally suited to convey information about the current environmental state (e.g. the target of reaching) for which an action needs to be chosen, while tonic inputs are ideally suited to convey information about the current context. Indeed, population dynamics in motor cortex during reaching have been well described by a mostly autonomous (i.e. not input-driven) dynamical system, in which different reaching directions correspond to different preparatory neural states to which the system is driven by appropriately tuned transient inputs (Kao et al. 2021b). Thus, the memory of a context, determining the mapping of environmental states to actions, is embedded in the dynamics of the circuit that determine how a neural trajectory evolves from an initial state to generate a sequence of motor commands to reach a target.

Due to the nonlinearity of neural circuit dynamics, different subspaces of the neural state space can support different local dynamics. Thus, these subspaces can form the dynamical substrates of independent modules capable of implementing context-specific memories (Wang et al. 2018, Flesch et al. 2022, Mante et al. 2013, Remington et al. 2018a). A particular context-dependent module can then be “addressed” by driving the neural state to the appropriate subspace by tonic (or slowly changing) context-dependent inputs (Mante et al. 2013, Remington et al. 2018a, Wang et al. 2018), providing a mechanism by which context-specific memories can be differentially expressed. Furthermore, the continuous nature of the state space means that context-specific memories can be interpolated between, for example, by driving the neural state to a preparatory state in between those for different contexts, allowing graded context probabilities to influence memory expression under context uncertainty. Alternatively, rather than selecting between different subspaces, context-dependent inputs might change neural gains (Stroud et al. 2018) or engage different thalamo-cortical loops via the basal ganglia (Logiaco et al. 2021), thus controlling the effective connectivity of the network and the resulting neural dynamics even within a single subspace. This mechanism might be particularly suitable for interpolating between different memories.

An elegant demonstration of these principles comes from recent studies of contextual motor learning in nonhuman primates. In these experiments, macaques performed different reaching movements while one of two opposing external force fields (corresponding to two different contexts) was applied to their arm. Recordings from motor cortex revealed that the subspace spanned by different preparatory neural states was context-dependent (Sun et al. 2022; Fig. 2d, the same colored points on each curve correspond to the same 12 reach directions). For example, learning to reach through two opposing force fields resulted in two parallel subspaces (red and blue) that were each parallel to the subspace spanned by the before-learning preparatory states (black, dimensions TDR1 and 2), and were separated along a dimension that was orthogonal to this subspace (context dimension). The common dimensions (TDR1 and 2) shared by these context-dependent subspaces may provide a mechanism by which learned behaviors can generalize across contexts.

Similar principles have been shown to underlie flexible motor timing (Remington et al. 2018a). In a time-interval reproduction task (Remington et al. 2018b), a random time interval between two visual flashes was presented that subjects needed to reproduce up to some context-dependent multiplicative factor (1 or 1.5), which changed over blocks and was indicated by color cues. Recordings from the dorsomedial frontal cortex revealed neural trajectories that were separated according to initial condition (determined by the presented time interval) and an orthogonal context-dependent axis, with trajectories in different parts of the state space evolving at different speeds to reproduce different timing intervals. Analogous results were also found in a variant of the same task, in which contexts were associated with different prior distributions over the possible time intervals that needed to be reproduced, rather than different multiplicative factors with which they needed to be reproduced (Sohn et al. 2019).

4.3. Memory updating

Within each context, memory updating should take into account uncertainty about the contingencies being inferred. In line with this, recent evidence suggests that synapses adjust their learning rates based on uncertainty, framing synaptic plasticity as Bayesian inference (Aitchison et al. 2021). Across contexts, behavioral studies have shown that memory updating is modulated by the posterior of contextual inference (Heald et al. 2021). A neural mechanism for such modulation, at the level of synapses, would require an additional component to simple two factor Hebbian mechanisms. One class of mechanisms that has been proposed is the three-factor mechanism in which synaptic modulation depends on presynaptic and postsynaptic activity as well as the influence of neuromodulators that can convey scalar information about novelty or reward (Frémaux & Gerstner 2015). For example, tonically active cholinergic neurons of the striatum have been suggested to gate the learning of striatum-dependent behaviors, providing a mechanism by which memories can be protected from unlearning during extinction (Crossley et al. 2013). However, conveying information about context probabilities requires more than just representing a single scalar. How neuromodulatory influences could achieve this remains an open question.

4.4. Memory creation

Memory creation involves two processes: novelty detection, that is determining whether sensory experience is explained by current representations or is novel, and memory instantiation. Novelty has been proposed to be encoded in neuromodulatory signals. Brain areas such as the ventral tegmental area (Lisman & Grace 2005, McNamara et al. 2014) and locus coeruleus (Takeuchi et al. 2016) signal novelty by releasing dopamine into the hippocampus. In this way, newly encoded hippocampal representations, which are initially labile, are stabilized (McNamara et al. 2014, Takeuchi et al. 2016), providing a mechanism by which new long-term memories can be created. Contextual novelty signals also arrive in the hippocampus from the hypothalamus (Chen et al. 2020) and could, in principle, be used to trigger the creation of a new map of space (Sanders et al. 2020). In addition to dopamine, norepinephrine (the main neurotransmitter produced by the locus coeruleus) has been suggested to signal “unexpected uncertainty”, when unsignaled context switches produce strongly unexpected observations (Yu & Dayan 2005). Critically, through its effects on synaptic plasticity, norepinephrine has also been implicated in the formation of memories (Palacios-Filardo & Mellor 2019), making it an ideal substrate for inducing memory creation.

The cerebellum may play a key role in memory creation in conditioning paradigms. Neuroimaging data show that a memory formed during fear conditioning remains within the cerebellum following extinction (Batsikadze et al. 2022), suggesting that distinct context-dependent memories have been formed for acquisition and extinction in the cerebellum. Conversely, in cerebellar patients performing an ABA renewal eye-blink conditioning paradigm, extinction (during B) is slowed and renewal (during the second A) is absent (Steiner et al. 2019), consistent with the idea that a single memory has been updated throughout learning, independent of context, and that an intact cerebellum is needed to create new context-specific memories in eye-blink conditioning.

At the circuit level, evidence of the instantiation of a new memory has been observed in the amygdala during fear conditioning and extinction in rodents. This was achieved by tracking a measure of representational ‘distance’ between the neural population responses to the conditioning stimulus (CS) and population responses to the CS pre-conditioning (Fig. 2e blue) and unconditioned stimulus (US, red; Grewe et al. 2017). CS responses became more similar to the US response during conditioning (red dashed line). During extinction, the distance to US response increased (red solid line) paralleling the reduction in freezing. However, the representation did not return to baseline, as indicated by the constant distance of responses from the initial CS representation (blue solid line). This is consistent with the idea that the neural circuit has been fundamentally changed by the incorporation of a new memory and hence cannot return to baseline. That is, extinction is not simply the reversal of learning. This result parallels that seen in monkey motor cortex, whereby following deadaptation to a previously learned force field, the neural activity did not return to baseline but instead retained a memory of the force field (Sun et al. 2022).

Further evidence that extinction results in two context-specific memories in the amygdala (conditioning and extinction memories) comes from studies demonstrating that unique neuronal ensembles emerge following extinction. That is “fear neurons” and “extinction neurons” co-exist and preferentially fire in response to the same CS when the animal freezes (renewal context) or does not (extinction context), respectively (Orsini et al. 2013).

In cortical areas that use different subspaces of the neural state space to implement context-specific computations (see Section 4.2), memory instantiation may correspond to expanding the neural repertoire into a previously unused (i.e. outside-manifold) subspace (Oby et al. 2019). Moreover, the creation of new memories may also be facilitated by increasing the number of neurons in the circuit by neurogenesis, for example in the dentate gyrus (Gershman et al. 2017b, Becker 2005).

5. CONTINUAL LEARNING

Contextual inference might also be key to understanding how the brain solves a fundamental problem that has long haunted learning in artificial neural networks (ANNs). Although ANNs can solve challenging computational tasks when learned individually (LeCun et al. 2015), albeit typically with extensive training to achieve high performance, crucially they have difficulty learning multiple tasks, especially when those tasks need to be learned sequentially (continual learning, also known as lifelong learning). As task-optimized ANNs have also been found to predict neural activity in a number of brain areas, including the visual cortex (Yamins et al. 2014, Echeveste et al. 2020), and prefrontal cortex (Mante et al. 2013, Stroud et al. 2021), understanding how they might be able to perform continual learning may provide useful clues as to how the brain achieves the same.

There are two fundamental factors that make multi-task and continual learning difficult in ANNs (Rolnick et al. 2019): interference and catastrophic forgetting. Interference arises when multiple tasks are incompatible, that is they have different input-output mappings. This happens regardless of whether the tasks are trained in an interleaved or blocked fashion (Kessler et al. 2021). In contrast, catastrophic forgetting can happen even when the tasks are not incompatible. In this case, the tasks are all well learned by an ANN when they are presented in an interleaved manner (standard multi-task learning), but when the tasks are experienced in a blocked fashion (continual learning), substantial forgetting is observed (French 1999). Such catastrophic forgetting occurs because the ANN weights are re-optimized for performance on each new task without reference to performance on previous tasks.

A variety of mechanisms have been explored to prevent these problems and promote continual learning in ANNs by using knowledge about context. A powerful solution is to create separate networks (Aljundi et al. 2017), or subnetworks (Li & Hoiem 2017, Rusu et al. 2016), for each task (context), and use an input representing the current context (task identity) to index the appropriate (sub)network that needs to be called upon. To avoid having to “grow” the network with time, which may limit generalization across tasks and require biologically implausible mechanisms, fixed network architectures with context-dependent gating have also been studied (Masse et al. 2018, Flesch et al. 2022, Podlaski et al. 2020). In these networks, a fraction of the units is used for each task (while the rest are gated by setting their activities to 0). Alternatively, contextual inputs have also been used to induce learned rotations of the input space (Zeng et al. 2019). These rotations allow the same inputs to map to different outputs for different tasks within the same network, thereby reducing interference. It remains an open question which, if any, of these mechanisms may be relevant to how context controls continual learning in biological circuits.

However, all these approaches are still task-aware: they require access to ground-truth information about task identity during training (and often at test time, too; Van de Ven & Tolias 2019). This information is often explicitly given in the form of task labels (Masse et al. 2018, Zeng et al. 2019, Aljundi et al. 2017, Rusu et al. 2016, Li & Hoiem 2017), or sometimes it is more implicit, e.g. when only the boundaries between tasks are sign-posted, but the identities of individual tasks are not provided (Zenke et al. 2017, Kirkpatrick et al. 2017, Shin et al. 2017, Lopez-Paz & Ranzato 2017, Rebuffi et al. 2017). Furthermore, to ensure that each task is learned equally well, several approaches also require networks to be provided with an equal amount of training for each task (Shin et al. 2017, Lopez-Paz & Ranzato 2017, Rebuffi et al. 2017, Kao et al. 2021a). Arguably, this is an unreasonable requirement for a lifelong learning algorithm, as, in general, an equal amount of experience per task cannot be guaranteed in the wild and should not be expected.

In contrast, biological neural networks do not seem to suffer from the same problems. Over the course of a lifetime, humans are able to learn a wide variety of tasks from a continuous stream of sensorimotor experience (Pisupati & Niv 2022). In fact, humans can even benefit from blocked training relative to interleaved training (Flesch et al. 2018) – the exact opposite of how the performance of ANNs depends on the training regimen. This effect could be reproduced in an ANN that received as contextual input a moving average of explicit information about task identity (Flesch et al. 2022). The “slugishness” of this moving average was similar to what can be expected from contextual inference under a generative model of context transitions that prefers self-transitions (Heald et al. 2021). This suggests that contextual inference may play a role in biological continual learning, such that different tasks are assigned to different contexts. In this way, context can be more reliably inferred when it is predictable, such as in a blocked design, and as a consequence, proper learning can also be more efficiently focused on the appropriate context-specific representations. In line with this (Lengyel 2022), interference is much reduced in roving paradigms in perceptual learning when using training protocols in which trials corresponding to each “task” (e.g. defined by the reference orientation in a fine orientation-discrimination paradigm) are either blocked (Dosher et al. 2020) or organized into predicable sequences (Zhang et al. 2008) compared to when they are randomly interleaved (Banai et al. 2010).

Importantly, humans are able to perform continual learning even without ever having been given explicit information about task labels, i.e. in a task-agnostic/task-free manner (cf. task-aware continual learning in ANNs). By leveraging contextual (task) inference, continual learning in ANNs can also begin to tackle the ecologically relevant and challenging task-agnostic setting. Some recent progress has been made in this direction using Bayesian nonparametric models (Xu et al. 2020, Jerfel et al. 2019, Nagabandi et al. 2018) that are broadly similar to the models that have been suggested to underlie contextual inference in humans and other animals (see Section 3.4). Other approaches have performed contextual inference without inverting a well-defined generative model. For example, in the Dynamic Mixture of Experts model, reinforcement learning was used to train a gating network that received input from the environment and output a decision regarding which expert to use for the current task (Tsuda et al. 2020). This model was also able to grow in capacity (like Bayesian nonparametric models), adding a new expert (also trained via reinforcement learning) whenever existing experts were unable to solve a task. Some of these approaches (Jerfel et al. 2019, Nagabandi et al. 2018) take context uncertainty into account when performing memory updating, modifying the parameters (in our terminology, contingencies) of all context-specific models in parallel based on the posterior probabilities of their corresponding contexts. However, none of these approaches (Xu et al. 2020, Jerfel et al. 2019, Nagabandi et al. 2018, Tsuda et al. 2020) take context uncertainty into account for expressing memories, as they only express a single context-specific model/expert (the one associated with the most probable context) at any moment.

6. CHALLENGES AND OPPORTUNITIES

We have reviewed the computations required for contextual continual learning and elements of their putative neural underpinnings. However, there are still many gaps in our understanding of the neural implementation of contextual inference and memory creation, expression and updating. For a full understanding across different domains of contextual learning, including for episodic events, motor skills and decision-making, there are five key computational elements than will need to be mapped onto neural circuit mechanisms.

First, neural circuits need to be able to maintain multiple memories simultaneously. There are mathematical theories for how synaptic and cellular forms of plasticity might achieve this, but comparatively little direct experimental evidence supporting these theories, especially in continual learning settings when multiple memories are explicitly tested. Second, contexts need to be continually inferred, incorporating not only current sensory information, but also prior experience with the probabilities of contexts and their transitions. Current experimental evidence for this is sporadic and mostly circumstantial. Outstanding questions include the neural representation of posterior distributions over contexts, and the division of labor – and interplay – between PFC, hippocampus and thalamus in contextual inference. Formal models of contextual inference, similar in spirit to the one we presented here, making quantitative predictions about posterior context distributions under specific conditions, should be useful for discovering and resolving the neural correlates of these posteriors. Third, the neural mechanisms of memory expression need to be context-dependent. Fourth, the updating of memories also need to be context-dependent. Fifth, there need to be distinct mechanisms for the creation of altogether new memories. While there are experimental demonstrations for each of these, it remains to be shown that they can go beyond all-or-none operations, and instead be graded or probabilistic – specifically as controlled by contextual inferences. Such graded forms of memory processing will likely rely on a large array of mechanisms that are traditionally studied in isolation, such as neural gain control, neuromodulation, synaptic plasticity, and large-scale interactions between cortical and sub-cortical regions. Understanding the neural bases of context-dependent continual learning will require studying these disparate mechanisms through the unifying lens of appropriate computational frameworks.

Glossary

Normative model

Normative models define a goal (e.g. maximizing reward), and find an optimal solution under constraints (e.g. available computation time, noise).

Markov decision process

A generative model in which the current state and action fully determine, albeit in general only probabilistically, the next state.

Partially observed Markov decision process

A Markov decision process in which states are hidden and need to be inferred (e.g. from sensory cues, actions, and sensory feedback).

Reinforcement learning

The study of how artificial or biological agents learn from experience to adapt their behavior so as to improve their performance as measured by cumulative rewards.

State

The features of the environment (and agent) that, together with the agent’s action, determine sensory feedback and the next state.

Sensory feedback

Sensory input that either has intrinsic value or is related to task performance (e.g. rewards, punishments, movement accuracy).

Sensory cue

Sensory input that is informative of the context but, unlike sensory feedback, has no intrinsic value and is not performance-related.

Primary contingencies

Parameters that control the statistics of how the current state, sensory feedback and sensory cues depend on previous state and actions.

Secondary contingencies

Hyperparameters that control the temporal dynamics of primary contingencies and contexts (e.g. the timescale on which the maze layout changes).

Within-context volatility

The trial-to-trial variability of contingencies within a given context.

Between-context volatility

The trial-to-trial variability of the context, as determined by the context transition probabilities. This is the inverse of environmental consistency.

Proper learning

An update to an existing memory or creation of a new memory.

Apparent learning

A change in how context-specific memories are differentially expressed due to a change in beliefs about the current context.

Probabilistic sampling

Instantaneous neural activities encode a single value of a hidden variable, such that over time they sample different values with frequencies proportional to the corresponding posterior probabilities.

Continual learning

The ability to learn multiple tasks sequentially without forgetting old tasks.

Interference

Degradation in task performance when two or more tasks are learned that are incompatible (i.e. require different outputs for the same inputs).

Catastrophic forgetting

Severe degradation of performance on previously learned tasks due to one or more subsequent tasks having been learned.

Task-aware

A continual learning setting where task identities and/or task boundaries are provided.

Perceptual learning

Repetitive fine perceptual discrimination between two stimuli improves across trials. One of the two stimuli, the reference, is typically the same across all trials.

Task-agnostic/task-free

A continual learning setting where neither task identities nor task boundaries are provided.