Evaluation of model‐based bioequivalence approach for single sample pharmacokinetic studies

Abstract

In a traditional pharmacokinetic (PK) bioequivalence (BE) study, a two‐way crossover study is conducted, PK parameters (namely the area under the time‐concentration curve [AUC] and the maximal concentration [$C_{\max }$]) are obtained by noncompartmental analysis (NCA), and the BE analysis is performed using the two one‐sided test (TOST) method. For ophthalmic drugs, however, only one sample of aqueous humor, in one eye, per eye can be obtained in each patient, which precludes the traditional BE analysis. To circumvent this issue, the U.S. Food and Drug Administration (FDA) has proposed an approach coupling NCA with either parametric or nonparametric bootstrap (NCA bootstrap). The model‐based TOST (MB‐TOST) has previously been proposed and evaluated successfully for various settings of sparse PK BE studies. In this paper, we evaluate, via simulations, MB‐TOST in the specific setting of single sample PK BE study and compare its performance to NCA bootstrap. We performed BE study simulations using a published PK model and parameter values and evaluated multiple scenarios, including study design (parallel or crossover), sampling times (5 or 10 spread across the dosing interval), and geometric mean ratio (of 0.8, 0.9, 1, and 1.25). Using the simulated structural PK model, MB‐TOST performed similarly to NCA bootstrap for AUC. For $C_{\max }$, the latter tended to be conservative and less powerful. Our research suggests that MB‐TOST may be considered as an alternative BE approach for single sample PK studies, provided that the PK model is correctly specified and the test drug has the same structural model as the reference drug.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

In bioequivalence (BE) studies for generic drug development of ophthalmic products, one sample of aqueous humor is taken at a certain timepoint per eye for measurement of drug concentration. Currently, the U.S. Food and Drug Administration (FDA) recommends a nonparametric or parametric bootstrap noncompartmental (NCA) approach in the BE evaluation of these products. Recent research has focused on nonlinear mixed effect models which have been evaluated for sparse pharmacokinetic (PK) BE studies.

• WHAT QUESTION DID THIS STUDY ADDRESS?

The present work compares a model‐based (MB) BE approach to the nonparametric NCA for PK BE studies with one sampling timepoint per subject and per occasion.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

Our simulations show that the MB BE approach controlled type I errors, and demonstrated a higher power for maximal concentration ($C_{\max }$) compared to nonparametric NCA with parallel study designs.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Results of our research suggest that an MB approach may potentially serve as an alternative method to evaluate BE for generic ophthalmic drug products. However, further research and assessment are needed.

INTRODUCTION

Pharmacokinetic (PK) bioequivalence (BE) studies are key to the development of generic (or test) drugs. Traditionally, a two‐treatment, two‐sequence, two‐period (two‐way) crossover study is conducted and the two one‐sided test (TOST) is performed on estimates of the area under the concentration‐time curve (AUC) and the maximal concentration ($C_{\max }$) obtained by noncompartmental analysis (NCA). In these BE studies, the AUC can be computed using the trapezoidal method and linear extrapolation, if sampling continues for at least three or more terminal elimination half‐lives of the drug and there are at least three sampling points after the peak. ¹

In PK BE studies for ophthalmic drug products, typically only one single sample of aqueous humor is collected from one eye of each patient, at one assigned sampling timepoint, to measure drug exposure. Recommendations from the U.S. Food and Drug Administration (FDA) on BE study designs for ophthalmic drug products have been previously described. ² , ³ A parallel design is typically used when only one sample is collected per patient. A crossover design may be used when using patients with bilateral disease (i.e., on both eyes), enabling the collection of two samples (i.e., one eye per period).

As such, PK BE studies of ophthalmic drug products present unique statistical challenges. Certainly, classical NCA is not feasible because it is not possible to calculate individual AUC values from a single concentration. To circumvent this issue, a nonparametric bootstrap NCA has been proposed by Shen et al. ⁴ This method involves resampling of the subjects, at each sampling time in both reference and test treatment groups, to generate nonparametric bootstrap datasets. Next, the arithmetic mean concentration is computed at each sampling time. ³ Then, AUC and $C_{\max }$ are computed by NCA from the arithmetic mean concentration in each treatment group for each bootstrap data set to assess the relevant BE criteria. The product‐specific guidance (PSG) for ophthalmic drug products generally recommends to use this method or a parametric method for BE analysis in PK studies. ⁵

Nonlinear mixed effects modeling (NLMEM) is a powerful tool used to describe the PK properties of a drug and may be used to support a lower number of subjects or reduced sampling in PK studies. ⁶ In the last 15 years, NLMEM has been demonstrated to be a useful tool in the design and analysis of PK BE studies. ⁷ For example, Panhard and Mentré ⁸ proposed to perform a TOST on empirical Bayes estimates (EBEs) of individual AUC and $C_{\max }$ or to analyze the data globally and perform two Wald tests on the model‐based treatment effect estimates (MB‐TOST). However, NLMEM requires specific estimation algorithms which may present certain challenges and concerns. For instance, Panhard and Mentré used the first‐order conditional estimates (FOCE) algorithm ⁹ which presents convergence issues that can be avoided with the more exact stochastic approximation expectation maximization (SAEM) algorithm. ¹⁰ Therefore, Dubois et al. ¹¹ evaluated the tests on EBE using SAEM, exploring various scenarios, and found the latter are not recommended when the shrinkage is above 20%. Furthermore, they evaluated the MB‐TOST using SAEM and identified an inflation of the test type I error rate due to departure from the asymptotic conditions. ¹² Consequently, Loingeville et al. ¹³ proposed alternative calculations of the standard errors (SEs) and showed that MB‐TOST using non‐asymptotic SE controls type I error rate on sparse PK BE studies with small sample sizes. In PK BE studies with large sample sizes, MB‐TOST using asymptotic SE derived from the observed Fisher information matrix (FIM) performed satisfactorily. ¹⁴ Yet, Möllenhoff et al. (2020) proposed the bioequivalence optimal test (BOT) which was shown to be more powerful while controlling type I error using either a model or NCA method to fit the concentrations. ¹⁵ Further, their simulation study highlighted the overly conservative type I error rate of the TOST method for drugs with large PK variability. Nonetheless, currently, the Agency recommends the reference‐scaled average BE approach for highly variable drugs. ¹ , ¹⁶

Our objective in the present work is to compare an MB approach to the FDA recommended NCA nonparametric bootstrap approach for single point designs.

METHODS

Two one‐sided tests

For most drug products, BE studies are focused on the release of the drug substance from the drug product into the systemic circulation. In these BE studies, the rate and extent of drug absorption of the test (T) product is compared to the reference (R) product using AUC and $C_{\max }$ metrics, respectively. For the drug exposure, one can estimate the AUC from time zero until the last sampling time (${\mathrm{AUC}}_{0-t_{\text{last}}}$) t _last or the AUC from time zero until infinity (${\mathrm{AUC}}_{0-\infty }$).

Let ${\beta }^T$ be the treatment effect (i.e., the difference between ${\mu }_T$ and ${\mu }_R$ [${\beta }^T={\mu }_T-{\mu }_R$]) the average means of the test and reference products for $\log \left(\mathrm{AUC}\right)$ or $\log \left(C_{\max }\right)$, then the null hypothesis for BE testing is:

$$H_0:{\beta }^T\ge \delta \text{or}{\beta }^T\le -\delta$$ (1)

with $\delta$ a given threshold

The TOST relies on the decomposition of the null hypothesis stated in Equation 1 in two one‐sided hypotheses $H_{0,-\delta }:\left\{{\beta }^T\le -\delta \right\}\text{and}{H}_{0,\delta }:\left\{{\beta }^T\ge \delta \right\}$ _. ¹⁷ Thereby the null hypothesis is rejected if

$$\frac{{\widehat{\beta }}^T+\delta }{\mathrm{SE}\left({\widehat{\beta }}^T\right)}\ge u_{1-\alpha }\text{and}\frac{{\widehat{\beta }}^T-\delta }{\mathrm{SE}\left({\widehat{\beta }}^T\right)}\le -u_{1-\alpha }$$ (2)

where ${\widehat{\beta }}^T$ and $\mathrm{SE}\left({\widehat{\beta }}^T\right)$ are the ${\beta }^T$ estimate and its standard error, and $u_{1-\alpha }$ is the $1-\alpha$ quantile of a reference distribution.

This method is equivalent to constructing a ($1-2\alpha$)‐confidence interval (CI) for ${\widehat{\beta }}^T$ and concluding BE if it is completely contained in the equivalence interval $\left[-\delta ;\delta \right]$. In conventional BE analysis, regulatory authorities set the threshold $\delta =\log \left(1.25\right)=-\log \left(0.8\right)$ and the significance level $\alpha =0.05$. ¹⁸ The BE acceptance criteria is for the 90% CI around the geometric mean ratio (GMR) of AUC or $C_{\max }$ to be included in the [80–125]% interval.

Single point study design

In BE studies for generic drug development of ophthalmic drug products, one sample of aqueous humor is taken at a certain timepoint per eye for measurement of drug concentration. A parallel study design involves sampling from only one eye, whereas crossover study designs involve sampling from both eyes, with test product in one eye and reference product in the other eye.

In both treatment arms of parallel studies, the subjects will be assigned to each of several prespecified sampling times $t_j$ with $j=1,\dots ,J$. Let $C_{\mathit{ij}}$ be the concentration of subject $i=1,\dots ,N_j$ at the sampling time $t_j$. The total number of samples is $n_{\mathrm{tot}}={\sum }_{j=1}^J{N}_j$ which is the same as the total number of subjects.

In the crossover studies, each subject with bilateral cataracts is randomly assigned for treatment with the test product in one eye and the reference product in the other eye.

A single sample of aqueous humor is collected from each eye at the same assigned sampling time $t_j$. Let $C_{\mathrm{ijk}}$ be the concentration of subject $i=1,\dots ,N_{\mathrm{kj}}$ at the same assigned sampling time $t_j$ at each period/in each eye $k=1,2$. So, the total number of samples in the study is $n_{\mathrm{tot}}={\sum }_{k=1}^2{\sum }_{j=1}^J{N}_{\mathrm{kj}}$ for crossover. The total number of subjects $N=n_{\mathrm{tot}}/2$.

MB‐TOST method

This approach uses NLMEM that account for the nonlinearity of the concentration versus time profile, as well as between‐ and within‐subject variability (BSV and WSV). ¹⁹

For crossover designs, the concentration $C_{\mathrm{ijk}}$ is described by a nonlinear function $f$ depending on the vector of individual parameters ${\varphi }_{\mathrm{ijk}}$ of subject $i$ sampled at time $t_j$ for period/eye $k$:

$$C_{\mathrm{ijk}}=f\left(t_j,{\varphi }_{\mathrm{ijk}}\right)+g\left(t_j,{\varphi }_{\mathrm{ijk}}\right){\epsilon }_{\mathrm{ijk}}$$ (3)

The $l^{\mathrm{th}}$ element of the vector ${\varphi }_{\mathrm{ijk}}$ (i.e., the $l^{\mathrm{th}}$ individual parameter ${\varphi }_{\text{ijkl}}$ $l=1,\dots ,n_p$ where $n_p$ is the number of PK parameters) can be decomposed as in the following equation:

$$\log \left({\varphi }_{\text{ijkl}}\right)=\log \left({\lambda }_l\right)+{\beta }_l^{T^{\prime }}{T}_{\mathrm{ijk}}+{\beta }_l^{P^{\prime }}{P}_k+{\beta }_l^{S^{\prime }}{S}_{\mathrm{ij}}+{\eta }_{\mathrm{ijl}}+{\kappa }_{\text{ijkl}},$$ (4)

with ${\lambda }_l$ the $l^{\mathrm{th}}$ element of the vector of fixed effects for the covariate reference class. $T_{\mathrm{ijk}}$, $P_k$, and $S_{\mathrm{ij}}$ are known vectors of treatment, period and sequence covariates, respectively. ${\beta }_l^T$, ${\beta }_l^P$, and ${\beta }_l^S$ are the vectors of coefficients of treatment, period and sequence effects, respectively, for the $l^{\mathrm{th}}$ individual parameter. ${\eta }_{\mathrm{ijl}}$ is the $l^{\mathrm{th}}$ element of the vector of random effects ${\eta }_{\mathrm{ij}}$ for subject $i$ at time $t_j$ capturing the BSV. ${\kappa }_{\text{ijkl}}$ is the $l^{\mathrm{th}}$ element of the vector of random effects ${\kappa }_{\mathrm{ijk}}$ for subject $i$ at time $t_j$ and period $k$, capturing WSV.

The random effect vectors ${\eta }_{\mathrm{ij}}$ and ${\kappa }_{\mathrm{ijk}}$ are independently and normally distributed, with mean zero and variance–covariance matrix $\mathrm{\Omega }$ and $\mathrm{\Gamma }$, respectively, of size $n_p\times n_p$. Let ${\omega }_l^2$ and ${\gamma }_l^2$ denote the $l^{\mathrm{th}}$ diagonal element of $\mathrm{\Omega }$ and $\mathrm{\Gamma }$, corresponding to the BSVs and WSVs of the $l^{\mathrm{th}}$ parameter, respectively.

The residual errors ${\epsilon }_{\mathrm{ijk}}$ are independently and identically distributed according to a normal centered distribution of variance ${\sigma }^2$. The associated error model can be additive $g\left(t_j,{\varphi }_{\mathrm{ijk}}\right)=a$, proportional $g\left(t_j,{\varphi }_{\mathrm{ijk}}\right)=bf\left(t_j,{\varphi }_{\mathrm{ijk}}\right)$, or combined $g\left(t_j,{\varphi }_{\mathrm{ijk}}\right)=a+bf\left(t_j,{\varphi }_{\mathrm{ijk}}\right)$.

For parallel designs, both Equations 1 and 2 simplify as follows (i.e., no period or sequence effect because there is only one period/eye and one sequence per subject):

$$\begin{array}{l}{C}_{\mathrm{ij}}=f\left(t_j,{\varphi }_{\mathrm{ij}}\right)+g\left(t_j,{\varphi }_{\mathrm{ij}}\right){\epsilon }_{\mathrm{ij}}\\ \log \left({\varphi }_{\mathrm{ijl}}\right)=\log \left({\lambda }_l\right)+{\beta }_l^{T^{\prime }}{T}_{\mathrm{ij}}+{\eta }_{\mathrm{ijl}},\end{array}$$ (5)

The full vector of parameters to be estimated in the NLMEM is $\theta =\left(\lambda ,{\beta }^T,{\beta }^P,{\beta }^S,\mathrm{\Omega },\mathrm{\Gamma },a,b\right)$ or $\left(\lambda ,{\beta }^T,\mathrm{\Omega },a,b\right)$ depending on the design. Let $\mathrm{VAR}\left(\widehat{\theta }\right)$ denote the asymptotic variance–covariance matrix of estimation, with the square root of its diagonal elements being the parameter asymptotic SEs. $\mathrm{VAR}\left(\widehat{\theta }\right)$ is derived as the inverse of the observed FIM.

The treatment effects on AUC and $C_{\max }$ (${\beta }_{\mathrm{AUC}}^T$ and ${\beta }_{C_{\max }}^T$, respectively) are functions of the reference effects $\lambda$ and the treatment effects ${\beta }^T$ on the PK model parameters. The delta‐method is used to obtain estimates of $\mathrm{SE}\left({\widehat{\beta }}_{\mathrm{AUC}}^T\right)$ and $\mathrm{SE}\left({\widehat{\beta }}_{C_{\max }}^T\right)$ _. ²⁰ These estimates and their SE are used to calculate the TOST statistics stated in Equation 2 to be compared to $z_{1-\alpha }$ the $\left(1-\alpha \right)$‐quantile of a normal distribution.

In this approach, the exposure can be captured by ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and ${\mathrm{AUC}}_{0-\infty }$, both being different functions of the reference effects $\lambda$ and the treatment effects ${\beta }^T$ on the PK model parameters.

Nonparametric bootstrap NCA

In recent years, the FDA has recommended parametric or nonparametric bootstrap NCA methods for the BE analysis of generic ophthalmic drug products. ³ , ⁴ , ⁵

For crossover designs, at each time $t_j$, the mean of the concentrations $C_{\mathrm{ijk}}$ are calculated, for each period k. Here, two versions of the nonparametric bootstrap NCA are evaluated (i) using the geometric mean of the concentrations or (ii) using the arithmetic mean of the concentrations. ³ In both versions, one value of $C_{\max }^k$ and ${\mathrm{AUC}}^k$ is derived from the $J^k$ (geometric or arithmetic) means at each timepoint, for each period (e.g., k = 1 for treatment T and 2 for treatment R).

Let $C_{\mathrm{hij}}$ be the $h^{\mathrm{th}}$ product concentration of the subject $i$ and sampling timepoint $t_j$, $h=T,R$, $i=1,\dots ,N_{\mathrm{hj}}$, and $j=1,\dots ,J$. Let ${\overline{C}}_{\mathrm{hj}}$ be the mean concentration of the $h^{\mathrm{th}}$ product at the $j^{\mathrm{th}}$ sampling timepoint, defined as follows:

$$\begin{array}{c}{\overline{C}}_{\mathrm{hj}}=\left\{\begin{array}{cc}{\sum }_{i=N_{\mathrm{hj}}}{C}_{\mathrm{hij}}/N_{\mathrm{hj}}\hfill & \text{if}\text{arithmetic}\text{mean}\\ \exp \left({\sum }_{i=N_{\mathrm{hj}}}\log \left(C_{\mathrm{hij}}\right)/N_{\mathrm{hj}}\right)& \text{if}\text{geometric}\text{mean}\end{array}\right.\hfill \end{array}$$ (6)

Thus, the AUC of the $h^{\mathrm{th}}$ product from the mean profile of drug concentration is calculated, using the trapezoidal rule, by:

$${\mathrm{AUC}}^h=t_1\times {\overline{C}}_{\mathrm{hj}}/2+\sum _{j=1}^{J-1}\left({\overline{C}}_{\mathrm{hj}}+{\overline{C}}_{h,j+1}\right)\cdot \left(t_{j+1}-t_j\right)/2$$ (7)

$C_{\max }$ is also obtained from the mean profile by:

$$C_{\max }^h=\underset{j\in \left(1,\dots ,J\right)}{\max }\left({\overline{C}}_{\mathrm{hj}}\right)$$ (8)

Then, the ratios $\frac{{\mathrm{AUC}}^T}{{\mathrm{AUC}}^R}$ and $\frac{C_{\max }^T}{C_{\max }^R}$ are calculated and the 90% CIs around these ratio estimates are obtained using nonparametric bootstrap as follows.

Let us consider $b\left(=1,\dots ,B\right)$ bootstrap samples. For each sampling time $t_j$, the concentrations of the $N_j$ individuals at both occasions $k$ (i.e., for treatments R and T) are re‐sampled with replacement. For each bootstrap sample, at each time $t_j$ the geometric and arithmetic mean of the concentrations $C_{\mathrm{ij}}$ are calculated for each treatment group, before deriving the respective treatment $\mathrm{AUC}$, $C_{\max }$ and the corresponding ratios. B ratio estimates $\frac{{\mathrm{AUC}}_b^T}{{\mathrm{AUC}}_b^R}$ and $\frac{C_{\text{max b}}^T}{C_{\text{max b}}^R}$ are obtained and the fifth and ${95}^{\mathrm{th}}$ percentiles of these distributions are used as the lower and upper bounds of the 90% CIs, respectively. Then, BE is concluded if the latter intervals are included in the [80–125]% interval.

To calculate the 90% bootstrap CIs for parallel designs, the concentrations of the $N_j$ individuals are bootstrapped in each treatment group separately.

In this approach, the exposure is captured by ${\mathrm{AUC}}_{0-t_{\text{last}}}$ (i.e., the trapezoidal rule is used to obtain the AUC and no extrapolation to infinity is made from the last sampling time). In the content of the following tables and figures, we refer to this approach as “NCA bootstrap Geometric and Arithmetic.”

Simulation study

Simulation settings

The PK data describing the PK of theophylline drug were simulated using the following one‐compartment PK model with first‐order absorption and elimination as in ref. 13, thereby assuming the test drug has the same PK structural model as the reference drug:

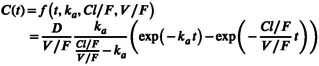(9)

where $F$ is the bioavailability, $D$ the dose, $V$ the distribution volume, $k_a$ the absorption rate constant, and $\mathit{Cl}$ the clearance of the drug. This PK model describes an exponential rise followed by a mono‐exponential decrease in the concentrations which would have fitted the data of the ophthalmic product described in ref. 4.

Parallel and two‐way crossover designs were considered, both with one sampling timepoint per subject. For each subject, the one sampling time was drawn from a rich or sparse set containing 10 or 5 sampling times, respectively, for selection. A total of 500 subjects was simulated with balanced sample sizes per sampling time and treatment group. For parallel designs, there were 25 subjects per sampling time in each treatment group for the rich set, and 50 subjects per sampling time in each treatment group for the sparse set. For crossover designs, there were 50 subjects per sampling time and per period/eye for the rich set, and 100 subjects per sampling time and period/eye for the sparse set.

The set of 10 sampling times was selected from: $t\in \left\{0.25,0.5,1,2,3.5,5,7,9,12,24\right\}$ h, and the set of 5 was selected from: $t\in \left\{0.25,1.5,3.35,12,24\right\}$ h. The latter was obtained by maximization of the determinant of the FIM with fixed sampling times at $\left\{\mathrm{1.5,12}\right\}$ h. ⁸ For the two‐way crossover design, the same timepoint after drug administration is assumed in both periods/eyes within each individual.

Each subject received $D=4$ mg. The fixed effects for the reference treatment group of subjects were ${\lambda }_{k_a}=1.5$/h, ${\lambda }_{V/F}=0.5$ L and ${\lambda }_{\mathit{Cl}/F}=40$ mL/h. Diagonal matrices were used for both BSV and WSV (only used when crossover design) with ${\omega }_{k_a}={\omega }_{V/F}={\omega }_{\mathit{Cl}/F}=52\%$ for parallel designs, and ${\omega }_{k_a}={\omega }_{V/F}={\omega }_{\mathit{Cl}/F}=50\%$ and ${\gamma }_{k_a}={\gamma }_{V/F}={\gamma }_{\mathit{Cl}/F}=15\%$ for crossover designs. We used a combined error model for the residual variance with $a=0.1$ mg/L and $b=10\%$.

The limit of quantification (LOQ) for simulated concentrations was set at 0.2 mg/L. Simulated concentrations below 0.2 mg/L, including negative concentrations ($<0$) and concentrations between 0 and 0.2 (0–0.2) mg/L were identified as below the limit of quantification (BLOQ). For MB‐TOST, BLOQ concentrations were handled in the likelihood calculations using the method described in ref. 21 (i.e., the likelihood for a BLOQ observation is taken to be the likelihood that it is between 0 and the LOQ, given the current model parameter estimates). For NCA bootstrap, the BLOQ data were set to LOQ/2 as in Ref. 4.

Evaluation

Both MB‐TOST and NCA bootstrap were evaluated for BE on ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$ (and not on ${\mathrm{AUC}}_{0-\infty }$) for the purpose of the comparison (see Supplementary Material S1 for the details of these metric calculations).

Despite the sparse sampling in our design, we used asymptotic SE for MB‐TOST due to the large sampling size evaluated ($N=500$). Indeed, with $\sqrt{N}$‐consistency for all PK parameters simulated and fitted with BSV (and WSV for crossover designs), we assumed asymptotic conditions were met.

For all approaches, the type I error was assessed under two different $H_0$ hypotheses by setting ${\beta }_{\mathit{Cl}/F}^T={\beta }_{V/F}^T=\log \left(0.8\right)$ and ${\beta }_{\mathit{Cl}/F}^T={\beta }_{V/F}^T=\log \left(1.25\right)$, corresponding to a simulated GMR for ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$ of 1.25 and 0.8, respectively (see Supplementary Material S1).

We simulated under two different $H_1$ hypotheses, first by setting ${\beta }_{\mathit{Cl}/F}^T={\beta }_{V/F}^T=\log \left(0.9\right)$ and second by setting ${\beta }_{\mathit{Cl}/F}^T={\beta }_{V/F}^T=\log \left(1\right)=0$, corresponding to a simulated GMR for ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$ of 1.111 and 1, respectively. In all scenarios, period and sequence effects were assumed to be null (i.e., ${\beta }^P={\beta }^S=0$).

Therefore, we simulated 16 scenarios: two study designs (parallel or two‐way crossover) times two sets of possible sampling times (5 or 10) and four hypotheses (${\beta }^T=\log \left(0.8\right)$, $\log \left(0.9\right)$, $\log \left(1\right)$, $\log \left(1.25\right)$). Subsequently, our notation $C10H_{0:0.8}$ refers to the scenario with a crossover design, a set of 10 sampling times to choose from and a simulated treatment effect ${\beta }^T$ of $\log \left(0.8\right)$.

Estimation errors (EEs; the differences between the estimates and the simulated value) were calculated for model‐based GMR and NCA bootstrap (geometric and arithmetic) mean ratio (MR) of AUC and $C_{\max }$. Similarly for all scenarios, we calculated the empirical 5th and 95th percentiles of the GMR for MB‐TOST (as the mean $\pm u_{1-\alpha }\times$ the standard deviation over all simulation estimates) and of the MR for the NCA bootstrap (geometric and arithmetic, as the 5th and 95th percentiles over all simulation estimates) to be compared to the distribution of the estimated 5th and 95th percentiles obtained on each simulated data sets, for AUC and $C_{\max }$.

For the MB approach, relative EE (REE), relative bias (Rbias) and relative root mean square error (RRMSE) were calculated for fixed effects, random effects, and error model parameters. ²² Because the treatment, sequence, and period effects were simulated at zero, we did not calculate REE, Rbias, and RRMSE for the latter but absolute values of the corresponding metrics.

MB‐TOST and NCA bootstrap were evaluated on 500 simulated data sets for each scenario. As NCA bootstrap runs faster, it was also evaluated on 10,000 simulated data sets for the challenging scenarios with 10 samples under one null and one alternative hypothesis: $P10H_{0:1.25}$, $P10H_{1:0.9}$, $C10H_{0:1.25}$, and $C10H_{1:0.9}$.

NCA bootstrap was evaluated with each of these scenarios, assuming there is no LOQ at 0.2 mg/L. Whereas MB‐TOST was evaluated on scenarios $P10H_{0:1.25}$ and $C10H_{0:1.25}$ with no LOQ at 0.2 mg/L. In the absence of a defined LOQ, concentrations simulated below zero were set to 0.0001.

MB‐TOST and NCA bootstrap were also evaluated on 500 simulated data sets for two parallel design scenarios with 10 possible sampling times and an increased residual variance at $b=30\%$ ($P10H_{1:0.9}{\mathrm{RUV}}_{0.3}$ and $P10H_{0:1.25}{\mathrm{RUV}}_{0.3}$) and two crossover design scenarios with 10 possible sampling times and increased WSV and residual variance at ${\gamma }_{k_a}={\gamma }_{V/F}={\gamma }_{\mathit{Cl}/F}=30\%$ and $b=30\%$ ($C10H_{1:0.9}{\text{WSVandRUV}}_{0.3}$ and $C10H_{0:1.25}{\text{WSVandRUV}}_{0.3}$).

Implementation

For the NCA bootstrap method, $B=5000$ bootstrap samples were performed in the R statistical software version 4.0.2.

For the model‐based approach, the Monolix 2018R2 software ²³ was used which implements the SAEM algorithm for parameters. ²⁴ Population parameters were estimated with 300 exploratory and 100 smoothing iterations, ensuring an appropriate convergence of SAEM visually assessed on a couple of data sets. Further, because there was only one observation per subject per occasion, 10 Markov chains were used to improve the precision of the estimation. This choice was motivated by a previous simulation study which already recommended to use 10 Markov chains with three sampling times per subject. ¹³ Initial values were set at the true value (i.e., the simulation value [see section simulation settings and Supplementary Material S2]) for all parameters except the treatment, period, and sequence effects all set to zero. Standard errors were computed using the stochastic approximation method. ²⁵

BE tests were performed on GMR for MB‐TOST and MR for NCA bootstrap (geometric and arithmetic), of ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$ in the R statistical software version 4.0.2.

RESULTS

Figure 1 represents a typical data set under the hypotheses of no BE (${\beta }_{Cl/F}^T={\beta }_{V/F}^T=\log \left(0.8\right)$ top two lines) and equivalence (${\beta }_{Cl/F}^T={\beta }_{V/F}^T=\log \left(1\right)$ bottom two lines) for scenarios with parallel (left column) and crossover (middle and right columns) designs and choosing the individual sample from a set of five or 10 possible times. As simulating ${\beta }_{Cl/F}^T={\beta }_{V/F}^T=\log \left(0.8\right)$ corresponds to ${\beta }_{\mathrm{AUC}}^T={\beta }_{C_{\max }}^T=\log \left(1.25\right)$ (see Supplementary Material S1), the test treatment curve appears above the reference treatment curve on plots A‐D of Figure 1. Consequently, simulating ${\beta }_{Cl/F}^T={\beta }_{V/F}^T=\log \left(1\right)$ leads to the reference and test treatment curves being overlaid on plots E‐H of Figure 1. There were very few BLOQ data in our simulations, with 0.2% to 1.6% of simulated concentrations below 0.2 mg/L at 12 and 24 h post‐dose respectively, for scenario $P10H_{0:1.25}$ which simulates the lowest concentrations in the treatment group.

FIGURE 1.

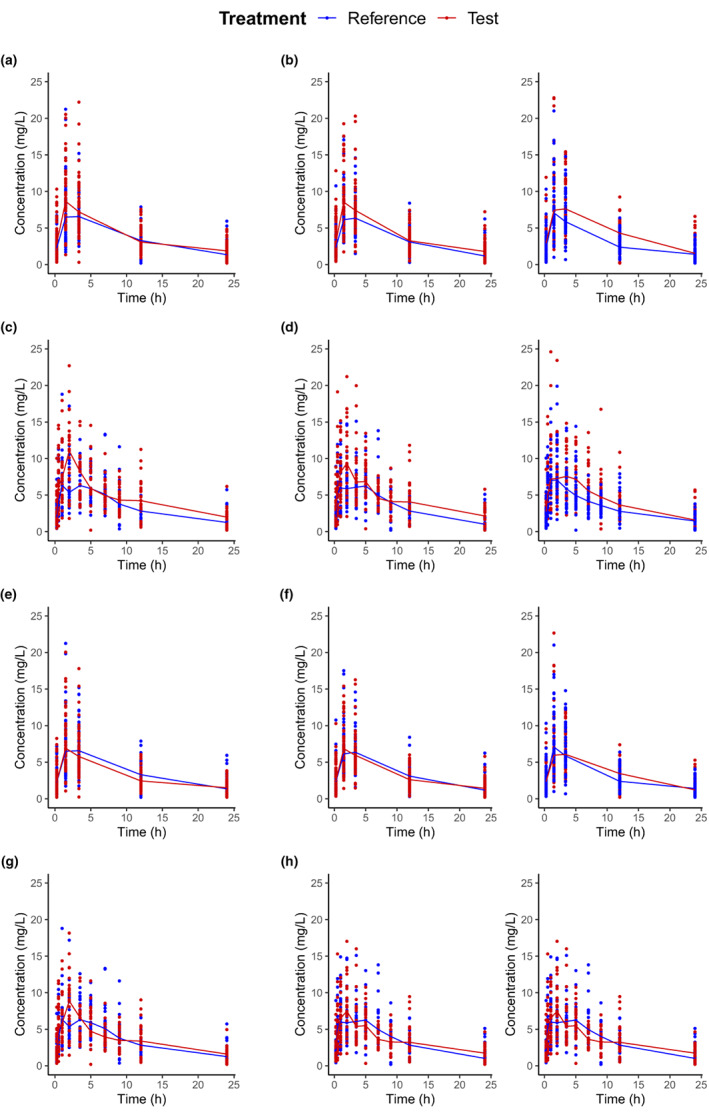
Concentrations versus time following the reference and test treatments for the first simulated clinical study for different simulation scenarios with parallel and two‐way crossover designs (period 1 on the left and period 2 on the right). The lines are connecting the median in each group successive timepoints. (a) $\mathrm{P}5{\mathrm{H}}_{0:0.8}$; (b) $\mathrm{C}5{\mathrm{H}}_{0:0.8}$; (c) $\mathrm{P}10{\mathrm{H}}_{0:0.8}$; (d) $\mathrm{C}10{\mathrm{H}}_{0:0.8}$; (e) $\mathrm{P}5{\mathrm{H}}_{1:1}$; (f) $\mathrm{C}5{\mathrm{H}}_{1:1}$; (g) $\mathrm{P}10{\mathrm{H}}_{1:1}$; and (h) $\mathrm{C}10{\mathrm{H}}_{1:1}$.

Model‐based GMR and NCA bootstrap MR (geometric and arithmetic) for ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$ were unbiased and precise (see Figures 2 and 3). These results validated the parameter estimation from both the model‐based and NCA approaches. The evaluation of the model parameter estimation is detailed in Supplementary Material S2.

FIGURE 2.

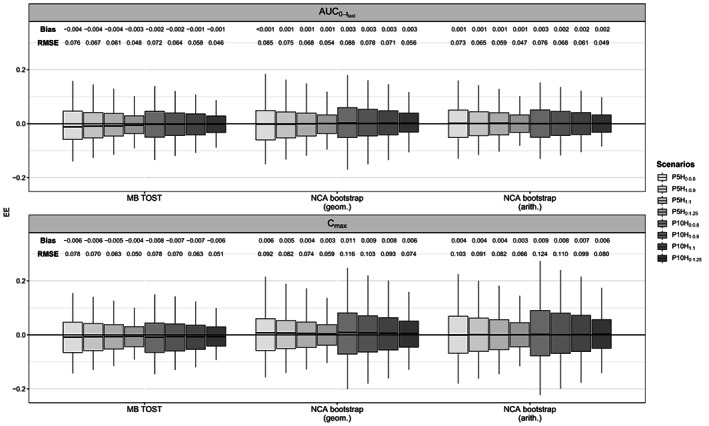
Boxplot (2.5th, 25th, 50th, 75th, and 97.5th percentiles) of estimation errors (EEs) of the geometric mean ratio (MB‐TOST) and the mean ratio (NCA bootstrap geometric and arithmetic) for ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$, for 500 simulated data sets with parallel designs. ${\mathrm{AUC}}_{0-t_{\text{last}}}$, area under the time‐concentration curve from time zero until the last sampling time; C _max, maximum concentration; EEs, estimation errors; MB‐TOST, model‐based two one‐sided test; NCA, noncompartmental analysis.

FIGURE 3.

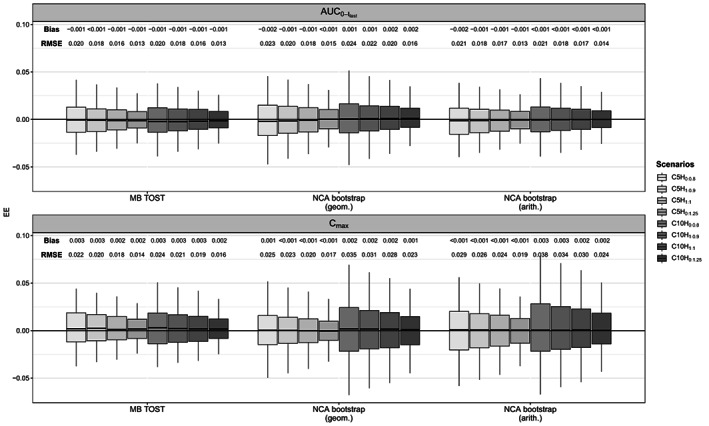
Boxplot (2.5th, 25th, 50th, 75th, and 97.5th percentiles) of EEs of the geometric mean ratio (MB‐TOST) and the mean ratio (NCA bootstrap geometric and arithmetic) for ${\mathrm{AUC}}_{0-t_{\text{last}}}$ and $C_{\max }$, for 500 simulated data sets with two‐way crossover designs. ${\mathrm{AUC}}_{0-t_{\text{last}}}$, area under the time‐concentration curve from time zero until the last sampling time; C _max, maximum concentration; EEs, estimation errors; MB‐TOST, model‐based two one‐sided test; NCA, noncompartmental analysis.

Compared to parallel studies, crossover studies resulted in smaller 90% CIs (see Figures S5 and S6) and consequently higher power estimates (see Table 1) close to 100%, as expected. The number of samples to choose from impacted only the percentiles of the NCA bootstrap MR for $C_{\max }$. Because the $\mathrm{AUC}$ is an average over the concentrations, it is expected to be less sensitive to the design than $C_{\max }$ which relies mostly on one measurement. Indeed, for designs with 10 rather than five samples to choose from, and consequently half of the sample size at each sampling time, the 90% CIs were significantly larger. This phenomenon led to 50% drops in power for parallel designs. For crossover designs, the drop in power was modest under the scenario with ${\beta }^T=\log \left(0.9\right)$. Indeed, in crossover designs, we simulated a rather low WSV which resulted in small 90% CIs and consequently a power close to one. Of note, 90% CIs derived from the empirical percentiles were even smaller.

TABLE 1.

Study power [95% CI] using parallel and two‐way crossover study designs with 500 simulated data sets (estimates in brackets are obtained with 10,000 simulated data sets).

	${\mathrm{AUC}}_{0-t_{\text{last}}}$			C max
	MB‐TOST	NCA bootstrap		MB‐TOST	NCA bootstrap
		Geometric	Arithmetic		Geometric	Arithmetic
P5H1:0.9	0.692 [0.649; 0.732]	0.600 [0.556; 0.643]	0.696 [0.654; 0.736]	0.598 [0.554; 0.641]	0.388 [0.345; 0.432]	0.378 [0.335; 0.422]
P10H1:0.9	0.696 [0.654; 0.736]	0.554 [0.509; 0.598] (0.565 [0.555; 0.575])	0.676 [0.633; 0.717] (0.681 [0.672; 0.690])	0.588 [0.543; 0.632]	0.194 [0.160; 0.231] (0.196 [0.188; 0.204])	0.170 [0.138; 0.206] (0.166 [0.159; 0.173])
P5H1:1	0.950 [0.927; 0.967]	0.916 [0.888; 0.939]	0.968 [0.949; 0.982]	0.926 [0.899; 0.947]	0.760 [0.720; 0.797]	0.664 [0.621; 0.705]
P10H1:1	0.968 [0.949; 0.982]	0.884 [0.853; 0.911]	0.970 [0.951; 0.983]	0.896 [0.866; 0.921]	0.370 [0.328; 0.414	0.294 [0.254; 0.336]
C5H1:0.9	0.998 [0.989; 1.000]	1 [0.993; 1.000]	1 [0.993; 1.000]	0.998 [0.989; 1.000]	1 [0.993; 1.000]	0.996 [0.986; 1.000]
C10H1:0.9	0.998 [0.989; 1.000]	1 [0.993; 1.000] (1 [1.000; 1.000])	1 [0.993; 1.000] (1 [1.000; 1.000])	0.998 [0.989; 1.000]	0.972 [0.953; 0.985] (0.973 [0.970; 0.976])	0.932 [0.906; 0.952] (0.949 [0.944; 0.953])
C5H1:1	1 [0.993; 1.000]	1 [0.993; 1.000]	1 [0.993; 1.000]	0.998 [0.989; 1.000]	1 [0.993; 1.000]	1 [0.993; 1.000]
C10H1:1	1 [0.993; 1.000]	1 [0.993; 1.000]	1 [0.993; 1.000]	0.998 [0.989; 1.000]	1 [0.993; 1.000]	1 [0.993; 1.000]

Note: The power estimates presented here are not corrected for the departure from the nominal level of the test.

Abbreviations: ${\mathrm{AUC}}_{0-t_{\text{last}}}$, area under the time‐concentration curve from time zero until the last sampling time; CI, confidence interval; C _max, maximum concentration; MB‐TOST, model‐based two one‐sided test; NCA, noncompartmental analysis.

For AUC, both MB‐TOST and NCA bootstrap (geometric and arithmetic) obtained controlled type I error rates on 500 simulated data sets (see Table 2) with the exception of a slightly inflated estimate in scenario $P10H_{0:0.8}$ for NCA bootstrap geometric (0.076).

TABLE 2.

Type I error rates [95% CI] using parallel and two‐way crossover study designs with 500 simulated data sets (estimates in brackets are obtained with 10,000 simulated data sets).

	${\mathrm{AUC}}_{0-t_{\text{last}}}$			C max
	MB‐TOST	NCA bootstrap		MB‐TOST	NCA bootstrap
		Geometric	Arithmetic		Geometric	Arithmetic
P5H0:0.8	0.068 [0.048; 0.094]	0.058 [0.039; 0.082]	0.064 [0.044; 0.089]	0.054 [0.036; 0.078]	0.026 [0.014; 0.044]	0.034 [0.020; 0.054]
P10H0:0.8	0.068 [0.048; 0.094]	0.076 [0.054; 0.103]	0.066 [0.046; 0.091]	0.060 [0.041; 0.085]	0.024 [0.012; 0.042]	0.026 [0.014; 0.044]
P5H0:1.25	0.038 [0.023; 0.059]	0.058 [0.039; 0.082]	0.052 [0.034; 0.075]	0.038 [0.023; 0.059]	0.028 [0.015; 0.047]	0.040 [0.025; 0.061]
P10H0:1.25	0.052 [0.034; 0.075]	0.064 [0.044; 0.089] (0.056 [0.052; 0.061])	0.066 [0.046; 0.091] (0.057 [0.052; 0.061])	0.032 [0.018; 0.051]	0.014 [0.006; 0.029] (0.020 [0.018; 0.023])	0.012 [0.004; 0.026] (0.020 [0.017; 0.023])
C5H0:0.8	0.044 [0.028; 0.066]	0.066 [0.046; 0.091]	0.062 [0.043; 0.087]	0.028 [0.015; 0.047]	0.016 [0.007; 0.031]	0.024 [0.012; 0.042]
C10H0:0.8	0.048 [0.031; 0.071]	0.052 [0.034; 0.075]	0.056 [0.038; 0.080]	0.026 [0.014; 0.044]	0.014 [0.006; 0.029]	0.014 [0.006; 0.029]
C5H0:1.25	0.060 [0.041; 0.085]	0.050 [0.033; 0.073]	0.050 [0.033; 0.073]	0.062 [0.043; 0.087]	0.024 [0.012; 0.042]	0.024 [0.012; 0.042]
C10H0:1.25	0.052 [0.034; 0.075]	0.068 [0.048; 0.094] (0.062 [0.057; 0.067])	0.070 [0.049; 0.096] (0.056 [0.052; 0.061])	0.060 [0.041; 0.085]	0.010 [0.003; 0.023] (0.013 [0.011; 0.015])	0.014 [0.006; 0.029] (0.015 [0.013; 0.018])

Abbreviations: ${\mathrm{AUC}}_{0-t_{\text{last}}}$, area under the time‐concentration curve from time zero until the last sampling time; CI, confidence interval; C _max, maximum concentration; MB‐TOST, model‐based two one‐sided test; NCA, noncompartmental analysis.

In terms of power, MB‐TOST and NCA bootstrap arithmetic obtained similar mean estimates, whereas NCA bootstrap geometric power estimates were consistently lower in parallel designs.

For $C_{\max }$, the 90% CIs of all approaches were larger than the 90% CIs derived from the empirical percentiles. Further, the 90% CIs of the NCA bootstrap (geometric and arithmetic) MR was wider than that for the model‐based GMR. Consequently, type I error rates were significantly conservative, for NCA bootstrap in general with the exception of scenario $P5H_{0:0.8}$ when using arithmetic means and for scenarios $C5H_{0:0.8}$ and $C10H_{0:0.8}$ for MB‐TOST.

In terms of power, MB‐TOST had a similar power as NCA bootstrap in crossover designs, but higher power than NCA bootstrap in parallel designs. Of note for $C_{\max }$, conversely to AUC, NCA bootstrap geometric had slightly higher power than NCA bootstrap arithmetic in parallel studies, but the two were similar in crossover designs.

On the scenarios where we investigated NCA bootstrap on 10,000 simulated data sets, the type I error rates converged closer to the 5% target value and with narrower CIs compared with 500 simulated data sets (Supplementary Material S5). Other trends were similar to those observed in Tables 1 and 2. When we analyzed the data without a LOQ at 0.2 mg/L, the results were generally consistent (Supplementary Material S6) for AUC.

We observed no impact of inflating the simulated RUV on the type I error of MB‐TOST and NCA bootstrap for AUC or $C_{\max }$ (Supplementary Material S4), in general. Inflating the simulated WSV only resulted in a slight inflation of the type I error of NCA bootstrap arithmetic for AUC in crossover designs. For a parallel design, the power estimate for AUC decreased by 28%, 21%, and 19% with MB‐TOST, NCA bootstrap geometric mean, and NCA bootstrap arithmetic, respectively, whereas on the crossover design they decreased by 8%, 17%, and 7%, respectively. Likewise, the power estimate for $C_{\max }$ decreased by 26% and 21% with MB‐TOST using a parallel and crossover design, respectively, and decreased by more than 60% for both NCA bootstrap methods and designs.

Overall, MB‐TOST and NCA bootstrap performed similarly for AUC. For $C_{\max }$, NCA bootstrap tended to be conservative and less powerful for parallel designs compared to MB‐TOST, likely due to the more precise estimates of MB‐TOST when the PK model is correctly specified.

DISCUSSION

In this study, we used NLME tools to simulate PK BE studies for a generic ophthalmic drug product with one sampling timepoint per subject and per occasion. Consistent with our previous research, we estimated treatment effects on all model parameters ¹² , ¹³ , ¹⁵ , ²⁶ and evaluated various scenarios, including the study design (parallel or crossover), set of sampling times, and GMR. The aim was to evaluate and compare the performances of MB‐TOST ¹⁵ and the NCA bootstrap ⁴ using concentration geometric or arithmetic means.

All model parameters were well‐estimated except for the additive term of the combined error model, possibly due to the limitations of using a single sample per patient (see Tables S1–S8 in Supplementary Material S2). Whether a proportional error model or fixing the additive term would have solved that issue requires further evaluation. ²⁷ It had, however, no impact on the estimation of the treatment, sequence, or period effects parameters as well as on the GMRs of AUC and $C_{\max }$.

Both MB‐TOST and the NCA bootstrap (geometric and arithmetic) performed similarly in terms of type I error rate for AUC. For $C_{\max }$, the NCA bootstrap approach almost always provided conservative type I error rates with values below 0.05. For parallel designs, NCA bootstrap, which does not need to specify the underlying PK model, led to noticeable lower power for $C_{\max }$ as compared to MB‐TOST when the underlying PK model is correctly specified and the test drug has the same PK structural model as the reference drug. We used optimal design to choose the sampling times of the sparse set which did not include the $t_{\max }$ according to the fixed effects. This may have favored MB‐TOST as NCA relies on observed sampling times to estimate $C_{\max }$. However, this advantage is difficult to appreciate as due to BSV all subjects had different $t_{\max }$. Power was also particularly impacted by the number of sampling timepoints. Indeed, with 10 sampling times to choose from, fewer subjects were allocated to informative timepoints, which reduced the informativeness of the design ²⁸ and led to larger 90% CIs of the GMR and MR for $C_{\max }$. The simulation showed that estimates for $C_{\max }$ were not as efficient as for AUC because $C_{\max }$ is only based on one value whereas AUC is based on an average over the concentrations.

This work presents a notable limitation in the use of the simulated PK model structure, as well as the simulated values as initial guess for the parameters (except for the treatment effects which were fixed to 0) in the MB approach, whereas the model structure and parameter values are unknown in reality. In this paper, we did not test the performance of MB‐TOST if the underlying PK model is not correctly specified, which is likely with a limited number of sampling points. This is mitigated, however, by the fact that BE studies occur downstream of the drug development process when a non‐negligible knowledge has been accumulated on the PKs of the drug at least in the reference treatment arm. ⁶ Moreover, the model would be subjected to a thorough evaluation prior to its use for the BE analysis. ⁷ Nonetheless, using the true model and parameter estimates provided a favorable setup for MB‐TOST and challenging its robustness to departure from the simulated PK model and parameter values needs to be explored in the future.

Another limitation is only 500 datasets were simulated under each of the 16 scenarios due to the limitation of computation power, which can impact the precision of the evaluation of the performance (e.g., bias, type 1 error rate, and power). Computing times ranged in average from 15 min per data set for parallel designs to 45 min per data set for crossover designs, on a similar computing setup. Notably, it is the default number for simulation‐based goodness of fit plots in PsN, a recognized tool for NLMEM. ²⁹ Additionally, the number of bootstraps for the NCA approaches could also have been increased from 5000 ⁴ to 10,000.

In addition, the lowest concentration level in real studies is zero, but, in simulation, negative concentration levels can happen, which is a limitation of using simulation to generate concentration data. For those concentrations simulated below zero, they are imputed as 0.0001 when no LOQ is defined. When a LOQ is defined, the likelihood is taken to be between zero and the LOQ for all simulated BLOQ concentrations including those with 0 to LOQ (e.g., 0.2) values as well as negative (<0) concentration values for MB‐TOST. Likewise, for NCA bootstrap, LOQ/2 is imputed for both 0–0.2 mg/L values and negative (<0) concentration values. These are typically used methods to handle BLOQ values, however, for simulated concentration values below zero, these imputations may impact bias, type 1 error rate, and power. This limitation also contributes to the observed inflated type 1 error rate above 0.05 in certain scenarios, besides the limited simulation data sets (500).

In addition, we considered the same magnitude of BSV and WSV for $k_a$, $\mathit{Cl}/F$, and $V/F$. Further, the initial 16 scenarios considered a residual variance at $b=10$% and a WSV at 15%, which are rather low. We explored the impact of increasing both variances at 30% in four additional scenarios and found no impact on MB‐TOST and NCA bootstrap type I error rate and, as expected, a decrease in power although to a remarkable extent for $C_{\max }$ with NCA bootstrap approaches on both parallel and crossover designs.

In conclusion, our simulations show that MB‐TOST demonstrates higher power and controlled type I error rate when compared to NCA‐TOST in single sample PK studies, provided that the underlying PK model is correctly specified, and the test drug has the same PK structural model as the reference drug. As such, MB‐TOST may potentially serve as an alternative approach to evaluate BE for generic ophthalmic drug products.

AUTHOR CONTRIBUTIONS

All authors wrote the manuscript. K.F., W.S., G.S., S.G., L.Z., L.F., F.M., and J.B. designed the research. C.T., F.L., and J.B. performed the research. C.T. analyzed the data.

FUNDING INFORMATION

This work was supported by the U.S. Food and Drug Administration, Silver Spring, MD 20993, USA, under FDA contract 75F40119C10111.

CONFLICT OF INTEREST STATEMENT

M.D., K.F., W.S., G.S., S.G., L.Z., and L.F. are employed by the U.S. Food and Drug Administration. As Editor‐in‐Chief of CPT:Pharmacometrics and Systems Pharmacology, F.M. was not involved in the review or decision process for this paper. The opinions expressed in this manuscript are those of the authors and should not be interpreted as the position of the U.S. Food and Drug Administration. All other authors declared no competing interests for this work.

Supporting information

Appendix S1

Tardivon C, Loingeville F, Donnelly M, et al. Evaluation of model‐based bioequivalence approach for single sample pharmacokinetic studies. CPT Pharmacometrics Syst Pharmacol. 2023;12:904‐915. doi: 10.1002/psp4.12960