Semantic projection recovers rich human knowledge of multiple object features from word embeddings

Abstract

How is knowledge about word meaning represented in the mental lexicon? Current computational models infer word meanings from lexical co-occurrence patterns. They learn to represent words as vectors in a multidimensional space, wherein words that are used in more similar linguistic contexts—that is, are more semantically related—are located closer together. However, whereas inter-word proximity captures only overall relatedness, human judgements are highly context dependent. For example, dolphins and alligators are similar in size but differ in dangerousness. Here, we use a domain-general method to extract context-dependent relationships from word embeddings: ‘semantic projection’ of word-vectors onto lines that represent features such as size (the line connecting the words ‘small’ and ‘big’) or danger (‘safe’ to ‘dangerous’), analogous to ‘mental scales’. This method recovers human judgements across various object categories and properties. Thus, the geometry of word embeddings explicitly represents a wealth of context-dependent world knowledge.

When we say that we know a word, what kind of knowledge do we mean we have? Words allow us to communicate the content of one human mind to another: they are representations of mental structures. More precisely, we use words to express concepts¹. Concepts correspond to our knowledge about regularities in the world—they are generalizations about the kinds of things that exist and the properties that they have. Words, in turn, associate such abstract knowledge with surface forms of sounds/letters/signs, and differences between word meanings correspond to many key distinctions that we can make between things, properties and events in the world^2–5. Consequently, the psycholinguistic study of word meanings in the mental lexicon (lexical semantics; see, for example, refs. ^6–9) is necessarily tightly linked to the cognitive study of the architecture of world knowledge in the human mind (semantic memory^10,11).

However, our world knowledge is broad, detailed and complex. Even an intuitively simple concept such as DOG (here and elsewhere we use all-caps to denote concepts) encompasses rich information about the animal it refers to, including its appearance, biological properties, behavioural tendencies, cultural roles, etc. Only a subset of this conceptual knowledge is communicated by the word ‘dog’, and different subsets may be communicated in different contexts (for a review, see ref. ¹²). Therefore, any theory of lexical semantics should specify the kinds of world knowledge that are captured in the lexicon (for example, ref. ¹³). In other words, such theories should identify which subset of semantic memory can be mapped onto language-specific representations of word meaning. Whereas this question is phrased in terms of correspondence between two memory stores (conceptual knowledge and language knowledge), one may alternatively phrase it in terms of a causal relationship between the two, that is, as a question about learnability: What kinds of world knowledge can—in principle—be implicitly learned from the patterns of language use?

Here, we focus on the kinds of world knowledge that might be embedded in a particular pattern of language use: how often different words co-occur with each other. We focus on word co-occurrences for two reasons. First, humans implicitly track such patterns with exquisite accuracy¹⁴, and start doing so early in development¹⁵, so word co-occurrences constitute a core part of our knowledge about language—that is, it is part of the mental lexicon—and it influences linguistic processing^16–21. Such data are consistent with a hypothesis that dates back to the origins of modern linguistics, namely that word meanings are influenced by their patterns of usage, that is, by the words they tend to appear with (the ‘distributional hypothesis’)^22–27. If co-occurrence patterns are part of the mental lexicon, then any kind of world knowledge that is (implicitly) embedded in such patterns and can be recovered from them is in effect stored in the mental lexicon. Second, word co-occurrences are a very simple form of language knowledge. It does not explicitly include, for example, syntactic relationships between words, or word-internal structure. Focusing on word co-occurrence patterns thus allows us to ask which kinds of conceptual knowledge can, in principle, be derived ‘bottom up’, based on a very simple mechanism of statistical learning over word-forms.

One approach for addressing this question is via computational methods. If a machine is granted access only to word-forms, with no a priori concepts, one can probe the semantic distinctions that are recoverable from the statistics of natural language alone. This approach applies the ‘distributional hypothesis’ to the artificial minds of machines. Specifically, by tracking the distribution of word co-occurrences in multi-billion word corpora, unsupervised algorithms can learn a representation of word meanings as vectors in a multidimensional space, where the proximity between these vectors increases with the co-occurrence probability of the corresponding words (for a related approach, see refs. ^28–30). The resulting space is called a ‘word embedding’ or a ‘distributional semantic model’^31–35.

Recent research has shown that inter-word distances in word embeddings correlate with human ratings of semantic similarity^35–38. Furthermore, these distances are geometrically consistent across different word pairs that share a common semantic relation. For instance, the location of $\overrightarrow{\text{man}}$ relative to $\overrightarrow{\text{woman}}$ is similar to the location of $\overrightarrow{\text{king}}$ relative to $\overrightarrow{\text{queen}}$. This consistency allows for geometric operations to simulate some conceptual relations, for example, $\overrightarrow{\text{king}}-\overrightarrow{\text{man}}+\overrightarrow{\text{woman}}\approx \overrightarrow{\text{queen}}$^39,40 (but see refs. ^41,42). These results demonstrate that, by simply tracking co-occurrence statistics, a machine with no a priori concepts can obtain a lexicon that contains certain kinds of semantic memory (albeit ungrounded in non-linguistic—for example, perceptual, motor and/or emotional—experience).

Despite these impressive capabilities, word embeddings appear to have a fundamental limitation: the proximity between any two word-vectors captures only a single, semantically rigid measure of overall similarity. In contrast, humans evaluate the conceptual similarity between items in semantic memory flexibly, in a context-dependent manner. Consider, for example, our knowledge of DOLPHINS and ALLIGATORS: when we compare the two on a mental scale of size, from small to big, they are relatively similar; in terms of their intelligence—on a scale from stupid to smart—they are somewhat different; and in terms of danger to us—on a scale from safe to dangerous—they differ significantly. Can such distinct relationships be inferred from word co-occurrence statistics? If so, how is such complex knowledge represented in word embeddings?

Here, we suggest that such conceptual knowledge is present in the structure of word embeddings and use a powerful, domain-general solution for extracting it: ‘semantic projection’ of word-vectors onto ‘feature subspaces’ that represent different features (or, more generally, contexts). For instance, to recover the similarities in size amongst nouns in a certain category (for example, animals), we project their representations onto the line that extends from the word-vector $\overrightarrow{\text{small}}$ to the word-vector $\overrightarrow{\text{big}}$ (a ‘semantic differential’^43,44); to compare their levels of intelligence, we project them onto the line connecting $\overrightarrow{\text{stupid}}$ and $\overrightarrow{\text{smart}}$; and to order them according to how dangerous they are, we project them onto the line connecting $\overrightarrow{\text{safe}}$ and $\overrightarrow{\text{dangerous}}$ (for an animation of this procedure, see Supplementary Video 1). We demonstrate that the resulting feature-wise similarities robustly predict human judgements across a wide range of everyday object categories and semantic features. These results corroborate evidence that rich conceptual knowledge can be extracted bottom up from the statistics of natural language, and establish that it is explicitly represented in the geometry of word embeddings, which can be flexibly manipulated in a simple, elegant manner to recover it. Thus, such rich conceptual knowledge must be stored in the mental lexicon.

Results

The rationale of semantic projection.

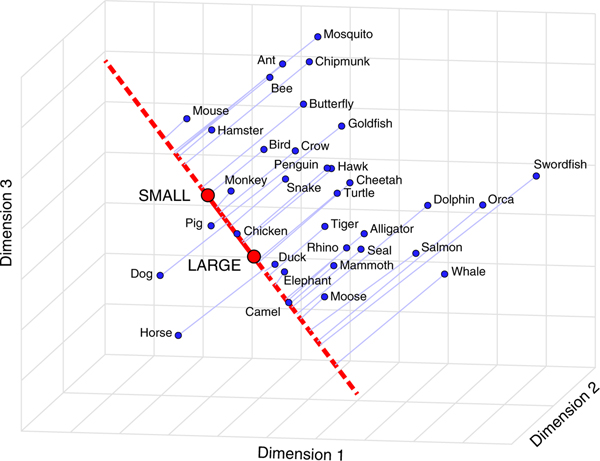
Semantic projection is a domain-general method for comparing word-vectors in the context of a certain semantic feature. A guiding example for applying this method in a simplified, three-dimensional word embedding space (for illustrative purposes) is depicted in Fig. 1 for the category ‘animals’ and the feature ‘size’. Intuitively, to compare animals in terms of this feature, we construct a scale—that is, a straight line in the word embedding space—on which animals could be ordered according to their size (Fig. 1, red line). This scale is constructed via a simple heuristic. We draw a line between antonyms—for example, the word-vector $\overrightarrow{\text{small}}$ and the word-vector $\overrightarrow{\text{large}}$—that denote opposite values of the feature ‘size’^43,44 (Fig. 1, red circles). This heuristic corresponds to taking a vector difference: $\overrightarrow{\text{″size″}}=\overrightarrow{\text{large}}-\overrightarrow{\text{small}}$ (we use double quotation marks to distinguish between our scale, obtained by subtracting two word-vectors, and the vector of the lexical entry $\overrightarrow{\text{size}}$). Then, by projecting word-vectors of different animals onto this scale, we can approximate common knowledge about their relative sizes. For example, to estimate the relative size of a horse, we would compute the inner product $\overrightarrow{\text{horse}}\cdot \overrightarrow{\text{″size″}}$ size (in Fig. 1, this orthogonal projection is represented by the blue line extending from the blue dot of $\overrightarrow{\text{horse}}$ to the red scale of $\overrightarrow{\text{″size″}}$).

Fig. 1 |. Schematic illustration of semantic projection.

Word-vectors in the category ‘animals’ (blue circles) are orthogonally projected (light-blue lines) onto the feature subspace for ‘size’ (red line), defined as the vector difference between $\overrightarrow{\text{large}}$ and $\overrightarrow{\text{small}}$ (red circles). The three dimensions in this figure are arbitrary and were chosen via principal component analysis to enhance visualization (the original GloVe word embedding has 300 dimensions, and projection happens in that space). For an animated version of this figure, see Supplementary Video 1.

The scale thus created is a one-dimensional subspace in which the feature ‘size’ governs similarity patterns between word-vectors such that, for example, $\overrightarrow{\text{horse}}$ and $\overrightarrow{\text{tiger}}$ are located close to each other because they are relatively similar in size (in Fig. 1 these two word-vectors, denoted by blue circles, map onto nearby locations on the red line denoting the scale). Critically, these size-related similarity patterns might be different from the global similarities in the original space where, for example, $\overrightarrow{\text{horse}}$ and $\overrightarrow{\text{tiger}}$ might be farther apart: despite their similarity in size (and other features), horses are perceived to be much less dangerous than tigers, belong to a different taxonomic order, occupy different habitats, etc. (in the schematic illustration of Fig. 1, the blue circle corresponding to $\overrightarrow{\text{horse}}$ is relatively far from that of $\overrightarrow{\text{tiger}}$, which happens to be closer to $\overrightarrow{\text{rhino}}$ and $\overrightarrow{\text{alligator}}$; see also Fig. 2).

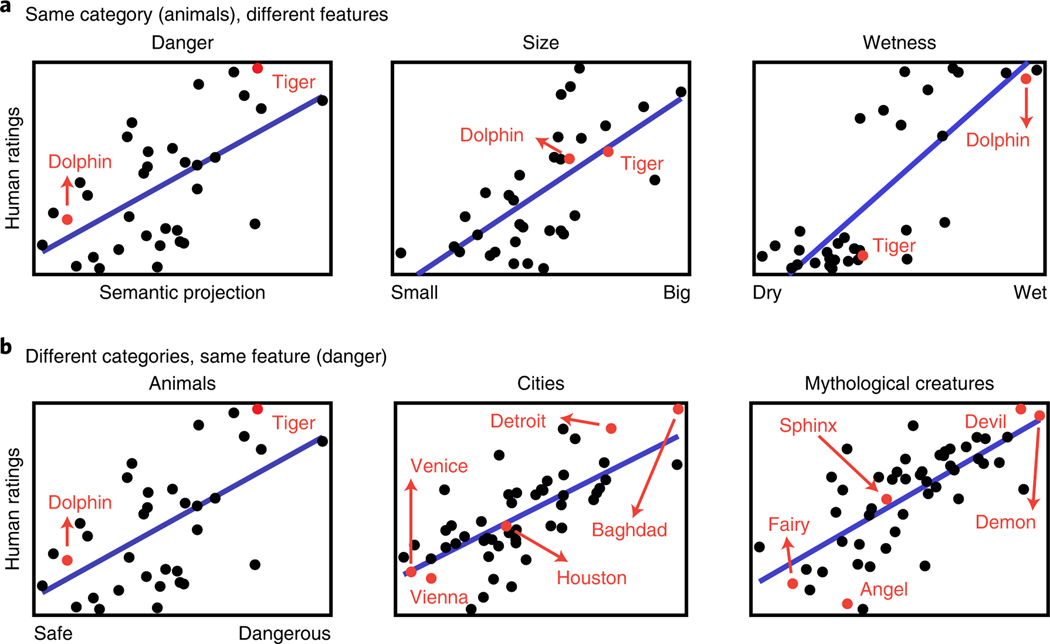
Fig. 2 |. Semantic projection predicts human judgements: sample cases.

a, Examples of three features for the same category (animals). Notice that the items—for instance, dolphin versus tiger—change their similarities to one another depending on context (feature), and semantic projection recovers these cross-feature differences. In other words, the model does not recover the same relationships across features. b, Examples of three categories for the same feature (danger). Sample items are highlighted in red for illustrative purposes. For descriptive and inferential statistics, see Table 1. Each panel is based on data from $n=25$ participants.

Note that ‘size’ is a semantic feature that applies to numerous categories of objects: not only animals, but also mythological creatures, world cities, states of the United States, etc. For each such category, its members could be projected onto the same size scale described above. Hence, semantic projection on a ‘feature subspace’ is a domain-general method. In this study, we limit ourselves to semantic features that can be represented by one-dimensional subspaces (‘scales’). However, other feature subspaces for other semantic features could be of higher dimensionality (Discussion).

Predicting human ratings using semantic projection.

We tested whether semantic projection could recover context-dependent conceptual knowledge. To operationalize context-dependent knowledge, we tested how objects from a given semantic category were rated based on a particular semantic feature. Overall, we ran 52 experiments, each testing a different category–feature pair. Pairs were distributed over nine object categories: animals, clothing, professions, weather phenomena, sports, mythological creatures, world cities, states of the United States and first names (most categories consisted of 50 items). Each category was matched with a subset of the following 17 semantic features: age, arousal, cost, danger, gender (here, limited to a man–woman continuum), intelligence, location (indoors versus outdoors), partisanship (liberal versus conservative), religiosity, size, speed, temperature, valence, (auditory) volume, wealth, weight and wetness. The matching of particular categories to particular features (to create the 52 tested pairs) relied on a combination of an online behavioural norming study and intuitive judgements by the authors (Methods).

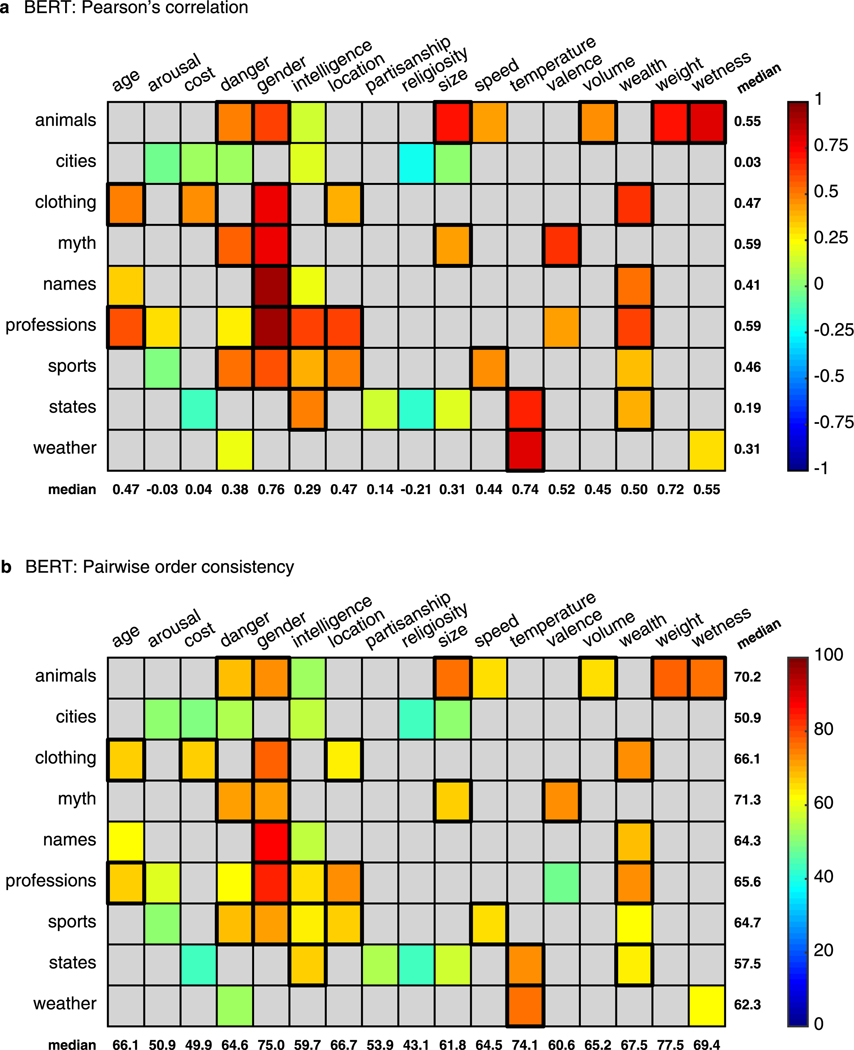
To implement semantic projection, we chose GloVe as the word embedding³⁷ (for results obtained with other models—FastText, word2vec, ELMo and BERT—see Supplementary Results and Extended Data Figs. 1–9). For each test case, we used linear projection to order category items along a line in GloVe that represented a particular semantic feature. This line (that is, one-dimensional ‘feature subspace’) was computed from vector differences between several antonym pairs that represent opposite ends of the feature continuum. For instance, the continuum for the size feature was anchored by the antonyms $\{\overrightarrow{\text{large}},\overrightarrow{\text{big}},\overrightarrow{\text{huge}}\}$ and $\{\overrightarrow{\text{small}},\overrightarrow{\text{little}},\overrightarrow{\text{tiny}}\}$; the subspace $\overrightarrow{\text{″size″}}$ was the average of $3\times 3=9$ pairwise lines between these antonyms. Onto this subspace, we projected the word-vectors of all category items.

Then, we quantified whether the result corresponded to behavioural ratings collected online from human participants ($n=25$ per experiment, for a total of 1,400 participants). Figure 2 shows scatterplots of human ratings against model predictions for some illustrative cases. Figures 3 and 4 and Table 1, show the results for each category–feature pair. The correspondence between semantic projection and human data was evaluated using two measures: (1) Pearson’s moment correlation and (2) ‘pairwise order consistency’$\left({\text{OC}}_{\text{p}}\right)$, that is, the percentage of item pairs $(i,j)$, out of all possible pairings, whose ordering was consistent between humans and semantic projection (for example, for the feature ‘size’, both rated $i$ as ‘bigger’ than $j$). The former is a strict measure of linear relationship, but potentially biased by outliers. The latter is a more lenient measure of correlation, but is more robust to outliers.

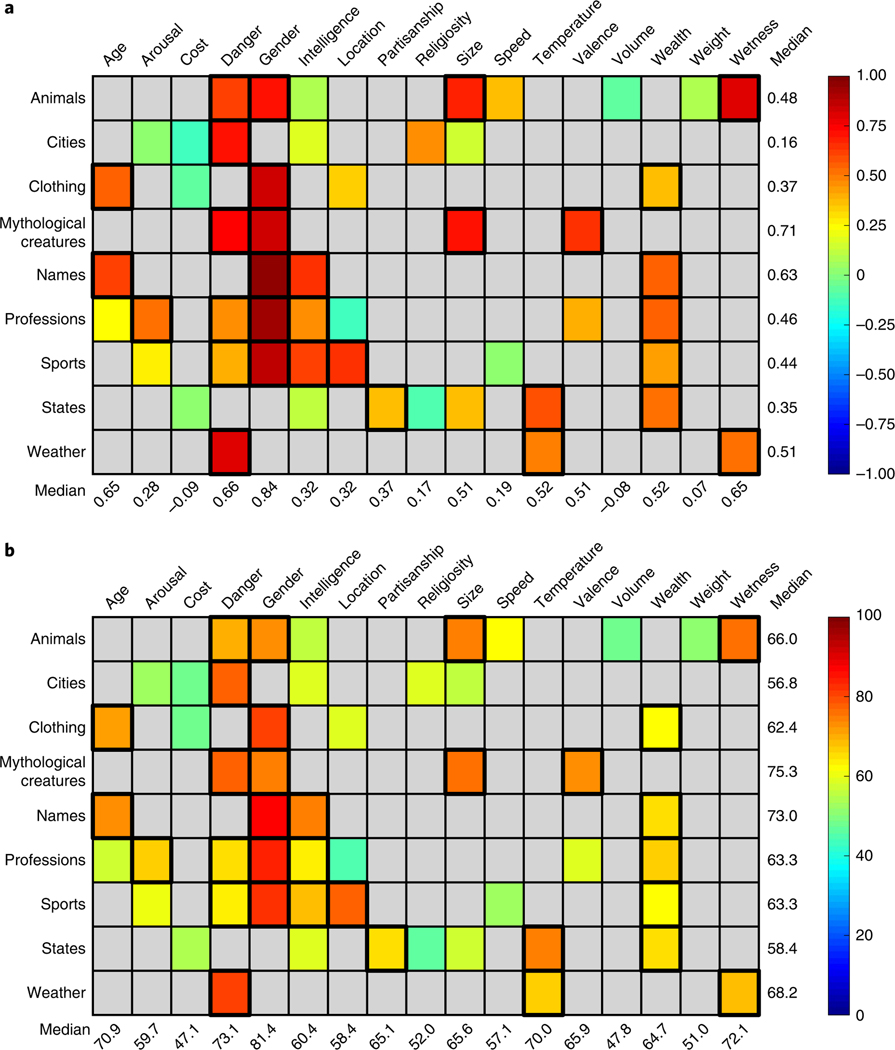
Fig. 3 |. Semantic projection predicts human judgements across diverse categories and features.

In each panel, each entry in the matrix has a colour corresponding to the strength of fit between semantic projection and human judgements for a given pairing of category (row) and feature (column). Statistically significant fits are surrounded with a thicker contour. For each category–feature pair, ratings were collected from $n=25$ participants; pairs that were not tested in our experiments are coloured in grey. a,b, Evaluation measures: Pearson’s correlation (a, median across experiments: 0.47, 95% CI 0.38–0.55) and pairwise order consistency (b, ${\text{OC}}_{\text{p}}$; median across experiments: 65%, 95% CI 62–68%). In each panel, median values per category are shown on the right whilst median values per feature are shown at the bottom. Evaluation measures are not adjusted for split-half reliability of behavioural ratings.

Fig. 4 |. Semantic projection predicts human judgements: detailed results.

For each of 52 category–feature pairs, scatterplots show the relationship between z scores of average item ratings across participants ($n=25$; y axis) and ratings predicted by semantic projection (x axis). Correlation and pairwise order consistency (${\text{OC}}_{\text{p}}$) values are presented below each scatterplot. Experiments for which both of these measures were significant are shown over a white background. Straight lines are linear regression fits to the data and, across figures, vary according to correlation strength from black (weak) to blue (strong).

Table 1 |.

Semantic projection predicts human judgements: detailed results^*

Category	Feature	Pearson’s r				${\text{OC}}_{\text{p}}$
		r	z	P (FDR)	95% CI	${\text{OC}}_{\text{p}}$	z	P (FDR)	95% CI
Clothing	Age	0.56	4.34	<0.001	0.35 to 0.74	0.71	4.28	<0.001	0.61 to 0.76
Names	Age	0.62	4.95	<0.001	0.44 to 0.76	0.72	4.59	<0.001	0.63 to 0.77
Professions	Age	0.24	1.65	0.33	−0.08 to 0.51	0.57	1.38	0.52	0.45 to 0.65
Cities	Arousal	0	−0.002	1	−0.26 to 0.29	0.52	0.46	1	0.41 to 0.61
Professions	Arousal	0.52	3.92	<0.001	0.32 to 0.69	0.66	3.20	0.008	0.56 to 0.72
Sports	Arousal	0.28	2.00	0.15	−0.01 to 0.55	0.60	2.02	0.16	0.48 to 0.69
Cities	Cost	−0.16	−1.07	1	−0.46 to 0.17	0.47	−0.61	1	0.36 to 0.57
Clothing	Cost	−0.09	−0.61	1	−0.32 to 0.17	0.47	−0.60	1	0.37 to 0.55
States	Cost	0.02	0.12	1	−0.20 to 0.27	0.54	0.91	1	0.44 to 0.62
Animals	Danger	0.60	3.89	<0.001	0.35 to 0.76	0.70	3.30	0.006	0.57 to 0.76
Cities	Danger	0.71	6.12	<0.001	0.57 to 0.82	0.77	5.45	<0.001	0.68 to 0.81
Mythological creatures	Danger	0.72	6.30	<0.001	0.58 to 0.84	0.78	5.78	<0.001	0.69 to 0.83
Professions	Danger	0.45	3.23	0.005	0.17 to 0.67	0.64	2.83	0.02	0.53 to 0.72
Sports	Danger	0.38	2.70	0.028	0.18 to 0.55	0.63	2.68	0.03	0.54 to 0.69
Weather	Danger	0.79	6.28	<0.001	0.67 to 0.88	0.80	5.19	<0.001	0.70 to 0.83
Animals	Gender	0.70	4.83	<0.001	0.45 to 0.85	0.73	3.83	<0.001	0.60 to 0.80
Clothing	Gender	0.81	7.83	<0.001	0.73 to 0.88	0.81	6.34	<0.001	0.74 to 0.84
Mythological creatures	Gender	0.82	7.78	<0.001	0.68 to 0.89	0.74	4.93	<0.001	0.65 to 0.79
Names	Gender	0.94	11.87	<0.001	0.90 to 0.97	0.87	7.62	<0.001	0.81 to 0.89
Professions	Gender	0.92	10.64	<0.001	0.87 to 0.95	0.84	6.90	<0.001	0.76 to 0.87
Sports	Gender	0.85	8.67	<0.001	0.76 to 0.92	0.82	6.50	<0.001	0.73 to 0.86
Animals	Intelligence	0.08	0.44	1	−0.26 to 0.42	0.55	0.77	1	0.40 to 0.66
Cities	Intelligence	0.18	1.24	0.674	−0.14 to 0.51	0.58	1.60	0.36	0.45 to 0.67
Names	Intelligence	0.65	5.32	<0.001	0.48 to 0.79	0.74	4.86	<0.001	0.65 to 0.79
Professions	Intelligence	0.47	3.45	0.003	0.21 to 0.67	0.62	2.54	0.045	0.53 to 0.69
Sports	Intelligence	0.61	4.92	<0.001	0.42 to 0.75	0.69	3.86	<0.001	0.58 to 0.75
States	Intelligence	0.11	0.75	1	−0.15 to 0.37	0.58	1.71	0.31	0.48 to 0.67
Clothing	Location	0.32	2.27	0.084	0.01 to 0.57	0.58	1.70	0.30	0.46 to 0.68
Professions	Location	−0.13	−0.86	1	−0.37 to 0.11	0.45	−1.04	1	0.35 to 0.53
Sports	Location	0.65	5.27	<0.001	0.52 to 0.76	0.77	5.50	<0.001	0.68 to 0.82
Animals	Loudness	−0.08	−0.45	1	−0.43 to 0.28	0.48	−0.37	1	0.34 to 0.59
States	Political	0.37	2.67	0.029	0.10 to 0.62	0.65	3.09	0.010	0.54 to 0.73
Cities	Religiosity	0.46	3.43	0.003	0.06 to 0.70	0.58	1.74	0.300	0.46 to 0.68
States	Religiosity	−0.11	−0.76	1	−0.35 to 0.15	0.45	−0.93	1	0.35 to 0.55
Animals	Size	0.67	4.48	<0.001	0.51 to 0.80	0.74	3.94	<0.001	0.63 to 0.78
Cities	Size	0.14	0.99	0.99	−0.10 to 0.37	0.56	1.19	0.708	0.45 to 0.64
Mythological creatures	Size	0.70	5.94	<0.001	0.54 to 0.82	0.76	5.33	<0.001	0.67 to 0.81
States	Size	0.35	2.43	0.055	0.05 to 0.57	0.58	1.53	0.41	0.46 to 0.66
Animals	Speed	0.36	2.10	0.124	0.12 to 0.58	0.62	2.06	0.14	0.50 to 0.70
Sports	Speed	0.03	0.20	1	−0.29 to 0.35	0.52	0.38	1	0.41 to 0.61
States	Temperature	0.57	4.42	<0.001	0.32 to 0.79	0.74	4.88	<0.001	0.63 to 0.81
Weather	Temperature	0.47	2.96	0.013	0.18 to 0.68	0.66	2.79	0.024	0.53 to 0.74
Mythological creatures	Valence	0.64	5.20	<0.001	0.50 to 0.77	0.73	4.73	<0.001	0.65 to 0.78
Professions	Valence	0.38	2.72	0.027	0.12 to 0.58	0.59	1.73	0.298	0.48 to 0.66
Clothing	Wealth	0.37	2.68	0.029	0.04 to 0.65	0.62	2.57	0.044	0.51 to 0.71
Names	Wealth	0.53	4.07	<0.001	0.29 to 0.70	0.65	3.19	0.008	0.55 to 0.72
Professions	Wealth	0.53	4.00	<0.001	0.32 to 0.70	0.67	3.37	0.005	0.56 to 0.74
Sports	Wealth	0.43	3.25	0.005	0.14 to 0.64	0.62	2.54	0.046	0.51 to 0.70
States	Wealth	0.52	3.91	<0.001	0.30 to 0.67	0.65	2.98	0.014	0.54 to 0.72
Animals	Weight	0.07	0.37	1	−0.32 to 0.42	0.51	0.17	1	0.37 to 0.63
Animals	Wetness	0.79	6.01	<0.001	0.66 to 0.89	0.76	4.34	<0.001	0.65 to 0.81
Weather	Wetness	0.51	3.27	0.005	0.22 to 0.73	0.68	3.17	0.008	0.56 to 0.76
‘

^*Pearson’s correlations are ‘raw’ values (not Fisher transformed); z scores are computed relative to the mean and s.d. of an empirical null distribution (based on 10,000 permutations), estimated with a Gaussian fit (one-tailed test); P values across the 52 experiments are corrected for multiple comparisons using FDR; Confidence intervals are empirically estimated based on 10,000 bootstrap re-samples of the data.

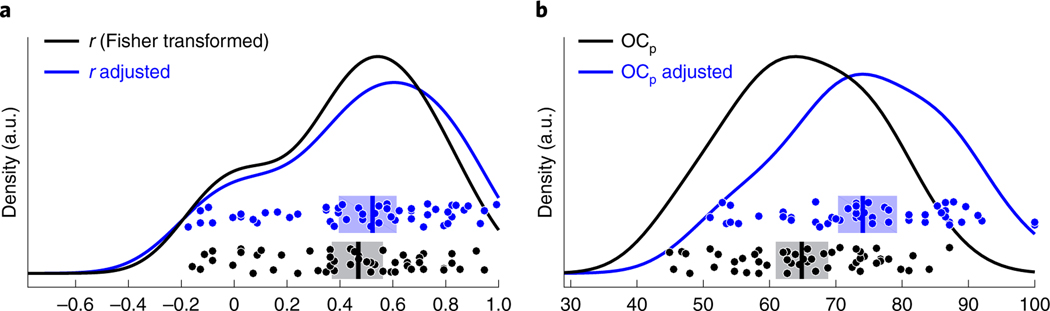
Overall, semantic projection successfully recovered human semantic knowledge. Moderate to strong correlations in ratings ($r>0.5$) were observed for nearly half of the pairs (25/52), and across all experiments, the median correlation was 0.47 (95% CI 0.38–0.55, IQR 0.21–0.65). Similarly, across all experiments, the median ${\text{OC}}_{\text{p}}$ was 65% (95% CI 62–68%, IQR 58–74%). We also adjusted these statistics based on split-half reliability of the behavioural ratings, which is an estimate of the noise ceiling, or ‘upper bound’, for our measurements (median split-half reliability across experiments: $r=0.94$, ${\text{OC}}_{\text{p}}=88\text{\%}$; Methods). The ‘adjusted median correlation’ was 0.52 (that is, the variability in human ratings captured by semantic projection was 27% of the upper bound, $\sqrt{0.27}=0.52$) (95% CI 0.41–0.60, IQR 0.23–0.74); the ‘adjusted median ${\text{OC}}_{\text{p}}$ ’ increased to 74% (that is, the pairwise order consistency in human ratings captured by semantic projection was 74% of the upper bound) (95% CI 72–78%, IQR 67–86%). In about half of the experiments (32/52), both the correlation and ${\text{OC}}_{\text{p}}$ measures were significant, as evaluated by permutation tests and corrected for multiple comparisons (Methods). Figure 5 summarizes the distribution of the evaluation measures across all experiments, both before and after normalizing these measures relative to split-half reliability. However, the fit between semantic projection and human ratings varied a lot across experiments, with the best fit observed for ratings of names by gender ($r=0.94$, ${\text{OC}}_{\text{p}}=87\text{\%}$) and the worst fits observed for ratings of cities by cost ($r=-0.15$, ${\text{OC}}_{\text{p}}=47\text{\%}$) and professions by location ($r=-0.12$, ${\text{OC}}_{\text{p}}=45\text{\%}$). We note that, across the 52 experiments, our evaluation measures did not correlate strongly with their corresponding split-half reliability measures (that is, upper bounds), so the cases where semantic projection fails to recover human knowledge are not simply those cases where humans disagree with one another in their judgements. Specifically, whereas the correlation between (Fisher-transformed) r and the split-half reliability of behavioural ratings across these experiments was 0.39 ($t_{(50)}=2.96$, $P=0.002$, based on 10,000 random permutations of experiment labels; 95% CI 0.09–0.61, based on 10,000 bootstrap samples), the correlation between ${\text{OC}}_{\text{p}}$ and the split-half reliability of behavioural ratings was 0.17 ($t_{(50)}=1.19$, $P=0.12$, 95% CI −0.06 to 0.40). We further consider this across-experiment variability in the Discussion.

Fig. 5 |. Distribution of evaluation scores for semantic projection.

a, Pearson’s correlation. b, Pairwise order consistency. Histograms across 52 category–feature pairs for linear correlations (left) and pairwise order consistency (${\text{OC}}_{\text{p}}$; right) between semantic projection ratings and human judgements ($n=25$ participants per category–feature pair), before (black) and after (blue) adjustment for inter-rater reliability in ratings. Points show category–feature pairs, vertical lines show medians and semi-transparent rectangles show 95% confidence intervals. Curves show approximated data distributions, with density (in arbitrary units) on the y axis.

Both ends of a scale contribute to semantic projection.

In defining a feature subspace (for example, $\overrightarrow{\text{″size″}}$^′) for semantic projection, we relied on antonymous adjectives (for example, $\overrightarrow{\text{small}}$ and $\overrightarrow{\text{big}}$) that can be intuitively thought of as defining opposite ends of a scale. The arithmetic difference between the antonymous word-vectors situates this scale within the word embedding space; that is, it defines a ‘diagnostic’ direction in the space along which concrete objects show high variation with regard to the feature in question. However, this subtraction might not be necessary if the diagnostic information were already sufficiently represented by each adjective vector on its own. In other words, the word-vector $\overrightarrow{\text{big}}$ might already define a size-related diagnostic direction in the space, such that subtracting $\overrightarrow{\text{small}}$ from it is redundant (this would be possible if, for example, these antonyms lay on opposite sides of the origin in the space). To test whether one end of a feature scale may be sufficient for predicting human knowledge, we repeated all experiments but this time compared behavioural ratings with semantic projection on either end of a feature scale (for example, for ‘size’, projection was performed once on the average of $\{\overrightarrow{\text{large}},\overrightarrow{\text{big}},\overrightarrow{\text{huge}}\}$ and, separately, on the average of $\{\overrightarrow{\text{small}},\overrightarrow{\text{little}},\overrightarrow{\text{tiny}}\}$).

Across the 52 experiments, projections on a single end had a median correlation of $r=0.06$ with human ratings. This projection scheme performed worse than our original semantic projection even when, for each category–feature pair, we chose from amongst the two ends of a feature scale the one that resulted in a better fit to human judgements ($t_{(51)}=4.04$, $P<0.001$, $d=0.74$, 95% CI 0.20–0.45, one-tailed test). Similar patterns emerged for the other evaluation score, namely pairwise order consistency. Across experiments, the alternative projection scheme had a median value of ${\text{OC}}_{\text{p}}=53\text{\%}$, worse than our original semantic projection ($t_{(51)}=4.04$, $P<0.001$, $d=0.57$, 95% CI 0.04–0.11). Performance was even worse when, instead of using projection, we computed the distance between each item in a category and either end of the feature scale, using either cosine or Euclidean distance. Therefore, the difference between the vectors of antonymous adjectives—rather than either vector in isolation—provides feature-specific ‘diagnostic’ dimensions in the word embedding space (see also ref. ⁴⁵).

Semantic projection is successful even without outlier items.

Might the correlation between human ratings and semantic projection have resulted from a few outliers that were rated as having extreme feature values by both humans and our method? For instance, when rating animals by size, semantic projection might be able to predict that whales are very big whilst mice are very small based on word co-occurrence statistics: the words ‘big’, ‘large’ or ‘huge’ (which define one end of the size subspace) might co-occur with some frequency around ‘whale’, whereas the words ‘small’, ‘little’ or ‘tiny’ (which define the other end of the size subspace) might co-occur with some frequency around ‘mouse’. Such extreme items could cause a strong fit between semantic projection and human ratings even if, for most animals with less extreme values, semantic projection cannot recover human knowledge. However, we do not believe this to be the case, because semantic projection showed high pairwise order consistency with human ratings, and this measure is not strongly biased by outliers.

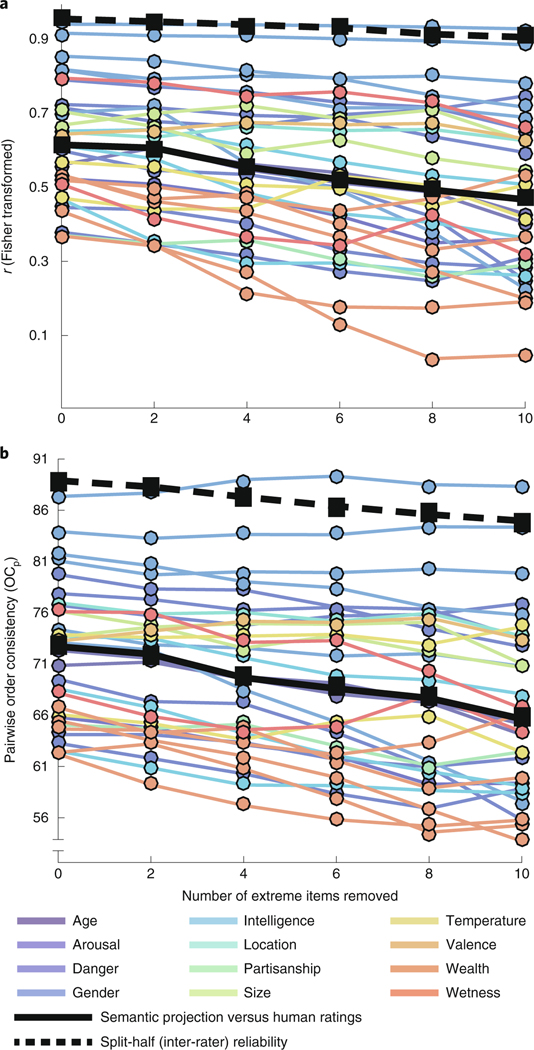
Nevertheless, to address this concern more directly, we repeated our analyses for each of the 32 significant experiments after removing the two items that received the most extreme (highest and lowest) average ratings. Then, we removed the next two most extreme items, repeated the analyses, and continued this process until 10 items (that is, 20% of the 50-item categories) had been removed. The results of this analysis are presented in Fig. 6. As extreme items were gradually removed from the dataset, both evaluation measures decreased somewhat. Across experiments, the median initial correlation of 0.61 decreased to 0.47 after removing the ten most extreme items. Similarly, the median initial ${\text{OC}}_{\text{p}}$ of 73% decreased to 66%. However, removing extreme items also resulted in less reliable human ratings (reflecting relatively higher noise or uncertainty for less extreme items). Across experiments, the median split-half reliability across behavioural ratings decreased from $r=0.95$ to $r=0.90$, and from ${\text{OC}}_{\text{p}}=89\text{\%}$ to ${\text{OC}}_{\text{p}}=85\text{\%}$.

Fig. 6 |. The fit of semantic projection to human ratings is not driven by outliers.

a,b, r (a, Fisher transformed) and ${\text{OC}}_{\text{p}}$ values (b) plotted as functions of the number of items with the most extreme human ratings that were removed from the data (note that, for b, the y axis is ‘broken’). Data from each of 32 category–feature pairs (those with significant results in our main experiment) are shown, with colour varying by feature. Continuous black lines show the average across the 32 pairs. Dotted black lines show the upper bound (split-half reliability across participants) averaged across these pairs. Notice that the continuous and black lines are mostly parallel: as extreme items are removed, the ability of semantic projection to recover human knowledge decreases, but the reliability of human knowledge itself similarly decreases. When predicting the decrease in these measures, the interaction between the number of removed items and the type of measure (critical measure versus its upper bound) is not significant (modelling r and its split-half reliability: ${\chi }_{(1)}^2=2.14$, $P=0.14$, $b=-0.02$, 95% CI −0.04 to 0.005; modelling ${\text{OC}}_{\text{p}}$ and its split-half reliability: ${\chi }_{(1)}^2=0.001$, $P=0.97$, $b<-{10}^{-4}$, 95% CI −0.004 to 0.003). Human data for each category/feature pair are based on $n=25$ participants.

To test whether our evaluation measures were more severely affected by the removal of extreme items, compared with the inter-participant reliability measures, we carried out a mixed-effects linear regression (using the R package lme4 (ref. ⁴⁶)) to predict the values of both measures based on: (1) the number of removed items, (2) the type of measure (raw versus upper bound/reliability) and (3) the interaction between (1) and (2). Random intercepts, and random slopes for (1), were included by category and by feature. For both evaluation measures, the interaction term did not significantly improve the model (modelling r and its split-half reliability: ${\chi }_{(1)}^2=2.14$, $P=0.14$, $b=-0.02$, 95% CI −0.04 to 0.005; modelling ${\text{OC}}_{\text{p}}$ and its split-half reliability: ${\chi }_{(1)}^2=0.001$, $P=0.97$, $b<-{10}^{-4}$, 95% CI −0.004 to 0.003). In other words, the decrease in the evaluation measures was statistically indistinguishable from the decrease in the corresponding split-half reliability across participants. We therefore do not find evidence that extreme feature values bias the success of semantic projection beyond the extent to which they increase certainty, or reduce noise, in semantic knowledge itself (as reflected by increased reliability of human judgements).

Discussion

We find that semantic projection of concrete and/or imageable nouns onto feature subspaces (that is, ‘semantic differentials’^43,44) can approximate human ratings of the corresponding entities along multiple, distinct feature continua. The method we use is simple yet robust and broadly applicable, successfully predicting human judgements across a range of everyday object categories and semantic features. These results demonstrate that semantic knowledge about context-dependent similarities is explicitly represented in the structure of word embeddings. Thus, extremely detailed conceptual knowledge can be constructed bottom up by merely tracking word co-occurrence statistics, and it can be expressed in a simple representational system (cf. deep neural networks where context sensitivity is engineered into the system via, for example, recurrence⁴⁷ or attention^48,49 mechanisms). These findings are consistent with previous reports demonstrating the richness of knowledge in word embeddings^50,51, including knowledge of social biases^52–55, and expert knowledge in specialized domains including, perhaps, yet-to-be-made scientific discoveries⁵⁶.

We go beyond these prior studies in three key respects. First, we cover a wide range of conceptual categories and their properties, including abstract and/or infrequently named properties. Second, where previous studies have relied on supervised learning algorithms, which are trained directly on human data to learn a mapping of word-vectors onto specific features^40,57–61, semantic projection is nearly unsupervised. It only requires that the task be specified in terms of antonyms (or, more broadly, ‘context-defining’ anchors), but can then generate predictions without any access to human data (except, of course, to evaluate its outputs). In this sense, our model does not require any training. The choice of antonyms amounts to the same level of supervision that is introduced in any evaluation that probes the quality of fixed word embeddings by choosing particular words and simply evaluating the similarity between their respective representations. Third, whereas supervised learning algorithms can learn any linear combination of the dimensions in a word embedding in order to optimize their prediction of human data, semantic projection guarantees a solution that is interpretable. It a priori defines a line that is intuitively analogous to a ‘scale’. With semantic projection, a single, general-purpose word embedding (unbiased towards any particular domain; cf. ref. ⁶²) can be re-structured to emphasize different properties. Therefore, its semantic knowledge is not only detailed, but can also be flexibly used. This is a hallmark of the human cognitive architecture, because language use is never ‘context-less’. Any reasonable model of the mental lexicon should employ context-sensitive representations.

The nature of semantic knowledge representations has been long debated, and continues to be central to the study of the human mind in cognitive science, neuroscience and philosophy (for reviews, see refs. ^4,63–66). In particular, knowledge about the relationships between object categories and the features characterizing them has been traditionally discussed in the context of symbolic representations such as feature lists^67,68, structured schemata⁶⁹ or highly elaborate intuitive theories^70,71 (for an early example of modelling context-dependent similarities, see ref. ⁷²). Prior studies that have attempted to extract such knowledge from natural corpora have had to augment the tracking of word co-occurrences with more elaborate information such as dependency parses or supervised identification of particular linguistic patterns^73–78. Our results instead suggest that the distributional, sub-symbolic representational format of word embeddings can support the flexible re-structuring of object categories to highlight specific features. Moreover, given that these spaces are hypothesized to approximate lexical semantics, the current study suggests that complex feature-specific knowledge is part of a word’s meaning.

We emphasize that the lexical knowledge in word embeddings is detached from, rather than grounded in, non-linguistic (for example, perceptual, motor or emotional) experience. Therefore, even though the geometry of word embeddings captures human knowledge that, for example, an ‘elephant’ is ‘bigger’ than a ‘mouse’ (a perceptual piece of knowledge), this model does not have access to the perceptual correlates of the words ‘elephant’, ‘big’ or ‘mouse’. In fact, it only knows the meaning of these words in terms of their relatedness to other words (that is, their intra-linguistic meaning). Nonetheless, our findings provide a proof of principle that world knowledge can be independently acquired from statistical regularities in natural language itself⁷⁹.

Therefore, the current study is consistent with the intriguing hypothesis that, like word embedding spaces, humans can use language as a gateway to acquiring conceptual knowledge^50,80–84. Indeed, humans are sensitive to patterns of word co-occurrence, and use them during language processing^14–21 (for tracking of relationships between words and linguistic contexts more generally, see refs. ^85–92). In addition, evidence from congenitally blind individuals suggests that such patterns may indeed be sufficient for acquiring some forms of perceptual knowledge, for example, similarities amongst colours or actions involving motion, and subtle distinctions between sight-verbs such as ‘look’, ‘see’ and ‘glance’^93–98. Thus, in the absence of direct (for example, perceptual) experience, language itself can serve as a source of semantic knowledge. Yet even without conjecturing about learnability, that is, a causal relationship from word co-occurrence patterns to world knowledge, our work supports a more general hypothesis: given that word co-occurrence patterns are stored in the mental lexicon (that is, constitute part of our knowledge about language) and that they contain the kinds of conceptual knowledge studied here, we conclude that the human mental lexicon contains a subset of semantic memory that is more rich, detailed and complex than has traditionally been assumed.

What kinds of category–feature relations could be acquired in this manner? Past research has suggested that word embedding spaces (prior to any semantic projection) capture gross knowledge about the sensory modalities associated with different objects⁹⁹, but they fare relatively poorly in approximating detailed perceptual properties in comparison with abstract (for example, encyclopaedic or functional) knowledge^76,100–103. The current results suggest a more nuanced view (Fig. 4). First, knowledge about some perceptual features (for example, size) was successfully predicted for some categories (animals, mythological creatures; see also ref. ⁶⁰). Second, whereas some abstract features (for example, gender and danger) could be recovered via semantic projection across all the categories with which they were paired, other abstract features (for example, intelligence) were only recovered for some categories but not others.

In addition, by re-structuring word embeddings, semantic projection may be able to resolve current debates concerning the particular object properties that are learnable via word co-occurrences (for example, refs. ^104–108). It is possible that some aspects of semantic knowledge may be captured to different degrees in the embedding space, depending on a variety of factors. For instance, sensory modalities may differ from one another in how consistently they are linguistically coded across speakers, and such differences across modalities also vary across languages¹⁰⁹. The more variable the words for a certain concept are, the fewer contexts of usage are available for each of those words in a corpus, potentially leading to both noisier vector representations for those words and a more diffuse influence of those words as contexts for learning other vectors. As a result, domains of knowledge whose linguistic coding is less consistent across speakers may be less learnable from word embeddings. This is a promising direction of research, in that such effects can be quantified and tested. Furthermore, even if concepts relevant to a given modality are consistently coded across individuals, it might be the case that this modality is not referred to in written language with the same frequency as spoken or signed language, or at all. If so, it would have less influence in structuring the embedding space or not be learnable at all. More generally, the factors underlying the variability in the performance of semantic projection across different feature–category pairs (and across different entities within a category) would be a fruitful area of future investigation.

Notwithstanding its variability in performance, we emphasize that semantic projection exhibits promising generalizability across both categories and features. Our categories span animate and inanimate categories (for example, animals versus clothing), natural and human-made categories (for example, weather versus clothing) and common and proper nouns (for example, professions versus cities). Future work may further test how well this method can recover knowledge about entities that are abstract rather than concrete, as well as about concepts that correspond to parts of speech other than nouns (for example, projecting verbs on subspaces defined by adverb antonym pairs). Similarly, our method generalizes across different ‘kinds’ of features: from those that are judged to be relatively binary (for example, the wetness of animals) to those that vary more continuously between two extremes (for example, the gender associated with articles of clothing). It may further extend to other kinds of features such as those with multiple, discrete values (for example, ‘colour’ or ‘number of legs’) and, more generally, to complex types of context-dependent knowledge represented in semantic subspaces with more than one dimension.

These prospects for generalizability raise deeper questions about semantic knowledge representation in word embeddings: Which sets of word-vectors constitute psychologically plausible categories?⁴ Which semantic subspaces represent features (or, more generally, contexts^110,111)? Which categories can be meaningfully described with which features?^112,113 And what geometric operations besides linear projection could capture different kinds of human knowledge? Addressing these questions could help characterize the structure of word embedding spaces and, critically, inform general theories of categories and features that are fundamental to the study of concepts. Specifically, if word embeddings are found to represent information that approximates human patterns of category formation, feature elicitation and context-dependent semantic judgements, then their structure could perhaps provide a principled way for deriving an ontology of concepts.

In conclusion, semantic projection in word embeddings is a powerful method for estimating human knowledge about the structure of categories under distinct contexts. Within the distributional semantics literature, this method continues the tradition of applying simple linear algebraic operations to perform useful semantic comparisons in word embeddings (for example, vector subtraction, cosine similarities and matrix multiplication^114,115). Moreover, compared with prior attempts at extracting semantic knowledge from patterns of natural language use, this method requires significantly less human supervision and/or corpus annotation. Most importantly, it obviates the need to define a priori a constrained ontology of semantic features that would span the vector space. Given an existing word embedding, which was not constructed based on any such ontology, semantic projection can flexibly recover a variety of semantic features. Therefore, we believe that we have only scratched the surface of the total volume of knowledge captured by word embeddings. We hope that semantic projection will provide a useful, generalizable framework for deeper exploration of such models.

Methods

All experimental procedures were approved by Massachusetts Institute of Technology’s Committee on the Use of Humans as Experimental Subjects. Informed consent was obtained from all participants, as required by the committee.

Materials.

We created a set of categories and features that met five criteria: (1) each category consisted of concrete and/or imageable objects/entities and had at least 30 members (most had 50); (2) each category could be characterized with respect to several features (to evaluate whether semantic projection generalized across features for a given category); (3) each feature was applicable to several categories (to evaluate whether semantic projection generalized across categories for a given feature); (4) each feature was one-dimensional; (5) categories and features spanned diverse aspects of everyday semantic knowledge. All categories and their constituent items were selected from an extensive set of nouns, generated for a large-scale study on lexical memory¹¹⁶.

Concept categories.

Our materials included nine semantic categories: animals, clothing, professions, weather phenomena, sports, mythological creatures, world cities, states of the United States and first names. These categories have been used in feature elicitation studies, with varying degrees of prevalence^{111,117–121}. The first four have been used frequently, and the next two less. The last three have been used rarely and, unlike the other categories, consisted of proper nouns. Items in all categories were used as cues in a mega-study of lexical knowledge using word associations¹²² (http://w3.usf.edu/FreeAssociation/).

Most categories consisted of 50 representative items (for example, the clothing category included words such as ‘hat’, ‘tuxedo’, ‘sandals’ and ‘skirt’; see Supplementary Methods for the full set of materials). The only exceptions were the categories of animals (34 items), weather phenomena (37 items) and professions (49 items). To ensure that items were representative of their respective category, we chose from a superset of nouns within each category (from ref. ¹¹⁶) the 50 most frequent nouns according to the SubtlexUS Word Frequency Database¹²³. We discarded multi-word expressions (except for states of the United States, for example, ‘North Dakota’) and words that did not appear in the vocabulary of the word embedding (see below).

For two categories, additional selection criteria were used to increase the variability for the ‘gender’ feature: for the first names category, we chose the 20 most common male names, the 20 most common female names and the 10 most common unisex names from the past 100 years, based on public data from the US Social Security Administration (www.ssa.gov/oact/babynames/decades/century.html; github.com/fivethirtyeight/data/tree/master/unisex-names). For the ‘professions’ category, efforts were made to balance the items by stereotypical gender, because the majority of the most frequently occurring profession nouns were traditionally male.

Semantic features.

Our materials included 17 semantic features, each associated with a subset of the categories above: size, temperature, valence, (auditory) volume, speed, location (indoors versus outdoors), intelligence, wetness, weight, wealth, gender (here, limited to a man–woman continuum), danger, age, religiosity, partisanship (liberal versus conservative), cost and arousal. These features have been produced in feature elicitation studies, with varying degrees of prevalence^111,119,120: the first four almost invariably, the next three frequently, the next six less frequently and the last four very rarely.

Choosing appropriate features for each concept category.

For each category in our set of materials, only some features provided meaningful contexts for rating category members. For instance, sports could be rated by ‘danger’ but not by ‘size’, and names could be rated by ‘gender’ but not by ‘temperature’. To select category–feature pairings to be used in the experiment, we relied on a combination of our own intuitive judgements and ratings obtained in a norming study. In particular, out of the set of 9 × 17 = 153 possible category–feature pairings, we first selected a subset of 45 pairs that appeared intuitively appropriate. In parallel, we asked participants (n = 50) on Amazon Mechanical Turk¹²⁴ (MTurk, www.mturk.com) to rate how likely they were to describe each category (for example, animals) in terms of each feature (for example, size). Instead of using feature names, we used the antonyms that represented opposite extreme values of that feature. For instance, a typical question read, ‘How likely are you to describe animals as large/big/huge or small/little/tiny?’. The 153 category–feature pairs were rated on a scale from 1 (‘not likely at all’) to 5 (‘extremely likely’).

We averaged the ratings of each category–feature pair across participants and selected those for which the mean rating exceeded the 75th percentile (corresponding to a mean rating of 3.44 or above on the likelihood scale). This subset consisted of 39 pairs. We further removed two pairs where the norming question was ambiguous or otherwise unclear: animals–age (we are likely to describe an animal as being young or old, but comparing different species in terms of their age is less meaningful) and cities–partisanship (we are likely to describe US cities as being liberal or conservative, but many items in this category were cities in other countries).

The remaining 37 pairs partially overlapped with the manually selected subset (26 pairs in common). The union of these two subsets, totalling 56 pairs, was used in the main experiment (four pairs were later removed because human knowledge about them was extremely noisy; see below). The inclusion of manually selected pairs that were not rated highly in the norming study could only weaken the performance of semantic projection. If human knowledge about these ‘unlikely’ category–feature pairs is noisy or uncertain, we do not expect to recover it from a word embedding via semantic projection. Despite there being other category–feature pairings that could be deemed appropriate for testing, we limited our study to 56 experiments because this number offered breadth of coverage whilst still being manageable given our resources.

Computational model.

The GloVe word embedding.

We chose to conduct our experiment in the GloVe word embedding³⁷, because it outperforms several other word embeddings in predicting word similarity judgements³⁸. We used 300-dimensional GloVe vectors derived from the Common Crawl corpus (http://commoncrawl.org/), which contains approximately 42 billion uncased tokens and a total vocabulary size of 1.9 million. To limit the vocabulary to words with robust co-occurrence estimates, we considered only the 500,000 most frequent words. See Supplementary Methods and Extended Data Figs. 1–9 for results obtained with two other word embeddings, as well as two deep language models that are trained to represent words in context (that is, process sentences).

Defining feature subspaces.

A one-dimensional feature subspace is approximated by the vector difference between antonyms that represent opposite ends of the feature continuum. In our implementation, each end was represented by three words similar in meaning that were chosen by the authors based on intuition from amongst the words used as cues in the word association study in ref. ¹²². For instance, for the feature ‘danger’, one end was represented by the three vectors $\{\overrightarrow{\text{dangerous}},\overrightarrow{\text{deadly}},\overrightarrow{\text{threatening}}\}$, and the other end by the three vectors $\{\overrightarrow{\text{safe}},\overrightarrow{\text{harmless}},\overrightarrow{\text{calm}}\}$. The feature subspace was then defined as the average of the $3\times 3=9$ possible vector differences (or ‘lines’) between the two ends.

This averaging procedure was used to obtain more robust approximations of feature subspaces that were not strongly dependent on (1) the particular choice of antonyms by the authors or (2) the representation of each individual antonym resulting from the particular training regime and corpus used to generate the GloVe space. Indeed, lines for a given feature subspace were not always strongly aligned, with the mean cosine similarity between one line and the average of the remaining eight being 0.533 (corresponding to an angle of $0.99\text{π}$ or 57°). Nevertheless, lines were still more aligned within a feature subspace than across subspaces: the mean cosine similarity between one line and the average of lines from another subspace was 0.095, which suggests that the subspaces are effectively orthogonal to each other.

Human ratings.

Common knowledge about the 56 category–feature pairs in our dataset was evaluated on MTurk. Each category–feature pair was evaluated in a separate ~5-min-long experiment with $n=25$ participants (for a total of 1,400 participants; age and gender information were not collected). Participants were paid US $4 for rating the items in a single category according to a single feature. Each item had a separate sliding scale from 0 to 100, where 0 corresponded to one end of the feature continuum (for example, ‘small, little or tiny’ for size) and 100 corresponded to the other end (for example, ‘large, big or huge’). The words describing each end of the scale were the same words that were used to define the feature subspaces in the GloVe space.

We limited participation to MTurk users in the United States who had previously completed at least 1,000 experiments (‘human information tasks’ (HITs)) with an acceptance rate of 95% or above. To account for participant idiosyncrasies in how the scale was used, we z-scored the ratings of each participant. To exclude participants who had provided random responses, we computed Pearson’s moment correlation coefficient between the scaled responses of each participant and the average of the scaled responses across the rest of the sample. For each experiment, this procedure thus resulted in 25 inter-subject correlation (ISC) values. These ISCs were Fisher transformed to improve the normality of their distribution¹²⁵, and participants whose ISC was inferior to the mean ISC in their sample by more than 2.5 s.d. (that is, participants whose ratings showed weak correlations with the rest of the group) were removed from further analysis. In the majority of experiments, no participants were excluded, and no more than two participants were excluded from any given experiment.

For a given category–feature pair, the average ISC across participants provides a measure of the noise, or uncertainty, in common knowledge about that pair. When examining the average ISC for each experiment, we identified four outlier experiments for which ISCs were low (<0.07): cities by temperature, cities by wealth, clothing by arousal and clothing by size. The ISC values for these four experiments were clear outliers relative to the distribution of ISC values across the remaining 52 experiments and, accordingly, we removed them from further analysis.

We note that the choice of $n=25$ participants per category–feature pair was based on our prior experience with rating studies. In the current dataset, the ISC between a single participant and the remaining 24 participants is nearly the same as the ISC between that participant and a random subset of only 14 other participants (namely, this difference never exceeds $r=0.025$). Thus, the agreement across 25 participants in their ratings is similar to the agreement that would be obtained with 15 participants, demonstrating that our sample size is sufficient for obtaining stable ratings.

Predicting human ratings using semantic projection.

For each category–feature pair, we evaluated how well the ratings produced by semantic projection predicted the human ratings, by using two complementary measures as described below. For each measure and each pair, we computed a 95% confidence interval based on 10,000 bootstrap samples. Across category–feature pairs, we computed the median, the inter-quartile range and 95% confidence intervals of the median.

Measure 1: linear correlation.

We used Pearson’s moment correlation coefficient to estimate how much of the variance in human ratings across items could be explained by the ratings from the semantic projection. This measure is sensitive to even minor shifts in ratings. A slight change in a single item would (in most cases) affect the s.d. of the entire rating distribution and, consequently, change the respective contribution of each item to the correlation value. Therefore, it provides a strict test for semantic projection. Nonetheless, it is strongly biased by outliers. A strong correlation might reflect not the overall quality of semantic projection but, rather, a few extreme ratings made by both humans and the semantic projection method.

Measure 2: pairwise order consistency.

This measure, which we denote ${\text{OC}}_{\text{p}}$, estimated the percentage of item pairs, out of all possible pairings, for which the difference in ratings had the same sign in both human judgements and the semantic projection. For example, in the animals–danger experiment, for every two animals (i, j) such that i was rated by humans as more dangerous than j, we tested whether the semantic projection had predicted the same (versus opposite) pattern. This measure is sensitive only to the direction of pairwise differences but not to their magnitude. For instance, in the animals–danger experiment, humans rate alligators to be more dangerous than dolphins, so we require that semantic projection makes the same judgement regardless of how far apart the two animals fall on the feature subspace. Here, a change in the rating of a single item would only affect those pairs that (1) include this item and (2) reversed the direction of their difference as a result of this change. This measure is therefore robust to outliers. We note that this measure is closely related to Kendall’s rank correlation coefficient (tau) but has a more intuitive interpretation due to its range of [0%, 100%] (instead of [−1, 1]).

Significance testing.

The significance of both evaluation measures for each experiment (that is, category–feature pair) was quantified via a permutation procedure. For each of 10,000 iterations, we randomly shuffled the labels of category items in the feature subspace (but not their labels in the human data) and recomputed our two evaluation measures to obtain their empirical null distributions. The significance of each veridical measure was then computed relative to the mean and s.d. of its null distribution, estimated with a Gaussian fit (one-tailed test). For each evaluation measure, P values across the 52 experiments were corrected for multiple comparisons using false discovery rate (FDR) correction¹²⁶.

We chose to rely on a Gaussian fit rather than the ‘raw’ distribution of permuted values because many permutation tests returned a count of 0 (that is, no permutation produced a better result than the empirical data). When zero probabilities are submitted to FDR correction, they remain at zero instead of increasing. In contrast, the Gaussian fit produces a P value that is numerically higher than absolute zero and is thus a conservative choice that allows for probabilities to ‘correct upward’. Moreover, we reasoned that a Gaussian fit would obtain probabilities that better reflect the full null distribution, not just those permutations that happened to be produced by the randomization code. Evidence for the quality of this fit is provided in the Supplementary Information. All the significant measures we report remain significant when P values from the Gaussian fits are replaced with ‘raw’ P values based on counting permutations (and all of the non-significant measures remain non-significant).

Estimating an upper bound (noise ceiling) for the evaluation measures.

Because semantic projection approximates human knowledge, its success is limited by the amount of noise or uncertainty in that knowledge. Specifically, if human ratings for a certain category–feature pair exhibit low inter-rater reliability, then testing whether semantic projection captures human knowledge for this pair makes little sense, given that people disagree with one another in their judgements. Therefore, for each experiment, we compared our first measure—linear correlation—with the (Fisher-transformed) split-half reliability of ratings across participants. Specifically, we divided the squared correlation (that is, the percentage of variance in human ratings explained by semantic projection) by the squared split-half reliability, and took the square root of the result. We followed a similar procedure for computing split-half pairwise order consistency (${\text{OC}}_{\text{p}}$) across participants, to obtain an upper bound for our second measure. Here, we divided the ${\text{OC}}_{\text{p}}$ from the semantic projection by split-half reliability. For both measures, values greater than 1 were set to 1. In the main text, ‘adjustment for upper bound’ refers to this normalization of our evaluation measures relative to inter-rater reliability in behavioural data.

We chose to use split-half reliability rather than inter-subject correlations (that is, the average agreement between each participant and the rest of the group, or a one-versus-all reliability) because the former is usually higher. Therefore, it provides a more conservative noise estimate against which to normalize our evaluation measures. In other words, we chose a reliability measure that would lead to less inflation in our evaluation measures.

Reporting summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

All behavioural data and GloVe vectors as reported in the paper are available on the Open Science Framework (https://osf.io/5r2sz/). The full database of GloVe vectors (including many words not used in this study) is available for download from https://nlp.stanford.edu/projects/glove/.

Code availability

Custom MATLAB codes for replicating the analyses are available on the Open Science Framework page referenced above (https://osf.io/5r2sz/). The outputs of these codes include all data visualized in Figs. 2–6.

Extended Data

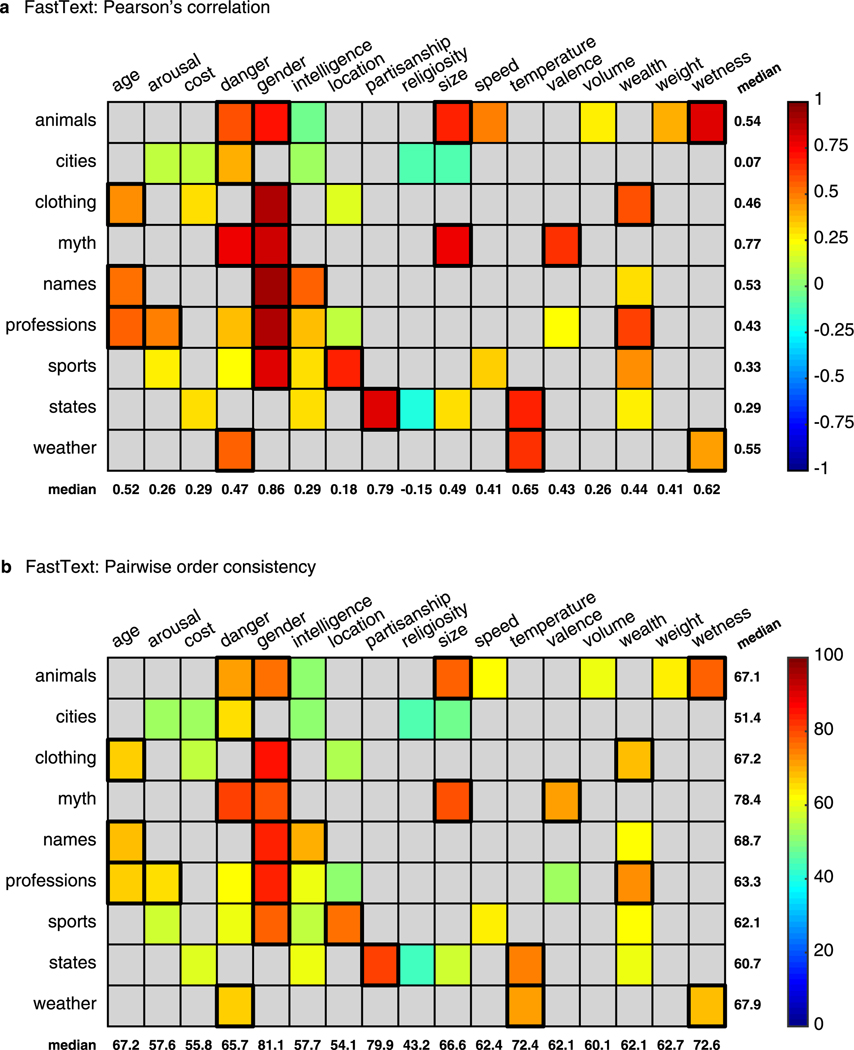
Extended Data Fig. 1 |. Correspondence between human judgments and semantic projection using FastText.

Conventions are the same as in Fig. 3 in the manuscript. Descriptive statistics across all tested pairs: (a) Pearson’s correlation: med = 0.41 ($C{l}_{95}=0.29-0.50$, $IQR=0.26-0.57$), adjusted med = 0.44 ($C{l}_{95}=0.35-0.53$, $IQR=0.29-0.60$). (b) $O{C}_p$: med = 64% ($C{l}_{95}=61-68\text{\%}$, $IQR=57-73\text{\%}$), adjusted med = 73% ($C{l}_{95}=70-78\text{\%}$, $IQR=67-81\text{\%}$).

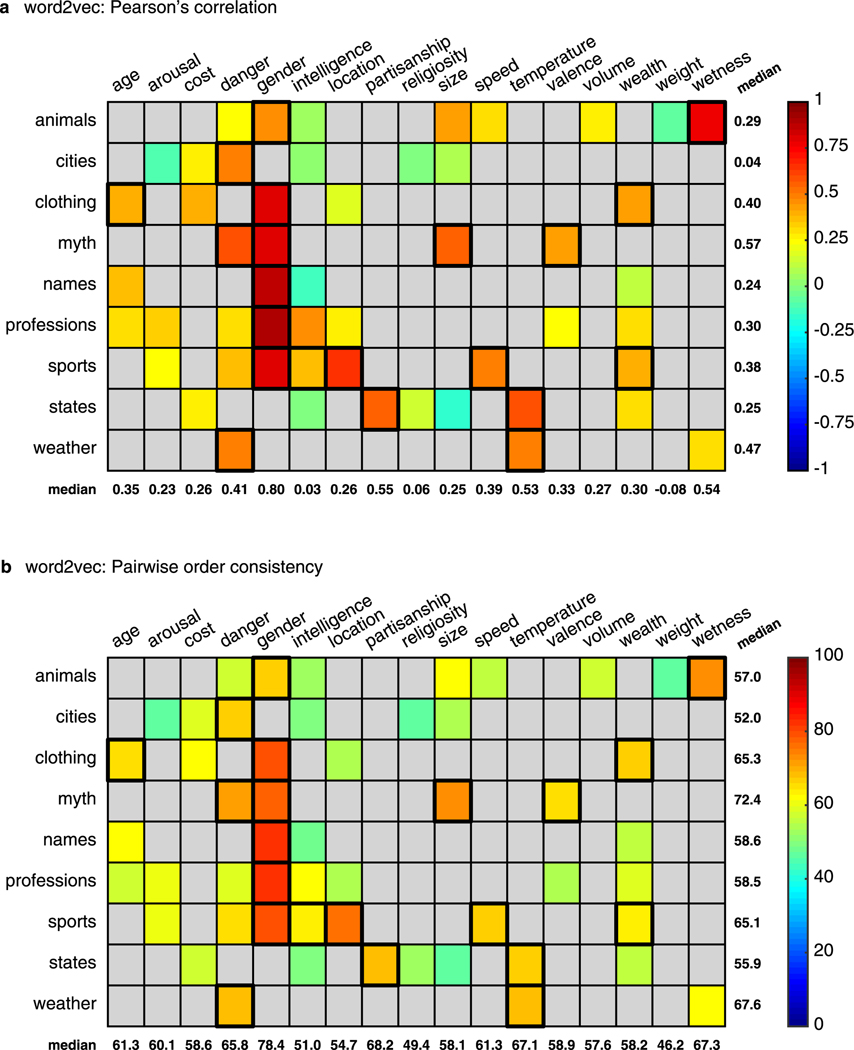
Extended Data Fig. 2 |. Correspondence between human judgments and semantic projection using word2vec.

Conventions are the same as in Fig. 3 in the manuscript. Descriptive statistics across all tested pairs: (a) Pearson’s correlation: med = 0.33 ($C{l}_{95}=0.27-0.40$, $IQR=0.22-0.44$), adjusted med = 0.35 ($C{l}_{95}=0.28-0.43$, $IQR=0.24-0.47$). (b) $O{C}_p$: med = 62% ($C{l}_{95}=57-65\text{\%}$, $IQR=55-67\text{\%}$), adjusted med = 71% ($C{l}_{95}=65-74\text{\%}$, $IQR=63-78\text{\%}$).

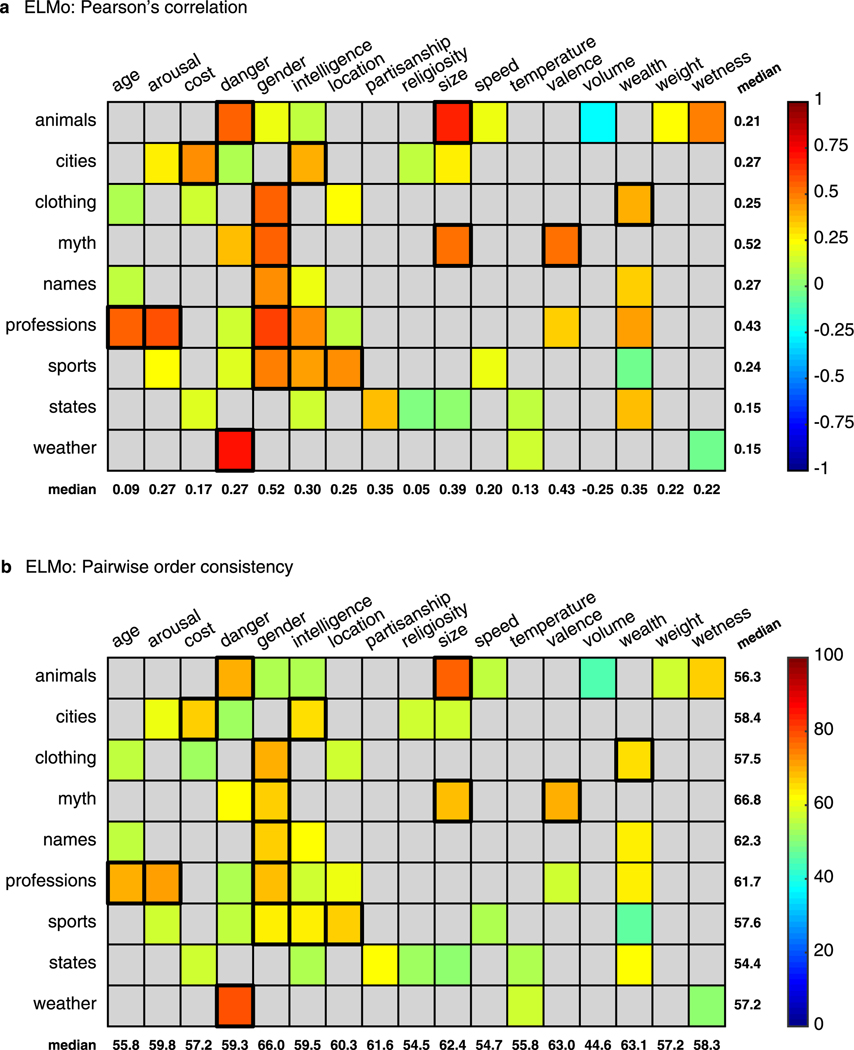
Extended Data Fig. 3 |. Correspondence between human judgments and semantic projection using ELMo.

Conventions are the same as in Fig. 3 in the manuscript. Descriptive statistics across all tested pairs: (a) Pearson’s correlation: med = 0.26 ($C{l}_{95}=0.20-0.36$, $IQR=0.14-0.43$), adjusted med = 0.31 ($C{I}_{95}=0.21-0.41$, $IQR=0.15-0.45$). (b) $O{C}_p$: med = 59% ($C{l}_{95}=57-63\text{\%}$, $IQR=55-66\text{\%}$), adjusted med = 70% ($C{l}_{95}=65-73\text{\%}$, $IQR=63-76\text{\%}$).

Extended Data Fig. 4 |. Correspondence between human judgments and semantic projection using BERT.

Conventions are the same as in Fig. 3 in the manuscript. Descriptive statistics across all tested pairs: (a) Pearson’s correlation: med = 0.42 ($C{l}_{95}=0.35-0.47,$, $IQR=0.20-0.54$), adjusted med = 0.44 ($C_{95}=0.40-0.50$, $IQR=0.25-0.57$). (b) $O{C}_p$: med = 65% ($C{l}_{95}=62-67\text{\%}$, $IQR=56-72\text{\%}$), adjusted med = 74% ($C{l}_{95}=72-76\text{\%}$, $IQR=67-80\text{\%}$).

Extended Data Fig. 5 |. Detailed results of semantic projection using FastText.

Conventions are the same as in Fig. 4 in the manuscript.

Extended Data Fig. 6 |. Detailed results of semantic projection using word2vec.

Conventions are the same as in Fig. 4 in the manuscript.

Extended Data Fig. 7 |. Detailed results of semantic projection using ELMo.

Conventions are the same as in Fig. 4 in the manuscript.

Extended Data Fig. 8 |. Detailed results of semantic projection using BERT.

Conventions are the same as in Fig. 4 in the manuscript.

Extended Data Fig. 9 |. Evaluating how well different word embeddings capture conceptual category structure.

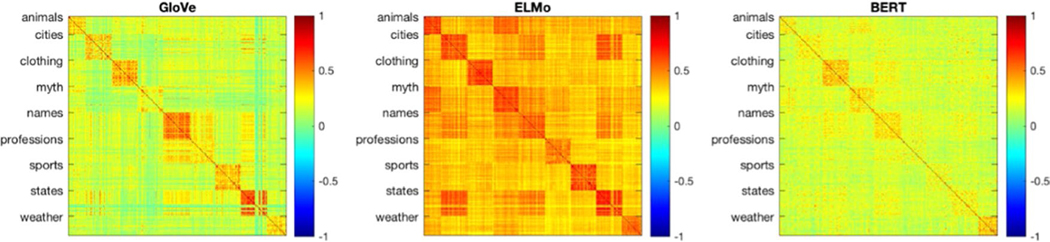
Each matrix shows Pearson’s correlations between all pairs of word vectors for all items used in our study, grouped by category (indicated on the y-axis), for a different embedding. Color corresponds to correlation strength, with dark blue corresponding to −1 and red corresponding to 1. Qualitatively, all three embeddings capture categorical structure, as is evidenced by the block-diagonal structure of the correlation matrix. Nonetheless, ELMo appears to generate highly similar vectors for words sharing a category (the diagonal blocks are colored in strong red), indicating a poorer ability to distinguish among within-category items, compared to the other two embeddings. In contrast, BERT appears to separate items from across different categories more poorly than the other two embeddings (the color differences between the diagonal blocks and the rest of the matrix are somewhat weak).