Abstract
Nature uses chromophore networks, with highly optimized structural and energetic characteristics, to perform important chemical functions. Due to its modularity, predictable aggregation characteristics, and established synthetic protocols, structural DNA nanotechnology is a promising medium for arranging chromophore networks with analogous structural and energetic controls. However, this high level of control creates a greater need to know how to optimize the systems precisely. This study uses the system’s modularity to produce variations of a coupled 14-Site chromophore network. It uses machine-learning algorithms and spectroscopy measurements to reveal the energy-transport roles of these Sites, paying particular attention to the cooperative and inhibitive effects they impose on each other for transport across the network. The physical significance of these patterns is contextualized, using molecular dynamics simulations and energy-transport modeling. This analysis yields insights about how energy transfers across the Donor–Relay and Relay–Acceptor interfaces, as well as the energy-transport pathways through the homogeneous Relay segment. Overall, this report establishes an approach that uses machine-learning methods to understand, in fine detail, the role that each Site plays in an optoelectronic molecular network.
Introduction
Inspired by natural systems like photosynthetic pigment–protein complexes, precise structural control using DNA scaffolds has been proposed for use-cases like molecular wires,1,3 photovoltaics,4 light-emitters,5 transistors,6 sensors,7 memory devices,8 and quantum gates.9,10 Natural systems use networks of chromophores to collect, transport, and process energy within their electronic and vibrational degrees of freedom.11–13 While pigment–protein complexes are highly optimized and can have very high energy-transport efficiencies,11 artificial systems typically have lower efficiencies due to less complete optimization which, for example, can result in excess energy-transport traps.14–16 To optimize a system, it is important to understand its nanoscale characteristics, such as its energy levels, electronic couplings, aggregation characteristics, environmental perturbations, and energy-transport dynamics.17 Moreover, it is important to map these factors to the bulk material functions on the lab bench. These details can become more difficult to understand in larger chromophore networks, because the greater size implies that the system is physically more complicated, yields more complex measurements, and is more expensive to model.
Electronic energy transport occurs because of the nanoscale interactions involving the electronic excited states (Sites) of the chromophores and their respective nuclear environments.4,18 (Here, Site refers to the lowest electronic excited state of a particular chromophore in its molecular basis set.) These processes can be understood using physical models, such as those based on Redfield theory, Förster theory, or the hierarchical equations of motion (HEOM).19,20 The physical models based on these theories are sensitive to the system’s structural arrangements and energy parameters, which can be obtained for example by analyzing their spectroscopic measurements.3,17,21–27 However, the challenge increases when these networks are composed of repeating monomer arrays, which are common in both natural and artificial systems. In that case, the contributions of individual chromophores are difficult to distinguish by distinct peaks in their optical spectra,16 due to their highly overlapping spectral features. Furthermore, though the spectra and dynamics are measured in terms of the Hamiltonian’s excitonic or vibronic eigenstates, the rational chemical design of molecular networks occurs in terms of their individual chromophores, so it is necessary to map sites to material functions directly. Therefore, one goal of this study is to understand empirically how Sites contribute to energy transport in scaffolded molecular networks.
Here, an approach is used that combines experimental measurements and computational modeling to understand energy transport in a large (14-Site) chromophore network. It uses Random Forest machine-learning algorithms to analyze spectroscopic measurements, inferring the energy-transport contributions of particular Sites (or clusters of Sites) within the network.28 Random Forest algorithms are capable of making both predictions and inferences. Predictions estimate unmeasured output values based on a given set of input values, while inferences determine the importance of each input variable (or clusters of them) for determining the output. The contributions from the Sites are not necessarily independent of each other. The Sites can inhibit or enhance each other, an interdependence quantified in this study. In addition to allowing more fine-tuned optimization for energy transport, knowing these parameters could also eventually enable the design of artificial systems with biologically inspired photoprotection mechanisms, in analogy to those where the presence of a couple atoms is enough to induce inhibiting effects that over-write the system’s function.29,30
The nanoscale factors that influence the energy-transport efficiencies include the aggregation characteristics, electronic energies and couplings, and system-environment interactions. These system-environment interactions are due to nuclear motions in the environmental baths coupled to the electronic states.31,32 Here, these dependencies are examined in a system whose energy transport is dominated by the Förster resonance energy transfer (FRET) mechanism, due to the multiple-nanometer distances between the neighboring Sites. This study considers a chromophore network embedded within a 6-helix bundle (6HB) DNA origami structure (Fig. 1a). The 6HB is comprised of a long, single-stranded DNA segment formed into six double helices with a honeycomb lattice pattern, created using a set of short staple strands. The details of this structure were reported previously.1 To create the molecular network, the site-specific staple strands were chemically modified at the 3′ or 5′ ends with one of three chromophores: Alexa Fluor 488 (AF488), Cyanine 3.5 (Cy3.5), or Alexa Fluor 647 (AF647). The Donor, Relay, and Acceptor segments are composed of two AF488, ten Cy3.5, and two AF647 Sites, respectively (Fig. 1). These species were selected to provide a downhill potential energy surface from the Donor segment to the Acceptor segment of the network. These monomers are labeled as Sites 1–14, starting from the Donor segment. The DNA scaffolds can precisely arrange the chromophore Sites,1,2,33–36 and they can be synthesized to exclude arbitrary Sites as detailed previously.1 DNA-scaffolded systems like this one are especially well-suited for machine-learning analysis, because their chromophores can be excluded systematically to produce a large library of related samples. In contrast, drastic, unintended changes to the structures of pigment–protein complexes or spin-coated organic materials can occur when their constituent chromophores are altered, which can significantly rewrite their structural and electronic characteristics.29,37
Fig. 1.
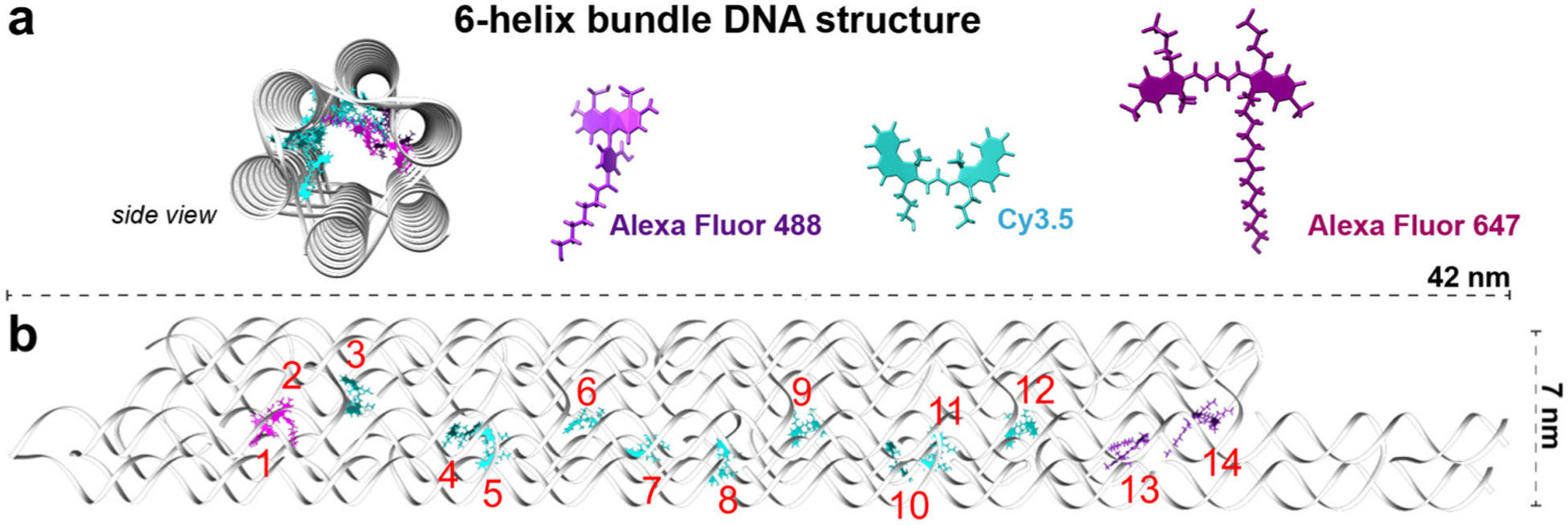
Schematic representing the DNA bundle and embedded chromophore network. (a) The DNA bundle is made of double helices arranged in a honeycomb lattice, as shown in the side view. The three chromophore types shown here were chemically attached to individual DNA strands within the bundle. (b) The front view of the DNA bundle (gray) with AF488 (1–2), Cy3.5 (3–12), and AF647 (13–14), numbered in red.
In the following sections, the relationships between the nanoscale characteristics and energy-transport efficiencies are investigated using molecular dynamics (MD) simulations, HEOM modeling, experimental FRET measurements, and Random Forest machine-learning algorithms. The FRET measurements are analyzed by the Random Forest algorithms to reveal the diverse, interdependent contributions the Sites provide for energy transport. Meanwhile, the MD simulations and HEOM models provide physical insight into how the system’s nanoscale parameters contribute to energy transport.
Methods
DNA photonic nanowire formation
The sample information used here was obtained from a previous publication by Klein et al.1 In that work, the DNA origami was prepared by utilizing a cleaved M13mp18 plasmid (Bayou Biolabs) prepared with the use of two restriction enzymes, EcoRI and BglII (New England Biolabs), to create a 704-nucleotide-long scaffold, along with excess staple strands. The DNA was annealed overnight in 1× TAE buffer with 15 mM MgCl2. To purify the formed photonic wire from excess strands, three washes with 50k Amicon centrifuge filters were used. The purified origami was then diluted with 1× TAE and 15 mM MgCl2 to ensure the sample concentration of 10 nM. The 29 nm-long, linear, photonic nanowire composed of 14 Sites was constructed within a 42 nm-long DNA nanostructure, based on a 6HB structure.38 By constructing samples where zero or more chromophores were absent within this motif, a library of related samples was constructed. The Site occupancy characteristics across the sample library are shown in Fig. S1 and S2 (ESI†).
Fluorescence
The raw data used here were reported previously by Klein et al.1 In that work, the steady-state fluorescence spectra were collected using a Tecan Infinite M1000 dual monochromator system (Tecan, Research Triangle Park, USA) with the excitation source tuned to 21 459 cm−1 (466 nm) or 17 094 cm−1 (585 nm). The samples were scanned in 96 well plates. The sample volume was set to , with a final concentration of 10 nM. The fluorescence spectra were collected with a 1 nm step size through a 490–800 nm range at 20 °C in 2.5 × PBS. The flash frequency was 400 Hz and the integration time was .
FRET analysis
Each of the samples’ fluorescence spectra was fit to a three-component linear combination, where the components were the fluorescence spectra from the individual AF488, Cy3.5, and AF647 chromophores attached to DNA. Because the chromophores were spaced 10 base pairs (typically >3 nm) apart, electronic mixing was assumed to distort the fluorescence spectra negligibly. This assumption was validated by the quality of the fit results (Fig. S1 and S2, ESI†). Using the weights from this fit, three figures of merit were obtained: the Donor-quenching (DQE, eqn (1), Relay-quenching (RQE, eqn (2), and wire-transfer efficiencies (WTE, eqn (3)).1
| (1) |
| (2) |
| (3) |
In these equations, A, R, and D correspond to the Acceptor, Relay, and Donor monomers, respectively; and S refers to the current sample configuration. S–A is the sample without any acceptors. is the fluorescence quantum yield of species , and is the fit coefficient in the fluorescence spectra of species after the excitation of the species containing only . The fluorescence quantum yields for AF488, Cy3.5, and AF647 were 0.95, 0.59, and 0.52, respectively.1 Eqn (1) assumes excitation of the Donor segment (21 459 cm−1; or 466 nm), eqn (2) assumes excitation of the Relay segment (17 094 cm−1; or 585 nm), and eqn (3) is subsequently investigated at both of these excitation frequencies.
For example, suppose the sample is the fully-occupied system. In that example, refers to the weight of the AF488 fluorescence spectrum in the three-component fit of the sample’s fluorescence spectrum. Meanwhile, refers to the fit component, for a sample containing only the Donor segment. Here, eqn (3) considers emission from the AF647 Acceptor after direct excitation of either the Donor or Relay segments. The AF647 fluorescence signal due to its direct excitation is measured on a system that only contains the Acceptor segment, and it is subtracted from the sample signal to yield only the signal component that occurred due to energy transport from the other monomers. In practice, sometimes these values were negative, indicating that the presence of non-Acceptor monomers was actually inhibiting Acceptor fluorescence. This effect was previously assigned to subtle differences in the origami formation efficiency and purification steps, which could have unexpected impacts including adding uncertainty.1
Random Forest method analysis
The data from the FRET measurements were used to map the Site 1–14 occupancies to the , and results across the unique samples shown in Fig. S1 and S2 (ESI†). Based on these measurements, the Random Forest method was used to infer the energy-transport roles of individual Sites, or clusters of Sites. The accuracies of these models are plotted in Fig. S3 (ESI†). The Random Forest method is well-suited for this problem, because it is scalable, requires no physical model, accommodates nonlinear (i.e., inter-dependent) degrees of freedom,39,40 and resists over-training in systems with many degrees of freedom.28 It has also been used previously to identify nonlinear dependencies of the input variables in a variety of contexts.41–43
The Random Forest algorithm has been described previously.28,44 Here, the method is summarized (Fig. 2a). Boot-strapping was used, which is the technique of resampling to use random subsets of the available data set to obtain statistical distributions.28,45 First, the data are resampled (with replacement, meaning predictors could be randomly selected more than once) into 1000 bootstrap aggregates (bags). Predictors are individual samples within the data set. The Random Forest method does not overfit the data as the number of bags increases, but the use of too few bags can increase prediction errors.28 The only penalty for an excessive bag quantity is an increased computational cost. Plots of the error magnitudes as a function of bag quantity (Fig. S4, ESI†) indicate that 1000 bags exceed the threshold for reducing this source of error. The dependence of the Random Forest output on the sample size was discussed in Fig. S5 and the subsequent text, within the ESI.†
Fig. 2.
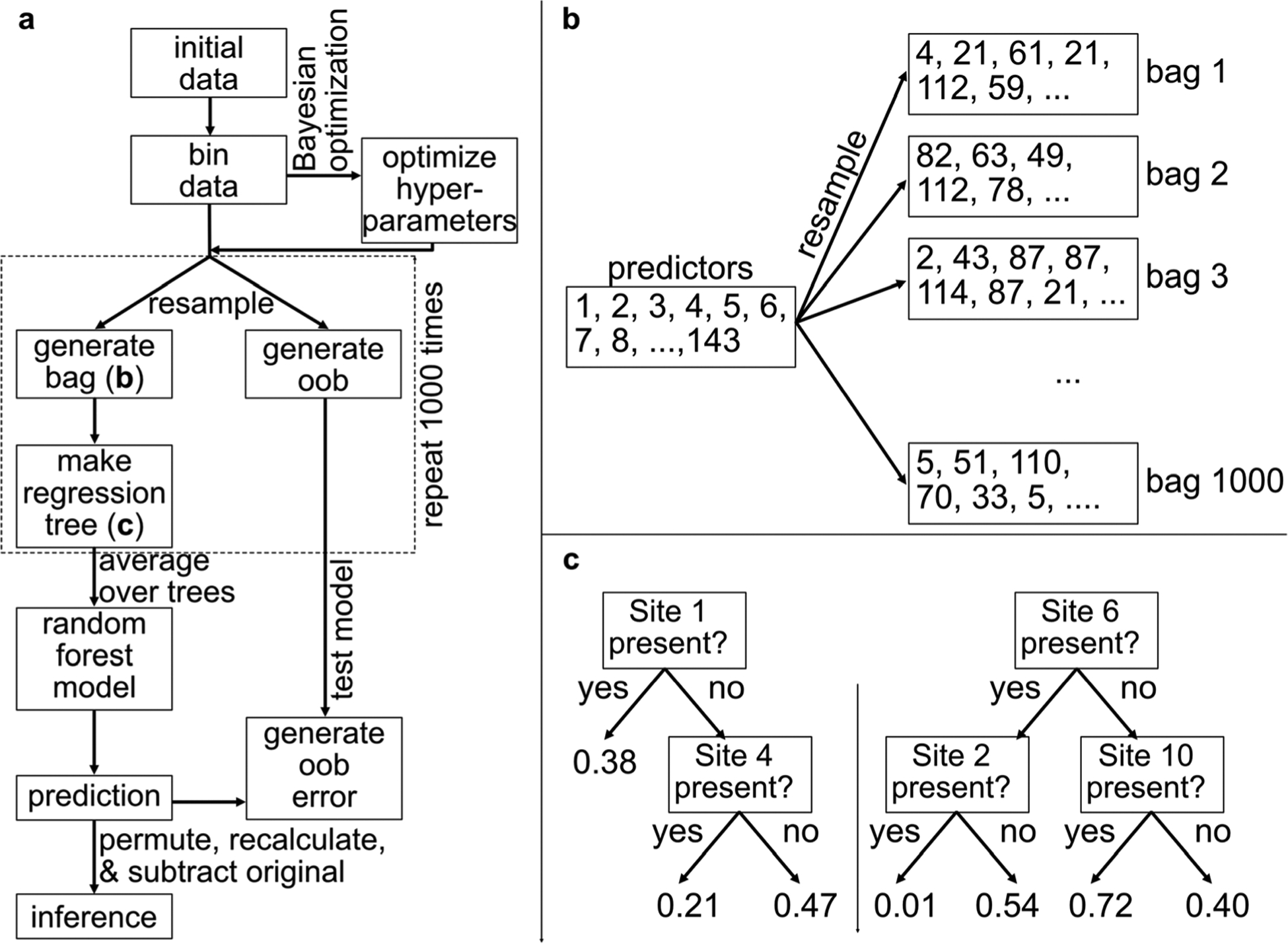
A diagram describing the Random Forest algorithm. (a) A schematic of the Random Forest algorithm used here is shown. Starting from the “initial data” box, the data are processed to generate a thousand regression trees, whose predictions are averaged to produce the model’s predictions. Based on input variable permutations, their inferences are also obtained. (b) The process of resampling to generate a bag is shown. From the 143 individual data sets, random individuals are selected with replacement, meaning that an individual can be chosen more than once. (c) Each bag is used to produce a binary regression tree, which is a set of nested if-statements leading predictions of an output variable, based on the corresponding bag’s average parameters. Two hypothetical examples of regression trees are shown here, though the actual regression trees in this study were not confined to only two levels of if-statements. The results of the trees’ predictions are averaged to produce the model’s predictions.
Taking the data set with a 21 459 cm−1 excitation for example, there were 143 individual measurements in the data set. Each individual sample includes the Site occupancy Booleans for each of the 14 Sites, a random Boolean value that is used to establish baselines (discussed subsequently), and the individual sample’s , and values. In this resampling process, individuals are selected one at a time from the data set for inclusion into the current bag (Fig. 2b). The bag is then used to train the model. The remaining predictors, that were not selected for the particular bag, are identified as its out-of-bag (oob) component.
The algorithm’s training procedure is the following. The bags were used to generate regression trees. The regression trees are nested if-statements (Fig. 2c) that result in predictions for a particular figure of merit, such as . The branching structures and nested if-statements are chosen at random by the algorithm, and they differ for each bag. Each regression tree is typically only weakly predictive; but when many trees are averaged, they become a more strongly predictive model that resists over-fitting.28 From the perspective of this model, the oob components are new measurements that were not used in the training process. Therefore, these models were trained using the bags, and then validated against the oob component to produce the oob error, which is the average error between the model prediction and the oob component. When the quantity of bags is increased, the oob error tends to decrease asymptotically and ultimately plateau.28 The quantity of bags used for this study was chosen to be several times the threshold where the oob error curves had plateaued (Fig. S4, ESI†). Regression trees that are too tall (i.e., include too many nested levels of if-statements) lead to over-fitting; however, averaging many short regression trees resists it.28
If the distribution of predictor outputs is too uneven, the resampling process under-samples the less population-dense regions, which can often diminish the role of the most important samples like the few top performers. To include these sparser regions of the search space, a rebalancing technique is used. The predictors were divided into equally wide bins depending on their output values, and the selections were sampled evenly from each bin. To minimize the influence of this technique on the results, only two bins were used here. Using more bins was found not to greatly impact the quality of the results. The practical trade-off for increasing the number of bins is to raise the baseline importance indicator for the input variables. To quantify the effect of rebalancing, a randomly generated Boolean input parameter was created that was uncorrelated to the outputs. The linear variable importance (LVI) of this uncorrelated input variable was used to set the threshold for determining the importance of the other input variables. This approach was repeated 9 times, and the results were averaged to determine this threshold.
The Random Forest algorithm’s hyperparameters were optimized using Bayesian optimization. These hyperparameters included the minimum number of observations per terminal node (a.k.a. the “minimum leaf size”), the maximum number of splits, and the number of predictors selected. To generate a bag, if predictors are selected (with replacement) from a data set with total predictors, the probability for predictor not to be selected in a particular bag is given by eqn (4).
| (4) |
Using eqn (4), for 143 or 126 predictors per data set (Fig. S1 and S2, ESI†), if predictors are selected, the number of predictors in the oob component is approximately 36.6% of the total data set. This value therefore represents the minimum typical proportion of the total data set used for validating the model, within the Bayesian optimization constraints used here. If the Bayesian optimization process assigns fewer predictor selections, then this percentage increases; however, it increases very gradually as the number of predictor selections decreases.
The approach used here is based conceptually on a cluster expansion, where the chromophores’ contributions to the material function can be separated into first-order contributions from individual Sites, second-order effects from pairs of these Sites, and so on. While a Site may individually have a strong contribution in the fully intact molecular network, as indicated for instance by a large decrease in function when only that Site is removed, cooperative (or inhibiting) effects involving multiple Sites can further direct the system’s functions. For example, in the second order, one Site may become a strong contributor only in the presence of a second Site. A similar example has been observed previously in the photoprotection mechanism of a pigment–protein complex, where energy transport through the molecular network was gated by the presence of two particular hydrogen atoms (and therefore, the system’s pH).29 It is possible to have higher-order effects as well. For example, if Sites 4–11 were removed from the network, then the energy transport would likely cease because the distance between Sites 3 and 12 becomes too large for efficient FRET. This would be a very high-order cluster contribution, involving 8 Sites. Here, the analysis is performed on first- and second-order clusters. This analysis gives insight into what Sites (or pairs of Sites) are acting as keystones for energy transport in the fully occupied system, which can assist in further optimization.
The LVI of each degree of freedom was obtained by randomly permuting that degree of freedom with respect to the output and recalculating the model.28 This method breaks any correlation of that particular input parameter to the output parameters, but it nonetheless preserves the overall data statistics to provide an apples-to-apples comparison between the permuted and unpermuted Random Forest models. Then, the permuted model’s output was compared to the unpermuted model’s output. If there is little change in the models’ predictions after the permutation of one input variable, then that input is not strongly correlated to the output and its variable importance is low. Conversely, a large change corresponds to a greater importance. This procedure was repeated 9 times to obtain statistical parameters, which are discussed in the Results section. These importances are obtained with respect to the fully occupied system, rather than the fully unoccupied one. The analysis is also performed at the level of two-Site clusters using the nonlinear variable importances (NVI). This metric was obtained by calculating the difference in LVI for Site A, depending on whether each distinct Site B was present or absent. These analyses used MatLab’s TreeBagger and BayesOpt functions.
Molecular structure and dynamics simulations
The atomic model of the 6HB scaffold and attached chromo-phores was created in UCSF Chimera.46 MD simulations were carried out with the Gromacs 2018 package47 on the DNA-dye complex using Amber OL15 force field parameters48 for the DNA and generalized amber force field (GAFF)49 for the dyes. Atomic partial net charges for the dyes were calculated from the fit to reproduce the electrostatic potential with the HF/6–31G* level. The starting structure was then solvated with the TIP3P water model in a triclinic box using a 15 Å buffer distance between the solute and the edge of the box. Periodic boundary conditions were employed for all directions. Then 15 mM MgCl2 were added to neutralize the system and match the experimental salt concentration. The long-range electrostatics were computed using the particle-mesh Ewald method with a real-space Coulomb cut-off of 1.0 nm. The van der Waals interactions were cut off at 1.0 nm. All bonds between the hydrogen atoms and heavy atoms were constrained using the LINCS algorithm.50 The neighbor-searching algorithm was used with a cut-off of 1.0 nm and the neighbor list was updated every tenth step. A time step of 2 fs was used for the simulation.
The solvated structure was first energy-minimized using the steepest-descent method for 10 000 steps in order to remove undesirable clashes between atoms. The system was then simulated for 1 ns at an isothermal–isochoric ensemble (constant volume and temperature, ) with harmonic constraints with the spring constant of 1000 kJ nm−2 imposed on DNA heavy atoms. The temperature was kept at 300 K using the Langevin thermostat with the coupling constant of 2 ps. The solvents and dyes were further equilibrated for another 2 ns by decreasing the spring constant for the position restraints down to 10 kJ nm−2. The system was relaxed for another 1 ns in the ensemble without any position restraint. The system was then equilibrated for 1 ns in the isothermal–isobaric ensemble using the Berendsen barostat51 to keep the pressure constant to a bath of the reference pressure (1 atm) with a coupling time of 2.0 ps. Finally, the production trajectories of the DNA-dye complex were calculated for keeping the number of particles, temperature, and pressure constant. The pressure was maintained at 1 atm isotropically with the Parinello–Rahman barostat52 and a coupling constant of 1.0 ps. The coordinates were written every 10 ps for analysis.
Hierarchical equations of motion
HEOM is a method to compute the quantum-mechanical evolution of an open quantum system under the influence of environmental perturbations. It has been described in detail previously.19,53,54 HEOM is used here, because alternatives like the Redfield or Förster theories use approximations that make them suitable for stronger inter-Site coupling with weaker system-environmental coupling, or vice versa, respectively. In contrast, HEOM does not depend on these limits.20,55,56 Though the present system is within the Förster limit due to its large inter-Site distances, HEOM is used here so that apples-to-apples comparisons to more closely-spaced chromophore networks can be made in future studies. Furthermore, HEOM includes more dynamical processes than FRET and yields more detailed, more exact results.53,57
The total Hamiltonian is composed of the system , environmental bath , and system-environmental coupling contributions (eqn (5)–(8)).58 In these equations, is the state energy, is the reorganization energy, and is the coupling for Sites and . Furthermore, is the mass, is the angular frequency, is the momentum operator, is the coupling, and is the position operator of Site and environmental bath oscillator .
| (5) |
| (6) |
| (7) |
| (8) |
Because the Sites are multiple nanometers apart, the couplings were calculated using the point-dipole approximation (eqn (9)).59 For Sites and is the orientation factor (eqn (10)), (in Debye) is the transition dipole magnitude (eqn (11)), is the refractive index, (in Angstroms) is the displacement, is the unit vector corresponding to the transition dipole, and is the unit vector for the displacement.59 In eqn (9), the medium’s dielectric constant is approximated by 59,60 In eqn (11), is the extinction coefficient at angular frequency is the elementary charge, is the mass of an electron, is the speed of light, and is the weighted average angular frequency of the absorption spectrum.61 The refractive index was set to 1.333, which is the value for water at room temperature.
| (9) |
| (10) |
| (11) |
To represent the environment, an overdamped Brownian oscillator model was applied, so that the system-environment coupling was represented by the Drude–Lorentz spectral density function (eqn (12)).62 This function includes the environmental relaxation rate .63 The value for used here was 10 ps−1, which corresponds to its assignment in other organic chromophore networks.55,64 Calculations were performed using a temperature of 298 K. Under these conditions, the high-temperature approximation applies, and a low-temperature correction is unnecessary.55
| (12) |
The system-environmental coupling term is used to determine the correlation function of the collective environment operator (eqn (13)).58 Independent environmental baths were used for each Site.
| (13) |
This correlation function is recast in terms of the Matsubara frequencies and their coefficients (eqn (14)–(18)), where the index formally spans to infinity but often provides good results when truncated to a hierarchy cut-off level , similar to previous reports of molecular network calculations.55,58 Here, is set to 2. This cut-off level is equivalent to the order in perturbation theory.65 In these equations, with Boltzmann constant and temperature is time, and is the imaginary number. The contributions of the hierarchy levels above are approximated by applying the Markovian approximation to maintain the detailed balance, following the truncation methods developed by Ishizaki and Tanimura.54,66 The implementation of this method has been described previously, along with comparative results.67
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
The time evolution of the density operator with index set is given by eqn (19).54,58,62,66 In this equation, the number of indices in scale with the hierarchy level as Pascal’s -simplex with , and the hierarchy level for each element is determined by the sum of its subscripted index numbers.62 is a non-negative index spanning the electronic states , and exponential indices that describe the environmental bath’s correlation functions in terms of the Matsubara frequencies. Here, is the number of Sites included in the calculation, and was set to 1. Furthermore, , where any negative index is set to zero. is the excitonic projection operator for state (eqn (20)).
| (19) |
| (20) |
The chromophores’ reorganization energies were approximated by using half of their measured Stokes’ shifts. These reorganization energies were 400, 196, and 204 cm−1 for AF488, Cy3.5, and AF647, respectively. These chromophores’ transition dipoles were 5.6, 14.2, and 15.3 D, respectively, based on estimates using the experimental spectra (eqn (11)). For the figures generated using HEOM, the time axis spans 0–1 ns in steps of 1 ps. The Quantum Toolbox in Python (QuTiP) library was used for the HEOM calculations.68,69
Results
Molecular structure and nuclear dynamics
The fully occupied system’s ground-state equilibrium structure was optimized using an energy-minimization method (Fig. 1b), and its nuclear motions were subsequently calculated using an MD simulation. Based on the average positions and orientations from the MD simulation results, histograms of the Sites’ center-to-center distances and couplings are shown in Fig. 3. These couplings are calculated using the point-dipole approximation (eqn (9)).59 The peaks for the couplings between Sites 1 and 2 were excluded for readability, because they average 665 cm−1 and are far greater than the positions of the other peaks. Other than Sites 1 and 2, the electronic couplings in this system are weak. In the MD simulation’s distance results (Fig. 3a), the distance distributions span approximately 20–300 Å, excluding the chromophores corresponding to Sites 1 and 2. Based on these multi-nanometer distances, even the closest neighbors have small coupling strengths on the order of tens of wavenumbers (eqn (9)). For most of the Site pairs, including all those that are not nearest neighbors, the couplings are extremely small (often <1 cm−1). Within this weak coupling regime, Sites 10–12 have comparatively strong coupling amongst each other, as do Sites 4–5, with long tails in their coupling histograms reaching magnitudes of 100 cm−1 in each case.
Fig. 3.
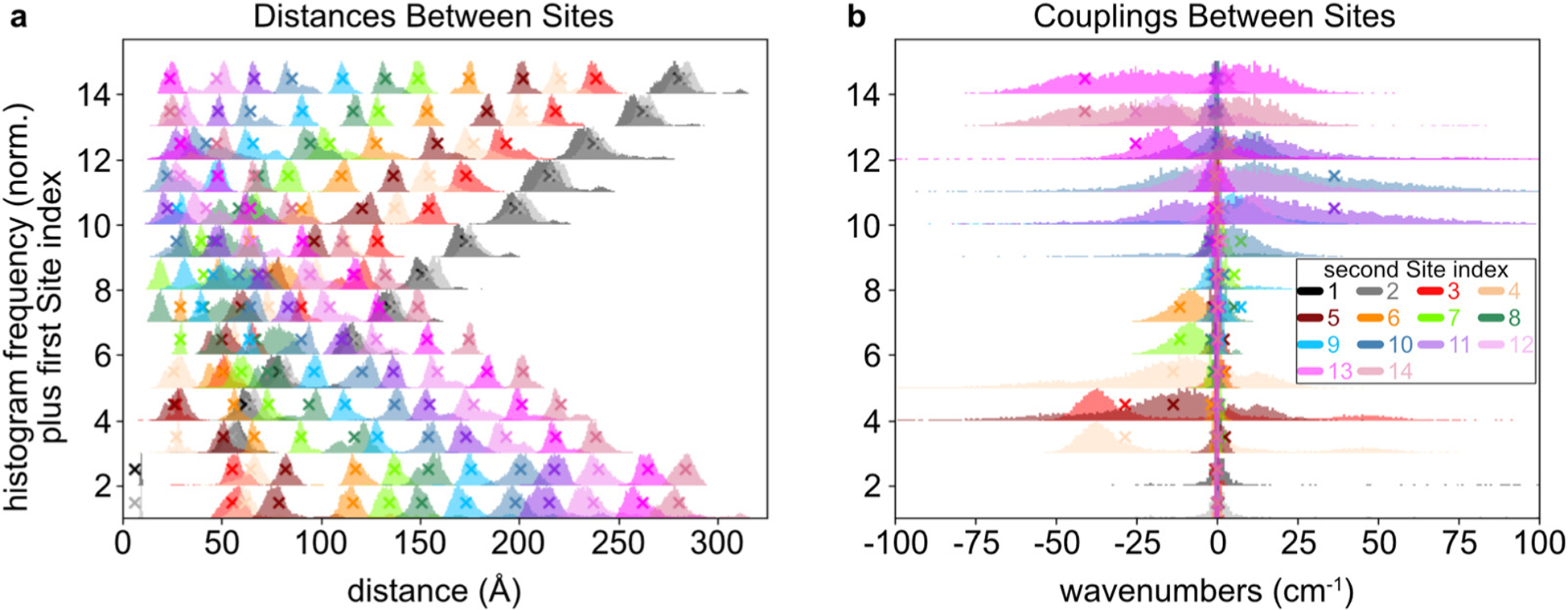
(a) The distributions of distances for the Site pairs are shown, as obtained by a molecular dynamics model. Each of the peaks is a normalized histogram, whose baseline is raised on the -axis to the corresponding first Site index. Therefore, Site pairs can be located by using the -axis baseline to identify the first Site index, and the color code to identify the second Site index. For example, the distance between Sites 3 and 7 appears with a -axis baseline of 3 and the light-green color, or equivalently with a -axis baseline of 7 and the red color. (b) The distributions of couplings are shown for each of the Sites. The histograms are overlaid to emphasize the Sites that have comparatively strong couplings to each other. In both panels, the histograms depend on pairs of Sites. The average couplings in panel b between Sites 1 and 2 are not shown because they are far outside of the plot range, at 665 cm−1. The X icons indicate the values obtained from the time-averaged monomer positions and orientations. Note that they are not obtained from the averages of the couplings, so the X may not coincide exactly with the histogram in some cases.
Next, the changes to the excitonic eigenstates are inspected in the presence of missing Sites. As eigenstates, they are stationary states by definition, so they provide an important view into the dynamics of the delocalized system. While molecular networks are typically designed in the Site basis, optical measurements probe the eigenstates instead. The eigenstate energies are shown in Fig. 4a for the fully occupied system (solid black line), as well as the system with each Site sequentially missing. Removing a Site causes a variable but small shift in the corresponding eigenstates’ energy levels, of approximately 10 cm−1 or less. Because the experiments are performed at room temperature , these shifts are relatively minor. For the fully occupied system, the frequencies and their distributions are shown for the Relay-centric eigenstates (3–12), due to the nuclear fluctuations in the MD simulation (Fig. 4b). In the presence of the nuclear motions, the wavenumbers of eigenstates 3–12 span 17 140–17 280 cm−1. This 140 cm−1 range is less than at room temperature. Therefore, the system is capable of energy transport in both directions along the relay chain at room temperature.
Fig. 4.
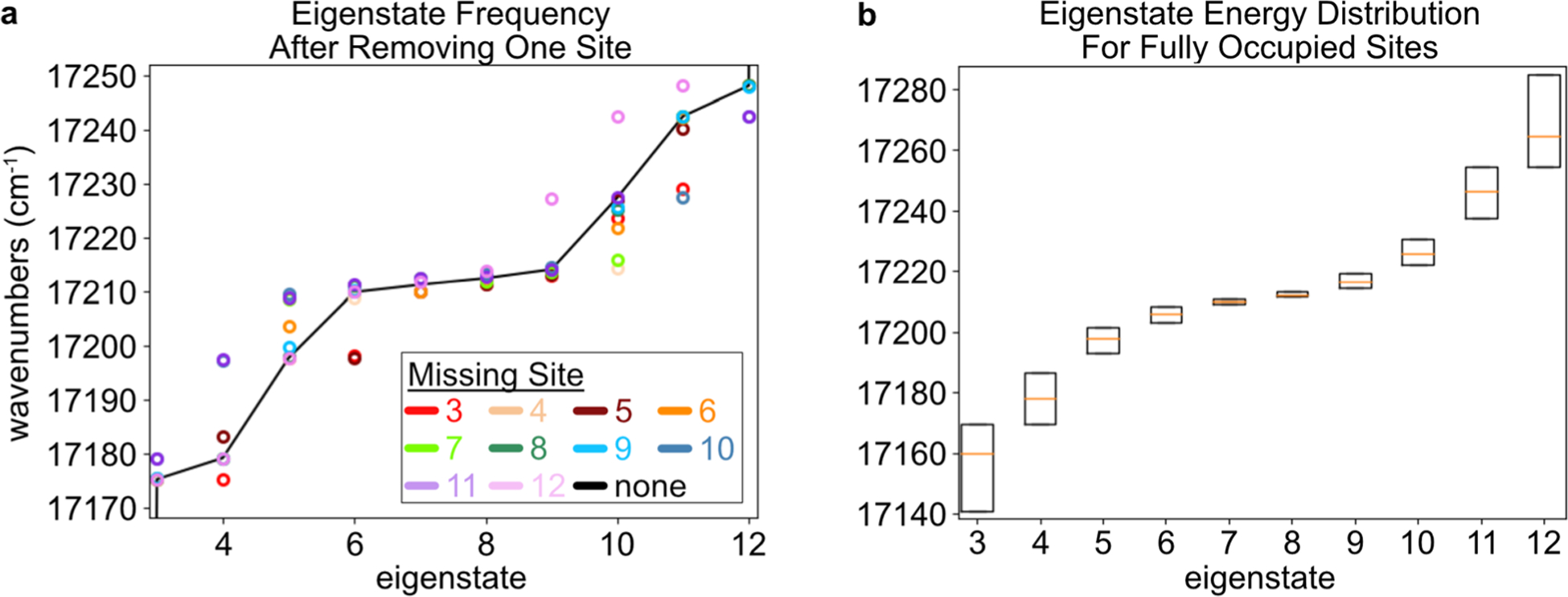
(a) The eigenstate wavenumbers are shown for the time-averaged Hamiltonian calculated based on the MD simulations. These values are calculated for the fully occupied system (black line), or when a single Site is missing according to the key. To aid visual inspection, the eigenstate index corresponding to the missing Site is skipped (e.g., there is no red marker for eigenstate 3). (b) Based on the couplings from the time steps within the MD simulation, the ranges of eigenfrequencies are shown for the system with all Sites occupied. The box plots indicate the first, second, and third quartiles of the distributions.
Machine-learning analysis of fluorescence measurements
Many unique sample configurations were synthesized with varying Site occupancies (Fig. S1 and S2, ESI†). The fluorescence spectra for these samples were measured by tuning the excitation frequency to target either the Donor (21 459 cm−1; or 466 nm) or Relay (17 094 cm−1; or 585 nm) segments. Each sample spectrum was fit to a linear combination of fluorescence spectra from the Donor, Relay, or Acceptor monomers attached to DNA (Fig. S1 and S2, ESI,† bottom). Using the FRET method to interpret the relative weights from these fits (see Methods section), the , and were calculated for each sample (eqn (1)–(3)). As a result, the total data set contained the occupancies of Sites 1–14 (as input variables), and the corresponding values for the , and (as output parameters).
Using this data set, Random Forest models were constructed to map these inputs to each output (see Methods section). The model was also used to infer the Feature Importance of each Site, with respect to each output parameter. For the Random Forest method, this Importance score reports how much each input variable influences each output variable.28 When only one input variable is considered at a time, the linear variable importance (LVI) is obtained. In addition, because the model is composed of nested if-statements (Fig. 2c), the model includes cooperative (or inhibitive) effects of these input variables. Therefore, conditional dependencies are quantified by the nonlinear variable importance (NVI). Nonlinear variable information in Random Forest models have been published previously in other contexts.41–43 For more information on these figures of merit, see the Methods section.
First, the Donor–Relay and Relay–Acceptor interfaces are considered. Because of the system’s 3D spatial structure, these interfaces should not be considered as a simple linear array, where only Site pairs [2, 3] or [12, 13] form the interfaces. Rather, multiple Sites are involved at each of these interfaces. For instance, the Donor–Relay interface is composed of Donor Sites 1–2, as well as the three nearest Relay Sites 3–5. Likewise, the Relay–Acceptor interface is composed of Relay Sites 10–12 and Acceptor Sites 13–14. Fig. 5 shows the LVI and NVI results corresponding to and , which report energy transport at the Donor–Relay or Relay–Acceptor interfaces, respectively. The LVI results indicate that Sites 3–5 are the most important for , while none of the other Sites individually contribute significantly. This result was expected, because of their proximity (eqn (9)). Fig. 5c and d display each NVI in terms of its Z-score , which is the number of standard deviations of the data point from the mean NVI score. It is defined by eqn (21), where is one NVI score, is the mean of the NVI scores, and is their standard deviation.
| (21) |
For the NVI results (Fig. 5c and d), most of the signals are in the range of ±1 standard deviation, though a few Site-pairs stand out. Fig. 5c shows a relatively strong cooperative effect for Site pairs [3, 5], [3, 7], [3, 8], and [3, 9]. Therefore, there exist cooperative effects even among non-adjacent monomers. Site 3’s prominence here is due to its location next to the Donor segment. There is also a strong inhibiting effect between Sites [3, 4], as indicated by its large negative intensity, which indicates competition between these Sites as energy-acceptor Sites for the Donor segment’s energy.
Fig. 5.
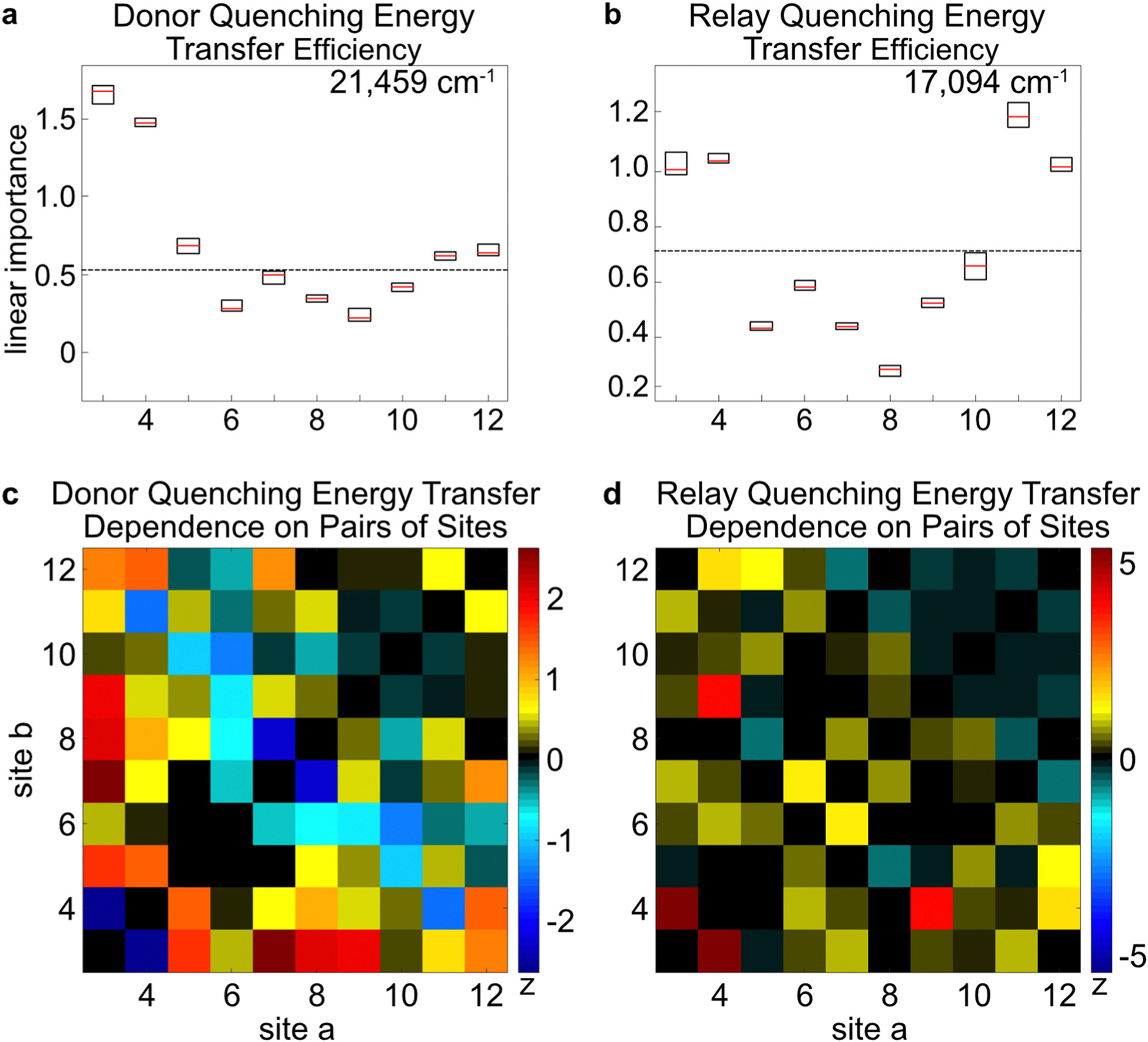
The linear and nonlinear variable importance indicators are shown for the DQE and RQE. (a and b) The excitation frequency is indicated in the top right corner. The box plots indicate the first, second, and third quartiles of the result distributions obtained after 9 repeats of the Random Forest algorithm. The horizontal, black, dotted line indicates the importance assigned to a randomly generated degree of freedom, which is taken as the baseline below which variables are uncorrelated to the output. Importance indicators do not necessarily indicate a positive correlation between each Site occupancy and the output. (c and d) The 2D figure indicates the importance of Site b, given the presence of Site a. The color scale of the 2D figure represents the -score, the number of standard deviations of each data point from the mean value. The excitation frequencies of the 2D plots correspond to those that were listed above in panels a and b. Though these figures are produced using random variations and are not exactly identical, a similar figure for panel a was published previously.1,2
For , the LVI results indicate that Sites 11 and 12 are especially important, as well as Sites 3 and 4. In the NVI chart, there are interspersed weak, positive cooperative effects, though not in the region of Sites 9–12. In the ideal case, when the Relay segment is excited directly, the Relay Sites further from the Relay–Acceptor interface act as antenna sites to capture more photoenergy and funnel it to the Relay–Acceptor interface. However, due to the small slope in Fig. 4 compared to at room temperature, this effect is likely weak. There are weak cooperative indications across several Sites, but the ones that stand out in particular are for Site pairs [3, 4] and [4, 9]. While the cooperative effects between pairs of adjacent Sites like [3, 4] can be attributed to coulombic interactions, but not aggregation effects because of their multi-nanometer distances, the longer-distance cooperative effects are more difficult to assign. For example, they could arise from delocalized energy-transport effects, such as changes in the eigenstate compositions or frequencies that affect the energy transport across the Relay segment. However, Fig. 4 shows that the eigenstates’ potential energy slope is not significantly affected by removal of individual Sites, so this effect would likely be negligible. Alternatively, they could happen due to subtle structural differences that may occur when particular dyes are excluded from the DNA scaffold.1 There are also reports demonstrating that, even when DNA origami includes particular dye-labeled strands, these can be non-emitting or have altered emission profiles.70 For multi-step energy transport processes, they could also occur from energy transport effects indirectly leading up to the process being probed, like transport through the Relay segment to the Relay–Acceptor interface, followed by Relay–Acceptor energy transfer. It remains a challenge to assign every cooperative effect. Nonetheless, the Random Forest inferences are able to reveal these outcomes without assuming a particular physical model.
The energy transport process across the chromophore network is investigated next, by considering the LVI and NVI results for the outputs. Based on the LVI results, Sites 3, 5, and 9–12 are the most important for (Fig. 6a). While Sites 3 and 5 are important for energy transport, as shown by their large Importance scores in the WTE LVI scores, Site 4 is excluded from meaningful transport through the relay chain despite its efficient quenching of the Donor Site excitations (Fig. 5a). Additionally, as expected, Sites 9–12 are important for energy transport from the Donor segment to the Acceptor segment, because they are part of the Relay–Acceptor interface. Fig. 6c shows the cooperative (or inhibitive) effects of Site pairs upon . The low Importance score of Site 4 appears in Fig. 5c to be due in part to strong inhibitive effects from Site 3, while Site 3 has a positive cooperative effect with Site 5. This pattern could help explain why Site 5 appears to be more important than Sites 3 and 4 in the .
Fig. 6.
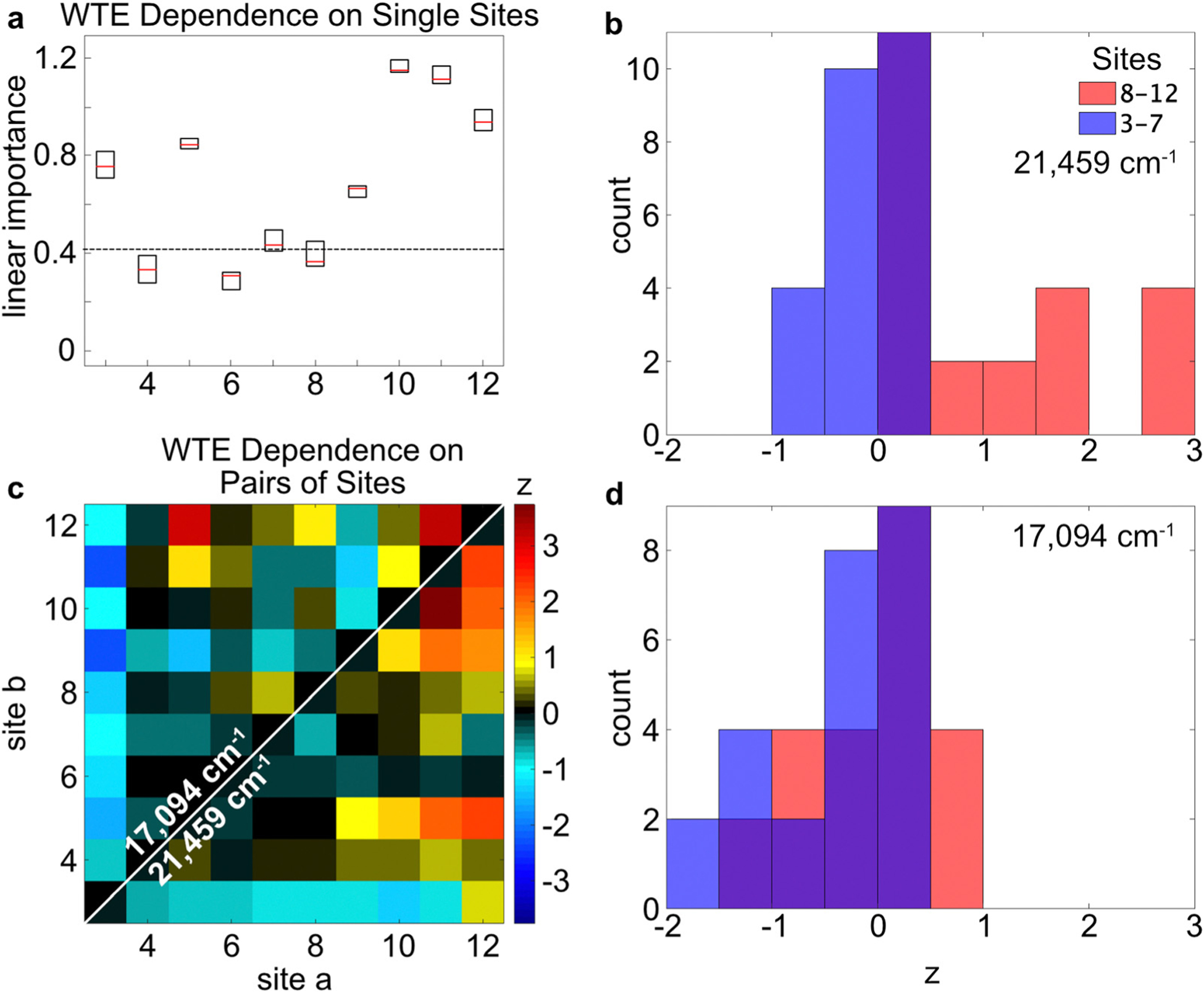
The linear (a) and nonlinear (c) importances of the WTE on the Sites 3–12 are shown, obtained from the Random Forest models. The excitation wavenumber in panel a was 21 459 cm−1. In panel c, because each data set is symmetric about the diagonal line for a given excitation energy, the data above or below the white diagonal line are overlaid to correspond to excitation targeting the Donor (21 459 cm−1) or Relay segments (17 094 cm−1), respectively. Histograms corresponding to sections of the 2D plot are shown in panels b and d, as indicated by the legend. For instance, the red histogram in panel b is obtained for the subsection with coordinates of [8–12, 8–12] in the 2D data set shown in panel c. Panels b and d correspond to excitation of the Donor and Relay segments, respectively. Though these figures are produced using random variations and are not exactly identical, a similar figure for panel a was published previously.1
Considering the different excitation energies in Fig. 6c, the cooperative effects in Sites 9–12 are the strongest when the Donor network is initially excited. This effect is observed more directly by comparing the red histograms in Fig. 6b and d. When the Donor segment is excited, Sites 9–12 have a higher average NVI score than when the Relay segment is excited. In contrast, Site 9 becomes inhibiting and Site 10 becomes less important when the Relay segment is excited directly. This pattern is consistent with an energy diffusion mechanism that, for excitations in Sites 9–12, can randomly transport the energy away from the Relay–Acceptor interface when Sites 3–8 are present. This effect becomes more apparent when the excitation is not guaranteed to begin at the Donor segment.
Hierarchical equations of motion
Using the Hamiltonian derived from the MD simulation results, the energy transport dynamics are modeled using HEOM. The system was separated into three segments that were modeled independently so that their individual roles could be observed: the Donor–Relay interface (Sites 1–5), Relay segment (Sites 3–12), and Relay–Acceptor interface (Sites 10–14). The calculations were performed using the Sites’ corresponding Hamiltonian elements, which were obtained based on the average couplings marked in Fig. 3b. Note that no ground-state was included in these calculations, so they only display the energy-transport behaviors among the excited-states.
First, the interfacial regions are investigated. In Fig. 7a, the electronic population dynamics of a system containing Sites 1–5 are modeled. This calculation assumes an equal initial population in Sites 1–2, and none in Sites 3–5. The energy transport is slow, because the couplings between Sites 1–2 and 3–5 are very small, as calculated from the MD simulation results. These couplings were unexpectedly on the order of 10−2–10−1 cm−1 (Fig. 3b). The reason is that monomers 1 and 2 tended to pull away from Sites 3–5 to an unexpectedly large distance of over 5 nm (Fig. 3a). Aside from that, there appears to be little distinction among the Donor monomers, or separately, the Relay monomers in Fig. 7a. Next, the dynamics of energy transport at the Relay–Acceptor interface are shown in Fig. 7b, with only the three interfacial Relay Sites (10–12) and the two Acceptor Sites (13–14) included. The initial population used in Fig. 7b is a contrived situation to understand the energy transport trends. It does not represent a realistic situation, because only three Relay Sites are included. Furthermore, only these Relay Sites are excited equally, while the experimental measurements involve either ten excited Relay Sites or two excited Donor Sites. Nonetheless, Fig. 7b is able to show how Sites 10–12 would perform energy-transport across the Relay–Acceptor interface. The dynamics shown here indicate that Site 12 donates energy to Sites 13–14 within approximately 100 ps, while Sites 10–11 do not donate energy very quickly. Meanwhile, Sites 13 and 14 receive their energy at nearly identical rates.
Fig. 7.
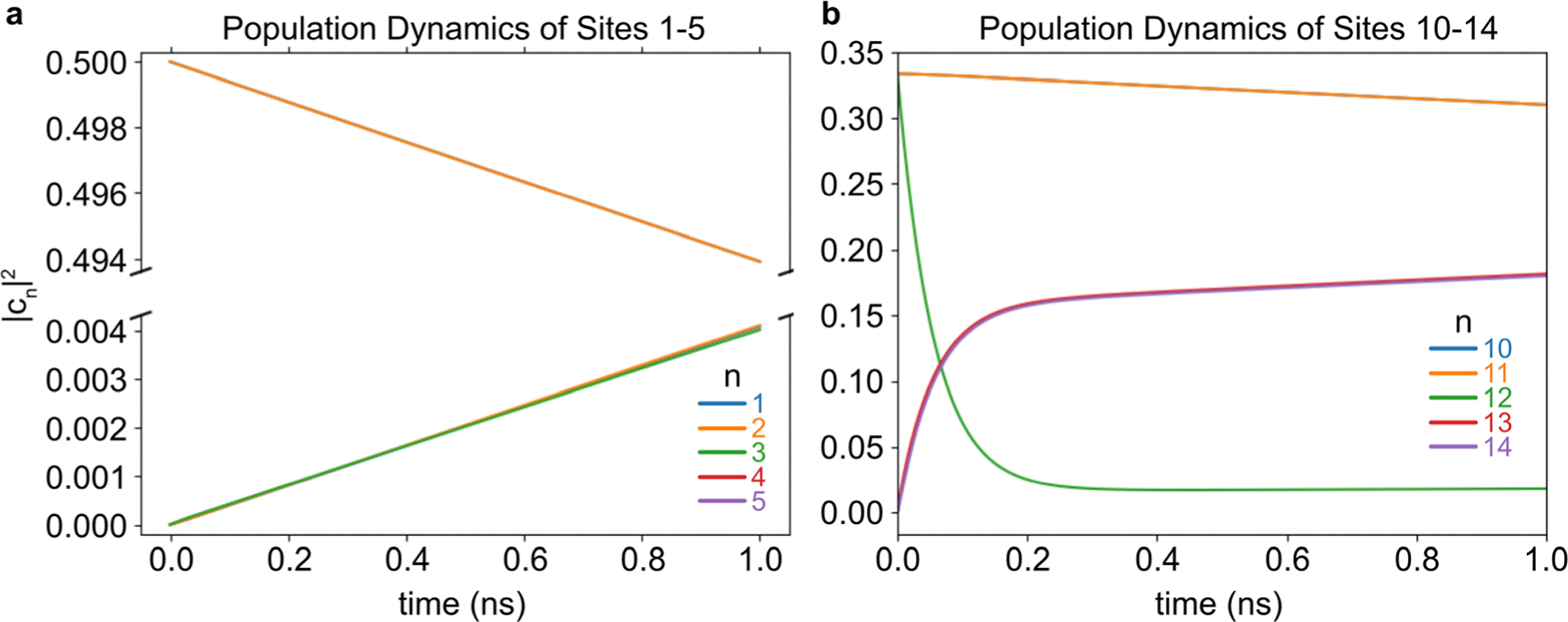
The energy transport dynamics of Sites 1–5 (a) and 10–14 (b) are shown. The Sites are designated by n, according to the color key. The excited-state dynamics were calculated using HEOM, assuming that the donor Sites (a) or Relay Sites (b) were initially occupied. In panel a, lines 1–2 and 3–5 each overlap. In panel b, lines 10–11 and 13–14 each overlap.
Next, the dynamics of the Relay segment (without the Donor or Acceptor segments) are investigated. Fig. 8 shows the dynamics when either Sites 3–5 are initially excited (Fig. 8a) or when the Relay segment is evenly excited (Fig. 8b). These two scenarios approximate the Donor-excitation or Relay-excitation initial conditions, respectively. When Sites 3–5 are initially excited, energy transport is directional toward Sites 10–12. The energy transports sequentially slower as the Site number rises, showing a transport distance dependence. In contrast, when the Relay segment is initially evenly excited, the population of each site does not change significantly because it is already near its equilibrium configuration. Therefore, Fig. 8b supports the earlier discussion about Fig. 4, which stated that the slope of the potential energy surface was too small compared to to significantly facilitate transport toward the Relay–Acceptor interface.
Fig. 8.
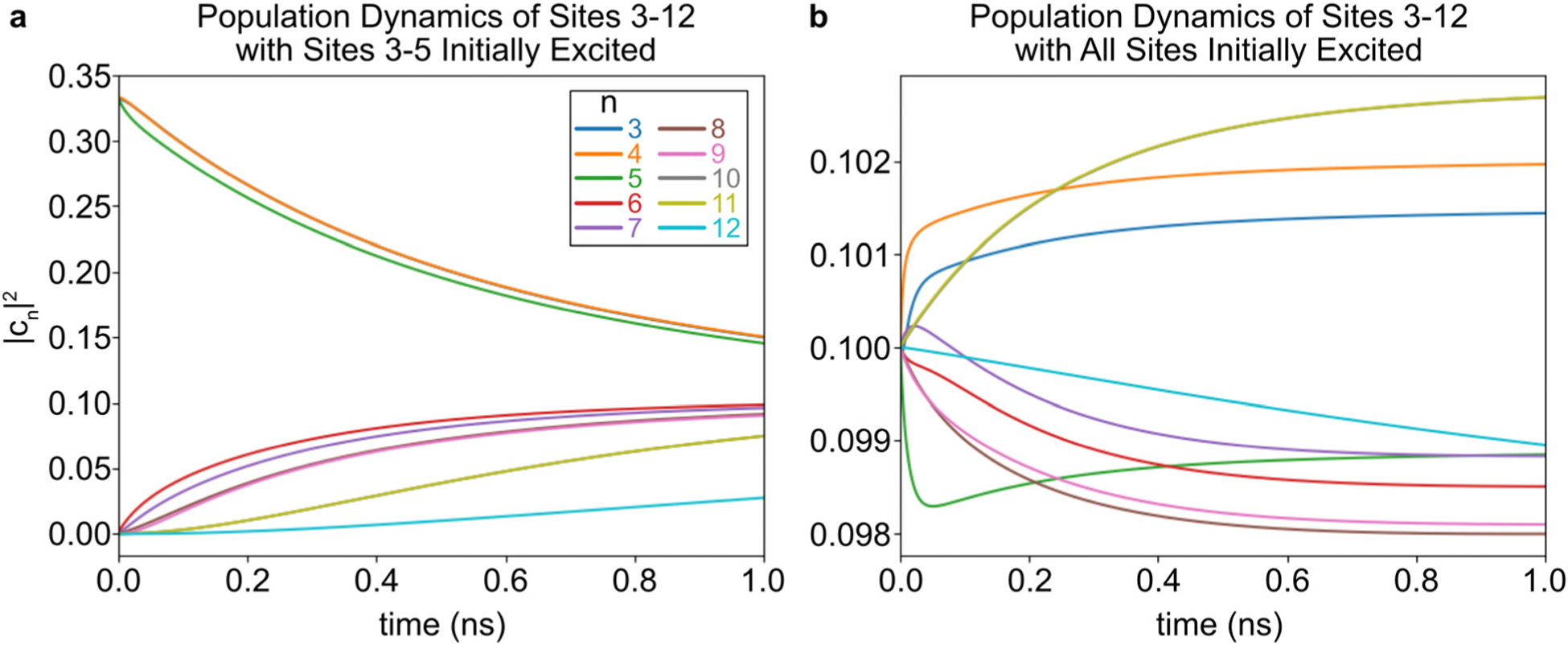
The energy transport dynamics are shown for the Relay segment. These plots assume that only Site 3 (a) or all of the Sites (b) are initially excited. These models leave out the Donor and Acceptor segments. The inset figure in panel a zooms in on the dynamics of Sites 9–12. In panel a, lines 3–4, 8–9, and 10–11 each overlap. In panel b, lines 10–11 overlap.
Discussion
The WTE importance indicators reveal that Sites 3, 5, and 10–12 were the most important for the wire-transport efficiency. These results could be due to the Donor–Relay, intra-Relay, and/or Relay–Acceptor energy-transport steps. The Donor–Relay energy-transfer step is not compelling, because the HEOM results indicate no special distinction for Sites 3 or 5 as an energy-acceptor to the Donor monomers (Fig. 7a). The Relay–Acceptor dynamics showed that Site 12 was the main energy-donor to the Acceptor segment, which explains its importance for the WTE. But these interfacial dynamics offered no explanation for why Sites 10–11 were important, because they did not engage in energy-transport significantly (Fig. 7b). Furthermore, the Importance indicators did not reveal any significant cooperative effects for Site 12 from Sites 10–11 (Fig. 5d). Among the Relay Sites (3–12), the average couplings were typically weak, with the strongest average couplings achieving only a few dozen wavenumbers (Fig. 3). However, Sites 4–5 and 9–12 exhibit the strongest transient couplings (in the long tails of their histo-grams in Fig. 3), which occasionally reached 100 cm−1, and these Sites also coincide with the strongest NVI scores in Fig. 6c. These large transient couplings were not included in the HEOM model, which only considered the Hamiltonian calculated using the average position and orientation of each Site from the MD simulation. The model shows that, when Sites 3–5 are initially excited, the energy eventually arrives in high proportion to Sites 10–11, compared to the small amount that arrives to Site 12. Therefore, the most consistent narrative is that the average transport processes are weak and slow when transporting energy from the Donor segment to Site 12, but the Site-pairs whose couplings that have the strongest variations are able to play an important role in energy transport by virtue of their stochastic moments of strong coupling. Sites 4–5 and 10–12 are the most capable of these momentary relatively strong couplings. Site 4 is less important, however, because it has inhibitive Donor-quenching interactions with Site 3 that compete with its advantages. Meanwhile, Site 3’s Donor-quenching interactions with Site 5 are cooperative instead (Fig. 5c).
The histograms for the WTE NVI results in Fig. 6b and d indicate that Sites 3–7 have an inhibiting effect on energy-transport, while Sites 9–12 have an enhancing effect on it. Site 3 in particular inhibits almost all of the other Sites’ WTE NVIs (Fig. 6c). The inhibiting effect stands in contrast to the Relay–Acceptor energy-transfer inferences (Fig. 5d), which report an enhancing effect for these Sites when the Relay segment is directly excited. When the excitation starts at the Donor side of the system, the energy must transport through the Relay segment to reach the Acceptor segment eventually. A longer Relay segment, in that case, lowers the transport efficiency because more transport steps must be taken. In contrast, when the Relay segment is excited directly, Sites 3–7 act as extra antennas that can capture more photoenergy, leading to cooperative effects in the RQE NVIs.
Next, the overlap of the eigenstates with the Sites is considered. A coherently excited system localizes to these eigenstates due to environmental perturbations. Despite the small electronic couplings, most of the system’s eigenstates (Table 1) are still delocalized across 2–6 Sites. The delocalization of the th eigenstate across Sites is expressed using the inverse participation ratio (eqn (22)), where is the overlap between the wavefunctions of Site and eigenstate (Table 2).71 Each eigenstate is delocalized over Sites on average, where the minimum possible value of 1 indicates complete excitonic localization on a single site and the maximum possible value of indicates complete eigenstate delocalization across all of the Sites.
| (22) |
Eigenstates 1–2 or 13–14 are completely delocalized over the Acceptor or Donor segments, respectively, because their inverse participation ratios are near 2, which is the total monomer length of these segments. Meanwhile, eigenstates 3–12 are mainly distributed within the Relay segment (Table 1). Relative to the Relay segment’s length of 10 monomers, these eigenstates are more localized than the ones on the Donor or Acceptor segments.
Table 1.
Overlap of Sites (rows) and eigenstates (columns) in the fully occupied system, using the couplings calculated from the average positions of the MD simulation
| Eigenstate 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Site | ||||||||||||||
| 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.71 | −0.71 |
| 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.71 | −0.71 |
| 3 | 0.00 | 0.00 | 0.43 | 0.02 | −0.05 | 0.00 | −0.12 | 0.75 | −0.13 | 0.16 | 0.43 | 0.01 | 0.00 | 0.00 |
| 4 | 0.00 | 0.00 | 0.71 | 0.02 | −0.07 | 0.00 | 0.00 | 0.00 | 0.01 | −0.06 | −0.70 | −0.03 | 0.00 | 0.00 |
| 5 | 0.00 | 0.00 | 0.55 | 0.01 | 0.02 | 0.00 | 0.10 | −0.60 | 0.08 | −0.01 | 0.56 | 0.02 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | 0.05 | −0.05 | 0.69 | 0.03 | −0.13 | 0.12 | 0.00 | −0.70 | 0.05 | 0.04 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.03 | −0.06 | 0.69 | 0.01 | −0.08 | −0.09 | −0.14 | 0.68 | −0.10 | −0.05 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.01 | 0.04 | −0.13 | 0.74 | 0.04 | −0.65 | −0.09 | −0.01 | 0.01 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | −0.02 | 0.09 | −0.16 | 0.15 | −0.61 | −0.21 | −0.72 | −0.08 | 0.00 | 0.05 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.01 | −0.66 | −0.07 | 0.41 | 0.04 | 0.00 | −0.06 | −0.04 | 0.03 | −0.62 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | −0.02 | 0.73 | 0.06 | 0.19 | 0.05 | 0.01 | 0.03 | −0.03 | 0.03 | −0.65 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | −0.14 | −0.02 | −0.87 | −0.19 | −0.03 | −0.05 | −0.05 | 0.03 | −0.43 | 0.00 | 0.00 |
| 13 | −0.71 | −0.71 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | −0.71 | 0.71 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Table 2.
Wavenumbers and inverse participation ratios of the excitonic eigenstates for the fully occupied system
| (cm−1) | ||
|---|---|---|
| 1 | 17 829 | 2.22 |
| 2 | 18 256 | 2.12 |
| 3 | 19 035 | 4.53 |
| 4 | 19 249 | 2.21 |
| 5 | 19 249 | 2.21 |
| 6 | 19 457 | 4.45 |
| 7 | 20 300 | 6.26 |
| 8 | 20 393 | 2.00 |
| 9 | 20 393 | 2.16 |
| 10 | 20 393 | 2.07 |
| 11 | 20 393 | 2.16 |
| 12 | 20 499 | 6.39 |
| 13 | 21 352 | 4.21 |
| 14 | 21 536 | 2.06 |
Because the stochastic energy fluctuations are important for processes like energy transport and dephasing, their roles in the Site and eigenstate basis sets are considered next. For a system with many identical, coupled Sites like the Relay segment studied here, even if the Sites individually experience the same stochastic perturbations on average from the environment, the eigenstates 3–12 will nonetheless distribute these perturbations so that the lowest- and highest-energy eigenstates experience them the most severely, while the eigenstates in between these extremes experience them less intensely (Fig. 4b). This pattern suggests that the highest- or lowest-energy eigenstates in the Relay segment benefit from greater frequency volatility, which could be useful for thermally assisted energy transport. Or conversely, if the goal is to produce systems with coherent transport, then designing them to interact mainly through their intermediate eigenstates, which have smaller perturbations, would be helpful because the muted stochastic perturbations would slow dephasing.72
Conclusion
Within a molecular network, the roles of the Sites for energy transport were studied using spectroscopy measurements, computational modeling, and machine-learning algorithms. The network’s large monomer length and repeating chromo-phore units made the roles of its individual Sites difficult to distinguish within its spectra, however the Random Forest method allowed these roles to be inferred based on experimental FRET measurements. Both the linear and nonlinear variable importance scores were obtained using this method. These Random Forest methods map the bulk effects to molecular characteristics and mechanisms. Compared to previous studies,1 this study introduced methods to investigate the cooperative or inhibiting roles that particular Sites have on each other, examined the effects and relationships between the bulk observations and nanoscale nuclear and electronic dynamics, and used HEOM and MD simulations to explain the Importance indicator patterns physically.
These results reveal a web of cooperative enhancements and inhibiting influences for energy transport through the network. Meanwhile, the energy-transport dynamics were calculated using HEOM on important subsections of the network. The energy transport dynamics indicated that, though the average Relay-segment couplings were weak, the Sites with the most strongly varying couplings benefited from stochastic moments of stronger coupling that transiently facilitated energy transport. These Sites were indicated as the most important for WTE in the Random Forest analysis. Longer range interdependencies were also observed, indicating that a nearest-neighbor design strategy may miss some possibilities for cooperative effects between distant Sites. For example, antenna effects were observed that bolstered the overall energy transfer efficiency from the Relay segment to the Acceptor segment, even with separation spanning ten Sites and tens of nanometers. However, the returns of adding additional Relay Sites were diminishing due to an increased chance of drawing the energy away from the Relay–Acceptor interface. The eigenstate structure was found to distribute more vibrational perturbations to eigenstates 3 and 12 and less to those in between, which implied the possibility of strategies to promote energy transport and coherent effects.
Supplementary Material
Acknowledgements
BSR was supported by the Jerome and Isabella Karle Distinguished Scholar Fellowship from the US Naval Research Laboratory. DM was supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number R00EB030013. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This work was supported by the US Naval Research Laboratory Institute for Nanoscience and the Office of Naval Research.
Footnotes
Electronic supplementary information (ESI) available: The sample configurations, fluorescence spectra and their fits, the Random Forest model accuracy, and the Random Forest model’s dependence on the number of predictors. See DOI: https://doi.org/10.1039/d2cp04960k
Conflicts of interest
There are no conflicts to declare.
References
- 1.Klein WP, Rolczynski BS, Oliver SM, Zadegan R, Buckhout-White S, Ancona MG, Cunningham PD, Melinger JS, Vora PM, Kuang W, Medintz IL and Díaz SA, ACS Appl. Nano Mater, 2020, 3, 3323–3336. [Google Scholar]
- 2.Buckhout-White S, Spillmann CM, Algar WR, Khachatrian A, Melinger JS, Goldman ER, Ancona MG and Medintz IL, Nat. Commun, 2014, 5, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hart SM, Chen WJ, Banal JL, Bricker WP, Dodin A, Markova L, Vyborna Y, Willard AP, Häner R, Bathe M and Schlau-Cohen G, Chem, 2021, 7, 752–773. [Google Scholar]
- 4.Park H, Heldman N, Rebentrost P, Abbondanza L, Iagatti A, Alessi A, Patrizi B, Salvalaggio M, Bussotti L, Mohseni M, Caruso F, Johnsen HC, Fusco R, Foggi P, Scudo PF, Lloyd S and Belcher AM, Nat. Mater, 2016, 15, 211–216. [DOI] [PubMed] [Google Scholar]
- 5.Varghese R and Wagenknecht H-A, Chemistry, 2009, 15, 9307–9310. [DOI] [PubMed] [Google Scholar]
- 6.Hamedi M, Elfwing A, Gabrielsson R and Inganäs O, Small, 2012, 9, 363–368. [DOI] [PubMed] [Google Scholar]
- 7.Parolo C, Greenwood AS, Ogden NE, Kang D, Hawes C, Ortega G, Arroyo-Currás N and Plaxco KW, Microsyst. Nanoeng, 2020, 6, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chu H-L, Lai J-J, Wu L-Y, Chang S-L, Liu C-M, Jian W-B, Chen Y-C, Yuan C-J, Wu T-S, Soo Y-L, Di Ventra M and Chang C-C, NPG Asia Mater, 2017, e430, DOI: 10.1038/am.2017.157. [DOI] [Google Scholar]
- 9.Cannon BL, Kellis DL, Davis PH, Lee J, Kuang W, Hughes WL, Graugnard E, Yurke B and Knowlton WB, ACS Photonics, 2015, 2, 398–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Castellanos MA, Dodin A and Willard AP, Phys. Chem. Chem. Phys, 2020, 22, 3048–3057. [DOI] [PubMed] [Google Scholar]
- 11.Blankenship R, Molecular Mechanisms of Photosynthesis, Wiley, Chichester, 2002. [Google Scholar]
- 12.Vinyard DJ, Ananyev GM and Charles Dismukes G, Annu. Rev. Biochem, 2013, 82, 577–606. [DOI] [PubMed] [Google Scholar]
- 13.Abramavicius D and Mukamel S, J. Chem. Phys, 2011, 134, 174504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Scholes GD and Rumbles G, Nat. Mater, 2006, 5, 683–696. [DOI] [PubMed] [Google Scholar]
- 15.Clarke TM and Durrant JR, Chem. Rev, 2010, 110, 6736–6767. [DOI] [PubMed] [Google Scholar]
- 16.Cho S, Rolczynski BS, Xu T, Yu L and Chen LX, J. Phys. Chem. B, 2015, 119, 7447–7456. [DOI] [PubMed] [Google Scholar]
- 17.Rolczynski BS, Díaz SA, Kim YC, Medintz IL, Cunningham PD and Melinger JS, J. Phys. Chem. A, 2021, 125, 9632–9644. [DOI] [PubMed] [Google Scholar]
- 18.Cunningham PD, Kim YC, Díaz SA, Buckhout-White S, Mathur D, Medintz IL and Melinger JS, J. Phys. Chem. B, 2018, 122, 5020–5029. [DOI] [PubMed] [Google Scholar]
- 19.Tanimura Y and Kubo R, J. Phys. Soc. Jpn, 1989, 58, 101–114. [Google Scholar]
- 20.Ishizaki A and Fleming GR, J. Chem. Phys, 2009, 130, 234110. [DOI] [PubMed] [Google Scholar]
- 21.Rolczynski BS, Yeh S-H, Navotnaya P, Lloyd LT, Ginzburg AR, Zheng H, Allodi MA, Otto JP, Ashraf K, Gardiner AT, Cogdell RJ, Kais S and Engel GS, J. Phys. Chem. B, 2021, 125, 2812–2820. [DOI] [PubMed] [Google Scholar]
- 22.Renger T and Marcus RA, J. Chem. Phys, 2002, 116, 9997–10019. [Google Scholar]
- 23.Adolphs J and Renger T, Biophys. J, 2006, 91, 2778–2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Friedl C, Renger T, Berlepsch HV, Ludwig K, Schmidt am Busch M and Megow J, J. Phys. Chem. C, 2016, 120, 19416–19433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cannon BL, Kellis DL, Patten LK, Davis PH, Lee J, Graugnard E, Yurke B and Knowlton WB, J. Phys. Chem. A, 2017, 121, 6905–6916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hayes D and Engel GS, Biophys. J, 2011, 100, 2043–2052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rolczynski BS, Zheng H, Singh VP, Navotnaya P, Ginzburg AR, Caram JR, Ashraf K, Gardiner AT, Yeh S-H, Kais S, Cogdell RJ and Engel GS, Chem, 2018, 4, 138–149. [Google Scholar]
- 28.Breiman L, Mach. Learn, 2001, 45, 5–32. [Google Scholar]
- 29.Orf GS, Saer RG, Niedzwiedzki DM, Zhang H, McIntosh CL, Schultz JW, Mirica LM and Blankenship RE, Proc. Natl. Acad. Sci. U. S. A, 2016, 113, E4486–E4493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rolczynski BS, Navotnaya P, Sussman HR and Engel GS, Proc. Natl. Acad. Sci. U. S. A, 2016, 113, 8562–8564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rebentrost P, Mohseni M, Kassal I, Lloyd S and Aspuru-Guzik A, New J. Phys, 2009, 11, 033003. [Google Scholar]
- 32.Chen L, Shenai P, Zheng F, Somoza A and Zhao Y, Molecules, 2015, 20, 15224–15272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mathur D, Kim YC, Díaz SA, Cunningham PD, Rolczynski BS, Ancona MG, Medintz IL and Melinger JS, J. Phys. Chem. C, 2020, 125, 1509–1522. [Google Scholar]
- 34.Dutta PK, Varghese R, Nangreave J, Lin S, Yan H and Liu Y, J. Am. Chem. Soc, 2011, 133, 11985–11993. [DOI] [PubMed] [Google Scholar]
- 35.Probst M, Langenegger SM and Häner R, Chem. Commun, 2014, 50, 159–161. [DOI] [PubMed] [Google Scholar]
- 36.Melinger JS, Khachatrian A, Ancona MG, BuckhoutWhite S, Goldman ER, Spillmann CM, Medintz IL and Cunningham PD, ACS Photonics, 2016, 3, 659–669. [Google Scholar]
- 37.Rolczynski BS, Szarko JM, Lee B, Strzalka J, Guo J, Liang Y, Yu L and Chen LX, J. Mater. Res, 2011, 26, 296–305. [Google Scholar]
- 38.Mathieu F, Liao S, Kopatsch J, Wang T, Mao C and Seeman NC, Nano Lett, 2005, 5, 661–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Strobl C, Boulesteix A-L, Kneib T, Augustin T and Zeileis A, BMC Bioinf, 2008, 9, 307–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.James G, Witten D, Hastie T and Tibshirani R, An Introduction to Statistical Learning, Springer, New York, 2015. [Google Scholar]
- 41.Auret L and Aldrich C, Miner. Eng, 2012, 35, 27–42. [Google Scholar]
- 42.Kelly C and Okada K, 2012 9th IEEE Int. Symp. Biomed. Imag, 2012, 154–1p57, DOI: 10.1109/ISBI.2012.6235507. [DOI] [Google Scholar]
- 43.Stephan J, Stegle O and Beyer A, Nat. Commun, 2015, 6, 1–10. [DOI] [PubMed] [Google Scholar]
- 44.Hastie T, Tibshirani R and Friedman J, The Elements of Statistical Learning, Springer, New York, 2nd edn, 2009. [Google Scholar]
- 45.Efron B, The Jackknife, the Bootstrap and Other Resampling Plans, SIAM, Philadelphia, 1982. [Google Scholar]
- 46.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC and Ferrin TE, J. Comput. Chem, 2004, 25, 1605–1612. [DOI] [PubMed] [Google Scholar]
- 47.Van Der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE and Berendsen HJC, J. Comput. Chem, 2005, 26, 1701–1718. [DOI] [PubMed] [Google Scholar]
- 48.Galindo-Murillo R, Robertson JC, Zgarbova M, Sponer J, Otyepka M, Jurecka P and Cheatham III TE, J. Chem. Theory Comput, 2016, 12, 4114–4127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang J, Wolf RM, Caldwell JW, Kollman PA and Case DA, J. Comput. Chem, 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- 50.Hess B, Bekker H, Berendsen HJC and Fraaije JGEM, J. Comput. Chem, 1997, 18, 1463–1472. [Google Scholar]
- 51.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A and Haak JR, J. Chem. Phys, 1984, 81, 3684–3690. [Google Scholar]
- 52.Parrinello M and Rahman A, J. Appl. Phys, 1981, 52, 7182–7190. [Google Scholar]
- 53.Tanimura Y, J. Chem. Phys, 2020, 153, 020901. [DOI] [PubMed] [Google Scholar]
- 54.Tanimura Y, J. Phys. Soc. Jpn, 2006, 75, 082001. [Google Scholar]
- 55.Ishizaki A and Fleming GR, J. Chem. Phys, 2009, 130, 234111. [DOI] [PubMed] [Google Scholar]
- 56.Scholes GD, Annu. Rev. Phys. Chem, 2003, 54, 57–87. [DOI] [PubMed] [Google Scholar]
- 57.Singh D, J. Phys. Chem. B, 2021, 125, 557–561. [DOI] [PubMed] [Google Scholar]
- 58.Yeh S-H and Kais S, J. Chem. Phys, 2014, 141, 234105. [DOI] [PubMed] [Google Scholar]
- 59.Sobakinskaya E, Schmidt am Busch M and Renger T, J. Phys. Chem. B, 2017, 122, 54–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Maillard J, Klehs K, Rumble C, Vauthey E, Heilemann M and Fürstenberg A, Chem. Sci, 2021, 12, 1352–1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Georgakopoulou S, van Grondelle R and van der Zwan G, Biophys. J, 2004, 87, 3010–3022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Strümpfer J and Schulten K, J. Chem. Theory Comput, 2012, 8, 2808–2816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Iles-Smith J, Lambert N and Nazir A, Phys. Rev. A: At., Mol., Opt. Phys, 2014, 90, 032114. [Google Scholar]
- 64.Ma J and Cao J, J. Chem. Phys, 2015, 142, 094106. [DOI] [PubMed] [Google Scholar]
- 65.Liu H, Zhu L, Bai S and Shi Q, J. Chem. Phys, 2014, 140, 134106. [DOI] [PubMed] [Google Scholar]
- 66.Ishizaki A and Tanimura Y, J. Phys. Soc. Jpn, 2005, 74, 3131–3134. [Google Scholar]
- 67.Lambert N, Raheja T, Ahmed S, Pitchford A and Nori F, arXiv, 2020, DOI: 10.48550/arXiv.2010.10806. [DOI] [Google Scholar]
- 68.Johansson JR, Nation PD and Nori F, Comput. Phys. Commun, 2013, 184, 1234–1240. [Google Scholar]
- 69.Johansson JR, Nation PD and Nori F, Comput. Phys. Commun, 2012, 183, 1760–1772. [Google Scholar]
- 70.Green CM, Hughes WL, Graugnard E and Kuang W, ACS Nano, 2021, 15, 11597–11606. [DOI] [PubMed] [Google Scholar]
- 71.Cho M, Vaswani HM, Brixner T, Stenger J and Fleming GR, J. Phys. Chem. B, 2005, 109, 10542–10556. [DOI] [PubMed] [Google Scholar]
- 72.Mukamel S, Nonlinear Optical Spectroscopy, Oxford University Press, Oxford, 1995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


